V-Shaped Dynamic Morphology Curve: A Sustainable Approach to Automotive Wheel Design
Abstract
1. Introduction
2. Methods
2.1. Overview of the VDMC Theory
2.2. Extraction and Classification of VDMC
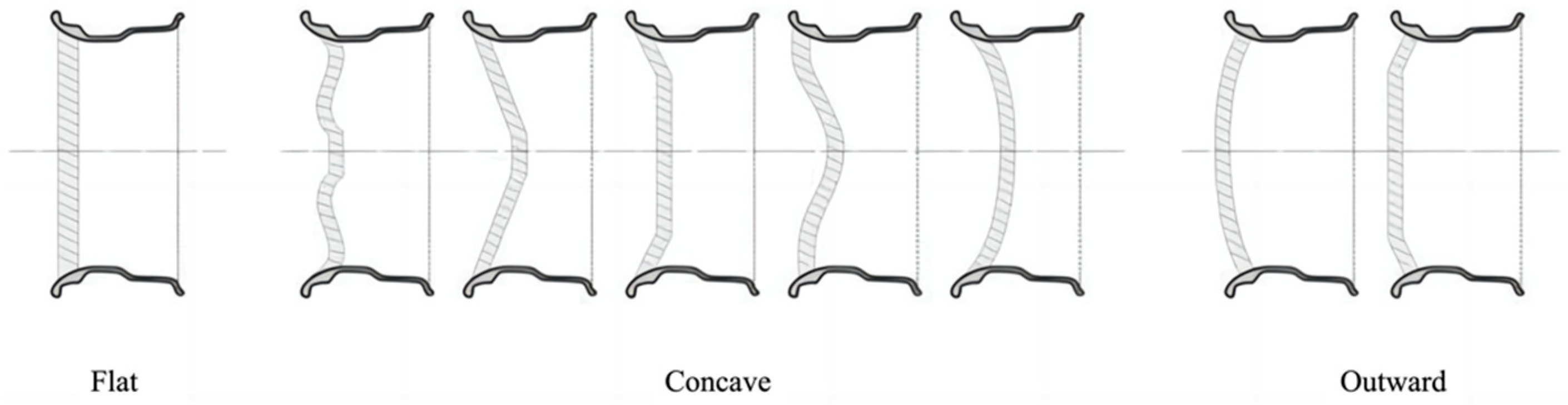
2.2.1. Curve Extraction and Classification
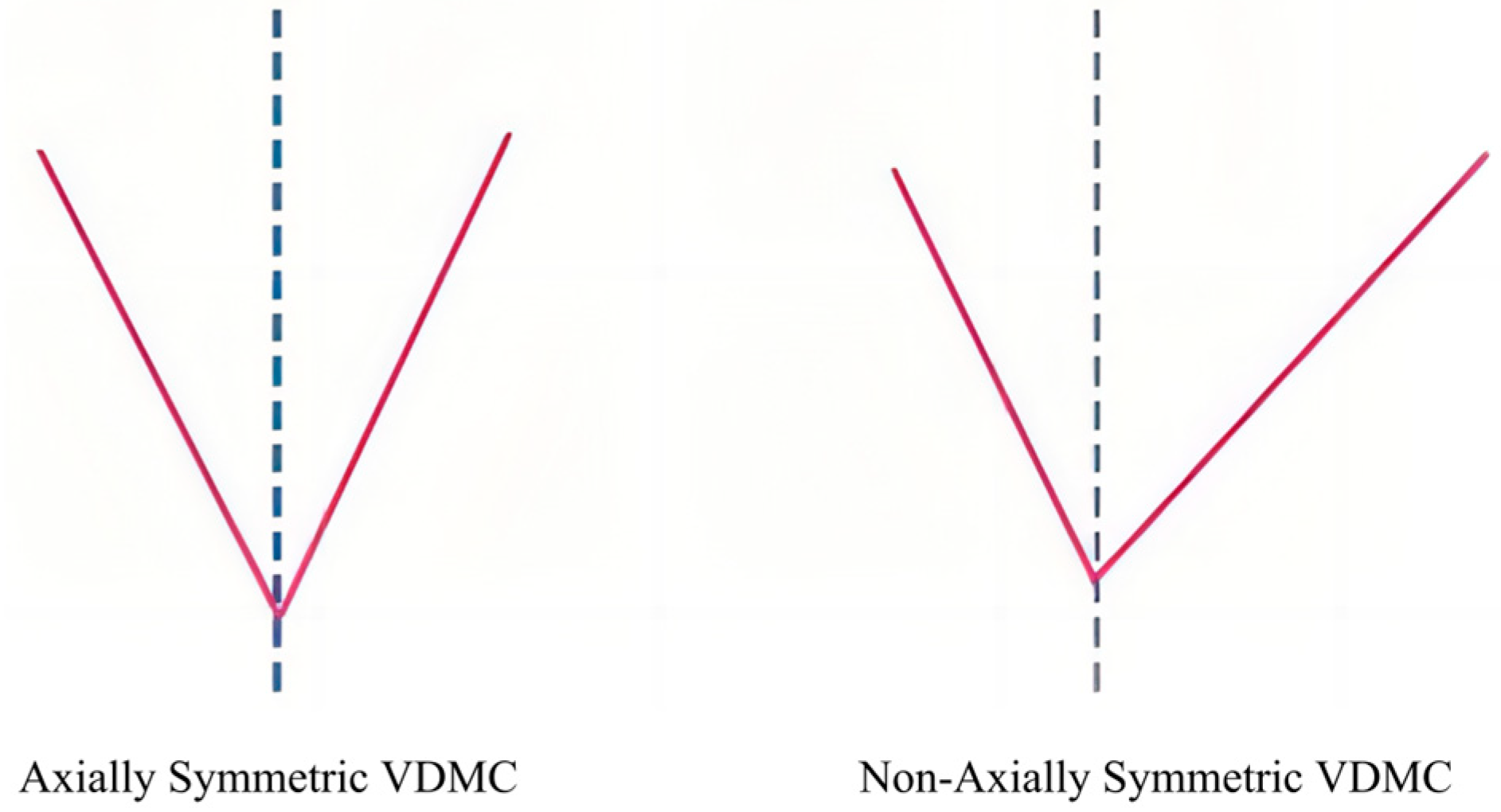
- Axially symmetric VDMCs: These curves are symmetrical with respect to a central axis, meaning that the left and right sides of the curve follow the same pattern of variation. This symmetry is typically seen in designs that emphasize balance and stability. Axially symmetric VDMCs are generally used in rim designs that emphasize simplicity and classic aesthetics.
- Non-axially symmetric VDMCs: These curves exhibit no symmetry with respect to a central axis, meaning the variations on the left and right sides of the curve differ in both form and progression. Non-axially symmetric VDMCs are often utilized in more dynamic and modern rim designs, where asymmetry is used to convey movement, innovation, and uniqueness. These curves allow for greater flexibility in shaping the rim’s aesthetic, particularly in designs that emphasize visual complexity or emphasize certain functional aspects of the wheel.
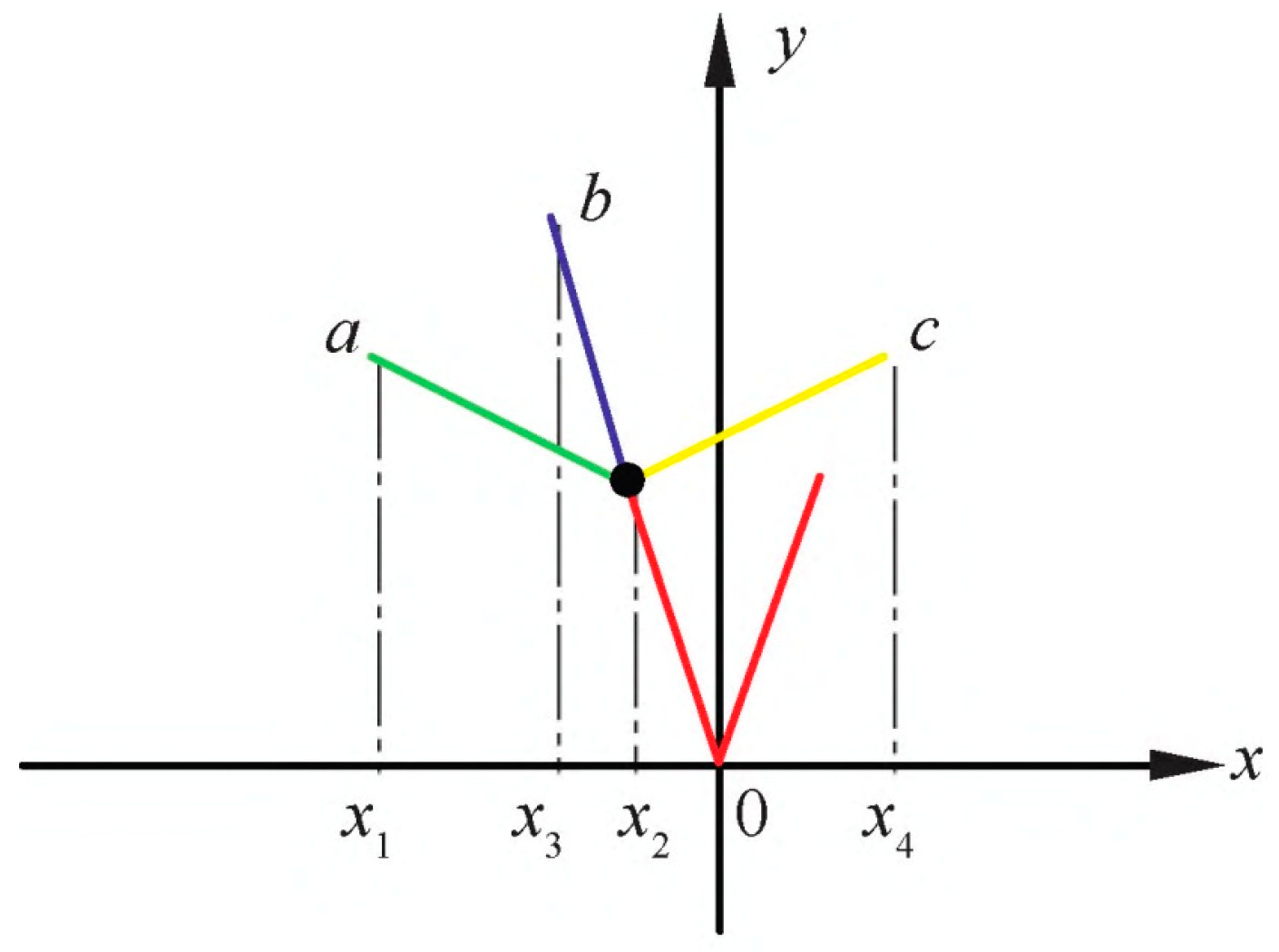
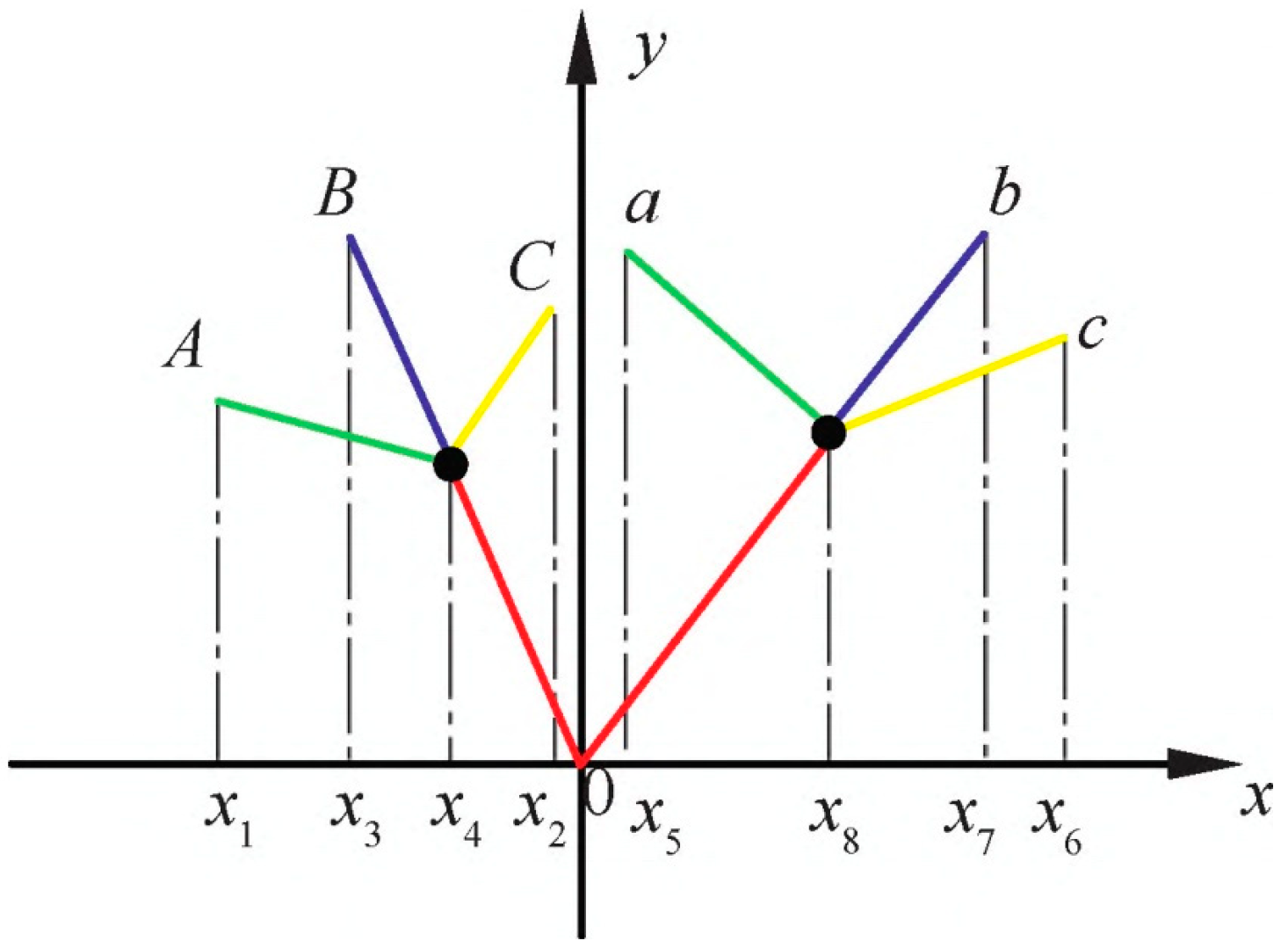
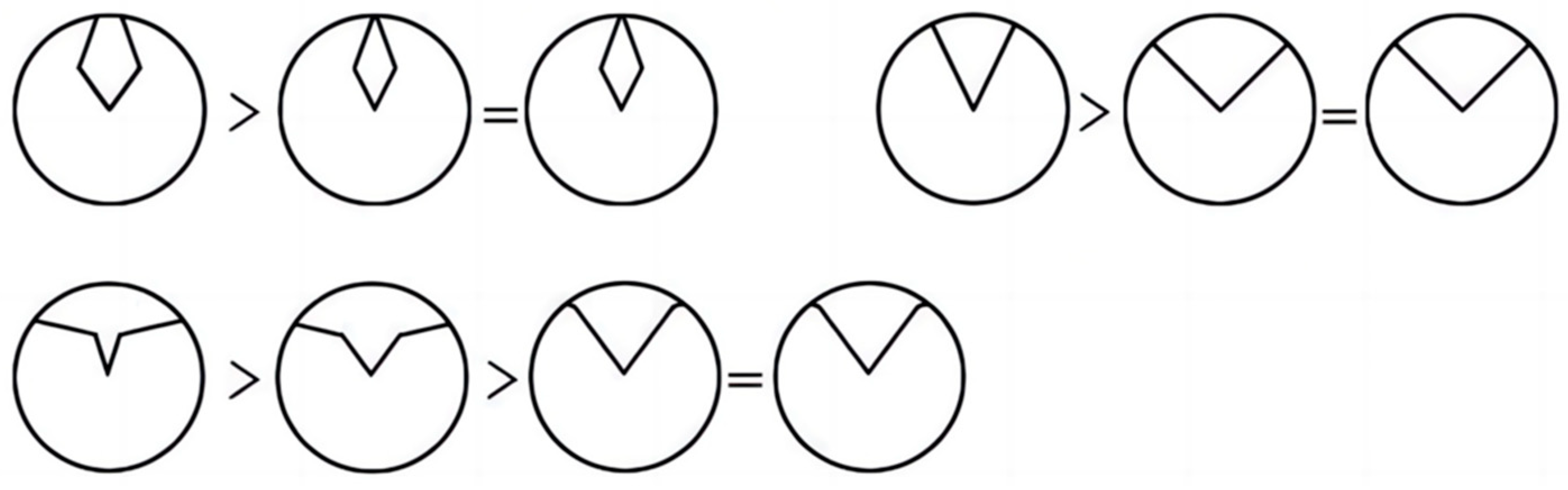
2.2.2. Control Point Analysis
- Category 1—Bb combination (double straight line basic form): In this category, the VDMC is in its basic form with 0 control points, representing a foundational shape for further transformations.
- Category 2—Ba combination (broken straight line inward curved form): For this configuration, the VDMC transforms into an inwardly curved broken straight line shape with 1 control point. This shape represents a transition from the basic shape to a more complex inward curvature, introducing a controlled, dynamic transformation.
- Category 3—Bc combination (broken straight line outward curved form): This category involves the VDMC transforming into an outwardly curved broken straight line shape, again with 1 control point. The outward curve represents a shift from the basic shape to a more expansive geometry, broadening the curve’s appearance and structure.
- Category 4—Cc combination (double broken line contraction–expansion form): In this transformation, the VDMC becomes a double broken line with contraction–expansion features, using 1 control point. The curve demonstrates a more intricate shape, where both inward and outward transitions occur within the same structure, contributing to a more dynamic and adaptable shape.
- Category 5—Ac combination (double broken line outward curved form): The VDMC in this category evolves into a double broken line with outward expansion characteristics, utilizing 1 control point. This shape maintains a more extended, outward-facing curve, providing a visually prominent and expansive shape while keeping the underlying symmetry intact.
- Category 6—Ca combination (double broken line contraction–expansion form): This configuration results in a double broken line inwardly curved shape, again with 1 control point. It represents the opposite of outward expansion, focusing on creating a more contained and inwardly bent structure, contributing to the overall compactness of the design.
2.3. VDMC-Based Structural Skeleton for Wheel Hub Design
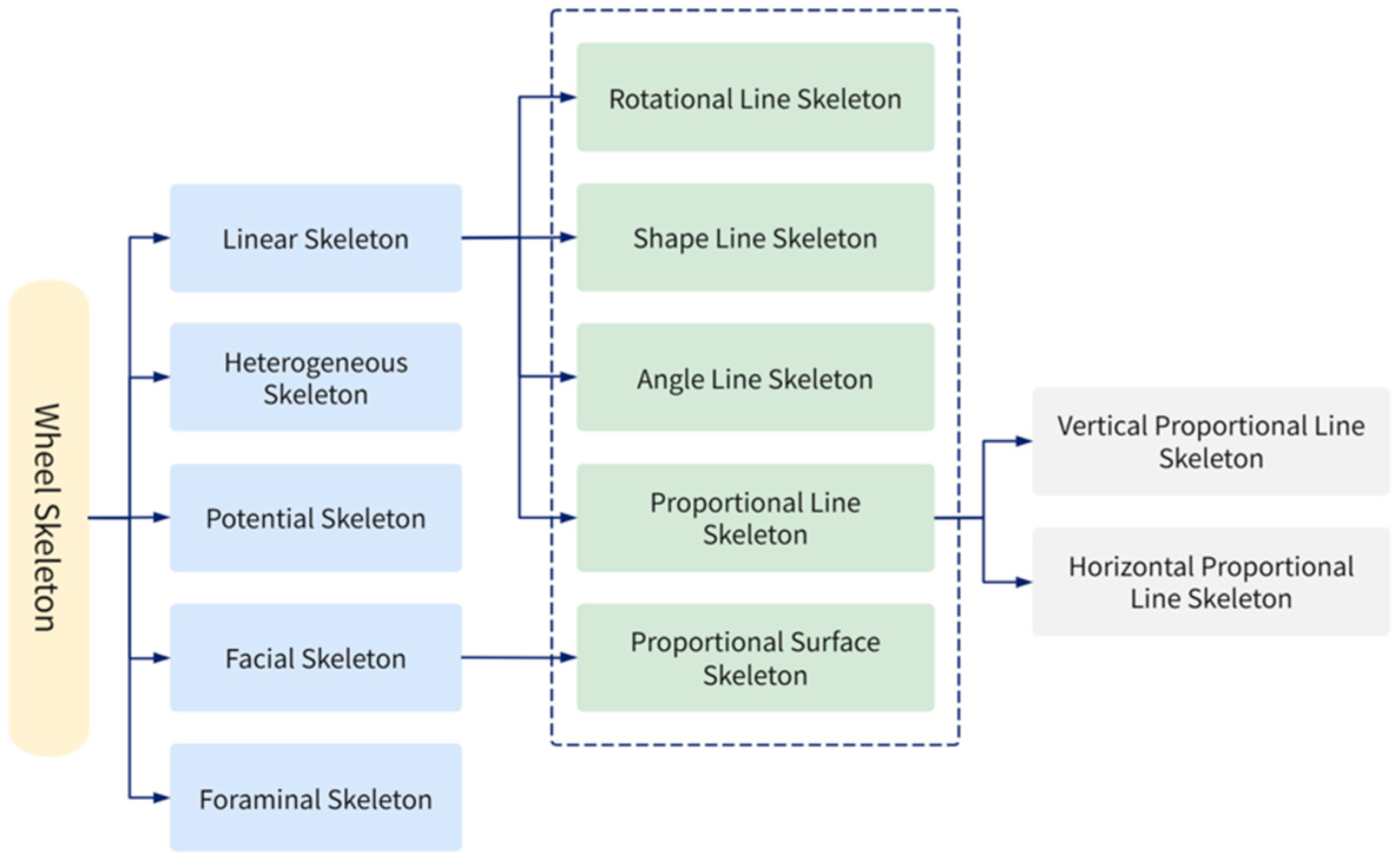
2.3.1. Definition and Types of Structural Skeletons
- Linear skeleton: This represents the basic structural characteristics of the spokes, including the form line skeleton (geometric layout of the spokes), angle line skeleton (angular positioning), proportional line skeleton (spoke proportions, further divided into horizontal and vertical), and rotational line skeleton (rotation dynamics of the spokes);
- Facial skeleton: This refers to the area-based features of the hub’s design, which includes the proportional facial skeleton;
- Foraminal skeleton: This denotes the skeletal features related to the bolt holes and central disc face in the hub’s structure;
- Potential skeleton: This represents the curve characteristics of the spokes when viewed from the side;
- Heterogeneous skeleton: This describes the skeletal features that correspond to local, detailed characteristics of the hub.
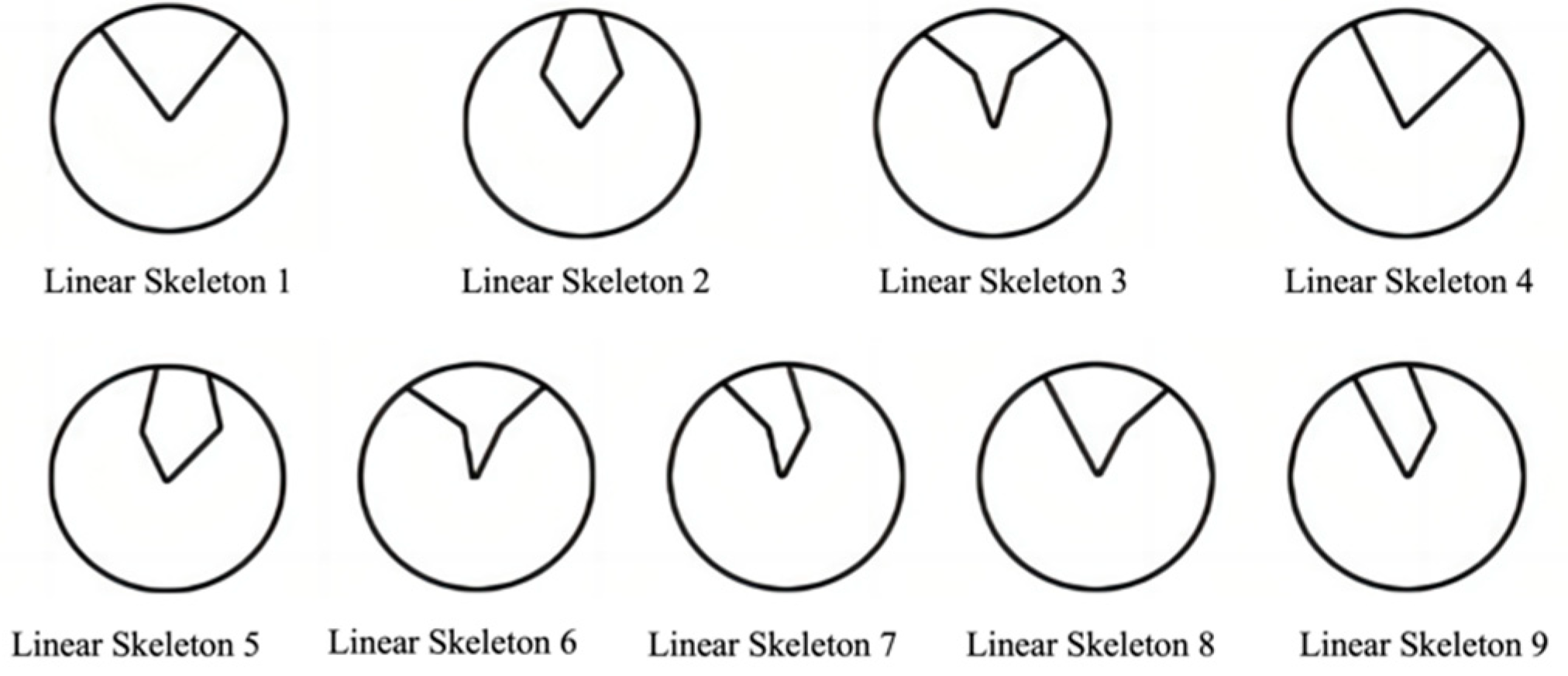
2.3.2. Linear Skeleton
- Shape line skeleton: Through a comprehensive analysis of wheel hub images combined with shape theory, the nine types of linear skeletons can be subdivided into different shape line skeletons. Each linear skeleton corresponds to multiple shape variants. The shape line skeleton modifies the VDMC by adjusting the slopes of the control points’ connecting lines, resulting in variations in the shape. The shape line skeleton is classified into six or nine types, depending on the symmetry of the linear skeleton. Asymmetrical skeletons (such as linear skeletons five, six, and seven) introduce complex variations, leading to more diverse results.
- Angular line skeleton: The angular line skeleton expresses the variation in the angle formed by the VDMC. By adjusting the angle of the VDMC, the overall shape of the wheel hub undergoes morphological changes. Each linear skeleton or morphological line skeleton corresponds to seven angular line skeletons, representing different spoke angles within the same structural type.
- Proportional line skeleton: The proportional line skeleton can be divided into vertical and horizontal types, with each guiding the movement of control points along the vertical or horizontal axes. This skeleton controls spoke profile variations through proportional adjustments. The vertical proportional skeleton is further categorized into seven or thirteen variations to represent the influence of vertical control point movements on the shape. In contrast, the horizontal proportional skeleton focuses on lateral control point adjustments, influencing the shape in the horizontal direction.
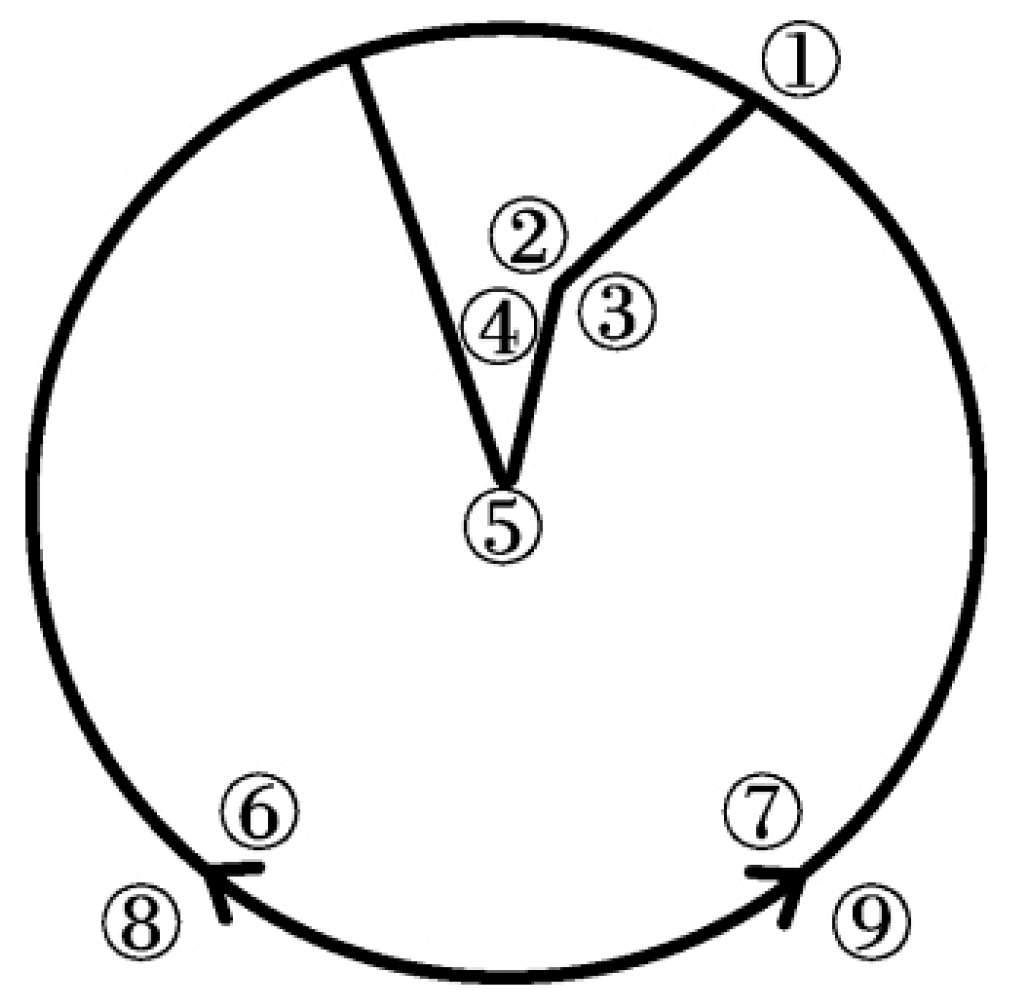
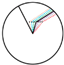
- Rotational line skeleton: The rotational line skeleton is based on the wheel’s rotation center and its associated rotational features. By rotating the VDMC clockwise or counterclockwise, the hub’s morphology is altered. There are several rotational line skeletons that describe different types of rotational behavior, including clockwise, counterclockwise, and mirrored rotational transformations along the centerline. For example, in Figure 7, the rotational line skeleton corresponding to linear skeleton eight is shown, where the spoke’s morphology changes due to rotational adjustments.
- Serial Number 1 (morphological skeletal line): This controls the slope of the polyline segments. Different serial numbers correspond to different variations in polyline shape.
- Serial Number 2 (vertical proportion skeletal line): This governs the vertical displacement of control points. Changes in the serial number directly influence the vertical positioning of these points.
- Serial Number 3 (horizontal proportion skeletal line): This governs the horizontal displacement of control points. Variations in the serial number adjust the horizontal position of these points.
- Serial Number 4 (angular skeletal line): This determines the included angle of the V-shaped curve. Different serial numbers correspond to different angle variations.
- Serial Number 5 (number of spokes): This defines the number of spokes in the structure, with the minimum number being three spokes.
- Serial Numbers 6 and 7 (first and second rotational skeletal lines): These represent the rotation centers of the spokes, determining their pivot points.
- Serial Numbers 8 and 9 (third rotational skeletal line): These define the mirrored rotational direction of the V-shaped curve along the centerline. A left arrow (←) indicates a clockwise rotation, whereas a right arrow (→) signifies a counterclockwise rotation.
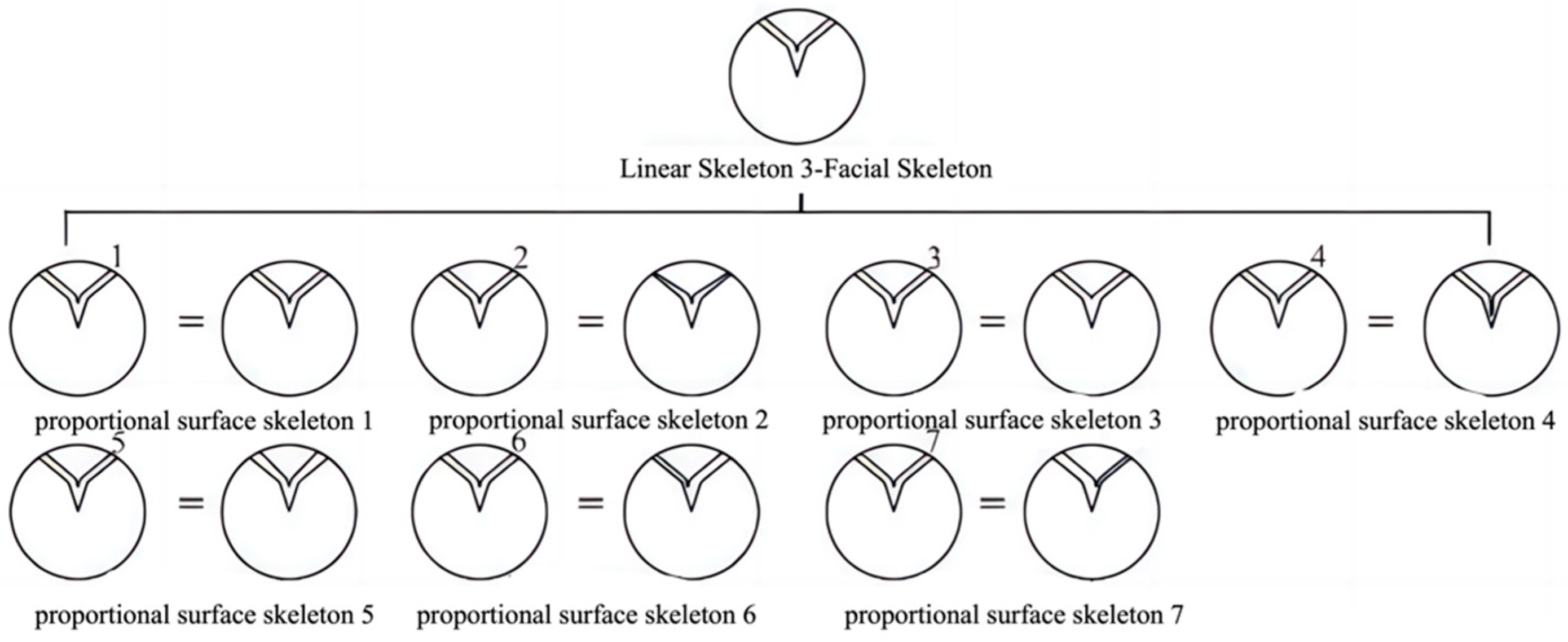
2.3.3. Facial Skeleton
2.3.4. Foraminal Skeleton
2.3.5. Potential Skeleton
2.3.6. Heterogeneous Skeleton
2.4. Wheel Skeleton Calculation Algorithm Based on VDMC
2.4.1. Skeleton Computation
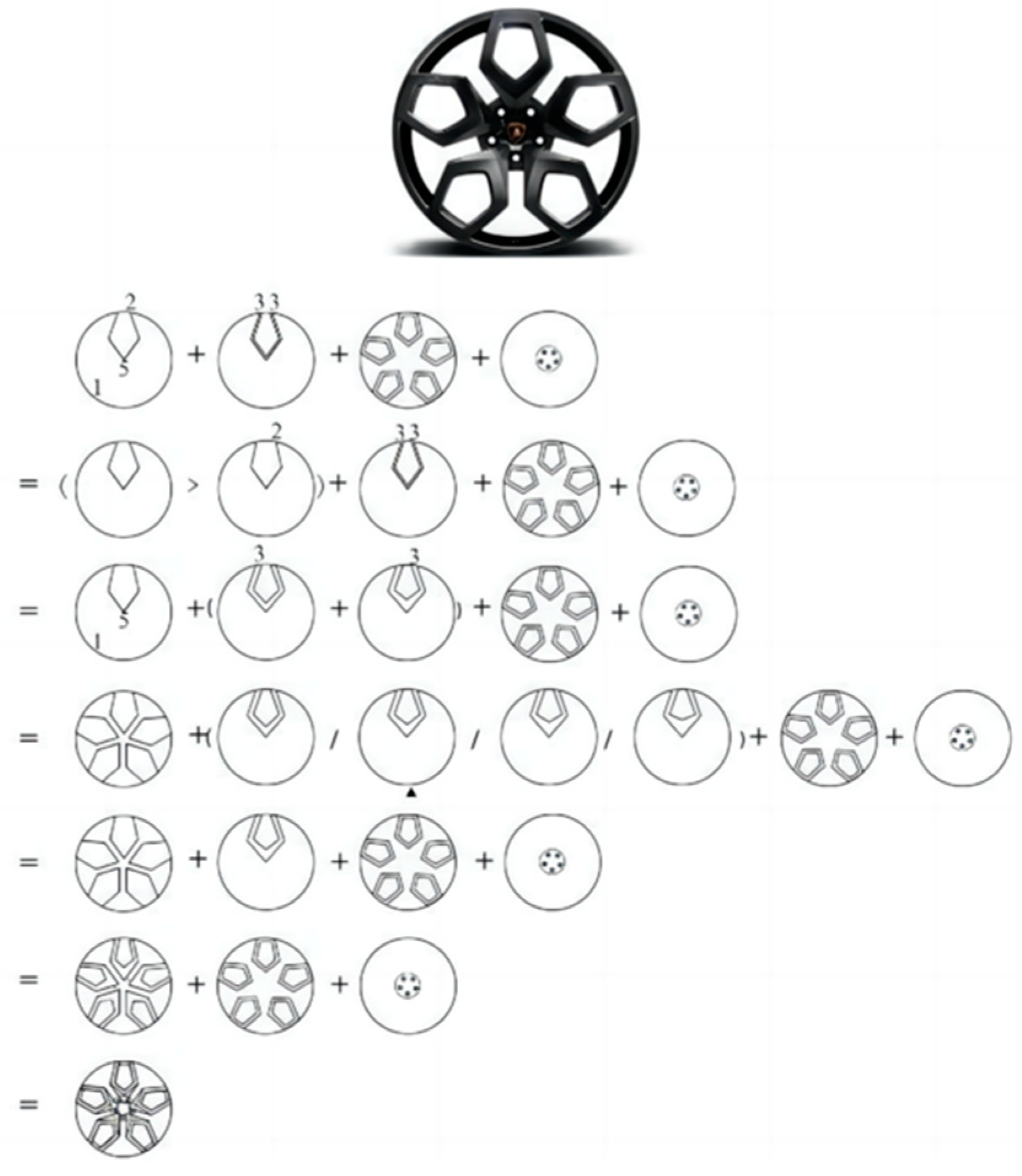
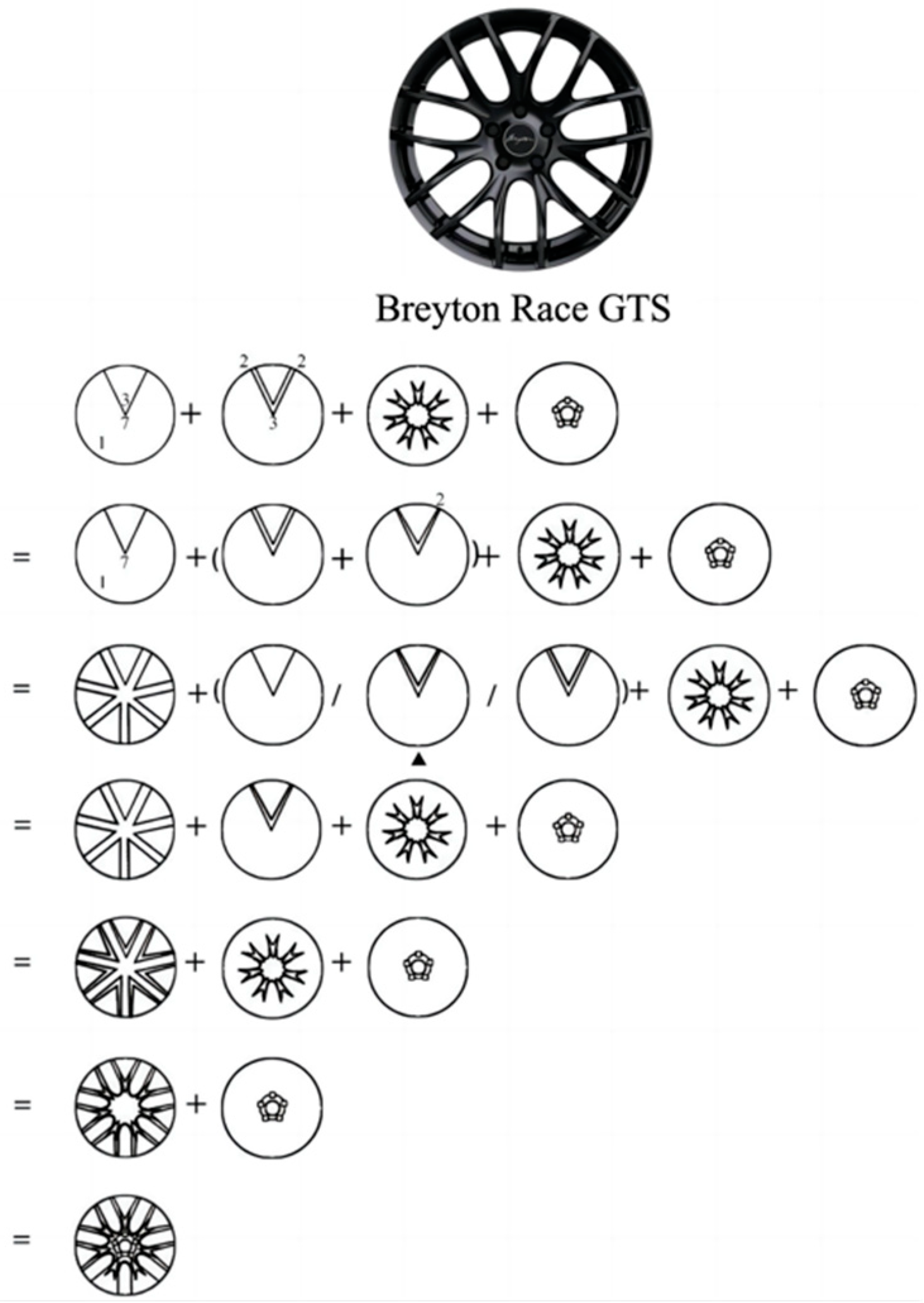
2.4.2. VDMC-Based Progressive Computation and Operational Rules
2.4.3. VDMC-Based Superposition Computation and Operational Rules
2.4.4. VDMC-Based Combination Computation and Operational Rules
3. The Practice of Deriving Hub Wheel Shapes Based on VDMC
4. Evaluation and Analysis of VDMC in Wheel Design
4.1. Participants Selection and Experimental Design
- Experimental group: Participants used the VDMC-based design approach, which was integrated into Rhinoceros 7.0 with the Grasshopper plugin. This parametric modeling tool allowed designers to generate multiple wheel design variants through parametric adjustments. Key parameters such as curvature, symmetry, and facial detailing were manipulated, enabling rapid iteration while ensuring brand consistency.
- Control group: Participants in the control group employed traditional CAD-based design methods, using AutoCAD 2023 and Rhinoceros 7.0. Designers manually created wheel variants by adjusting parameters through these CAD modeling platforms, requiring several iterations to refine the designs and maintain adherence to the brand’s visual identity standards.
4.2. Experimental Procedure
- Design time: This encompassed total time spent on the creation of all five wheel variants. To ensure the accuracy of design time measurement, screen-monitoring software (ManicTime) was used to track the active working time of each participant. The timer started when the designer opened the design file and stopped when the final design was saved. Non-active periods, such as breaks or software loading times, were automatically excluded from the recorded time. This approach ensured that the recorded design time reflected only the actual time spent on the task.
- Brand consistency: This evaluated how closely each design adhered to the brand’s visual identity, rated by a panel of experts. To evaluate brand consistency, a detailed scoring rubric was developed based on the brand’s core design guidelines, including the following key design indicators weighted according to their significance. Symmetry was assigned the highest weight at 20%, followed by the V-shaped curve angle range (±5°) and the spoke area gradient pattern (e.g., “thin-to-thick” or “thick-to-thin”), each contributing 15%. The central hole and bolt hole arrangement accounted for 10%, as did the heterogeneous skeleton features. The remaining 30% was allocated to other local details, such as edge chamfering and surface texture, which play a crucial role in overall design refinement. Each indicator was assessed on a 0–1 scale, with the total score calculated as a weighted sum and converted to a 10-point scale to ensure a standardized evaluation of design consistency.
- Resource utilization: This was measured by tracking design process efficiency (e.g., the number of iterations or design modifications) and the computational resources consumed during the design process (e.g., time spent on design software or hardware usage).
- Design modification: This was measured by the number of design iterations made by each designer.
4.3. Experimental Results and Analysis
4.3.1. Design Efficiency
- Experimental group: On average, the experimental group completed the five-wheel design task in 18.3 h.
- Control group: The control group took an average of 26.7 h to complete the same task.
4.3.2. Brand Consistency
- Experimental group: The designs generated by the experimental group were rated with an average brand consistency score of 9.1/10.
- Control group: The control group’s designs were rated with an average score of 7.8/10.
4.3.3. Sustainability Outcomes
- Experimental group: The average number of design iterations per variant was 4.2 iterations. The average number of modifications required to finalize a design was 2.6 modifications per design.
- Control group: The control group required an average of 7.9 iterations per variant. The control group required an average of 5.3 modifications per design.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Norman, D.A. Emotional Design: Why We Love (or Hate) Everyday Things; Basic Books: New York, NY, USA, 2004. [Google Scholar]
- Schmitt, B.H. Experiential Marketing: How to Get Customers to Sense, Feel, Think, Act, and Relate to Your Company and Brands; Simon and Schuster: New York, NY, USA, 1999. [Google Scholar]
- Keller, K.L. Strategic Brand Management: Building, Measuring, and Managing Brand Equity; Pearson Education India: Tamil Nadu, India, 2013. [Google Scholar]
- Kotler, P.; Armstrong, G. Principles of Marketing; Pearson Education: London, UK, 2018. [Google Scholar]
- Singh, J.; Sarkar, P. Understand and quantify the consumers’ cognitive behavior for the appropriateness features of product aesthetics through the eye-tracking technique. Int. J. Interact. Des. Manuf. 2023, 19, 1–34. [Google Scholar]
- Hekkert, P.; van Dijk, M. Vision in Design: A Guidebook for Innovators; BIS Publishers: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Lundgren, B. Customer-perceived value in residential developments: The case of Hornsberg Strand, Sweden. Int. Real Estate Rev. 2013, 16, 1–27. [Google Scholar] [CrossRef] [PubMed]
- Reichelt, F.; Holder, D.; Maier, T. The vehicle development process where engineering meets industrial design. IEEE Eng. Manag. Rev. 2023, 51, 102–123. [Google Scholar] [CrossRef]
- Bocken, N.M.; De Pauw, I.; Bakker, C.; Van Der Grinten, B. Product design and business model strategies for a circular economy. J. Ind. Prod. Eng. 2016, 33, 308–320. [Google Scholar] [CrossRef]
- Zheng, Q.; Ding, G.; Xie, J.; Li, Z.; Qin, S.; Wang, S.; Zhang, K. Multi-stage cyber-physical fusion methods for supporting equipment’s digital twin applications. Int. J. Adv. Manuf. Technol. 2024, 132, 5783–5802. [Google Scholar] [CrossRef]
- Belhocine, A.; Abdullah, O.I. Finite element analysis (FEA) of frictional contact phenomenon on vehicle braking system. Mech. Based Des. Struct. Mach. 2022, 50, 2961–2996. [Google Scholar] [CrossRef]
- Lawson, B. How Designers Think: The Design Process Demystified; Routledge: London, UK, 2006. [Google Scholar]
- Charter, M.; Tischner, U. (Eds.) Sustainable Solutions: Developing Products and Services for the Future; Routledge: London, UK, 2017. [Google Scholar]
- Füller, J.; Matzler, K.; Hoppe, M. Brand community members as a source of innovation. J. Prod. Innov. Manag. 2008, 25, 608–619. [Google Scholar] [CrossRef]
- Li, Z.; Hamidi, A.S.; Yan, Z.; Sattar, A.; Hazra, S.; Soulard, J.; Tailor, F. A circular economy approach for recycling Electric Motors in the end-of-life Vehicles: A literature review. Resour. Conserv. Recycl. 2024, 205, 107582. [Google Scholar] [CrossRef]
- Okoth, G.H.; Ndeda, R.; Raghupatruni, P.; Olakanmi, E.O. Trends in Lightweighting for Automotive Applications: A Case Study. J. Sustain. Res. Eng. 2024, 8, 50–67. [Google Scholar]
- McDonough, W.; Braungart, M. Cradle to Cradle: Remaking the Way We Make Things; North Point Press: Berkeley, CA, USA, 2002. [Google Scholar]
- Wang, G.G.; Shan, S. Review of metamodeling techniques in support of engineering design optimization. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Philadelphia, PA, USA, 10–13 September 2006; Volume 4255, pp. 116–123. [Google Scholar]
- Wu, J.T.; Mao, Q.; Sun, L. Intelligent Customization Design of Wheel Hub Based on Meta Symbol and Extenics. Boletín Técnico 2017, 55, 116–123. [Google Scholar]
- Sun, L.; Wu, J.T.; Lv, Q.H. Method of Recommending Wheel Hub Based on User Preferences. Boletín Técnico 2017, 55, 64–73. [Google Scholar]
- Sun, L.; Wu, J.T.; Li, T. Product Family Shape Based on Similar Characteristics. J. Comput. 2014, 3, 758–765. [Google Scholar] [CrossRef]
- Liu, X.; Yang, S. Study on product form design via Kansei engineering and virtual reality. J. Eng. Des. 2022, 33, 412–440. [Google Scholar] [CrossRef]
- Yuan, C. Deep Neural Network Architectures for User-Centered Design Concept Generation and Evaluation. Ph.D. Thesis, Northeastern University, Boston, MA, USA, 2022. [Google Scholar]
- Elkafafy, M.; Csurcsia, P.; Cornelis, B.; Risaliti, E.; Janssens, K. Machine learning and system identification for the estimation of data-driven models: An experimental case study illustrated on a tire-suspension system. In Proceedings of the ISMA 2020, International Conference on Noise and Vibration Engineering, CD-ROM, Online, 7–9 September 2020. [Google Scholar]
- Tovey, M.; Porter, S.; Newman, R. Sketching, concept development and automotive design. Des. Stud. 2003, 24, 135–153. [Google Scholar] [CrossRef]
- Sharma, A.; Yadav, R.; Sharma, K. Optimization and investigation of automotive wheel rim for efficient performance of vehicle. Mater. Today Proc. 2021, 45, 3601–3604. [Google Scholar] [CrossRef]
- Liu, N.; Liu, X.; Jiang, Y.; Liu, P.; Gao, Y.; Ding, H.; Zhao, Y. Bionic Optimization Design and Fatigue Life Prediction of a Honeycomb-Structured Wheel Hub. Biomimetics 2024, 9, 611. [Google Scholar] [CrossRef] [PubMed]
- Dong, X.; Yao, L.; Liu, H.; Ding, Y. Research on topology optimization method of surface support structure based on leaf vein growth process. AIP Adv. 2023, 13, 095001. [Google Scholar] [CrossRef]
- Xu, P.F.; Duan, S.Y.; Wang, F. Reverse modeling and topological optimization for lightweight design of automobile wheel hubs with hollow ribs. Int. J. Comput. Methods 2020, 17, 1950064. [Google Scholar] [CrossRef]
- Hirz, M.; Dietrich, W.; Gfrerrer, A.; Lang, J. Integrated Computer-Aided Design in Automotive Development; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Gao, J.; Chen, C.; Fang, X.; Zhou, X.; Gao, L.; Nguyen, V.P.; Rabczuk, T. Multi-objective topology optimization for solid-porous infill designs in regions-divided structures using multi-patch isogeometric analysis. Comput. Methods Appl. Mech. Eng. 2024, 428, 117095. [Google Scholar] [CrossRef]
- Koronis, G.; Silva, A.; Fontul, M. Green composites: A review of adequate materials for automotive applications. Compos. Part B Eng. 2013, 44, 120–127. [Google Scholar] [CrossRef]
- Llopis-Albert, C.; Rubio, F.; Valero, F. Impact of digital transformation on the automotive industry. Technol. Forecast. Soc. Change 2021, 162, 120343. [Google Scholar] [CrossRef] [PubMed]
- Tofail, S.A.; Koumoulos, E.P.; Bandyopadhyay, A.; Bose, S.; O’Donoghue, L.; Charitidis, C. Additive manufacturing: Scientific and technological challenges, market uptake and opportunities. Mater. Today 2018, 21, 22–37. [Google Scholar] [CrossRef]
- Goel, R.; Gupta, P. Robotics and Industry 4.0. In A Roadmap to Industry 4.0: Smart Production, Sharp Business and Sustainable Development; Springer: Berlin, Heidelberg, Germany, 2020; pp. 157–169. [Google Scholar]
- Wegst, U.G.K. Natural materials for making things. Mater. Today 2010, 13, 40–44. [Google Scholar]
- Ashby, M.F.; Johnson, K. Materials and design: The Art and Science of Material Selection in Product Design; Butterworth-Heinemann: Oxford, UK, 2019. [Google Scholar]
- Akande, T.O.; Alabi, O.O.; Oyinloye, J.B. A Review of Generative Models for 3D Vehicle Wheel Generation and Synthesis. J. Comput. Theor. Appl. 2024, 1, 368–385. [Google Scholar] [CrossRef]
- Akande, T.O.; Alabi, O.O.; Rizwan, A.; Ajagbe, S.A.; Olaleye, A.O.; Adigun, M.O. AI-assisted Design of Lightweight and Strong 3D-Printed Wheels for Electric Vehicles. PLoS ONE 2024, 19, e0308004. [Google Scholar] [CrossRef]
- Sun, L.; Wu, J.T.; Liang, X.X. Computerized Automatic Generation Method of Categorized Hub Spectrum According to Its Form. Adv. Mater. Res. 2014, 933, 521–526. [Google Scholar] [CrossRef]
- Bo, W.; Qiu, Y.R.; Jin, H. Research on Parametric Generation of Automobile Styling Based on Grasshopper. In Proceedings of the 2024 IEEE 24th International Conference on Software Quality, Reliability, and Security Companion (QRS-C), Cambridge, UK, 1–5 July 2024; pp. 998–1003. [Google Scholar]
- Puangchaum, W.; Rooppakhun, S.; Phunpeng, V. Parametric Design and Optimization of Alloy Wheel Based on Dynamic Cornering Fatigue Test. In Proceedings of the 5th IIAE International Conference on Industrial Application Engineering, Kitakyushu, Japan, 27–31 March 2017. [Google Scholar]










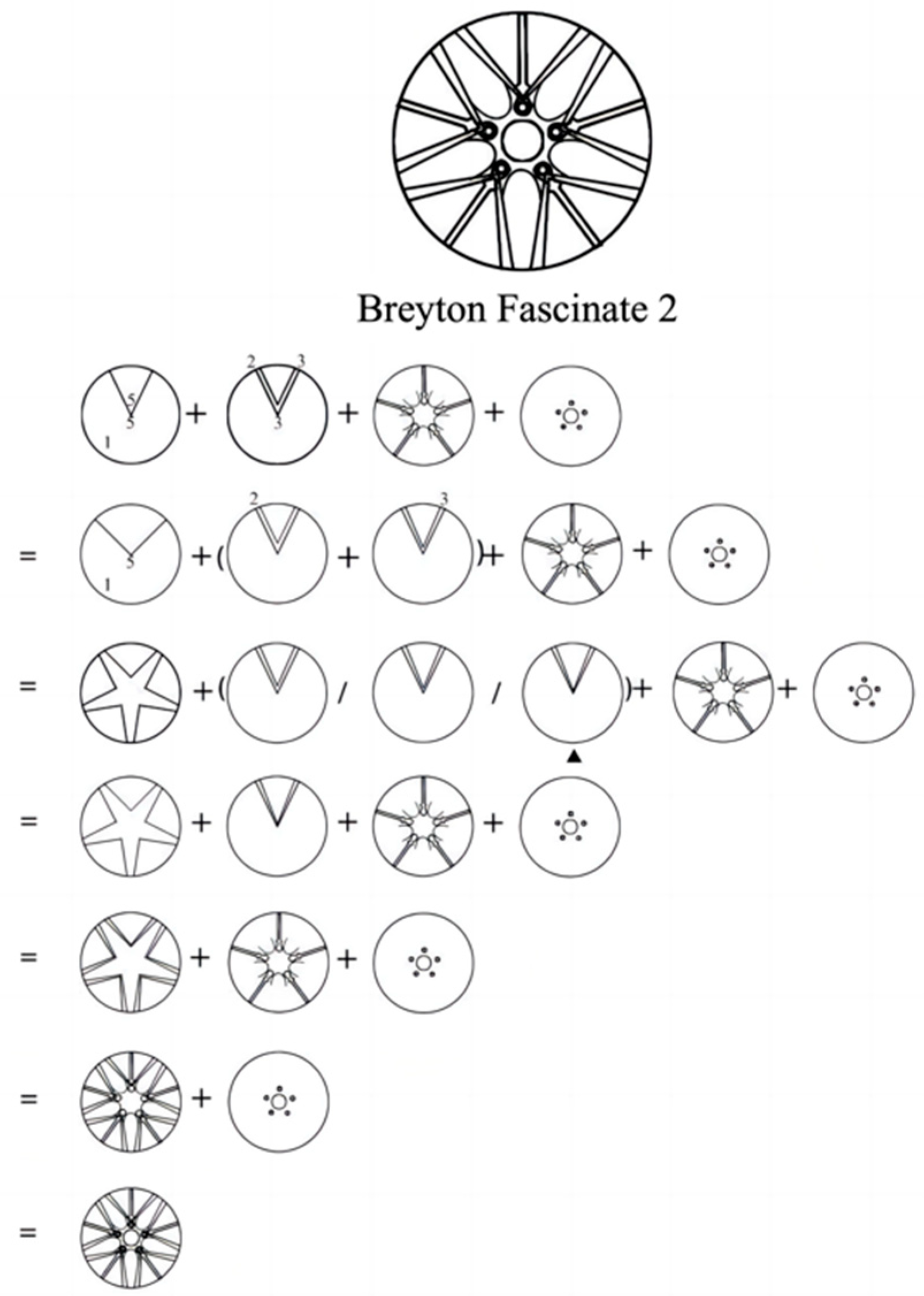

| Type | Basic Shape | Inward-Retracted Shape | Outward-Retracted Shape |
|---|---|---|---|
| V-shaped diagram | 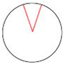 |  | 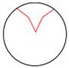 |
| Wheel hub diagram |  |  |  |
| Type | Double Straight Line Basic Form | Double Broken Line Contraction– Expansion Form | Double Broken Line Inward Curved Form | Double Broken Line Outward Curved Form | Broken Straight Line Inward Curved Form | Broken Straight Line Outward Curved Form |
|---|---|---|---|---|---|---|
| V-shaped diagram |  | 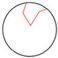 |  | 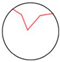 |  | 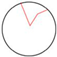 |
| Wheel hub diagram |  |  |  |  |  |  |
| Type | Linear Skeleton Eight’s Corresponding Shape Linear Skeleton | Linear Skeleton Eight’s Corresponding Angular Line Skeleton | Linear Skeleton Eight’s Corresponding Vertical Proportional Skeleton | Linear Skeleton Eight’s Corresponding Horizontal Proportional Skeleton |
|---|---|---|---|---|
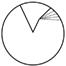 |  | 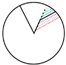 |  |
| Hub Diagram | Variation 1 | Variation 2 | Variation 3 |
|---|---|---|---|
| Control slope |  |  |  |
| Control point movement |  |  |  |
| Angle variation |  |  |  |
| Rotation variation |  |  |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Sun, L.; Ai, W.; Wu, J.; Qin, Z.; Yu, H.; Song, H.; Wang, Q.; Jiang, C.; Li, J. V-Shaped Dynamic Morphology Curve: A Sustainable Approach to Automotive Wheel Design. Sustainability 2025, 17, 2463. https://doi.org/10.3390/su17062463
Chen Y, Sun L, Ai W, Wu J, Qin Z, Yu H, Song H, Wang Q, Jiang C, Li J. V-Shaped Dynamic Morphology Curve: A Sustainable Approach to Automotive Wheel Design. Sustainability. 2025; 17(6):2463. https://doi.org/10.3390/su17062463
Chicago/Turabian StyleChen, Yongliang, Li Sun, Wen Ai, Jiantao Wu, Zhongzhi Qin, Hongfei Yu, Hao Song, Qi Wang, Changhong Jiang, and Jiangnan Li. 2025. "V-Shaped Dynamic Morphology Curve: A Sustainable Approach to Automotive Wheel Design" Sustainability 17, no. 6: 2463. https://doi.org/10.3390/su17062463
APA StyleChen, Y., Sun, L., Ai, W., Wu, J., Qin, Z., Yu, H., Song, H., Wang, Q., Jiang, C., & Li, J. (2025). V-Shaped Dynamic Morphology Curve: A Sustainable Approach to Automotive Wheel Design. Sustainability, 17(6), 2463. https://doi.org/10.3390/su17062463




