Dynamic Response Analysis of Large-Diameter Monopile Foundation Under Ice Load
Abstract
1. Introduction
2. Model Description
2.1. Modeling of Level Ice Sheet
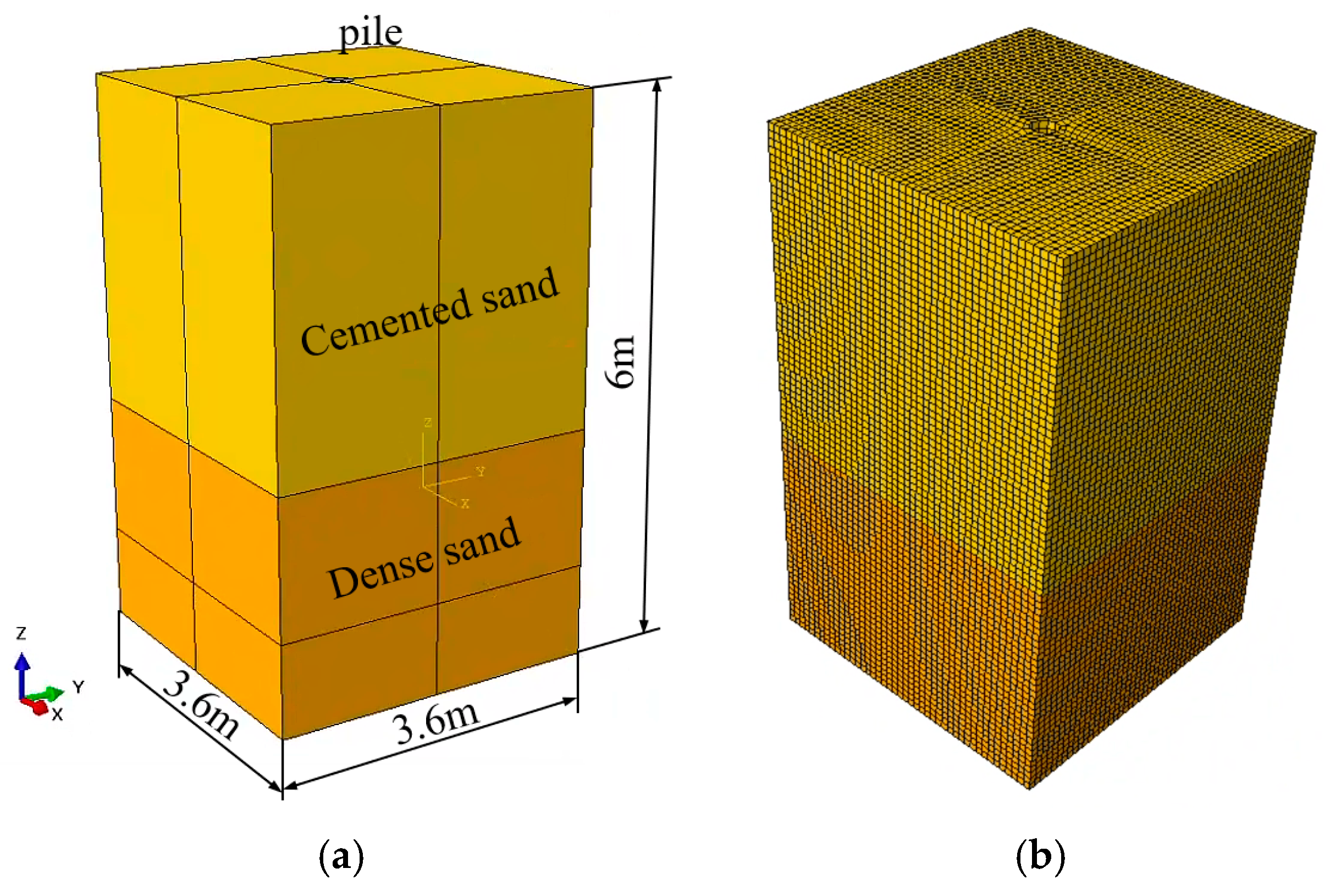
2.2. Modeling of Soil
| Parameters | Value |
|---|---|
| (kg/m3) | 2000 |
| Poisson’s ratio, μ | 0.3 |
| Friction angle, φ (°) | 38 |
| Dilatancy angle, ψ (°) | 15 |
| Elastic modulus, E (MPa) | 130 |
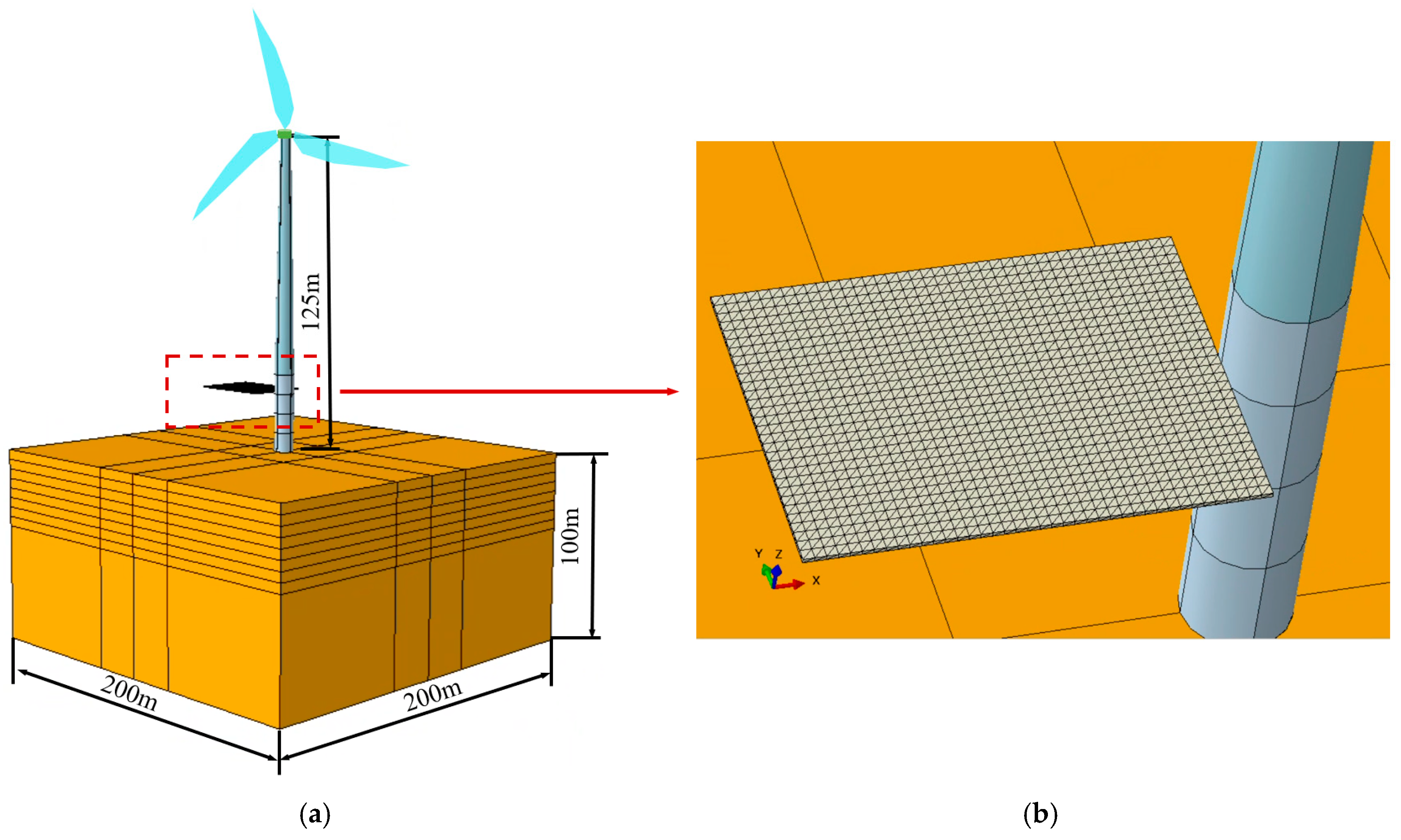
2.3. Modeling of Monopile OWT
3. Model Validation
3.1. Test Setup and Experimental Approach
3.2. Validation of Ice Failure and Fragments Accumulation
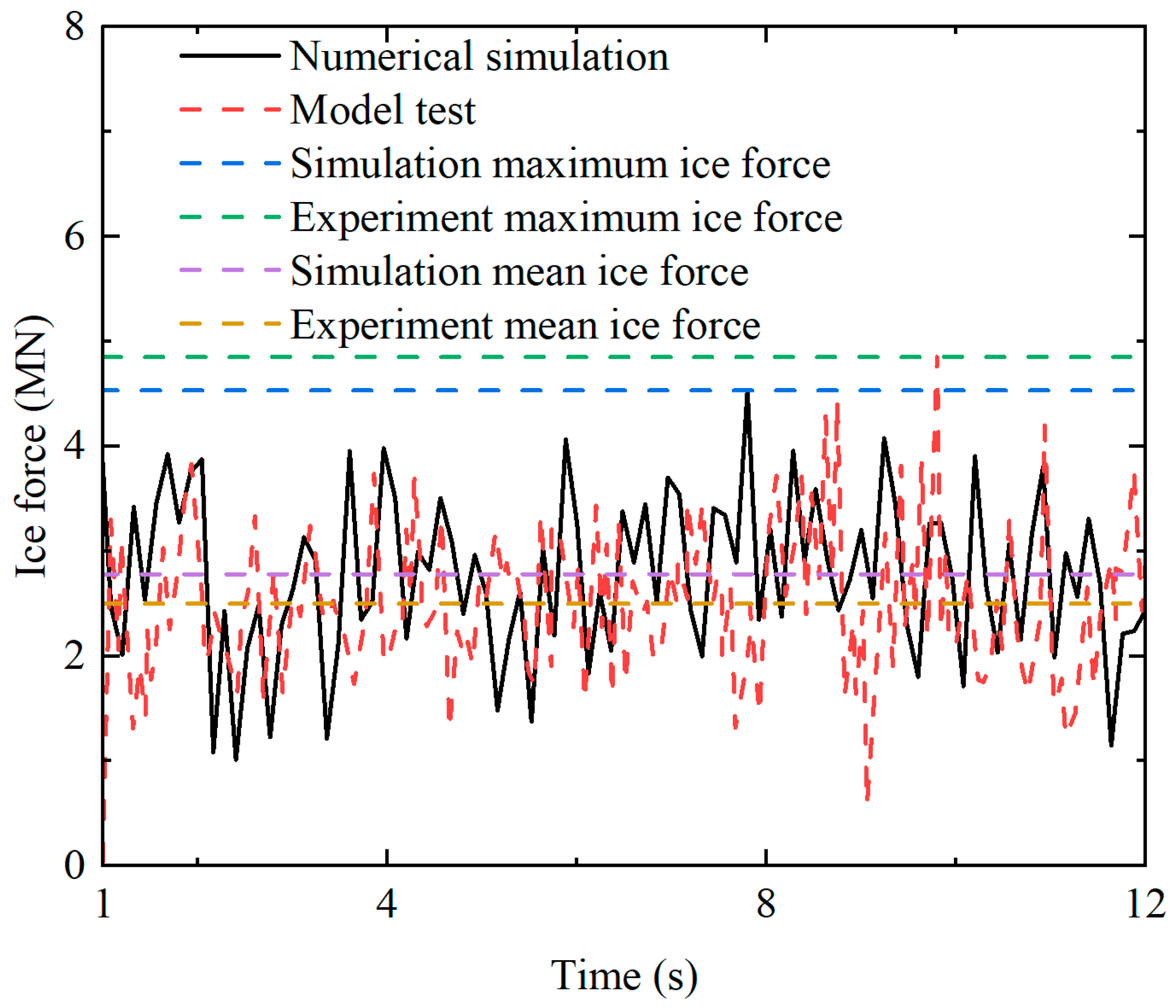
3.3. Validation of the Ice Force
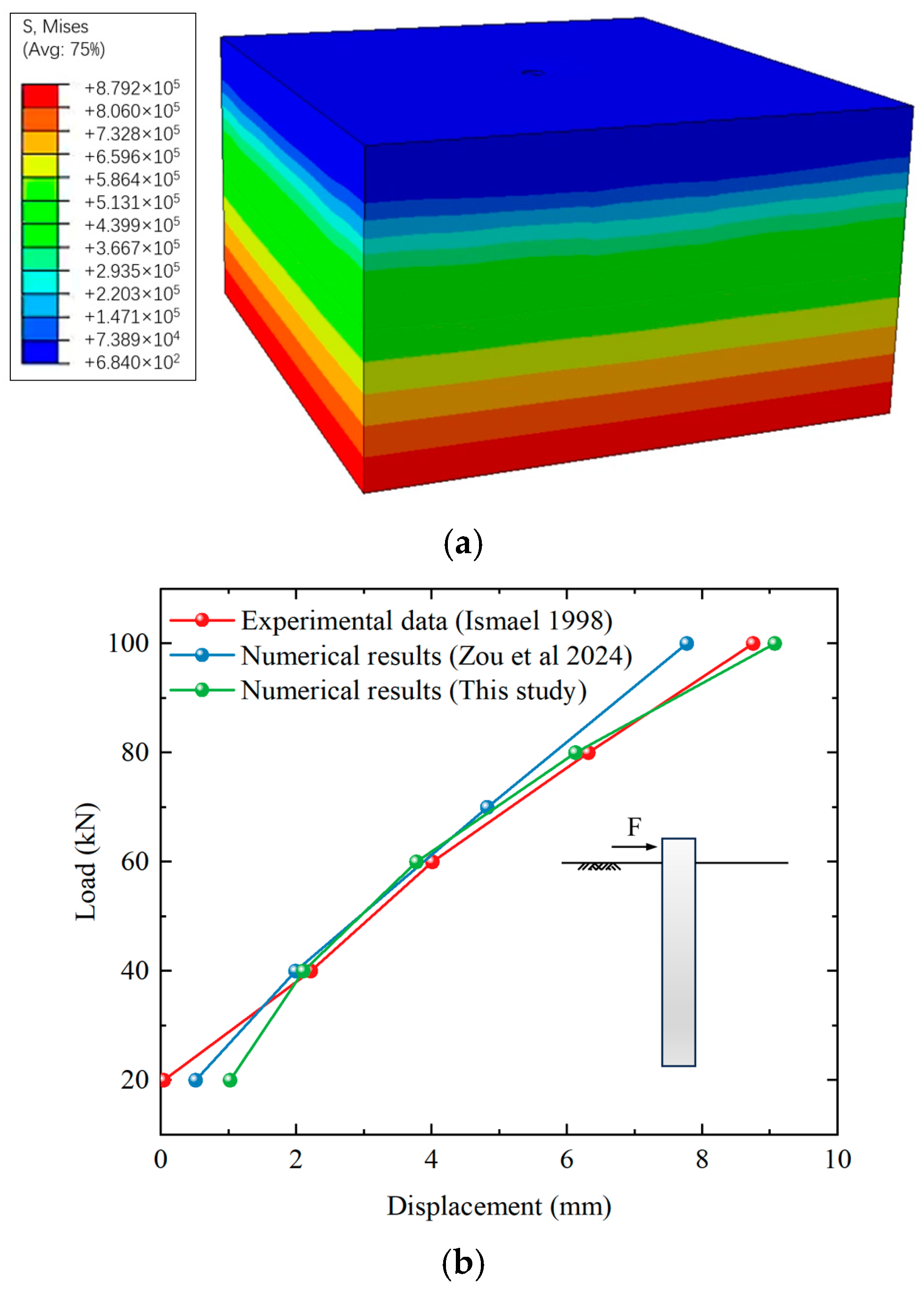
3.4. Validation of the Soil-Pile Interaction
4. Numerical Results and Analysis
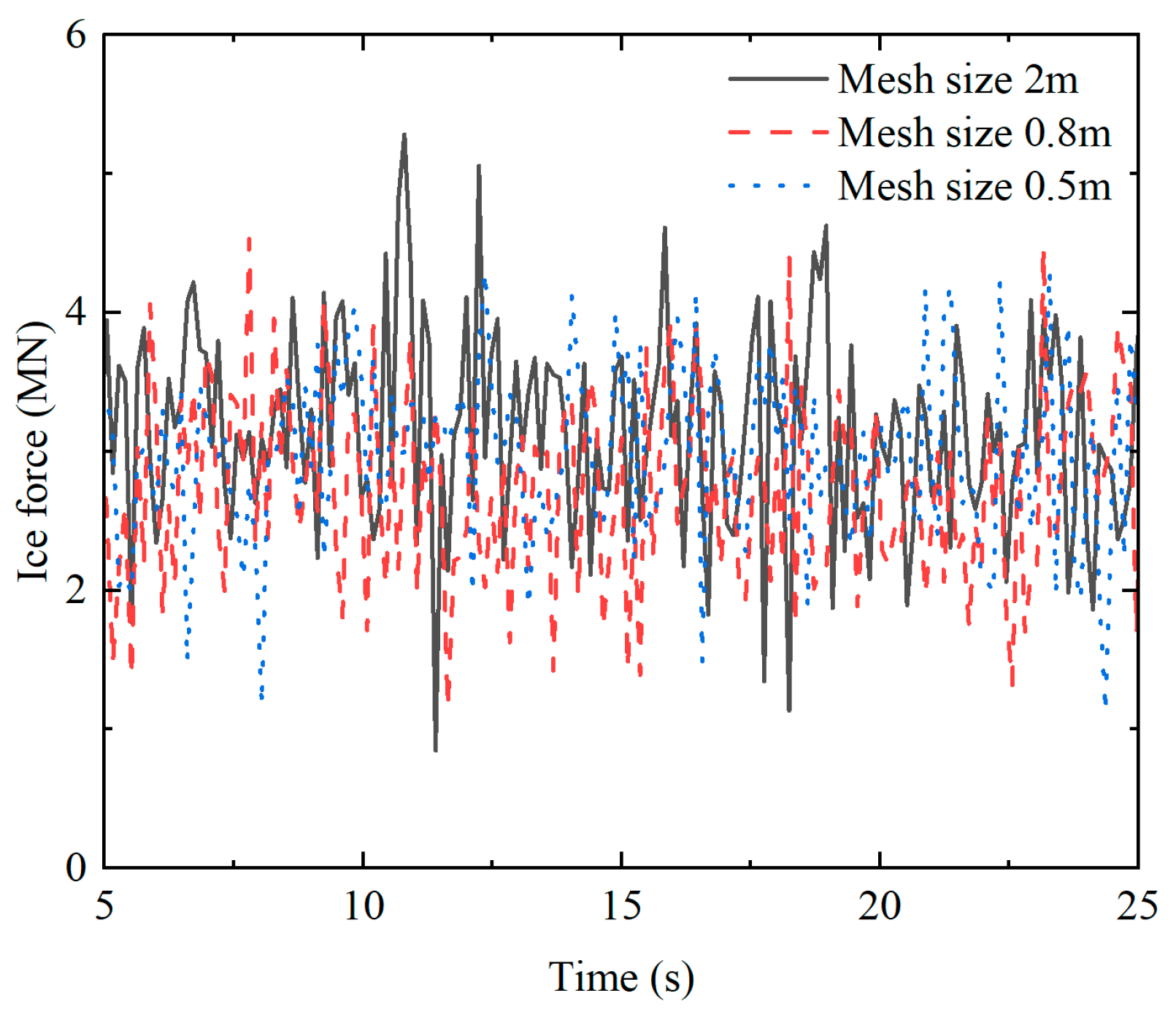
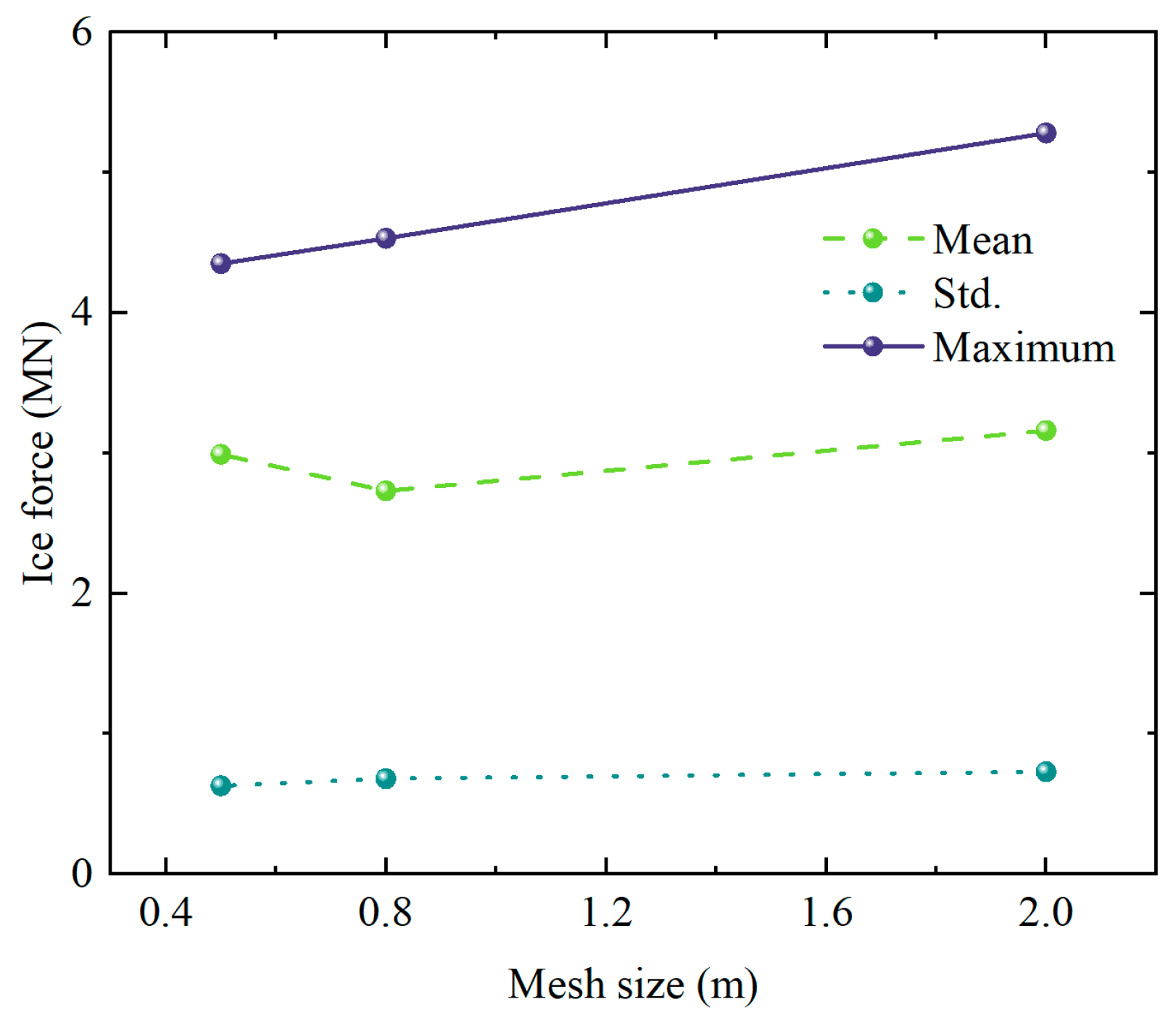
4.1. Influence of Ice Mesh Size
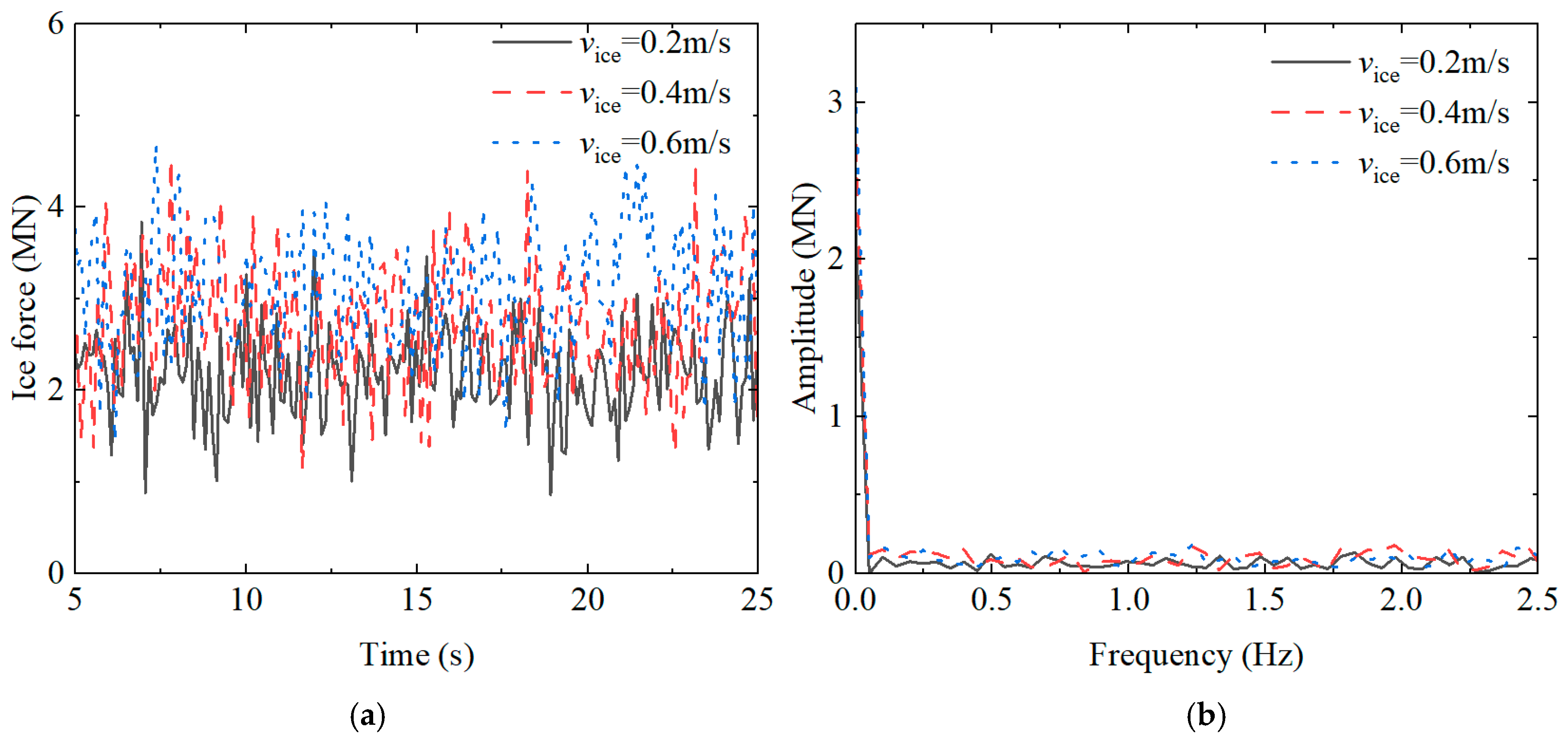
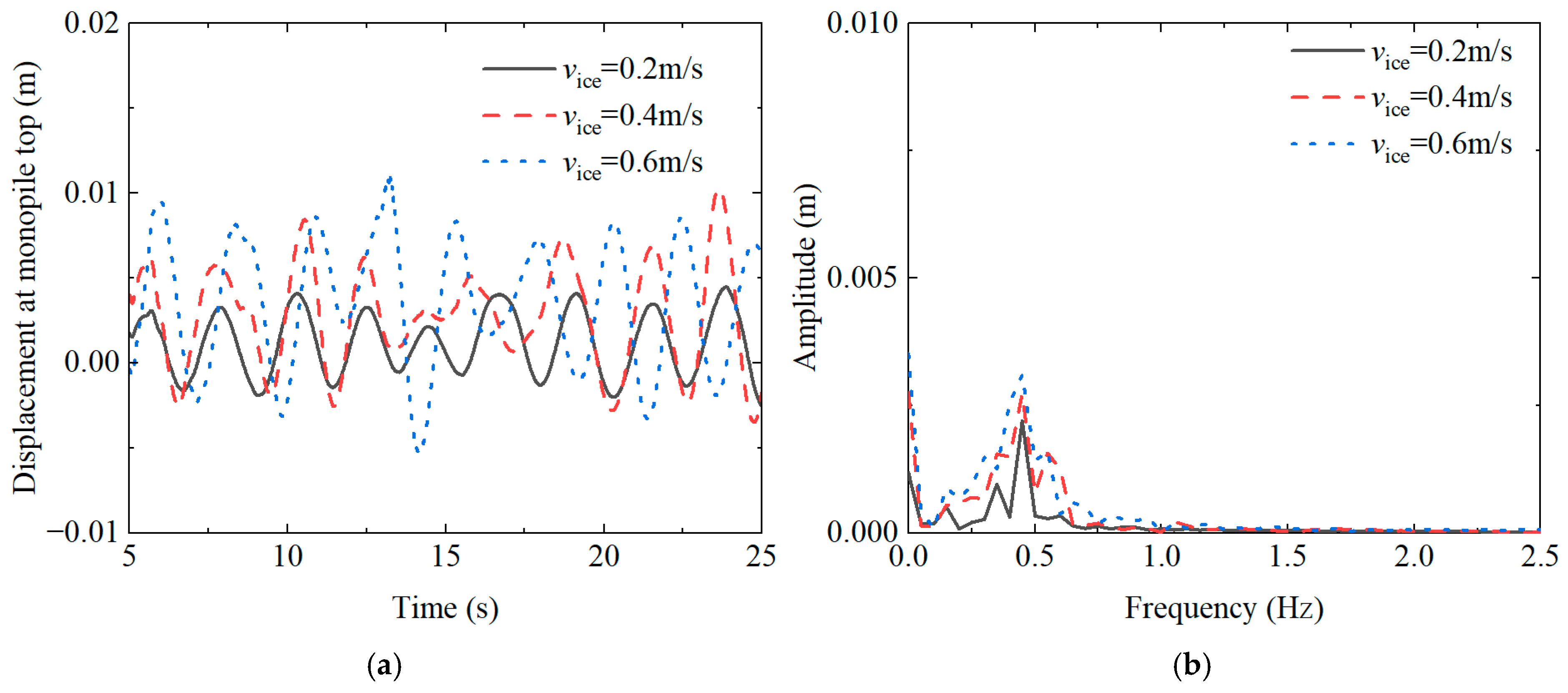
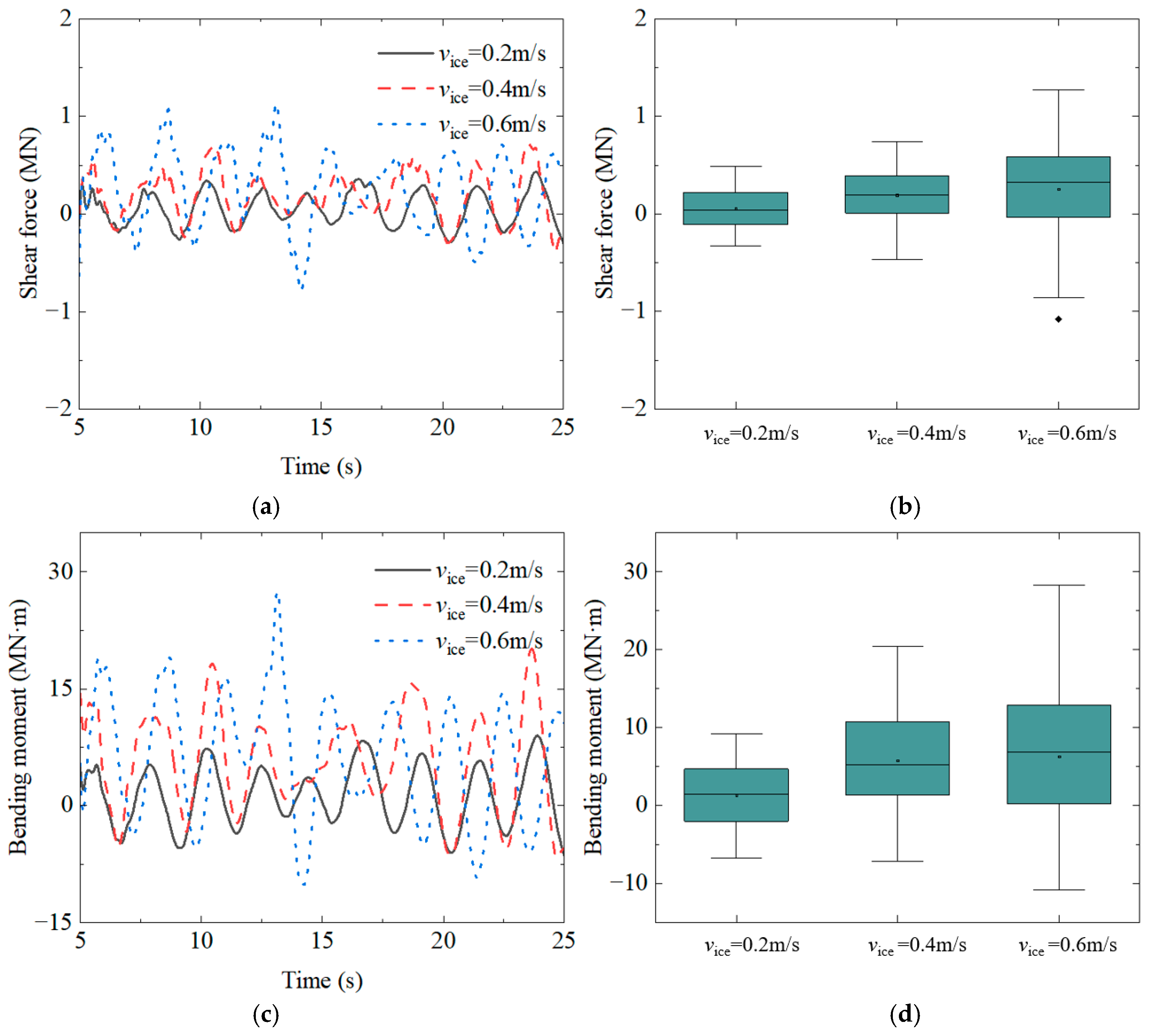
4.2. Influence of Ice Velocities
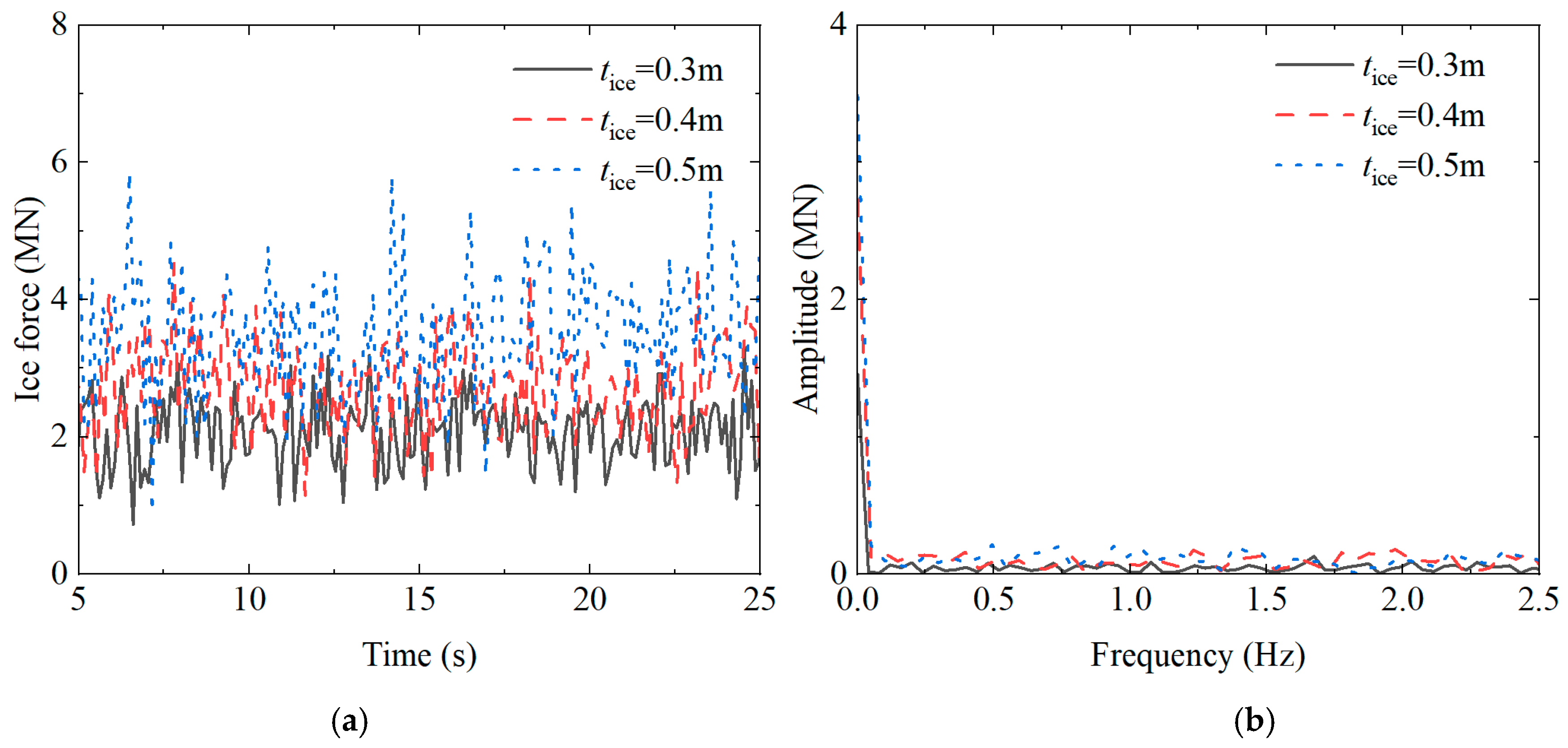
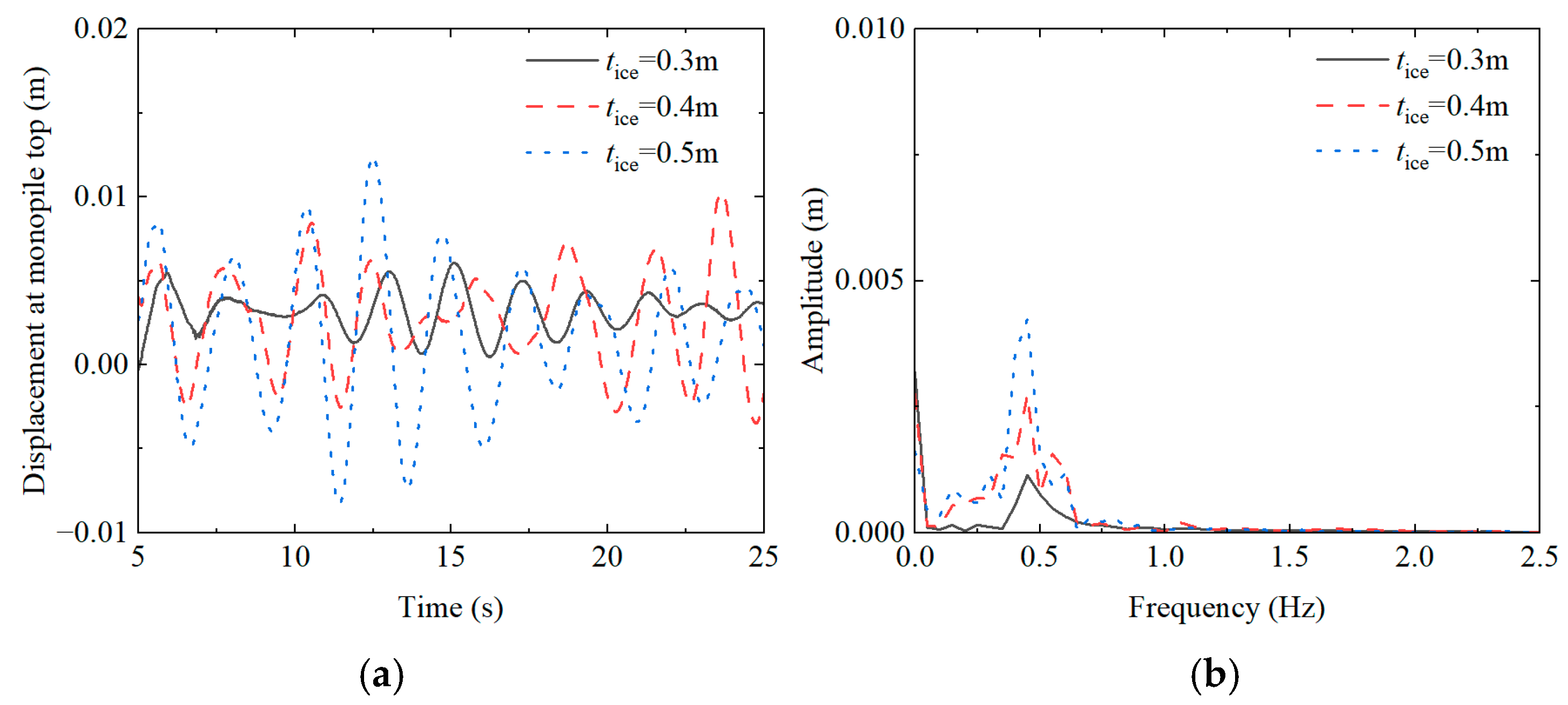
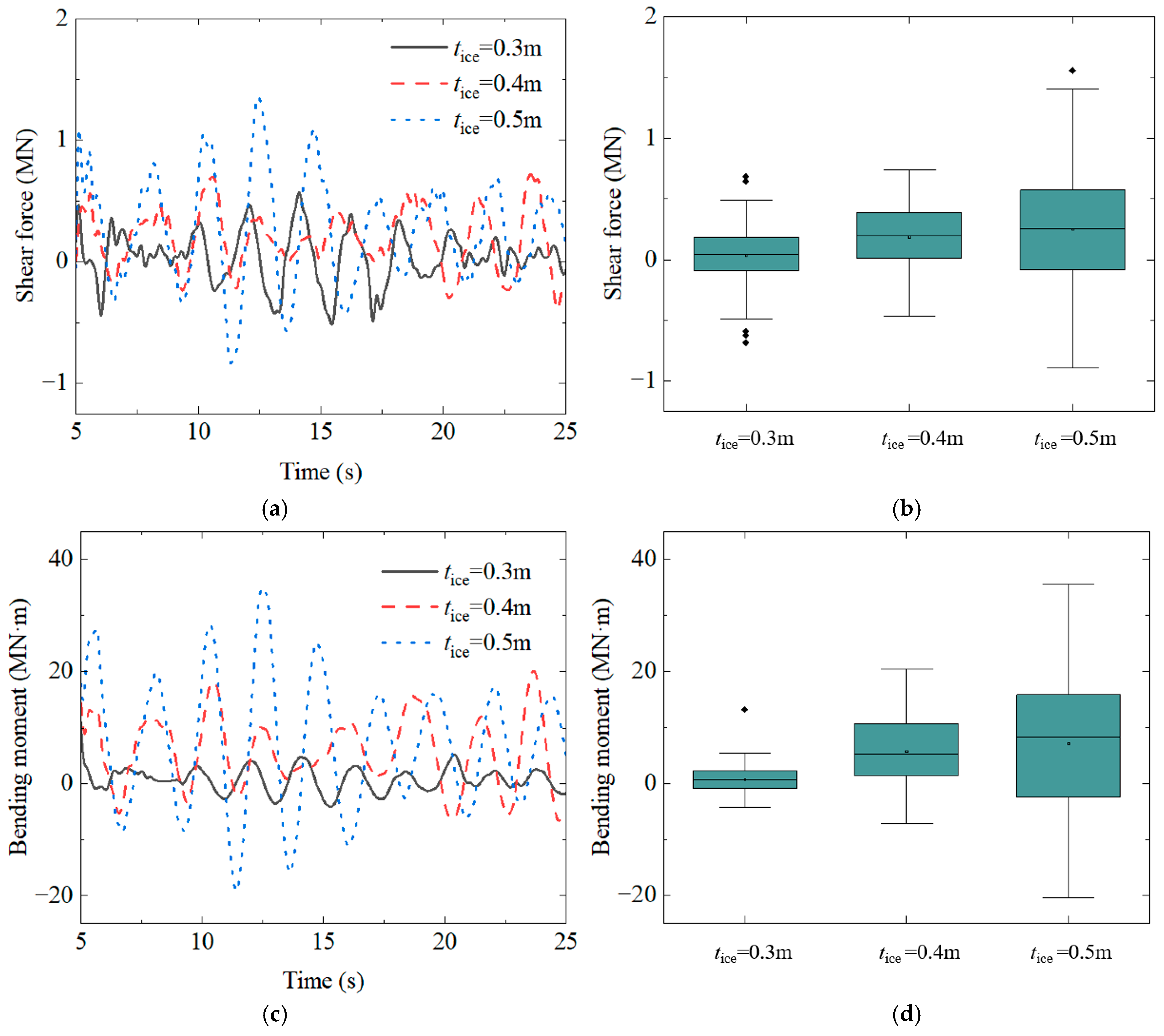
4.3. Influence of Ice Thicknesses
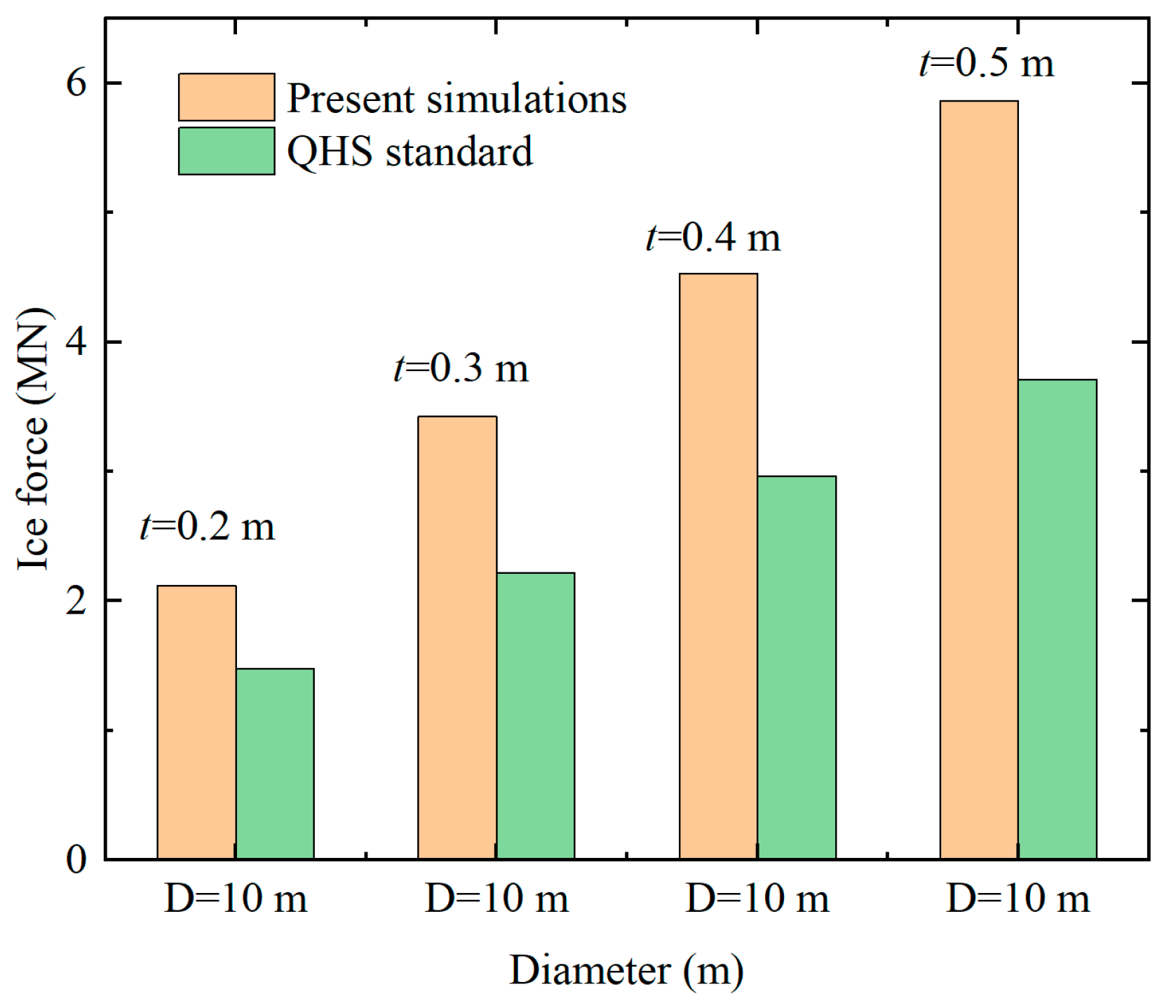
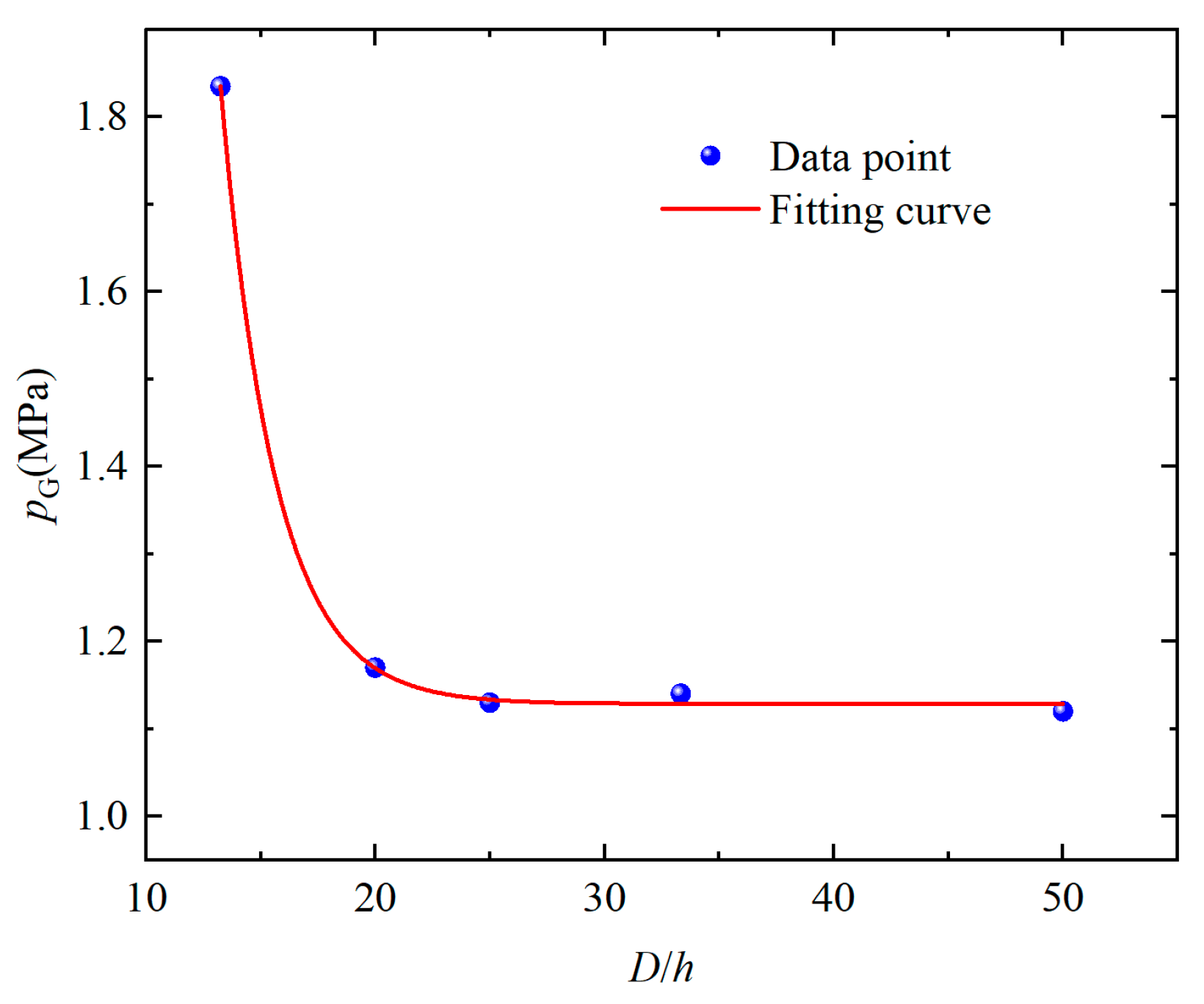
5. Semi-Empirical Method for Calculating Ice Pressure Incorporating Diameter-to-Thickness Ratio Effects
6. Conclusions
- (1)
- Following the completion of model tests, an ice–structure–soil interaction model was developed. The results demonstrate that this model accurately simulates the ice-crushing processes and the dynamic response of the large-diameter monopile foundation;
- (2)
- This study analyzed the influence of parameters, including mesh size, ice sheet velocity, and thickness, on the dynamic response of large-diameter monopile foundations. Results indicated that the dynamic response intensifies with increasing ice sheet velocity and thickness. Under constant conditions, variations in ice thickness demonstrated a more pronounced impact on the monopile foundation’s dynamic response compared to ice velocity;
- (3)
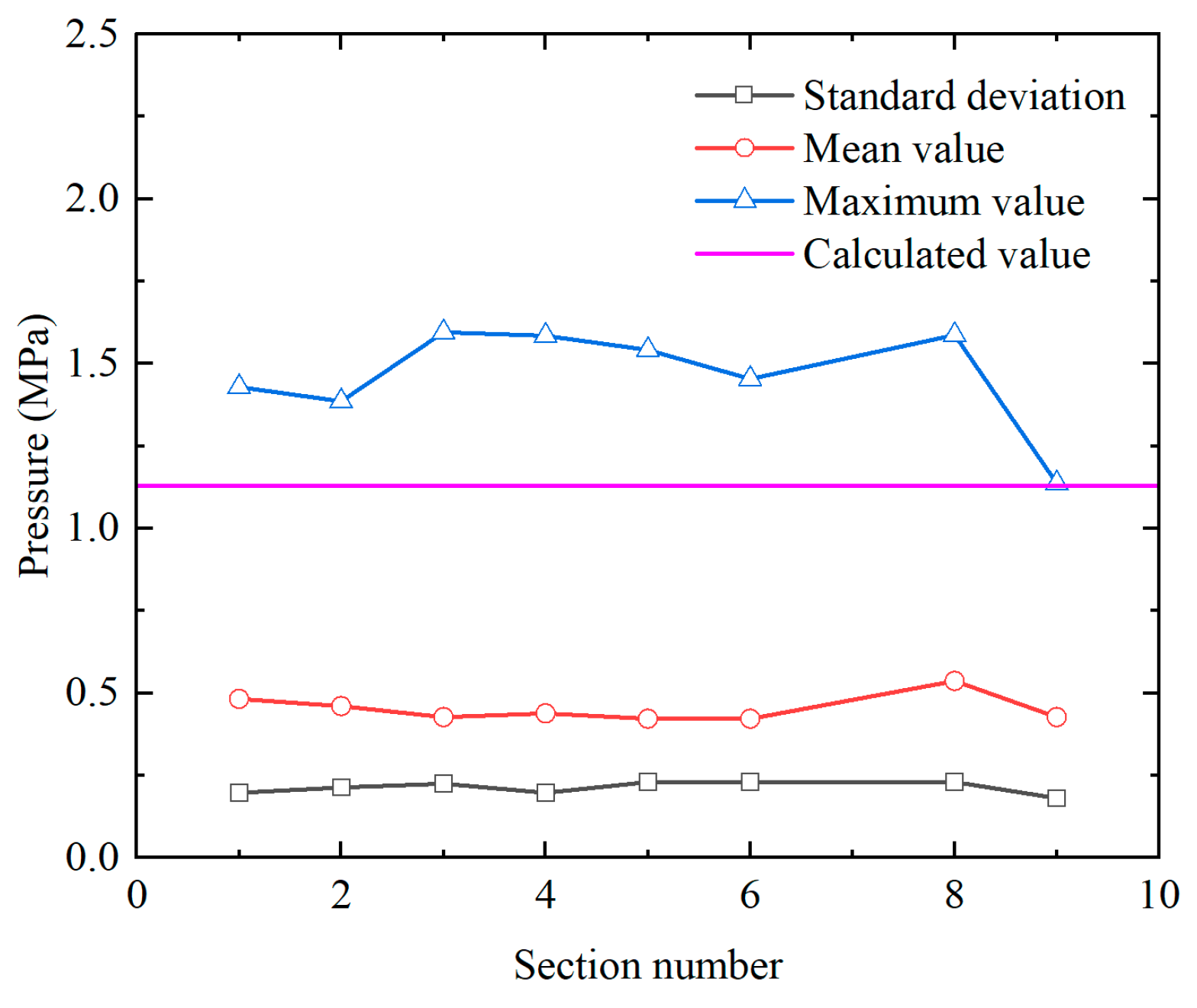
- A comparison between the extreme ice force values derived from numerical results and those calculated according to established standards revealed significant underestimation in the values calculated using “China’s Sea Ice Conditions and Applications Regulations QHS 3000-2002”. To address this discrepancy, a semi-empirical calculation method incorporating the aspect ratio effect was developed. This method was subsequently validated using field monitoring data of ice loads from the Norströmsgrund lighthouse in Norwegian waters. The results demonstrate that the proposed calculation method effectively accounts for the influence of the aspect ratio on the global ice pressure for large-diameter monopile foundations;
- (4)
- In contrast to conventional ice pressure calculation, the proposed method incorporates a more comprehensive consideration of the aspect ratio’s influence on large-diameter monopile foundations. This approach offers more direct and valuable insights for OWT design during the construction phase.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jahangiri, V.; Sun, C. Integrated bi-directional vibration control and energy harvesting of monopile offshore wind turbines. Ocean Eng. 2019, 178, 260–269. [Google Scholar] [CrossRef]
- Abdi, A.P.; Damci, A.; Kirca, O.; Turkoglu, H.; Arditi, D.; Demirkesen, S.; Korkmaz, M.; Arslan, A.E. A Spatial Decision-Support System for Wind Farm Site Selection in Djibouti. Sustainability 2024, 16, 9635. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Y.; Wang, R.; Hu, Y. Cost–Benefit Analysis of Cross-Regional Transmission of Renewable Electricity: A Chinese Case Study. Sustainability 2024, 16, 10538. [Google Scholar] [CrossRef]
- GWEC. Global Wind Report 2019; GWEC: Brussels, Belgium, 2020. [Google Scholar]
- Yang, X.; Zeng, X.; Wang, X. Lateral-moment loading capacity and bearing behavior of suction bucket foundations for offshore wind turbines in sand. Int. J. Geomech. 2018, 18, 04018152. [Google Scholar] [CrossRef]
- Gupta, B.K.; Basu, D. Offshore wind turbine monopile foundations: Design perspectives. Ocean Eng. 2020, 213, 107514. [Google Scholar] [CrossRef]
- Fu, D.F.; Zhou, Z.F.; Yan, Y.; Pradhan, D.L.; Hennig, J. A method to predict the torsional resistance of suction caisson with anti-rotation fins in clay. Mar. Struct. 2021, 75, 102866. [Google Scholar] [CrossRef]
- Xu, N.; Yue, Q.J. Dynamic ice force analysis on a conical structure based on direct observation and measurement. J. Offshore Mech. Arct. Eng. 2014, 136, 014501. [Google Scholar] [CrossRef]
- Zhu, B.; Sun, C.; Jahangiri, V. Characterizing and mitigating ice-induced vibration of monopile offshore wind turbines. Ocean Eng. 2021, 219, 108406. [Google Scholar] [CrossRef]
- Hammer, T.C.; Willems, T.; Hendrikse, H. Dynamic ice loads for offshore wind support structure design. Mar. Struct. 2023, 87, 103335. [Google Scholar] [CrossRef]
- Gravesen, H.; Petersen, B.; Sørensen, S.L.; Vølund, P. Ice forces to wind turbine foundations in Denmark. In Proceedings of the 17th International Conference on Port and Ocean Engineering under Arctic conditions, Trondheim, Norway, 16–19 June 2003. [Google Scholar]
- Gravesen, H.; Sørensen, S.L.; Vølund, P.; Barker, A.; Timco, G. Ice loading on Danish wind turbines: Part 2. Analyses of dynamic model test results. Cold Reg. Sci. Technol. 2005, 41, 25–47. [Google Scholar] [CrossRef]
- Määttänen, M.; Marjavaara, P.; Saarinen, S.; Laakso, M. Ice crushing tests with variable structural flexibility. Cold Reg. Sci. Technol. 2011, 67, 120–128. [Google Scholar] [CrossRef]
- Barker, A.; Timco, G.; Gravesen, H.; Vølund, P. Ice loading on Danish wind turbines: Part 1: Dynamic model tests. Cold Reg. Sci. Technol. 2005, 41, 1–23. [Google Scholar] [CrossRef]
- Bekker, A.T.; Sabodash, O.A.; SeJiverstov, V.; Koff, G.; Pipko, E. Estimation of limit ice loads on engineering offshore structures in the Sea of Okhotsk. In Proceedings of the 19th International Offshore and Polar Engineering Conference, Osaka, Japan, 21–26 June 2009. ISOPE-I-09-007. [Google Scholar]
- Gürtner, A.; Bjerkas, M.; Kuhnlein, W.; Jochmann, P.; Konuk, I. Numerical simulation of ice action to a lighthouse. In Proceedings of the 28th International Conference on Ocean, Offshore and Arctic Engineering (OMAE), Honolulu, HI, USA, 31 May–5 June 2009. OMAE2009-80164. [Google Scholar]
- Heinonen, J.; Hetmanczyk, S.; Strobel, M. Introduction of ice loads in overall simulation of offshore wind turbines. In Proceedings of the International Conference on Port and Ocean Engineering Under Arctic Conditions, Montreal, QC, Canada, 10–14 July 2011. POAC11-024. [Google Scholar]
- Wang, B.; Liu, Y.Z.; Zhang, J.H.; Shi, W.; Li, X.; Li, Y. Dynamic analysis of offshore wind turbines subjected to combined wind and ice loads based on cohesive element method. Front. Mar. Sci. 2022, 9, 956032. [Google Scholar] [CrossRef]
- Shi, W.; Liu, Y.Z.; Wang, W.H.; Cui, L.; Li, X. Numerical study of an ice-offshore wind turbine structure interaction with the pile-soil interaction under stochastic wind loads. Ocean Eng. 2023, 273, 113984. [Google Scholar] [CrossRef]
- Zou, P.; Bricker, J.D.; Fujisaki-Manome, A.; Garcia, F.E. Characteristics of ice-structure-soil interaction of an offshore wind turbine. Ocean Eng. 2024, 295, 116975. [Google Scholar] [CrossRef]
- Gravesen, H.; Kärnä, T. Ice loads for offshore wind turbines in Southern Baltic Sea. In Proceedings of the 20th International Conference on Port and Ocean Engineering under Arctic Conditions, Luleå, Sweden, 9–12 June 2009; pp. 20–31. [Google Scholar]
- Zhou, L.; Riska, K.; Polach, R.V.B.; Moan, T.; Su, B. Experiments on level ice loading on an icebreaking tanker with different ice drift angles. Cold Reg. Sci. Technol. 2013, 85, 79–93. [Google Scholar] [CrossRef]
- Taylor, R.S.; Richard, M. Development of a probabilistic ice load model based on empirical descriptions of high pressure zone attributes. In Proceedings of the 33rd International Conference on Ocean, Offshore and Arctic Engineering (OMAE), San Francisco, CA, USA, 8–13 June 2014. OMAE2014-24353. [Google Scholar]
- Murray, J.; LeGuennec, S.; Spencer, D.; Yang, C.K.; Yang, W. Model tests on a spar in level ice and ice ridge conditions. In Proceedings of the 28th International Conference on Ocean, Offshore and Arctic Engineering (OMAE), Honolulu, HI, USA, 31 May–5 June 2009; pp. 123–134. [Google Scholar]
- Yue, Q.J.; Guo, F.; Kärnä, T. Dynamic ice forces of slender vertical structures due to ice crushing. Cold Reg. Sci. Technol. 2009, 123, 121–139. [Google Scholar] [CrossRef]
- Popko, W.; Heinonen, J.; Hetmanczyk, S.; Vorpahl, F. State-of-the-art comparison of standards in terms of dominant sea ice loads for offshore wind turbine support structures in the Baltic Sea. In Proceedings of the 22nd International Offshore and Polar Engineering Conference, Rhodes, Greece, 17–22 June 2012. ISOPE-I-12-094. [Google Scholar]
- Bekker, A.T.; Sabodash, O.A.; Balakin, B.V. Numerical prediction of contact surface between hummock and ice fields for estimation of ice loads on structure. In Proceedings of the 23rd International Offshore and Polar Engineering Conference, Anchorage, AK, USA, 30 June–5 July 2013. ISOPE-I-13-142. [Google Scholar]
- Spencer, P.; Morrison, T.; Ausenco, C. Quantile regression as a tool for investigating local and global ice pressures. In Proceedings of the Offshore Technology Conference, Arctic Technology Conference, Houston, TX, USA, 5–8 May 2014. OTC-24550-MS. [Google Scholar]
- Zvyagin, P.; Sazonov, K. Analysis and probabilistic modelling of the stationary ice loads stochastic process with lognormal distribution. In Proceedings of the 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014. OMAE2014-24713. [Google Scholar]
- Nord, T.S.; Lourens, E.M.; Øiseth, O.; Metrikine, A. Model-based force and state estimation in experimental ice-induced vibrations by means of Kalman filtering. Cold Reg. Sci. Technol. 2015, 111, 13–26. [Google Scholar] [CrossRef]
- Shi, W.; Tan, X.; Gao, Z.; Moan, T. Numerical study of ice-induced loads and responses of a monopile-type offshore wind turbine in parked and operating conditions. Cold Reg. Sci. Technol. 2016, 123, 121–139. [Google Scholar] [CrossRef]
- Xing, W.Q.; Cong, S.Y.; Ling, X.Z.; Li, X.Y.; Cheng, Z.H.; Tang, L.J. Numerical study of ice loads on different interfaces based on cohesive element formulation. Sci. Rep. 2023, 13, 14434. [Google Scholar] [CrossRef]
- Konuk, I.; Gürtner, A.; Yu, S. A cohesive element framework for dynamic ice structure interaction problems—Part I: Review and formulation. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering (OMAE), Honolulu, HI, USA, 31 May–6 June 2009. [Google Scholar]
- Gürtner, A.; Bjerkås, M.; Forsberg, J.; Hilding, D. Numerical modelling of a full scale ice event. In Proceedings of the 20th IAHR International Symposium on Ice, Lahti, Finland, 14–17 June 2010; pp. 77–88. [Google Scholar]
- Lu, W.; Lubbad, R.; Løset, S. Simulating ice-sloping structure interactions with the cohesive element method. J. Offshore Mech. Arct. Eng. 2014, 136, 16. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, D.; Yue, Q.; Yu, S. Study on the dynamic ice load of offshore wind turbines with installed ice-breaking cones in cold regions. Energies 2022, 15, 3357. [Google Scholar] [CrossRef]
- Zhang, X.L.; Zhou, R.; Zhang, G.L.; Han, Y. A corrected p-y curve model for large-diameter pile foundation of offshore wind turbine. Ocean Eng. 2023, 273, 114012. [Google Scholar] [CrossRef]
- Velarde, J.; Bachynski, E.E. Design and fatigue analysis of monopile foundations to support the DTU 10 MW offshore wind turbine. Energy Procedia 2017, 137, 3–13. [Google Scholar] [CrossRef]
- Velarde, J. Design of Monopile Foundations to Support the DTU 10 MW Offshore Wind Turbine. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2016. [Google Scholar]
- Ismael, N.F. Lateral loading tests on bored piles in cemented sands. In Deep Foundations on Bored and Auger Piles; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- ISO 19906; Petroleum and Natural Gas Industries—Arctic Offshore Structures. ISO: Geneva, Switzerland, 2019.
- Q/HS 3000-2002; Regulations for Offshore Ice Condition Application in China Sea. China National Offshore Oil Corporation: Beijing, China, 2002. (In Chinese)
- Wu, H.B.; Huang, Y.; Li, W. Experimental study on the ice load of large-diameter monopile wind turbine foundations. Ocean Eng. 2018, 36, 83–91. (In Chinese) [Google Scholar]
- Kärnä, T.; Qu, Y.; Bi, X.; Yue, Q.; Kuehnlein, W. A Spectral Model for Forces Due to Ice Crushing. J. Offshore Mech. Arct. Eng. 2007, 129, 138–145. [Google Scholar] [CrossRef]
- Fransson, L.; Lundqvist, J.E. A statistical approach to extreme ice loads on lighthouse Norströmsgrund. In Proceedings of the 25th International Conference on Offshore Mechanics and Arctic Engineering, Hamburg, Germany, 4–9 June 2006. OMAE2006-92465. [Google Scholar]
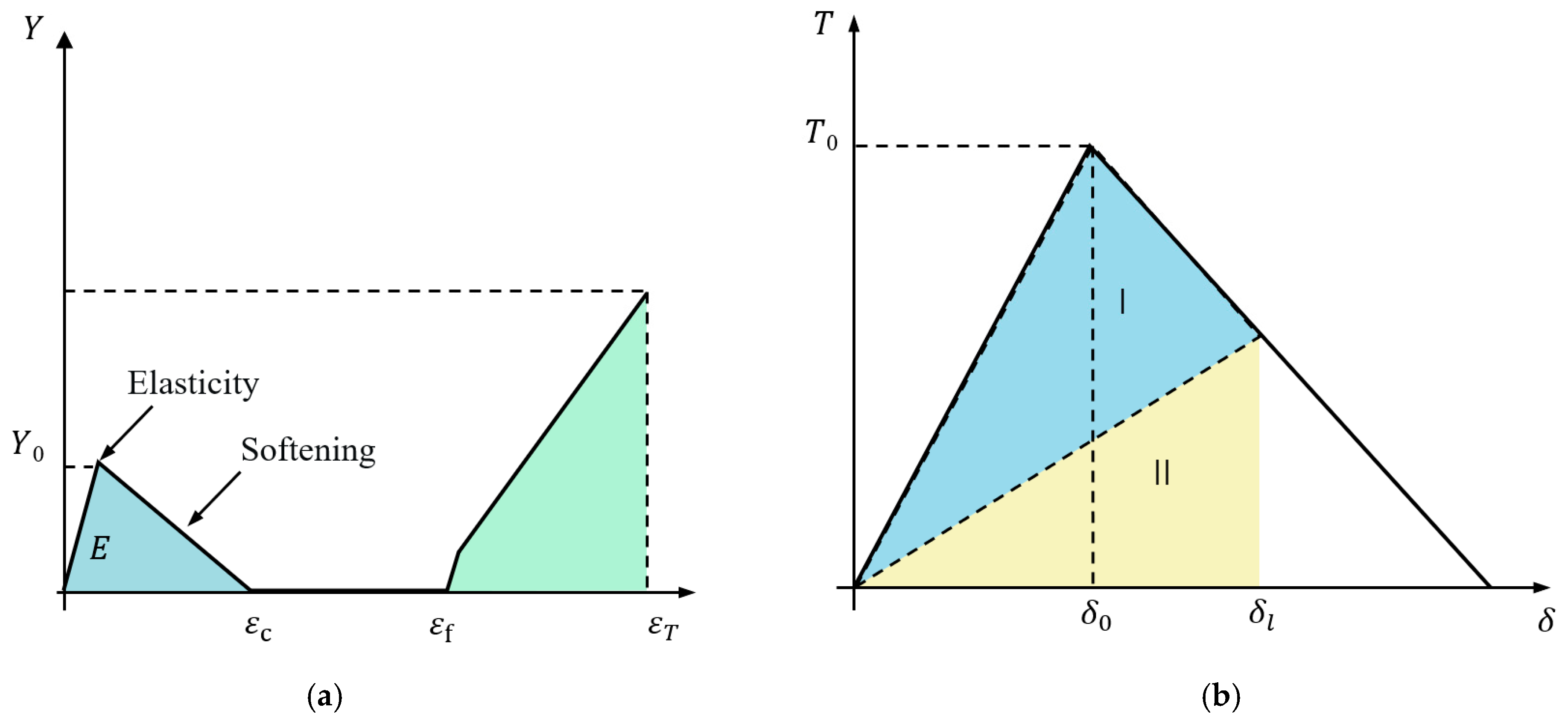
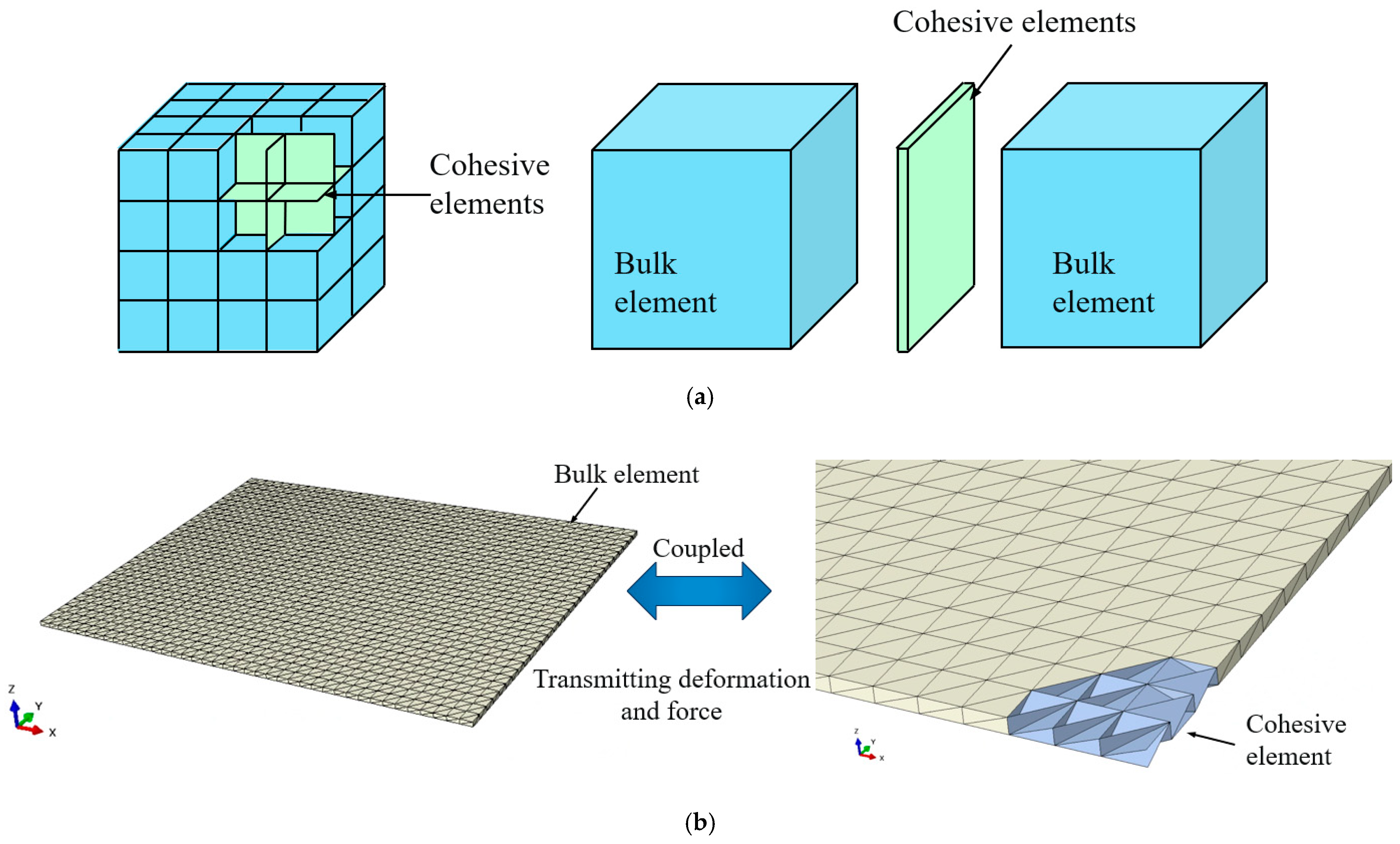

| Parameters | Bulk Elements | Cohesive Elements |
|---|---|---|
| Young’s modulus/(GPa) | 5 | 5 |
| Poisson’s ratio | 0.3 | 0.3 |
| Density (kg/m3) | 900 | 900 |
| Yield strength/(MPa) | 2 | – |
| Yield strain | 4 × 10−4 | – |
| Fracture energy (N/m) | – | 100 |
| Fracture strength/(MPa) | – | 1.5/1.1/1.1 |
| Failure strain | 0.4 | – |
| Parameter | Value |
|---|---|
| Monopile diameter (m) | 10 |
| Monopile thickness (m) | 0.125 |
| Rated power (MW) | 10 |
| Tower mass (t) | 628 |
| Rotor mass (t) | 228 |
| Nacelle quality control method (t) | 446 |
| Hub diameter (m) | 5.6 |
| Hub center height (m) | 178.3 |
| Cut in, rated, cut out wind speed (m/s) | 4, 11.4, 25 |
| Physical Parameters | Similarity Ratio |
|---|---|
| Displacement (D) | λ |
| Mass (kg) | λ3 |
| Elasticity modulus (E) | λ |
| Velocity (m/s) | λ1/2 |
| Time (t) | λ1/2 |
| Gravitational acceleration (g) | 1 |
| Force (N) | λ3 |
| Material | Weight (kN/m3) | Young’s Modulus (Pa) | Cohesion (kPa) | Friction Angle (°) | Poisson’s Ratio |
|---|---|---|---|---|---|
| Medium-dense silty sand | 18 | 1.3 × 107 | 20 | 35 | 0.30 |
| Medium-dense to very dense silty sand | 19 | 1.3 × 107 | – | 45 | 0.30 |
| Pile | 25 | 2.3 × 1010 | – | – | 0.15 |
| Mode Number | Natural Frequency (Hz) | Mode Shape |
|---|---|---|
| 1 | 0.25 | Fore–aft bending mode of the tower |
| 2 | 0.25 | Side–side bending mode of the tower |
| 3 | 1.09 | Fore–aft global bending mode |
| 4 | 1.1 | Side–side global bending mode |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Cong, S.; Ling, X.; Tang, L. Dynamic Response Analysis of Large-Diameter Monopile Foundation Under Ice Load. Sustainability 2025, 17, 2300. https://doi.org/10.3390/su17052300
Liu S, Cong S, Ling X, Tang L. Dynamic Response Analysis of Large-Diameter Monopile Foundation Under Ice Load. Sustainability. 2025; 17(5):2300. https://doi.org/10.3390/su17052300
Chicago/Turabian StyleLiu, Shuxing, Shengyi Cong, Xianzhang Ling, and Liang Tang. 2025. "Dynamic Response Analysis of Large-Diameter Monopile Foundation Under Ice Load" Sustainability 17, no. 5: 2300. https://doi.org/10.3390/su17052300
APA StyleLiu, S., Cong, S., Ling, X., & Tang, L. (2025). Dynamic Response Analysis of Large-Diameter Monopile Foundation Under Ice Load. Sustainability, 17(5), 2300. https://doi.org/10.3390/su17052300