Exploring the Relationship Between Growth Strain and Growth Traits in Eucalyptus cloeziana at Different Age Stages
Abstract
1. Introduction
2. Materials and Methods
2.1. Growth Strain Measurement
2.2. Measurement of Density and Heartwood Percentage
2.3. Determination of Fiber Cell Morphology
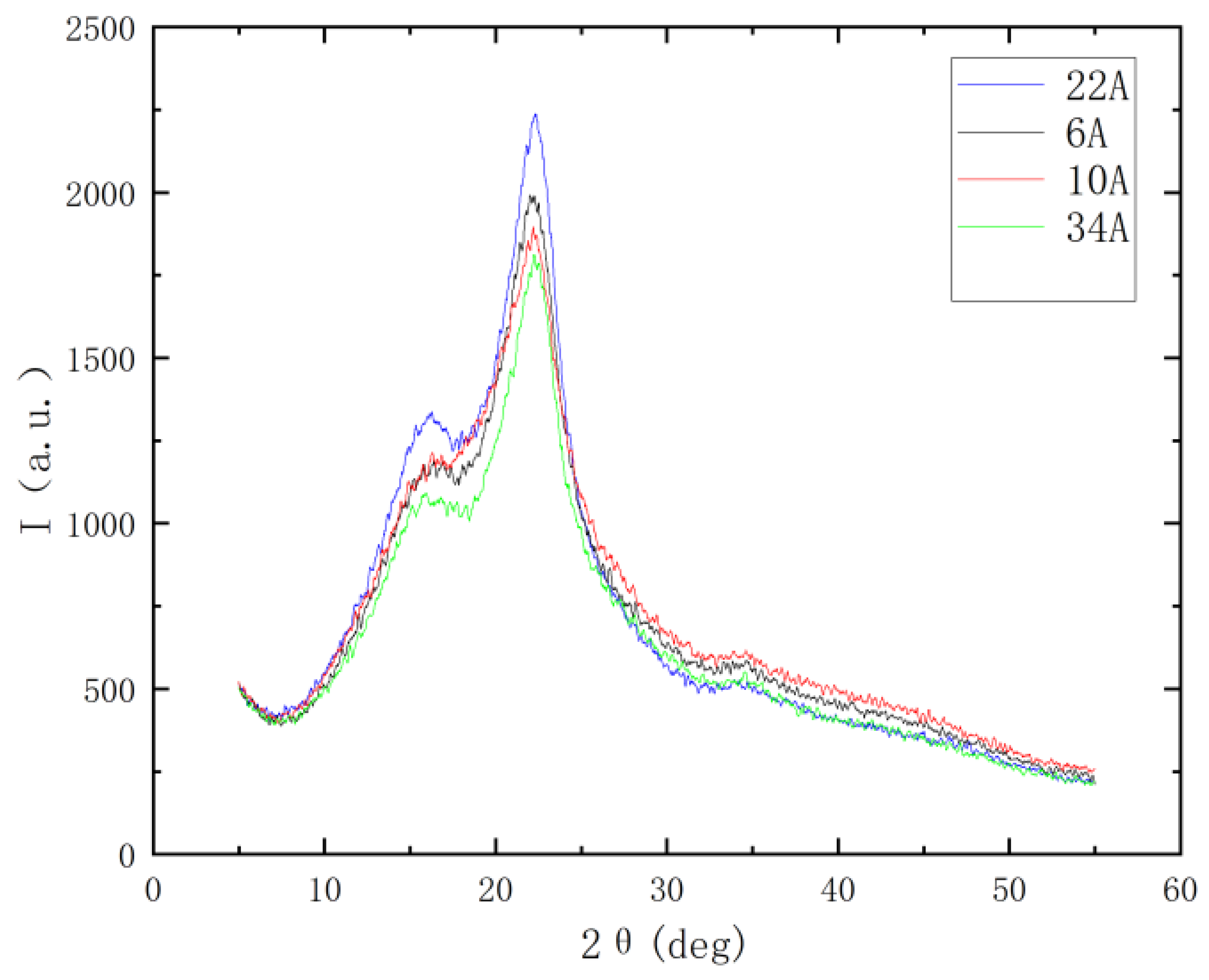
2.4. Determination of Crystallinity
2.5. Determination of Relative Content of Lignin by Fourier Transform Infrared Spectroscopy
2.6. Data Processing
3. Results
3.1. Analysis of Growth Traits of E. cloeziana in Four Age Groups
3.2. The Changes In Density and Heartwood Percentage of E. cloeziana at Four Age Stages
3.3. Growth Strain Analysis of E. cloeziana in Four Age Stages
Effects of Growth Traits and Physical Properties on Growth Strain
3.4. Correlation Analysis of Fiber Morphology and Growth Strain
3.5. Correlation Analysis Between Crystallinity and Growth Strain
3.6. Lignin Content and Correlation Analysis with Growth Strain
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DBH | Diameter at breast height |
References
- Yingna, L. Eucalyptus large-diameter timber cultivation technology. Guangdong Seric. 2023, 57, 53–55. [Google Scholar] [CrossRef]
- Guofang, S. Afforestation Technology of Main Tree Species in China; China Forestry Publishing House: Beijing, China, 2020. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, J.; Chen, Z.; Wang, L.; Guo, H. Current situation and research prospect of domestic genetic breeding of Eucalyptus cloeziana. Sichuan For. Sci. Technol. 2018, 39, 17–21. [Google Scholar] [CrossRef]
- Chen, G.; Zheng, J.; Meng, F.; Chen, S.; Chen, Y.; Wang, J. Wood fiber characteristics and variation of six Eucalyptus plantations. J. Cent. South Univ. For. Technol. 2020, 40, 137–142+168. [Google Scholar] [CrossRef]
- Xin, L.; Heng, L.; Shenyang, W.; Yaqi, P.; Hanfu, Q.; Yunlin, F. Study on the properties of 17-year-old Eucalyptus cloeziana. Jiangxi Agric. 2020, 32, 45–49. [Google Scholar] [CrossRef]
- Haikang, Q.; Heng, L.; Xingcheng, J.; Penglian, W.; Zhongcai, M.; Yunlin, F. A comparative study on the mechanical processing performance of 29-year-old and 35-year-old Eucalyptus cloeziana wood. Eucalyptus Sci. Technol. 2023, 40, 93–96. [Google Scholar] [CrossRef]
- Lei, Z.; Heng, L.; Liqiang, C.; Weiqing, Z.; Benliang, Z.; Yunlin, F. Effect of tree age on physical properties of Eucalyptus cloeziana wood. Agric. For. Sci. Technol. Ningxi 2020, 61, 27–29. [Google Scholar] [CrossRef]
- Jianzhong, W.; Heng, L.; Linbo, Q.; Weiqing, Z. Xiaoyun, F.; Yunlin, F. Effect of tree age on mechanical properties of Eucalyptus cloeziana wood. Heilongjiang Agric. Sci. 2020, 4, 78–81. [Google Scholar] [CrossRef]
- Dril, J.; Jullien, D.; Bardet, S.; Yamamoto, H. Tree Growth Stress and Related Problems. J. Wood Sci. 2017, 63, 411–432. [Google Scholar] [CrossRef]
- Murphy, T.; Henson, M.; Vanclay, J. Growth stress in Eucalyptus dunnii. Aust. For. 2005, 68, 144–149. [Google Scholar] [CrossRef][Green Version]
- Boyd, J.D. Tree growth stresses—Part V: Evidence of an origin in differentiation and lignification. Wood Sci. Technol. 1972, 6, 251–262. [Google Scholar] [CrossRef]
- Bamber, R.K. The Origin of Growth Stresses: A Rebuttal. IAWA Bull. 1987, 8, 80–84. [Google Scholar] [CrossRef]
- Beltrame, R.; Peres, M.D.; Lazarotto, M.; Gatto, D.A.; Schneid, E.; Haselein, C.R. Growth stress and its relationship with end splits in logs of Eucalyptus spp. Sci. For. 2015, 43, 63–74. [Google Scholar]
- Yang, J.L.; Gary, W. Growth stress its measurement and effects. Aust. For. 2002, 64, 127–135. [Google Scholar] [CrossRef]
- Chafe, S.C. Growth stress in trees. Aust. For. Res. 1979, 9, 203–223. [Google Scholar] [CrossRef]
- Wang, G. Reducing growth stresses in standing trees. Aust. For. Res. 1977, 7, 215–218. [Google Scholar] [CrossRef]
- Ferrand, J. Study of growth stresses Eucalyptus delegatensis and Eucalyptus nitens influence of silviculture and site index. Ann. Sci. Forest. 1982, 39, 355–378. [Google Scholar] [CrossRef]
- Malan, F.S.; Gerischer, G.F.R. Wood property differences in South African grown Eucalyptus grandis trees of different growth stress intensity. Holzforschung 1987, 41, 331–335. [Google Scholar] [CrossRef]
- Trugilho, P.; Oliveira, J. Relationships and estimates of longitudinal growth stress in Eucalyptus dunnii at different ages. Rev. Arvore 2008, 32, 723–729. [Google Scholar] [CrossRef]
- Biechele, T.; Nutto, L.; Becker, G. Growth Strain in Eucalyptus nitens at Different Stages of Development. Silva Fenn. 2009, 43, 669–679. [Google Scholar] [CrossRef][Green Version]
- Nicholson, J.E. A rapid method for estimating longitudinal growth stresses in logs. Wood Sci. Technol. 1971, 5, 40–48. [Google Scholar] [CrossRef]
- Xiao, W. Study on the Relationship Between Growth Strain and Wood Properties of Tension Wood of Poplar. Master’s Thesis, Anhui Agricultural University, Hefei, China, 2022. [Google Scholar] [CrossRef]
- Tianhui, W. Study on the Influencing Factors and Formation Mechanism of High Growth Strain of Eucalyptus urophylla. Master’s Thesis, Guangxi University, Nanning, China, 2023. [Google Scholar] [CrossRef]
- GB1928.2-2021; Test Method for Physical and Mechanical Properties of Flawless Small Sample Wood. China Standard Publishing House: Beijing, China, 2021. [CrossRef]
- Bonham, V.A.; Barnatt, J.R. Fibre length and microfibril angle in silver birch (Betula pendula Roth). Holzforschung 2001, 2, 159–162. [Google Scholar] [CrossRef]
- Yang, K.; Xu, X.; Sun, H.; Chen, L.; Qiang, T. Effects of pruning intensity on growth and stem form of Fraxinus mandshurica plantation. J. Northeast. For. Univ. 2024, 52, 10–16. [Google Scholar] [CrossRef]
- Peng, W.; Chen, J.; Yongli, Z. Study on wood physical and mechanical properties and vertical variation characteristics of Liriodendron chinense natural forest. Sichuan For. Sci. Technol. 2018, 39, 27–31. [Google Scholar]
- Song, K.; Yin, Y.; Salmén, L.; Xiao, F.; Jiang, X. Changes in the properties of wood cell walls during the transformation from sapwood to heartwood. Mater. Sci. 2014, 49, 1734–1742. [Google Scholar] [CrossRef]
- Kramer, R.D.; Sillett, S.C.; Carroll, A.L. Carroll, Structural development of redwood branches and its effects on wood growth. Tree Physiol. 2014, 34, 314–330. [Google Scholar] [CrossRef]
- Cangwei, L.; Minglei, S.; Xianwu, S.; Rongjun, Z.; Jianxiong, L.; Yurong, W. Study on lignin content and micro-area distribution of transgenic poplar cell wall by FTIR and CLSM. Spectrosc. Spectr. Anal. 2017, 37, 3404–3408. [Google Scholar]
- Fournies, M. Growth-stress pattern in tree stems: A model assuming evolution with the tree age of maturation strain. Wood Sci. Technol. 1990, 24, 131–142. [Google Scholar] [CrossRef]
- Trugilho, P.F.; Lima, J.T.; de Pádua, F.A.; de Carvalho Soragi, L.; Andrade, C.R. Deformação residual longitudinal (DRL) e tangencial (DRT) em seis clones de Eucalyptus spp. Cerne 2006, 12, 279–286. [Google Scholar]
- Jiqing, H.; Xiaomei, J.; Zhuqiang, H.; Yafang, Y. Preliminary study on strain variation of axial growth of Eucalyptus in three plantations. Wood Ind. 2000, 06, 9–11. [Google Scholar] [CrossRef]
- Okuyama, T.; Sasaki, Y.; Kikata, Y.; Kawai, N. The seasonal change in growth stresses in the tree trunk. Wood Res. Soc. 1981, 24, 77–78. [Google Scholar] [CrossRef]
- Aggarwal, P.K.; Chauhan, S.S.; Karmarkar, A. Growth Strains in Acacia auriculaeformis Trees of Different Age: Their Relationship with Growth Rate and Height. Inst. Wood Sci. 2006, 17, 212–215. [Google Scholar] [CrossRef]
- Yamamoto, H.; Okuyama, T.; Yoshida, M. Generation process of growth stresses in cell walls, 6: Analysis of growth stress generation by using a cell model having three layers (S1, S2, and I+P). J. Jpn. Wood Res. Soc. 1995, 41, 1–8. [Google Scholar] [CrossRef]
- Jullien, D.; Widmann, R.; Loup, C.; Thibaut, B. Relationship between tree morphology and growth stress in mature European beech stands. Ann. For. Sci. 2012, 70, 133–142. [Google Scholar] [CrossRef]
- Jianxiong, L.; Yafang, Y.; Youke, Z.; Xiaomei, J. Evaluation of growth strain level of different Eucalyptus plantation species in southern China. J. Beijing For. Univ. 2005, 27, 69–72. [Google Scholar] [CrossRef]

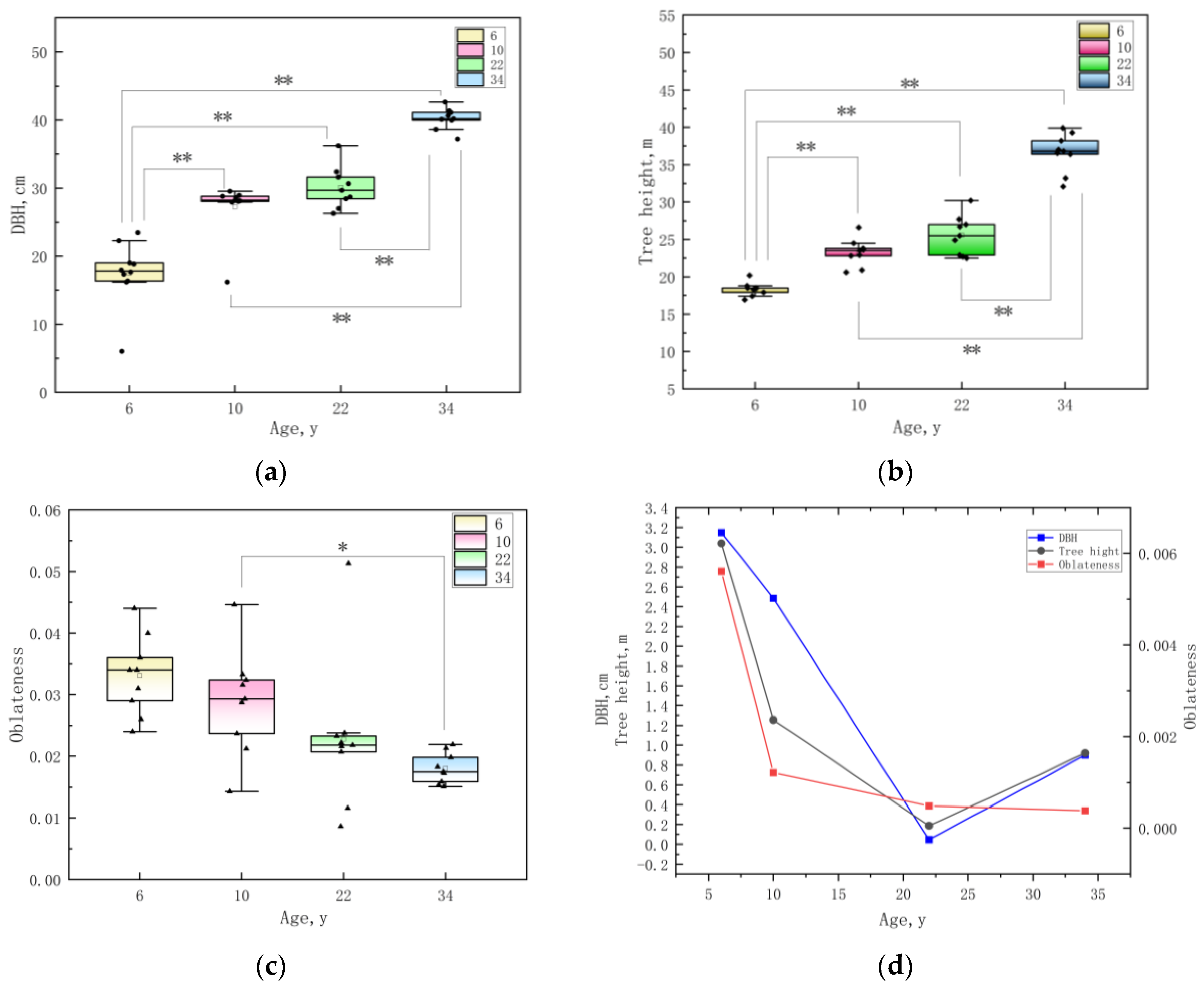
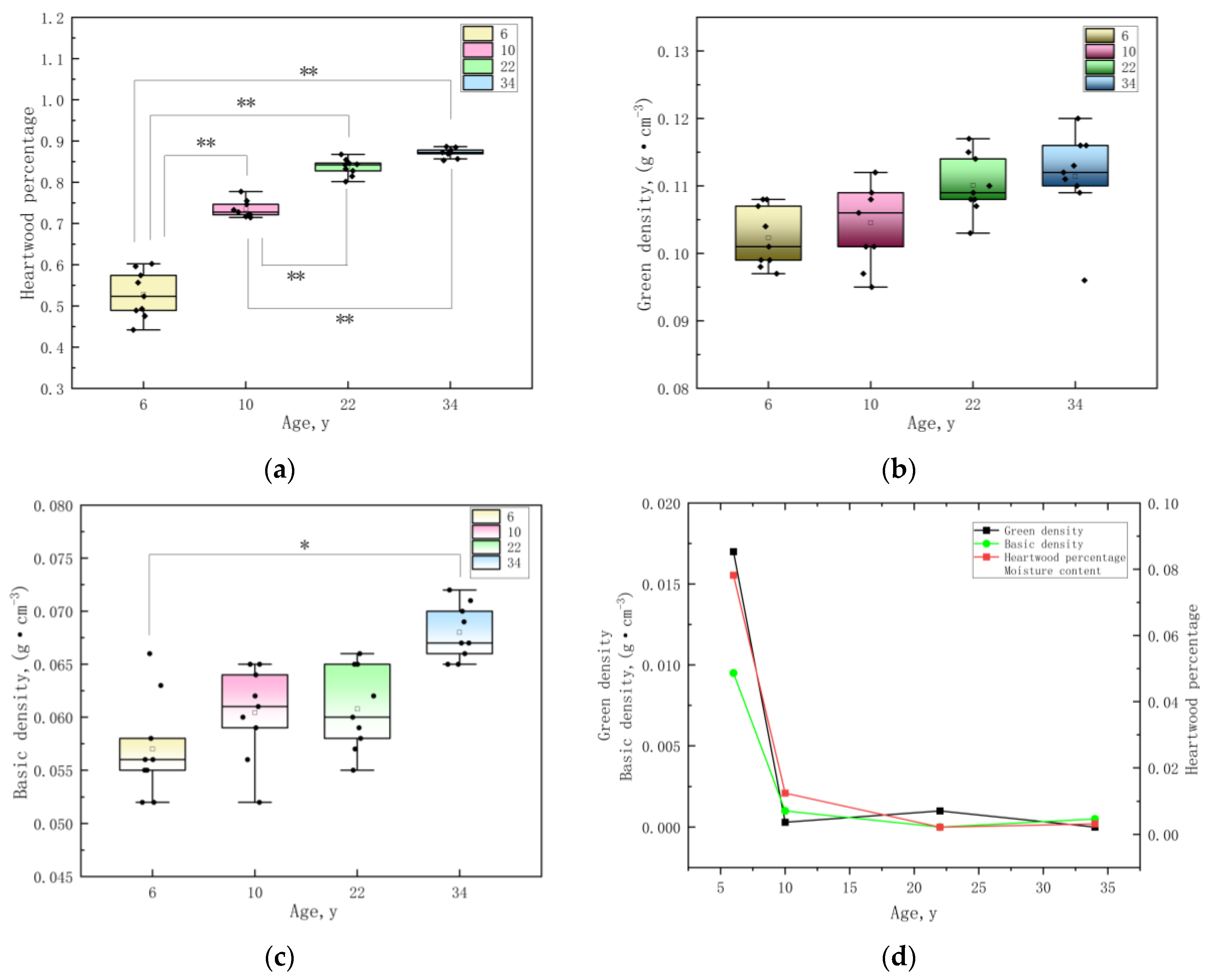
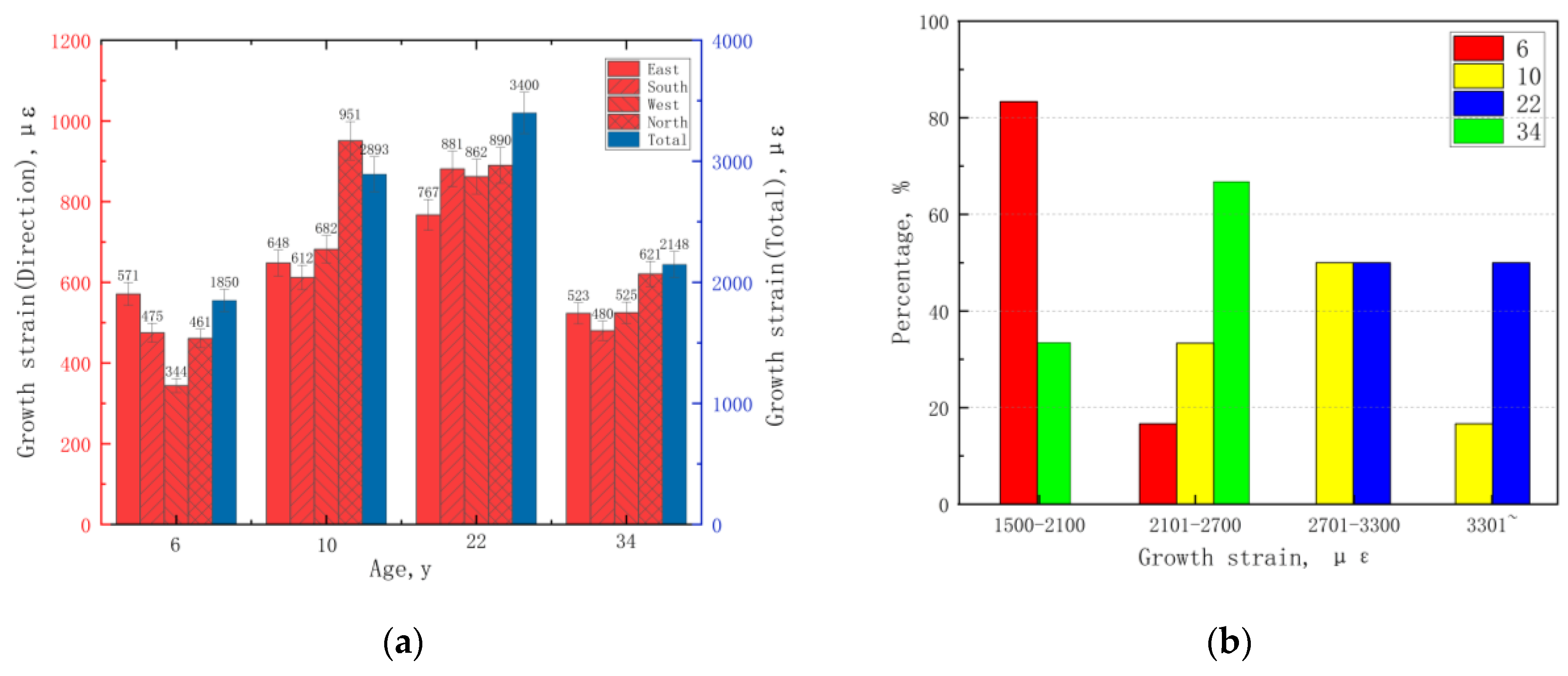
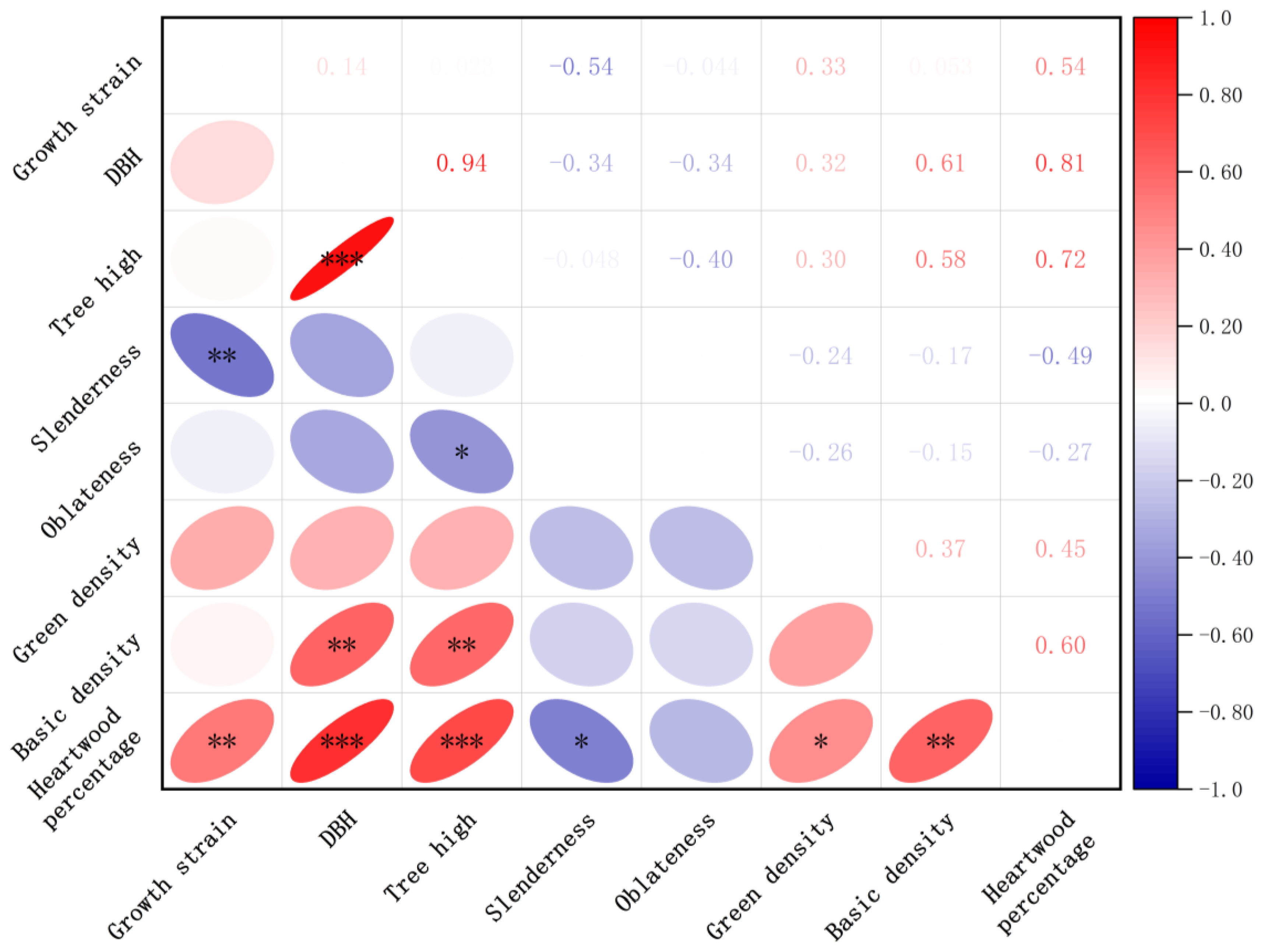

| Age, y | DBH, cm | Tree Height, m | Oblateness | Slenderness |
|---|---|---|---|---|
| 6 | 18.89 ± 2.38 | 18.23 ± 0.88 | 0.03 ± 0.01 | 0.98 ± 0.13 |
| 10 | 28.83 ± 0.76 | 23.26 ± 1.64 | 0.03 ± 0.01 | 0.78 ± 0.05 |
| 22 | 29.39 ± 2.88 | 25.50 ± 2.46 | 0.02 ± 0.01 | 0.81 ± 0.03 |
| 34 | 40.19 ± 1.57 | 36.54 ± 2.57 | 0.02 ± 0.00 | 0.89 ± 0.05 |
| Device | Model | Manufacturers | Country |
|---|---|---|---|
| Strain meter | YJW-8 | Beijing Tairui Venus Instrument Co., Ltd. | Beijing, China |
| Strain gage | BE120-10AA-P150 | AVIC Electric Measuring Instrument Co., Ltd. manufactured | Shanxi, China |
| Brulai altimeter | DGQ-1 | Harbin Optical Instrument Co., Ltd. | Harbin, China |
| Electronic balance | YH-A3003 | Yingheng Electric Co., Ltd. | Ruian, China |
| Vernier caliper | SF2000 | Guilin Guanglu Digital Measurement and Control Co., Ltd. | Guilin, China |
| Oven | ED260 | Binder GmbH | Tutlingen, Germany |
| X-ray diffractometer | A24A10 | BRUKER AXS GMBH | Karlsruhe, Germany |
| Fourier transform infrared spectrometer | IRTracer-100 | Shimadzu Corporation | Shima, Japan |
| Sample Group | Sample Size | Test Method | Test Statistic | p |
|---|---|---|---|---|
| East | 36 | Kruskal–Wallis | 3.487 | 0.322 |
| South | 36 | Kruskal–Wallis | 5.460 | 0.141 |
| West | 36 | Kruskal–Wallis | 10.370 | 0.016 |
| North | 36 | Kruskal–Wallis | 11.587 | 0.009 |
| Total | 36 | Kruskal–Wallis | 16.913 | 0.001 |
| Sample Group | Multiple Comparisons, Age | Test Statistic | Standard Error | Standard Test Statistic | Significance | Adjusted Significance |
|---|---|---|---|---|---|---|
| Total | 6–34 | −3.500 | 4.082 | −0.857 | 0.391 | 1.000 |
| 6–10 | −10.660 | 4.082 | −2.613 | 0.009 | 0.054 | |
| 6–22 | −15.160 | 4.082 | −3.715 | 0.000 | 0.001 | |
| 34–10 | 7.167 | 4.082 | 1.755 | 0.079 | 0.475 | |
| 34–22 | 11.667 | 4.082 | 2.858 | 0.004 | 0.026 | |
| 10–22 | −4.500 | 4.082 | −1.102 | 0.270 | 1.000 |
| Age, y | Fiber Length, μm | Cavity Diameter Value, μm | Double Wall Thickness, μm | Wall and Cavity Ratio, % |
|---|---|---|---|---|
| 6 | 1172.883 ± 94.085 a (0.080) | 9.506 ± 1.360 a (0.143) | 12.193 ± 0.489 a (0.040) | 1.693 ± 0.250 a (0.147) |
| 10 | 1235.567 ± 21.488 b (0.017) | 8.985 ± 1.324 ab (0.147) | 14.433 ± 0.718 ab (0.050) | 1.886 ± 0.415 ab (0.220) |
| 22 | 1343.782 ± 63.516 bc (0.047) | 6.418 ± 0.712 b (0.111) | 15.467 ± 0.670 b (0.043) | 2.785 ± 0.376 b (0.135) |
| 34 | 1517.681 ± 55.495 c (0.037) | 6.478 ± 0.932 b (0.144) | 16.967 ± 0.586 c (0.035) | 2.937 ± 0.437 c (0.149) |
| Age, y | Growth Strain, με | Fiber Length Correlation Coefficient | Cavity Diameter Value Correlation Coefficient | Double Wall Thickness Correlation Coefficient | Correlation Coefficient of Wall–Cavity Ratio | ||||
|---|---|---|---|---|---|---|---|---|---|
| Age | Growth Strain | Age | Growth strain | Age | Growth Strain | Age | Growth Strain | ||
| 6 | 1850.17 | 0.893 ** | 0.121 | −0.719 ** | −0.402 | 0.885 ** | 0.374 | 0.785 ** | 0.352 |
| 10 | 2574.17 | ||||||||
| 22 | 3080.50 | ||||||||
| 34 | 2148.17 | ||||||||
| Age (I) | Growth Strain, με | Crystallinity, % | Age (J) | Average Difference in Crystallinity (I–J) | Significance | Correlation Between Crystallinity and Growth Strain | |
|---|---|---|---|---|---|---|---|
| sig. (Double Tail) | Pearson Correlation | ||||||
| 6 | 1850.17 | 36.37 | 10 | −1.29000 | 0.331 | 0.014 | 0.683 * |
| 22 | −3.05000 * | 0.040 | |||||
| 34 | 1.52000 | 0.257 | |||||
| 10 | 2574.17 | 37.66 | 6 | 1.29000 | 0.331 | ||
| 22 | −1.76000 | 0.195 | |||||
| 34 | 2.81000 | 0.054 | |||||
| 22 | 3080.50 | 39.42 | 6 | 3.05000 * | 0.040 | ||
| 10 | 1.76000 | 0.195 | |||||
| 34 | 4.57000 ** | 0.006 | |||||
| 34 | 2148.17 | 34.85 | 6 | −1.52000 | 0.257 | ||
| 10 | −2.81000 | 0.054 | |||||
| 22 | −4.57000 ** | 0.006 | |||||
| Age, y | Growth Strain, με | Characteristic Peak Height Ratio | The Relative Content of Lignin and Growth Strain Correlation | |||
|---|---|---|---|---|---|---|
| I1510/I1377 | I1510/I1745 | I1510/I1425 | sig. (Double Tail) | Pearson Correlation | ||
| 4 | 1850.17 | 0.971 ± 0.066 a (0.068) | 0.984 ± 0.040 a (0.041) | 0.981 ± 0.043 a (0.043) | 0.044 | 0.588 * |
| 10 | 2574.17 | 0.985 ± 0.028 a (0.028) | 0.979 ± 0.022 a (0.022) | 0.996 ± 0.041 a (0.041) | ||
| 22 | 3080.50 | 0.987 ± 0.015 a (0.015) | 1.011 ± 0.025 a (0.026) | 0.986 ± 0.013 a (0.013) | ||
| 34 | 2148.17 | 0.981 ± 0.015 a (0.015) | 0.981 ± 0.026 a (0.026) | 0.991 ± 0.025 a (0.025) | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Wang, J.; Pan, Y.; Zeng, H.; Fu, Y.; Wei, P. Exploring the Relationship Between Growth Strain and Growth Traits in Eucalyptus cloeziana at Different Age Stages. Sustainability 2025, 17, 2229. https://doi.org/10.3390/su17052229
Huang Y, Wang J, Pan Y, Zeng H, Fu Y, Wei P. Exploring the Relationship Between Growth Strain and Growth Traits in Eucalyptus cloeziana at Different Age Stages. Sustainability. 2025; 17(5):2229. https://doi.org/10.3390/su17052229
Chicago/Turabian StyleHuang, Ying, Jianzhong Wang, Yuan Pan, Haibo Zeng, Yunlin Fu, and Penglian Wei. 2025. "Exploring the Relationship Between Growth Strain and Growth Traits in Eucalyptus cloeziana at Different Age Stages" Sustainability 17, no. 5: 2229. https://doi.org/10.3390/su17052229
APA StyleHuang, Y., Wang, J., Pan, Y., Zeng, H., Fu, Y., & Wei, P. (2025). Exploring the Relationship Between Growth Strain and Growth Traits in Eucalyptus cloeziana at Different Age Stages. Sustainability, 17(5), 2229. https://doi.org/10.3390/su17052229





