Developing a Novel Robust Model to Improve the Accuracy of River Ecosystem Health Assessment in the Qinghai–Tibet Plateau
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Sampling Sites
2.2. Data Collection and Processing
2.2.1. Indicator System
2.2.2. Sample Collection and Testing
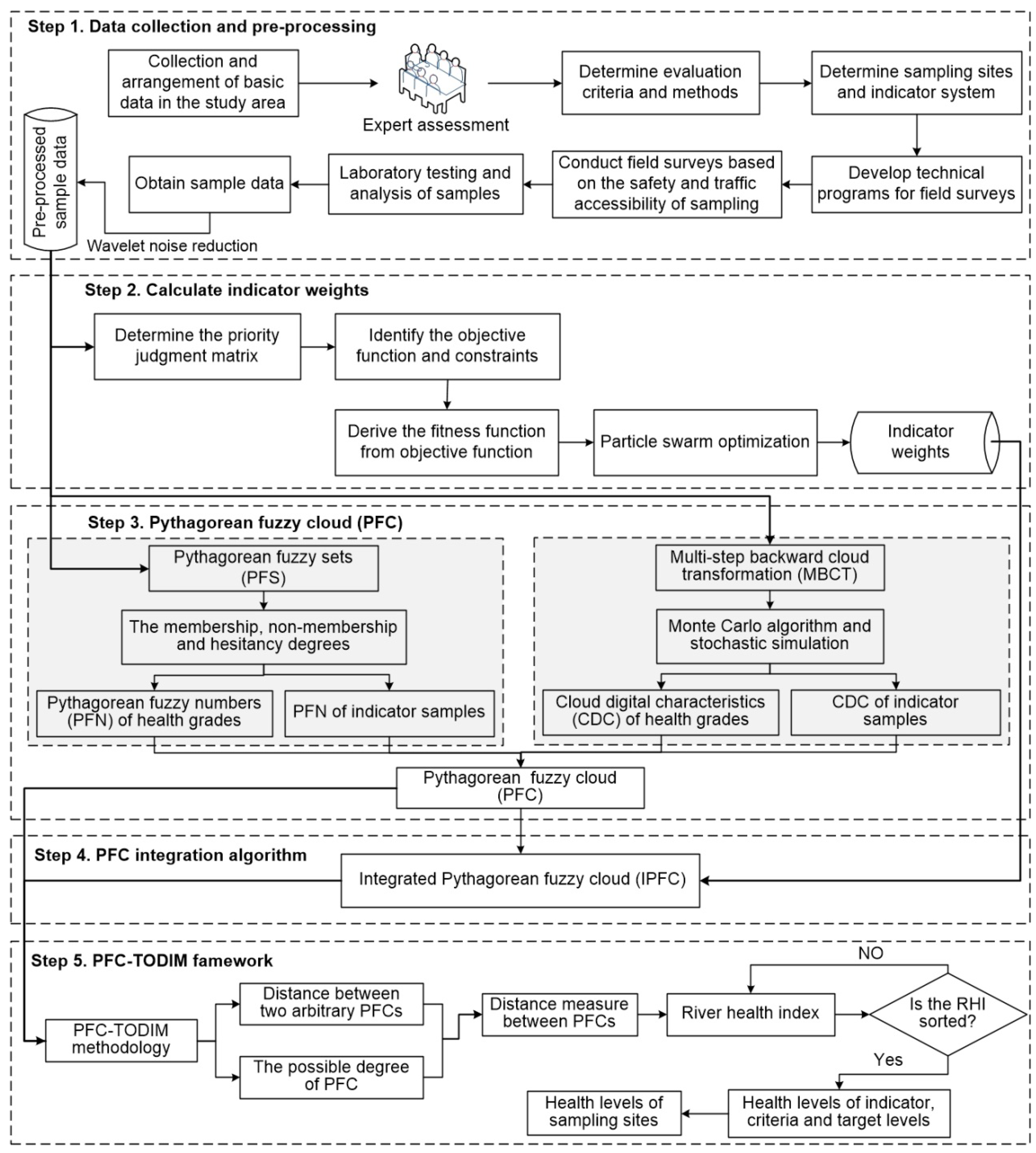
2.3. Hybrid Decision-Making Model
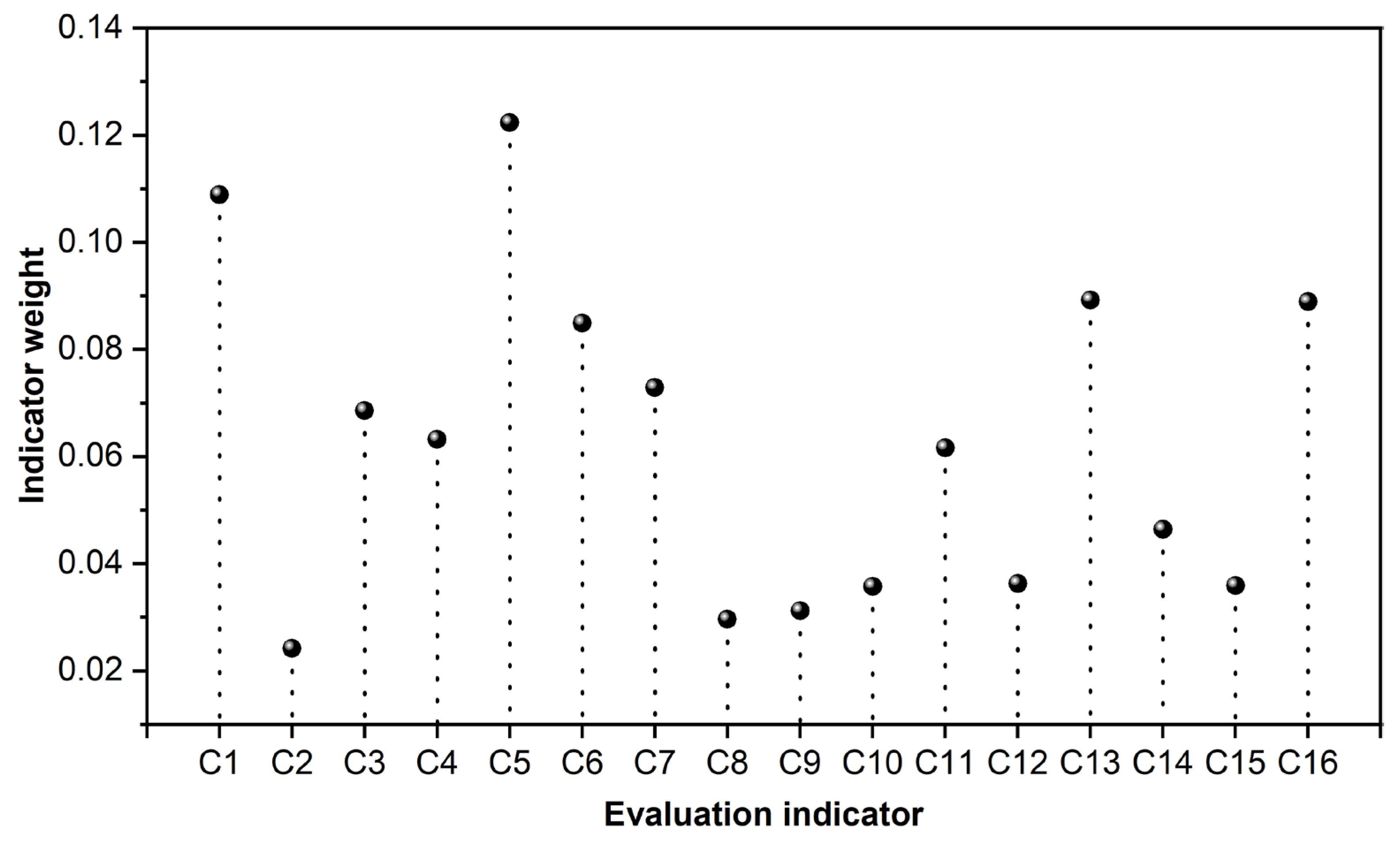
2.3.1. Indicator Weights
2.3.2. Pythagorean Fuzzy Cloud
2.3.3. PFC-TODIM Framework
3. Results
3.1. Health Conditions Indicator Level
3.1.1. PFC of Evaluation Indicators
3.1.2. Health Conditions of Evaluation Indicators
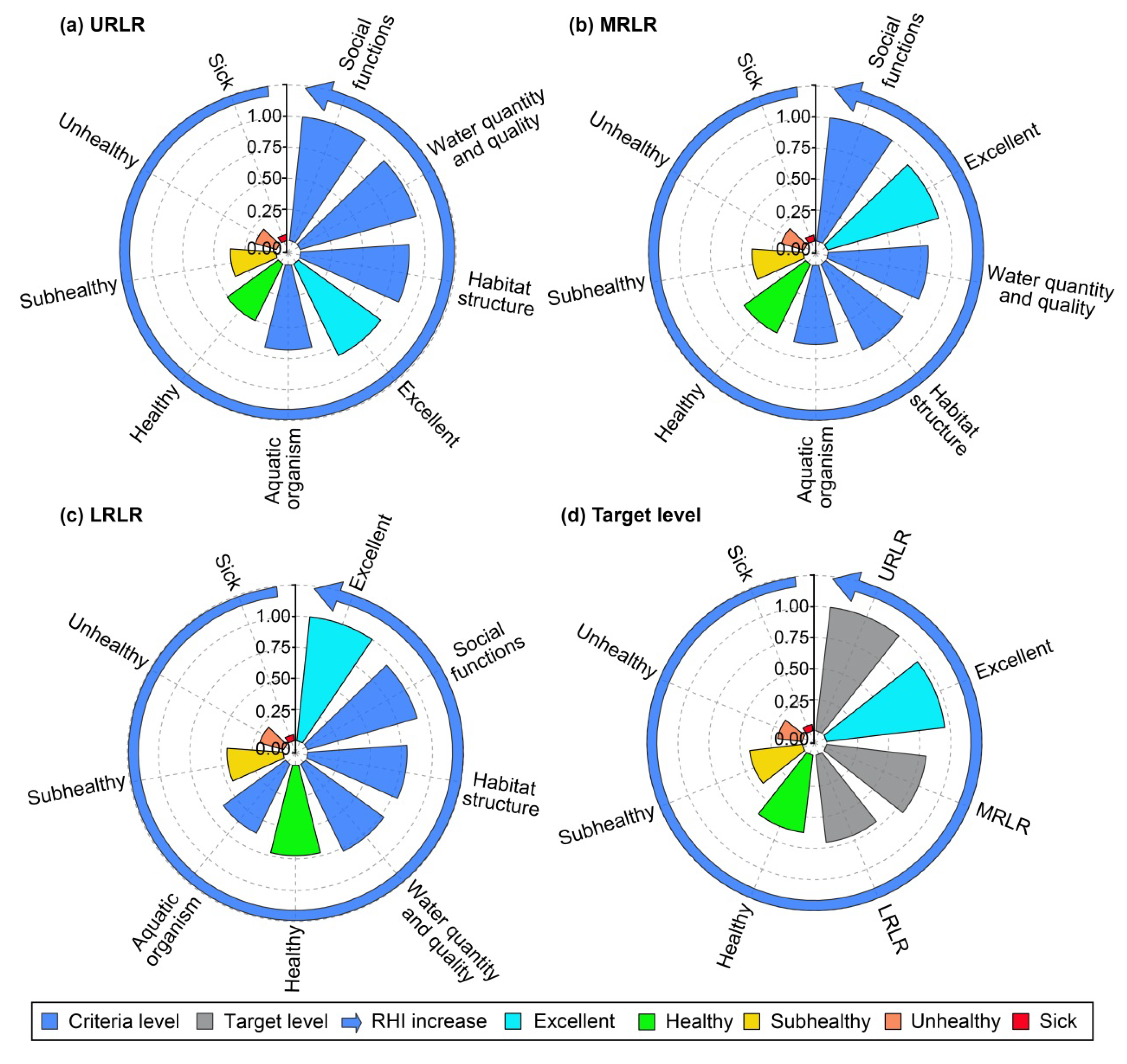
3.2. Health Conditions of Criteria and Target Levels
3.2.1. IPFC of Criteria and Target Levels
3.2.2. Health Status of Criteria and Target Levels
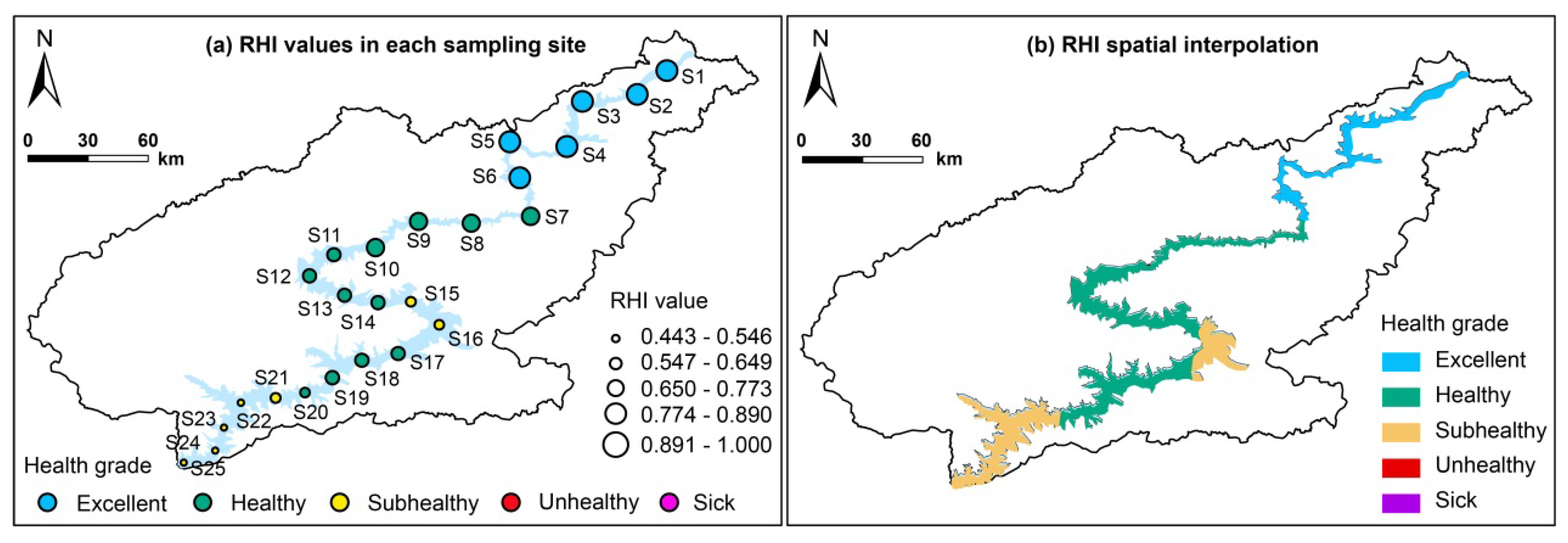
3.3. Health Conditions of Sampling Sites
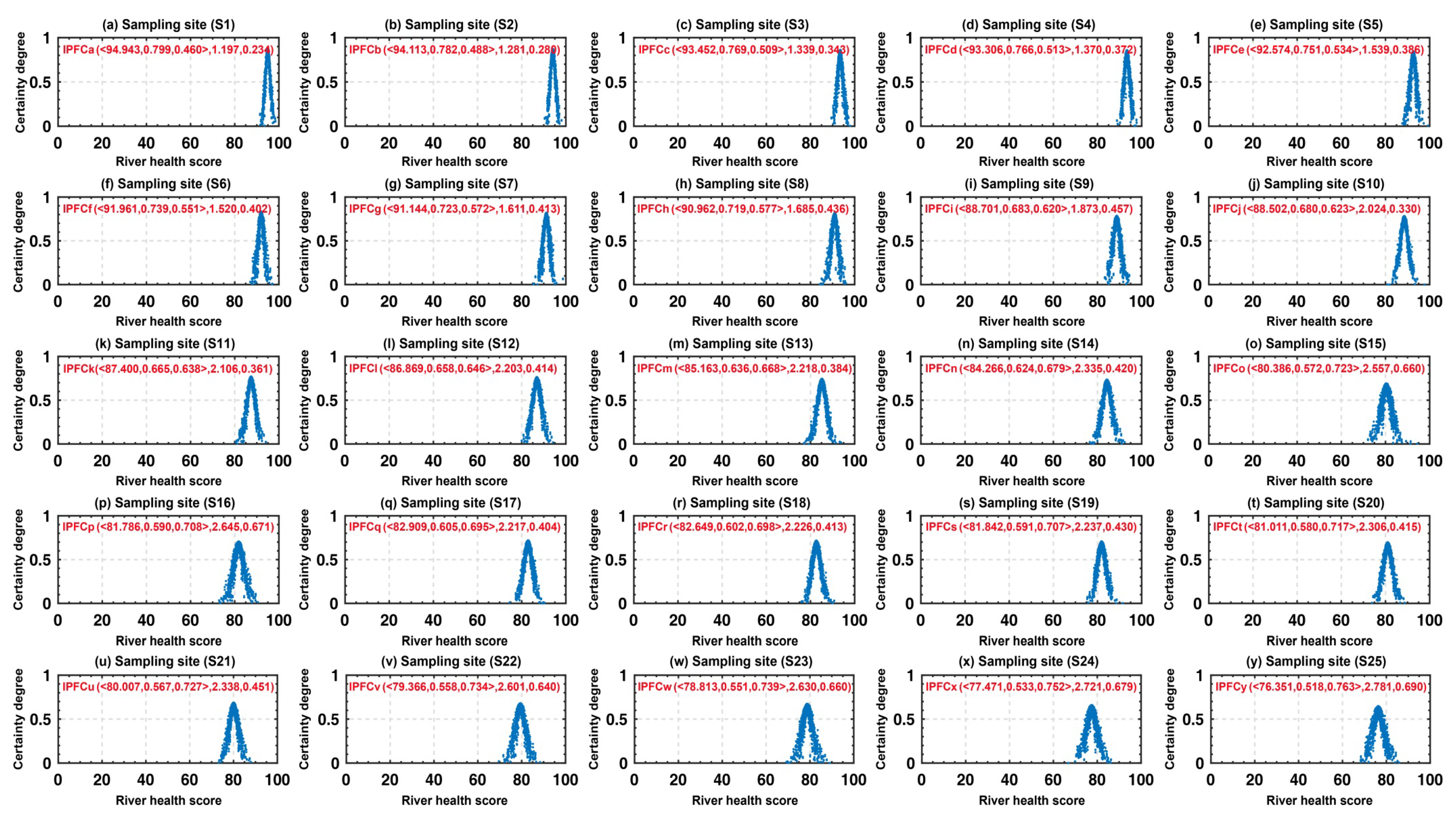
3.3.1. IPFC of Sampling Sites
3.3.2. Health Status of Sampling Sites
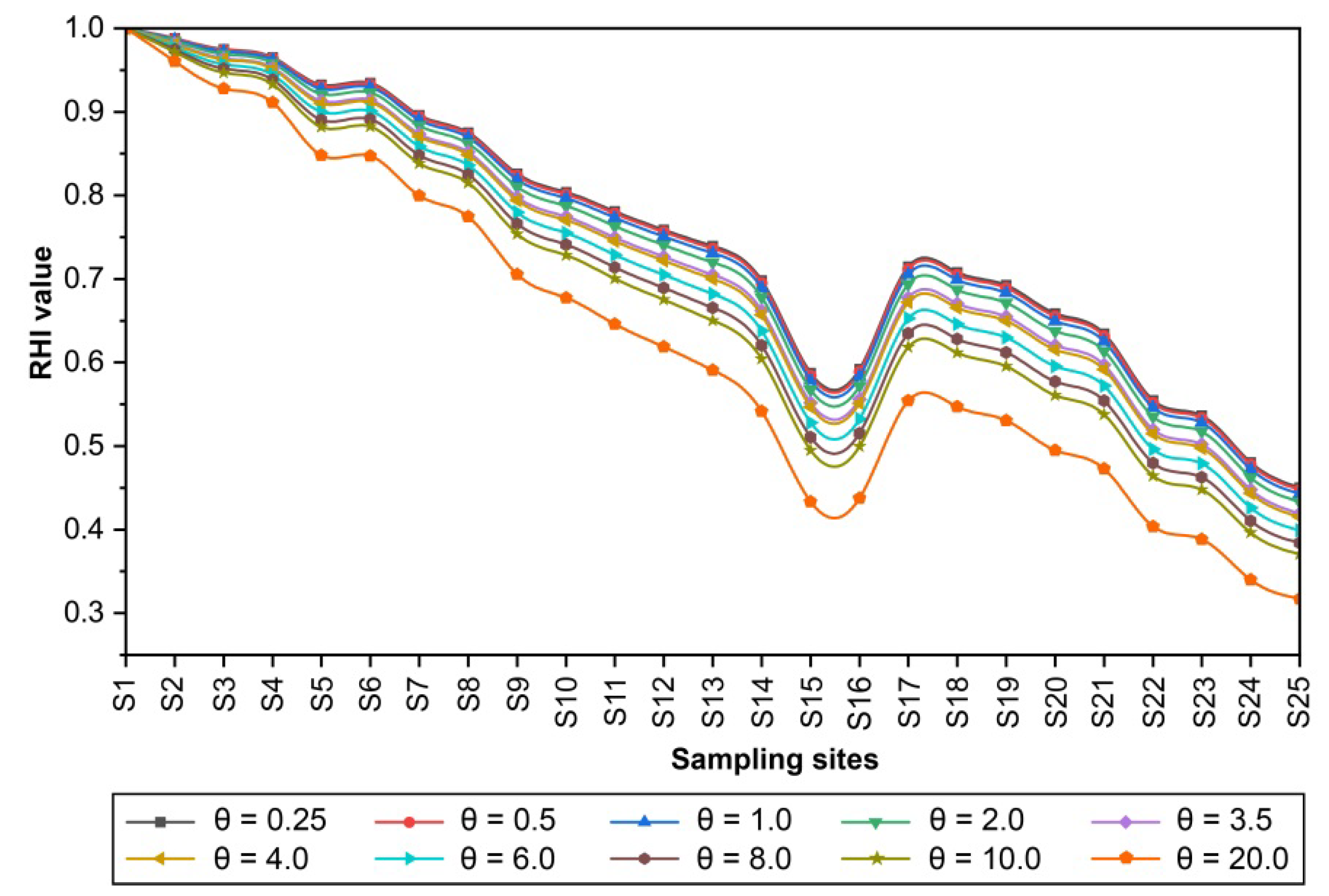
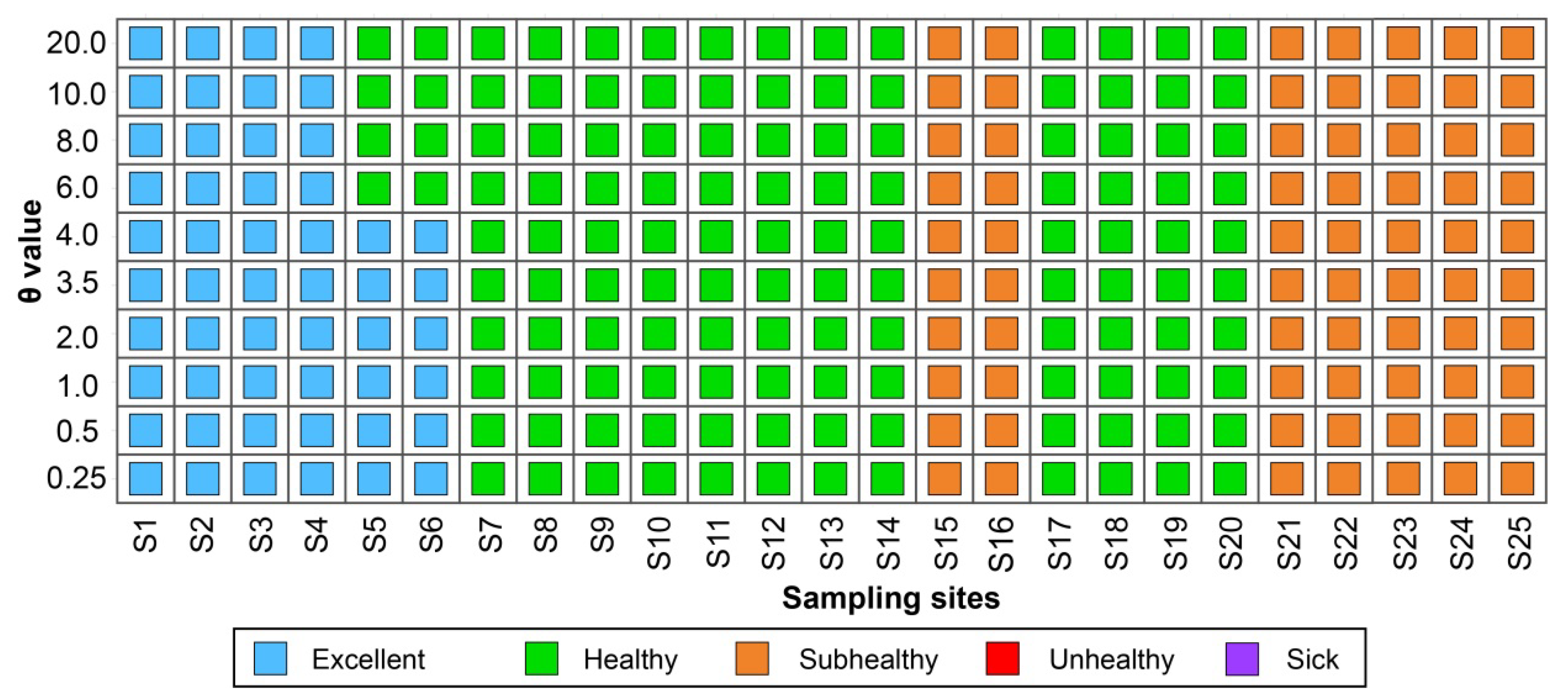
3.4. Comparison of Different Parameters and Methods
3.4.1. Comparison of Different Parameters
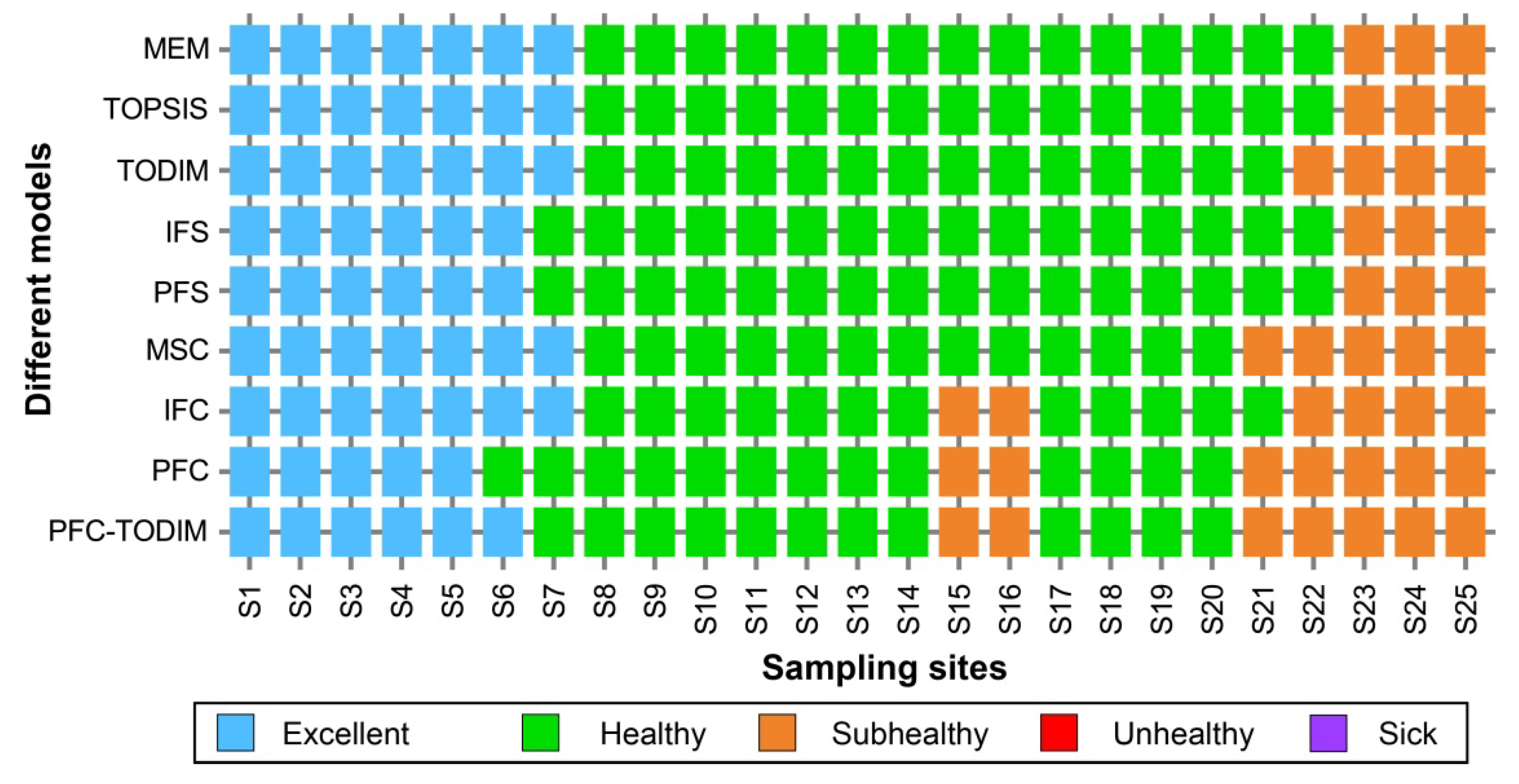
3.4.2. Comparison of Different Methods
4. Discussion
4.1. Driving Factors for River Ecosystem Health
4.2. Robustness of the PFC-TODIM Model
4.3. Model Advantage
4.4. Adaptive Management Measures
- (1)
- Improvement of river connectivity
- (2)
- Fine management of riparian
- (3)
- Conservation of natural wetlands
- (4)
- Reduction in water environment pollution
4.5. Limitations and Future Research
5. Conclusions
- (1)
- The URLR were relatively less disturbed by human activities, and the health status of evaluation indicators was better than the MRLR and LRLR. Affected by human activities, obvious spatial differences were noted in the health status of the URLR, MRLR and LRLR. During the study period, the health compliance rates in the URLR, MRLR, and LRLR were 100%, 81.25%, and 62.5%, respectively;
- (2)
- The RHI and health status of each monitoring site showed a decreasing tendency from the URLR to the LRLR. During the study period, there were no unhealthy and sick sampling sites, and the number of sampling sites in the subhealthy, healthy, and excellent states accounted for 28%, 48%, and 24% of the total, respectively;
- (3)
- Simulation results demonstrated that the PFC-TODIM model did not need to establish reference points for calculating the absolute prospect value of alternatives. It employed pairwise comparisons to compute relative dominance under different attribute states, thereby reducing the complexity and improving decision-making efficiency;
- (4)
- The bounded rationality of decision-makers will affect the REHA results. When evaluating a river with poor health and weak self-repair ability, a smaller θ value (0 < θ ≤ 1) can be chosen to reflect the decision-maker’s risk aversion. Given the enhanced capacity for self-repair and external risk resistance, a larger θ value (θ > 1) may be more appropriate, taking into account the decision-maker’s risk appetite psychology;
- (5)
- The PFC-TODIM model optimizes the PFC model by absorbing the bounded rationality of decision-makers. This model can effectively consider multiple uncertainties (input uncertainty, environmental stochasticity, and a decision-maker’s bounded rationality), thereby improving the REHA accuracy and robustness. It also enriched the REHA methodologies and provided a foundation for managing river ecosystems in the QTP.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Karr, J.R. Defining and Measuring River Health. Freshw. Biol. 1999, 41, 221–234. [Google Scholar] [CrossRef]
- Norris, R.H.; Thoms, M.C. What Is River Health? Freshw. Biol. 1999, 41, 197–209. [Google Scholar] [CrossRef]
- Norris, R.H.; Hawkins, C.P. Monitoring River Health. Hydrobiologia 2000, 435, 5–17. [Google Scholar] [CrossRef]
- Fairweather, P.G. State of Environment Indicators of ‘River Health’: Exploring the Metaphor. Freshw. Biol. 1999, 41, 211–220. [Google Scholar] [CrossRef]
- Singh, P.K.; Saxena, S. Towards Developing a River Health Index. Ecol. Indic. 2018, 85, 999–1011. [Google Scholar] [CrossRef]
- Pinto, U.; Maheshwari, B.L. River Health Assessment in Peri-Urban Landscapes: An Application of Multivariate Analysis to Identify the Key Variables. Water Res. 2011, 45, 3915–3924. [Google Scholar] [CrossRef]
- An, K.-G.; Park, S.S.; Shin, J.-Y. An Evaluation of a River Health Using the Index of Biological Integrity along with Relations to Chemical and Habitat Conditions. Environ. Int. 2002, 28, 411–420. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Q.; Yang, T.; Zhang, L.; Li, X.; Chen, J. River Health Assessment: Proposing a Comprehensive Model Based on Physical Habitat, Chemical Condition and Biotic Structure. Ecol. Indic. 2019, 103, 446–460. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Y.; Wang, X.; Zhu, L.; Li, H.; Liu, Y.; Tang, N.; Xu, Y.; Hu, Q. Investigating River Health and Potential Risks Using a Novel Hybrid Decision-Making Framework with Multi-Source Data Fusion in the Qinghai-Tibet Plateau. Environ. Impact Assess. Rev. 2022, 96, 106849. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Y.; Wang, X.; Li, H.; Zheng, F.; Liao, Y.; Tang, N.; Chen, G.; Yang, C. Assessment of River Health Based on a Novel Multidimensional Similarity Cloud Model in the Lhasa River, Qinghai-Tibet Plateau. J. Hydrol. 2021, 603, 127100. [Google Scholar] [CrossRef]
- Zhao, Y.W.; Yang, Z.F. Integrative Fuzzy Hierarchical Model for River Health Assessment: A Case Study of Yong River in Ningbo City, China. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1729–1736. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, X.; Li, Y.; Liu, Y.; Xu, Y.; Li, J.; Ding, W.; Li, H.; Yang, H. River Ecosystem Health Assessment in the Qinghai-Tibet Plateau: A Novel Hybrid Method Based on Artificial Intelligence and Multi-Source Data Fusion. Expert Syst. Appl. 2024, 251, 124078. [Google Scholar] [CrossRef]
- Wang, X.; Liu, X.; Wang, L.; Yang, J.; Wan, X.; Liang, T. A Holistic Assessment of Spatiotemporal Variation, Driving Factors, and Risks Influencing River Water Quality in the Northeastern Qinghai-Tibet Plateau. Sci. Total Environ. 2022, 851, 157942. [Google Scholar] [CrossRef] [PubMed]
- Cai, N.; Wang, X.; Wang, W.; Wang, L.; Tian, S.; Zhu, H.; Zhang, X. Accumulation, Ecological Health Risks, and Source Identification of Potentially Toxic Elements in River Sediments of the Qinghai-Tibet Plateau, China. Process Saf. Environ. Prot. 2024, 182, 703–718. [Google Scholar] [CrossRef]
- Jiang, W.; Lü, Y.; Liu, Y.; Gao, W. Ecosystem Service Value of the Qinghai-Tibet Plateau Significantly Increased during 25 Years. Ecosyst. Serv. 2020, 44, 101146. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, X.; Zhang, Z. Spatiotemporal dynamics and anthropogenic drivers of geological hazard prevention efficiency in China. Cities. 2023, 143, 104607. [Google Scholar] [CrossRef]
- Chen, J.; Mei, Y.; Xiao, W. Establishment of the Ecological Relationships and Properties of the Lhasa River Basin Water Resources System, China. Sustain. Cities Soc. 2019, 47, 101477. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, Y.; Yao, Z.; Gong, T.; Wang, H.; Chu, D.; Liu, L.; Zhang, F. The Trend on Runoff Variations in the Lhasa River Basin. J. Geogr. Sci. 2008, 18, 95–106. [Google Scholar] [CrossRef]
- Su, Y.; Li, W.; Liu, L.; Hu, W.; Li, J.; Sun, X.; Li, Y. Health Assessment of Small-to-Medium Sized Rivers: Comparison between Comprehensive Indicator Method and Biological Monitoring Method. Ecol. Indic. 2021, 126, 107686. [Google Scholar] [CrossRef]
- SL/T 793-2020; Technical Guideline for River Health Assessment in China. Ministry of Water Resources of the People’s Republic of China: Beijing, China, 2020.
- Zhang, Z.; Liu, Y.; Li, Y.; Wang, X.; Li, H.; Yang, H.; Ding, W.; Liao, Y.; Tang, N.; He, F. Lake Ecosystem Health Assessment Using a Novel Hybrid Decision-Making Framework in the Nam Co, Qinghai-Tibet Plateau. Sci. Total Environ. 2022, 808, 152087. [Google Scholar] [CrossRef]
- Yi, Y.; Lin, C.; Wang, W.; Song, J. Habitat and Seasonal Variations in Bacterial Community Structure and Diversity in Sediments of a Shallow Lake. Ecol. Indic. 2021, 120, 106959. [Google Scholar] [CrossRef]
- Lin, Z.; Xu, Y.; Wang, Q.; Luo, S.; Lu, M.; Yu, Z. River System Changes under Urban Expansion: Insights from the Suzhou-Wuxi-Changzhou Metropolitan Area, China. J. Hydrol. Reg. Stud. 2024, 53, 101766. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Z.; Huang, X. A Novel Coupling Cloud Decision-Making Framework for Investigating Population-Economy-Water Consumption Nexus in the Inner Mongolia Reaches of the Yellow River, China. Environ. Impact Assess. Rev. 2023, 98, 106923. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean Membership Grades in Multicriteria Decision Making. IEEE Trans. Fuzzy Syst. 2014, 22, 958–965. [Google Scholar] [CrossRef]
- Yao, J.; Wang, G.; Wang, L.; Zhang, X.; Wang, P. Assessing the Spatiotemporal Variability of Lake Water Quality Using a Novel Multidimensional Shape—Position Similarity Cloud Model. J. Hydrol. 2021, 599, 126379. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Y.; Wang, X.; Liu, Y.; Tang, W.; Ding, W.; Han, Q.; Shang, G.; Wang, Z.; Chen, K.; et al. Investigating River Health across Mountain to Urban Transitions Using Pythagorean Fuzzy Cloud Technique under Uncertain Environment. J. Hydrol. 2023, 620, 129426. [Google Scholar] [CrossRef]
- Ren, P.; Xu, Z.; Gou, X. Pythagorean Fuzzy TODIM Approach to Multi-Criteria Decision Making. Appl. Soft Comput. 2016, 42, 246–259. [Google Scholar] [CrossRef]
- Llamazares, B. An Analysis of the Generalized TODIM Method. Eur. J. Oper. Res. 2018, 269, 1041–1049. [Google Scholar] [CrossRef]
- Deng, X.; Xu, Y.; Han, L.; Yu, Z.; Yang, M.; Pan, G. Assessment of River Health Based on an Improved Entropy-Based Fuzzy Matter-Element Model in the Taihu Plain, China. Ecol. Indic. 2015, 57, 85–95. [Google Scholar] [CrossRef]
- Xu, W.; Dong, Z.; Ren, L.; Ren, J.; Guan, X.; Zhong, D. Using an Improved Interval Technique for Order Preference by Similarity to Ideal Solution to Assess River Ecosystem Health. J. Hydroinformatics 2019, 21, 624–637. [Google Scholar] [CrossRef]
- Ashofteh, P.-S.; Golfam, P.; Loáiciga, H.A. Evaluation of River Water Transfer Alternatives with the TODIM Multi-Criteria Decision Making Method. Water Resour. Manag. 2020, 34, 4847–4863. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic Fuzzy Sets. In Intuitionistic Fuzzy Sets: Theory and Applications; Atanassov, K.T., Ed.; Studies in Fuzziness and Soft Computing; Physica-Verlag HD: Heidelberg, Germany, 1999; pp. 1–137. ISBN 978-3-7908-1870-3. [Google Scholar]
- Mao, G.; Zhao, Y.; Zhang, F.; Liu, J.; Huang, X. Spatiotemporal Variability of Heavy Metals and Identification of Potential Source Tracers in the Surface Water of the Lhasa River Basin. Environ. Sci. Pollut. Res. 2019, 26, 7442–7452. [Google Scholar] [CrossRef]
- Tian, P.; Lu, H.; Feng, W.; Guan, Y.; Xue, Y. Large Decrease in Streamflow and Sediment Load of Qinghai–Tibetan Plateau Driven by Future Climate Change: A Case Study in Lhasa River Basin. Catena 2020, 187, 104340. [Google Scholar] [CrossRef]
- Liu, Y.; Su, W.; Zhu, Y.; Xiao, L.; Hu, T. Endocrine Disrupting Compounds in the Middle and Lower Reaches of the Lhasa River Basin: Occurrence, Distribution, and Risk Assessment. Sci. Total Environ. 2020, 727, 138694. [Google Scholar] [CrossRef]
- You, Y.; Li, Z.; Gao, P.; Hu, T. Impacts of Dams and Land-Use Changes on Hydromorphology of Braided Channels in the Lhasa River of the Qinghai-Tibet Plateau, China. Int. J. Sediment Res. 2022, 37, 214–228. [Google Scholar] [CrossRef]
- Du, B.; Ge, J.; Yang, R.; Han, X.; Chen, H.; Li, J.; Zeng, L. Altitude-Dependent Accumulation of Short Chain Chlorinated Paraffins in Fish from Alpine Lakes and Lhasa River on the Tibetan Plateau. Environ. Pollut. 2019, 250, 594–600. [Google Scholar] [CrossRef]
- Alali, F.; Tolga, A.C. Portfolio Allocation with the TODIM Method. Expert Syst. Appl. 2019, 124, 341–348. [Google Scholar] [CrossRef]
- Kumar, R.; Edalatpanah, S.A.; Jha, S.; Singh, R. A Pythagorean Fuzzy Approach to the Transportation Problem. Complex Intell. Syst. 2019, 5, 255–263. [Google Scholar] [CrossRef]
- Yang, T.; Zhang, Q.; Wan, X.; Li, X.; Wang, Y.; Wang, W. Comprehensive Ecological Risk Assessment for Semi-Arid Basin Based on Conceptual Model of Risk Response and Improved TOPSIS Model-a Case Study of Wei River Basin, China. Sci. Total Environ. 2020, 719, 137502. [Google Scholar] [CrossRef]
- Krohling, R.A.; Pacheco, A.G.C.; Siviero, A.L.T. IF-TODIM: An Intuitionistic Fuzzy TODIM to Multi-Criteria Decision Making. Knowl.-Based Syst. 2013, 53, 142–146. [Google Scholar] [CrossRef]
- Prata, J.C.; Padrão, J.; Khan, M.T.; Walker, T.R. Do’s and Don’ts of Microplastic Research: A Comprehensive Guide. Water Emerg. Contam. Nanoplastics 2024, 3, 8. [Google Scholar] [CrossRef]
- Ihsanullah, I.; Khan, M.T.; Hossain, M.F.; Bilal, M.; Ali Shah, I. Eco-Friendly Solutions to Emerging Contaminants: Unveiling the Potential of Bioremediation in Tackling Microplastic Pollution in Water. Adv. Sustain. Syst. 2024, 8, 2400172. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Li, Y.; Wang, X.; Zhang, J.; Zhang, Z. Developing a Novel Robust Model to Improve the Accuracy of River Ecosystem Health Assessment in the Qinghai–Tibet Plateau. Sustainability 2025, 17, 2041. https://doi.org/10.3390/su17052041
Xu Y, Li Y, Wang X, Zhang J, Zhang Z. Developing a Novel Robust Model to Improve the Accuracy of River Ecosystem Health Assessment in the Qinghai–Tibet Plateau. Sustainability. 2025; 17(5):2041. https://doi.org/10.3390/su17052041
Chicago/Turabian StyleXu, Yuan, Yun Li, Xiaogang Wang, Jianmin Zhang, and Zhengxian Zhang. 2025. "Developing a Novel Robust Model to Improve the Accuracy of River Ecosystem Health Assessment in the Qinghai–Tibet Plateau" Sustainability 17, no. 5: 2041. https://doi.org/10.3390/su17052041
APA StyleXu, Y., Li, Y., Wang, X., Zhang, J., & Zhang, Z. (2025). Developing a Novel Robust Model to Improve the Accuracy of River Ecosystem Health Assessment in the Qinghai–Tibet Plateau. Sustainability, 17(5), 2041. https://doi.org/10.3390/su17052041








