Vapor Pressure Deficit as an Indicator of Condensation in a Greenhouse with Natural Ventilation Using Numerical Simulation Techniques
Abstract
1. Introduction
2. Materials and Methods
2.1. Acquisition of Experimental Data
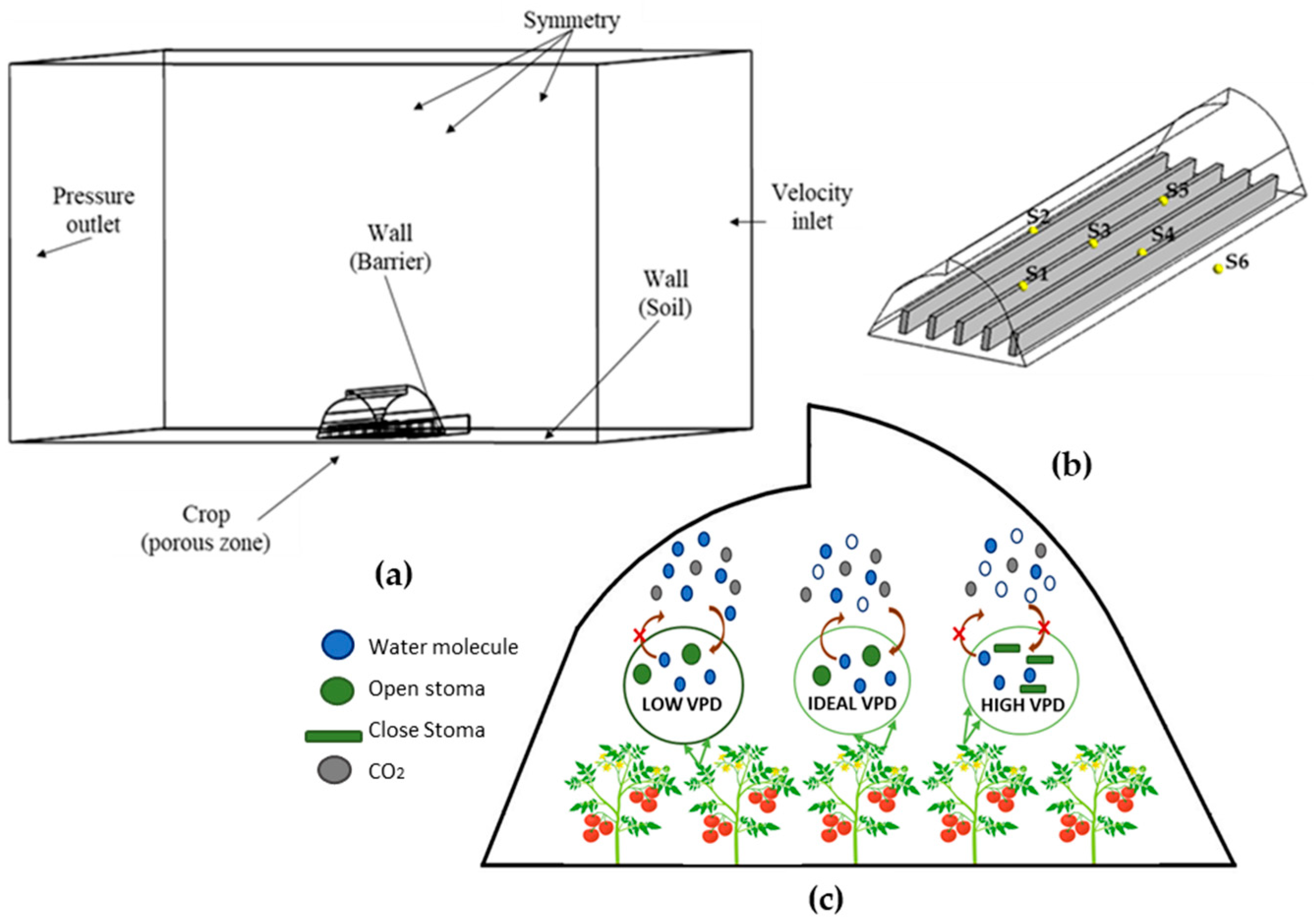
2.2. Mathematical Model
- The simulation was carried out in steady state
- A stable mass fraction was considered (ignoring crop transpiration)
- The crop was considered as a porous zone
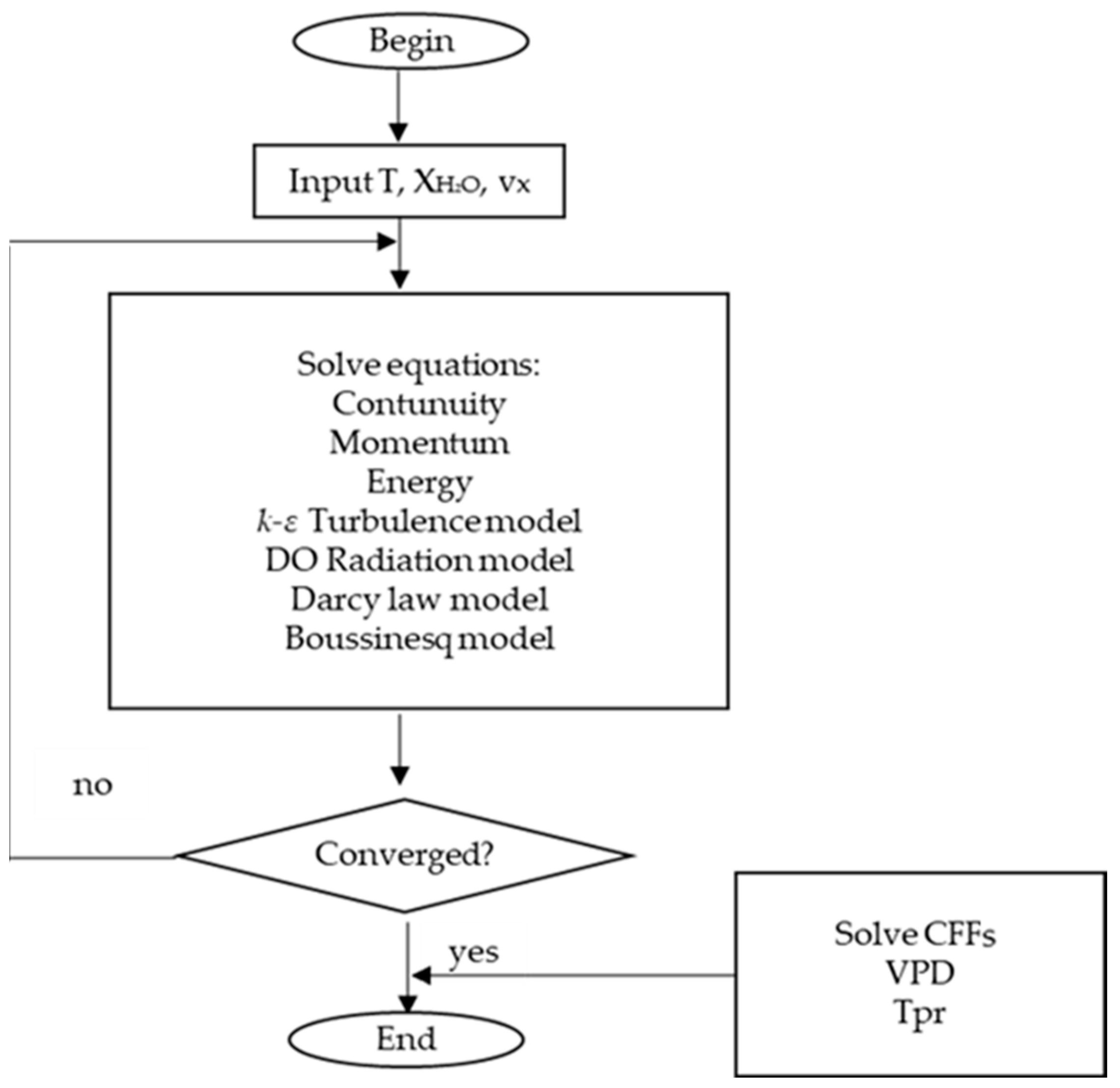
2.3. Governing Equations
2.4. Simulated Scenarios
3. Results and Discussion
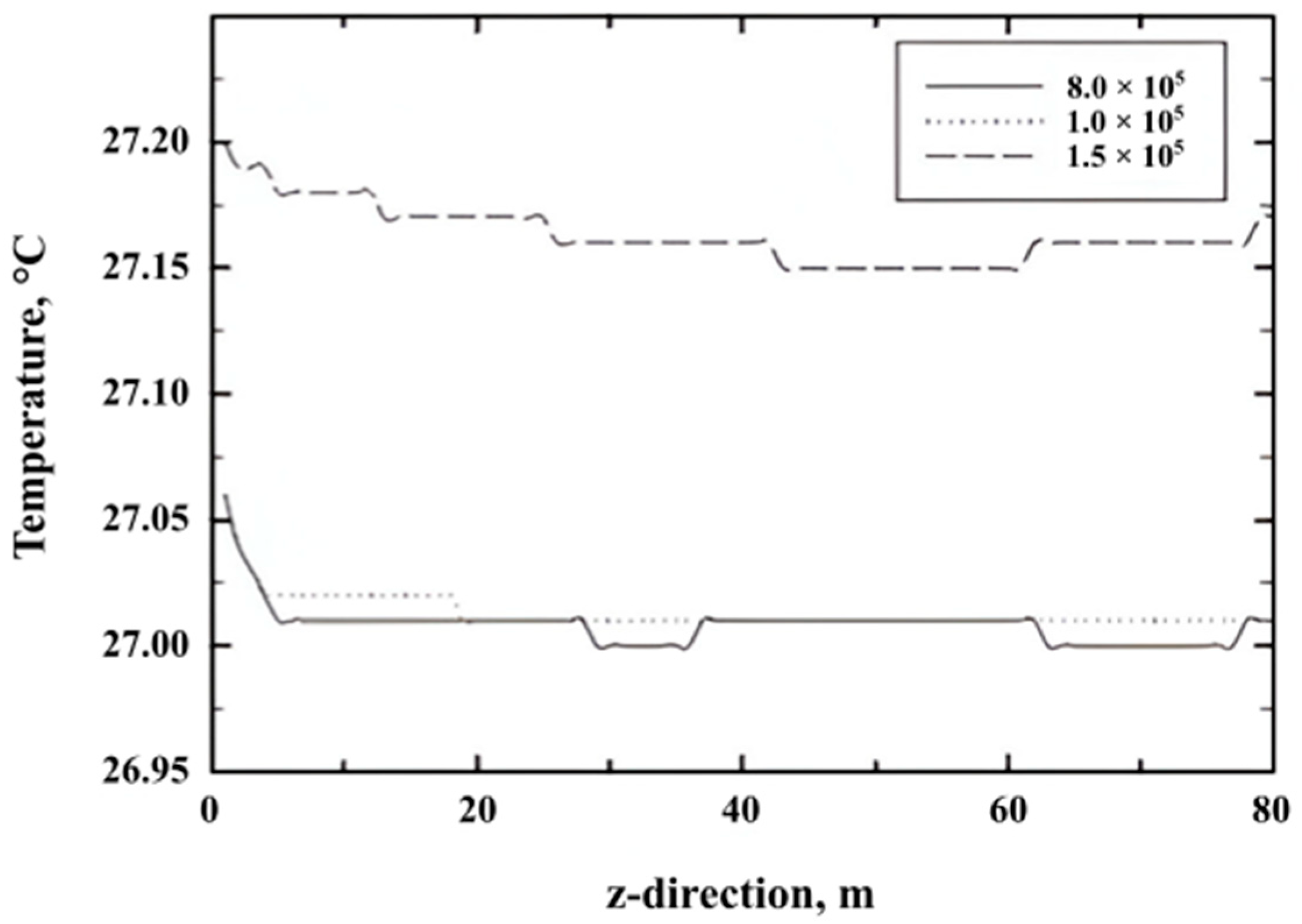
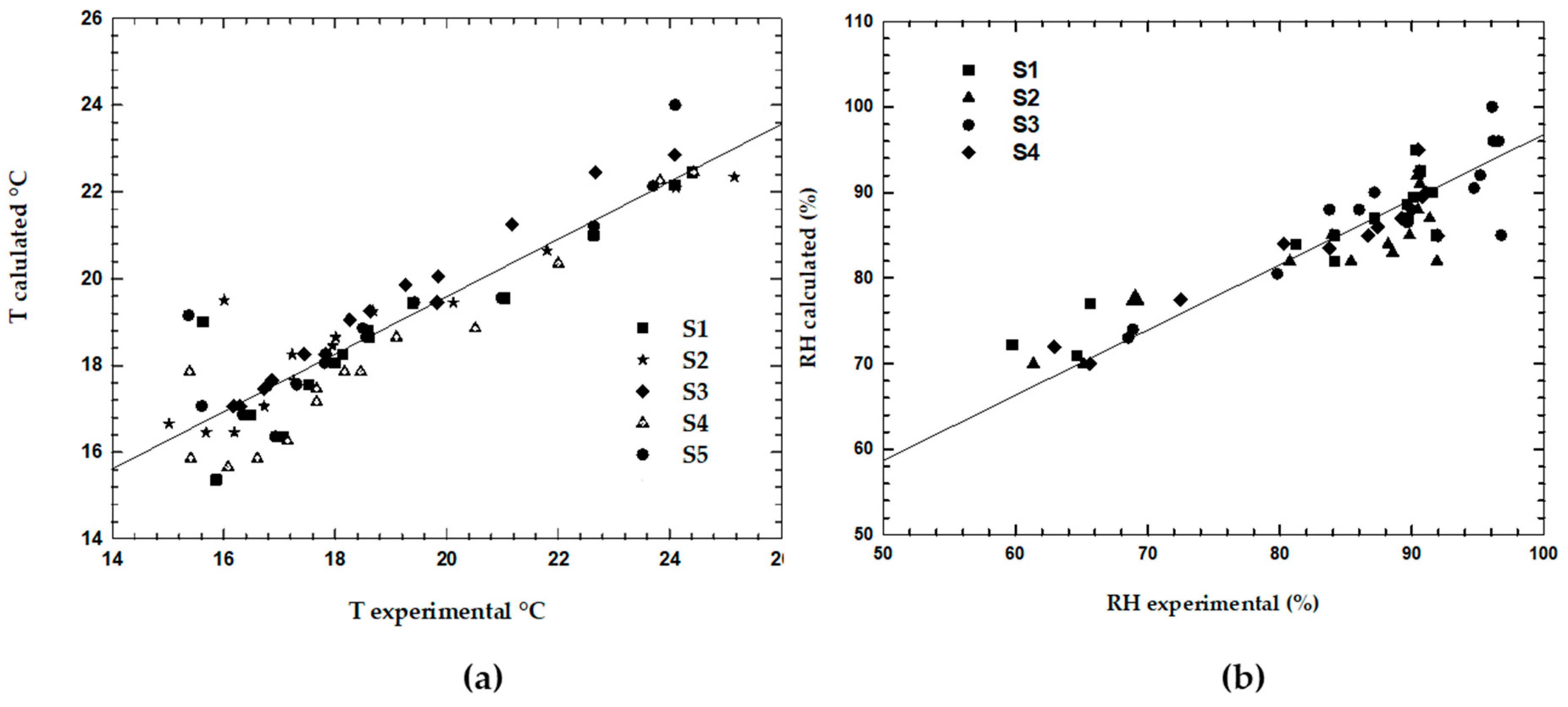
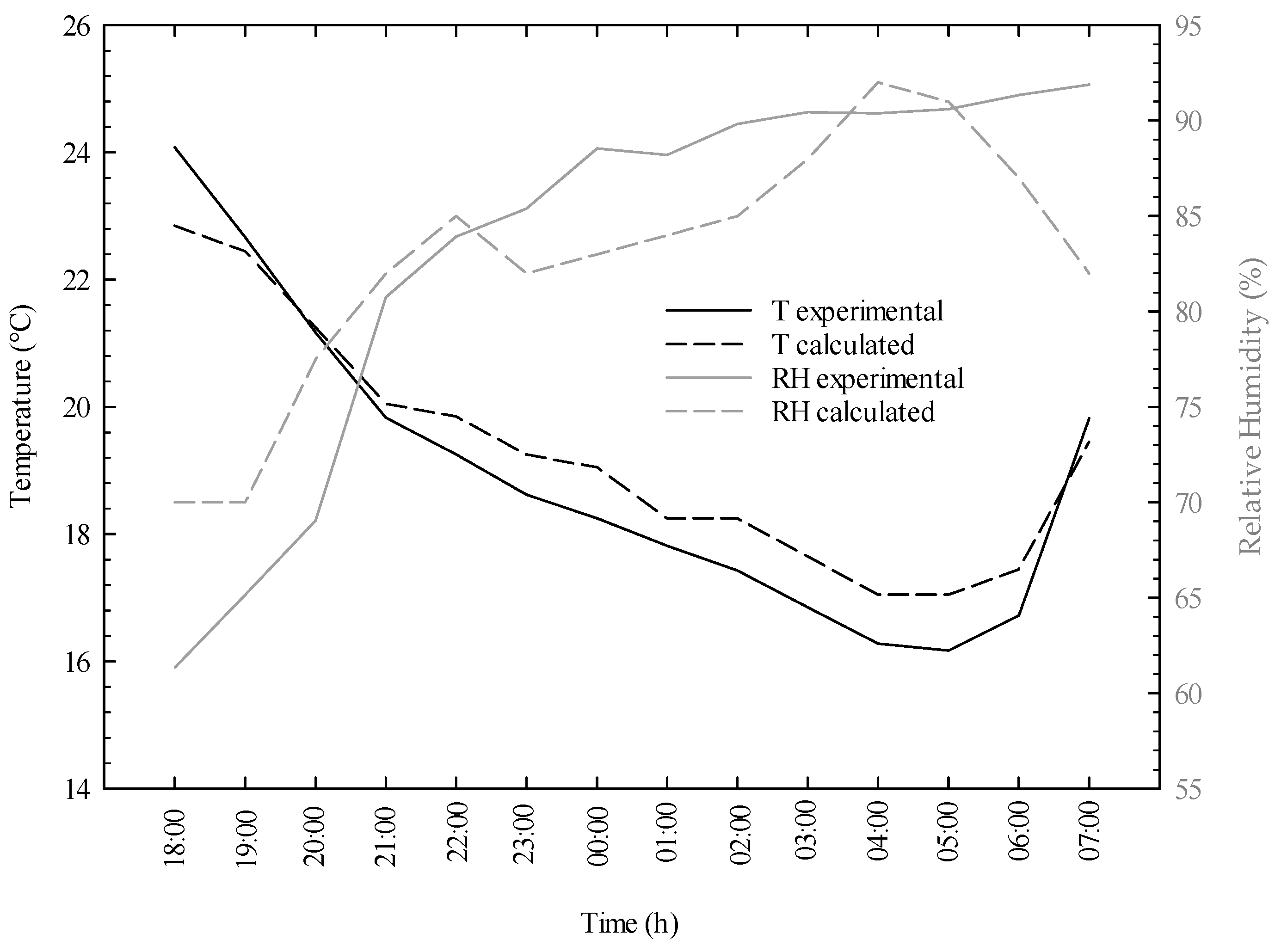
3.1. Model Validation
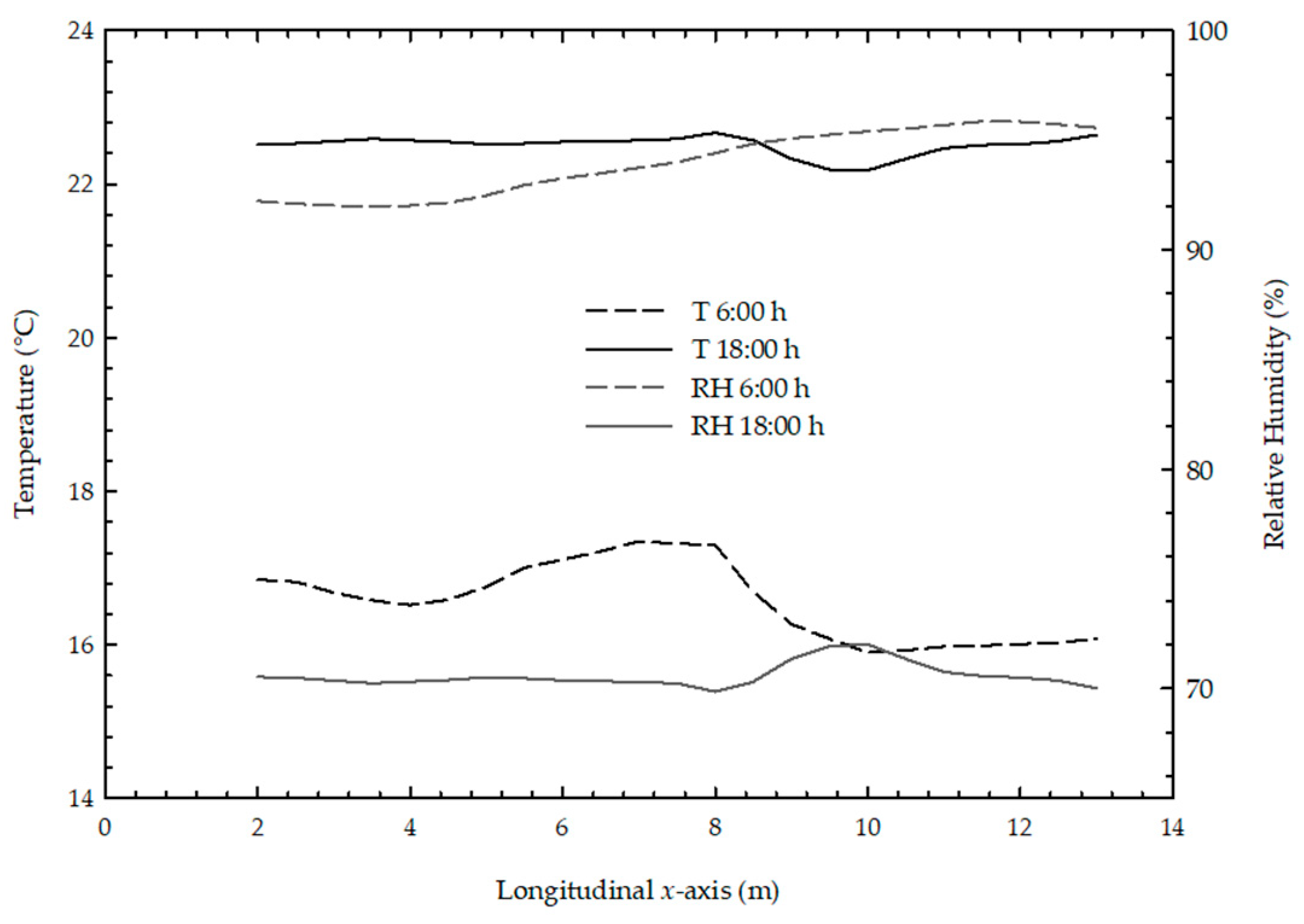
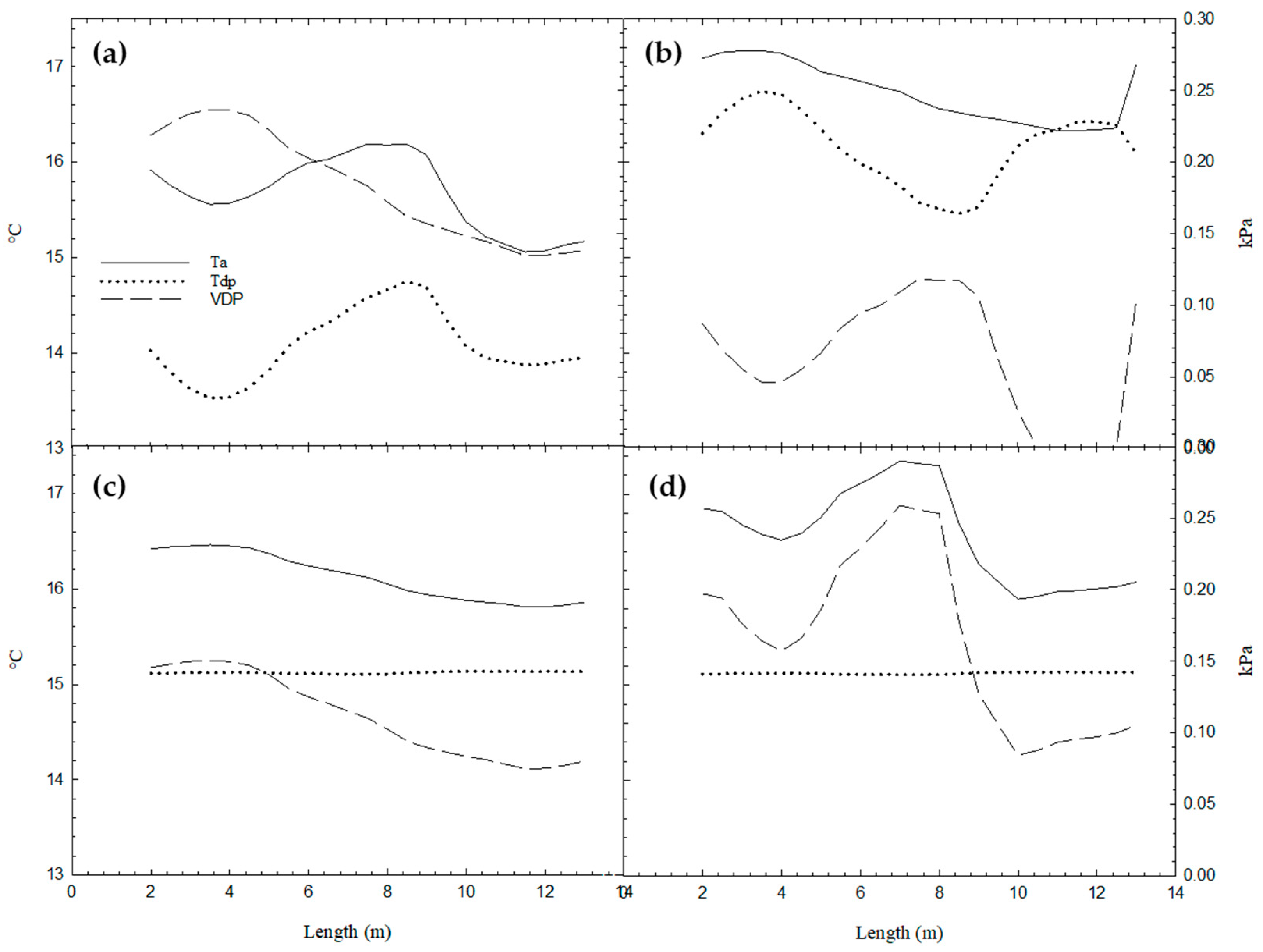
3.2. Simulation 6:00 and 18:00 h
3.3. Simulation Scenarios
4. Conclusions
- The time with the highest risk of condensation is 6:00 a.m., with humidity levels of up to 97%. At dusk, humidity levels are not high enough to generate conditions for this phenomenon since they are below 75%.
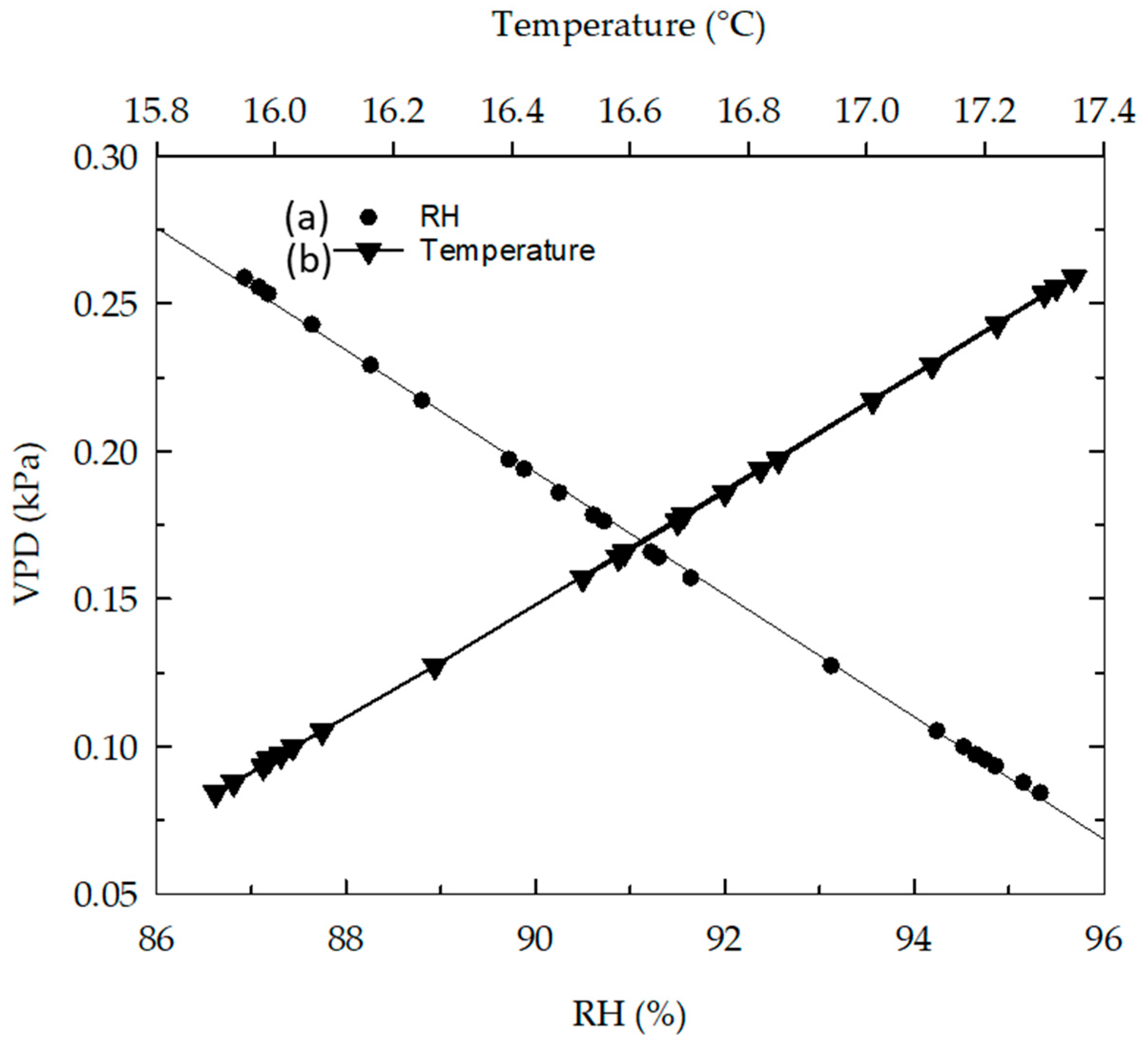
- The VPD can be used as an indicator of the presence of condensation inside the greenhouse. As its value approaches zero, the probability of condensation increases. The risk of condensation is seen from values less than 0.1 kPa.
- The dew point temperature can be considered as an alternative to determine the risk of condensation by analyzing the behavior of the difference between its values and those of the ambient temperature.
- Under the simulated conditions, fully opening the windows can prevent the VPD from reaching zero and, therefore, condensation. Timely opening of the windows can also help decrease the relative humidity and increase the difference between ambient temperature and Tdp.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Velázquez, J.F.; Saenz, E.M.; Camacho, J.I.M.; Rojano, A. Análisis numérico del clima interior en un invernadero de tres naves con ventilación mecánica. Agrociencia 2011, 45, 545–560. [Google Scholar]
- Fatnassi, H.; Boulard, T.; Benamara, H.; Roy, J.; Suay, R.; Poncet, C. Increasing the height and multiplying the number of spans of greenhouse: How far can we go? Acta Hortic. 2017, 1170, 137–144. [Google Scholar] [CrossRef]
- Villagran, E.A.; Bojaca, C. Numerical evaluation of passive strategies for nocturnal climate optimization in a greenhouse designed for rose production (Rosa spp.). Ornam. Hortic. 2019, 25, 351–364. [Google Scholar] [CrossRef]
- López, A.; Valera, D.L.; Molina Aiz, F. Sonic anemometry to measure natural ventilation in greenhouses. Sensors 2011, 11, 9820–9838. [Google Scholar] [CrossRef] [PubMed]
- Rocha Ortiz, G.A.; Pichimata, M.A.; Villagran, E. Research on the Microclimate of Protected Agriculture Structures Using Numerical Simulation Tools: A Technical and Bibliometric Analysis as a Contribution to the Sustainability of Under-Cover Cropping in Tropical and Subtropical Countries. Sustain. Sci. 2021, 13, 10433. [Google Scholar] [CrossRef]
- Tong, G.; Christopher, D.M.; Li, B. Numerical modelling of temperature variations in a Chinese solar greenhouse. Comput. Electron. Agric. 2009, 68, 129–139. [Google Scholar] [CrossRef]
- Fitz Rodriguez, E.; Kubota, C.; Giacomelli, G.A.; Tignor, M.E.; Wilson, S.B.; McMahon, M. Dynamic modeling and simulation of greenhouse environments under several. Comput Electron Agric. 2010, 70, 105–116. [Google Scholar] [CrossRef]
- Piscia, D.; Montero, J.I.; Baeza, E.; Baely, B.J. Un modelo CFD de condensación nocturna en invernadero. Ing. Biosist. 2012, 111, 141–154. [Google Scholar]
- Willits, D.H.; Peet, M.M. El efecto de la temperatura nocturna sobre los rendimientos de tomates cultivados en invernadero en climas cálidos. Agric. Meteorol. 1998, 92, 191–202. [Google Scholar] [CrossRef]
- Villagran Munar, E.A.; Bojaca Aldana, C.R. Simulación de microclima en un invernadero utilizado para la producción de rosas en condiciones de clima intertropical. Chil. J. Agric. Anim. Sci. 2019, 35, 137–150. [Google Scholar] [CrossRef]
- Piscia, D.; Flores, J.; Montero, J. Predicting nocturnal condensation in a multi-span greenhouse using computational fluid dynamics simulations. Acta Hortic. 2010, 927, 627–634. [Google Scholar] [CrossRef]
- Díaz Rodriguez, A. Métodos de Predicción y Técnicas de Control de la Condensación en Invernaderos. Ph.D. Thesis, Universidad Politécnica de Madrid, Madrid, Spain, 2009. [Google Scholar] [CrossRef]
- Bounet, P.E. Assessing greenhouse climate using CFD: A focus on air humidity issues, International Symposium on New Technologies for Environment Control, Energy-Saving and Crop Production in Greenhouse and Plant. Acta Hortic. 2014, 1037, 971–985. [Google Scholar] [CrossRef]
- Leal, I.; Alcorta García, E.; Rodriguez Fuentes, H. Modelado del clima en invernaderos. Ingenierías 2006, 9, 7–13. [Google Scholar]
- Both, A.J.; Franklin, J.; Benjamin, L.; Holroyd, G.; Incoll, L.D.; Lefsrud, M.G.; Pitkin, G. Guidelines for measuring and reporting environmental parameters for experiments in greenhouses. Plant Methods 2015, 11, 43. [Google Scholar] [CrossRef] [PubMed]
- Baptista, F.J.; Bailey, B.J.; Meneses, J.F. Effect of nocturnal ventilation on the occurrence of Botrytis cinerea in Mediterranean unheated tomato greenhouses. Crop Prot. 2012, 32, 144–149. [Google Scholar] [CrossRef]
- Huertas, L. El control ambiental en invernaderos: Humedad relativa. Horticultura 2008, 205, 52–54. [Google Scholar]
- Aguilar Rodriguez, C.E.; Flores Velazquez, J.; Rojano, F.; Flores Magdaleno, H.; Rubiños Panta, E. Simulation of Water Vapor and Near Infrared Radiation to Predict Vapor Pressure Deficit in a Greenhouse Using CFD. Processes 2021, 9, 1587. [Google Scholar] [CrossRef]
- Cuellar Murcia, C.A.; Suarez Salazar, J.C. Sap flow and water potential in tomato plants (Solanum lycopersicum L.) under greenhouse conditions. Rev. Colom. Cienc. Hortícolas 2018, 12, 104–112. [Google Scholar] [CrossRef]
- Zhang, D.; Du, Q.; Zhang, Z.; Xiaocong, J.; Song, X.; Li, J. Vapour pressure deficit control in relation to water transport and water productivity in greenhouse tomato production during summer. Sci. Rep. 2017, 7, 43461. [Google Scholar] [CrossRef]
- Rivano, F.; Jara, J. Estimación de la evapotranspiración de referencia en la localidad de Remehue-Osorno, X región. Agro Sur. 2005, 33, 49–61. [Google Scholar] [CrossRef]
- BioAgro Tecnologies. Available online: https://brioagro.es/dpv-deficit-de-presion-de-vapor/ (accessed on 26 June 2024).
- Luo, W.; Goudriaan, J. Dew formation on rice under varying durations of nocturnal radiative loss. Agric. Meteorol. 2000, 104, 303–313. [Google Scholar] [CrossRef]
- Lu, N.; Kamimura, N.; Taichi, K.; Dalong, Z.; Ikusaburo, K.; Michiko, T.; Toru, M.; Toyoki, K.; Wataru, Y. Control of vapor pressure deficit (VPD) in greenhouse enhancedtomato growth and productivity during the winter season. Sci. Hortic. 2015, 197, 17–23. [Google Scholar] [CrossRef]
- Tamimi, E.; Kacira, M.; Choi, C.Y.; An, L. Analysis of microclimate uniformity in a naturally vented greenhouse with a high-pressure fogging system. Trans. ASABE 2013, 56, 1241–1254. [Google Scholar] [CrossRef]
- Villagran, E.; Flores Velázquez, J.; Mohamed, A.; Bojaca, C. Influencia de la altura en un invernadero multitúnel colombiano en la ventilación natural y el comportamiento térmico: Enfoque de modelación. Sustain. Sci. 2021, 13, 136331. [Google Scholar] [CrossRef]
- Baxevanou, C.; Fidardos, D.; Bartzanas, T.; Kittas, C. Numerical simulation of solar radiation, air flow and temperature. Ing. Agrícola Int. CIGR J. 2010, 12, 48–67. [Google Scholar]
- Li, A.; Huang, L.; Zhang, T. Field test and analysis of microclimate in naturally ventilated single-sloped greenhouses. Energy Build 2017, 138, 479–489. [Google Scholar] [CrossRef]
- Slatni, Y.; Djezzar, M.; Messai, T.; Brahim, M. Numerical simulation of thermal behavior in a naturally ventilated greenhouse. Int. J. Comput. Sci. Eng. 2022, 11, 2150034. [Google Scholar] [CrossRef]
- Bouhoun, A.H.; Bournet, P.E.; Danjou, V.; Migeon, C. CFD analysis of the climate inside a closed greenhouse at night including condensation and crop transpiration. Acta Hortic. 2015, 1170, 53–60. [Google Scholar] [CrossRef]
- Montero, J.I.; Muñoz, P.; Sánchez Gerrero, M.C.; Medrano, E.; Piscia, D.; Lorenzo, E. Shading screens for the improvement of the night-time climate of unheated greenhouses. Span. J. Agric. Res. 2013, 11, 32–46. [Google Scholar] [CrossRef]
- Iglesias, N.; Montero, J.I.; Muñoz, P.; Antón, A. Estudio del clima nocturno y el empleo de doble cubierta de techo como alternativa pasiva para aumentar la temperatura nocturna de los invernaderos utilizando un modelo basado en la Mecánica de Fluidos Computacional (CFD). Hort. Argent. 2009, 28, 18–23. [Google Scholar]
- Fidardos, D.K.; Bexevanou, C.A.; Bartzanas, T.; Kittas, C. Numerical simulation of thermal behavior of a ventilated arc greenhouse during a solar day. Renew. Energy 2010, 35, 1380–1386. [Google Scholar] [CrossRef]
- Fidardos, D.; Kittas, C.; Baxevanou, C.; Bartzanas, T. Solar radiation distribution in a tunnel greenhouse. Acta Hortic. 2008, 801, 855–862. [Google Scholar] [CrossRef]
- Alduchov, O.A.; Eskridge, R. Improved Magnus form approximation of saturation vapor pressure. J. Appl. Meteorol. 1996, 601–609. [Google Scholar] [CrossRef]
- Marquez Vera, M.A.; Ramos Fernandez, J.C.; Cerecero Natale, L.F.; Lafont, F.; Balmat, J.F.; Esparza Villanueva, J.I. Temperature control in a MISO greenhouse by inverting its fuzzy model. Comput. Electron. Agric. 2016, 124, 168–174. [Google Scholar] [CrossRef]
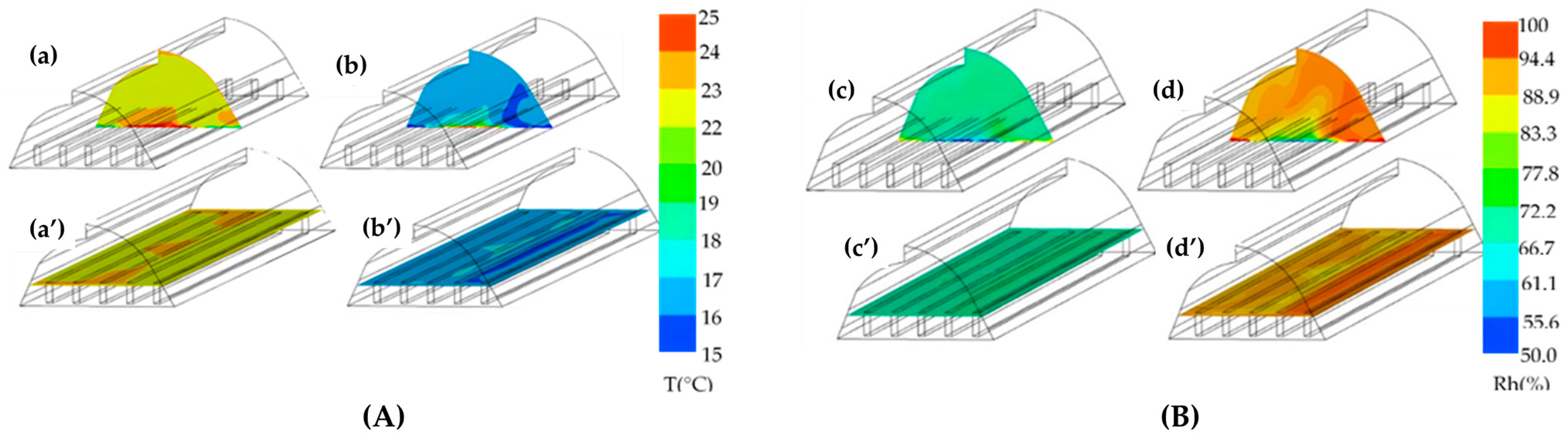
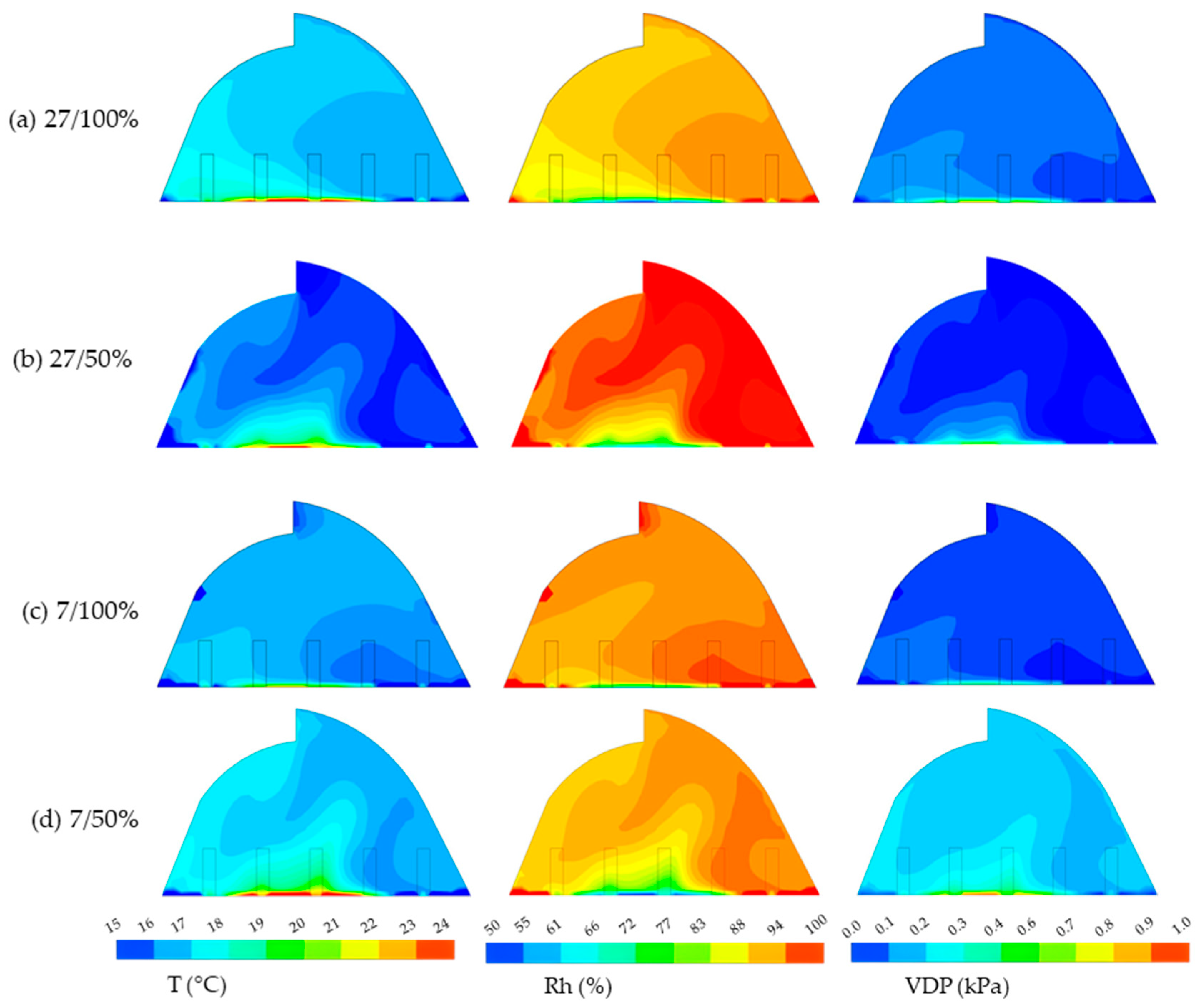
| Scenario | Day/Window Opening Configuration |
|---|---|
| (a) | 7/100% |
| (b) | 7/50% |
| (c) | 27/100% |
| (d) | 27/50% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acevedo-Romero, M.M.; Hernández-Bocanegra, C.A.; Aguilar-Rodríguez, C.E.; Ramos-Banderas, J.Á.; Solorio-Díaz, G. Vapor Pressure Deficit as an Indicator of Condensation in a Greenhouse with Natural Ventilation Using Numerical Simulation Techniques. Sustainability 2025, 17, 1957. https://doi.org/10.3390/su17051957
Acevedo-Romero MM, Hernández-Bocanegra CA, Aguilar-Rodríguez CE, Ramos-Banderas JÁ, Solorio-Díaz G. Vapor Pressure Deficit as an Indicator of Condensation in a Greenhouse with Natural Ventilation Using Numerical Simulation Techniques. Sustainability. 2025; 17(5):1957. https://doi.org/10.3390/su17051957
Chicago/Turabian StyleAcevedo-Romero, Mirka Maily, Constantin Alberto Hernández-Bocanegra, Cruz Ernesto Aguilar-Rodríguez, José Ángel Ramos-Banderas, and Gildardo Solorio-Díaz. 2025. "Vapor Pressure Deficit as an Indicator of Condensation in a Greenhouse with Natural Ventilation Using Numerical Simulation Techniques" Sustainability 17, no. 5: 1957. https://doi.org/10.3390/su17051957
APA StyleAcevedo-Romero, M. M., Hernández-Bocanegra, C. A., Aguilar-Rodríguez, C. E., Ramos-Banderas, J. Á., & Solorio-Díaz, G. (2025). Vapor Pressure Deficit as an Indicator of Condensation in a Greenhouse with Natural Ventilation Using Numerical Simulation Techniques. Sustainability, 17(5), 1957. https://doi.org/10.3390/su17051957







