Abstract
Exploring pathways for sustainable synergistic development is a challenging issue for the construction industry, which is currently in a critical period of transformation. Current research has confirmed that industrial clusters are an important organizational form for promoting sustainable synergistic development. However, the existing research on construction industry clusters has overly focused on cluster attribute analysis and evaluation. Investigating the core mechanisms of synergistic development within construction industry clusters is particularly crucial. From the perspectives of ecological and synergetic theories, this paper constructs the ecosystem of the construction industry cluster and analyzes its synergistic development process. It identifies the driving factors of the synergistic development of the construction industry cluster and uses the ISM model to determine the structural hierarchical relationships among factors. Taking Shandong Province as the data sample, this study employs the Haken model to conduct an empirical investigation of the level of synergy and its driving mechanisms, establishing a three-stage framework for the driving mechanisms. The results show the following results: (1) Operating efficiency and innovation ability are the top factors to promote the synergistic development of the construction industry. (2) Market demand, as an order parameter, is an important condition for triggering and amplifying fluctuations in the construction industry cluster system, and it acts as a controlling factor to promote the system’s self-organization evolution to a new ordered and stable state. (3) The construction industry cluster in Shandong Province is in the initial stage of low synergy and is gradually evolving to moderate synergy. From a new research perspective, this study helps construction industry planners and policymakers understand the mechanisms of evolution and key driving factors of construction industry clusters.
1. Introduction
Industrial clusters have long been regarded as the core engine of urban and regional development [1]. Currently, the global economy faces numerous challenges, including increasing resource constraints and environmental regulations, as well as the increasingly fierce competition in the market, which has led to industrial clusters gradually becoming a key driver of national competitiveness [2]. As a vital pillar industry, the construction industry plays an especially important role in national economic development. Promoting the new industrialization of the construction industry, with prefabricated buildings as an example, to comprehensively transform and upgrade the construction industry is a development strategy for the construction sector globally in many countries. As China’s construction industry enters a critical period of transformation and upgrading, the advantages of coordinated development in construction industry clusters in enhancing the competitiveness of the construction industry, promoting regional economic improvement, and achieving high-quality development in the construction industry are gradually becoming apparent. During the 14th Five-Year Plan period, various provinces and cities in China, such as Guangdong Province [3] and Shandong Province [4], have issued a series of planning measures to foster the creation of modern construction industry clusters, new construction industrialization industry clusters, and construction industry aggregation areas. These diverse and highly functional construction industry clusters will contribute to the high-quality and coordinated development of the construction industry.
Industrial clusters, as the best strategy for enhancing regional comprehensive competitiveness [5], have become the organizational choice for many enterprises due to their high capital utilization rates and external economic advantages [2,6,7]. Scholars have also explored the clustering phenomenon in the construction field and found that construction industry clusters can improve the efficiency of construction enterprises’ production activities and create competitive advantages for cluster enterprises [8]; the agglomeration effects that generate technological, financial, and talent advantages can enhance the productivity of construction enterprises and reduce resource consumption [9]. After long-term development, the importance of clusters as a form of organization has gradually been realized, and the coordinated development of industrial clusters is key to the rational allocation and efficient use of industrial factors of production. Hengjiang Liu et al. [10] believe that the synergistic development of industrial clusters is a dynamically evolving process: industrial clusters continuously develop in a regular and stable way under the influence of endogenous driving mechanisms and exogenous stimulating mechanisms. Xuyun Li and Jia He [11] believe that the synergistic development within regional industries should focus on the overall industrial layout adjustment of industrial clusters and deepen the cooperative development through the rational construction of industrial chain ecology. Weidong Sun [12] proposes that small- and medium-sized enterprises (SMEs) and other actors within industrial clusters need to rely on external innovative resources to achieve coordinated development.
At present, a number of theories have been put forward to explain why closely related firms are geographically co-located and how this can induce knowledge spillovers, innovation, etc. [13,14]. Research on construction industry clusters in China is primarily focused on cluster identification, analysis of cluster types and patterns, and cluster evaluation. The research team led by Jian Sun [15,16], based on industrial cluster theory, uses Location Quotient analysis to identify construction industry clusters and classify them according to their causes and industrial characteristics. By dissecting real-case scenarios, they analyzed the internal and external mechanisms of construction industry clusters, highlighting scale, efficiency, firm density, and entrepreneurial spirit as significant factors influencing cluster competitiveness. Furthermore, Long Gao et al. [17] were the first to explore the formation and development paths of Chinese construction clusters, noting that these clusters are gradually ascending from the lower levels of the industrial chain. Jiangpeng Zhang et al. [18] delineated the construction cluster network system, suggesting that the evolution of construction clusters is a process in which the main organizations within the network enhance their competitive advantage by improving their resource acquisition capabilities through competitive and cooperative interaction mechanisms. It is evident that while some regional construction industry clusters have preliminarily formed, the state of their collaborative development remains uncertain. How to sustain their development and prevent decline is an urgent issue that needs to be addressed, which necessitates research into the core mechanisms of synergetic development within industrial clusters.
With the application of ecosystem thinking in the field of industrial economics and the increasing complexity of the business environment, the concept of the ecosystem has increasingly been used to describe the growing interdependencies among participants [19]. The ecological characteristics exhibited by industrial clusters have demonstrated the applicability of ecological theory in the study of cluster development and evolution [20,21], offering a new perspective on the synergetic development of industrial organizations. Despite extensive discussions on ecosystems in the management literature [22,23], research on ecosystems within the context of construction industry clusters remains scarce [24,25].
In summary, existing research on construction industry clusters lacks an in-depth analysis of the core mechanisms of cluster synergistic development from new research perspectives. Therefore, this study adopts an ecological perspective by dissecting the ecosystem model of construction industry clusters and analyzing the intrinsic patterns and dynamic mechanisms of their synergistic development. This study provides theoretical references for the synergistic development of construction industry clusters and explores pathways towards their sustainable development.
2. Analysis of the Synergistic Development of Construction Industry Clusters from an Ecological Perspective
2.1. Composition of the Construction Industry Cluster Ecosystem
Organizational evolution is the result of both environmental selection and managerial selection [26,27]. Construction industry clusters, along with their living environment, form an ecosystem that exhibits the basic characteristics of general ecosystems [28]. This cluster ecosystem is a complex system formed by the interactions of various entities, including upstream and downstream enterprises in the construction industry chain and intermediary institutions. The main bodies of the construction industry cluster include construction enterprises, financial institutions, government agencies, and research institutions, as well as related industries and sectors such as manufacturing, services, and transportation. The enterprises and institutions that make up the construction industry cluster act as Producers, Consumers, and Decomposers based on their positions in the industrial chain, forming organizational communities within the construction industry cluster. The cluster organizational community interacts with the natural, political, economic, and social external environments in which the cluster is situated, jointly facilitating the flow of resources such as materials, energy, information, and capital, and together maintaining the dynamic balance of the construction industry cluster ecosystem. The structure of the construction industry cluster ecosystem is primarily composed of three hierarchical networks: the Core System, the Support System, and the External Environment System, as shown in Figure 1.
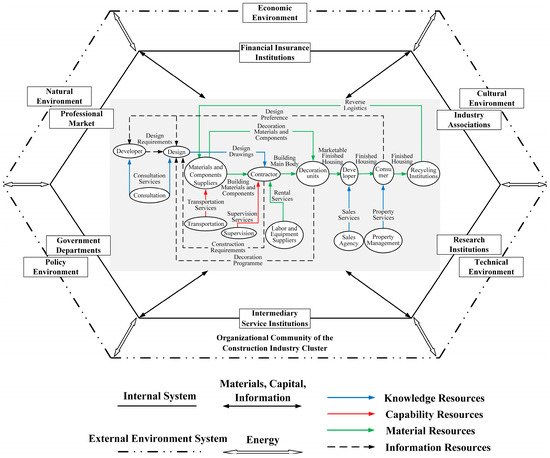
Figure 1.
Structural diagram of the construction industry cluster ecosystem.
Natural ecosystems can be divided into two parts: the biological community (Internal System) and the inorganic environment in which they live (External System). The construction industry cluster ecosystem operates analogously to natural ecosystems, sharing similar component structures, and can be divided into Internal and External Systems.
- (1)
- Internal System
The Internal System encompasses the Core System and the Support System. The Core System possesses the central knowledge and professional expertise, consisting of key construction enterprise organizations such as construction companies, survey and design firms, and material suppliers. The Support System ensures the normal operation of the Core System by providing the cluster with human resources, technology, capital, infrastructure, and intermediary services, including research institutions, financial and insurance organizations, government departments, industry associations, and other intermediary service agencies. Each entity within the Internal System belongs to either the Producer Population, Consumer Population, or Decomposer Population, forming Food Chains within the system. For instance, enterprises acting as Producers by supplying construction materials provide the nutrients necessary for enterprises acting as Consumers to carry out their operations. The residual materials and waste from construction production and operation activities are recycled by energy-saving and recycling institutions acting as Decomposers and then supplied back to the Producers for the next cycle. Multiple Food Chains within the construction industry cluster form a Food Web, constituting the organizational community of the construction industry cluster.
- (2)
- External System
The External System refers to the external environment in which the construction industry cluster organizational community is situated, that is, the outer environmental system at the outermost layer of the system’s structure, which serves as the external driving force for industrial agglomeration development. It mainly includes the natural resource environment and the constantly evolving Social Environments such as technology, economy, policy, and culture. Between the two, the Social Environment has a more critical impact on the human-led construction industry cluster ecosystem. The external environment can directly influence the core structure of the system by establishing regulations and rules, and it can also indirectly affect the core structure through the Support System, providing a favorable environment for the development of construction industry clusters.
2.2. The Synergistic Development Process of the Construction Industry Cluster Ecosystem
According to the Dissipative Structure theory (DST) [29] and synergetic theory, the emergence and function of synergy require certain conditions in the evolutionary development process of the construction industry cluster ecosystem. When these necessary conditions are met, the synergistic development trends exhibited by the system constitute the Natural Laws of industrial cluster evolution. Specifically, the basic conditions that should be satisfied include Openness, Disequilibrium, and the Unimpeded Interconnectivity of Elements. The disequilibrium within the open construction industry cluster ecosystem and the smooth interconnectivity between various elements allow the different components of the system to develop through competition and cooperation, laying the foundation for achieving synergistic development goals in construction industry clusters.
Synergistic development is a macroscopic manifestation of system evolution, a process primarily achieved through the synergistic interactions between the Internal System and External System. For the construction industry cluster ecosystem, competition creates the foundational conditions for synergistic development. The development of individual enterprises fosters competition, and various entities within the system move toward synergy through their interactions. This synergy, in turn, sparks higher-level competition. The system forms a synergistic mechanism under the influence of competition and cooperation among relevant factors, transforming some of these factors into competitive advantages. For instance, the synergistic mechanism promotes the application of new technologies by the main bodies of cluster construction enterprises, converting technological factors into competitive advantages for system development through innovative activities. Therefore, the synergistic development of the construction industry cluster ecosystem is mainly driven by the interactions between entities within the system and between the Internal System and the External System, with these interactions primarily manifesting as competition and cooperation.
Only by inducing a Mutation in the system can the dissipative structure of the system truly be catalyzed, prompting the system to evolve towards a more ordered and stable structure, thereby achieving synergistic development in the construction industry cluster ecosystem. The key to this Mutation lies in the random fluctuations that arise from the interplay between the system’s self-organizing characteristics and synergistic driving factors. When a driving factor in the development of the construction industry cluster ecosystem changes, fluctuations occur randomly at various points within the system, such as fluctuations in the policy environment, capital investment, and Market Demand. These fluctuations, either occurring independently or interwoven, exert a subtle influence on the system’s development, called Micro Fluctuations. When the intensity of the driving factor reaches the system’s own threshold, Micro Fluctuations are amplified into Giant Fluctuations, propelling the construction industry cluster ecosystem to break through its original steady state and form a new dissipative structure. As the system crosses the critical point, the synergistic actions among its internal constituents based on the industrial chain gradually strengthen, and the interactions between various driving factors inside and outside the system are amplified, leading to the formation of the order parameter that exerts a dominant influence. Therefore, the order parameter for the synergistic development of the construction industry cluster ecosystem primarily originates from the system’s random fluctuations, which are the result of the collective action of individual enterprises, enterprise populations, organizational communities, and the external environment, determining the type and direction of development of the construction industry cluster ecosystem.
Based on the above discussion of the conditions, dynamics, and pathways for the synergistic development of the construction industry cluster system, a theoretical model for synergistic development is constructed. As shown in Figure 2, from an ecological perspective, the synergetic development model of the construction industry cluster system is as follows: the system’s main bodies are influenced by internal and external driving factors, leading to competitive and collaborative relationships that cause the system to depart from its original steady state. The collective synergistic response of groups of construction-related enterprises and institutions, along with system-driving factors, generates a force. When the cumulative effect of this force exceeds the system’s threshold for Mutation, Micro Fluctuations within the system are amplified into Giant Fluctuations. Micro Fluctuations do not disrupt the system’s equilibrium state; the system can maintain its original dynamic balance through self-regulation. However, Giant Fluctuations push the system in a direction that is far from its own equilibrium state, causing the system to become unstable. During the fluctuation process, the nonlinear interactions among various state variables in the system lead to the emergence of system order parameters, which then dominate the upgrading and development of the original system structure into a higher-level new stable state. Subsequently, the system, based on this new steady state, will undergo interactions between internal and external driving factors, creating new conditions for fluctuations for the next round of evolution. It is within this cyclical process of evolution that the construction industry cluster ecosystem achieves its goal of synergistic development.
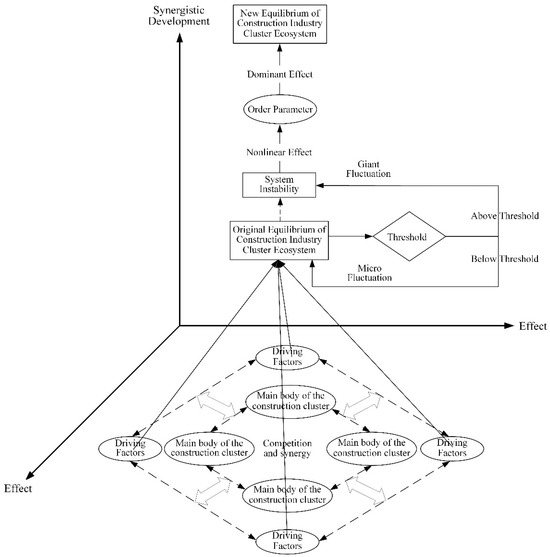
Figure 2.
Theoretical model of synergy development in construction industry clusters.
3. Analysis of Synergistic Driving Factors in Construction Industry Clusters
3.1. Construction of the Synergistic Driving Factors Indicator System
Synthesizing the aforementioned analysis, the construction industry cluster ecosystem, which is composed of a three-tiered network that includes the Core System, the Support System, and the External Environment System, is subject to the synergistic influence of various factors. On one hand, different enterprises and organizations within the Internal System, in pursuit of profit objectives, form a dynamic balance of competition and cooperation through complementary advantages and innovation research. On the other hand, the construction industry cluster interacts with the constantly changing External Environment System. Changes in cluster elements, Industrial Structure, and the external environment cause cluster enterprises to continuously adjust their ecological niches for development, engaging in collaborative development under the influence of both internal and external factors. Based on the analysis of the synergetic development of the construction industry cluster ecosystem, combined with the research on industrial cluster collaboration by scholars Zhiguo Chen [30], Junjie Fan [31], and Yibing Gao [32], the synergistic driving factors of the construction industry cluster are identified from two dimensions: the Internal System and the External System. The internal synergistic driving factors are summarized into three major categories: Operational Efficiency, Innovation Capability, and Industrial Structure, while the external synergistic driving factors are summarized into three major categories: Market Demand, Resource Endowment, and Social Environment.
Additionally, by reviewing existing research findings and referring to the relevant literature on building industrialization, industrial cluster collaboration, and evaluation indicators for industrial synergetic development, over 20 representative documents were selected. In conjunction with the characteristics of construction industry clusters and the accessibility of data, 23 high-frequency measurement indicators across six levels of indicators were identified, as shown in Table 1.

Table 1.
Indicator system of synergistic driving factors in construction industry clusters.
3.2. Hierarchical Effects of Synergistic Driving Factors
Interpretive Structural Modeling (ISM) is a classic systems analysis method that can analyze the structural relationships among various influencing factors in complex network systems through a multi-level extraction approach. Compared to other alternative methods, ISM not only helps to discover the hierarchical organization of various factors [33] but also provides order and direction for the complex relationships among elements within the system [34]. Therefore, to clarify the hierarchical structure of the driving factors in the synergistic development of construction industry clusters, this paper employs ISM to analyze the relationships and hierarchical structure among the driving factors of Operational Efficiency (N1), Innovation Capability (N2), Industrial Structure (N3), Market Demand (N4), Resource Endowment (N5), and Social Environment (N6). A 10-person ISM expert group was formed, and expert opinions in the field of construction were collected via a survey questionnaire. After verification and rationalization, an adjacency matrix A, representing the direct impact relationships among the synergistic driving factors, was obtained. In this matrix, a direct influence of synergistic driving factor Ni on Nj is represented as “”, and no direct influence as “”. The influence relationship of factors on themselves is not judged, so the diagonal values are fixed at 0.
The identity matrix I is introduced to the adjacency matrix A and the resulting matrix (A + I) is further processed according to the rules of Boolean matrix operations; when it satisfies , the reachable matrix M can be obtained as . The logical AND operation rules for Boolean matrices are as follows: 0 + 0 = 0; 0 + 1 = 1; 1 + 1 = 1; 1 × 0 = 0; 0 × 1 = 0; and 1 × 1 = 1. Using MATLAB software for auxiliary calculations, the reachable matrix M can be derived.
By using set operations and continuously extracting the same elements from the reachable set and the intersection set, a hierarchical classification Table 2 can be obtained.

Table 2.
Hierarchical classification table of driving factors.
Based on the hierarchical classification results of the various factors, the hierarchical structure of the synergistic driving factors of the construction industry cluster is depicted as shown in Figure 3.
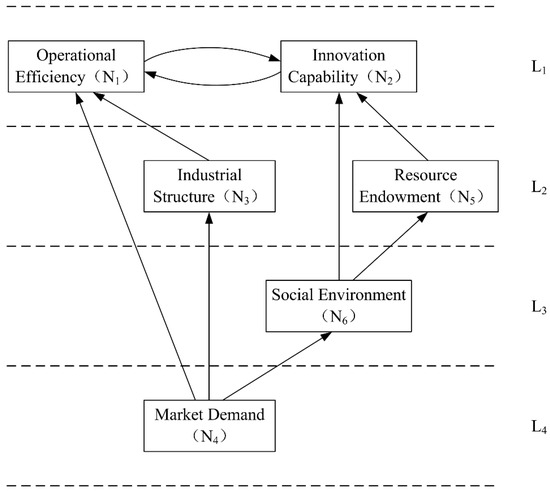
Figure 3.
Hierarchical structure of synergy driving factors in construction industry clusters.
The ISM model constructed in this study for the synergistic driving factors of the construction industry cluster is a four-tiered hierarchical directed structure model, where arrows represent the direction of the influence of the synergistic driving factors. This model has preliminarily determined the structural hierarchical relationships among the six major categories of synergistic driving factors, ranging from L1 to L4, with layers transitioning from superficial to deeper as the level number increases. At level L1, Operational Efficiency (N1) and Innovation Capability (N2) are top-level factors that directly affect the synergistic development of the construction industry. At the bottom level, L4, Market Demand (N4) is a deep-layer driving factor that often influences the target from the root. At the intermediate levels, L2 and L3, Industrial Structure (N3), Resource Endowment (N5), and Social Environment (N6) indirectly influence the target by affecting the top-level factors and serve as a bridge linking the top-level driving factors with the deep-layer driving factors.
Based on the ISM model, the logical structural relationships and driving pathways of the synergistic driving factors within the construction industry cluster can be preliminarily clarified. However, the specific nature of the interactions between these factors—such as whether they are positive or negative—and the definition of synergistic order parameters still require further elaboration.
4. Analysis of Synergistic Dynamics Mechanism in Construction Industry Clusters Based on the Haken Model
4.1. Haken Model
The synergetic theory is considered to be the theory that studies the laws governing the formation of synergistic structures within complex systems [35], providing methodological guidance for exploring complex systems characterized by both synergy and competition [36]. The Haken model [37] is an important model in synergetic theory for measuring the system’s orderliness. By distinguishing between fast and slow variables within the system, it identifies the order parameters that dominate the orderly structural development process of complex systems. This allows for the determination of the key factors influencing the interactions between subsystems and variables within the system, as well as the overall evolution of the system. The model is capable of describing the interaction mechanisms among state variables within the system through various parameters. The construction industry cluster ecosystem meets the application conditions of the Haken model with characteristics such as self-organization, Openness, non-equilibrium, and nonlinearity. The Haken model can be used to identify the order parameters for the synergistic development of construction industry clusters, thereby revealing the driving mechanisms that lead the overall development of construction industry clusters towards a more orderly structured collaboration.
The core content of the Haken model includes the adiabatic approximation assumption, the evolution equation of order parameters, and the potential function, which mainly involves two state variables. By selecting two variables, and , from the construction industry cluster ecosystem, their model relationship can be established as follows:
where and are damping coefficients, while a and b are interaction strength coefficients. According to the adiabatic approximation assumption, the damping coefficients must satisfy and the two values must differ by at least one order of magnitude. At this point, is the slow variable that dominates and controls the system’s evolution, i.e., the system’s order parameter. It can be set that , which provides the following:
Substituting (3) into (1), the system’s order parameter evolution equation is obtained as follows:
To facilitate practical analysis, the Haken model is discretized as follows:
The potential function can determine the stability of the system’s potential energy and thus explore the evolutionary trend of the system. Integrating the negative of in Equation (4) yields the system’s potential function as follows:
When the system is in a stable state, . At this time, the equilibrium points of the potential function can be found as follows: when , the equation has a unique solution of 0; when , the equation has three solutions.
At this point, any point in the system that deviates from the equilibrium point will eventually return to the equilibrium point, and the stability of any point is determined by the straight-line distance between that point and the equilibrium point.
4.2. Data Sources and Analysis
Quantitative indicator data were selected from the comprehensive data of Shandong Province, China, spanning from 2015 to 2022. The data were primarily sourced from various statistical websites, including statistical yearbooks at different levels, annual reports on the construction industry, the Shandong Provincial Government website, and so on. The initial indicator values were derived from the organization and analysis of relevant statistical materials.
Qualitative indicator data were obtained through the distribution of questionnaires. Given the accessibility of data and the specialized nature of the indicators being investigated, the distribution of questionnaires was limited to practitioners in construction enterprises or individuals engaged in research related to the construction industry. Distributed online, a total of 220 questionnaires were collected. After excluding invalid questionnaires with identical answers and those with short response times, 172 valid questionnaires were obtained, resulting in an effective response rate of 78.2%. The collected questionnaire data were analyzed for reliability and validity using SPSS 26. The Cronbach’s α value of 0.832 (greater than 0.7) indicates good consistency within the sample data and a high degree of credibility. The KMO value of 0.811 (greater than 0.7) and the significance level (Sig.) of 0.000 (less than 0.05) suggest that the questionnaire has a relatively ideal level of stability and consistency [38].
The data were processed using the range transformation method, and the Entropy Weight Method (EWM) was employed to assign weights to the various indicators of the driving factors in the synergistic development of the construction industry cluster, which were then used for simulation calculations.
4.3. Model Calculation and Analysis
- (1)
- Order Parameter Identification
Using Eviews13, the six variables mentioned above were combined in pairs for analysis, with the requirement that at least two variables’ coefficients must pass the significance test [39]. After processing the data with the software, a total of 30 sets of calculation results were output. Due to space limitations, the specific steps of the software operation and the selection process of the regression results are omitted in this paper. Only the 12 results where the motion equations are established (with the significance levels of and reaching 10%) are listed, as shown in Table 3.

Table 3.
Partial results of Haken model variable analysis.
From the table, it can be seen that under the assumption ④ and the condition that the motion equation is established, , which satisfy the adiabatic approximation assumption that and . Therefore, Market Demand (N4) is the order parameter, Q1, and Innovation Capability (N2) is another state variable, Q2. This indicates that compared to other driving forces, the stimulation of Market Demand has a greater impact on the synergistic development of the cluster, and the interaction path between Market Demand and Innovation Capability is the main driving path for the cluster to develop in an orderly and synergistic direction.
The parameter indicates that a positive feedback mechanism has been established within the system between the Market Demand drive and the continuous improvement in Innovation Capability, promoting the system to gradually evolve towards an orderly direction. This also implies that the market environment is becoming more conducive to the synergistic development of the construction industry cluster. The parameter indicates that a stable positive feedback mechanism between the Market Demand drive and the interactive development of Innovation Capability has not yet fully formed within the system. That is, the existing Market Demand still needs further stimulation for cluster development, and the efficiency of innovation in cluster enterprises is not high enough, which means the driving path from Market Demand to Innovation Capability needs further improvement.
The parameter indicates that the order parameter Market Demand (N4) can promote the development of the state parameter Innovation Capability (N2), meaning that the synergistic driving factor Market Demand ultimately plays a promoting role in the factor Innovation Capability. indicates that the state parameter Innovation Capability (N2) can to some extent inhibit the growth of the order parameter Market Demand (N4), meaning that the synergistic driving factor Innovation Capability can exert a hindering effect on Market Demand by influencing other factors on the driving path. According to the results of the interaction of the two factors, the role of cluster innovation on Market Demand can be divided into two stages: in the initial stage, innovative activities are the key means to meet Market Demand, and the innovative achievements of the cluster are used to satisfy the economic market’s demand for construction products. Market demand will not continue to grow in the short term, meaning that the factor of Innovation Capability has a hindering effect on the factor of Market Demand. However, this hindering effect will not last forever because innovation can not only open up new market spaces for limited Market Demand but also change the structure and patterns of Market Demand, providing new choices and possibilities for Market Demand. At this time, the role of cluster innovation in Market Demand enters an advanced stage, where innovation drives continuous changes in Market Demand.
- (2)
- Potential Function Solution
Based on the aforementioned analysis results, the evolution equation for the order parameter of the construction industry cluster ecosystem is obtained as follows:
Integrating the negative of in Equation (8) yields the potential function for the system’s evolution as follows:
Since , it is known that setting results in three solutions for the potential function: , , . The potential function graph is illustrated in Figure 4.
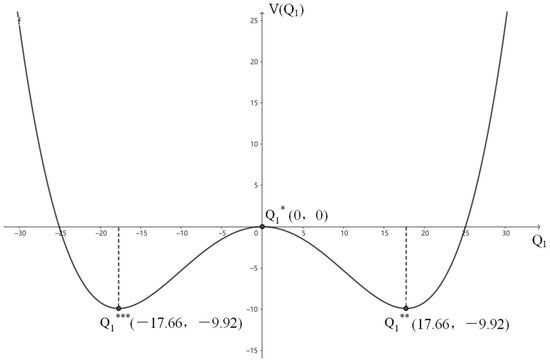
Figure 4.
Synergistic development potential function graph of construction industry clusters.
The potential function maps the development and evolution path of the system. As shown in Figure 4, when Q > 0, the system’s stable point is ; when Q < 0, the system’s stable point is . The point is an unstable point and will eventually return to the stable points or . When the control variables are appropriate, the Market Demand (N1) and Innovation Capability (N2) within the construction industry cluster ecosystem will have a non-zero effect.
Considering the actual situation, the order parameter for Market Demand is a positive variable, which means a new stable solution forms at 17.66. The distance of any point from determines the state of that point. The system state evaluation function is as follows:
The closer the state point is to the stable point , the smaller the d value, indicating a higher degree of system synergy. To facilitate the comparison of score values, the d value is normalized to a positive indicator within the [0,1] range, known as the synergy score S:
where is the maximum value of the sample data and is the minimum value of the sample data. The range of synergy score S will be mapped to the [0,1] interval, with higher S values indicating a higher level of synergetic development. This study refers to Jinhua Zhang’s [40] research, using the trisection points of the interval as the boundary of the synergetic level, dividing the synergy score into three stages: (0,0.333] for low synergy; (0.334,0.666] for moderate synergy; and (0.667,1] for high synergy. The synergy scores for the synergistic development of construction industry clusters in 16 cities in Shandong Province, China, from 2015 to 2022, are shown in the following table.
To clearly present the synergistic development status of construction industry clusters in various regions of Shandong Province, a trend chart was created based on the synergy scores of each city from Table 4, as shown in Figure 5 below:

Table 4.
Synergistic score values of Shandong Province’s construction industry clusters.
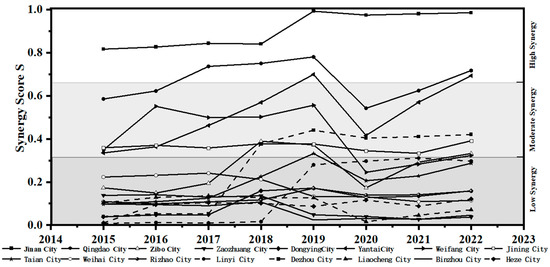
Figure 5.
Development trend of synergy in Shandong Province’s construction industry clusters.
Based on the data from Table 4 and Figure 5, it can be observed that from 2015 to 2022, the synergy scores of the majority of cities in Shandong Province fell within the low synergy range and gradually increased. This indicates that the overall level of synergistic development of construction industry clusters in various regions of Shandong Province is in the initial stage and shows an upward trend year by year, evolving towards moderate synergy. Additionally, the synergy scores of the majority of regions declined in 2020 and then slowly rebounded. Analysis of the actual development situation reveals that the outbreak of COVID-19 at the end of 2019 led to the first significant decline in the total output value of Shandong Province’s construction industry in nearly five years in 2020. The stagnation of construction production and business activities, the retreat of the construction market, and the suspension of work in other industries were a series of unfavorable factors that collectively caused the overall level of synergistic development of construction industry clusters in various regions of Shandong Province to decrease. Subsequently, with the strengthening of policy support from the Shandong Provincial Government, the level of synergistic development of construction industry clusters began to show an upward trend.
Regionally, Jinan City (0.907) and Qingdao City (0.670) have reached a high level of synergy in the development of their construction industry clusters, placing them in the first tier of synergistic development among construction industry clusters in Shandong Province. Jinan City has particularly maintained a high level of synergy for eight consecutive years. Yantai City (0.513), Weifang City (0.414), and Jining City (0.364) are at a moderate level of synergy, positioning them in the second tier of synergistic development. The remaining 11 cities are all at a low level of synergy. Binzhou City (0.065) and Zaozhuang City (0.087), which rank at the bottom two in terms of synergy scores, show a significant gap compared to other cities. This indicates a considerable disparity in the synergistic development of construction industry clusters across different regions in Shandong Province. Jinan and Qingdao, driven by Market Demand, have faster speeds in cluster synergistic development and structural adjustment compared to other regions, and they are more capable of adapting to changes in the external environment of the clusters.
4.4. Design of the Dynamics Mechanism
Based on the order parameter evolution equation and potential function of the Haken model, the driving mechanism of the synergistic development of construction industry clusters can be revealed: taking Shandong Province as an example, Market Demand is the order parameter that dominates the synergistic development of its construction industry clusters. The path of action between Market Demand and Innovation Capability is the main driving path for the cluster to develop towards an orderly and synergistic direction. The interaction of various synergistic driving factors collectively promotes the construction industry cluster to break through its original stable state, evolving from disorder to order and from a lower level to a higher level of synergistic development. Combining the relevant synergetic theories and the hierarchical structure model of synergistic driving factors, the driving mechanism for the synergistic development of construction industry clusters was designed as shown in Figure 6.
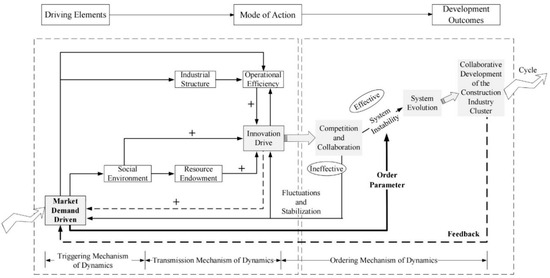
Figure 6.
Model of the driving mechanism for the synergistic development of the construction industry cluster.
The dynamic triggering mechanism is the fundamental driving force behind the synergistic development of construction industry clusters, reflecting the source of momentum and the process from nothing to something. The Openness of the construction industry cluster system determines that the cluster will be influenced by the economic market environment. Under the drive of Market Demand, changes occur in the Industrial Structure and corporate behavior of the cluster, leading to random fluctuations that cause the cluster system to undergo Mutations, thereby triggering the formation of new orderly structures within the construction industry cluster. Specifically, the construction products generated by construction production and operation activities usually start with meeting Market Demand. At the same time, only enterprises that meet Market Demands can have the advantage of development. Changes in demand will guide the spatial selection of construction industry cluster aggregation, adjustment of Industrial Structure, expansion of overall scale, and transformation of development methods, thus becoming the primary external driving force in the process of synergistic development of construction industry clusters. The order parameter of the cluster plays different roles at different times; the role of Market Demand may not be obvious in the initial stage, but when demand changes reach a certain level, it forms a driving force for the synergistic development of the construction industry cluster.
The dynamic transmission mechanism is the process by which synergistic development and the continuous operation of the cluster are driven. Driven by Market Demand, construction industry clusters exhibit fluctuations that are amplified into Giant Fluctuations through the positive feedback of various synergistic driving factors. Specifically, Market Demand transmits its promotional effect on innovation drive by driving environmental changes, resource aggregation, industrial transformation, and the maximization of benefits. Innovation drive, in turn, provides positive feedback to Market Demand. According to the hierarchical structure of the factors’ influence, there are four pathways through which the driving effect of Market Demand is transmitted: Market Demand → Industrial Structure → Operational Efficiency → Innovation Drive, Market Demand → Operational Efficiency → Innovation Drive, Market Demand → Social Environment → Resource Endowment → Innovation Drive, and Market Demand → Social Environment → Innovation Drive. Under the impetus of Market Demand, enterprises within the construction industry cluster will spontaneously adjust and optimize their Industrial Structure, strengthen collaborative cooperation, and increase investment in innovative activities to form an innovation drive. Market demand also reshapes the Social Environment in which clusters are embedded, and with government regulation and technological knowledge spillovers, clusters will attract the entry of innovative resource elements. The augmentation of exploitable resources within the cluster further bolsters the innovation drive, enabling various pathways to collectively shape the cluster’s overall innovation drive as they convey the impetus of Market Demand. This process is also subject to feedback from other pathways, which serves to amplify the driving force of Market Demand. It is this positive feedback mechanism between the Market Demand drive and innovation drive that achieves the continuous and synergistic development of construction industry clusters. Furthermore, to gain market competitive advantage as well as meet diverse and multi-level Market Demands, cluster enterprises will further promote industrial agglomeration by establishing a stable, efficient, and resilient industrial chain system. Clusters focused on complementing and strengthening the chain make the industrial chain layout more rational and complete, enhancing the technological spillover effects between industries and the resilience of the industrial chain. This is the process by which the synergy within construction industry clusters is enhanced.
The dynamic orderly mechanism is attributed to the self-organizing evolution capability of the construction industry cluster system. When the effects of various synergistic driving factors do not reach the system’s threshold, the cluster’s own regulatory function will quell the fluctuations caused by the driving factors, and the system maintains its original equilibrium at this time. When the effects of the factors are strong enough, fluctuations are amplified into Giant Fluctuations, and the system becomes unstable and evolves. The system then reaches a higher level of synergy under the dominance of the order parameter, Market Demand, and the construction industry cluster achieves a new state of orderly stability, entering a virtuous cycle until new fluctuations emerge. Market demand drives the synergistic development of the construction industry cluster, and in turn, the construction industry cluster, while meeting various industrial and consumer demands, will induce new demands, thereby driving a new round of development. This cycle repeats, making Market Demand a significant and sustained driving force for the synergistic development of construction industry clusters. The orderly process of synergistic development in construction industry clusters manifests as a cyclical pattern of Market Demand changes → synergistic driving factor effects → synergistic effects → system instability → structural change → increase in synergy → new Market Demand changes.
5. Discussion
5.1. Academic Value and Contribution
The construction industry in China is a pillar of the national economy, encompassing multiple fields and a vast industrial chain. Currently, the construction industry is facing multiple challenges such as declining Market Demand, rising costs, and difficulties in financing; especially, the rapid downturn in the real estate market has had a significant impact on the construction engineering industry market. With the aim of achieving China’s Dual Carbon goals, the innovation of low-carbon production technology, energy saving and emission reduction, and prefabricated construction have become new directions for the development of the construction industry, making sustainable development of the construction industry an urgent task. Industrial clusters are an important organizational form to promote sustainable synergistic development; therefore, this paper analyzes the hierarchical relationship and driving mechanisms of the driving factors of construction industry clusters, finding that Operational Efficiency and Innovation Capability can directly promote the synergistic development of construction industry clusters, while Market Demand can trigger system changes and dominate the cluster system to achieve a new stable state. In addition, this paper analyzes the construction industry cluster from an ecological perspective, filling the research gap in existing construction industry cluster theories. At the same time, as a new research perspective, the three-stage driving mechanism framework for synergistic development of construction industry clusters formed in this paper provides a theoretical basis and reference for subsequent mechanism studies of construction industry clusters.
5.2. Limitations
Given the limited conditions, this study has formed some conclusions but still has the following limitations:
- (1)
- The index system for the driving factors of construction industry cluster collaboration needs further refinement. This study identified six types of synergistic driving factors from a macro perspective based on the synergistic development patterns of the construction industry cluster ecosystem and selected measurement indicators through literature research. However, the construction industry cluster is a complex system involving numerous driving factors, and there may still be omitted elements.
- (2)
- The sample data for empirical analysis needs to be further expanded. This study conducted an empirical analysis using data from Shandong Province from 2015 to 2022 as the sample, which has limited coverage and capacity. It does not fully consider the imbalance in development across different regions, making it difficult to fully and accurately reflect the overall situation of synergistic development in China’s construction industry clusters.
In subsequent research, the index system can be improved based on a more comprehensive understanding and consideration of the specific development details and characteristics of the clusters. Specific analysis of the order parameters in other provinces and regions can be conducted to formulate synergistic driving mechanisms tailored to the current state of development of China’s construction industry clusters, making the empirical results more universally applicable.
6. Conclusions and Suggestions
Based on the construction industry-related data from Shandong Province, China, from 2015 to 2022, and using the Haken model for empirical analysis, the following conclusions were drawn according to the system’s order parameter evolution equation and potential function: The synergistic development of construction industry clusters in various regions of Shandong Province is generally in the initial stage of low synergy and is gradually evolving towards moderate synergy. Market Demand is the order parameter driving the synergistic development of its construction industry clusters, meaning that Market Demand is the key synergistic driving factor that pushes cluster development beyond the critical point toward a new, more orderly steady state. At the same time, the path driven mainly by Market Demand and Innovation Capability propels the synergistic development of the construction industry cluster ecosystem. This dynamic mechanism framework primarily consists of three stages: the Market Demand-oriented dynamic triggering mechanism, the dynamic transmission mechanism characterized by interactions among the Social Environment, Resource Endowment, Industrial Structure, Operational Efficiency, and cluster innovation, and the dynamic orderly mechanism of systemic synergistic evolution.
The synergistic development of construction industry clusters is influenced by a variety of internal and external factors. The key to promoting synergistic development within clusters is to grasp the order parameters and regulate the relationships between various synergistic driving factors. Based on the research conclusions, the policy recommendations for promoting the synergistic development of construction industry clusters from the perspectives of enterprises, clusters, and governments are as follows:
- (1)
- Enterprises are the main drivers of cluster development, and innovation is the most crucial factor for synergistic development within these clusters. Cluster enterprises should enhance their R&D and innovation awareness, actively introduce scientific research institutions, and build innovation cooperation platforms that are enterprise-led and market-oriented, integrating industry–university–research–innovation. They should fully leverage the driving effect of core enterprises to strengthen the momentum of enterprise aggregation in construction industry clusters. Additionally, they should continuously optimize the internal relationships and production structures of enterprises within construction industry clusters, and promote specialized division of labor and differentiated development among enterprises, thereby expanding effective supply and meeting the demands of the construction economy market.
- (2)
- Construction industry clusters can continuously innovate and upgrade through industrial agglomeration, knowledge spillovers, and collective action, promoting close interaction between related enterprises and institutions to accelerate synergistic development. Clusters need to deploy innovation chains centered on the construction industry chain and cultivate innovative clusters. They should value the role of construction industry associations and jointly build cluster intermediary platforms that serve the synergistic development of the industry. Furthermore, they should break through the geographical constraints of construction industry clusters and develop virtual industry clusters, such as combining Geographic Information System (GIS) technology and Google Earth applications to break the traditional geographical and spatial limitations of construction industry clusters, achieving cross-regional integration of the industry chain.
- (3)
- The government should act as a key facilitator, strengthening the construction of market-oriented systems that benefit both the market and the government, to provide a favorable policy and institutional environment as well as a market supply and demand environment for the synergistic development of construction industry clusters. Government departments should refine the market standards and legal frameworks related to construction industry clusters. They should enhance support and promotion for the development of these clusters, actively support and guide the aggregation of innovative resources towards the clusters, and advance mixed development within the industry.
Author Contributions
Conceptualization, J.Z. and L.Z.; methodology, L.Z. and Y.X.; formal analysis, L.Z. and Y.X.; investigation, L.Z., X.Y. and Y.X.; resources, X.Y. and Y.X.; data curation, L.Z. and X.Y.; writing—original draft preparation, J.Z., L.Z. and Y.X.; writing—review and editing, J.Z. and L.Z.; supervision, J.Z.; project administration, J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors wish to thank the anonymous reviewers and editors who reviewed this manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Tan, Y.; Gu, Z.; Chen, Y.; Li, J. Industry Linkage and Spatial Co-Evolution Characteristics of Industrial Clusters Based on Natural Semantics: Taking the Electronic Information Industry Cluster in the Pearl River Delta as an Example. Sustainability 2022, 14, 14047. [Google Scholar] [CrossRef]
- Dyrdonova, A.N.; Shinkevich, A.I.; Fomin, N.Y.; Andreeva, E.S. Formation and development of industrial clusters in the regional economy. Rev. Espac. 2019, 40, 21–28. Available online: https://api.semanticscholar.org/CorpusID:158668298 (accessed on 28 December 2023).
- Guangdong Provincial People’s Government Office. Notification on the Issuance of Several Measures to Promote High-Quality Development of the Construction Industry in Guangdong: Guangdong Provincial People’s Government Office [2021] No. 11. Available online: https://www.gd.gov.cn/zwgk/gongbao/2021/23/content/post_3496254.html (accessed on 20 April 2024).
- Shandong Provincial Department of Housing and Urban-Rural Development. Opinions on Promoting the Development of the Whole Industry Chain of Modern Industrialization of Architecture: Shandong Provincial Department of Housing and Urban-Rural Development [2022] No. 5. Available online: http://zjt.shandong.gov.cn/art/2023/12/14/art_103756_10337079.html (accessed on 20 April 2024).
- Porter, M.E. Location, competition, and economic development: Local clusters in a global economy. Econ. Dev. Q. 2000, 14, 15–34. [Google Scholar] [CrossRef]
- Adeyemi, O.S.; Adeyemi, O.; Olawale, O. Does indu 124240001400105 strial cluster influence firms’ growth? Evidence from Oluyole industrial estate, Ibadan Oyo State, Nigeria. J. Econ. Allied Res. 2020, 4, 38–49. Available online: https://jearecons.com/index.php/jearecons/article/view/160 (accessed on 20 June 2023).
- Long, C.; Zhang, X. Patterns of China’s industrialization: Concentration, specialization, and clustering. China Econ. Rev. 2012, 23, 593–612. [Google Scholar] [CrossRef]
- Zagidullina, G.; Ivanova, R.; Nugumanova, G.; Sirazetdinov, R.; Zaripova, A. The improvement of construction industry innovative potential through the creation of a cluster. In Proceedings of the International Scientific Conference on Socio-Technical Construction and Civil Engineering (STCCE-2020), Kazan, Russian, 29 April–15 May 2020; Volume 890, p. 012121. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Y.; Philbin, S.P.; Ballesteros-Pérez, P.; Ouyan, Y.; Cheng, J. Influence of agglomeration and selection effects on the Chinese construction industry. Eng. Sustain. 2021, 174, 9–22. [Google Scholar] [CrossRef]
- Liu, H.; Chen, J. Elements, driving mechanisms, and competitive advantages: The development logic of industrial clusters. China Soft Sci. 2005, 2, 125–130. [Google Scholar]
- Li, X.; He, J. Research on the circular economy development issues in the Beijing-Tianjin-Hebei region. Public Financ. Econ. Res. 2016, 1, 144–151. [Google Scholar]
- Sun, W. Research on the business model innovation and transformation and upgrading path of SMEs in industrial clusters: From the perspective of collaborative innovation. Contemp. Econ. Manag. 2019, 41, 24. [Google Scholar] [CrossRef]
- Porter, M. On Competition; Harvard Business School Press: Boston, MA, USA, 1998. [Google Scholar]
- Bresnahan, T.; Gambardella, A. Building a High-Tech Cluster: Silicon Valley and Beyond; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Sun, J. Construction Industry Clusters—Mechanisms, Effects, and Development Strategies; Chemical Industry Press: Beijing, China, 2012; pp. 54–76. [Google Scholar]
- Sun, J.; Li, F. Construction of a competitiveness evaluation index system for construction industry clusters. Stat. Decis. 2017, 21, 57–59. [Google Scholar] [CrossRef]
- Gao, L.; Wang, X. Analysis of the evolution and growth of construction industry clusters in China. Mod. Urban Res. 2012, 12, 1–5. [Google Scholar]
- Zhang, J.; Zhang, P.; Liu, L. The impact of construction industry cluster network evolution on competitiveness: An empirical analysis based on SEM. Sci. Technol. Manag. Res. 2016, 36, 148–156. [Google Scholar]
- Aarikka-Stenroos, L.; Ritala, P. Network management in the era of ecosystems: Systematic review and management framework. Ind. Mark. Manag. 2017, 67, 23–36. [Google Scholar] [CrossRef]
- Meyer, K.E.; Peng, M.W. Theoretical foundations of emerging economy business research. J. Int. Bus. Stud. 2016, 47, 3–22. [Google Scholar] [CrossRef]
- Hu, Y. Industrial cluster ecosystems: Themes, evolution, and methods. Foreign Econ. Manag. 2022, 44, 114–135. [Google Scholar] [CrossRef]
- Adner, R. Ecosystem as structure. J. Manag. 2017, 43, 39–58. [Google Scholar] [CrossRef]
- Thomas, L.D.W.; Autio, E. Oxford Research Encyclopedia of Business and Management; Oxford University Press: Oxford, UK, 2020. [Google Scholar] [CrossRef]
- Ghaffar, S.H.; Burman, M.; Braimah, N. Pathways to circular construction: An integrated management of construction and demolition waste for resource recovery. J. Clean. Prod. 2020, 244, 118710. [Google Scholar] [CrossRef]
- Wijewickrama, M.K.C.S.; Rameezdeen, R.; Chileshe, N. Information brokerage for circular economy in the construction industry: A systematic literature review. J. Clean. Prod. 2021, 313, 127938. [Google Scholar] [CrossRef]
- Madhok, A.; Liu, C. A coevolutionary theory of the multinational firm. J. Int. Manag. 2006, 12, 1–21. [Google Scholar] [CrossRef]
- Okhmatovskiy, I. Performance implications of ties to the government and SOEs: A political embeddedness perspective. J. Manag. Stud. 2010, 47, 1020–1047. [Google Scholar] [CrossRef]
- Liu, T.; Chen, X. Research on the ecological attributes and behavioral characteristics of industrial clusters. Sci. Res. Stud. 2006, 2, 197–201. [Google Scholar] [CrossRef]
- Prigogine, I.; Lefever, R. Theory of Dissipative Structures. In Synergetics; Haken, H., Ed.; Vieweg+ Teubner Verlag: Wiesbaden, Germany, 1973. [Google Scholar] [CrossRef]
- Chen, Z. Study on the Evolution Mechanism of Collaborative Innovation in Trans-Regional Industrial Clusters. Ph.D. Thesis, Capital University of Economics and Business, Beijing, China, 2016. [Google Scholar]
- Fan, J. Research on the Evolution and Evaluation of Urban Logistics Industry Cluster Ecosystems. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2018. [Google Scholar]
- Gao, Y. Driving factors of collaborative innovation in the Pearl River Delta urban agglomeration: A dynamic analysis based on the Haken model. Sci. Technol. Manag. Res. 2020, 40, 85–93. [Google Scholar]
- Janes, F. Interpretive structural modelling: A methodology for structuring complex issues. Trans. Inst. Meas. Contr. 1988, 10, 145–154. [Google Scholar] [CrossRef]
- Jindal, A.; Sangwan, K.S. Development of an Interpretive Structural Model of Barriers to Reverse Logistics Implementation in Indian Industry. In Glocalized Solutions for Sustainability in Manufacturing; Springer: Berlin/Heidelberg, Germany, 2011; pp. 448–453. [Google Scholar]
- Tognoli, E.; Zhang, M.; Fuchs, A.; Beetle, C.; Kelso, J.A.S. Coordination dynamics: A foundation for understanding social behavior. Front. Hum. Neurosci. 2020, 14, 317. [Google Scholar] [CrossRef]
- Zhang, X.; Shen, J.; Sun, F.; Wang, S.; Zhang, S.; Chen, J. Allocation of flood drainage rights in watershed using a hybrid fbwm-grey-topsis method: A case study of the Jiangsu section of the Sunan Canal, China. Int. J. Environ. Res. Public Health 2022, 19, 8180. [Google Scholar] [CrossRef]
- Haken, H. Synergetics: An Introduction; Springer: Berlin/Heidelberg, Germany, 1977. [Google Scholar]
- Chen, X. Modern Statistical Analysis Methods: Theory and Application; National Defense Industry Press: Beijing, China, 2016; pp. 222–223. [Google Scholar]
- Li, Q.; Hu, Y. Study on the Evolution Mechanism of China’s Big Data Industry Based on the Haken Model. Ind. Technol. Econ. 2020, 39, 125–131. [Google Scholar] [CrossRef]
- Zhang, J. Research on the Influencing Factors and Effects of Industrial Collaborative Development in the Yangtze River Delta Region. Ph.D. Thesis, Nanjing University, Nanjing, China, 2021. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).