Investigating a Sustainable Inventory System with Controlled Non-Instantaneous Deterioration for Green Products via the Dragonfly Algorithm
Abstract
1. Introduction
2. Literature Survey
2.1. Models Related to Inventory
2.2. Inventory Model with Sustainability
3. Notation
Assumption
4. Mathematical Formulation
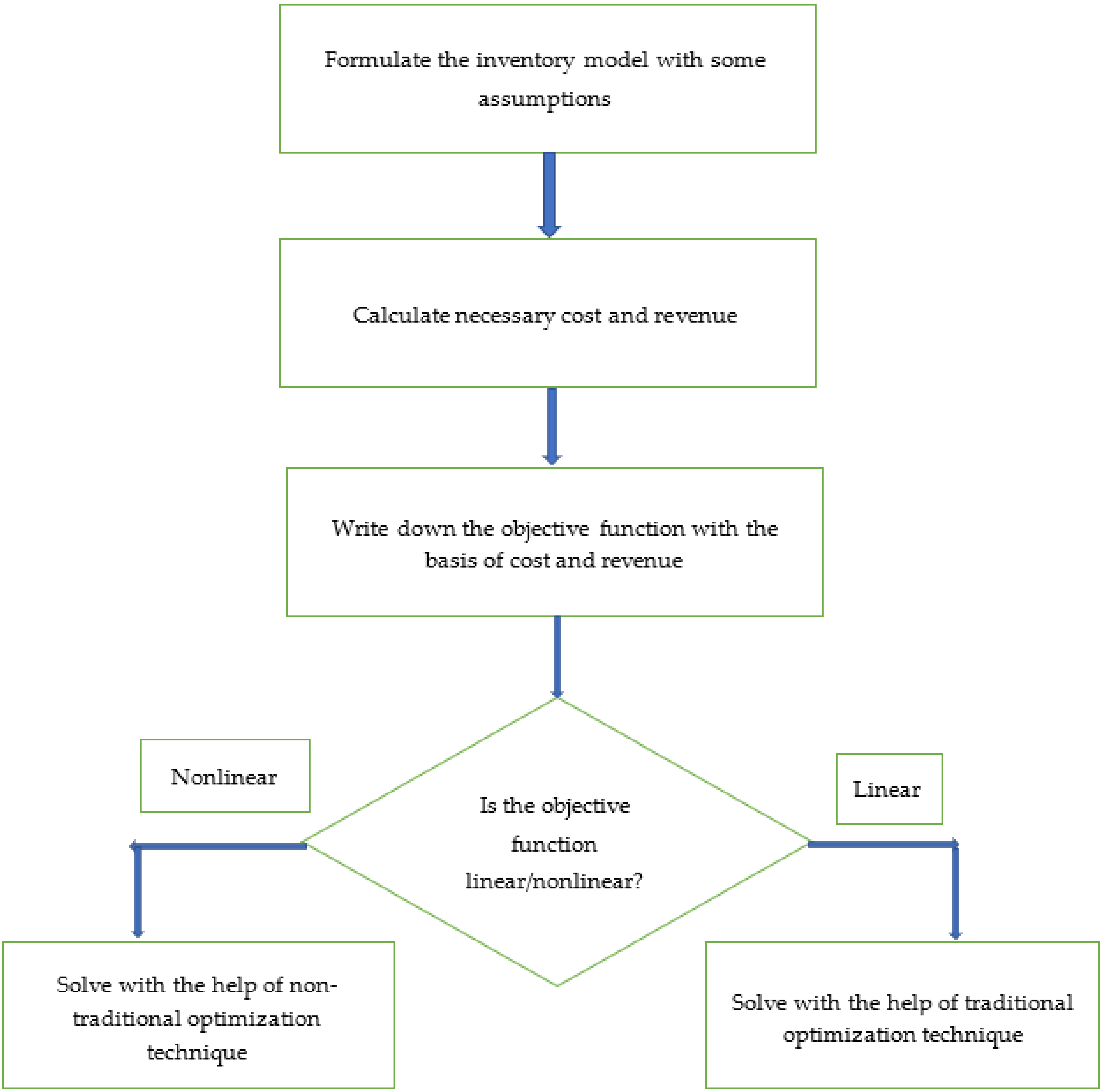
5. Solution Methodology
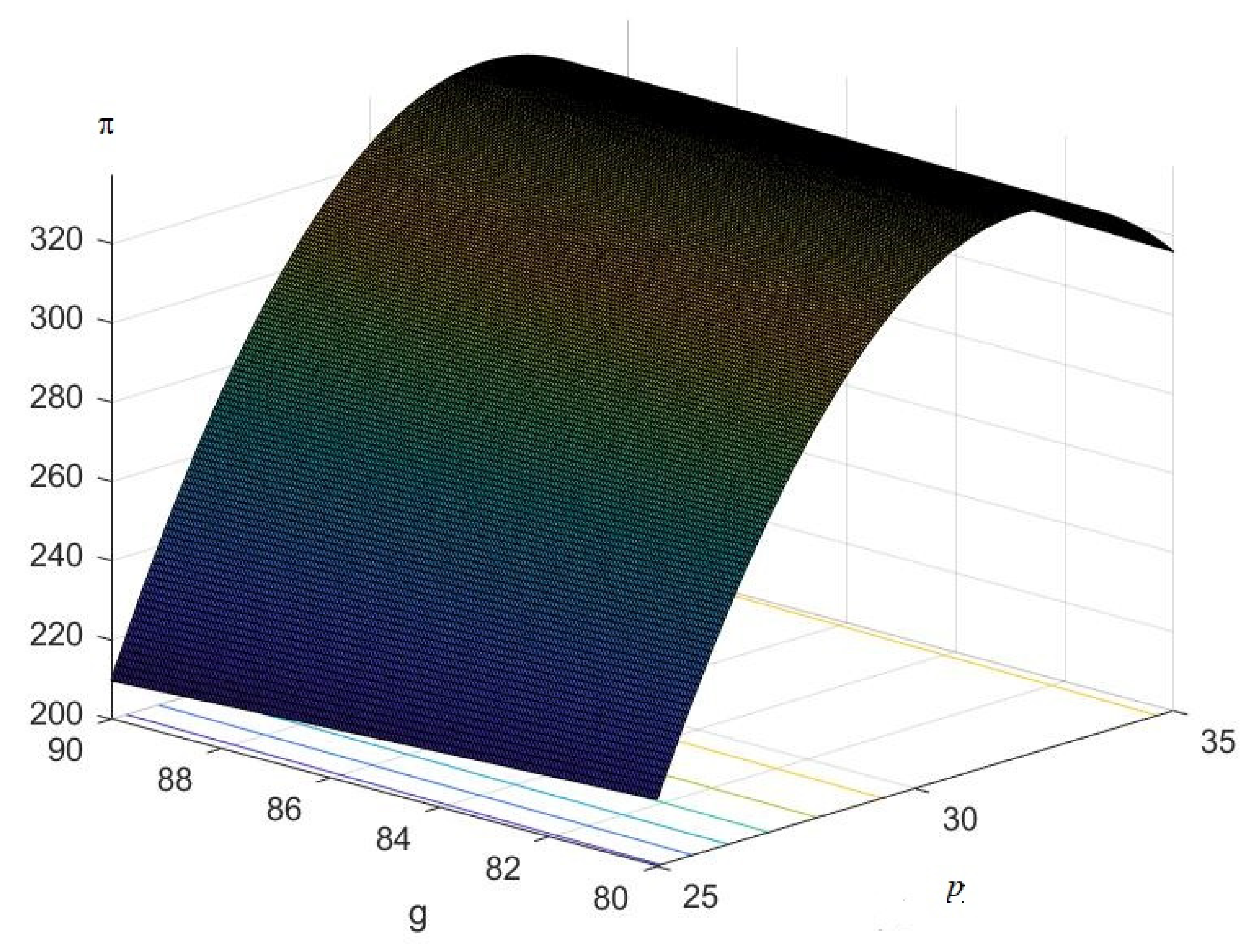
6. Numerical Explanation
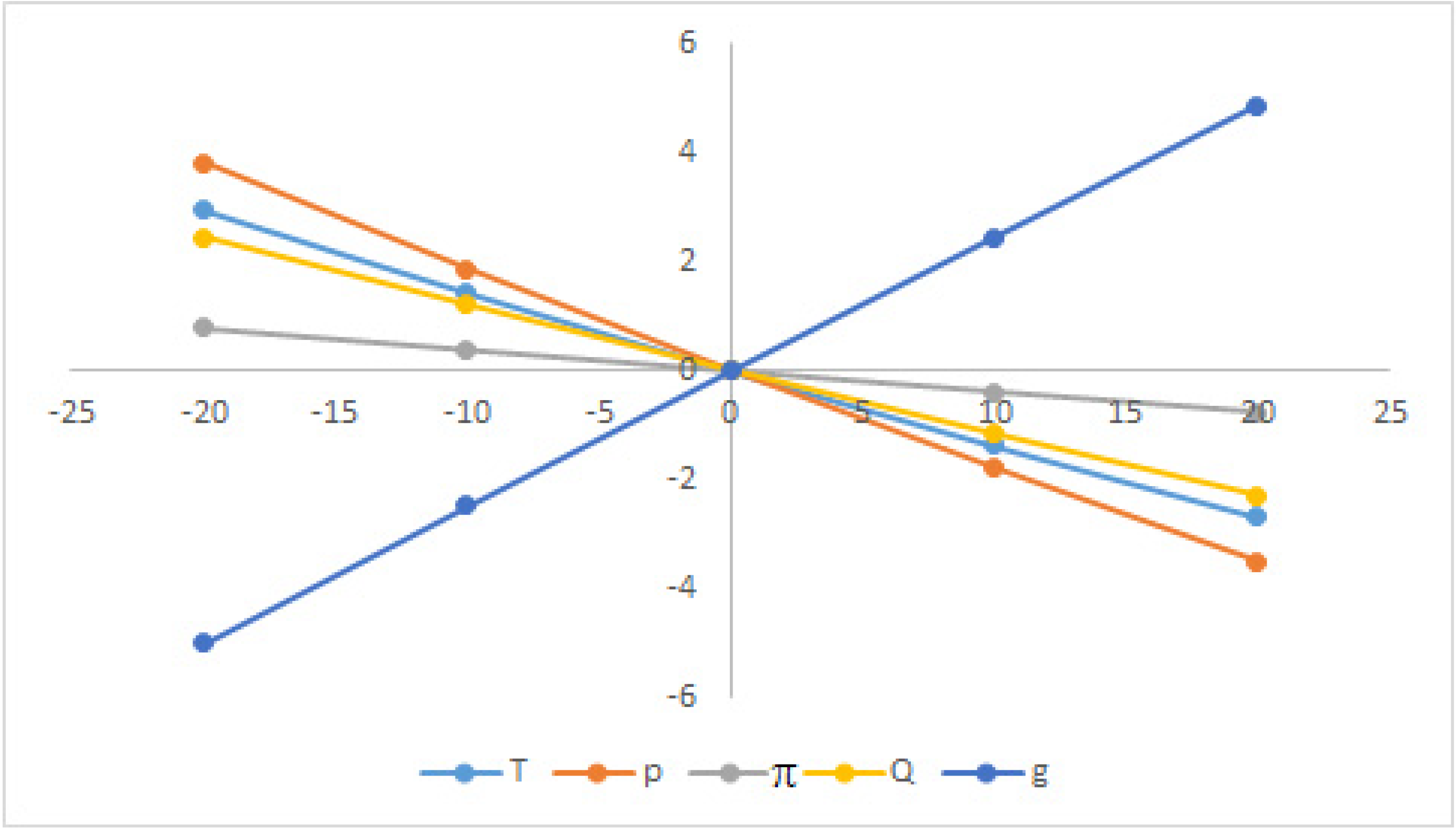
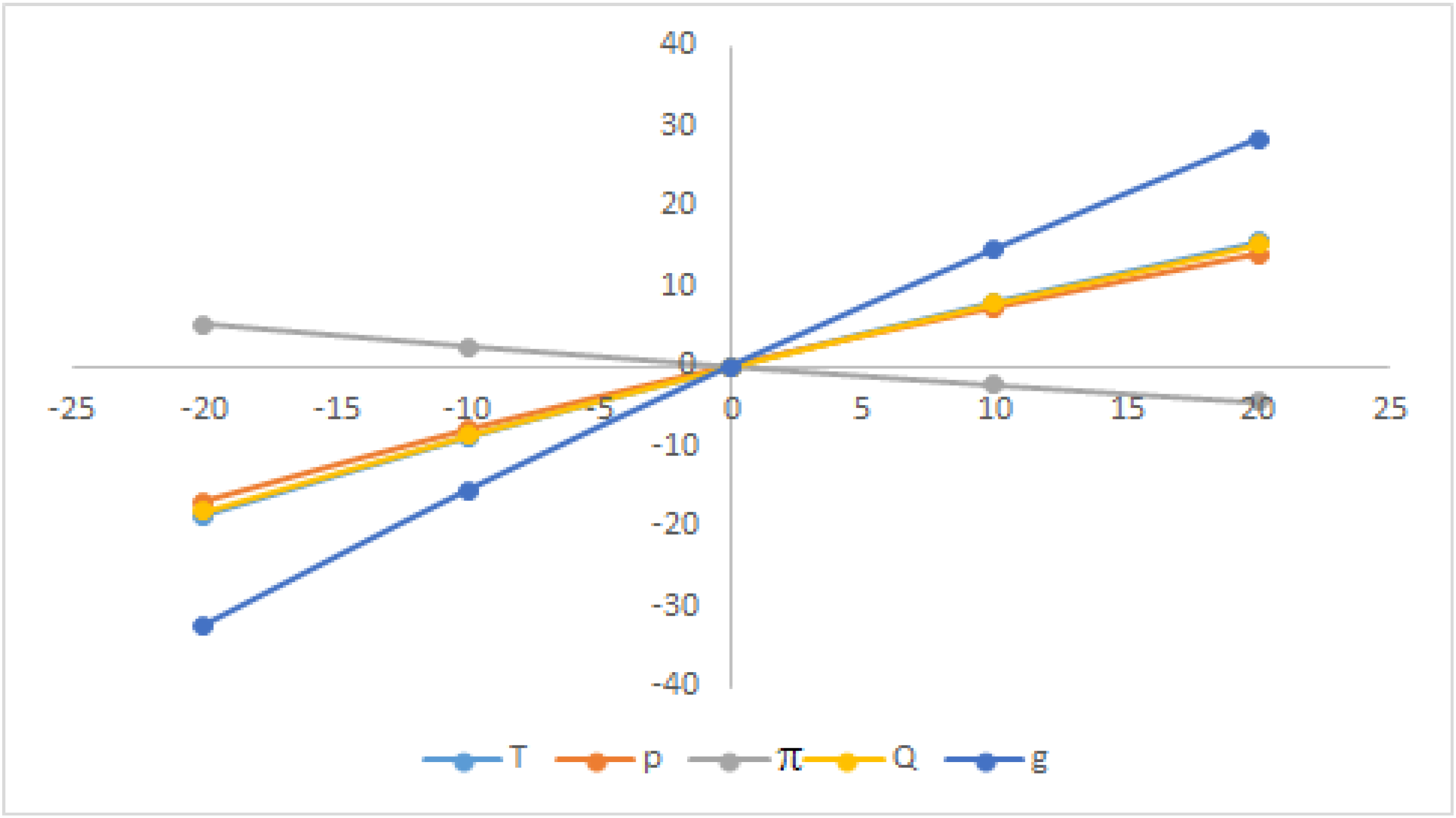
7. Post-Optimality Analyses
Managerial Implication
8. Conclusions
Specific Future Research Directions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lin, H.J. Investing in transportation emission cost reduction on environmentally sustainable EOQ models with partial backordering. J. Appl. Sci. Eng. 2018, 21, 291–303. [Google Scholar]
- Annadurai, K.; Uthayakumar, R. Ordering cost reduction in inventory model with defective items and backorder price discount. J. Opt. 2014, 2014, 767943. [Google Scholar] [CrossRef]
- Lee, W.C.; Wu, J.W.; Lei, C.L. Computational algorithmic procedure for optimal inventory policy involving ordering cost reduction and back-order discounts when lead time demand is controllable. Appl. Math. Comput. 2007, 189, 186–200. [Google Scholar] [CrossRef]
- Chang, H.C.; Ouyang, L.Y.; Wu, K.S.; Ho, C.H. Integrated vendor–buyer cooperative inventory models with controllable lead time and ordering cost reduction. Eur. J. Oper. Res. 2006, 170, 481–495. [Google Scholar] [CrossRef]
- Teng, J.T.; Cardenas-Barron, L.E.; Chang, H.J.; Wu, J.; Hu, Y. Inventory lot-size policies for deteriorating items with expiration dates and advance payments. Appl. Math. Model. 2016, 40, 8605–8616. [Google Scholar] [CrossRef]
- Dye, C.-Y.; Yang, C.T. Sustainable trade credit and replenishment decisions with credit-linked demand under carbon emission constraints. Eur. J. Oper. Res. 2015, 244, 187–200. [Google Scholar] [CrossRef]
- Baker, R.C.; Urban, T.L. A deterministic inventory system with an inventory level dependent demand rate. J. Oper. Res. Soc. 1988, 39, 823–831. [Google Scholar] [CrossRef]
- Hou, K.L.; Lin, L.C. An EOQ model for deteriorating items with price-and stock-dependent selling rates under inflation and time value of money. Int. J. Syst. Sci. 2006, 37, 1131–1139. [Google Scholar] [CrossRef]
- Min, J.; Zhou, Y.W. A perishable inventory model under stock-dependent selling rate and shortage-dependent partial backlogging with capacity constraint. Int. J. Syst. Sci. 2009, 40, 33–44. [Google Scholar] [CrossRef]
- Geetha, K.V.; Uthayakumar, R. Economic design of an inventory policy for non-instantaneous deteriorating items under permissible delay in payments. J. Comput. Appl. Math. 2010, 223, 2492–2505. [Google Scholar] [CrossRef]
- Deane, J.; Agarwal, A. Scheduling online advertisements to maximize revenue under variable display frequency. Omega 2012, 40, 62–70. [Google Scholar] [CrossRef]
- Shah, N.H.; Soni, H.N.; Patel, K.A. Optimizing inventory and marketing policy for non-instantaneous deteriorating items with generalized type deterioration and holding cost rates. Omega 2013, 41, 421–430. [Google Scholar] [CrossRef]
- Pando, V.; Garcıa-Lagunaa, J.; San-Jose, L.A.; Sicilia, J. Maximizing profits in an inventory model with both demand rate and holding cost per unit time dependent on the stock level. Comput. Ind. Eng. 2012, 62, 599–608. [Google Scholar] [CrossRef]
- Maihami, R.; Abadi, I.N.K. Joint control of inventory and its pricing for non-instantaneously deteriorating items under permissible delay in payments and partial backlogging. Math. Comput. Model. 2012, 55, 1722–1733. [Google Scholar]
- Pal, S.; Mahapatra, G.S. An inventory model of price and stock dependent demand rate with deterioration under inflation and delay in payment. Int. J. Syst. Assur. Eng. Manage. 2014, 5, 591–601. [Google Scholar] [CrossRef]
- Yang, C.T. An inventory model with both stock-dependent demand rate and stock-dependent holding cost rate. Int. J. Prod. Econ. 2014, 155, 214–221. [Google Scholar] [CrossRef]
- Maihami, R.; Karimi, B. Optimizing the pricing and replenishment policy for non-instantaneous deteriorating items with stochastic demand and promotional efforts. Comput. Oper. Res. 2014, 51, 302–312. [Google Scholar] [CrossRef]
- Chang, C.T.; Cheng, M.C.; Ouyang, L.Y. Optimal pricing and ordering policies for non-instantaneously deteriorating items under order size dependent delay in payments. Appl. Math. Model. 2015, 39, 747–763. [Google Scholar] [CrossRef]
- Dye, C.Y.; Hsieh, T.P. An optimal replenishment policy for deteriorating items with effective investment in preservation technology. Eur. J. Oper. Res. 2012, 218, 106–112. [Google Scholar]
- Dye, C.Y. The effect of preservation technology investment on a non-instantaneous deteriorating inventory model. Omega 2013, 41, 872–880. [Google Scholar] [CrossRef]
- He, Y.; Huang, H. Optimizing inventory and pricing policy for seasonal deteriorating products with preservation technology investment. J. Ind. Eng. 2013, 2013, 793568. [Google Scholar] [CrossRef]
- Hsieh, T.P.; Dye, C.Y. A production-inventory model incorporating the effect of preservation technology investment when demand is fluctuating with time. J. Comput. Appl. Math. 2013, 239, 25–36. [Google Scholar] [CrossRef]
- Mishra, U. An inventory model for deteriorating items under trapezoidal type demand and controllable deterioration rate. Prod. Eng. 2015, 9, 351–365. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, J.; Tang, W. Joint dynamic pricing and investment strategy for perishable foods with price-quality dependent demand. Ann. Oper. Res. 2015, 226, 397–416. [Google Scholar] [CrossRef]
- Alfares, H.K.; Ghaithan, A.M. Inventory and pricing model with price-dependent demand, time-varying holding cost, and quantity discounts. Comput. Ind. Eng. 2016, 94, 170–177. [Google Scholar] [CrossRef]
- Mishra, U. An inventory model for controllable probabilistic deterioration rate under shortages. Evolv. Syst. 2016, 7, 287–307. [Google Scholar] [CrossRef]
- Bardhan, S.; Pal, H.; Giri, B.C. Optimal replenishment policy and preservation technology investment for a non-instantaneous deteriorating item with stock-dependent demand. Oper. Res. 2017, 19, 347–368. [Google Scholar] [CrossRef]
- Sarkar, B.; Ahmed, W.; Choi, S.B.; Tayyab, M. Sustainable inventory management for environmental impact through partial backordering and multi-trade-credit-period. Sustainability 2018, 10, 4761. [Google Scholar] [CrossRef]
- Taleizadeh, A.A.; Soleymanfar, V.R.; Govindan, K. Sustainable economic production quantity models for inventory systems with shortage. J. Clean. Prod. 2018, 174, 1011–1020. [Google Scholar] [CrossRef]
- Tiwari, S.; Ahmed, W.; Sarkar, B. Sustainable ordering policies for non-instantaneous deteriorating items under carbon emission and multi-trade-credit-policies. J. Clean. Prod. 2019, 240, 118183. [Google Scholar] [CrossRef]
- Tiwari, S.; Daryanto, Y.; Wee, H.M. Sustainable inventory management with deteriorating and imperfect quality items considering carbon emission. J. Clean. Prod. 2018, 192, 281–292. [Google Scholar] [CrossRef]
- Ahmadini, A.A.H.; Modibbo, U.M.; Shaikh, A.A.; Ali, I. Multi-objective optimization modelling of sustainable green supply chain in inventory and production management. Alex. Eng. J. 2021, 60, 5129–5146. [Google Scholar] [CrossRef]
- Manna, A.K.; Bhunia, A.K. Investigation of green production inventory problem with selling price and green level sensitive interval-valued demand via different metaheuristic algorithms. Soft Comput. 2022, 26, 10409–10421. [Google Scholar] [CrossRef]
- Goli, A.; Tirkolaee, E.B.; Weber, G.W. A perishable product sustainable supply chain network design problem with lead time and customer satisfaction using a hybrid whale-genetic algorithm. In Logistics Operations and Management for Recycling and Reuse; Springer: Berlin/Heidelberg, Germany, 2020; pp. 99–124. [Google Scholar]
- Mashud, A.H.M.; Pervin, M.; Mishra, U.; Daryanto, Y.; Tseng, M.L.; Lim, M.K. A sustainable inventory model with controllable carbon emissions in green-warehouse farms. J. Clean. Prod. 2021, 298, 126777. [Google Scholar] [CrossRef]
- Pan, L.; Shan, M.; Li, L. Optimizing Perishable Product Supply Chain Network Using Hybrid Metaheuristic Algorithms. Sustainability 2023, 15, 10711. [Google Scholar] [CrossRef]
- Sadeghi, A.H.; Bani, E.A.; Fallahi, A.; Handfield, R. Grey wolf optimizer and whale optimization algorithm for stochastic inventory management of reusable products in a two-level supply chain. IEEE Access 2023, 11, 40278–40297. [Google Scholar] [CrossRef]
- Das, S.C.; Akhtar, F.; Alrasheedi, A.F.; Shaikh, A.A. Application of water cycle algorithm with demand follows green level and nonlinear power pattern of the product for an inventory system. Sci. Rep. 2024, 14, 20995. [Google Scholar] [CrossRef] [PubMed]
- Benjaafar, S.; Li, Y.; Daskin, M. Carbon footprint and the management of supply chains: Insights from simple models. IEEE Trans. Autom. Sci. Eng. 2013, 10, 99–116. [Google Scholar] [CrossRef]
- Chen, X.; Benjaafar, S.; Elomri, A. The carbon-constrained EOQ. Oper. Res. Lett. 2013, 41, 172–179. [Google Scholar] [CrossRef]
- Toptal, A.; Özlü, H.; Konur, D. Joint decisions on inventory replenishment and emission reduction investment under different emission regulations. Int. J. Prod. Res. 2014, 52, 243–269. [Google Scholar] [CrossRef]
- Lou, G.X.; Xia, H.Y.J.; Zhang, Q.; Fan, T.J. Investment strategy of emission-reduction technology in a supply Chain. Sustainability 2015, 7, 10684–10708. [Google Scholar] [CrossRef]
- Manna, A.K.; Das, S.; Shaikh, A.A.; Bhunia, A.K.; Moon, I. Carbon emission controlled investment and warranty policy based production inventory model via meta-heuristic algorithms. Comput. Ind. Eng. 2023, 177, 109001. [Google Scholar] [CrossRef]
- Qin, J.; Bai, X.; Xia, L. Sustainable trade credit and replenishment policies under the capand-trade and carbon tax regulations. Sustainability 2015, 7, 16340–16361. [Google Scholar] [CrossRef]
- Datta, T.K. Effect of green technology investment on a production-inventory system with carbon tax. Adv. Oper. Res. 2017, 2017, 4834839. [Google Scholar] [CrossRef]
- Hovelaque, V.; Bironneau, L. The carbon-constrained EOQ model with carbon emission dependent demand. Int. J. Prod. Econ. 2015, 164, 285–291. [Google Scholar] [CrossRef]
- Tiwari, S.; Cárdenas-Barrón, L.E.; Goh, M.; Shaikh, A.A. Joint pricing and inventory model for deteriorating items with expiration dates and partial backlogging under two-level partial trade credits in supply chain. Int. J. Prod. Econ. 2018, 200, 16–36. [Google Scholar] [CrossRef]
- Tiwari, S.; Ahmed, W.; Sarkar, B. Multi-item sustainable green production system under trade-credit and partial backordering. J. Clean. Prod. 2018, 204, 82–95. [Google Scholar] [CrossRef]
- Ahmed, W.; Sarkar, B. Impact of carbon emissions in a sustainable supply chain management for a second generation biofuel. J. Clean. Prod. 2018, 186, 807–820. [Google Scholar] [CrossRef]
- Alharbi, M.G. Carbon reduction technology based on imperfect production system for deteriorating items with warranty periods and greenness dependent demand. Sustainability 2022, 14, 15061. [Google Scholar] [CrossRef]
- Taleizadeh, A.A.; Rezvan-Beydokhti, S.; Cárdenas-Barrón, L.E. Joint determination of the optimal selling price, refund policy and quality level for complementary products in online purchasing. Eur. J. Ind. Eng. 2018, 12, 332–363. [Google Scholar] [CrossRef]
- Dey, B.K.; Sarkar, B.; Sarkar, M.; Pareek, S. An integrated inventory model involving discrete setup cost reduction, variable safety factor, selling price dependent demand, and investment. RAIRO Oper. Res. 2019, 53, 39–57. [Google Scholar] [CrossRef]
- Lu, C.J.; Yang, C.T.; Yen, H.F. Stackelberg game approach for sustainable production-inventory model with collaborative investment in technology for reducing carbon emissions. J. Clean. Prod. 2020, 270, 121963. [Google Scholar] [CrossRef]
- Sepehri, A.; Mishra, U.; Sarkar, B. A sustainable production-inventory model with imperfect quality under preservation technology and quality improvement investment. J. Clean. Prod. 2021, 310, 127332. [Google Scholar] [CrossRef]
- Becerra, P.; Mula, J.; Sanchis, R. Green supply chain quantitative models for sustainable inventory management: A review. J. Clean. Prod. 2021, 328, 129544. [Google Scholar] [CrossRef]
- Becerra, P.; Mula, J.; Sanchis, R. Sustainable inventory management in supply chains: Trends and further research. Sustainability 2022, 14, 2613. [Google Scholar] [CrossRef]
- Salas-Navarro, K.; Serrano-Pájaro, P.; Ospina-Mateus, H.; Zamora-Musa, R. Inventory models in a sustainable supply chain: A bibliometric analysis. Sustainability 2022, 14, 6003. [Google Scholar] [CrossRef]
- Pervin, M.; Roy, S.K.; Sannyashi, P.; Weber, G.W. Sustainable inventory model with environmental impact for non-instantaneous deteriorating items with composite demand. RAIRO Oper. Res. 2023, 57, 237–261. [Google Scholar] [CrossRef]
- San-José, L.A.; Sicilia, J.; Cárdenas-Barrón, L.E.; González-de-la-Rosa, M. A sustainable inventory model for deteriorating items with power demand and full backlogging under a carbon emission tax. Int. J. Prod. Econ. 2024, 268, 109098. [Google Scholar] [CrossRef]
- Mishra, U.; Cárdenas-Barrón, L.E.; Tiwari, S.; Shaikh, A.A.; Treviño-Garza, G. An inventory model under-price and stock dependent demand for controllable deterioration rate with shortages and preservation technology investment. Ann. Oper. Res. 2017, 254, 165–190. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly algorithm: A new metaheuristic optimization technique for solving singleobjective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Amroune, M.; Bouktir, T.; Musirin, I. Power system voltage stability assessment using a hybrid approach combining dragonfly optimization algorithm and support vector regression. Arab. J. Sci. Eng. 2018, 43, 3023–3036. [Google Scholar] [CrossRef]
- Babayigit, B. Synthesis of concentric circular antenna arrays using dragonfly algorithm. Int. J. Electron. 2018, 105, 784–793. [Google Scholar] [CrossRef]
- Jafari, M.; Chaleshtari, M.H.B. Using dragonfly algorithm for optimization of orthotropic infinite plates with a quasi-triangular cut-out. Eur. J. Mech.-A/Solids 2017, 66, 1–14. [Google Scholar] [CrossRef]
- Baiche, K.; Meraihi, Y.; Hina, M.D.; Ramdane-Cherif, A.; Mahseur, M. Solving graph coloring problem using an enhanced binary dragonfly algorithm. Int. J. Swarm. Intell. Res. (IJSIR) 2019, 10, 23–45. [Google Scholar] [CrossRef]
- Hariharan, M.; Sindhu, R.; Vijean, V.; Yazid, H.; Nadarajaw, T.; Yaacob, S.; Polat, K. Improved binary dragonfly optimization algorithm and wavelet packet based non-linear features for infant cry classification. Comput. Methods Progr. Biomed. 2018, 155, 39–51. [Google Scholar] [CrossRef] [PubMed]
- Rahman, C.M.; Rashid, T.A. Dragonfly algorithm and its applications in applied science survey. Comput. Intell. Neurosci. 2019, 2019, 9293617. [Google Scholar] [CrossRef] [PubMed]
- Sayed, G.I.; Tharwat, A.; Hassanien, A.E. Chaotic dragonfly algorithm: An improved metaheuristic algorithm for feature selection. Appl. Intell. 2019, 49, 188–205. [Google Scholar] [CrossRef]
- Neelima, P.; Reddy, A.R.M. An efficient load balancing system using adaptive dragonfly algorithm in cloud computing. Clust. Comput. 2020, 23, 2891–2899. [Google Scholar] [CrossRef]
- Bao, X.; Jia, H.; Lang, C. Dragonfly algorithm with opposition-based learning for multilevel thresholding color image segmentation. Symmetry 2019, 11, 716. [Google Scholar] [CrossRef]







| Symbols | Units | Common Interpretations |
|---|---|---|
| A | USD/order | Ordering cost |
| USD/order | Fixed ordering cost | |
| Demand of the product | ||
| % | Investment of preservation | |
| % | Emission cost related to the environment | |
| Average emission cost | ||
| I(t) | units | |
| Kg/unit | Carbon cap | |
| $/unit/time unit | Cost of unit holding per time unit | |
| $/time unit | Deterioration cost | |
| Q | units | Arranging the sizes in every cycle |
| $/unit/time | Cost of opportunity against capital investment | |
| $/unit | Unit cost of purchase | |
| Deterioration rate | ||
| $/time unit | Profit per unit time | |
| Decision variables | ||
| T | Time unit | Cycle length. |
| USD/unit | Price of sale per unit | |
| -- | Green level |
| Variables | Optimal Values Obtain from DA | Optimal Values Obtain from CDA | Optimal Values Obtain from ADA | Optimal Values Obtain from OBDA |
|---|---|---|---|---|
| g | 86.58237% | 86.58237% | 86.58237% | 86.58237% |
| 5.476035 months | 5.476035 months | 5.476035 months | 5.476035 months | |
| 332.2873 | 332.2873 | 332.2873 | 332.2873 | |
| USD 32.17468 | USD 32.17468 | USD 32.17468 | USD 32.17468 | |
| USD 337.3759 | USD 337.3759 | USD 337.3759 | USD 337.3759 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alharbi, M. Investigating a Sustainable Inventory System with Controlled Non-Instantaneous Deterioration for Green Products via the Dragonfly Algorithm. Sustainability 2025, 17, 1156. https://doi.org/10.3390/su17031156
Alharbi M. Investigating a Sustainable Inventory System with Controlled Non-Instantaneous Deterioration for Green Products via the Dragonfly Algorithm. Sustainability. 2025; 17(3):1156. https://doi.org/10.3390/su17031156
Chicago/Turabian StyleAlharbi, Majed. 2025. "Investigating a Sustainable Inventory System with Controlled Non-Instantaneous Deterioration for Green Products via the Dragonfly Algorithm" Sustainability 17, no. 3: 1156. https://doi.org/10.3390/su17031156
APA StyleAlharbi, M. (2025). Investigating a Sustainable Inventory System with Controlled Non-Instantaneous Deterioration for Green Products via the Dragonfly Algorithm. Sustainability, 17(3), 1156. https://doi.org/10.3390/su17031156





