A Numerical Simulation Study on the Critical Erosion of Laboratory-Scale Debris Flow
Abstract
1. Introduction
2. Materials and Methods
2.1. Coupling Logics
2.2. Experiments for Validation
2.3. Procedure for Formal Simulation Experiments
3. Results
3.1. Erosion Phases
3.2. Factors Contributing to Eroding Dynamics
3.3. Mechanical Factors
4. Discussion
4.1. Mechanisms of the Critical Erosion
4.2. Limitations of This Study
5. Conclusions
- (1)
- The process of erosion can be categorized into three distinct phases: the initial erosion phase, the net erosion phase, and the post-erosion phase, wherein the net erosion phase is responsible for the most significant erosive effects. Increasing both the grain size D and the Froude number of debris flow can enhance the erosion depth normal to the bed, and the eroded length L and the critical transport of the basal sediment are both positively correlated with the total mass M of the debris flow.
- (2)
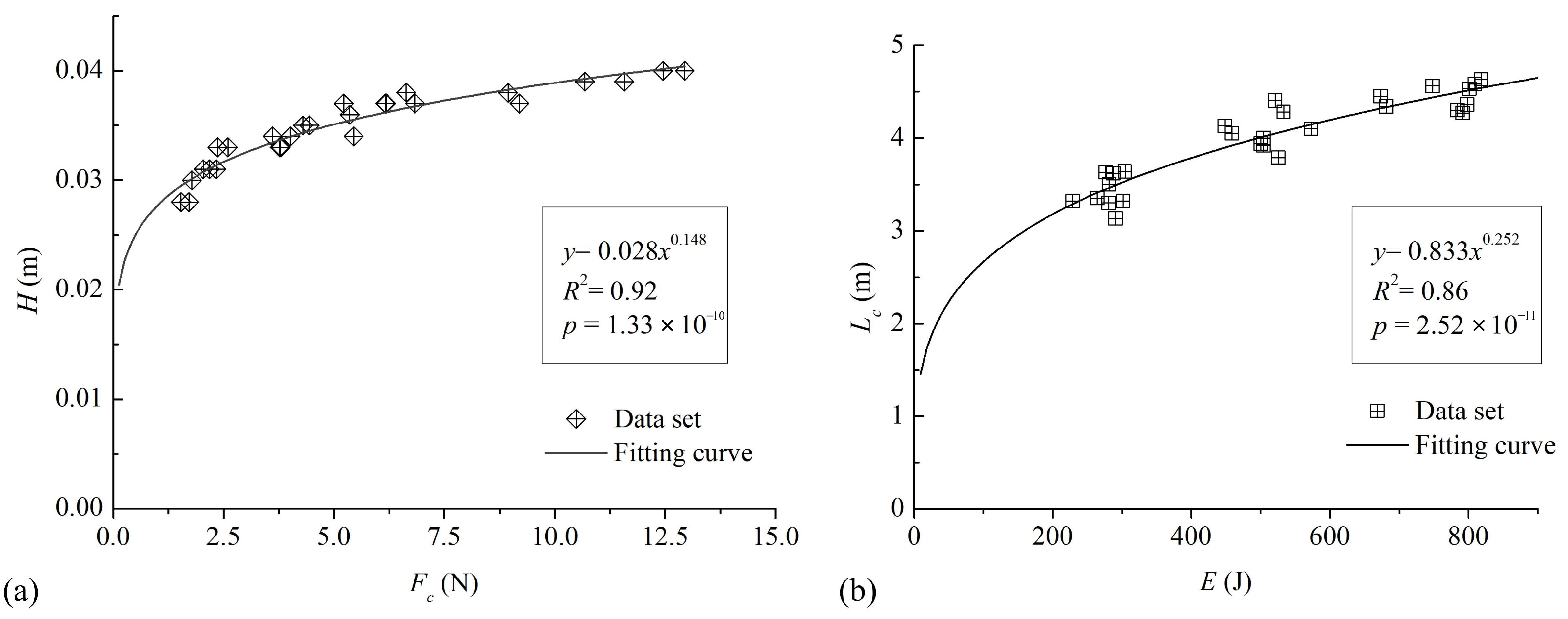
- The erosion depth H is described by a power function that correlates with the collisional point load computed by the normal impact force per unit of the debris-flow head. Furthermore, the critical entrainment transport is also represented as a power function of the impact energy E estimated by the averaged thickness of the debris flow head. Despite uncertainties, the impact energy estimation provides a practical approach for assessing the preliminary magnitude of debris flow in fields.
- (3)
- Furthermore, thresholds for both the collisional point load and the impact energy that predict the attenuated rates of the erosive depth and the critical transport of entrainment, respectively, are obtained through regression analyses.
- (4)
- The idea for the mechanisms of the erosion proposed by previous studies is verified by the presented coupled simulation that the collisional point load is key to initiating the net erosion process, while frictional shearing is the factor that sustains the flow mobility.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| D | Uniform grain size of debris flow |
| M | Total mass of debris flow |
| V | Solid fraction of debris flow |
| H | Erosion depth |
| L | Erosion length |
| Lc | Critical entrainment transport |
| Fr | Froude number |
| U | Velocity of the debris flow head |
| Ue | Velocity of the eroded material |
| Un | Velocity of the entrainment |
| h | Thickness of debris flow |
| g | Gravity acceleration |
| Fc | Collisional point load |
| E | Impact energy of debris flow |
Appendix A. Appendix for Main Results
| Serial ID. | H (m) | L (m) | (m) | U (m/s) | (m/s) | h (m) | |
|---|---|---|---|---|---|---|---|
| D4M115V45 | 2.85 | 0.035 | 1.62 | 3.32 | 2.46 | 0.09 | 0.040 |
| D4M115V50 | 2.52 | 0.037 | 1.66 | 3.5 | 2.54 | 0.12 | 0.060 |
| D4M115V55 | 2.16 | 0.037 | 1.61 | 3.62 | 2.30 | 0.13 | 0.076 |
| D4M150V45 | 4.04 | 0.037 | 1.75 | 4.05 | 2.37 | 0.15 | 0.034 |
| D4M150V50 | 2.86 | 0.038 | 1.85 | 4.13 | 2.54 | 0.18 | 0.060 |
| D4M150V55 | 2.82 | 0.039 | 1.92 | 4.40 | 2.46 | 0.20 | 0.071 |
| D4M185V45 | 3.86 | 0.039 | 1.94 | 4.45 | 2.46 | 0.20 | 0.044 |
| D4M185V50 | 3.14 | 0.040 | 1.94 | 4.56 | 2.51 | 0.23 | 0.070 |
| D4M185V55 | 2.74 | 0.040 | 2.10 | 4.63 | 2.59 | 0.24 | 0.095 |
| D3M115V45 | 1.65 | 0.031 | 1.47 | 3.32 | 2.15 | 0.08 | 0.113 |
| D3M115V50 | 2.03 | 0.033 | 1.57 | 3.35 | 2.08 | 0.10 | 0.077 |
| D3M115V55 | 1.97 | 0.033 | 1.63 | 3.63 | 2.24 | 0.11 | 0.083 |
| D3M150V45 | 2.25 | 0.035 | 1.83 | 3.92 | 2.13 | 0.13 | 0.097 |
| D3M150V50 | 2.47 | 0.034 | 1.67 | 4.00 | 2.18 | 0.13 | 0.085 |
| D3M150V55 | 2.33 | 0.037 | 1.80 | 4.28 | 2.21 | 0.17 | 0.098 |
| D3M185V45 | 2.92 | 0.036 | 1.89 | 4.34 | 2.26 | 0.17 | 0.071 |
| D3M185V50 | 2.75 | 0.037 | 2.02 | 4.36 | 2.13 | 0.18 | 0.092 |
| D3M185V55 | 2.36 | 0.038 | 1.94 | 4.58 | 2.28 | 0.18 | 0.118 |
| D2M115V45 | 1.65 | 0.028 | 1.46 | 3.13 | 1.65 | 0.07 | 0.109 |
| D2M115V50 | 1.87 | 0.028 | 1.56 | 3.30 | 1.71 | 0.08 | 0.091 |
| D2M115V55 | 1.73 | 0.030 | 1.62 | 3.64 | 1.72 | 0.10 | 0.108 |
| D2M150V45 | 2.19 | 0.031 | 1.65 | 3.79 | 1.68 | 0.11 | 0.105 |
| D2M150V50 | 2.12 | 0.031 | 1.76 | 3.94 | 1.70 | 0.13 | 0.105 |
| D2M150V55 | 2.17 | 0.033 | 1.85 | 4.10 | 1.72 | 0.14 | 0.116 |
| D2M185V45 | 2.45 | 0.033 | 1.95 | 4.27 | 1.73 | 0.14 | 0.109 |
| D2M185V50 | 2.89 | 0.034 | 1.86 | 4.30 | 1.87 | 0.15 | 0.084 |
| D2M185V55 | 1.93 | 0.034 | 1.87 | 4.53 | 1.81 | 0.16 | 0.154 |
References
- Berti, M.; Genevois, R.; LaHusen, R.; Simoni, A.; Tecca, P.R. Debris flow monitoring in the acquabona watershed on the Dolomites (Italian alps). Phys. Chem. Earth Part B Hydrol. Ocean. Atmos. 2000, 25, 707–715. [Google Scholar] [CrossRef]
- Yang, Z.Q.; Zhao, X.G.; Chen, M.; Zhang, J.; Yang, Y.; Chen, W.T.; Bai, X.F.; Wang, M.M.; Wu, Q. Characteristics, dynamic analyses and hazard assessment of Debris flows in Niumiangou valley of Wenchuan County. Appl. Sci. 2023, 13, 1161. [Google Scholar] [CrossRef]
- Abdel-Karim, A.-A.M.; Gad, A. Precious and base metal minerals in black sands of the egyptian mediterranean coast: Mineralogical and geochemical attributes. Resources 2024, 13, 109. [Google Scholar] [CrossRef]
- Li, C.J.; Hu, Y.X.; Li, H.B.; Zhou, J.W. Deciphering the dynamics of debris flows through basal stress responses in model experiments. Acta Geotech. 2025, 20, 1777–1794. [Google Scholar] [CrossRef]
- Hungr, O.; McDougall, S.; Bovis, M. Entrainment of material by debris flows. In Debris-Flow Hazards and Related Phenomena; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Li, J.; Cao, Z.X.; Hu, K.H.; Pender, G.; Liu, Q.Q. A depth-averaged two-phase model for debris flows over fixed beds. Int. J. Sediment Res. 2018, 43, 462–477. [Google Scholar] [CrossRef]
- Shen, P.; Zhang, L.M.; Wong, H.F.; Peng, D.L.; Zhou, S.Y.; Zhang, S.; Chen, C. Debris flow enlargement from entrainment: A case study for comparison of three entrainment models. Eng. Geol. 2020, 270, 105581. [Google Scholar] [CrossRef]
- Wang, Y.H.; Mao, W.W.; Yang, P.; Huang, Y.; Zheng, H. CFD-DEM study on the entrainment induced by debris flows with the HBP rheological model. IOP Conf. Ser. Earth Environ. Sci. 2021, 861, 072012. [Google Scholar] [CrossRef]
- Stoffel, M.; Mendlik, T.; Schneuwly-Bollschweiler, M.; Gobiet, A. Possible impacts of climate change on debris-flow activity in the Swiss Alps. Clim. Change 2014, 122, 141–155. [Google Scholar] [CrossRef]
- Jiang, Y.; Song, P.; Choi, C.E.; Choo, J. Erosion and transport of dry soil bed by collisional granular flow: Insights from a combined experimental– numerical investigation. J. Geophys. Res. Earth Surf. 2023, 128, e2023JF007073. [Google Scholar] [CrossRef]
- Berger, C.; Mcardell, B.W.; Schlunegger, F. Direct measurement of channel erosion by debris flows, Illgraben, Switzerland. J. Geophys. Res.-Earth Surf. 2011, 116, F01002. [Google Scholar] [CrossRef]
- Iverson, R.M.; Reid, M.E.; Logan, M.; LaHusen, R.G.; Godt, J.W.; Griswold, J.P. Positive feedback and momentum growth during debris-flow entrainment of wet bed sediment. Nat. Geosci. 2011, 4, 116–121. [Google Scholar] [CrossRef]
- Iverson, R.M. Elementary theory of bed-sediment entrainment by debris flows and avalanches. J. Geophys. Res. Earth Surf. 2012, 117, F03006. [Google Scholar] [CrossRef]
- Egashira, S.; Honda, N.; Itoh, T. Experimental study on the entrainment of bed material into debris flow. Phys. Chem. Earth Part C Solar Terr. Planet. Sci. 2001, 26, 645–650. [Google Scholar] [CrossRef]
- Choi, C.E.; Song, P. New unsaturated erosion model for landslide: Effects of flow particle size and debunking the importance of frictional stress. Eng. Geol. 2023, 315, 107024. [Google Scholar] [CrossRef]
- Zheng, H.; Hu, X.; Shi, Z.; McArdell, B.; de Haas, T. Volumetric growth of debris flow on erodible bed by basal shear and collision: Theory and observations. Earth Planet. Sci. Lett. 2025, 662, 119404. [Google Scholar] [CrossRef]
- Ning, L.; Hu, K.; Li, P.; Cheng, H.; Liu, S.; Zhang, Q. Peak discharge amplication of debris flows in colluvial channels with varying cross-sections. Environ. Earth Sci. 2025, 84, 217. [Google Scholar] [CrossRef]
- Mcdougall, S.; Hungr, O. Dynamic modelling of entrainment in rapid landslides. Can. Geotech. J. 2005, 42, 1437–1448. [Google Scholar] [CrossRef]
- Zhao, J.; Shan, T. Coupled CFD-DEM simulation of fluid-particle interaction in geomechanics. Powder Technol. 2013, 239, 248–258. [Google Scholar] [CrossRef]
- Kong, Y.; Zhao, J.D.; Li, X.Y. Coupled CFD/DEM Modeling of Multiphase Debris Flow over a Natural Erodible Terrain: The Yu Tung Road Case. In Proceedings of the Second JTC1 Workshop, Hongkong, China, 3–5 December 2018; The Hong Kong Geotechnical Society: Hong Kong, China, 2018. [Google Scholar]
- Razavi, F.; Komrakova, A.; Lange, C.F. CFD–DEM Simulation of Sand-Retention Mechanisms in Slurry Flow. Energies 2021, 14, 3797. [Google Scholar] [CrossRef]
- Kong, Y.; Li, X.; Zhao, J. Quantifying the transition of impact mechanisms of geophysical flows against flexible barrier. Eng. Geol. 2021, 289, 106188. [Google Scholar] [CrossRef]
- Kong, Y.; Li, X.; Zhao, J.; Guan, M. Load–deflection of flexible ring-net barrier in resisting debris flows. Géotechnique 2022, 74, 486–498. [Google Scholar] [CrossRef]
- Han, Z.; Chen, G.; Li, Y.; Tang, C.; Xu, L.; He, Y.; Huang, X.; Wang, W. Numerical simulation of debris-flow behavior incorporating a dynamic method for estimating the entrainment. Eng. Geol. 2015, 190, 52–64. [Google Scholar] [CrossRef]
- Liu, D.; Fu, X.; Wang, G. Volume fraction allocation using characteristic points for coupled CFD-DEM calculations. J. Tsinghua Univ. Technol. 2018, 7, 720–727. (In Chinese) [Google Scholar]
- Schiller, L.A.; Nauman, A. A drag coefficient correlation. Z. Vereines Ingenieure 1935, 77, 318–320. [Google Scholar]
- Brazhenko, V.; Mochalin, I. Terminal velocity and drag coefficient of a smooth steel sphere moving in the water-filled vertical and inclined glass pipe (Newton regime). Z. Powder Technol. 2024, 446, 120120. [Google Scholar] [CrossRef]
- Li, X.; Zhao, J. Dam-break of mixtures consisting of non-Newtonian liquids and granular particles. Powder Technol. 2018, 338, 493–505. [Google Scholar] [CrossRef]
- Li, X.; Zhao, J.; Kwan, J.S.H. Assessing debris flow impact on flexible ring net barrier: A coupled CFD-DEM study. Comput. Geotech. 2020, 128, 103850. [Google Scholar] [CrossRef]
- Li, X.; Zhao, J.; Soga, K. A new physically based impact model for debris flow. Géotechnique 2021, 71, 674–685. [Google Scholar] [CrossRef]
- Zhao, T.X.; Li, X. Numerical Investigation on Sediment Bed Erosion Based on CFD-DEM. In Dam Breach Modelling and Risk Disposal, Proceedings of the ICED 2020, Beijing, China, 5–7 June 2020; Zhang, J.M., Zhang, L., Wang, R., Eds.; Springer Series in Geomechanics and Geoengineering; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Levenspiel, O.; Haider, A. Drag Coefficient and Terminal Velocity of Spherical and Nonspherical Particles. Powder Technol. 1989, 58, 63–70. [Google Scholar] [CrossRef]
- George, D.; Iverson, R.M. A two-phase debris-flow model that includes coupled evolution of volume fractions, granular dilatancy, and pore-fluid pressure. Ital. J. Eng. Geol. Environ. 2011, 415–424. [Google Scholar] [CrossRef]
- Liu, W.; He, S.; Li, X. A finite volume method for two-phase debris flow simulation that accounts for the pore-fluid pressure evolution. Environ. Earth Sci. 2016, 75, 206. [Google Scholar] [CrossRef]
- Iverson, R.M.; Denlinger, R.P. Flow of variably fluidized granular masses across three-dimensional terrain: 1 Coulomb mixture theory. J. Geophys. Res. 1989, 58, 537–552. [Google Scholar] [CrossRef]
- Tayyebi, S.M.; Pisano, M.; Stickle, M.M. Two-phase SPH numerical study of pore-water pressure effect on debris flows mobility: Yu Tung debris flow. Comput. Geotech. 2021, 132, 103973. [Google Scholar] [CrossRef]
- Huo, M.; Lambert, S.; Fontaine, F.; Piton, G. Capture of near-critical debris flows by flexible barriers: An experimental investigation. Nat. Hazards Earth Syst. Sci. 2025, 25, 4115–4134. [Google Scholar] [CrossRef]
- Song, P.J.; Choi, E.C. Revealing the importance of capillary and collisional stresses on soil bed erosion induced by debris flows. J. Geophys. Res. Earth Surf. 2021, 126, e2020JF005930. [Google Scholar] [CrossRef]
- Iverson, R.M. The physics of debris flows. Rev. Geophys. 1997, 35, 245–296. [Google Scholar] [CrossRef]
- Ouyang, C.; He, S.; Tang, C. Numerical analysis of dynamics of debris flow over erodible beds in Wenchuan earthquake-induced area. Eng. Geol. 2015, 194, 62–72. [Google Scholar] [CrossRef]
- Zheng, H.; Shi, Z.; Peng, M.; Yu, S. Coupled CFD-DEM model for the direct numerical simulation of sediment bed erosion by viscous shear flow. Eng. Geol. 2018, 245, 309–321. [Google Scholar] [CrossRef]
- Sarno, L.; Carleo, L.; Papa, M.N.; Villani, P. Experimental investigation on the effects of the fixed boundaries in channelized dry granular flows. Rock Mech. Rock Eng. 2018, 51, 203–225. [Google Scholar] [CrossRef]
- Komatsu, T.; Inagaki, S.; Nakagawa, N.; Nasuno, S. Creep motion in a granular pile exhibiting steady surface flow. Phys. Rev. Lett. 2001, 86, 1757–1760. [Google Scholar] [CrossRef]
- Pudasaini, S.P.; Krautblatter, M. The mechanics of landslide mobility with erosion. Nat. Commun. 2021, 12, 6793. [Google Scholar] [CrossRef]
- Liu, H.W.; Zhao, X.Y.; Frattini, P.; Crosta, G.B.; De Blasio, F.V.; Wan, Y.H.; Zhu, X.Z. Mobility and erosion of granular flows travelling on an erodible substrate: Insights from the small-scale flume experiments. Eng. Geol. 2023, 326, 107316. [Google Scholar] [CrossRef]
- Pandey, N.K.; Satyam, N. Entrainment-driven morphological changes in debris flow deposits by varying water content at laboratory scale. Bull. Eng. Geol. Environ. 2025, 84, 215. [Google Scholar] [CrossRef]
- Iverson, R.M.; Logan, M.; LaHusen, R.; Berti, M. The perfect debris flow? Aggregated results from 28 large-scale experiments. J. Geophys. Res. Earth Surf. 2010, 115, F03005. [Google Scholar] [CrossRef]
- Iverson, R.M. Scaling and design of landslide and debris-flow experiments. Geomorphology 2015, 244, 9–20. [Google Scholar] [CrossRef]
- Federico, F.; Cesali, C. An energy-based approach to predict debris flow mobility and analyze empirical relationships. Can. Geotech. J. 2015, 52, 2113–2133. [Google Scholar] [CrossRef]

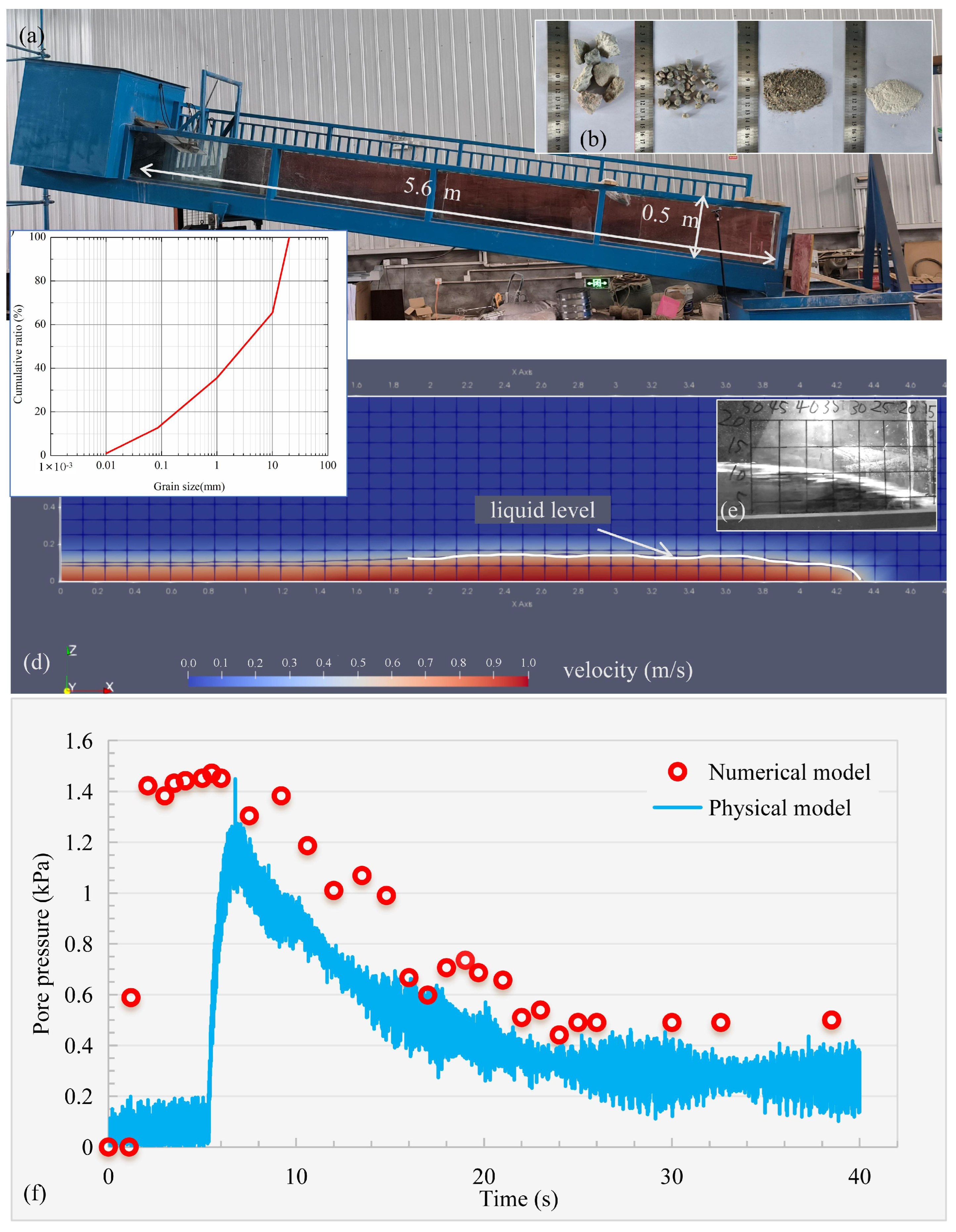
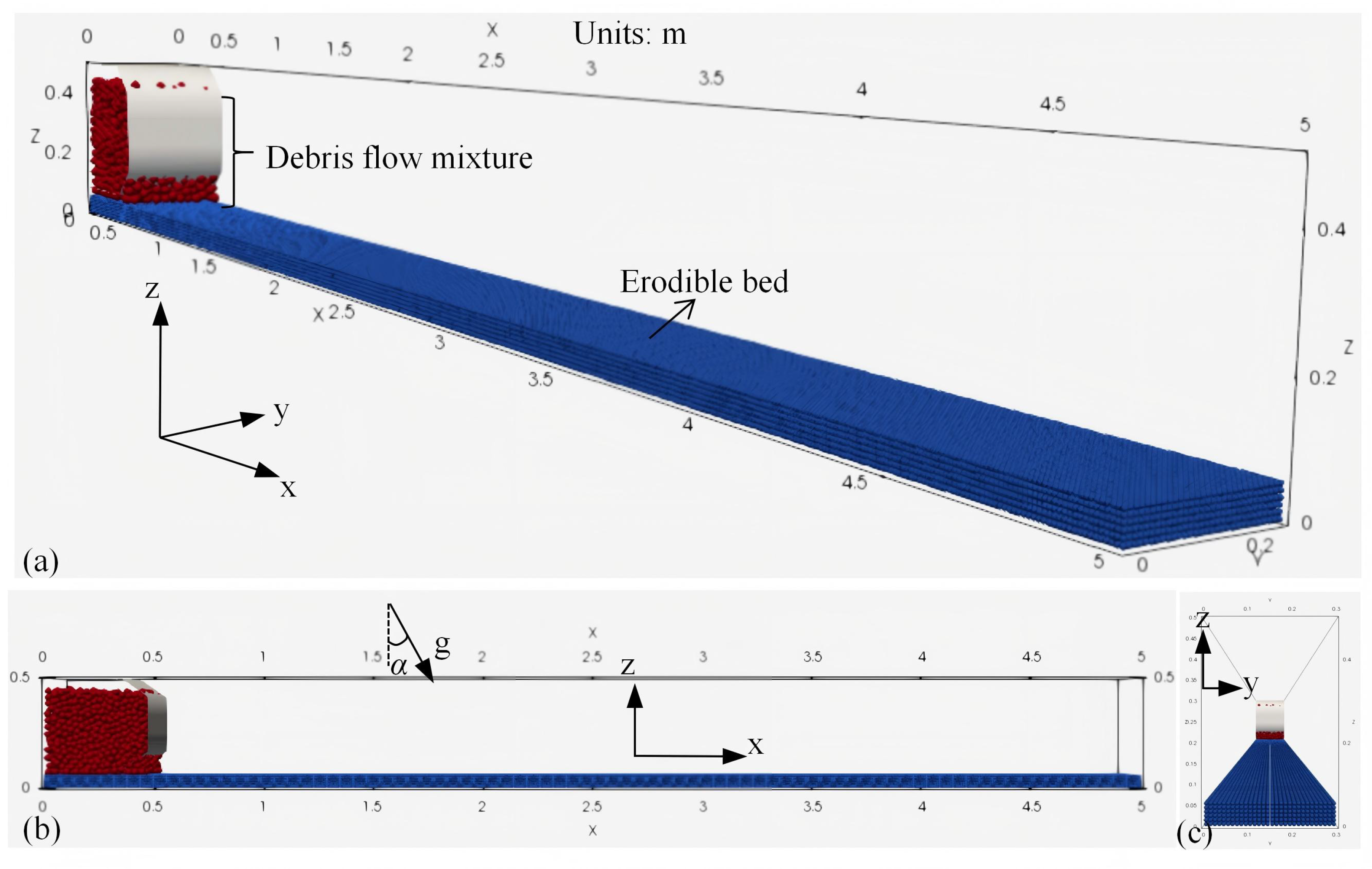
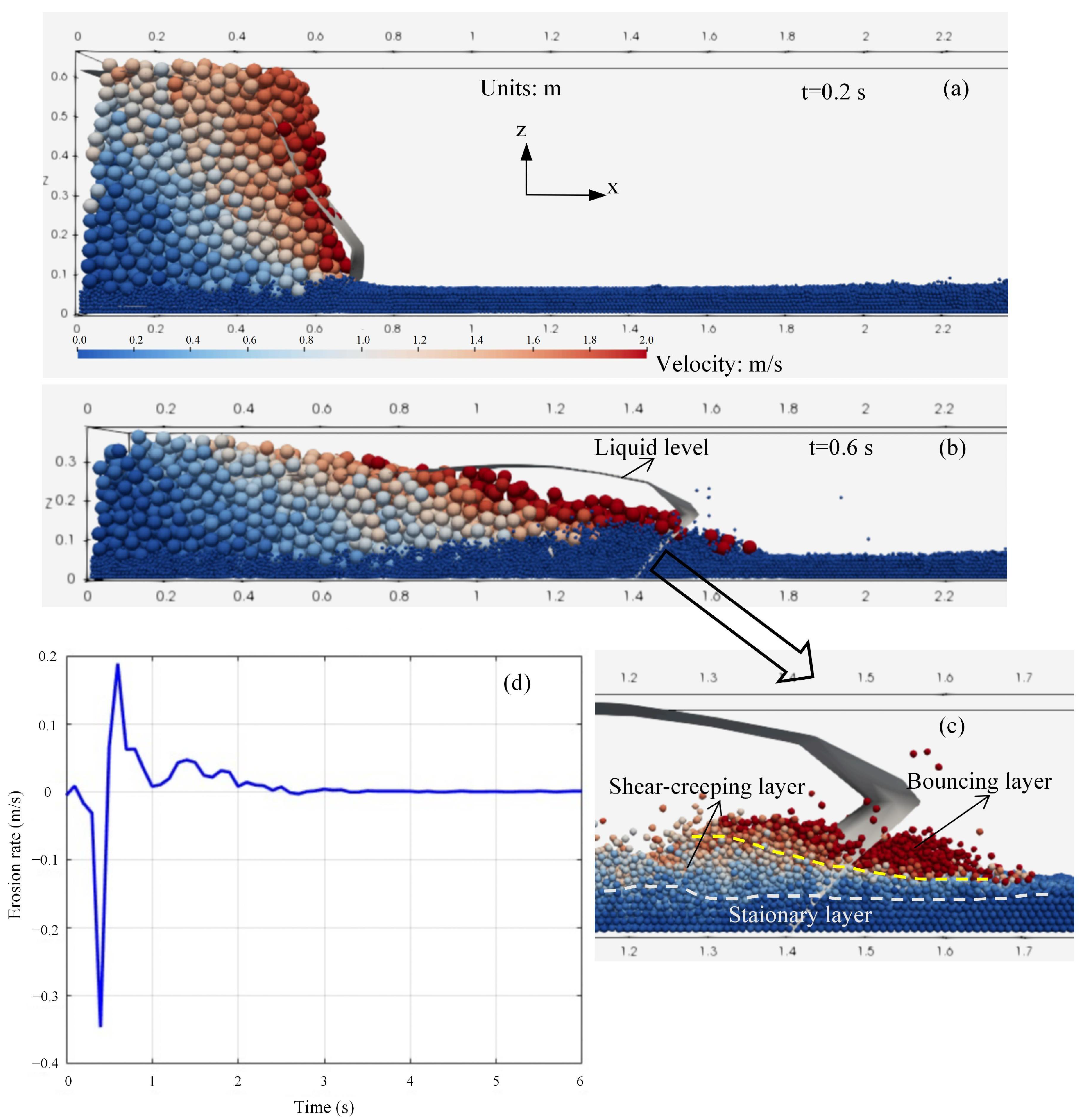

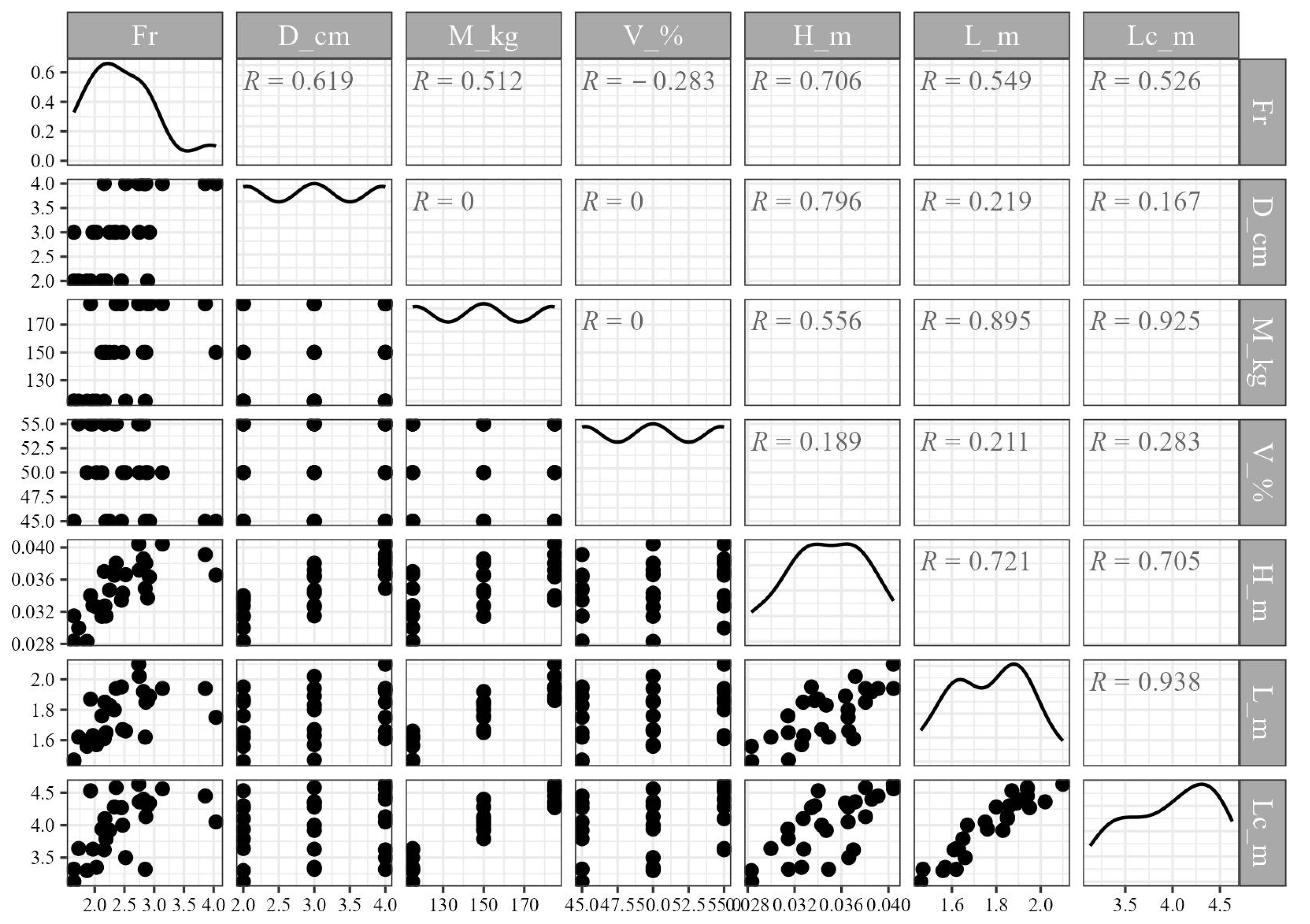
| Parameters | Sinking Sphere | Erodible Bed | Debris Flow |
|---|---|---|---|
| Cell size for CFD domain (mm) | 20 × 20 × 20 | 60 × 100 × 60 | 60 × 100 × 60 |
| Mean particle diameter (mm) | 1 | 10 | 20/30/40 1 |
| Gravity acceleration (m/s2) | 9.81 | 9.81 | 9.81 |
| Dynamic viscosity of liquid (Pa·s) | 0.001 | 0.001 | 0.001 |
| Message exchange resolution (time steps) | 10 | 10 | 10 |
| Particle density (kg/m3) | 2650 | 2650 | 2650 |
| Young’s modulus for particle–particle contact (GPa) | - | 0.5 | 0.5 |
| Rolling friction coefficient for particle–particle contact | - | 0.1 | 0.1 |
| Shearing friction coefficient for particle–particle contact | 0.7 | 0.7 | 0.7 |
| Rebound coefficient for particle–particle contact | 0.4 | 0.4 | 0.4 |
| Poisson’s ratio for particle–particle contact | - | 0.3 | 0.3 |
| Time step (s) | 0.01 | 0.001 | 0.001 |
| Solid fraction | - | 1 | 0.45/0.50/0.55 2 |
| Results | Physical Model | Numerical Model |
|---|---|---|
| Pore pressure dissipation time (s) | 38 | 26 |
| Mean flow velocity U (m/s) | 1.32 | 2.30 |
| Mean flow thickness (m) | 0.10 | 0.15 |
| 1.68 | 1.93 | |
| Deposit depth (m) | 0.15 | 0.16 |
| 0.7 | 0.5 |
| Solid Fraction (%) | Uniform Diameter of Debris Flow (cm) | Total Mass (kg) | Serial ID. |
|---|---|---|---|
| 55 | 4 | 115 | D4M115V55 |
| 150 | D4M150V55 | ||
| 185 | D4M185V55 | ||
| 55 | 3 | 115 | D3M115V55 |
| 150 | D3M150V55 | ||
| 185 | D3M185V55 | ||
| 55 | 2 | 115 | D2M115V55 |
| 150 | D2M150V55 | ||
| 185 | D2M185V55 | ||
| 50 | 4 | 115 | D4M115V50 |
| 150 | D4M150V50 | ||
| 185 | D4M185V50 | ||
| 50 | 3 | 115 | D3M115V50 |
| 150 | D3M150V50 | ||
| 185 | D3M185V50 | ||
| 50 | 2 | 115 | D2M115V50 |
| 150 | D2M150V50 | ||
| 185 | D2M185V50 | ||
| 45 | 4 | 115 | D4M115V45 |
| 150 | D4M150V45 | ||
| 185 | D4M185V45 | ||
| 45 | 3 | 115 | D3M115V45 |
| 150 | D3M150V45 | ||
| 185 | D3M185V45 | ||
| 45 | 2 | 115 | D2M115V45 |
| 150 | D2M150V45 | ||
| 185 | D2M185V45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huo, M.; Xu, S.; Renqing, D.; Liu, J.; Jiang, C.; Zhang, L.; Yang, P. A Numerical Simulation Study on the Critical Erosion of Laboratory-Scale Debris Flow. Sustainability 2025, 17, 9690. https://doi.org/10.3390/su17219690
Huo M, Xu S, Renqing D, Liu J, Jiang C, Zhang L, Yang P. A Numerical Simulation Study on the Critical Erosion of Laboratory-Scale Debris Flow. Sustainability. 2025; 17(21):9690. https://doi.org/10.3390/su17219690
Chicago/Turabian StyleHuo, Miao, Shuang Xu, Duoji Renqing, Jiawei Liu, Chenjie Jiang, Lili Zhang, and Ping Yang. 2025. "A Numerical Simulation Study on the Critical Erosion of Laboratory-Scale Debris Flow" Sustainability 17, no. 21: 9690. https://doi.org/10.3390/su17219690
APA StyleHuo, M., Xu, S., Renqing, D., Liu, J., Jiang, C., Zhang, L., & Yang, P. (2025). A Numerical Simulation Study on the Critical Erosion of Laboratory-Scale Debris Flow. Sustainability, 17(21), 9690. https://doi.org/10.3390/su17219690







