Multi-Dimensional Risks and Eco-Environmental Responses of Check Dam Systems: Evidence from a Typical Watershed in China’s Loess Plateau
Abstract
1. Introduction
2. Materials and Methods
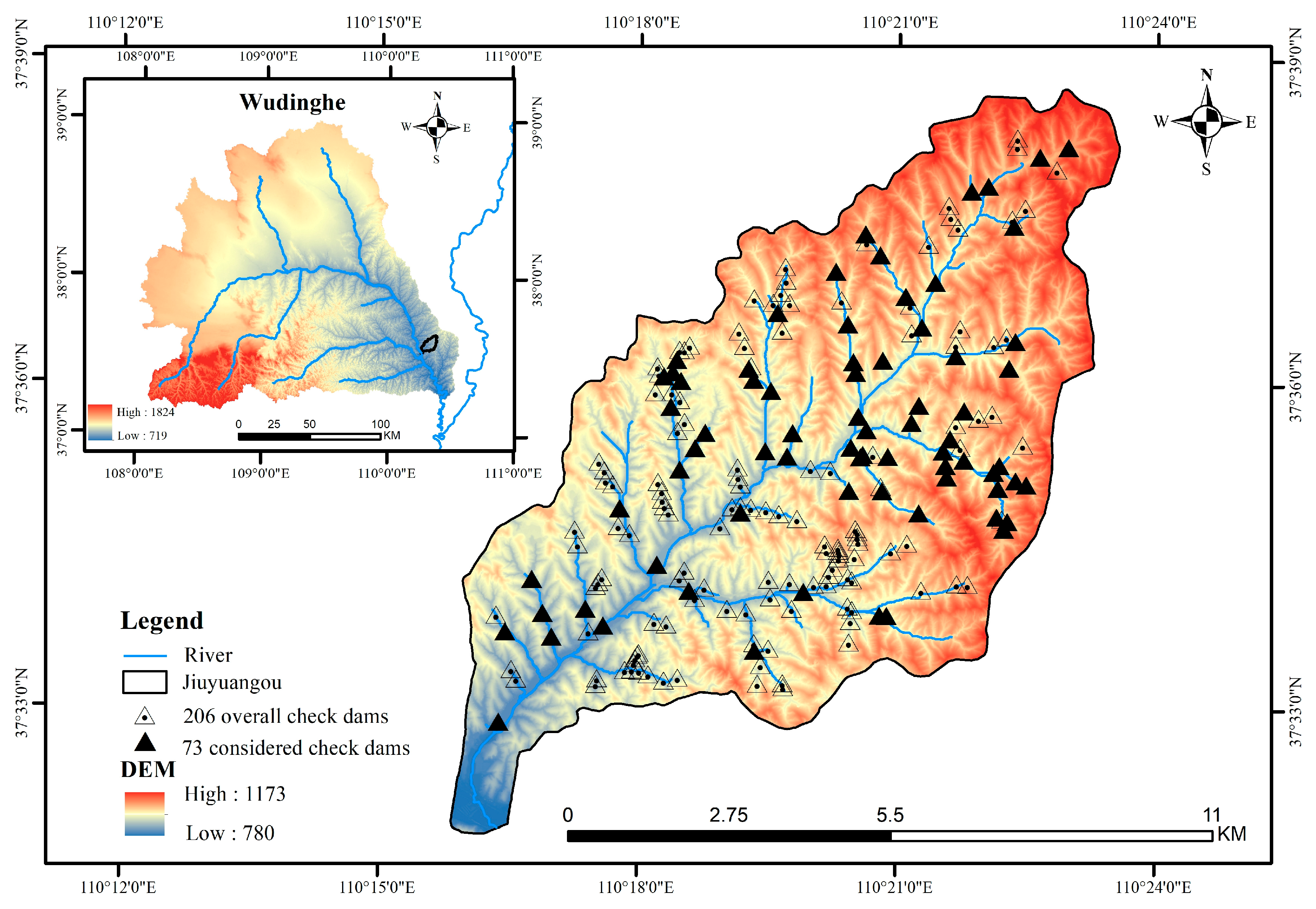
2.1. Overview of the Study Area
2.2. Data Source and Processing
2.3. Research Method
2.3.1. Risk Assessment Index System for Check Dam Operations
- Engineering risk ()
- Low design standards are often inadequate, notably characterized by insufficient dam height, limited reservoir capacity, or an overly short design service life, failing to meet flood retention requirements. This issue was particularly prevalent in the 1960s and 1970s. A representative example occurred from 1977 to 1988 in Northern Shaanxi, where several heavy rainstorms caused damage to approximately 70% of small check dams. Most of these structures were built by local communities with low standards and poor construction quality, and about 60% consisted solely of embankments without spillways or drainage facilities.Check dams serve two primary functions: sediment interception (silt trapping) and flood mitigation. However, a functional conflict exists between these objectives: an increase in sedimentation capacity reduces available flood storage capacity, thereby weakening the dam’s overall flood control performance. Consequently, the design risk of check dams is influenced by multiple factors, including flood storage capacity, accumulated sediment volume, and flood design frequency. Thus, the design risk of a check dam can be defined as follows. This indicator uniquely assesses the mismatch between the original design capacity and the actual hydrological load, independent of the dam’s current physical condition or ancillary facilities.where represents the design risk index of the check dam, where a higher value indicates a greater level of risk, with a maximum possible value of 1; denotes the designed flood return period (in years) that the check dam is intended to intercept; refers to the return period (in years) of the flood event currently encountered; indicates the designed flood storage capacity of the check dam (in 104 m3); represents the current siltation storage capacity already accumulated in the dam (in 104 m3); and is a conversion factor used to quantify the flood mitigation capabilities of the check dam.
- Damage to dam body is primarily caused by factors such as intense precipitation, poor construction quality, and lack of maintenance, leading to cracks, gullies, breaches, and even collapse. This risk indicator () specifically quantifies the threat to the dam’s structural integrity based on its observed physical state, irrespective of its original design or the functionality of its drainage facilities. Complete collapse is relatively rare; most failures result from enlarged gullies due to prolonged erosion. Generally, a significant breach renders the check dam unable to retain floods. Field observations show that most breaches initiate from overtopping-induced erosion at the crest, which progressively expands and may lead to full failure. In other cases, scour at the base forms cavities, causing sudden instability and collapse of the upper dam structure. Gullies often develop due to long-term erosion, particularly in poorly maintained dams, and can evolve into breaches. Cracks, typically arising from construction defects, foundation settlement, or seismic activity, often appear within 1–3 years after construction and can be remedied by backfilling or grouting.According to the extent of damage, the threat of check dam failure is quantified as follows: cracks pose the lowest risk, followed by gullies, with breaches and collapse being the most severe. This study considers that a breach represents a complete failure of flood retention capacity, with an assigned risk value of 1. Cracks, being limited and repairable, have an upper risk limit denoted as . Gullies can be numerically characterized by their transverse depth and longitudinal depth . When reaches the average dam width , and exceeds the remaining retention height (height from sediment surface to dam crest), the gully is considered to have developed into a breach, indicating functional failure. Thus, dam damage risk can be described using these parameters.In the formula, is the risk index for structural damage to the check dam, where an elevated number signifies increased peril, with a maximum threshold of 1; represents the transverse depth of the crack across the dam’s breadth (m), denotes the longitudinal depth corresponding to the height of the dam (m), aligns with the mean width of the check dam (m), and denotes the residual flood retention height, characterized as the vertical distance from the sediment surface to the dam crest (m).
- Damage to drainage facilities—such as shafts, inclined pipes, or spillways—may result in the collapse of a check dam due to insufficient discharge capacity, complete absence of such structures, or functional impairment during operation. This indicator () exclusively evaluates the performance and adequacy of the water release system. Its calculation is based on a hydraulic balance between inflow and outflow, making it conceptually and computationally separate from the structural damage indicator (). In practice, the design grade of a check dam is determined based on its controlled watershed area and flood regulation coordination with upstream and downstream structures. When the inflow volume exceeds the designed storage capacity, additional water release facilities should be installed to reduce flood retention pressure. The absence or impairment of these facilities introduces safety risks, influenced by factors including precipitation duration, watershed area, average precipitation depth, runoff coefficient, discharge capacity per unit time, and available remaining storage.
- Management risk ()
- Environmental risk ()
- Extreme rainstorms denote precipitation that significantly surpasses the average annual precipitation or prolonged precipitation that far exceeds the average for the corresponding duration. This indicator () is calculated based on precipitation data (), making it independent of the streamflow-based flood indicator (). It specifically captures risks from direct, intense rainfall over the watershed. By analyzing long-term historical records of maximum precipitation events and conducting frequency analysis, the maximum event precipitation under different design frequencies can be determined. A higher precipitation value corresponds to a greater risk level for the check dam. The water volume in front of the dam must be calculated based on runoff and concentration, and compared with the flood detention capacity of the check dam. The higher the ratio of water volume produced by precipitation to the flood detention capacity, the more perilous the check dam becomes. When the ratio is greater than 1, the check dam overflows and loses its flood detention capacity, and this is likely to cause dam failure due to overtopping. In this study, when a check dam overflows, it will collapse, and the risk will reach its maximum. The formula for calculation is as follows:
- where represents the risk index for extreme rainstorm hazards associated with the check dam, with higher values indicating greater danger, with a maximum value of 1; denotes the duration of precipitation, in hours (h); represents the length of each precipitation interval, in hours (h); represents the unit precipitation depth during the -th interval, in millimeters (mm); represents the controlling region of the check dam, expressed as square kilometers (km2); represents the runoff coefficient, representing the ratio of flow depth at the inner diameter per unit time to precipitation depth; indicates the flooding outflow volume of the check dam during the period, representing the average discharge of flood control facilities each period of time, measured in cubic meters per hour (m3/h); and signifies the remaining amount of storage of the warping dam, expressed in cubic meters (m3).
- 2.
- Over-standard flood refers to a flood that is beyond the flood prevention thresholds of a check dam, hence heightening the risk associated with flood management. In contrast to the precipitation-based , this indicator () is calculated using direct flood discharge data () or reliably derived flow estimates. This clear distinction in input data ensures that the contributions of rainfall and riverine flooding are not conflated. In a river basin, multiple precipitation gauges are typically deployed. Areal precipitation can be estimated through spatial interpolation techniques. However, streamflow gauges are generally only located at the basin outlet, where long-term monitoring data are available. It remains challenging to accurately estimate or back-calculate the runoff corresponding to each individual check dam based solely on outlet discharge measurements. Therefore, on the basis of analyzing the relationship between precipitation and runoff, we assume that precipitation and floods have the same frequency, convert precipitation into runoff, and calculate the inundation procedure in front of the dam. The research indicates that the risk indicators for excessive flooding are associated with the flood process, length, discharge facilities, and detention capacity:
- where represents the risk index for exceeding standard flood levels at the check dam, with higher values indicating greater danger, with a maximum value of 1. represents the flood frequency in hours (h); signifies the duration of the unit period in seconds (s). symbolizes the flow during period in cubic meters per second (m3/s). indicates the flood drainage capability of the check dam over time period , specifically the average release of flood disposal facilities per unit time, in cubic meters per second (m3/s). refers to the residual storage capacity of the warping dam, defined as cubic meters (m3).
- 3.
- Seismic hazard refers to the risks induced by geological movements during earthquakes, such as cracking, collapse, settlement, and damage to hydraulic structures in check dams. According to historical records [32], the magnitude 8.0 Wenchuan earthquake on 12 May (also known as the “5·12” earthquake) triggered multiple magnitude 6.0 aftershocks in Gansu Province, causing severe damage to check dams in the region. As of 26 May 2008, survey figures indicated that 124 check dams were compromised, comprising 93 key dams, 27 medium-sized dams, and 4 small dams, reflecting a highly serious level of impact. There has been very limited research on seismic risk to check dams, making it particularly challenging to quantify corresponding seismic risk indicators.Seismic intensity denotes the extent of shaking and its impact on the ground surface and engineering structures. Utilizing the mean damage index derived from the China Seismic Intensity Scale (Table 3) as the seismic risk indicator for check dams, a relationship between this indicator and earthquake magnitude can be established as follows:
- where is the seismic disaster risk index of the check dam, and the greater its value, the more dangerous it is, and the maximum value is 1; is the earthquake magnitude; , , and are the seismic disaster risk coefficients of the check dam, taking = −0.0214, = 0.4115, = −2.2853, and = 3.8883, respectively.
- Risk of loss ()
- Socioeconomic losses denote economic detriments resulting from the failure of check dams, leading to the inundation of agricultural land, residences, thoroughfares, urban neighborhoods, and industrial zones. Generally, estimates can be made on the basis of the extent of flooding. The measurement of the risk of socioeconomic losses is related not only to the magnitude of the losses caused but also to the local economic level, that is, the ratio of the magnitude of the losses to the disaster resistance capacity. The disaster resistance capacity can be measured by the funds available for flood control and disaster relief in the local area:
- where represents the socioeconomic loss risk index of the check dam; a higher value indicates greater danger. The upper limit is 1; represents socioeconomic losses, measured in tens of thousands of yuan; and represents the funds available locally for flood control and disaster relief, in tens of thousands of yuan.
- 2.
- Eco-environmental loss pertains to the degradation of the ecological landscape due to the failure of check dams, leading to the inundation of ecological zones or riverbanks, which exposes loess and induces significant soil erosion. The extent of the risk of damage to the environment can be evaluated through the financial resources required for ecological restoration and the funds designated for local environmental development:
- where represents the eco-environmental loss risk index of the check dam. The index value correlates positively with risk, with an upper bound amount of 1; denotes the amount of environmental loss, measured in 10,000 yuan; and signifies local accessible finances for eco-environmental construction, also in 10,000 yuan.
- 3.
- Personnel losses refer to harm to personnel, such as being injured, missing, or killed, due to not evacuating in time after the collapse of a check dam and the subsequent flooding. The RESCDAM technique [33,34] simplifies the assessment of mortality attributable to the dam failure by including many criteria, including alert time, at-risk population, and flood intensity.
- In the formula, is the risk indicator for loss of life due to check dam failure The index value correlates positively with risk, with an absolute highest of 1; denotes the population at risk; represents the number of fatalities within this demographic; indicates the severity of the flood disaster; and is the life loss correction coefficient of the check dam, primarily reflecting the impact of the prediction and early warning system as well as emergency rescue capabilities on life loss.
2.3.2. Determination of Indicator Weights Based on Fuzzy Analytic Hierarchy Process (FAHP)
- Establishment of the Fuzzy Consistent Judgment Matrix
- Determining Indicator Weights from the Fuzzy Consistent Judgment Matrix
- Weighting of Operational Risk Assessment Indicators for Check Dam Systems
- Fuzzy Consistent Judgment Matrices for Operational Risk Indicators of Check Dam Systems
- (1)
- First-level Fuzzy Consistent Judgment Matrix:
- (2)
- Second-level Fuzzy Consistent Judgment Matrix for Engineering Risk:
- (3)
- Second-level Fuzzy Consistent Judgment Matrix for Management Risk:
- (4)
- Second-level Fuzzy Consistent Judgment Matrix for Environmental Risk:
- (5)
- Second-level Fuzzy Consistent Judgment Matrix for Risk of Loss:
- 2.
- Calculation of Operational Risk Indicator Weights for Check Dam Systems
2.3.3. Evaluation of Risks Associated with the Check Dam System in the Jiuyuangou Watershed
3. Results
3.1. Operational Risk of Check Dam Systems Across Varying Precipitation Frequencies
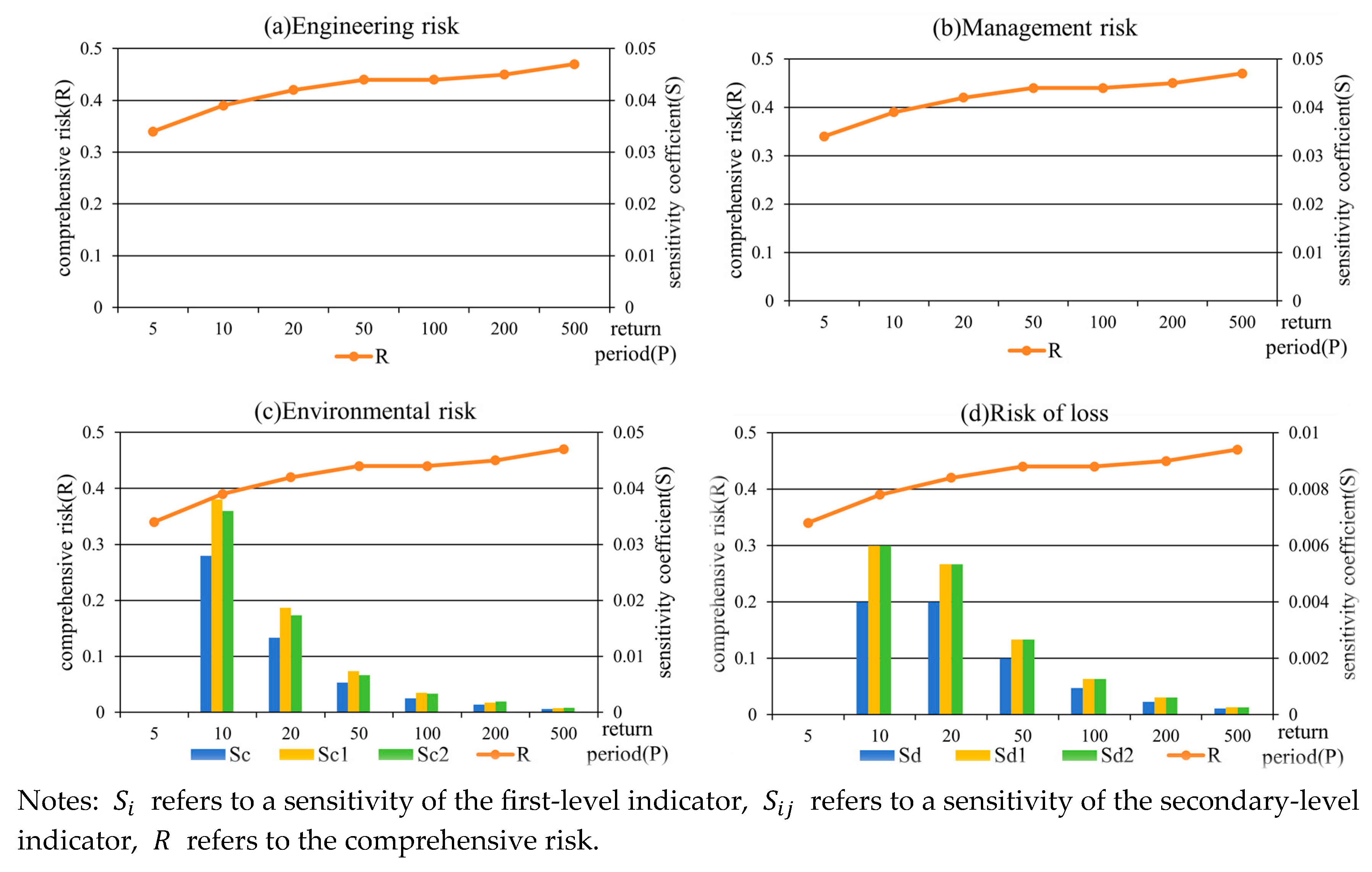
3.2. Sensitivity Analysis of Various Levels of Risks of the Check Dam System to Precipitation Return Period
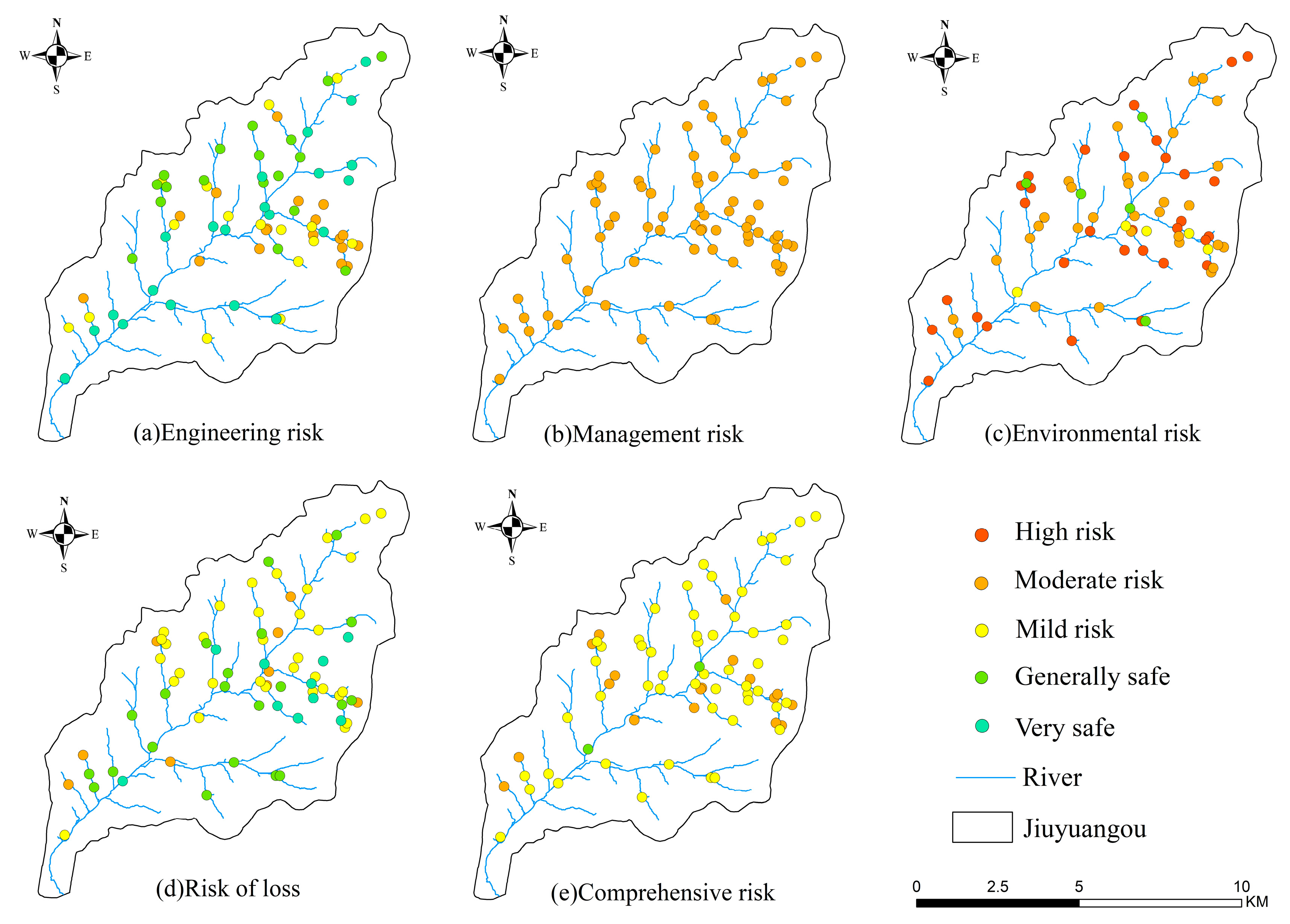
3.3. Different Risk Situations of 73 Check Dams in the Jiuyuangou Watershed
4. Discussion
4.1. Regional Context and Methodological Validation in an Eco-Environmental Framework
4.2. Risk-Informed Mitigation Strategies and Transferability of the Framework
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, Y.; Ran, W.; Xu, X.; Luan, X.; Fan, G.; Yang, T.; Ma, H.; Yang, Y.; Li, L.; Yang, Z. Linear Polygonal Faults Initiated Gully System around the Margin Slope of Middle Miocene Carbonate Platform in the Northwest South China Sea. Mar. Pet. Geol. 2023, 147, 106022. [Google Scholar] [CrossRef]
- Yu, Z.; Xuan, H.; Dong, S. Bibliometric Analysis of Environmental Effects of Check Dams on the Loess Plateau Based on Web of Science Database. Soil Water Conserv. 2021, 19, 126–131. [Google Scholar] [CrossRef]
- Jian, S.; Xiao, P.; Tang, Y.; Jiao, P. Runoff–Sediment Simulation of Typical Small Watershed in Loess Plateau of China. Sustainability 2023, 15, 4894. [Google Scholar] [CrossRef]
- Huo, A.; Li, P.; Zhao, Y.; Abuarab, M.E.-S.; Elsayed, S.; Zhang, J. The Application and Development of Innovative Models in the Sustainable Management of Natural Gully Consolidation and Highland Protection Projects. Sustainability 2025, 17, 4329. [Google Scholar] [CrossRef]
- Wen, Y.; Zhong, X.; Yun, W. Analysis of Runoff Change in the Yellow River Basin under the Background of Climate Change. Meteorol. Environ. Sci. 2009, 32, 1–6. [Google Scholar] [CrossRef]
- Wang, J.; Li, M.; Li, X.; Wang, S.; Li, Q.; Li, Y.; Zhang, L. Response Study of Streamflow and Sediment Reduction in the Northeast Region of the Loess Plateau under Changing Environment. Sustainability 2024, 16, 1475. [Google Scholar] [CrossRef]
- Zu, C.; Zhan, L.; Zhao, W. Some Thoughts on Strategic Positioning of Check Dam Construction on the Loess Plateau. Soil Water Conserv. China 2020, 32–38. [Google Scholar] [CrossRef]
- Wang, S.; Xu, C.; Liu, Y.; Xu, B. Zonal Intelligent Inversion of Viscoelastic Parameters of High Arch Dams Using an HEST Statistical Model. J. Civ. Struct. Health Monit. 2022, 12, 207–223. [Google Scholar] [CrossRef]
- Tan, F.; Lahmer, T. Shape Optimization Based Design of Arch-Type Dams under Uncertainties. Eng. Optimiz. 2018, 50, 1470–1482. [Google Scholar] [CrossRef]
- Wang, Z.; Deng, X.; Li, X.; Zhou, Q.; Yan, H. Impact Analysis of Government Investment on Water Projects in the Arid Gansu Province of China. Phys. Chem. Earth Parts A/B/C 2015, 79–82, 54–66. [Google Scholar] [CrossRef]
- Chen, H.-E.; Chen, T.-Y.; Zheng, Y.-L.; Chiu, Y.-Y.; Chen, S.-C. Optimizing Sediment Control by Adjusting the Relative Spacing between Trusses/Beams in an Open-Type Check Dam. Landslides 2025, 22, 551–565. [Google Scholar] [CrossRef]
- Azman, A.; Ng, F.C.; Zawawi, M.H.; Abas, A.; Rozainy, M.A.Z.M.R.; Abustan, I.; Adlan, M.N.; Tam, W.L. Effect of Barrier Height on the Design of Stepped Spillway Using Smoothed Particle Hydrodynamics and Particle Image Velocimetry. KSCE J. Civ. Eng. 2020, 24, 451–470. [Google Scholar] [CrossRef]
- Andreasen, M.H.; Agergaard, J.; Allotey, A.N.M.; Møller-Jensen, L.; Oteng-Ababio, M. Built-in Flood Risk: The Intertwinement of Flood Risk and Unregulated Urban Expansion in African Cities. Urban Forum 2023, 34, 385–411. [Google Scholar] [CrossRef]
- Najafi, S.; Kiani-Harchegani, M.; Dragovich, D. Check Dams: Distribution, Purposes and Effectiveness. Sci. Total Environ. 2025, 980, 179468. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Mao, Y.; Qi, Y.; Su, H.; Yuan, J.; Qi, Z.; Du, X. Reliability Analysis of Concrete Gravity Dams Based on the Bayesian Line Sampling Algorithm and Global Sensitivity Analysis Method. Expert Syst. Appl. 2025, 281, 127663. [Google Scholar] [CrossRef]
- Krasko, V.; Rebennack, S. Two-Stage Stochastic Mixed-Integer Nonlinear Programming Model for Post-Wildfire Debris Flow Hazard Management: Mitigation and Emergency Evacuation. Eur. J. Oper. Res. 2017, 263, 265–282. [Google Scholar] [CrossRef]
- Kucukoglu, I.; Korucu, M.K. A Nonlinear Programming Model for Long-Term Planning of Municipal Solid Waste Management Systems: The Desire for Global Optima. Environ. Model. Assess. 2024, 29, 1131–1149. [Google Scholar] [CrossRef]
- Chen, W.; Huang, L.; Wang, D.; Liu, C.; Xu, L.; Ding, Z. Effects of Siltation and Desiltation on the Wave-Induced Stability of Foundation Trench of Immersed Tunnel. Soil Dyn. Earthq. Eng. 2022, 160, 107360. [Google Scholar] [CrossRef]
- Wei, Y.; Jiao, J.; Li, Y. Evolution of Historical Sediment Yield Using Check-Dam Systems as Carriers: A Case Study in a Restored Agricultural Catchment on the Loess Plateau, China. CATENA 2022, 210, 105877. [Google Scholar] [CrossRef]
- Lee, M.-J.; Bae, S.; Shin, J.H.; Baek, J.B. Fuzzy Bayesian Network Analysis for Quantifying Risk Reduction Rate of Hierarchy of Controls. J. Loss Prev. Process Ind. 2024, 90, 105350. [Google Scholar] [CrossRef]
- Ullah, I.; Kovacs, G.; Lenner, T. Impact of Climate Change on Flood Risk with Urban Resilience Perspective Using Fuzzy Logic Model. Earth Sci. Inform. 2025, 18, 346. [Google Scholar] [CrossRef]
- Jibhakate, S.M.; Timbadiya, P.V.; Patel, P.L. Dam-Break Flood Hazard and Risk Assessment of Large Dam for Emergency Preparedness: A Study of Ukai Dam, India. J. Hydrol. 2024, 640, 131659. [Google Scholar] [CrossRef]
- Orojloo, M.; Hashemy Shahdany, S.M.; Roozbahani, A. Developing an Integrated Risk Management Framework for Agricultural Water Conveyance and Distribution Systems within Fuzzy Decision Making Approaches. Sci. Total Environ. 2018, 627, 1363–1376. [Google Scholar] [CrossRef]
- Meng, Y.; Li, P.; Xiao, L.; Wang, R.; Yang, S.; Han, J.; Hu, B. Heavy Metal Content and Pollution Assessment in Typical Check Dam Sediment in a Watershed of Loess Plateau, China. Sustainability 2022, 14, 8597. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, M.; Lu, J.; Zhou, Q.; Ma, W. Evaluation of Ecological City and Analysis of Obstacle Factors under the Background of High-Quality Development: Taking Cities in the Yellow River Basin as Examples. Ecol. Indic. 2020, 118, 106771. [Google Scholar] [CrossRef]
- Li, E. Effects of Extreme Rainfall Change on Sediment Load in the Huangfuchuan Watershed, Loess Plateau, China. Sustainability 2024, 16, 7457. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, Y.; Yu, S.; Wang, L.; Chen, Z.; Zhou, J. Rapid Quantitative Study of Check Dam Breach Floods under Extreme Rainstorm. Nat. Hazards 2023, 116, 2011–2031. [Google Scholar] [CrossRef]
- Nikolić Popadić, S. Flood Prevention in Serbia and Legal Challenges in Obtaining the Land for Flood Risk Management. Environ. Sci. Policy 2021, 116, 213–219. [Google Scholar] [CrossRef]
- Bao, H.; Liu, L.; Lan, H.; Peng, J.; Yan, C.; Xu, J.; Wang, J.; Zhang, K.; Wei, W. Progressive Hydraulic Failure Mechanism and Multi-Stage Instability Risk Early Warning for Loess Check Dams. J. Hydrol. 2025, 663, 134226. [Google Scholar] [CrossRef]
- Zhang, B.; Guo, J.; Fang, H.; Wu, S.; Feng, H.; Siddique, K.H.M. Soil Erosion Projection and Response to Changed Climate and Land Use and Land Cover on the Loess Plateau. Agric. Water Manag. 2024, 306, 109187. [Google Scholar] [CrossRef]
- Xue, Y.; Xu, W.; Luo, S.; Chen, H.; Li, N.; Xu, L. Experimental Study of Dam-Break Flow in Cascade Reservoirs With Steep Bottom Slope. J. Hydrodyn. 2011, 23, 491–497. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, C.; Yuan, R. 2.21—Earthquake-Triggered Landslides. In Treatise on Geomorphology, 2nd ed.; Shroder, J.F., Ed.; Academic Press: Oxford, UK, 2022; pp. 583–614. ISBN 978-0-12-818235-2. [Google Scholar]
- Dyer, J.S. Remarks on the Analytic Hierarchy Process. Manag. Sci. 1990, 36, 249–258. [Google Scholar] [CrossRef]
- Maranzoni, A.; D’Oria, M.; Rizzo, C. Probabilistic Mapping of Life Loss Due to Dam-Break Flooding. Nat. Hazards 2024, 120, 2433–2460. [Google Scholar] [CrossRef]
- Wang, M.; Zhu, H.; Yao, J.; Hu, L.; Kang, H.; Qian, A. Assessing Large-Scale Flood Risks: A Multi-Source Data Approach. Sustainability 2025, 17, 5133. [Google Scholar] [CrossRef]
- Luo, Q.; Zhen, L.; Hu, Y. The Effects of Restoration Practices on a Small Watershed in China’s Loess Plateau: A Case Study of the Qiaozigou Watershed. Sustainability 2020, 12, 8376. [Google Scholar] [CrossRef]
- Zhang, J. Fuzzy Analytical Hierarchy Process (FAHP). Fuzzy Syst. Math. 2000, 14, 80–88. [Google Scholar]
- Chauhan, S.; Bhardwaj, D.R. Suitability Mapping of Agroforestry in Shimla District, Himachal Pradesh, India, Using Analytic Hierarchy Process (AHP) and Fuzzy Analytic Hierarchy Process (Fuzzy AHP). Agroforest. Syst. 2025, 99, 95. [Google Scholar] [CrossRef]
- Chen, Y.; Li, J.; Jiao, J.; Bai, L.; Wang, N.; Chen, T.; Zhang, Z.; Xu, Q.; Han, J. Assessing the Risk of Check Dam Failure Due to Heavy Rainfall Using Machine Learning on the Loess Plateau, China. Int. Soil Water Conserv. Res. 2024, 12, 506–520. [Google Scholar] [CrossRef]
- Li, P.; Liang, C. Risk Analysis for Cascade Reservoirs Collapse Based on Bayesian Networks under the Combined Action of Flood and Landslide Surge. Math. Probl. Eng. 2016, 2016, 2903935. [Google Scholar] [CrossRef]
- Li, Z.; Chen, B.; Liu, Y.; Peng, J.; Xu, Q.; Jiang, L.; Du, J.; Song, C.; Ding, M.; Zhu, W. Long-Term Three-Dimensional Deformation Monitoring and Risk Assessment of the Guba Landslide, Tibetan Plateau. Sci. China Earth Sci. 2025, 68, 3288–3305. [Google Scholar] [CrossRef]
- Rui, Y.; Zi, L.; Dan, W.; Shui, Y. Safety Evaluation of Check Dam System in Small Watershed of Loess Plateau. J. Yanan Univ. (Nat. Sci. Ed.). 2018, 37, 41–45. [Google Scholar] [CrossRef]
- Bing, X.; Kun, Y.; Zhan, L.; Peng, L.; Ming, P.; Peng, H.; Gao, H.; Jian, Y.; Wen, Z. Comprehensive Risk Warning of Check Dam System in the Jiuyuangou Watershed. Sci. Soil Water Conserv. 2022, 20, 102–108. [Google Scholar] [CrossRef]
- Ke, G.; Cheng, S.; Li, Z.; Wang, T.; Wu, H.; Zhen, Y. Impact of Different Types of Sediment-Filled Check Dam Systems on Runoff Erosion Dynamics in a Loess Plateau Watershed. Int. J. Sediment Res. 2025, 40, 322–332. [Google Scholar] [CrossRef]
- Hai, G.; Zhan, L.; Peng, L.; Zong, R.; Yuan, Y.; Jie, W. Path and Control of Rainstorm Sediment Yield in the Loess Plateau—Based on the Understanding of Rainstorm in Wuding River Basin on July 26, 2017. Sci. Soil Water Conserv. 2018, 16, 66–72. [Google Scholar] [CrossRef]
- Gu, C.; Zhu, Y.; Li, R.; Yao, H.; Mu, X. Effects of Different Soil and Water Conservation Measures on Hydrological Extremes and Flood Processes in the Yanhe River, Loess Plateau, China. Nat. Hazards 2021, 109, 545–566. [Google Scholar] [CrossRef]
| Target Layer | First-Level Indicators | Second-Level Indicators |
|---|---|---|
| Risk assessment indicators for the operation of silt dam systems () | Engineering risk () | Low design standards () |
| Damage to dam body () | ||
| Damage to drainage facilities () | ||
| Management risk () | Personnel duty situation () | |
| Emergency warning capability () | ||
| Management architecture () | ||
| Environmental risk () | Extreme rainstorm () | |
| Over standard flood () | ||
| Seismic hazard () | ||
| Risk of loss () | Socio-economic losses () | |
| Eco-environmental loss () | ||
| Personnel losses () |
| Indicator Component | Check Dam Project Management Risk Level | ||||
|---|---|---|---|---|---|
| Level 1/0 | Level 2/0.2 | Level 3/0.5 | Level 4/0.8 | Level 5/1 | |
| Personnel duty situation | Each check dam has dedicated supervision and regular maintenance | Most check dams have dedicated supervision and regular maintenance | Only thorough inspections are conducted before each flood season | Almost no responsible personnel perform check dam inspections | No operational supervision of check dams |
| Emergency warning capability | Rapid warning with timely evacuation | Relatively rapid warning with delayed evacuation | Slow warning with delayed evacuation | No warning; self-organized evacuation occurs | No warning; lack of crisis awareness |
| Management architecture | Comprehensive and well-implemented system | Relatively sound system | Relatively outdated system | Outdated and inefficient system | No relevant policies in place |
| Intensity | Magnitude | Mean Damage Index | Phenomenological Description |
|---|---|---|---|
| I | 1.9 | 0 | Detected only by instruments. |
| II | 2.5 | 0 | Perceived by a limited number of individuals while stationary indoors; suspended items may oscillate somewhat. |
| III | 3.1 | 0 | Perceived indoors by numerous individuals, outdoors by a select few; suspended items oscillate, unstable objects tremble. |
| IV | 3.7 | 0 | Perceived indoors by the majority, outdoors by a minority; windows and doors tremble, and wall surfaces may fissure. |
| V | 4.3 | 0 | Felt outdoors by most; animals become restless; doors and windows creak; fine cracks may appear in walls. |
| VI | 4.9 | 0~0.1 | People feel unsteady; animals flee; objects fall off shelves; simple sheds damaged; slope failures may occur. |
| VII | 5.5 | 0.11~0.3 | Slight damage to buildings; monuments and chimneys damaged; ground cracks and sand boils may appear. |
| VIII | 6.1 | 0.31~0.5 | Many buildings damaged, a few collapsed; road embankments failed; underground pipes ruptured. |
| IX | 6.7 | 0.51~0.7 | Most buildings severely damaged, some collapsed; monuments and chimneys toppled; railway tracks bent. |
| X | 7.3 | 0.71~0.9 | Widespread building collapse; roads destroyed; large rockfalls occur; large waves on water bodies. |
| XI | 7.9 | 0.91~1.0 | Majority of buildings collapse; long sections of embankments and roads destroyed; significant ground deformation. |
| XII | 8.5 | 1.0 | Total destruction of all structures; dramatic changes in topography; annihilation of plant and animal life |
| Scale | Definition | Description |
|---|---|---|
| 0.5 | Equally Important | Two elements are equally important. |
| 0.6 | Slightly Important | One element is slightly more important than the other. |
| 0.7 | Obviously Important | One element is obviously more important than the other. |
| 0.8 | Much More Important | One element is much more important than the other. |
| 0.9 | Extremely Important | One element is extremely more important than the other. |
| 0.1~0.4 | Reciprocal Comparison | If the comparison of element ai with yields judgment then the comparison of with yields . |
| Target Layer | Weight of First-Level Indicators | Weight of Second-Level indicators | |
|---|---|---|---|
| Risk assessment indicators for the operation of silt dam systems () | Engineering risk | Low design standards | |
| Damage to dam body | |||
| Damage to drainage facilities | |||
| Management risk | Personnel duty situation | ||
| Emergency warning capability | |||
| Management architecture | |||
| Environmental risk | Extreme rainstorm | ||
| Over standard flood | |||
| Seismic hazard | |||
| Risk of loss | Socio-economic losses | ||
| Eco-environmental loss | |||
| Personnel losses | |||
| Risk Level | Description of Risk Degree | Range |
|---|---|---|
| Level 1 | High risk | [0.7, 1] |
| Level 2 | Moderate risk | [0.5, 0.7) |
| Level 3 | Mild risk | [0.3, 0.5) |
| Level 4 | Generally safe | [0.1, 0.3) |
| Level 5 | Very safe | [0, 0.1) |
| Return Period | 5 | 10 | 20 | 50 | 100 | 200 | 500 |
| Engineering risk | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| Low design standard | 0.47 | 0.47 | 0.47 | 0.47 | 0.47 | 0.47 | 0.47 |
| Dam damage | 0.42 | 0.42 | 0.42 | 0.42 | 0.42 | 0.42 | 0.42 |
| Damage to drainage facilities | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 |
| Management risk | 0.55 | 0.55 | 0.55 | 0.55 | 0.55 | 0.55 | 0.55 |
| Personnel duty situation | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 |
| Emergency early warning capability | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| Management Architecture | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| Environmental risk | 0.34 | 0.48 | 0.54 | 0.58 | 0.58 | 0.61 | 0.64 |
| Extreme Rainstorm | 0.53 | 0.72 | 0.81 | 0.86 | 0.86 | 0.87 | 0.91 |
| Over standard flood | 0.41 | 0.59 | 0.67 | 0.71 | 0.73 | 0.79 | 0.83 |
| Seismic hazard | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Risk of loss | 0.25 | 0.27 | 0.31 | 0.34 | 0.34 | 0.34 | 0.36 |
| Socioeconomic loss | 0.62 | 0.65 | 0.7 | 0.74 | 0.74 | 0.74 | 0.75 |
| Eco-environmental loss | 0.17 | 0.24 | 0.33 | 0.4 | 0.4 | 0.41 | 0.44 |
| Personnel losses | 0 | 0 | 0 | 0 | 0 | 0 | 0.01 |
| Comprehensive risk | 0.34 | 0.39 | 0.42 | 0.44 | 0.44 | 0.45 | 0.47 |
| Risk level | Level 3 | Level 3 | Level 3 | Level 3 | Level 3 | Level 3 | Level 3 |
| Name of Check Dam | Type | Increase Dam Height (m) | Increase Storage Capacity (104 m3) | Drainage Facilities | Design Criteria | Risk Transfer |
|---|---|---|---|---|---|---|
| Wangjiagou No. 1 dam | Small dam | 1 | 3.1 | Share downstream risks | ||
| Guandaogou No. 1 dam | Medium-sized dam | 1 | 11.5 | Additional spillway | 10 → 50 | Risk transfer downward |
| Guandaogou No. 2 dam | Small dam | 1 | 3.0 | 5 → 10 | Share downstream risks | |
| Majiagou guaigou dam | Small dam | 0 | 0 | Additional shaft/horizontal pipe | 5 → 10 | Risk transfer downward |
| Yayaogou dam | Backbone dam | 1 | 3.5 | 20 → 100 | Share downstream risks | |
| Tuanwougou No. 2 dam | Small dam | 1 | 0.8 | 5 → 10 | Share downstream risks | |
| Xiangtagou No. 3 dam | Small dam | 3 | 3.6 | Share downstream risks | ||
| Xiangtagou No. 1 dam | Medium-sized dam | 0 | 0 | Additional spillway | 10 → 50 | Risk transfer downward |
| Chaijiagou No. 1 dam | Backbone dam | 1 | 1.7 | 5 → 100 | Share downstream risks | |
| Mazhangzui dam | Backbone dam | 1 | 4.0 | 20 → 100 | Share downstream risks | |
| Laolimao dam | Medium-sized dam | 0 | 0 | Additional spillway | Risk transfer downward | |
| Haojialiang dam | Backbone dam | 1 | 2.8 | 20 → 100 | Share downstream risks | |
| Xiyangou Goukou dam | Backbone dam | 1 | 5.6 | 20 → 100 | Share downstream risks | |
| Guandigou No. 4 dam | Medium-sized dam | 0 | 0 | Additional spillway | 10 → 50 | Risk transfer downward |
| Guandigou No. 3 dam | Small dam | 1 | 1.2 | 5 → 10 | Share downstream risks | |
| Madizui dam | Medium-sized dam | 1 | 1.8 | 10 → 50 | Share downstream risks | |
| Nianyangou No. 1 dam | Medium-sized dam | 0 | 0 | Additional spillway | 10 → 50 | Risk transfer downward |
| Weijiayan No. 3 dam | Medium-sized dam | 0 | 0 | Additional spillway | 10 → 50 | Risk transfer downward |
| Yangquanzui dam | Medium-sized dam | 0 | 0 | Additional spillway | 10 → 50 | Risk transfer downward |
| Liushugou dam | Backbone dam | 1 | 3.2 | 20 → 100 | Share downstream risks | |
| Wujiagou dam | Medium-sized dam | 0 | 0 | Additional spillway | 20 → 50 | Risk transfer downward |
| Nanzuigou dam | Medium-sized dam | 1 | 0.9 | 10 → 50 | Share downstream risks | |
| Erlangcha No. 1 dam | Backbone dam | 1 | 4.5 | 20 → 100 | Share downstream risks |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Cheng, S.; Hang, P.; Li, Z.; Wu, H.; Ke, G.; Guo, X.; Zhen, Y. Multi-Dimensional Risks and Eco-Environmental Responses of Check Dam Systems: Evidence from a Typical Watershed in China’s Loess Plateau. Sustainability 2025, 17, 9477. https://doi.org/10.3390/su17219477
Yang Y, Cheng S, Hang P, Li Z, Wu H, Ke G, Guo X, Zhen Y. Multi-Dimensional Risks and Eco-Environmental Responses of Check Dam Systems: Evidence from a Typical Watershed in China’s Loess Plateau. Sustainability. 2025; 17(21):9477. https://doi.org/10.3390/su17219477
Chicago/Turabian StyleYang, Yujie, Shengdong Cheng, Penglei Hang, Zhanbin Li, Heng Wu, Ganggang Ke, Xingyue Guo, and Yunzhe Zhen. 2025. "Multi-Dimensional Risks and Eco-Environmental Responses of Check Dam Systems: Evidence from a Typical Watershed in China’s Loess Plateau" Sustainability 17, no. 21: 9477. https://doi.org/10.3390/su17219477
APA StyleYang, Y., Cheng, S., Hang, P., Li, Z., Wu, H., Ke, G., Guo, X., & Zhen, Y. (2025). Multi-Dimensional Risks and Eco-Environmental Responses of Check Dam Systems: Evidence from a Typical Watershed in China’s Loess Plateau. Sustainability, 17(21), 9477. https://doi.org/10.3390/su17219477






