Machine Learning-Based Prediction of Root-Zone Temperature Using Bio-Based Phase-Change Material in Greenhouse

Abstract

The study focuses on the experimental investigation of the impact of using coconut oil (CO) as a phase-change material (PCM) for heat storage on the root-zone temperature within a greenhouse in Adana, Türkiye. The study examines the efficacy of PCM as latent heat-storage material and predicts root-zone temperature using three machine learning algorithms. The dataset used in the analysis consists of 2658 data at hourly resolution with six variables from February to April in 2022. A greenhouse with PCM shows a remarkable increase in both ambient (0.9–4.1 °C) and root-zone temperatures (1.1–1.6 °C) especially during the periods without sunlight compared to a conventional greenhouse. Machine learning algorithms used in this study include Multivariate Adaptive Regression Splines (MARS), Support Vector Regression (SVR), and Extreme Gradient Boosting (XGBoost). Hyperparameter tuning was performed for all three models to control model complexity, flexibility, learning rate, and regularization level, thereby preventing overfitting and underfitting. Among these algorithms, R² values for testing data listed from largest to smallest are MARS (0.95), SVR (0.96), and XGBoost (0.97), respectively. The results emphasize the potential of machine learning approaches for applying thermal energy storage systems to agricultural greenhouses. In addition, it provides insight into a net-zero energy greenhouse approach by storing heat in a bio-based PCM, alongside its implementation and operational procedures.

1. Introduction

Greenhouses are specialized agricultural structures designed to enable continuous plant growth by mitigating the adverse effects of climatic fluctuations. These systems function by reducing thermal exchange between interior and exterior environments. However, to maintain optimal plant productivity, microclimatic parameters such as temperature, humidity, and solar radiation must be actively or passively regulated, particularly during unfavorable weather conditions.

Geographical latitude significantly affects the energy demand for greenhouse operations. While greenhouse cultivation is most economically feasible between 30° and 40° latitudes, heating requirements increase above the 40th parallel and cooling costs escalate below the 30th [1]. Among energy demands, heating constitutes the most significant share, accounting for approximately 65–85% of total energy consumption in northern climates [2], with other studies reporting ranges from 50% to 88% [3,4].

The environment inside the greenhouse is regulated using active or passive systems. While active heating systems often rely on nonrenewable fossil fuels, passive systems offer a more sustainable approach by utilizing naturally stored thermal energy. The semi-closed architecture of greenhouses makes them particularly suited for passive heating, capturing and storing solar radiation during the day for nighttime use, which is a principle aligned with the net-zero energy greenhouse concept. Consequently, enhancing energy efficiency through effective thermal storage techniques is vital not only for reducing operational costs but also for minimizing greenhouse gas emissions and promoting sustainable greenhouse agriculture [5,6,7,8].

Phase-Change Materials (PCMs) have gained increasing attention for passive thermal energy storage due to their ability to absorb and release latent heat at specific temperature ranges. Various studies demonstrate that PCM integration in greenhouses can enhance nighttime temperatures by 1–6 °C [9,10,11,12]. However, most applications focus on heating the greenhouse air volume rather than directly targeting the root zone, which is more energy-efficient and critical for crop productivity. Llorach-Massana et al. have shown that maintaining root-zone temperatures between 10 and 15 °C improves crop yield and reduces total energy usage [13]. Moreover, using PCM for root-zone heating can significantly reduce CO₂ emissions up to 10.95 tons CO₂/ha.year and improve net profits for growers.

Despite the promise of PCMs, paraffin-based materials derived from petroleum remain dominant, representing a sustainability concern due to their high carbon footprint [14]. Bio-based PCMs, such as vegetable oils, present a promising alternative due to their renewability, non-toxicity, thermal stability, and environmental compatibility [15,16]. Nevertheless, studies exploring bio-based PCMs for localized root-zone heating remain scarce.

Accurate modeling of greenhouse thermal behavior, particularly in systems using PCMs, is essential for optimizing energy use. Both mathematical and artificial intelligence (AI)-based models have been applied to this problem, with machine learning (ML) techniques showing high potential for managing the complex and nonlinear interactions among climatic variables [17,18,19,20]. ML algorithms can develop predictive models based on empirical input–output datasets, offering faster and often more accurate outcomes than traditional physical modeling.

The motivation of this study is to model the thermal dynamics of root-zone temperature in a greenhouse utilizing coconut oil (Cocos nucifera), a bio-based PCM through machine learning approaches. This study is among the first to address this gap, as highlighted by [21,22] and also responds to the call for the adoption of open-source platforms like RStudio (2025.09.1) over proprietary tools like MATLAB [23].

A unique aspect of this study is its focus on root-zone heating with a biologically derived PCM rather than traditional air volume heating, addressing a critical but underexplored area in greenhouse climate control. Furthermore, despite the growing literature on PCM use in greenhouses, there is a gap in the application of machine learning techniques specifically for modeling root-zone temperature in systems using latent heat storage. This study fills this gap and contributes to the broader goal of decarbonizing greenhouse agriculture by demonstrating the feasibility of replacing petroleum-based PCMs with sustainable, bio-based alternatives.

2. Materials and Methods

This section describes the experimental design, measurement system, and modeling approach adopted to investigate the thermal performance of coconut oil (CO) as a bio-based phase-change material (PCM) in greenhouse root-zone heating. Details on the greenhouse structure, environmental and thermal measurements, instrumentation accuracy, and data-acquisition procedures are presented. Furthermore, the section outlines the construction and optimization of the machine learning models MARS, SVR, and XGBoost used to predict root-zone temperature based on key climatic and internal parameters. The methodological framework aims to ensure the reproducibility, reliability, and statistical robustness of both experimental and computational analyses.

2.1. Experimental Setup

An experimental study was conducted on two similar greenhouse sections, one with and one without PCM (CO), each with an area of 60 m², covered by a single layer of polyethylene in Adana (37°00′38″ N, 35°20′21″ E) in the south of Türkiye to explore the thermal behavior of root zone in greenhouse (Figure 1) in February, March and April 2022. Dimensions of the plastic greenhouse are 10 m (length), 6 m (width), and 3.75 m (height). The greenhouse frame is made of aluminum and steel materials, positioned in the north–south direction. A single layer of polyethylene (PE) cover with a thickness of 0.35 mm is used as the cover material in the greenhouse. The experimental study started on 4 February 2022 with cleaning of the greenhouse, preparation of stands where PCMs will be placed, setup of the plant-growing environment, and ended on 26 May 2022. As a plant-growing medium, a mixture of 50% cocopeat and 50% pumice materials was used instead of soil. These materials were filled into pots with a width of 44 cm, a height of 35 cm, and a volume of 27 L. For irrigation and fertilization, micro drippers were added to the irrigation line and positioned inside the pots. A total of 190 pots were placed in both greenhouses (95 pots each).

According to the General Directorate of Meteorology of Türkiye [24], average ambient air temperatures for the coldest months (December, January, and February) are 11.2 °C, 9.5 °C, and 10.3 °C, with the lowest average ambient temperatures for these months recorded at 7.0 °C, 5.2 °C, and 6 °C, respectively. Additionally, negative ambient temperatures can be observed in some years during winter in the province. To prevent heat transfer from greenhouse air to the soil, black plastic cover material was laid at the base of both greenhouses. Temperature changes in the indoor air, PCM, and root zones in the greenhouse were measured and logged using an Onset Computer Hobo UX120-006M (Bourne, MA, USA) with a resolution of 1 h, resulting in a total of 2658 datasets collected from the experiment (Figure 2). Outside temperature, radiation, relative humidity, and wind speed were measured by the NG Field Climate (Weiz, Austria) local meteorological station located 50 m away from the experimental greenhouse.

In the greenhouse equipped with PCM, using disposable ice packages as a macro-packaged heat-storage medium. These disposable ice packages that are readily available in markets were hung on a wire prepared near the pots. The packages were chosen in a transparent color to observe the thermal behavior of CO (Figure 3).

2.2. Uncertainty Analysis

The accuracy of measured values is very important for experimental studies. In this study, uncertainty propagation analysis was used to calculate the uncertainties of calculated results. Using the approach outlined by [25], uncertainty of calculated findings is derived by using the values

Table 1. Uncertainty for each equipment of measurement system.

Device/Material	Measurement Range/Accuracy
Temperature measurement	−20 + 80 °C, ±0.5 °C
Moisture measurement	10–90%, ±3%
Pyranometer	400–1100 W/m2, ±10 W/m2
Anemometer	0–50 m/s, ±0.25 m/s
Mettler Toledo (Differential Scanning Calorimetry 3+)	−170 + 700 °C, ±0.2 °C
HotDisk TPS 2500S (Thermal Conductivity)	0.005–1800 W/m/K, 5%

and Equation (1).

According to the method, if a result R is a given function of the independent variables x₁, x₂, x₃, x₄, …, x_n. Thus,

$${\omega }_R={\left[{\left({\displaystyle \frac{{\partial }_R}{{\partial }_{x1}}}{\omega }_1\right)}^2+{\left({\displaystyle \frac{{\partial }_R}{{\partial }_{x2}}}{\omega }_2\right)}^2+{\left({\displaystyle \frac{{\partial }_R}{{\partial }_{x3}}}{\omega }_3\right)}^2+\cdots +{\left({\displaystyle \frac{{\partial }_R}{{\partial }_{xn}}}{\omega }_n\right)}^2\right]}^{1/2}$$

(1)

Here R is a calculated result, x₁, x₂, x₃, …, x_n are the measured values. $\omega$₁, $\omega$₂, $\omega$₃, …, $\omega$_n is the uncertainty of the values x₁, x₂, x₃, …, measured, respectively. ${\omega }_R$ is the absolute uncertainty of the outcome R and ${\omega }_R$/R is the percentage uncertainty of the outcome R. In this study, the experiments are conducted at 6.0% uncertainty.

2.3. Model Construction

Greenhouses represent highly complex and nonlinear systems that dynamically adapt to various shocks, predominantly influenced by weather-related factors. Given their ability to universally approximate, machine learning techniques are increasingly recognized as a versatile solution for addressing challenges inherent in nonlinear systems. Models were constructed by utilizing RStudio software (2025.09.1) using R programming language. During the model employed, various libraries were used, such as earth, caret, tidyverse, ggplot2, ehaGoF, phych, xgboost, corrplot, dalex. Model construction processes are illustrated in Figure 4.

Multivariate Adaptive Regression Splines (MARS), Support Vector Regression (SVR), Extreme Gradient Boosting (XGBoost), which are used and are powerful predictors in practice, were applied in this study. MARS was chosen because it contributes particularly to interpretability, thanks to its ability to capture nonlinear and interactive relationships between variables with segment-based flexible regression curves. SVR was preferred because it shows high generalization performance, especially in small- and medium-sized datasets and can model nonlinear relationships with kernel functions. XGBoost was used due to its fast computational capability, ability to cope with missing data, and success in modeling complex interactions between variables with high accuracy. These models were selected owing to their ability to deal with complex and nonlinear connection among inputs and output (

Table 2. Input and output parameters used in study.

Parameters	Variables	Definitions
Inputs	Rad	Radiation (W/m2): Global solar radiation on horizontal surface
	Wv	Wind velocity (m/s): Wind velocity is necessary for calculation of the greenhouse heat loss.
	Moist	Air moisture (%): It is important to grow healthy plants in a greenhouse and is also proportional to the heat that the air inside the greenhouse can absorb.
	Tamb	Ambient temperature (°C): Outdoor air temperature
	Tghot	Greenhouse air temperature (°C): Indoor temperature of greenhouse equipped with PCM
	Tpcm	PCM temperature (°C): Temperature of phase-change material (CO)
Output	Tpot	Root-zone temperature (°C): It is taken from 3 different points in the pot, and these 3 measurements were averaged.

).

A total of 2658 samples of root-zone temperatures were randomly selected with a proportion of 70% for training and 30% for testing datasets. To ensure an unbiased selection of data, a standard type of cross-validation (CV), namely K-fold CV, was employed [26]. Although there is no strict rule for determining the value of K, it is common practice to use 5 or 10 folds in machine learning algorithms and for this study K-fold CV was selected as 10 according to [27,28,29].

$$Y_i={\sum }_{k=1}^{K}fk\left(x_i\right), fk ϵ F, i=1,\dots ,n$$

(2)

where $Y_i$ is the prediction of the $i$-th sample after iterations. K is the representation of all CART trees, $fk\left(x_i\right)$ is the prediction results of $x_i$ in the k-th tree, and $\mathcal{F}$ denotes the space of all possible CART trees.

In machine learning models, numerous parameters significantly influence model effectiveness, generalization ability, and the computational time and complexity required for training. To avoid issues such as overfitting and underfitting and to achieve robust model performance, grid search was employed during the training phase. This method involves training the model over a predefined set of hyperparameter combinations and evaluating performance using a selected methodology, typically cross-validation. The primary advantage of the grid search lies in its simplicity and ease of implementation. However, its major drawback is the high computational cost associated with large hyperparameter spaces [30]. Optimized hyperparameter values for XGBoost, SVR, and MARS are given in

Table 3. Optimized hyperparameter results for XGBoost.

XGBoost
nrounds	max_depth		eta			gamma	min_child_weight			colsample_bytree
751	5		0.532			1.354	10			0.533
SVR
gamma				c					epsilon
0.186				100					0.23
MARS
degree		nprune			penalty			thresh			nk
2		100			2			0.005			6

.

Multivariate Adaptive Regression Splines (MARS), a non-parametric regression method, is designed to be used in cubic and linear basis function developed by [31] to understand connection of datasets between predictors and responses. MARS consists of linear models that automatically recognize nonlinear situations between parameters of a problem. Recent statistical modeling studies have comparatively assessed the prediction capabilities of decision tree, artificial neural networks, random forest, and MARS algorithms over the last decade. The method can be used for linear and nonlinear modeling, and it is suitable for engineering problems based on dynamic physical systems. The MARS algorithm’s equation is represented mathematically by [32]:

$$y={\beta }_0+{\sum }_{m=1}^M{\beta }_m{\prod }_{k=1}^{K_m}{h}_{km}\left(X_{v(k,m)}\right)$$

(3)

Here, y defines output or dependent parameters, ${\beta }_0$ is the regression constant, ${\beta }_m$ represents coefficients of basis functions of the MARS model, $h_{km}\left(X_{v(k.m)}\right)$ are basis functions, in which $v(k,m)$ is an index of the independent variable in the $m^{th}$ component of the $k^{th}$ product. $K_m$ is the parameter restrictive of the order of interaction.

These basis functions allow MARS to adaptively partition the input space and fit piecewise models, thereby capturing nonlinear dependencies effectively. To enhance the model performance with the MARS algorithm, the following optimized hyperparameter configuration was employed: degree set to 2, nprune to 100, penalty to 2, and thresh to 0.005.

SVM (Support Vector Machine) is known as a classification algorithm in two-dimensional space. SVR that is an extension of SVM was modified by [33] and is an important method used in solving regression-type problems by fitting various lines and curves in both linear and nonlinear cases. SVR creates a symmetrical tubular function with a minimal radius that eliminates high and low values in a dataset.

$$f\left(x\right)=w·x+b$$

(4)

$${\left|\xi \right|}_{\epsilon }=f\left(x\right)=\left\{\begin{array}{r}0 if \left|\xi \right|\le ϵ, \\ \left|\xi \right|-ϵ otherwise, \end{array}\right. minimize: {\displaystyle \frac{1}{2}}\left(\omega ·\omega \right)+c{\sum }_{i=1}^N\left({\xi }_i^{+}+{\xi }_i^{+}\right)$$

(5)

Here, $x$ and $b$ are bias values, and $w$ is the weighting of the vector. Minimizing test errors is achieved by minimizing the weight vector. This means that some deviations of size ε are acceptable, but those larger than +ε and −ε Equation (5) are ignored. The kernel type used for modeling nonlinear complex relationships is the radial basis function (RBF), with the model’s error tolerance controlled by the parameters gamma (0.186), C (set to 100), and sigma (set to 0.23).

2.4. Model Evaluation

Some evaluation criteria have been determined in the literature to measure performance of models created to predict output data. These criteria to be used specifically for this study are Root Mean Square Error (RMSE; Equation (6)), Standard Deviation Ratio (SDR; Equation (7)), Mean Absolute Percentage Error (MAPE; Equation (8)), Mean Absolute Deviation (MAD; Equation (9)), Coefficient of Determination (R²; Equation (10)). Evaluation of the algorithms depends on goodness of fit criteria that are defined as follows [34,35]:

$$RMSE= \sqrt{{\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{\left(y_i-y_{ip}\right)}^2}$$

(6)

$$SDratio={\displaystyle \frac{S_m}{S_d}}$$

(7)

$$MAPE={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n\left|{\displaystyle \frac{y_i-y_{ip}}{y_i}}\right|\times 100$$

(8)

$$MAD={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n\left|y_i-y_{ip}\right|$$

(9)

$$R^2=1-\left({\displaystyle \frac{{\sum }_{i=1}^n{\left(y_i-y_{ip}\right)}^2}{{\sum }_{i=1}^n{\left(y_i-\overline{y}\right)}^2}}\right)$$

(10)

where n is the total number of samples used for training and testing, $y_i$ is the actual value that was measured, $y_{ip}$ is the value that was predicted, and $\overline{y}$ is the mean of the measured values. Algorithms and performance metrics were both computed with the help of R software (2025.09.1).

3. Results

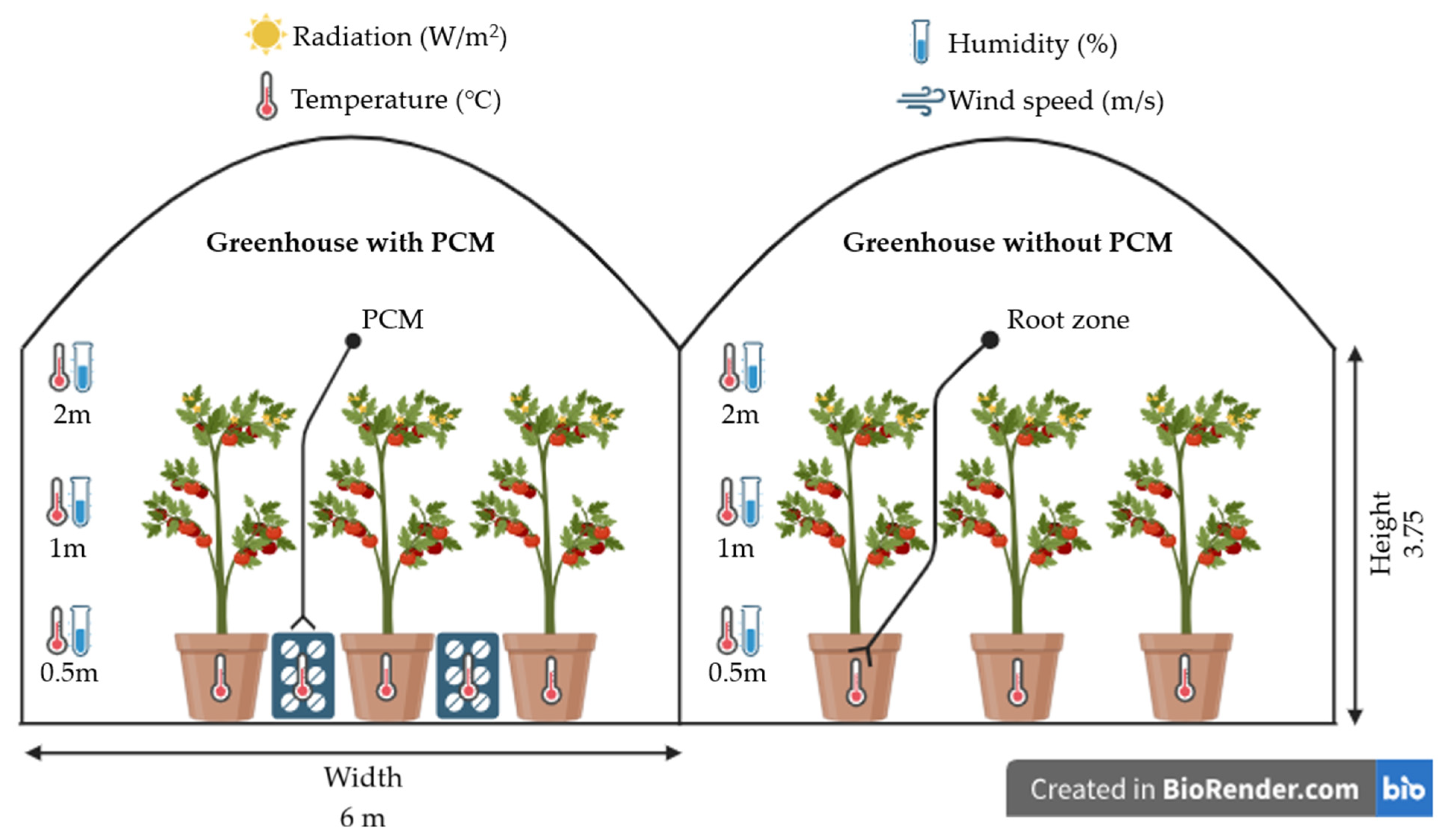
The findings are structured to evaluate the thermophysical properties and stability of coconut oil, its effectiveness as a heat-storage medium, and its influence on greenhouse root-zone temperatures under real climatic conditions. In addition, the predictive performance of the applied machine learning models is compared through statistical metrics, feature importance, and sensitivity analyses. The results collectively highlight the potential of coconut oil-based PCM systems for improving thermal management and energy efficiency in greenhouse environments.

3.1. Selection Criteria of Coconut Oil

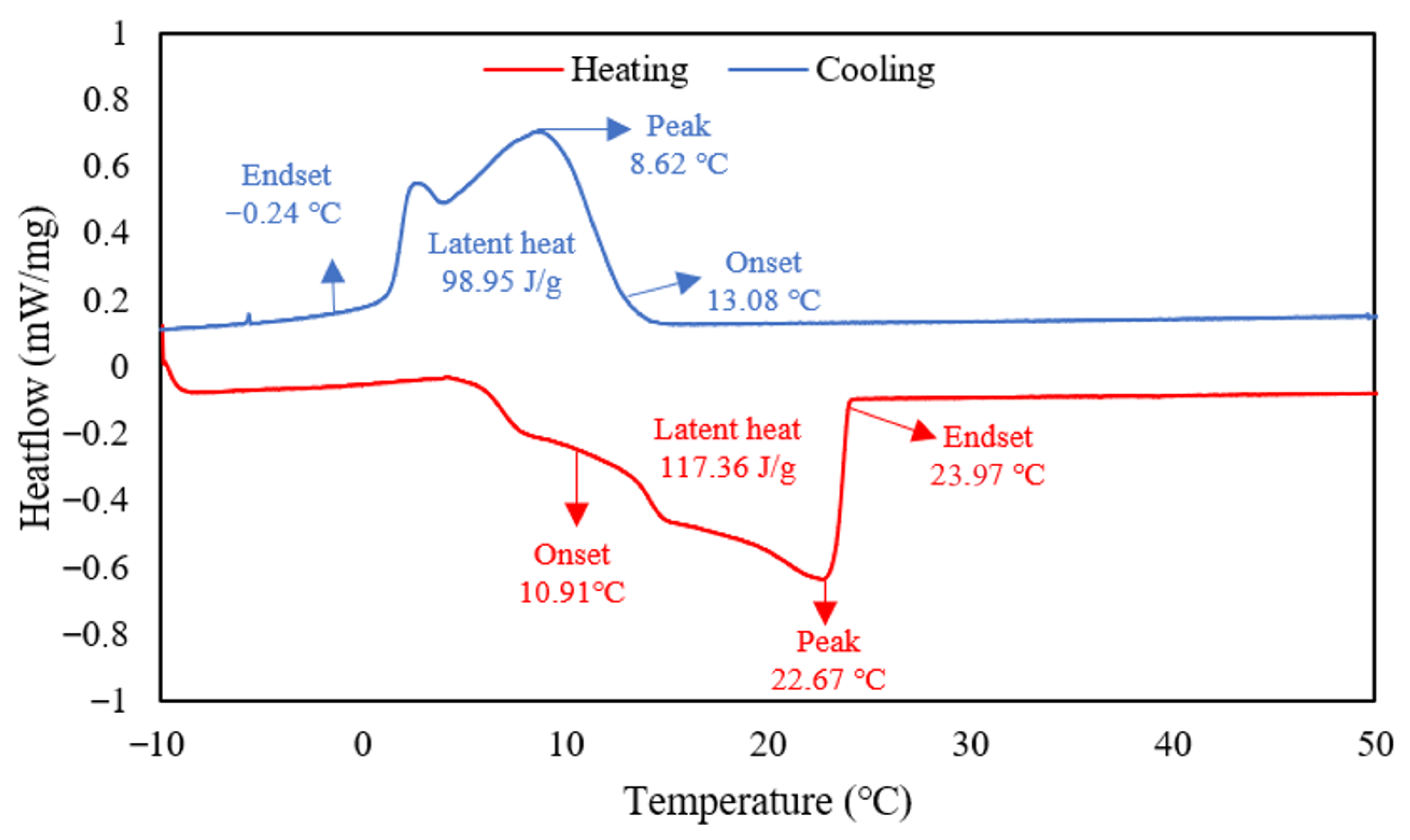
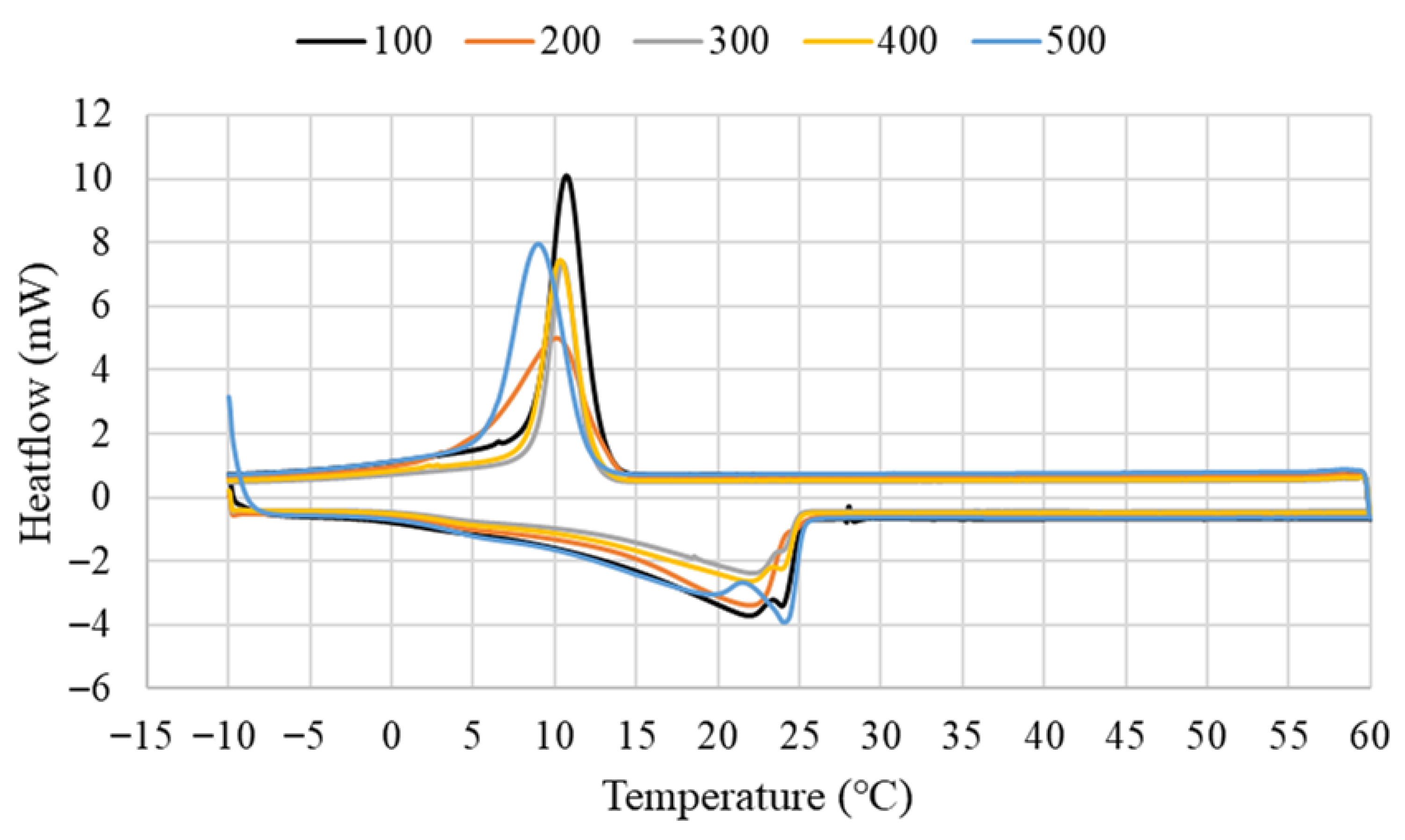
Differential Scanning Calorimetry (DSC) is the most used method to determine the melting/freezing points, phase-change heat and specific heat capacity of PCMs. In this study, DSC measurements were carried out with a Mettler Toledo brand device located at Cukurova University Central Research Laboratory, using a 10 mg CO sample in a nitrogen atmosphere with a nitrogen flow rate of 40 mL/min and a heating–cooling rate of 1 °C/min. Each sample was heated from −10 °C to 60 °C and similarly cooled from 60 °C to −10 °C. Also, thermal conductivity of CO was measured using HotDisk2500S with capton sensor at 25 °C ambient temperature. Differential scanning calorimetry and thermal conductivity analysis of coconut oil used in the study is given in Figure 5 and

Table 4. Thermophysical properties of coconut oil.

Properties	Heating	Cooling
Peak temperature (°C)	22.67	8.62
Onset temperature (°C)	10.91	13.8
Endset temperature (°C)	23.97	−0.24
Heat of fusion (J/g)	117.36	98.95
Thermal conductivity (W/m·K)	0.193
Thermal diffusivity (mm2/s)	0.159

. Investigation of the usability of coconut oil as a PCM, the specific enthalpy and thermal conductivity values were like other studies in the literature as expected [36,37,38,39]. CO gives back 98.95 J/g of the 117.36 J/g of energy it takes in during heating, and its storage efficiency is 84.3%. Although the thermal conductivity coefficient of the sample is low at 0.193 W/m.K, it is a product with development potential due to the abundance of CO, its natural origin, and the ability to increase the thermal conductivity coefficient with nanoparticles.

CO possesses desirable thermal properties, such as a phase-change temperature between 17 and 26 °C [36,37], a moderate latent heat of fusion of 102–103 kJ/kg [38], and a thermal conductivity ranging from 0.161–0.321 W/m·K [39], in addition to its ecofriendly bio-based nature.

The biochemical stability of coconut oil, classified under the fatty acid group in PCM classification, is reported to withstand 200 thermal cycles [40] or more than two years, making it also cost-effective. Overall, studies suggest that coconut oil is suitable for thermal applications for building as a heat-storage material [15,37,41,42,43]. 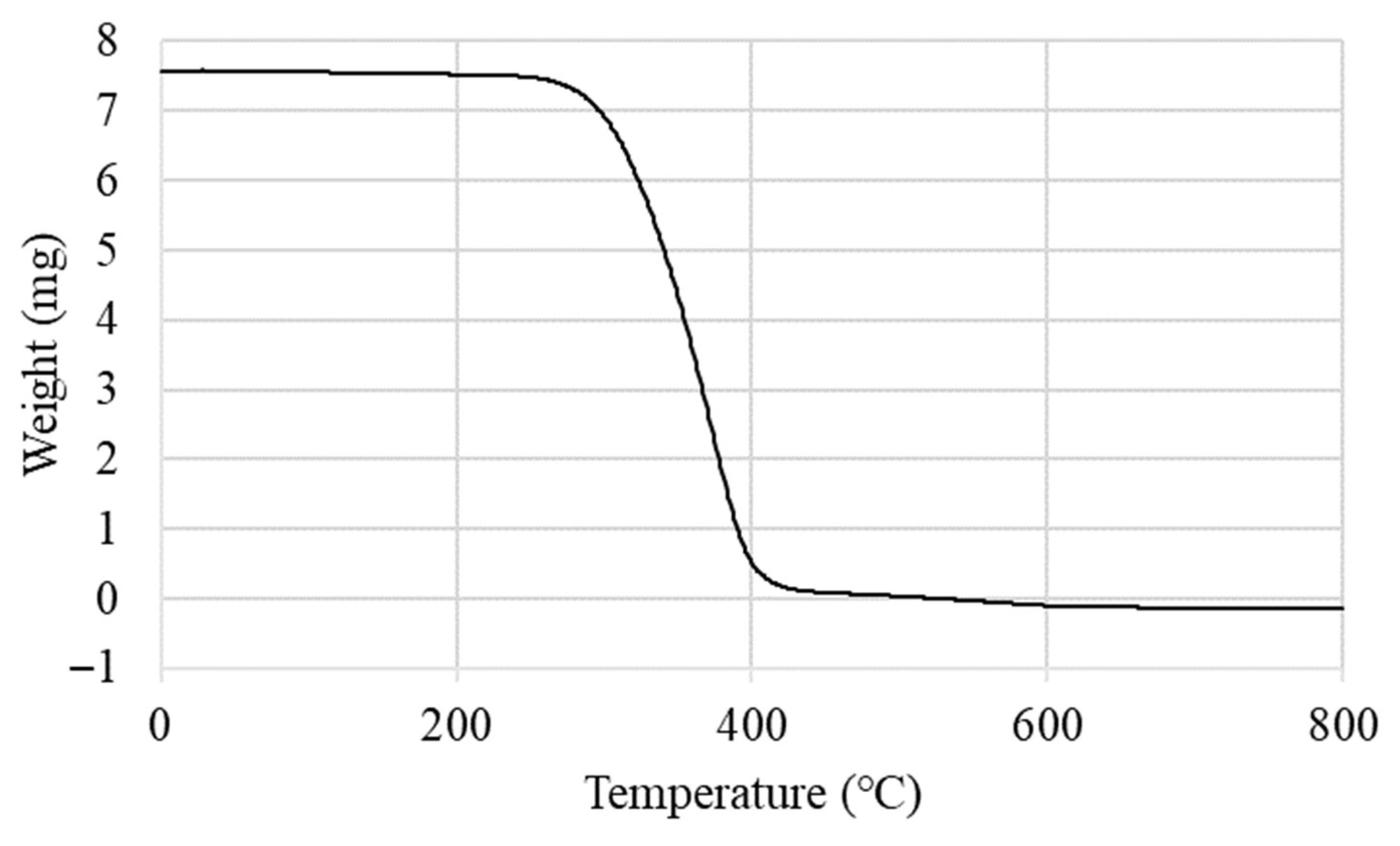Thermal stability analysis of CO was performed with different numbers of cycles (100, 200, 300, 400, and 500), and results are given in Figure 6.

Thermogravimetric analysis gives curves showing the weight loss of a substance against temperature. The weight of the CO sample remains constant until the decomposition starts. The mass loss observed afterwards is the result of the temperature increase in the boiling phase and the evaporation in the test phase. The initial temperature of the thermal decomposition of coconut oil was found to be 252 °C for this study. Majority portion of the mass loss (95%) occurred between 200 and 400 °C. When the degradation curve of CO is examined, it falls into the classification of medium volatile oil (200–600 °C). There is a two-stage thermal degradation in the curve shown in Figure 7. The reason for this is that the chain length of the fatty acids, a branch of the chain, and the degree of unsaturation are factors that affect the thermo-oxidative properties of the fatty ester [44].

3.2. Thermal Behavior and Performance of Coconut Oil as Heat-Storage Medium

The thermal performance of PCM on root-zone temperatures for tomato plants in greenhouses were examined and compared. According to the results obtained from the experimental study, it was observed that the greenhouse indoor air, PCM temperature, and root-zone temperatures started to decrease as of 15:00 local time, when the energy gain resulting from solar radiation was lower than the heat loss in the greenhouse indoor. The average of global solar radiation of the investigated months are 173.9, 252.2, and 338.5 W/m², February, March, and April, respectively. Of hourly average ambient temperatures (Tamb) examined, the coldest month for both daytime (09:00–18:00) and nighttime (18:00–09:00) is March. The average ambient daytime–nighttime temperatures for February are 14.8 °C, and 9.9 °C, respectively. These temperatures are 13.9 °C and 8.6 °C for March and 24.2 °C, and 16.9 °C for April. Indoor air temperatures of the PCM-equipped greenhouse were 1.2 °C, 1.3 °C, and 4.5 °C higher than the control greenhouse indoor temperature during daytime for February, March, and April, respectively. These temperatures were 1.8 °C, 2.4 °C, and 0.4 °C higher than the control greenhouse in the PCM-equipped greenhouse indoor air (Figure 8). The average difference between root-zone temperatures in the greenhouse (with PCM) compared to root-zone temperatures in the control greenhouse (without PCM) are 1.76 °C, 0.91 °C, and 1.46 °C higher for February, March, and April, respectively (Figure 9). The findings obtained from the experimental study are similar [6,8].

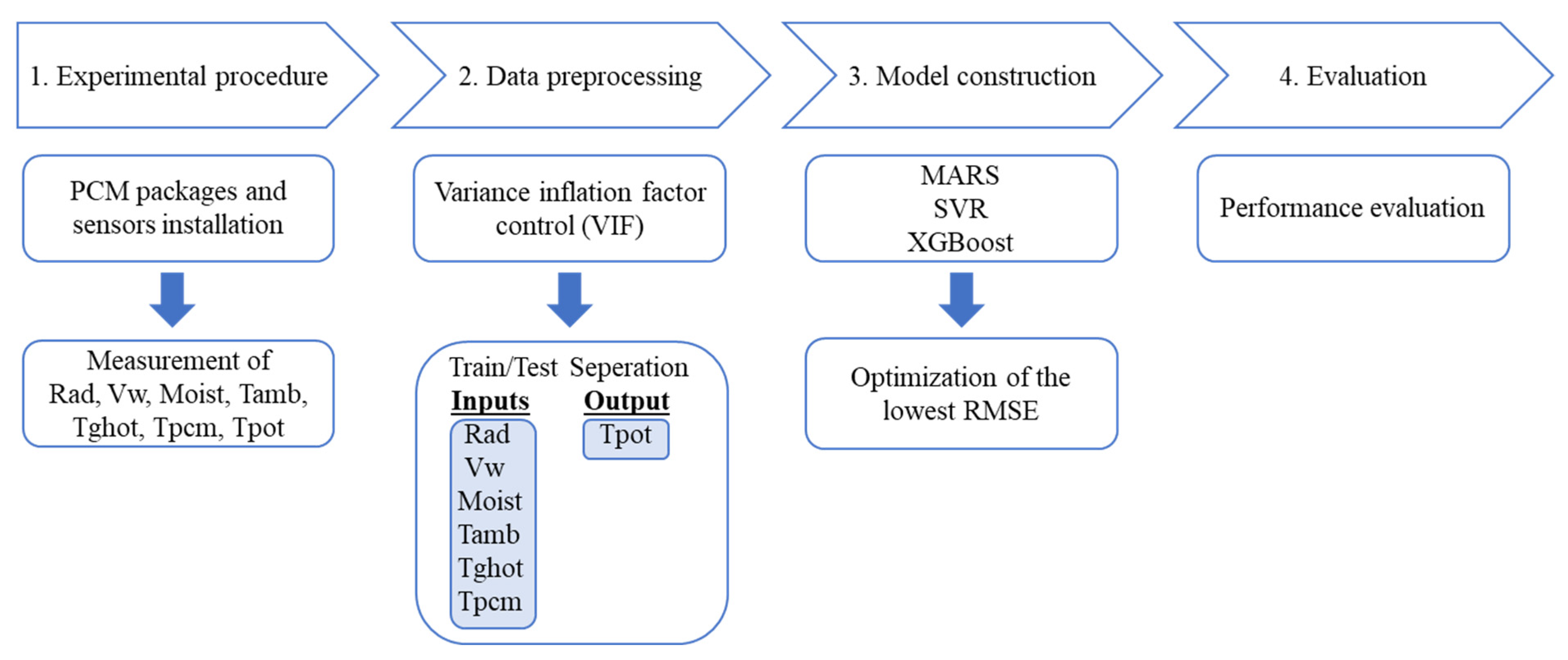
3.3. Statistics and Machine Learning for Experiment

Machine learning has been applied to predict the root-zone temperature to determine the impacts of heat storage with PCM in a greenhouse. It is important to evaluate properly the training and test sets for machine learning applications to eliminate underfitting, overfitting, and multicollinearity. Before starting the analysis, whether there was a multicollinearity problem among the input parameters was examined. The Variance Inflation Factor (VIF) value of the parameters whose multicollinearity was controlled are Rad (3.962), Vw (1.329), Moist (2.066), Tamb (7.296), Tghot (9.787), and Tpcm (3.260), respectively. Results show that there is no multicollinearity problem when VIF is lower than 10 [45,46]; thus, there is no multicollinearity problem in this study. Descriptive statistics of the measured parameters in this experiment are presented in

Table 5. Descriptive statistics of experimental data.

Variables	n	Mean ± Standard Error	sd	Min	Max	Skewness	Kurtosis
Rad	2658	187.26 ± 5.41	279.12	0	1051	1.36	0.50
Vw		0.44 ± 0.01	0.48	0	2.6	1.26	1.10
Moist		61.33 ± 0.54	27.91	8.51	100.0	−0.07	−1.36
Tamb		16.01 ± 0.13	6.70	−1.70	34.4	0.24	−0.45
Tghot		18.98 ± 0.18	9.21	−1.77	42.69	0.29	−0.78
Tpcm		18.62 ± 0.18	9.51	−1.84	44.65	0.33	−0.51
Tphot		21.84 ± 0.17	8.59	3.30	44.65	0.23	−0.70

. The average root-zone temperature (Tphot) ranges between 3.30 °C and 44.65 °C. The average of Tpcm, which is thought to be the most effective parameter on Tphot, varies between −1.84 °C and 44.65 °C.

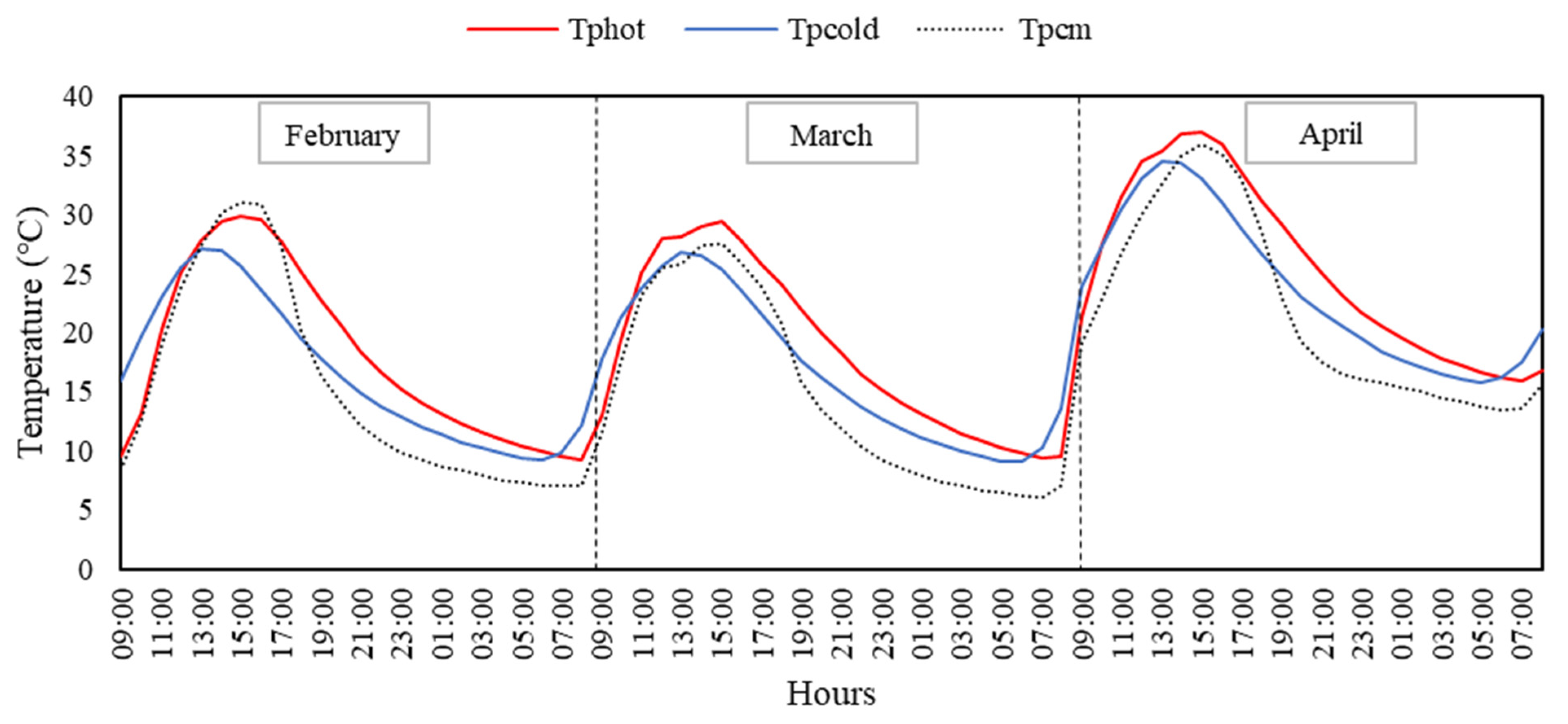
According to the results of the paired t-test, a statistically significant difference was observed between the soil temperatures of the heated pots (Tphot) and the unheated pots (Tpcold) (t = 18.558, df = 2657, p < 0.001). The confidence interval (95%) for the mean difference was (1.39, 1.72), indicating that the average soil temperature in the heated pots was 1.55 °C higher than in the unheated pots. This finding concludes that the application of phase-change materials (PCMs) is effective in increasing root-zone temperatures.

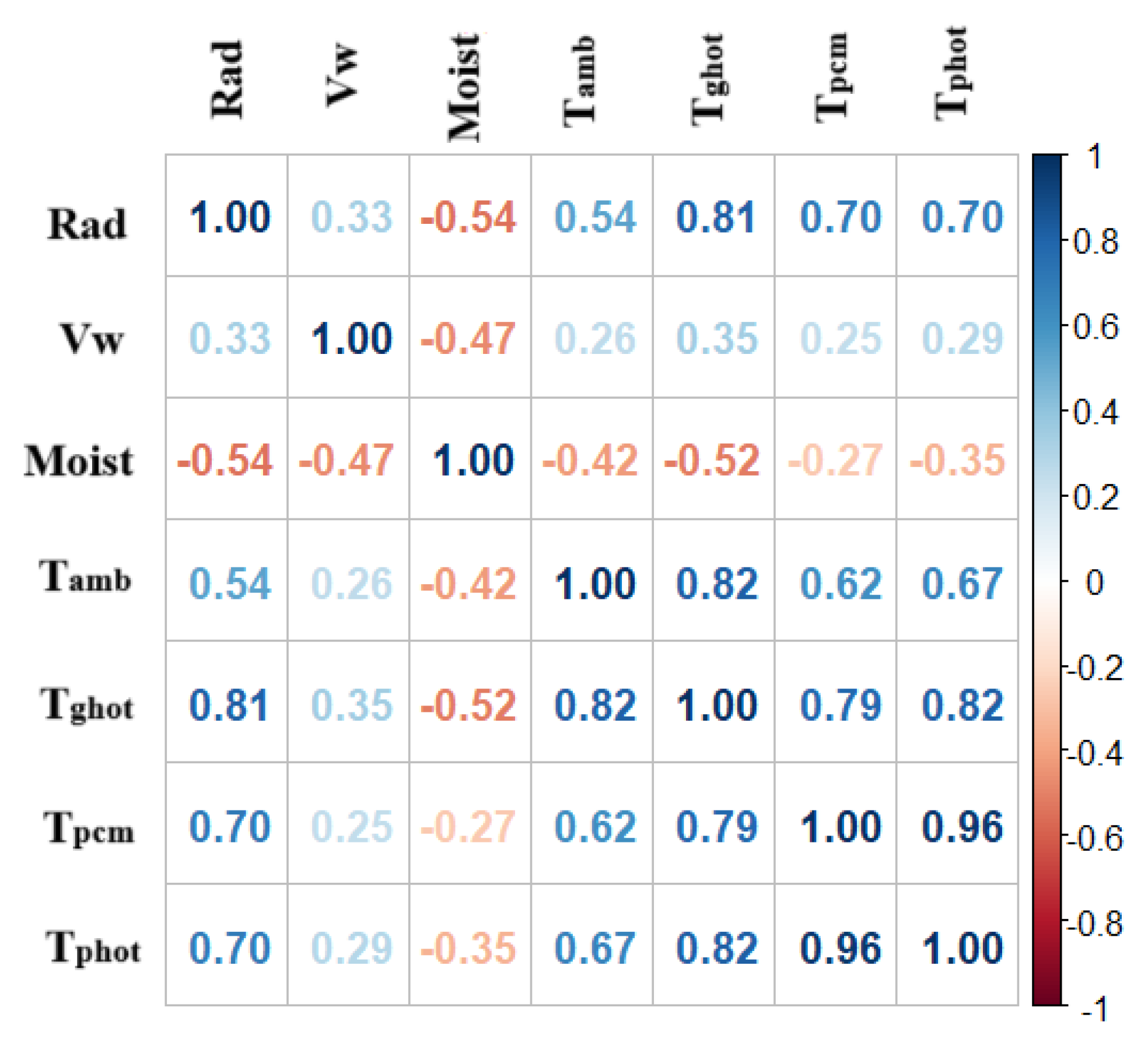
Linear relationship between measured parameters were determined using Pearson correlation coefficient (R), and the results are illustrated (Figure 10). As can be seen from Figure 10, Tphot has a positive and highly significant correlation (p < 0.001) with Tpcm (0.96), Tghot (0.82), Rad (0.70) and Tamb (0.67). Rad positively correlated with Tghot, Tpcm, and Tphot, with R ranging from 0.70 to 0.81, and Moist is negatively correlated with Tamb, Tghot, Tpcm, and Tphot (p < 0.001).

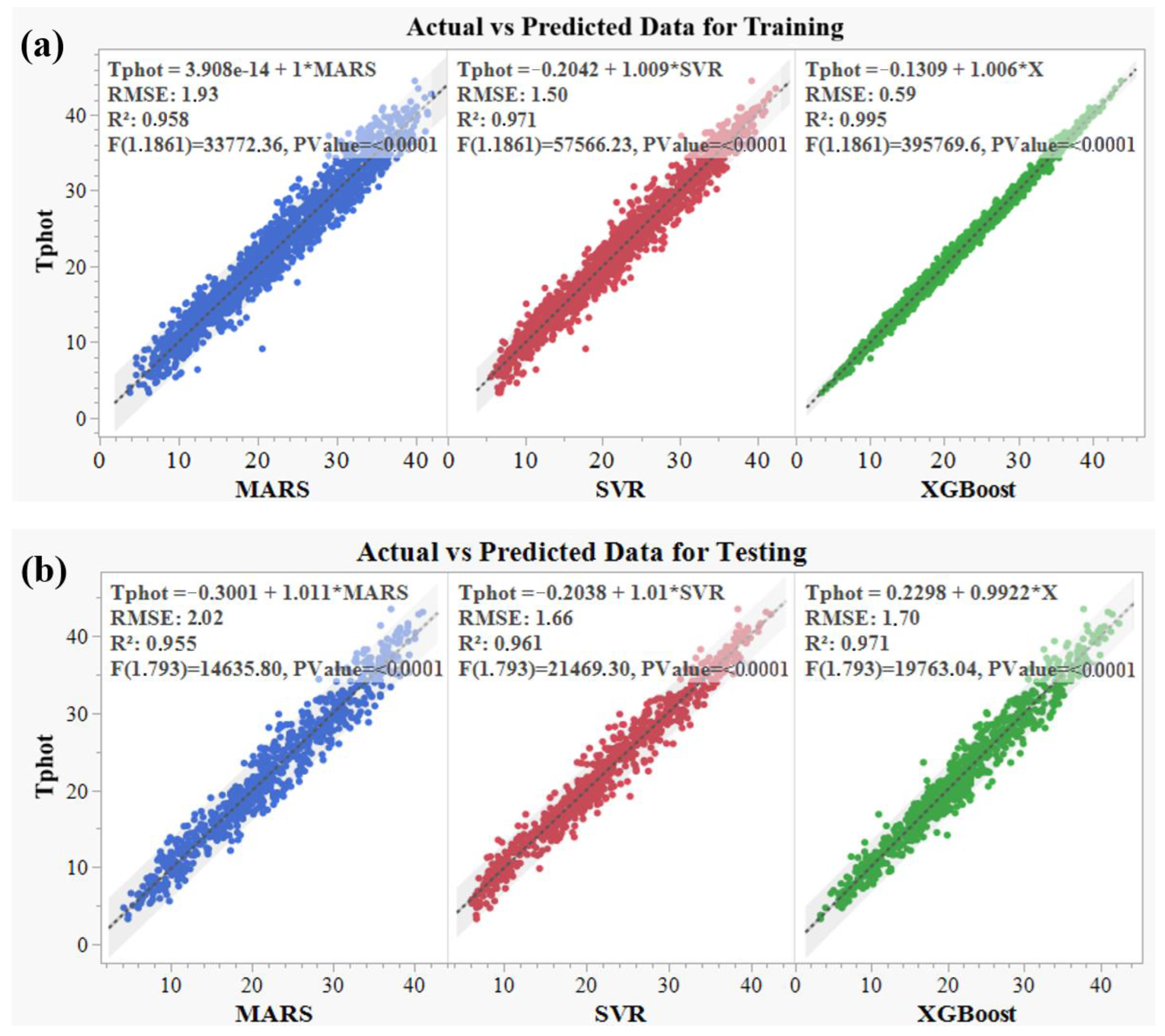
To determine the predictive power of a model, it needs to be evaluated with various criteria. For this reason, the evaluation results made with six different criteria are summarized in

Table 6. Goodness-of-fit results of training and test sets for each model used in the study.

Evaluation Matrix	MARS		SVR		XGBoost
	Train	Test	Train	Test	Train	Test
Root mean square error (RMSE)	1.93	2.02	1.50	1.66	0.59	1.70
Standard deviation ratio (SDR)	0.23	0.23	0.18	0.19	0.07	0.18
Mean absolute percentage error (MAPE)	8.01	8.35	6.35	7.15	2.48	6.90
Mean absolute deviation (MAD)	1.52	1.55	1.15	1.26	0.46	1.28
Coefficient of determination (R2)	0.958	0.955	0.971	0.961	0.995	0.971

. The smallest RMSE for training is 0.59 °C in XGBoost and for testing is 1.66 °C for SVR. Ref. [47] tried to determine the RMSE values between 2.05 and 3.54 °C, and in [46] the smallest RMSE of 1.61 was found. SDR ratios in the study ranged between 0.07 and 0.23. The minimum SDR is observed in XGBoost for both training and testing datasets.

MAPE and MAD were smallest for training in XGBoost at 2.48 and 0.46. These indices were the smallest for testing in XGBoost and SVR at 6.90 and 1.26, respectively. When R² values are examined, it is observed that all three algorithms obtain strong models (>95%). XGBoost showed better results (99%) for training datasets than others, while testing dataset’s R² values are equal in SVR and XGBoost (96%). The results of the evaluation criteria shown in Table 6 are within the ideal limits. All three algorithms achieved strong results in modeling the root-zone temperature. While the XGBoost algorithm achieved the best results during the training of the dataset, XGBoost and SVR achieved similar results during the evaluation of the test set. Figure 11 shows the linear regression between the observed and predicted values of the models used in the study for both training and testing sets.

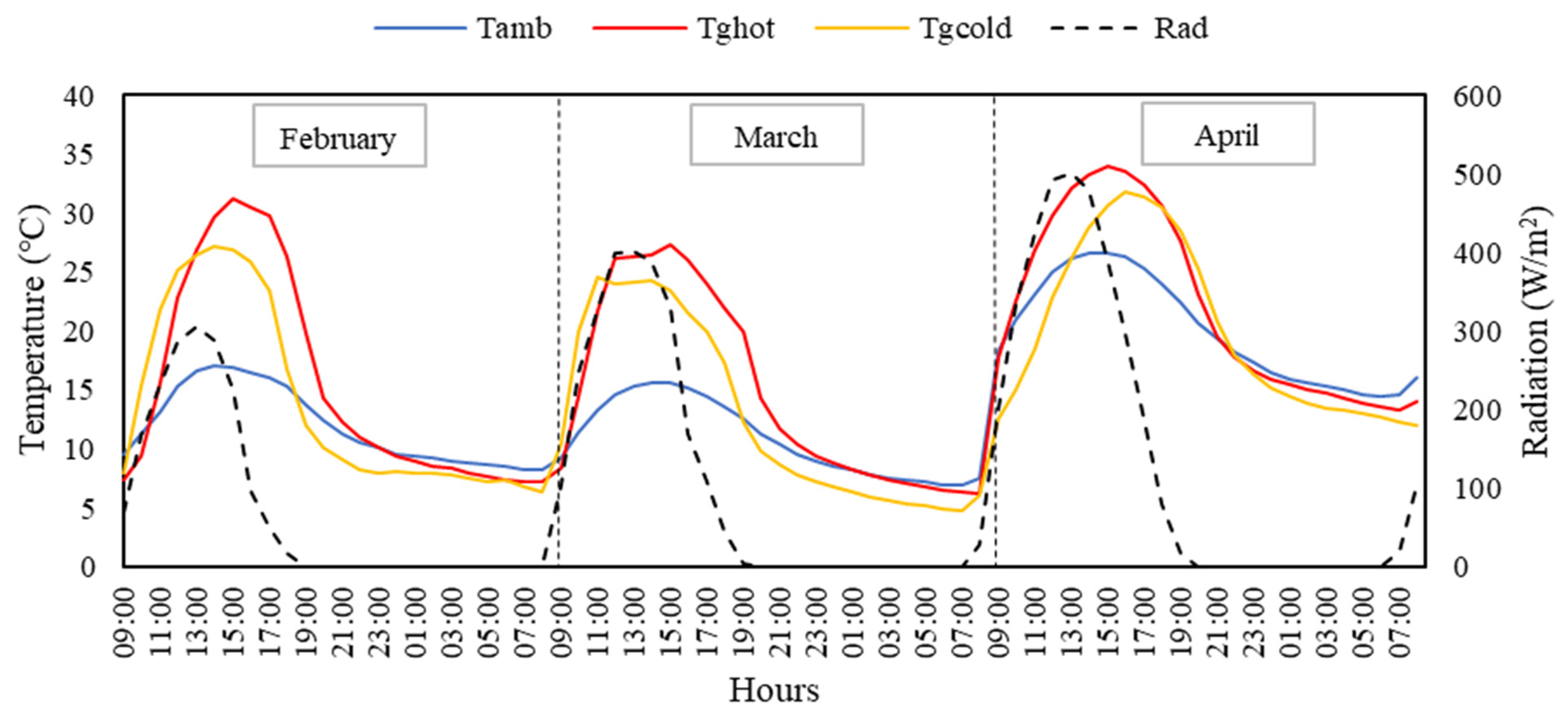
Heating requirements of greenhouses in the Mediterranean region are lower than in other regions. The annual average energy consumption of a greenhouse in the Mediterranean region for a 90-day heating period is approximately 150 kW. The amount of fuel oil required to meet this demand is 0.055 L/m², and the amount of coal is 0.1 kg/m² [48]. Ref. [49] heat storage on the soil surface can meet up to 13–19% of total daily heat requirement of a greenhouse. Ref. [50] reported that the air temperature inside the greenhouse should be 12 °C higher than the air temperature outside. With the proposed heat-storage application, both greenhouse indoor temperatures and root-zone temperatures were found to be higher than control groups. Root-zone temperatures in the greenhouse compartment where the heat-storage application was made showed better results during the night hours compared to the control group. The reason why the plant root-zone temperatures in the greenhouse with heat storage are lower before noon is that the PCM has collected and stored heat from the interior, and both the interior and root-zone temperatures have decreased. Indoor temperatures were found to be 1.8 °C, 2.4 °C, and 0.4 °C higher than the control greenhouse in February, March, and April, respectively, with a short-term (day to night) heat-storage process. Root-zone temperatures were observed to be 1.76 °C, 0.91 °C, and 1.46 °C higher than control pots for the same months, respectively.

This study clarifies the effectiveness of machine learning models (SVR, MARS, XGBoost) in analyzing factors and PCM on root-zone temperature and predicting future values. The models combine climatic factors such as temperature, humidity, solar radiation, and wind velocity and internal factors like air temperature in the greenhouse and PCM temperature. These models try to reveal nonlinear relationships between inputs and outputs. With these learning models, target output can be predicted with a very accurate percentage using existing input data.

Ref. [51] achieved a low Root Mean Square Error (RMSE) value of 3.7 °C for the test dataset in their study, employing Artificial Neural Networks (ANNs) to predict temperature fluctuations in a high tunnel greenhouse. In another study, ref. [52] utilized ANNs to estimate greenhouse temperatures, yielding R² values of 0.959 (winter) and 0.955 (summer) within a 95% confidence interval. Ref. [53] attempted to forecast temperature and humidity levels in a Chinese greenhouse, employing various machine learning approaches. Support Vector Machine (SVM) demonstrated an RMSE of 2.78 °C and an R² of 0.89 for temperature prediction, along with an RMSE of 4.55% and an R² of 0.87 for humidity. Ref. [54] conducted a comparative analysis of machine learning models including Random Forest, SVM, Multiple Linear Regression (MLP), Long Short-Term Memory (LSTM), and Gated Recurrent Unit (GRU) for predicting minimum greenhouse temperatures. The random forest model exhibited the highest R² (0.87) with the lowest RMSE (4.43 °C), while SVM yielded an R² of 0.87 and an RMSE of 4.52 °C. SVM has been utilized for understanding greenhouse indoor temperatures and the energy-storage performance of phase-change materials in solar collectors. Ref. [22] utilized the Nonlinear Autoregressive Networks with Exogenous Input (NARX) algorithm to model indoor air temperatures in greenhouses with and without Phase-Change Materials (PCMs). Ref. [55] applied NARX and Recurrent Neural Network (RNN) algorithms to model indoor temperatures, achieving R² values of 0.9986 and 0.9893, respectively. These findings underscore the efficacy of machine learning techniques in developing heat-storage systems. Ref. [56] compared ANN and Multivariate Adaptive Regression Splines (MARS) methods for estimating indoor temperatures in greenhouses, noting MARS’s provision of more detailed results. MARS data-mining algorithm has been utilized across various domains, including agricultural studies [32,57,58].

Determining which variables are significant and assessing their impact on model performance is of paramount importance in machine learning. To this end, feature importance analysis was conducted for each model, and the results are presented in

Table 7. Feature importance and sensitivity results for ML models.

XGBoost
Importance Level	Sensitivity Level	Features	Gain	Mean Dropout Loss
1	1	Tpcm	0.688	9.245
2	2	Rad	0.184	1.984
3	3	Tghot	0.085	1.728
4	4	Tamb	0.022	1.629
5	5	Moist	0.015	1.406
6	6	Wv	0.006	0.849
SVR
Importance Level	Sensitivity Level	Features	Gain	Mean Dropout Loss
1	1	Tpcm	0.475	10.808
2	2	Tamb	0.196	5.347
3	3	Tghot	0.127	3.935
4	4	Rad	0.118	3.766
5	5	Moist	0.056	2.598
6	6	Wv	0.027	1.992
MARS
Importance Level	Sensitivity Level	Features	Gain	Mean Dropout Loss
1	1	Tpcm	0.435	10.074
3	3	Rad	0.184	4.256
2	2	Tghot	0.185	4.265
5	5	Moist	0.089	2.057
4	4	Tamb	0.107	2.500
6	NA	Wv-unused	0	NA

. Additionally, sensitivity analysis which evaluates how variations in each variable affect model performance, provides critical insights into model accuracy, robustness, and hyperparameter tuning. The sensitivity metrics are also included in Table 7.

Upon examination of Table 7, it was observed that in the XGBoost and SVR models, all six input variables contributed to model performance, whereas in the MARS model, Vw was found to be ineffective and was thus excluded. Across all three models, Tpcm was identified as the most influential factor affecting Tphot. The increase in temperature of the phase-change material (coconut oil) led to a corresponding rise in root-zone temperatures.

Feature importance analysis was employed to evaluate the impact of input variables on the output variable by calculating their gain values. The sum of all variable gains equals one. The influence of Tpcm on Tphot was determined to be 68.8% in XGBoost, 47.5% in SVR, and 43.5% in MARS. While XGBoost and MARS models identified Rad (18.4%) as the second-most significant parameter after Tpcm, the SVR model indicated Tamb (19.6%) as the secondary influential factor.

According to the sensitivity analysis results, which demonstrate the effect of variations in each variable on model performance, the Moist and Vw variables influence the model output, albeit with relatively lower importance scores in all algorithms except MARS. Mean dropout loss values indicate that even minor changes in Tpcm would lead to significant differences in model performance across all three algorithms.

4. Discussion

The experimental and modeling results of this study demonstrate that coconut oil (CO), as a bio-based phase-change material (PCM), effectively stabilizes the root-zone temperature (RZT) in greenhouse conditions and reduces nocturnal cooling fluctuations. The PCM-integrated greenhouse achieved a 1.1–1.6 °C increase in RZT and a 0.9–4.1 °C rise in indoor air temperature compared to the control greenhouse, particularly during non-solar hours. These findings align with previous reports in arid regions such as the 1–10 °C temperature gains obtained using PCM systems in Ghardaia and Borj Cedria [11,12] but diverge from the more modest results observed in temperate climates like Barcelona, where PCM alone could not supply sufficient night-time heat due to limited stored energy [13]. The results therefore confirm that the effectiveness of latent-heat-based root-zone heating depends strongly on climatic context, with the continental Mediterranean setting of Adana favoring the passive utilization of CO-based PCM.

Compared to paraffin-based phase-change materials, coconut oil (CO) exhibits distinct thermophysical, environmental, and economic characteristics. While paraffin (C16-C18) provides a higher latent heat capacity of approximately 150–160 J g⁻¹, coconut oil stores around 72–120 J g⁻¹, making it slightly less efficient in terms of heat storage [38,40]. Both materials share similar melting temperature ranges (18–27 °C for paraffin and 24 °C for CO), suitable for low-temperature thermal applications such as greenhouse heating. However, the embodied carbon emissions of coconut oil (1.54 kg CO₂ eq kg⁻¹) are nearly 50% lower than those of paraffin (3.02 kg CO₂ eq kg⁻¹), reflecting its renewable and bio-based origin. Economically, coconut oil is about half the cost of paraffin (USD 4.18 kg⁻¹ vs. USD 8.8–11.6 kg⁻¹), which enhances its feasibility in large-scale or low-cost applications [41]. Although paraffin achieves slightly better heating and cooling load reductions due to its higher energy density, coconut oil presents a more sustainable alternative with a smaller environmental footprint. Life-cycle assessments indicate that, despite lower thermal efficiency, CO’s renewable sourcing and reduced carbon emissions make it a promising eco-friendly substitute for paraffin-based PCMs, especially in low-enthalpy systems such as agricultural greenhouses. Life-cycle assessments further indicate that despite its lower thermal efficiency, CO’s renewable origin and biodegradability make it a more sustainable alternative for low-enthalpy agricultural heating compared with petroleum-derived PCMs [14,15].

Thermal reliability remains a key consideration. Refs. [59,60] observed that organic PCMs can maintain latent heat variation within ±3% after 2000–10,000 thermal cycles, with only minor shifts in melting temperature (−0.37 °C) and latent heat (−7.6%). In the current experiment, CO maintained stable phase-transition behavior after 500 cycles, confirming its durability under cyclic heating and cooling. The oxidative degradation of fatty acid-based PCMs, often evidenced by FTIR-detected hydroperoxide and aldehyde formation [61,62], is mitigated in CO due to its high saturated fatty acid fraction, providing greater stability than palm or rapeseed oils. Palm oil (33–39 °C) and its derivatives (30–60 °C), particularly hydrogenated palm stearin, typically exhibit higher melting points, rendering them more suitable for medium-to-high temperature thermal storage applications rather than low-enthalpy greenhouse heating. Nevertheless, palm oil is abundant and inexpensive as an agro-industrial byproduct, offering economic advantages in large-scale systems. Rapeseed oil, while widely available and low-cost, contains a higher proportion of unsaturated fatty acids, which leads to greater susceptibility to oxidation and degradation, thereby necessitating encapsulation or chemical modification to enhance stability. From a practical standpoint, coconut oil offers a favorable balance between thermal properties and sustainability, making it an effective bio-based alternative to paraffin for low-temperature thermal energy storage in greenhouse applications, whereas palm and rapeseed oils may require additional processing or system-specific adjustments to achieve similar performance [63,64,65,66,67]. However, encapsulation or packaging remains essential to ensure long-term reliability.

PCM placement configuration significantly affects heat-transfer performance. In this study, CO packages positioned near plant pots directly influenced root-zone heat transfer. Comparable enhancements were reported for macro-encapsulated PCMs beneath the substrate [12], north wall PCM tubes [68], and PCM-integrated coatings and bricks [69]. Nasimi et al. [70] confirm that near the root zone or wall-integrated PCMs provide superior thermal regulation by minimizing convective losses. Future applications should therefore evaluate multiple integration strategies including substrate embedding, wall incorporation, and cascading PCMs with varying melting points to maximize both heat-storage range and operational practicality.

The machine learning (ML) results reinforce the experimental observations. Among the three algorithms, XGBoost achieved the best predictive accuracy (R² = 0.971, RMSE = 1.70 °C), while SVR (R² = 0.961) and MARS (R² = 0.955) also yielded robust results, indicating that RZT dynamics are moderately nonlinear and can be effectively modeled with both ensemble and regression spline approaches. Although XGBoost achieved the highest accuracy among the three algorithms, the comparable performance of MARS and SVR (all R² values above 0.95) indicates that the relationships among environmental variables and root-zone temperature were relatively well defined and moderately nonlinear. This suggests that greenhouse thermal dynamics can be effectively modeled using simpler and more interpretable algorithms without a significant loss of accuracy. Therefore, while XGBoost demonstrates the capability of ensemble-based methods to capture complex interactions, MARS and SVR provide practical alternatives for predictive modeling in greenhouse systems where computational efficiency and interpretability are equally important.

Feature importance analysis revealed that Tpcm (PCM temperature) was the dominant predictor, contributing 68.8% (XGBoost), 47.5% (SVR), and 43.5% (MARS) to model performance, followed by solar radiation (Rad) and greenhouse air temperature (Tghot). Sensitivity analysis confirmed that small perturbations in Tpcm caused the largest changes in model accuracy (mean dropout loss > 9), highlighting the strong thermal coupling between PCM and the root zone. These outcomes are consistent with [22,46], who reported that ensemble models capture complex nonlinear interactions among climatic variables in PCM-assisted greenhouses. Moreover, MARS’s interpretable basis functions identified breakpoints near 22–24 °C, closely matching CO’s melting interval, thereby offering a valuable tool for operational control.

Economically, the observed heating energy reduction of 25–30% corresponds well with previously reported energy saving ranges of 20–60% for PCM-integrated systems [71]. Reported payback periods for paraffin-based PCM walls span 3–23 years depending on climate [41], but CO’s lower cost and renewable origin could substantially shorten this timeframe, improving feasibility for small-scale or low-budget greenhouses. Nevertheless, further full-scale validation is needed, since scaling up from a 60 m² pilot compartment may introduce non-uniform heat distribution, increased encapsulation costs, and maintenance complexity [72,73].

Collectively, these findings indicate that bio-based PCMs such as coconut oil, when combined with data driven predictive control, can substantially improve the energy efficiency and thermal stability of greenhouse systems, particularly in climates with strong diurnal temperature gradients. The hybrid use of latent and sensible heat storage and incorporation of real-time ML models trained on historical datasets [5,6] could further enhance system reliability and move greenhouse agriculture toward the net-zero-energy and low-carbon objectives of sustainable food production.

5. Conclusions

The study aims to apply three machine learning approach to estimate the root-zone temperature of PCM placed in a greenhouse environment with some climatic parameters such as radiation, relative humidity, wind speed, and greenhouse indoor temperature in a plastic greenhouse located in the Mediterranean region. Training and test sets were used at 70–30%; it was concluded that the XGBoost model was quite successful in predicting root-zone temperatures compared to the MARS and SVR. In addition, the results obtained bring to light that those models provide optimal energy management conditions in greenhouses. The following conclusions can be drawn from the study:

• Integration of bio-based coconut oil as a heat-storage material into Mediterranean greenhouses is proposed.
• Experimental results show that coconut oil can increase the indoor temperature of a greenhouse between 0.86 and 4.09 °C. Root-zone temperatures were higher compared to the pots in the control greenhouse at 1.25 °C, 1.61 °C and 1.46 °C for February, March, and April, respectively.
• While the effects of Vw and Moist on Tghot, Tpcm, and Tphot are statistically insignificant, Rad is significant on these parameters between 70 and 96%.
• Using CO for greenhouses with large-scale production may cause some difficulties due to the high cost. However, the integration of CO with active greenhouse heating systems can provide benefits in terms of operating and installation costs.
• To reduce root-zone heat losses at night-time, it would be appropriate to change mixture ratios of materials placed in the pot as the growing medium and different materials that have a high heat capacity should be added.
• In addition to the disadvantages of CO compared to other PCMs, such as its low latent heat of fusion and its use as human food, it also has some advantages for low-enthalpy applications due to its biological origin and abundance.

Limitations and Future Perspectives

Despite the promising results, several limitations should be noted. First, the current experimental duration covered only one cultivation season, and long-term degradation phenomena such as oxidation of coconut oil or leakage from encapsulation materials were not quantified. Future studies should evaluate multi-year thermal cycling and investigate protective encapsulation methods to ensure phase stability. Second, while the ML models achieved high predictive performance, their generalizability to different climates, crop species, and growing medium remains to be validated. Coupling these models with process-based simulations or multi-location datasets could enhance their robustness.

Additionally, integrating real-time sensor data with predictive algorithms can enable adaptive PCM management, allowing dynamic control of air circulation or irrigation systems based on predicted temperature trajectories. From a sustainability perspective, a full life-cycle assessment (LCA) and life-cycle cost (LCC) evaluation should be conducted to quantify the net environmental and economic gains. Earlier analyses have shown that PCM integration can reduce CO₂ emissions by up to 6–8 tons per year and cut total greenhouse operation costs by as much as 50–60%, which indicates significant potential if implemented on a commercial scale.