Integrated Optimization of Train Schedules and Transportation Plans for a Passenger–Freight Metro Line
Abstract
1. Introduction
1.1. Literature Review
- (1)
- Passenger and freight co-transportation (PFCT).
- (2)
- Urban rail transit schedule (URTS).
1.2. Focus of This Study
- (1)
- We propose a new framework in which both trains and passenger (or freight) flows select potential space–time trajectories (PSTTs). This contrasts with the traditional approach, where trains select PSTTs and passenger (or freight) flows are assigned to specific trains. By adopting this approach, the resulting model becomes linear.
- (2)
- The ILP model incorporates headway constraints, flow equilibrium constraints, capacity constraints, time window constraints, and coupling constraints. The objective function is designed to minimize the generalized total cost.
- (3)
- Through an equivalent transformation, the primal problem can be solved more efficiently by commercial solvers. This efficiency is validated through numerical experiments conducted on examples of varying scales.
- (4)
- The results demonstrate that integrating train schedule optimization with co-transportation planning significantly enhances transportation efficiency, thereby achieving the greatest potential improvement in system performance.
2. Mathematical Formulation
2.1. Problem Statement
2.2. Optimization Model
2.3. Model Relaxation
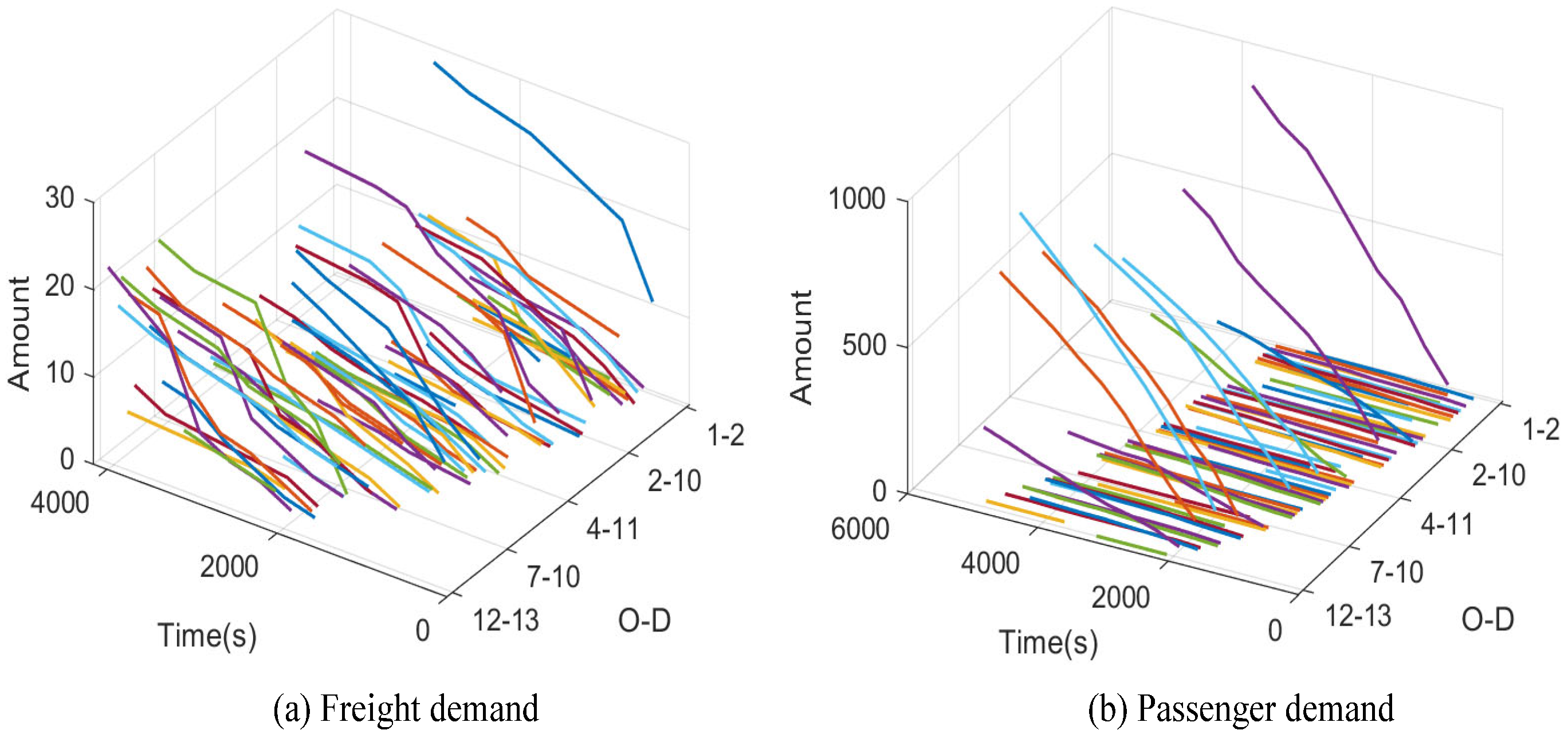
3. Numerical Experiments
3.1. Computational Efficiency Analysis
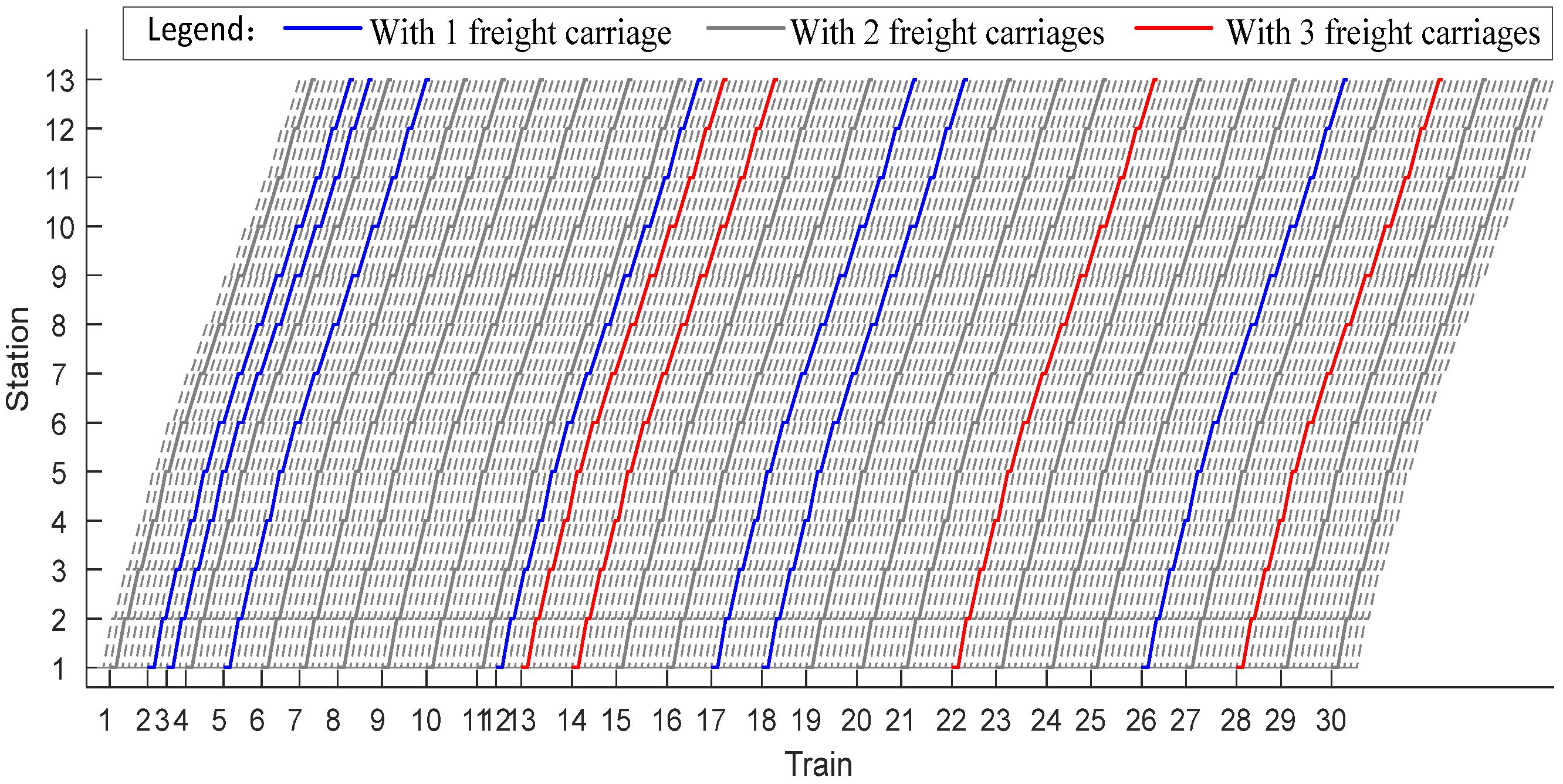
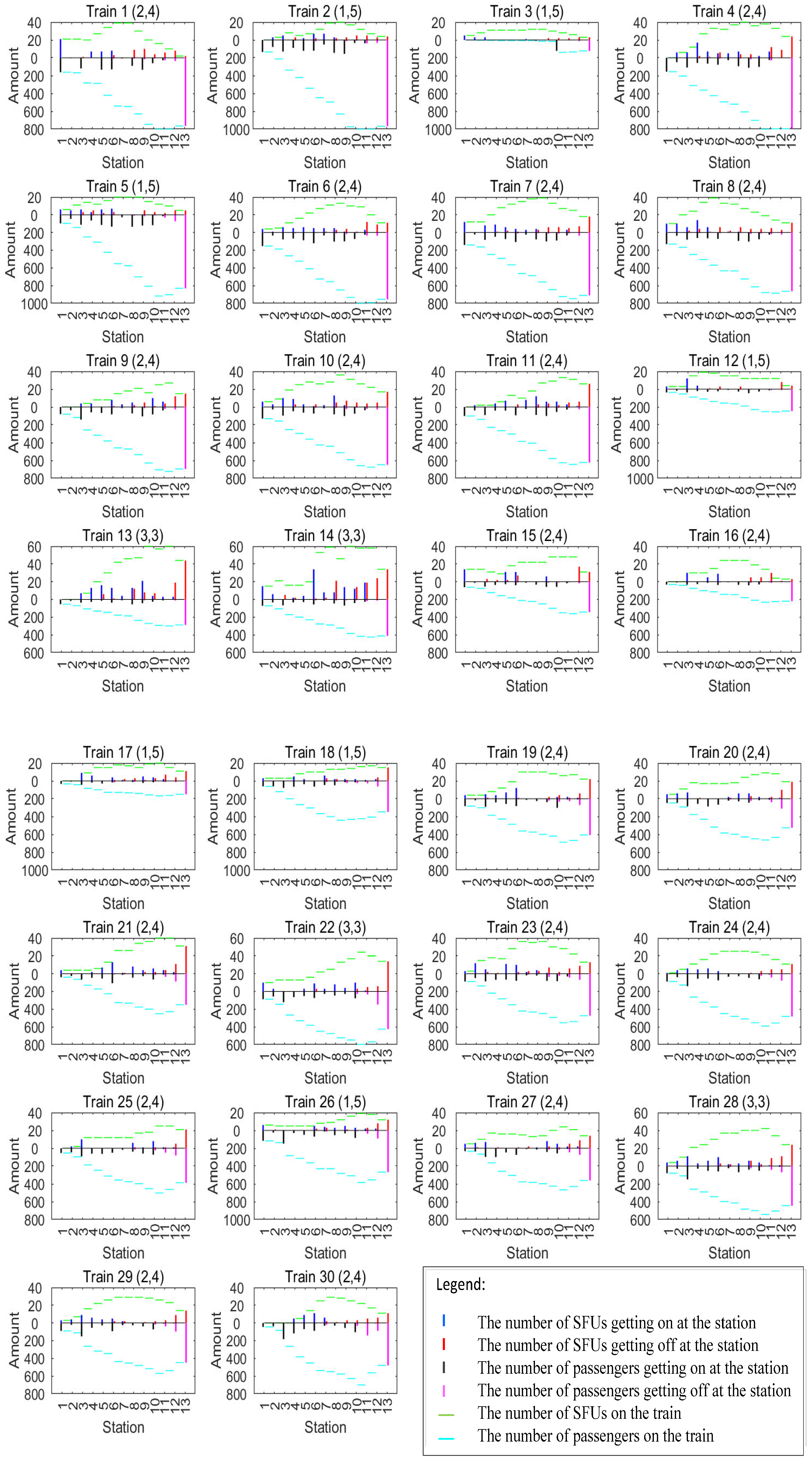
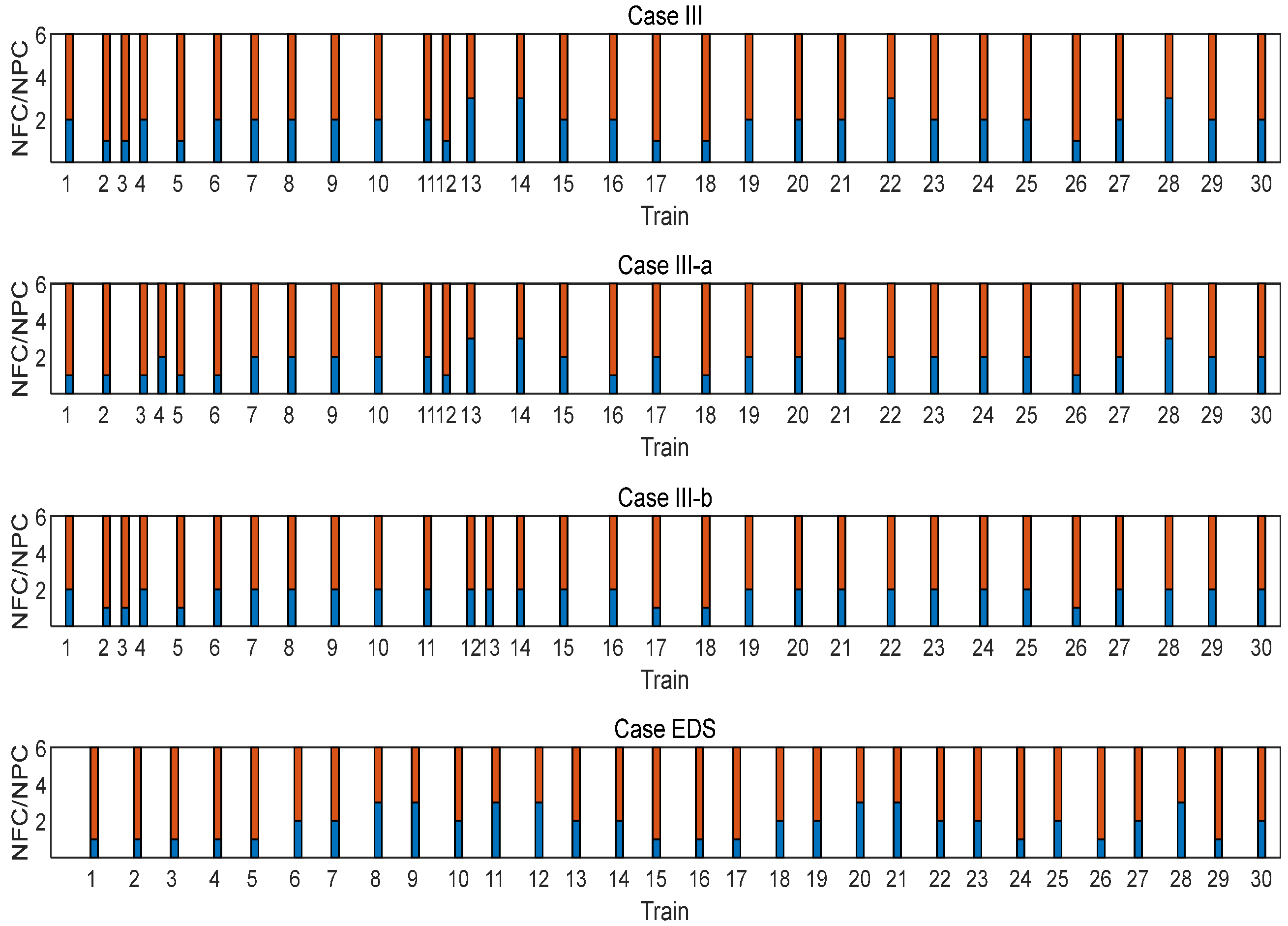
3.2. Solution Analysis of Case III
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Macioszek, E. Analysis of the volume of passengers and cargo in rail and road transport in Poland in 2009–2019. Sci. J. Silesian Univ. Technol. (Ser. Transp.) 2021, 113, 133–143. [Google Scholar] [CrossRef]
- Macioszek, E. Analysis of the rail cargo transport volume in Poland in 2010–2021. Sci. J. Silesian Univ. Technol. (Ser. Transp.) 2023, 119, 125–140. [Google Scholar] [CrossRef]
- Anupriya; Graham, D.J.; Carbo, J.M.; Anderson, R.J.; Bansal, P. Understanding the costs of urban rail transport operations. Transp. Res. Part B 2020, 138, 292–316. [Google Scholar] [CrossRef]
- Cochrane, K.; Saxe, S.; Roorda, M.J.; Shalaby, A. Moving freight on public transit: Best practices, challenges, and opportunities. Int. J. Sustain. Transp. 2016, 11, 120–132. [Google Scholar] [CrossRef]
- Kikuta, J.; Ito, T.; Tomiyama, I.; Yamamoto, S.; Yamada, T. New subway-integrated city logistics szystem. Procedia Soc. Behav. Sci. 2012, 39, 476–489. [Google Scholar] [CrossRef]
- Marinov, M.; Giubilei, F.; Gerhardt, M.; Ozkan, T.; Stergiou, E.; Papadopol, M.; Cabecinha, L. Urban freight movement by rail. J. Transp. Lit. 2013, 7, 87–116. [Google Scholar] [CrossRef]
- Motraghi, A.; Marinov, M.V. Analysis of urban freight by rail using event based simulation. Simul. Model. Pract. Theory 2012, 25, 73–89. [Google Scholar] [CrossRef]
- Dampier, A.; Marinov, M. A study of the feasibility and potential implementation of metro-based freight transportation in Newcastle upon Tyne. Urban Rail Transit 2015, 1, 164–182. [Google Scholar] [CrossRef]
- Howe, J. Filling the middle: Uganda’s appropriate transport services. Transp. Rev. 2003, 23, 161–176. [Google Scholar] [CrossRef]
- Hu, W.; Dong, J.; Hwang, B.; Ren, R.; Chen, Z. Hybrid optimization procedures applying for two-echelon urban underground logistics network planning: A case study of Beijing. Comput. Ind. Eng. 2020, 144, 106452. [Google Scholar] [CrossRef]
- Zhu, S.; Bell, M.G.H.; Schulz, V.; Stokoe, M. Co-modality in city logistics: Sounds good, but how? Transp. Res. Part A 2023, 168, 103578. [Google Scholar] [CrossRef]
- Cavallaro, F.; Nocera, S. Integration of passenger and freight transport: A concept-centric literature review. Res. Transp. Bus. Manag. 2022, 43, 100718. [Google Scholar] [CrossRef]
- Di, Z.; Yang, L.; Shi, J.; Zhou, H.; Yang, K.; Gao, Z. Joint optimization of carriage arrangement and flow control in a metro-based underground logistics system. Transp. Res. Part B 2022, 159, 1–23. [Google Scholar] [CrossRef]
- Hou, Z.; He, R.; Liu, C.; Wan, S.; Yang, K.; Dai, C. Optimization of passenger and freight collaborative transportation for urban rail transit under virtual coupling condition. Eng. Lett. 2024, 32, 179–192. [Google Scholar]
- Li, F.; Guo, X.; Zhou, L.; Wu, J.; Li, T. A capacity matching model in a collaborative urban public transport system: Integrating passenger and freight transportation. Int. J. Prod. Res. 2022, 60, 6303–6328. [Google Scholar] [CrossRef]
- Bruzzone, F.; Cavallaro, F.; Nocera, S. The integration of passenger and freight transport for first-last mile operations. Transp. Policy 2021, 100, 31–48. [Google Scholar] [CrossRef]
- Donne, D.D.; Alfandari, L.; Archetti, C.; Ljubic, I. Freight-on-Transit for urban last-mile deliveries: A strategic planning approach. Transp. Res. Part B 2023, 169, 53–81. [Google Scholar] [CrossRef]
- Machado, B.; Pimentel, C.; Sousa, A. Integration planning of freight deliveries into passenger bus networks: Exact and heuristic algorithms. Transp. Res. Part A 2023, 171, 103645. [Google Scholar] [CrossRef]
- Li, S.; Zhu, X.; Shang, P.; Li, T.; Liu, W. Optimizing a shared freight and passenger high-speed railway system: A multi-commodity flow formulation with Benders decomposition solution approach. Transp. Res. Part B 2023, 172, 1–31. [Google Scholar] [CrossRef]
- Xu, G.; Zhong, L.; Wu, R.; Hu, X.; Guo, J. Optimize train capacity allocation for the high-speed railway mixed transportation of passenger and freight. Comput. Ind. Eng. 2022, 174, 108788. [Google Scholar] [CrossRef]
- Dong, J.; Hu, W.; Yan, S.; Ren, R.; Zhao, X. Network planning method for capacitated metro-based underground logistics system. Adv. Civ. Eng. 2018, 2018, 6958086. [Google Scholar] [CrossRef]
- Kelly, J.; Marinov, M. Innovative interior designs for urban freight distribution using light rail systems. Urban Rail Transit 2017, 3, 238–245. [Google Scholar] [CrossRef]
- Behiri, W.; Belmokhtar-Berraf, S.; Chu, C. Urban freight transport using passenger rail network: Scientific issues and quantitative analysis. Transp. Res. Part E 2018, 115, 227–245. [Google Scholar] [CrossRef]
- Ye, Y.; Guo, J.; Yan, L. A metro freight plan for mixed passenger and freight transportation. J. Adv. Transp. 2022, 2022, 6602387. [Google Scholar] [CrossRef]
- Di, Z.; Luo, J.; Shi, J.; Qi, J.; Zhang, S. Integrated optimization of capacity allocation and timetable rescheduling for metro-based passenger and freight cotransportation. Tunn. Undergr. Space Technol. 2025, 155, 106186. [Google Scholar] [CrossRef]
- Li, Z.; Shalaby, A.; Roorda, M.J.; Mao, B. Urban rail service design for collaborative passenger and freight transport. Transp. Res. Part E 2021, 147, 102205. [Google Scholar] [CrossRef]
- Ozturk, O.; Patrick, J. An optimization model for freight transport using urban rail transit. Eur. J. Oper. Res. 2018, 267, 1110–1121. [Google Scholar] [CrossRef]
- Sahli, A.; Behiri, W.; Belmokhtar-Berraf, S. An effective and robust genetic algorithm for urban freight transport scheduling using passenger rail network. Comput. Ind. Eng. 2021, 173, 108645. [Google Scholar] [CrossRef]
- Li, X.; Lo, H.K. An energy-efficient scheduling and speed control approach for metro rail operations. Transp. Res. Part B 2014, 64, 73–89. [Google Scholar] [CrossRef]
- Yin, J.; Yang, L.; Tang, T.; Gao, Z.; Ran, B. Dynamic passenger demand oriented metro train scheduling with energy-efficiency and waiting time minimization: Mixed-integer linear programming approaches. Transp. Res. Part B 2017, 97, 178–210. [Google Scholar] [CrossRef]
- Niu, H.; Zhou, X.; Gao, R. Train scheduling for minimizing passenger waiting time with time-dependent demand and skip-stop patterns: Nonlinear integer programming models with linear constraints. Transp. Res. Part B 2015, 76, 117–135. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, T.; Ning, B.; Meng, L. Integrated optimization of regular train schedule and train circulation plan for urban rail transit lines. Transp. Res. Part E 2017, 105, 83–104. [Google Scholar] [CrossRef]
- Wang, Y.; D’Ariano, A.; Yin, J.; Meng, L.; Tang, T.; Ning, B. Passenger demand oriented train scheduling and rolling stock circulation planning for an urban rail transit line. Transp. Res. Part B 2018, 118, 193–227. [Google Scholar] [CrossRef]
- Shi, J.; Yang, L.; Yang, J.; Gao, Z. Service-oriented train timetabling with collaborative passenger flow control on an oversaturated metro line: An integer linear optimization approach. Transp. Res. Part B 2018, 110, 26–59. [Google Scholar] [CrossRef]
- Liu, R.; Li, S.; Yang, L. Collaborative optimization for metro train scheduling and train connections combined with passenger flow control strategy. Omega 2020, 90, 101990. [Google Scholar] [CrossRef]
- Pan, H.; Liu, Z.; Yang, L.; Liang, Z.; Wu, Q.; Li, S. A column generation-based approach for integrated vehicle and crew scheduling on a single metro line with the fully automatic operation system by partial supervision. Transp. Res. Part E 2021, 152, 102406. [Google Scholar] [CrossRef]
- Li, S.; Xu, R.; Han, K. Demand-oriented train services optimization for a congested urban rail line: Integrating short turning and heterogeneous headways. Transp. A 2019, 15, 1459–1486. [Google Scholar] [CrossRef]
- Pan, H.; Yang, L.; Liang, Z. Demand-oriented integration optimization of train timetabling and rolling stock circulation planning with flexible train compositions: A column-generation-based approach. Eur. J. Oper. Res. 2023, 305, 184–206. [Google Scholar] [CrossRef]
- Yang, L.; Gao, Y.; D’Ariano, A.; Xu, S. Integrated optimization of train timetable and train unit circulation for a Y-type urban rail transit system with flexible train composition mode. Omega 2024, 122, 102968. [Google Scholar] [CrossRef]
- Wang, D.; D’Ariano, A.; Zhao, J.; Zhan, S.; Peng, Q. Joint rolling stock rotation planning and depot deadhead scheduling in complicated urban rail transit lines. Eur. J. Oper. Res. 2024, 314, 665–684. [Google Scholar] [CrossRef]
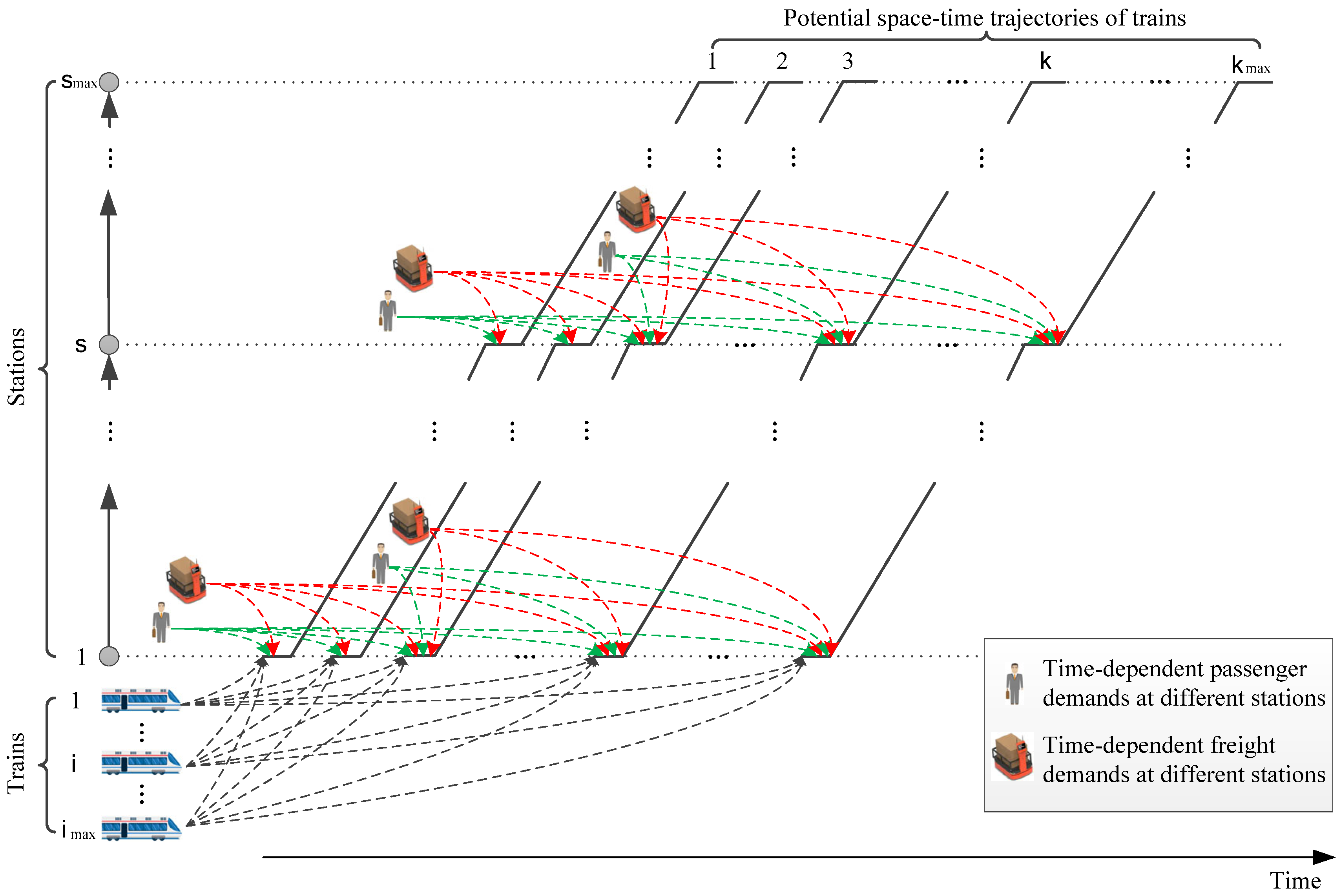


| Research | Model Type | Solution Method | Flow Assignment Strategy |
|---|---|---|---|
| [23] | Nonlinear | Heuristic | To trains |
| [26] | Nonlinear | Solver and Heuristic | To trains |
| [24] | Nonlinear | VNS 1 | To trains |
| [14] | Nonlinear | NSGA 2 | To trains |
| [25] | Nonlinear | Heuristic | To trains |
| This study | Linear | Solver | To trajectories |
| Notation | Definition |
|---|---|
| Given time domain | |
| Set of time-dependent freight demands | |
| Set of time-dependent passenger demands | |
| Parameter to represent the number of carriages of a train | |
| Parameter to represent the capacity of a carriage for freights | |
| Parameter to represent the capacity of a carriage for passengers | |
| Variable | Definition |
|---|---|
| . | |
| Case | Num. of Trains | Num. of PSTTs | Demand Parameters | Stop Cond. (Gap) | Comp. Time of Gurobi | ||
|---|---|---|---|---|---|---|---|
| Freight | Passenger | Model PP | Model RP | ||||
| I | 10 | 60 | (339, 726) | (469, 7927) | 10−4 | 25 s | 18 s |
| II | 20 | 124 | (192, 936) | (889, 10,914) | 10−4 | 30 s | 21 s |
| III | 30 | 199 | (605, 1278) | (1206, 18,378) | 10−4 | 99 s | 78 s |
| IV | 40 | 266 | (902, 1977) | (1502, 23,439) | 10−4 | 2381 s | 915 s |
| V | 65 | 336 | (1179, 5208) | (1779, 27,681) | 10−4 | 13,744 s | 4871 s |
| Case | Parameters | Passenger Demand | TNPC/TNFC * | Freight Demand | |||||
|---|---|---|---|---|---|---|---|---|---|
| TWT * (s) | SWT * (s) | ADSW * | TWT * (s) | SWT * (s) | ADSW * | ||||
| III | 0.1 | 3 | 1,478,430 | 69,685 | 161 | 123/57 | 122,670 | 6360 | 12 |
| III-a | 1 | 3 | 1,367,370 | 0 | 0 | 125/55 | 169,890 | 14,980 | 26 |
| III-b | 0.1 | 2 | 1,546,350 | 102,260 | 208 | 126/54 | 139,950 | 10,460 | 22 |
| EDS * | 0.1 | 3 | 4,912,230 | 44,095 | 95 | 124/56 | 498,210 | 72,115 | 59 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di, Z.; Zuo, H.; Zhou, H.; Qi, J.; Zhang, S. Integrated Optimization of Train Schedules and Transportation Plans for a Passenger–Freight Metro Line. Sustainability 2025, 17, 730. https://doi.org/10.3390/su17020730
Di Z, Zuo H, Zhou H, Qi J, Zhang S. Integrated Optimization of Train Schedules and Transportation Plans for a Passenger–Freight Metro Line. Sustainability. 2025; 17(2):730. https://doi.org/10.3390/su17020730
Chicago/Turabian StyleDi, Zhen, Hanqi Zuo, Housheng Zhou, Jianguo Qi, and Shenghu Zhang. 2025. "Integrated Optimization of Train Schedules and Transportation Plans for a Passenger–Freight Metro Line" Sustainability 17, no. 2: 730. https://doi.org/10.3390/su17020730
APA StyleDi, Z., Zuo, H., Zhou, H., Qi, J., & Zhang, S. (2025). Integrated Optimization of Train Schedules and Transportation Plans for a Passenger–Freight Metro Line. Sustainability, 17(2), 730. https://doi.org/10.3390/su17020730






