Optimization of Microgrid Dispatching by Integrating Photovoltaic Power Generation Forecast
Abstract
1. Introduction
- (1)
- This paper presents an in-depth study on the application of new energy photovoltaic power generation, and proposes an effective forecasting and scheduling method, which better solves the imbalance in the distribution of microgrid power resources due to the volatility of renewable energy production.
- (2)
- In terms of photovoltaic power generation forecast, this paper proposes a neural network model based on CNN-BiLSTM, which can consider multiple influencing factors in the process of photovoltaic power generation at the same time to make the forecasting results more accurate.
- (3)
- This paper introduces the group intelligence algorithm in the prediction model to optimize the original structure. Sparrow search algorithm is used to optimize the weights as well as the thresholds of the CNN-BiLSTM neural network to improve the robustness of the model and to increase the attentional mechanism to improve the predictive accuracy of the model while reducing the computational cost more, and to improve the generalization ability of the model.
- (4)
- A microgrid distributed power scheduling model is established by this paper, which focuses on how to reasonably allocate the weights of economic objectives as well as environmental objectives in the multi-objective scheduling problem, and introduces the quantum particle swarm algorithm based on differential evolutionary algorithm to solve the problem, and constructs an optimization model aimed at minimization of the system operation cost.
2. Photovoltaic Power Generation Prediction Model Based on Cluster Analysis and SSA-CNN-BiLSTM-ATT
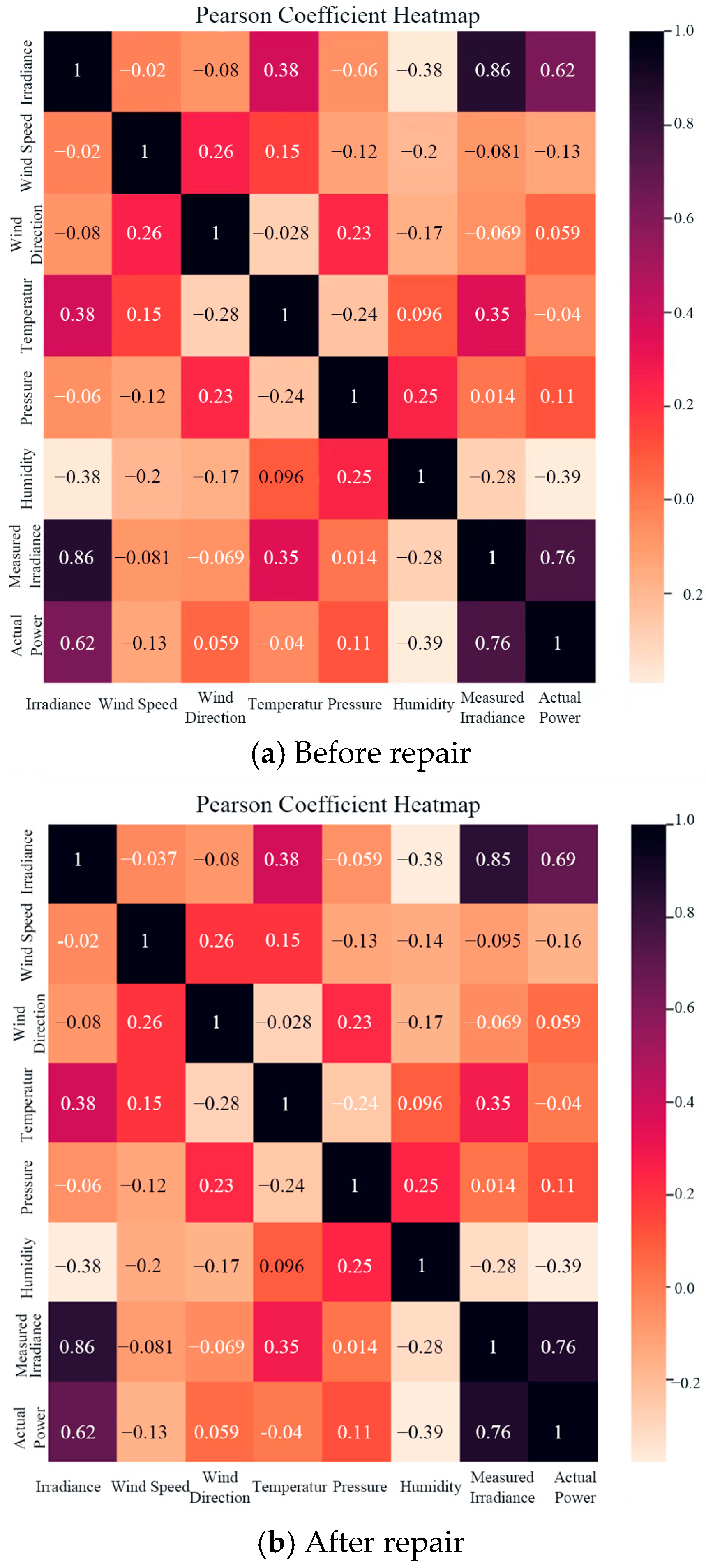
2.1. Correlation Analysis of Influencing Factors
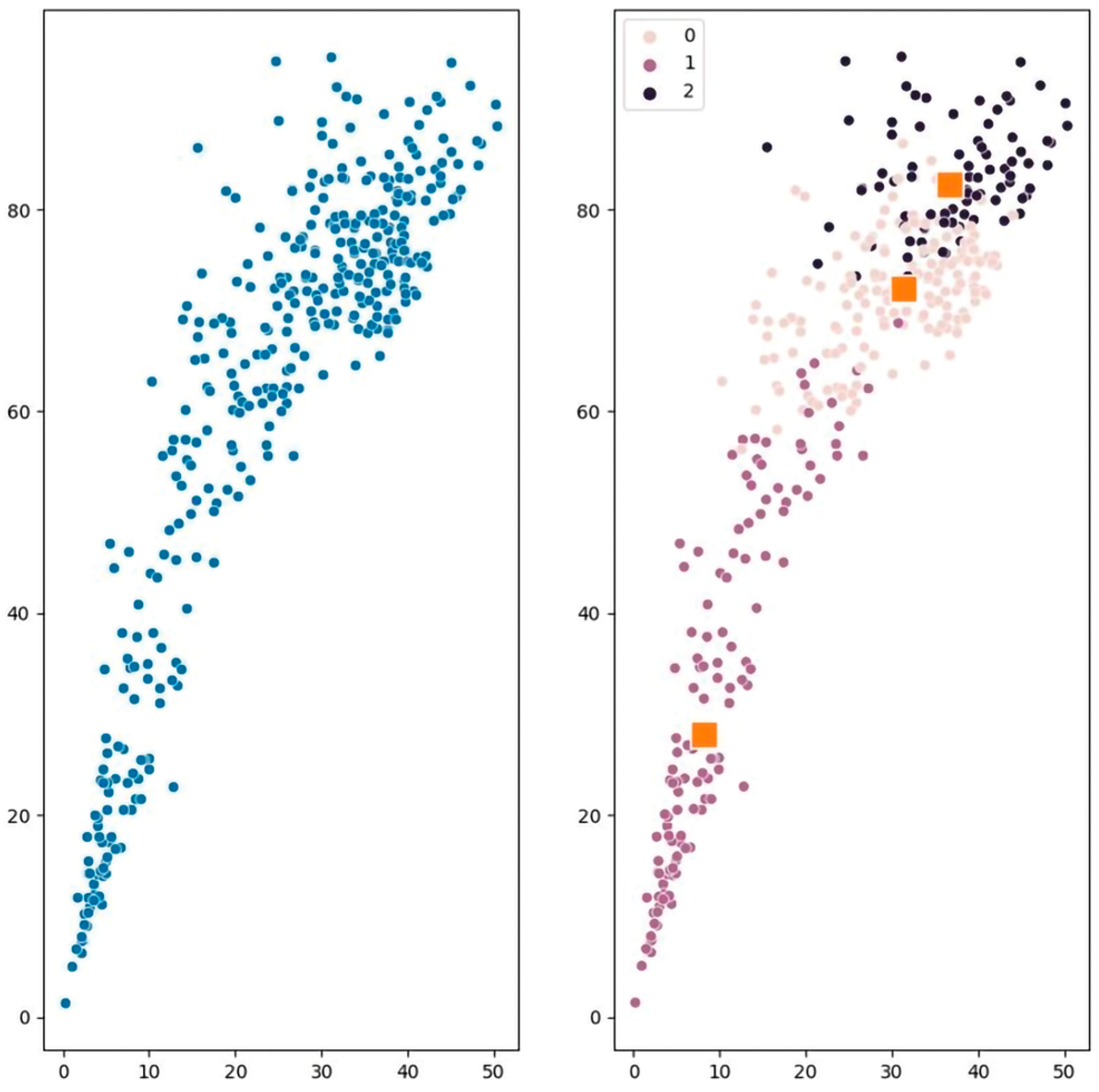
2.2. Data Preprocessing Based on Fuzzy C-Means Algorithm
2.2.1. Cluster Analysis of Photovoltaic Data
- (1)
- Initialization of the clustering center, .
- (2)
- Calculate the different affiliation matrices:
- (3)
- Update the clustering center:
- (4)
- Repeat (2) and (3) until Equation (2) converges and reaches the maximum number of iterations.
2.2.2. Photovoltaic Data Preprocessing
- (1)
- Check the continuity of the data and mark missing or duplicate data points. The timestamp format can be used to calculate the time difference between two consecutive points.
- (2)
- Remove anomalous data based on the maximum power value.
- (3)
- Remove consecutive missing power data.
- (4)
- Normalize the data to remove unit differences between different factors.
2.2.3. Data Dimensionality Reduction Based on Principal Component Analysis
- (1)
- The core idea of PCA is a matrix compression algorithm that converts the original matrix of into a lower dimensional matrix of .
- (2)
- Inputs in the model of PCA are the original variables, and the target variables are obtained after PCA and satisfy . The original sample is the matrix of :
- (3)
- Steps of PCA algorithm: Let the original data X be a matrix of .
- (a)
- Find the eigenvalues, eigenvectors of the covariance matrix.
- (b)
- Ranking the eigenvalues and selecting the appropriate k components, the resulting principal components are:
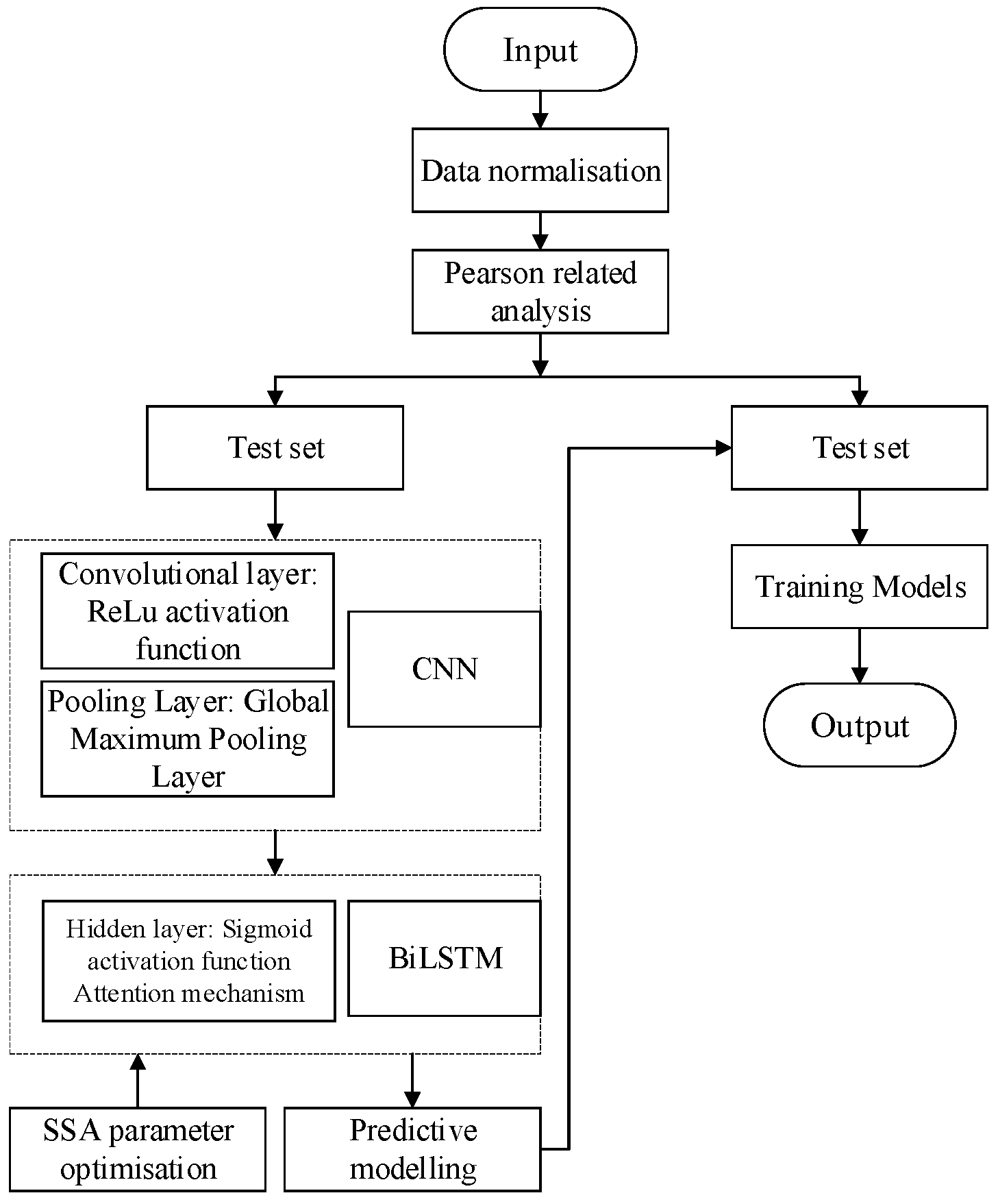
2.3. Based on SSA-CNN-BiLSTM-ATT Predictive Model Construction
2.3.1. Sparrow Search Algorithm
2.3.2. Convolutional Neural Network
2.3.3. BiLSTM Neural Network
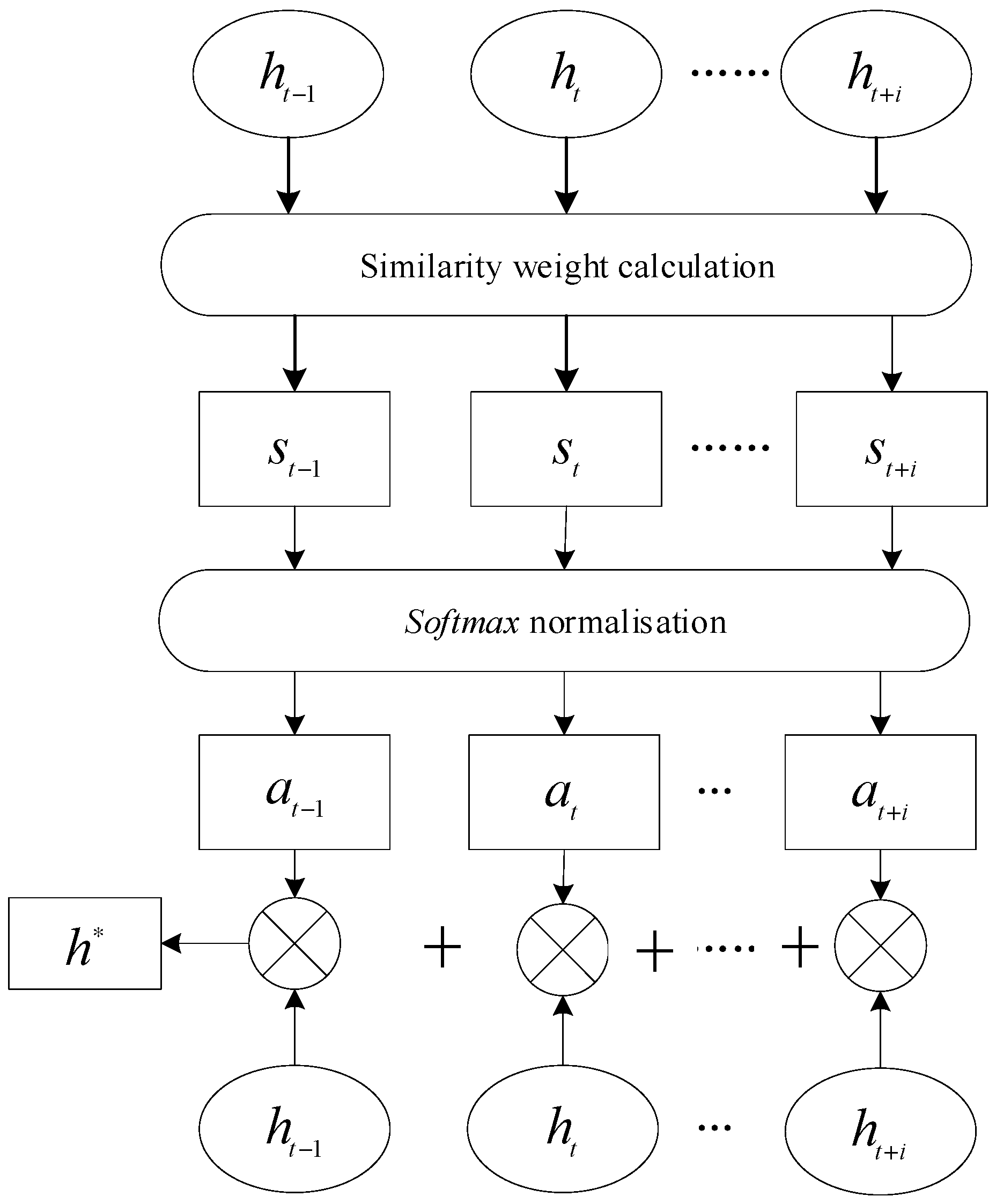
2.3.4. Attention Mechanism
2.3.5. SSA-CNN-BiLSTM-ATT-Based Photovoltaic Power Generation Forecasting Process
- (1)
- Pearson’s correlation coefficient is used to analyze the actual operating data of PV arrays, determining the correlation coefficients between the variables. Heat maps are then plotted based on the correlation coefficients to visualize the relationships between the variables.
- (2)
- Fuzzy C-means cluster analysis classifies the historical photovoltaic power generation sequence samples into three categories: sunny weather changes, cloudy weather changes, and rainy weather changes.
- (3)
- To identify the optimal component parameter k, the historical PV power generation sequence undergoes decomposition. Variational modal decomposition is applied to each weather type, assuming k modal components exist for slow weather conditions.
- (4)
- Empirical direct observation divides the k modal components derived from step (3) into high-frequency and low-frequency components.
- (5)
- A two-layer prediction framework is designed. A CNN model is used for the low-frequency part, and a BiLSTM model is used for the high-frequency part. In order to improve the model performance, the model parameters are optimized using the improved sparrow algorithm, and the attention mechanism is introduced so that the model can pay more attention to the key features.
- (6)
- By feeding real-time environmental data into the trained neural network, the model predicts the high-frequency and low-frequency components separately and combines the predictions to arrive at the predicted value of PV power generation.
2.4. Evaluation of Photovoltaic Power Generation Forecasting Models
2.4.1. Mechanism Analysis of Photovoltaic Power Generation Prediction Error Generation
- (1)
- The NWP model is a time- as well as space-discretized continuum time-space method, which is bound to have some errors.
- (2)
- There are anomalies in the observed data, which will further generate errors when assimilated into the NWP model.
- (3)
- The atmospheric system is very complex, and the use of partial differential equations to describe its system is highly sensitive to the existence of errors in the initial conditions, but the errors will gradually accumulate with the passage of time.
2.4.2. Indicators for Evaluating Projected Results
3. Distributed Power Scheduling Model for Microgrids
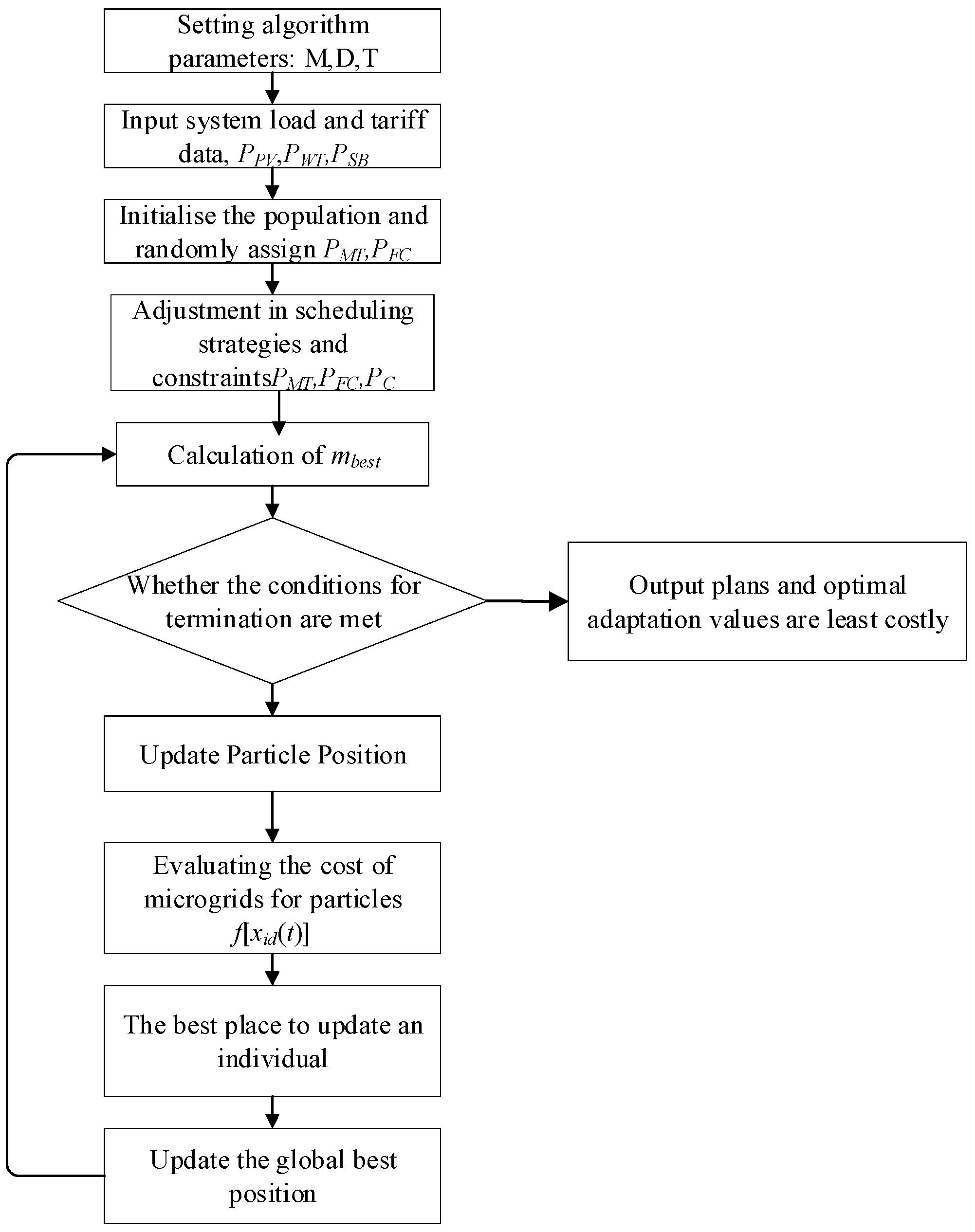
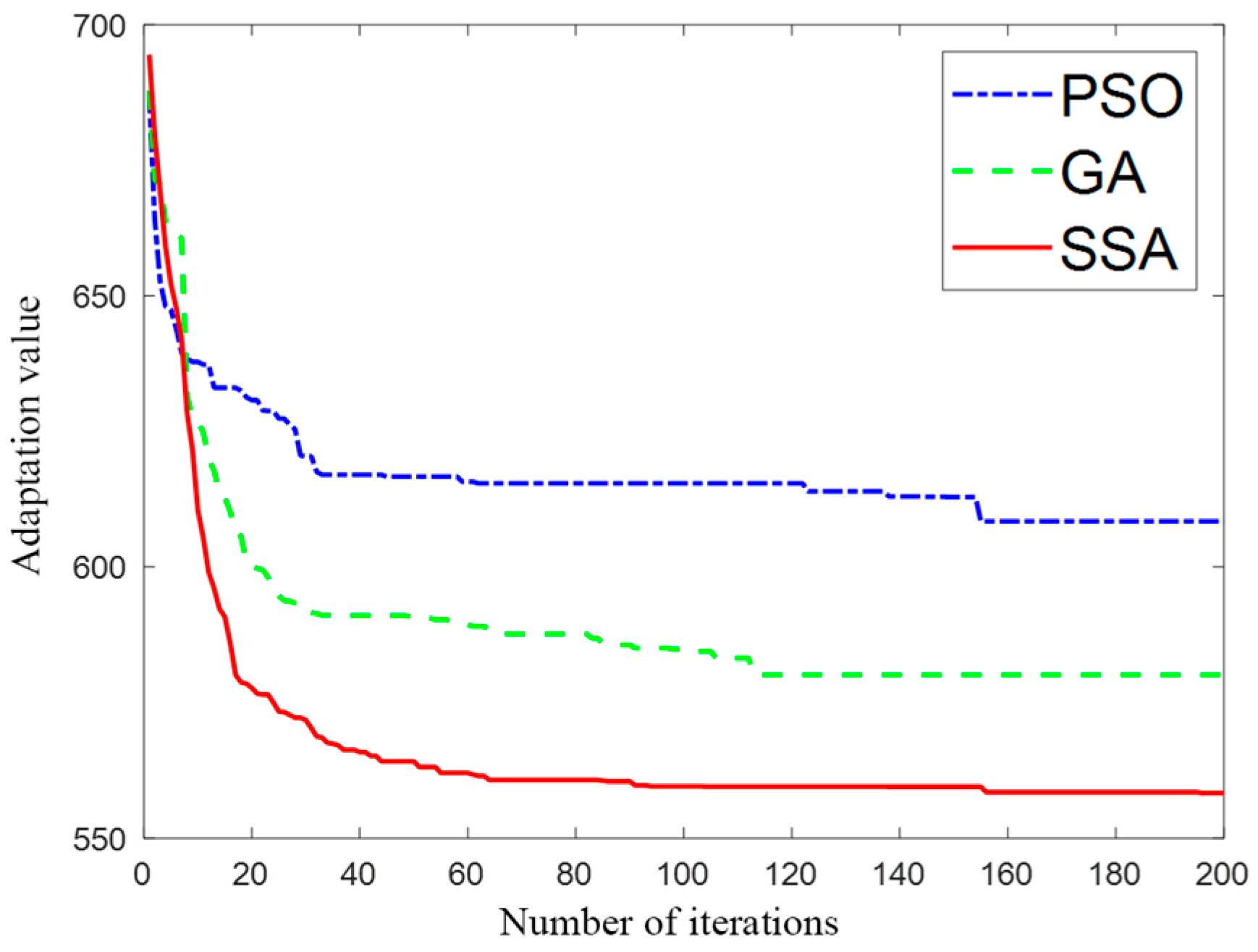
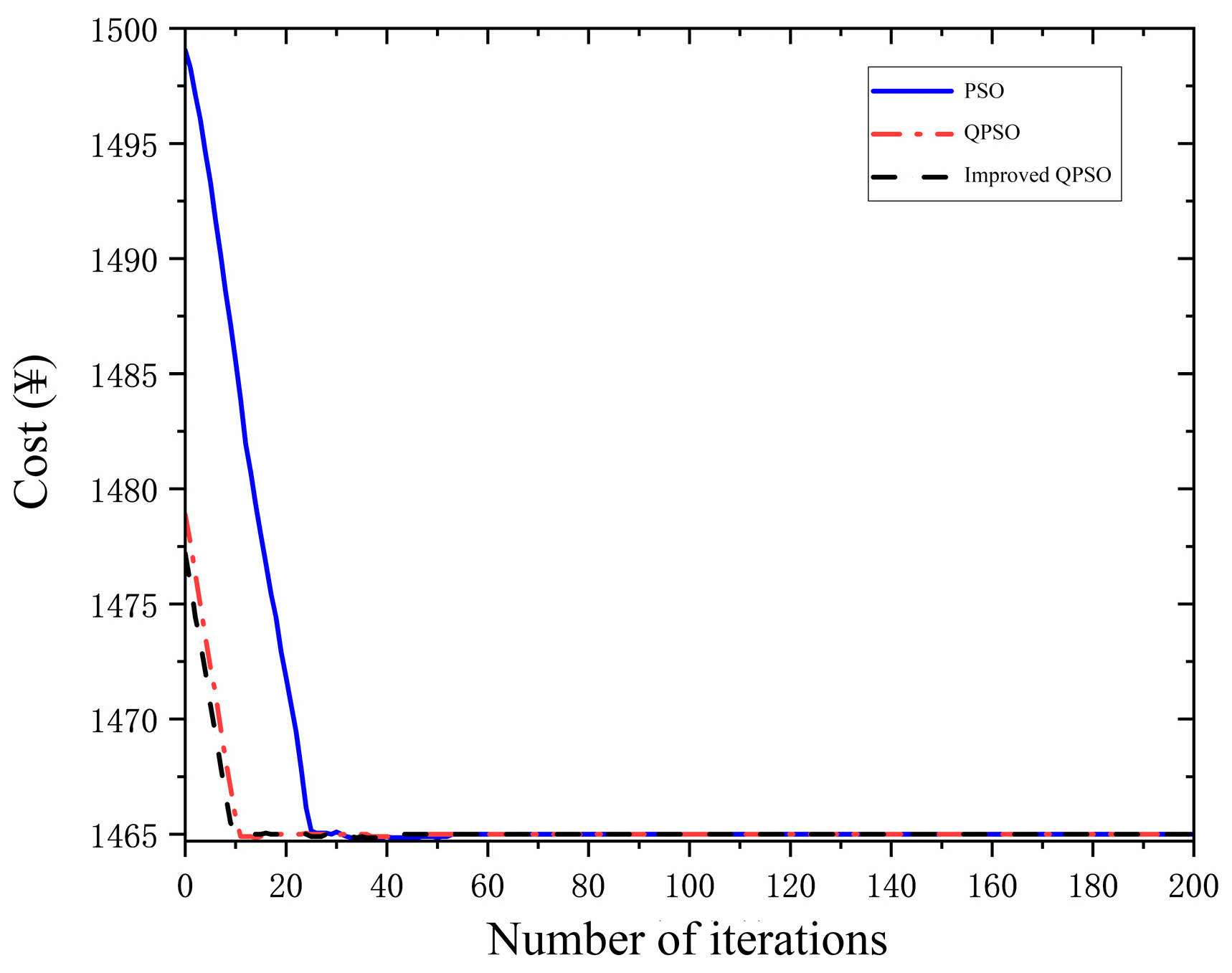
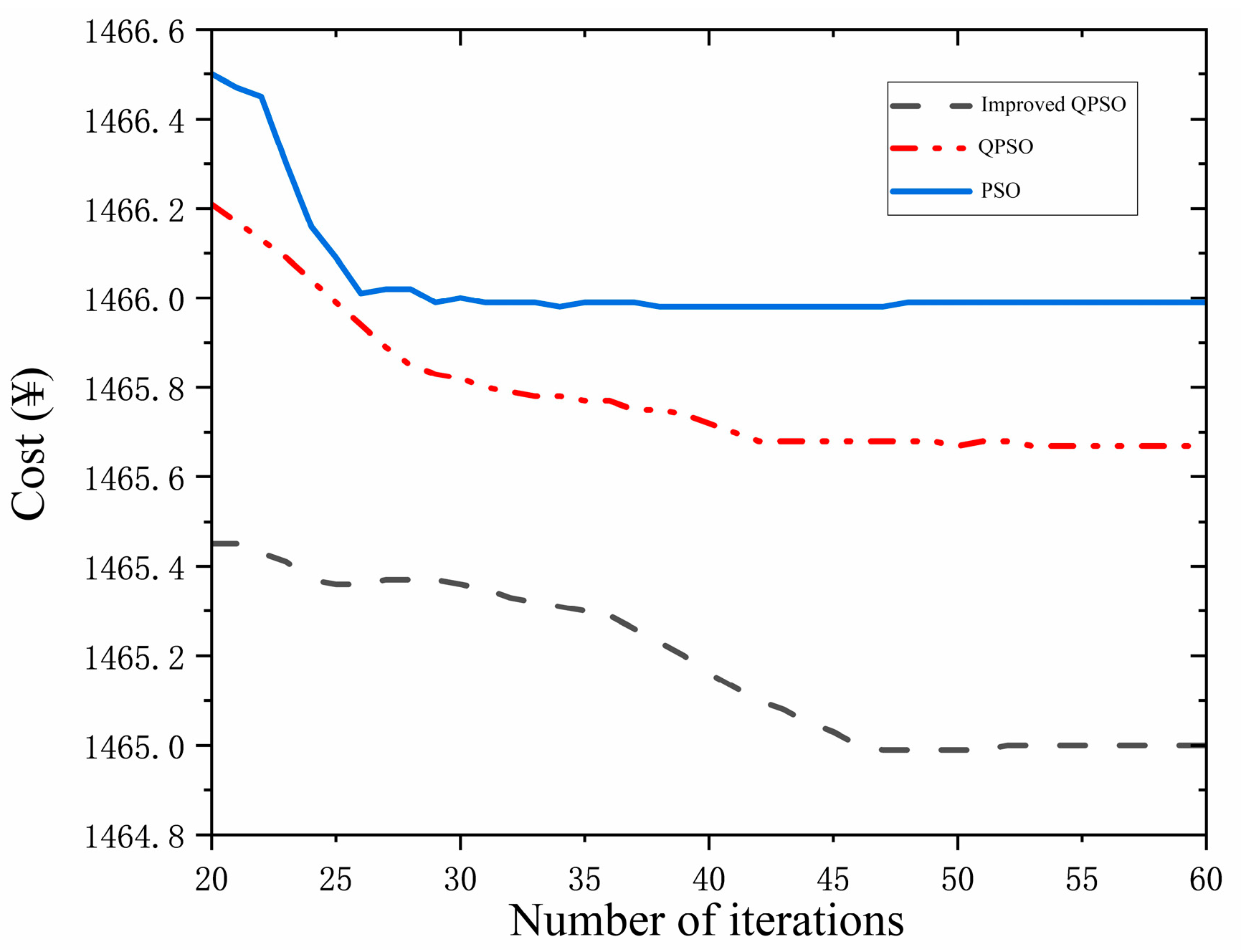
3.1. Improved Quantum Particle Swarm Algorithms
3.2. Microgrid Scheduling Model
3.2.1. Scheduling Model
- (1)
- Objective function
- (2)
- Binding conditions
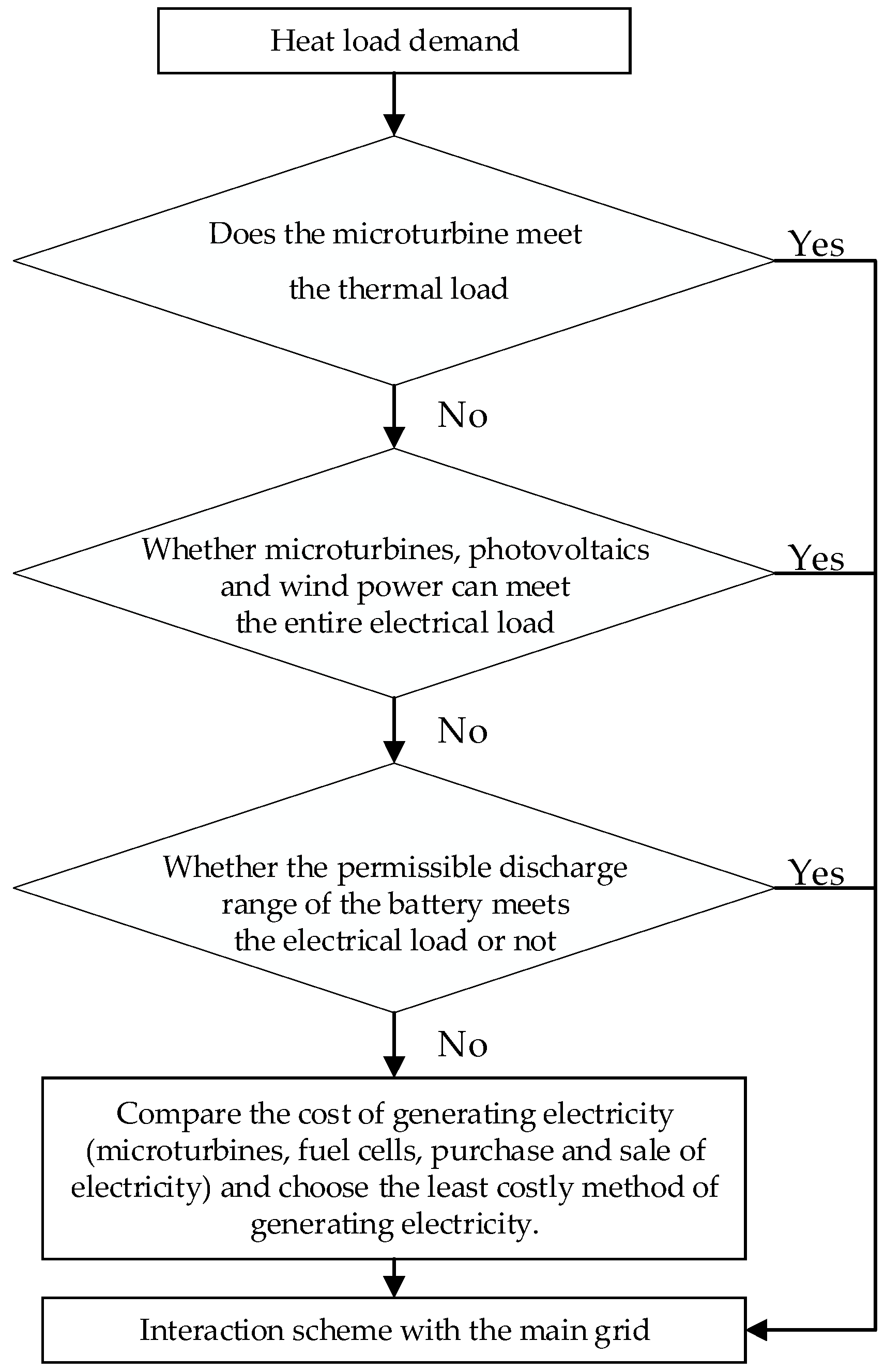
3.2.2. Dispatch Strategy
- (1)
- Low periods of electricity consumption
- (2)
- Flat periods of electricity consumption
- (3)
- Peak periods of electricity consumption
4. Practical Case Studies
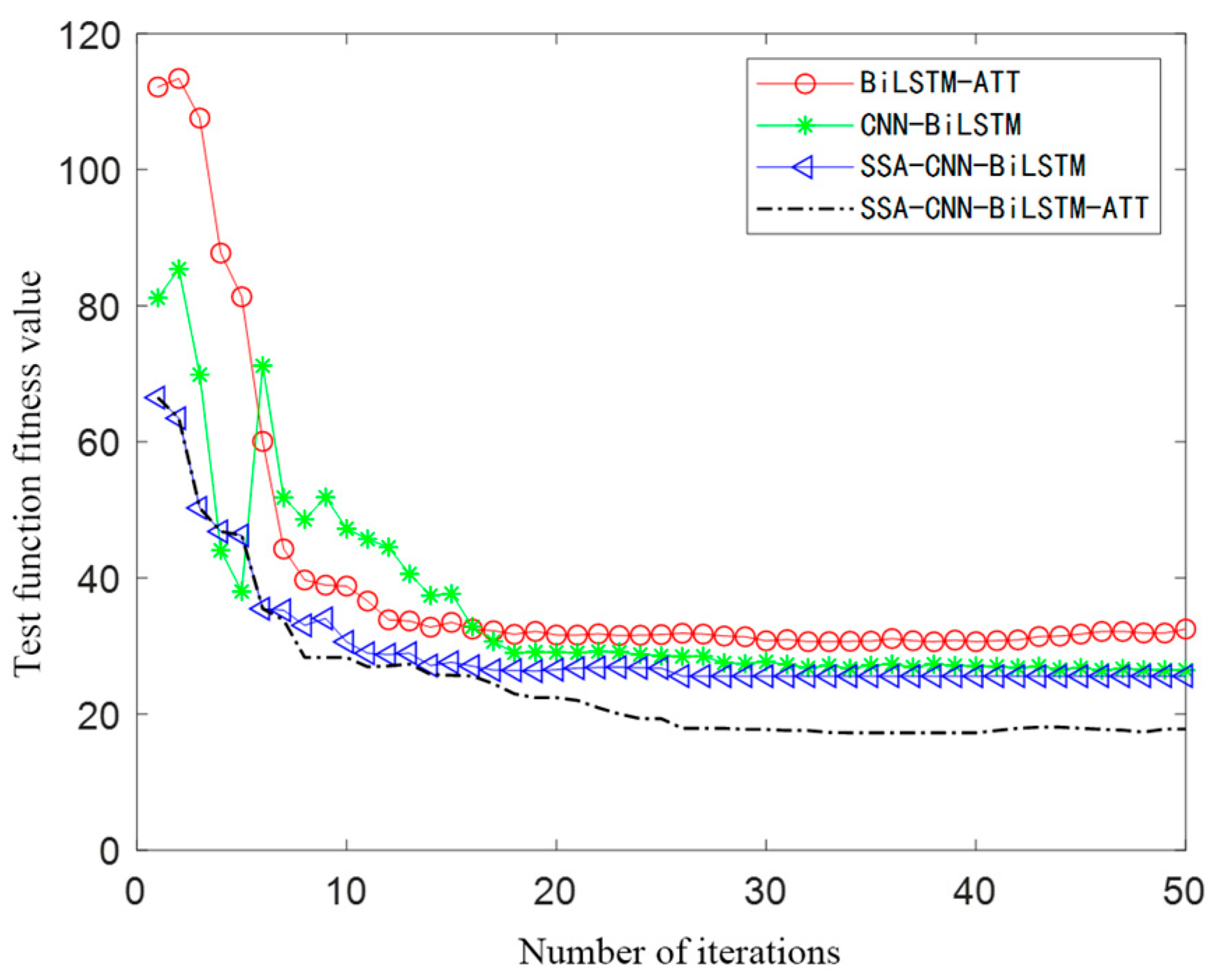
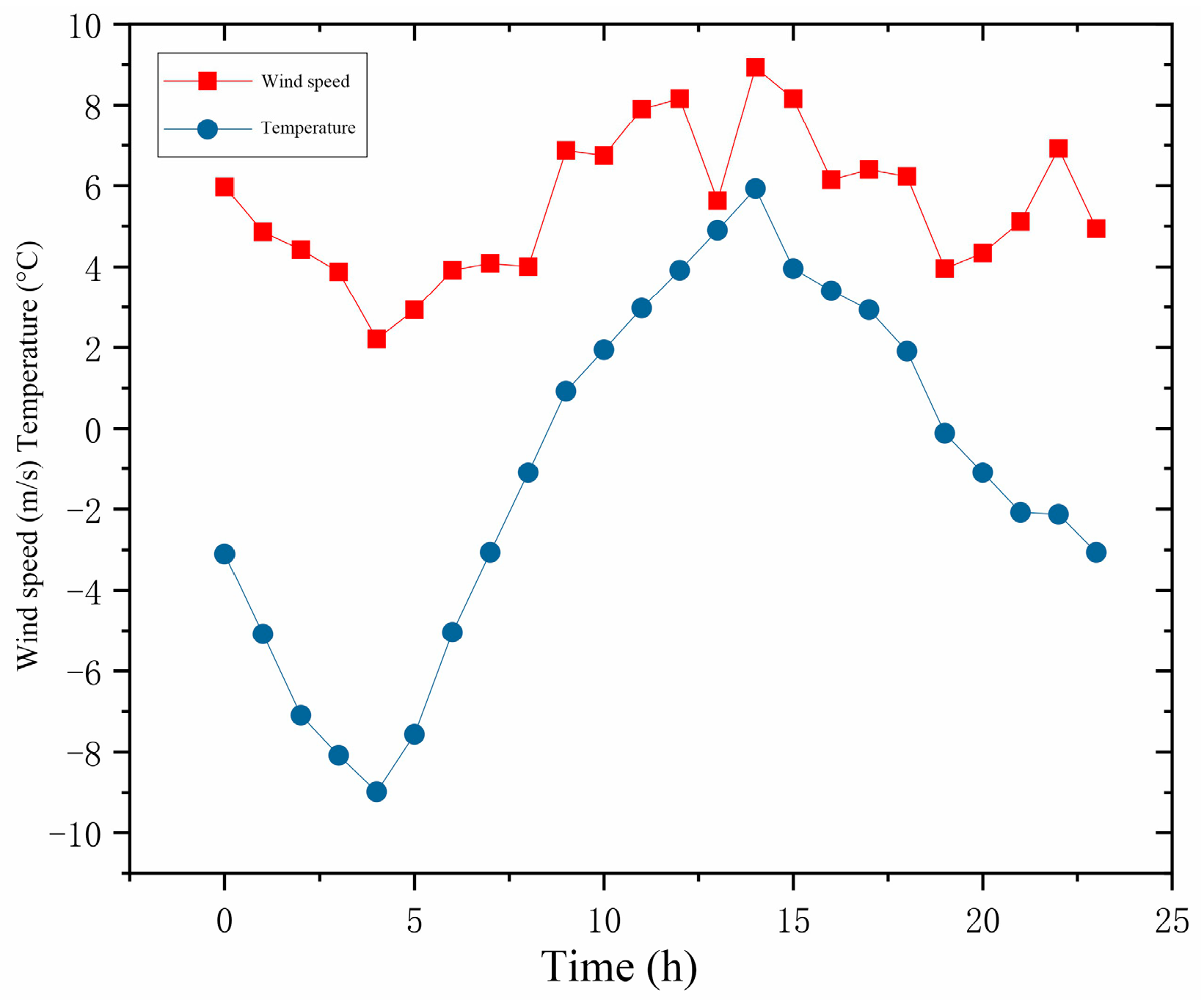
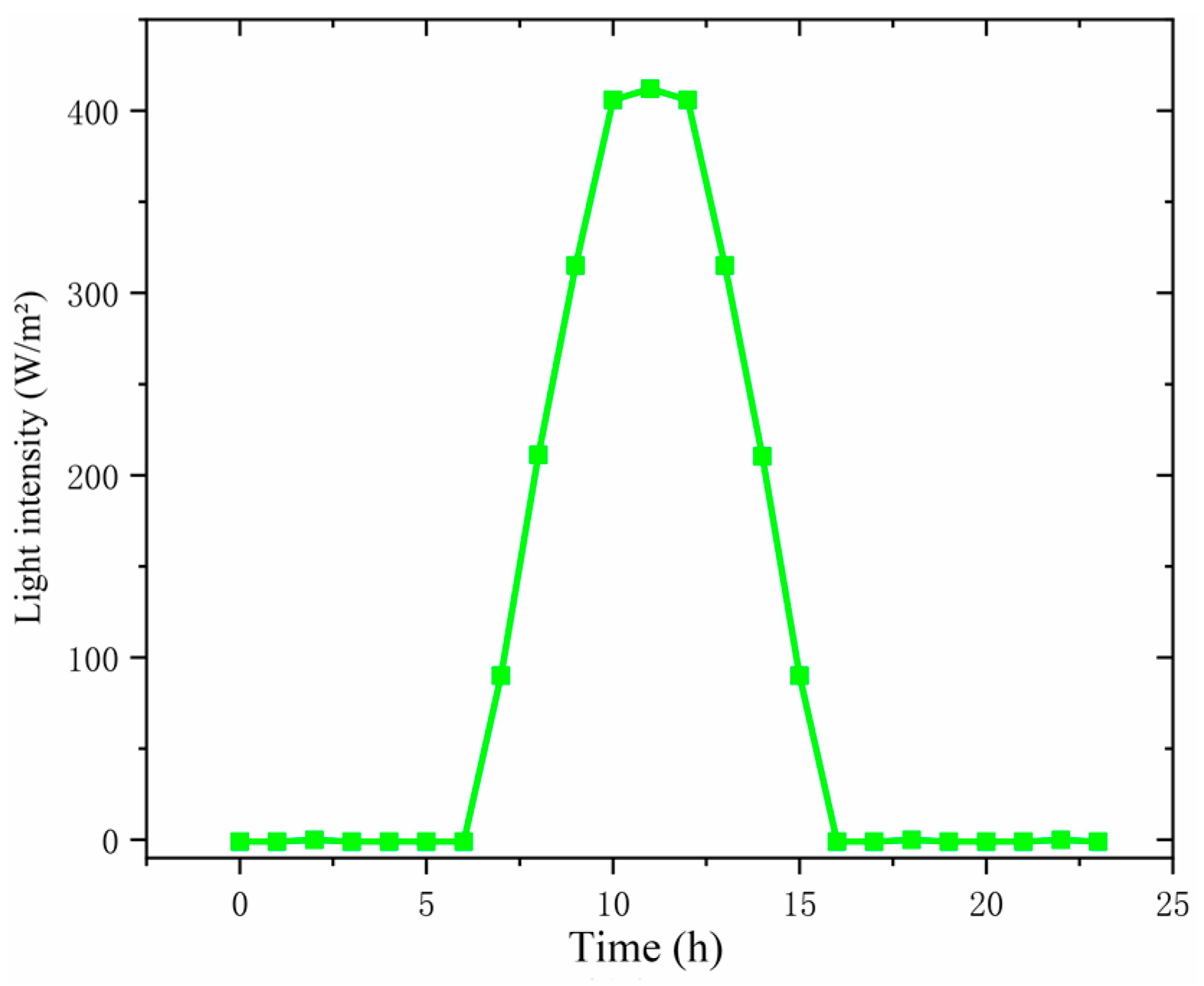
4.1. Example Simulation of Photovoltaic Power Generation Prediction
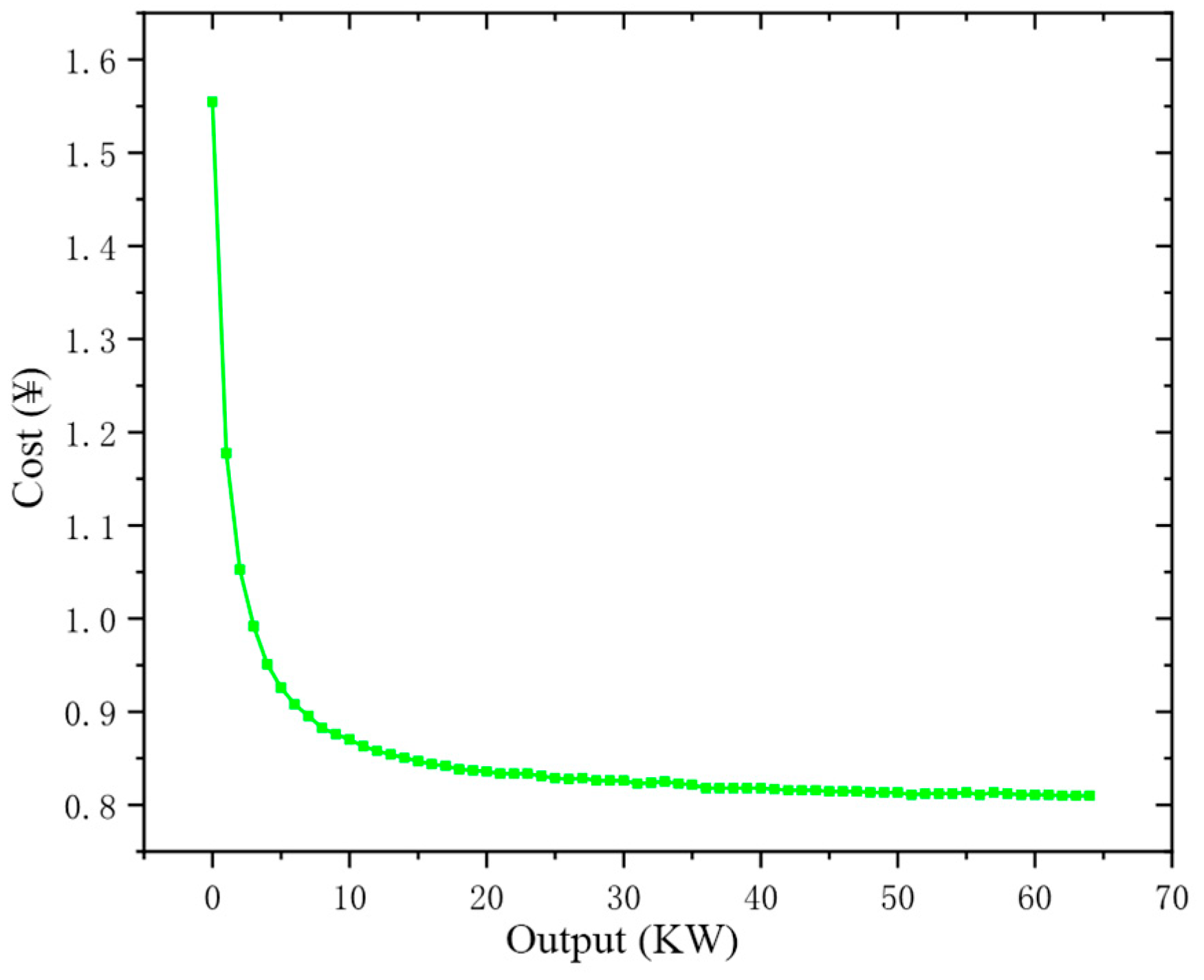
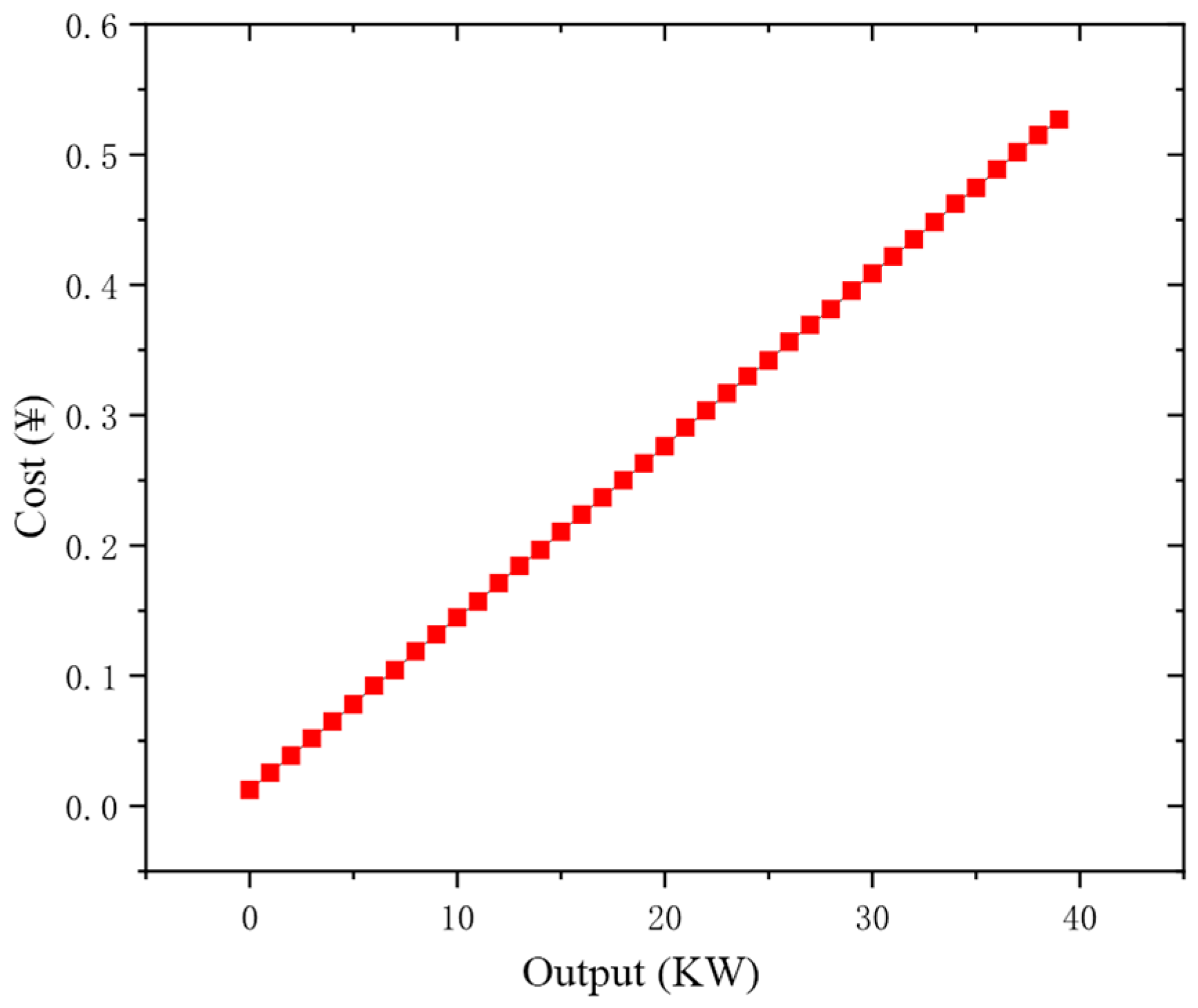
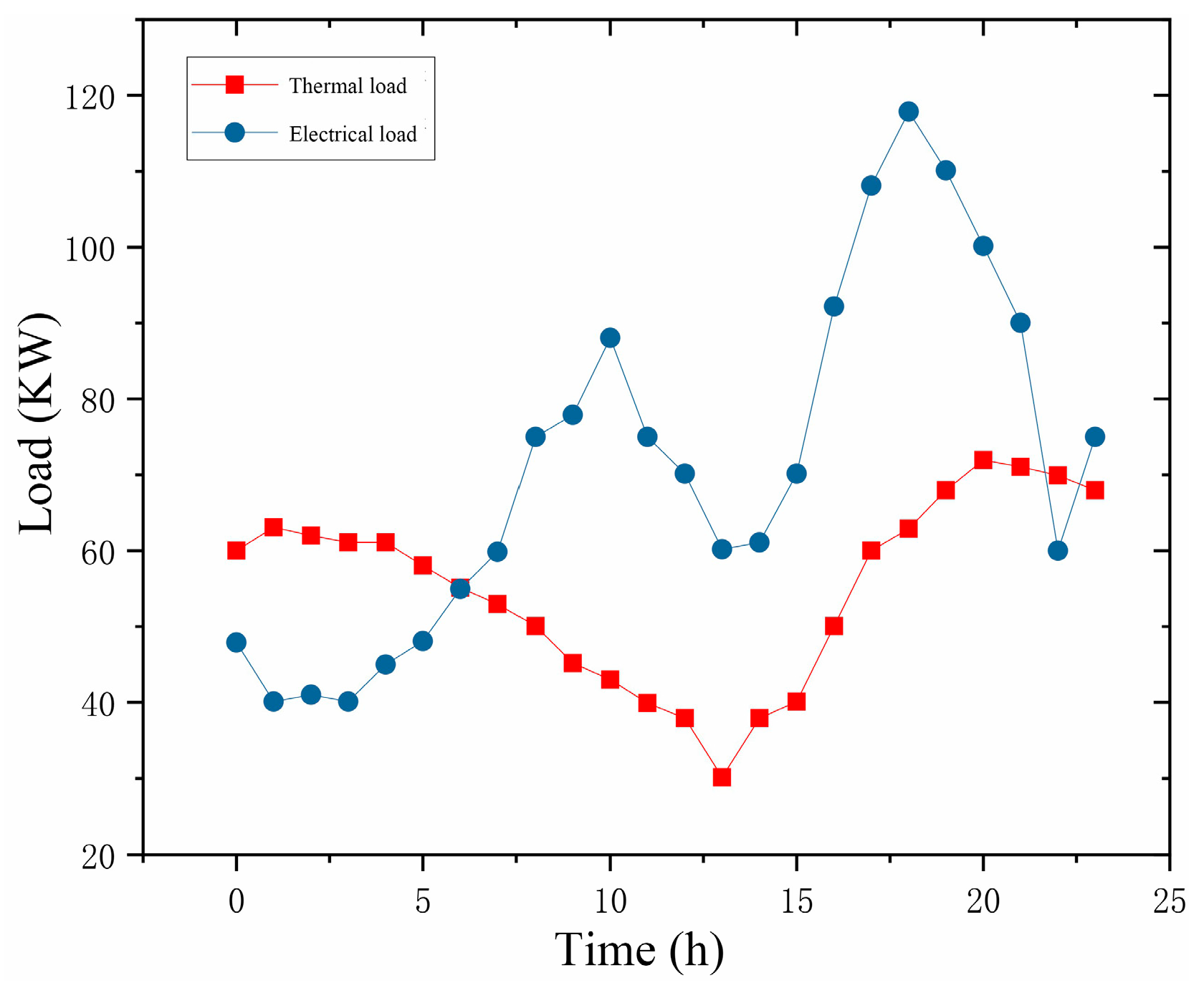
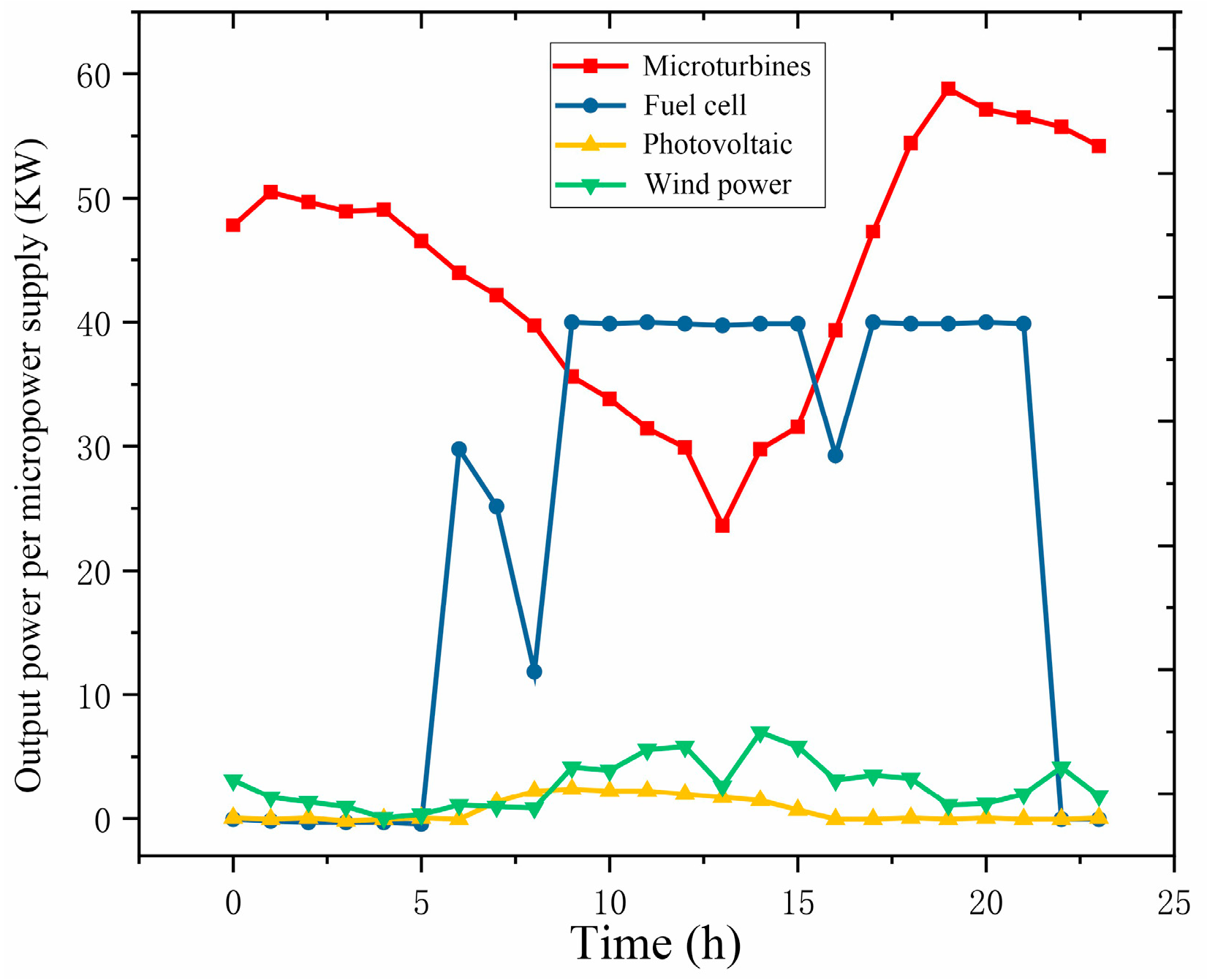
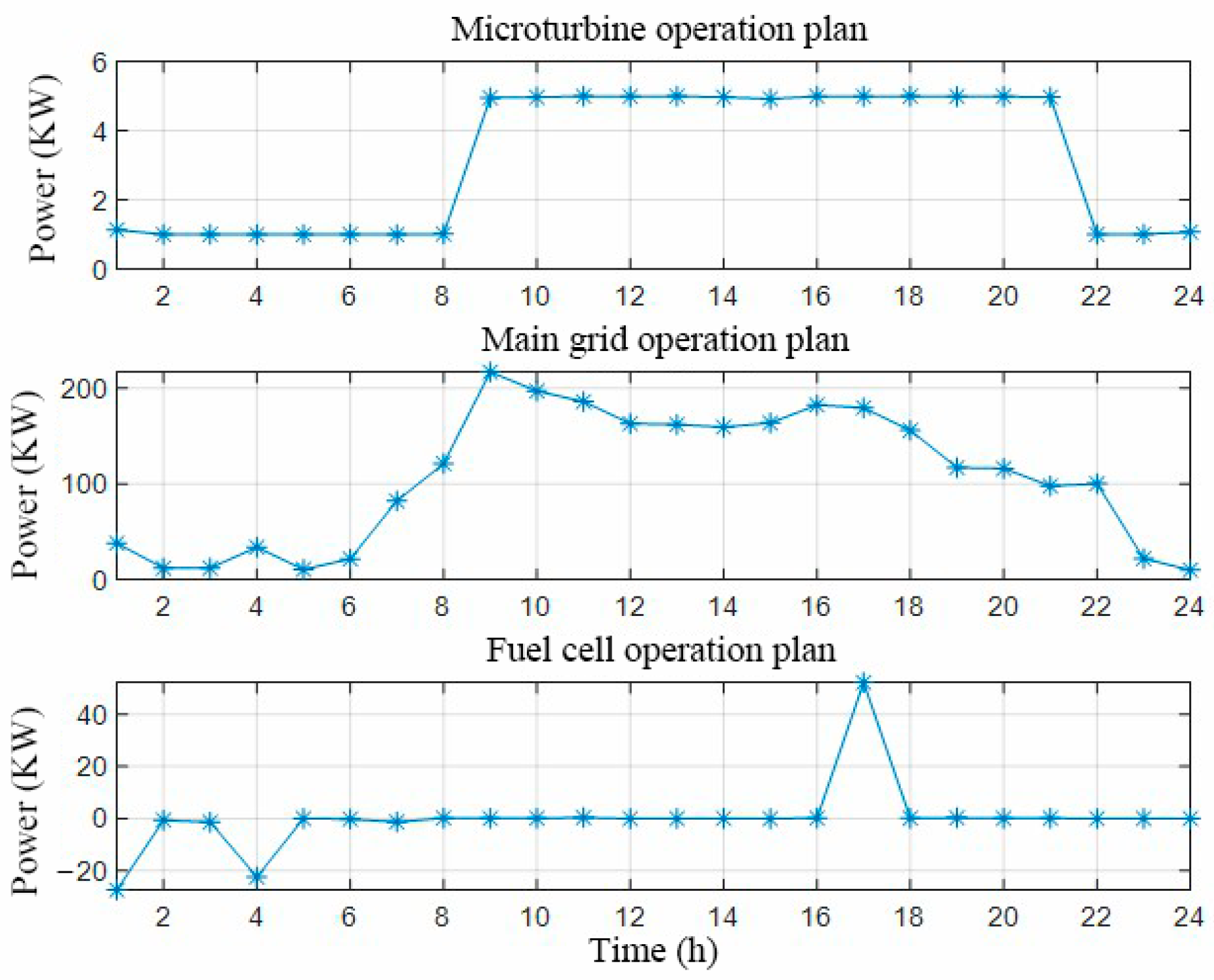
4.2. Simulation of a Microgrid Distributed Energy Dispatch Example
- (1)
- Low periods of electricity consumption (23:30–06:30)
- (2)
- Flat periods of electricity consumption (07:30–09:30, 15:30–17:30, 21:30–22:30)
- (3)
- Peak periods of electricity consumption (10:30–14:30, 18:30–20:30)
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cao, R.; Tian, H.; Li, D.; Feng, M.; Fan, H. Short-Term Photovoltaic Power Generation Prediction Model Based on Improved Data Decomposition and Time Convolution Network. Energies 2023, 17, 33. [Google Scholar] [CrossRef]
- Abdellatif, A.; Mubarak, H.; Ahmad, S.; Ahmed, T.; Shafiullah, G.M.; Hammoudeh, A.; Abdellatef, H.; Rahman, M.M.; Gheni, H.M. Forecasting Photovoltaic Power Generation with a Stacking Ensemble Model. Sustainability 2022, 14, 11083. [Google Scholar] [CrossRef]
- Wei, X.; Wang, M. Research on Data Model and Integration Technology of New Energy Power System. In Proceedings of the 2017 4th International Conference on Information Science and Control Engineering (ICISCE), Changsha, China, 21–23 July 2017; pp. 1135–1139. [Google Scholar] [CrossRef]
- Leva, S.; Dolara, A. Analysis and Vlidation of 24 Hours Ahead Neural Network Forecasting of Photovoltaic Output Power. Math. Comput. Simul. 2017, 131, 1325–1340. [Google Scholar] [CrossRef]
- Tan, Z.; De, G.; Li, M. Combined Electricity Heat-cooling-gas Load Forecasting Model for Integrated Energy System Based on Multi-task Learning and Least Square Support Vector Machine. Clean. Prod. 2020, 248, 119252–119263. [Google Scholar] [CrossRef]
- Aslam, S.; Herodotou, H.; Mohsin, S.M. A Survey on Deep Learning Methods for Power Load and Renewable Energy Forecasting in Smart Microgrids. Renew. Sustain. Energy Rev. 2021, 144, 524–536. [Google Scholar] [CrossRef]
- Kim, M.K.; Kim, Y.-S. Predictions of Electricity Consumption in a Campus Building Using Occupant Rates and Weather Elements with Sensitivity Analysis: Artificial Neural Network vs. Linear Regression. Sustain. Cities Soc. 2020, 62, 515–530. [Google Scholar] [CrossRef]
- Kalliola, J.; Kapočiūtė-Dzikienė, J.; Damaševičius, R. Neural Network Hyperparameter Optimization for Prediction of Real Estate Prices in Helsinki. PeerJ Comput. Sci. 2021, 7, 434–444. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Hu, Q.; Hu, Z. An Adaptive Hyper Parameter Tuning Model for Ship Fuel Consumption Prediction under Complex Maritime Environments. J. Ocean. Eng. Sci. 2021, 5, 260–265. [Google Scholar] [CrossRef]
- Netsanet, S.; Zheng, D.; Zhang, W.; Teshager, G. Short-Term PV Power Forecasting Using Variational Mode Decomposition Integrated with Ant Colony Optimization and Neural Network. Energy Rep. 2022, 10, 8. [Google Scholar] [CrossRef]
- Liang, L.; Su, T.; Gao, Y.; Qin, F.; Pan, M. FCDT-IWBOA-LSSVR: An Innovative Hybrid Machine Learning Approach for Efficient Prediction of Short-To-Mid-Term Photovoltaic Generation. J. Clean. Prod. 2023, 385, 135716. [Google Scholar] [CrossRef]
- Dhiman, G. MOSHEPO: A Hybrid Multi-Objective Approach to Solve Economic Load Dispatch and Micro Grid Problems. Appl. Intell. 2020, 50, 119–137. [Google Scholar] [CrossRef]
- Prasad, T.N.; Devakirubakaran, S.; Muthubalaji, S.; Srinivasan, S.; Kamel, S. Power Management in Hybrid ANFIS PID Based AC–DC Microgrids with EHO Based Cost Optimized Droop Control Strategy. Energy Rep. 2022, 8, 15081–15094. [Google Scholar] [CrossRef]
- Luo, S.; Guo, X. Multi-Objective Optimization of Multi-Microgrid Power Dispatch under Uncertainties Using Interval Optimization. J. Ind. Manag. Optim. 2023, 19, 823–851. [Google Scholar] [CrossRef]
- Li, S.; Chen, X.; Yin, L.; Zhang, F.; Wu, P.; Zhao, S.T. Evaluation and Research of Photovoltaic Power Generation Model Considering Climate Change. Acta Energiae Solaris Sin. 2022, 43, 79–84. [Google Scholar] [CrossRef]
- Peng, O.; Ren, T.; Wang, Y. Short-term Wind Power Prediction by Optimizing Deep Learning Network Hyper-Parameters Based on ISSA. Smart Power 2023, 51, 31–38+52. [Google Scholar]
- Huang, X.; Li, Q.; Tai, Y.; Chen, Z.; Liu, J.; Shi, J.; Liu, W. Time series forecasting for hourly photovoltaic power using conditional generative adversarial network and Bi-LSTM. Energy 2022, 246, 123403. [Google Scholar] [CrossRef]
- Kim, T.Y.; Cho, S.B. Predicting residential energy consumption using CNN-LSTM neural networks. Energy 2019, 182, 72–81. [Google Scholar] [CrossRef]
- Zhang, X.; Shang, J.; Yu, G. Bearing Fault Diagnosis Based on Attention for Multi-Scale Convolutional Neural Network [J/OL]. J. Jilin Univ. Eng. Technol. Ed. 2023, 1–10. [Google Scholar] [CrossRef]
- Yao, Z.; Lu, Z.; Li, C. Improved CEEMDAN-PSO-BiLSTM Model for Short-term Passenger Flow Prediction at Bus Stops. J. Beijing Jiaotong Univ. 2023, 47, 74–80. [Google Scholar]
- Sun, H.; Li, F. Photovoltaic Hot Spot Recognition Based on Attention Mechanism. Acta Electron. Sin. 2023, 44, 453–459. [Google Scholar] [CrossRef]
- Zhou, H.; Bai, H.; Cai, Z. Container Quota Optimization Algorithm Based on GRNN and LSTM. Acta Electron. Sin. 2022, 50, 366–373. [Google Scholar]
- Qu, W.; Chen, G.; Zhang, T. An adaptive noise reduction approach for remaining useful life prediction of lithium-ion batteries. Energies 2022, 15, 7422. [Google Scholar] [CrossRef]
- Kang, L.; Zhang, X.; Oleg, K. SLSL-QPSO: Quantum-behaved particle swarm optimization with short-lived swarm layers. SoftwareX 2023, 24, 101536. [Google Scholar] [CrossRef]
- Zhu, X.T.; Xu, B. Power short-term load forecasting based on QPSO-SVM. Adv. Mater. Res. 2012, 591, 1311–1314. [Google Scholar] [CrossRef]

| Relevant Relation | Degree of Relevance | ||
|---|---|---|---|
| Perfect linear correlation | extremely weak correlation | ||
| no linear correlation | weak correlation | ||
| positive correlation | moderately relevant | ||
| negative correlation | strong correlation | ||
| Highly relevant | |||
| Principal Component | Variance Contribution (%) | Cumulative Variance Contribution (%) |
|---|---|---|
| 1 | 33.378 | 33.379 |
| 2 | 15.965 | 49.347 |
| 3 | 13.076 | 62.418 |
| 4 | 9.34 | 71.768 |
| 5 | 7.08 | 78.858 |
| 6 | 5.131 | 83.992 |
| 7 | 4.514 | 88.507 |
| 8 | 3.495 | 92.006 |
| 9 | 2.778 | 94.778 |
| 10 | 1.936 | 96.716 |
| 11 | 1.491 | 98.204 |
| 12 | 1.456 | 99.661 |
| 13 | 0.245 | 99.907 |
| 14 | 0.084 | 99.991 |
| 15 | 0.006 | 99.998 |
| 16 | 0.002 | 100 |
| 17 | 2.778 | 94.778 |
| Typology | External Discount Cost (CNY/kg) | Emission Factor (kg/MW) | ||
|---|---|---|---|---|
| Micro Turbine | Fuel Cell | Primary Network | ||
| 8.00 | 0.2 | 0.014 | 1.6 | |
| 6.00 | 0.0036 | 0.0027 | 1.8 | |
| 0.023 | 724 | 489 | 889 | |
| Module Type | Wind Turbine | Photovoltaic | Micro Turbine | Fuel Cell | Storage Battery |
|---|---|---|---|---|---|
| Installation cost (CNY/kW) | 23,750.00 | 66,500.00 | 18,500.00 | 52,710.00 | — |
| Maintenance cost factor | 0.02941 | 0.00962 | 0.00963 | 0.02911 | 0.0452 |
| Depreciation cost factor | 0.71 | 2.793 | 0.0111 | 0.251 | — |
| Upper limit power (kW) | 10.00 | 10.00 | 65.00 | 40.00 | 20.00 |
| Life span (years) | 10.00 | 20.00 | 15.00 | 10.00 | 5.00 |
| Phase | Cost Comparisons | Analysis |
|---|---|---|
| Low periods of electricity consumption | Fuel cells do not generate electricity | |
| Microturbines do not generate electricity after encountering thermal loads | ||
| Flat periods of electricity consumption | Fuel cells do not generate electricity after encountering an electrical load | |
| Microturbines do not generate electricity after encountering thermal loads | ||
| Peak periods of electricity consumption | Fuel cell full power generation | |
| Microturbines do not generate electricity after encountering thermal loads | ||
| Micro-turbine power generation to meet electrical loads |
| Typology | Parameters |
|---|---|
| Activation function | ReLU function |
| Number of iterations | 50 |
| Learning rate | 0.001 |
| Fine-tuning learning rate | 0.1 |
| Regularization parameter | 0.5 |
| Modelling | Number of Iterations | Population size | Learning Rate | Hidden Node 1, 2 | Fully Connected Node |
|---|---|---|---|---|---|
| CNN-BiLSTM | 50 | 20 | 0.001 | 10 | 10 |
| BiLSTM-ATT | 60 | 10 | 0.001 | 10 | 10 |
| SSA-CNN-BiLSTM | 100 | 20 | 0.001 | 10 | 10 |
| SSA-CNN-BiLSTM-ATT | 150 | 20 | 0.002 | 10 | 20 |
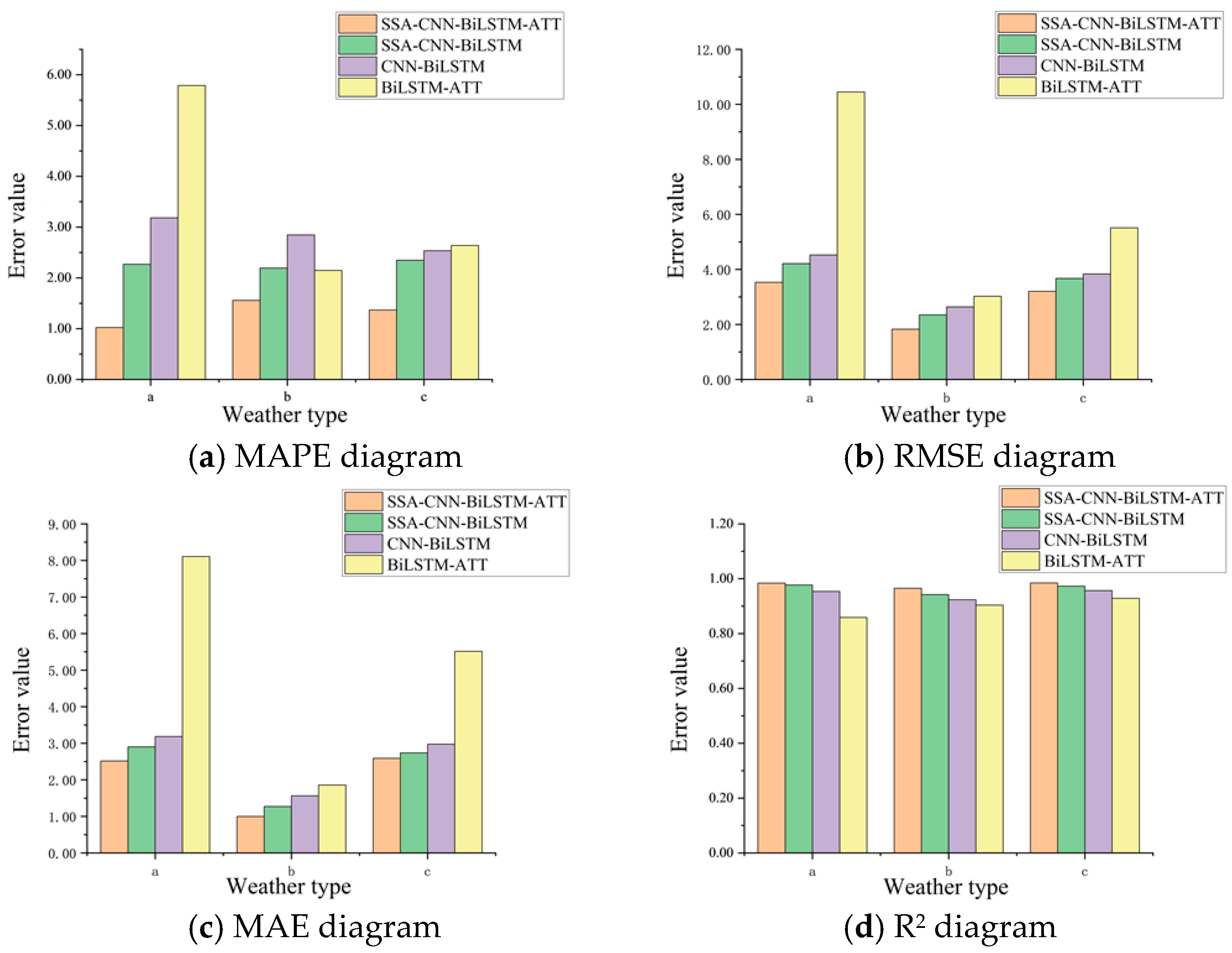
| Error Parameter | Weather Types | SSA-CNN-BiLSTM-ATT | SSA-CNN-BiLSTM | CNN-BiLSTM | BiLSTM-ATT |
|---|---|---|---|---|---|
| MAPE | a | 1.0225 | 2.2689 | 3.1825 | 5.7866 |
| b | 1.5562 | 2.1935 | 2.8462 | 2.1464 | |
| c | 1.3673 | 2.3472 | 2.5347 | 2.6372 | |
| RMSE | a | 3.5292 | 4.2110 | 4.5231 | 8.4481 |
| b | 1.8258 | 2.3490 | 2.6374 | 3.0254 | |
| c | 3.2021 | 3.6725 | 3.8354 | 5.5128 | |
| MAE | a | 2.5150 | 2.9021 | 3.1852 | 8.1065 |
| b | 0.9986 | 1.2703 | 1.5632 | 1.8591 | |
| c | 2.5876 | 2.7354 | 2.9756 | 5.5128 | |
| R2 | a | 0.9839 | 0.9770 | 0.9536 | 0.8586 |
| b | 0.9650 | 0.9420 | 0.9235 | 0.9038 | |
| c | 0.9845 | 0.9728 | 0.9568 | 0.9286 |
| Mode | Period | Tariff Price (CNY/kWh) |
|---|---|---|
| Electricity purchase | Peak period (10:30–14:30, 18:30–20:30) | 0.83 |
| Regular period (7:30–9:30, 15:30–17:30, 21:30–22:30) | 0.49 | |
| Bottom period (23:30–06:30) | 0.17 | |
| Electricity sale | Peak period (10:30–14:30, 18:30–20:30) | 0.65 |
| Regular period (7:30–9:30, 15:30–17:30, 21:30–22:30) | 0.38 | |
| Bottom period (23:30–06:30) | 0.13 |
| Name of Algorithm | Average Rankings |
|---|---|
| PSO | 2.85 |
| QPSO | 2.02 |
| Improved QPSO | 1.12 |
| Number of Iterations | Improved QPSO | QPSO | PSO |
|---|---|---|---|
| 1 | 1478.53 | 1496.1404 | 1499.975 |
| 5 | 1475.13 | 1492.835 | 1497.8886 |
| 10 | 1470.49 | 1477.8428 | 1494.6328 |
| 15 | 1465.49 | 1467.2558 | 1489.274 |
| 20 | 1465.43 | 1466.5655 | 1489.0882 |
| 25 | 1465.4 | 1466.0593 | 1488.829 |
| 30 | 1465.38 | 1466.3064 | 1488.7039 |
| 35 | 1465.37 | 1466.30439 | 1488.6686 |
| 40 | 1465.32 | 1466.3038 | 1488.6327 |
| 45 | 1465.24 | 1466.3037 | 1488.5629 |
| 50 | 1465.08 | 1466.3037 | 1488.5631 |
| 55 | 1464.97 | 1466.3037 | 1488.5631 |
| 60–230 (stable value) | 1464.97 | 1466.3037 | 1488.5631 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Zhao, W.; He, Q.; Xu, J. Optimization of Microgrid Dispatching by Integrating Photovoltaic Power Generation Forecast. Sustainability 2025, 17, 648. https://doi.org/10.3390/su17020648
Zhang T, Zhao W, He Q, Xu J. Optimization of Microgrid Dispatching by Integrating Photovoltaic Power Generation Forecast. Sustainability. 2025; 17(2):648. https://doi.org/10.3390/su17020648
Chicago/Turabian StyleZhang, Tianrui, Weibo Zhao, Quanfeng He, and Jianan Xu. 2025. "Optimization of Microgrid Dispatching by Integrating Photovoltaic Power Generation Forecast" Sustainability 17, no. 2: 648. https://doi.org/10.3390/su17020648
APA StyleZhang, T., Zhao, W., He, Q., & Xu, J. (2025). Optimization of Microgrid Dispatching by Integrating Photovoltaic Power Generation Forecast. Sustainability, 17(2), 648. https://doi.org/10.3390/su17020648






