Hydro-Climatic Trends in Central Italy: A Case Study from the Aterno-Pescara River Watershed
Abstract
1. Introduction
2. Study Area and Data
3. Methodology
4. Results and Discussion
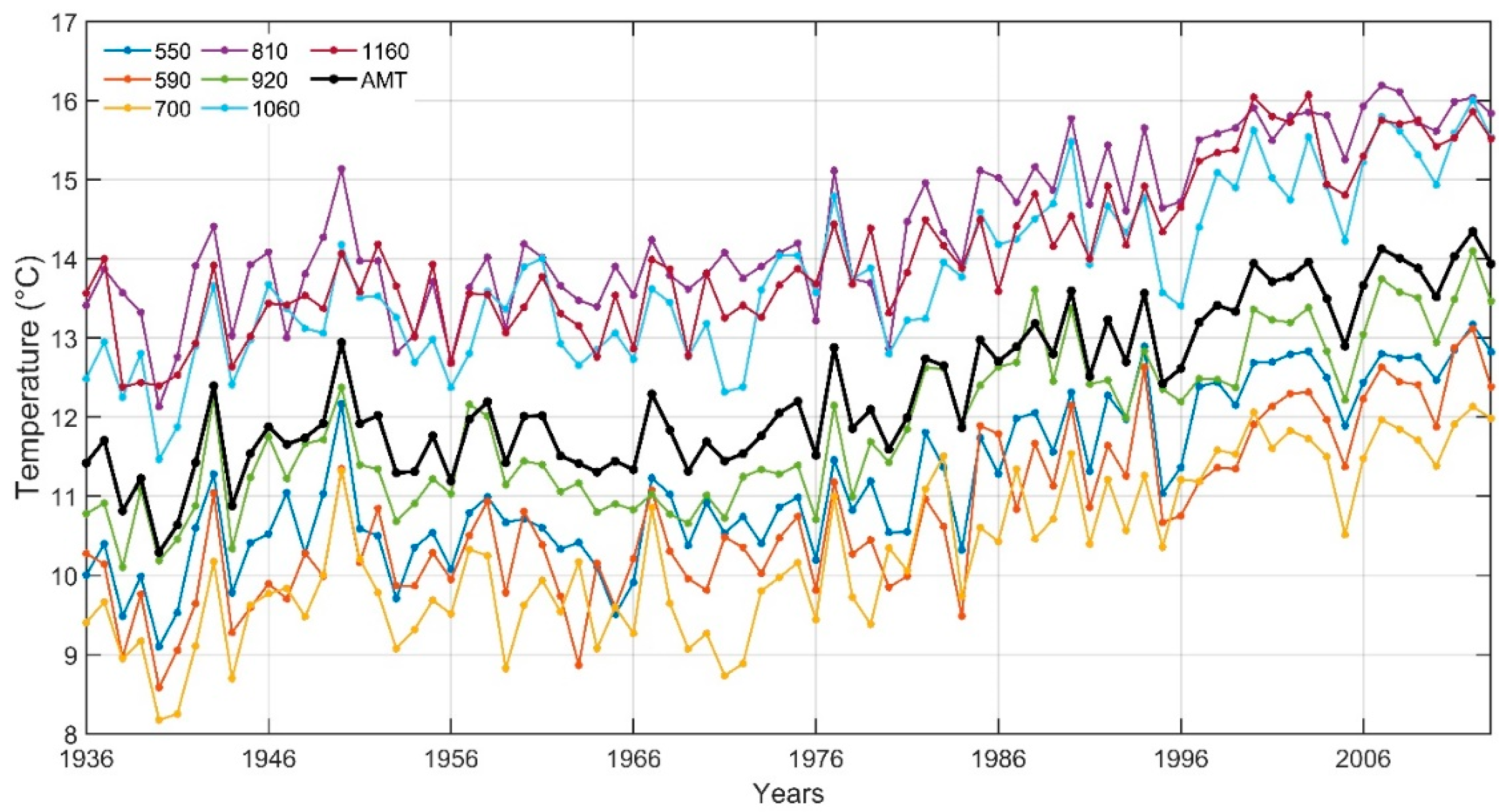
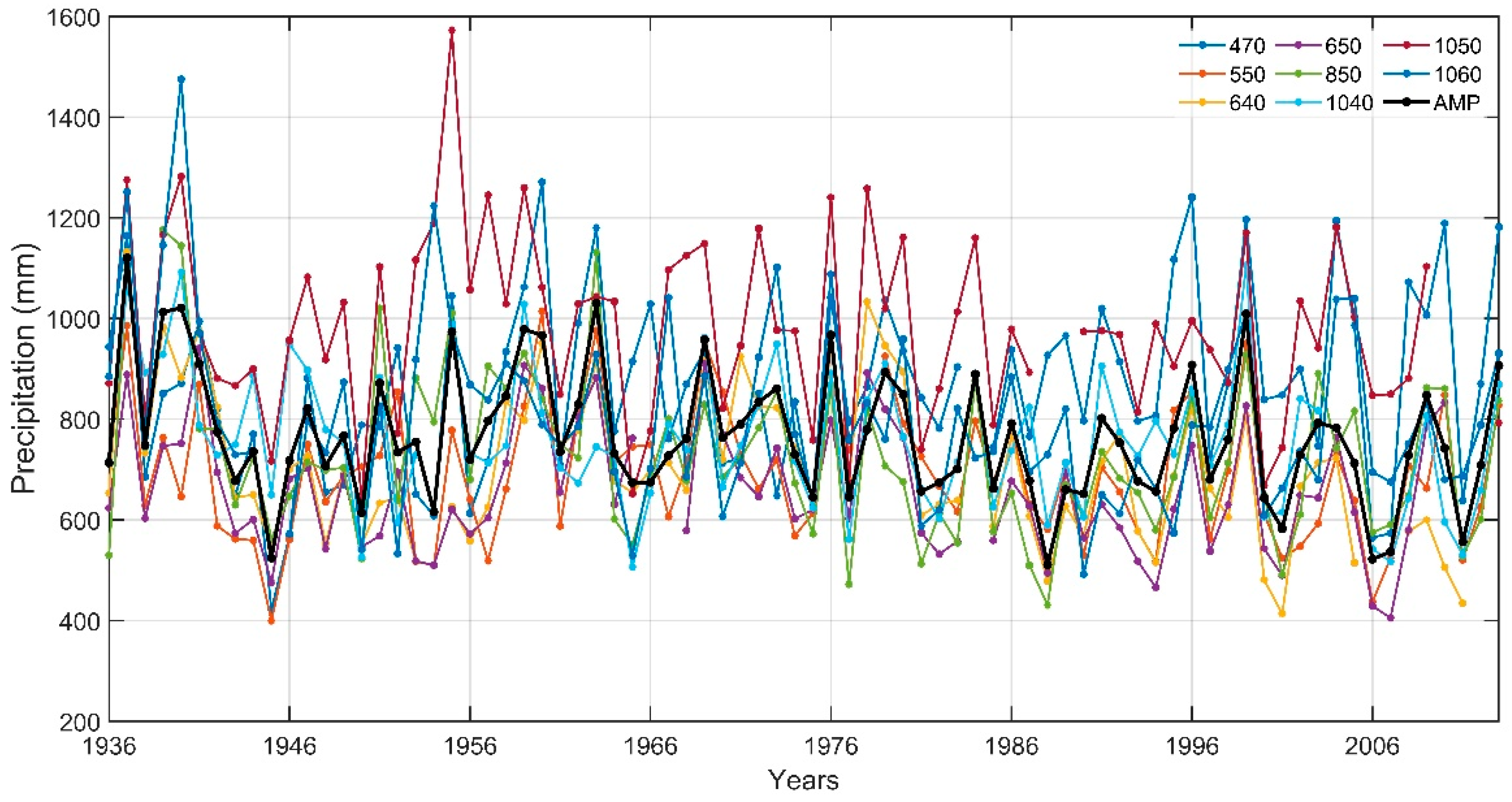
4.1. Summary Statistics of Variables
4.2. Trend Analysis
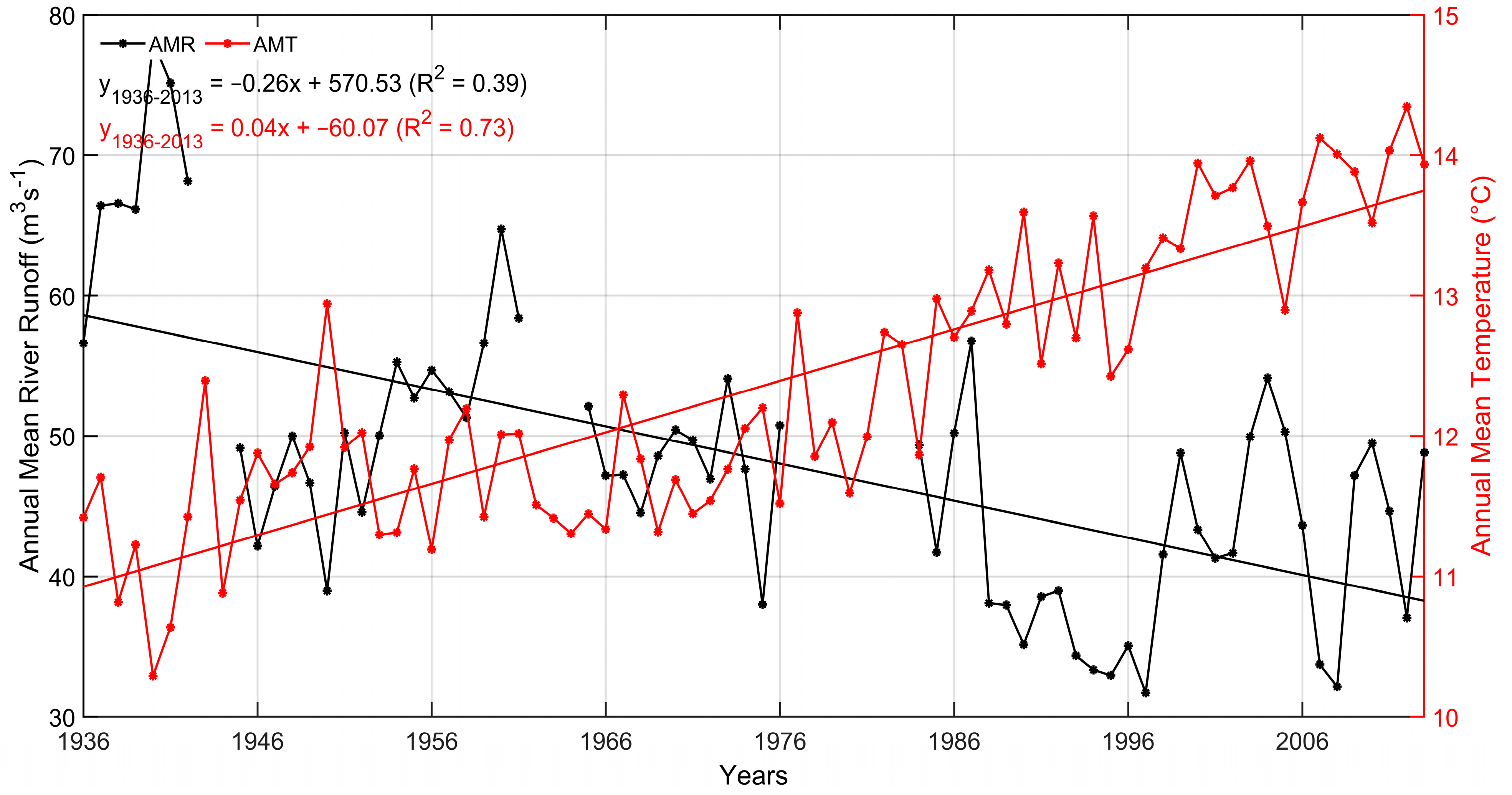
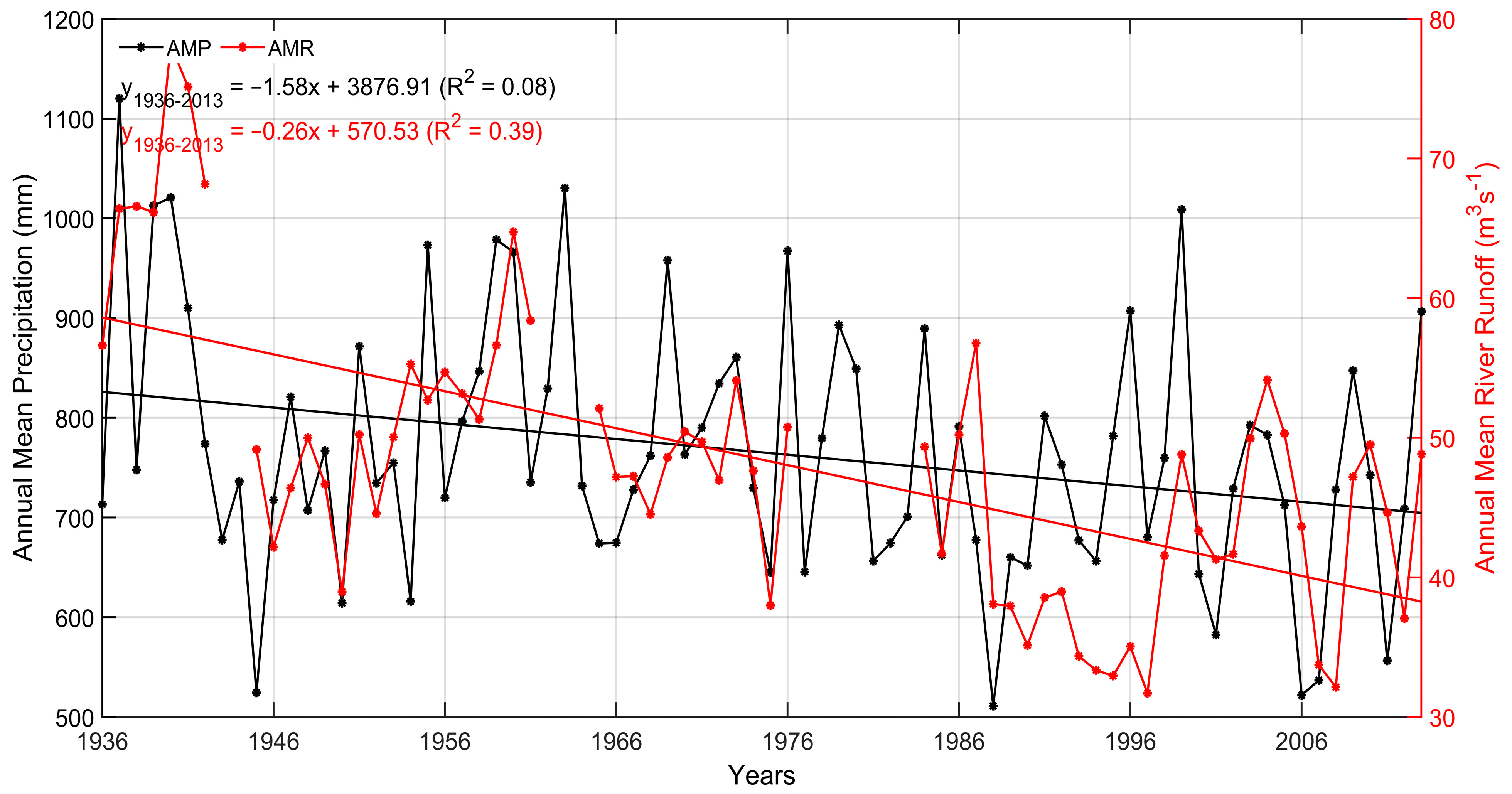
4.2.1. Linear Regression
4.2.2. Mann–Kendall and Sen’s Slope Estimator Tests
4.2.3. Spearman’s Correlation Test
5. Discussion
6. Conclusions
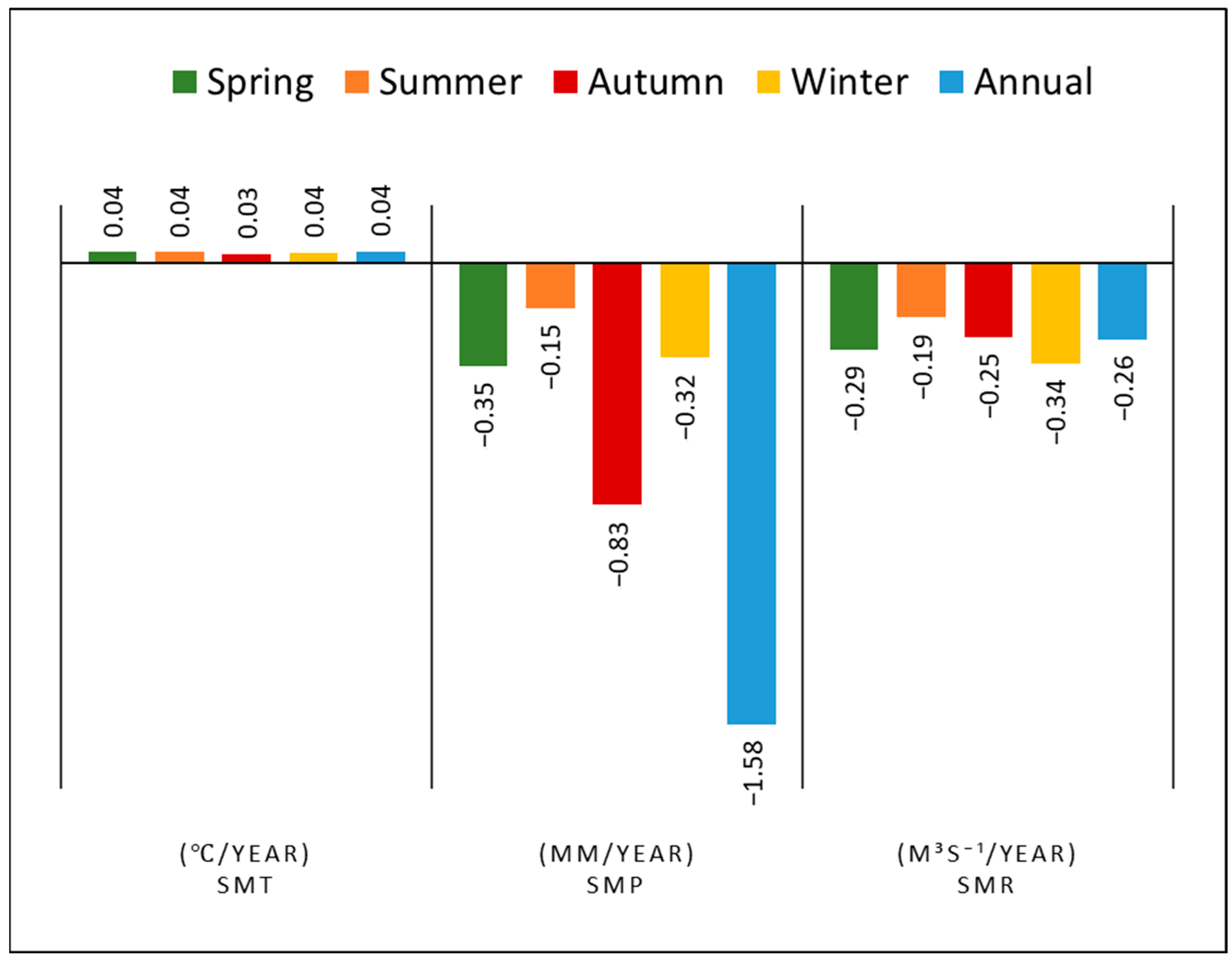
- The annual mean temperature on the watershed scale increased at a rate of 0.037 °C/year. Spring and summer remained the hottest seasons, significantly exhibiting an increasing trend of 0.038 °C/year.
- The cumulative precipitation average exhibited a significant decreasing trend on the annual scale and for the autumn season only. Other seasons showed an insignificant decreasing trend. The autumn season held a major contribution of −0.68 mm/year towards annual precipitation (−1.81 mm/year).
- In association with increasing temperatures and decreasing precipitation, the hydrologic variable, i.e., RR, showed a significant decreasing trend annually (−0.29 m3 s−1/year) and seasonally, notably with the highest rate of decrease in winters (−0.41 m3 s−1/year).
- A significant correlation was observed among all the variables, albeit with varying magnitudes of strength. To comprehensively understand their contributions towards the reduction in precipitation and RR rate, the inclusion of additional variables, such as wind matrices, water abstraction, and land use, would help.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rahmani, F.; Fattahi, M.H. Climate change-induced influences on the nonlinear dynamic patterns of precipitation and temperatures (case study: Central England). Theor. Appl. Climatol. 2023, 152, 1147–1158. [Google Scholar] [CrossRef]
- Nikzad Tehrani, E.; Sahour, H.; Booij, M. Trend analysis of hydro-climatic variables in the north of Iran. Theor. Appl. Climatol. 2019, 136, 85–97. [Google Scholar] [CrossRef]
- Alexander, L.V.; Zhang, X.; Peterson, T.C.; Caesar, J.; Gleason, B.; Klein Tank, A.; Haylock, M.; Collins, D.; Trewin, B.; Rahimzadeh, F. Global observed changes in daily climate extremes of temperature and precipitation. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Dey, R.; Lewis, S.C.; Arblaster, J.M.; Abram, N.J. A review of past and projected changes in Australia’s rainfall. Wiley Interdiscip. Rev. Clim. Chang. 2019, 10, e577. [Google Scholar] [CrossRef]
- Philandras, C.; Nastos, P.; Kapsomenakis, J.; Douvis, K.; Tselioudis, G.; Zerefos, C. Long term precipitation trends and variability within the Mediterranean region. Nat. Hazards Earth Syst. Sci. 2011, 11, 3235–3250. [Google Scholar] [CrossRef]
- Ren, L.; Arkin, P.; Smith, T.M.; Shen, S.S. Global precipitation trends in 1900–2005 from a reconstruction and coupled model simulations. J. Geophys. Res. Atmos. 2013, 118, 1679–1689. [Google Scholar] [CrossRef]
- Cortesi, N.; González-Hidalgo, J.C.; Brunetti, M.; Martin-Vide, J. Daily precipitation concentration across Europe 1971–2010. Nat. Hazards Earth Syst. Sci. 2012, 12, 2799–2810. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Jones, P.D.; Ambenje, P.; Bojariu, R.; Easterling, D.; Tank, A.K.; Parker, D.; Rahimzadeh, F.; Renwick, J.A.; Rusticucci, M. Observations: Surface and atmospheric climate change. In Climate Change 2007: The Physical Science Basis. Contribution of Working Group 1 to the 4th Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Luterbacher, J.; Dietrich, D.; Xoplaki, E.; Grosjean, M.; Wanner, H. European seasonal and annual temperature variability, trends, and extremes since 1500. Science 2004, 303, 1499–1503. [Google Scholar] [CrossRef] [PubMed]
- Alpert, P.; Krichak, S.O.; Shafir, H.; Haim, D.; Osetinsky, I. Climatic trends to extremes employing regional modeling and statistical interpretation over the E. Mediterranean. Glob. Planet. Chang. 2008, 63, 163–170. [Google Scholar] [CrossRef]
- Tuel, A.; Eltahir, E.A. Why is the Mediterranean a climate change hot spot? J. Clim. 2020, 33, 5829–5843. [Google Scholar] [CrossRef]
- Climate Change 2022: Impacts, Adaptation, and Vulnerability. Contribution of Working Group II to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2022.
- Jackson, R.B.; Carpenter, S.R.; Dahm, C.N.; McKnight, D.M.; Naiman, R.J.; Postel, S.L.; Running, S.W. Water in a changing world. Ecol. Appl. 2001, 11, 1027–1045. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Boulange, J.; Do, H.X.; Gosling, S.N.; Grillakis, M.G.; Koutroulis, A.G.; Leonard, M.; Liu, J.; Müller Schmied, H.; Papadimitriou, L. Globally observed trends in mean and extreme river flow attributed to climate change. Science 2021, 371, 1159–1162. [Google Scholar] [CrossRef] [PubMed]
- Donnelly, C.; Greuell, W.; Andersson, J.; Gerten, D.; Pisacane, G.; Roudier, P.; Ludwig, F. Impacts of climate change on European hydrology at 1.5, 2 and 3 degrees mean global warming above preindustrial level. Clim. Chang. 2017, 143, 13–26. [Google Scholar] [CrossRef]
- Noto, L.V.; Cipolla, G.; Francipane, A.; Pumo, D. Climate change in the mediterranean basin (part I): Induced alterations on climate forcings and hydrological processes. Water Resour. Manag. 2023, 37, 2287–2305. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Peña-Gallardo, M.; Hannaford, J.; Murphy, C.; Lorenzo-Lacruz, J.; Dominguez-Castro, F.; López-Moreno, J.I.; Beguería, S.; Noguera, I.; Harrigan, S. Climate, irrigation, and land cover change explain streamflow trends in countries bordering the northeast Atlantic. Geophys. Res. Lett. 2019, 46, 10821–10833. [Google Scholar] [CrossRef]
- Hao, X.; Chen, Y.; Xu, C.; Li, W. Impacts of climate change and human activities on the surface runoff in the Tarim River Basin over the last fifty years. Water Resour. Manag. 2008, 22, 1159–1171. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Seneviratne, S.I.; Zhang, X. Anthropogenic climate change detected in European renewable freshwater resources. Nat. Clim. Chang. 2017, 7, 813–816. [Google Scholar] [CrossRef]
- Brunetti, M.; Maugeri, M.; Nanni, T. Variations of temperature and precipitation in Italy from 1866 to 1995. Theor. Appl. Climatol. 2000, 65, 165–174. [Google Scholar] [CrossRef]
- Caloiero, T.; Coscarelli, R.; Ferrari, E.; Mancini, M. Trend detection of annual and seasonal rainfall in Calabria (Southern Italy). Int. J. Climatol. 2011, 31, 44–56. [Google Scholar] [CrossRef]
- Vergni, L.; Todisco, F. Spatio-temporal variability of precipitation, temperature and agricultural drought indices in Central Italy. Agric. For. Meteorol. 2011, 151, 301–313. [Google Scholar] [CrossRef]
- Toreti, A.; Desiato, F. Temperature trend over Italy from 1961 to 2004. Theor. Appl. Climatol. 2008, 91, 51–58. [Google Scholar] [CrossRef]
- Gentilucci, M.; Materazzi, M.; Pambianchi, G.; Burt, P.; Guerriero, G. Assessment of variations in the temperature-rainfall trend in the province of Macerata (Central Italy), comparing the last three climatological standard normals (1961–1990; 1971–2000; 1981–2010) for biosustainability studies. Environ. Process. 2019, 6, 391–412. [Google Scholar] [CrossRef]
- Aruffo, E.; Di Carlo, P. Homogenization of instrumental time series of air temperature in Central Italy (1930–2015). Clim. Res. 2019, 77, 193–204. [Google Scholar] [CrossRef]
- Scorzini, A.R.; Leopardi, M. Precipitation and temperature trends over central Italy (Abruzzo Region): 1951–2012. Theor. Appl. Climatol. 2019, 135, 959–977. [Google Scholar] [CrossRef]
- Curci, G.; Guijarro, J.A.; Di Antonio, L.; Di Bacco, M.; Di Lena, B.; Scorzini, A.R. Building a local climate reference dataset: Application to the Abruzzo region (Central Italy), 1930–2019. Int. J. Climatol. 2021, 41, 4414–4436. [Google Scholar] [CrossRef]
- Farroni, A.; Magaldi, D.; Tallini, M. Total sediment transport by the rivers of Abruzzi (Central Italy): Prediction with the Raizal model. Bull. Eng. Geol. Environ. 2002, 61, 121–127. [Google Scholar]
- Lastoria, B.; Miserocchi, F.; Lanciani, A.; Monacelli, G. An estimated erosion map for the Aterno-Pescara river basin. Eur. Water 2008, 21, 29–39. [Google Scholar]
- Tariq, M.; Rohith, A.; Cibin, R.; Aruffo, E.; Abouzied, G.A.A.; Di Carlo, P. Understanding future hydrologic challenges: Modelling the impact of climate change on river runoff in central Italy. Environ. Chall. 2024, 15, 100899. [Google Scholar] [CrossRef]
- WMO. Analyzing Long Time Series of Hydrological Data with Respect to Climate Variability; World Meteorological Organization: Geneva, Switzerland, 1988. [Google Scholar]
- Darvini, G.; Memmola, F. Assessment of the impact of climate variability and human activities on the runoff in five catchments of the Adriatic Coast of south-central Italy. J. Hydrol. Reg. Stud. 2020, 31, 100712. [Google Scholar] [CrossRef]
- Anghileri, D.; Pianosi, F.; Soncini-Sessa, R. Trend detection in seasonal data: From hydrology to water resources. J. Hydrol. 2014, 511, 171–179. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; American Psychological Association: Washington, DC, USA, 1948. [Google Scholar]
- Aalijahan, M.; Karataş, A.; Lupo, A.R.; Efe, B.; Khosravichenar, A. Analyzing and modeling the spatial-temporal changes and the impact of GLOTI index on precipitation in the Marmara region of Türkiye. Atmosphere 2023, 14, 489. [Google Scholar] [CrossRef]
- Camuffo, D.; Bertolin, C.; Diodato, N.; Cocheo, C.; Barriendos, M.; Dominguez-Castro, F.; Garnier, E.; Alcoforado, M.J.; Nunes, M. Western Mediterranean precipitation over the last 300 years from instrumental observations. Clim. Chang. 2013, 117, 85–101. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C.Y. Applicability of prewhitening to eliminate the influence of serial correlation on the Mann-Kendall test. Water Resour. Res. 2002, 38, 4-1–4-7. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C. The Mann-Kendall test modified by effective sample size to detect trend in serially correlated hydrological series. Water Resour. Manag. 2004, 18, 201–218. [Google Scholar] [CrossRef]
- Sandeep Kumar, P.; Nicole, O.B. Modifiedmk: Modified Versions of Mann Kendall and Spearman’s Rho Trend Tests. 2021, R Package Version 1.6. Available online: https://CRAN.R-project.org/package=modifiedmk (accessed on 10 November 2023).
- Wang, W.; Yin, S.; Gao, G.; Papalexiou, S.; Wang, Z. Increasing trends in rainfall erosivity in the Yellow River basin from 1971 to 2020. J. Hydrol. 2022, 610, 127851. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar]
- Yue, S.; Pilon, P.; Cavadias, G. Power of the Mann–Kendall and Spearman’s rho tests for detecting monotonic trends in hydrological series. J. Hydrol. 2002, 259, 254–271. [Google Scholar] [CrossRef]
- Klein Tank, A.M.G.; Wijngaard, J.B.; Können, G.P.; Böhm, R.; Demarée, G.; Gocheva, A.; Mileta, M.; Pashiardis, S.; Hejkrlik, L.; Kern-Hansen, C.; et al. Daily dataset of 20th-century surface air temperature and precipitation series for the European Climate Assessment. Int. J. Climatol. 2002, 22, 1441–1453. [Google Scholar] [CrossRef]
- Ventura, F.; Pisa, P.R.; Ardizzoni, E. Temperature and precipitation trends in Bologna (Italy) from 1952 to 1999. Atmos. Res. 2002, 61, 203–214. [Google Scholar] [CrossRef]
- Kumar, P.V.; Bindi, M.; Crisci, A.; Maracchi, G. Detection of variations in air temperature at different time scales during the period 1889–1998 at Firenze, Italy. Clim. Chang. 2005, 72, 123–150. [Google Scholar] [CrossRef]
- Bartolini, G.; Morabito, M.; Crisci, A.; Grifoni, D.; Torrigiani, T.; Petralli, M.; Maracchi, G.; Orlandini, S. Recent trends in Tuscany (Italy) summer temperature and indices of extremes. Int. J. Climatol. 2008, 28, 1751–1760. [Google Scholar] [CrossRef]
- Viola, F.; Liuzzo, L.; Noto, L.V.; Lo Conti, F.; La Loggia, G. Spatial distribution of temperature trends in Sicily. Int. J. Climatol. 2014, 34, 1–17. [Google Scholar] [CrossRef]
- Moonen, A.C.; Ercoli, L.; Mariotti, M.; Masoni, A. Climate change in Italy indicated by agrometeorological indices over 122 years. Agric. For. Meteorol. 2002, 111, 13–27. [Google Scholar] [CrossRef]
- Longobardi, A.; Buttafuoco, G.; Caloiero, T.; Coscarelli, R. Spatial and temporal distribution of precipitation in a Mediterranean area (southern Italy). Environ. Earth Sci. 2016, 75, 1–20. [Google Scholar] [CrossRef]
- Caporali, E.; Lompi, M.; Pacetti, T.; Chiarello, V.; Fatichi, S. A review of studies on observed precipitation trends in Italy. Int. J. Climatol. 2021, 41, E1–E25. [Google Scholar] [CrossRef]
- Kubiak-Wójcicka, K.; Nagy, P.; Pilarska, A.; Zeleňáková, M. Trend analysis of selected hydroclimatic variables for the Hornad catchment (Slovakia). Water 2023, 15, 471. [Google Scholar] [CrossRef]
- López-Moreno, J.; Vicente-Serrano, S.; Morán-Tejeda, E.; Lorenzo-Lacruz, J.; Kenawy, A.; Beniston, M. Effects of the North Atlantic Oscillation (NAO) on combined temperature and precipitation winter modes in the Mediterranean mountains: Observed relationships and projections for the 21st century. Glob. Planet. Chang. 2011, 77, 62–76. [Google Scholar] [CrossRef]
- Fernández, J.; Sáenz, J.; Zorita, E. Analysis of wintertime atmospheric moisture transport and its variability over southern Europe in the NCEP Reanalyses. Clim. Res. 2003, 23, 195–215. [Google Scholar] [CrossRef]
- Quadrelli, R.; Pavan, V.; Molteni, F. Wintertime variability of Mediterranean precipitation and its links with large-scale circulation anomalies. Clim. Dyn. 2001, 17, 457–466. [Google Scholar] [CrossRef]
- Memmola, F.; Darvini, G. Changes in Precipitation-Runoff Relationship in Six Catchments of the Adriatic Coast of Central Italy. EPiC Ser. Eng. 2018, 3, 1373–1381. [Google Scholar]
- Saidi, H.; Dresti, C.; Manca, D.; Ciampittiello, M. Quantifying impacts of climate variability and human activities on the streamflow of an Alpine river. Environ. Earth Sci. 2018, 77, 1–16. [Google Scholar] [CrossRef]
- Gentilucci, M.; Djouohou, S.I.; Barbieri, M.; Hamed, Y.; Pambianchi, G. Trend Analysis of Streamflows in Relation to Precipitation: A Case Study in Central Italy. Water 2023, 15, 1586. [Google Scholar] [CrossRef]





| River | Basin Area (km2) | Area Percentage to the Total Watershed (%) |
|---|---|---|
| Raio River | 260.36 | 8.21 |
| Sagittario River | 612.90 | 19.33 |
| Gizio River | 253.50 | 8.05 |
| Orta River | 165.56 | 5.22 |
| Vera River | 137.89 | 4.35 |
| Tirino River | 369.47 | 11.73 |
| Nora River | 137.66 | 4.34 |
| Station Name | Type | Elevation (m) Above Sea Level | NHS Code |
|---|---|---|---|
| Montereale | Pcp | 913.00 | 470 |
| L’Aquila a S. Elia | Pcp | 595.00 | 550 |
| Beffi | Pcp | 608.00 | 640 |
| Campana | Pcp | 563.00 | 650 |
| Popoli | Pcp | 250.00 | 850 |
| Alanno | Pcp | 285.00 | 1040 |
| Manoppello | Pcp | 297.00 | 1050 |
| Chieti | Pcp | 278.00 | 1060 |
| L’Aquila a S. Elia | Tmp | 595.00 | 550 |
| Assergi | Tmp | 992.00 | 590 |
| Scanno | Tmp | 1045.00 | 700 |
| Sulmona | Tmp | 372.00 | 810 |
| Barisciano | Tmp | 978.00 | 920 |
| Chieti | Tmp | 278.00 | 1060 |
| Pescara | Tmp | 2.00 | 1160 |
| Pescara a Santa Teresa | Hydro | 4.50 | 6140 |
| Months | 1936–2013 | ||||||
|---|---|---|---|---|---|---|---|
| Tmin | Tmax | Tday | STDTday | Sk | Kr | Cv (%) | |
| January | 0.40 | 6.93 | 3.66 | 1.70 | 0.19 | 0.54 | 46.51 |
| February | 0.73 | 8.17 | 4.45 | 1.70 | 0.19 | 0.53 | 38.08 |
| March | 3.16 | 11.39 | 7.27 | 1.68 | 0.15 | 1.13 | 23.06 |
| April | 6.14 | 15.04 | 10.59 | 1.72 | 0.18 | 1.27 | 16.26 |
| May | 10.07 | 19.78 | 14.92 | 1.73 | 0.22 | 1.30 | 11.60 |
| June | 13.52 | 24.15 | 18.83 | 1.84 | 0.15 | 1.22 | 9.78 |
| July | 15.84 | 27.51 | 21.67 | 1.71 | 0.16 | 1.37 | 7.88 |
| August | 15.92 | 27.56 | 21.74 | 1.64 | 0.07 | 1.51 | 7.55 |
| September | 12.94 | 23.16 | 18.05 | 1.71 | 0.05 | 0.97 | 9.45 |
| October | 9.11 | 17.65 | 13.38 | 1.75 | 0.11 | 0.75 | 13.04 |
| November | 5.12 | 12.13 | 8.62 | 1.82 | 0.23 | 0.61 | 21.13 |
| December | 1.76 | 7.93 | 4.85 | 1.87 | 0.21 | 0.78 | 38.54 |
| Months | 1936–2013 | 1936–2013 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| PCP | STD | Sk | Kr | Cv (%) | RR | STD | Sk | Kr | Cv (%) | |
| January | 70.94 | 12.20 | 1.31 | 5.17 | 17.20 | 55.04 | 14.91 | 0.82 | 3.73 | 27.09 |
| February | 63.34 | 7.67 | 1.40 | 4.24 | 12.11 | 57.14 | 15.50 | 0.50 | 2.91 | 27.12 |
| March | 61.68 | 10.96 | 1.24 | 5.16 | 17.78 | 58.20 | 15.21 | 0.25 | 2.45 | 26.13 |
| April | 67.34 | 12.46 | 0.61 | 3.11 | 18.51 | 58.77 | 16.81 | 0.80 | 3.30 | 28.60 |
| May | 57.15 | 8.10 | 1.25 | 2.79 | 14.17 | 48.94 | 13.34 | 1.03 | 3.55 | 27.26 |
| June | 47.61 | 7.17 | −0.07 | 1.02 | 15.07 | 41.20 | 11.60 | 1.58 | 6.72 | 28.15 |
| July | 34.70 | 4.90 | −0.77 | 2.19 | 14.12 | 35.88 | 7.68 | 1.33 | 6.89 | 21.40 |
| August | 39.20 | 8.13 | 0.14 | 1.38 | 20.73 | 34.92 | 7.76 | −0.71 | 8.72 | 22.23 |
| September | 61.77 | 10.35 | 0.06 | 1.28 | 16.75 | 39.43 | 8.11 | 0.91 | 3.91 | 20.57 |
| October | 78.91 | 11.92 | 1.08 | 4.77 | 15.11 | 43.51 | 10.44 | 1.45 | 6.98 | 24.00 |
| November | 97.67 | 9.55 | 0.96 | 2.53 | 9.78 | 49.94 | 12.75 | 0.75 | 3.36 | 25.54 |
| December | 92.59 | 13.12 | 1.32 | 4.75 | 14.17 | 55.90 | 15.66 | 1.23 | 5.80 | 28.01 |
| Time Period | MK Test | SSE Test | |||||||
|---|---|---|---|---|---|---|---|---|---|
| TMP | PCP | RR | TMP | PCP | RR | ||||
| Z | Sig. | Z | Sig. | Z | Sig. | bsen | bsen | bsen | |
| 1936–2013 | 6.15 | ** | −2.47 | * | −2.29 | * | 0.037 | −1.81 | −0.29 |
| Spring | 6.06 | ** | −1.34 | + | −2.72 | ** | 0.038 | −0.42 | −0.35 |
| Summer | 5.56 | ** | −0.6 | + | −2.35 | * | 0.038 | −0.16 | −0.18 |
| Autumn | 5.52 | ** | −2.55 | * | −3.52 | ** | 0.031 | −0.68 | −0.28 |
| Winter | 5.82 | ** | −1.20 | + | −3.21 | ** | 0.034 | −0.38 | −0.41 |
| Time Period | TMP vs. PCP | TMP vs. RR | PCP vs. RR | |||
|---|---|---|---|---|---|---|
| rs | Sig. | rs | Sig. | rs | Sig. | |
| 1936–2013 | −0.40 | ** | −0.62 | ** | 0.46 | ** |
| Spring | −0.31 | ** | −0.56 | ** | 0.47 | ** |
| Summer | −0.42 | ** | −0.53 | * | 0.21 | ** |
| Autumn | −0.28 | * | −0.45 | ** | 0.40 | ** |
| Winter | −0.29 | ** | −0.61 | ** | 0.52 | ** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tariq, M.; Aruffo, E.; Chiacchiaretta, P.; Di Carlo, P. Hydro-Climatic Trends in Central Italy: A Case Study from the Aterno-Pescara River Watershed. Sustainability 2025, 17, 493. https://doi.org/10.3390/su17020493
Tariq M, Aruffo E, Chiacchiaretta P, Di Carlo P. Hydro-Climatic Trends in Central Italy: A Case Study from the Aterno-Pescara River Watershed. Sustainability. 2025; 17(2):493. https://doi.org/10.3390/su17020493
Chicago/Turabian StyleTariq, Mohsin, Eleonora Aruffo, Piero Chiacchiaretta, and Piero Di Carlo. 2025. "Hydro-Climatic Trends in Central Italy: A Case Study from the Aterno-Pescara River Watershed" Sustainability 17, no. 2: 493. https://doi.org/10.3390/su17020493
APA StyleTariq, M., Aruffo, E., Chiacchiaretta, P., & Di Carlo, P. (2025). Hydro-Climatic Trends in Central Italy: A Case Study from the Aterno-Pescara River Watershed. Sustainability, 17(2), 493. https://doi.org/10.3390/su17020493








