Towards Sustainable Rockfall Protection: An Interaction Matrix Method for Assessing Flexible Barrier Siting Adaptability
Abstract
1. Introduction
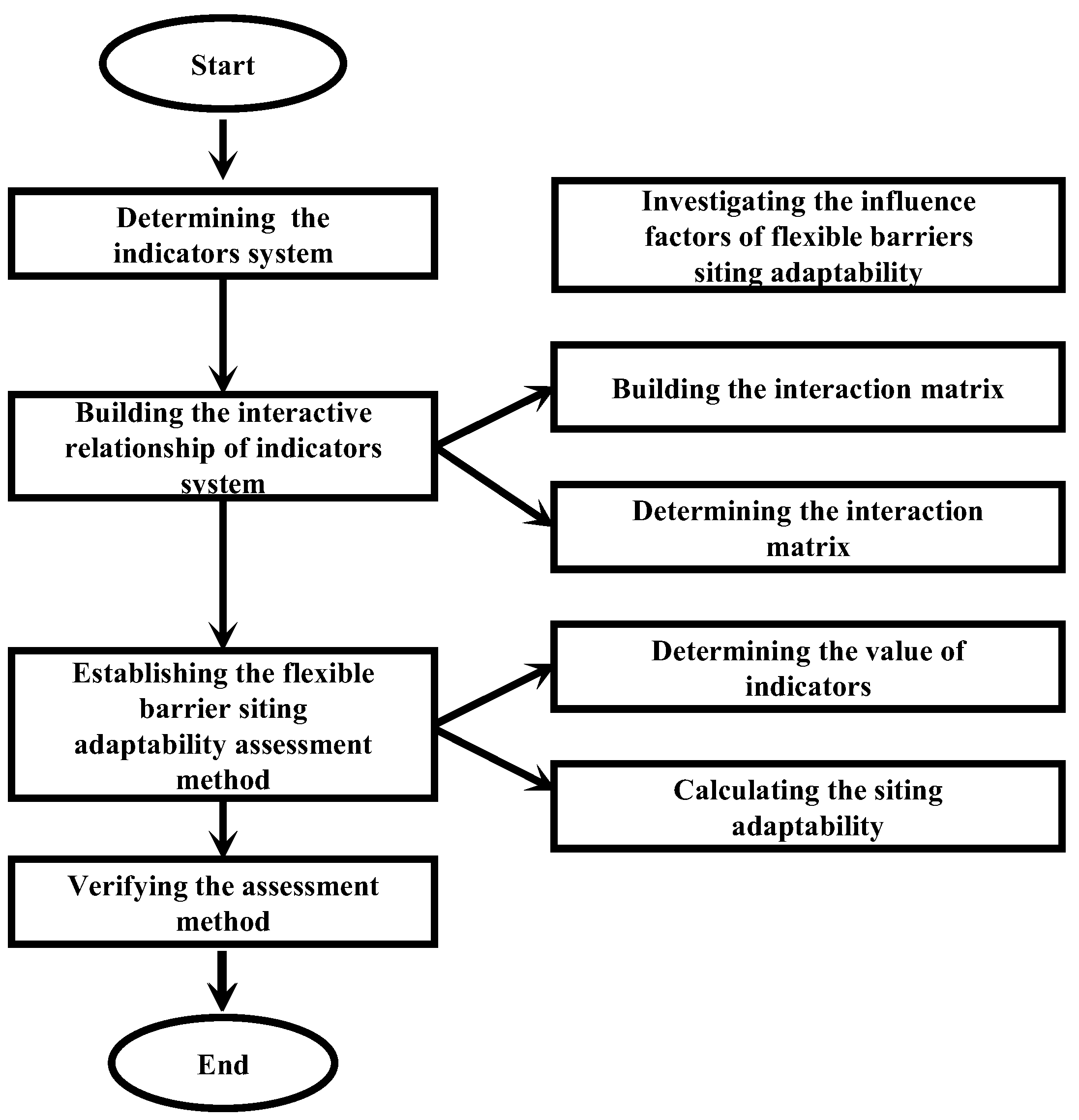
2. Materials and Methods
2.1. Overview
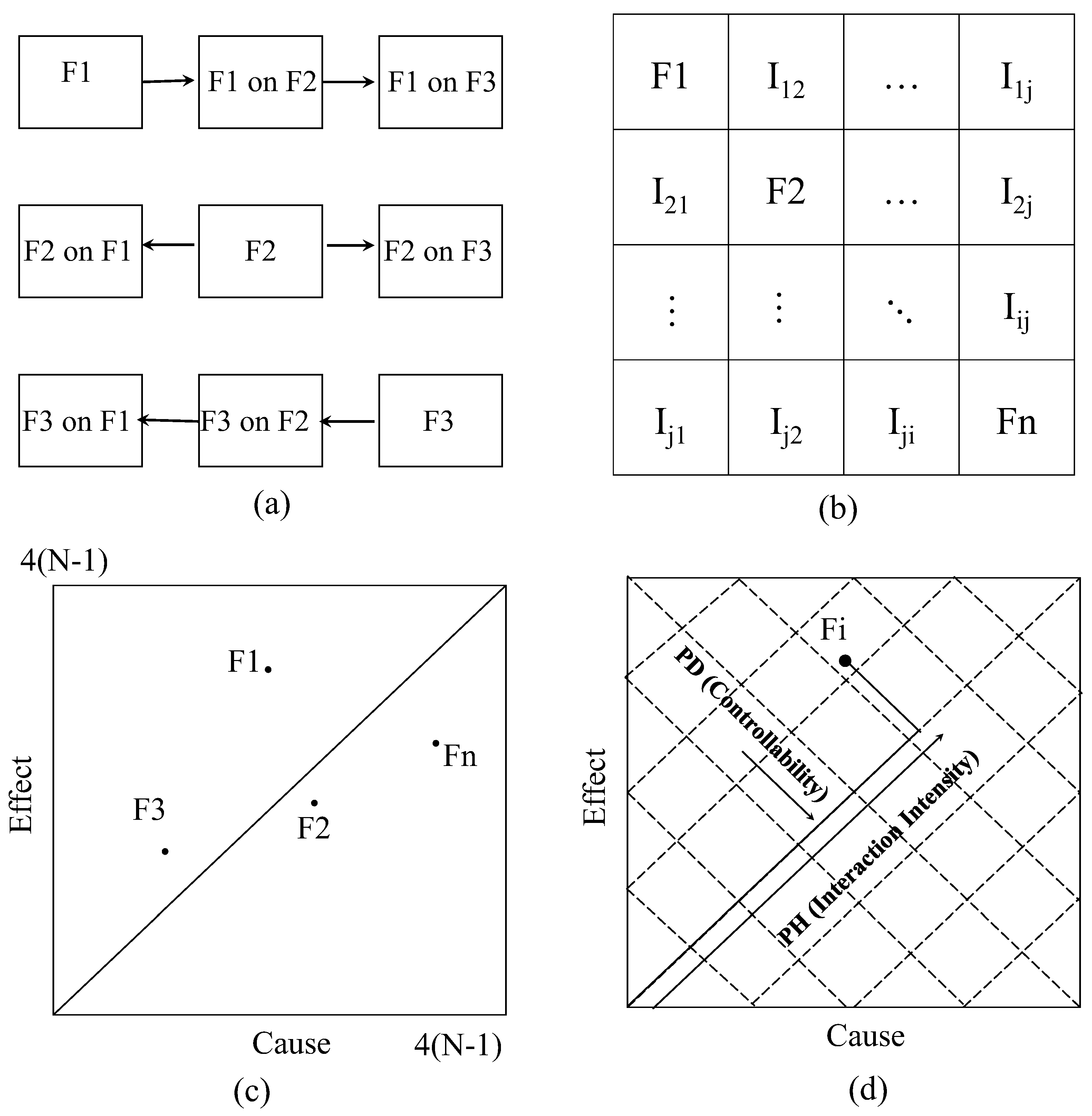
2.2. Details of the Interaction Matrix
3. Establishing the Flexible Barrier Siting Adaptability Assessment System
3.1. Selecting the Evaluation Indicators
3.2. Building the Interaction Relationship of Evaluation Indicators
Building the Interaction Matrix
- (1)
- Ensuring that if factor A strongly influences factor B, the reverse interaction (B on A) was evaluated independently and assigned a logically consistent value.
- (2)
- Checking that the assigned intensity aligned with the defined criteria (e.g., value of 4 was reserved only for direct, deterministic relationships).
- (3)
- Comparing the relative strengths of different interactions to maintain a consistent scale across the matrix.
- (1)
- No Interaction (0 points)
- (2)
- Minor Interaction (1 point)
- (3)
- Moderate Interaction (2 points)
- (4)
- Significant Interaction (3 points)
- (5)
- Strong Interaction (4 points)
3.3. Calculating the Flexible Barrier Siting Adaptability
4. Case Study
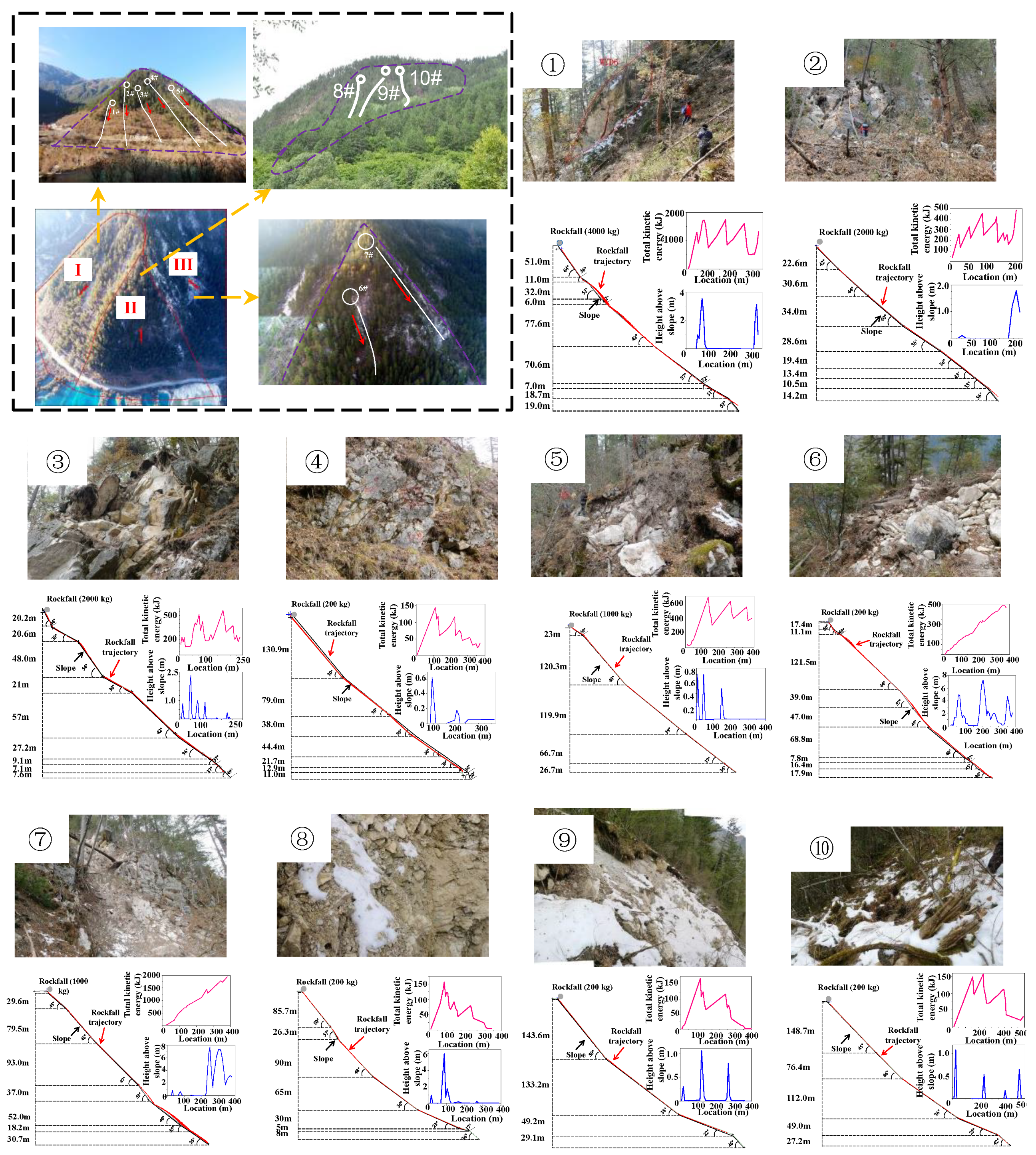
4.1. Study Area
4.2. Assessing the Flexible Barrier Siting Adaptability
4.3. Results and Analysis
4.4. Impact of Variations in Slope Angle on Rocks' Bouncing Behavior
5. Discussion and Conclusions
- (1)
- This study developed a novel sustainability-oriented assessment framework for flexible barrier siting. The ten key factors and their interactions, quantified through the interaction matrix, provide a holistic view that encompasses not only engineering performance but also implicit environmental and constructability (economic) concerns.
- (2)
- It was found that variations in slope angle significantly affect rockfall bounce height; specifically, as the gentle slope angle increases (in steep-to-gentle transitions), the minimum angle difference required to induce bouncing motion decreases.
- (3)
- Most significantly, the proposed method itself embodies a sustainable approach. Its simplicity and low computational requirements make it a rapid, low-energy, and accessible tool for engineers, particularly in the critical planning and feasibility stages. This promotes resource-efficient design by ensuring that barriers are correctly sited from the outset, thereby extending service life, reducing maintenance needs, and avoiding the substantial embodied carbon costs associated with failed or over-designed structures.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ge, Z.; Liu, H. Effects of three-directional seismic wave on dynamic response and failure behavior of high-steep rock slide. Appl. Sci. 2022, 12, 20. [Google Scholar] [CrossRef]
- Margreth, S.; Roth, A. Interaction of flexible rockfall barriers with avalanches and snow pressure. Cold Reg. Sci. Technol. 2008, 51, 168–177. [Google Scholar] [CrossRef][Green Version]
- Tian, Y.; Luo, L.; Yu, Z.; Xu, H.; Ni, F. Noncontact vision-based impact force reconstruction and spatial-temporal deflection tracking of a flexible barrier system under rockfall impact. Comput. Geotech. 2023, 153, 105070. [Google Scholar] [CrossRef]
- Xia, C.; Zhang, Z.; Liu, C.; Zhang, H.; Tian, S. Study on numerical model and dynamic response of ring net in flexible rockfall barriers. Sustainability 2022, 14, 4406. [Google Scholar] [CrossRef]
- Brighenti, R.; Segalini, A.; Ferrero, A.M. Debris flow hazard mitigation: A simplified analytical model for the design of flexible barriers. Comput. Geotech. 2013, 54, 1–15. [Google Scholar] [CrossRef]
- Peila, D.; Peilizza, S.; Sassudelli, F. Evaluation of behaviour of rockfall restraining nets by full scale tests. Rock Mech. Rock Eng. 1998, 31, 1–24. [Google Scholar] [CrossRef]
- Tan, D.; Yin, J.; Feng, W.; Qin, J.m.; Zhu, Z. New simple method for measuring impact force on a flexible barrier from rockfall and debris flow based on large-scale flume tests. Eng. Geol. 2020, 279, 105881. [Google Scholar] [CrossRef]
- Zhao, L.; He, J.; Yu, Z.; Liu, Y.; Zhou, Z.; Chan, S. Coupled numerical simulation of a flexible barrier impacted by debris flow with boulders in front. Landslides 2020, 17, 2723–2736. [Google Scholar] [CrossRef]
- Volkwien, A.; Wendeler, C.; Guasti, G. Design of Flexible Debris Flow Barriers. Ital. J. Eng. Geol. Environ. 2011, 1093–1100. [Google Scholar] [CrossRef]
- Liu, C.; Liang, L. A coupled SPH–DEM–FEM approach for modeling of debris flow impacts on flexible barriers. Arab. J. Geosci. 2022, 15, 10. [Google Scholar] [CrossRef]
- Li, X.; Zhao, J. A unified CFD-DEM approach for modeling of debris flow impacts on flexible barriers. Int. J. Num. Anal. Met. 2018, 42, 1643–1670. [Google Scholar] [CrossRef]
- Leonardi, A.; Wittel, K.; Mendoza, M.; Vetter, R.; Hermann, H. Particle–fluid–structure interaction for debris flow impact on flexible barriers. Comp.-Aided. Civ. Inf. 2016, 31, 323–333. [Google Scholar] [CrossRef]
- Geobrugg. Report on Testing SL–150 a Protection System Against Shallow Landslides; Test report No. 10–17; Geobrugg AG: Hong Kong, China, 2011. [Google Scholar]
- Cheung, A.; Yiu, J.; Lam, H.; Sze, E. Advanced numerical analysis of landslide debris mobility and barrier interaction. HKIE Trans. 2018, 25, 76–89. [Google Scholar] [CrossRef]
- Wu, H.; Wu, Y.; Ma, L. Design of passive flexible barrier against rockfall impact with 8 000 kJ energy level. Explos. Shock. Waves 2025, 45, 1–8. (In Chinese) [Google Scholar] [CrossRef]
- Pimpinella, F.; Marchelli, M.; De, V. A weight-based efficiency measure for energy dissipating devices for flexible rockfall barriers. Int. J. Prot. Struct. 2024, 151, 10. [Google Scholar] [CrossRef]
- Taboni, B.; Umili, G.; Malbertelli, L.; Tagliaferri, L. Surveying existing rockfall flexible barriers: A combined method for gathering data, managing information and prioritizing maintenance. J. Mt. Sci. 2024, 21, 4112–4130. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, L.; Yu, Z.; Qi, X.; Zhang, Y. A case study on the energy capacity of a flexible rockfall barrier in resisting landslide debris. Forests 2022, 13, 1384. [Google Scholar] [CrossRef]
- Castanon, L.; Blanco, E.; Castro, D.; Ballester, F. Energy Dissipating Devices in Falling Rock Protection Barriers. Rock Mech. Rock Eng. 2016, 50, 603–619. [Google Scholar] [CrossRef]
- Escallón, J.; Wendeler, C.; Chatzi, E.; Bartelt, P. Parameter identification of rockfall protection barrier components through an inverse formulation. Eng. Struct. 2014, 77, 1–16. [Google Scholar] [CrossRef]
- Xu, H.; Gentilini, C.; Yu, Z.; Qi, X.; Zhao, S. An energy allocation based design approach for flexible rockfall protection barriers. Eng. Struct. 2018, 173, 831–852. [Google Scholar] [CrossRef]
- Berger, S.; Hofmann, R.; Preh, A. Impacts on embankments, rigid and flexible barriers against rockslides: Model experiments vs. DEM simulations. Rock Mech. Rock Eng. 2024, 57, 2793–2808. [Google Scholar] [CrossRef]
- Sha, S.; Dyson, A.; Kefayati, G.; Tolooiya, A. An equivalent stiffness flexible barrier for protection against boulders transported by debris flow. Int. J. Civ. Eng. 2024, 22, 705–722. [Google Scholar] [CrossRef]
- Huo, M.; Zhou, J.; Zhao, J.; Zhou, H.; Li, J.; Liu, X. The normal impact stiffness of a debris-flow flexible barrier. Sci. Rep. 2023, 13, 3969. [Google Scholar] [CrossRef] [PubMed]
- Spadari, M.; Giacomini, A.; Buzzi, O.; Hambleton, J. Prediction of the Bullet Effect for Rockfall Barriers: A Scaling Approach. Rock Mech. Rock Eng. 2012, 45, 131–144. [Google Scholar] [CrossRef]
- Yu, Z.; Zhao, L.; Liu, Y.; Zhao, S.; Xu, H.; Chan, S. Studies on flexible rockfall barriers for failure modes, mechanisms and design strategies: A case study of Western China. Landslides 2019, 16, 347–362. [Google Scholar] [CrossRef]
- Albaba, A.; Lambert, S.; Kneib, F.; Chareyre, B.; Nicot, F. DEM modeling of a flexible barrier impacted by a dry granular flow. Rock Mech. Rock Eng. 2017, 50, 3029–3048. [Google Scholar] [CrossRef]
- Guo, L.; He, S.; Yu, Z.; Jin, Y. Damage assessment of ring nets in flexible barriers subjected to consecutive rockfall impacts. Can. Geotech. J. 2025, 62, 1–21. [Google Scholar] [CrossRef]
- He, Y.; Nie, L.; Lv, Y.; Wang, H.; Jiang, S.; Zhao, X. The study of rockfall trajectory and kinetic energy distribution based on numerical simulations. Nat. Hazards 2021, 106, 213–233. [Google Scholar] [CrossRef]
- Koo, R.; Kwan, J.; Lam, C.; Ng, C.; Yiu, J.; Choi, C.; Ng, A.; Ho, K.; Pun, W. Dynamic response of flexible rockfall barriers under different loading geometries. Landslides 2017, 14, 905–916. [Google Scholar] [CrossRef]
- Qi, X.; Zhao, L.; Meng, Q. Prediction method for the tension force of support ropes in flexible rockfall barriers based on full-scale experiments and numerical analysis. Sci. Rep. 2024, 141, 9969. [Google Scholar] [CrossRef]
- Yu, Z.; Luo, L.; Liu, C.; Guo, L.; Qi, X.; Zhao, L. Dynamic response of flexible rockfall barriers with different block shapes. Land-slides 2021, 18, 2621–2637. [Google Scholar] [CrossRef]
- Xiong, H.; Hao, M.; Zhao, D.; Gan, X.; Yin, Z.; Chen, X. A fully resolved SPH-DEM for simulation of debris flows with arbitrary particle shapes impacting flexible barriers. Acta Geotech. 2025, 203, 1403–1430. [Google Scholar] [CrossRef]
- Paronuzzi, P. Rockfall-induced block propagation on a soil slope, northern Italy. Environ. Geol. 2009, 58, 1451–1466. [Google Scholar] [CrossRef]
- Gili, J.; Ruiz, R.; Matas, G.; Moya, J.; Prades, A.; Corominas, J.; Lantada, N.; Núñez-Andrés, M.A.; Buill, F.; Puig, C.; et al. Rockfalls: Analysis of the block fragmentation through field experiments. Landslides 2022, 193, 1009–1029. [Google Scholar] [CrossRef]
- Xu, H.; Cheng, Y.; Zhao, L.; Liu, Y.; Yu, Z. Experimental study on bearing capacity reduction of the steel wire-rings in flexible barriers due to corrosion. Constr. Build. Mater. 2024, 439, 137341. [Google Scholar] [CrossRef]
- Saroglou, H.; Berger, F.; Bourrier, F.; Asteriou, P.; Tsiambao, G.; Tsagkas, D. Effect of forest presence on rockfall trajectory, an example from Greece. In Engineering Geology for Society and Territory-Volume 2; Springer International Publishing: Cham, Switzerland, 2015; pp. 1451–1466. [Google Scholar]
- Boulaud, R.; Douthe, C. A comparative assessment of ASM4 rockfall barrier modelling. Eng. Struct. 2022, 251 Pt B, 113512. [Google Scholar] [CrossRef]
- Hambleton, J.; Buzzi, O.; Giacomini, A.; Spadari, M.; Sloan, S. Perforation of flexible rockfall barriers by normal block impact. Rock Mech. Rock Eng. 2013, 46, 515–526. [Google Scholar] [CrossRef]
- Liu, C.; Yu, Z.; Zhao, S. Quantifying the impact of a debris avalanche against a flexible barrier by coupled DEM-FEM analyses. Landslides 2020, 17, 33–47. [Google Scholar] [CrossRef]
- Zhao, L.; Yu, Z.; Liu, Y.; He, J.; Chan, S.; Zhao, S. Numerical simulation of responses of flexible rockfall barriers under impact loading at different positions. J. Constr. Steel Res. 2020, 167, 105953. [Google Scholar] [CrossRef]
- Kong, Y.; Li, X.; Zhao, J. Quantifying the transition of impact mechanisms of geophysical flows against flexible barrier. Eng. Geol. 2021, 289, 106188. [Google Scholar] [CrossRef]
- Lambert, S.; Toe, D.; Mentani, A.; Bourrier, F. A Meta-Model-Based Procedure for Quantifying the On-Site Efficiency of Rockfall Barriers. Rock Mech. Rock Eng. 2021, 54, 487–500. [Google Scholar] [CrossRef]
- Zhang, Y.; Ci, H.; Yang, H.; Wang, R.; Yan, Z. Rainfall-Induced Geological Hazard Susceptibility Assessment in the Henan Section of the Yellow River Basin: Multi-Model Approaches Supporting Disaster Mitigation and Sustainable Development. Sustainability 2025, 17, 4348. [Google Scholar] [CrossRef]
- Tsou, C.-Y.; Yamagishi, H.; Kawakami, R.; Tsai, M.-F.; Miwa, T. Investigating the Relationship between Plant Species Composi-tion and Topography in the Tomeyama Landslide: Implications for Environmental Education and Sustainable Management in the Happo-Shirakami Geopark, Japan. Sustainability 2023, 15, 16572. [Google Scholar] [CrossRef]
- Zheng, X.; Zhao, Q.; Peng, S.; Wu, L.; Dou, Y.; Chen, K. Analysis of Failure Mechanism of Medium-Steep Bedding Rock Slopes under Seismic Action. Sustainability 2024, 16, 7729. [Google Scholar] [CrossRef]
- Kikuchi, T.; Nishiyama, S.; Hatano, T. Unveiling Deep-Seated Gravitational Slope Deformations via Aerial Photo Interpretation and Statistical Analysis in an Accretionary Complex in Japan. Sustainability 2024, 16, 5328. [Google Scholar] [CrossRef]
- Sotiriadis, D.; Klimis, N.; Dokas, I.M. Updated Predictive Models for Permanent Seismic Displacement of Slopes for Greece and Their Effect on Probabilistic Landslide Hazard Assessment. Sustainability 2024, 16, 2240. [Google Scholar] [CrossRef]
- Kumar, P.; Kumara, A.; Reddy, U. Making quality agglomerates using lean iron ores for sustainable iron-making. J. Saf. Sustain. 2024, 1, 257–263. [Google Scholar] [CrossRef]
- Shen, Z.; Liu, Y.; Xu, J.; Zhou, Y.; Yang, L.; Fang, Y.; Yuan, B. Self-powered smart fire-alarm materials: Advances and perspective. J. Saf. Sustain. 2025, 2, 81–94. [Google Scholar] [CrossRef]
- EOTA. Falling Rock Protection Kits. 2018. Available online: https://www.eota.eu/download?file=/2014/14-34-0059/ead%20for%20ojeu/ead%20340059-00-0106_ojeu2018.pdf (accessed on 27 August 2025).
- Volkwein, A.; Gerber, W.; Klette, J.; Spescha, G. Review of approval of flexible rockfall protection systems according to ETAG 027. Geosciences 2019, 9, 49. [Google Scholar] [CrossRef]
- Hudson, J. Rock mechanics principles in engineering practice. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1989, 26, 289. [Google Scholar] [CrossRef]
- Hudson, J.; Arnold, P.; Tamai, A. Rock Engineering Mechanisms Information Technology (REMIT): Part 1—The basic method: Part II—Illustrative case examples: Hudson, J A; Arnold, P N; Tamai, A Proc 7th ISRM International Congress on Rock Mechanics, Aachen, 16–20 September 1991V2, P1113–1119. Publ Rotterdam: A A Balkema, 1991. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1993, 30, 302. [Google Scholar] [CrossRef]
- Hudson, J.; Harrisin, J. A new approach to studying complete rock engineering problems. Q. J. Eng. Geol. 1992, 25, 93–105. [Google Scholar] [CrossRef]
- Rocscience Inc. ROCFALL-Computer Program for Risk Analysis of Falling Rocks on Steep Slopes, Version 4.0; Rocscience Inc.: Toronto, ON, Canada, 2022. [Google Scholar]
- Huang, C.; Hu, Q.; Cai, Q.; Li, M. Post-earthquake spatiotemporal evolution characteristics of typical landslide sources in the Jiuzhaigou meizoseismal area. Bull. Eng. Geol. Environ. 2024, 83, 1–19. [Google Scholar] [CrossRef]
- Yang, Z.; Du, G.; Zhang, Y.; Xu, C.; Yu, P.; Shao, W.; Mai, X. Seismic landslide hazard assessment using improved seismic motion parameters of the 2017 Ms 7.0 Jiuzhaigou earthquake, Tibetan Plateau. Front. Earth Sci. 2024, 12, 1–16. [Google Scholar] [CrossRef]
- Ling, S.; Sun, C.; Li, X.; Ren, Y.; Xu, J.; Huang, T. Correction to: Characterizing the distribution pattern and geologic and geo-morphic controls on earthquake-triggered landslide occurrence during the 2017 Ms 7.0 Jiuzhaigou earthquake, Sichuan, China. Landslides 2021, 18, 1293. [Google Scholar] [CrossRef]
- Stevens, W. Rockfall: A Tool for Probabilistic Analysis, Design of Remedial Measures and Prediction of Rockfalls. Master’s Thesis, Department of Civil Engineering, University of Toronto, Toronto, ON, Canada, 1998. [Google Scholar]
- Wang, X.; Zhang, L.; Wang, S.; Agliardi, F.; Frattini, P.; Crosta, G.B.; Yang, Z. Field investigation and rockfall hazard zonation at the Shijing Mountains Sutra caves cultural heritage (China). Environ. Earth Sci. 2012, 66, 1897–1908. [Google Scholar] [CrossRef]



| Protection Level | Height Requirement | Setback Distance |
|---|---|---|
Ed: design energy level; Er: protection energy level; : safety factor. | hi: design intercept height; hp: rockfall height (95% reliability) from analyzing the rockfall trajectory; f: 0.5 times average rockfall size. | da: maximum flexible barrier elongation; dp: distance to protected area; : safety factor. |
| Element | ID | Descriptions |
|---|---|---|
| Kinetic energy of falling rocks | P1 | When kinetic energy exceeds 10,000 kJ, flexible barriers are not suitable for use. |
| Rockfall size | P2 | Oversized rockfalls with excessive kinetic energy cannot be effectively intercepted. |
| Dispersion of perilous rock masses | P3 | Passive flexible barriers are preferred when rockfalls are numerous and dispersed. |
| Rockfall event frequency | P4 | Evaluate the expected number of rockfall events per unit time |
| Slope roughness | P5 | Smooth rock faces and loose deposits affect frictional energy dissipation. |
| Slope height | P6 | Increased slope height results in greater kinetic energy, potentially exceeding barrier capacity. |
| Slope gradient variation (rockfall bounce height) | P7 | Flexible barriers are unsuitable if rockfall bounce heights are excessive. |
| Vegetation coverage | P8 | Vegetation dissipates kinetic energy. Tall trees can intercept falling rocks. |
| Hydrological conditions | P9 | Acidic groundwater corrodes anchor bolts; surface runoff can undermine slope toe stability. |
| Seismic activity | P10 | Flexible protection measures are preferred in high-seismic zones due to their ability to undergo large deformations and dissipate energy through ductile behavior, unlike rigid structures that are prone to brittle failure under seismic inertial forces. Their integrated connections allow for better coordination during ground motions, maintaining system integrity. |
| Construction conditions | P11 | Flexible barriers are suitable for difficult-to-access sites (accessibility—transport/installation difficulty, and maintenance conditions—ease of inspection/component replacement). |
| Environmental and social sustainability | P12 | Evaluate the environmental and social impacts of flexible barriers throughout their entire life cycle, encompassing aspects such as material recyclability, ecological disturbance caused by construction, visual landscape impact, and long-term maintenance requirements. |
| Iij | Ii1 | Ii2 | Ii3 | Ii4 | Ii5 | Ii6 | Ii7 | Ii8 | Ii9 | Ii10 | Ii,11 | Ii,12 | Ci | Ci + Ej | Ci − Ej | ki(%) | PH | PD |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I1j | P1 | - | - | - | 3 | - | - | - | - | - | 2 | 2 | 7 | 23 | −9 | 10.27 | 16.27 | −6.36 |
| I2j | 4 | P2 | 2 | - | - | - | - | - | - | - | - | 1 | 7 | 15 | −1 | 6.70 | 10.61 | −0.71 |
| I3j | 2 | 2 | P3 | 2 | - | - | - | - | - | - | 1 | 2 | 9 | 22 | −4 | 9.82 | 15.56 | −2.83 |
| I4j | - | - | - | P4 | - | - | - | 1 | - | - | 3 | 2 | 6 | 17 | −5 | 7.59 | 12.02 | −3.54 |
| I5j | 3 | 2 | 2 | 1 | P5 | - | 1 | 3 | - | - | 1 | - | 13 | 21 | 5 | 9.38 | 14.85 | 3.54 |
| I6j | 4 | - | 3 | 1 | 1 | P6 | 2 | 1 | - | - | 1 | - | 13 | 14 | 12 | 6.25 | 9.90 | 8.49 |
| I7j | 3 | 1 | 1 | - | 1 | - | P7 | 2 | - | - | - | - | 8 | 14 | 2 | 6.25 | 9.90 | 1.41 |
| I8j | - | 2 | 2 | - | 2 | - | 3 | P8 | 1 | - | 2 | - | 12 | 24 | 0 | 10.71 | 16.97 | 0.00 |
| I9j | - | - | - | 3 | - | - | - | 1 | P9 | - | 1 | 2 | 7 | 12 | 2 | 5.36 | 8.49 | 1.41 |
| I10j | - | 1 | 3 | 4 | 1 | 1 | - | - | - | P10 | 4 | 2 | 16 | 16 | 16 | 7.14 | 11.32 | 11.32 |
| I11,j | - | - | - | - | - | - | - | 1 | 1 | - | P11 | 2 | 4 | 23 | −15 | 10.27 | 16.27 | −10.61 |
| I12,j | - | - | - | - | - | - | - | 3 | 3 | - | 4 | P12 | 10 | 23 | −3 | 10.27 | 16.27 | −2.12 |
| Ej | 16 | 8 | 13 | 11 | 8 | 1 | 6 | 12 | 5 | 0 | 19 | 13 |
| Factor | P1 | P2 | P3 | P4 | P5 | P6 | |
| Level | |||||||
| Ⅰ (Suitable) | <2000 kJ * | <4 m3 * | concentrated | 1 event/year | rock | <30 m * | |
| Ⅱ (Unsuitable) | ≥2000 kJ * | ≥4 m3 * | dispersed | 1 event/year | soil | ≥30 m * | |
| Factor | P7 | P8 | P9 | P10 | P11 | P12 | |
| Level | |||||||
| Ⅰ (Suitable) | 8 m | tree | acidic | seismic activity | difficult | recyclable | |
| Ⅱ (Unsuitable) | 8 m | none/shrub | neutral | no seismic activity | simple | non-recyclable | |
| Site ID | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | P10 | P11 | P12 | W |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 69.2 |
| 2 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 72.33 |
| 3 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 75.45 |
| 4 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 76.34 |
| 5 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 83.04 |
| 6 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 70.54 |
| 7 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 54.02 |
| 8 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 54.02 |
| 9 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 60.27 |
| 10 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 73.22 |
| upper slope angle (°) | 35 | 40 | 45 | 50 | 55 | 60 | 65 |
| lower slope angle (°) | 48 | 50 | 55 | 58 | 63 | 66 | 70 |
| angle difference (°) | 13 | 10 | 10 | 8 | 7 | 6 | 5 |
| upper slope angle (°) | 55 | 60 | 65 | 70 | 75 | 80 | 85 |
| lower slope angle (°) | 16 | 25 | 36 | 50 | 62 | 71 | 77 |
| angle difference (°) | 39 | 35 | 29 | 20 | 13 | 9 | 8 |
| Site ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Case | |||||||||||
| maximum kinetic energy (kJ) | 1741 | 487 | 570 | 145 | 689 | 490 | 1792 | 156 | 172 | 157 | |
| maximum bounce height (m) | 3.56 | 1.78 | 2.31 | 0.63 | 0.70 | 7.31 | 7.73 | 6.01 | 1.04 | 1.08 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, Z. Towards Sustainable Rockfall Protection: An Interaction Matrix Method for Assessing Flexible Barrier Siting Adaptability. Sustainability 2025, 17, 8675. https://doi.org/10.3390/su17198675
Ge Z. Towards Sustainable Rockfall Protection: An Interaction Matrix Method for Assessing Flexible Barrier Siting Adaptability. Sustainability. 2025; 17(19):8675. https://doi.org/10.3390/su17198675
Chicago/Turabian StyleGe, Ziwei. 2025. "Towards Sustainable Rockfall Protection: An Interaction Matrix Method for Assessing Flexible Barrier Siting Adaptability" Sustainability 17, no. 19: 8675. https://doi.org/10.3390/su17198675
APA StyleGe, Z. (2025). Towards Sustainable Rockfall Protection: An Interaction Matrix Method for Assessing Flexible Barrier Siting Adaptability. Sustainability, 17(19), 8675. https://doi.org/10.3390/su17198675






