Impact of Filter Inductance on Transient Synchronization Stability of Grid-Connected Systems with Grid-Following Converters Under Voltage Sag Faults
Abstract
1. Introduction
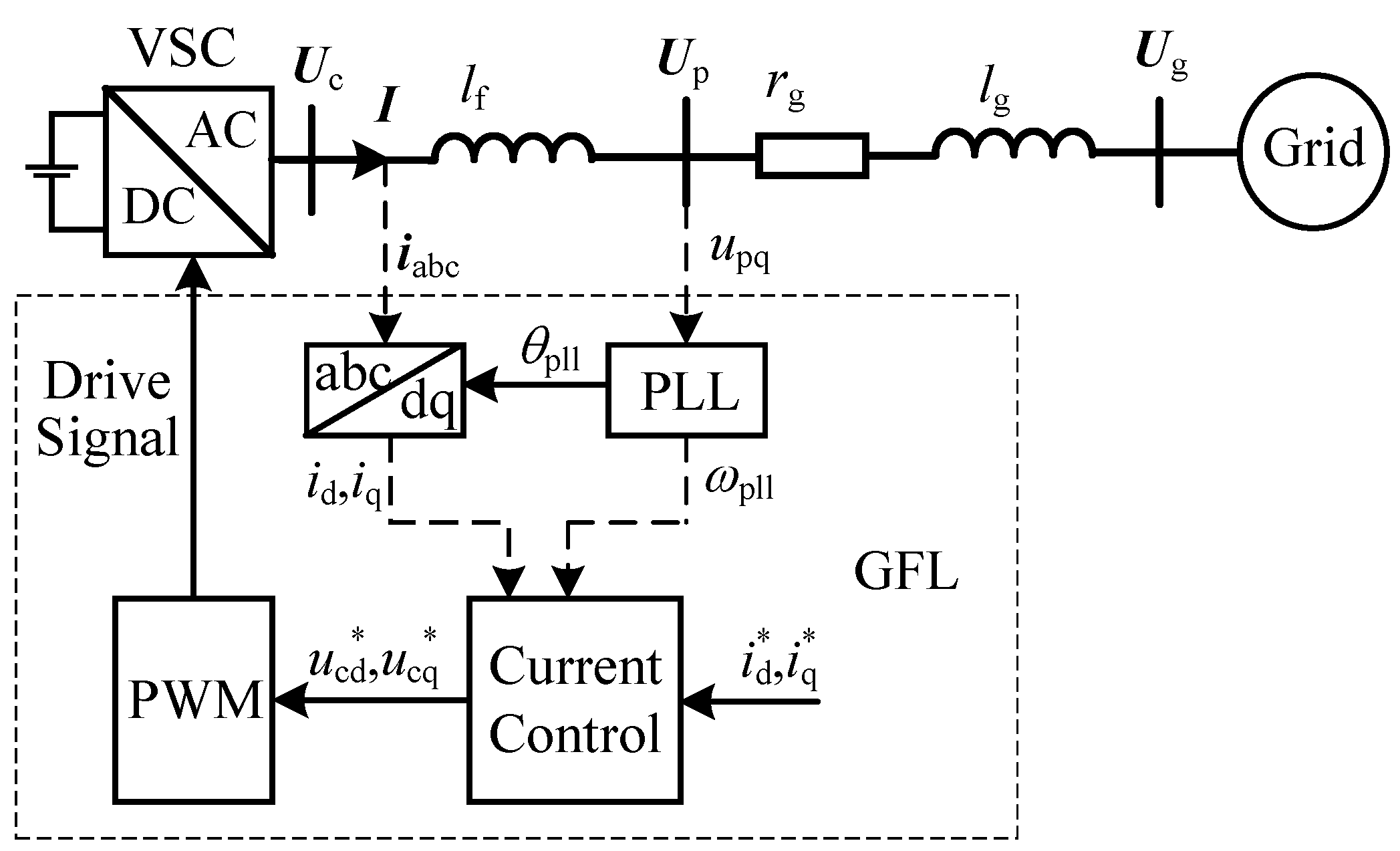
2. Necessity of Considering Filter Inductance in Synchronous Stability Analysis
3. Analysis of Filter Inductance Impact on Transient Stability
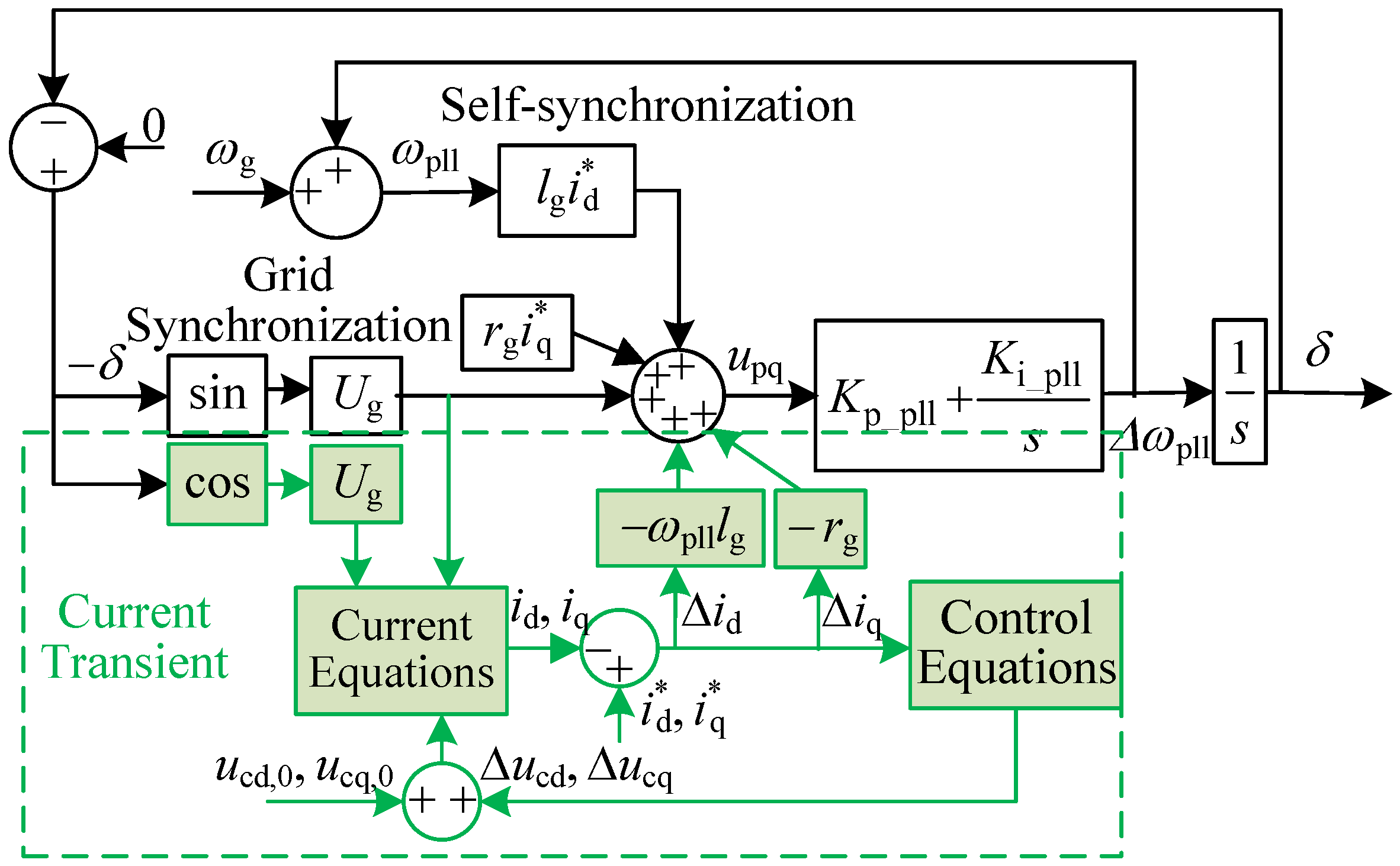
3.1. Modeling of Filter Inductance Impact on Synchronization Stability
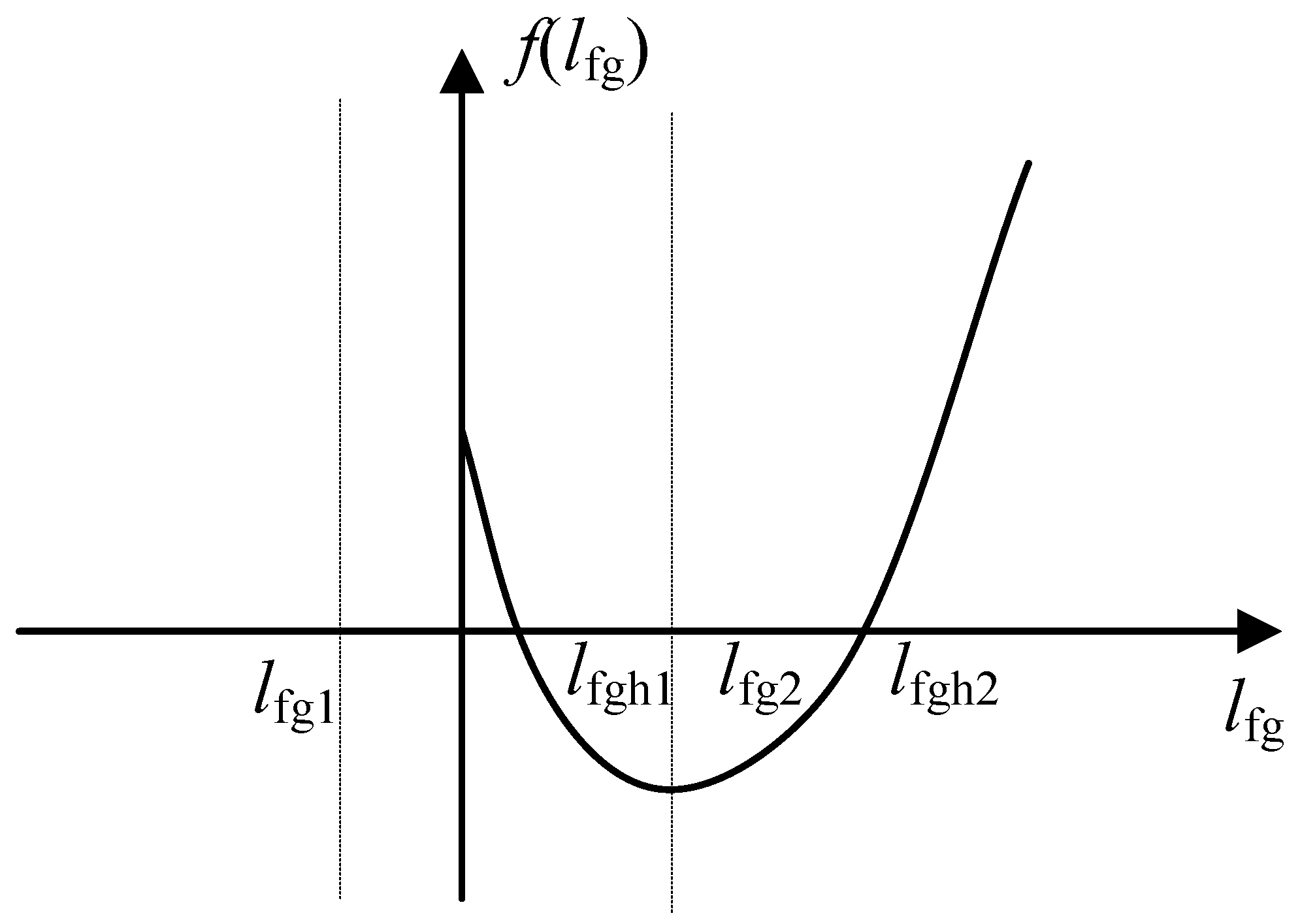
3.2. Impact of Filter Inductance on Synchronization Stability in Different Cases
3.2.1. Case of
3.2.2. Case of
3.2.3. Case of
4. Simulations and Validations
4.1. Impact of Filter Inductance on Transient Stability
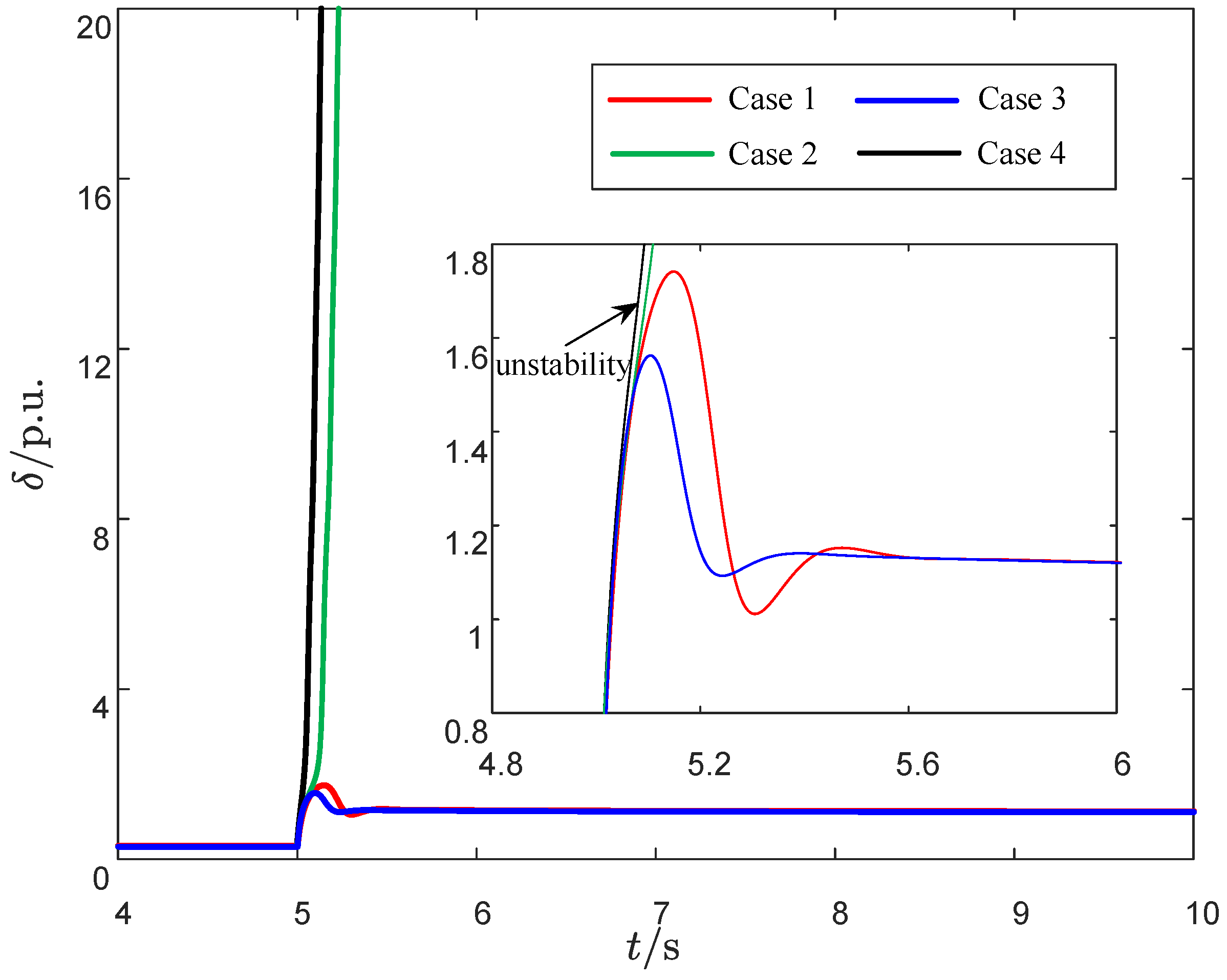
4.2. Impact of Control Parameters on Transient Stability
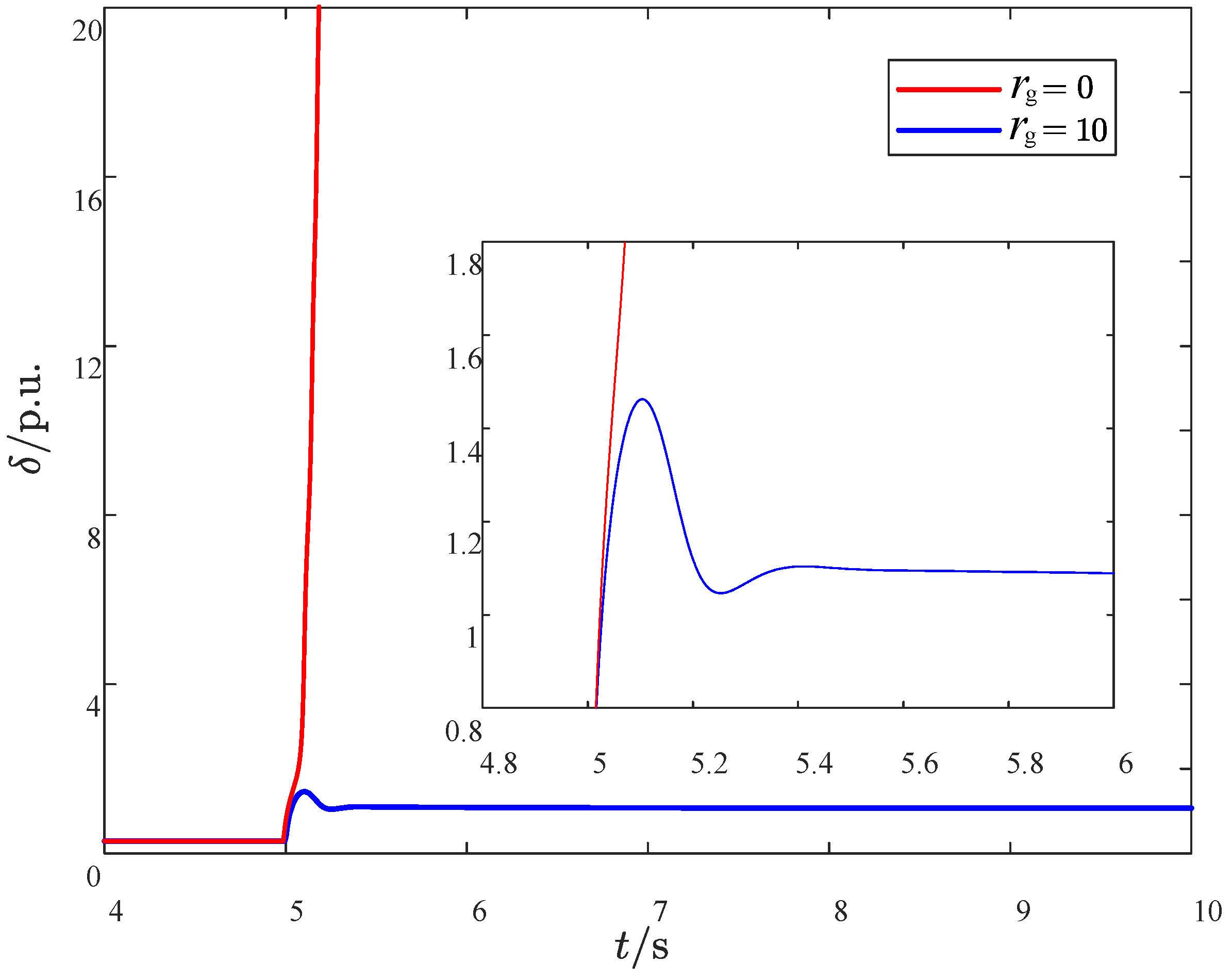
4.3. Impact of Grid Resistance on Transient Stability
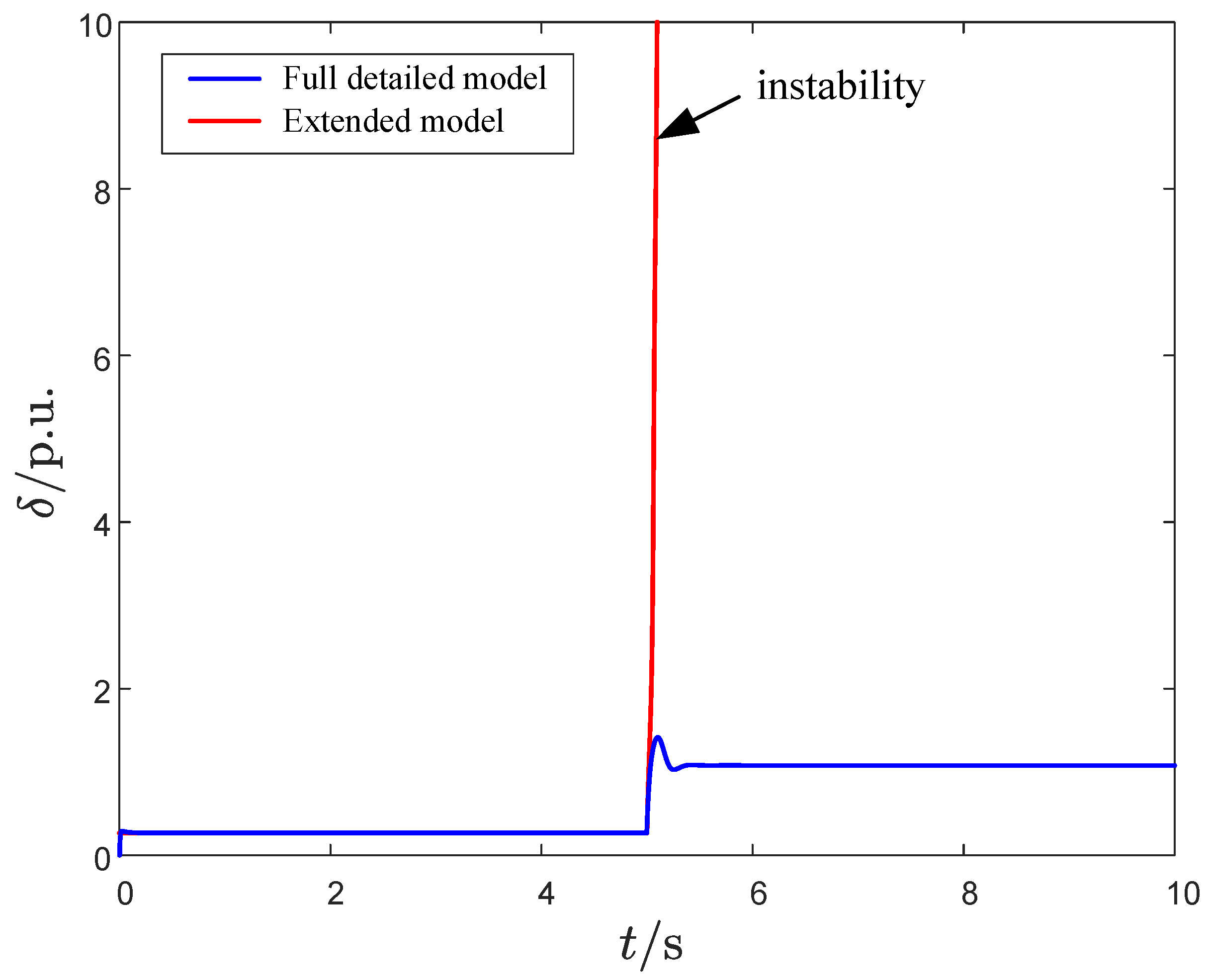
4.4. Comparative Study Between the Conventional Full-Detail Model and the Model Considering Current Transients
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GFL | Grid-following |
| PLL | Phase-locked loop |
| PCC | Point of common coupling |
| VSC | Voltage source converter |
| PWM | Pulse width modulation |
| KCL | Kirchhoff’s current law |
Appendix A. Mathematical Formulas
Appendix A.1. Supplementary Mathematical Derivation Steps
Appendix A.2. Supplementary Mathematical Derivation Steps When α 2 >0
Appendix A.3. Supplementary Mathematical Derivation Steps When α 2 <0
References
- Wang, G.; Fu, L.; Hu, Q.; Liu, C.; Ma, Y. Transient Synchronization Stability of Grid-Forming Converter During Grid Fault Considering Transient Switched Operation Mode. IEEE Trans. Sustain. Energy 2023, 14, 1504–1515. [Google Scholar] [CrossRef]
- Li, B.; Wang, Y. Enhanced Low-Voltage Ride-Through Scheme for Grid-Forming Converters Considering Current Limitation and Transient Stability Simultaneously. Sustainability 2025, 17, 1428. [Google Scholar] [CrossRef]
- Li, Y.; Xia, Y.; Ni, Y.; Peng, Y.; Feng, Q. Transient Stability Analysis for Grid-Forming VSCs Based on Nonlinear Decoupling Method. Sustainability 2023, 15, 11981. [Google Scholar] [CrossRef]
- Wang, Z.; Guo, L.; Li, X.; Wang, Z.; Zang, X.; Zhu, J.; Zhou, X.; Wang, C. Transient Synchronization Stability of Grid-Tied Multi-VSCs System Considering Nonlinear Damping and Transient Interactions. IEEE Trans. Power Electron. 2024, 39, 16775–16791. [Google Scholar] [CrossRef]
- Rigo, P.D.; Siluk, J.C.M.; Lacerda, D.P.; Spellmeier, J.P. Competitive Business Model of Photovoltaic Solar Energy Installers in Brazil. Renew. Energy 2022, 181, 39–50. [Google Scholar] [CrossRef]
- Liu, C.C.; Yang, J.; Tse, C.K.; Huang, M. Transient Synchronization Stability of Grid-Following Converters Considering Nonideal Current Loop. IEEE Trans. Power Electron. 2023, 38, 13757–13769. [Google Scholar] [CrossRef]
- Ali, Z.; Christofides, N.; Hadjidemetriou, L.; Kyriakides, E.; Yang, Y.; Blaabjerg, F. Three-Phase Phase-Locked Loop Synchronization Algorithms for Grid-Connected Renewable Energy Systems: A Review. Renew. Sustain. Energy Rev. 2018, 90, 434–452. [Google Scholar] [CrossRef]
- Zarei, S.F.; Mokhtari, H.; Ghasemi, M.A.; Peyghami, S.; Davari, P.; Blaabjerg, F. Control of Grid-Following Inverters Under Unbalanced Grid Conditions. IEEE Trans. Energy Convers. 2020, 35, 184–192. [Google Scholar] [CrossRef]
- Elkhidir, L.; Khan, K.; Al-Muhaini, M.; Khalid, M. Enhancing Transient Response and Voltage Stability of Renewable Integrated Microgrids. Sustainability 2022, 14, 3710. [Google Scholar] [CrossRef]
- Chen, J.; Liu, M.; Geng, H.; O’Donnell, T.; Milano, F. Impact of PLL Frequency Limiter on Synchronization Stability of Grid Feeding Converter. IEEE Trans. Power Syst. 2022, 37, 2487–2490. [Google Scholar] [CrossRef]
- Yang, J.; Tse, C.K.; Huang, M.; Liu, D. Bifurcations of Grid-Following Rectifiers and Routes to Voltage Instability in Weak AC Grids. IEEE Trans. Power Syst. 2023, 38, 1702–1713. [Google Scholar] [CrossRef]
- Yang, S.; Ma, R.; Wen, J.; Cheng, S. Equivalent circuit model of grid-forming-converter based power grids: Visualizing control loop interactions on synchronization stability. Int. J. Electr. Power Energy Syst. 2025, 168, 110692. [Google Scholar] [CrossRef]
- Wang, Y.; Ruan, L.; Yang, M.; Xiao, X.; Chen, S.; Gomis-Bellmunt, O. Control interaction analysis of hybrid system with grid-following and grid-forming inverters based on admittance decomposition. Int. J. Electr. Power Energy Syst. 2024, 162, 110267. [Google Scholar] [CrossRef]
- He, Y.; Xiang, W.; Meng, P.; Wen, J. Investigation on grid-following and grid-forming control schemes of cascaded hybrid converter for wind power integrated with weak grids. Int. J. Electr. Power Energy Syst. 2024, 155, 109524. [Google Scholar] [CrossRef]
- Hatziargyriou, N.; Milanovic, J.; Rahmann, C.; Ajjarapu, V.; Canizares, C.; Erlich, I.; Hill, D.; Hiskens, I.; Kamwa, I.; Pal, B.; et al. Definition and Classification of Power System Stability—Revisited & Extended. IEEE Trans. Power Syst. 2021, 36, 3271–3281. [Google Scholar] [CrossRef]
- Chen, J.; Liu, M.; O’Donnell, T.; Milano, F. Impact of Current Transients on the Synchronization Stability Assessment of Grid-Feeding Converters. IEEE Trans. Power Syst. 2020, 35, 4131–4134. [Google Scholar] [CrossRef]
- Lin, X.; Peng, J.C.-H.; Macii, D.; Petri, D.; Yu, J.; Wen, H. Frequency-domain small-signal stability analysis methods for grid-following converters systems—An overview. Renew. Sustain. Energy Rev. 2025, 211, 115283. [Google Scholar] [CrossRef]
- Tian, X.; Zhang, Y.; Xu, Y.; Zheng, L.; Zhang, L.; Yuan, Z. Transient synchronous stability modeling and comparative analysis of grid-following and grid-forming new energy power sources. Electronics 2024, 13, 3308. [Google Scholar] [CrossRef]
- Agbemuko, A.J.; Domínguez-García, J.L.; Gomis-Bellmunt, O.; Harnefors, L. Passivity-Based Analysis and Performance Enhancement of a Vector Controlled VSC Connected to a Weak AC Grid. IEEE Trans. Power Deliv. 2021, 36, 156–167. [Google Scholar] [CrossRef]
- Tian, H.; Zhang, Z.; Liu, W.; Wu, C.; Wu, Y. Influence of Filter Inductance on Synchronization Stability of Grid-Connected Converter. In Proceedings of the 2023 International Conference on Power System Technology (PowerCon), Wuhan, China, 21–23 November 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Si, W.; Fang, J. Transient Stability Improvement of Grid-Forming Converters Through Voltage Amplitude Regulation and Reactive Power Injection. IEEE Trans. Power Electron. 2023, 38, 12116–12125. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, L.; Xu, X.; Li, D.; Liang, Z.; Ye, N. Transient Synchronization Stability in Grid-Following Converters: Mechanistic Insights and Technological Prospects—A Review. Energies 2025, 18, 1975. [Google Scholar] [CrossRef]
- Li, Y.; Fu, L.; Li, Q.; Wang, W.; Jia, Y.; Dong, Z.Y. Small-signal modelling and stability analysis of grid-following and grid-forming inverters dominated power system. Glob. Energy Interconnect. 2023, 6, 363–374. [Google Scholar] [CrossRef]

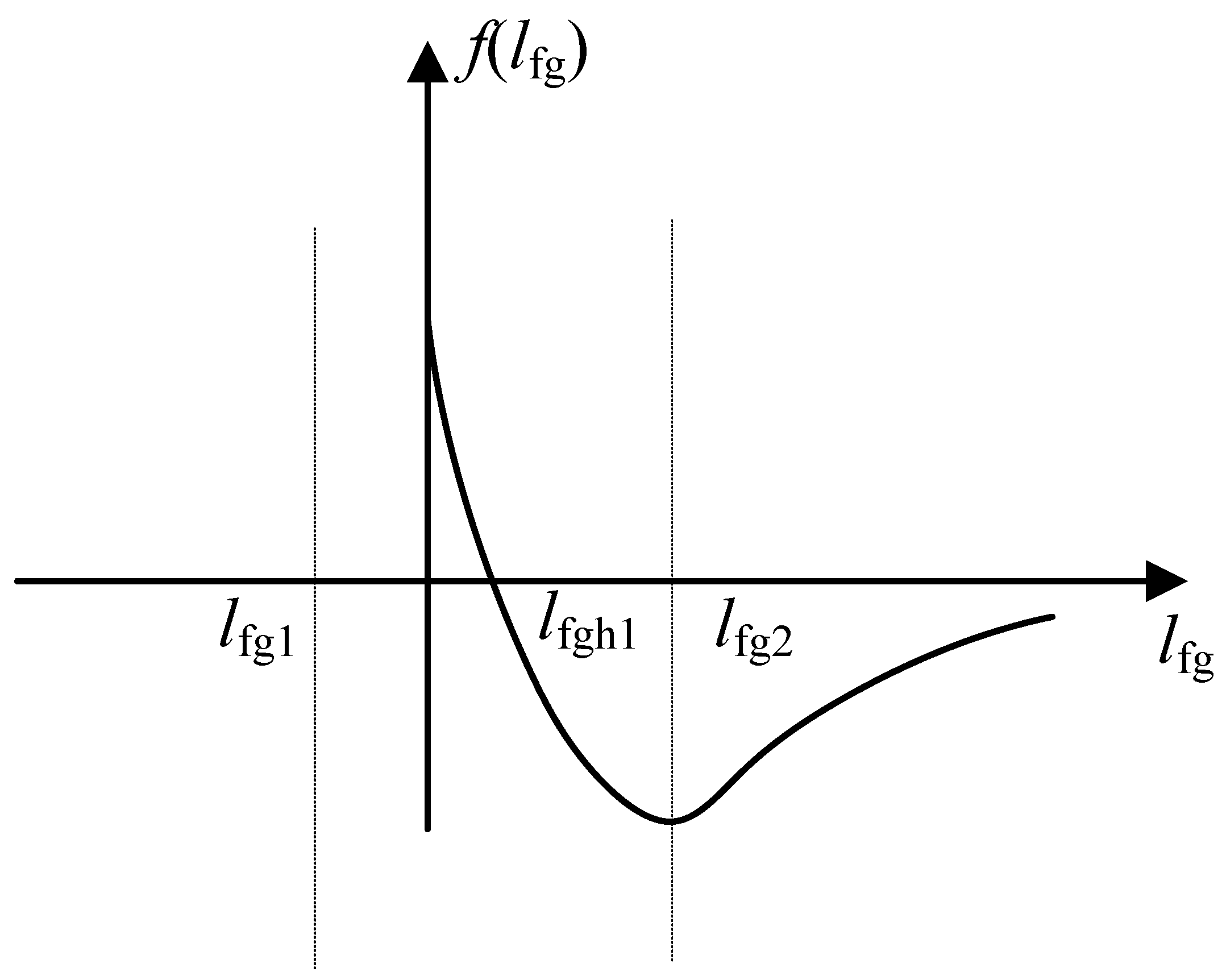
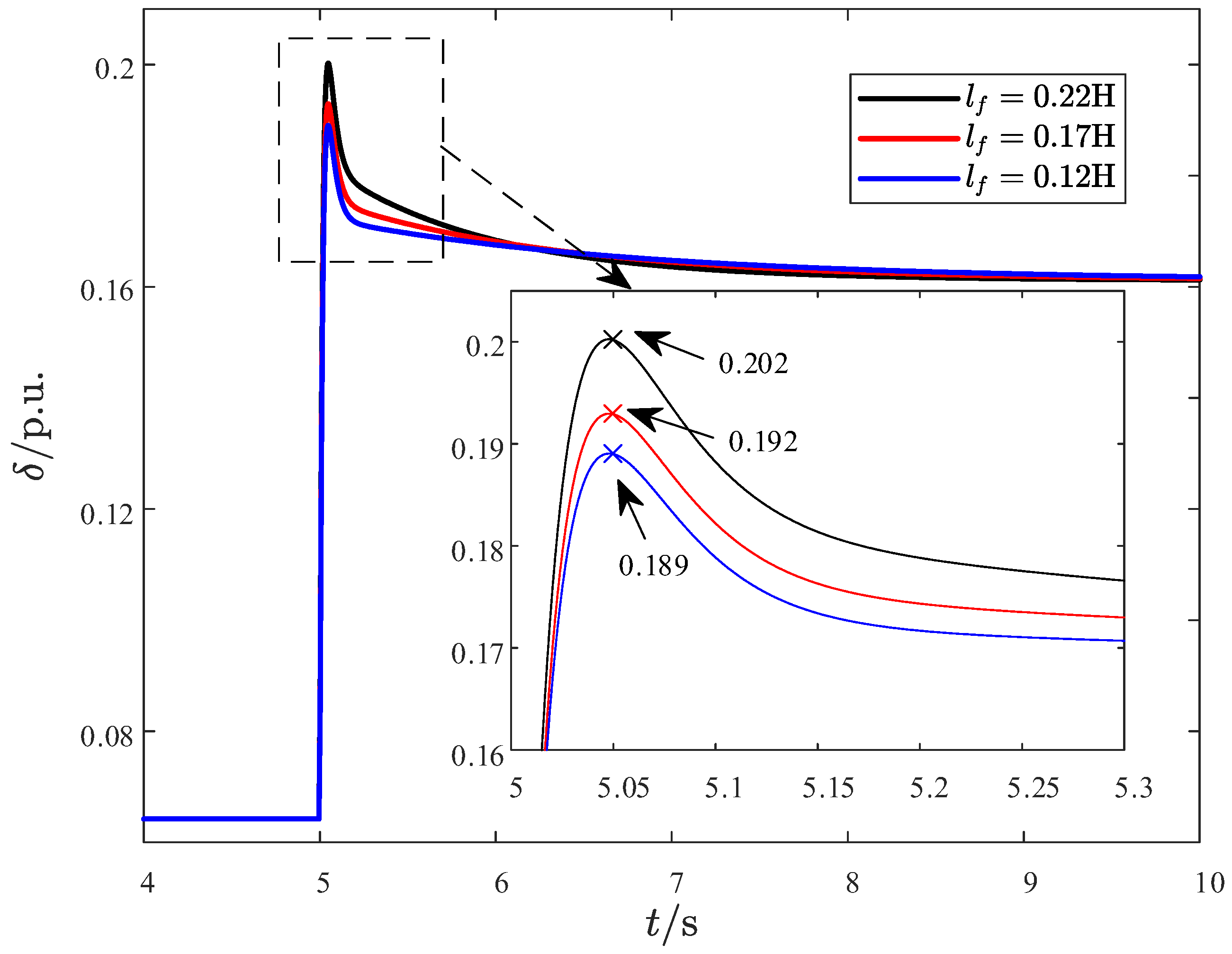
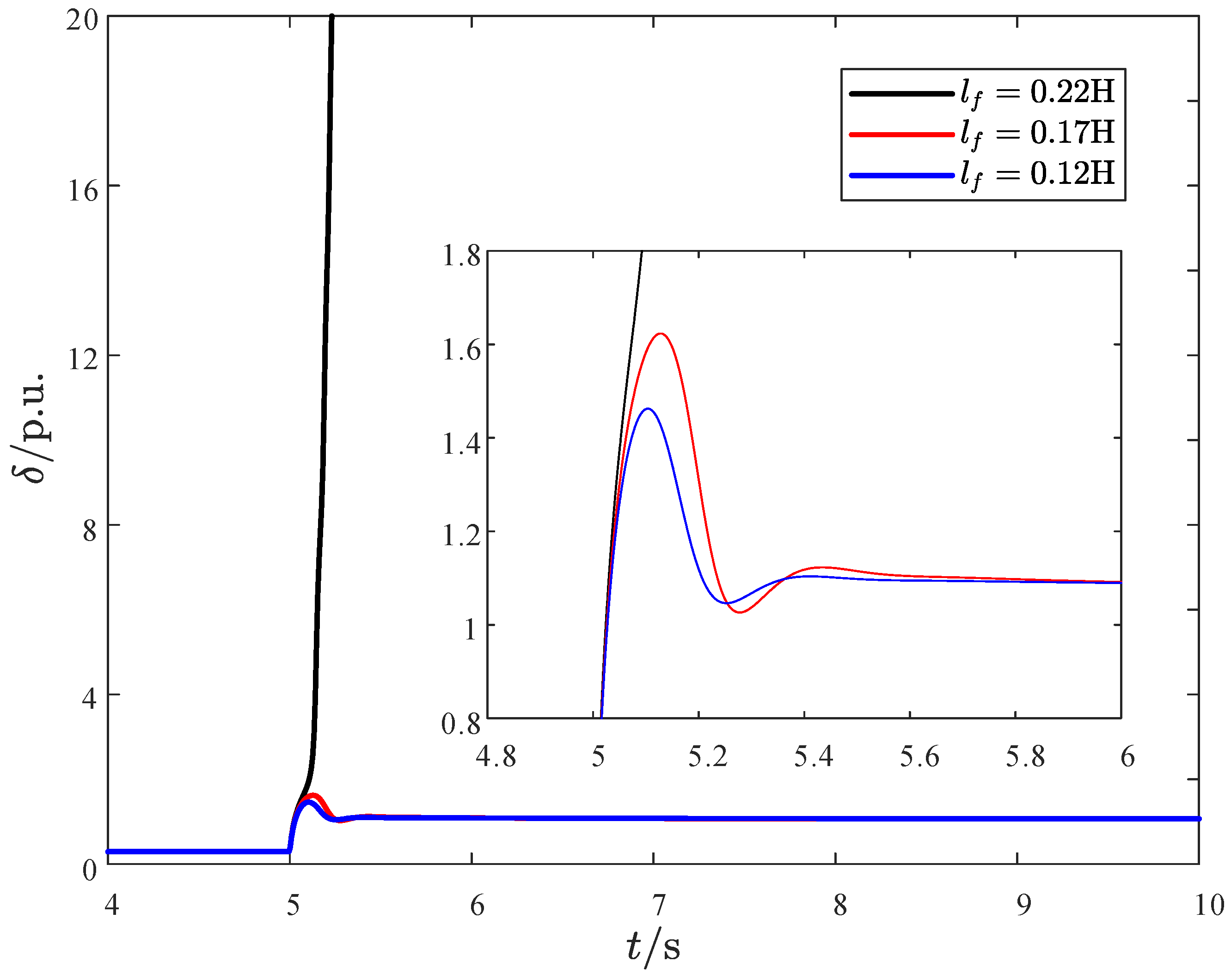

| Classification of Situations | Filter Inductor Variation | Transient Stability Variation |
|---|---|---|
| tan | ↓ | |
| tan | , ↓ | |
| , ↑ | ||
| , ↓ | ||
| tan | , ↑ | |
| , ↓ | ||
| , ↑ | ||
| tan | , ↑ | |
| , ↓ | ||
| , ↑ | ||
| , ↓ |
| Parameter | Actual Value | Per-Unit Value |
|---|---|---|
| Rated capacity /MW | 1 | - |
| Rated voltage /kV | 10 | - |
| Rated frequency /Hz | 50 | - |
| Line inductance /H | 0.1 | 0.3 |
| d-axis current command value /A | 81.65 | 1.00 |
| q-axis current command value /A | −40.82 | −0.50 |
| Current loop integral coefficient | 2433.00 | 4.87 |
| PLL proportional coefficient | 0.022 | 180.000 |
| PLL integral coefficient | 0.392 | 3200.000 |
| Simulation Example | |||||
|---|---|---|---|---|---|
| 0.0482 | 0.5737 | 0.1 | 0.2870 | 0.12 + 0.1 | |
| 0.17 + 0.1 | |||||
| 0.22 + 0.1 | |||||
| 0.0130 | 0.1300 | 0.0841 | 0.1162 | 0.22 + 0.1 | |
| 0.32 + 0.1 | |||||
| 0.42 + 0.1 |
| Voltage Drop | Sensitivity | ||
|---|---|---|---|
| 30 | 0.3 | 0.22 | 22.1744 |
| 30 | 0.3 | 0.17 | 21.5134 |
| 30 | 0.3 | 0.12 | 21.1826 |
| 10 | 0.3 | 0.22 | 42.8528 |
| 10 | 0.3 | 0.17 | 32.7740 |
| 10 | 0.3 | 0.12 | 29.8500 |
| 10 | 0.33 | 0.22 | 46.7631 |
| 10 | 0.33 | 0.17 | 35.0317 |
| 10 | 0.33 | 0.12 | 32.0640 |
| Case | Stability | |||
|---|---|---|---|---|
| 1 | 0.17 H | 0.022 | 0.392 | stable |
| 2 | 0.22 H | 0.022 | 0.392 | unstable |
| 3 | 0.17 H | 0.03 | 0.5 | stable |
| 4 | 0.22 H | 0.03 | 0.5 | unstable |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mou, Q.; Yuan, J.; Wu, Y.; Sun, S.; Xing, J. Impact of Filter Inductance on Transient Synchronization Stability of Grid-Connected Systems with Grid-Following Converters Under Voltage Sag Faults. Sustainability 2025, 17, 8634. https://doi.org/10.3390/su17198634
Mou Q, Yuan J, Wu Y, Sun S, Xing J. Impact of Filter Inductance on Transient Synchronization Stability of Grid-Connected Systems with Grid-Following Converters Under Voltage Sag Faults. Sustainability. 2025; 17(19):8634. https://doi.org/10.3390/su17198634
Chicago/Turabian StyleMou, Qianying, Jingxiu Yuan, Yuhan Wu, Shumin Sun, and Jiawei Xing. 2025. "Impact of Filter Inductance on Transient Synchronization Stability of Grid-Connected Systems with Grid-Following Converters Under Voltage Sag Faults" Sustainability 17, no. 19: 8634. https://doi.org/10.3390/su17198634
APA StyleMou, Q., Yuan, J., Wu, Y., Sun, S., & Xing, J. (2025). Impact of Filter Inductance on Transient Synchronization Stability of Grid-Connected Systems with Grid-Following Converters Under Voltage Sag Faults. Sustainability, 17(19), 8634. https://doi.org/10.3390/su17198634





