Abstract
Groundwater level (GWL) prediction in arid regions faces two fundamental challenges in conventional numerical modeling: (i) irreducible parameter uncertainty, which systematically reduces predictive accuracy; (ii) oversimplification of nonlinear process interactions, which leads to error propagation. Although machine learning (ML) methods demonstrate strong nonlinear mapping capabilities, their standalone applications often encounter prediction bias and face the accuracy–generalization trade-off. This study proposes a hybrid TCN–Transformer–LSTM (TTL) model designed to address three key challenges in groundwater prediction: high-frequency fluctuations, medium-range dependencies, and long-term memory effects. The TTL framework integrates TCN layers for short-term features, Transformer blocks to model cross-temporal dependencies, and LSTM to preserve long-term memory, with residual connections facilitating hierarchical feature fusion. The results indicate that (1) at the monthly scale, TTL reduced RMSE by 20.7% (p < 0.01) and increased R2 by 0.15 compared with the Groundwater Modeling System (GMS); (2) during abrupt hydrological events, TTL achieved superior performance (R2 = 0.96–0.98, MAE < 0.6 m); (3) PCA revealed site-specific responses, corroborating the adaptability and interpretability of TTL; (4) Grad-CAM analysis demonstrated that the model captures physically interpretable attention mechanisms—particularly evapotranspiration and rainfall—thereby providing clear cause–effect explanations and enhancing transparency beyond black-box models. This transferable framework supports groundwater forecasting, risk warning, and practical deployment in arid regions, thereby contributing to sustainable water resource management.
1. Introduction
Groundwater is the planet’s most vital freshwater resource and serves as a critical buffer for agricultural irrigation, municipal supply, and ecological conservation in arid and semiarid regions [1,2]. Intensifying climate change and anthropogenic activities present dual challenges to groundwater systems: declining quantity and deteriorating quality. Aquifer degradation is accelerating due to over-extraction, reduced surface runoff, and agricultural as well as industrial contamination [3]. Consequently, developing groundwater prediction models with both high accuracy and strong generalizability is essential for effective water resource management, particularly in arid zones where prolonged water table decline critically threatens ecological security [4,5]. Globally, over-extraction in arid regions has led to persistent groundwater level declines, jeopardizing water security and ecosystem stability [6,7,8,9,10,11]. Conventional approaches such as MODFLOW [12] simulate groundwater flow based on governing equations and provide strong physical interpretability. However, these models demand high-quality inputs, complex parameter calibration, and substantial computational resources, thereby limiting their efficiency and applicability for long-term forecasting and large-scale, multi-site deployment [13,14,15].
Data-driven approaches have become central to groundwater level (GWL) for forecasting. These methods range from statistical techniques (e.g., ARIMA, SVR, and RF) and classic machine learning algorithms (e.g., GMDH, GA-ANN, and ELM) to deep neural networks (e.g., CNN, LSTM, and GRU), all of which demonstrate strong capabilities for modeling nonlinear dynamics (NLDs) [16,17,18,19,20,21]. To reduce model complexity and data dependency, a variety of AI and hybrid strategies have been proposed. For instance, ELM and its enhanced variants (e.g., ORELM) enable extremely fast training and often exhibit good generalization in aquifer-scale forecasting [22,23,24,25,26,27]. Stochastic and ensemble techniques (e.g., bootstrap and bagging) can provide high-accuracy predictions without full numerical simulation [28,29]. TCNs, which employ causal and dilated convolutions, effectively capturelocal features while modeling long-range temporal dependencies [30,31]. Deep learning models can extract predictive patterns from historical observations independently of explicit physical assumptions, achieving high accuracy even with limited datasets Recent advances further underscore their potential in hydrological and environmental forecasting [32,33,34]. Nevertheless, stability and generalizability in long-term forecasting remain major challenges. Hybrid and interdisciplinary frameworks have therefore gained momentum, integrating machine learning with physical modeling and data-driven optimization to improve both accuracy and robustness [35,36,37,38,39].
In summary, although a of data-driven and hybrid approaches have been employed for GWL forecasting, several critical limitations persist. Existing models frequently encounter difficulties in (i) concurrently capturing multiscale hydroclimatic signals, (ii) maintaining robustness under abrupt groundwater fluctuations, (iii) ensuring computational efficiency without compromising predictive accuracy. These challenges underscore the necessity of a compact yet powerful modeling framework that effectively balances predictive performance with model simplicity.
Therefore, this study proposes a hybrid TTL model for groundwater level prediction in an arid inland basin. In contrast to existing hybrids architectures such as TCN + LSTM or Transformer + LSTM, the TTL model explicitly separates multiscale feature extraction (TCN), long-range dependency modeling (Transformer), and temporal memory representation (LSTM) into dedicated sequential modules. This design forms a synergistic pipeline capable of capturing both local fluctuations and global trends while preserving long-term temporal dependencies. Hierarchical feature fusion is achieved through residual connections across modules, facilitating effective gradient propagation and feature reuse. Although residual connections are commonly employed in deep learning, their integration into a compact hybrid model for groundwater prediction under arid conditions represents a novel contribution.
Daily observations from wells KY4, WS5, and WS10 in the Kuitun River Basin (2019–2021) were employed for model validation. The proposed TTL model was compared against CNN-BiLSTM-Attention (CBA), CNN-GRU-Attention (CGA), and the Groundwater Modeling System (GMS), with performance evaluated in terms of predictive accuracy, robustness to abrupt groundwater fluctuations, and computational efficiency.
2. Materials and Methods
2.1. Description of the Study Area
The Kuitun River Basin (83.37–85.78° E, 43.50–45.07° N) lies at the ecotone between the northern Tianshan Mountains and the southwestern Junggar Basin, exhibiting characteristic inland arid-zone hydrology (Figure 1). Its boundaries are defined by the Turgu–Bayingou composite water system to the east, the Tuotuo River alluvial fan to the west, the Ili–Kix River divide to the south, and the Maiyir–Saiwaer tectonic belt to the north. Covering approximately 28,300 km2 with a ~360km main channel, the basin features a three-tiered terrace system [40,41], with elevations ranging from 205 m in the Junggar Basin lowlands to 4882 m in the Tianshan headwaters. A pronounced continental climate prevails, with a mean annual temperature ≈ 7 °C (January ≈ −16 °C; July ≈ 26 °C), a precipitation-to-evaporation ratio of ~1:11 (precipitation 168 ± 19 mm yr−1 versus evaporation 1815 ± 115 mm yr−1), and an aridity index exceeding 20 [42,43]. The Kuitun River network comprises the mainstem and principal tributaries (Gurtu River and Sikeshu River), with a total annual discharge of 1.256 × 109 m3, supplying ≈80.9% of basin’s water resources and forming a fan-shaped drainage pattern. The multilayered aquifer system consists of an upper Quaternary phreatic aquifer (<10 m depth) overlying a thick confined aquifer (>150 m thickness) with a potentiometric surface at ~20–70 m depth. These two units are separated by a continuous aquitard. This recharge–storage configuration, coupled with pronounced groundwater gradients in the Nanwa Depression, renders the basin an ideal site for studying groundwater dynamics and validating predictive models and sustainable extraction thresholds.
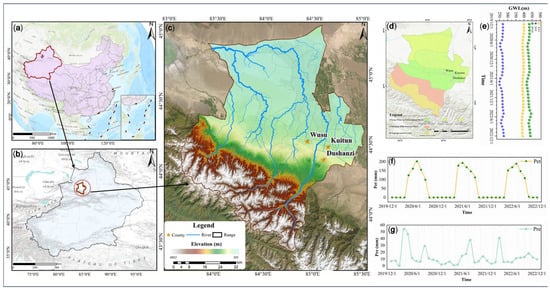
Figure 1.
Location map of the Study Area. (a) Location of the study area within China. (b) Position of the basin in Xinjiang Province. (c) Digital elevation model (DEM) and river network of the Kuitun River Basin. (d) Hydrogeological zoning map. (e) GWL observations from wells KY4, WS5, and WS10. (f) Daily potential evapotranspiration (Pet). (g) Daily precipitation (Pre).
2.2. Data Sources and Preprocessing
Daily GWL observations from representative monitoring wells (KY4, WS5, WS10) in the Kuitun River Basin were collated along with concurrent meteorological records for the study period (2019–2021).
(1) Well water levels: Daily water level measurements (2019–2021) were obtained from local hydrometric stations. The raw time series were visually inspected, and extreme values exceeding ±3σ were flagged and removed after confirmation.
(2) Meteorological data: Daily precipitation, evaporation, and mean air temperature data were acquired from the China Meteorological Administration (CMA; Station ID: XJ-QL-03; Latitude: 44.4333° N; Longitude: 84.6667° E; Altitude: 478.7 m). All timestamps were aligned to UTC before merging with well observations.
The TTL model was trained using four raw daily input variables: precipitation (mm), evaporation (mm), mean air temperature (°C), and antecedent groundwater levels (lagged GWLs, m). No engineered features (e.g., moving averages or cumulative indices) or external forcings were included. To ensure training stability, all continuous variables were normalized to the range [0,1] using min–max scaling. A summary of the input variables is provided in Table 1.

Table 1.
Summary of input variables used for model training.
(3) Preprocessing procedures:
(a) Missing value imputation: Short gaps were linearly interpolated within adjacent temporal windows, whereas longer or spatially isolated gaps were filled using spatially weighted averaging via inverse-distance weighting (IDW).
(b) Outlier handling: To mitigate the influence of extreme values, the water level time series was processed to fill short gaps via interpolation. Additionally, eight points (≈0.7% of the 1097 daily observations) were identified as outliers using the Grubbs test (α = 0.01) within a sliding-window framework, and cross-validated against Mann–Kendall trend checks and visual inspection. These points were removed prior to interpolation, ensuring a continuous and consistent dataset for subsequent analysis.
(c) Data standardization: Numerical predictors were standardized using Z-score normalization (μ = 0, σ = 1), while categorical variables (if present) were encoded using one-hot representation.
2.3. Groundwater Flow Model Construction
After geomorphological screening and data-completeness assessment, mountainous, desert, and uninhabited zones were excluded, resulting in an effective modeling domain of 14,894.98 km2 within the Kuitun River Basin. The domain was conceptualized as a three-dimensional, heterogeneous, anisotropic, and transient groundwater-flow system implemented using the Groundwater Modeling System (GMS). Spatial discretization employed uniform finite-difference grids comprising 250 rows × 291 columns × 5 layers (363,750 active cells,) with a horizontal resolution of 500 m × 500 m. The transient simulation encompassed 24 monthly stress periods from January 2019 to December 2020. Boundary conditions reflected topographic and structural controls, including structurally constrained inflow boundaries in the southern and northern sectors, outflow boundaries in the western sector, and recharge-controlled inflow in the eastern sector. Vertical recharge was represented using an RCH-type recharge module, integrating geological controls with precipitation intensity. Recharge parameters were calibrated against long-term water-balance analyses and observed groundwater depths for 2019–2020.
2.4. TTL Model Architecture
This study developed a deep learning model trained on 1097 consecutive daily observations (1 January 2019–31 December 2021) to achieve high-precision, daily-scale GWL predictions. Model inputs included daily precipitation, evaporation, mean air temperature, and antecedent groundwater levels, with the current-day GWL saving the target variable. The TTL model was implemented asa single-step autoregressive predictor, wherein each forecast corresponds to the GWL at day t in the basin with a sliding window of antecedent conditions. Although multi-step predictions can be generated recursively, this study focused exclusively on single-step forecasts.
The principal TTL architecture is illustrated in Figure 2. In this framework, the TCN blocks and the Transformer attention layer are connected in a strictly serial (stacked) manner. Specifically, input sequences are first processed by the TCN blocks to extract multiscale local features, and the output of the final TCN block is subsequently fed into the Transformer attention layer to capture long-range dependencies. The outputs of the TCN and Transformer are integrated via residual addition, effectively fusing local and global information before being passed to the LSTM layer for temporal modeling and, ultimately, to a fully connected layer for prediction. Residual pathways ensure that low-level features extracted by the TCN are preserved and progressively integrated, enhancing the representation of nonlinear, nonstationary hydrologic series. A schematic flow diagram illustrating inter-module feature transmission, residual connections, and output aggregation is provided in Figure 2 to facilitate interpretation.
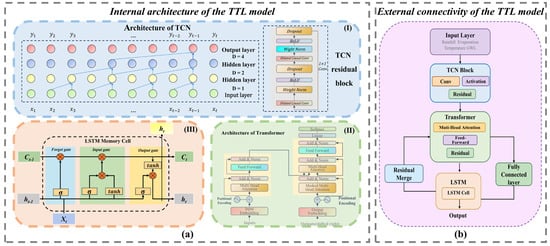
Figure 2.
Architecture of the TTL neural network model: (a) internal structure; (b) external connections.
Three comparative architectures—TTL, CBA, and CGA—were trained using identical four-dimensional inputs and evaluated under a combined validation framework of time-series K-fold cross-validation (Time SeriesSplit, n_splits = 5) and walk-forward (rolling-origin) validation. TimeSeriesSplit partitionedthe 1097-day record into six sequential segments, iteratively using the first i folds for training and the (i + 1)-th fold for validation to assess model stability. Walk-forward validation initialized an initial training window of 731 days (1 January 2019–31 December 2020), subsequently updating at monthly or quarterly intervals to emulate online learning and test robustness to dataset growth.
Model performance was quantified using R2, RMSE, MSE, and MAE (Equations (1)–(4)). Grouped bar charts and boxplots were employed to visualize means, standard deviations, and correlation coefficients across models, facilitating the selection of architectures that minimize error while maintaining stability. This multi-tiered validation strategy ensures fair comparability for trend fitting and rigorously evaluates daily-scale fluctuations and extreme-event capture, thereby enhancing the reliability and practical applicability of the conclusions. To improve interpretability, the internal mechanisms of TTL were analyzed using Transformer attention visualization and temporal Gradient-weighted Class Activation Mapping (Grad-CAM). These techniques enable identification of dominant input features and critical time periods contributing the most to predictions, thereby increasing model transparency.
where denotes the i-th observed value, represents the -th simulated value, and are the mean values of the observed and simulated data, respectively, and denote the i-th observed and predicted values for MAE and MSE calculations, and n indicates the total number of observations.
2.5. Hyperparameter Optimization
All hyperparameter combinations were trained under identical conditions to ensure fair evaluation and preserve temporal integrity. Specifically, the chronological order of the dataset (2019–2021) was strictly maintained, with 2019–2020 used for training/validation and 2021 reserved for testing. No shuffling was applied, preventing information leakage and ensuring proper time-series forecasting.
Hyperparameter ranges—including TCN dilations {1, 2, 4}, kernel sizes {2, 3, 5}, Transformer attention heads {2, 4, 8}, and LSTM hidden units {20, 50, 100}—were determined based on established time-series deep learning practices and preliminary exploratory trials. The dilation pattern captures multiscale temporal dependencies, kernel sizes balance receptive field width and computational efficiency, Transformer heads facilitate extraction of global context at multiple scales, and LSTM units span small to moderate memory capacities, ensuring stable convergence and practical feasibility.
An exhaustive grid search was conducted to systematically evaluate all candidate hyperparameter combinations. This approach avoids ad hoc tuning, enhances training stability, and improves the reproducibility and reliability of the final model selection. To prevent overfitting during prolonged training (up to 10,000 epochs), dropout (p = 0.2) was applied after the LSTM block, L2 weight decay (1 × 10−4) was incorporated into the optimizer, and early stopping with a 10-epoch patience criterion was employed based on validation RMSE.
Training was performed in a CPU-only environment to ensure reproducibility. Although this constraint increases runtime, it does not compromise the fairness, convergence, or validity of the hyperparameter evaluation, as all combinations were trained under identical computational conditions. The final selected configuration comprised TCN dilations [1,2,4], kernel size = 3, four Transformer attention heads, and 50 LSTM hidden units.
3. Results
3.1. Numerical Simulation Results
Prior to groundwater level (GWL) prediction, rigorous validation and parameter calibration of the numerical groundwater-flow model were conducted to ensure physical consistency and simulation reliability. Figure 3 shows the model grid and the initial hydraulic head distribution for the study domain, which establish the essential initial and boundary conditions for subsequent simulations. A structured sensitivity analysis and calibration workflow was applied to identify the dominant parameters controlling model responses and to reinforce both physical plausibility and numerical stability. Observed hydraulic head time series from multiple monitoring wells were incorporated into the calibration, and model performance was evaluated using the root mean square error (RMSE) and coefficient of determination (R2), supplemented by visual diagnostics (time-series overlays, residual plots, and scatterplots). The calibrated model exhibited close agreement with observations and maintained numerical stability in both steady-state and transient simulations, thereby supporting its application to subsequent DR modeling. Figure 4 presents a cloud–rain plot of monthly simulation errors in the plain sector, along with statistical descriptors (mean error, variance, and extremum distribution), to summarize model performance and the spatiotemporal structure of residuals.
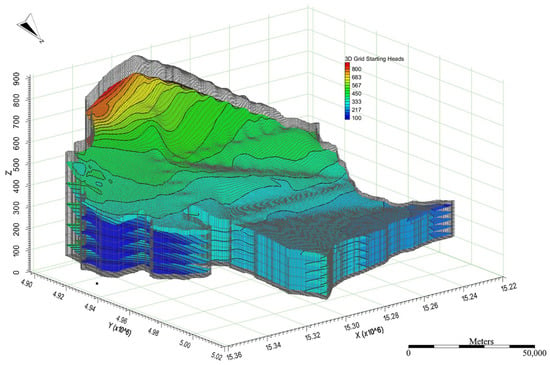
Figure 3.
Numerical simulation model framework and initial hydraulic head distribution in the study area.
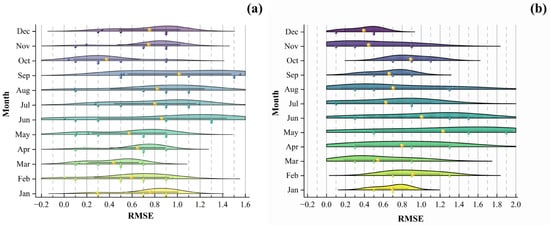
Figure 4.
RMSE values of simulated GWLs in the MODFLOW model. (a) Calibration and (b) validation phase.
3.2. Artificial Intelligence-Based GWL Prediction
To evaluate the feasibility of artificial neural network–based temporal prediction as an alternative to traditional numerical models under data-limited conditions, this study analyzed daily GWL series (2019–2021) from three representative monitoring wells (KY4, WS5, WS10) in the Kuitun River Basin. Table 2 summarizes the key characteristics of these wells, including their geographic coordinates, observation period, and mean groundwater level. The TTL model generated daily predictions that were aggregated into calendar-month averages for monthly analysis, using daily precipitation, evaporation, mean air temperature, and antecedent groundwater levels as inputs. Input data were obtained from piezometer measurements, and model training followed a rolling-window scheme with a standardized training budget of approximately 10,000 epochs to ensure comparability across experiments. The model outputs represented current-month plain-aquifer GWLs and were evaluated using RMSE, MSE, MAE, and R2 to quantify both fitting accuracy and dynamic response capability. Results are presented in Figure 5 (daily prediction–observation time-series comparisons) and Figure 6 (scatterplots of predicted versus observed values). Performance metrics across wells and models (TTL, CBA, CGA, GMS) are summarized in Table 3, enabling systematic comparison of goodness-of-fit and error distributions. The multiscale validation and aggregation framework confirmed the feasibility and robustness of TTL for high-precision GWL forecasting under realistic input constraints.

Table 2.
Basic information of the representative monitoring wells in the Kuitun River Basin.
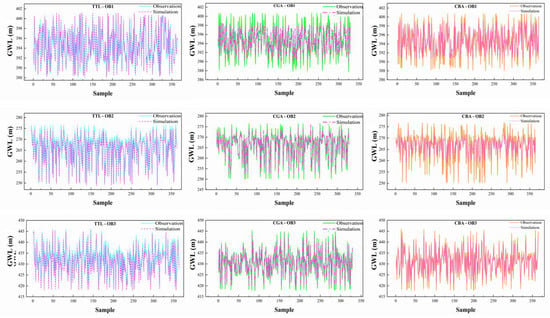
Figure 5.
Simulated versus observed GWL variations at three representative monitoring wells using three distinct models.
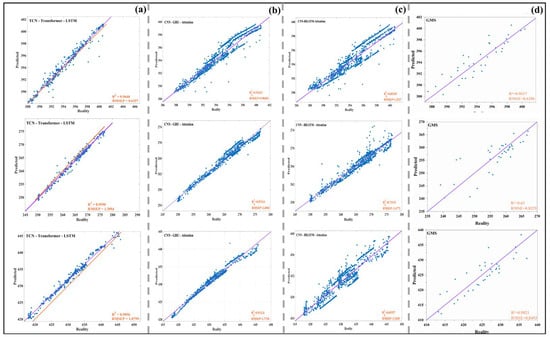
Figure 6.
Scatter regression plots of GWLs predicted versus observed from three distinct models at representative monitoring wells. Subplots correspond to (a) TTL (TCN–Transformer–LSTM model), (b) CGA (CNN-GRU-Attention model), (c) CBA (CNN-BiLSTM-Attention model), (d) GMS (Groundwater Modeling System).

Table 3.
Comparison of the GWL prediction performance of different models with different monitoring wells.
4. Discussion
4.1. Model Performance Analysis
The results shows that the TTL model consistently outperformed the benchmark methods at the OB1–OB3 monitoring wells. Across sites, TTL achieved R2 values of 0.905–0.964, RMSEs of 0.636–1.880 m, and MAEs = 0.446–1.760 m. In contrast, the CBA model exhibited lower accuracy (R2 = 0.759–0.853; RMSE = 1.25–3.24 m), while the CGA model achieved intermediate performance (R2 = 0.933–0.957), outperforming CBA on most metrics. The conventional numerical model (GMS) yielded competitive results at OB1 (R2 = 0.9617; RMSE = 0.6286 m) but showed markedly reduced accuracy at the more complex OB2 and OB3 sites. By comparison, TTL maintained stable performance across all scenarios, demonstrating enhanced robustness and generalization capability. The relatively high R2 of the GMS at OB1 can be attributed to the simpler hydrogeological conditions at this site, where groundwater fluctuations are primarily governed by antecedent water storage and evapotranspiration. In such settings, physically based models can effectively capture the dominant processes. Nevertheless, TTL exhibited superior adaptability under more heterogeneous and nonlinear hydroclimatic conditions. Previous studies support the superiority of Transformer–LSTM hybrids over single-framework models. For example, Shi, J. reported that hybrid architectures consistently outperformed standalone CNN, LSTM, and Transformer models in mine water inflow prediction across all metrics [44,45,46]. Similarly, Zong, R. demonstrated that TCN-based models achieved R2 > 0.999 in coastal aquifer forecasting, surpassing LSTM performance [47]. Furthermore, conventional numerical methods (e.g., MODFLOW/GMS) require substantial prior information and incur high computational costs, whereas ANN-based approaches deliver superior accuracy under comparable conditions [48]. Chen et al. (2023) specifically verified the superiority of CNNs over MODFLOW under identical simulation settings [49]. Considering that CBA and CGA already represent state-of-the-art architectures that outperforming conventional single-framework models such as LSTM or GRU, additional comparisons with simpler baselines are unnecessary and would yield limited further insight. Nonetheless, we recommend reporting uncertainty bounds (e.g., bootstrapped confidence intervals), per-site statistical tests, and computational cost metrics alongside point estimates to fully substantiate comparative claims.
4.2. Comparative Analysis of TTL Versus Conventional Benchmark Models
TTL integrates the complementary strengths of the TCN, Transformer, and LSTM architectures, with each module supported by established theoretical principles and empirical evidence. TCNs employ dilated causal convolutions with residual connections to enlarge the receptive field while preserving temporal causality, thereby enabling efficient long-range pattern extraction and stable deep-network training [50]. Previous studieshave shown that TCNs often outperform traditional RNNs in long-horizon pattern recognition while offering superior computational efficiency. The Transformer’s self-attention adaptively weights sequence elements to capture global dependencies; however, without appropriate positional encodings or local feature extractors, it may underemphasize temporal order and multiscale locality. Wang, M. (2024) demonstrated that attention mechanisms can impair temporal scale perception, rendering Transformers suboptimal for long-horizon forecasting compared with convolutional hybrids [51]. TTL addresses these limitations by placing Transformer modules after TCN layers: TCNs first extract robust local and multiscale representations, the Transformer applies dynamic global attention to these representations, and the LSTM layers subsequently perform temporal memorization and sequential prediction. This serial–parallel fusion leverages TCNs for local sensitivity and multiscale context, the Transformer for flexible global weighting, and LSTM for stable long-term state propagation—mitigating the individual limitations of each component. Empirical evidence (e.g., Chen et al.; Shi et al.) further corroborates that hybrid convolutional–recurrent or convolutional–attention–recurrent architectures generally outperform single-framework designs in multi-horizon forecasting tasks [52]. Thus, TTL synthesizes convolutional feature extraction, attentional dependency modeling, and recurrent multi-step forecasting into a compact, trainable architecture well suited to nonlinear, nonstationary hydrologic time series.
4.3. Composition of Principal Component and Hydrometeorological Control Mechanisms
Figure 7 presents the sample distribution and factor-loading vectors for the three monitoring wells (KY4, WS5, and WS10) projected onto the PC1–PC2 plane. The loadings indicate that PC1 is characterized by negative precipitation and positive air-temperature contributions, whereas PC2 is positively associated with antecedent water level and negatively with evapotranspiration. Accordingly, PC1 captures a precipitation–temperature gradient, while PC2 reflects aquifer storage versus evapotranspiration regulation mechanisms [53,54]. Mechanistically, increased precipitation raises GWLs, whereas higher air temperatures lower GWLs through enhanced evapotranspiration. Elevated antecedent levels represent greater baseline storage and exert lagged, cumulative influences on current fluctuations [55]. Kidmose, J. reported linear correlations between monthly GWL variations and climatic drivers (precipitation and evapotranspiration), consistent with the PCA-derived dominant factor trends identified in this study. Variance partitioning shows that PC1 explains ~45% of the variance at KY4 and WS5 (PC2 ~25%), confirming the dominance of precipitation–temperature controls at those sites. WS10 exhibits a lower PC1 contribution (~38%) but a larger PC2 share, indicating a greater influence of antecedent storage and evapotranspiration [56]. Across all wells, loading directions are consistent (precipitation negative on PC1; temperature positive on PC1; antecedent water level positive and evapotranspiration negative on PC2) [57]. Longer loading vectors indicate stronger influence: antecedent level and evapotranspiration vectors are relatively long for WS10, whereas temperature and precipitation vectors dominate at KY4 and WS5 [58].

Figure 7.
GWL samples from three monitoring wells projected onto the PC1–PC2 space with corresponding factor-loading vectors.
Interannual sample clustering further highlights temporal shifts in dominant drivers. At KY4 (left panel), 2019 samples cluster in the PC1-positive quadrant (temperature-dominated), 2020 samples shift into the PC1-negative quadrant (precipitation-dominated), and 2021 samples extend furthest along the PC2-positive quadrant (enhanced baseline storage). WS5 (center) shows a similar sequence (2019 → PC1-positive; 2020 → PC1-negative; 2021 → PC2-positive). WS10 (right) displays the reverse early-year pattern (2019 → PC1-negative; 2020 → PC1-positive), followed by a 2021 expansion toward PC2, underscoring strong antecedent-level control. These spatiotemporal shifts—consistent with Mohammed and related studies—indicate that “hot” years amplify PC1 temperature control, whereas “wet” years enhance PC2 storage effects [59,60].
Overall, the PCA confirms precipitation and temperature as the primary drivers on PC1, and antecedent storage plus evapotranspiration as the main controls on PC2, with site-specific heterogeneity in their relative importance. Figure 8 further visualizes the GWL sample distribution and factor-loading vectors in the PC1–PC2 space. The clustering patterns align with the PCA results: KY4 and WS5 samples predominantly span the PC1-positive to PC1-negative quadrants, reflecting the precipitation–temperature gradient captured by PC1, whereas WS10 samples extend more strongly along PC2, emphasizing the influence of antecedent storage and evapotranspiration. These visual patterns corroborate the site-specific heterogeneity in dominant hydroclimatic controls revealed by the PCA loadings.
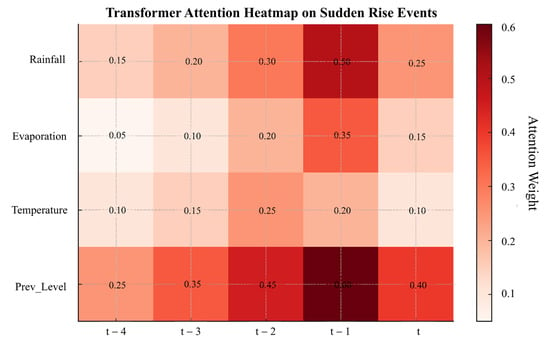
Figure 8.
Transformer attention heatmap (abrupt event response samples).
4.4. Analysis of Model Interpretability and Abrupt Event Response Mechanisms
To link the PCA results with the attention mechanism analysis, we observe that high attention weights during drought periods spatially correspond to areas with negative PC2 loadings associated with reduced evapotranspiration. This alignment suggests that TTL dynamically identifies aquifer-specific drivers consistent with the dominant hydro-meteorological patterns revealed by PCA, providing a coherent interpretation across both analyses. These relationships establish a standardized framework for event-specific analyses across all monitoring wells. To further elucidate the internal mechanisms underlying TTL’s superior performance during abrupt events, we applied two interpretability techniques: (1) Transformer attention visualization and (2) temporal Grad-CAM mapping. Unlike conventional CNNs or RNNs, TTL integrates multiscale convolutions, attention mechanisms, and recurrent units—achieving not only higher predictive accuracy but also structural interpretability in its responses to abrupt hydroclimatic events [61,62,63].
For attention visualization, we extracted weight matrices from all Transformer attention heads to construct temporal heatmaps, quantifying the relative importance of historical inputs at each time step. Figure 8 shows that precipitation and antecedent water level inputs from t − 3 to t − 1 days receive higher attention weights, underscoring the TTL model’s ability to capture key factors with temporal lag effects [64]. These attention patterns are consistent across hydrological regimes: drought periods emphasize antecedent water levels and evapotranspiration over rainfall, whereas wet periods prioritize short-term precipitation [65]. This behavior aligns with PCA-derived components—PC1 (rainfall–temperature dominance) and PC2 (storage–evapotranspiration regulation)—confirming that TTL’s attention allocation reflects the statistical structure of dominant hydro-meteorological drivers [66,67]. Grad-CAM analysis further reveals response peaks in temperature and evapotranspiration channels at t − 2 to t − 4 during abrupt events, verifying the model’s capacity to identify evapoconsumptive drivers within critical windows [68]. In contrast, rainfall surges produce maximum responses in precipitation channels at t − 1, indicating precise detection of triggers for rapid water level rise. Such channel-level response mapping substantially enhances interpretability for extreme-event detection, surpassing the “black-box” limitations of standalone LSTM or CNN models.
Overall, these analyses demonstrate that TTL excels not only in predictive accuracy but also in its structural capacity for dynamic feature focusing and causal attribution. The attention mechanism adaptively weights features according to prevailing hydrological regimes, while Grad-CAM leverages gradients from the final convolutional layers to generate class-specific heatmaps—revealing spatial–channel response patterns and enabling dual-level interpretation of both observed phenomena and their causal drivers [69,70].
5. Conclusions
- The proposed TTL framework integrates multiscale convolutions, self-attention mechanisms, and LSTM units, thereby addressing the parameter uncertainty of physical models and the feature-extraction limitations of single-type neural networks. Validation results demonstrate that TTL effectively captures hydro-meteorologically driven temporal patterns and abrupt groundwater fluctuations, achieving consistently higher accuracy and stability than benchmark models.
- The PCA results reveal pronounced spatial variability in the dominant groundwater-level (GWL) drivers: rainfall–temperature interactions primarily control KY4 and WS5, whereas antecedent water storage and evapotranspiration exert stronger influence at WS10. Moreover, integrating PCA findings with Transformer attention visualization and temporal Grad-CAM mapping provides robust interpretability.
- To enhance practical applicability, TTL forecasts should be translated into operational indicators, such as time-specific irrigation thresholds and graded groundwater-extraction warnings aligned with watershed management units (WMUs). This requires spatial aggregation or interpolation of point or gridded forecasts to the WMU scale, as well as temporal aggregation to the planning horizon (e.g., daily to weekly or monthly), combined with probability-based outputs derived from ensembles or uncertainty propagation. When processed in this manner, these indicators can be integrated into basin-scale scheduling and real-time allocation platforms via standardized data formats (e.g., NetCDF, GeoTIFF, JSON), enabling rule-based triggers and risk-informed resource allocation.
- Due to data limitations, this study did not consider key drivers such as soil moisture, runoff generation, and pumping records. Future research should incorporate these variables using data assimilation, remote sensing, or hybrid physics–data models. Additionally, emerging machine learning architectures capable of handling heterogeneous covariates and probabilistic forecasting (e.g., the Temporal Fusion Transformer, TFT) should be evaluated to enhance model robustness and predictive reliability. These findings lay the groundwork for the development of practical decision-support tools aimed at promoting sustainable groundwater management in arid inland basins.
Author Contributions
Conceptualization, Y.L. and M.D.; methodology, Y.L. and Z.T.; software, Y.L.; validation, X.M.; formal analysis, S.H.; investigation, Y.L., X.M. and S.H.; resources, Z.T. and S.H.; data curation, Z.T.; writing—original draft preparation, Y.L.; writing—review and editing, M.D.; supervision, M.D. and X.M.; funding acquisition, Y.L. and M.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Xinjiang Uygur Autonomous Region Major Science and Technology Special Project Funding (2024A03007-3).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data will be made available on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wada, Y.; van Beek, L.P.H.; Sperna Weiland, F.C.; Chao, B.F.; Wu, Y.H.; Bierkens, M.F.P. Past and Future Contribution of Global Groundwater Depletion to Sea-level Rise. Geophys. Res. Lett. 2012, 39, 1–6. [Google Scholar] [CrossRef]
- Beyene, T.D.; Zimale, F.A.; Gebrekristos, S.T. A Review on Sources of Uncertainties for Groundwater Recharge Estimates: Insight into Data Scarce Tropical, Arid, and Semiarid Regions. Hydrol. Res. 2023, 55, 51–66. [Google Scholar] [CrossRef]
- Williams, M.L.; MacCoy, D.E.; Maret, T.R. Evaluation of Mercury in Rainbow Trout Collected from Duck Valley Indian Reservation Reservoirs, Southwestern Idaho and Northern Nevada, 2007, 2009, and 2013; U.S. Geological Survey Scientific Investigations Report; U.S. Geological Survey: Reston, VA, USA, 2015; Volume 5079, 18p. [Google Scholar] [CrossRef]
- Seifi, A.; Ehteram, M.; Singh, V.P.; Mosavi, A. Modeling and Uncertainty Analysis of GWL Using Six Evolutionary Optimization Algorithms Hybridized with ANFIS, SVM, and ANN. Sustainability 2020, 12, 4023. [Google Scholar] [CrossRef]
- Gholami, V. Spatial Modeling of Groundwater Depth Fluctuations Using Co-Active Neuro-Fuzzy Inference System (CANFIS) and Geographic Information System (GIS). Appl. Water Sci. 2022, 12, 24. [Google Scholar] [CrossRef]
- Kumar, H.; Syed, T.H.; Amelung, F.; Agrawal, R.; Venkatesh, A.S. Space-Time Evolution of Land Subsidence in the National Capital Region of India Using ALOS-1 and Sentinel-1 SAR Data: Evidence for Groundwater Overexploitation. J. Hydrol. 2022, 605, 127329. [Google Scholar] [CrossRef]
- Fan, B.; Shi, X.; Luo, G.; Hellwich, O.; Ma, X.; Shang, M.; Wang, Y.; Ochege, F.U. Ground Subsidence and Disaster Risk Induced by Groundwater Overexploitation: A Comprehensive Assessment from Arid Oasis Regions. Int. J. Disaster Risk Reduct. 2025, 119, 105328. [Google Scholar] [CrossRef]
- Lezzaik, K.; Milewski, A.; Mullen, J. The Groundwater Risk Index: Development and Application in the Middle East and North Africa Region. Sci. Total Environ. 2018, 628–629, 1149–1164. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Liu, C.; Zhen, P.; Guo, X.; Wang, S. Groundwater Quality Variability with Inter-Basin Water Transfer and Overexploitation Control in an Agriculture-Dominant Subregion of North China Plain. Agric. Water Manag. 2025, 317, 109660. [Google Scholar] [CrossRef]
- Lu, T.; Luo, P.; Wang, J.; Lu, Y.; Huo, A.; Liu, L. Soil Salinity Accumulation and Groundwater Degradation Due to Overexploitation over Recent 40-Year Period in Yaoba Oasis, China. Soil Tillage Res. 2024, 248, 106398. [Google Scholar] [CrossRef]
- Schuch, C.S.; Galvão, P.; de Melo, M.C.; Pereira, S. Overexploitation Assessment in an Urban Karst Aquifer: The Case of Sete Lagoas (MG), Brazil. Environ. Res. 2023, 236, 116820. [Google Scholar] [CrossRef]
- Mo, Y.; Xu, J.; Zhu, S.; Xu, B.; Wu, J.; Jin, G.; Wang, Y.-G.; Li, L. Spatial Heterogeneity of Groundwater Depths in Coastal Cities and Their Responses to Multiple Factors Interactions by Interpretable Machine Learning Models. Geosci. Front. 2025, 16, 102033. [Google Scholar] [CrossRef]
- Goodarzi, M.R.; Bana Bafrouei, H.; Vazirian, M. Insight into GWL Prediction with Feature Effectiveness: Comparison of Machine Learning and Numerical Methods. Hydrol. Res. 2024, 56, 74–92. [Google Scholar] [CrossRef]
- Di Salvo, C. Improving Results of Existing Groundwater Numerical Models Using Machine Learning Techniques: A Review. Water 2022, 14, 2307. [Google Scholar] [CrossRef]
- Khan, J.; Lee, E.; Balobaid, A.S.; Kim, K. A Comprehensive Review of Conventional, Machine Learning, and Deep Learning Models for GWL (GWL) Forecasting. Appl. Sci. 2023, 13, 2743. [Google Scholar] [CrossRef]
- Pourmorad, S.; Kabolizade, M.; Dimuccio, L.A. Artificial Intelligence Advancements for Accurate GWL Modelling: An Updated Synthesis and Review. Appl. Sci. 2024, 14, 7358. [Google Scholar] [CrossRef]
- Thakur, A.; Chandel, A.; Shankar, V. Prediction of GWLs Using a Long Short-Term Memory (LSTM) Technique. J. Hydroinform. 2024, 27, 51–68. [Google Scholar] [CrossRef]
- Sun, J.; Hu, L.; Li, D.; Sun, K.; Yang, Z. Data-Driven Models for Accurate GWL Prediction and Their Practical Significance in Groundwater Management. J. Hydrol. 2022, 608, 127630. [Google Scholar] [CrossRef]
- Patra, S.R.; Chu, H.-J. Convolutional long short-term memory neural network for groundwater change prediction. Front. Water 2024, 6, 1471258. [Google Scholar] [CrossRef]
- Igwebuike, N.; Ajayi, M.; Okolie, C.; Kanyerere, T.; Halihan, T. Application of Machine Learning and Deep Learning for Predicting GWLs in the West Coast Aquifer System, South Africa. Earth Sci. Inform. 2025, 18, 6. [Google Scholar] [CrossRef]
- Larsen, E.W.; Gossel, W.S.; Kuni, T. MODFLOW-2000, The U.S. Geological Survey Modular Ground-Water Model—User Guide to Modularization Concepts and the Ground-Water Flow Process; U.S. Geological Survey: Reston, VA, USA, 2000; Volume 38, pp. 1–130. [Google Scholar]
- Pandey, K.; Kumar, S.; Malik, A.; Kuriqi, A. Artificial Neural Network Optimized with a Genetic Algorithm for Seasonal Groundwater Table Depth Prediction in Uttar Pradesh, India. Sustainability 2020, 12, 8932. [Google Scholar] [CrossRef]
- Roy, D.K.; Biswas, S.K.; Mattar, M.A.; El-Shafei, A.A.; Murad, K.F.I.; Saha, K.K.; Datta, B.; Dewidar, A.Z. GWL Prediction Using a Multiple Objective Genetic Algorithm-Grey Relational Analysis Based Weighted Ensemble of ANFIS Models. Water 2021, 13, 3130. [Google Scholar] [CrossRef]
- Barzegar, R.; Fijani, E.; Asghari Moghaddam, A.; Tziritis, E. Forecasting of GWL Fluctuations Using Ensemble Hybrid Multi-Wavelet Neural Network-Based Models. Sci. Total Environ. 2017, 599–600, 20–31. [Google Scholar] [CrossRef]
- Yadav, B.; Ch, S.; Mathur, S.; Adamowski, J. Assessing the suitability of extreme learning machines (ELM) for GWL prediction. J. Water Land Dev. 2017, 32, 103–112. [Google Scholar] [CrossRef]
- Liu, W.; Yu, H.; Yang, L.; Yin, Z.; Zhu, M.; Wen, X. Deep Learning-Based Predictive Framework for GWL Forecast in Arid Irrigated Areas. Water 2021, 13, 2558. [Google Scholar] [CrossRef]
- Kombo, O.; Kumaran, S.; Sheikh, Y.; Bovim, A.; Jayavel, K. Long-Term GWL Prediction Model Based on Hybrid KNN-RF Technique. Hydrology 2020, 7, 59. [Google Scholar] [CrossRef]
- Monir, M.d.M.; Sarker, S.C.; Islam, A.R.M.T. A Critical Review on GWL Depletion Monitoring Based on GIS and Data-Driven Models: Global Perspectives and Future Challenges. HydroResearch 2024, 7, 285–300. [Google Scholar] [CrossRef]
- Gong, Y.; Wang, Z.; Xu, G.; Zhang, Z. A Comparative Study of GWL Forecasting Using Data-Driven Models Based on Ensemble Empirical Mode Decomposition. Water 2018, 10, 730. [Google Scholar] [CrossRef]
- Xu, Y.; Hu, C.; Wu, Q.; Li, Z.; Jian, S.; Chen, Y. Application of Temporal Convolutional Network for Flood Forecasting. Hydrol. Res. 2021, 52, 1455–1468. [Google Scholar] [CrossRef]
- Haider, A.; Lee, G.; Jafri, T.H.; Yoon, P.; Piao, J.; Jhang, K. Enhancing Accuracy of GWL Forecasting with Minimal Computational Complexity Using Temporal Convolutional Network. Water 2023, 15, 4041. [Google Scholar] [CrossRef]
- Abegeja, D.; Nedaw, D. Identification of groundwater potential zones using geospatial technologies in Meki Catchment, Ethiopia. Geol. Ecol. Landsc. 2024, 10, 1–16. [Google Scholar] [CrossRef]
- Li, R.; Zhu, G.; Chen, L.; Qi, X.; Lu, S.; Meng, G.; Wang, Y.; Li, W.; Zheng, Z.; Yang, J.; et al. Global Stable Isotope Dataset for Surface Water. Earth Syst. Sci. Data 2025, 17, 1–11. [Google Scholar] [CrossRef]
- You, J.; Wang, S.; Ha, M.; Kang, A.; Lei, X.; Chen, B.; Yu, Y.; Chai, B. Comparative hydrologic performance of cascading and distributed green-gray infrastructure: Experimental evidence for spatial optimization in urban waterlogging mitigation. J. Hydrol. 2025, 662, 133979. [Google Scholar] [CrossRef]
- Yu, W.; Wang, P.; Zhao, M.; Qu, Y.; Du, X. Fluid-structure interaction simulation of floating structure interacting with the combined effect of wave-current-earthquake based on CFD method. Ocean Eng. 2025, 339, 122192. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, J.; Zhu, T.; Li, J. Experimental and MPM modelling of widened levee failure under the combined effect of heavy rainfall and high riverine water levels. Comput. Geotech. 2025, 184, 107259. [Google Scholar] [CrossRef]
- Kishor, K.; Aggarwal, A.; Srivastava, P.K.; Sharma, Y.K.; Lee, J.; Ghobadi, F. A Systematic Literature Review of MODFLOW Combined with Artifcial Neural Networks(ANNs) for Groundwater Flow Modelling. Water 2025, 17, 2375. [Google Scholar] [CrossRef]
- Saqr, A.M.; Kartal, V.; Karakoyun, E.; Abd-Elmaboud, M.E. Improving the Accuracy of GWL Forecasting by Coupling Ensemble Machine Learning Model and Coronavirus Herd Immunity Optimizer. Water Resour. Manag. 2025, 27, 106268. [Google Scholar] [CrossRef]
- Makhlouf, A.; El-Rawy, M.; Kanae, S.; Ibrahim, M.G.; Sharaan, M. Integrating MODFLOW and Machine Learning for Detecting Optimum Groundwater Abstraction Considering Sustainable Drawdown and Climate Changes. J. Hydrol. 2024, 637, 131428. [Google Scholar] [CrossRef]
- Qiao, C.; Wang, Y.; Liu, Y.; Li, J.; Zhang, H.; Lu, J. Study of Water Resources Optimal Operation Model of Multireservoir: A Case Study of Kuitun River Basin in Northwestern China. Wirel. Commun. Mob. Comput. 2022, 17, 919. [Google Scholar] [CrossRef]
- Li, Q.; Tao, H.; Aihemaiti, M.; Jiang, Y.; Su, Y.; Yang, W. Spatial Distribution Characteristics and Enrichment Factors of High-Fluorine Groundwater in the Kuitun River Basin of Xinjiang Uygur Autonomous Region in China. Desalination Water Treat. 2021, 223, 208–217. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Z.; Mou, J.; He, H. Impact of Glacier Change on Water Resources in the Kuytun River Basin, Tianshan Mountains During the Recent 50 Years. Geogr. Sin. 2017, 37, 1771–1777. [Google Scholar] [CrossRef]
- Zhao, L.; Sun, M.; Sun, H.; Gong, N.; Yan, L. Discharge Simulation and Sensitivity to Climate Change of the Kuytun River Basin on the North Slope of Tianshan Mountains, China. J. Mt. Res. 2018, 36, 722–730. [Google Scholar] [CrossRef]
- Shi, J.; Wang, S.; Qu, P.; Shao, J. Time Series Prediction Model Using LSTM-Transformer Neural Network for Mine Water Inflow. Sci. Rep. 2024, 14, 8214. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Liu, C.; Xu, Y.; Niu, C.; Li, R.; Li, M.; Hu, C.; Tian, L. An Interpretable Hybrid Deep Learning Model for Flood Forecasting Based on Transformer and LSTM. J. Hydrol. Reg. Stud. 2024, 54, 101873. [Google Scholar] [CrossRef]
- Motawej, H. Integrating MODFLOW and LSTM Models for Enhanced Groundwater Management in the Coastal Plains of Lattakia Governorate. Water Pract. Technol. 2024, 20, 413–423. [Google Scholar] [CrossRef]
- Zong, R.; Wang, Z.; Li, W.; Ayantobo, O.O.; Li, h.; Song, L. Assessing the impact of seasonal freezing and thawing on the soil microbial quality in arid northwest China. Sci. Total Environ. 2023, 863, 161029. [Google Scholar] [CrossRef]
- Zhang, X.; Dong, F.; Chen, G.; Dai, Z. Advance Prediction of Coastal GWLs with Temporal Convolutional and Long Short-Term Memory Networks. Hydrol. Earth Syst. Sci. 2023, 27, 83–96. [Google Scholar] [CrossRef]
- Chen, H.-Y.; Lo, Z.V.; Lee, J.-W. GWL Prediction with Deep Learning Methods. Water 2023, 15, 3118. [Google Scholar] [CrossRef]
- Lara-Benítez, P.; Carranza-García, M.; Luna-Romera, J.M.; Riquelme, J.C. Temporal Convolutional Networks Applied to Energy-Related Time Series Forecasting. Appl. Sci. 2020, 10, 2322. [Google Scholar] [CrossRef]
- Wang, M.; Qin, F. A TCN-Linear Hybrid Model for Chaotic Time Series Forecasting. Entropy. 2024, 26, 467. [Google Scholar] [CrossRef]
- Guo, D.; Duan, P.; Yang, Z.; Zhang, X.; Su, Y. Convolutional Neural Network and Bidirectional Long Short-Term Memory (CNN-BiLSTM)-Attention-Based Prediction of the Amount of Silica Powder Moving in and out of a Warehouse. Energies 2024, 17, 3757. [Google Scholar] [CrossRef]
- Zhang, X.; Guo, X.; Liu, S.; Shang, X.; Xu, Z.; Zhao, J. A Study on GWL Calculation Based on PCA-CIWOABP. Front. Earth Sci. 2024, 12, 1445241. [Google Scholar] [CrossRef]
- Haji-Aghajany, S.; Amerian, Y.; Amiri-Simkooei, A. Impact of Climate Change Parameters on GWL: Implications for Two Subsidence Regions in Iran Using Geodetic Observations and Artificial Neural Networks (ANN). Remote Sens. 2023, 15, 1555. [Google Scholar] [CrossRef]
- Li, W.; Finsa, M.M.; Laskey, K.B.; Houser, P.; Douglas-Bate, R. GWL Prediction with Machine Learning to Support Sustainable Irrigation in Water Scarcity Regions. Water 2023, 15, 3473. [Google Scholar] [CrossRef]
- Kidmose, J.; Refsgaard, J.C.; Troldborg, L.; Seaby, L.P.; Escrivà, M.M. Climate Change Impact on GWLs: Ensemble Modelling of Extreme Values. Hydrol. Earth Syst. Sci. 2013, 17, 1619–1634. [Google Scholar] [CrossRef]
- Baud, B.; Lachassagne, P.; Dumont, M.; Toulier, A.; Hendrayana, H.; Fadillah, A.; Dorfliger, N. Review: Andesitic Aquifers—Hydrogeological Conceptual Models and Insights Relevant to Applied Hydrogeology. Hydrogeol. J. 2024, 32, 1259–1286. [Google Scholar] [CrossRef]
- Tian, C.; Wang, L.; Li, F.; Zhang, X.; Jiao, W.; Medici, M.; Kaseke, F.; Beysens, D. The Moisture Origin of Dew: Insights from Three Sites with Contrasting Climatic Conditions. Hydrol. Process. 2023, 37, e14902. [Google Scholar] [CrossRef]
- Mohammed, M.A.A.; Szabó, N.P.; Mikita, V.; Szűcs, P. Tracking the Spatiotemporal Evolution of Groundwater Chemistry in the Quaternary Aquifer System of Debrecen Area, Hungary: Integration of Classical and Unsupervised Learning Methods. Environ. Sci. Pollut. Res. 2025, 32, 6884–6903. [Google Scholar] [CrossRef]
- Di Lena, F.; Berardi, M.; Masciale, R.; Portoghese, I. Network Dynamics for Modelling Artificial Groundwater Recharge by a Cluster of Infiltration Basins. Hydrol. Process. 2023, 37, 14876. [Google Scholar] [CrossRef]
- Wan, R.; Tian, C.; Zhang, W.; Deng, W.; Yang, F. A Multivariate Temporal Convolutional Attention Network for Time-Series Forecasting. Electronics 2022, 11, 1516. [Google Scholar] [CrossRef]
- Parasar, P.; Krishna, A.P. Explainable AI-driven assessment of hydro climatic interactions shaping river discharge dy-namics in a monsoonal basin. Sci Rep. 2025, 15, 27302. [Google Scholar] [CrossRef] [PubMed]
- Lim, B.; Arık, S.Ö.; Loeff, N.; Pfister, T. Temporal Fusion Transformers for Interpretable Multi-Horizon Time Series Forecasting. Int. J. Forecast. 2021, 37, 1748–1764. [Google Scholar] [CrossRef]
- Liu, C.; Liu, D.; Mu, L. Improved Transformer Model for Enhanced Monthly Streamflow Predictions of the Yangtze River. IEEE Access. 2022, 10, 58240–58253. [Google Scholar] [CrossRef]
- Dikshit, A.; Pradhan, B.; Assiri, M.E.; Almazroui, M.; Park, H.J. Solving Transparency in Drought Forecasting Using Attention Models. Sci. Total Environ. 2022, 837, 155856. [Google Scholar] [CrossRef]
- Shakoor, A.; Shah, S.A.; Sattar, M.N.; Ogunrinde, A.T.; Alharbi, R.S.; Rehman, F.u. Hydroclimate Drivers and Spatiotem-poral Dynamics of Reference Evapotranspiration in a Changing Climate. Water. 2025, 17, 2586. [Google Scholar] [CrossRef]
- Santos, J.F.; Carriço, N.; Miri, M.; Raziei, T. Distributed Composite Drought Index Based on Principal Component Analy-sis and Temporal Dependence Assessment. Water 2025, 17, 17. [Google Scholar] [CrossRef]
- Xiang, X.; Guo, S.; Cui, Z.; Wang, L.; Xu, C.-Y. Improving Flood Forecast Accuracy Based on Explainable Convolutional Neural Network by Grad-CAM Method. J. Hydrol. 2024, 642, 131867. [Google Scholar] [CrossRef]
- Noor, F.; Haq, S.; Rakib, M.; Ahmed, T.; Jamal, Z.; Siam, Z.S.; Hasan, R.T.; Adnan, M.S.G.; Dewan, A.; Rahman, R.M. Water Level Forecasting Using Spatiotemporal Attention-Based Long Short-Term Memory Network. Water 2022, 14, 612. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Chang, T.-Y.; Chow, H.-Y.; Li, S.-L.; Ou, C.-Y. Using Convolutional Neural Networks to Build a Lightweight Flood Height Prediction Model with Grad-CAM for the Selection of Key Grid Cells in Radar Echo Maps. Water 2022, 14, 155. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).