Sustainability and Algorithmic Comparison of Segmented PVRP for Healthcare Waste Collection: A Brazilian Case Study
Abstract
1. Introduction
- A segmentation-based PVRP formulation that reflects realistic HCW generator behavior.
- A computational comparison of CW and PSO, highlighting convergence performance and robustness.
- An environmental impact assessment, quantifying CO2 reductions via optimized routing.
- A real-world case study showing applicability in developing urban contexts.
2. Related Work
- (1)
- Homogeneous customer modeling: Many studies assume uniform HCW generation behavior across clients, disregarding variations in waste type and volume. This limits the realism and applicability of routing solutions.
- (2)
3. Methods
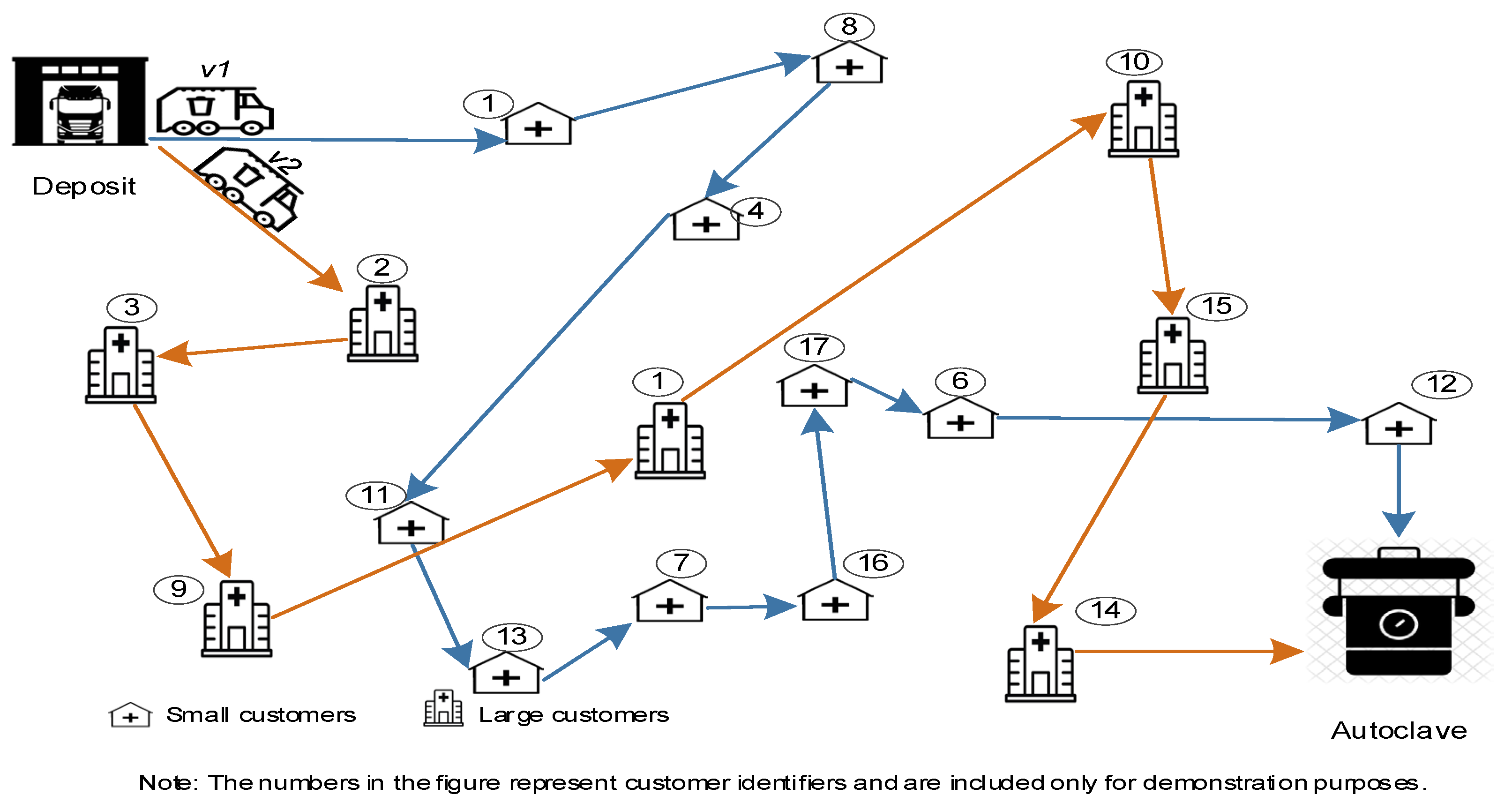
3.1. PVRP Model for HCW
- Large Generators: Hospitals and clinics generating between 176 kg and 550 kg of HCW per day.
- Small Generators: Medical offices, laboratories, dental practices, optical centers, and pharmacies, generating up to 175 kg/day.
- Single visit per customer per day
- Full coverage: All customers must be served on their scheduled days.
- Depot start and end: Each route must begin and end at the depot.
- Vehicle capacity: Waste collected must not exceed the vehicle’s capacity.
- Exclusive service: Each customer is served only once per day by one vehicle.
Mathematical Formulation
| Index and sets |
| . |
| . |
| . |
| Parameters |
- Decision variables
- Objective functionMinimize total traveled distance over all days and vehicles:
- ConstraintsSchedule selection and day activation:Visit exactly once on activated days (arrival/departure linking):Depot flow balance per vehicle and day:Vehicle capacity per day:Variable domains:
3.2. Solution Approach
- CW, for its low computational cost and ability to produce feasible, structured initial routes.
- PSO, for its swarm intelligence-inspired adaptability and capacity to refine complex, constraint-laden solutions.
3.2.1. Clarke and Wright (CW) Heuristic
| Algorithm 1: Pseudo-code Clarke and Wright (CW) algorithm for a PVRP |
| Definition of the capacities of both small and large vehicles |
| Definition of parameters, customer demand, and geographical coordinates for collection |
| Calculate distance |
| Input: Set of vertices and set of edges , maximum vehicle capacity Output: List of ordered in descending order of saving 1 route create_initial_routes ; 2 saving_list = { }; 3 For each customer pair do 4 ; 5 saving list in descending order ; 6 end 7 sort_decreasing ; 8 return the optimized route structure |
3.2.2. Particle Swarm Optimization (PSO)
| Algorithm 2: Pseudo-code of the PSO algorithm |
| Input: W Output: swarm of size ( position vetors) Initialize , randomly generate the position of each particle within the bounds Initialize all velocities to zero; Initialize best positions * (and respective values) for individual particles and find *; Choose randomly two values in [0,1] for and ; Iteration ; Initialize While do Calculate inertia ; For each particle in , the values for iteration are: 1 Update velocity big customer: ; 2 Update velocity small customer: ; 3 Update position: ; 4 Compute the value of the new position according to ; 5 Check / Update: (Optional) check for convergence; Increment iteration counter: ; End Return |
3.2.3. Parameter Settings and Calibration
- Vehicle capacity: Based on operational data provided by the company responsible for HCW collection, vehicle capacities of 1500 kg were adopted for routes serving large generators and 1000 kg for those serving small generators. This differentiation is essential to accurately reflect the heterogeneity in waste generation volumes.
- Route savings criteria: Two strategies were evaluated: one based on the distance between customers and another on the volume of waste collected. The distance-based savings criterion was selected based on its direct alignment with the primary objective of minimizing travel distance. This choice was subsequently validated through statistical comparison using the Mann–Whitney U test, confirming its superior performance over volume-based alternatives for small and large customer segments (see Section 5).
- Distance matrix: The distances between waste generators, the central depot, and the treatment facility (autoclave) were calculated using real geographic coordinates and the Euclidean distance formula. This step was critical to ensure accuracy in estimating logistical costs and to support effective route optimization.
- Total distance traveled (km): The primary optimization metric is directly associated with operational costs and environmental impact.
- Feasibility rate (% of feasible solutions): Reflects the robustness of the solution concerning vehicle capacity and service frequency constraints.
- CO2 emissions (kg CO2): The DEFRA emission factor (2.68 kg CO2 per liter of diesel) is estimated based on the average fuel consumption of the vehicles used in the waste collection service.
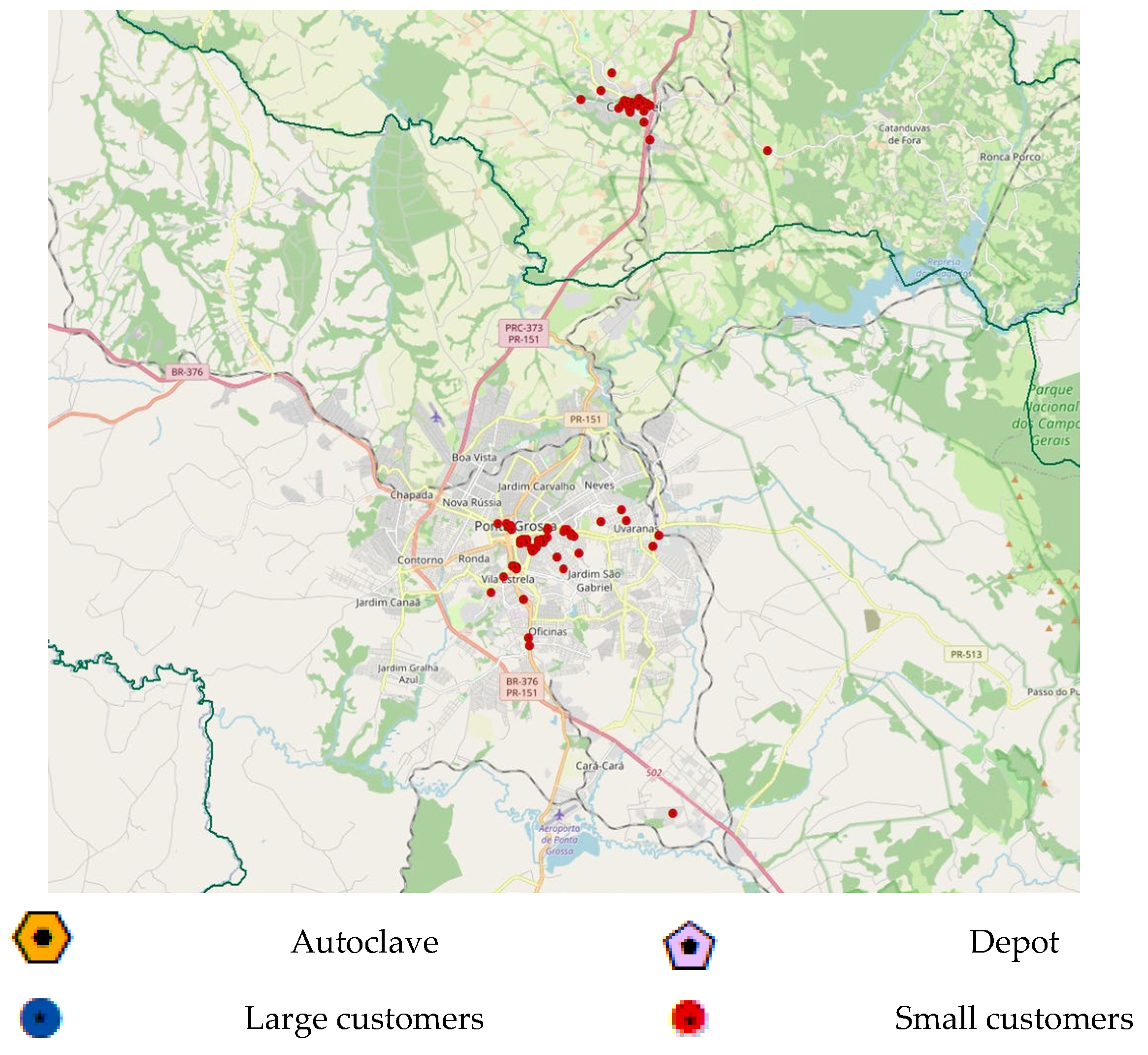
4. Case Study
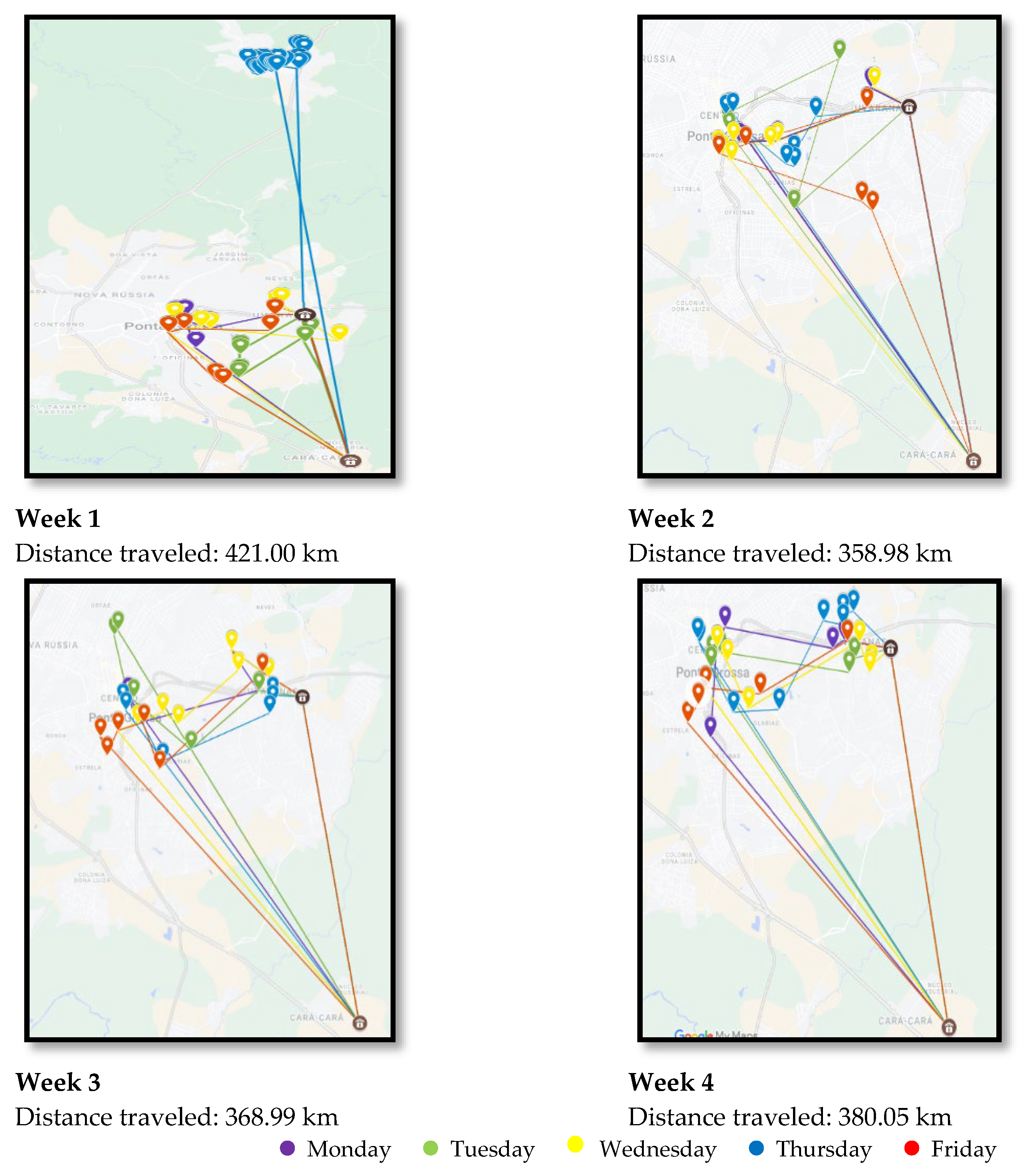
5. Results
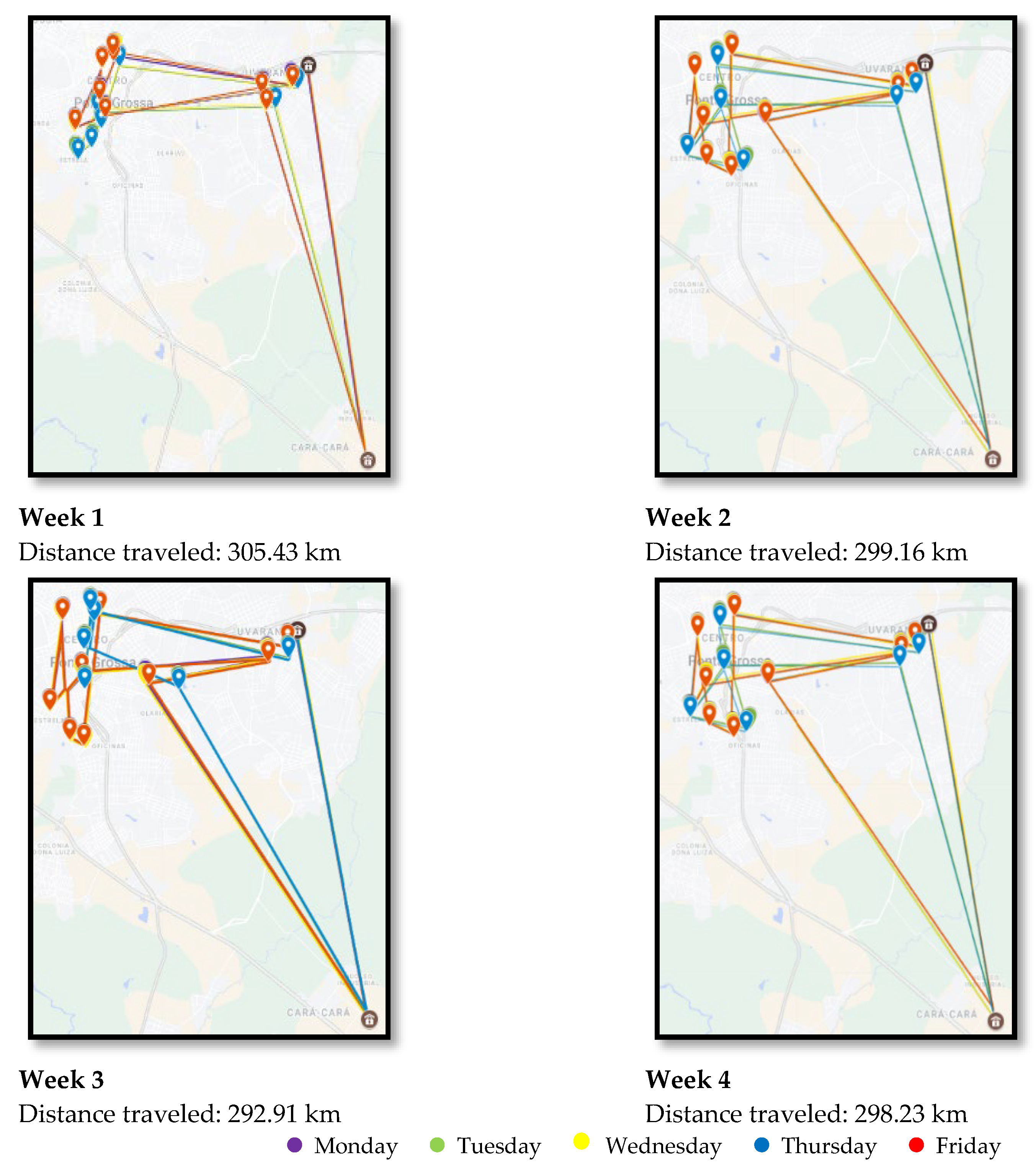
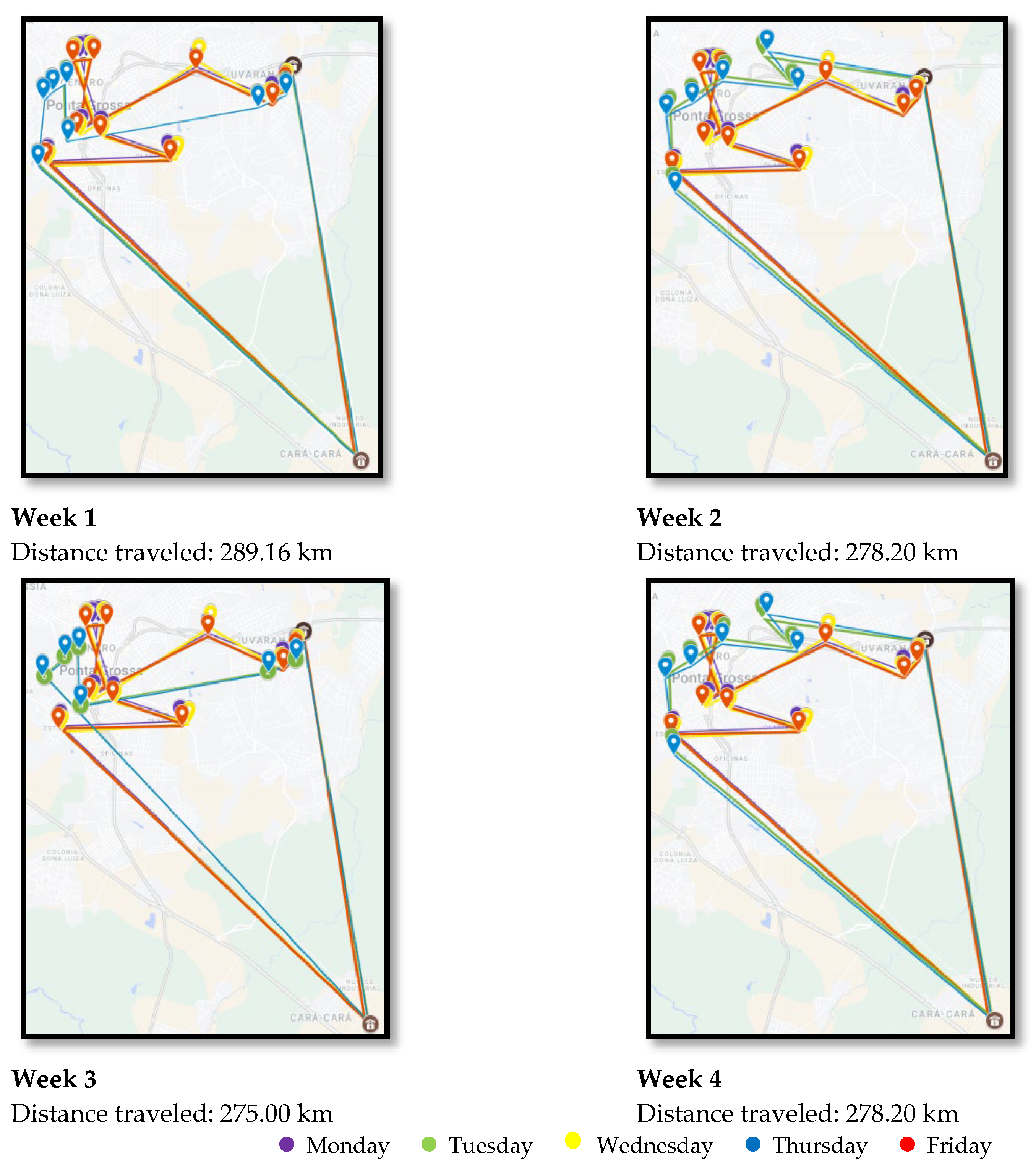
5.1. Small HCW Generators
5.2. Large HCW Generators
5.3. Environmental Impact Assessment
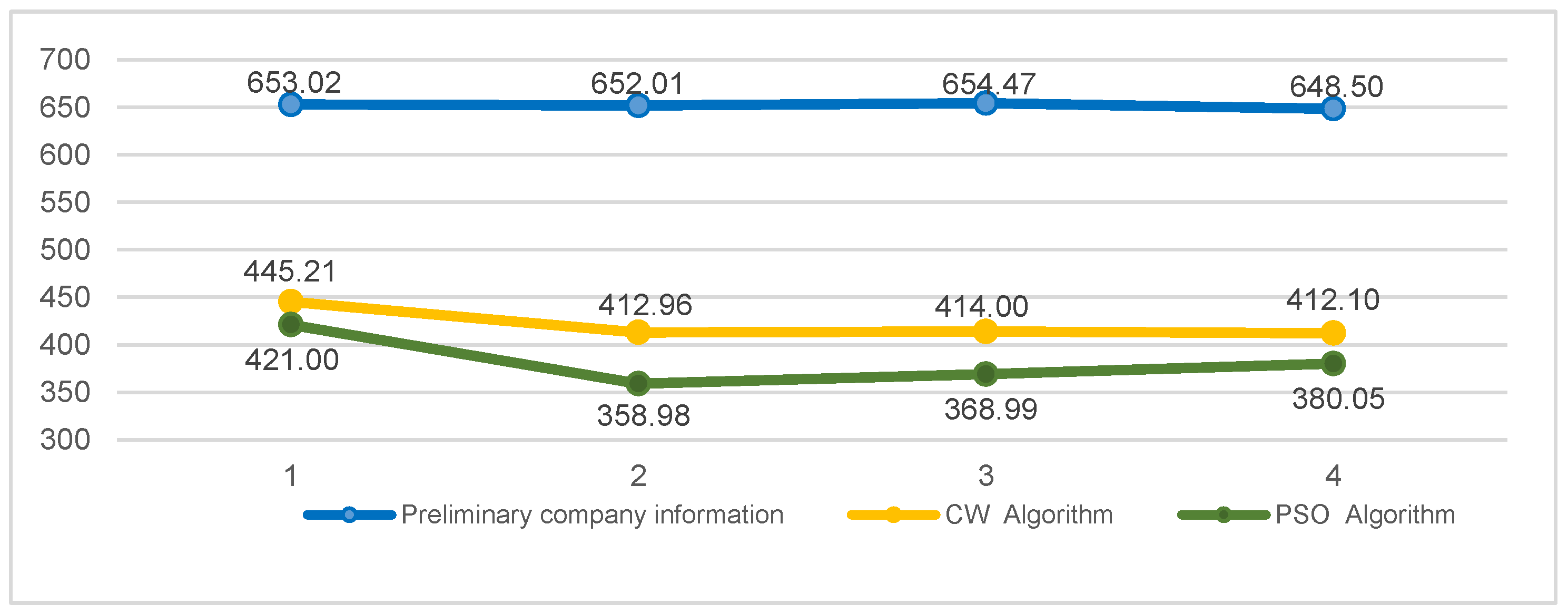
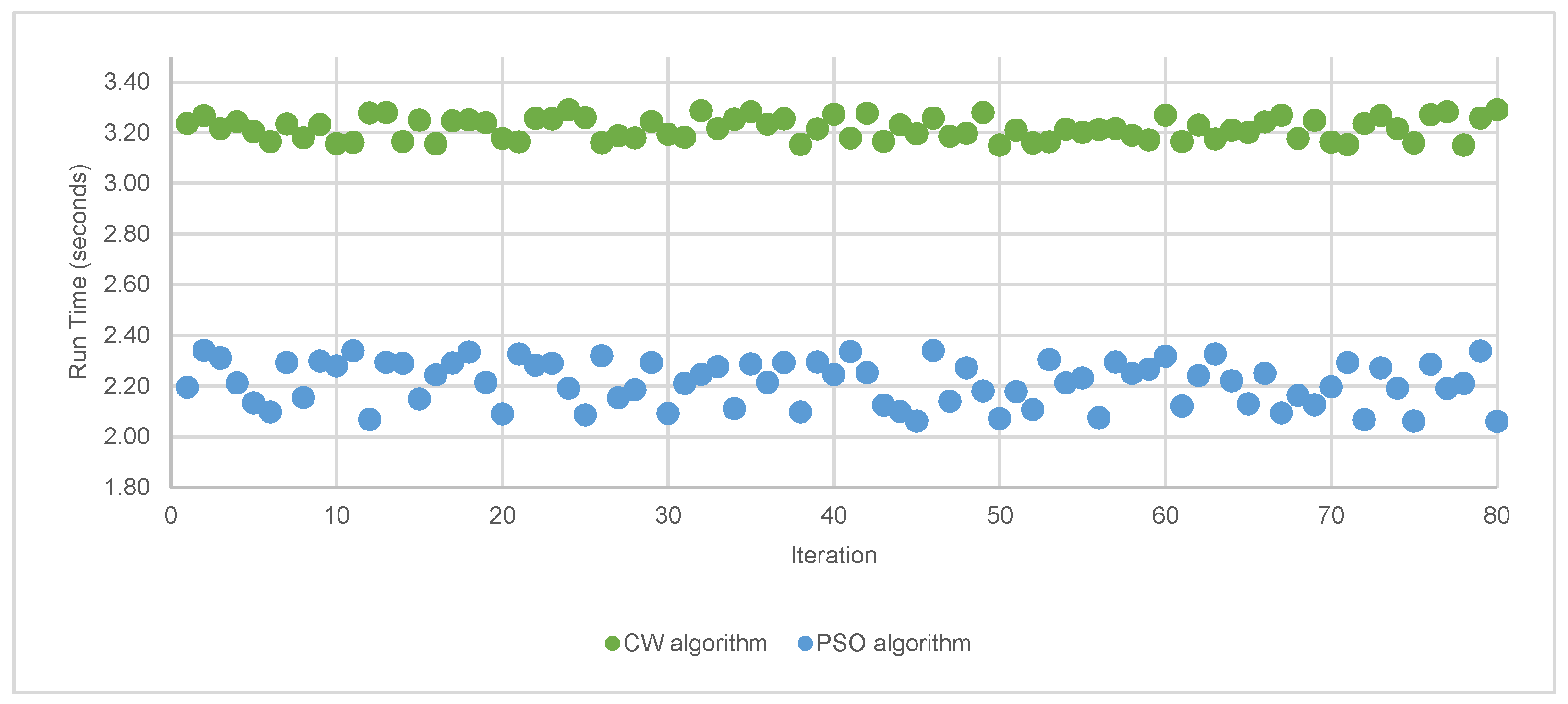
5.4. Algorithmic Performance Comparison
6. Conclusions and Future Work
- Extending the analysis to different problem sizes, operational configurations (e.g., fleet capacity, regulations), and geographical contexts (other cities/countries) to rigorously validate scalability and improve generalizability.
- Incorporating additional critical variables into the model and segmentation, such as waste type (infectious, sharps), time windows, health-related priorities, and real-time data from IoT sensors.
- Conducting broader comparative studies with other advanced metaheuristics (e.g., Genetic Algorithms, Variable Neighborhood Search) and focusing on systematic parameter calibration tailored to the HCW routing problem.
- Although the 176 kg/day limit was set based on established operational practices, we may investigate alternative limits derived from optimization models, considering different scenarios of fleet capacity, collection frequencies, and waste generation patterns.
- Although the PSO parameters were initially set based on widely accepted literature recommendations, future research could focus on systematic parameter calibration and sensitivity analysis specifically for the HCW routing problem.
- Integrating socio-economic indicators and multi-criteria decision-making frameworks to evaluate the holistic sustainability and social impact of routing strategies.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Customer | Week 1 | Week 2 | Week 3 | Week 4 | Total |
|---|---|---|---|---|---|
| 1 | 500 | 450 | 462 | 489 | 1901 |
| 2 | 518 | 454 | 470 | 449 | 1891 |
| 3 | 320 | 497 | 315 | 482 | 1614 |
| 7 | 437 | 320 | 454 | 320 | 1531 |
| 8 | 519 | 319 | 445 | 318 | 1601 |
| 9 | 456 | 525 | 319 | 448 | 1748 |
| 13 | 487 | 440 | 476 | 491 | 1894 |
| 27 | 319 | 320 | 318 | 312 | 1269 |
| 37 | 543 | 539 | 447 | 470 | 1999 |
| 38 | 318 | 317 | 319 | 317 | 1271 |
| Customer | Week 1 | Week 2 | Week 3 | Week 4 | Total |
|---|---|---|---|---|---|
| 4 | 93 | 99 | 166 | 183 | 541 |
| 5 | 92 | 122 | 199 | 160 | 573 |
| 6 | 112 | 126 | 179 | 211 | 628 |
| 10 | 120 | 114 | 232 | 298 | 764 |
| 11 | 94 | 100 | 128 | 99 | 421 |
| 12 | 120 | 113 | 269 | 254 | 756 |
| 14 | 99 | 97 | 90 | 147 | 433 |
| 15 | 117 | 119 | 195 | 274 | 705 |
| 16 | 101 | 149 | 214 | 271 | 735 |
| 17 | 94 | 99 | 178 | 92 | 463 |
| 18 | 53 | 73 | 109 | 82 | 317 |
| 19 | 80 | 98 | 158 | 80 | 416 |
| 20 | 71 | 100 | 249 | 172 | 592 |
| 21 | 79 | 96 | 181 | 157 | 513 |
| 22 | 65 | 97 | 156 | 161 | 479 |
| 23 | 82 | 99 | 132 | 124 | 437 |
| 24 | 132 | 145 | 161 | 251 | 689 |
| 25 | 56 | 94 | 139 | 160 | 449 |
| 26 | 150 | 185 | 348 | 301 | 984 |
| 28 | 107 | 131 | 162 | 334 | 734 |
| 29 | 88 | 128 | 160 | 145 | 521 |
| 30 | 108 | 123 | 176 | 128 | 535 |
| 31 | 104 | 125 | 196 | 173 | 598 |
| 32 | 75 | 130 | 152 | 128 | 485 |
| 33 | 68 | 95 | 204 | 128 | 495 |
| 34 | 76 | 98 | 184 | 154 | 512 |
| 35 | 71 | 84 | 168 | 178 | 501 |
| 36 | 101 | 121 | 181 | 273 | 676 |
| 39 | 99 | 90 | 111 | 165 | 465 |
| 40 | 87 | 94 | 139 | 107 | 427 |
| 41 | 139 | 185 | 296 | 332 | 952 |
| 42 | 107 | 125 | 198 | 282 | 712 |
| 43 | 76 | 125 | 162 | 181 | 544 |
| 44 | 71 | 75 | 161 | 188 | 495 |
| 45 | 85 | 147 | 178 | 259 | 669 |
| 46 | 102 | 151 | 216 | 299 | 768 |
| 47 | 15 | 17 | 12 | 9 | 53 |
| 48 | 20 | 5 | 10 | 15 | 50 |
| 49 | 12 | 15 | 9 | 6 | 42 |
| 50 | 9 | 10 | 8 | 13 | 40 |
| 51 | 11 | 7 | 7 | 8 | 33 |
| 52 | 14 | 12 | 15 | 10 | 51 |
| 53 | 10 | 6 | 10 | 12 | 38 |
| 54 | 19 | 10 | 14 | 11 | 54 |
| 55 | 15 | 12 | 13 | 11 | 51 |
| 56 | 10 | 9 | 11 | 12 | 42 |
| 57 | 9 | 11 | 12 | 14 | 46 |
| 58 | 18 | 12 | 8 | 11 | 49 |
| 59 | 8 | 10 | 5 | 5 | 28 |
| 60 | 11 | 9 | 10 | 3 | 33 |
| 61 | 11 | 10 | 16 | 18 | 55 |
| 62 | 18 | 8 | 11 | 11 | 48 |
| 63 | 13 | 10 | 10 | 20 | 53 |
| 64 | 12 | 16 | 10 | 14 | 52 |
| 65 | 14 | 9 | 10 | 11 | 44 |
| 66 | 9 | 8 | 6 | 9 | 32 |
| 67 | 10 | 15 | 9 | 6 | 40 |
| 68 | 10 | 6 | 8 | 8 | 32 |
| 69 | 5 | 8 | 7 | 11 | 31 |
| 70 | 84 | 149 | 168 | 220 | 621 |
| 71 | 93 | 169 | 307 | 297 | 866 |
| 72 | 103 | 128 | 200 | 185 | 616 |
| 73 | 61 | 82 | 232 | 172 | 547 |
| TOTAL | 3998 | 4915 | 7665 | 8053 | 24,631 |
References
- Ghannadpour, S.F.; Zandieh, F.; Esmaeili, F. Optimizing triple bottom-line objectives for sustainable health-care waste collection and routing by a self-adaptive evolutionary algorithm: A case study from tehran province in Iran. J. Clean. Prod. 2021, 287, 125010. [Google Scholar] [CrossRef]
- Chauhan, A.; Jakhar, S.K.; Chauhan, C. The interplay of circular economy with industry 4.0 enabled smart city drivers of healthcare waste disposal. J. Clean. Prod. 2021, 279, 123854. [Google Scholar] [CrossRef] [PubMed]
- Janik-Karpinska, E.; Brancaleoni, R.; Niemcewicz, M.; Wojtas, W.; Foco, M.; Podogrocki, M.; Bijak, M. Healthcare waste—A serious problem for global health. Healthcare 2023, 11, 242. [Google Scholar] [CrossRef] [PubMed]
- Taslimi, M.; Batta, R.; Kwon, C. Medical waste collection considering transportation and storage risk. Comput. Oper. Res. 2020, 120, 104966. [Google Scholar] [CrossRef]
- Neves, A.C.; Maia, C.C.; de Castro e Silva, M.E.; Vimieiro, G.V.; Gomes Mol, M.P. Analysis of healthcare waste management in hospitals of Belo Horizonte, Brazil. Environ. Sci. Pollut. Res. 2022, 29, 90601–90614. [Google Scholar] [CrossRef]
- Zamparas, M.; Kapsalis, V.C.; Kyriakopoulos, G.L.; Aravossis, K.G.; Kanteraki, A.E.; Vantarakis, A.; Kalavrouziotis, I.K. Medical waste management and environmental assessment in the Rio University Hospital, Western Greece. Sustain. Chem. Pharm. 2019, 13, 100163. [Google Scholar] [CrossRef]
- Erdem, M. Designing a sustainable logistics network for hazardous medical waste collection a case study in COVID-19 pandemic. J. Clean. Prod. 2022, 376, 134192. [Google Scholar] [CrossRef]
- Gao, J.; Li, H.; Wu, J.; Lyu, J.; Tan, Z.; Jin, Z. Routing Optimisation of Urban Medical Waste Recycling Network considering Differentiated Collection Strategy and Time Windows. Sci. Program. 2021, 2021, 5523910. [Google Scholar] [CrossRef]
- Rahmanifar, G.; Mohammadi, M.; Sherafat, A.; Hajiaghaei-Keshteli, M.; Fusco, G.; Colombaroni, C. Heuristic approaches to address vehicle routing problem in the Iot-based waste management system. Expert Syst. Appl. 2023, 220, 119708. [Google Scholar] [CrossRef]
- Erdem, M. Optimisation of sustainable urban recycling waste collection and routing with heterogeneous electric vehicles. Sustain. Cities Soc. 2022, 80, 103785. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, D.; Van Woensel, T.; Xu, G.; Guo, J. Green vehicle routing using mixed fleets for cold chain distribution. Expert Syst. Appl. 2023, 233, 120979. [Google Scholar] [CrossRef]
- International Energy Agency, CO2 Emiss. Available online: https://www.iea.org/reports/co2-emissions-in-2023 (accessed on 3 May 2024).
- Ben-Romdhane, H.; Ouertani, N.; Krichen, S.; Nouaouri, I. On optimizing healthcare waste routing systems using waste separation policies: A case study. Appl. Soft Comput. 2023, 146, 110615. [Google Scholar] [CrossRef]
- Zhang, M.; Cui, W.; Jiang, Q.; Wang, N.; Shang, Y. Vehicle Routing for Infectious Healthcare Waste Collection with Transit Points: A Problem Incorporating Multiple Types of Risks and Two Solution Methods from Different Perspectives. IEEE Access 2025, 13, 83542–83560. [Google Scholar] [CrossRef]
- Nikzamir, M.; Baradaran, V. A healthcare logistic network considering stochastic emission of contamination: Bi-objective model and solution algorithm. Transp. Res. Part E Logist. Transp. Rev. 2020, 142, 102060. [Google Scholar] [CrossRef]
- Zhang, M.; Cui, W.; Jiang, Q.; Wang, N. Routing Optimization for Healthcare Waste Collection with Temporary Storing Risks and Sequential Uncertain Service Requests. IEEE Access 2024, 12, 2868–2881. [Google Scholar] [CrossRef]
- Cárdenas-León, I.; Koeva, M.; Nourian, P.; Davey, C. Urban digital twin-based solution using geospatial information for solid waste management. Sustain. Cities Soc. 2024, 115, 105798. [Google Scholar] [CrossRef]
- SDG. United Nations. Department of Economic and Social Affairs Sustainable Development. 2021. Available online: https://sdgs.un.org/goals (accessed on 8 October 2024).
- Liu, L.; Liao, W. Optimization and profit distribution in a two-echelon collaborative waste collection routing problem from economic and environmental perspective. Waste Manag. 2021, 120, 400–414. [Google Scholar] [CrossRef]
- Akbarpour, N.; Salehi-Amiri, A.; Hajiaghaei-Keshteli, M.; Oliva, D. An innovative waste management system in a smart city under stochastic optimization using vehicle routing problem. Soft Comput. 2021, 25, 6707–6727. [Google Scholar] [CrossRef]
- Chen, R.-M.; Shen, Y.-M.; Hong, W.-Z. Neural-like encoding particle swarm optimization for periodic vehicle routing problems. Expert Syst. Appl. 2019, 138, 112833. [Google Scholar] [CrossRef]
- Zhang, W.; Zeng, M.; Guo, P.; Wen, K. Variable Neighborhood Search for Multi-Cycle Medical Waste Recycling Vehicle Routing Problem with Time Windows. Int. J. Environ. Res. Public Health 2022, 19, 12887. [Google Scholar] [CrossRef]
- Bouya, S.; Balouchi, A.; Rafiemanesh, H.; Amirshahi, M.; Dastres, M.; Moghadam, M.P.; Behnamfar, N.; Shyeback, M.; Badakhsh, M.; Allahyari, J. Global prevalence and device related causes of needle stick injuries among health care workers: A systematic review and meta-analysis. Ann. Glob. Health 2020, 86, 35. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.T.; Rafi, M.A.; Hasan, M.J. Knowledge, attitude and practice of health care workers on solid medical waste management in two urban hospitals of Bangladesh: A mixed-method study. J. Health Popul. Nutr. 2025, 44, 34. [Google Scholar] [CrossRef] [PubMed]
- Wang, N.; Cui, W.; Zhang, M.; Jiang, Q. Routing optimization for medical waste collection considering infectious risk and multiple disposal centers. Expert Syst. Appl. 2023, 234, 121035. [Google Scholar] [CrossRef]
- Shih, L.-H.; Lin, Y.-T. Optimal routing for infectious waste collection. J. Environ. Eng. 1999, 125, 479–484. [Google Scholar] [CrossRef]
- Shih, L.-H.; Chang, H.-C. A routing and scheduling system for infectious waste collection. Environ. Model. Assess. 2001, 6, 261–269. [Google Scholar] [CrossRef]
- Huang, D.; Gu, Y.; Wang, S.; Liu, Z.; Zhang, W. A two-phase optimization model for the demand-responsive customized bus network design. Transp. Res. Part C Emerg. Technol. 2020, 111, 1–21. [Google Scholar] [CrossRef]
- Eren, E.; Rıfat Tuzkaya, U. Safe distance-based vehicle routing problem: Medical waste collection case study in COVID-19 pandemic. Comput. Ind. Eng. 2021, 157, 107328. [Google Scholar] [CrossRef]
- Babaee Tirkolaee, E.; Aydin, N.S. A sustainable medical waste collection and transportation model for pandemics. Waste Manag. Res. 2021, 39, 34–44. [Google Scholar] [CrossRef]
- Shih, L.-H.; Lin, Y.-T. Multicriteria optimization for infectious medical waste collection system planning. Pract. Period. Hazard. Toxic Radioact. Waste Manag. 2003, 7, 78–85. [Google Scholar] [CrossRef]
- Wu, H.; Tao, F.; Qiao, Q.; Zhang, M. A chance-constrained vehicle routing problem for wet waste collection and transportation considering carbon emissions. Int. J. Environ. Res. Public Health 2020, 17, 458. [Google Scholar] [CrossRef]
- Xu, X.; Wu, T.; Wang, S.; Zhang, S.; Xu, Z.; Yang, B.; Ding, Z.; Shen, L. Optimization of reliable vehicle routing problem for medical waste collection with time windows in stochastic transportation networks. Eng. Optim. 2025, 57, 2109–2139. [Google Scholar] [CrossRef]
- Shen, L.; Xu, X.; Shao, F.; Shao, H.; Ge, Y. A multi-objective optimization model for medical waste recycling network design under uncertainties. Transp. Res. Part E Logist. Transp. Rev. 2024, 184, 103492. [Google Scholar] [CrossRef]
- Tang, C.; Wei, Q.; Zhang, D.; Sun, J.; Perboli, G.; Guo, Z.; Li, K. An improved adaptive large neighborhood search algorithm to solve a bi-level medical waste location-routing problem with infection control. Waste Manag. 2025, 197, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Shen, X.; Lou, H.; Ge, Z. A two-stage scheduling algorithm for dynamic interval multi-objective vehicle routing problem in medical waste collection. Comput. Ind. Eng. 2025, 2025, 111136. [Google Scholar] [CrossRef]
- Sasikumar, P.; Kannan, G.; Haq, A.N. A heuristic based approach to vehicle routing model for Third Party Reverse Logistics provider. Int. J. Serv. Technol. Manag. 2009, 12, 106–125. [Google Scholar] [CrossRef]
- Hannan, M.A.; Akhtar, M.; Begum, R.A.; Basri, H.; Hussain, A.; Scavino, E. Capacitated vehicle-routing problem model for scheduled solid waste collection and route optimization using PSO algorithm. Waste Manag. 2018, 71, 31–41. [Google Scholar] [CrossRef]
- Pisinger, D.; Ropke, S. A general heuristic for vehicle routing problems. Comput. Oper. Res. 2007, 34, 2403–2435. [Google Scholar] [CrossRef]
- Seyyedhasani, H.; Dvorak, J.S. Using the Vehicle Routing Problem to reduce field completion times with multiple machines. Comput. Electron. Agric. 2017, 134, 142–150. [Google Scholar] [CrossRef]
- Cengiz Toklu, M. A fuzzy multi-criteria approach based on Clarke and Wright savings algorithm for vehicle routing problem in humanitarian aid distribution. J. Intell. Manuf. 2023, 34, 2241–2261. [Google Scholar] [CrossRef]
- GHG Emissions Calculation Tool. Available online: https://eaesp.fgv.br/centros/centro-estudos-sustentabilidade/projetos/programa-brasileiro-ghg-protocol (accessed on 12 September 2024).
- Defra. Department for Environment, Food & Rural Affairs. Nature Recovery Network; 2020. Available online: https://www.gov.uk/government/publications/nature-recovery-network/nature-recovery-network (accessed on 17 March 2024).
| Parameter | Symbol | Value | Justification |
|---|---|---|---|
| Population size (particles) | 20 | Standard size for medium-scale routing problem [21] | |
| Inertia weight | 0.5 | Balances global and local search [8] | |
| Cognitive coefficient | 0.5 | Encourages self-exploration | |
| Social coefficient | 0.5 | Encourages convergence via swarm best | |
| Max iterations | 10 | Empirically defined to ensure convergence without excessive runtime | |
| Velocity bounds | [−1, 1] | Prevents overshooting feasible space |
| Customer Type | Number of Customers | Planning Period (Days) | Maximum Fleet (u/Day) | Daily Demand (kg) | Visit Frequency |
|---|---|---|---|---|---|
| Small | 63 | 5 | 1 | ≤100 | 1 |
| 101 to 135 | 2 | ||||
| 136 to 175 | 3 | ||||
| Large | 10 | 5 | 1 | 176 to 325 | 3 |
| 326 to 550 | 5 |
| Item Description | Information |
|---|---|
| Small customer (number) | 63 |
| Large customer (number) | 10 |
| Depot (number) | 1 |
| Autoclave (number) | 1 |
| Vehicles (number) | 2 |
| Small vehicle capacity (kg) | 1000 |
| Large vehicle capacity (kg) | 1500 |
| Week | Total Distances Traveled (km) | Difference in Distances | ||
|---|---|---|---|---|
| CW Algorithm | PSO Algorithm | km | % | |
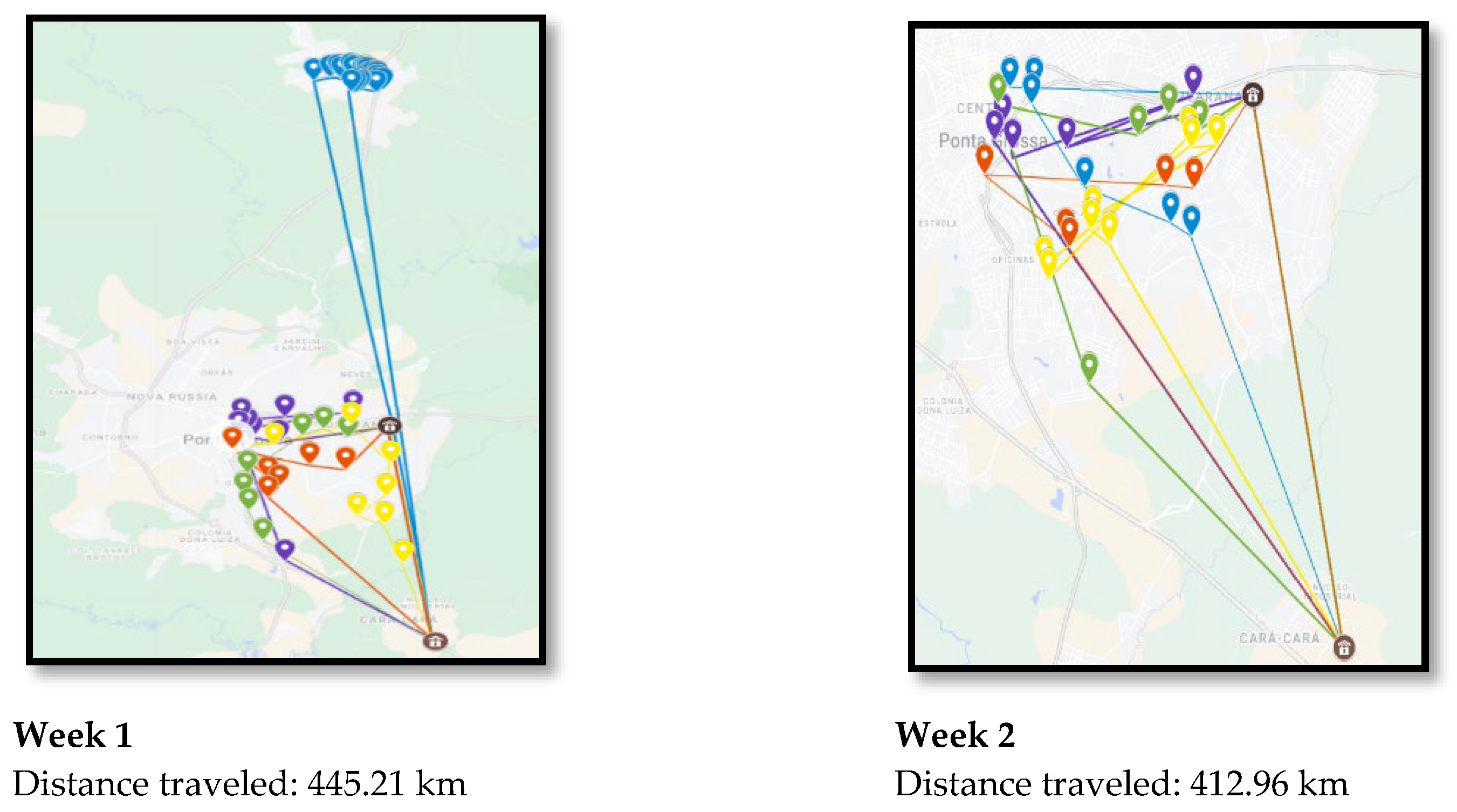
| 1 | 445.21 | 421.00 | 24.21 | 5% |
| 2 | 412.96 | 358.98 | 53.98 | 13% |
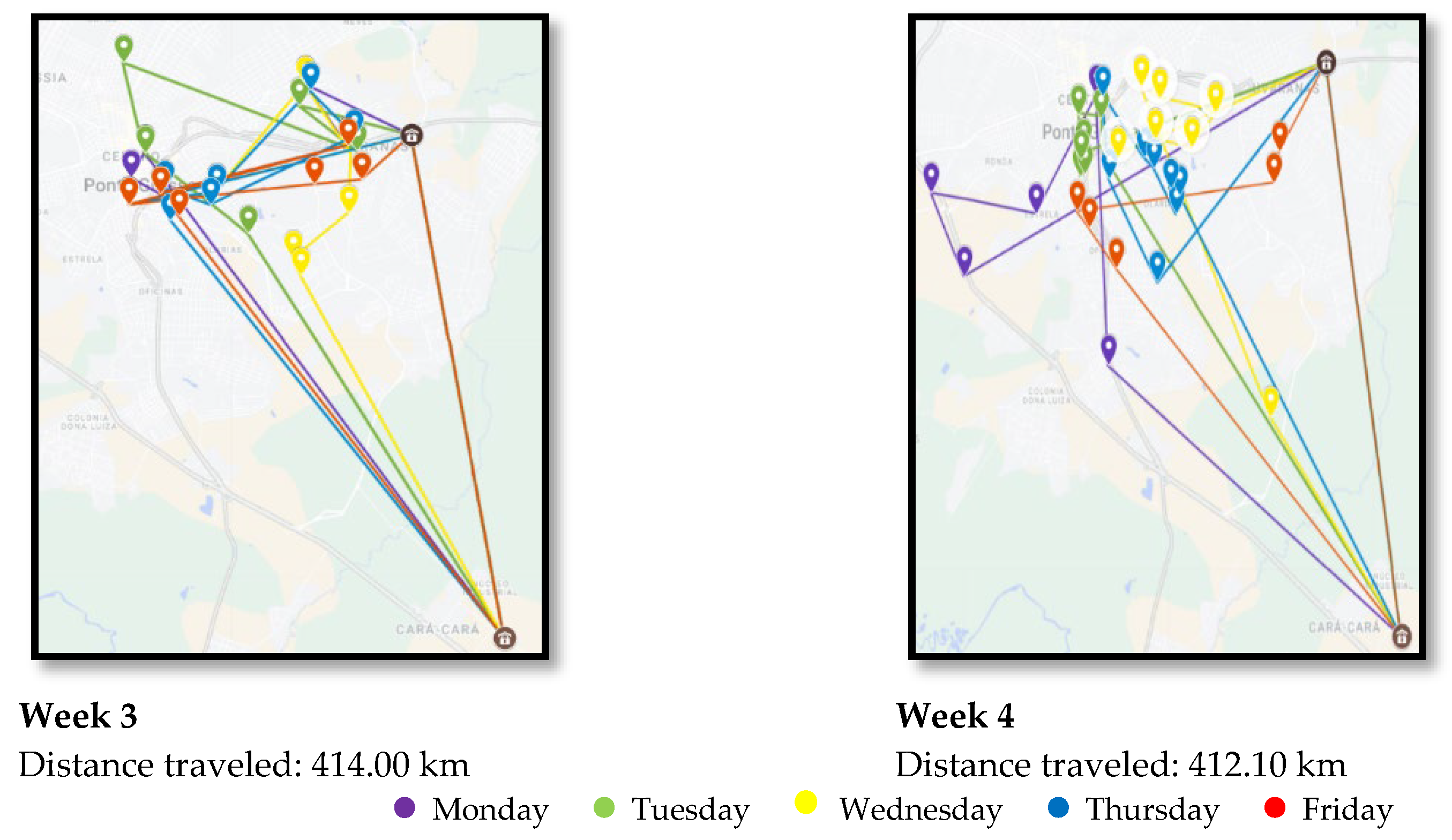
| 3 | 414.00 | 368.99 | 45.01 | 11% |
| 4 | 412.10 | 380.05 | 32.05 | 8% |
| Week | CW (Mean ± SD) | PSO (Mean ± SD) | p-Value (Mann–Whitney–Wilcoxon Test) |
|---|---|---|---|
| W1 | 445.21 ± 2.54 | 421.00 ± 2.37 | 1.45 × 10−11 |
| W2 | 412.96 ± 2.38 | 358.98 ± 3.23 | 1.45 × 10−11 |
| W3 | 414.00 ± 3.34 | 368.99 ± 3.26 | 1.45 × 10−11 |
| W4 | 412.10 ± 2.75 | 380.05 ± 3.06 | 1.45 × 10−11 |
| Week | Total Distances Traveled (km) | Difference in Distances | ||
|---|---|---|---|---|
| CW Algorithm | PSO Algorithm | km | % | |
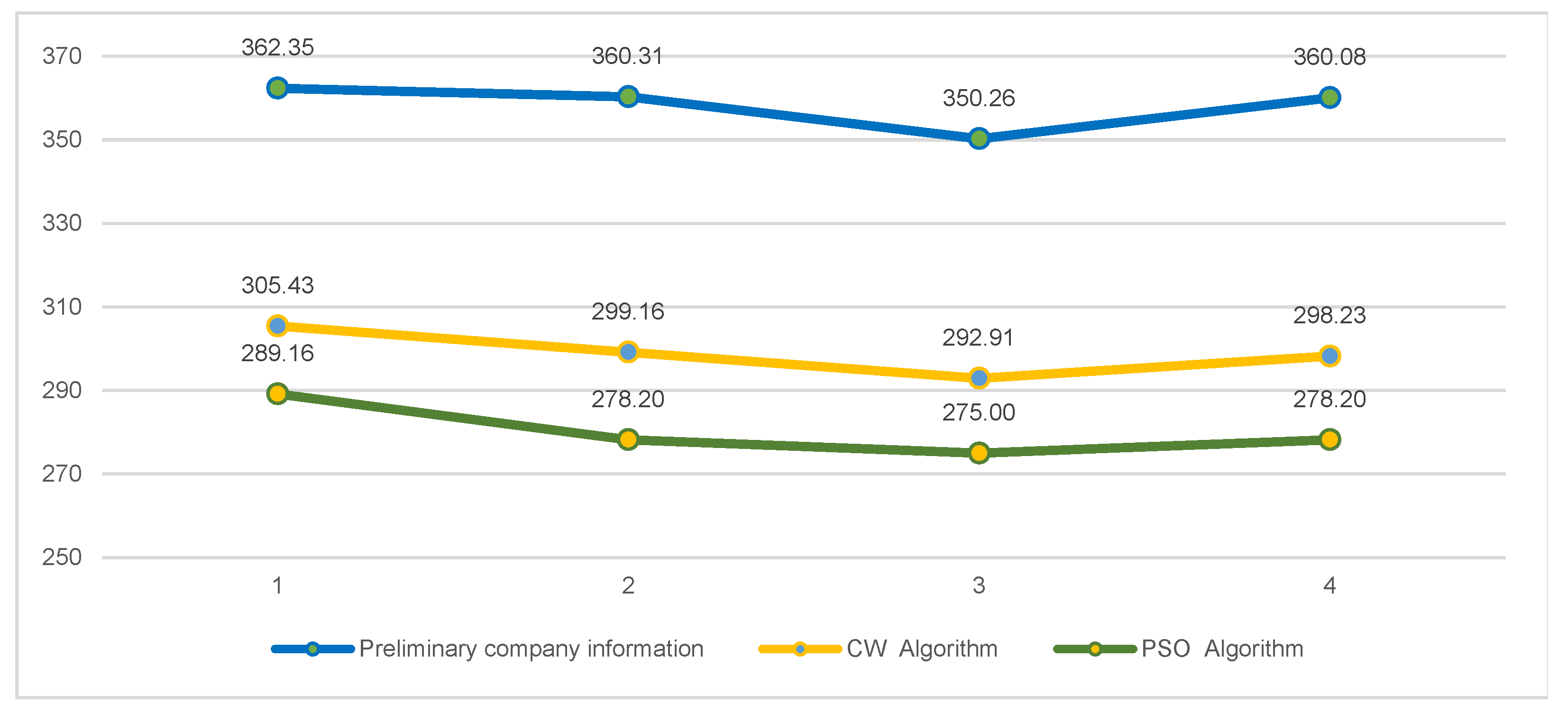
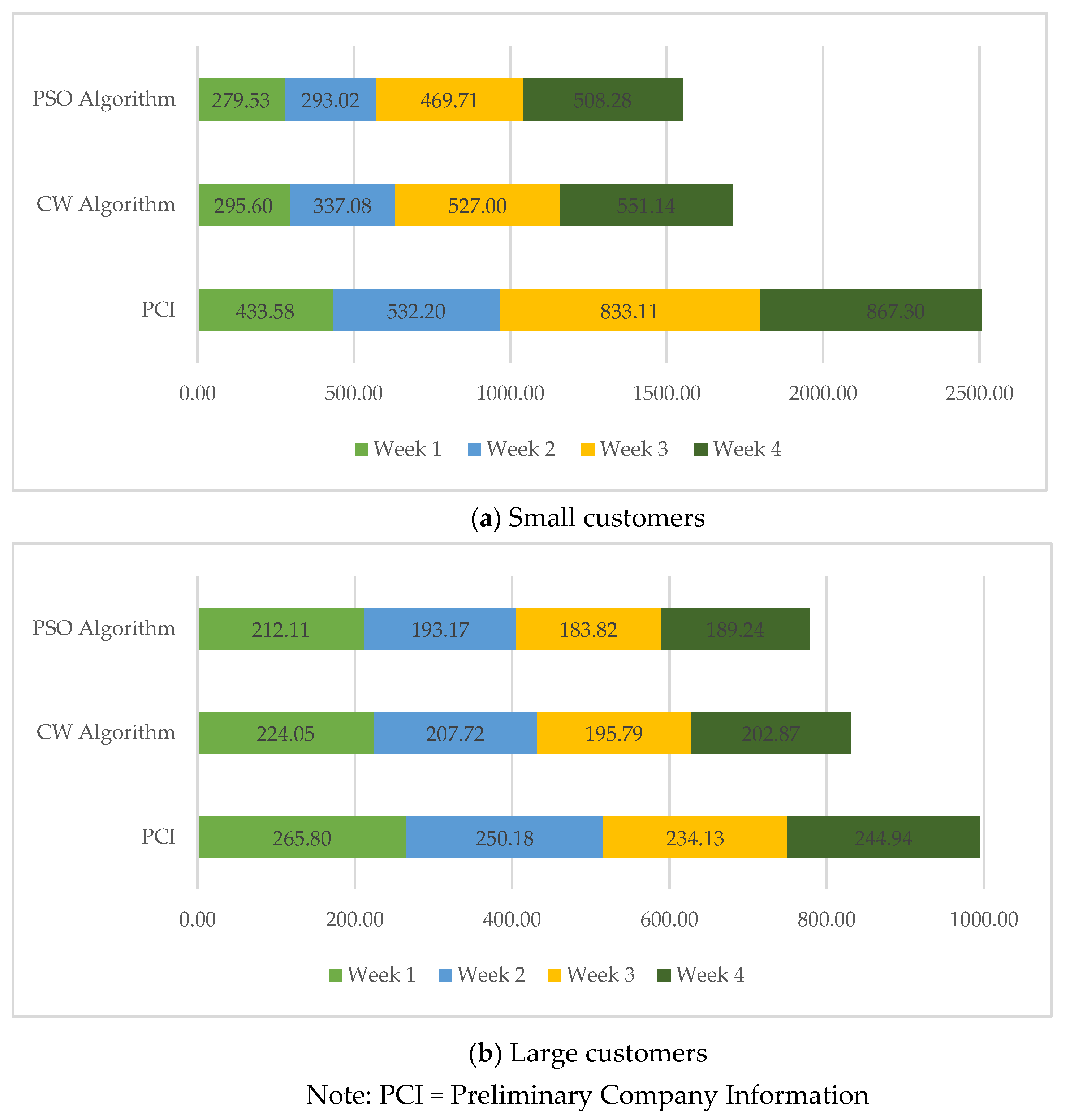
| 1 | 305.43 | 289.16 | 16.27 | 5% |
| 2 | 299.16 | 278.20 | 20.96 | 7% |
| 3 | 292.91 | 275.00 | 17.91 | 6% |
| 4 | 298.23 | 278.20 | 20.03 | 7% |
| Week | CW (Mean ± SD) | PSO (Mean ± SD) | p-Value (Mann–Whitney–Wilcoxon Test) |
|---|---|---|---|
| W1 | 305.43 ± 2.11 | 289.16 ± 2.52 | 1.45 × 10−11 |
| W2 | 299.16 ± 3.35 | 278.20 ± 3.05 | 1.45 × 10−11 |
| W3 | 292.91 ± 3.41 | 275.00 ± 2.85 | 1.45 × 10−11 |
| W4 | 298.23 ± 3.23 | 278.20 ± 2.55 | 1.45 × 10−11 |
| Vehicle Type | Trips/Month | Quantity (T/Day) | Operational Days | Fuel Cost (R$/month) |
|---|---|---|---|---|
| Volkswagen Delivery (Volkswagen AG, Wolfsburg, Germany) | 300 | 1.5 | 5 | 1169.89 |
| Hyundai HR (Hyundai Motor Company, Seoul, South Korea) | 653 | 1.0 | 5 | 1315.47 |
| DEFRA Factor (kg CO2/L) | Baseline–Small | CW–Small | PSO–Small | Baseline–Large | CW–Large | PSO–Large |
|---|---|---|---|---|---|---|
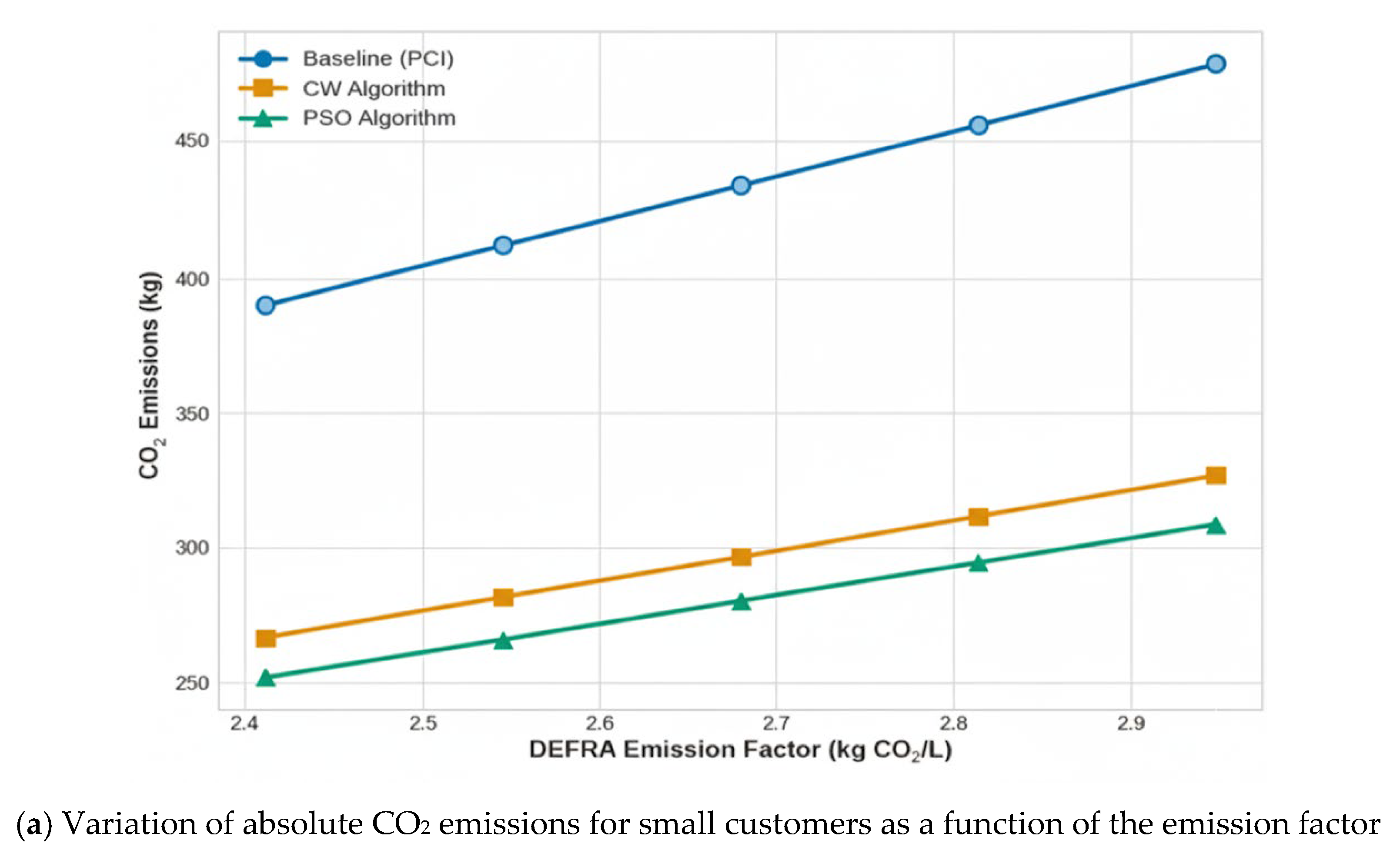
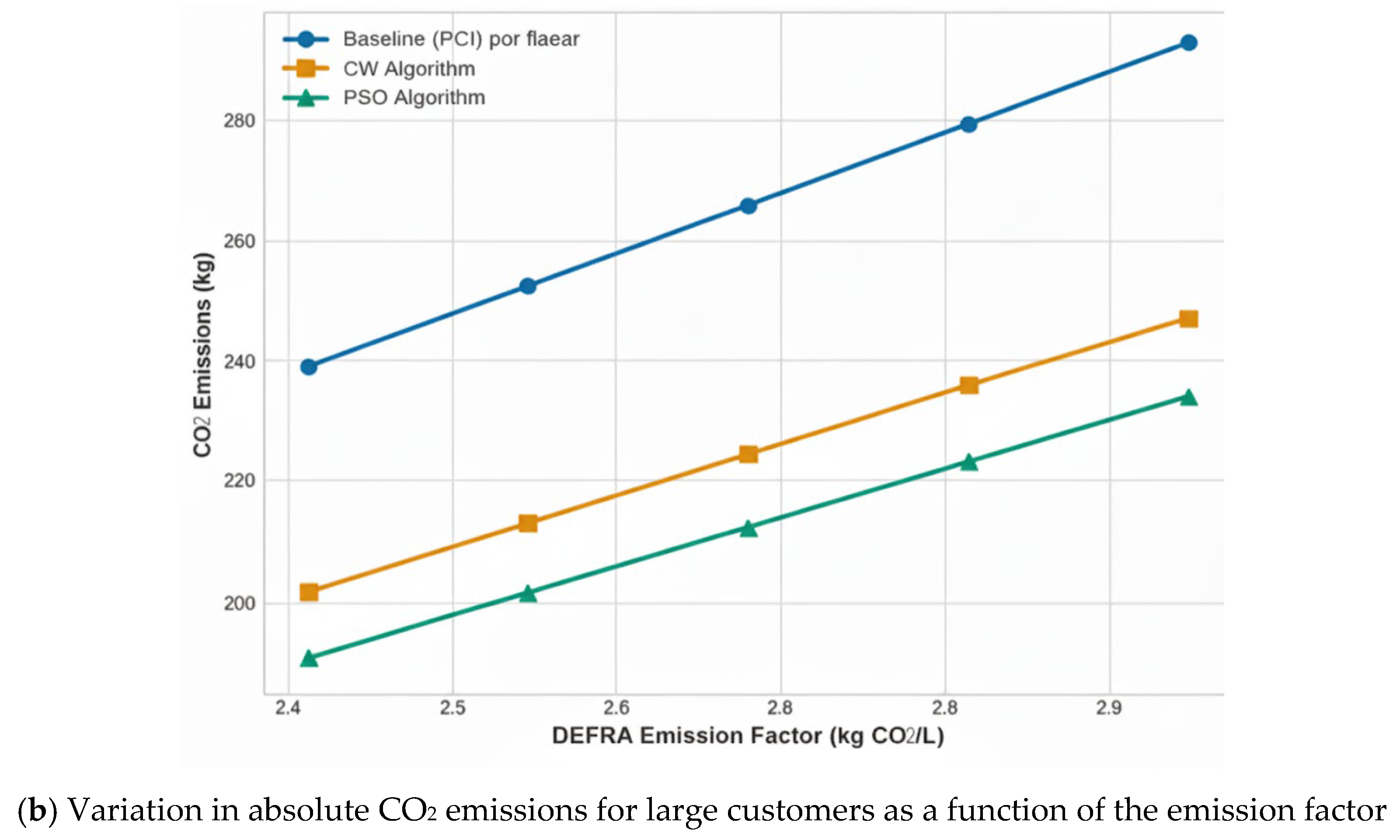
| 2.412 (–10%) | 398.9 | 271.2 | 250.1 | 1025.6 | 855.9 | 801.4 |
| 2.680 (Base) | 442.9 | 301.2 | 277.8 | 1138.5 | 949.9 | 888.3 |
| 2.948 (+10%) | 486.9 | 331.3 | 305.5 | 1251.3 | 1043.9 | 975.2 |
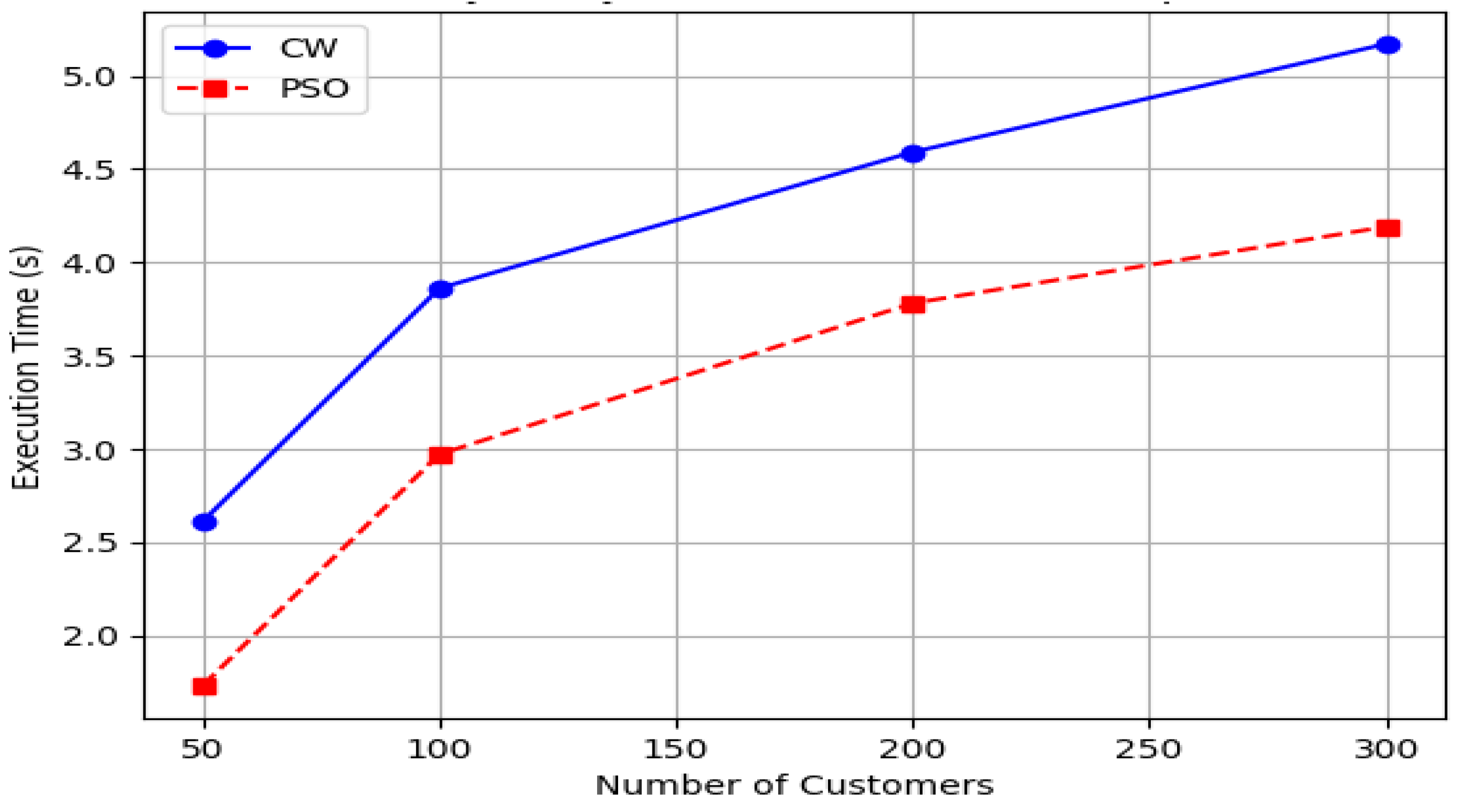
| Number of Customers | CW Time (s) | PSO Time (s) | Percentage Difference (%) |
|---|---|---|---|
| 50 | 2.61 | 1.73 | 33.72 |
| 100 | 3.86 | 2.97 | 23.06 |
| 200 | 4.59 | 3.78 | 17.65 |
| 300 | 5.17 | 4.19 | 18.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castillo Ulloa, M.I.; Ramos Huarachi, D.A.; Moretti, V.; Hluszko, C.; Neves Puglieri, F.; Monteiro Obal, T.; Carlos de Francisco, A. Sustainability and Algorithmic Comparison of Segmented PVRP for Healthcare Waste Collection: A Brazilian Case Study. Sustainability 2025, 17, 8536. https://doi.org/10.3390/su17198536
Castillo Ulloa MI, Ramos Huarachi DA, Moretti V, Hluszko C, Neves Puglieri F, Monteiro Obal T, Carlos de Francisco A. Sustainability and Algorithmic Comparison of Segmented PVRP for Healthcare Waste Collection: A Brazilian Case Study. Sustainability. 2025; 17(19):8536. https://doi.org/10.3390/su17198536
Chicago/Turabian StyleCastillo Ulloa, Micaela Ines, Diego Alexis Ramos Huarachi, Vinicius Moretti, Cleiton Hluszko, Fabio Neves Puglieri, Thalita Monteiro Obal, and Antonio Carlos de Francisco. 2025. "Sustainability and Algorithmic Comparison of Segmented PVRP for Healthcare Waste Collection: A Brazilian Case Study" Sustainability 17, no. 19: 8536. https://doi.org/10.3390/su17198536
APA StyleCastillo Ulloa, M. I., Ramos Huarachi, D. A., Moretti, V., Hluszko, C., Neves Puglieri, F., Monteiro Obal, T., & Carlos de Francisco, A. (2025). Sustainability and Algorithmic Comparison of Segmented PVRP for Healthcare Waste Collection: A Brazilian Case Study. Sustainability, 17(19), 8536. https://doi.org/10.3390/su17198536






