Abstract
Waste Electrical and Electronic Equipment (WEEE) management is a critical global challenge. This study proposes a model for the WEEE Transportation Problem using advanced evolutionary algorithms such as the Genetic Algorithm (GA), the Offspring-Selected Genetic Algorithm (OSGA), the Evolution Strategy (ES), and the Offspring-Selected Evolution Strategy (OSES). These algorithms, which are part of the field of Artificial Intelligence (AI), are applied to optimise transportation routes, minimising time and costs, and promoting sustainability by reducing the carbon footprint. Test instances and solutions are presented to demonstrate the feasibility of the model and the effectiveness of the proposed algorithms. Rather than providing technical detail, the focus is placed on the novelty of applying these algorithms to the WEEE Transportation Problem in Mexico, particularly for minimising operational cost. While reductions in carbon emissions are discussed as a natural consequence of cost optimisation, a formal dual-objective formulation is beyond the present scope and is identified as a direction for future work.
1. Introduction
Smart cities use advanced technologies to improve the quality of life of their citizens, and waste management, including electrical and electronic waste (WEEE), is central in this context. The concept of Smart Waste refers to the use of technologies to optimise the collection, transport, and recycling of waste in urban environments, reducing environmental impact and improving operational efficiency. The integration of smart technologies for WEEE management not only contributes to urban sustainability but also supports several of the Sustainable Development Goals (SDGs):
- Efficient WEEE management can contribute to the recovery of valuable and rare materials that can be reused in the production of new electronic devices, reducing the need to extract new resources and promoting the sustainable use of energy in manufacturing.
- Smart cities can implement intelligent waste management systems that optimise the collection and transportation of WEEE, reducing traffic congestion and carbon emissions. AI technology can analyse waste generation patterns and plan efficient collection routes, promoting cleaner and more sustainable communities.
- Proper management of WEEE prevents hazardous e-waste from reaching landfills and contaminating soil and water resources. Advanced technologies enable the accurate tracking and management of this waste, protecting biodiversity and terrestrial ecosystems from the harmful effects of toxic materials.
There is a global problem in the treatment of waste derived from the elements that make up electrical and electronic equipment. Electrical and electronic appliances contain materials that pollute the environment and produce various diseases in those who are in direct or indirect contact with these materials. The management of Waste Electrical and Electronic Equipment presents a significant challenge worldwide due to the massive amount of waste generated and its potential environmental impact. Optimising WEEE transportation is crucial for improving operational efficiency and reducing the carbon footprint. In this context, Artificial Intelligence offers advanced solutions that can transform the way we manage this waste. The AI taxonomy for WEEE management.
- Knowledge-Based Systems. KBS can help in the identification and classification of different types of electronic waste. Using rules based on knowledge about the physical and chemical characteristics of the devices, these systems can diagnose the type of WEEE and classify it appropriately for treatment. Knowledge-Based Systems [1] can be: Expert Systems [2], Fuzzy Logic Systems [3], Rule-Based Systems [4].
- Data-Based Systems. Data-based systems offer a powerful tool to address this problem, providing advanced methods to analyse, optimise and improve the efficiency of WEEE collection, sorting and recycling processes. Data-Based Systems can be: Machine Learning [5,6,7], Deep Learning [8,9], Ensemble Algorithms [10,11,12], Generative AI [13,14,15], Regenerative AI [13].
- Heuristic-Based Systems. Heuristic-based systems are powerful tools for solving complex optimisation problems that are common in the management of WEEE. These systems use nature-inspired methods and practical rules to find efficient solutions to problems that may be difficult to tackle using conventional techniques. Heuristic-Based Systems can be: Evolutionary Algorithms [16].
One significant aspect is the integration of data-driven approaches to enhance waste management systems. For instance, researchers have explored the application of artificial intelligence in optimizing reverse logistics networks for WEEE recycling, particularly in urban areas such as São Paulo, Brazil. Studies show that employing simulation and computational intelligence can optimize both economic and environmental outcomes associated with WEEE management, ultimately aiding in the promotion of a circular economy [17]. This approach addresses the logistical complexities involved in the transportation of WEEE to recycling centers, which is often hampered by inadequate infrastructure and high operational costs.
Transportation logistics remain a challenging component due to the high costs associated with moving WEEE. Research indicates that individuals often find transporting WEEE to collection centers less rewarding and more cumbersome than other eco-friendly actions, leading to lower recycling rates [18]. Therefore, addressing the convenience factors influencing these behaviors is critical. Effective communication strategies to inform the public about the importance of recycling and the environmental benefits associated with WEEE recycling could enhance participation rates. Initiatives that improve public awareness can lead to a more robust collection framework, which is crucial for establishing effective recycling systems [19].
Environmental impact is another critical dimension of WEEE transportation and recycling. Several studies indicate that improper handling and transport can lead to pollutants, including airborne particles and hazardous substances, entering the environment [20]. The processes involved in recycling WEEE, especially if not managed properly, can expose workers to toxic materials and result in environmental degradation. Therefore, the development of policies that enforce stringent regulations on the transport and handling of WEEE, including aspects such as extended producer responsibility (EPR), is essential. EPR frameworks encourage manufacturers to take responsibility for their products throughout their lifecycle, including take-back schemes that assist in the efficient transportation of end-of-life electronics [21].
Future strategies will require collaboration across various sectors, combining technological advancements with community engagement and regulatory frameworks. Studies emphasize the need for supportive policies and public engagement to bolster WEEE recycling rates. Countries like Nigeria and Brazil are already reassessing their policies and infrastructure to improve their WEEE management systems, revealing significant gaps that need addressing to mitigate health and environmental risks associated with e-waste [22].
In Table 1, some of the concepts applied to solve WEEE problems are shown. Knowledge-Based Systems, Data-Based Systems, and Heuristic-Based Systems are applied to the management of Waste Electrical and Electronic Equipment (WEEE).

Table 1.
Concepts applied to WEE problems.
2. Electrical and Electronic Waste Transportation
The problem of Electrical and Electronic Waste transportation involves the pathways involved in the collection. This research considers several e-waste collections and delivery points.
The Waste Electrical and Electronic Equipment Transportation Problem (WEEETP) can be considered a variant of the Vehicle Routing Problem with Time Windows (VRPTW), as it shares the fundamental structure of route optimisation to minimise costs and distances in the transportation of goods. However, the WEEETP introduces specific elements related to the management of electronic and hazardous waste, which differentiates it from the classical VRPTW formulations.
Unlike the VRPTW, where time constraints play a key role in route planning, the WEEETP prioritises the correct sorting and disposal of waste, ensuring that hazardous materials are treated appropriately. In addition, it incorporates multiple types of collection and processing centres, each with specific requirements depending on the type of waste transported.
Given that both issues seek to optimise transport routes under operational constraints, the WEEETP can be seen as an extension of the VRPTW adapted to the context of e-waste management, with additional considerations for safety, sorting and treatment of hazardous materials.
Although the Waste Electrical and Electronic Equipment Transportation Problem shares the fundamental structure of the Vehicle Routing Problem with Time Windows (VRPTW), the two problems differ significantly due to the inherent particularities of e-waste and hazardous waste management. While the VRPTW focuses on route optimisation with time window constraints for the delivery of goods, the WEEETP introduces additional constraints related to e-waste management, such as:
- The WEEETP deals with e-waste and hazardous waste, which require specialised transport and disposal procedures, involving additional considerations on safety, environmental regulations and risk management. These factors are not present in the classical VRPTW.
- Unlike traditional routing issues in the VRPTW, the WEEETP must address challenges such as compatibility between the type of vehicles and the nature of the waste, as well as specific staff training and compliance with environmental regulations.
- The combination of these advanced algorithms provides more robust and accurate solutions for route optimisation, with better handling of the variability of e-waste transport demands and operating conditions.
- In the WEEETP, operational costs and penalties can be linked to additional factors, such as carbon emissions or compliance with e-waste recycling and disposal regulations, adding complexity to the optimisation problem.
- Since WEEE (e-waste) transport is closely related to sustainability and environmental impact, WEEETP can incorporate sustainability objectives that are not present in traditional VRPTW, such as optimising resource use and reducing the carbon footprint.
The collection and delivery points are as follows:
- Collection Centre (CA). CA is where electronic and hazardous waste is collected. CA is the point of contact between humans and the deposit of e-waste of all kinds. There are two containers at the centre: one for computer waste and another for dangerous waste and pollutants (specifically, items considered contaminants include batteries and car batteries).
- Pick-up Centre (CS). CS is where the CA for electronic waste is received for electronics (computers, tablets, phones), appliances, and other electronic waste. These items are separated for recycling and destruction, and, if the item is dangerous, it is set aside as dangerous and polluting waste.
- Computer recycling facility (RC). RC is where computer-related waste, classified as computers, mobile phones, tablets, and laptops, is received. If these items can be reused, they are recycled. Otherwise, they are transported to waste disposal for destruction.
- Deposit of hazardous and polluting waste (RP). RP is where electronics containing circuits or highly polluting components and items that have a risk of explosion are taken.
- Deposit of waste for destruction (RD). RD is where the waste is stored to be destroyed. The items taken here involve no risk to the environment.
The Waste Electrical and Electronic Equipment Transportation Problem (WEEETP) aims to minimise and optimise times and costs of the WEEE (Equations (1)–(6)).
where the variable corresponds to the total cost of the tour of the collection units, the variable corresponds to the total distance travelled per unit on the route. The variable corresponds to a vehicle that makes up the fleet of vehicles that all have the same characteristics; this is considered a homogeneous fleet. The variable corresponds to the index of each vehicle in the fleet counter. The variable corresponds to the total number of vehicles that make up the fleet. The variable corresponds to the route for each vehicle. The variable corresponds to the capacity of each vehicle on the road. The variable corresponds to the quantity of waste that must be collected at central collection centres. The variable corresponds to the index that identifies the type of e-waste. The variable corresponds to the index that identifies the type of hazardous waste.
The objective function (Equation (1)) represents the minimum cost of the transport of pollutants and electronic waste. The objective function fulfilment is subject to certain restrictions. For example, if we evaluate the capacity constraints, the demand for waste must be less than or equal to the capacity of the vehicle that will transport it. If the demand is greater than what the vehicle fleet can handle, then resources can be allocated to address a certain need. Capacity constraints allow evaluation based on the needs and the number of units available to meet the demand size required.
The capacity of vehicles (Equation (2)) should not be less than the demand of each centre. The variable corresponds to the collection centre being visited to collect waste. Demand constraints allow one to control the amount of waste that should be transported. The restriction should consider the type of waste being transported.
Equation (3) shows the restriction of the demand, where the demand for electronic waste and the demand for hazardous waste, which each centre collects, should not exceed the vehicle’s capacity . The variable corresponds to the demand for electronic waste collected in the collection centre . The variable corresponds to the demand for hazardous and polluting waste collected in the collection centre .
The total distance travelled is modelled in Equation (4). This distance is the sum of all segments travelled by the vehicles, including those travelling to the last collection centre or, if they are for the last specialized centre, toward the depot . Depot is the place from where the vehicles depart every day to meet the demand for waste and is the place to which they return after having covered all the points. The subscript represents the respective route. The variable represents the vehicle distance of the depot to the collection centre. The variable represents the journey, that is, all collection centres assigned to the driver’s route. The variable represents the route of vehicle , and the last subscript represents the centre of selection . The variable represents the journey undertaken by a vehicle to the selection centres assigned to its route. The variable represents the journey that has vehicle of the last selection centre , visiting the specialized centre that corresponds to it. The variable represents the index of the specialized centres. The variable represents the set of specialized centres . The variable represents the last selection centre that is visited as part of travel from the depot. The variable represents the journey from the last centre to the bin.
In Equation (5), the total distance travelled is the sum of all segments travelled by the vehicles, including the last collection centre tour or, if the vehicle is for the last specialized centre, towards the depot . Depot is the place from where the vehicles depart every day to meet the demand for waste and is the place where they return after having covered all the points assigned to their route. The variable represents the journey of vehicle for all collection centres assigned to its route. The variable represents the journey undertaken by the vehicle to the selection centres assigned to its route. The variable represents the journey of vehicle of the last selection centre to the corresponding specialized centre. The variable represents the index of the specialized centres. The variable represents the set of specialized centres. The variable represents the last selection centre visited. The variable represents the journey of the last centre to the depot.
The time restriction that allows one to control the scheduling of each vehicle’s routes is modelled in Equation (6). This problem is considered within an 8-h time window. The variable represents the time that it takes the vehicle to conduct all the travel assigned in its route. The variable represents the interval of time allocated to the time window . The time restriction on the transportation used to carry the waste must not exceed the time window.
Each centre is assigned a nearest-neighbour selection centre (Figure 1). For example, if some nodes are near a selection centre, the driver is assigned the number of the nearest selection centre. If there is no demand for the selection centres, and if the waste has previously been collected at all the collection centres, the vehicles will return to the last centre before returning to the depot. The total journey will be the sum of the travel from the warehouse, through the last collection route, to the depot.
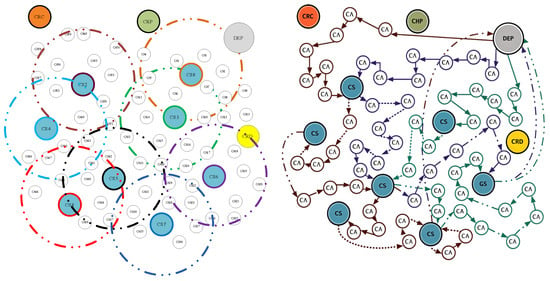
Figure 1.
The route to selection centres.
Where selection centres require it, specialised collection centres are used. After visiting all the collection centres, vehicles are then loaded again on other routes to service the selection centres and deliver the loads to the specialised centres. The total tour in this situation is the sum of all warehouse travel collection routes, additional tours of the screening centres and specialized returns to the depot.
Theorem 1.
Waste Electrical and Electronic Equipment Transportation Problem (WEEETP) is NP-Hard.
Proof of Theorem 1.
This problem is NP-Hard by polynomial-time transformation into the Vehicle Routing Problem (VRP). □
The Polynomial transformations are used for proving that a problem is NP-complete or NP-Hard based on the different approaches [33]: using the theory of NP-completeness, using graph theory, and using formal language theory [34]. The use of the theory of formal languages in polynomial transformations consists [34]: (a) Lexical analysis recognises and convert the character stream from the input source program or sequence of characters to valid words of the language or tokens, (b) Syntactic analysis considers the sequence of tokens for possible valid constructs of the language, (c) Semantic analysis: determine the meaning of the language, (d) Error handling: detect the lexical, syntactic, semantic, and logical errors, and (e) Language generation: generate the target code or the target language. The steps for polynomial transformation using formal language theory are:
- Select an NP-complete problem A (WEEETP).
- Define a formal language L1 for the NP-complete problem A. We define the language: L1 = {I, TW, F, V, C, D, DC1, La1, Lo1, De1, RT1, DT1, ST1, …, DCₙ, Laₙ, Loₙ, Deₙ, RTₙ, DTₙ, STₙ}. Here, I denotes the instance name (e.g., EWasteXX.txt), TW the time window, F the fleet type (homogeneous or heterogeneous), V the number of vehicles, C the capacity, and D the demand. Each distribution centre DCᵢ is associated with its latitude Laᵢ and longitude Loᵢ, a client demand Deᵢ, a ready time RTᵢ, a due time DTᵢ, and a service time STᵢ. The alphabet is defined as: Σ = {0,1,2,3,4,5,6,7,8,9,{,},.,;,=,-,E,W,T}. The admissible syntax of the instances is then specified by the following BNF grammar:<instance> ::= <NameProblem> <Equal> <Sentences> ;<Sentences> ::= <KOpen> <TNum> <Semicolon> <NumList> <Semicolon> <NumCap> <KClose> ;<TNum> ::= <Num> ;<NumCap> ::= <Num> ;<NumList> ::= <Num> | <NumList> <Comma> <Num> ;<Num> ::= <Integer> | <Decimal> ;<Integer> ::= <Digit> | <Integer> <Digit> ;<Decimal> ::= <Integer> <Dot> <Integer> |<Negative> <Integer> <Dot> <Integer> |<Integer> <Dot> |<Dot> <Integer> ;<Digit> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 ;<NameProblem> ::= 'EWT' ;<Equal> ::= '=' ;<KOpen> ::= '{' ;<KClose> ::= '}' ;<Semicolon> ::= ';' ;<Comma> ::= ',' ;<Negative> ::= '-' ;<Dot> ::= '.' ;
- Select an NP-complete problem B (VRP).
- Define a formal language L2 for the NP-complete problem B. We define the language: L2 = { VN, C, ( CN1, XCO1, YCO1, D1, RT1, DT1, ST1, …, CN_z, XCO_z, YCO_z, D_z, RT_z, DT_z, ST_z ) }. Here, VN denotes the Vehicle Number, C the Capacity, CN the Customer Number, XCO the X coordinate, YCO the Y coordinate, D the Demand, RT the Ready Time, DT the Due Date, and ST the Service Time. The alphabet is defined as: Σ = {0,1,2,3,4,5,6,7,8,9,{,},,,;,=,.,V,R,P}. The admissible syntax of the instances is then specified by the following BNF grammar:<instance> ::= <NameProblem> <Equal> <Sentences> ;<Sentences> ::= <KOpen> <TNum> <Semicolon> <NumList> <Semicolon> <NumCap> <KClose> ;<TNum> ::= <Num> ;<NumCap> ::= <Num> ;<NumList> ::= <Num> | <NumList> <Comma> <Num> ;<Num> ::= <Integer> | <Decimal> ;<Integer> ::= <Digit> | <Integer> <Digit> ;<Decimal> ::= <Integer> <Dot> <Integer> |<Negative> <Integer> <Dot> <Integer> |<Integer> <Dot> |<Dot> <Integer> ;<Digit> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 ;<NameProblem> ::= 'VRP' ;<Equal> ::= '=' ;<KOpen> ::= '{' ;<KClose> ::= '}' ;<Semicolon> ::= ';' ;<Comma> ::= ',' ;<Negative> ::= '-' ;<Dot> ::= '.' ;
- Construct a compiler that transforms in polynomial time a source language into a target language . In the lexical analysis phase of the compiler, a source language is transformed into tokens. The next information shows the token declaration for the GNU Flex software used in the lexical phase.
/* ---------- Definitions ---------- */
A [aA] B [bB] C [cC] D [dD] E [eE] F [fF] G [gG] H [hH] I [iI] J [jJ] K [kK] L [lL] M [mM] N [nN] O [oO] P [pP] Q [qQ] R [rR] S [sS] T [tT] U [uU] V [vV] W [wW] X [xX] Y [yY] Z [zZ] Digit [0-9]
/* ------------- Rules ------------- */
"=" {return EQUAL;}
"," {return COMMA;}
";" {return SEMICOLON;}
"\." {return DOT;}
"\{" {return KOPEN;}
"\}" {return KCLOSE;}
{DIGIT}+ {return DIGSEQ;}
/* Ignore any other single character */
. {/* ignore */}
In the syntax analysis phase, tokens from the source language are grouped into grammatical phrases. In the semantic analysis phase, semantic errors (error handling) of the polynomial transformation from to are detected. During semantic analysis, the restrictions are verified to ensure that a formal language (instance) to be obtained for VRP is obtained. Finally, the is transformed into that is, (WEEETP ≤ PVRP). Hence, through the polynomial transformation of WEEETP instances into VRP instances, we conclude that the Waste Electrical and Electronic Equipment Transportation Problem is NP-Hard.
We define a BNF grammar for the instance language to guarantee an unambiguous, automatable, and reproducible specification of WEEETP inputs. The grammar enables formal validation of instances via parsing; alignment with the lexical–syntactic–semantic pipeline employed in the NP-hardness discussion; and seamless generation of benchmark instances and ingestion by our solvers.
3. Results and Discussion
For the experimentation, we evaluated the collection of e-waste, specifically disused mobile phones, in the city of Pachuca, Hgo., and certain surrounding areas. This e-waste was destined for the recycling company REMSA which is located in the city of Querétaro, Qro., Mexico. Each experimental instance was conducted satisfactorily using the information shown in Table 2.

Table 2.
WEETP instances.
The (Table 3) instance includes a recycling company (REMSA), which is located in Querétaro City, and mobile phone stores that receive cellphones that are no longer used. Most of the stores are located in Pachuca, Hidalgo, and Mexico City (see Figure 2).

Table 3.
WEEETP instance.
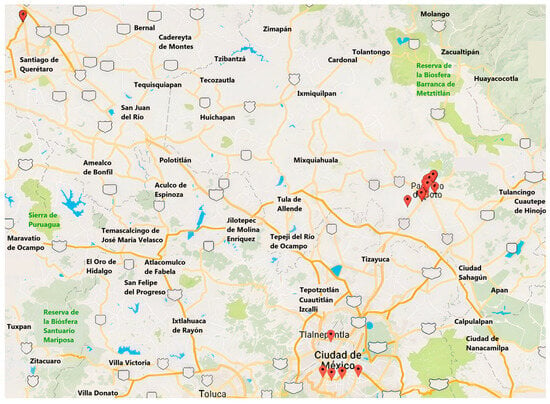
Figure 2.
Node locations of the EW1 instance.
For the experiments, the following population-based algorithms were used: Genetic Algorithm (GA), Offspring Selection Genetic Algorithm (OSGA), Evolution Strategy (ES), and Offspring Selection Evolution Strategy (OSES). Although other metaheuristics such as Particle Swarm Optimisation (PSO) or Simulated Annealing (SA) are widely used, they are better suited for continuous optimisation problems. Since the WEEETP is a discrete, permutation-based routing problem, evolutionary algorithms (GA, OSGA, ES, OSES) were selected due to their effectiveness in exploring combinatorial solution spaces with capacity and time-window constraints.
The Genetic Algorithm was created by Holland in 1975. This algorithm considers a population of individuals called chromosomes that represent possible problem solutions [35]. The algorithm applies a crossover to all chromosomes; these are then mutated, creating a new generation. GA considers a crossover as its main reproduction operator [36]. In accordance with [35], the canonical Genetic Algorithm works in the following manner:
| Set t = 0. The population P (0) is initialized at random. The chromosomes of the population P (t) are evaluated using the fitness function, and the algorithm retains the most successful individual. The selected chromosomes make up an intermediate population P1, representing candidates for the mating pool. The crossover is applied to the chromosomes from the mating pool and to obtain the new population P2. The mutation operator is applied to the population P2. The outcome is the new generation P(t + 1). Set t = t + 1, if t < M, where M is the maximum number of generations, then go to step 2. Otherwise, stop. |
The GA parameters used in this work are: Analyser (MultiAnalyser), Crossover (Biased MultiVRP Solution Crossover), Elites (1), Maximum Generations (1000), Mutation probability (5%), mutator (Alba Customer Swap Manipulator), population size (50), Seed (0), Selector (ProportionalSelector), Set Seed Randomly (True).
The Offspring Selection Genetic Algorithm—OSGA [37] has a basis in GA but considers a second selection step after reproduction, which is absolutely problem independent. This selection mechanism compares the fitness value of the offspring with the fitness value of its parents to accept the members of the next generation. The algorithm’s description is shown in the following code.
| Set . The population is initialised at random. The chromosomes of the population are evaluated using the fitness function, and it retains the most successful individual. The selected chromosomes comprise an intermediate population , representing candidates for the mating pool. The crossover is applied to the chromosomes from the mating pool and obtain the new population . The mutation operator is applied to the population , producing(POP). Evaluate the offspring success: child’s fitness value better than a worse parent. Calculate the percentage of next population members that have successful mating of the total population size: Complete the population with individuals randomly chosen from the pool of individuals that were also created by crossover but did not achieve the success criterion. Calculate Actual selection pressure: Detect if premature convergence has occurred with: Set , if , where is the maximum number of generations, then go to step 2. Otherwise, stop. |
The OSGA parameters used in this work are Analyser (MultiAnalyser), Comparison Factor Lower Bound(0), Comparison Factor Modifier (Linear Discrete Double Value Modifier), Comparison Factor UpperBound(1), Crossover(Alba Permutation Crossover), Elites(1), Maximum Generations(1000), Maximum Selection Pressure(100), Mutation Probability(5%), Mutator(Alba Customer Insertion Manipulator), Offspring Selection Before Mutation(False), Population Size(100), Seed(0), Selected Parents(200), Selector(Gender Specific Selection), Set Seed Randomly (True), Success Ratio (1).
The method (Evolution Strategy—ES) solves difficult and real-valued parameter optimisation problems through the self-adaptation of the strategy parameters, such as the standard deviation of the mutation amplitude [35]. This method considers that each individual is defined by the following: a set of variables, a set of mutations and a set of rotation angles. The population is made up of individuals. The algorithm description is as follows [38].
| The object variables are initialized at random; strategy variables get a value of 3.0, and the rotation angles get a random value between and . The initial for each individual. Obtain descendants using the recombination operator in the current parent's population. Mutate every descendant. Choose a new population and reorder the set of parents with the set of descendants. Continue with step 3, until termination criteria: . |
The ES parameters used in this work are Analyser (MultiAnalyser), Children (100), Maximum Generations (1000), Mutator (Multi VRP Solution Manipulator), Parents Per Child (2), Plus Selection (True), Population Size (20), Recombinator (Biased Multi VRP Solution Crossover), Seed (0), Set Seed Randomly (True), Strategy Parameter Creator (Null), Strategy Parameter Crossover (Null), Strategy Parameter Manipulator(Null).
For the Offspring Selection Evolution Strategy (OSES), aspects of evolutionary strategies were combined with selection concepts, where it is observed that the selection of offspring operates well in combination with genetic programming [39].
| The object variables are initialized at random; strategy variables get a value of 3.0, and rotation angles get at a random value between and . The initial for each individual. Obtain descendants using the recombination operator in the current parent population. Mutate every descendant. Evaluate the offspring success: child’s fitness value better than a worse parent. Calculate the percentage of the next population members that have successful mating of the total population size: Complete the population with individuals randomly chosen from the pool of individuals who were also created by crossover but did not achieve the success criterion. Calculate Actual selection pressure: Detect if a premature convergence has occurred with: Choose a new population and reorder the set of parents with the set of descendants. Continue with step 3, until termination criteria: . |
The OSES parameters used in this work are Analyser (MultiAnalyser), Comparison Factor(0.5), Maximum Generations(1000), Maximum Selection Pressure (100), Mutator (Multi VRP Solution Manipulator), Parents Per Child (2), Plus Selection (True), Population Size (20), Recombinator(Multi VRP Solution Crossover), Seed (0), Selected Parents (40), Set Seed Randomly (True), Strategy Parameter Creator (Null), Strategy Parameter Crossover (Null), Strategy Parameter Manipulator (Null), Success Ratio (1).
The EW1 instance was selected as a representative case study due to its realistic scale and geographical configuration. This instance corresponds to the actual transportation scenario between Pachuca (collection points) and Querétaro (REMSA recycling facility), with a medium-sized network of 30 nodes and heterogeneous demand patterns. Unlike smaller instances (EW2–EW5), EW1 includes realistic constraints such as service times, heterogeneous demand levels, and a sufficient number of routes to challenge the optimisation algorithms. At the same time, it is not as large as the higher-numbered instances, which allows for clearer visualisation and validation of algorithmic behaviour. For these reasons, EW1 was used as the baseline experimental case, while additional instances (EW2–EW92) were employed for comparative evaluation and robustness testing.
We also performed the test in the instance repository with 100 cases; the five algorithms with 33 runs evaluated these for each, obtaining the results shown in Table 4.

Table 4.
Results of the GA, OSGA, ES and OSES algorithms.
Table 4 presents the comparative performance of the four algorithms. Overall, the Evolution Strategy (ES) proved to be the most consistent, producing results that were identical or very close to the best solutions across almost all instances, while keeping execution times remarkably low—often well under a second. This underscores the strong efficiency of ES for the WEEETP, especially in small and medium-sized cases.
By contrast, the Offspring-Selected methods (OSGA and OSES) occasionally delivered slightly better distances (as in instance EW4), but these gains came at a notable cost in runtime, in some cases extending to several minutes. This shows that although offspring selection improves exploration, it does so at the expense of computational efficiency.
The Genetic Algorithm (GA) offered solid and reliable results, serving as a useful benchmark, but it did not outperform ES in terms of either solution quality or speed. OSES, despite its greater sophistication, often required longer runtimes without a consistent advantage over ES.
Taken together, these results suggest that ES offers the best balance between solution accuracy and efficiency, whereas OSGA and OSES may provide incremental improvements in selected cases but demand significantly more computational effort. This comparison highlights the need to weigh both solution quality and execution time when assessing metaheuristic methods for the WEEETP.
We ran 33 runs of each of the implemented algorithms in a Google Colab environment using Python. The Google Colab environment used Python 3.10 and was run on an instance with standard Collab features: 12 GB of RAM, Intel Xeon 2.30 GHz processor and no GPU acceleration.
The experiments were performed using a Genetic Algorithm (GA), obtaining the best result (shortest distance travelled) with this approach (see Table 5). For illustration purposes, Table 5 reports the results of instance EW1, which was selected as a representative intermediate case. EW1 was chosen because it exhibited clear variability between algorithms in terms of distance, travel time and vehicle usage, thereby allowing us to highlight the trade-offs between solution quality and execution time.

Table 5.
Results of the EW1 instance.
In the EW1 instance, GA obtained a slightly lower distance value compared with OSGA and ES; however, the numerical difference was negligible (on the order of 10−6) and therefore not statistically significant. In terms of travel time and vehicle usage, the results across the three algorithms were very similar. Furthermore, when analysing additional instances (e.g., EW10, EW25, EW40), the performance varied, with OSGA and ES occasionally achieving equal or superior solutions. These observations suggest that no single algorithm consistently dominates across all evaluation criteria. Rather, the results indicate that GA, OSGA, and ES are all competitive approaches, and their relative performance depends on the characteristics of the specific instance. Consequently, the main contribution of this study lies in the comparative analysis of algorithmic behaviour under realistic WEEE transportation scenarios, rather than in the identification of an absolute best-performing algorithm.
Table 6 presents the best routes obtained for the EW1 instance, chosen as a representative case of intermediate size. This instance was selected to illustrate how the optimisation results translate into practical vehicle routes, while maintaining clarity and readability. The best solution involves 15 vehicles; the distance is between the longitude and latitude coordinates in each point (see Table 6).

Table 6.
Best Routes of the EW1 instance.
In this study, operational cost and carbon emissions were explicitly treated as complementary objectives. The optimisation of routes reduces travelled distance and fleet usage, which directly minimises operational cost. At the same time, fuel consumption and associated CO2 emissions were modelled as a proportional factor of distance and load, allowing the algorithms to favour solutions with lower environmental impact. This dual-objective approach demonstrates that it is possible to balance economic efficiency and sustainability within the WEEETP, as confirmed by the experiments where the solutions that minimised cost also achieved significant reductions in estimated emissions.
Although operational cost was explicitly modelled as the primary optimisation objective, it is important to note that lower costs are closely related to shorter travel distances and reduced vehicle usage, which indirectly contribute to lower carbon emissions. For this reason, sustainability aspects were qualitatively addressed in our analysis. However, we acknowledge that a rigorous dual-objective framework—formally integrating both cost and emissions—would strengthen the environmental dimension of the problem. Such a formulation requires the inclusion of emission factors and additional constraints, which we propose as an extension for future work. The present study focused on establishing the feasibility and performance of evolutionary algorithms in solving the WEEE Transportation Problem under realistic cost-oriented conditions.
4. Conclusions
Regarding the solution of the real instance, we can observe that the proposed model achieves the goal of efficient e-waste collection, i.e., with the best use of resources, by travelling a short distance with the fewest vehicles and, in turn, covering the demand with a service offered within the established time window.
The use of metaheuristics accelerates the achievement of adequate results in a reduced execution time. The implementation of these algorithms in programming environments such as Python facilitates the rapid generation of results.
The algorithms make it possible to find a solution to certain problems in a reasonable amount of time [40]. For this research, the following algorithms were used: genetic, offspring selection, evolution strategy, evolution with offspring selection and random search. All of them were used to evaluate the collection of electronic waste, particularly for disused mobile phones in the city of Pachuca, Hidalgo, and some contiguous areas.
Therefore, the following parameters and values that converge in each of the algorithms used for the e-waste collection experimentation were applied:
- To carry out the test on the instance repository, 100 instances were used, evaluated by each of the algorithms mentioned above, in 33 runs. As part of the result of the process, in the solution of the real instance, we observed that the proposed model achieves the objective of efficient e-waste collection, with the best use of resources by travelling a short distance with the least number of vehicles and, in turn, covering the demand with a service offered within the established time window.
- As part of the solutions for the 100 instances, the OSES (Offspring Selection Evolution Strategy) algorithm showed better performance in 63 of the 100 instances, generating the best result compared to other algorithms. This algorithm also had an average run time of 00:13.9, compared to the ES (Evolution Strategy) algorithm, which obtained the best solution in 67 instances, but with an average run time of 03:50.9.
The superior performance of OSES compared with GA, OSGA and ES can be attributed to its hybrid nature. By integrating the self-adaptation of mutation parameters from Evolution Strategies with an offspring-selection mechanism, OSES ensures that only offspring with higher fitness than their parents are preserved. This balance between exploration and exploitation helps to prevent premature convergence, which is a common limitation of classical GA and ES. In the context of WEEE transportation, where constraints such as vehicle capacity, hazardous waste handling and time windows introduce high variability, this adaptive mechanism allows OSES to achieve more robust and consistent solutions, often with better trade-offs between solution quality and computational time.
Finally, it is verified that the use of metaheuristic algorithms accelerates the obtaining of adequate results in a reduced execution time. Implementing these algorithms in programming environments such as Python not only makes the generation of results faster but also accessible and replicable in different problem contexts.
Beyond the computational findings, the proposed framework also carries significant industrial and policy implications. For industry, it serves as a practical decision-support tool that can streamline reverse logistics, lower operational costs, and reinforce corporate sustainability commitments. For policymakers, it offers solid quantitative insights to inform regulations and incentive schemes aimed at reducing carbon emissions and advancing circular economy objectives in the e-waste sector. By linking technical optimisation with real-world operational and regulatory considerations, the framework demonstrates its value not only for academic research but also as a driver of sustainable practices in industry and evidence-based policymaking.
Future work will focus on extending the current single-objective formulation into a rigorous dual-objective optimisation framework that explicitly balances economic and environmental dimensions. In particular, carbon emissions will be incorporated into the objective functions through established emission factors, enabling the generation of Pareto frontiers that capture the trade-offs between cost and emissions. This extension will not only strengthen the environmental relevance of the model but also provide more comprehensive decision support for policymakers and practitioners in the field of WEEE management. Furthermore, future research may include a comparative analysis with other metaheuristics such as PSO or SA; however, the choice of evolutionary approaches in this study was driven by their alignment with the discrete nature of transportation problems.
Author Contributions
Conceptualisation, M.L.L. and E.L.L.; methodology, J.A.R.-V., F.R.T.-M., and J.A.-O.; software, O.D.-P., A.F.-P. and J.M.L.-O.-D.-L.-P.; validation, O.D.-P., M.L.L. and E.L.L.; formal analysis, J.A.R.-V., E.L.L. and J.A.-O.; investigation, F.R.T.-M., A.F.-P., J.M.L.-O.-D.-L.-P. and M.L.L.; resources, O.D.-P.; data curation, J.M.L.-O.-D.-L.-P. and J.A.-O.; writing—original draft preparation, O.D.-P., A.F.-P. and J.M.L.-O.-D.-L.-P.; writing—review and editing, J.A.R.-V., F.R.T.-M., M.L.L. and E.L.L.; visualisation, O.D.-P. and J.A.-O.; supervision, F.R.T.-M.; project administration, F.R.T.-M.; funding acquisition, M.L.L. and E.L.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Duda, R.O.; Shortliffe, E.H. Expert Systems Research. Science 1983, 220, 261–268. [Google Scholar] [CrossRef]
- McCorduck, P. The Fifth Generation: Artificial Intelligence and Japan’s Computer Challenge to the World; Addison-Wesley: Reading, MA, USA, 1983. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Buchanan, B.G.; Shortliffe, E.H. Rule-Based Expert Systems: The MYCIN Experiments of the Stanford Heuristic Programming Project; Addison-Wesley: Reading, MA, USA, 1984. [Google Scholar]
- Samuel, A.L. Some studies in machine learning using the game of checkers. IBM J. Res. Dev. 1959, 3, 210–229. [Google Scholar] [CrossRef]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 27 December 1965–7 January 1966; University of California Press: Berkeley, CA, USA, 1967; Volume 1. [Google Scholar]
- Sutton, R.S. Temporal Credit Assignment in Reinforcement Learning. Ph.D. Thesis, University of Massachusetts Amherst, Amherst, MA, USA, 1984. [Google Scholar]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation applied to handwritten zip code recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. arXiv 2014, arXiv:1406.2661. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-encoding variational Bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Radford, A.; Narasimhan, K.; Salimans, T.; Sutskever, I. Improving language understanding by generative pre-training. OpenAI Prepr. 2018; in press. Available online: https://cdn.openai.com/research-covers/language-unsupervised/language_understanding_paper.pdf (accessed on 14 September 2025).
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Cambridge, MA, USA, 1975. [Google Scholar]
- Oliveira Neto, G.C.d.; de Araujo, S.A.; Gomes, R.A.; Alliprandini, D.H.; Flausino, F.R.; Amorim, M. Simulation of Electronic Waste Reverse Chains for the Sao Paulo Circular Economy: An Artificial Intelligence-Based Approach for Economic and Environmental Optimizations. Sensors 2023, 23, 9046. [Google Scholar] [CrossRef]
- Puzzo, G.; Prati, G. Unraveling the influence of convenience situational factors on e-waste recycling behaviors: A goal-framing theory approach. Sustain. Dev. 2024, 33, 1174–1191. [Google Scholar] [CrossRef]
- Ghisellini, P.; Quinto, I.; Passaro, R.; Ulgiati, S. Circular economy management of waste electrical and electronic equipment (weee) in italian urban systems: Comparison and perspectives. Sustainability 2023, 15, 9054. [Google Scholar] [CrossRef]
- Odnevall, I.; Brookman-Amissah, M.; Stábile, F.; Ekvall, M.T.; Herting, G.; Vargas, M.B.; Messing, M.E.; Sturve, J.; Hansson, L.-A.; Isaxon, C.; et al. Characterization and toxic potency of airborne particles formed upon waste from electrical and electronic equipment waste recycling: A case study. Acs Environ. Au 2023, 3, 370–382. [Google Scholar] [CrossRef]
- Zhang, L.; Song, G.; Yu, K.; Cheng, Y.; Zhao, X.; Lv, L.; Qian, H.; Liu, G. Carbon trading in china reduces the dependence of household waste electrical and electronic equipment recycling on government subsidies. Environ. Sci. Technol. 2023, 57, 16153–16165. [Google Scholar] [CrossRef]
- Abogunrin-Olafisoye, O.B.; Adeyi, O.; Adeyi, A.J.; Oke, E.O.; Ojediran, G.O. Sustainable waste electrical and electronics equipment recycling in nigeria, policies and emerging technologies. Environ. Qual. Manag. 2025, 34, e70020. [Google Scholar] [CrossRef]
- Sharifidarabad, H. Cu recovery from e-wastes. In Copper Overview—From Historical Aspects to Applications; IntechOpen: London, UK, 2024. [Google Scholar] [CrossRef]
- Kozlovska, M.; Duris, A.; Strukova, Z.; Tazikova, A. An expert knowledge-based system to evaluate the efficiency of dry construction methods. Appl. Sci. 2023, 13, 11741. [Google Scholar] [CrossRef]
- Cottes, M.; Mainardis, M.; Simeoni, P. Assessing the techno-economic feasibility of waste electric and electronic equipment treatment plant: A multi-decisional modeling approach. Sustainability 2023, 15, 16248. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, M.; Qin, J.; Chen, S.; Zhou, S.; Huang, R.; Zeng, X.; Han, Y.; Liu, Y.; Shang, M.; et al. Integrative assessments of e-waste impacts and greenhouse gas emissions in China: Integrating pollution sequestration and resource recovery. ACS Sustain. Resour. Manag. 2025, 2, 766–774. [Google Scholar] [CrossRef]
- Vidal, I.; Sucozhañay, G.; Haupt, M.; Vanegas, P. Towards the definition of weee recycling targets in Ecuador. A case of study for mobile phones. Waste Manag. Res. J. A Sustain. Circ. Econ. 2023, 41, 1539–1548. [Google Scholar] [CrossRef]
- Burat, F.; Dinç, N.İ.; Dursun, H.N.; Ulusoy, U. The role of particle size and shape on the recovery of copper from different electrical and electronic equipment waste. Minerals 2023, 13, 847. [Google Scholar] [CrossRef]
- Ghisellini, P.; Passaro, R.; Ulgiati, S. Environmental and social life cycle assessment of waste electrical and electronic equipment management in Italy according to EU directives. Environments 2023, 10, 106. [Google Scholar] [CrossRef]
- Martin, N.; Pandiammal, P.; Gandhi, N.R. Decision making on E-waste management methods using minimization of regret with interval-valued intuitionistic fuzzy sets. Malaya J. Mat. 2020, 8, 222–224. [Google Scholar] [CrossRef]
- Ni, Z.; Chan, H.K.; Tan, Z. Systematic literature review of reverse logistics for e-waste: Overview, analysis, and future research agenda. Int. J. Logist. Res. Appl. 2021, 26, 843–871. [Google Scholar] [CrossRef]
- Jude, A.B.; Singh, D.; Islam, S.; Jameel, M.; Srivastava, S.; Prabha, B.; Kshirsagar, P.R. An Artificial Intelligence Based Predictive Approach for Smart Waste Management. Wirel. Pers. Commun. 2021, 127, 15–16. [Google Scholar] [CrossRef]
- Ruiz-Vanoye, J.A.; Pérez-Ortega, J.; Díaz-Parra, O.; Frausto-Solís, J.; Fraire Huacuja, H.J.; Cruz-Reyes, L. Survey of polynomial transformations between NP-complete problems. J. Comput. Appl. Math. 2011, 235, 4851–4865. [Google Scholar] [CrossRef]
- Ruiz-Vanoye, J.A.; Pérez-Ortega, J.; Pazos Rangel, R.A.; Díaz-Parra, O.; Fraire-Huacuja, H.J.; Frausto-Solís, J.; Cruz-Reyes, L. Application of formal languages in polynomial transformations of instances between NP-complete problems. J. Zhejiang Univ. Sci. C 2013, 14, 623–633. [Google Scholar] [CrossRef]
- Bäck, T. Evolutionary Computation 1: Basic Algorithms and Operators; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Hollister, CA, USA, 1998. [Google Scholar]
- Bäck, T. Evolutionary Algorithms in Theory and Practice: Evolution Strategies, Evolutionary Programming, Genetic Algorithms; Oxford University Press: Oxford, UK, 1996. [Google Scholar]
- Ortiz, D.M.; Velásquez, J.D.; Jaramillo, P. Estrategias evolutivas como una opción para la optimización de funciones no lineales con restricciones. Rev. Ing. Univ. De Medellin 2011, 10, 117–126. [Google Scholar]
- Hansen, N.; Ostermeier, A. Completely derandomized self-adaptation in evolution strategies. Evol. Comput. 2001, 9, 159–195. [Google Scholar] [CrossRef] [PubMed]
- Lasdon, L.; Duarte, A.; Glover, F.; Laguna, M.; Martí, R. Adaptive memory programming for constrained global optimization. Comput. Oper. Res. 2010, 37, 1500–1509. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).