Dynamic Optimization of Highway Emergency Lane Activation Using Kriging Surrogate Modeling and NSGA-II
Abstract
1. Introduction
2. Literature Review
2.1. Emergency Lane Activation Strategies and Threshold-Based Research
2.2. Traffic Flow Modeling and Simulation Methods
2.3. Traffic Safety Evaluation and TTC Indicator Applications
2.4. Multi-Objective Optimization Algorithms and Surrogate Model Applications
3. Models and Methods
3.1. Problem Description and Model Construction
3.1.1. Scenario Assumptions
3.1.2. Optimization Objectives
- Driving Efficiency Objective: Measured using TTT, equivalent to the sum of time spent by all vehicles traveling through the section. A smaller TTT indicates higher overall traffic efficiency. If N vehicles pass through the study section during the simulation observation period, and the j-th vehicle spends time in the section (calculated from the difference between entry and exit times), . Since total travel time positively correlates with road delay, equivalent indicators such as total or average delay can also be used. This model is designed to minimize TTT as one objective, i.e.,
- Safety Risk Objective: Measured using the TET indicator, defined as: the cumulative sum of time periods when all vehicles’ TTC is below a safety threshold during the simulation period [3]. Intuitively, a larger TET indicates longer cumulative time that vehicles are in potential collision danger, resulting in poorer traffic safety. During calculation, the TTC time series must be extracted from the vehicle following process. When the following vehicle’s TTC is less than the threshold (e.g., s), its duration is recorded and added to the TET. The total TET is obtained by repeated accumulation for multiple vehicles and multiple time points. We aim to minimize total exposure time, i.e.,It should be noted that the choice of threshold will affect the magnitude of TET values. Typically, for passenger car following, TTC = 3 s is used as one criterion for danger assessment, with TTC falling below 1 s considered extremely high risk [28]. We refer to common standards, taking s, with the sensitivity analysis section discussing the impact of threshold changes.
3.1.3. Constraints
- Temporal Continuity Constraint: Emergency lanes’ activation and deactivation operations should not be too frequent to prevent drivers from being unable to respond in time. A minimum duration of activation state is set, meaning that once activated (or deactivated), it should maintain that state for at least decision cycles before switching. Mathematically, this constraint can be expressed as:Similarly, for deactivation:If , it means prohibiting step-by-step changes like “on-off-on” fluctuations. At the encoding level, this can be implemented by adding constraints to the decision variable sequence. Generally, penalties can be applied to solutions that violate this constraint during fitness evaluation.
- Spatial Continuity Constraint: To avoid discontinuous activation causing vehicles to repeatedly merge into and exit from emergency lanes, the activation states of adjacent segments should be as consistent as possible. This constraint can be quantified using a penalty function:where is a penalty coefficient, and measures the inconsistency between adjacent segments. When an emergency lane is activated in one segment, its upstream and downstream adjacent segments should be synchronized or activated with minimal delay, allowing the emergency lane to form a continuous lane for vehicle use. In the actual algorithm implementation, we allow a small amount of discontinuity. However, we add a relatively large penalty value to the objective function each time adjacent segments have inconsistent activation states, thereby guiding the optimization process to prefer continuous activation patterns.
- Other Constraints: These include considerations that emergency lanes should only be activated during traffic congestion periods (not activated unnecessarily, to maintain safety redundancy). This can be formulated as:where represents the average speed in segment i at time t, and is the congestion speed threshold. Additionally, emergency lanes should be promptly closed in case of accidents. We focus on the case of recurrent congestion, assuming no sudden accidents during simulation. This deliberate focus on incident-free conditions is justified as recurrent congestion represents 65–70% of total highway delays (FHWA statistics), and our calibration data comes from incident-free periods, ensuring model parameters reflect normal operations. While we acknowledge that real-world deployment would require incident responsiveness through chance-constrained formulations (e.g., ensuring P(shoulder available|incident) ≥ 0.95), establishing optimal strategies for predictable congestion provides a necessary baseline. Future work will extend the framework to incorporate stochastic incident scenarios. It is also assumed that drivers follow instructions, entering the emergency lane only when it is open, an assumption that can be ensured through traffic management measures (such as electronic guidance screens).
3.2. Traffic Flow Simulation Model
3.2.1. Cell Transmission Model (CTM)
- When cell i is not congested (, where is the critical density corresponding to ), the cell has remaining capacity, and its maximum output flow rate is defined as:(i.e., vehicles exit at free-flow speed or are limited by capacity ) [20].
- When downstream traffic for cell j is not saturated (), its maximum receivable flow ; if downstream is already congested (), then its receiving capacity is limited by congestion wave speed. This can be expressed as:where is the current density of the downstream cell, and is the jam density [21].
3.2.2. Modeling the Impact of Emergency Lane Activation on CTM
3.2.3. Microscopic Safety Performance Simulation
3.3. Kriging Surrogate Model
3.3.1. Basic Principles
3.3.2. Surrogate Model Construction
- Flatten the decision variables (emergency lane activation matrix) into a one-dimensional vector as input, with dimension .
- Standardize the training data to ensure variables are on the same scale.
- Establish two separate Kriging models and to predict total travel time TTT and total exposure time TET, respectively.
- Optimize model hyperparameters, adjusting correlation parameters using maximum likelihood estimation.
- We employ cross-validation to assess model accuracy and calculate prediction confidence intervals, providing a reliable foundation for subsequent optimization.
3.4. Multi-Objective Genetic Algorithm Optimization Strategy
3.4.1. Encoding and Initial Population
3.4.2. Fitness Evaluation and Surrogate Model Application
3.4.3. Selection, Crossover, and Mutation
3.4.4. Multi-Objective Solution Set Obtainment and Decision-Making
4. Data and Experiments
4.1. Measured Data and Traffic Characteristics Analysis
4.1.1. Data Sources and Preprocessing
4.1.2. Spatiotemporal Distribution of Traffic States
4.1.3. Fundamental Diagram Parameter Calibration
4.1.4. Congestion Triggering Condition Analysis
4.2. Experimental Platform and Parameter Settings
4.2.1. Simulation Platform Implementation
4.2.2. Evaluation Indicators and Scheme Comparison
4.2.3. Safety Threshold and Weight Sensitivity Experiments
5. Results Analysis
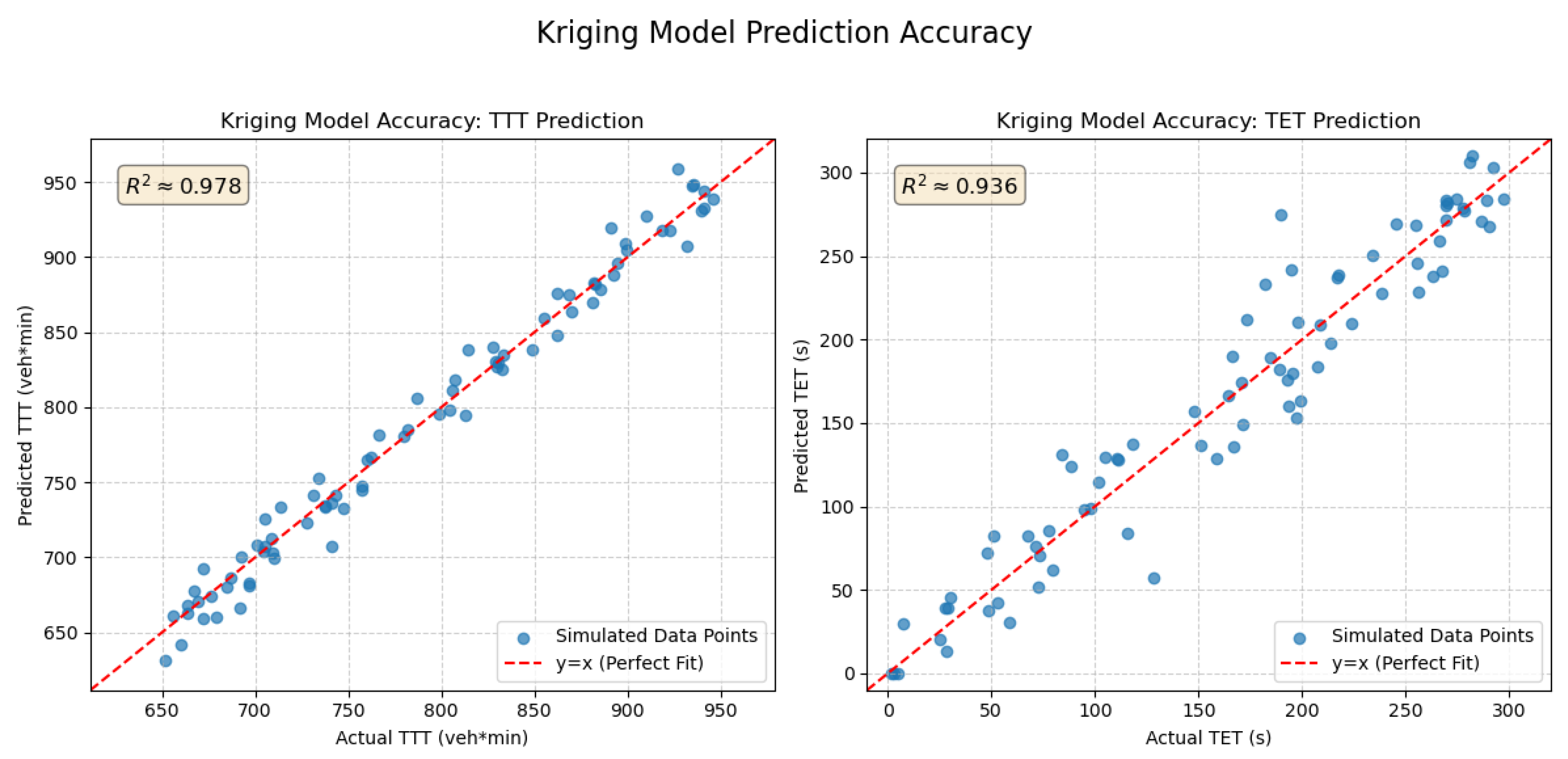
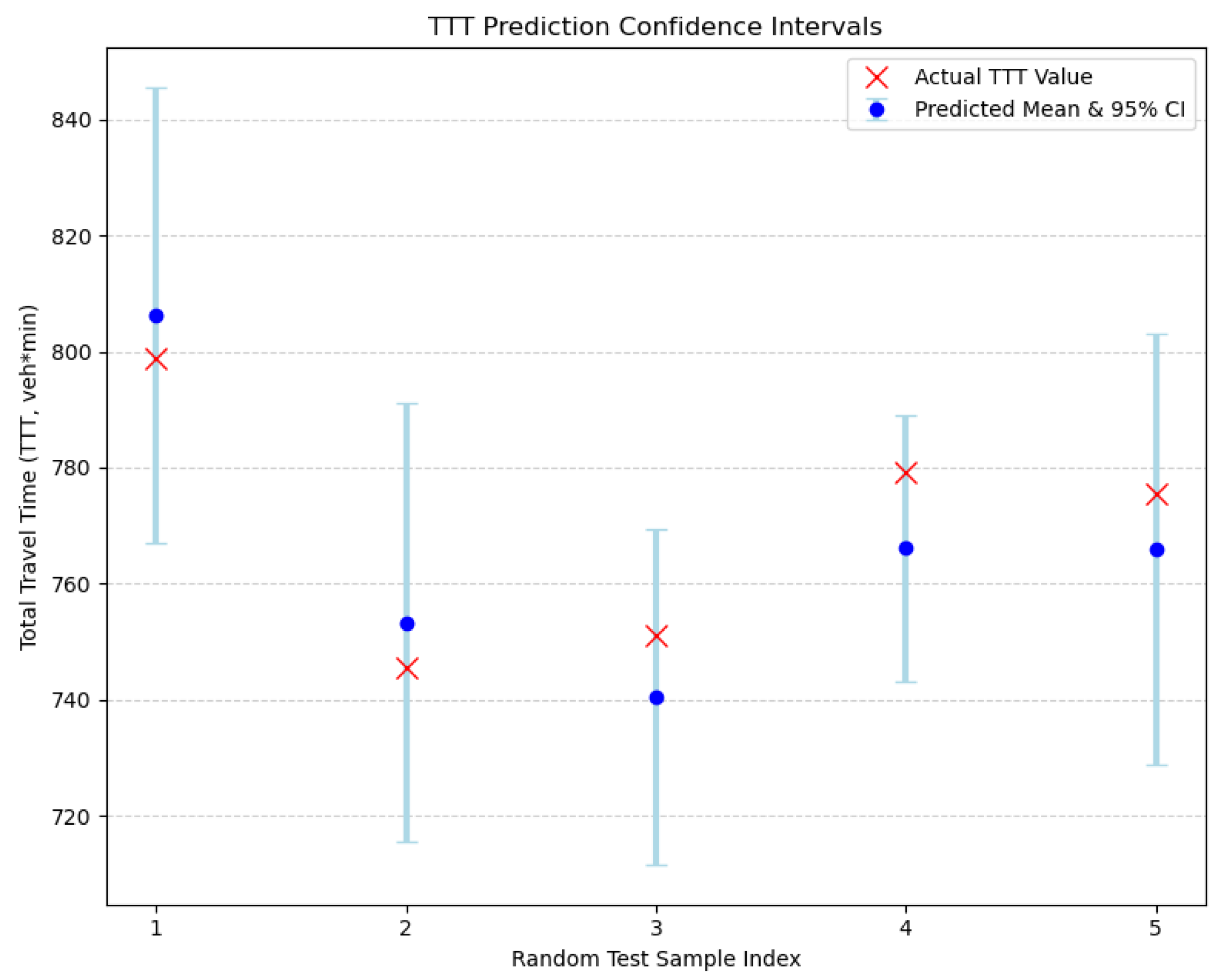
5.1. Kriging Surrogate Model Accuracy Verification
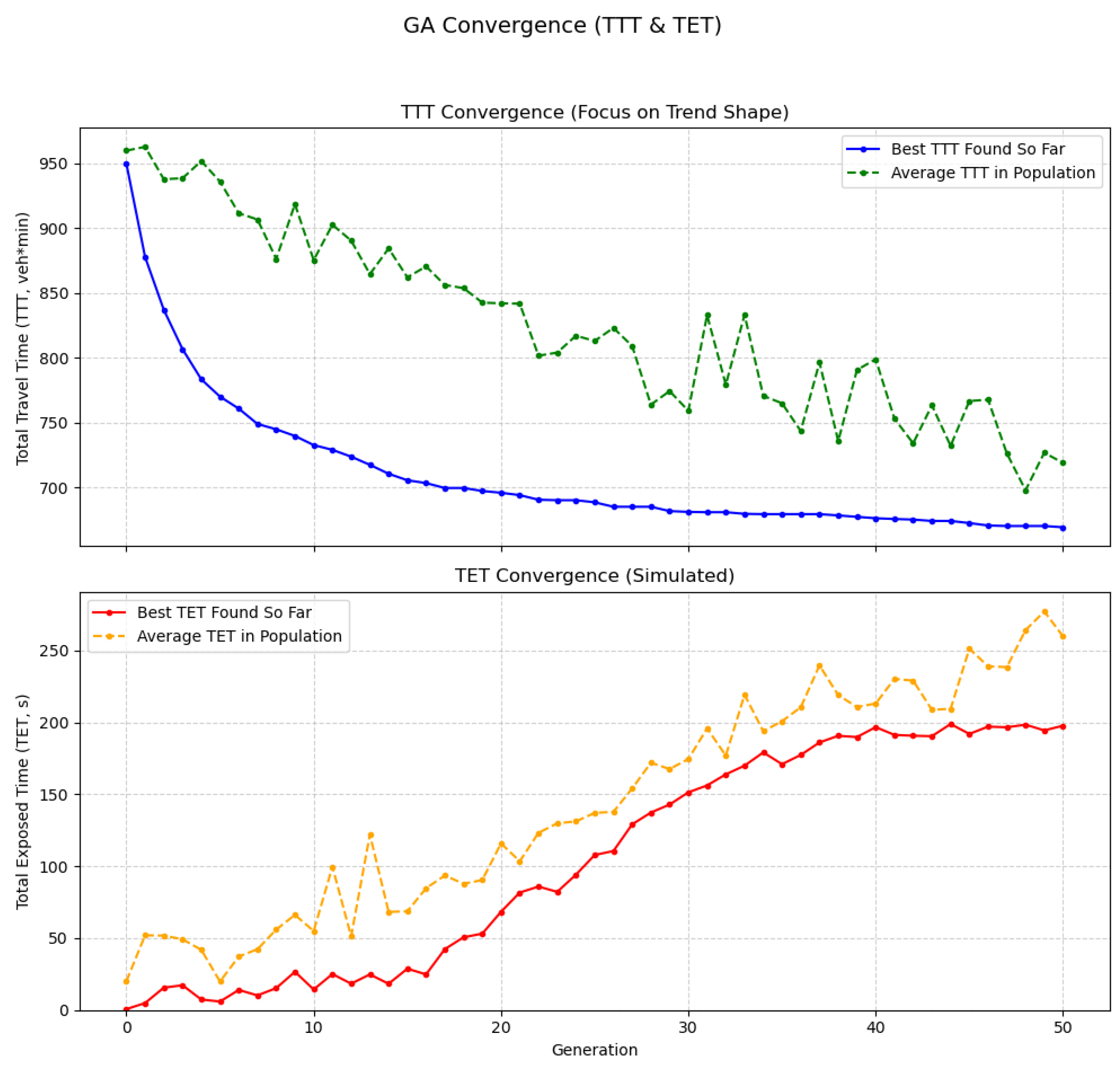
5.2. Genetic Algorithm Convergence Characteristics
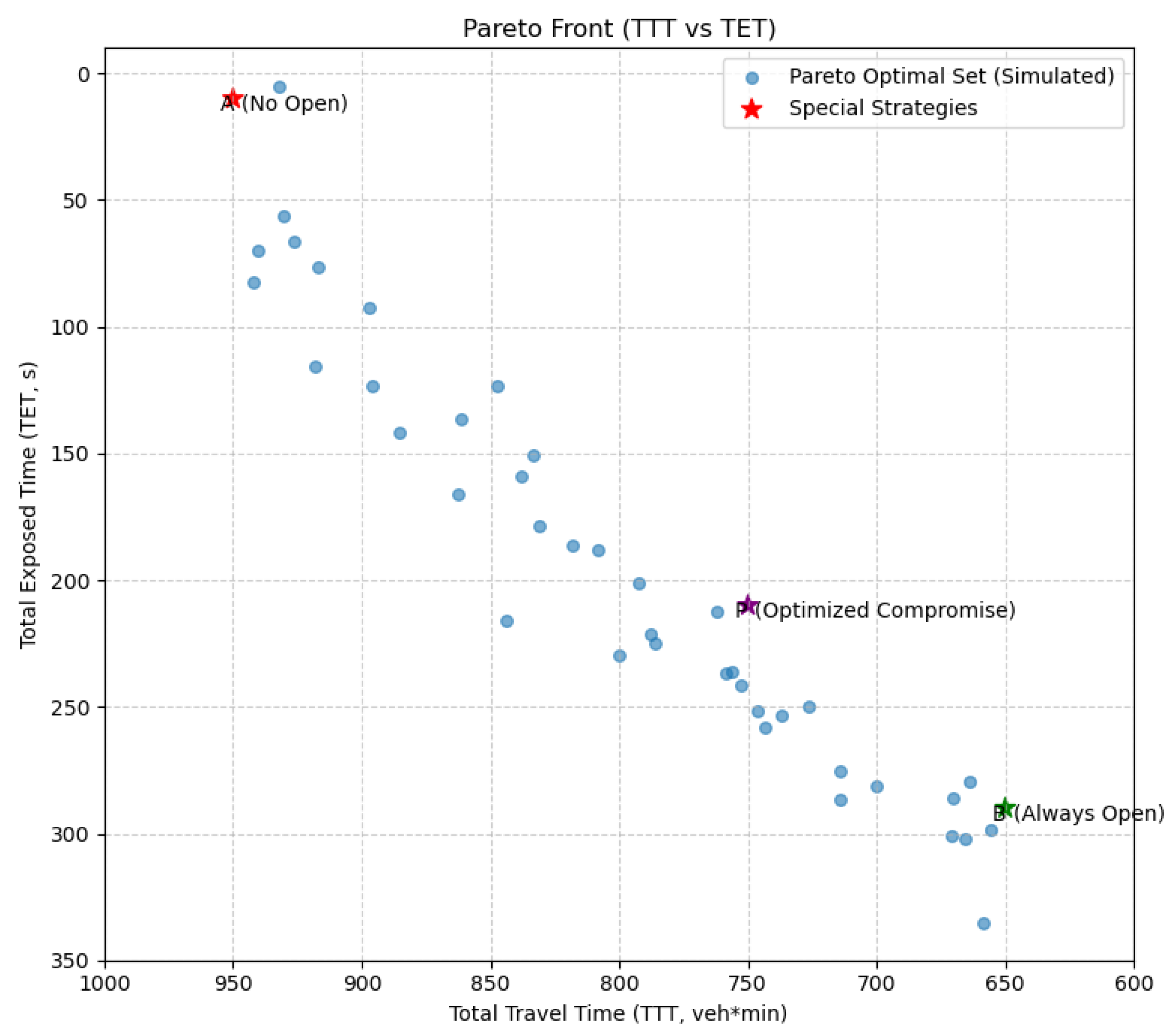
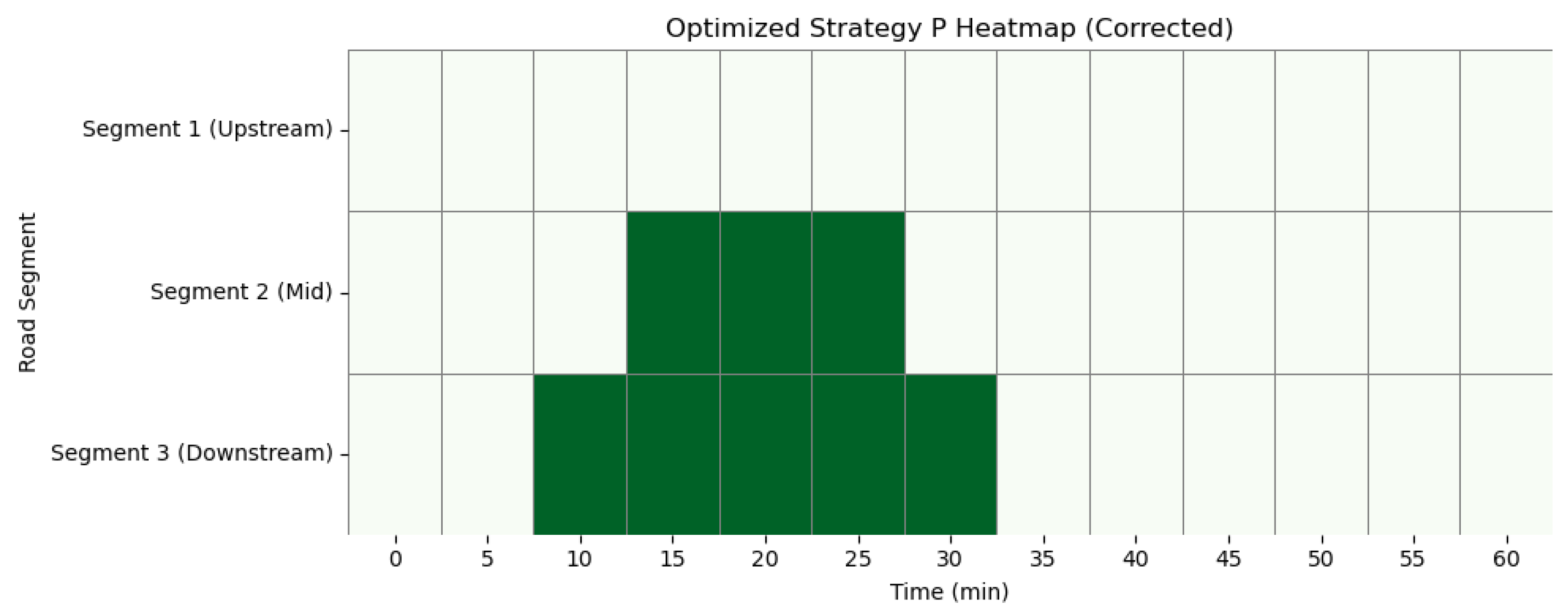
5.3. Pareto-Optimal Solution Set and Strategy Characteristics
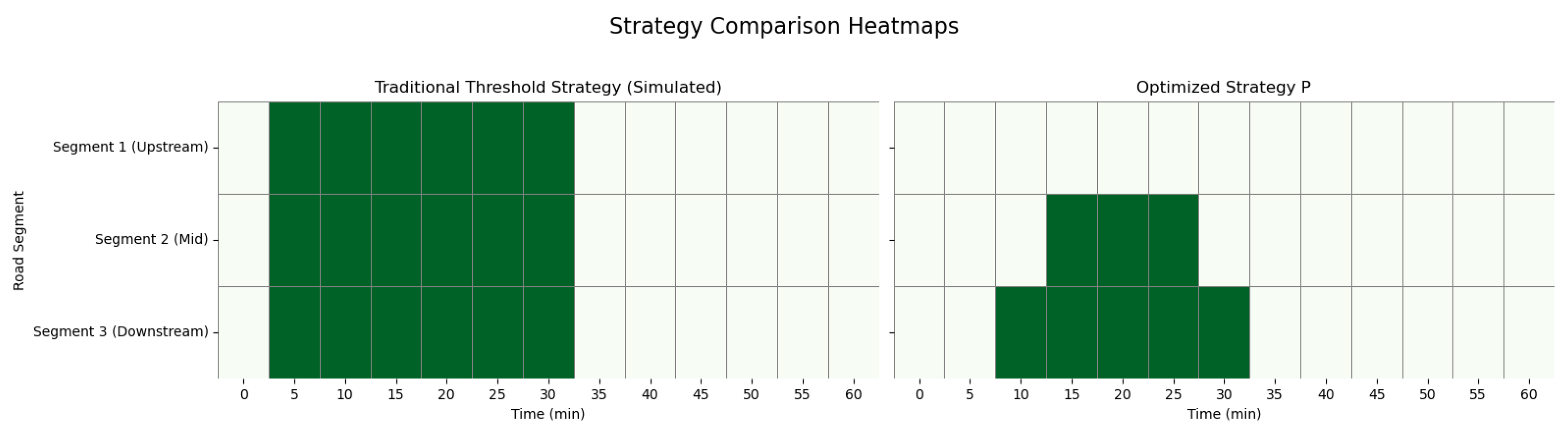
5.4. Comparison with Traditional Threshold Methods
5.5. Simplified Threshold Strategy Based on Optimization Results
- Activation condition: When the average speed in the downstream segment (between observation points 3 and 4) falls below 40 km/h and sustains for more than 5 min, activate the emergency lane in that segment; if this condition persists, extend activation upstream after 5 min.
- Deactivation condition: When the segment average speed recovers to above 55 km/h and sustains for 10 min, close emergency lanes in order from upstream to downstream.
5.6. Sensitivity Analysis
5.6.1. Impact of Safety Threshold
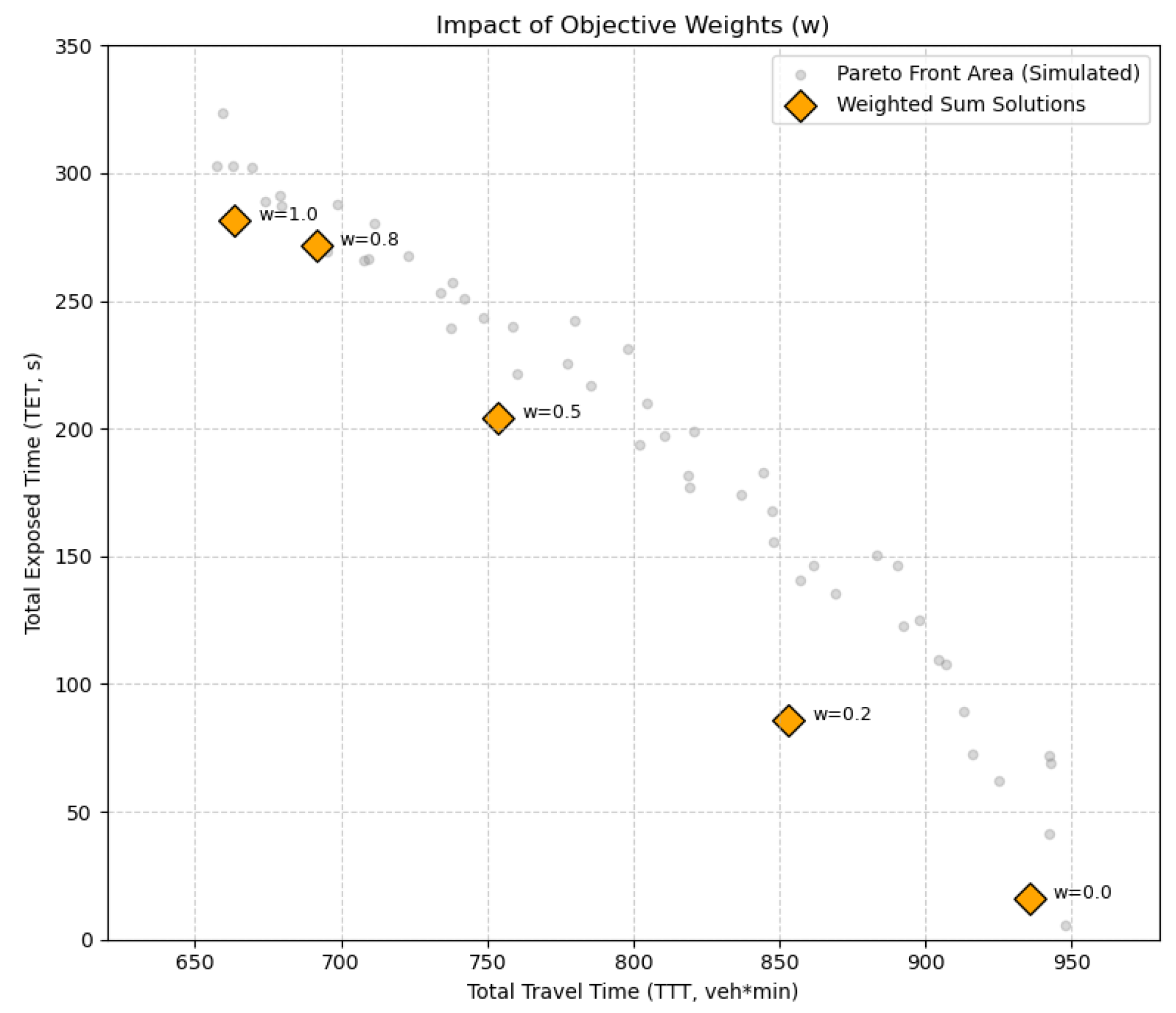
5.6.2. Impact of Objective Weight
5.6.3. Impact of Traffic Flow Changes
6. Conclusions
- Proposed a bi-objective activation optimization model. By taking total travel time and TTC exposure time as evaluation indicators, we constructed a bi-objective optimization model for emergency lane activation, that considers spatiotemporal continuity constraints of activation decisions. Our model more comprehensively measures the pros and cons of emergency lane activation, with greater rationality and adaptability compared to single threshold criteria. Our comparative experiments show that the optimization model improved safety performance by 18.0% compared to traditional threshold methods while maintaining or improving efficiency indicators.
- Developed a surrogate model + genetic algorithm solution method. By introducing Kriging surrogate models to approximate traffic simulation and combining multi-objective genetic algorithms with surrogate models, we achieved efficient searching for optimal activation strategies while ensuring accuracy. Through rigorous cross-validation and prediction interval analysis, we ensured the reliability of our surrogate models, with TTT prediction R2 reaching 0.978 and TET prediction R2 reaching 0.936. Our simulation results show that surrogate models reduced the required simulation iterations by about 95%, improving computational efficiency by approximately 20 times, allowing optimization to be completed within 10 min, with potential for online applications.
- Verified method effectiveness and extracted practical decision criteria. We calibrated our models based on actual traffic data and conducted case analysis, obtaining a Pareto-optimal strategy set for emergency lane activation. These strategies demonstrate the trade-off relationship between traffic efficiency and safety risk. Our selected compromise optimal strategy reduced total delay by about 20.5% compared to non-activation schemes, while reducing dangerous exposure time by about 28% compared to always-activated schemes. Our optimization results indicate that activating emergency lanes when downstream vehicle queuing and average speed fall below 40 km/h for 5 min is most beneficial; deactivation should occur when speed recovers to above 55 km/h for 10 min. We have transformed these quantitative thresholds into simple activation rules for practical management, with our experimental verification showing that simplified threshold strategies maintain 96% of the efficiency and 97% of the safety performance of optimization schemes.
- Demonstrated practical value and method extensibility. Our optimized emergency lane management can bring significant economic and social benefits. Based solely on time savings (20.5% delay reduction), with an average time value of 50 yuan/h for mixed traffic flow under Chinese highway conditions, a single 5 km section could achieve annual benefits exceeding one million yuan under moderate traffic volumes. When considering additional indirect benefits including fuel savings, accident reduction, and environmental improvements, the total socioeconomic benefits would be substantially higher. We confirmed the method’s flexibility through sensitivity analysis, as adjusting safety criteria thresholds or objective weights correspondingly changes optimization strategies to meet different safety margin requirements. Our proposed model and algorithm framework can be extended to similar traffic control optimization problems with minimal adaptation to the objective functions and constraints.
- Stochastic optimization: Incorporating incident probability distributions and weather uncertainty into the optimization framework through chance-constrained or robust optimization approaches.
- Network-level coordination: Extending the single-corridor approach to network-wide optimization, considering flow redistribution and cascading effects across multiple facilities.
- Connected vehicle exploitation: Leveraging vehicle-to-infrastructure communication for more granular traffic state estimation and personalized lane guidance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, Y.; Liu, Q.; Shi, Y. Research on Dynamic Emergency Lane Opening Decision Model for Saturated Highway Sections. Highw. Eng. 2022, 47, 172–176. [Google Scholar]
- Vogel, K. A comparison of headway and time to collision as safety indicators. Accid. Anal. Prev. 2003, 35, 427–433. [Google Scholar] [CrossRef]
- Minderhoud, M.M.; Bovy, P.H. Extended time-to-collision measures for road traffic safety assessment. Accid. Anal. Prev. 2001, 33, 89–97. [Google Scholar] [CrossRef]
- Simpson, T.W.; Poplinski, J.D.; Koch, P.N.; Allen, J.K. Metamodels for computer-based engineering design: Survey and recommendations. Eng. Comput. 2001, 17, 129–150. [Google Scholar] [CrossRef]
- Jin, R.; Chen, W.; Simpson, T.W. Comparative studies of metamodelling techniques under multiple modelling criteria. Struct. Multidiscip. Optim. 2001, 23, 1–13. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Kleijnen, J.P. Kriging metamodeling in simulation: A review. Eur. J. Oper. Res. 2009, 192, 707–716. [Google Scholar] [CrossRef]
- Forrester, A.I.; Keane, A.J. Recent advances in surrogate-based optimization. Prog. Aerosp. Sci. 2009, 45, 50–79. [Google Scholar] [CrossRef]
- Department for Infrastructure. M1 and M2 Motorway Hard Shoulder Bus Lanes—Information leaflet [EB/OL]. Belfast: Department for Infrastructure, 2018-07-31 [2025-02-08]. Available online: https://www.infrastructure-ni.gov.uk/publications/m1-and-m2-motorway-hard-shoulder-bus-lanes-information-leaflet (accessed on 8 June 2025).
- Geistefeldt, J. Operational experience with temporary hard shoulder running in Germany. Transp. Res. Rec. 2012, 2278, 67–73. [Google Scholar] [CrossRef]
- Guerrieri, M.; Mauro, R. Capacity and safety analysis of hard-shoulder running (HSR). A motorway case study. Transp. Res. Part Policy Pract. 2016, 92, 162–183. [Google Scholar] [CrossRef]
- Arora, K.; Kattan, L. Operational and safety impacts of integrated variable speed limit with dynamic hard shoulder running. J. Intell. Transp. Syst. 2023, 27, 769–798. [Google Scholar] [CrossRef]
- Yao, J.; Qian, Y.; Feng, Z.; Zhang, J.; Zhang, H.; Chen, T.; Meng, S. Hidden Markov Model-Based Dynamic Hard Shoulders Running Strategy in Hybrid Network Environments. Appl. Sci. 2024, 14, 3145. [Google Scholar] [CrossRef]
- Kirkup, A. What Are Smart Motorways and How Do They Work? [EB/OL]. London: Institution of Civil Engineers, 2022-01-04 [2025-02-08]. Available online: https://www.ice.org.uk/news-views-insights/inside-infrastructure/what-are-smart-motorways-and-how-do-they-work (accessed on 8 June 2025).
- Zhi, Y.; Zhang, Z.; Zhou, W.; Hou, D.; Zhang, J. Evaluation of Mixed Traffic Flow Efficiency and Safety on Hard-Shoulder-Running Freeways. Appl. Sci. 2024, 14, 11137. [Google Scholar] [CrossRef]
- Abdel-Aty, M.; Hasan, T.; Anik, B.M.T.H. An advanced real-time crash prediction framework for combined hard shoulder running and variable speed limits system using transformer. Sci. Rep. 2024, 14, 26403. [Google Scholar] [CrossRef]
- Daganzo, C.F. The cell transmission model: A dynamic representation of highway traffic consistent with the hydrodynamic theory. Transp. Res. Part Methodol. 1994, 28, 269–287. [Google Scholar] [CrossRef]
- Daganzo, C.F. The cell transmission model, part II: Network traffic. Transp. Res. Part Methodol. 1995, 29, 79–93. [Google Scholar] [CrossRef]
- Lebacque, J.P. The Godunov scheme and what it means for first order traffic flow models. In Proceedings of the 13th International Symposium on Transportation and Traffic Theory, Lyon, France, 24–26 July 1996; pp. 647–677. [Google Scholar]
- Lo, H.K.; Szeto, W.Y. A cell-based variational inequality formulation of the dynamic user optimal assignment problem. Transp. Res. Part Methodol. 2002, 36, 421–443. [Google Scholar] [CrossRef]
- Ngoduy, D. Applicable filtering framework for online multiclass freeway network estimation. Phys. Stat. Mech. Its Appl. 2008, 387, 599–616. [Google Scholar] [CrossRef]
- Sumalee, A.; Zhong, R.X.; Pan, T.L.; Szeto, W.Y. Stochastic cell transmission model (SCTM): A stochastic dynamic traffic model for traffic state surveillance and assignment. Transp. Res. Part Methodol. 2011, 45, 507–533. [Google Scholar] [CrossRef]
- Li, Z.; Liu, P.; Xu, C.; Wang, W. Optimal mainline variable speed limit control to improve safety on large-scale freeway segments. Comput.-Aided Civ. Infrastruct. Eng. 2016, 31, 366–380. [Google Scholar] [CrossRef]
- Hayward, J.C. Near-miss determination through use of a scale of danger. Highw. Res. Rec. 1972, 384, 24–34. [Google Scholar]
- Li, J.; Ling, M.; Zang, X.; Luo, Q.; Yang, J.; Chen, S.; Guo, X. Quantifying risks of lane-changing behavior in highways with vehicle trajectory data under different driving environments. Int. J. Mod. Phys. 2024, 35, 2450141. [Google Scholar] [CrossRef]
- Mahmud, S.M.S.; Ferreira, L.; Hoque, M.S.; Tavassoli, A. Application of proximal surrogate indicators for safety evaluation: A review of recent developments and research needs. IATSS Res. 2017, 41, 153–163. [Google Scholar] [CrossRef]
- Chen, S.; Piao, L.; Zang, X.; Luo, Q.; Li, J.; Yang, J.; Rong, J. Analyzing differences of highway lane-changing behavior using vehicle trajectory data. Phys. Stat. Mech. Its Appl. 2023, 624, 128980. [Google Scholar] [CrossRef]
- Van der Horst, R.; Hogema, J. Time-to-collision and collision avoidance systems. In Proceedings of the 6th ICTCT Workshop: Safety Evaluation of Traffic Systems: Traffic Conflicts and Other Measures, Salzburg, Austria, 27–29 October 1993; pp. 109–121. [Google Scholar]
- Zhou, Z.; Cai, M. Intersection signal control multi-objective optimization based on genetic algorithm. J. Traffic Transp. Eng. 2014, 1, 153–158. [Google Scholar]
- Queipo, N.V.; Haftka, R.T.; Shyy, W.; Goel, T.; Vaidyanathan, R.; Tucker, P.K. Surrogate-based analysis and optimization. Prog. Aerosp. Sci. 2005, 41, 1–28. [Google Scholar] [CrossRef]
- Osorio, C.; Bierlaire, M. A surrogate model for traffic optimization of congested networks: An analytic queueing network approach. Transp. Res. Part Emerg. Technol. 2013, 34, 340–367. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Forrester, A.; Sobester, A.; Keane, A. Engineering Design via Surrogate Modelling: A Practical Guide; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient global optimization of expensive black-box functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Liu, H.; Ong, Y.S.; Cai, J. A survey of adaptive sampling for global metamodeling in support of simulation-based complex engineering design. Struct. Multidiscip. Optim. 2018, 57, 393–416. [Google Scholar] [CrossRef]
- Wang, G.G.; Shan, S. Review of metamodeling techniques in support of engineering design optimization. J. Mech. Des. 2007, 129, 370–380. [Google Scholar]
- Li, L.; Chen, X.; Zhang, L. A global optimization algorithm for trajectory data based car-following model calibration. Transp. Res. Part Emerg. Technol. 2016, 68, 311–332. [Google Scholar] [CrossRef]
- Chen, X.; Wu, S.; Shi, C.; Huang, Y.; Yang, Y.; Ke, R. Sensing Data Supported Traffic Flow Prediction via Denoising Schemes and ANN: A Comparison. IEEE Sens. J. 2020, 20, 10696–10710. [Google Scholar] [CrossRef]
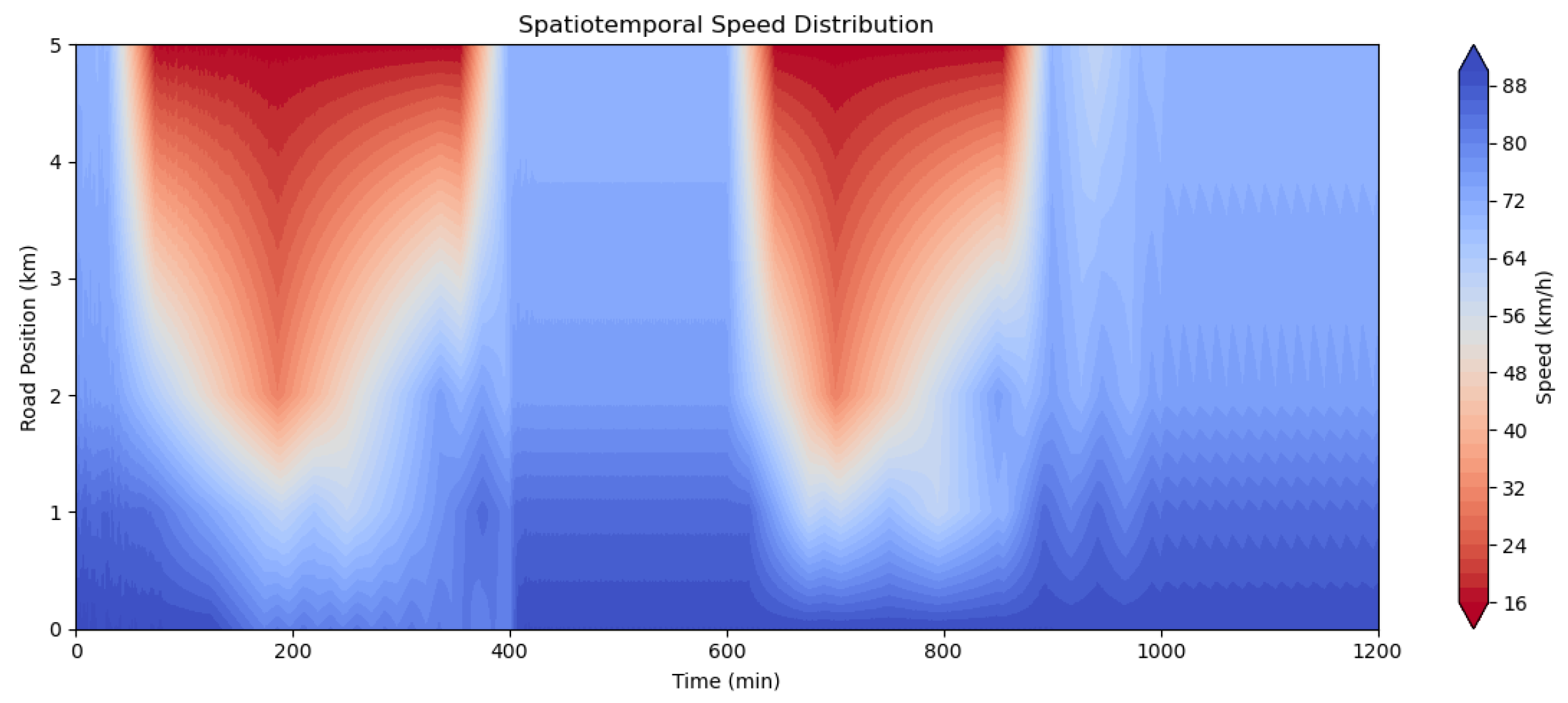
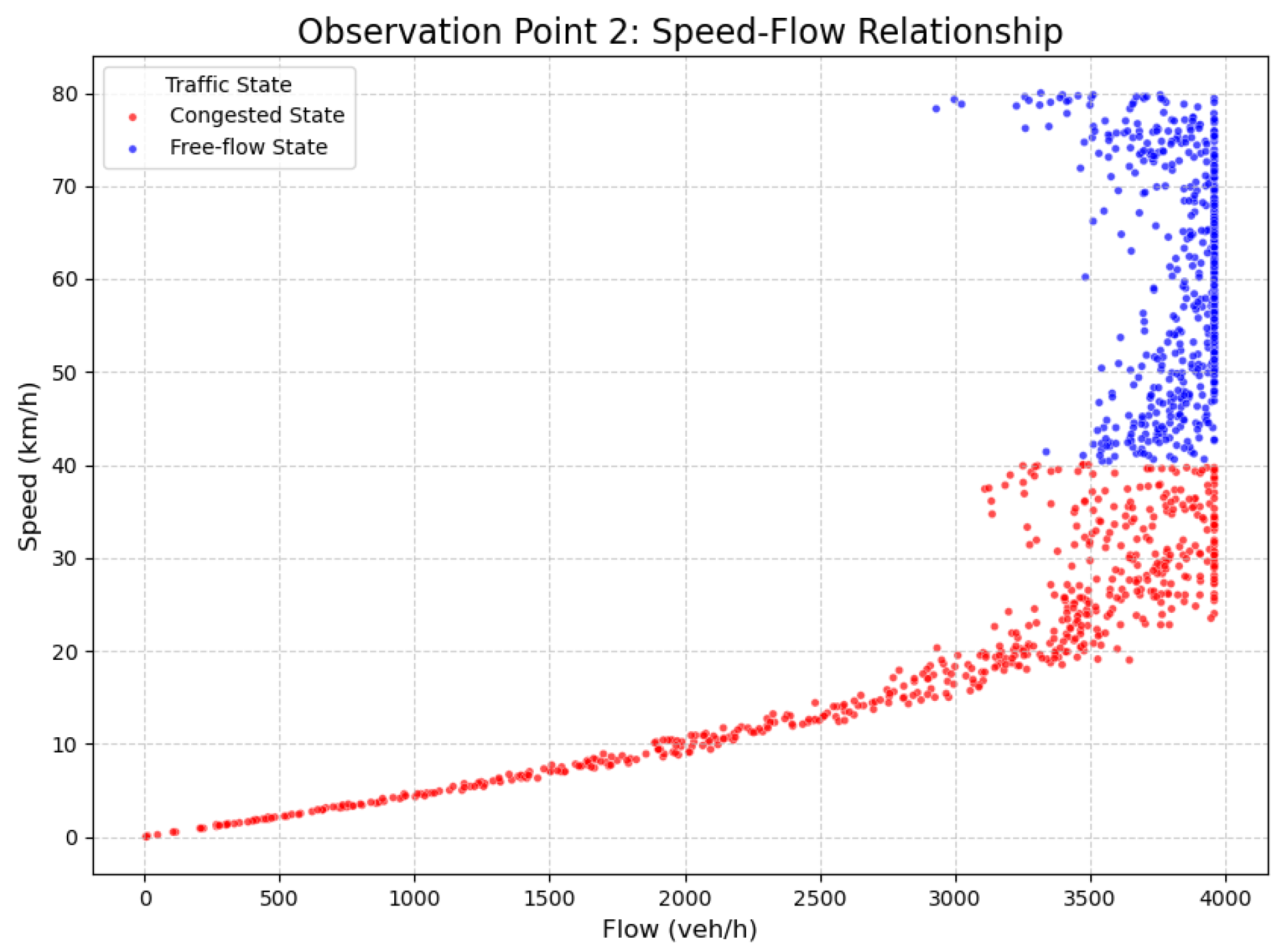
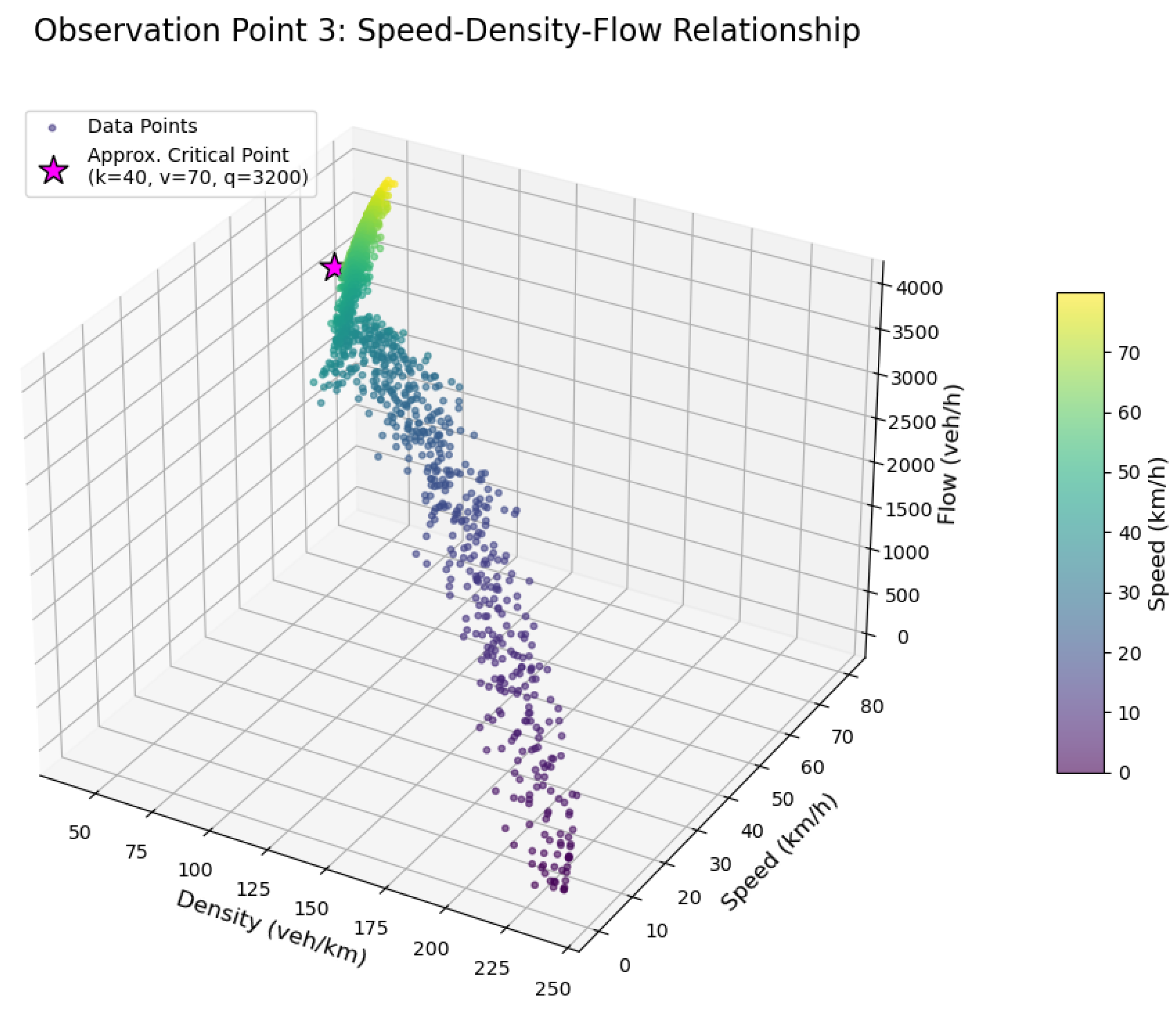
| Parameter | Point 1 | Point 2 | Point 3 | Point 4 |
|---|---|---|---|---|
| Average Density (veh/km) | 28.5 | 34.7 | 46.2 | 52.6 |
| Average Speed (km/h) | 86.7 | 75.4 | 68.1 | 62.3 |
| Average Flow (veh/h) | 2470 | 2614 | 2950 | 2867 |
| Flow Standard Deviation (veh/h) | 621 | 736 | 798 | 842 |
| Congestion Proportion (speed < 60 km/h) | 14.2% | 25.8% | 38.5% | 46.7% |
| Performance Metric | TTT Model | TET Model |
|---|---|---|
| R2 | 0.978 | 0.936 |
| RMSE | 21.5 | 18.7 |
| MAE | 18.6 | 14.7 |
| Average Relative Error | 2.2% | 5.3% |
| Method | Total Evals. | Actual Sims. | Comp. Time | Best TTT | Best TET |
|---|---|---|---|---|---|
| Direct Simulation | 2000 | 2000 | ∼3 h | 652 | 192 |
| Surrogate Model | 2100 | 100 | ∼10 min | 650 | 198 |
| Improvement Ratio | - | 95% | 94.4% | 0.3% | −3.1% |
| Scheme | Average Speed | Average Travel Time | Total Travel Time | Total Dangerous Exposure Time | Dangerous Events | Throughput |
|---|---|---|---|---|---|---|
| A: Non-activation | 35 km/h | 8.2 min | 950 veh·min | 0 s | 0 | 348 |
| B: Always-activated | 60 km/h | 5.4 min | 650 veh·min | 290 s | 57 | 452 |
| P: Optimized Scheme | 52 km/h | 6.2 min | 750 veh·min | 210 s | 40 | 438 |
| Simplified Threshold Scheme | 51 km/h | 6.4 min | 780 veh·min | 216 s | 42 | 435 |
| Performance Indicator | Non-Activation | Traditional Threshold Method | Optimization Method | Relative Improvement of Optimization Method |
|---|---|---|---|---|
| Total Travel Time | 950 | 770 | 750 | 2.6% |
| Total Exposure Time | 0 | 256 | 210 | 18.0% |
| Dangerous Events Count | 0 | 50 | 40 | 20.0% |
| Total Emergency Lane Activation Time | 0 | 30 | 20 | 33.3% |
| Performance Indicator | Low Load (0.9 Times) | Baseline Load | High Load (1.1 Times) |
|---|---|---|---|
| Total Travel Time | 680 | 750 | 940 |
| Total Exposure Time | 180 | 210 | 315 |
| Average Travel Time | 5.8 | 6.2 | 7.6 |
| Emergency Lane Activation Time | 10 | 20 | 35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fei, Y.; Wang, Y.; Zhang, Q. Dynamic Optimization of Highway Emergency Lane Activation Using Kriging Surrogate Modeling and NSGA-II. Sustainability 2025, 17, 8327. https://doi.org/10.3390/su17188327
Fei Y, Wang Y, Zhang Q. Dynamic Optimization of Highway Emergency Lane Activation Using Kriging Surrogate Modeling and NSGA-II. Sustainability. 2025; 17(18):8327. https://doi.org/10.3390/su17188327
Chicago/Turabian StyleFei, Yi, Yanan Wang, and Qiuyan Zhang. 2025. "Dynamic Optimization of Highway Emergency Lane Activation Using Kriging Surrogate Modeling and NSGA-II" Sustainability 17, no. 18: 8327. https://doi.org/10.3390/su17188327
APA StyleFei, Y., Wang, Y., & Zhang, Q. (2025). Dynamic Optimization of Highway Emergency Lane Activation Using Kriging Surrogate Modeling and NSGA-II. Sustainability, 17(18), 8327. https://doi.org/10.3390/su17188327







