Smart Sustainable Disassembly Systems for Circular Economy
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Research Gap and Objectives
2. Related Work and Background
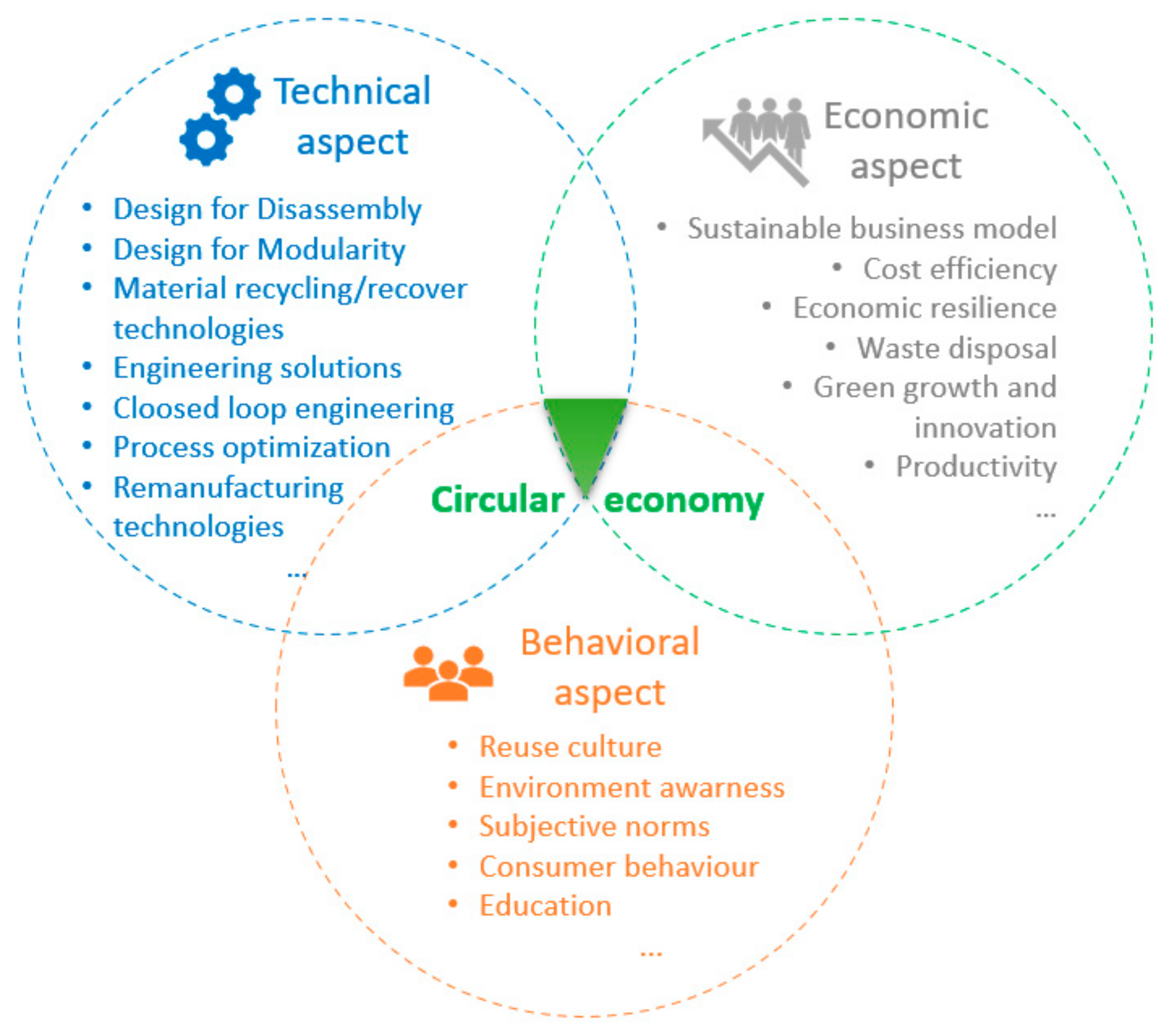
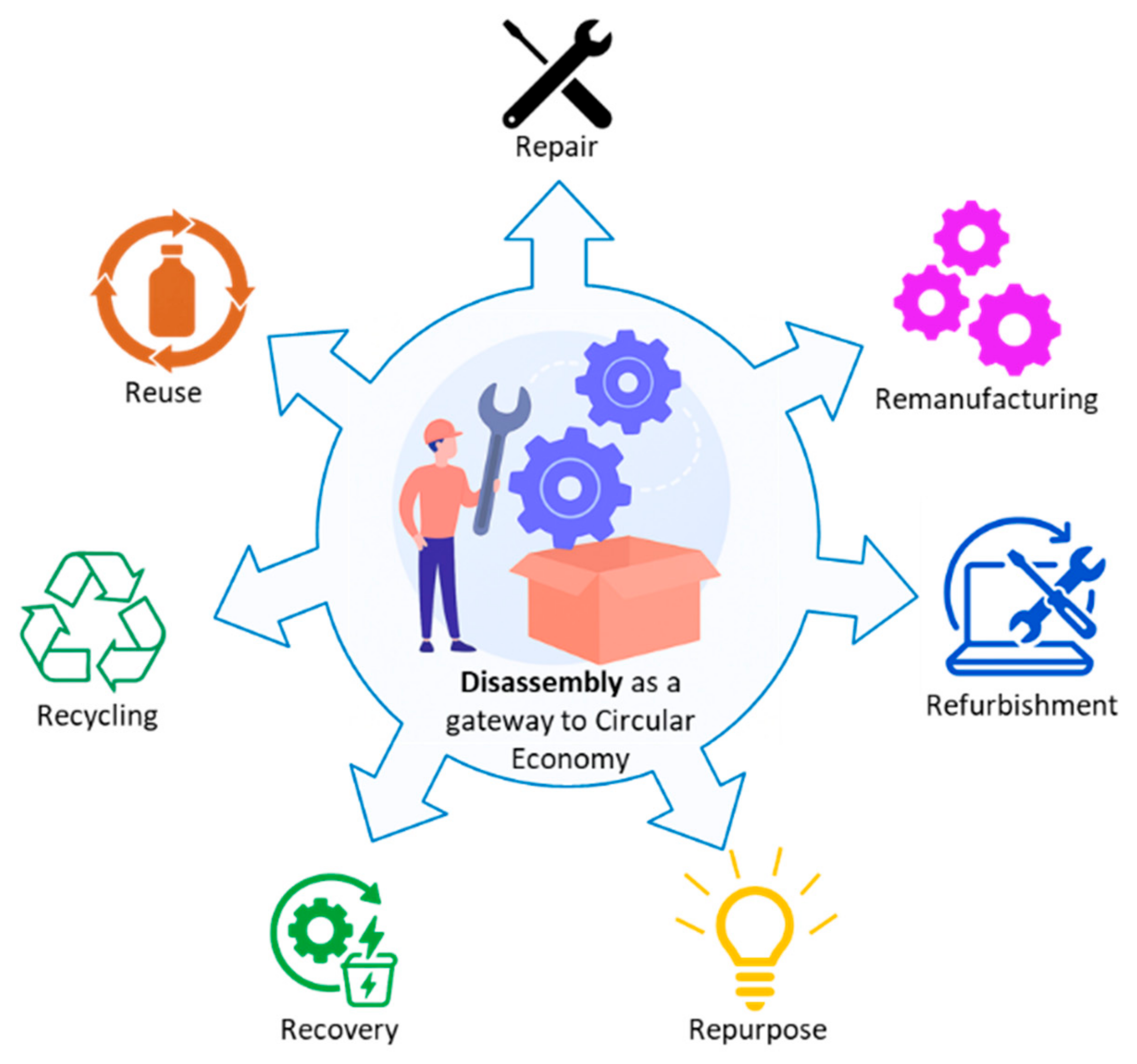
2.1. Importance of Disassembly Within the Circular Economy Framework
2.2. Design for Disassembly
2.2.1. Strategic Benefits
2.2.2. Operational Benefits
2.2.3. Sustainability Benefits
2.3. The Role of Disassembly Systems Today and Product Complexity
3. Linear Programming-Based Model for Optimizing Disassembly
3.1. Managing Product Complexity
- is the fitting index for category A in the Lucas DfA method—Part Placing and Fastening.
- is the theoretical maximum value for the fitting index (12.4).
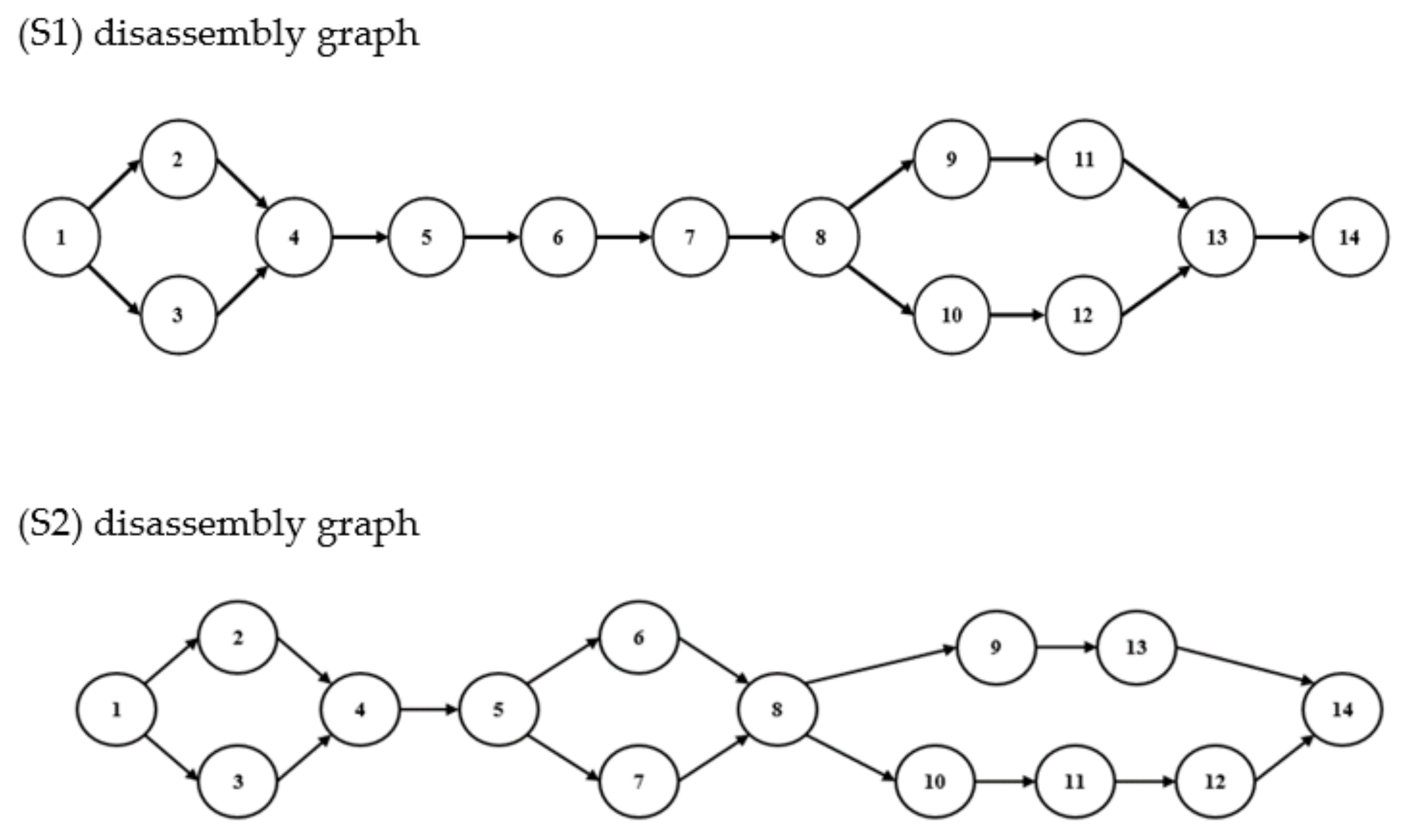
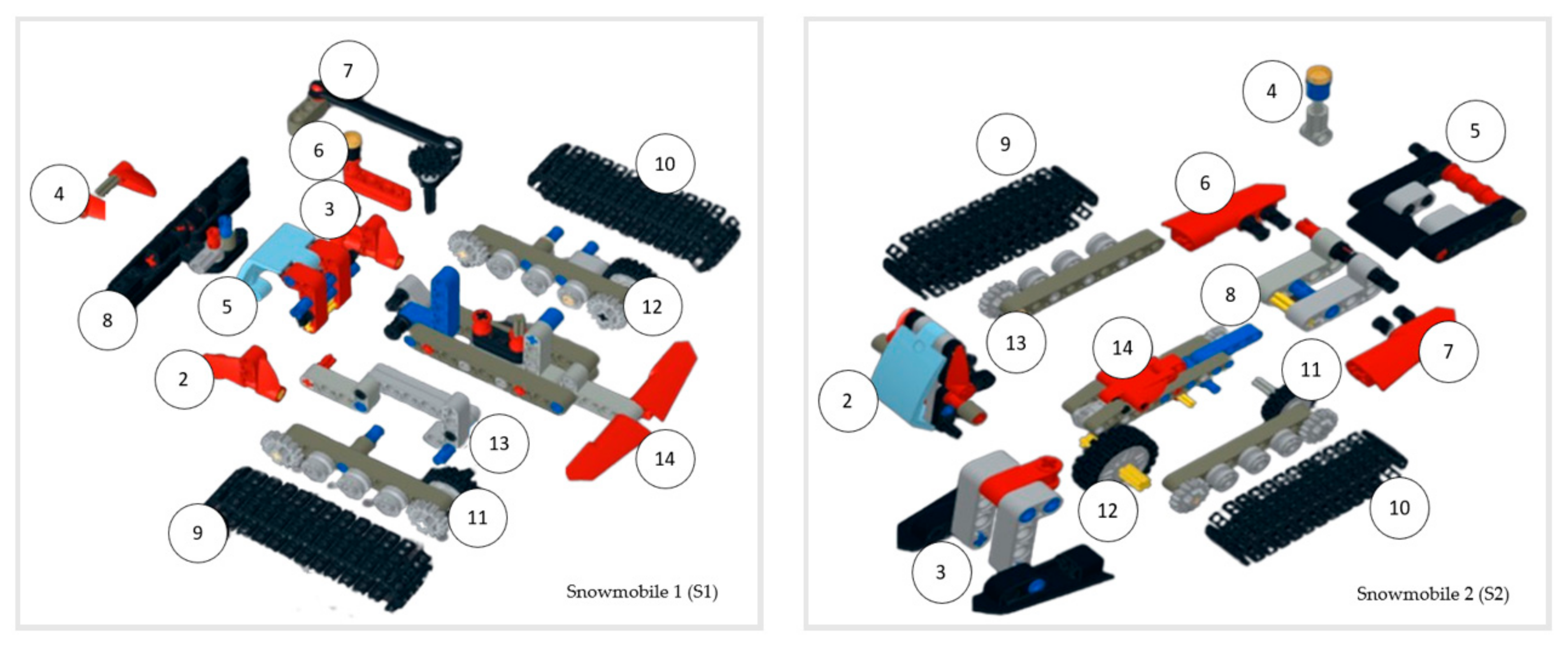
3.2. Products and Disassembly Process Design
3.3. Development of Disassembly Model and Maximization of Disassembly Throughput
- is the number of disassembled products ;
- is interface complexity for disassembly of product ;
- is the penalty parameter.
- is the constraint for disassembly workstation , for;
- is disassembly time for specific product ;
- is amount of time to complete disassembly tasks at specific workstation .
4. Results and Discussion
4.1. Product Complexity Calculation
4.2. Linear Programming Results
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- European Commission. Directorate-General for Communication. Circular Economy Action Plan: For a Cleaner and More Competitive Europe; Publication Office of the European Union: Luxembourg, 2020. [Google Scholar] [CrossRef]
- De Fazio, F.; Bakker, C.; Flipsen, B.; Balkenende, R. The Disassembly Map: A new method to enhance design for product repairability. J. Clean. Prod. 2021, 320, 128552. [Google Scholar] [CrossRef]
- Bocken, N.; De Pauw, I.; Bakker, C.; Van der Grinten, B. Product and design business model strategies for a circular economy. J. Ind. Prod. Eng. 2016, 33, 308–320. [Google Scholar] [CrossRef]
- Mani, V.; Das, S.; Caudill, R. Disassembly complexity and recyclability analysis of new designs from CAD file data. In Proceedings of the 2001 IEEE International Symposium on Electronics and the Environment. 2001 IEEE ISEE (Cat. No. 01CH37190), Denver, CO, USA, 9 May 2001; pp. 10–15. [Google Scholar]
- Benabdellah, A.; Bouhaddou, I.; Benghabrit, A.; Benghabrit, O. A systematic review of design for X techniques from 1980 to 2018: Concepts, applications, and perspectives. Int. J. Adv. Manuf. Technol. 2019, 102, 3473–3502. [Google Scholar] [CrossRef]
- Formentini, G.; Prioli, J.; Ko, J.; Hapuwatte, B.; Ferrero, V.; Badurdeen, F.; Rickli, J.L.; Ramanujan, D. A review of disassembly systems for circular product design. J. Clean. Prod. 2025, 506, 145459. [Google Scholar] [CrossRef]
- Lindemann, U.; Maurer, M.; Braun, T. Complexity in the Conteyt of Product Design; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Vanegas, P.; Peeters, J.R.; Cattrysse, D.; Tecchio, P.; Ardente, F.; Mathieux, F.; Dewulf, W.; Duflou, J.R. Ease of disassembly of products to support circular economy strategies. Resour. Conserv. Recycl. 2018, 135, 323–334. [Google Scholar] [CrossRef]
- Zhang, Q.; Xing, Y.; Yao, M.; Guo, X.; Qin, S.; Zhu, H.; Qi, L.; Hu, B. Optimizing Robotic Disassembly-Assembly Line Balancing with Directional Switching Time via an Improved Q(λ) Algorithm in IoT-Enabled Smart Manufacturing. Electronics 2025, 14, 3499. [Google Scholar] [CrossRef]
- Cong, L.; Zhao, F.; Sutherland, J. Integration of dimantling operations into a value recovery plan for circular economy. J. Clean. Prod. 2017, 149, 378–386. [Google Scholar] [CrossRef]
- Kirchherr, J.; Yang, N.; Schulze-Spuntrup, F.; Heerink, M.; Hartley, K. Conceptualizing the circular economy (revisited): An analysis of 221 definitions. Resour. Conserv. Recycl. 2023, 194, 107001. [Google Scholar] [CrossRef]
- Kret-Grzeskowiak, A.; Baborska-Narozny, M. Guidelines for disassembly and adaptation in architectural design compared to circular economy goals—A literature review. Sustain. Prod. Consum. 2023, 39, 1–12. [Google Scholar] [CrossRef]
- Al Assadi, A.; Goes, D.; Baazouzi, S.; Staudacher, M.; Malczyk, P.; Kraus, W.; Nägele, F.; Huber, M.F.; Fleischer, J.; Peuker, U.; et al. Challenges and prospects of automated disassembly of fuel cells for a circular economy. Resour. Conserv. Recycl. Adv. 2023, 19, 200172. [Google Scholar] [CrossRef]
- Reike, D.; Vermeulen, W.; Witjes, S. The circular economy: New or refurbished as CE 3.0?—Exploring controversies in the conceptualization of the circular economy through a focus on history and resource value retention options. Resour. Conserv. Recycl. 2018, 135, 246–264. [Google Scholar] [CrossRef]
- Formentini, G.; Ramanujan, D. Design for circular disassembly: Evaluating the impacts of product end-of-life status on circularity through the parent-action-child model. J. Clean. Prod. 2023, 405, 137009. [Google Scholar] [CrossRef]
- Ohnemuller, G.; Beller, M.; Rosemann, B.; Dopper, F. Disassembly and Its Obstacles: Challenges Facing Remanufacturers of Lithium-Ion Traction Batteries. Processes 2025, 13, 123. [Google Scholar] [CrossRef]
- Battaia, O.; Dolgui, A.; Heragu, S.; Meerkov, S.; Tiwari, M.K. Design for manufacturing and assembly/disassembly: Joint design of products and production systems. Int. J. Prod. Res. 2017, 56, 7181–7189. [Google Scholar] [CrossRef]
- Benatha, M.; Battaia, O.; Doulgui, A.; Hu, J. Dealing with Uncertainty in Disassembly Line Design. CIRP Ann.-Manuf. Technol. 2014, 63, 21–24. [Google Scholar] [CrossRef]
- Wang, X.; Ong, S.; Nee, A. A comprehensive survey of augmented reality assembly research. Adv. Manuf. 2016, 4, 1–22. [Google Scholar] [CrossRef]
- Nee, A.; Ong, S.; Chryssolouris, G.; Mourtzis, D. Augmented reality applications in design and manufacturing. CIRP Ann. 2012, 61, 657–679. [Google Scholar] [CrossRef]
- Alkan, B.; Vera, D.; Ahmad, B. A method to assess assembly complexity of industrial products in early design phase. IEEE Access 2017, 6, 989–999. [Google Scholar] [CrossRef]
- Chatras, C.; Giard, V.; Sali, M. Mass customisation impact on bill of materials structure and master production schedule development. Int. J. Prod. Res. 2015, 54, 5634–5650. [Google Scholar] [CrossRef]
- Shannon, C. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Park, K.; Kremer, G.O. Assessment of static complexity in design and manufacturing of a product family and its impact on manufacturing performance. Int. J. Prod. Econ. 2015, 169, 215–232. [Google Scholar] [CrossRef]
- Alkan, B.; Vera, D.; Ahmand, M.; Ahmad, B.; Harrison, R. Design evaluation of automated manufacturing processes based on complexity of control logic. Procedia CIRP 2016, 50, 141–146. [Google Scholar] [CrossRef]
- Zeltzer, L.; El-Houssaine, A.; Limere, V. Workload balancing and manufacturing complexity levelling in mixed-model assembly lines. Int. J. Prod. Res. 2016, 55, 2829–2844. [Google Scholar] [CrossRef]
- Herrera-Vidal, G.; Coronado-Hernández, J.R.; Paredes, B.P.M.; Ramos, B.O.S.; Sierra, D.M. Systematic configurator for complexity management in manufacturing systems. Entropy 2024, 26, 747. [Google Scholar] [CrossRef]
- Modrak, V.; Soltysova, Z. Development of operational complexity measure for selection of optimal layout design alternative. Int. J. Prod. Res. 2017, 56, 7280–7295. [Google Scholar] [CrossRef]
- Modrak, V.; Soltysova, Z. Novel Complexity Indicator of Manufacturing Process Chains and Its Relations to Indirect Complexity Indicators. Complexity 2017, 2017, 9102824. [Google Scholar] [CrossRef]
- Frizelle, G.; Suhov, Y. The measurement of complexity in production and other commercial systems. Proc. R. Soc. A: Math. Phys. Eng. Sci. 2008, 464, 2649–2668. [Google Scholar] [CrossRef]
- Liu, H.; Xu, K.; Pan, Z. Modeling and application of mixed model assembly system complexity introduced by auto-body personalization. Int. J. Adv. Manuf. Technol. 2015, 93, 43–54. [Google Scholar] [CrossRef]
- Sinha, K. Structural Complexity and Its Implications for Design of Cyber Phisical Systems. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2014. [Google Scholar]
- Chan, V.; Salustri, F. DFA: The Lucas Method. 2005. Available online: https://ebrary.net/191720/business_finance/lucas_evaluation_method (accessed on 29 January 2019).

| Category | Option | Value |
|---|---|---|
| A. Part placing and fastening (Select one of the following *) | Self-holding orientation Requires holding | 1.0 2.0 |
| (* Plus one of the following lists) | Self-securing (i.e., snaps) | 1.3 |
| Screwing | 4.0 | |
| Riveting | 4.0 | |
| Bending | 4.0 | |
| B. Process direction (Select one of the following *) | Straight line from above Straight line not from above | 0 0.1 |
| Not a straight line | 1.6 | |
| C. Insertion (Select one of the following *) | Single Multiple insertions | 0 0.7 |
| Simultaneous multiple insertions | 1.2 | |
| D. Access and/or vision (Select one of the following *) | Direct Restricted | 0 1.5 |
| E. Alignment (Select one of the following *) | Easy to align Difficult to align | 0 0.7 |
| F. Insertion force (Select one of the following *) | No resistance to insertion Resistance to insertion | 0 0.6 |
| Connection | Total Complexity Index | Subassemblies | Assembly |
|---|---|---|---|
| 1-2 | 0.33 | 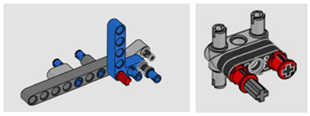 | 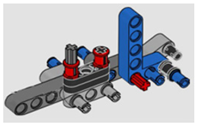 |
| 2-3 | 0.26 | 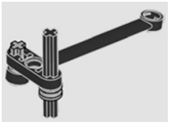 |  |
| 3-4 | 0.32 |  | 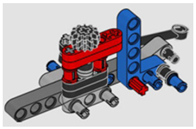 |
| Connection | Lucas DfA Method and Analysis | Index | Total Complexity Index |
|---|---|---|---|
| 1-2 | A. Part Placing and Fastening | 2 1.3 | 0.33 |
| B. Process Direction | 0.1 | ||
| C. Insertion | 0.7 | ||
| D. Access and/or Vision | 0 | ||
| E. Alignment | 0 | ||
| F. Force | 0 | ||
| 2-3 | A. Part Placing and Fastening | 2 1.3 | 0.26 |
| B. Process Direction | 0 | ||
| C. Insertion | 0 | ||
| D. Access and/or Vision | 0 | ||
| E. Alignment | 0 | ||
| F. Force | 0 | ||
| 3-4 | A. Part Placing and Fastening | 2 1.3 | 0.32 |
| B. Process Direction | 0 | ||
| C. Insertion | 0.7 | ||
| D. Access and/or Vision | 0 | ||
| E. Alignment | 0 | ||
| F. Force | 0 |
| Disassembly Workstation | Disassembly Time (S1) Time [s] | Disassembly Time (S1) Time [s] | Constraints Time [s] | ||
|---|---|---|---|---|---|
| 1 | 0.99 | 60 | 0.77 | 20 | 20,171 |
| 2 | 0.65 | 10 | 0.77 | 20 | 15,171 |
| 3 | 0.80 | 30 | 0.77 | 35 | 28,300 |
| 4 | 1.32 | 35 | 0.77 | 35 | 28,300 |
| 5 | 1.10 | 40 | 1.03 | 35 | 28,300 |
| sum | 4.86 | 4.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Crnjac Žižić, M.; Aljinović Meštrović, A.; Mladineo, M.; Gjeldum, N. Smart Sustainable Disassembly Systems for Circular Economy. Sustainability 2025, 17, 8289. https://doi.org/10.3390/su17188289
Crnjac Žižić M, Aljinović Meštrović A, Mladineo M, Gjeldum N. Smart Sustainable Disassembly Systems for Circular Economy. Sustainability. 2025; 17(18):8289. https://doi.org/10.3390/su17188289
Chicago/Turabian StyleCrnjac Žižić, Marina, Amanda Aljinović Meštrović, Marko Mladineo, and Nikola Gjeldum. 2025. "Smart Sustainable Disassembly Systems for Circular Economy" Sustainability 17, no. 18: 8289. https://doi.org/10.3390/su17188289
APA StyleCrnjac Žižić, M., Aljinović Meštrović, A., Mladineo, M., & Gjeldum, N. (2025). Smart Sustainable Disassembly Systems for Circular Economy. Sustainability, 17(18), 8289. https://doi.org/10.3390/su17188289






