A Hybrid System Approach to Energy Optimization in Gas–Electric Hybrid Powertrains
Abstract
1. Introduction
- (1)
- A unified hybrid modeling framework is developed based on MLD, enabling rigorous representation of both discrete and continuous dynamics in the MGHPS. This framework forms the foundation for subsequent control design.
- (2)
- An HMPC-based energy management strategy is proposed, which dynamically adjusts control weights in response to varying mission profiles to achieve a balanced improvement in fuel economy and emission reduction. A simulation platform is developed to validate the proposed approach under representative operating conditions, demonstrating its effectiveness in enhancing control performance and energy efficiency.
2. Modeling Theory and Methods
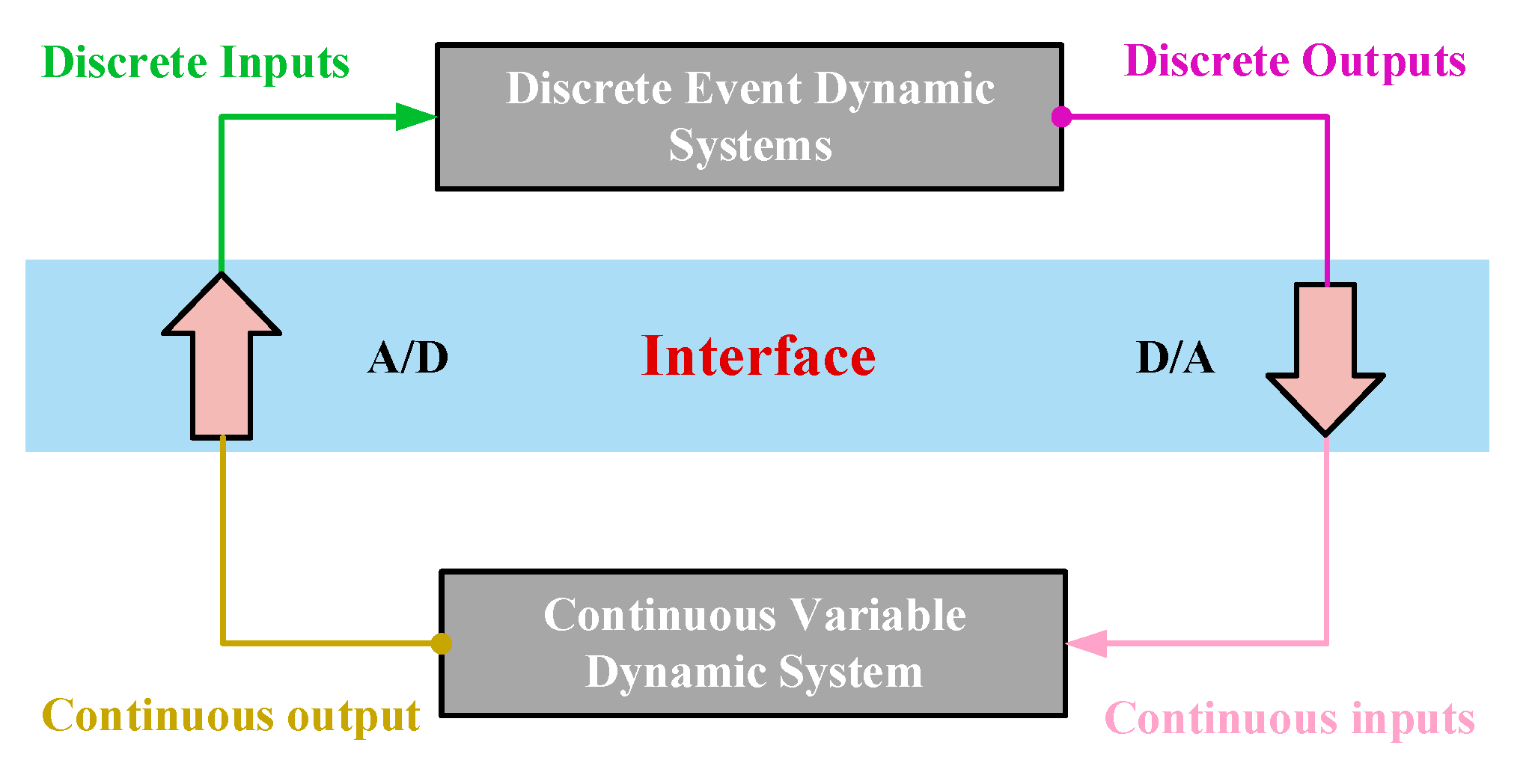
2.1. Hybrid Systems Theory
2.2. Modeling Methods for Hybrid Systems
3. Energy Management Applications for MGHPS
3.1. Research Objects
3.2. Gas–Electric Hybrid Modeling Based on Hybrid System Theory
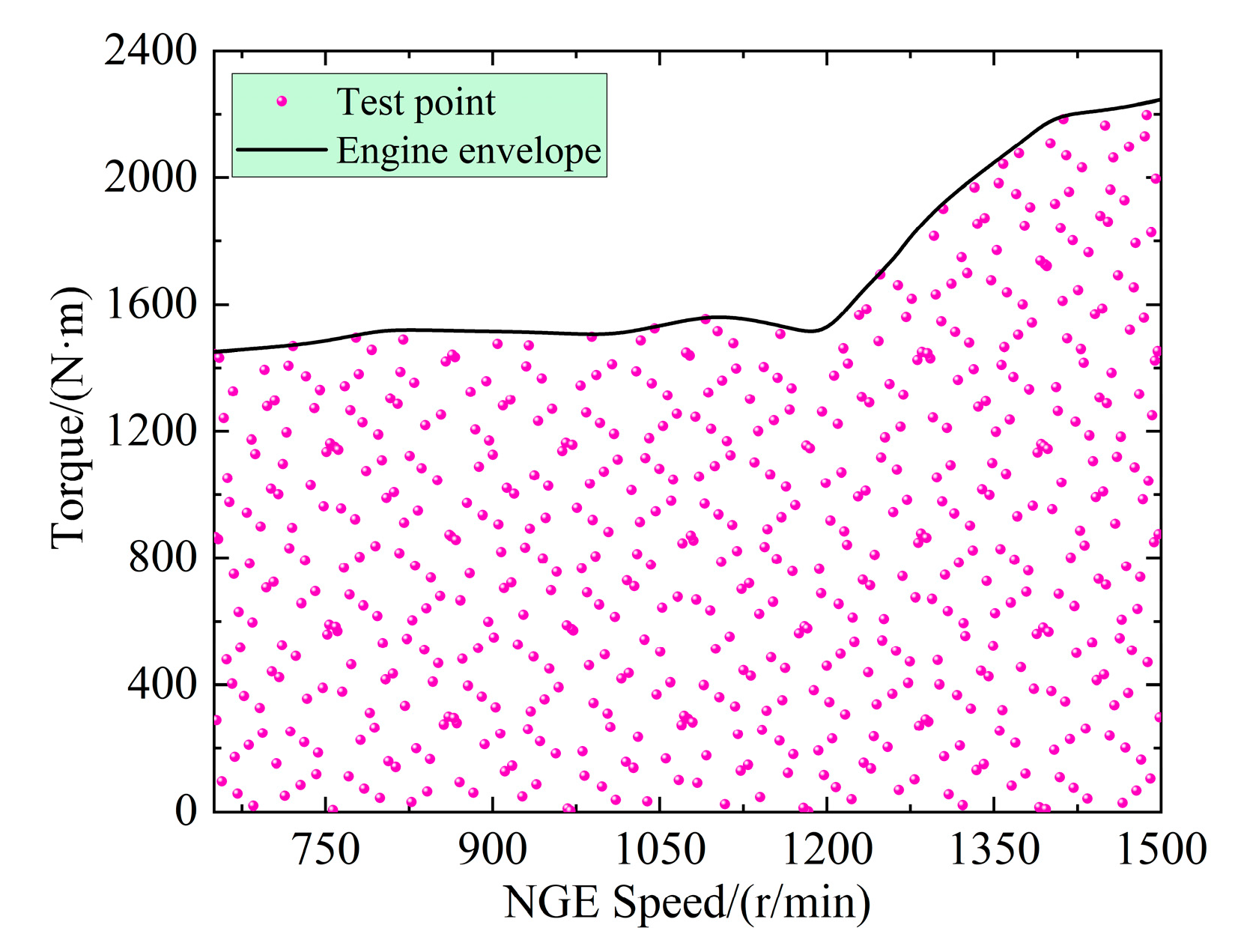
3.2.1. NGE Model
3.2.2. Motor-Energy Storage Systems
3.2.3. Coupled Power Output
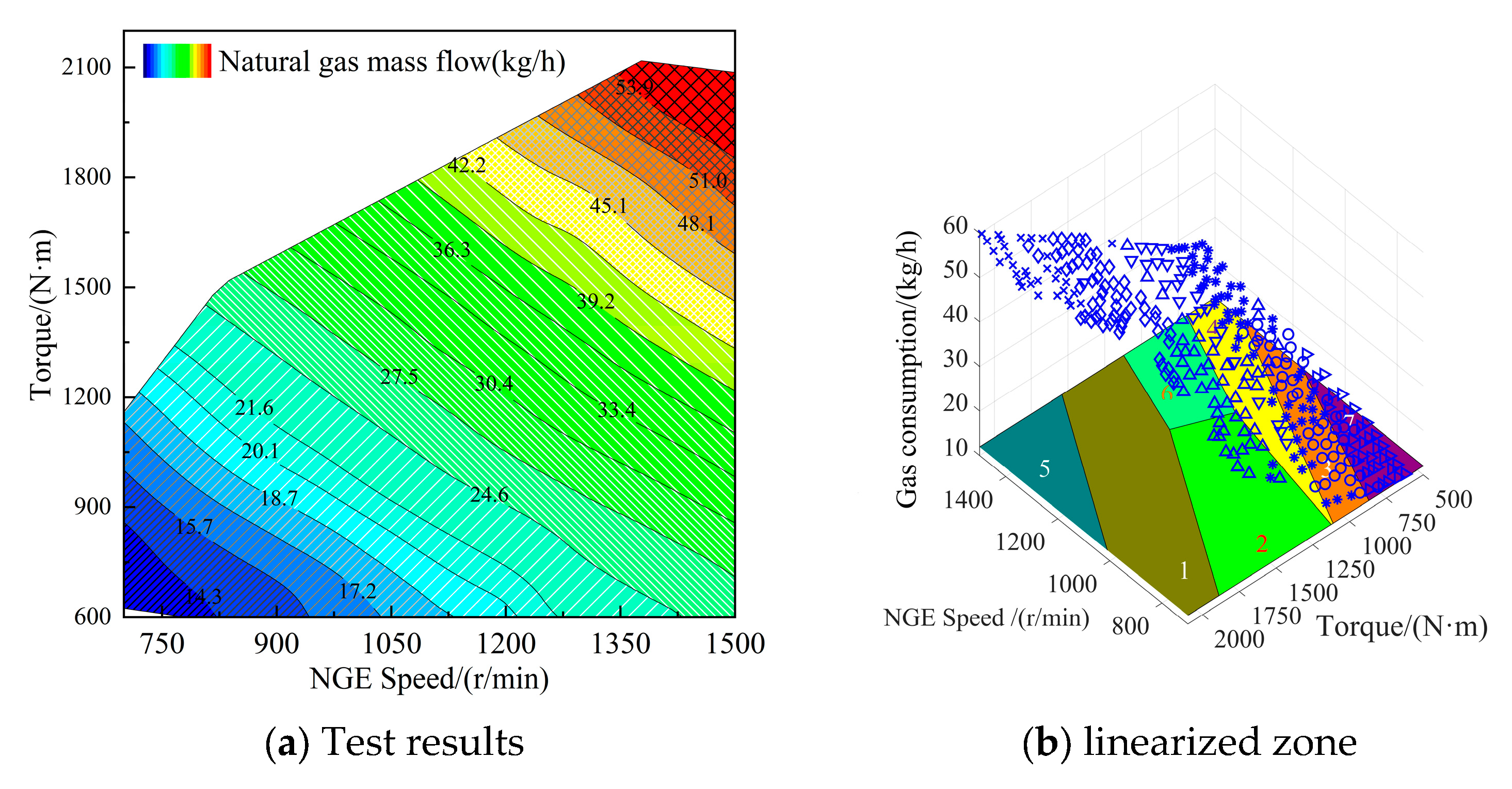
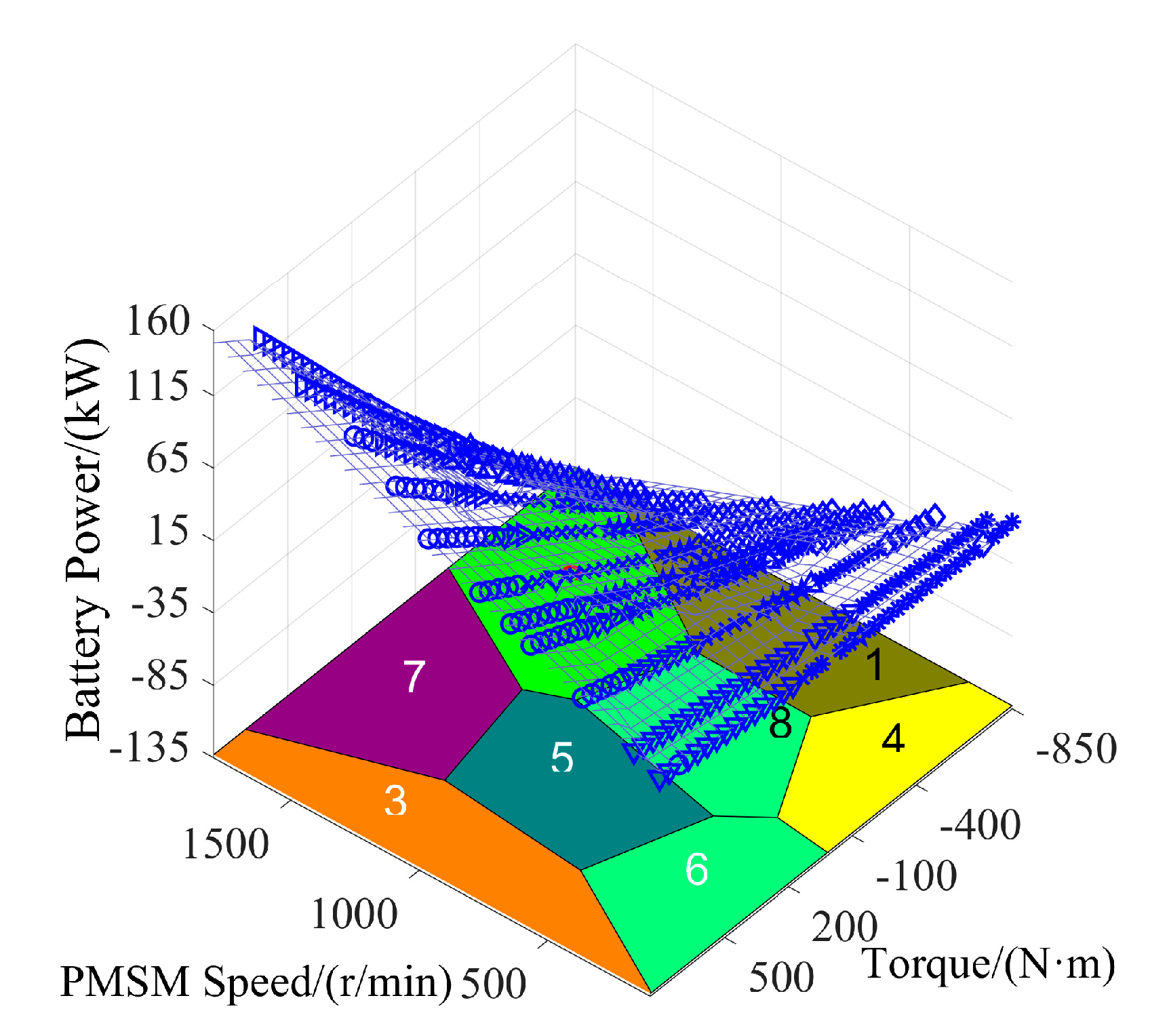
3.2.4. Linearization of External Characteristic Constraints
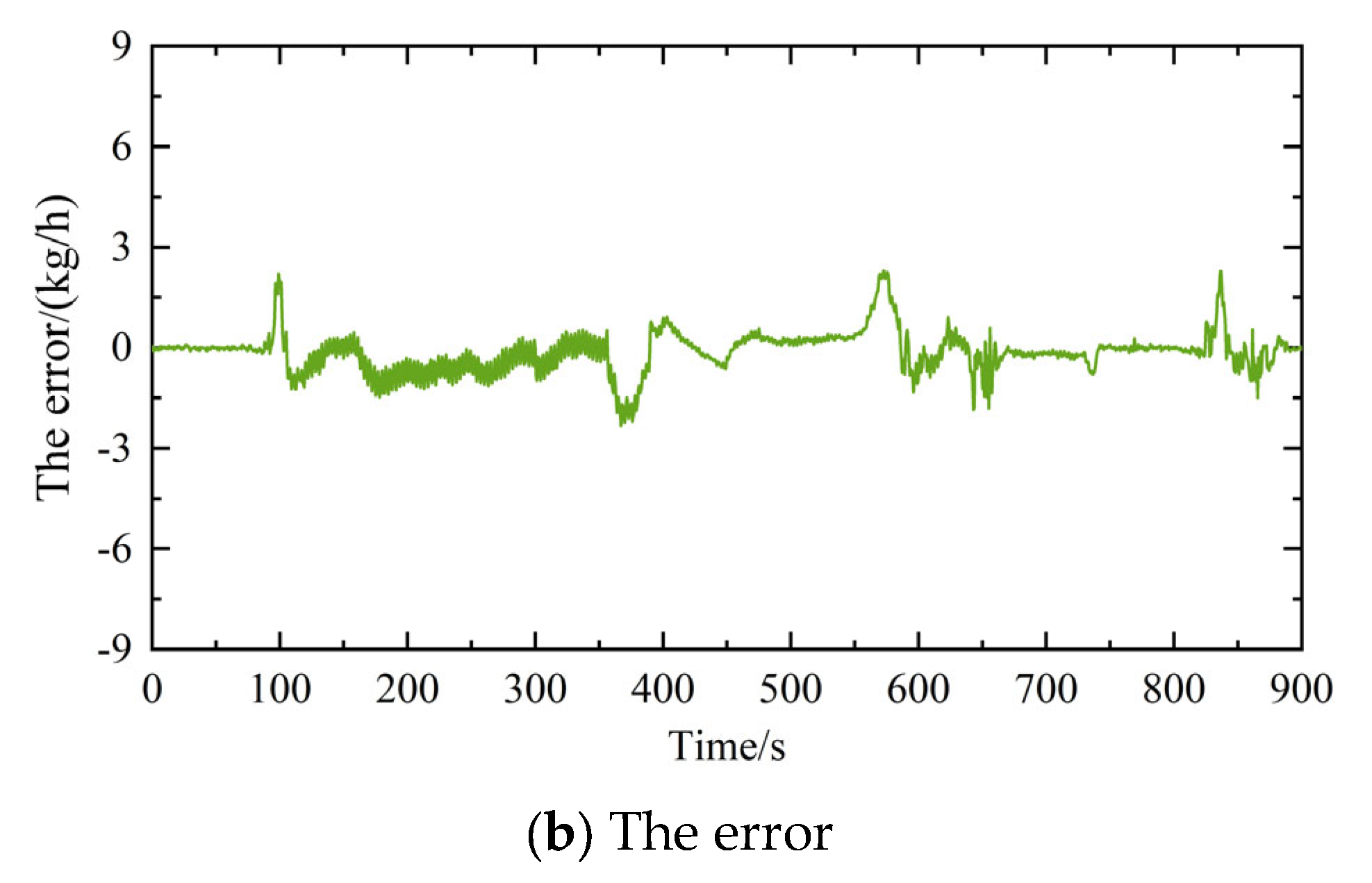
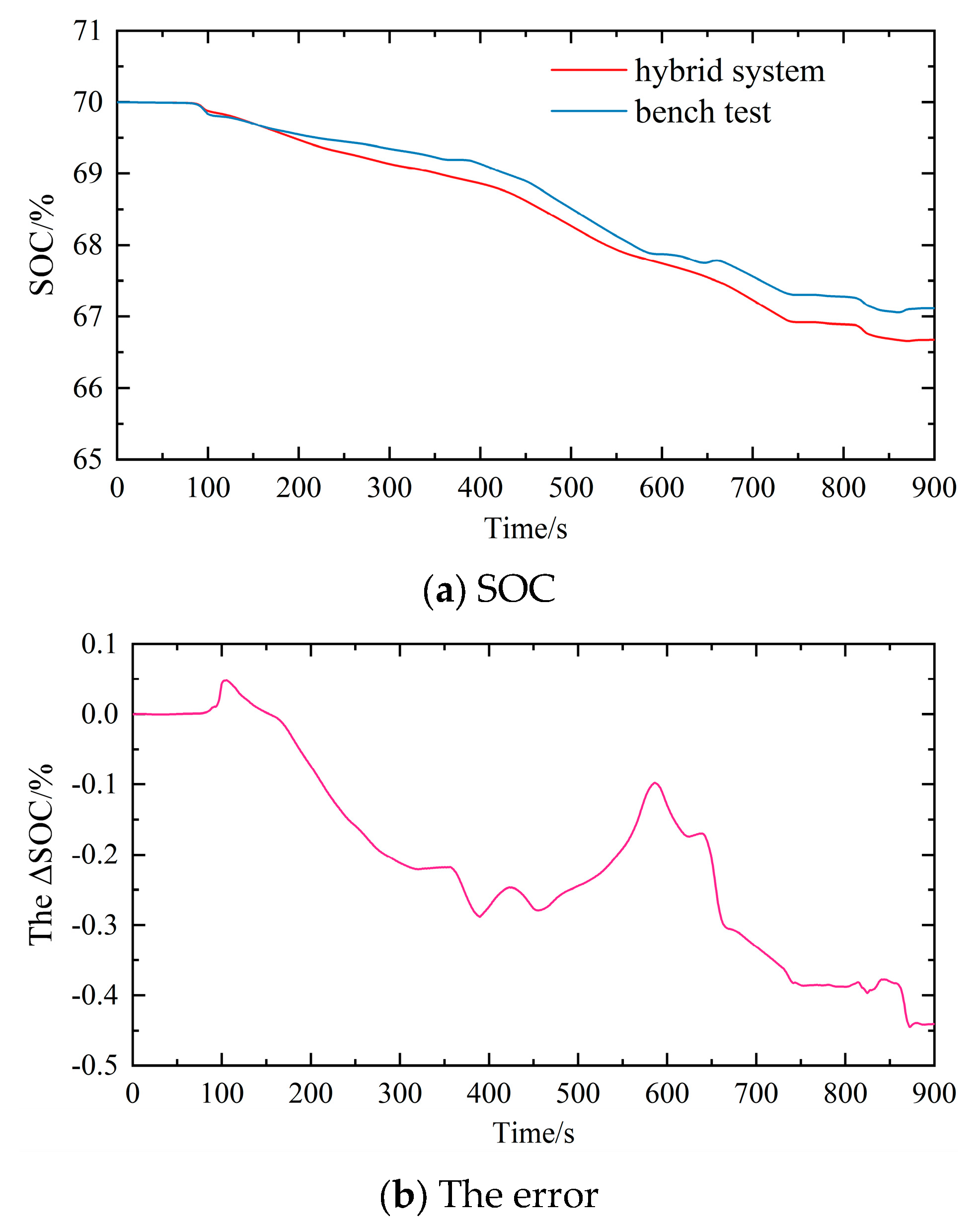
3.3. Cumulative Error Analysis of Hybrid Model
3.4. Energy Management Allocation Based on Hybrid Control
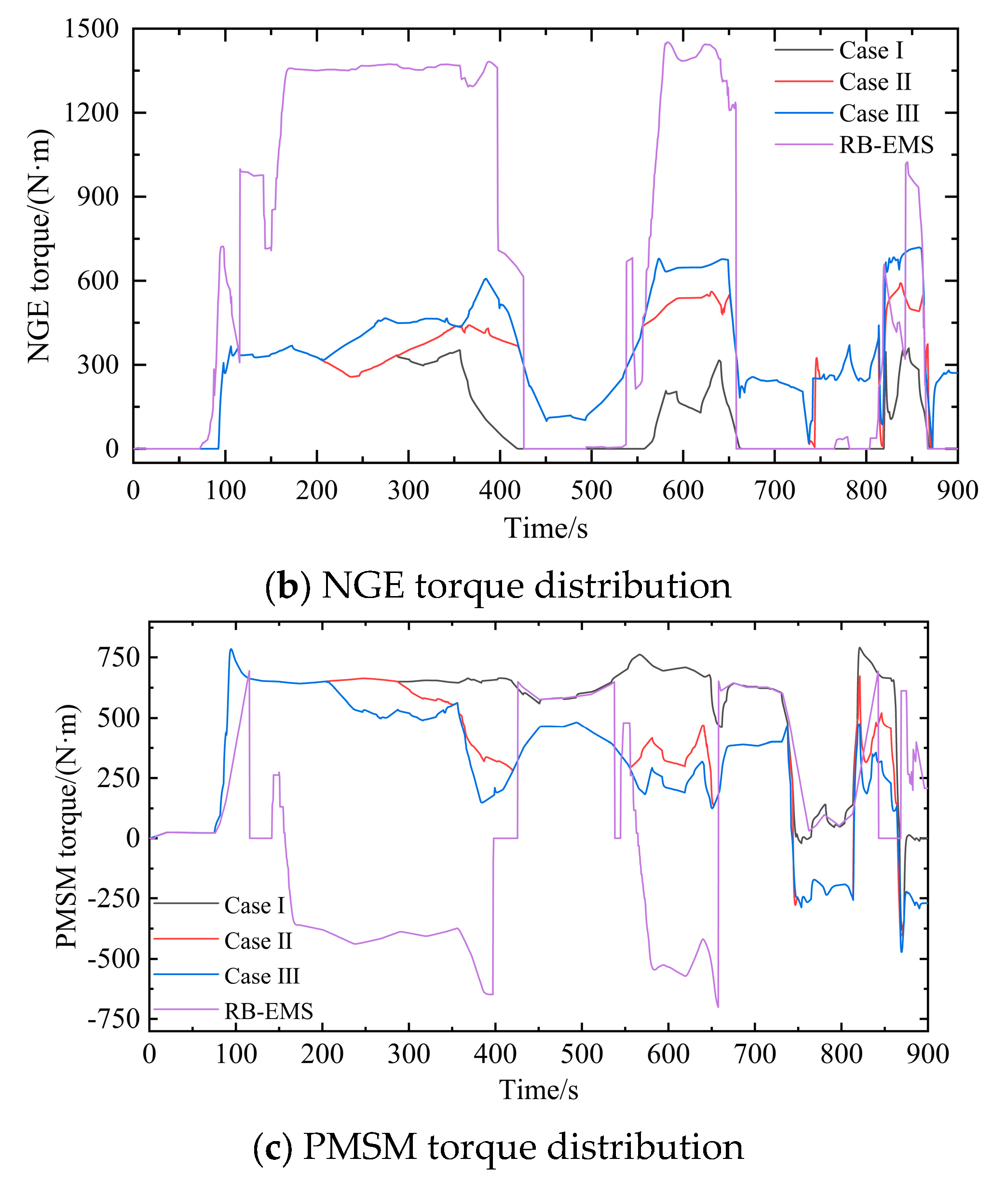
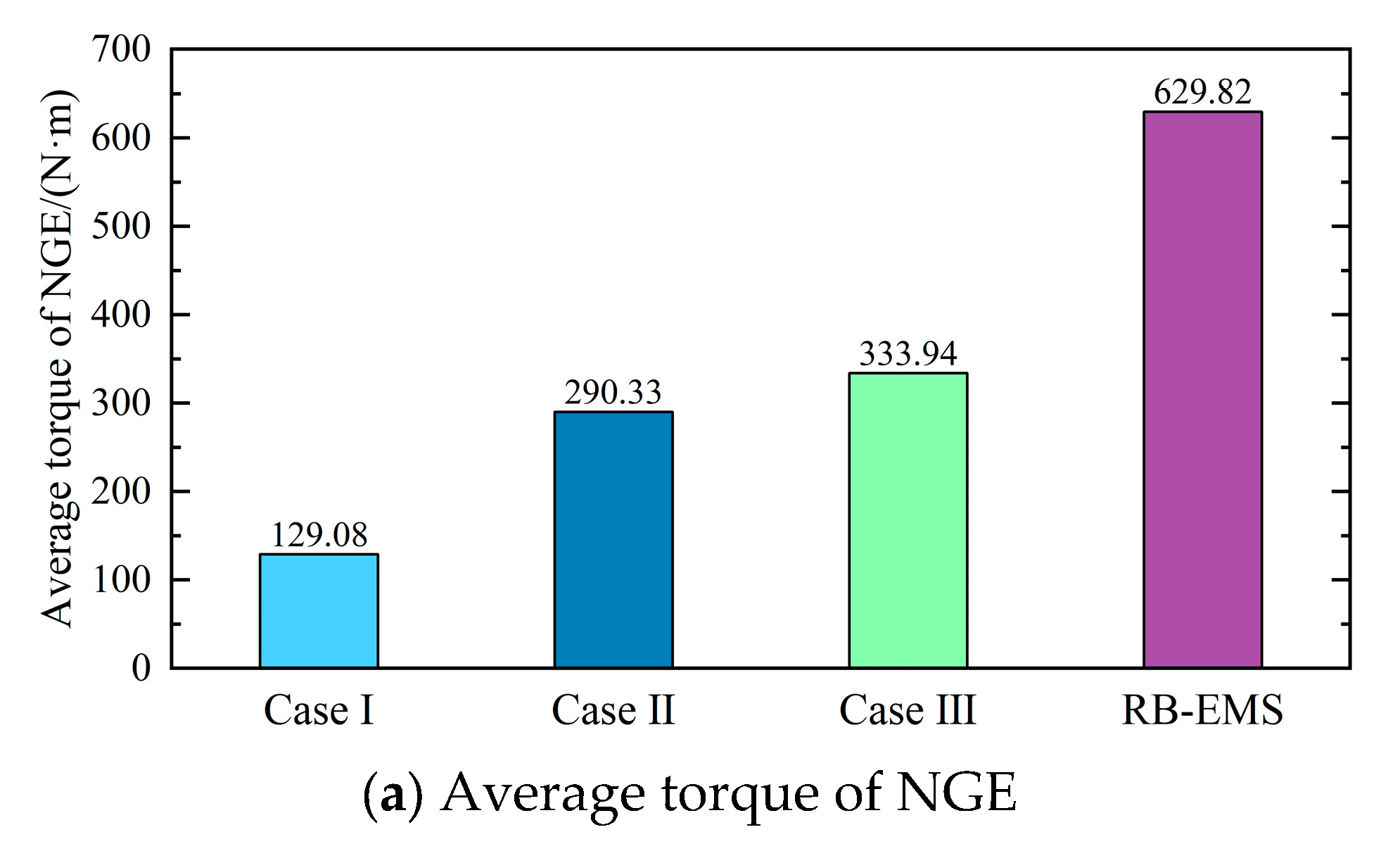
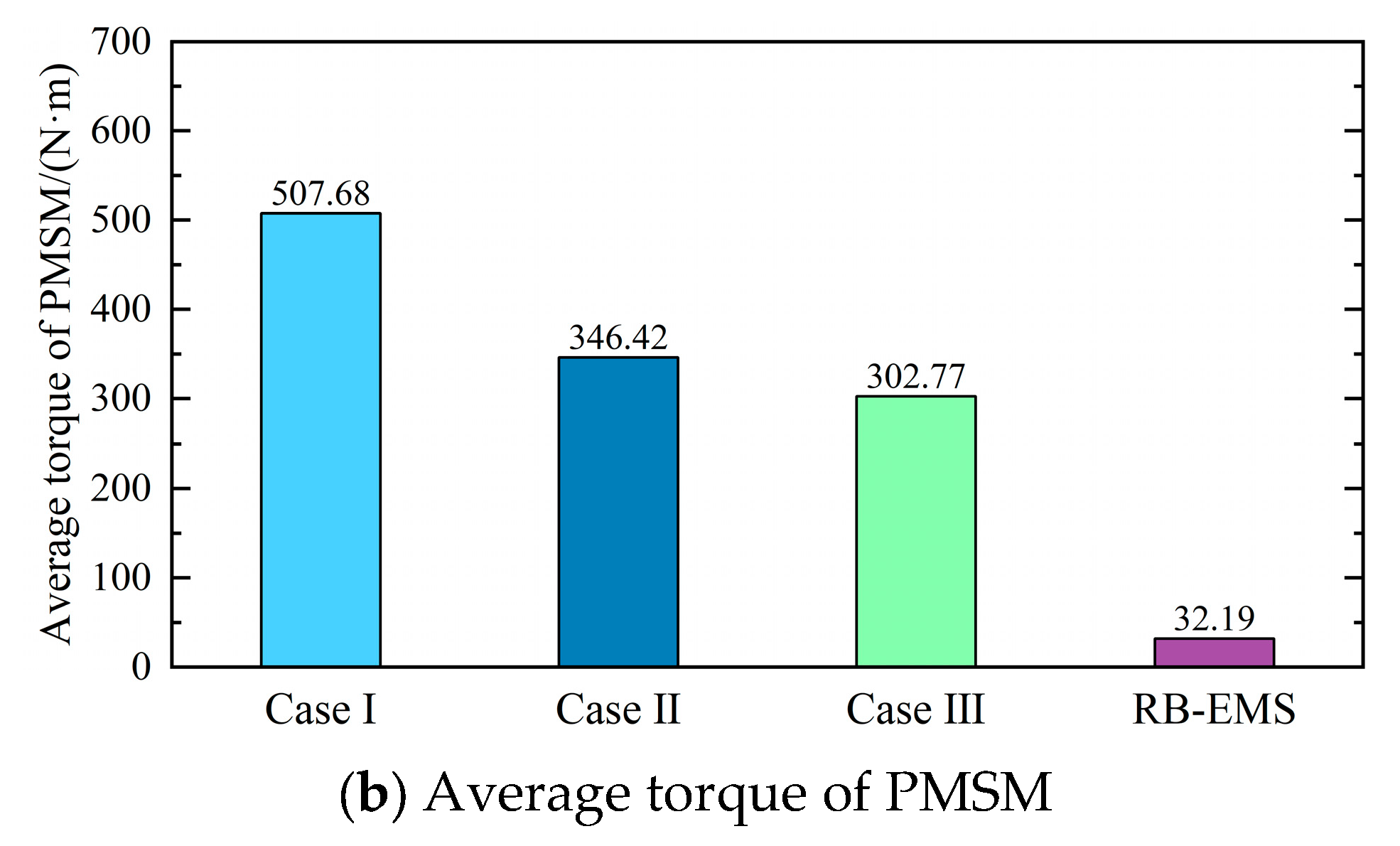
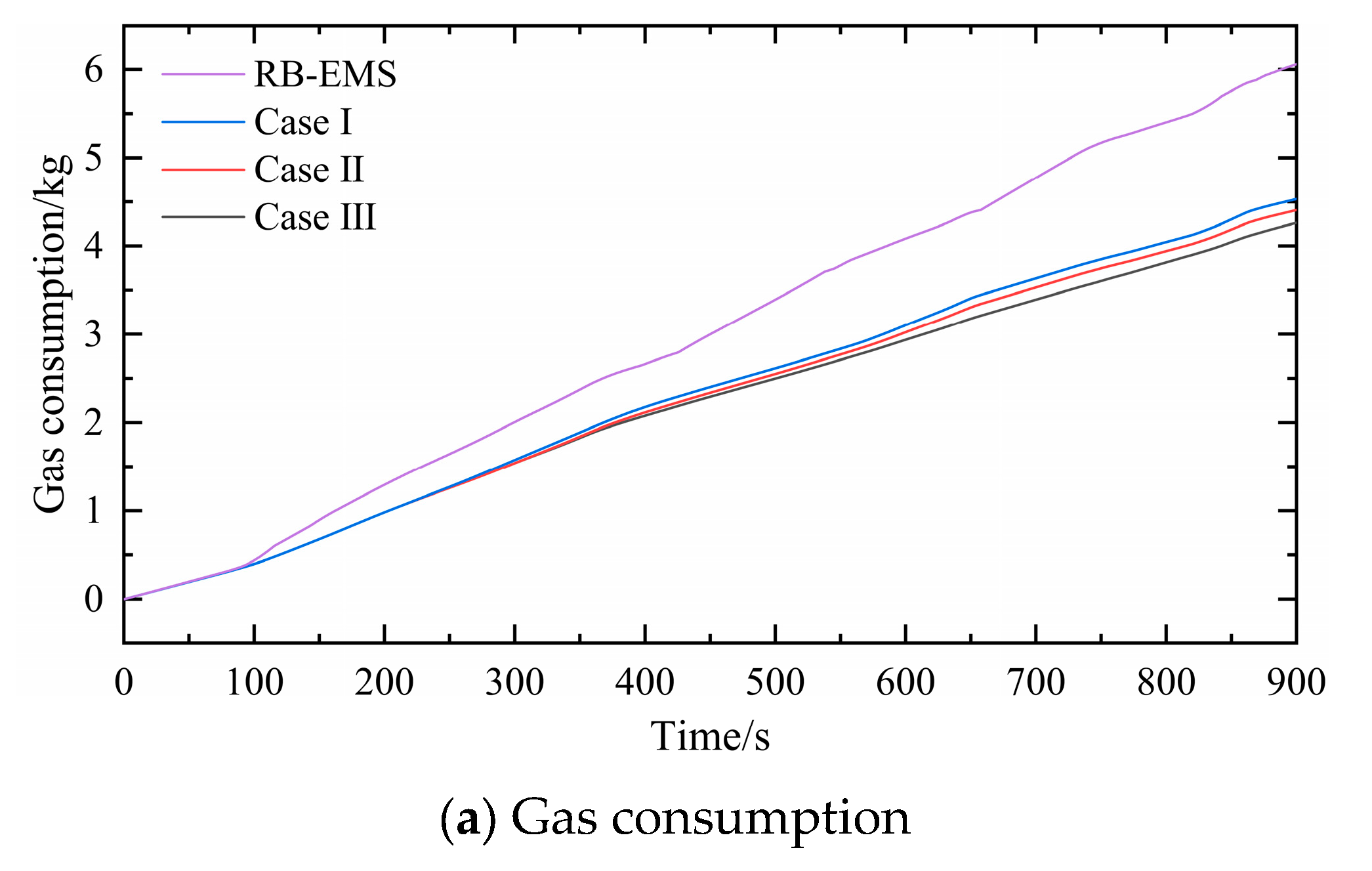
4. Results and Discussion
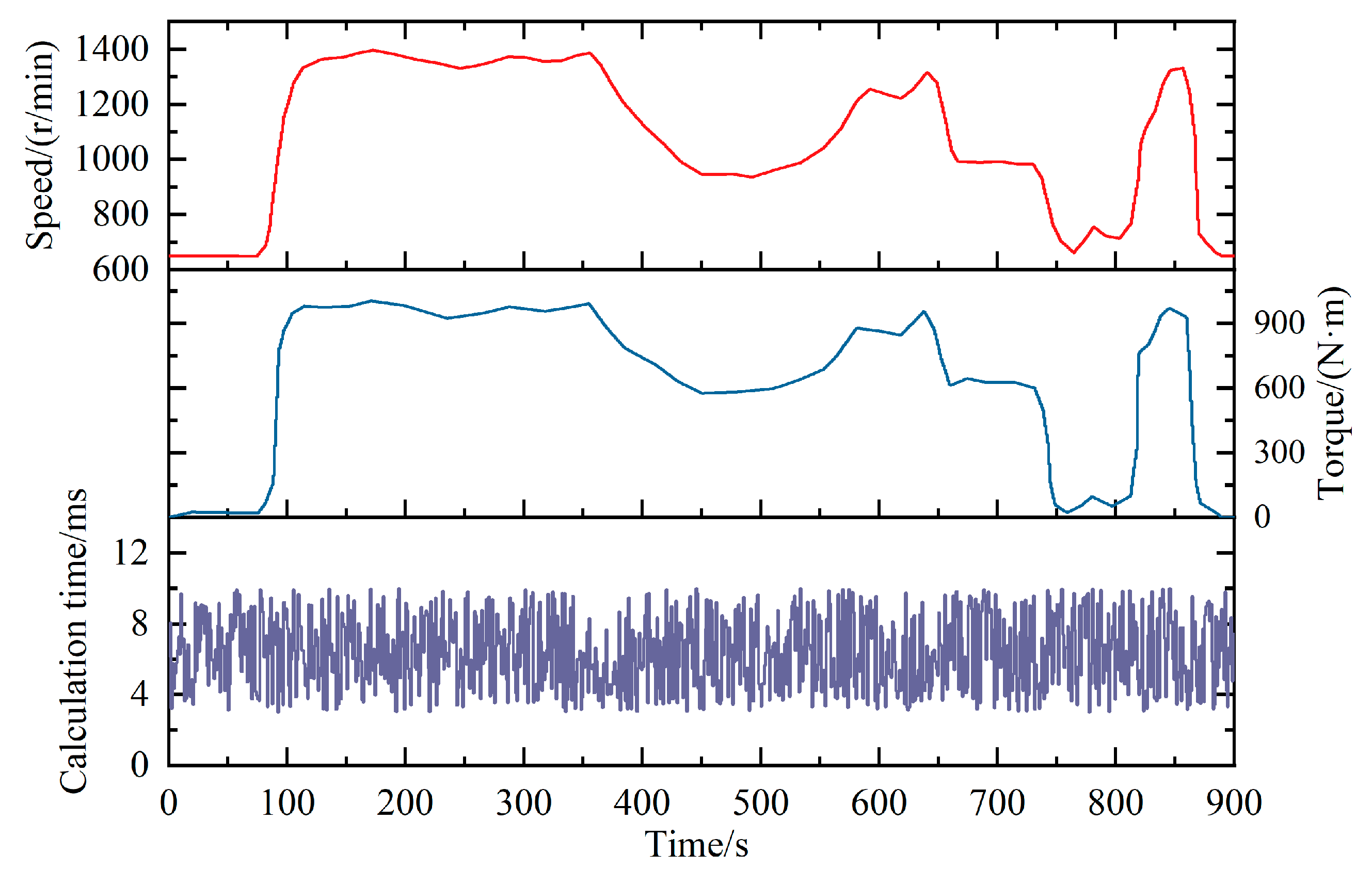
4.1. Experimental Scheme
4.2. Result Analysis
5. Conclusions
- (1)
- The modeling of the MGHPS can be effectively achieved using hybrid systems theory, which has been demonstrated to be both practical and efficient.
- (2)
- The hybrid model of the MGHPS provides the foundation for developing an energy management controller capable of efficiently managing the operational states of each power source within the system.
- (3)
- By adjusting the weights in the hybrid model predictive controller (HMPC), the MGHPS can operate under various states, enabling the ship to meet the performance requirements for different operating conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Wei, W.; Li, G.; Zhang, Z.; Long, Y.; Huang, Y.; Zhang, H.; Zhou, M. Fuel Consumption and NOx Emissions Optimization of a Marine Natural Gas Engine with Lean-Burn and Reformed Exhaust Gas Recirculation Strategies. Fuel 2024, 357, 129970. [Google Scholar] [CrossRef]
- Lu, Z.; Ma, M.; Wang, T.; Lu, T.; Wang, H.; Feng, Y.; Shi, L. Numerical Research of the In-Cylinder Natural Gas Stratification in a Natural Gas-Diesel Dual-Fuel Marine Engine. Fuel 2023, 337, 126861. [Google Scholar] [CrossRef]
- Sun, X.; Yao, C.; Song, E.; Liu, Z.; Ke, Y.; Ding, S. Novel Enhancement of Energy Distribution for Marine Hybrid Propulsion Systems by an Advanced Variable Weight Decision Model Predictive Control. Energy 2023, 274, 127269. [Google Scholar] [CrossRef]
- Sun, X.; Yao, C.; Song, E.; Yang, Q.; Yang, X. Optimal Control of Transient Processes in Marine Hybrid Propulsion Systems: Modeling, Optimization and Performance Enhancement. Appl. Energy 2022, 321, 119404. [Google Scholar] [CrossRef]
- Taghavian, A.; Safi, A.; Khanmirza, E. Constrained Computational Hybrid Controller for Input Affine Hybrid Dynamical Systems. J. Frankl. Inst. 2024, 361, 107142. [Google Scholar] [CrossRef]
- Li, X.; Zhao, T.; Xu, J. Research on MLD Modeling and Predictive Control of Magnetically Coupled Resonant Bidirectional WPT System. Electronics 2024, 13, 1290. [Google Scholar] [CrossRef]
- Cai, B.; Ning, Z.; Ji, W.; Zhu, Y.; Han, M. Quantized Output-Feedback Control of Piecewise-Affine Systems with Reachable Regions of Quantized Measurements. Inf. Sci. 2024, 677, 120828. [Google Scholar] [CrossRef]
- Yadav, P.K.; Karuppaiah, P. On Finiteness of the Solution Set of Extended Horizontal Linear Complementarity Problem. Oper. Res. Lett. 2024, 54, 107112. [Google Scholar] [CrossRef]
- Zhang, X.; Ling, K.V.; Lu, Z.; Zhang, X.; Liao, W.; Lim, W.S. Piece-Wise Affine MPC-Based Attitude Control for a CubeSat during Orbital Manoeuvres. Aerosp. Sci. Technol. 2021, 118, 106997. [Google Scholar] [CrossRef]
- Mansoor, M.; Stadler, M.; Zellinger, M.; Lichtenegger, K.; Auer, H.; Cosic, A. Optimal Planning of Thermal Energy Systems in a Microgrid with Seasonal Storage and Piecewise Affine Cost Functions. Energy 2021, 215, 119095. [Google Scholar] [CrossRef]
- Mei, Z.; Li, Z.; Su, L.; Wang, J.; Li, F. Quantized H∞ Filtering for Networked Persistent Dwell-Time Switched Piecewise-Affine Systems. ISA Trans. 2023, 136, 173–181. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Chen, M.; Zhang, Q. Research on Mixed Logic Dynamic Modeling and Finite Control Set Model Predictive Control of Multi-Inverter Parallel System. Energy Eng. 2023, 120, 649–664. [Google Scholar] [CrossRef]
- Wang, F.; Wu, T.; Ni, Y.; Ye, P.; Cai, Y.; Guo, J.; Wang, C. Torsional Oscillation Suppression-Oriented Torque Compensate Control for Regenerative Braking of Electric Powertrain Based on Mixed Logic Dynamic Model. Mech. Syst. Signal Process. 2023, 190, 110114. [Google Scholar] [CrossRef]
- Zhao, H.; Xing, Y.; Zhou, C.; Wang, Y.; Duan, H.; Liu, K.; Jiang, S. Research on Hybrid Logic Dynamic Model and Voltage Predictive Control of Photovoltaic Storage System. Energies 2024, 17, 4285. [Google Scholar] [CrossRef]
- Dassios, I.; Vaca, A.; Milano, F. On Hybrid Dynamical Systems of Differential–Difference Equations. Chaos Solitons Fractals 2024, 187, 115431. [Google Scholar] [CrossRef]
- Zhang, Y.; Chu, X.; Liu, Y.; Liu, Y. A Modelling and Control Approach for a Type of Mixed Logical Dynamical System Using in Chilled Water System of Refrigeration System. Math. Probl. Eng. 2019, 2019, 7131380. [Google Scholar] [CrossRef]
- Papalambrou, G.; Planakis, N.; Kyrtatos, N. Transient and Disturbed Propeller Load Compensation in Hybrid Propulsion Using Propeller Estimator and Predictive Control. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2022, 236, 86–102. [Google Scholar] [CrossRef]
- Khajiyeva, L.; Sabirova, Y.; Kudaibergenov, A.; Kudaibergenov, A. Application of the Lumped-Parameter Method for Modeling Nonlinear Vibrations of Drill Strings with Stabilizers in a Supersonic Gas Flow. Appl. Math. Model. 2022, 110, 748–766. [Google Scholar] [CrossRef]
- Planakis, N.; Papalambrou, G.; Kyrtatos, N. Ship Energy Management System Development and Experimental Evaluation Utilizing Marine Loading Cycles Based on Machine Learning Techniques. Appl. Energy 2022, 307, 118085. [Google Scholar] [CrossRef]




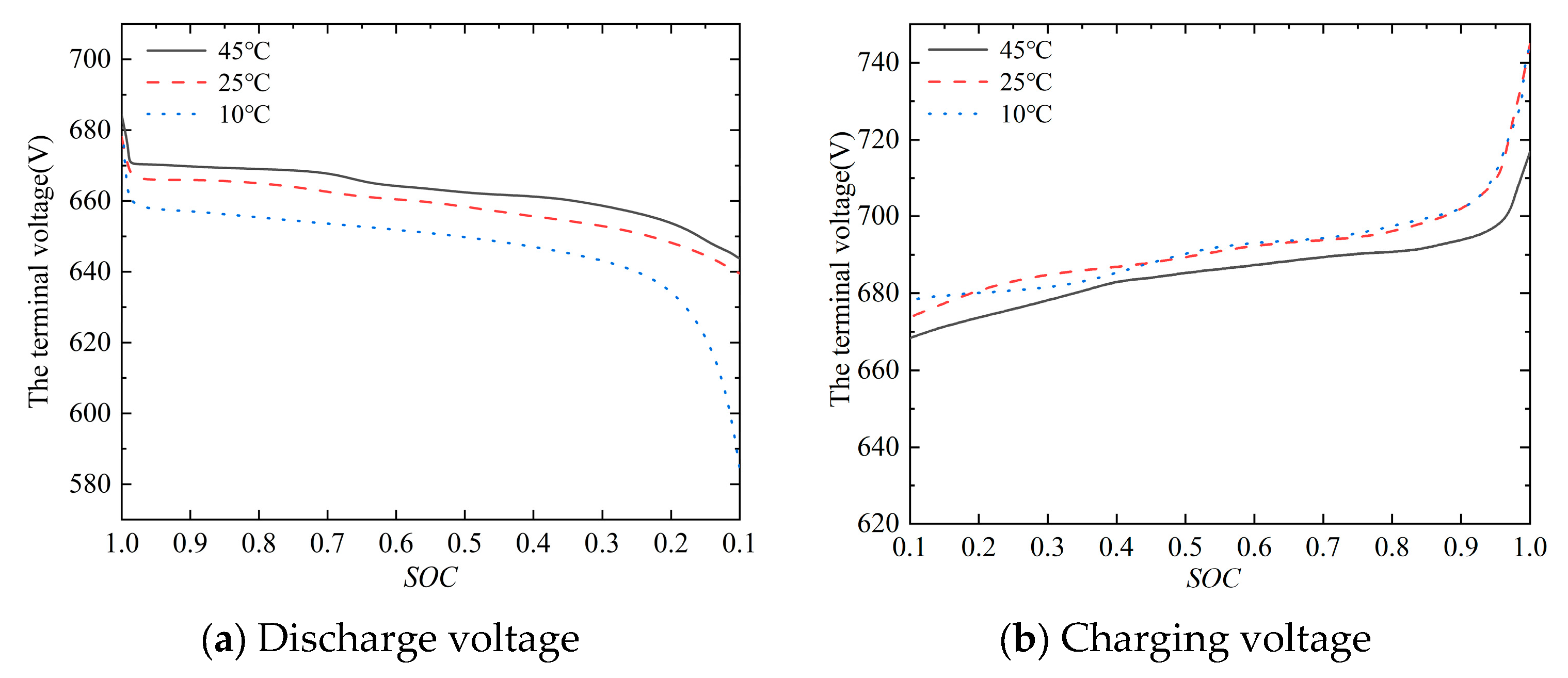
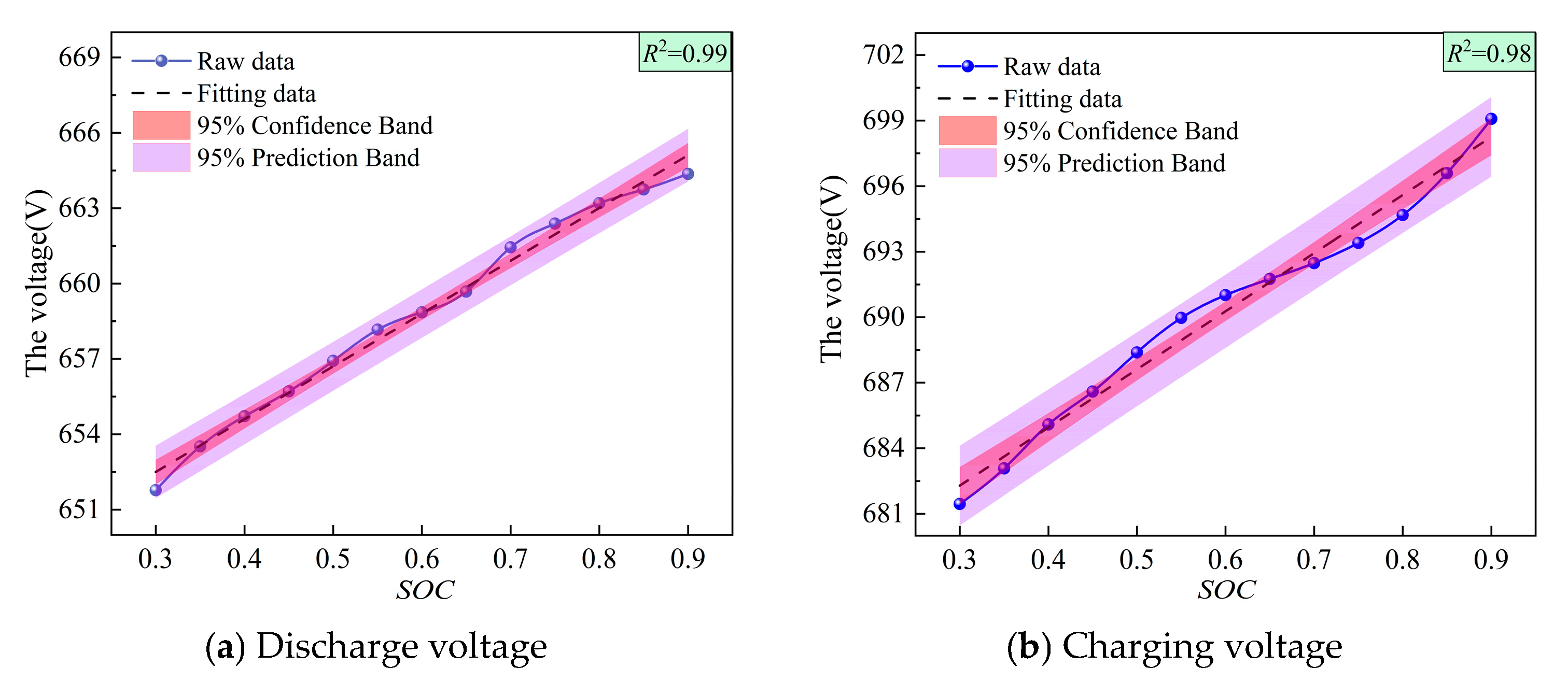



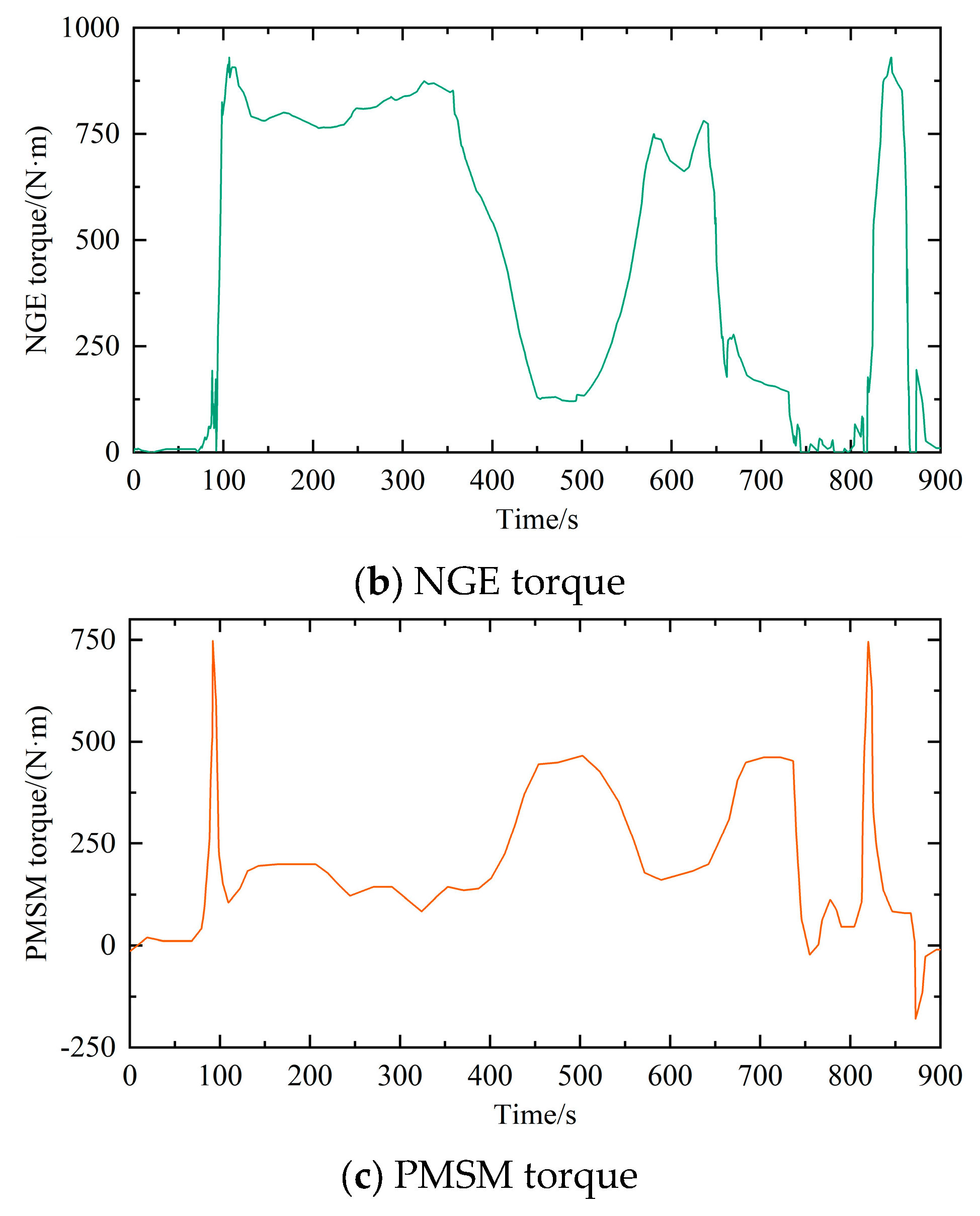
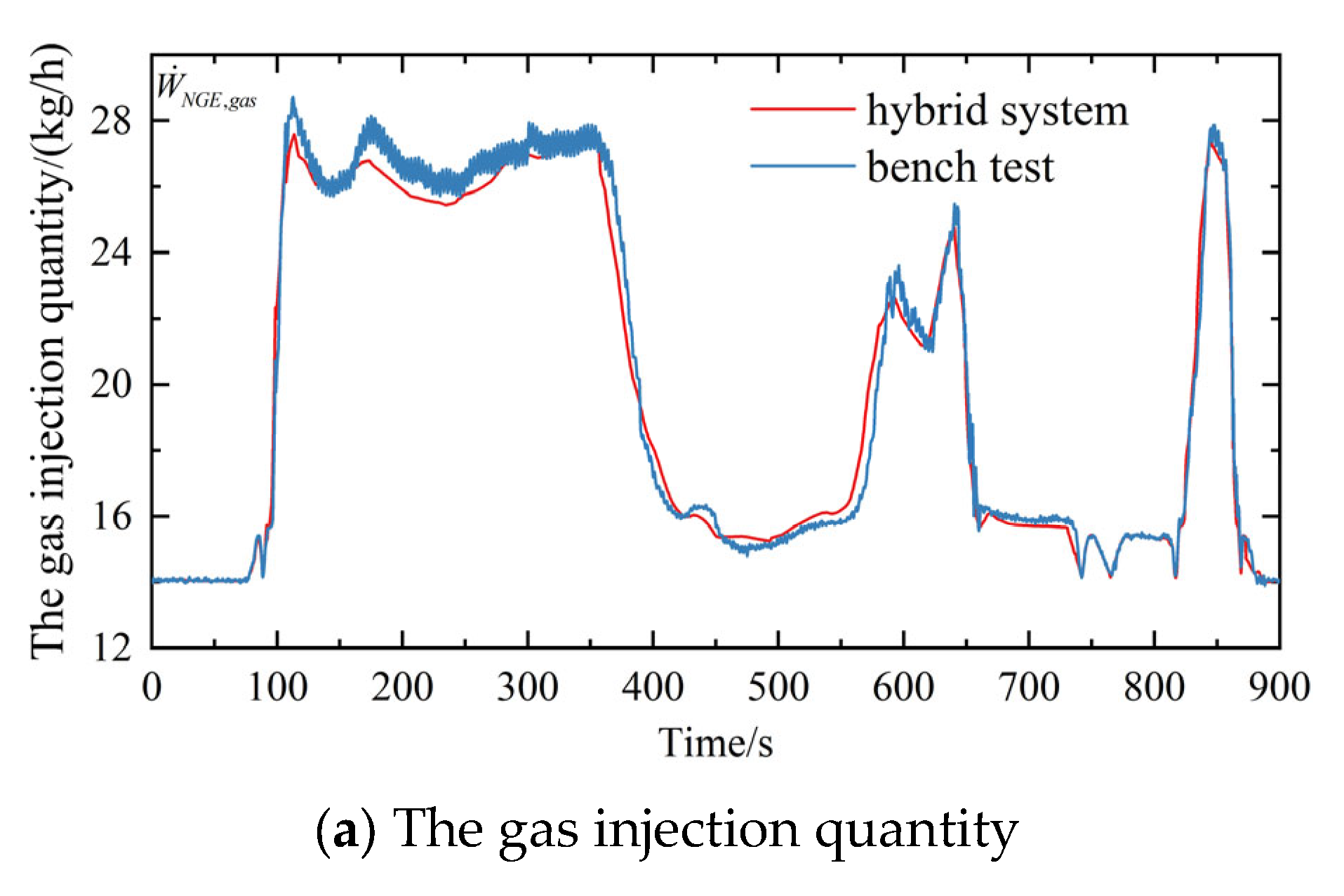


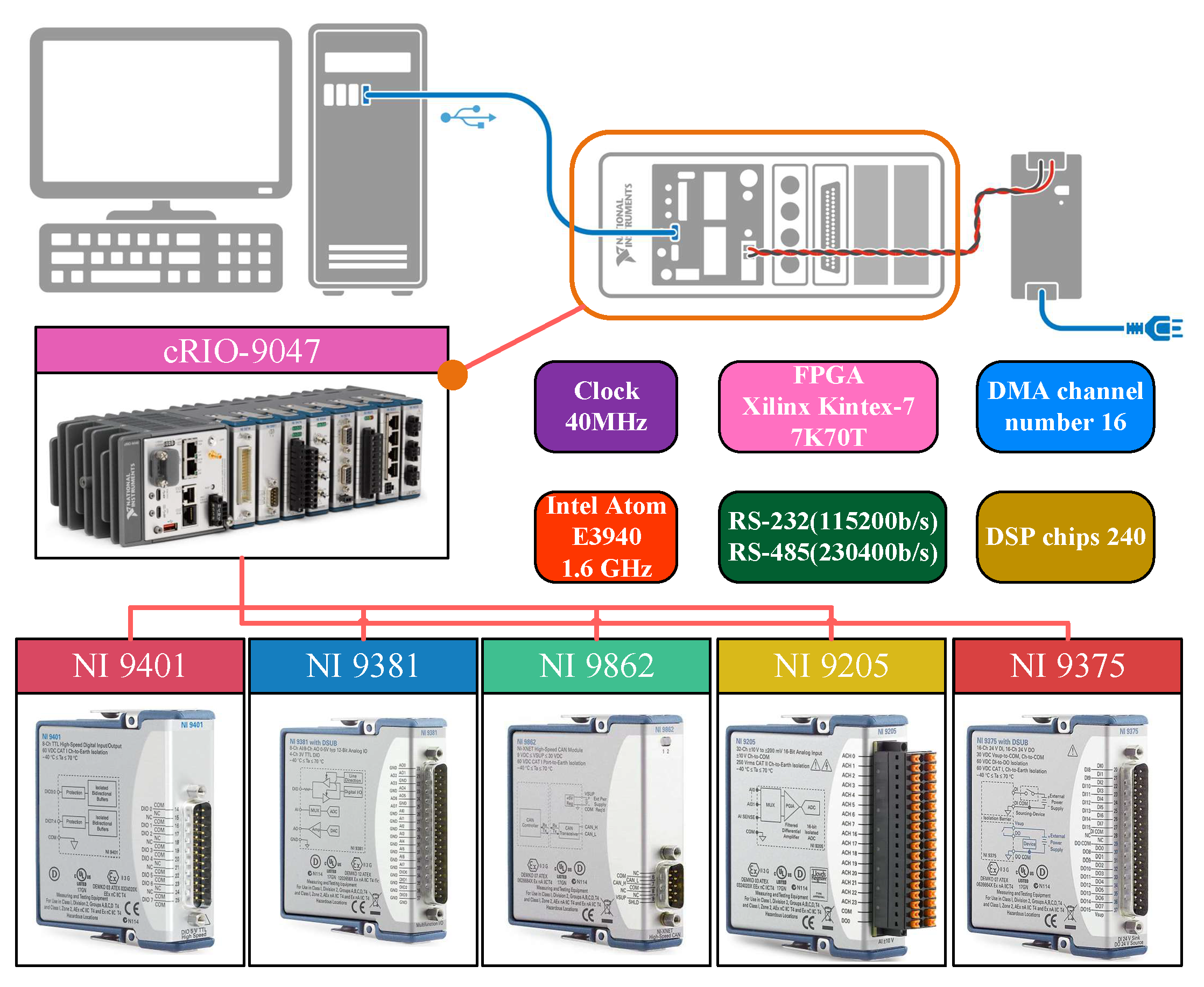


| No. | Equipment | Model Number | Parameters | Function |
|---|---|---|---|---|
| 1 | NGE | 6M33 | Minimum no-load stabilized speed: 650 r/min Rated power: 330 kW Rated speed: 1500 r/min | Power source |
| 2 | PMSM | surface mounted | Rated power: 98 kW Rated voltage: 380 V Rated current: 285 A | Power source |
| 3 | Energy storage systems | LiFePO4 | Battery storage: 205.6 kW·h Capacity: 315 Ah Rated voltage: 652.8 V | Provides power to the PMSM and energy storage. |
| Operating Area | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| MSE | 0.0341 | 0.0621 | 0.0393 | 0.0503 | 0.0450 | 0.0567 | 0.0264 |
| Operating Area | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| MSE | 0.0703 | 0.0103 | 0.0183 | 0.0760 | 0.0789 | 0.0121 |
| Operating Area | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| MSE | 0.6965 | 0.7688 | 1.1468 | 0.4718 | 2.1473 | 0.7021 | 1.6541 | 0.5790 |
| Pdmd Boundary Conditions | SOC Boundary Conditions | NGE Power/(kW) | PMSM Power/(kW) |
|---|---|---|---|
| Operating Conditions | ||||
|---|---|---|---|---|
| Case I | 0.2 | 0.8 | 1 | 10 |
| Case II | 0.5 | 0.5 | 1 | 10 |
| Case III | 0.8 | 0.2 | 1 | 10 |
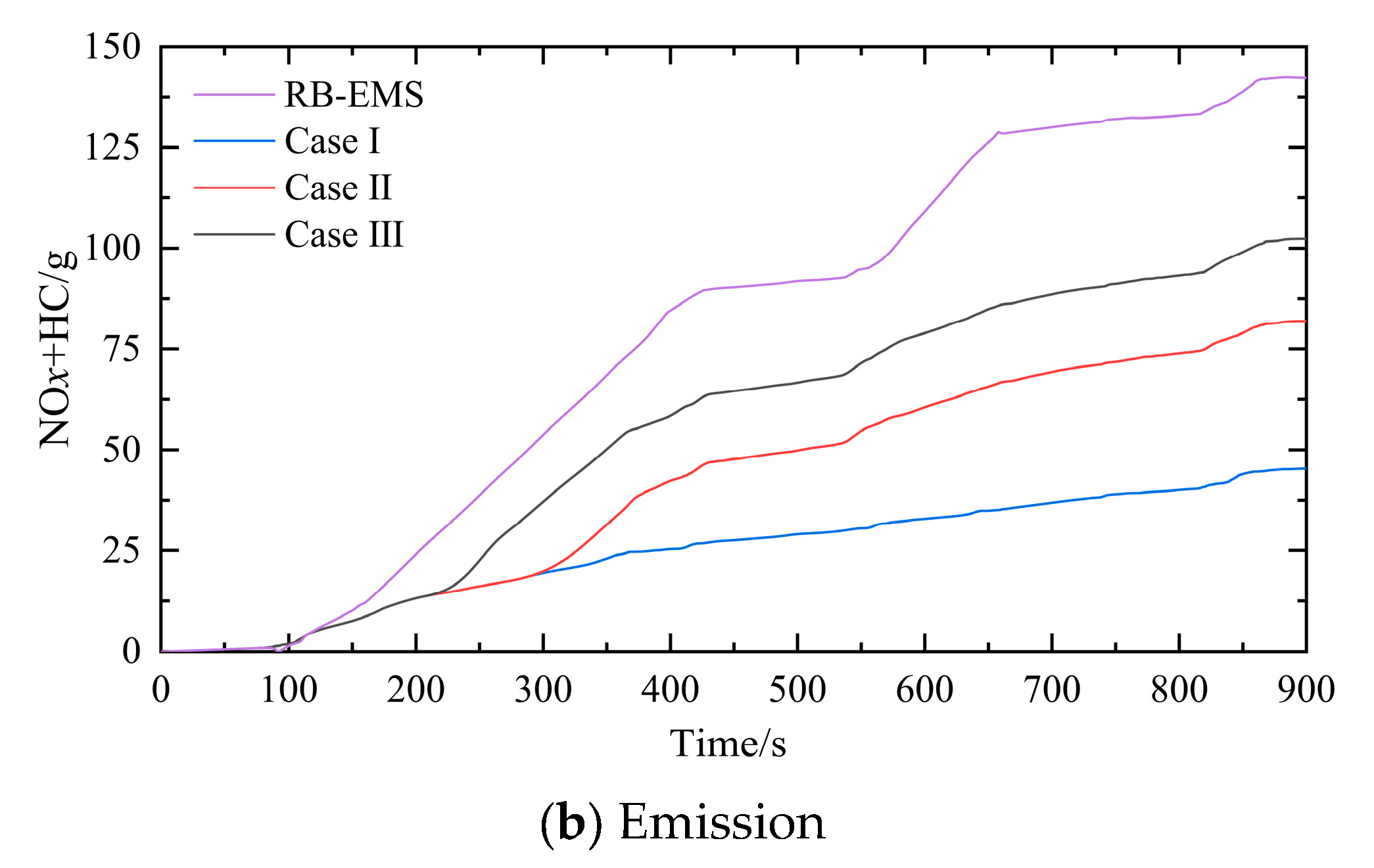
| EMS | Gas Consumption(kg) | VS RB-EMS(%) | Emission(g) | VS RB-EMS(%) |
|---|---|---|---|---|
| RB-EMS | 6.05838 | / | 142.21448 | / |
| HMPC(Case I) | 4.56710 | 24.62 | 45.46057 | 68.03 |
| HMPC(Case II) | 4.44236 | 26.67 | 81.98105 | 42.35 |
| HMPC(Case III) | 4.30216 | 28.99 | 102.42616 | 27.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Zhang, B.; Zhu, J.; Yao, C. A Hybrid System Approach to Energy Optimization in Gas–Electric Hybrid Powertrains. Sustainability 2025, 17, 8160. https://doi.org/10.3390/su17188160
Sun X, Zhang B, Zhu J, Yao C. A Hybrid System Approach to Energy Optimization in Gas–Electric Hybrid Powertrains. Sustainability. 2025; 17(18):8160. https://doi.org/10.3390/su17188160
Chicago/Turabian StyleSun, Xiaojun, Benrong Zhang, Jiangning Zhu, and Chong Yao. 2025. "A Hybrid System Approach to Energy Optimization in Gas–Electric Hybrid Powertrains" Sustainability 17, no. 18: 8160. https://doi.org/10.3390/su17188160
APA StyleSun, X., Zhang, B., Zhu, J., & Yao, C. (2025). A Hybrid System Approach to Energy Optimization in Gas–Electric Hybrid Powertrains. Sustainability, 17(18), 8160. https://doi.org/10.3390/su17188160







