Hybrid Deep Learning Combining Mode Decomposition and Intelligent Optimization for Discharge Forecasting: A Case Study of the Baiquan Karst Spring
Abstract
1. Introduction
2. Study Area and Data Acquisition
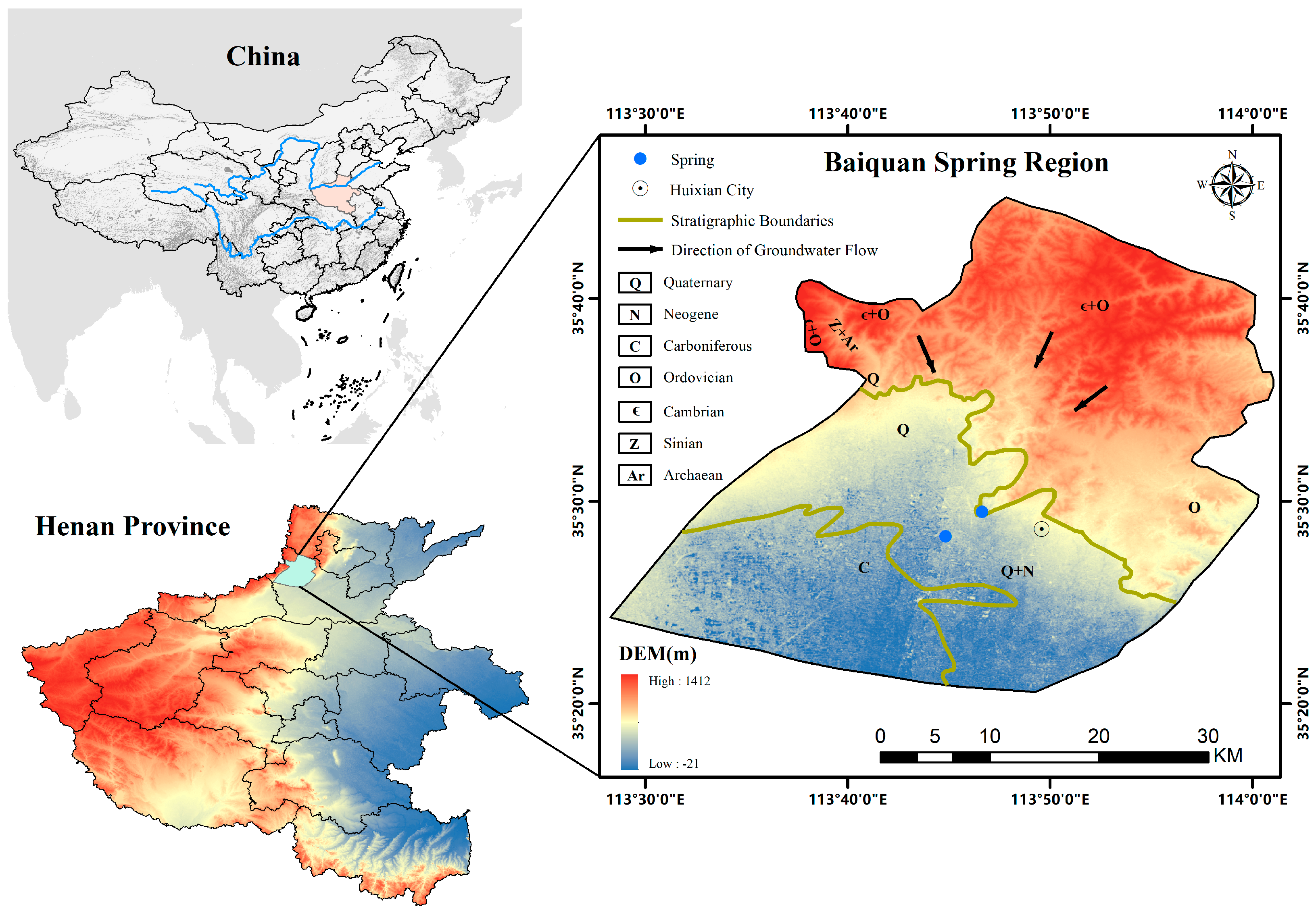
2.1. Study Area
2.2. Data Collection
2.3. Experimental Setup
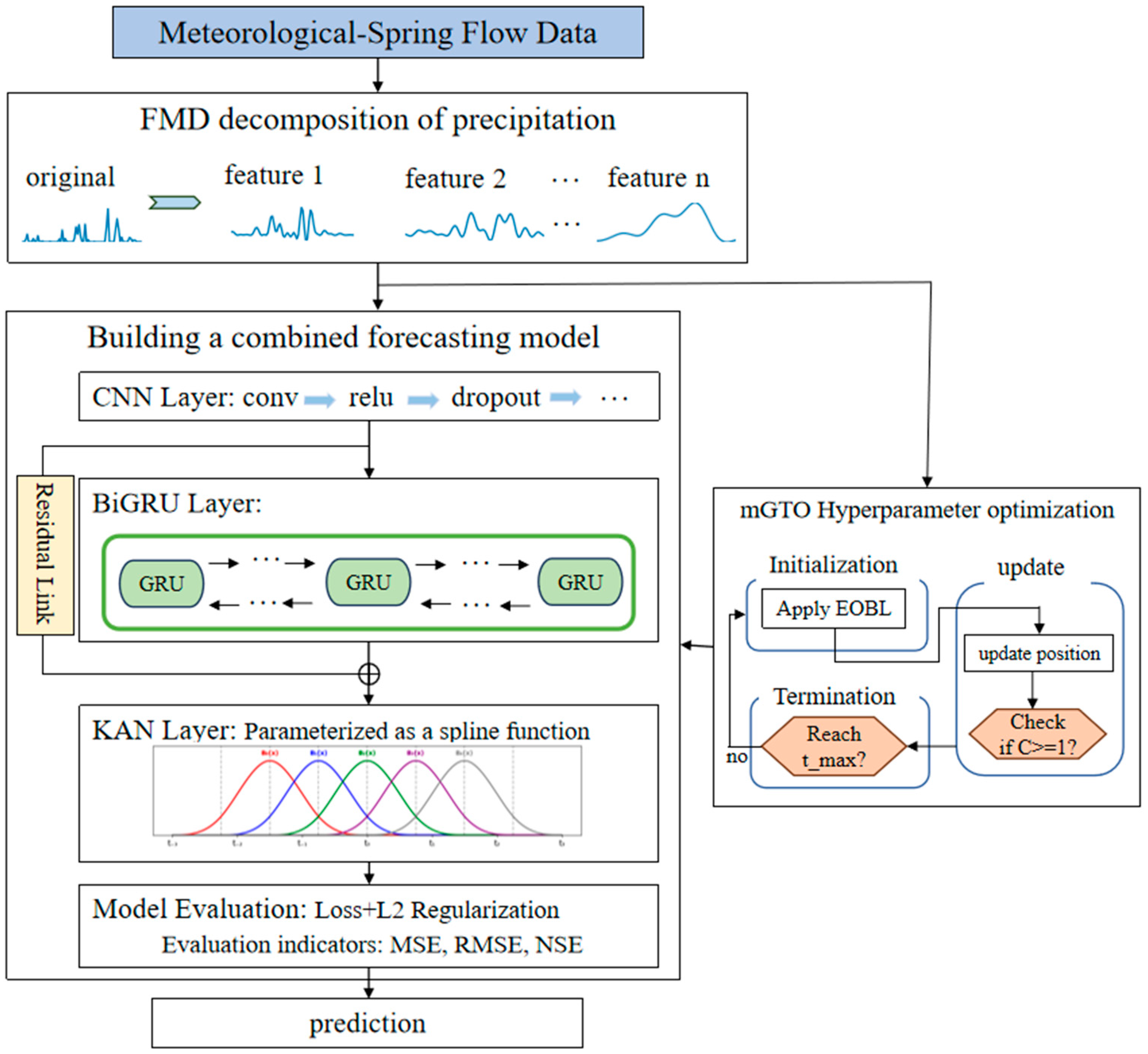
3. Methods
3.1. Feature Mode Decomposition
- (1)
- Adaptive FIR Filter Bank
- (2)
- Filter Update and Period Estimation
- (3)
- Mode Selection
3.2. Bidirectional Gated Recurrent Unit
3.3. Kolmogorov–Arnold Networks
3.4. An Improved Gorilla Troops Optimizer
3.5. Evaluation Indicators
4. Results
4.1. Determination of Parameters of FMD Characteristic Modes
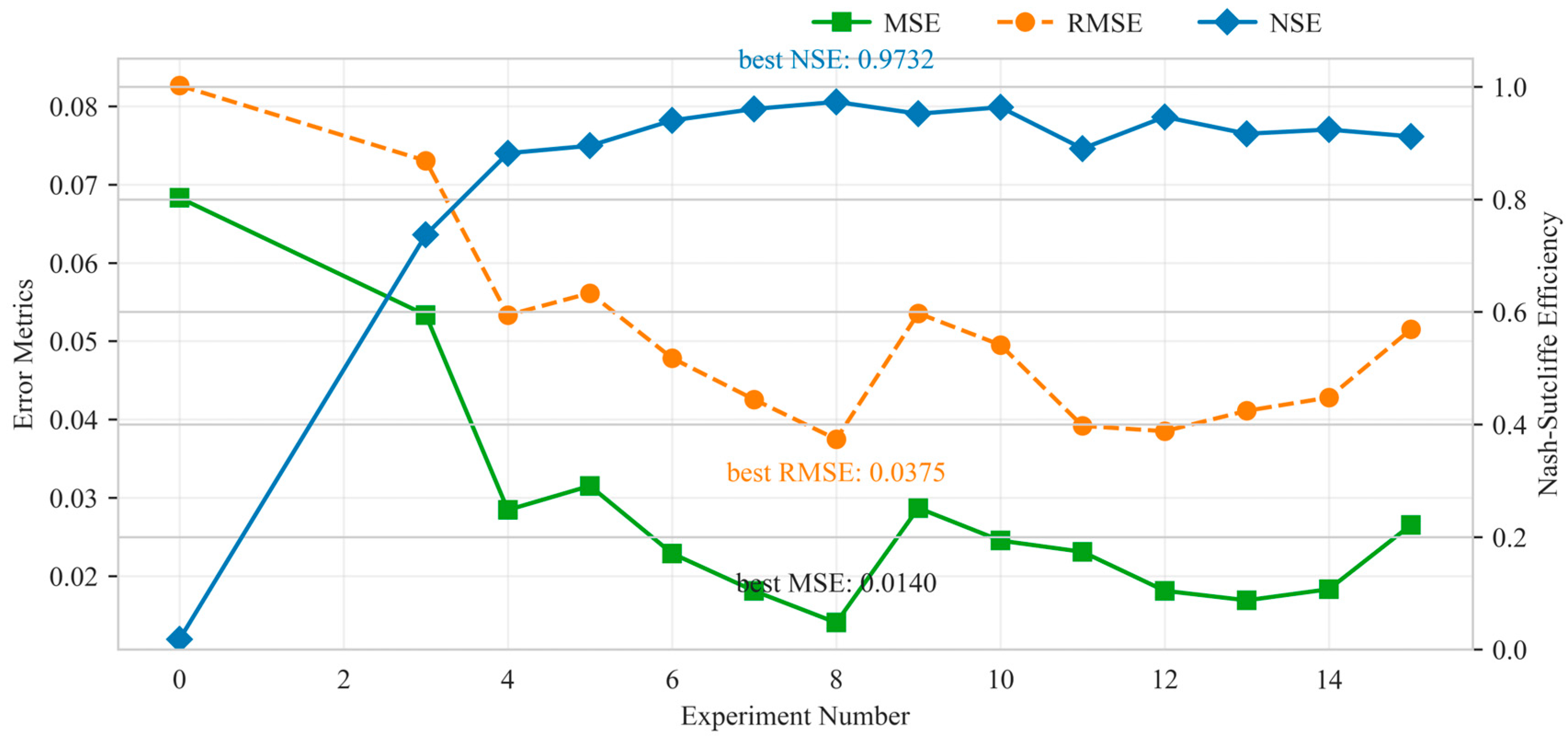
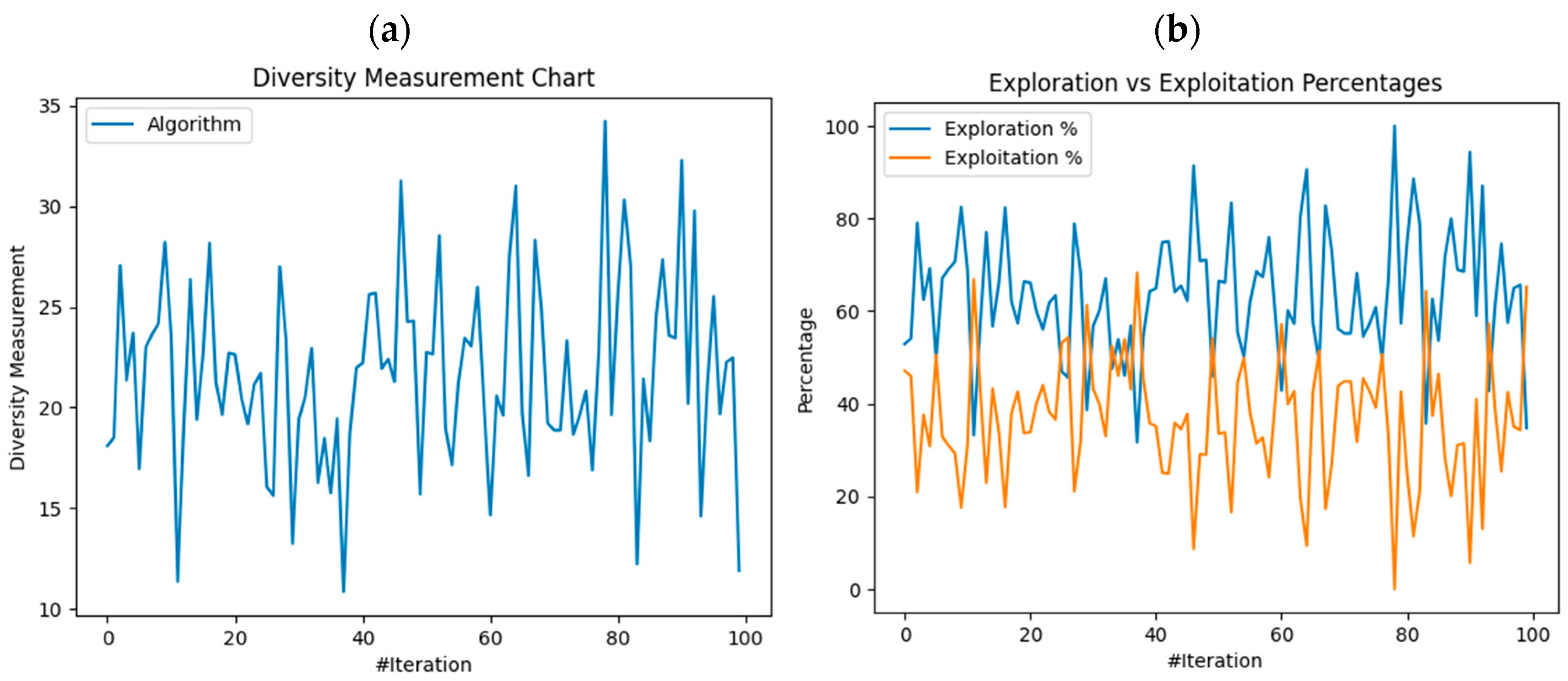
4.2. Intelligent Optimization Algorithm for Hyperparameter Optimization
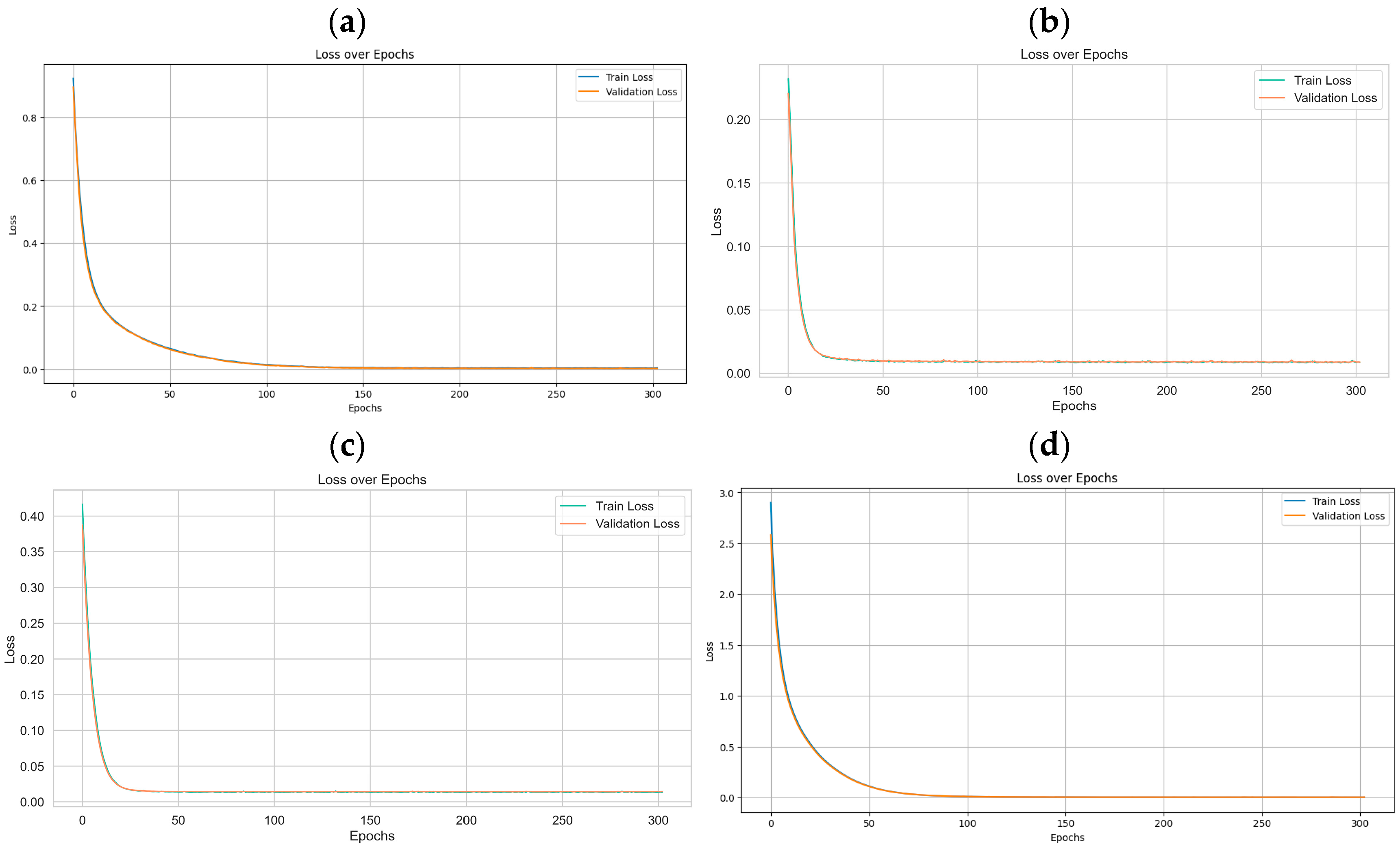
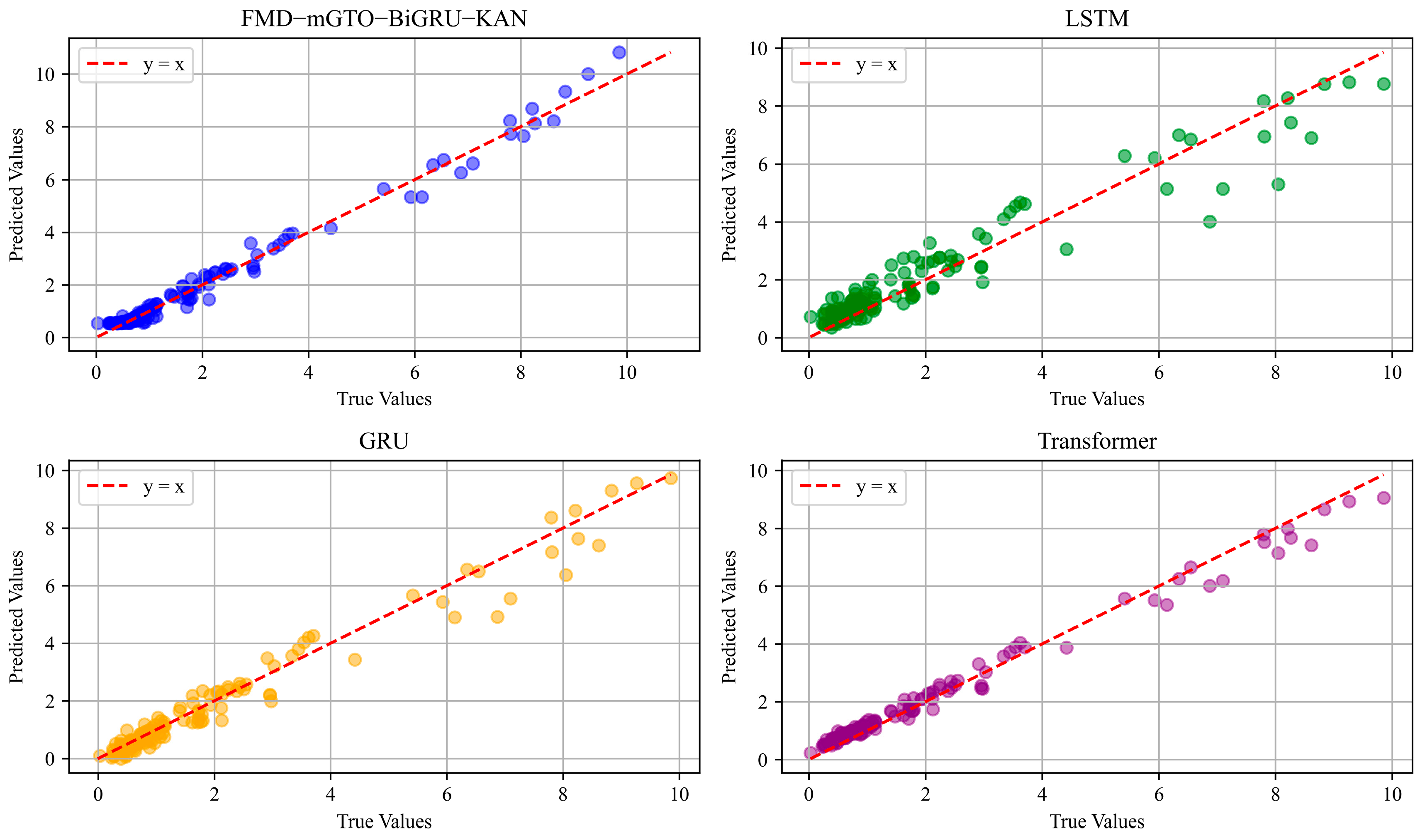
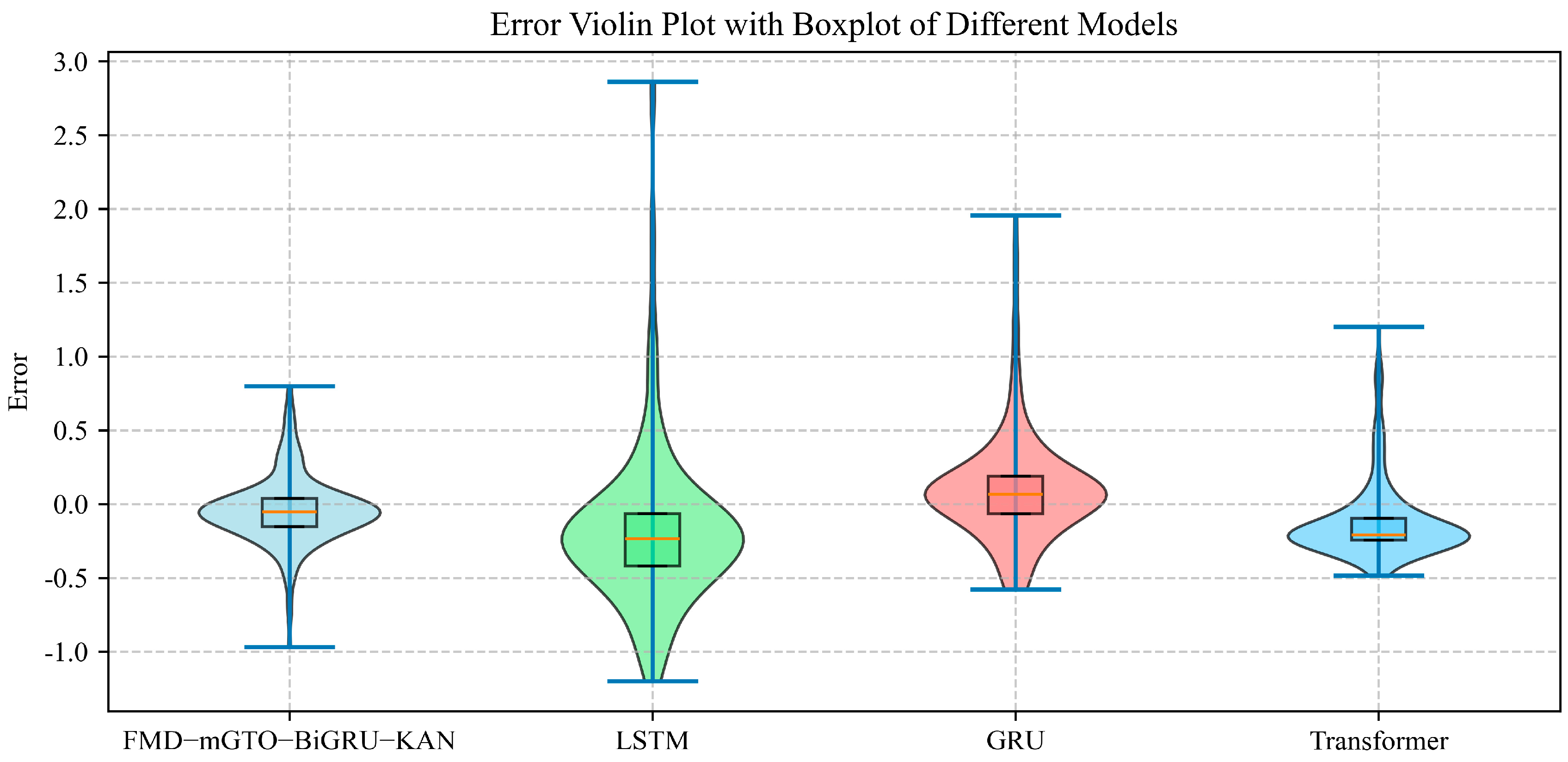
4.3. Comparison of Prediction Effects of Different Models
5. Conclusions
6. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Goldscheider, N.; Chen, Z.; Auler, A.S.; Bakalowicz, M.; Broda, S.; Drew, D.; Hartmann, J.; Jiang, G.; Moosdorf, N.; Stevanovic, Z.; et al. Global Distribution of Carbonate Rocks and Karst Water Resources. Hydrogeol. J. 2020, 28, 1661–1677. [Google Scholar] [CrossRef]
- Hartmann, A.; Goldscheider, N.; Wagener, T.; Lange, J.; Weiler, M. Karst Water Resources in a Changing World: Review of Hydrological Modeling Approaches. Rev. Geophys. 2014, 52, 218–242. [Google Scholar] [CrossRef]
- Bakalowicz, M. Karst Groundwater: A Challenge for New Resources. Hydrogeol. J. 2005, 13, 148–160. [Google Scholar] [CrossRef]
- Ahmed, S. Application of Geostatistics in Hydrosciences. In Groundwater; Springer: Dordrecht, The Netherlands, 2007; pp. 78–111. [Google Scholar]
- Broderick, C.; Matthews, T.; Wilby, R.L.; Bastola, S.; Murphy, C. Transferability of Hydrological Models and Ensemble Averaging Methods between Contrasting Climatic Periods. Water Resour. Res. 2016, 52, 8343–8373. [Google Scholar] [CrossRef]
- Tóth, Á.; Kovács, S.; Kovács, J.; Mádl-Szőnyi, J. Springs Regarded as Hydraulic Features and Interpreted in the Context of Basin-Scale Groundwater Flow. J. Hydrol. 2022, 610, 127907. [Google Scholar] [CrossRef]
- Barman, P.; Ghosh, J.; Deb, S. Study of Water Quality, Socio-Economic Status and Policy Intervention in Spring Ecosystems of Tripura, Northeast India. Discov. Water 2022, 2, 7. [Google Scholar] [CrossRef]
- Gallegos, J.J.; Hu, B.X.; Davis, H. Simulating Flow in Karst Aquifers at Laboratory and Sub-Regional Scales Using MODFLOW-CFP. Hydrogeol. J. 2013, 21, 1749–1760. [Google Scholar] [CrossRef]
- Efstratiadis, A.; Nalbantis, I.; Koukouvinos, A.; Rozos, E.; Koutsoyiannis, D. HYDROGEIOS: A Semi-Distributed GIS-Based Hydrological Model for Modified River Basins. Hydrol. Earth Syst. Sci. 2008, 12, 989–1006. [Google Scholar] [CrossRef]
- Çallı, S.S.; Çallı, K.Ö.; Tuğrul Yılmaz, M.; Çelik, M. Contribution of the Satellite-Data Driven Snow Routine to a Karst Hydrological Model. J. Hydrol. 2022, 607, 127511. [Google Scholar] [CrossRef]
- Diodato, N.; Guerriero, L.; Fiorillo, F.; Esposito, L.; Revellino, P.; Grelle, G.; Guadagno, F.M. Predicting Monthly Spring Discharges Using a Simple Statistical Model. Water Resour. Manag. 2014, 28, 969–978. [Google Scholar] [CrossRef]
- Katsanou, K.; Maramathas, A.; Lambrakis, N. Simulation of Karst Springs Discharge in Case of Incomplete Time Series. Water Resour. Manag. 2015, 29, 1623–1633. [Google Scholar] [CrossRef]
- Kazakis, N.; Chalikakis, K.; Mazzilli, N.; Ollivier, C.; Manakos, A.; Voudouris, K. Management and Research Strategies of Karst Aquifers in Greece: Literature Overview and Exemplification Based on Hydrodynamic Modelling and Vulnerability Assessment of a Strategic Karst Aquifer. Sci. Total Environ. 2018, 643, 592–609. [Google Scholar] [CrossRef] [PubMed]
- Farzin, M.; Avand, M.; Ahmadzadeh, H.; Zelenakova, M.; Tiefenbacher, J.P. Assessment of Ensemble Models for Groundwater Potential Modeling and Prediction in a Karst Watershed. Water 2021, 13, 2540. [Google Scholar] [CrossRef]
- Granata, F.; Saroli, M.; de Marinis, G.; Gargano, R. Machine Learning Models for Spring Discharge Forecasting. Geofluids 2018, 2018, 8328167. [Google Scholar] [CrossRef]
- Song, X.; Hao, H.; Liu, W.; Wang, Q.; An, L.; Jim Yeh, T.-C.; Hao, Y. Spatial-Temporal Behavior of Precipitation Driven Karst Spring Discharge in a Mountain Terrain. J. Hydrol. 2022, 612, 128116. [Google Scholar] [CrossRef]
- An, L.; Hao, Y.; Yeh, T.-C.J.; Liu, Y.; Liu, W.; Zhang, B. Simulation of Karst Spring Discharge Using a Combination of Time–Frequency Analysis Methods and Long Short-Term Memory Neural Networks. J. Hydrol. 2020, 589, 125320. [Google Scholar] [CrossRef]
- Zhou, R.; Zhang, Y.; Wang, Q.; Jin, A.; Shi, W. A Hybrid Self-Adaptive DWT-WaveNet-LSTM Deep Learning Architecture for Karst Spring Forecasting. J. Hydrol. 2024, 634, 131128. [Google Scholar] [CrossRef]
- Pölz, A.; Blaschke, A.P.; Komma, J.; Farnleitner, A.H.; Derx, J. Transformer Versus LSTM: A Comparison of Deep Learning Models for Karst Spring Discharge Forecasting. Water Resour. Res. 2024, 60, e2022WR032602. [Google Scholar] [CrossRef]
- Hua, Q.; Fan, Z.; Mu, W.; Cui, J.; Xing, R.; Liu, H.; Gao, J. A Short-Term Power Load Forecasting Method Using CNN-GRU with an Attention Mechanism. Energies 2024, 18, 106. [Google Scholar] [CrossRef]
- Liu, F.; Cai, M.; Wang, L.; Lu, Y. An Ensemble Model Based on Adaptive Noise Reducer and Over-Fitting Prevention LSTM for Multivariate Time Series Forecasting. IEEE Access 2019, 7, 26102–26115. [Google Scholar] [CrossRef]
- Zhou, R.; Wang, Q.; Jin, A.; Shi, W.; Liu, S. Interpretable Multi-Step Hybrid Deep Learning Model for Karst Spring Discharge Prediction: Integrating Temporal Fusion Transformers with Ensemble Empirical Mode Decomposition. J. Hydrol. 2024, 645, 132235. [Google Scholar] [CrossRef]
- Zhang, W.; Duan, L.; Liu, T.; Shi, Z.; Shi, X.; Chang, Y.; Qu, S.; Wang, G. A Hybrid Framework Based on LSTM for Predicting Karst Spring Discharge Using Historical Data. J. Hydrol. 2024, 633, 130946. [Google Scholar] [CrossRef]
- Akay, B.; Karaboga, D.; Akay, R. A Comprehensive Survey on Optimizing Deep Learning Models by Metaheuristics. Artif. Intell. Rev. 2022, 55, 829–894. [Google Scholar] [CrossRef]
- Dodangeh, E.; Panahi, M.; Rezaie, F.; Lee, S.; Tien Bui, D.; Lee, C.-W.; Pradhan, B. Novel Hybrid Intelligence Models for Flood-Susceptibility Prediction: Meta Optimization of the GMDH and SVR Models with the Genetic Algorithm and Harmony Search. J. Hydrol. 2020, 590, 125423. [Google Scholar] [CrossRef]
- Mostafa, R.R.; Gaheen, M.A.; Abd ElAziz, M.; Al-Betar, M.A.; Ewees, A.A. An Improved Gorilla Troops Optimizer for Global Optimization Problems and Feature Selection. Knowl. Based Syst. 2023, 269, 110462. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Soleimanian Gharehchopogh, F.; Mirjalili, S. Artificial Gorilla Troops Optimizer: A New Nature-Inspired Metaheuristic Algorithm for Global Optimization Problems. Int. J. Intell. Syst. 2021, 36, 5887–5958. [Google Scholar] [CrossRef]
- Hussien, A.G.; Bouaouda, A.; Alzaqebah, A.; Kumar, S.; Hu, G.; Jia, H. An In-Depth Survey of the Artificial Gorilla Troops Optimizer: Outcomes, Variations, and Applications. Artif. Intell. Rev. 2024, 57, 246. [Google Scholar] [CrossRef]
- Singh, N.K.; Gope, S.; Koley, C.; Dawn, S.; Alhelou, H.H. Optimal Bidding Strategy for Social Welfare Maximization in Wind Farm Integrated Deregulated Power System Using Artificial Gorilla Troops Optimizer Algorithm. IEEE Access 2022, 10, 71450–71461. [Google Scholar] [CrossRef]
- Tayab, U.B.; Hasan, K.N.; Hayat, M.F. Short-Term Industrial Demand Response Capability Forecasting Using Hybrid EMD-AGTO-LSTM Model. In Proceedings of the 2023 IEEE International Conference on Energy Technologies for Future Grids (ETFG), Wollongong, Australia, 3–6 December 2023; IEEE: New York, NY, USA, 2023; pp. 1–5. [Google Scholar]
- Cho, K.; van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations Using RNN Encoder–Decoder for Statistical Machine Translation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; Association for Computational Linguistics: Stroudsburg, PA, USA, 2014; pp. 1724–1734. [Google Scholar]
- Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljačić, M.; Hou, T.Y.; Tegmark, M. Kan: Kolmogorov—Arnold Networks. arXiv 2024. [Google Scholar] [CrossRef]
- Miao, Y.; Zhang, B.; Li, C.; Lin, J.; Zhang, D. Feature Mode Decomposition: New Decomposition Theory for Rotating Machinery Fault Diagnosis. IEEE Trans. Ind. Electron. 2023, 70, 1949–1960. [Google Scholar] [CrossRef]
- Li, Z.; Jiang, B.; Lu, J.; Wang, X. Application of the Grey Theory to Dynamic Analyses of the Baiquan Spring Flow Rate in Xinxiang. Hydrogeol. Eng. Geol. 2023, 2, 34–43. [Google Scholar] [CrossRef]
- Jiang, B.; Xu, L.; Cui, J.; Zhao, G. Dynamic Prediction of Spring Flow and Resources Evaluation of Baiquan at Xinxiang. Yellow River 2014, 12, 71–72. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Greff, K.; Srivastava, R.K.; Koutnik, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A Search Space Odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2222–2232. [Google Scholar] [CrossRef] [PubMed]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Polosukhin, I. Attention Is All You Need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 6000–6010. [Google Scholar]
- Diniz, P.S.R. Adaptive Filtering; Springer: Boston, MA, USA, 2013; ISBN 978-1-4614-4105-2. [Google Scholar]
- Woods, R.; McAllister, J.; Yi, Y.; Lightbody, G. FPGA-Based Implementation of Signal Processing Systems; Wiley: Hoboken, NJ, USA, 2017; ISBN 9781119077954. [Google Scholar]
- Ke, Q.; Kanade, T. Robust L1 Norm Factorization in the Presence of Outliers and Missing Data by Alternative Convex Programming. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; IEEE: New York, NY, USA, 2005; pp. 739–746. [Google Scholar]
- Yildiz, B.S.; Pholdee, N.; Bureerat, S.; Yildiz, A.R.; Sait, S.M. Enhanced Grasshopper Optimization Algorithm Using Elite Opposition-Based Learning for Solving Real-World Engineering Problems. Eng. Comput. 2022, 38, 4207–4219. [Google Scholar] [CrossRef]





| Parameter | Range |
|---|---|
| look back | 3~30 |
| learning rate | 5 × 10−5~1 × 10−3 |
| num epochs | 200~600 |
| batch size | 16~128 |
| Parameter | Look Back | Learning Rate | Num Epochs | Batch Size |
|---|---|---|---|---|
| result | 6 | 8.44306 × 10−4 | 303 | 61 |
| FMD-mGTO-BiGRU-KAN | LSTM | GRU | Transformer | |
|---|---|---|---|---|
| MSE-Train | 0.0014 | 0.0038 | 0.0044 | 0.0027 |
| RMSE-Train | 0.0376 | 0.0618 | 0.0663 | 0.0515 |
| NSE-Train | 0.9637 | 0.8954 | 0.8797 | 0.9274 |
| MSE-Val | 0.0007 | 0.0039 | 0.0048 | 0.0038 |
| RMSE-Val | 0.0260 | 0.0625 | 0.0693 | 0.0620 |
| NSE-Val | 0.9835 | 0.9237 | 0.9063 | 0.9248 |
| MSE-Pred | 0.0706 | 0.3515 | 0.4840 | 0.3734 |
| RMSE-Pred | 0.2658 | 0.5929 | 0.6957 | 0.6111 |
| NSE-Pred | 0.9825 | 0.9213 | 0.8916 | 0.9163 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Dong, T.; Shao, Y.; Mao, X. Hybrid Deep Learning Combining Mode Decomposition and Intelligent Optimization for Discharge Forecasting: A Case Study of the Baiquan Karst Spring. Sustainability 2025, 17, 8101. https://doi.org/10.3390/su17188101
Li Y, Dong T, Shao Y, Mao X. Hybrid Deep Learning Combining Mode Decomposition and Intelligent Optimization for Discharge Forecasting: A Case Study of the Baiquan Karst Spring. Sustainability. 2025; 17(18):8101. https://doi.org/10.3390/su17188101
Chicago/Turabian StyleLi, Yanling, Tianxing Dong, Yingying Shao, and Xiaoming Mao. 2025. "Hybrid Deep Learning Combining Mode Decomposition and Intelligent Optimization for Discharge Forecasting: A Case Study of the Baiquan Karst Spring" Sustainability 17, no. 18: 8101. https://doi.org/10.3390/su17188101
APA StyleLi, Y., Dong, T., Shao, Y., & Mao, X. (2025). Hybrid Deep Learning Combining Mode Decomposition and Intelligent Optimization for Discharge Forecasting: A Case Study of the Baiquan Karst Spring. Sustainability, 17(18), 8101. https://doi.org/10.3390/su17188101





