Load-Bearing Capacity Analysis on Rubber-Sand Mixture Cored Composite Block as Low-Cost Isolation Bearing for Rural Houses Based on DEM Simulations
Abstract
1. Introduction
2. DEM Procedure and Test
2.1. Model and Materials
2.2. Test and Validation of DEM
2.3. Further Parameter Analysis
3. Particulate-Scale Results
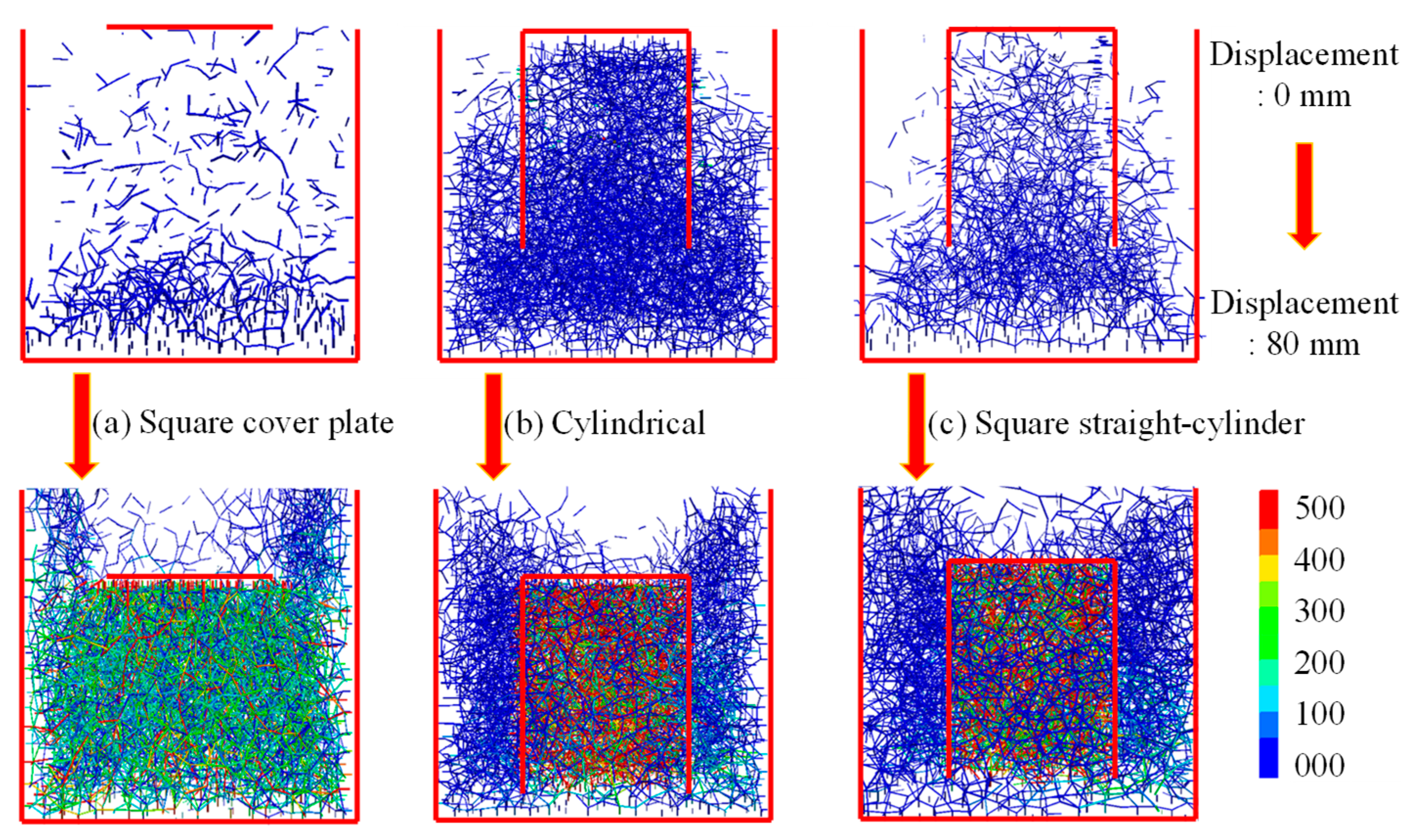
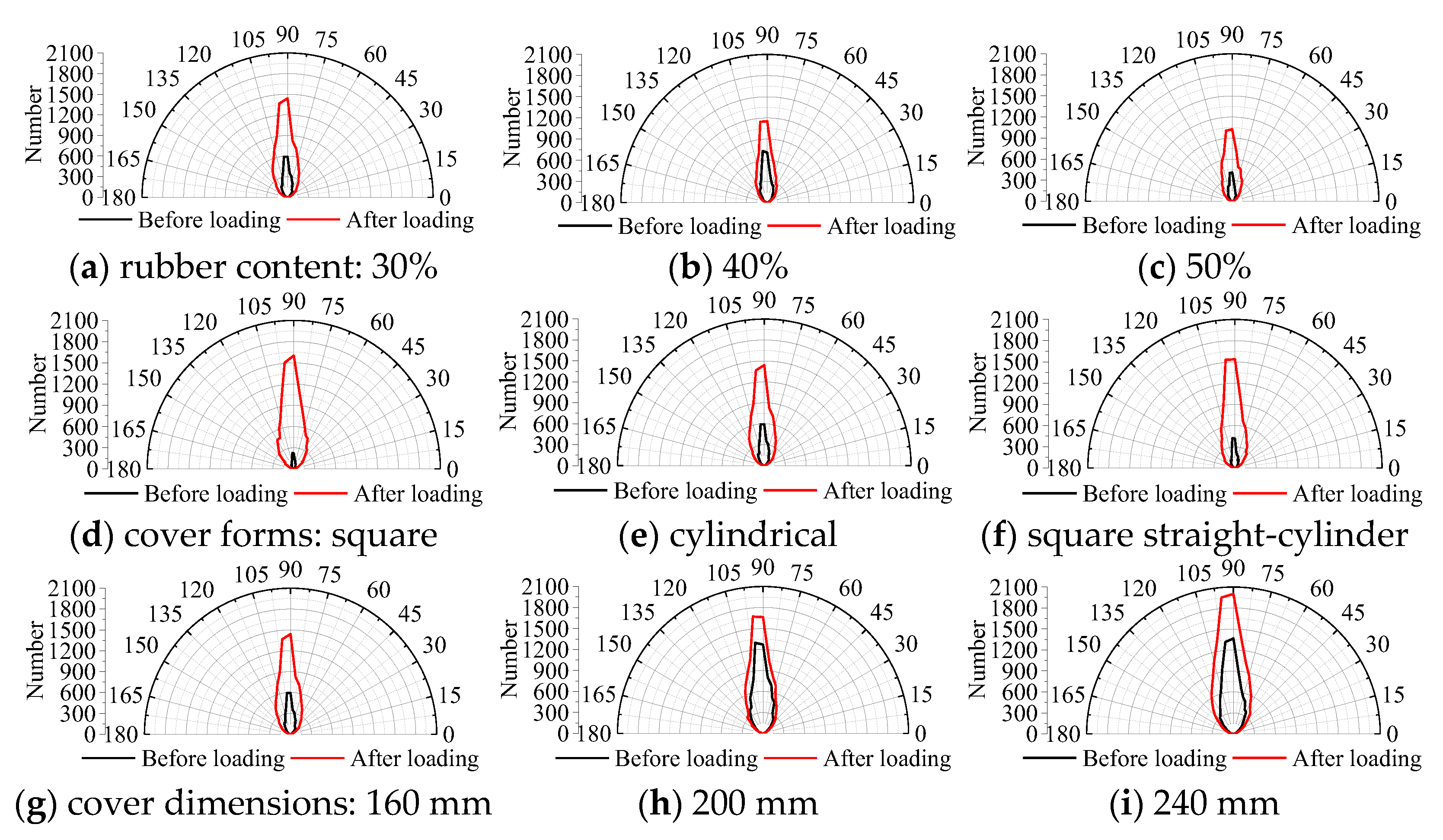
3.1. Inter-Particle Forces
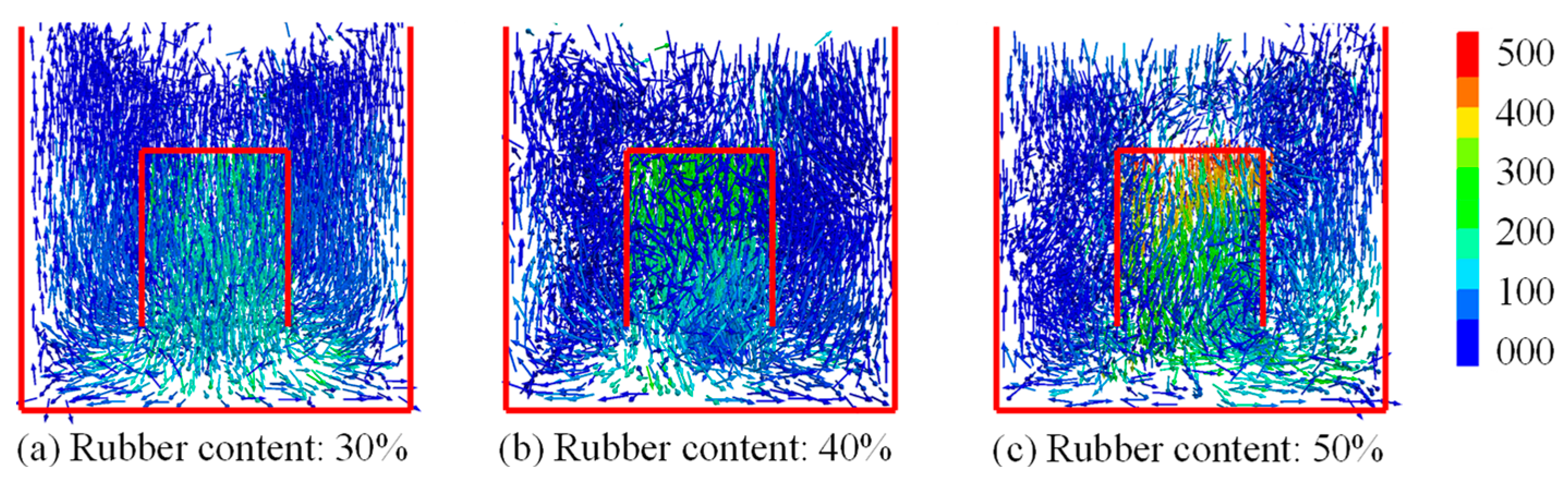
3.2. Particle Displacement Vector
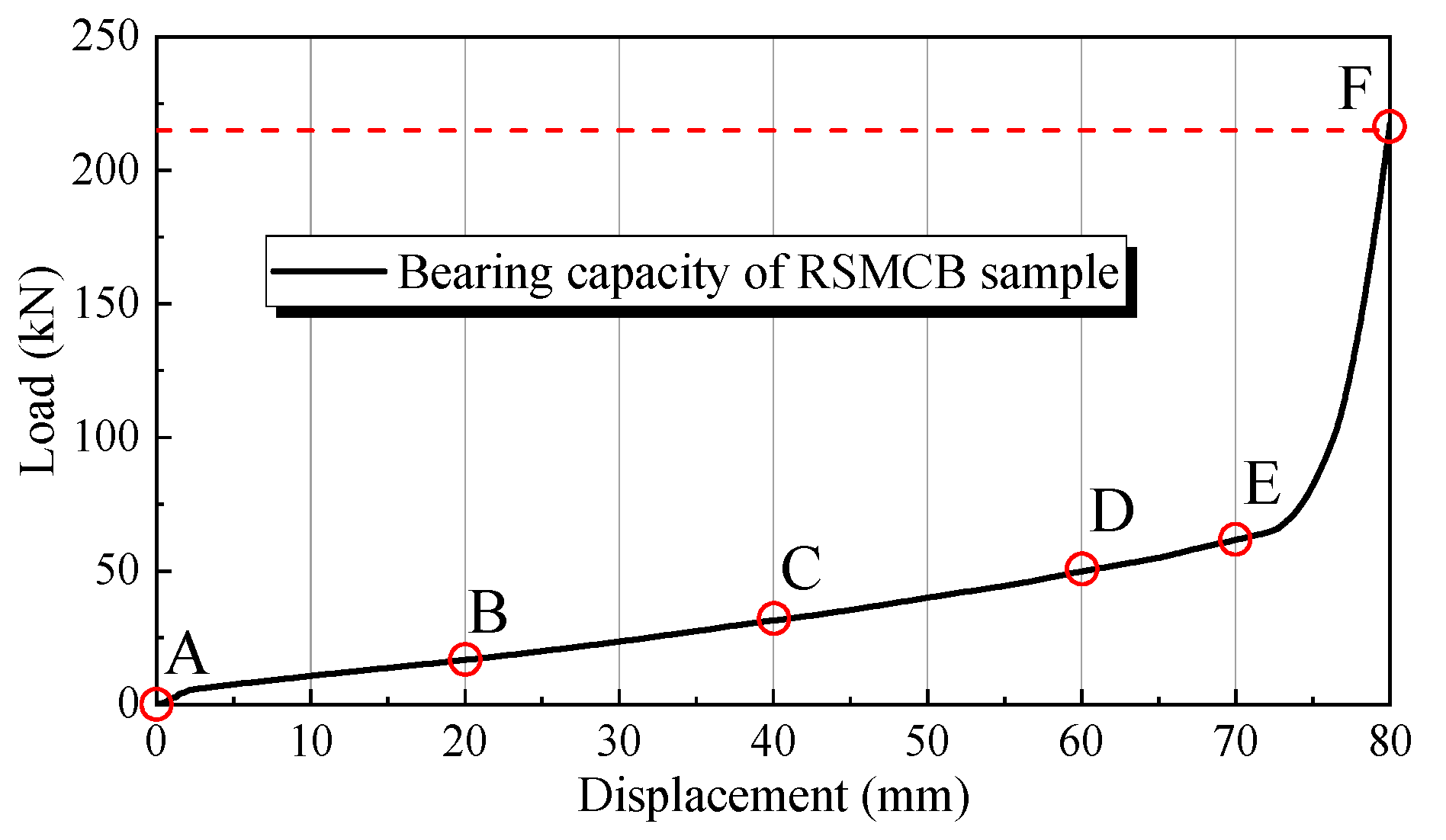
4. Bearing Capacity Analysis of RSMCB
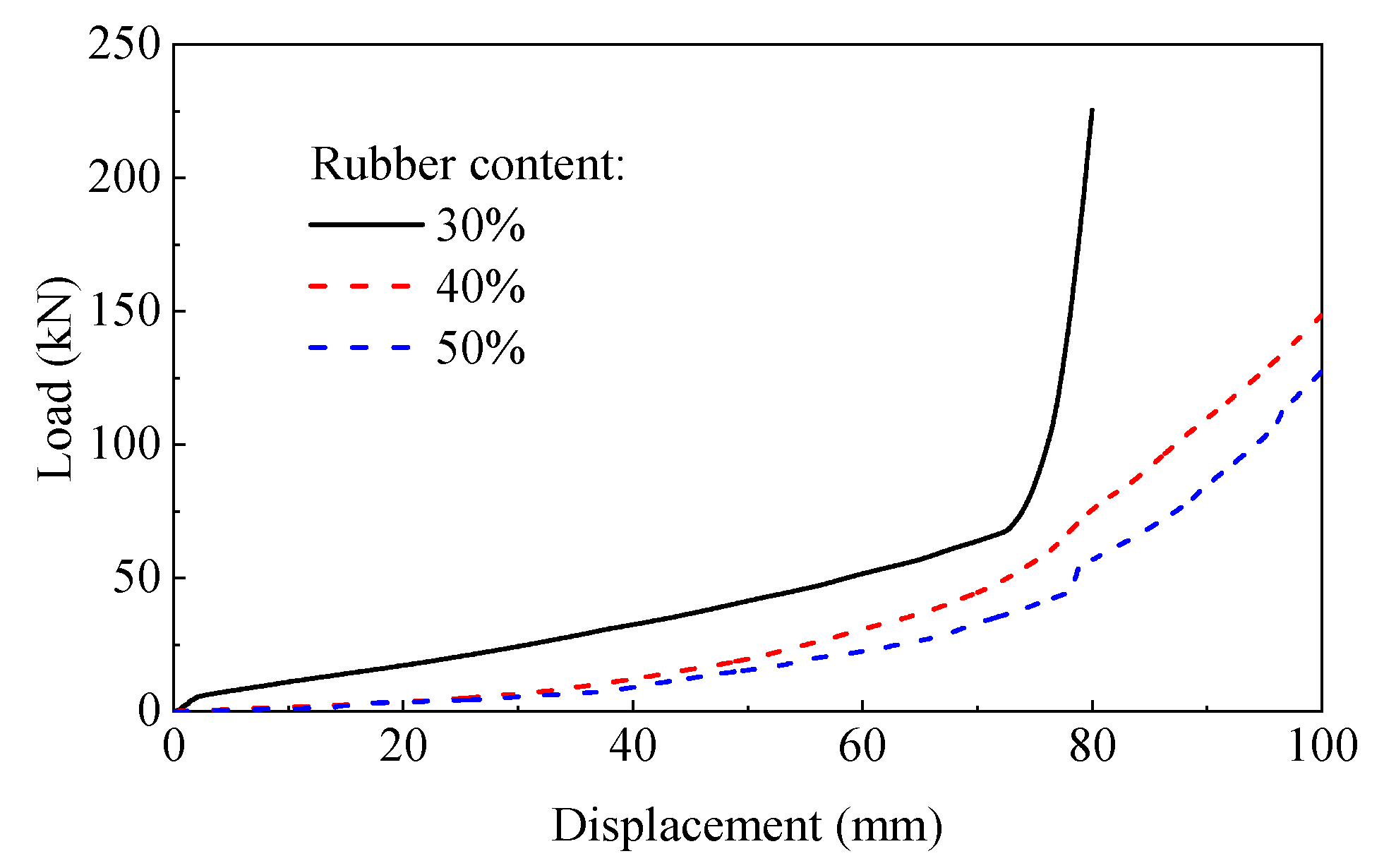
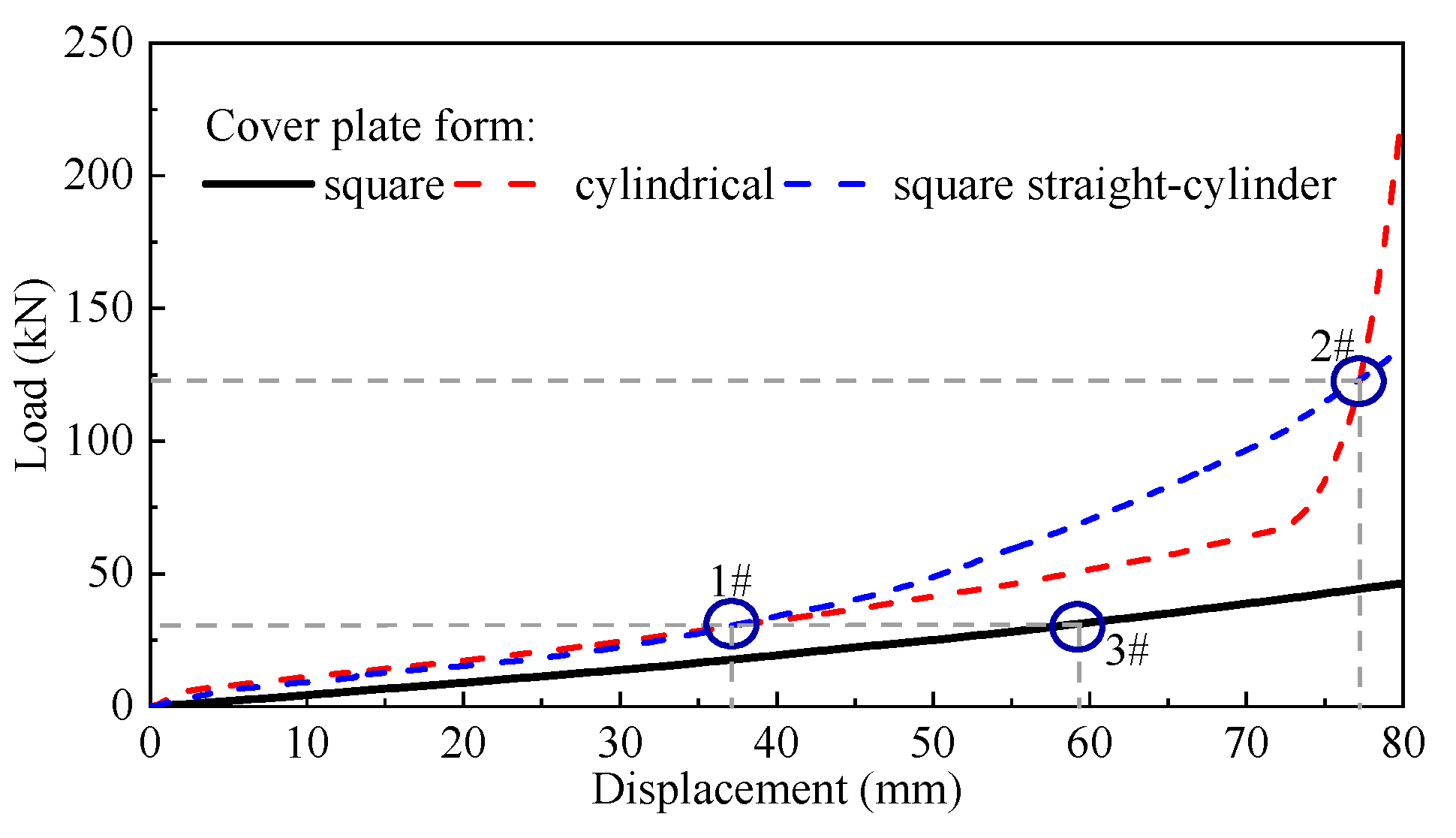
4.1. Effect of Rubber Content and Cover Plate Form
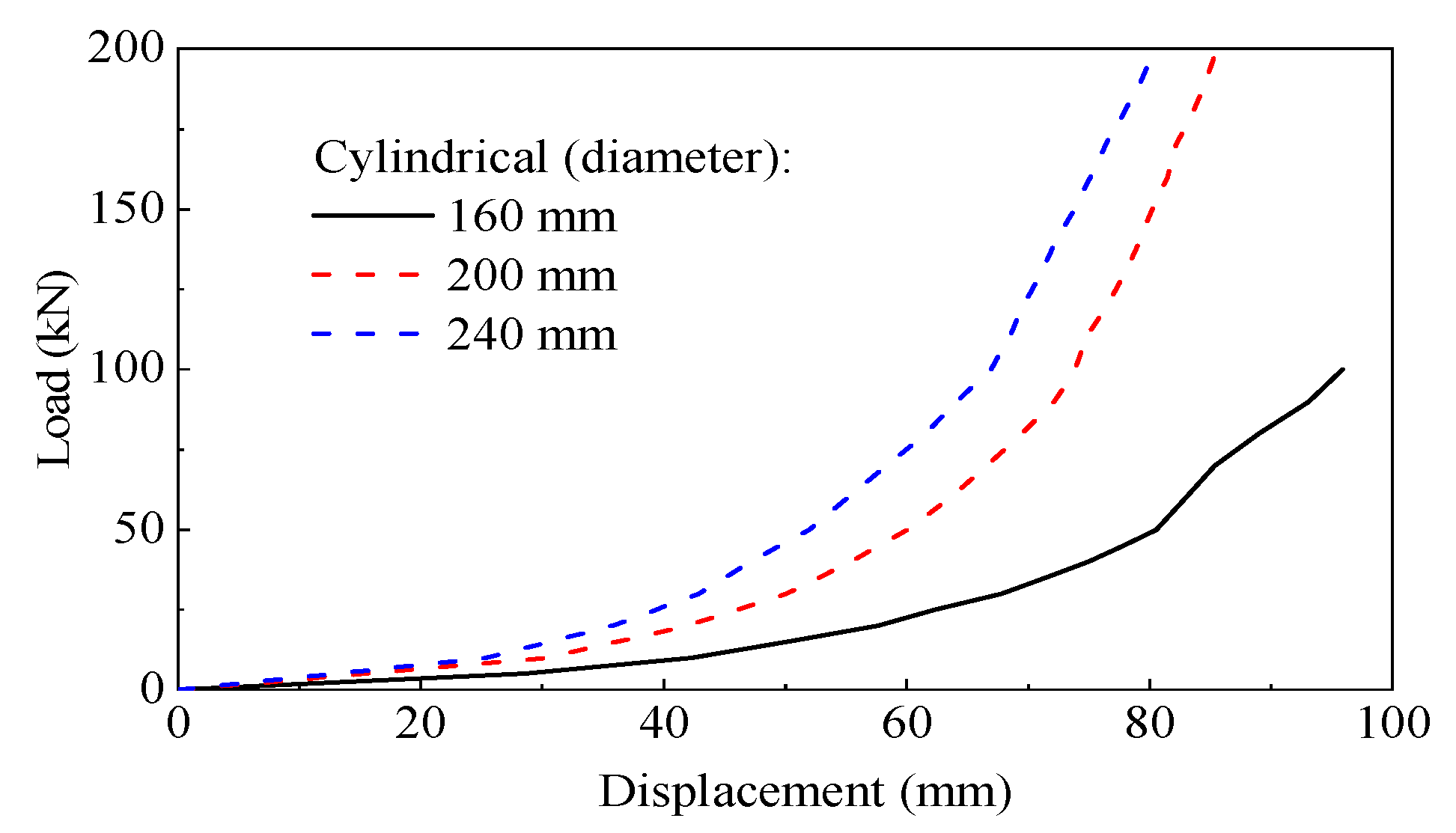
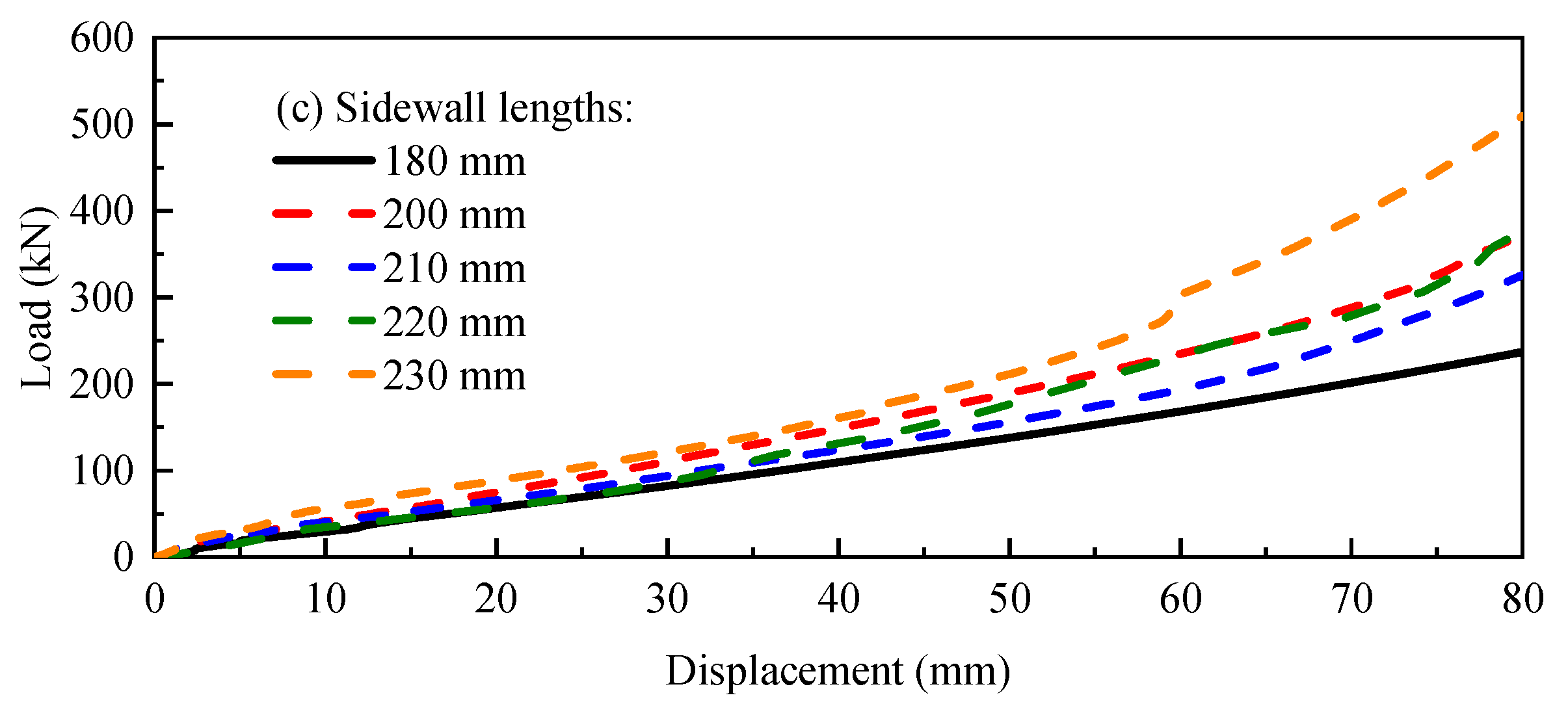
4.2. Effect of Cover Plate Dimension and Sidewall Length
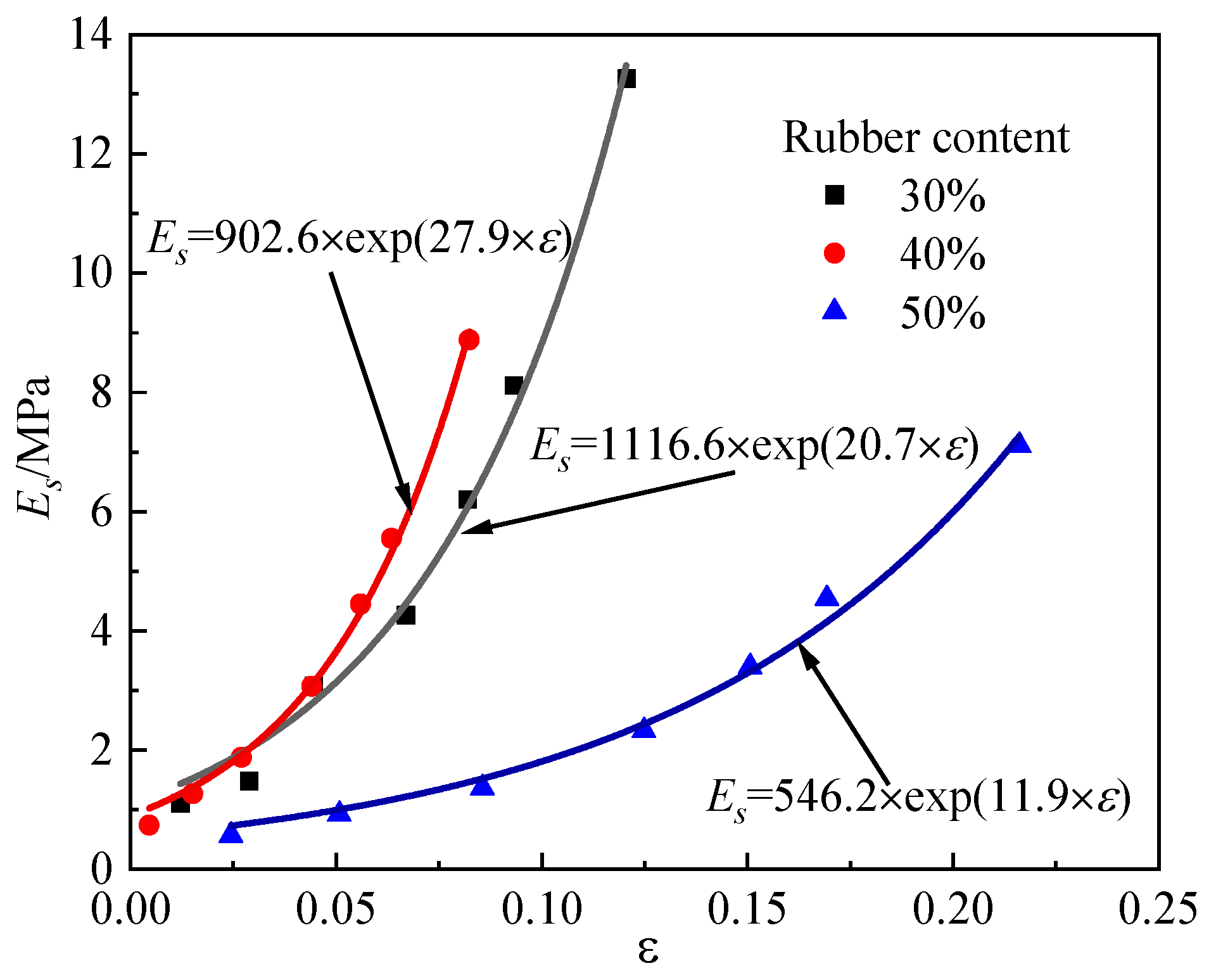
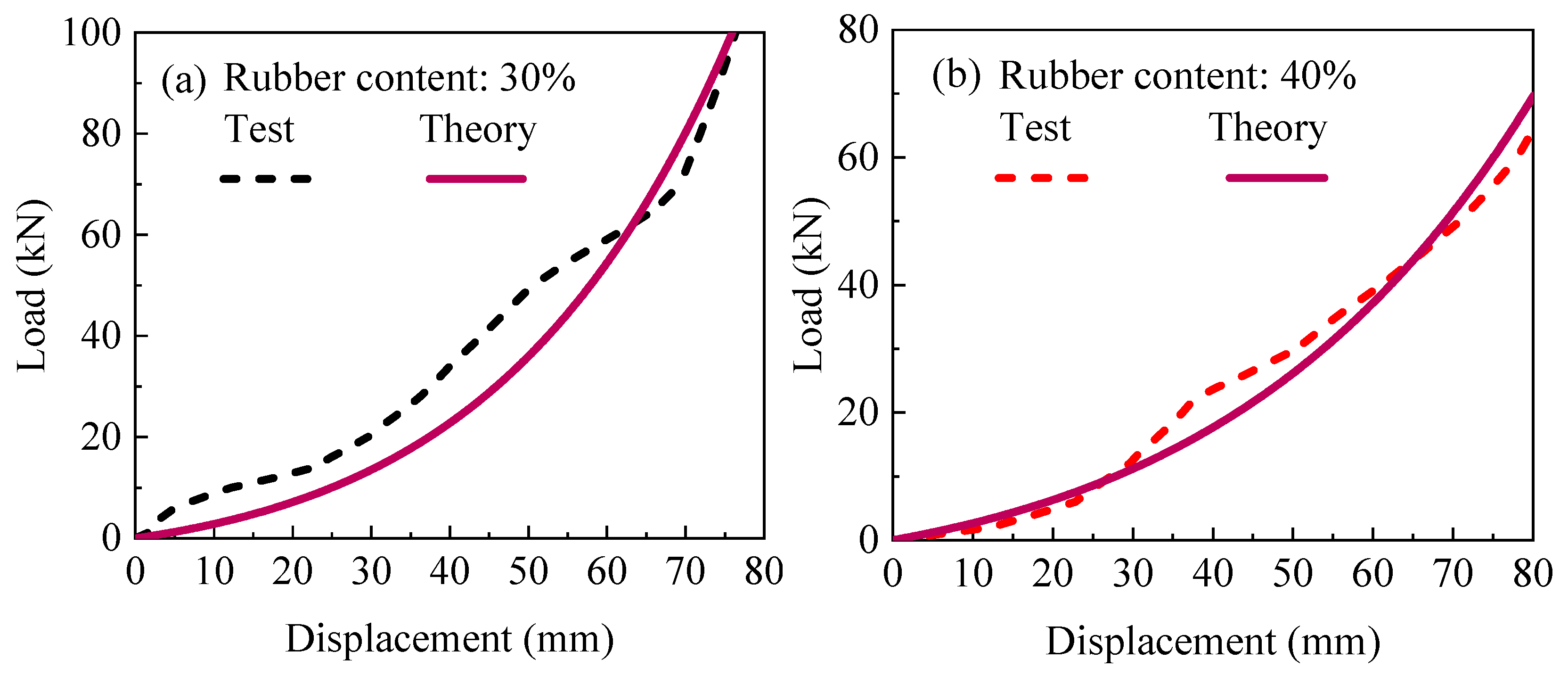
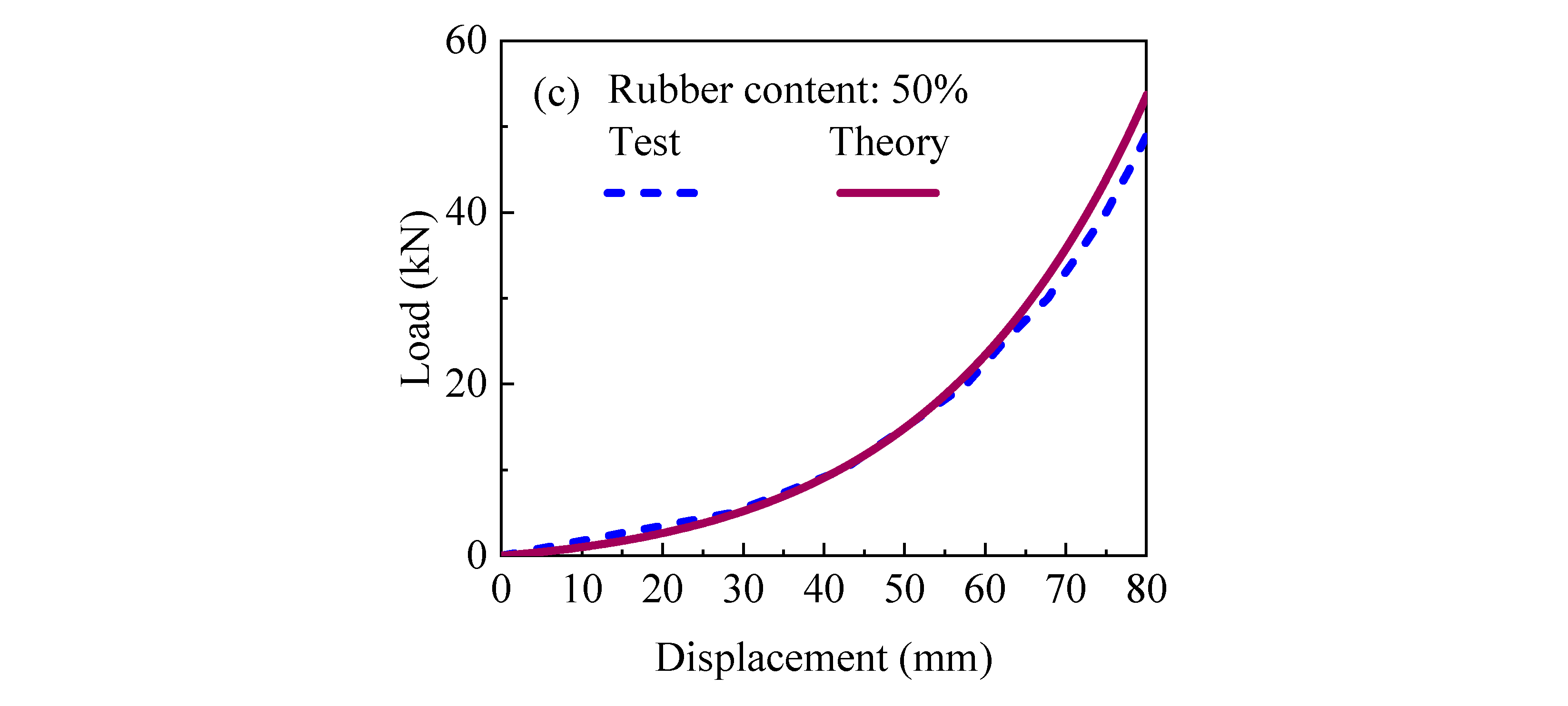
4.3. Theoretical Exploration of RSMCB
4.4. Implementation and Challenges for RSMCB in Rural Construction
5. Conclusions
6. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kuang, A.; Sridhar, A.; Garven, J.; Gutschmidt, S.; Rodgers, G.W.; Chase, J.G.; MacRae, G.A. Christchurch Women’s Hospital: Performance analysis of the base-isolation system during the series of canterbury earthquakes 2011–2012. J. Perform. Constr. Facil. 2016, 30, 04015096. [Google Scholar] [CrossRef]
- Chen, H.; Xie, Q.; Feng, B.; Liu, J.; Huang, Y.; Chen, H. Seismic performance to emergency centers, communication and hospital facilities subjected to Nepal earthquakes, 2015. J. Earthq. Eng. 2018, 22, 1537–1568. [Google Scholar] [CrossRef]
- Yu, Q.Q.; Wu, J.Y.; Gu, X.L.; Zhou, F.Y. Experimental study on effects of U-shape dampers on earthquake responses of a base-isolated LNG inner tank. Eng. Struct. 2022, 269, 114841. [Google Scholar] [CrossRef]
- Chen, P.; Wang, B.; Dai, K.; Li, T. Analytical and numerical investigations of base isolation system with negative stiffness devices. Eng. Struct. 2022, 268, 114799. [Google Scholar] [CrossRef]
- Chen, P.; Wang, B.; Zhang, Z.; Li, T.; Dai, K. A generalized model of lead rubber bearing considering large strain stiffening and degradation. Eng. Struct. 2023, 275, 115264. [Google Scholar] [CrossRef]
- Hadad, H.A.; Calabrese, A.; Strano, S.; Serino, G. A base isolation system for developing countries using discarded tyres filled with elastomeric recycled materials. J. Earthq. Eng. 2017, 21, 246–266. [Google Scholar] [CrossRef]
- Xiang, N.; Li, J. Experimental and numerical study on seismic sliding mechanism of laminated-rubber bearings. Eng. Struct. 2017, 141, 159–174. [Google Scholar] [CrossRef]
- Valdes, J.R.; Evans, T.M. Sand–rubber mixtures: Experiments and numerical simulations. Can. Geotech. J. 2008, 45, 588–595. [Google Scholar] [CrossRef]
- Masad, E.; Taha, R.; Ho, C.; Papagiannakis, T. Engineering properties of tire/soil mixtures as a lightweight fill material. Geotech. Test. J. 1996, 19, 297–304. [Google Scholar] [CrossRef]
- Ghazavi, M.; Sakhi, M.A. Influence of optimized tire shreds on shear strength parameters of sand. Int. J. Geomech. 2005, 5, 58–65. [Google Scholar] [CrossRef]
- Liu, F.; Zheng, K.; Jia, B.; Yang, J.; Wu, M. Shear modulus and damping ratio of granulated rubber-sand mixtures: Influence of relative particle size. Constr. Build. Mater. 2024, 427, 136205. [Google Scholar] [CrossRef]
- Lee, C.; Shin, H.; Lee, J.S. Behavior of sand–rubber particle mixtures: Experimental observations and numerical simulations. Int. J. Numer. Anal. Methods Geomech. 2014, 38, 1651–1663. [Google Scholar] [CrossRef]
- Foose, G.J.; Benson, C.H.; Bosscher, P.J. Sand reinforced with shredded waste tires. J. Geotech. Eng. 1996, 122, 760–767. [Google Scholar] [CrossRef]
- Balunaini, U.; Yoon, S.; Prezzi, M.; Salgado, R. Pullout response of uniaxial geogrid in tire shred–sand mixtures. Geotech. Geol. Eng. 2014, 32, 505–523. [Google Scholar] [CrossRef]
- Bernal, A.; Salgado, R.; Swan, R.H.; Lovell, C. Interaction between tire shreds, rubber-sand and geosynthetics. Geosynth. Int. 1997, 4, 623–643. [Google Scholar] [CrossRef]
- Edil, T.B. A review of mechanical and chemical properties of shredded tires and soil mixtures. In Proceedings of the Recycled Materials in Geotechnics Sessions at ASCE Civil Engineering Conference and Exposition, Baltimore, MD, USA, 19–21 October 2004; pp. 1–21. [Google Scholar] [CrossRef]
- Uchimura, T.; Chi, N.; Nirmalan, S.; Sato, T.; Meidani, M.; Towhata, I. Shaking table tests on effect of tire chips and sand mixture in increasing liquefaction resistance and mitigating uplift of pipe. In Proceedings of the International Workshop on scrap Tire Derived Geomaterials—Opportunities and Challenges, Yokosuka, Japan, 23–24 March 2007; pp. 179–186. [Google Scholar]
- Fan, K.; Yang, G.; Zou, W.; Han, Z.; Shen, Y. Lateral earth pressure of granular backfills on retaining walls with expanded polystyrene geofoam inclusions under limited surcharge loading. J. Rock Mech. Geotech. Eng. 2024, 16, 1388–1397. [Google Scholar] [CrossRef]
- Fan, K.; Zou, W.; Zhang, P.; Wang, X.; Shen, Y. Laboratory investigation and theoretical analysis of lateral pressure exerted by expansive soils on retaining walls with expanded polystyrene geofoam block upon water infiltration. Geotext. Geomembr. 2024, 52, 332–341. [Google Scholar] [CrossRef]
- Lee, J.H.; Salgado, R.; Bernal, A.; Lovell, C.W. Shredded tires and rubber-sand as lightweight backfill. J. Geotech. Geoenvironmental Eng. 1999, 125, 132–141. [Google Scholar] [CrossRef]
- Xiao, M.; Bowen, J.; Graham, M.; Larralde, J. Comparison of seismic responses of geosynthetically reinforced walls with tire-derived aggregates and granular backfills. J. Mater. Civ. Eng. 2012, 24, 1368–1377. [Google Scholar] [CrossRef]
- Tafreshi, S.M.; Mehrjardi, G.T.; Dawson, A.R. Buried pipes in rubber-soil backfilled trenches under cyclic loading. J. Geotech. Geoenvironmental Eng. 2012, 138, 1346–1356. [Google Scholar] [CrossRef]
- Ecemis, N.; Valizadeh, H.; Karaman, M. Sand-granulated rubber mixture to prevent liquefaction-induced uplift of buried pipes: A shaking table study. Bull. Earthq. Eng. 2021, 19, 2817–2838. [Google Scholar] [CrossRef]
- Bosscher, P.J.; Edil, T.B.; Kuraoka, S. Design of highway embankments using tire chips. J. Geotech. Geoenvironmental Eng. 1997, 123, 295–304. [Google Scholar] [CrossRef]
- Edeskar, T. Use of Tyre Shreds in Civil Engineering Applications—Technical and Environmental Properties. Ph.D. Dissertation, Lulea University of Technology, Department of Civil and Environmental Engineering, Division of Mining and Geotechnical Engineering, Luleå, Sweden, 2006. [Google Scholar]
- Reddy, K.R.; Saichek, R.E. Characterization and performance assessment of shredded scrap tires as leachate drainage material in landfills. In Proceedings of the 14th International Conference on Solid Waste Technology and Management, Chester, PA, USA, 1–4 November 1998. [Google Scholar]
- Wang, J.; Wu, M.; Liu, F.; Bin, J.; He, J. Rubber-sand infilled soilbags as seismic isolation cushions: Experimental validation. Geosynth. Int. 2025, 32, 205–218. [Google Scholar] [CrossRef]
- Wu, M.; Liu, F.; Li, Z.; Bu, G. Micromechanics of granulated rubber–soil mixtures as a cost-effective substitute for geotechnical fillings. Mech. Adv. Mater. Struct. 2022, 30, 2701–2717. [Google Scholar] [CrossRef]
- Liu, B.; Vu-Bac, N.; Zhuang, X.; Lu, W.; Fu, X.; Rabczuk, T. Al-DeMat: A web-based expert system platform for computationally expensive models in materials design. Adv. Eng. Softw. 2023, 176, 103398. [Google Scholar] [CrossRef]
- Tsang, H.H.; Lo, S.H.; Xu, X.; Neaz Sheikh, M. Seismic isolation for low-to-medium-rise buildings using granulated rubber–soil mixtures: Numerical study. Earthq. Eng. Struct. Dyn. 2012, 41, 2009–2024. [Google Scholar] [CrossRef]
- Liu, F.; Wang, J.; Zhou, B.; Wu, M.; He, J.; Bin, J. Shaking table study on rubber-sand mixture cored composite block as low-cost isolation bearing for rural houses. J. Build. Eng. 2023, 76, 107413. [Google Scholar] [CrossRef]
- Zhang, C.; Ali, A.; Sun, L. Investigation on low-cost friction-based isolation systems for masonry building structures: Experimental and numerical studies. Eng. Struct. 2021, 243, 112645. [Google Scholar] [CrossRef]
- Tsiavos, A.; Sextos, A.; Stavridis, A.; Dietz, M.; Dihoru, L.; Alexander, N.A. Large-scale experimental investigation of a low-cost PVC ’sand-wich’ (PVC-s) seismic isolation for developing countries. Earthq. Spectra 2020, 36, 1886–1911. [Google Scholar] [CrossRef]
- Tsang, H.H. Seismic isolation by rubber–soil mixtures for developing countries. Earthq. Eng. Struct. Dyn. 2008, 37, 283–303. [Google Scholar] [CrossRef]
- Fan, K.; Pei, Q.; Liu, L.; Han, Z.; Zou, W. Strength and microstructure of a lignin fiber-reinforced expansive soil in cold regions. Geosynth. Int. 2022, 29, 622–629. [Google Scholar] [CrossRef]
- Dondi, G.; Simone, A.; Vignali, V.; Manganelli, G. Numerical and experimental study of granular mixes for asphalts. Powder Technol. 2012, 232, 31–40. [Google Scholar] [CrossRef]
- Xu, W.J.; Wang, S.; Zhang, H.Y.; Zhang, Z.L. Discrete element modelling of a soil-rock mixture used in an embankment dam. Int. J. Rock Mech. Min. Sci. 2016, 86, 141–156. [Google Scholar] [CrossRef]
- He, H.; Zheng, J.; Li, Z. Accelerated simulations of direct shear tests by physics engine. Comput. Part. Mech. 2021, 8, 471–492. [Google Scholar] [CrossRef]
- Gu, X.; Huang, M.; Qian, J. DEM investigation on the evolution of microstructure in granular soils under shearing. Granul. Matter 2014, 16, 91–106. [Google Scholar] [CrossRef]
- Dai, B.B.; Yang, J.; Zhou, C.Y. Micromechanical origin of angle of repose in granular materials. Granul. Matter 2017, 19, 24. [Google Scholar] [CrossRef]
- Zhou, T.; Qian, X.; Zhang, B. Investigation and analysis of damage to rural houses in Lushan earthquake. Earthq. Eng. Eng. Vib. 2013, 33, 53–58. [Google Scholar]
- Perez, J.C.L.; Kwok, C.Y.; Senetakis, K. Effect of rubber size on the behaviour of sand-rubber mixtures: A numerical investigation. Comput. Geotech. 2016, 80, 199–214. [Google Scholar] [CrossRef]
- Wang, C.; Deng, A.; Taheri, A. Three-dimensional discrete element modeling of direct shear test for granular rubber–sand. Comput. Geotech. 2018, 97, 204–216. [Google Scholar] [CrossRef]
- Reddy, N.S.; He, H.; Senetakis, K. DEM analysis of small and small-to-medium strain shear modulus of sands. Comput. Geotech. 2022, 141, 104518. [Google Scholar] [CrossRef]
- Liu, F.-C.; Zhang, Y.-F.; Ren, D.-B. Stress-strain characteristics of rubber-sand mixtures in united triaxial shear and simple shear tests. Rock Soil Mech. 2016, 37, 2769–2779. [Google Scholar] [CrossRef]
- Itasca, C. PFC 3D-User Manual; Itasca Consulting Group: Minneapolis, MN, USA, 1999; p. 435. [Google Scholar]
- Zhou, Q.; Shen, H.H.; Helenbrook, B.T.; Zhang, H. Scale dependence of direct shear tests. Sci. Bull. 2009, 54, 4337–4348. [Google Scholar] [CrossRef]
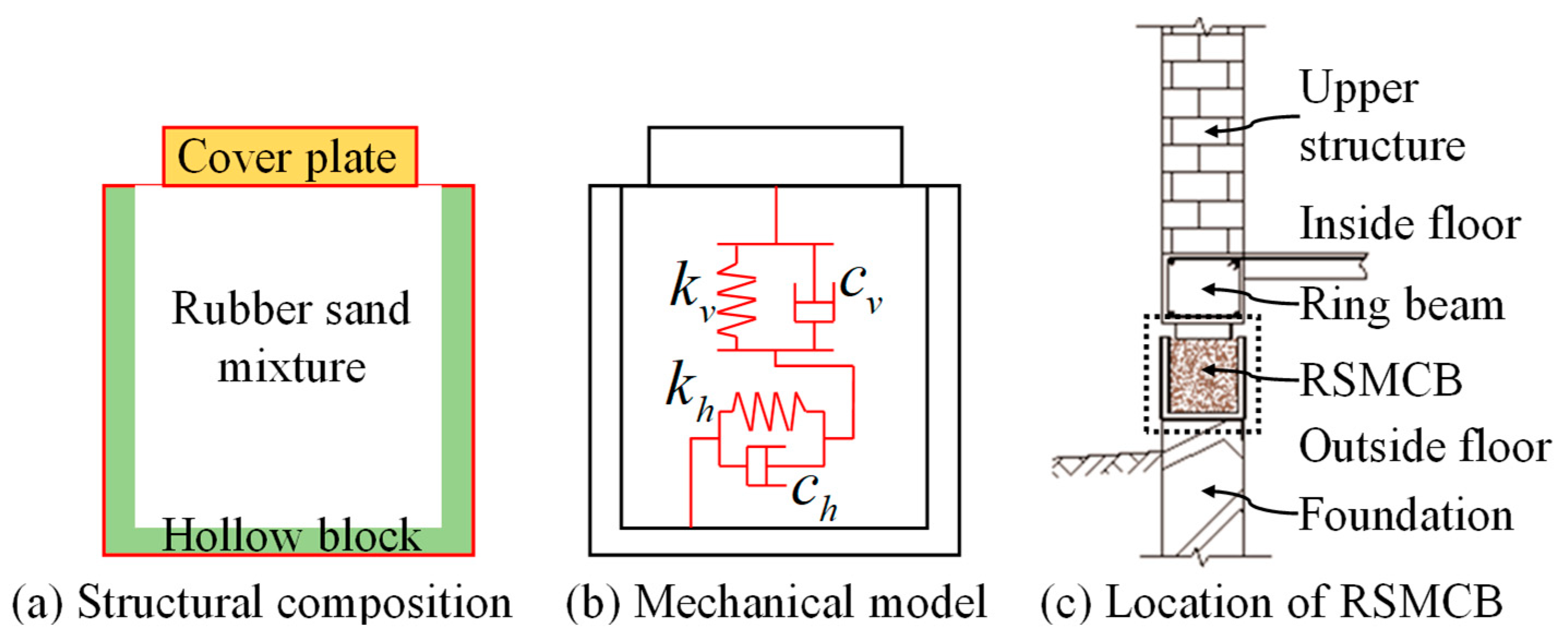

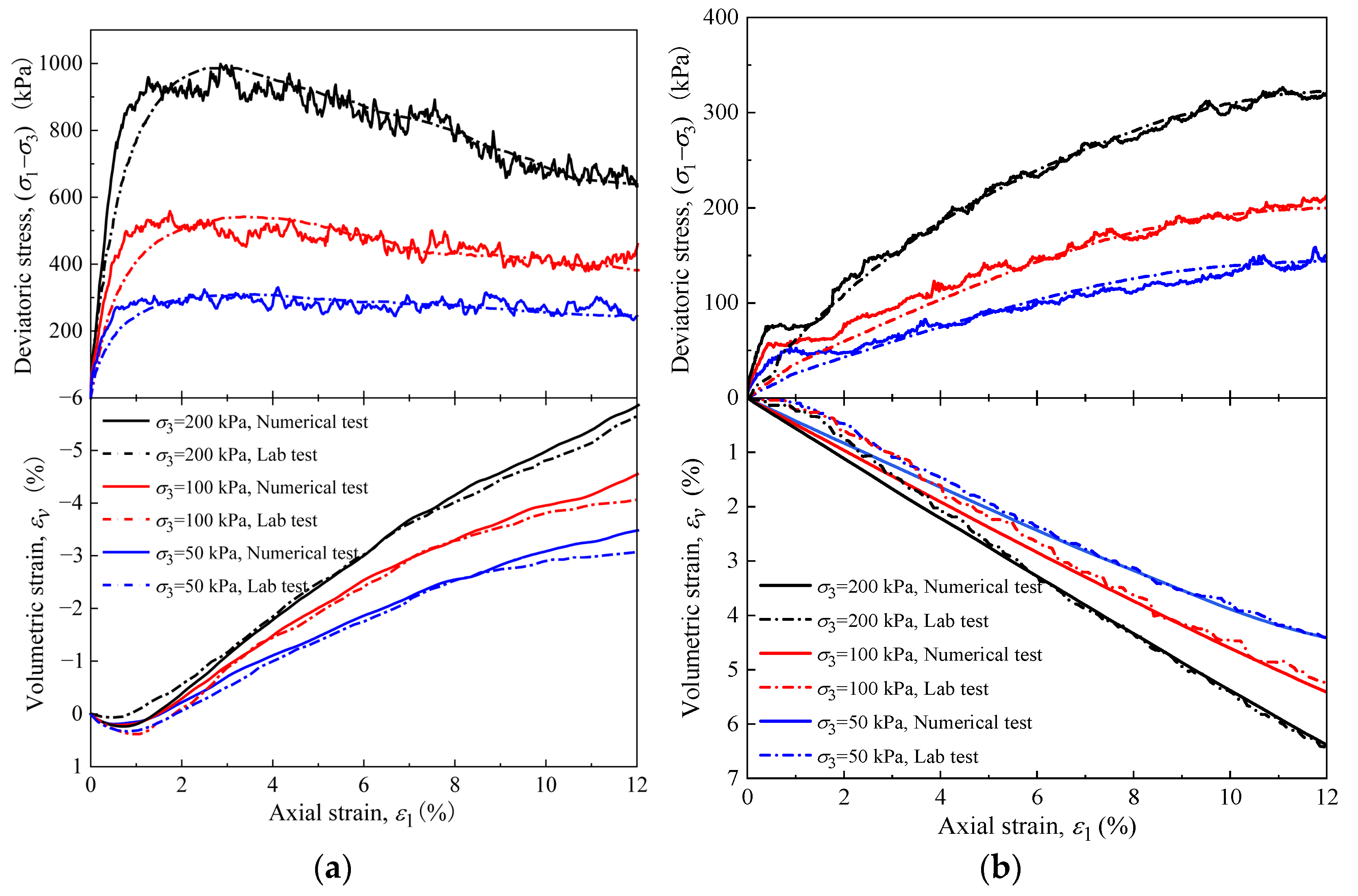
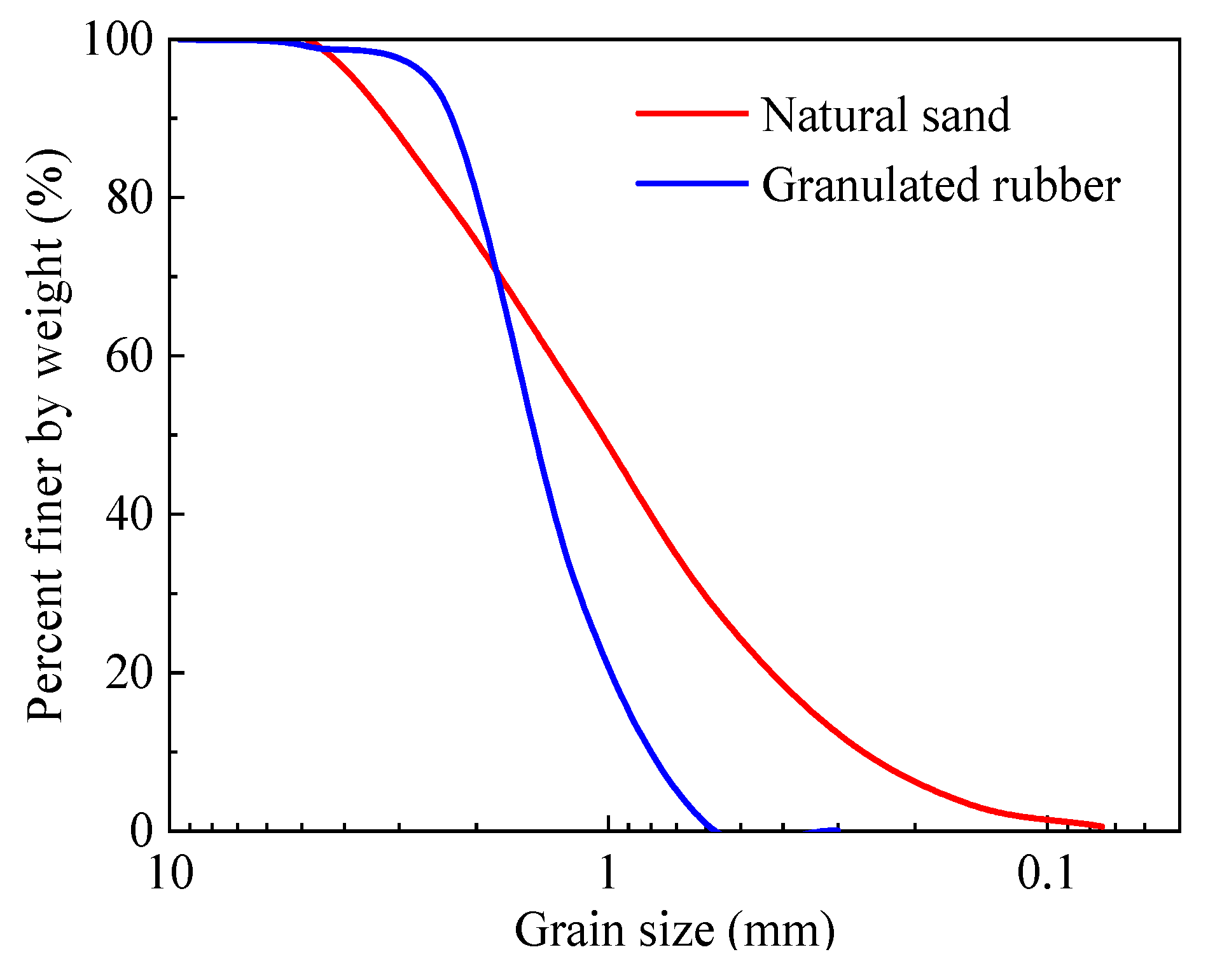
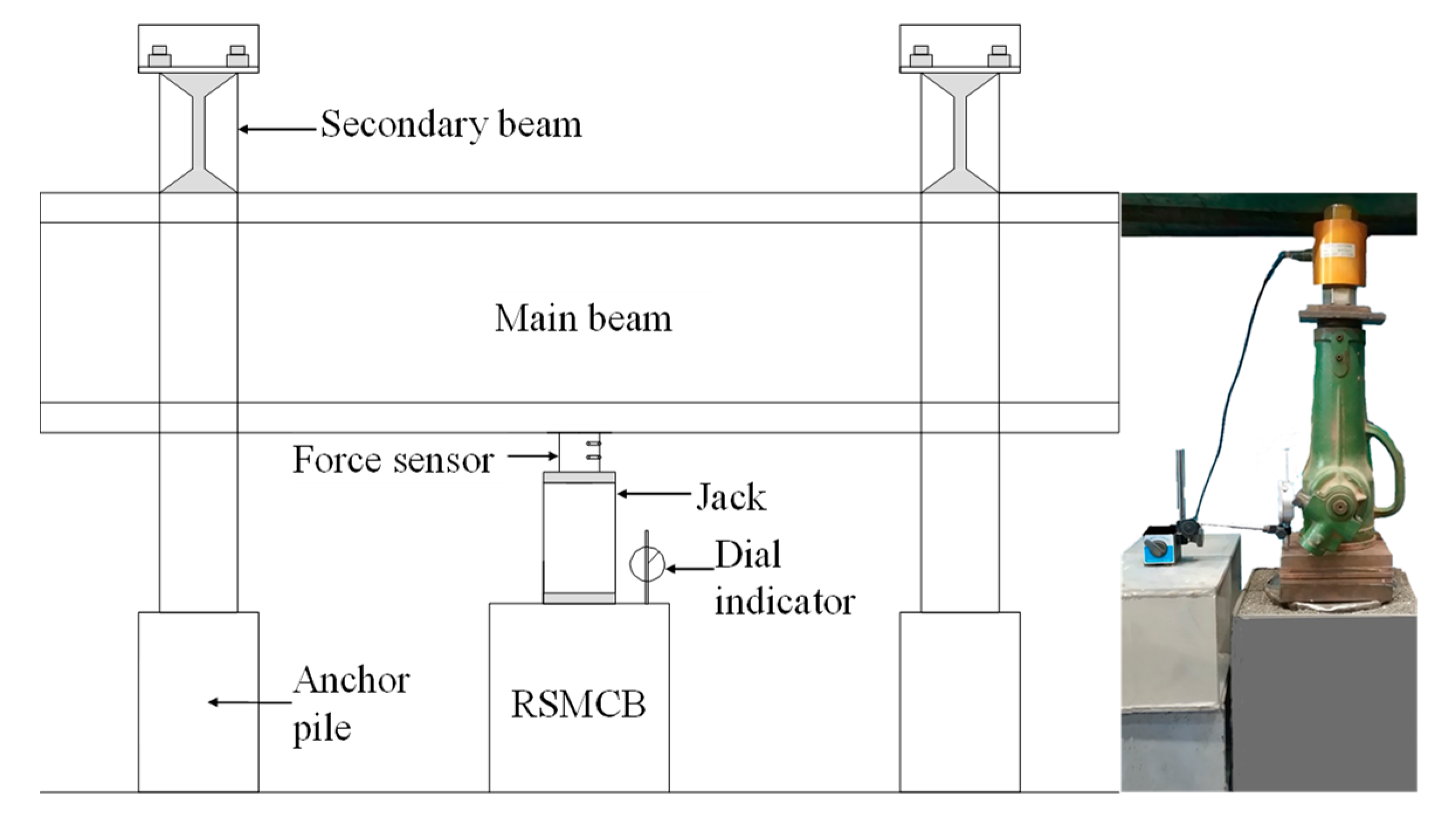




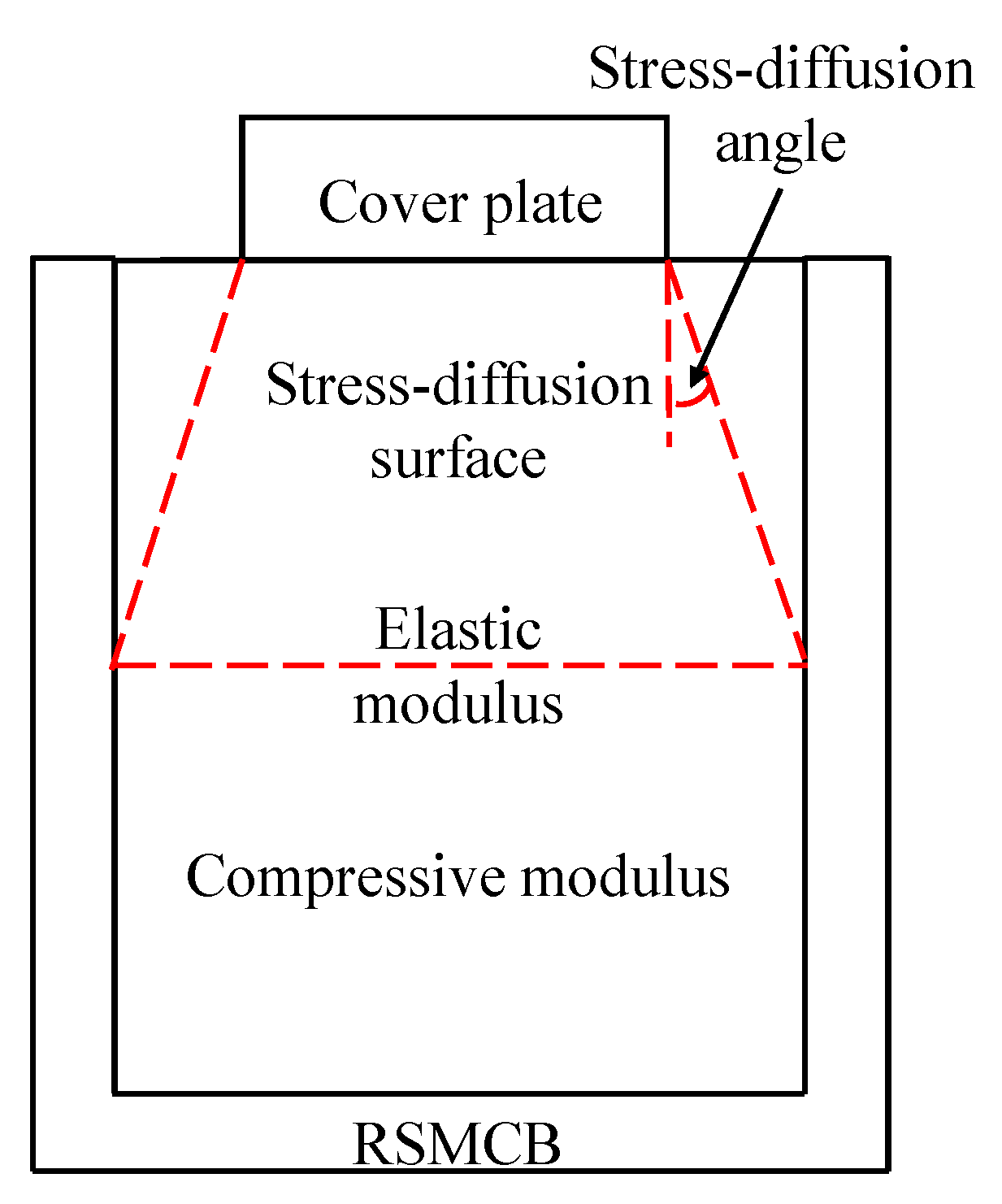
| Equation Content | Application Scenario | No. |
|---|---|---|
| Determining the total particle number to control initial porosity ratio | (1) | |
| Calculating normal contact stiffness between particles to simulate elastic deformation of RSM | (2) | |
| Matching tangential deformation characteristics of rubber-sand particles | (3) | |
| Additional conditions of stiffness | (4) | |
| A represents the initial cross-sectional area, R denotes the radius of a single particle, and L refers to the spacing between particles. | (5) |
| Experiment Material | Specific Gravity (Gs) | Grain Size (mm) | Average Particle Size (D50) | Coefficient of Nonuniformity (Cu) |
|---|---|---|---|---|
| Granulated rubber | 1.17 | 0.6~2.5 | 1.52 | 1.42 |
| Natural sand | 2.56 | 0~4.8 | 0.31 | 1.32 |
| Rubber Content (%) | Cover Form | Cover Dimension (Diameter or Side Length (mm)) | Cover Sidewall Length (mm) |
|---|---|---|---|
| 30, 40, 50 | Square, Cylindrical, Square straight-cylinder | 160, 200, 240 | 20, 40, 60, 80, 100, 120, 140, 160, 180, 200, 210, 220, 230 |
| Rubber Content | μ | β | A | B | C |
|---|---|---|---|---|---|
| 30% | 0.38 | 0.50 | 1116.6 | 20.7 | 0.34 |
| 40% | 0.41 | 0.43 | 902.6 | 27.9 | 0.25 |
| 50% | 0.43 | 0.35 | 546.2 | 11.9 | 0.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Liu, F.; Tian, W. Load-Bearing Capacity Analysis on Rubber-Sand Mixture Cored Composite Block as Low-Cost Isolation Bearing for Rural Houses Based on DEM Simulations. Sustainability 2025, 17, 8092. https://doi.org/10.3390/su17188092
Wang J, Liu F, Tian W. Load-Bearing Capacity Analysis on Rubber-Sand Mixture Cored Composite Block as Low-Cost Isolation Bearing for Rural Houses Based on DEM Simulations. Sustainability. 2025; 17(18):8092. https://doi.org/10.3390/su17188092
Chicago/Turabian StyleWang, Jiang, Fangcheng Liu, and Wenhui Tian. 2025. "Load-Bearing Capacity Analysis on Rubber-Sand Mixture Cored Composite Block as Low-Cost Isolation Bearing for Rural Houses Based on DEM Simulations" Sustainability 17, no. 18: 8092. https://doi.org/10.3390/su17188092
APA StyleWang, J., Liu, F., & Tian, W. (2025). Load-Bearing Capacity Analysis on Rubber-Sand Mixture Cored Composite Block as Low-Cost Isolation Bearing for Rural Houses Based on DEM Simulations. Sustainability, 17(18), 8092. https://doi.org/10.3390/su17188092






