Balancing Temperature and Humidity Control in Storage Location Assignment: An Optimization Perspective in Refrigerated Warehouses

Abstract

As consumer awareness grows and regulations regarding the quality and safety of perishable goods become stricter, careful management of environmental conditions throughout the supply chain is becoming essential. Among these factors, storage temperature plays a crucial role in preserving the physicochemical characteristics of products. Therefore, an effective approach to ensure quality and safety up to the final customer is to continuously monitor the temperature within warehouses, using specific location-mapping techniques and stocking optimization methods. This study proposes a dynamic optimization model for the storage location assignment problem, integrating both temperature and humidity constraints into the placement of stock-keeping units. The model operates under a multi-period, multi-product framework and leverages real-time sensor data to account for spatial temperature stratification and environmental variability within the warehouse, contributing to the reduction in the energy consumption. Two alternative optimization strategies are explored: one focused on minimizing thermal and humidity stress, and another targeting the reduction in average storage cycle time. A detailed what-if analysis is conducted across three scenarios, varying warehouse fill rates and incoming load volumes, in order to prove the effectiveness of the proposed model in a real-data context. The results show that the approach minimizing environmental stress consistently outperforms traditional methods in quality-related metrics, maintaining superior objective function values.

1. Introduction

Over recent decades, the global food trade has increasingly addressed consumer concerns about the so-called credence attributes—aspects like quality, safety, sustainability, and fair-trade practices [1]. Events such as food safety scandals have heightened public sensitivity and boosted consumers’ demand for transparency and adherence to strict standards [2].

Environmental factors, including temperature, humidity, and vibrations, significantly influence the shelf life and sensory qualities (such as taste and freshness) of perishable goods like food and pharmaceuticals [3]. Managing these conditions effectively is especially critical at storage points such as warehouses, where products remain for extended periods [4]. Among these environmental variables, temperature [5] and humidity [6] are widely recognized as the most critical factors in safeguarding product integrity. Numerous studies have shown that poor temperature control leads to chemical and physical degradation, accelerating spoilage and compromising safety. Consequently, regulatory bodies have developed safety and quality standards to guide companies in ensuring proper storage conditions during distribution [7,8]. Moreover, the phenomenon of air stratification in the storage area and the facility’s structural features of refrigerated warehouses (such as insulation quality, exposure to sunlight, and internal layout) reduce the effectiveness of storage zones in maintaining safe conditions for stock-keeping units (SKUs) [9].

Monitoring the temperature conditions in warehouses is considered best practice. Therefore, quality managers are typically required to conduct temperature mapping to track fluctuations over time, and different techniques were proposed in the past from this perspective [5]. These techniques are fast-evolving in the era of Industry 5.0, where temperature monitoring in logistics and warehousing has become increasingly sophisticated and data-driven [10]. Advanced technologies such as Internet of Things (IoT) sensors, wireless data loggers, and real-time monitoring systems are now commonly employed to continuously track temperature conditions throughout the supply chain. These devices transmit data to cloud platforms, enabling predictive analytics and proactive decision-making. From this perspective, optimization techniques play a pivotal role in enhancing the efficiency and responsiveness of storage and retrieval operations within refrigerated warehouses. These environments demand precise coordination to minimize energy consumption, reduce product handling time, and maintain strict temperature control, all while ensuring rapid access to perishable goods. Leveraging AI-driven algorithms, digital twins, and real-time data analytics enables dynamic decision-making that optimizes warehouse layout, the routing of autonomous vehicles, and inventory rotation strategies [11]. This not only improves operational sustainability, but also enhances worker safety and adaptability, aligning with the core principles of Industry 5.0—collaboration between humans and machines for resilient and value-driven logistics [12,13].

In warehousing, optimizing the assignment of SKUs to storage locations is a well-recognized critical activity for improving the overall performance and responsiveness of warehouse operations [14]. Strategic SKU placement directly impacts picking efficiency, travel time, and inventory accessibility, especially in high-throughput environments. Moreover, an intelligent SKU assignment strategy helps balance workload across different zones, avoids congestion, and supports more accurate space utilization. This becomes even more essential in dynamic inventory settings, where demand patterns fluctuate and real-time adaptability is required [15]. These aspects become more relevant within refrigerated warehouses.

The proper placement of SKUs not only improves picking efficiency and reduces travel time, but also ensures that sensitive items are stored in zones with the most appropriate environmental conditions, controlling temperature and humidity. For instance, products with stricter thermal requirements can be positioned closer to more stable cooling zones, while less sensitive goods may be stored in peripheral areas. This strategic allocation helps maintain consistent climate conditions by minimizing unnecessary door openings, reducing air circulation disruptions, and limiting exposure to external temperatures [9]. Additionally, optimizing SKU locations reduces energy consumption by supporting better airflow and reducing the workload in refrigeration systems. In this way, intelligent SKU-to-location mapping contributes not only to operational efficiency, but also to the sustainability and regulatory compliance of cold chain logistics [16]. Moreover, proper air distribution and SKUs’ allocation in cold warehouses supports the emerging concept of green warehousing [17], by promoting sustainable practices that reduce energy consumption and carbon emissions. Through the integration of energy-efficient technologies, smart inventory placement, and environmentally conscious design, it not only lowers operational costs, but also enhances the overall sustainability of the cold supply chain.

This paper advances the cold warehousing literature on the storage assignment problem by introducing an original dynamic optimization model for the allocation of perishable products. The model is inspired by a real refrigerated warehouse used by a company operating in the cold food chain for storing frozen foods, considering a stocking area with capacity of 5000 food-grade plastic pallets (referred as unit loads hereinafter). The refrigerated storage area has recently undergone modernization and has been equipped with sensors capable of detecting the warehouse’s temperature and humidity levels in real time, for mapping the temperature profile. The company aims to leverage this information to improve the storage process of incoming load units. With this aim, the proposed model integrates both temperature and humidity control into the decision-making process for SKUs placement on storage racks. Additionally, a what-if analysis is conducted through a case study to evaluate the impact of storage decisions driven by environmental control considerations.

The remainder of the paper is arranged as follows: Section 2 organizes a review of the literature and a description of the methodology; Section 3 illustrates the optimization model, Section 4 showcases the methodology with a case study and introduces computational results, while, and Section 5 presents the study’s conclusions and provides goals for further research developments.

2. Materials and Methods

Within refrigerated warehouses, the typical storage and retrieval operations are influenced by several factors related to the specific boundary conditions. Below is a detailed overview of studies addressing these conditions and those combining these considerations with SKU storage strategies, as well as the description of the proposed methodology.

2.1. Perishable Products Storage Conditions Literature Review

Within the food industry, improper control of warehouse temperature and humidity accelerates microbial growth and causes physical degradation of products, altering flavor, texture, and appearance [18]. Two key indicators are commonly used to monitor quality: shelf life, which measures the period during which a product retains acceptable quality (also known as stability period), and the freshness gauge, which evaluates freshness based on remaining shelf life [6]. Accurate determination of shelf life is critical for setting expiration and sell-by dates.

Indoor climate conditions also affect worker health and productivity, further highlighting the need for precise environmental control in industrial storage spaces [19]. A major challenge is air stratification, where temperature gradients develop vertically in high-ceiling warehouses, leading to inefficient heating and non-uniform temperatures [20,21,22]. Porras-Amores et al. [23] recently analyzed vertical temperature gradients in warehouses, highlighting the impact of air stratification, especially in facilities with passive or active cooling systems. Similarly, Ho et al. [24] examined air velocity and temperature distribution in refrigerated warehouses, recommending the placement of products near cooling units, within the limits allowed by safety regulations, as best practice.

The warehouse layout—along with elements such as skylights, loading docks, and fan airflow—can exacerbate thermal imbalances. Although computational fluid dynamics has been suggested to simulate these environments [20], it is often impractical due to its cost and complexity. Instead, many facilities use temperature mapping with data loggers to empirically assess how heat distribution varies over time and space. Temperature mapping involves monitoring how temperature levels change over time within storage environments, such as cold chambers, industrial refrigerators, or warehouses. The goal is to ensure that the environmental conditions match the storage requirements specified for the products. This process helps detect temperature variations caused by structural characteristics, facility design, or human activity. This method helps identify problem zones, even as external weather conditions change [5].

2.2. Storage Location Assignment Problem Literature Review

One of the most critical challenges in warehouse management is the storage location assignment problem (SLAP) [25], which involves determining the optimal placement of items within a storage system to improve the overall efficiency. Yingde and Smith [26] classify storage assignment problems based on demand profiles: static (with stable SKU flows) and dynamic (with fluctuating inventory due to factors like seasonality or product turnover). In dynamic contexts, external influences—such as marketing, stock-outs, or supply chain disruptions—affect performance, making the periodic reorganization of storage, referred as re-warehousing, essential to maintain efficiency [27]. In this paper, we refer to the static version of the problem, accordingly with this definition. Poor assignment strategies can lead to increased travel time, labor costs, and order picking delays [15]. SLAP is particularly complex due to the variety of constraints and objectives involved, such as minimizing retrieval times, balancing workload, and accommodating product-specific storage requirements. Several variants have emerged in the literature, including random assignment, class-based assignment, and volume-based assignment. Random assignment offers simplicity but sacrifices efficiency [28], while class-based methods group items by demand frequency to improve pick performance (e.g., assigning fast-moving SKUs closer to dispatch zones). More advanced approaches include correlated storage [29], where items frequently ordered together are stored nearby to minimize picker travel distance. Optimization-based solutions often rely on heuristics, metaheuristics (e.g., genetic algorithms), or integer programming to solve these problems under realistic constraints. Recent studies have also explored dynamic assignment models [9], which adjust item locations over time based on evolving demand patterns and warehouse usage, trying to avoid re-warehousing operations. These dynamic methods are increasingly relevant in fast-paced environments such as e-commerce or cold chain logistics, where adaptability is key to maintaining service levels and operational efficiency.

Unlike conventional settings, in cold storage environments, SLAP must not only account for operational efficiency, but also for product-specific temperature and humidity requirements, shelf-life constraints, and energy optimization goals [30]. Objective functions in this context typically aim to minimize travel distance, reduce order picking time, and optimize energy usage by clustering goods with similar thermal profiles [9]. Some variants of SLAP incorporate thermal zoning strategies, assigning products to storage zones based on their sensitivity to temperature fluctuations, while others focus on first-expired-first-out (FEFO) policies to ensure product freshness [31]. Additionally, multi-criteria decision models may consider factors such as product turnover rate, weight, volume, and compatibility with other SKUs. Constraints often include limited space in cold zones, restricted access due to condensation or frost, and energy-intensive equipment operation schedules. More advanced formulations leverage mixed-integer programming or metaheuristics to balance competing objectives [32], such as minimizing total retrieval time while adhering to strict cold chain compliance [33]. In complex cases, the combined optimization of storage and picking is performed for improving efficiency and safety [34,35]. Moreover, hybrid algorithm techniques, combining optimization and machine learning, are recently introduced [36]. These specialized SLAP models are increasingly relevant in the management of pharmaceuticals, fresh products, and frozen foods, where preserving product integrity is as critical as achieving logistical efficiency. For a complete overview of the field, the reader can refer to the surveys of Yurtseven et al. [16], Muhammad et al. [37], and Ren et al. [38].

2.3. Contribution to the Literature

This paper contributes to the literature proposing a storage location assignment problem with innovative characteristics customized on the company perspective, and it is configured as an extension of the problem proposed in Baruffaldi et al. [5]. In particular,

• A multi-period SLAP model has been proposed for storage management over a specific planning horizon. This model is particularly suited to the dynamic nature of warehouses and allows for the management of refrigerated storage activities using simple rolling horizon approaches, while accounting for the variability of boundary conditions;
• The model features an objective function composed of two main terms: one related to maintaining the safety temperature, and the other related to humidity level. The analysis of this aspect was inspired by Woo et al. [6]. This characteristic is entirely novel within the class of SLAPs, which often consider only temperature conditions, or focus on optimizing operational metrics such as time and energy reduction, without taking product quality into account;
• The model supports the general hypothesis of a warehouse operating with traditional selective racking, offering high operational flexibility and allowing free retrieval without enforcing FIFO or FEFO rules. This neutral infrastructure does not impose any inherent storage policy, which has to be suggested by the optimization;
• The model also accounts for the multi-product scenario, which reflects a realistic condition in warehouse management—particularly in refrigerated warehouses. In such contexts, the need to maintain the cold storage area at a suitable temperature, combined with the phenomenon of air stratification, often clashes with the specific, and sometimes heterogeneous, temperature requirements of different products;
• A real case-study is introduced for a refrigerated warehouse, where the temperature measuring is provided by sensors, and a what-if-analysis is presented for evaluating the storage–retrieval cycle efficiency and the quality considerations introduced into the model.

While Baruffaldi et al. [5] propose an optimization model for the storage of perishable products—considering temperature constraints and product demand—their contribution remains theoretical, as no computational experiments are presented. Similarly, Woo et al. [6] introduce a freshness-based performance indicator and suggest guidelines for storage assignment, but without integrating routing dynamics or providing quantitative validation. In contrast, our work combines storage under temperature and humidity constraints, and provides a full numerical evaluation across multiple realistic scenarios.

Note that several models in the literature address demand-based allocation through class-based or correlated storage policies. These strategies group SKUs by turnover rate or picking co-occurrence, and are typically applied in ambient-temperature warehouses. However, such approaches require a predefined zoning logic, which is not compatible with the neutral, dynamic racking layout considered in this work.

Finally, note that also if the proposed model does not directly optimize for energy consumption (as necessary for companies that are interested in testing the efficiency of new sensors), but implicitly supports energy efficiency (as a fundamental concept of sustainable green warehousing) by leveraging environmental data for optimal SKU placement. Specifically,

• It minimizes thermal and humidity stress, thereby reducing the load on refrigeration systems;
• It allocates SKUs in thermally stable areas, limiting fluctuations caused by door openings and air stratification, which results in lower compressor activity;
• It avoids areas frequently exposed to thermal disturbances, also reducing the amount of energy used for material handling.

Future developments aim to integrate direct energy metrics into the optimization objective, for strongly enhancing sustainability performance.

2.4. Methodology

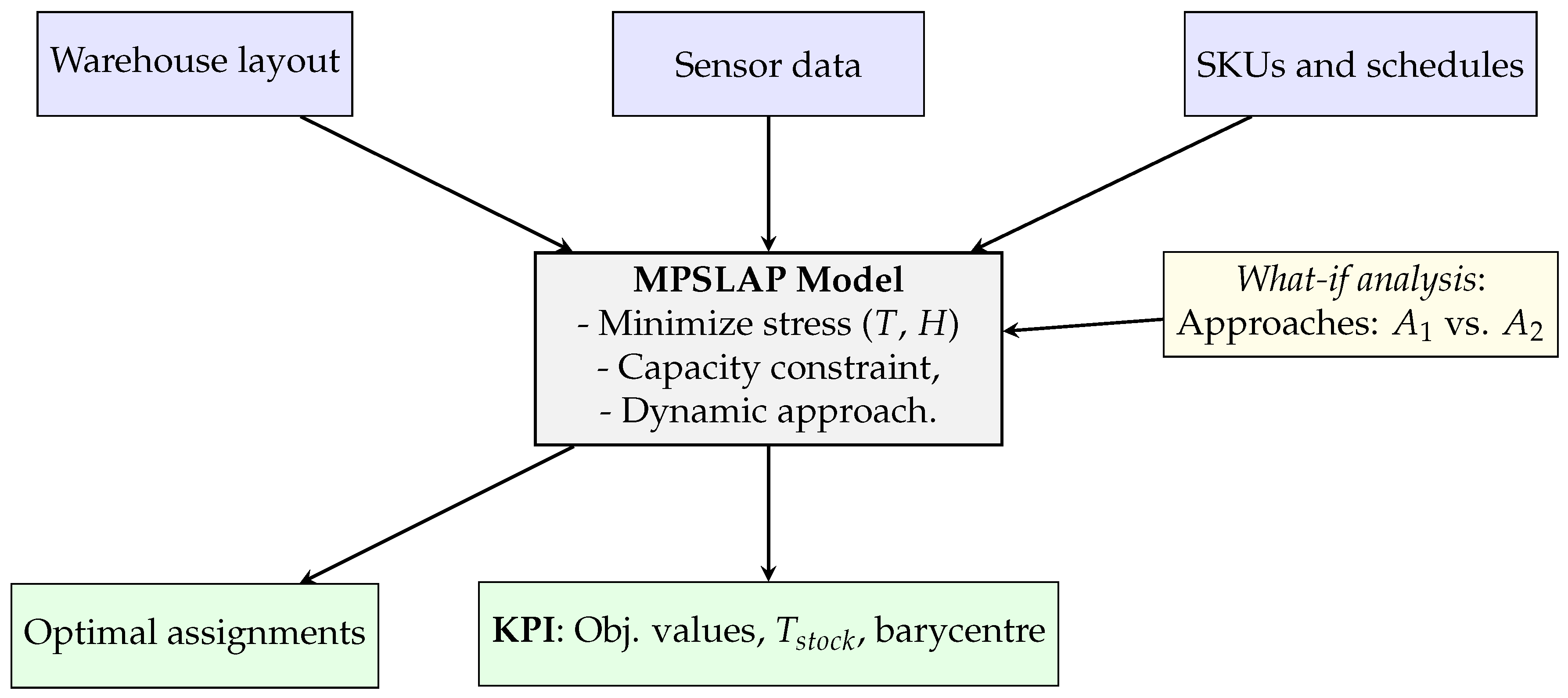
The methodological framework is articulated into different main stages (see Figure 1) that reflects the logical structure of the proposed work.

• Input acquisition: the process begins with the collection of key operational and environmental data from the company. This includes the geometric layout of the warehouse, real-time measurements of temperature and humidity captured by embedded sensors, and information on incoming unit loads, including their arrival schedule and characteristics. These data form the basis for all subsequent optimization steps and scenario analysis definition;
• Optimization: at the core of the methodology lies the multi-period multi-product storage location assignment problem (MPSLAP), which integrates environmental constraints, such as thermal stratification and humidity thresholds, into the decision-making process.
• What-if analysis: to assess the robustness and adaptability of the proposed model, a what-if analysis is carried out across multiple operational scenarios. These scenarios vary key parameters such as warehouse fill rates and incoming load volumes, allowing for the comparison of the MPSLAP, which minimizes environmental stress, and a second approach, which aims to reduce average storage cycle time under realistic and dynamic conditions. The analysis highlights trade-offs between environmental performance and operational efficiency, supporting informed decision-making in practical applications.
• Output and performance evaluation: the final stage generates an optimized assignment plan and evaluates the resulting system performance. Key indicators include the average storage time, the value of the objective function, and the barycentre of assigned SKUs within the warehouse. Empirical insights into the trade-offs between efficiency and environmental compliance are described.

Although the optimization model was inspired by the operational context of a specific company, it is designed to be sufficiently general, scalable, and adaptable to other applications. For this reason, it is presented first, in Section 3, as a theoretical contribution. In contrast, Section 4 focuses on the practical implementation and analysis of the case study, emphasizing its real-world applicability.

3. Mathematical Formulation

This section illustrates the SLAP optimization model designed to determine the best storage for incoming unit loads, using the temperature-mapping data of a specific storage area. It concerns selecting the most appropriate storage location for an incoming pallet of a specific SKU, with the aim of optimizing a general convenience-related objective function.

The model is developed under the assumption that sensors provide data to a tool processing thermal loggers, to generate a detailed map of both historical and real-time indoor storage conditions. This enables the development of storage assignment models focused on reducing thermal stress on the inventory throughout its lifecycle.

The rest of this section is dedicated to formalizing the MPSLAP, where the quality of conservation conditions serves as the core criterion for the optimization process. The MPSLAP is modeled considering the following:

• The set I representing the storage locations in the stocking area;
• The set S introducing the different stock keeping units (SKUs);
• The set T describing the time horizon;
• The set $U_t$ representing an ordered list of unit-loads of different SKUs to be stocked at each time $t\in T$. It can be partitioned as follows: $U_t=U_{1t}\cup U_{2t}\cup \cdots \cup U_{st}$, with $s\in S$. Note that $|U_{st}|$ represents the number of unit-loads of type s to be stocked in period t.

The following parameters are considered:

• $K_i\left(t\right)$: temperature measured at location $i\in I$ in period $t\in T$;
• $[K_u^{saf{e}^{-}},K_u^{saf{e}^{+}}]$: safe temperature range for unit-load $u\in U_{st},t\in T$ and $s\in S$;
• $H_{ui}$: humidity for unit load $u\in U_{st},t\in T,s\in S$ measured at the location $i\in I$;
• $\beta$: weight to scale the effect of humidity in comparison with temperature considerations, with $\beta \in (0,1)$;
• $H_{target}$: target humidity;
• ${\gamma }_{it}$: takes value 1 if the location $i\in I$ is empty during period $t\in T$, 0 otherwise;
• $d_{ui}^{t,H}$: distance between the location $i\in I$ and the optimal location for the unit-load $u\in U_{st},t\in T,s\in S$ according to the highest safe temperature $K_u^{saf{e}^{+}}$ and the target humidity $H_{target}$. This parameter pushes the assignment of the incoming unit-loads according to the highest expected temperature stress that is measured in that location $i\in I$ along a time horizon from t to $t+{\Delta }_s$. The term ${\Delta }_s$ is the average period that a pallet is stored in the warehouse, computed considering historical data on SKU $s\in S$;
• $K_{ui}^{stress}\left(t\right)$: expected stress temperature for unit-load $u\in U_{st}$ measured at the location $i\in I$ during the ${\Delta }_s$, starting from period $t\in T$.

Parameter $K_{ui}^{stress}\left(t\right)$ is computed assuming that a storage location occupied until the corresponding SKU is removed for ${\Delta }_s$ periods, may be exposed to stress or critical temperature conditions that could compromise the load’s safe preservation. It is determined as follows:

$$K_{ui}^{stress}\left(t^{\ast }\right)=\left\{\begin{array}{cc}max\left\{K_i\left(t\right):t^{\ast }<t\le t^{\ast }+\Delta s\right\}\hfill & \mathrm{if}\left|max\left\{K_i\left(t\right):t^{\ast }<t\le t^{\ast }+\Delta s\right\}-K_u^{saf{e}^{+}}\right|\ge \left|max\left\{K_i\left(t\right):t^{\ast }<t\le t^{\ast }+\Delta s\right\}-K_u^{saf{e}^{-}}\right|\hfill \\ min\left\{K_i\left(t\right):t^{\ast }<t\le t^{\ast }+\Delta s\right\}\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(1)

Using (1), is possible to measure the highest stress temperature during the time frame $[t, t+{\Delta }_s$] for the unit-load $u\in U_{st},s\in S$ and location $i\in I$. The distance $d_{ui}^{t,H}$ is consequently computed as follows:

$$d_{ui}^{t,H}=|K_u^{saf{e}^{+}}-K_{ui}^{stress}\left(t\right)|+\beta (H_{ui}-H_{target})$$

(2)

Note that the closer the temperature $K_{ui}^{stress}\left(t\right)$ is to the safe storage range $[K_u^{saf{e}^{-}},K_u^{saf{e}^{+}}]$ for load $u\in U_{st}$, the more the configuration aligns with optimal storage conditions.

The unique set of decision variables is $x_{uit}$; that is, a binary variable taking a value of 1 if the unit-load $u\in U_{st},s\in S,t\in T$ is assigned to the location $i\in I$ during the period $t\in T$, and 0 otherwise. Then, the model is formulated as follows and solved with a rolling horizon approach [39]; for each period, $t\in T$:

$$\begin{array}{cc}\hfill & minz\left(x\right)=\sum _{s\in S}\sum _{u\in U_{st}}\sum _{i\in I}{d}_{ui}^{t,H}{x}_{uit}\hfill \\ \hfill s.v\end{array}$$

(3)

$$\begin{array}{cc}\hfill & \sum _{i\in I}{x}_{uit}=1\forall u\in U_{st},s\in S\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & \sum _{s\in S}\sum _{u\in U_{st}}{x}_{uit}\le {\gamma }_{it}\forall i\in I\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill & x_{uit}\in \{0,1\}\forall u\in U_{st},s\in S,i\in I\hfill \end{array}$$

(6)

The objective function (3) represents the quality preservation measuring how much the current storage setup deviates from the configuration that would minimize the stress temperature and the humidity slack from the target. Constraint (4) forces the assignment of load $u\in U_{st}$ to a single storage location $i\in I$. Constraint (5) guarantees that each storage location $i\in I$ is filled by a unit-load only if location $i\in I$ is empty. Constraint (6) shows the binary nature of the decision variables.

The objective of the model is to optimize the overall benefit derived from the periodically allocation of incoming unit loads to available storage locations. This benefit depends on the storage conditions observed at each location. By considering the maximum expected stress temperature at a given location over the time range $[t,t+\Delta s]$ and a humidity target, the model directs the assignment of unit-load $u_s$ to the most suitable available location $i\in I$. It should be noted that the rolling horizon approach is applied through updating the set $U_t$ of storage units to be allocated, and the parameter ${\gamma }_{it}$, which accounts for the positions that were occupied and those that have been emptied due to retrieval operations in the period $t-1$.

4. Context Description and What-If Analysis

This section is dedicated to the context description, the what-if analysis and computational experiments.

As previously mentioned, the case study is inspired by a real stocking area of 5000 unit loads capacity, equipped with sensors for monitoring humidity and temperature. With this aim, a what-if analysis is conducted considering three cases (referred to hereinafter as scenarios), on the basis of different settings of the $|U_{st}|,s\in S,t\in T$ and of the storage fill rate of the stocking area.

What-if analysis is a decision-making tool used to evaluate the potential outcomes of different scenarios by changing the input variables in a model, allowing the exploration of how variations in assumptions—such as cost increases, sales volume fluctuations, or resource changes—affect the final results. It is widely used in warehouse process simulations to evaluate how changes in variables—such as staffing levels or equipment configurations—affect operations. This approach enables organizations to optimize performance and make informed decisions without disrupting actual workflows [40].

The MPSLAP was implemented using Lingo 21.0 (https://www.lindo.com/, accessed 4 July 2025), a powerful optimization software that supports various problem types, including mixed-integer programming. Lingo applies the branch-and-bound method for integer problems and enhances performance through preprocessing and cutting techniques for linear mixed-integer models, improving solution times. For more details, see the Lingo manual (https://www.lindo.com/downloads/PDF/LINGO.pdf, accessed 4 July 2025).

The computer used for the computational experiments is equipped with an AMD Ryzen 7 3700U with a Radeon Vega Mobile Gfx processor, 8.00 GB of RAM, and Windows 11 Professional 64-bit.

4.1. Description of the Case Study

The considered storage area is characterized by the following features:

• $\left|I\right|=5000$, represents the capacity of the storage area, a building measuring $69.60$ m along the x-axis and $56.75$ m along the y-axis;
• The unit loads are handled with forklifts;
• The safe temperature range for the storage area is [−26 °C, −21 °C];
• The target humidity chosen is $H_{target}=0.7$;
• The measured values for $H_{ui}$ for unit load $u\in U_{st}$ at the location i are within the interval $[0.6;0.8]$.
• The parameter $\beta$ is set to a value of 0.6 based on preliminary sensitivity analysis, reflecting the greater criticality of temperature over humidity in the frozen storage context (−26 °C to −21 °C);
• Random lists $U_{st},s\in S,t\in T$ are generated for each scenario;
• One period of planning is considered in the time horizon;
• The parameter ${\gamma }_{it}$ is assigned a value of 1 or 0 randomly, depending on the specific scenario considered, to show if the location i is empty or not, respectively.

The warehouse operates under a “random storage policy”, meaning that SKUs are dynamically assigned to storage locations based on current availability. As a result, the allocation of SKUs changes over time depending on the real-time occupancy of the storage space. This policy allows for maximum utilization of the available storage space. Each unit-load u must be automatically identified—using any identification method (e.g., RFID scanning)—in order to continuously update the database of storage locations occupied by stored unit loads u. This update occurs at the end of every storage or retrieval operation.

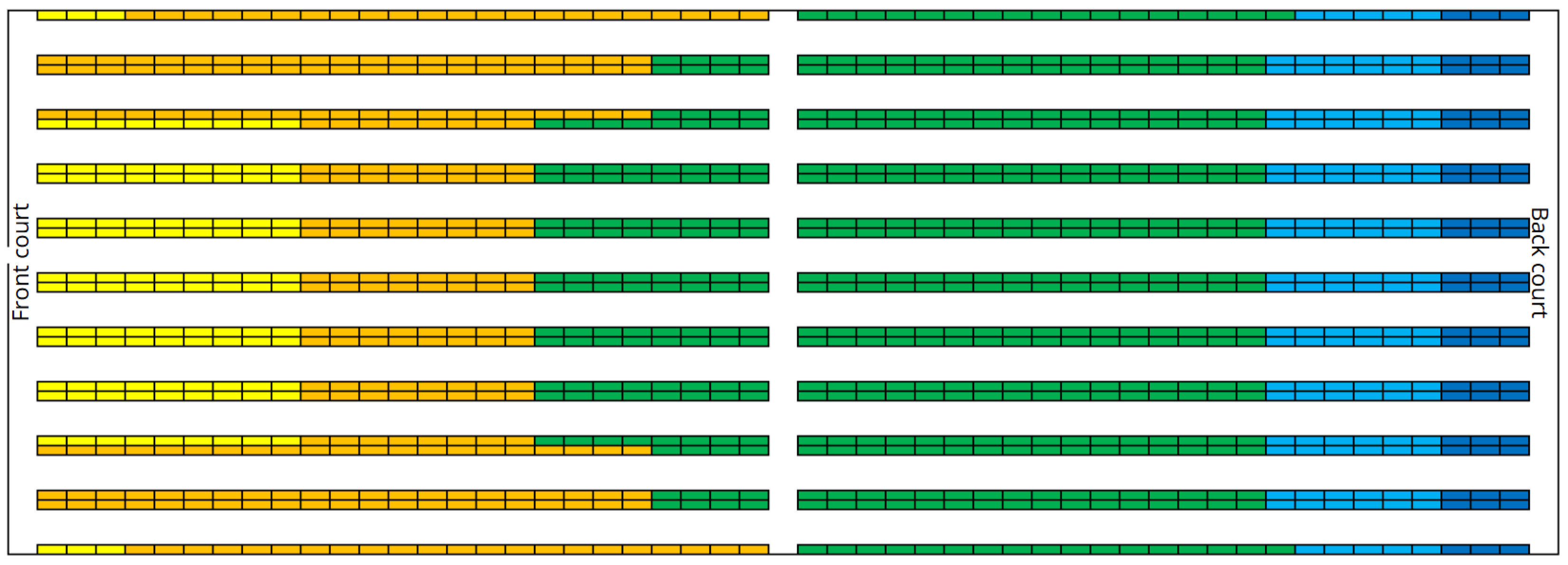
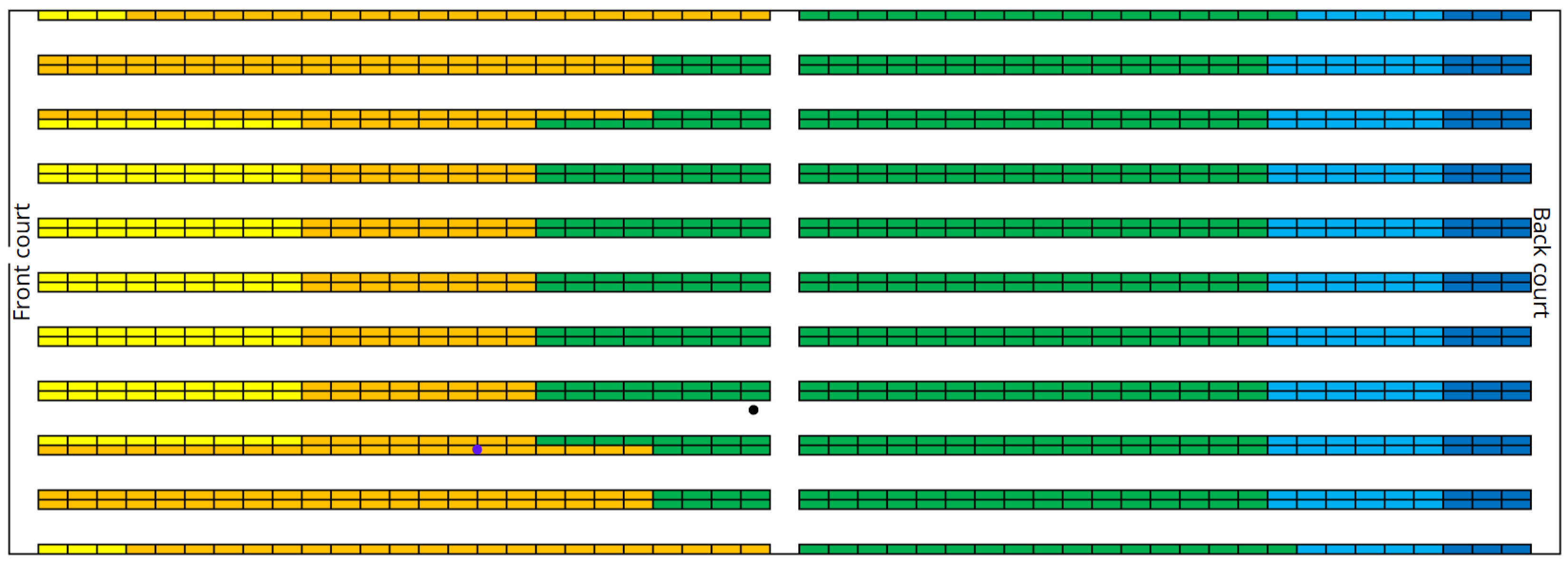
The warehouse is structured into two blocks, each containing 20 aisles of selective racking, for a total of 40 storage locations arranged along the y-axis—two of which are positioned against the walls. Each shelving unit includes 25 storage locations along the x-axis and is divided into 5 vertical levels. Figure 2 shows a top view of the refrigerated storage area layout, indicating the front and the back courts. Note that the entrance door is positioned on the front court.

The parameters considered in the analysis are listed in

Table 1. Parameters related to warehouse layout and forklift operations.

Parameter	Description	Value
$w_x$	Width of the aisles along x-axis	2 m
$w_y$	Width of the aisles along y-axis	4 m
$l_x$	Length of each unit load	1.2 m
$l_y$	Width of each unit load	0.8 m
h	Height for each storage level	1.5 m
c	Clearance distance within each load	0.075 m
$v_u$	Travel speed of an empty forklift truck	3.5 m/s
$v_l$	Travel speed of a loaded forklift truck	3 m/s
$v_{au}$	Unloaded fork ascending speed	0.5 m/s
$v_{al}$	Loaded fork ascending speed	0.3 m/s
$v_{du}$	Unloaded fork descending speed	0.5 m/s
$v_{dl}$	Loaded fork descending speed	0.5 m/s
$t_f$	Pallet forking and deforking time	60 s

. Each rack has a length, denoted by $b_x=(25\times l_x)+(24\times c)=31.8\mathrm{m}$. The width of a storage location is given by $b_y=(2\times l_y)+c=1.675\mathrm{m}$, so the width of a single row is $b_y/2$. Accordingly, the total length of the storage area is $L_x=(2\times b_x)+(3\times w_x)=69.6\mathrm{m}$ and the total width of the storage area is $L_y=10\times (b_y+w_y)=56.75\mathrm{m}$.

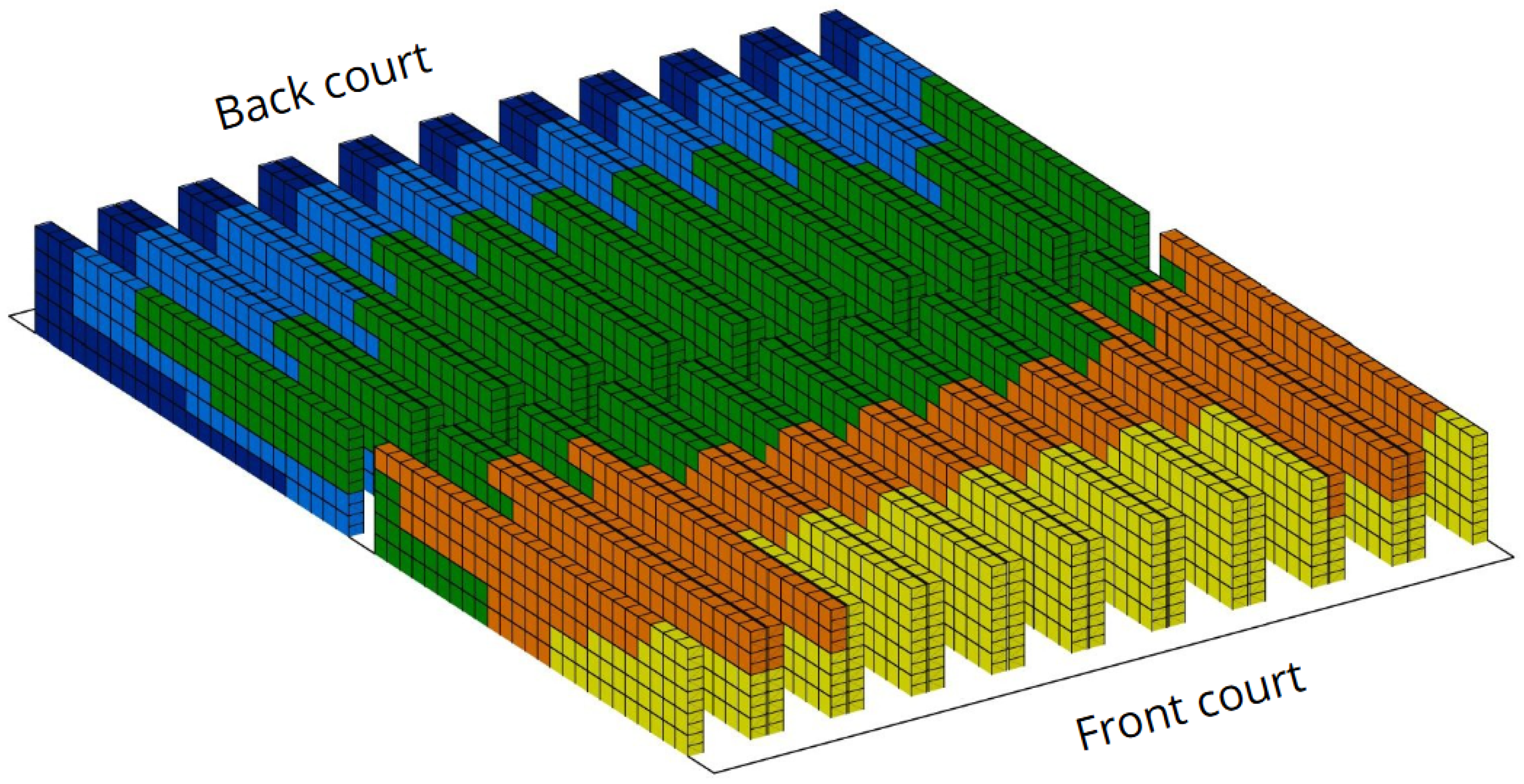
Figure 3 visually illustrates the layout of the refrigerated warehouse, highlighting the temperature gradient that transitions from colder to warmer zones throughout the facility. The cold airflow source is located in the back court of the building, at the ground level. Notably, it emphasizes the progressive temperature increase from the back—closer to the airflow source—toward the rear of the storage racks, a pattern primarily driven by diminished air circulation and localized heat accumulation, as well as from the air stratification from the floor to the top of the building. This thermal distribution is derived from on-site sensor data collected at various rack depths and heights, enabling a spatially resolved understanding of temperature dynamics. Such a thermal profile is instrumental for optimizing product placement by aligning storage zones with temperature stability, thereby ensuring the preservation of temperature-sensitive goods and enhancing overall energy efficiency. This technical illustration was developed in Autodesk Inventor, ensuring dimensional precision and realistic representation.

For each storage location, the time required to complete both the storage cycle $T^{stock}$ and the retrieval cycle $T^{retr}$ has been calculated. These times depend on the distance ${\tau }_i,i\in I$ that the forklift must travel to reach the respective location. The storage time $T^{stock}$ and the retrieval time $T^{retr}$ are calculated as follows:

$$T^{stock}={\displaystyle \frac{{\tau }_i}{v_l}}+{\displaystyle \frac{h}{v_{al}}}+t_f+{\displaystyle \frac{h}{v_{du}}}+{\displaystyle \frac{{\tau }_i}{v_u}}$$

(7)

$$T^{retr}={\displaystyle \frac{{\tau }_i}{v_u}}+{\displaystyle \frac{h}{v_{au}}}+t_f+{\displaystyle \frac{h}{v_{dl}}}+{\displaystyle \frac{{\tau }_i}{v_l}}$$

(8)

All the data used in the study were either provided directly by the company, or, where unavailable, reasonably estimated based on established technical and managerial knowledge in the field.

4.2. What-If Analysis

The what-if analysis is conducted considering three different scenarios, associated with various configurations of storage filling rate and number of incoming unit loads, as introduced in the following:

• First scenario (S1). A progressive increase in warehouse occupancy levels was considered, based on a total of 5000 storage locations. Four different fill rates were analyzed—20%, 40%, 60%, and 80%—while keeping the number of incoming unit-loads constant ($|U_t|=625$). Specifically,
  • At 20% warehouse occupancy, 875 locations were already occupied and 4125 were available. After the placement of the 625 incoming unit-loads, the number of free locations decreased to 3500;
  • At 40% occupancy, 1750 locations were occupied and 3250 were available. After allocation, the number of free locations reduced to 2625;
  • At 60% occupancy, 2625 locations were occupied and 2375 were available. After placement, free locations decreased to 1750;
  • At 80% occupancy, 3500 locations were already occupied, leaving 1500 available. After adding the incoming unit-loads, the remaining free locations were reduced to 875.
• Second scenario (S2). In this case, the number of incoming unit-loads was varied across four levels (250, 500, 750, and 1000) to assess the impact of load volume on warehouse operations, assuming a fixed warehouse occupancy rate of 50%. The following cases were considered:
  • For 250 incoming unit-loads, a total of 4750 storage locations were considered. Prior to their arrival, 2625 positions were available; following placement, 2375 remained free and 2375 were occupied;
  • For 500 incoming unit-loads, the total number of storage locations was 4500. Before placement, 2750 positions were available; afterward, 2250 remained free and 2250 were occupied;
  • For 750 incoming unit-loads, 4250 storage locations were considered. Initially, 2875 positions were available; after placement, 2125 remained free and 2125 were occupied;
  • For 1000 incoming unit-loads, the total number of storage locations was 4000. Before their arrival, 3000 positions were available; after allocation, 2000 remained free and 2000 were occupied.
• Third scenario (S3). In this scenario, the number of incoming unit-loads was set to 250, 500, 750, and 1000, while maintaining a fixed warehouse occupancy level of 50%, corresponding to 2500 free and 2500 occupied storage locations at the initial state. The outcomes for each case are as follows:
  • With 250 incoming unit-loads, the number of available storage locations decreased to 2250, while the number of occupied positions increased to 2750;
  • With 500 incoming unit-loads, the available storage locations decreased to 2000, and occupied positions increased to 3000;
  • With 750 incoming unit-loads, the available storage locations decreased to 1750, and occupied positions increased to 3250;
  • With 1000 incoming unit-loads, the available storage locations decreased to 1500, and occupied positions increased to 3500.

4.2.1. Description of the Computational Approach

The MPSLAP (3)–(6) is solved considering the three proposed scenarios under different warehouse conditions. The scope is to assess the importance of minimizing the distance between the target temperature $K_{ui}^{stress}\left(t\right)$ and humidity target $H_{target}$ during the storage location process. From this perspective, the storage cycle time for each stocked pallet ($T^{stock}$) is considered, finally computing the average value for each time period ($T_{average}^{stock}$). This approach is referred as a posteriori analysis for calculating the average storage cycle time. This method enables the evaluation of how distance-based storage allocation influences the duration of storage operations, assuming that locations with easier access are associated with shorter handling times. The approach involving the resolution of the model (3)–(6) is referred to as $A_1$ hereinafter.

In order to provide a comparison of the adopted metric, a new version of the problem is solved. The objective function (3) is substituted by (9), where the distance component $d_{ui}^{t,H}$ is replaced with the storage cycle time $T_{ui}^{stock}$. The model (9) and (4)–(6) is re-solved accordingly.

$$minz\left(x\right)=\sum _{s\in S}\sum _{u\in U_{st}}\sum _{i\in I}{T}_{ui}^{stock}{x}_{uit}$$

(9)

The purpose of the revised objective function (9) is to minimize the overall storage cycle time by directly optimizing the allocation of incoming products to storage locations. Subsequently, the average storage cycle time $T_{average}^{stock}$ is computed. This formulation aims to promote storage locations that reduce handling distance, but also ensure faster product turnover. The approach involving the resolution of the model (9) and (4)–(6) is referred as $A_2$ hereinafter.

Finally, for $A_1$ and $A_2$ and for each scenario, the barycentre for each $U_t,t\in T$ is calculated. For the evaluation of barycentre, the following features are considered:

• $(x_u,y_u,z_u)$ are the coordinates of the storage location $u\in U_{st}$;
• $x_u$ represents the lengthwise position (i.e., the distance from the entrance) of the storage location $u\in U_{st}$;
• $y_u$ represents the transverse position (i.e., the reference lane) of the storage location $u\in U_{st}$;
• $z_u$ represents the vertical position (i.e., the shelf level) of the storage location $u\in U_{st}$.

The barycentre coordinates $(x_{bar},y_{bar},z_{bar})$, for $U_t,t\in T$ are computed as

$$x_{bar}={\displaystyle \frac{{\sum }_{u=1}^{U_t}{x}_u}{|U_t|}}$$

(10)

$$y_{bar}={\displaystyle \frac{{\sum }_{u=1}^{U_t}{y}_u}{|U_t|}}$$

(11)

$$z_{bar}={\displaystyle \frac{{\sum }_{u=1}^{U_t}{z}_u}{|U_t|}}$$

(12)

By analyzing the barycentre resulting from both allocation strategies, it becomes possible to evaluate how these approaches shape the spatial distribution of stored unit loads within the warehouse layout. The barycentre is calculated using the geometric coordinates of the assigned storage locations and acts as a spatial indicator of how centralized or dispersed the allocation is with respect to key reference points, such as the warehouse entrance or high-traffic zones. A more centralized barycentre may indicate a more efficient configuration, potentially reducing travel distances and handling times. Conversely, a more dispersed barycentre might reflect less efficient space utilization or a deliberate trade-off that prioritizes thermal stability over proximity to access points. Comparing the barycentres derived from distance-based and storage cycle-time-based optimization strategies allows for an assessment of how each method balances operational efficiency with cold chain integrity. This spatial perspective adds a valuable layer of analysis, revealing how model-driven decisions influence not only key performance metrics, but also the physical deployment of goods across the warehouse grid. The results are summarized in the following subsections, one for each scenario.

4.2.2. Discussion of the Results

In the following, the results obtained for S1, S2, and S3 using two different approaches, $A_1$ and $A_2$, are described. As previously mentioned, the what-if-analysis is conducted on two main performance indicators: $T_{average}^{stock}$ and barycentre.

• Results for S1

Table 2. Values of $T_{average}^{stock}$ and objective function for each sub-case within S1 and for $A_1$ and $A_2$.

Case	${\mathit{T}}_{\mathit{average}}^{\mathit{stock}}$ (${\mathit{A}}_1$)	${\mathit{T}}_{\mathit{average}}^{\mathit{stock}}$ (${\mathit{A}}_2$)	Obj. (${\mathit{A}}_1$)	Obj. (${\mathit{A}}_2$)
	[s]	[s]
20%	105.595	79.898	3264.047	3379.724
40%	105.665	82.148	3267.904	3381.443
60%	105.971	85.129	3272.375	3379.263
80%	106.426	89.466	3282.571	3382.956

presents the average stock time values $T_{average}^{stock}$ and the objective function for four different sub-cases related to the increasing fill rate of the storage area (20%, 40%, 60%, and 80%) under S1, using two different approaches: $A_1$ and $A_2$. It is possible to observe the following:

• $A_1$ consistently yields higher average stock times than $A_2$ across all cases.
• As the case percentage increases from 20% to 80%, there is a slight increasing trend in average stock time for both approaches, with values for $A_1$ ranging from 105.595 to 106.426, and for $A_2$ from 79.898 to 89.466 (see Figure 4).
• The objective function values are lower for approach $A_1$ than for $A_2$, indicating better performance; indeed, $A_1$ maintains a clear advantage, with an average gap of 3.33% compared to $A_2$.

Table 3. Coordinates of barycentre $(x_{bar},y_{bar},z_{bar})$ for each sub-case within S1 and for $A_1$ and $A_2$.

Case	$({\mathit{x}}_{\mathit{bar}},{\mathit{y}}_{\mathit{bar}},{\mathit{z}}_{\mathit{bar}})$ (${\mathit{A}}_1$)	$({\mathit{x}}_{\mathit{bar}},{\mathit{y}}_{\mathit{bar}},{\mathit{z}}_{\mathit{bar}})$ (${\mathit{A}}_2$)
	[m]	[m]
20%	(33.485, 13.805, 3.060)	(14.751, 10.652, 0.782)
40%	(33.704, 14.071, 3.017)	(16.491, 10.975, 0.965)
60%	(33.427, 14.430, 3.065)	(18.663, 11.261, 1.238)
80%	(34.263, 14.412, 3.055)	(21.726, 11.979, 1.613)

shows the coordinates of the barycentre for each sub-case related to the increasing fill rate of the storage area, under the same scenario S1, again comparing the two approaches, $A_1$ and $A_2$. For each case (20%, 40%, 60%, and 80%), a set of 3D coordinates is provided representing the central point (barycentre) of the positions assigned to the incoming unit loads. It is possible to observe the following:

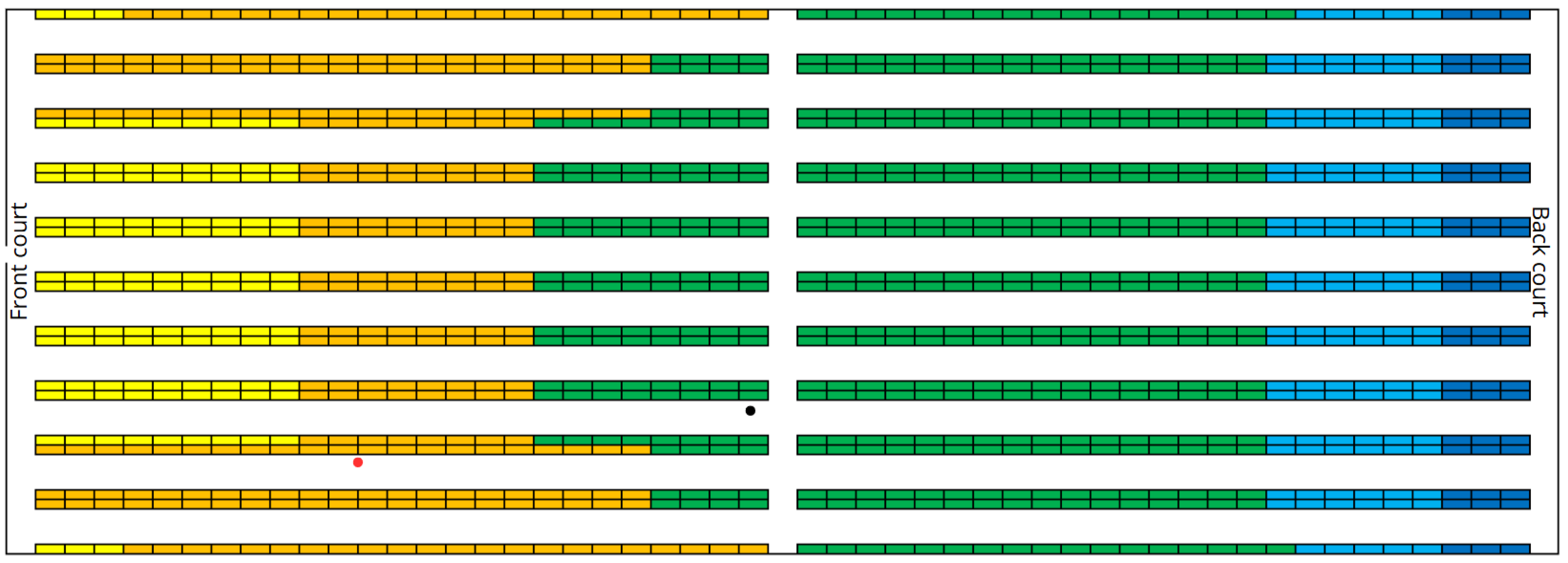
• The barycentre coordinates show that in case $A_1$, the height is usually higher (around the third shelf level), while in case $A_2$, it stays close to the floor. This is because the goal in case $A_1$ is to protect the temperature of the load units, so the model places pallets mostly in cooler areas.
• As the filling rate increases, it is possible to observe that the barycentre also shifts across the building floor plan, with varying degrees of significance. Specifically, in case $A_1$, the barycentre shows slight fluctuations along the x and y-axis, always remaining in a central position within the building layout; in case $A_2$, the barycentre moves significantly away from the entrance as the number of occupied positions increases.
• By observing the two barycentre plotted together in Figure 5, Figure 6, Figure 7 and Figure 8 for each sub-case, it can be seen that the approach based on minimizing total storage time ($A_2$), which is the more traditional method, shifts the barycentre of the assigned positions closer to the entrance door with respect to case $A_1$. This exposes the load units in case $A_2$ to higher temperatures and greater fluctuations due to the door opening. The other approach, which is based on a metric specifically designed for refrigerated scenarios, instead places the load units not too far from the door, but still in significantly cooler areas.

• Results for S2

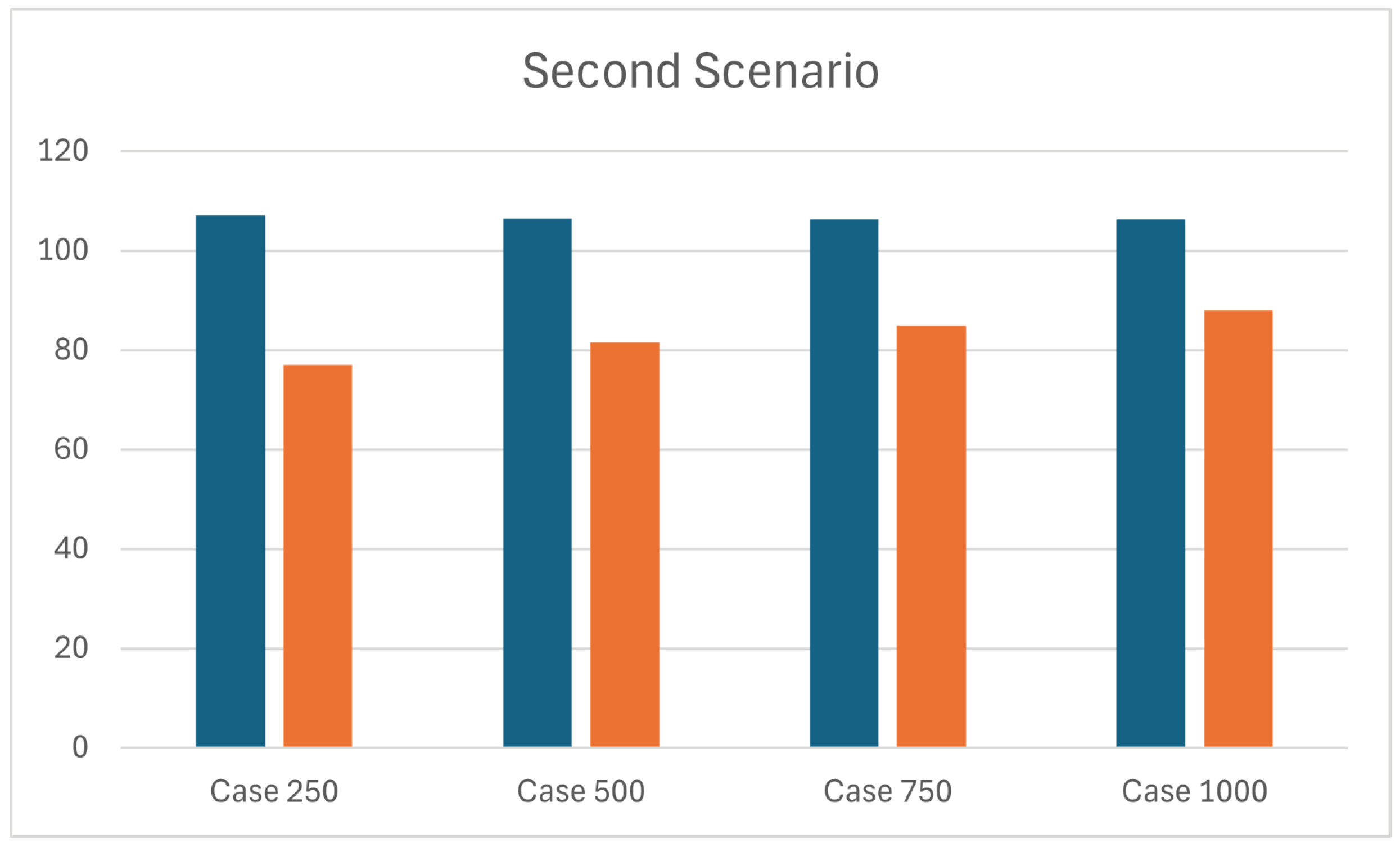
As for the first scenario,

Table 4. Values of $T_{average}^{stock}$ and objective values for each sub-case within S2 and for $A_1$ and $A_2$.

Case	${\mathit{T}}_{\mathit{average}}^{\mathit{stock}}$ (${\mathit{A}}_1$)	${\mathit{T}}_{\mathit{average}}^{\mathit{stock}}$ (${\mathit{A}}_2$)	Obj. (${\mathit{A}}_1$)	Obj. (${\mathit{A}}_2$)
	[s]	[s]
250	107.088	77.034	1345.351	1394.363
500	106.431	81.434	2565.075	2655.783
750	106.249	84.917	3768.603	3901.689
1000	106.157	87.840	5227.062	5396.946

and Figure 9 compare the average $T_{average}^{stock}$ and objective function for two different approaches, $A_1$ and $A_2$, across four different sub-cases (250, 500, 750, 1000 number of unit-loads incoming). The results clearly indicate that the average $T_{average}^{stock}$ increases in parallel with the increasing number of unit loads in $A_2$, as expected, while this effect is less evident in $A_1$. This is due to the position of the barycentre that presents the same behavior of the scenario S1 (see

Table 5. Coordinates of barycentre $(x_{bar},y_{bar},z_{bar})$ for each sub-case within S2 and for $A_1$ and $A_2$.

Case	$({\mathit{x}}_{\mathit{bar}},{\mathit{y}}_{\mathit{bar}},{\mathit{z}}_{\mathit{bar}})$ (${\mathit{A}}_1$)	$({\mathit{x}}_{\mathit{bar}},{\mathit{y}}_{\mathit{bar}},{\mathit{z}}_{\mathit{bar}})$ (${\mathit{A}}_2$)
	[metres]	[metres]
250	(34.530, 13.983, 3.198)	(12.977, 9.319, 0.606)
500	(34.632, 13.413, 3.129)	(16.271, 10.730, 0.885)
750	(34.317, 14.530, 3.002)	(18.114, 11.539, 1.230)
1000	(34.655, 14.435, 2.957)	(20.611, 11.775, 1.461)

). Similarly to $S_1$, $A_1$ maintains an average gap of 3.49% compared to $A_2$ between objective functions.

• Results for S3

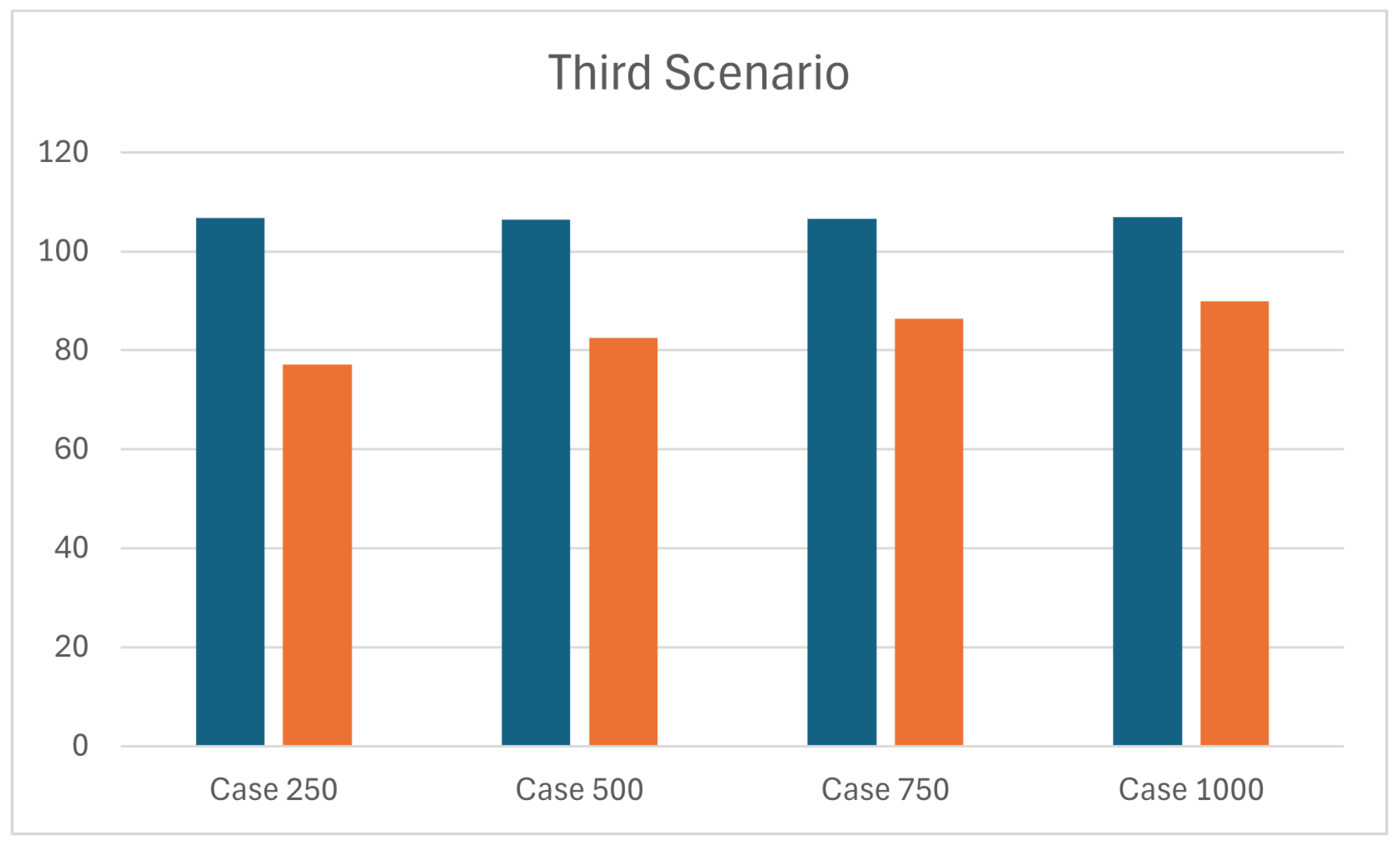
As for the previous scenarios,

Table 6. Values of $T_{average}^{stock}$ for each sub-case within S3 and for $A_1$ and $A_2$.

Case	${\mathit{T}}_{\mathit{average}}^{\mathit{stock}}$ (${\mathit{A}}_1$)	${\mathit{T}}_{\mathit{average}}^{\mathit{stock}}$ (${\mathit{A}}_2$)	Obj. (${\mathit{A}}_1$)	Obj. (${\mathit{A}}_2$)
	[s]	[s]
250	106.790	77.074	1346.136	1394.286
500	106.373	82.503	2566.401	2658.568
750	106.558	86.462	3773.918	3904.967
1000	106.920	89.851	5237.148	5398.805

and Figure 10 compare the average $T_{average}^{stock}$ and objective functions for two different approaches, $A_1$ and $A_2$, across four different sub-cases (250, 500, 750, 1000 number of units loads incoming). The results clearly indicate that the average $T_{average}^{stock}$ increases in parallel with the increasing number of unit loads in approach $A_2$, as expected, while this effect is less evident in approach $A_1$. This is due to the position of the barycentre that presents the same behavior of the scenario S1 (see

Table 7. Coordinates of barycentre $(x_{bar},y_{bar},z_{bar})$ for each sub-case within S3 and for $A_1$ and $A_2$.

Case	$({\mathit{x}}_{\mathit{bar}},{\mathit{y}}_{\mathit{bar}},{\mathit{z}}_{\mathit{bar}})$ (${\mathit{A}}_1$)	$({\mathit{x}}_{\mathit{bar}},{\mathit{y}}_{\mathit{bar}},{\mathit{z}}_{\mathit{bar}})$ (${\mathit{A}}_2$)
	[m]	[m]
250	(33.214, 14.457, 3.240)	(12.803, 9.713, 0.588)
500	(33.770, 14.467, 3.096)	(16.136, 10.273, 1.038)
750	(34.589, 14.843, 2.992)	(18.998, 11.756, 1.392)
1000	(34.757, 14.674, 3.060)	(21.751, 12.008, 1.679)

). Similarly to $S_2$, $A_1$ maintains an average gap of 3.43 % compared to $A_2$ between objective functions.

4.3. Results Comparison

The analysis conducted under S1, S2, and S3 highlights the trade-off between temperature-aware optimization and cycle-time efficiency in refrigerated warehouse operations. The results show that $A_1$, which prioritizes environmental conditions (temperature and humidity), consistently leads to higher average storage cycle times compared to $A_2$, which minimizes handling time.

• Temporal stability across scenarios.$A_1$ maintains highly stable values of average stock duration $T_{\mathrm{stock}}$ around 106 s, regardless of changes in fill rate (S1) or the number of units (S2 and S3). In contrast, $A_2$ exhibits a more marked increase in average storage time, especially when moving from 250 to 1000 units, both in S2 and S3, from around 77s to around 89s.
• Objective function gap trend. The average gap between $A_1$ and $A_2$ in terms of objective function remains relatively constant, ranging from approximately 3.33% in S1 to 3.49% in S2 and 3.43% in S3. This highlights the robustness of the environmentally driven approach $A_1$ across different operational configurations.
• Spatial behavior and barycentre patterns. Despite its higher cycle time, $A_1$ ensures improved product preservation by assigning unit loads to cooler and more stable storage zones, as demonstrated by the barycentre coordinates. $A_1$ placements are more centralized and higher along the z-axis, leveraging stratified cooler air, while $A_2$ tends to cluster goods near the entrance, exposing them to potential thermal fluctuations due to frequent door openings.
• Operational trade-offs between scenarios. While increasing fill rate in S1 leads to moderate increases in average storage time, in S2 and S3, the impact of increasing the number of unit loads is more pronounced, especially under $A_2$. This highlights how the robustness of $A_1$ ensures better environmental consistency, whereas $A_2$ favors reduced cycle time at the cost of greater environmental exposure.
• Managerial implications. For operations involving increasing fill levels (S1), $A_1$ appears more suitable due to its consistent environmental performance even under congestion. In contrast, under variable workload conditions (S2 and S3), $A_2$ provides faster turnover, but may require additional monitoring to control thermal risks.

These findings validate the proposed optimization model’s ability to integrate environmental metrics into storage decisions, showing that even a moderate sacrifice in operational speed can significantly enhance quality control for perishable goods. Note that comparing the results of the proposed model with those of similar studies is not straightforward, as warehouse optimization problems are typically tailored to specific layouts, operational constraints, and product characteristics. Moreover, unlike class-based strategies, which depend on SKU popularity or order profiles, the proposed model assigns unit loads dynamically based on environmental fit; while this logic is orthogonal to demand-driven policies, the two could be integrated in future hybrid models to optimize both quality and efficiency.

4.4. Sensitive Analysis on Parameter $\beta$

In the proposed model, the $\beta$ parameter plays a crucial role in balancing the influence of temperature and humidity within the distance metric used for storage location assignment (see Equation (3)). To assess the impact of this parameter, a sensitivity analysis was carried out under a fixed warehouse fill rate of 40% with 625 stocking units incoming, testing $\beta$ values ranging from 0.0 (full priority to temperature) to 1 (full priority tu humidity).

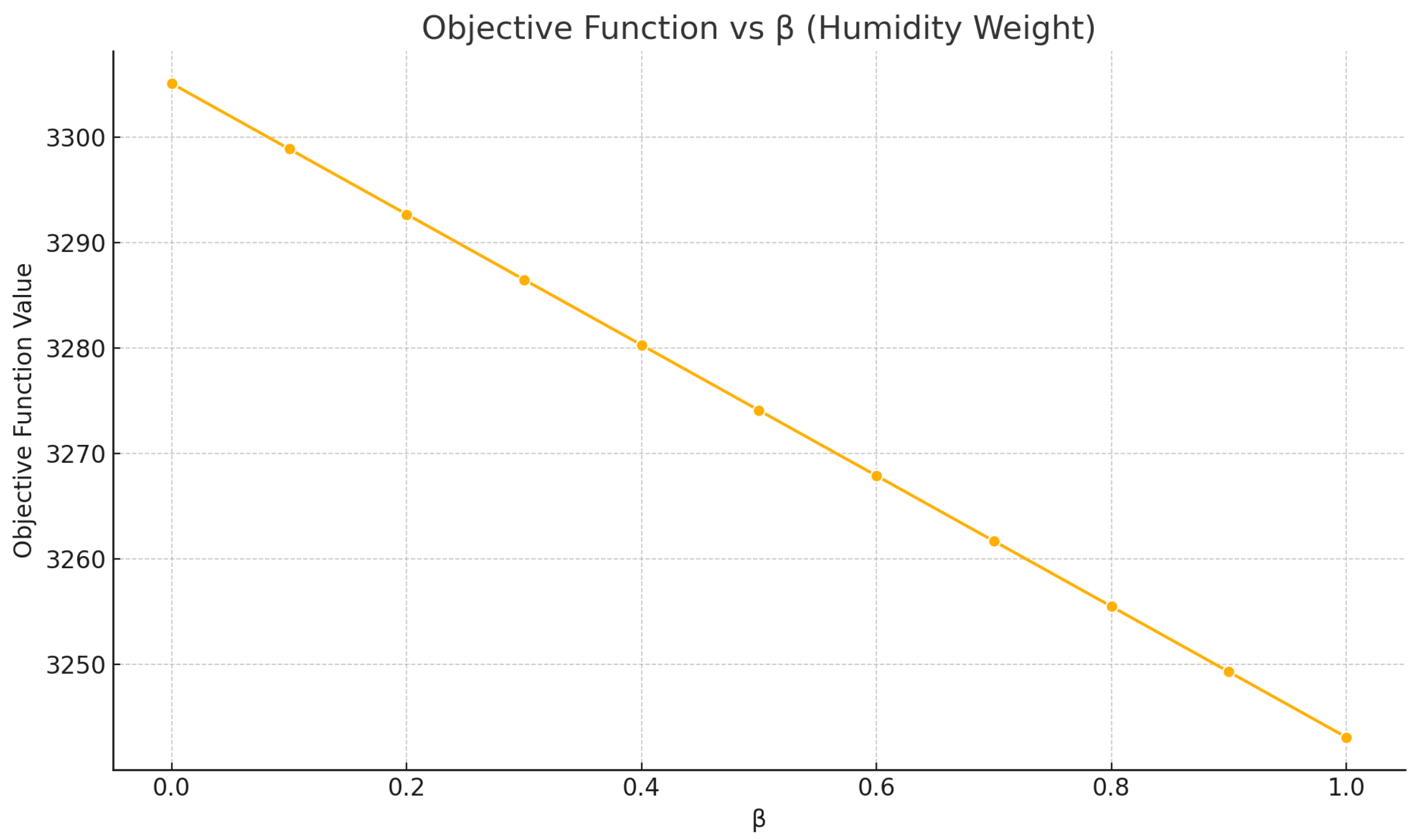
Environmental Impact. As shown in Figure 11, the objective function—representing the combined thermal and humidity stress—decreases monotonically as $\beta$ increases. This behavior is consistent with expectations: assigning greater importance to humidity leads the model to prioritize locations that better match the target humidity level, thus lowering the overall environmental penalty. This confirms that $\beta$ acts as a tunable lever for environmental compliance, allowing warehouse managers to calibrate the model according to the nature of stored products (e.g., those particularly sensitive to humidity).

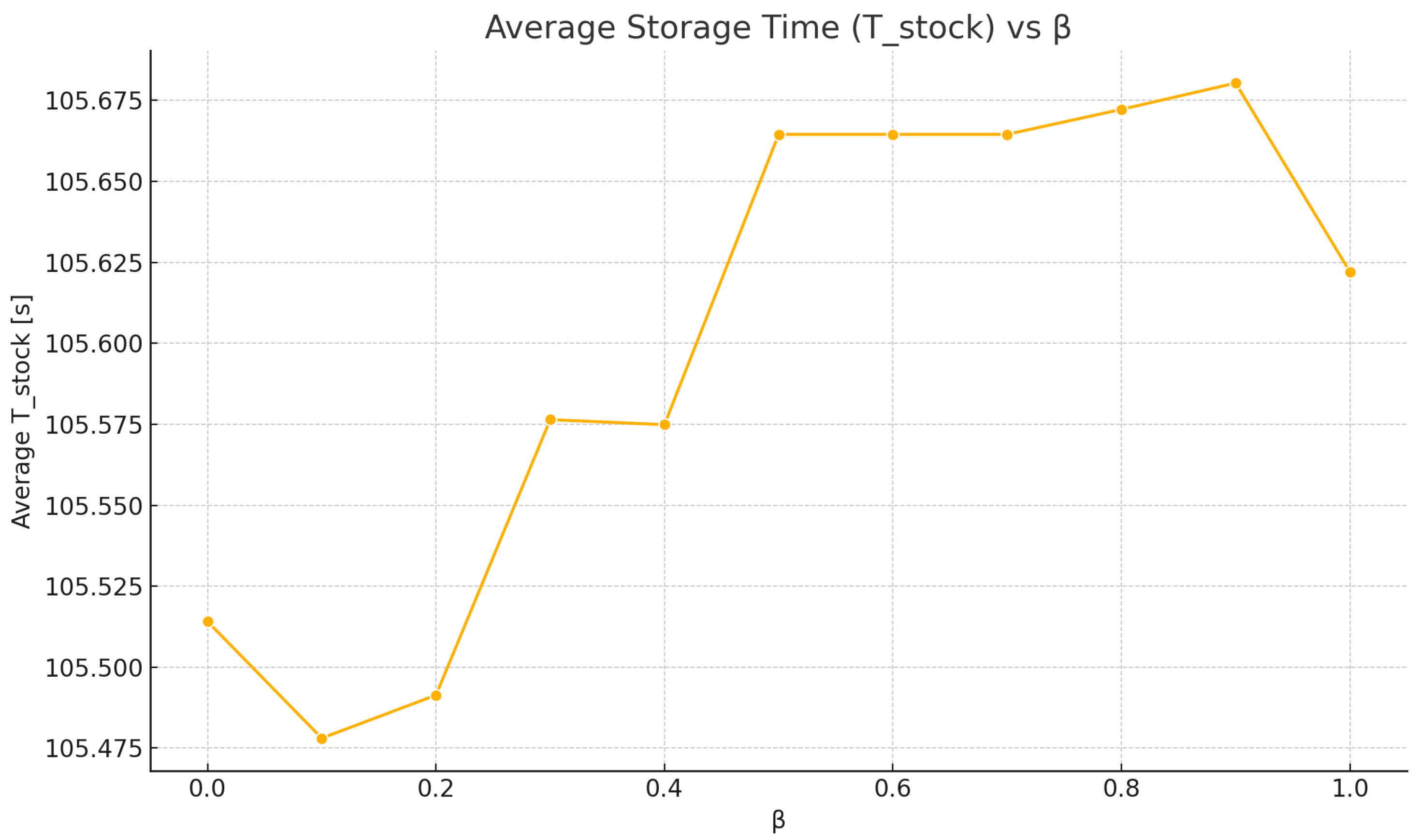
Operational Performance. Interestingly, as depicted in Figure 12, the average storage cycle time ($T_{\mathrm{stock}}$) remains nearly constant across all tested values of $\beta$, with variations limited to a few tenths of a second. This suggests that humidity control improvements in environmental conditions do not significantly compromise operational efficiency. In practical terms, the model is capable of improving environmental stability without elongating storage operations—a desirable feature in time-sensitive cold chains. Moreover, a sort of stability in the average storage time is reached around the value $\beta =0.6$.

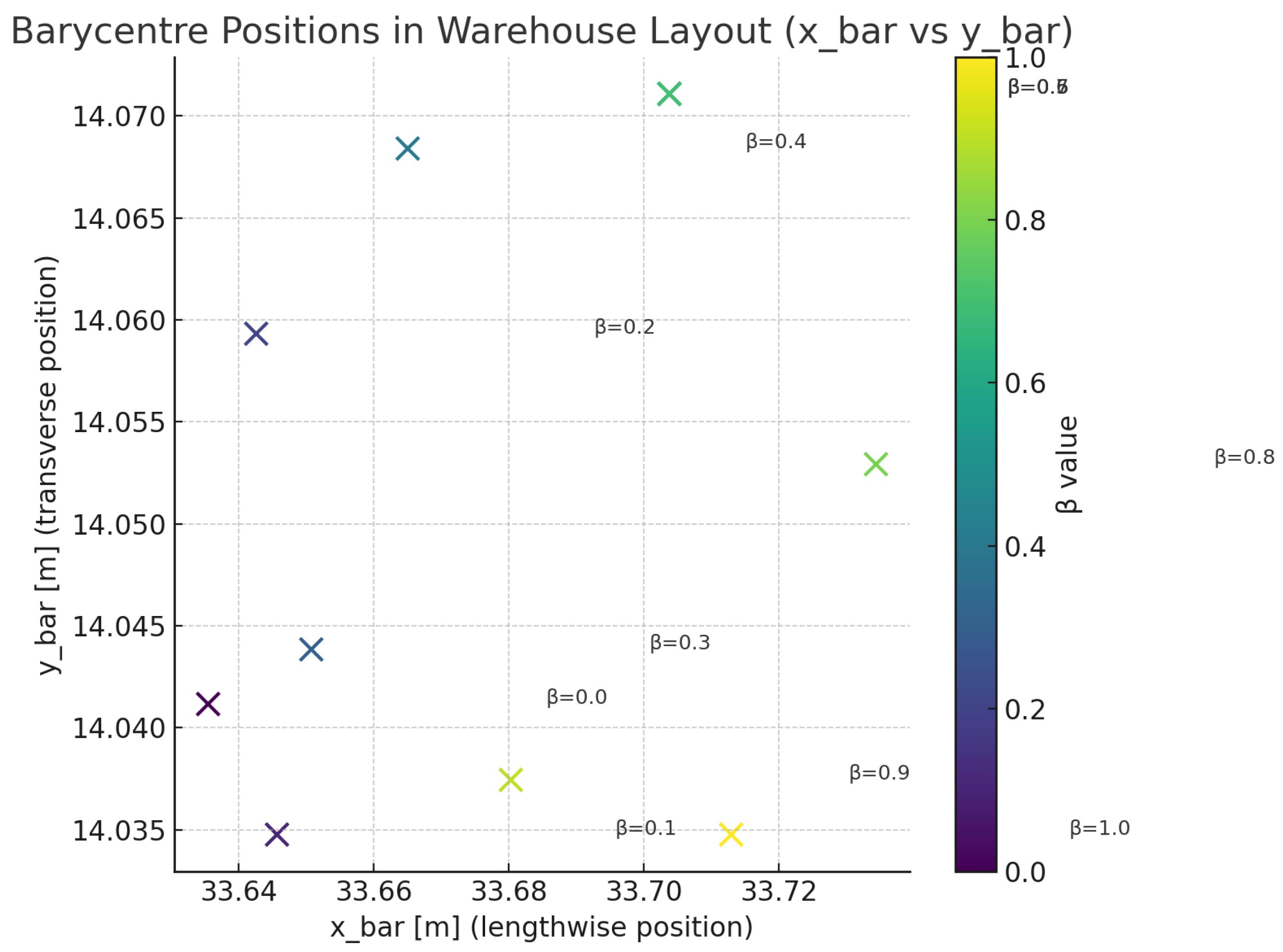
Spatial Allocation Stability. A deeper insight into the spatial behavior of the model is offered by the barycentre analysis.

Table 8. Barycentre coordinates $(x_{\mathrm{bar}},y_{\mathrm{bar}},z_{\mathrm{bar}})$ for different $\beta$ values.

$\mathit{\beta }$	$({\mathit{x}}_{\mathbf{bar}},{\mathit{y}}_{\mathbf{bar}},{\mathit{z}}_{\mathbf{bar}})$ [m]
0.0	(33.635, 14.041, 3.000)
0.1	(33.646, 14.035, 2.993)
0.2	(33.643, 14.059, 2.993)
0.3	(33.651, 14.044, 3.010)
0.4	(33.665, 14.068, 3.005)
0.5	(33.704, 14.071, 3.017)
0.6	(33.704, 14.071, 3.017)
0.7	(33.704, 14.071, 3.017)
0.8	(33.734, 14.053, 3.017)
0.9	(33.680, 14.037, 3.026)
1	(33.713, 14.035, 3.012)

reports the coordinates $(x_{\mathrm{bar}},y_{\mathrm{bar}},z_{\mathrm{bar}})$ associated with the unit load allocations under different $\beta$ settings.

• The vertical coordinate $z_{\mathrm{bar}}$ remains consistently close to level 3, indicating that the model favors mid-to-high vertical zones, which tend to be more thermally stable due to stratification effects.
• The horizontal coordinates $x_{\mathrm{bar}}$ (lengthwise) and $y_{\mathrm{bar}}$ (transverse) exhibit only slight fluctuations. This implies that the distribution of stored units does not shift significantly along the warehouse plane, preserving the overall layout balance.

Figure 13 illustrates this behavior in a 2D scatterplot, showing the barycentre positions for each tested $\beta$ value. The compactness and coherence of the points confirm the robustness of the model: changes in the humidity weight do not induce erratic shifts or concentration in thermally unfavorable zones (e.g., near entrances or high-disturbance aisles).

Managerial Implications. These findings highlight the practical usability of $\beta$ as a control parameter for warehouse managers. It enables scenario-specific calibration without compromising the model’s efficiency or distorting its spatial logic. For instance, in regulatory contexts where humidity thresholds are critical, increasing $\beta$ could improve compliance without requiring structural reconfiguration or operational slowdown.

The model’s ability to maintain both thermal humidity compliance and operational stability under varying $\beta$ settings enhances its value as a decision-support tool, particularly in the context of sustainable and intelligent cold chain logistics.

5. Conclusions and Future Works

Theoretical Contributions and Novelty. This work introduces an original optimization framework for the storage location assignment problem (SLAP) in refrigerated warehouses, where thermal and humidity conditions are explicitly integrated into the decision-making process. In contrast to the majority of existing models—typically oriented toward minimizing travel distance, labor cost, or maximizing retrieval efficiency—our approach focuses on the minimization of environmental stress during the storage phase. This shift represents a conceptual advancement in the modelling of cold chain logistics, addressing an underexplored yet operationally relevant dimension: spatial microclimatic variability.From a theoretical standpoint, the model contributes to the literature in multiple ways. First, it proposes a spatial distance metric that simultaneously accounts for temperature deviation and humidity mismatch, encapsulated through a weighted function governed by the parameter $\beta$. Second, it embeds this logic within a mixed-integer linear programming (MILP) structure adapted to a rolling horizon implementation, allowing for dynamic allocation of incoming unit loads. The formulation remains tractable, even for large-scale warehouse instances (up to 5000 storage locations), thus offering a mathematically rigorous yet computationally viable solution for real-world applications.

Managerial and Operational Implications. Beyond its formal structure, the proposed model holds important implications for cold storage operations. By optimizing for environmental compatibility rather than for spatial proximity alone, it enables more intelligent allocation strategies that can reduce thermal shocks, preserve product quality, and mitigate the risk of regulatory non-compliance—particularly relevant in frozen or highly sensitive environments.

Simulation results show that prioritizing environmental metrics (A1) leads to a moderate increase in storage cycle time, but achieves significant improvements in terms of exposure to thermal and humidity deviations. Conversely, minimizing storage time (Approach A2) may compromise product safety due to placement in climatically unstable areas. These findings provide warehouse managers with a transparent understanding of the trade-offs involved in different policy choices. Furthermore, the analysis of baricentric shifts, fill rate evolution, and thermal stress distribution confirms the robustness of the model under a range of operational conditions.

Limitations and Model Assumptions. We acknowledge that the current version of the model includes some simplifying assumptions. Notably, it does not account for product-specific expiration dates or retrieval sequencing policies such as FIFO/FEFO. Moreover, it assumes uniform probabilities of location release, and does not incorporate demand class information, item correlations, or affinity-based zoning.

These exclusions were deliberate, allowing us to isolate the effect of environmental control and maintain model transparency. However, they also represent natural boundaries of the present formulation. The warehouse layout under study, featuring selective racking, provides a neutral infrastructure that supports such assumptions without introducing structural bias. Still, expanding the model to include more complex rotation rules or correlated storage strategies would require a redefinition of the constraint system and objective prioritization, which remains a promising direction for future work.

Future Research Directions. Several meaningful extensions are currently under consideration. First, the integration of expiration date logic and perishable inventory rotation (e.g., FIFO/FEFO) would enhance the model’s applicability to fresh and short-shelf-life products. This would entail introducing time-stamped unit loads and additional constraints on retrieval accessibility. Second, the model may be extended to support a formal multi-objective framework, combining environmental, temporal, and economic criteria. Scalarization techniques or adaptive objective switching could then be used to reflect dynamic operational priorities.

Another promising avenue is the personalization of the $\beta$ parameter through data-driven or expert-informed calibration. In this study, $\beta =0.6$ was selected based on preliminary sensitivity analysis tailored to a frozen storage range (−26 °C to −21 °C), where temperature fluctuations are more critical than humidity variations. However, in other contexts (e.g., pharmaceutical storage, fresh produce), humidity may play a more dominant role. Future developments may include machine learning or reinforcement learning methods to dynamically adjust $\beta$ based on spoilage data, product typology, or real-time sensor feedback.

Finally, coupling the optimization model with Internet of Things (IoT) systems and predictive environmental mapping tools could unlock further potential for anticipatory decision-making. Indeed, the current implementation of the model assumes a uniform probability of availability for storage locations (${\gamma }_{it}$), which may not fully reflect real-world retrieval dynamics. In practice, access frequency varies significantly across SKUs based on demand patterns, shelf-life, or service level agreements. Future developments should consider integrating a stochastic retrieval component, where parameter ${\gamma }_{it}$ is determined by product-specific turnover rates or probabilistic models derived from historical data. This would enable warehouse control systems to proactively adjust storage policies based on incoming load profiles and evolving microclimatic patterns, aligning with the broader vision of intelligent and sustainable logistics.