Ensemble Learning and SHAP Interpretation for Predicting Tensile Strength and Elastic Modulus of Basalt Fibers Based on Chemical Composition
Abstract
1. Introduction
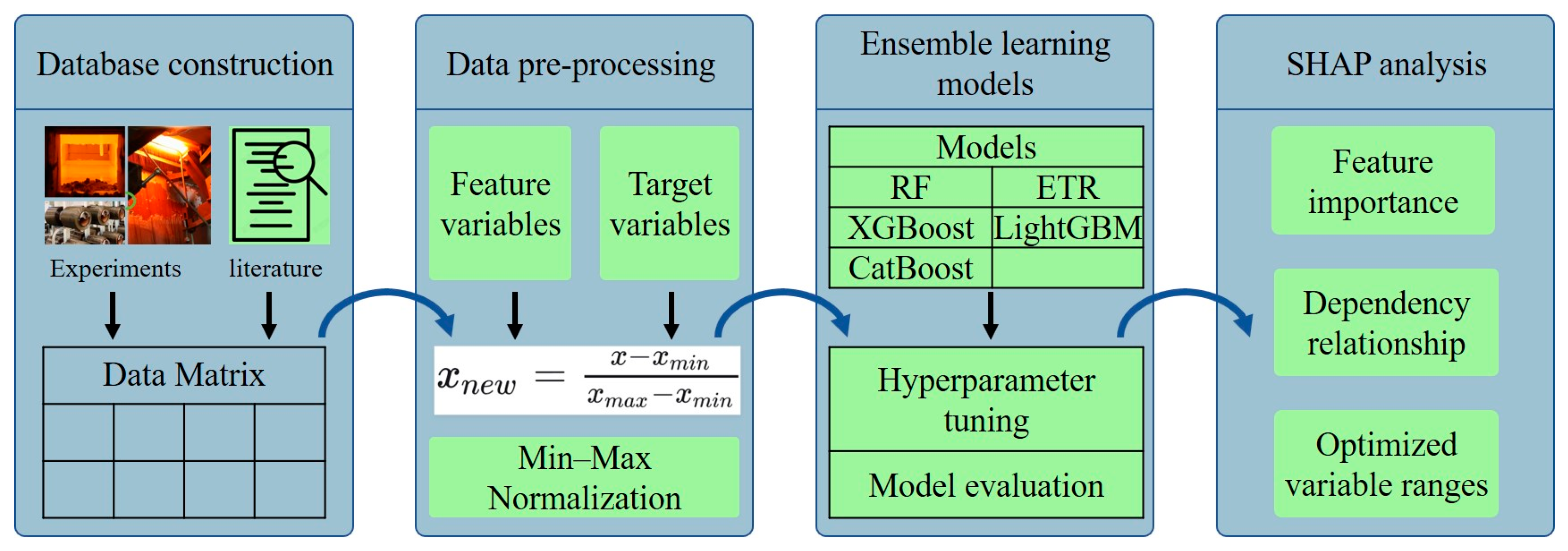
2. Materials and Methods
2.1. Database Construction
2.2. Data Preprocessing
2.3. Ensemble Learning Models
2.3.1. RF
2.3.2. ETR
2.3.3. XGBoost
2.3.4. LightGBM
2.3.5. CAT Boost
2.4. Hyperparameter Tuning and Model Evaluation
2.5. SHAP Analysis
3. Results and Discussion
3.1. Data Description
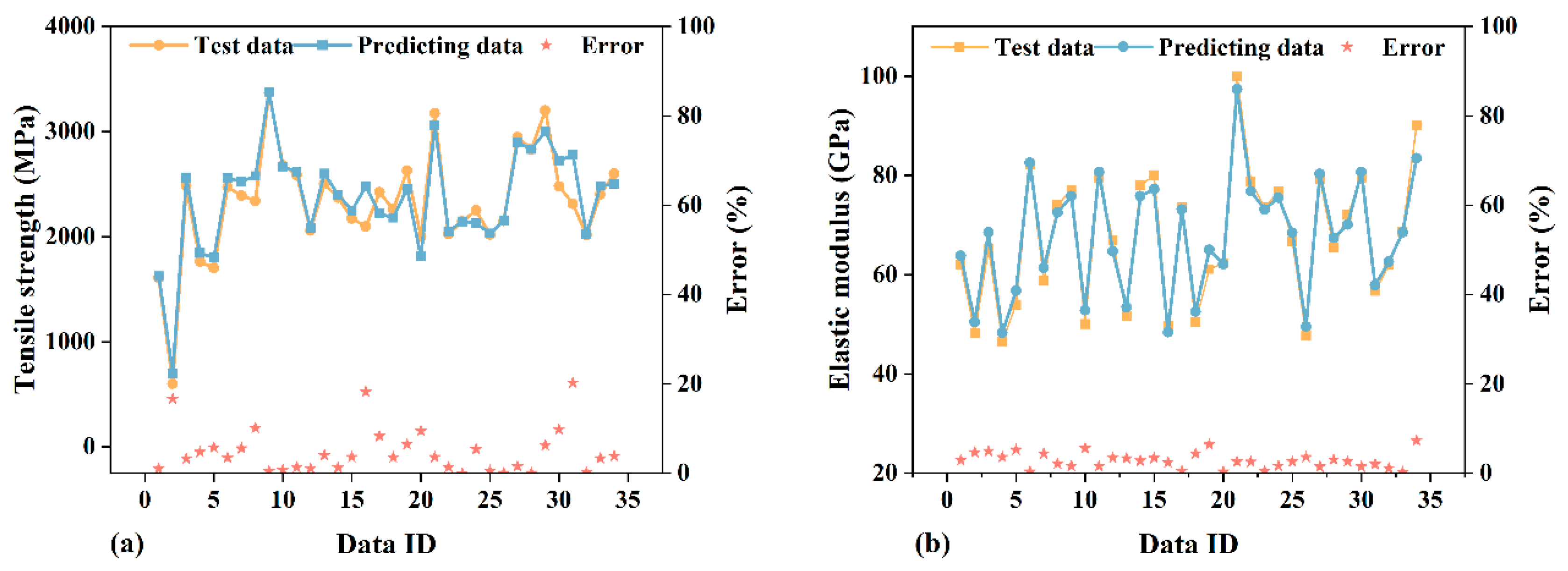
3.2. The Performance of Ensemble Learning Models
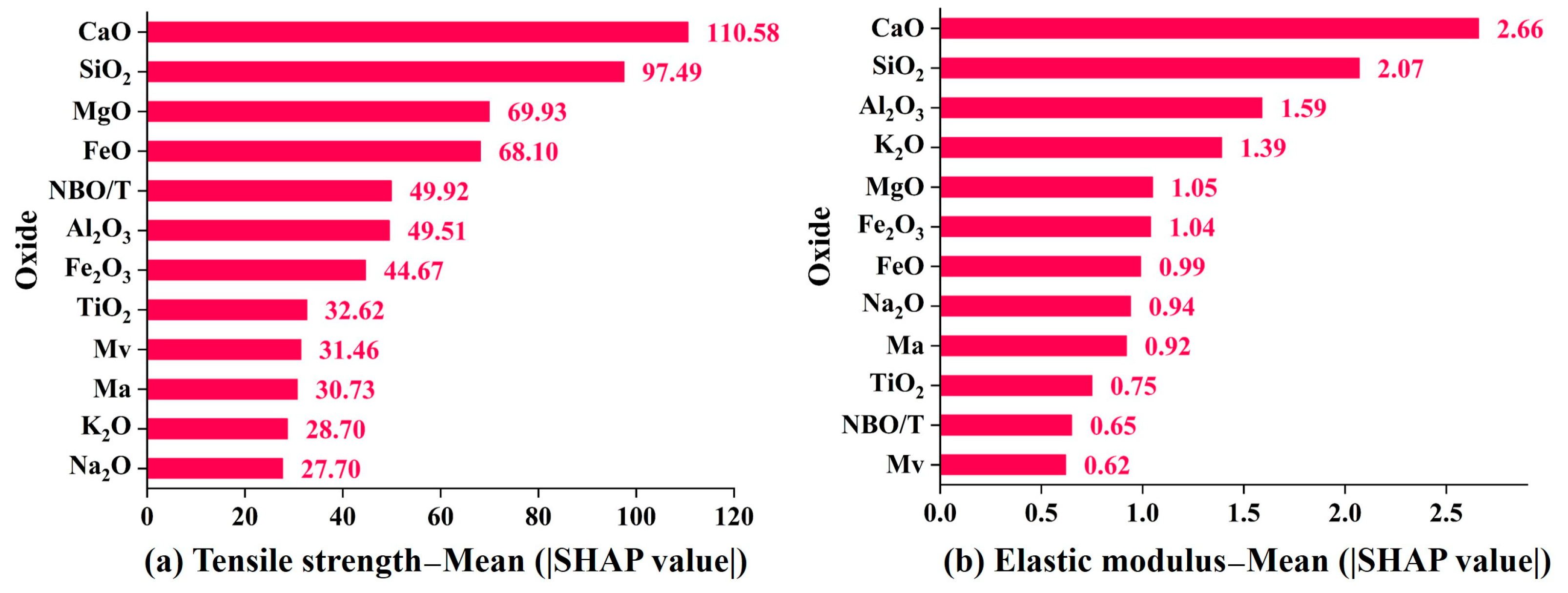
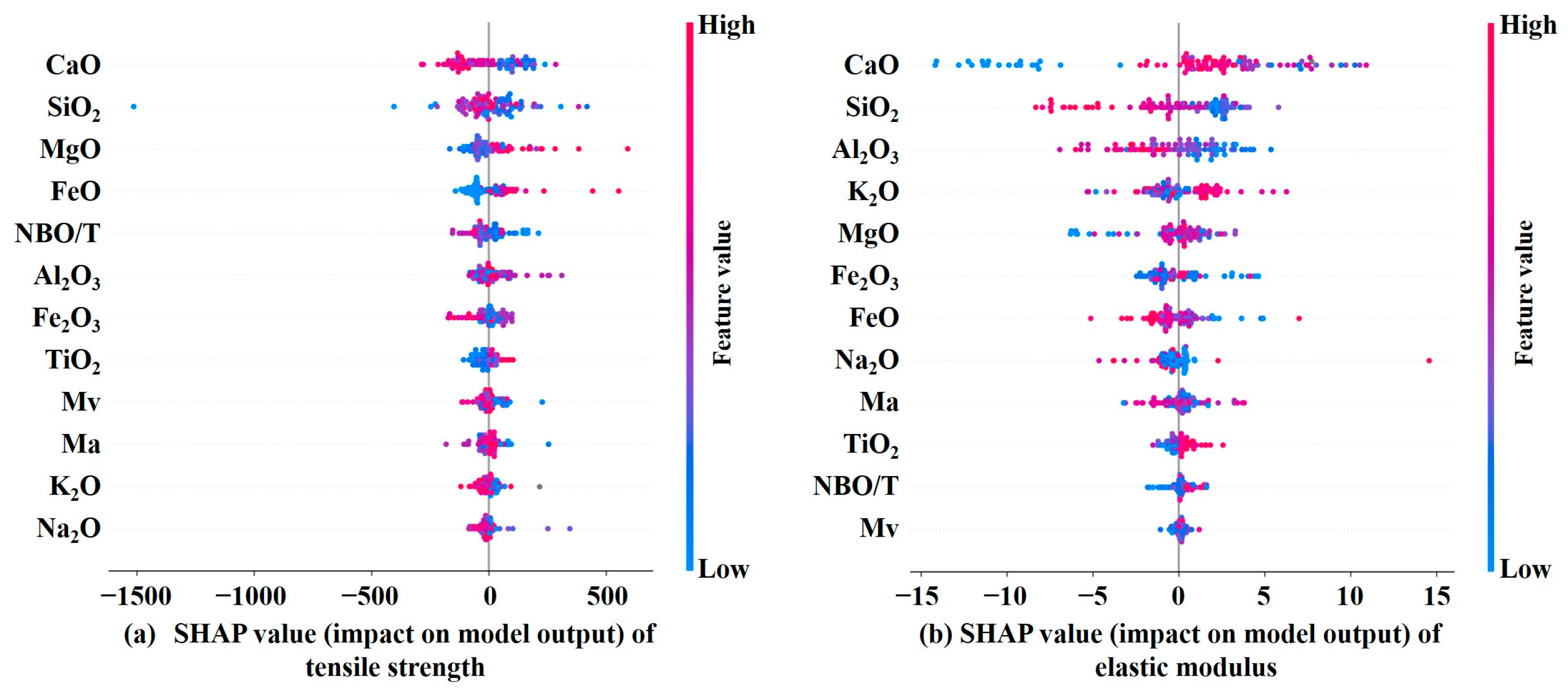
3.3. Feature Importance Measured by SHAP Analysis
3.4. Optimal Oxide Ranges for Predicting the Tensile Strength and Possible Mechanism
3.5. Optimal Oxide Ranges for Predicting the Elastic Modulus and Possible Mechanism
3.6. Limitations and Future Directions
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Deák, T.; Czigány, T. Chemical Composition and Mechanical Properties of Basalt and Glass Fibers: A Comparison. Text. Res. J. 2009, 79, 645–651. [Google Scholar] [CrossRef]
- Girnis, A.V. Partition of Trace Elements between Minerals and Melt: Parameterization of Experimental Data on Olivine, Pyroxene, and Feldspars. Geochem. Int. 2024, 62, 221–233. [Google Scholar] [CrossRef]
- Khater, G.A.; Gomaa, M.M.; Kang, J.; Mahmoud, M.A. Effect of CaO/SiO2 molar ratio on the electrical and physical properties of basaltic glass materials. Heliyon 2019, 5, e01248. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Yang, J.; Chen, M.; Lei, L.; Wu, Z. Effect of SiO2, Al2O3 on heat resistance of basalt fiber. Thermochim. Acta 2018, 660, 56–60. [Google Scholar] [CrossRef]
- Soares, B.; Preto, R.; Sousa, L.; Reis, L. Mechanical behavior of basalt fibers in a basalt-UP composite. Procedia Struct. Integr. 2016, 1, 82–89. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, L.; Lai, C.; Fu, D.; Lin, J.; Hou, H.; Zhao, Y.; Zhang, Z.; Bu, C.; Zheng, X. Prediction of tensile strength of basalt continuous fiber from chemical composition using machine learning models. Polym. Compos. 2023, 44, 6634–6645. [Google Scholar] [CrossRef]
- Yan, L.; Chu, F.; Tuo, W.; Zhao, X.; Wang, Y.; Zhang, P.; Gao, Y. Review of research on basalt fibers and basalt fiber-reinforced composites in China (I): Physicochemical and mechanical properties. Polym. Polym. Compos. 2021, 29, 1612–1624. [Google Scholar] [CrossRef]
- Adesina, A. Performance of cementitious composites reinforced with chopped basalt fibres—An overview. Constr. Build. Mater. 2021, 266, 120970. [Google Scholar] [CrossRef]
- Balaji, K.V.; Shirvanimoghaddam, K.; Rajan, G.S.; Ellis, A.V.; Naebe, M. Surface treatment of Basalt fiber for use in automotive composites. Mater. Today Chem. 2020, 17, 100334. [Google Scholar] [CrossRef]
- Ding, C.; Xue, K.; Yi, G. Research on fire resistance and economy of basalt fiber insulation mortar. Sci. Rep. 2023, 13, 17288. [Google Scholar] [CrossRef]
- Bhat, T.; Chevali, V.; Liu, X.; Feih, S.; Mouritz, A.P. Fire structural resistance of basalt fibre composite. Compos. Part A-Appl. Sci. Manuf. 2015, 71, 107–115. [Google Scholar] [CrossRef]
- Jagadeesh, P.; Rangappa, S.M.; Siengchin, S. Basalt fibers: An environmentally acceptable and sustainable green material for polymer composites. Constr. Build. Mater. 2024, 436, 136834. [Google Scholar] [CrossRef]
- Fiore, V.; Scalici, T.; Di Bella, G.; Valenza, A. A review on basalt fibre and its composites. Compos. Part B Eng. 2015, 74, 74–94. [Google Scholar] [CrossRef]
- Moiseev, E.A.; Gutnikov, S.I.; Malakho, A.P.; Lazoryak, B.I. Effect of iron oxides on the fabrication and properties of continuous glass fibers. Inorg. Mater. 2008, 44, 1026–1030. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, Y.; Huo, H.; Wu, Z. Improving the tensile strength of continuous basalt fiber by mixing basalts. Fibers Polym. 2017, 18, 1796–1803. [Google Scholar] [CrossRef]
- Gutnikov, S.I.; Malakho, A.P.; Lazoryak, B.I.; Loginov, V.S. Influence of alumina on the properties of continuous basalt fibers. Russ. J. Inorg. Chem. 2009, 54, 191–196. [Google Scholar] [CrossRef]
- Farouk, M.; Soltan, A.; Schlüter, S.; Hamzawy, E.; Farrag, A.; El-Kammar, A.; Yahya, A.; Pollmann, H. Optimization of microstructure of basalt-based fibers intended for improved thermal and acoustic insulations. J. Build. Eng. 2021, 34, 101904. [Google Scholar] [CrossRef]
- Si, J.; Wang, Z.; Li, J.; Zuo, C.; Zhang, P.; Wei, C.; Wang, J.; Li, W.; Miao, S. Effects of CaO added to raw basalt on producing continuous basalt fibers and their mechanical properties. J. Non-Cryst. Solids 2021, 568, 120941. [Google Scholar] [CrossRef]
- Meng, Y.; Liu, J.; Xia, Y.; Liang, W.; Ran, Q.; Xie, Z. Preparation and characterization of continuous basalt fibre with high tensile strength. Ceram. Int. 2021, 47, 12410–12415. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, Y.; Huo, H.; Wu, Z. Study of high tensile strength of natural continuous basalt fibers. J. Nat. Fibers 2020, 17, 214–222. [Google Scholar] [CrossRef]
- Gutnikov, S.I.; Manylov, M.S.; Lipatov, Y.V.; Lazoryak, B.I.; Pokholok, K.V. Effect of the reduction treatment on the basalt continuous fiber crystallization properties. J. Non-Cryst. Solids 2013, 368, 45–50. [Google Scholar] [CrossRef]
- Manylov, M.S.; Gutnikov, S.I.; Lipatov, Y.V.; Malakho, A.P.; Lazoryak, B.I. Effect of deferrization on continuous basalt fiber properties. Mendeleev Commun. 2015, 25, 386–388. [Google Scholar] [CrossRef]
- Xing, D.; Xi, X.Y.; Ma, P.C. Factors governing the tensile strength of basalt fibre. Compos. Part A-Appl. Sci. Manuf. 2019, 119, 127–133. [Google Scholar] [CrossRef]
- Wu, Y. From ensemble learning to deep ensemble learning: A case study on multi-indicator prediction of pavement performance. Appl. Soft Comput. J. 2024, 166, 112188. [Google Scholar] [CrossRef]
- Dong, X.; Yu, Z.; Cao, W.; Shi, Y.; Ma, Q. A survey on ensemble learning. Front. Comput. Sci. 2020, 14, 241–258. [Google Scholar] [CrossRef]
- Maleki, S.; Karimi-Jashni, A.; Mousavifard, M. Removal of Ni(II) ions from wastewater by ion exchange resin: Process optimization using response surface methodology and ensemble machine learning techniques. J. Environ. Chem. Eng. 2024, 12, 112417. [Google Scholar] [CrossRef]
- Almohammed, F.; Thakur, M.S.; Lee, D.; Kumar, R.; Singh, T. Flexural and split tensile strength of concrete with basalt fiber: An experimental and computational analysis. Constr. Build. Mater. 2024, 414, 134936. [Google Scholar] [CrossRef]
- Qiao, L.; Miao, P.; Xing, G.; Luo, X.; Ma, J.; Farooq, M.A. Interpretable machine learning model for predicting freeze-thaw damage of dune sand and fiber reinforced concrete. Case Stud. Constr. Mater. 2023, 19, e02453. [Google Scholar] [CrossRef]
- Cakiroglu, C.; Shahjalal, M.; Islam, K.; Mahmood, S.M.F.; Billah, A.H.M.M.; Nehdi, M.L. Explainable ensemble learning data-driven modeling of mechanical properties of fiber-reinforced rubberized recycled aggregate concrete. J. Build. Eng. 2023, 76, 107279. [Google Scholar] [CrossRef]
- Machello, C.; Aghabalaei Baghaei, K.; Bazli, M.; Hadigheh, A.; Rajabipour, A.; Arashpour, M.; Mahdizadeh Rad, H.; Hassanli, R. Tree-based machine learning approach to modelling tensile strength retention of Fibre Reinforced Polymer composites exposed to elevated temperatures. Compos. B Eng. 2024, 270, 111132. [Google Scholar] [CrossRef]
- Ding, L.; Liu, Y.; Liu, J.; Wang, X. Correlation analysis of tensile strength and chemical composition of basalt fiber roving. Polym. Compos. 2019, 40, 2959–2966. [Google Scholar] [CrossRef]
- Eduard, K.; Rainer, G.; Jona, S. Basalt, glass and carbon fibers and their fiber reinforced polymer composites under thermal and mechanical load. AIMS Mater. Sci. 2016, 3, 1561–1576. [Google Scholar] [CrossRef]
- Wei, B.; Cao, H.; Song, S. Tensile behavior contrast of basalt and glass fibers after chemical treatment. Mater. Design. 2010, 31, 4244–4250. [Google Scholar] [CrossRef]
- Sergey, I.G.; Evgeniya, S.Z.; Sergey, S.P.; Bogdan, I.L. Correlation of the chemical composition, structure and mechanical properties of basalt continuous fibers. AIMS Mater. Sci. 2019, 6, 806–820. [Google Scholar] [CrossRef]
- Wang, L. Study on Effect of Basalt Fiber Component on Elastic Modulus. Master’s Thesis, Southeast University, Nanjing, China, 2021. [Google Scholar] [CrossRef]
- Kuzmin, K.L.; Gutnikov, S.I.; Zhukovskaya, E.S.; Lazoryak, B.I. Basaltic glass fibers with advanced mechanical properties. J. Non-Cryst. Solids 2017, 476, 144–150. [Google Scholar] [CrossRef]
- Kuzmin, K.L.; Zhukovskaya, E.S.; Gutnikov, S.I.; Pavlov, Y.V.; Lazoryak, B.I. Effects of Ion Exchange on the Mechanical Properties of Basaltic Glass Fibers. Int. J. Appl. Glass Sci. 2016, 7, 118–127. [Google Scholar] [CrossRef]
- Wu, Z.; Liu, J.; Jiang, M.; Wang, Y.; Lei, L. A High-Temperature Resistant Basalt Fiber Composition. China Patent No. 201410139342.1, 30 July 2014. [Google Scholar]
- Wang, X.; Sun, K.; Shao, J.; Ma, J. Fracture properties of graded basalt fiber reinforced concrete: Experimental study and Mori-Tanaka method application. Constr. Build. Mater. 2023, 398, 132510. [Google Scholar] [CrossRef]
- Ramachandran, B.E.; Velpari, V.; Balasubramanian, N. Chemical durability studies on basalt fibres. J. Mater. Sci. Technol. 1981, 16, 3393–3397. [Google Scholar] [CrossRef]
- Dong, J.F.; Wang, Q.Y.; Guan, Z.W.; Chai, H.K. High-temperature behaviour of basalt fibre reinforced concrete made with recycled aggregates from earthquake waste. J. Build. Eng. 2022, 48, 103895. [Google Scholar] [CrossRef]
- Xing, D.; Chang, C.; Xi, X.Y.; Hao, B.; Zheng, Q.; Gutnikov, S.I.; Lazoryak, B.I.; Ma, P.C. Morphologies and mechanical properties of basalt fibre processed at elevated temperature. J. Non-Cryst. Solids 2022, 582, 121439. [Google Scholar] [CrossRef]
- Nasir, V.; Karimipour, H.; Taheri-Behrooz, F.; Shokrieh, M.M. Corrosion behaviour and crack formation mechanism of basalt fibre in sulphuric acid. Corros. Sci. 2012, 64, 1–7. [Google Scholar] [CrossRef]
- Li, R.; Gu, Y.; Zhang, G.; Yang, Z.; Li, M.; Zhang, Z. Radiation shielding property of structural polymer composite: Continuous basalt fiber reinforced epoxy matrix composite containing erbium oxide. Compos. Sci. Technol. 2017, 143, 67–74. [Google Scholar] [CrossRef]
- Ahmad, M.R.; Chen, B. Effect of silica fume and basalt fiber on the mechanical properties and microstructure of magnesium phosphate cement (MPC) mortar. Constr. Build. Mater. 2018, 190, 466–478. [Google Scholar] [CrossRef]
- Vejmelková, E.; Koňáková, D.; Scheinherrová, L.; Doleželová, M.; Keppert, M.; Černý, R. High temperature durability of fiber reinforced high alumina cement composites. Constr. Build. Mater. 2018, 162, 881–891. [Google Scholar] [CrossRef]
- Qin, J.; Qian, J.; Li, Z.; You, C.; Dai, X.; Yue, Y.; Fan, Y. Mechanical properties of basalt fiber reinforced magnesium phosphate cement composites. Constr. Build. Mater. 2018, 188, 946–955. [Google Scholar] [CrossRef]
- Tang, C.; Jiang, H.; Zhang, X.; Li, G.; Cui, J. Corrosion Behavior and Mechanism of Basalt Fibers in Sodium Hydroxide Solution. Mater. 2018, 11, 1381. [Google Scholar] [CrossRef]
- Li, M.; Gong, F.; Wu, Z. Study on mechanical properties of alkali-resistant basalt fiber reinforced concrete. Constr. Build. Mater. 2020, 245, 118424. [Google Scholar] [CrossRef]
- Gutnikov, S.I.; Popov, S.S.; Efremov, V.A.; Ma, P.C.; Lazoryak, B.I. Correlation of Phase Composition, Structure, and Mechanical Properties of Natural Basalt Continuous Fibers. Nat. Resour. Res. 2021, 30, 1105–1119. [Google Scholar] [CrossRef]
- Morozov, N.N.; Bakunov, V.S.; Morozov, E.N.; Aslanova, L.G.; Granovskii, P.A.; Prokshin, V.V.; Zemlyanitsyn, A.A. Materials Based on Basalts from the European North of Russia. Glass Ceram. 2001, 58, 100–104. [Google Scholar] [CrossRef]
- Khan, A.A.; Chaudhari, O.; Chandra, R. A review of ensemble learning and data augmentation models for class imbalanced problems: Combination, implementation and evaluation. Expert Syst. Appl. 2024, 244, 122778. [Google Scholar] [CrossRef]
- Bakır, R.; Orak, C.; Yüksel, A. Optimizing hydrogen evolution prediction: A unified approach using random forests, lightGBM, and Bagging Regressor ensemble model. Int. J. Hydrogen Energy 2024, 67, 101–110. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar] [CrossRef]
- Huang, X.; Liu, W.; Guo, Q.; Tan, J. Prediction method for the dynamic response of expressway lateritic soil subgrades on the basis of Bayesian optimization CatBoost. Soil Dyn. Earthq. Eng. 2024, 186, 108943. [Google Scholar] [CrossRef]
- Zhou, Z.; Cao, J.; Shi, X.; Zhang, W.; Huang, W. Probabilistic rutting model using NGBoost and SHAP: Incorporating other performance indicators. Constr. Build. Mater. 2024, 438, 137052. [Google Scholar] [CrossRef]
- Yang, F.; Wen, C.; Zhu, S.; Feng, Y.; Ye, Z.; Peng, H.; Guan, P. Machine learning model of plant fiber/PLA composite: Prediction and analysis of mechanical strength. Compos. Part Appl. Sci. Manuf. 2025, 199, 109201. [Google Scholar] [CrossRef]
- Golkarnarenji, G.; Naebe, M.; Badii, K.; Milani, A.S.; Jazar, R.N.; Khayyam, H. A machine learning case study with limited data for prediction of carbon fiber mechanical properties. Comput. Ind. 2019, 105, 123–132. [Google Scholar] [CrossRef]
- Chokshi, S.; Gohil, P.; Lalakiya, A.; Patel, P.; Parmar, A. Tensile strength prediction of natural fiber and natural fiber yarn: Strain rate variation upshot. Mater. Today Proc. 2020, 27, 1218–1223. [Google Scholar] [CrossRef]
- Wu, Z.; Liu, J.; Chen, X. The role of chemical composition in continuous basalt fibers. In Continuous Basalt Fiber Technology; Chemical Industry Press: Beijing, China, 2020; pp. 45–48. [Google Scholar]
- Cao, H.; Yan, Y.; Yue, L.; Zhao, J. Microscopic fine structure. In Basalt Fiber; National Defense Industry Press: Beijing, China, 2017; pp. 43–45. [Google Scholar]

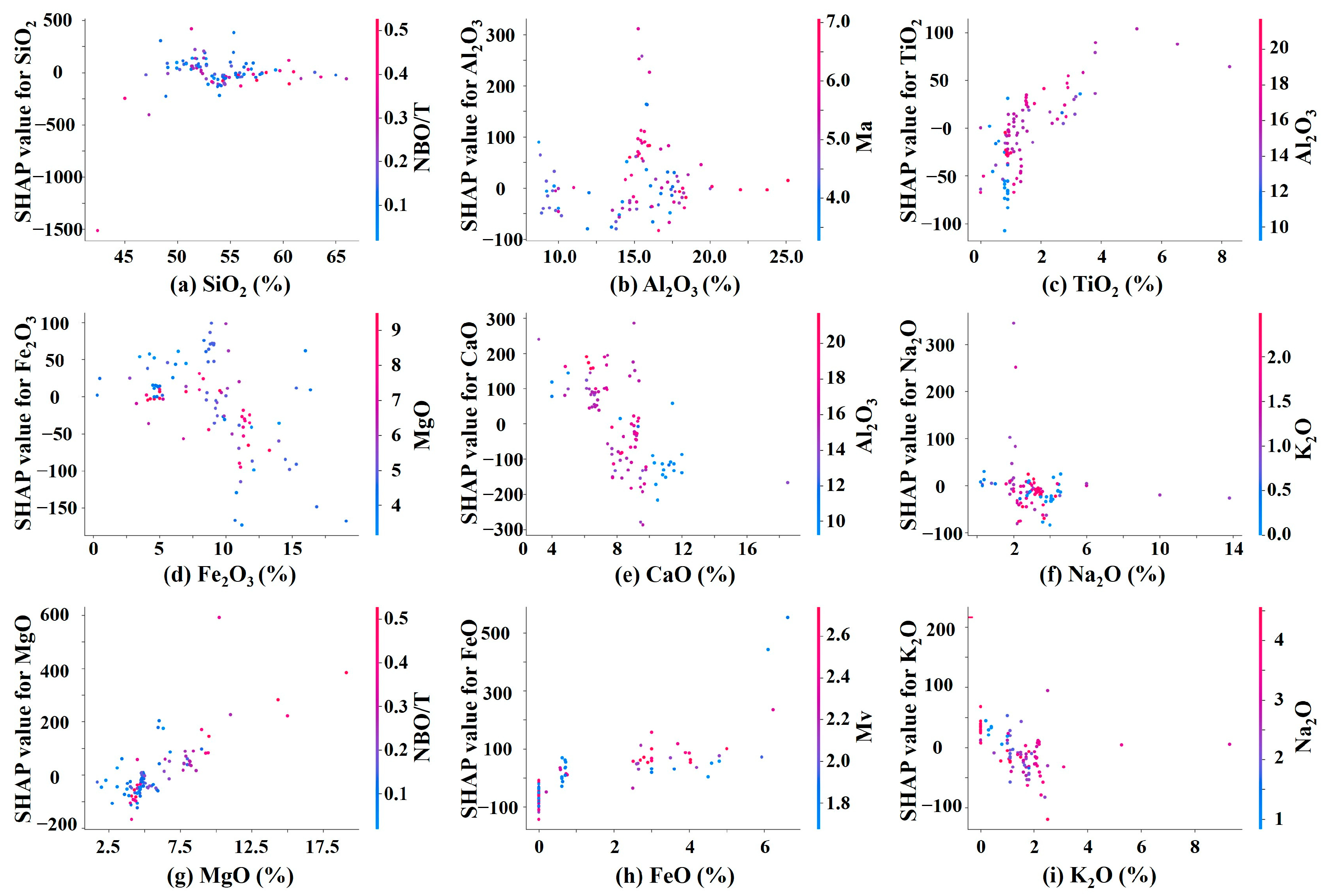
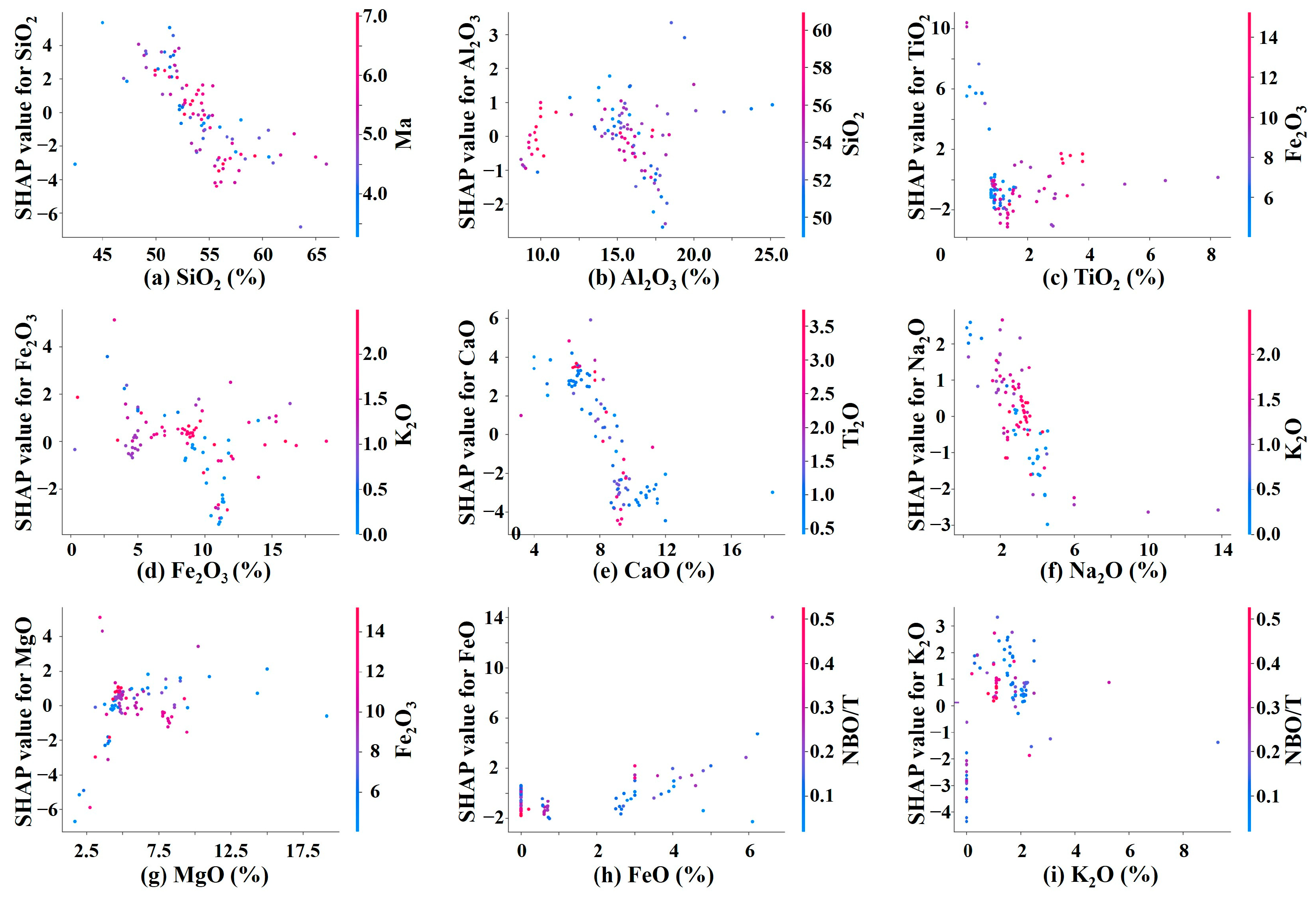
| Feature | Al2O3 | CaO | Fe2O3 | FeO | K2O | Ma | MgO | Mv | NBO/T | Na2O | SiO2 | TiO2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K-S Statistic | 0.120 | 0.117 | 0.208 | 0.120 | 0.121 | 0.126 | 0.105 | 0.160 | 0.135 | 0.113 | 0.153 | 0.093 |
| p-value | 0.779 | 0.802 | 0.164 | 0.783 | 0.775 | 0.728 | 0.889 | 0.439 | 0.655 | 0.838 | 0.490 | 0.953 |
| Model | Metrics | RF | ETR | XGBoost | LightGBM | CatBoost |
|---|---|---|---|---|---|---|
| Tensile strength prediction | R2 train | 0.8357 | 0.9964 | 0.9974 | 0.6538 | 0.9939 |
| R2 test | 0.6607 | 0.8677 | 0.9152 | 0.8596 | 0.8751 | |
| MSE train | 0.7042 | 0.0189 | 0.0145 | 1.4837 | 0.0260 | |
| MSE test | 1.9816 | 0.7424 | 0.2867 | 1.3424 | 0.5645 | |
| RMSE train | 0.8392 | 0.1375 | 0.1204 | 1.2181 | 0.1614 | |
| RMSE test | 1.4077 | 0.8616 | 0.5354 | 1.1586 | 0.7513 | |
| MAE train | 0.6728 | 0.0007 | 0.0014 | 0.9943 | 0.1283 | |
| MAE test | 1.1277 | 0.3809 | 0.6091 | 0.9676 | 0.6193 | |
| Elastic modulus prediction | R2 train | 0.8560 | 0.9974 | 0.9998 | 0.9927 | 0.9986 |
| R2 test | 0.5575 | 0.8061 | 0.9303 | 0.9664 | 0.9803 | |
| MSE train | 0.9449 | 0.7045 | 0.5260 | 0.4546 | 0.0024 | |
| MSE test | 6.5861 | 2.0246 | 0.4306 | 0.2309 | 0.1209 | |
| RMSE train | 0.9719 | 0.8390 | 0.7113 | 0.6743 | 0.0491 | |
| RMSE test | 2.5663 | 1.4229 | 0.6562 | 0.4805 | 0.3478 | |
| MAE train | 0.8163 | 0.6452 | 0.5577 | 0.4582 | 0.0384 | |
| MAE test | 1.9726 | 1.2149 | 0.5299 | 0.3782 | 0.2692 |
| Study (Year) | Material | Input Features | Output Targets | Model Type | Performance |
|---|---|---|---|---|---|
| Our work | Basalt fiber | Oxide composition | Tensile strength, elastic modulus | XGBR CatBoost | 0.92, 0.98 |
| Yang et al. ([58]) | Plant fiber/PLA composite | Grammage, PLA content, beating degree, calendering temperature, calendering pressure, fiber length, and fiber width | Tensile strength bursting strength density | Support Vector Regression (SVR), Artificial Neural Network (ANN), Decision Tree GBR | (R2 = 0.90, RMSE = 0.44), (R2 = 0.91, RMSE = 4.56), (R2 = 0.92, RMSE = 0.06) |
| Golkarnarenji et al. ([59]) | Carbon fiber | Cyclization, dehydrogenation, and oxidation | Tensile strength, Young’s modulus | ANN-LMA | Average error of less than ± 3.7%, less than ± 2.4% |
| Chokshi et al. ([60]) | Natural bamboo fiber | Strain rate | Tensile strength | Polynomial model | 0.80 |
| % | SiO2 | Al2O3 | TiO2 | Fe2O3 | CaO | Na2O | MgO | FeO | K2O |
|---|---|---|---|---|---|---|---|---|---|
| Tensile strength | [48.39, 63.00] | [8.70, 25.13] | [0, 8.26] | [0.30, 16.37] | [3.20, 11.41] | [0.20, 6.00] | [3.10, 15.00] | [0.57, 6.62] | [0, 9.30] |
| Elastic modulus | [45.01, 55.34] | [9.28, 25.13] | [0.11, 10.38] | [0.50, 10.96] | [3.20, 9.05] | [0.20, 3.20] | [3.42, 15.00] | [0, 6.62] | [0.20, 5.27] |
| Ma | Mv | NBO/T | |||||||
| Tensile strength | [2.15, 8.56] | [1.32, 3.34] | [0.02, 0.37] | ||||||
| Elastic modulus | [3.80, 8.56] | [1.39, 3.34] | [0.02, 0.36] | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Zheng, L.; Long, P.; Yang, L.; Zhang, L. Ensemble Learning and SHAP Interpretation for Predicting Tensile Strength and Elastic Modulus of Basalt Fibers Based on Chemical Composition. Sustainability 2025, 17, 7387. https://doi.org/10.3390/su17167387
Liu G, Zheng L, Long P, Yang L, Zhang L. Ensemble Learning and SHAP Interpretation for Predicting Tensile Strength and Elastic Modulus of Basalt Fibers Based on Chemical Composition. Sustainability. 2025; 17(16):7387. https://doi.org/10.3390/su17167387
Chicago/Turabian StyleLiu, Guolei, Lunlian Zheng, Peng Long, Lu Yang, and Ling Zhang. 2025. "Ensemble Learning and SHAP Interpretation for Predicting Tensile Strength and Elastic Modulus of Basalt Fibers Based on Chemical Composition" Sustainability 17, no. 16: 7387. https://doi.org/10.3390/su17167387
APA StyleLiu, G., Zheng, L., Long, P., Yang, L., & Zhang, L. (2025). Ensemble Learning and SHAP Interpretation for Predicting Tensile Strength and Elastic Modulus of Basalt Fibers Based on Chemical Composition. Sustainability, 17(16), 7387. https://doi.org/10.3390/su17167387







