Green Product Innovation Coordination in Aluminum Building Material Supply Chains with Innovation Capability Heterogeneity: A Biform Game-Theoretic Approach
Abstract
1. Introduction
2. Literature Review
2.1. Decision Making and Coordination of Supply Chain on Green Innovation
2.2. The Application of Biform Game in SCM
2.3. The Operational Research on Firm Heterogeneity
2.4. Statement of Our Contributions
3. Models
3.1. Assumptions and Notions
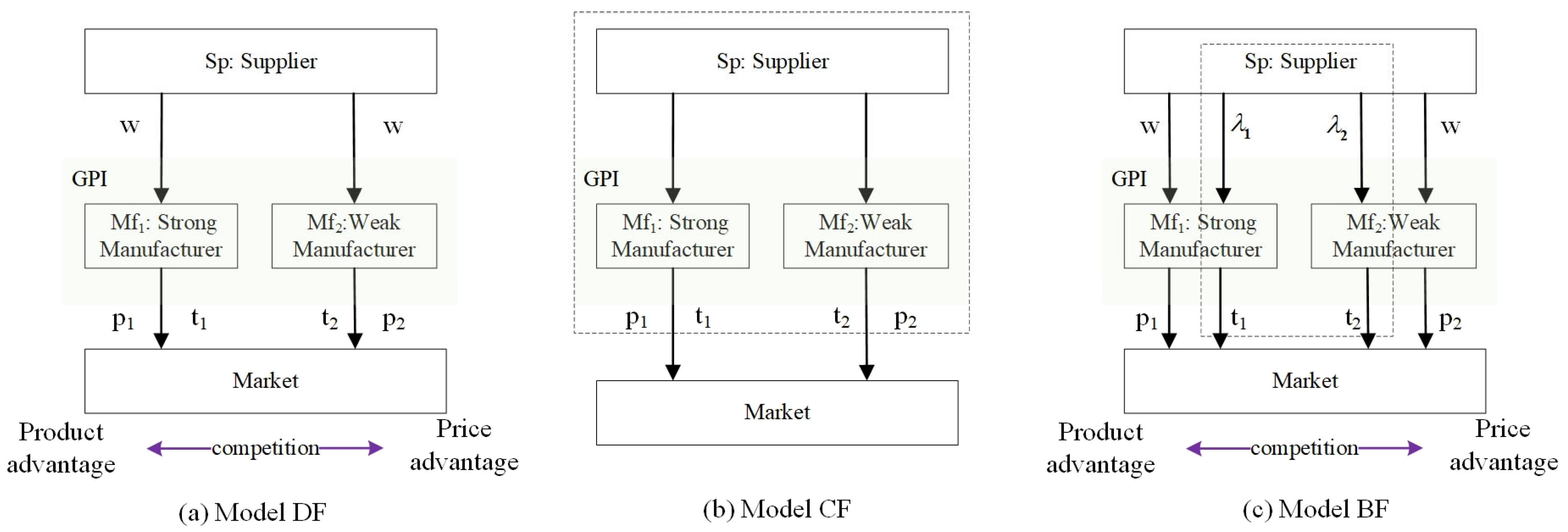
3.2. Decentralized AlBSC (Model DF)
3.3. Centralized AlBSC (Model CF)
3.4. Biform Game-Based AlBSC (Model BF)
3.4.1. Cooperative Game Part
3.4.2. Non-Cooperative Game Part
4. Analysis
- (1)
- .
- (2)
- .
- (3)
- ; ; if , otherwise .
- (4)
- , .
- (1)
- , , .
- (2)
- ; if ; otherwise ; .
- (3)
- , , .
- (4)
- .
- (1)
- , , , .
- (2)
- ; ; when , , ; when , , .
- (3)
- , , , .
- (4)
- , , .
5. Extension
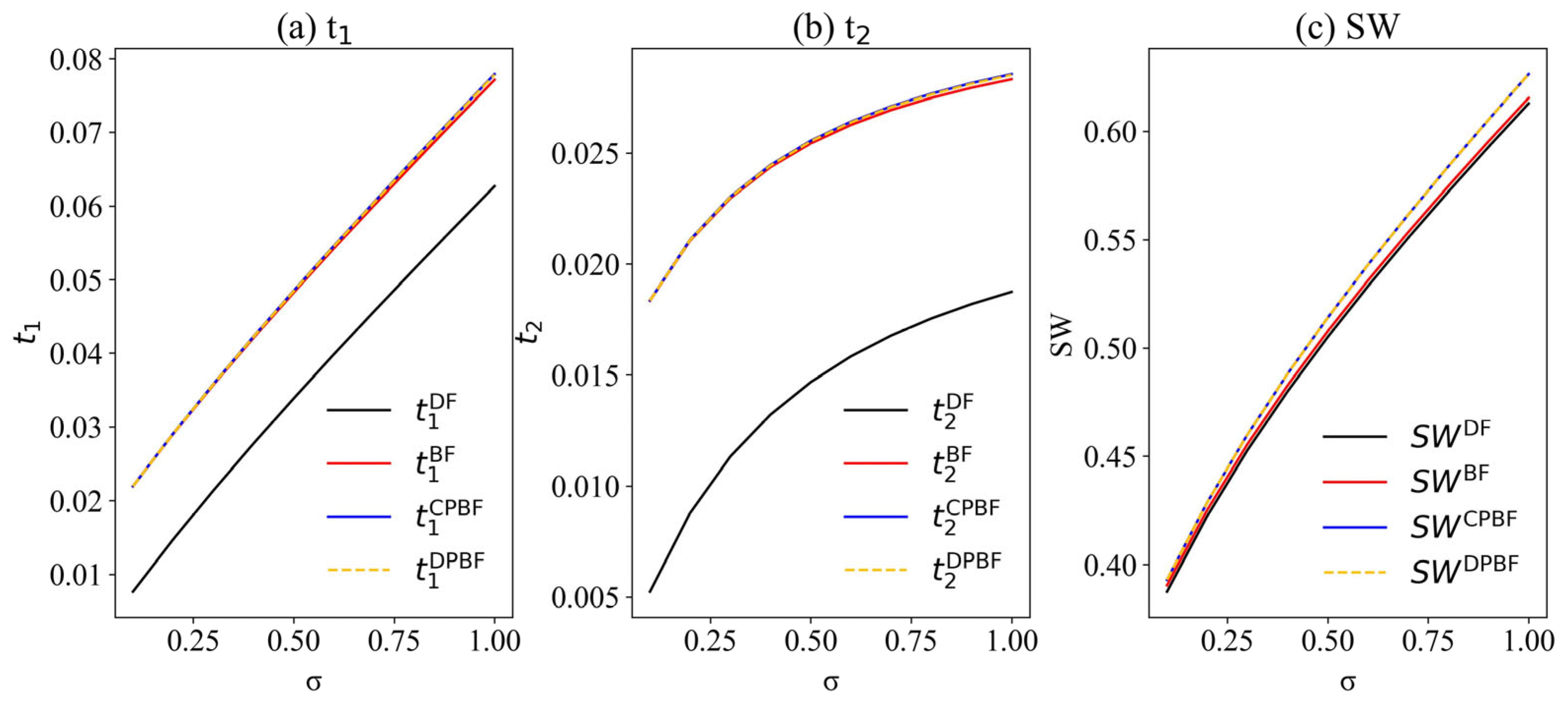
6. Numerical Results
6.1. Parameter Setting
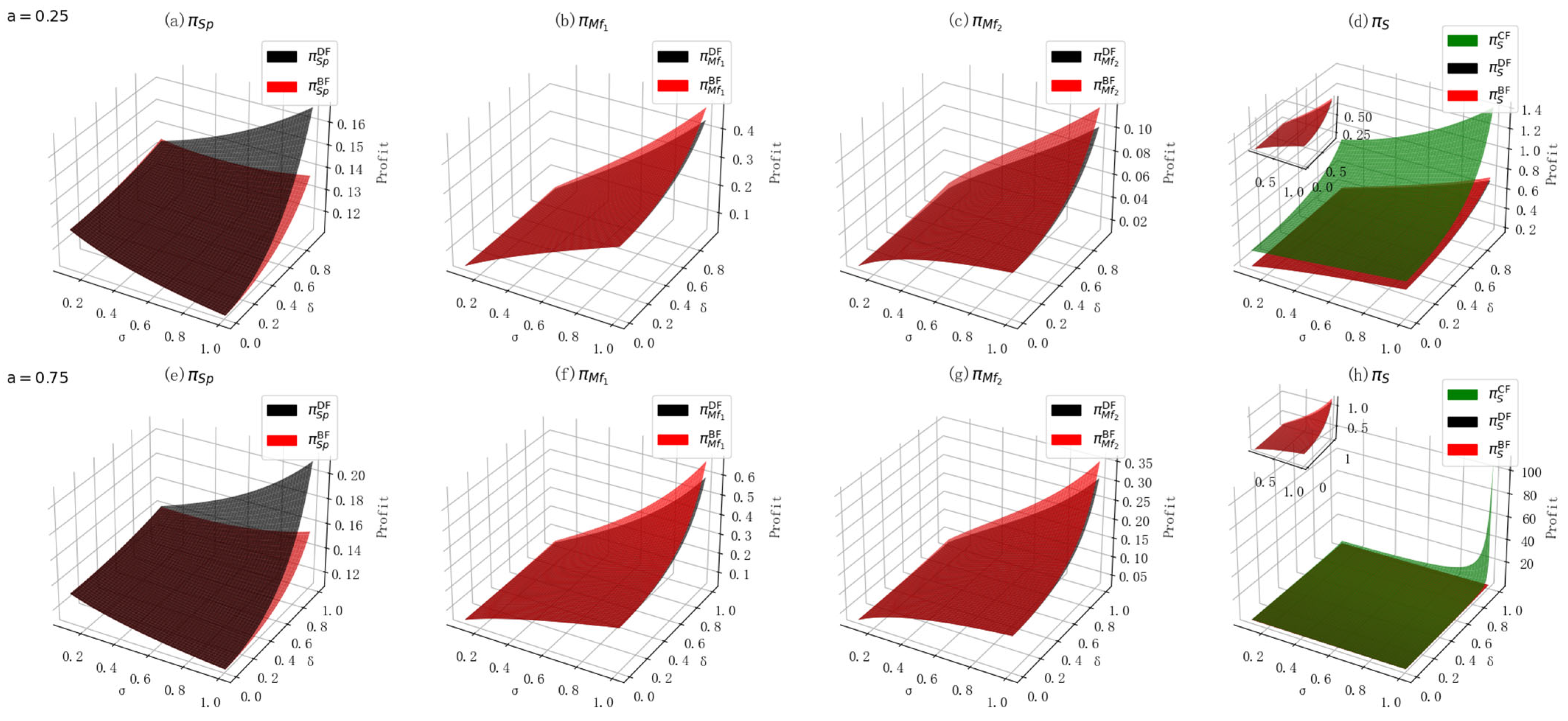
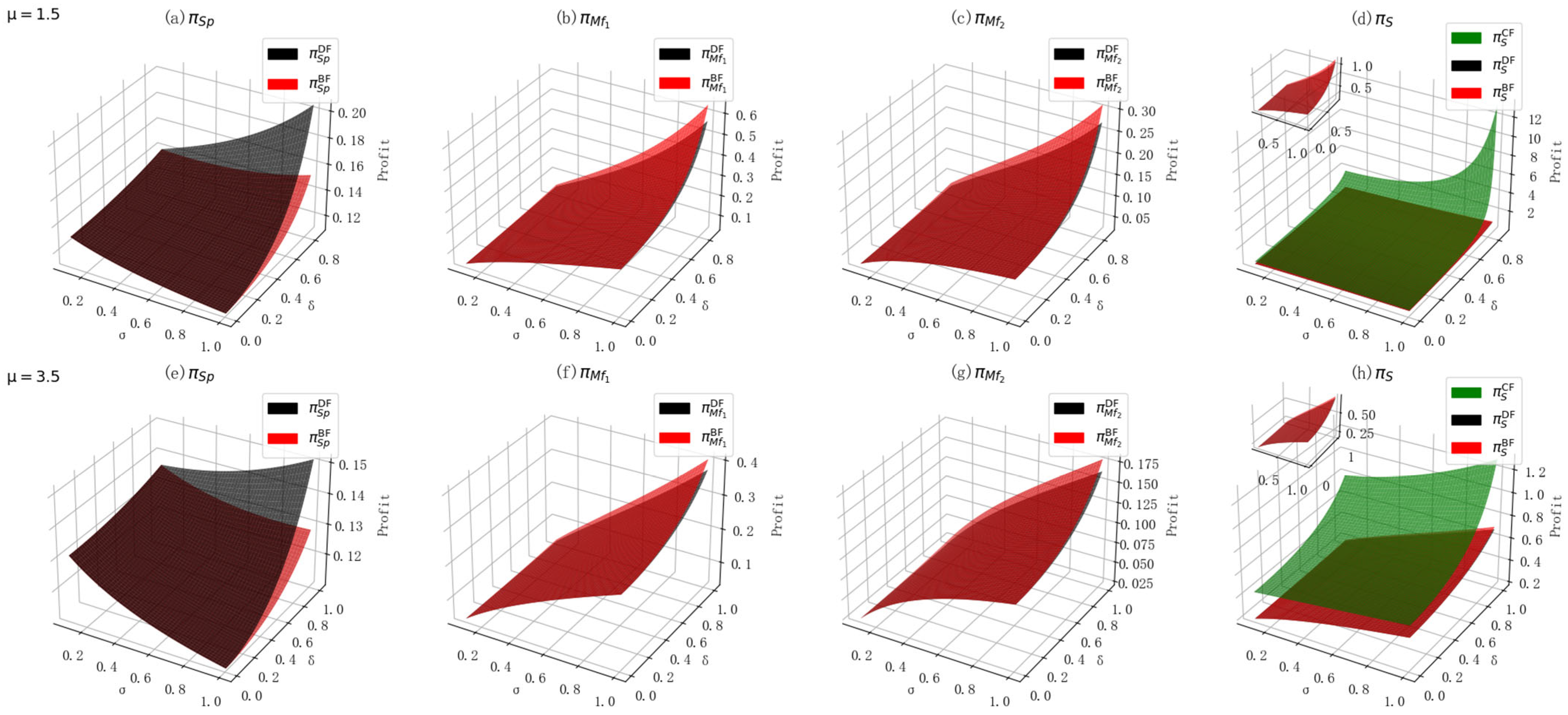
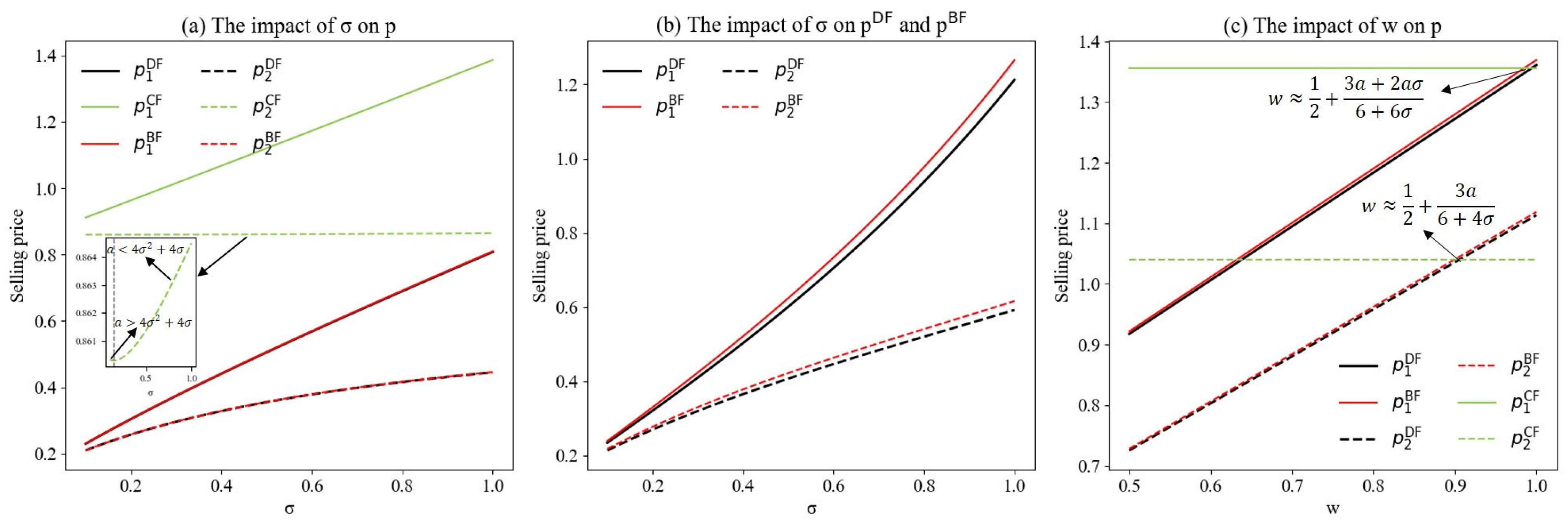
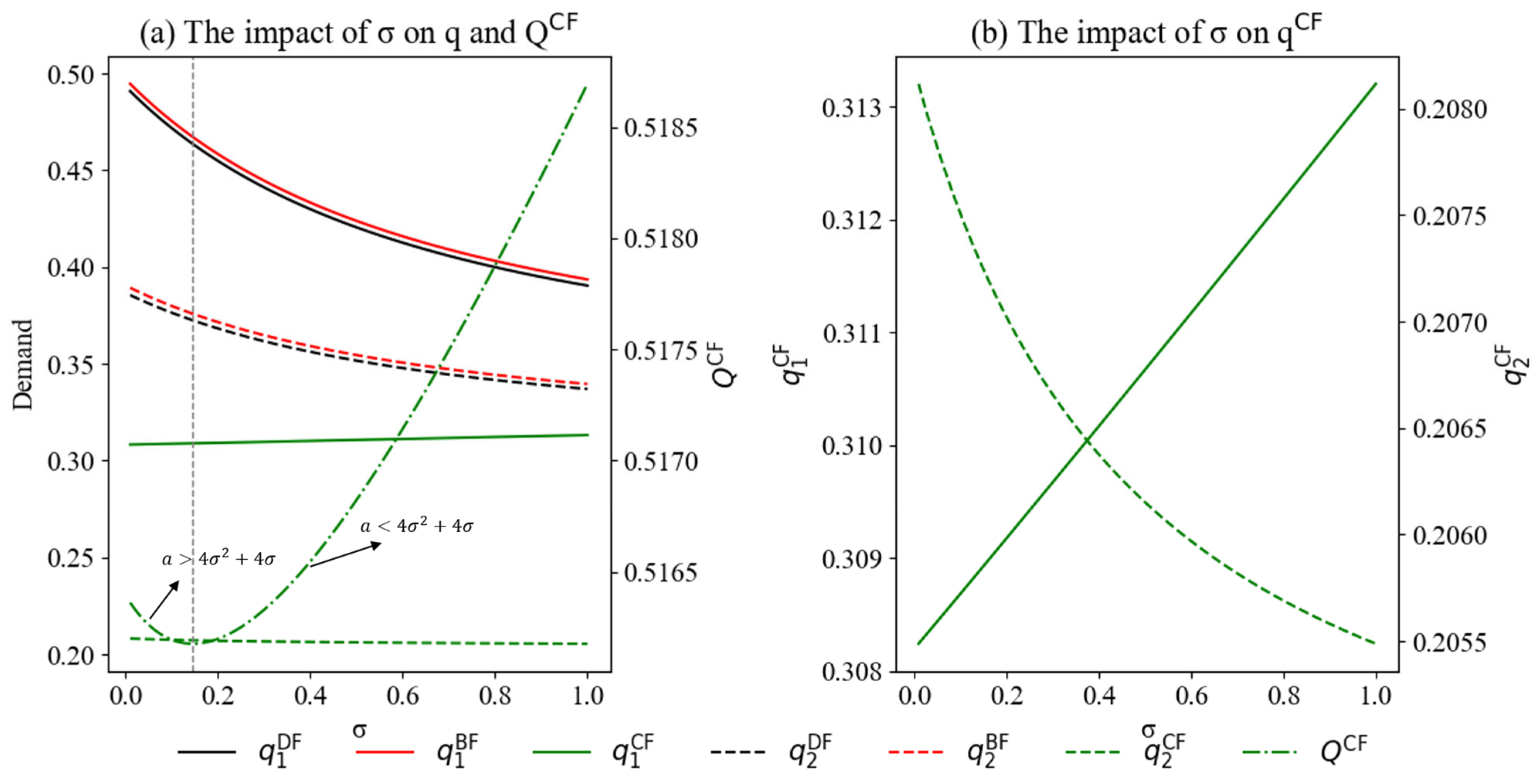
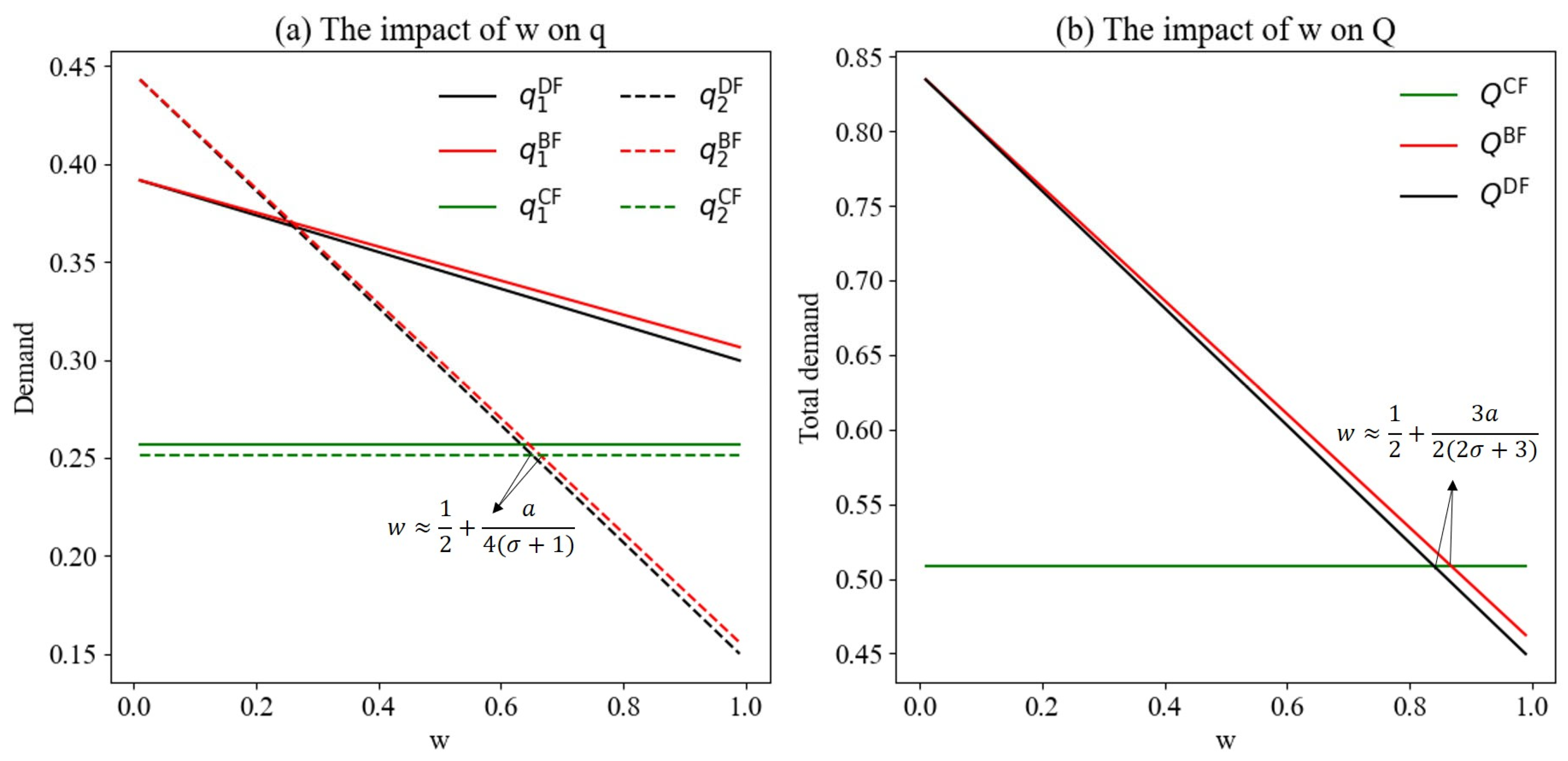
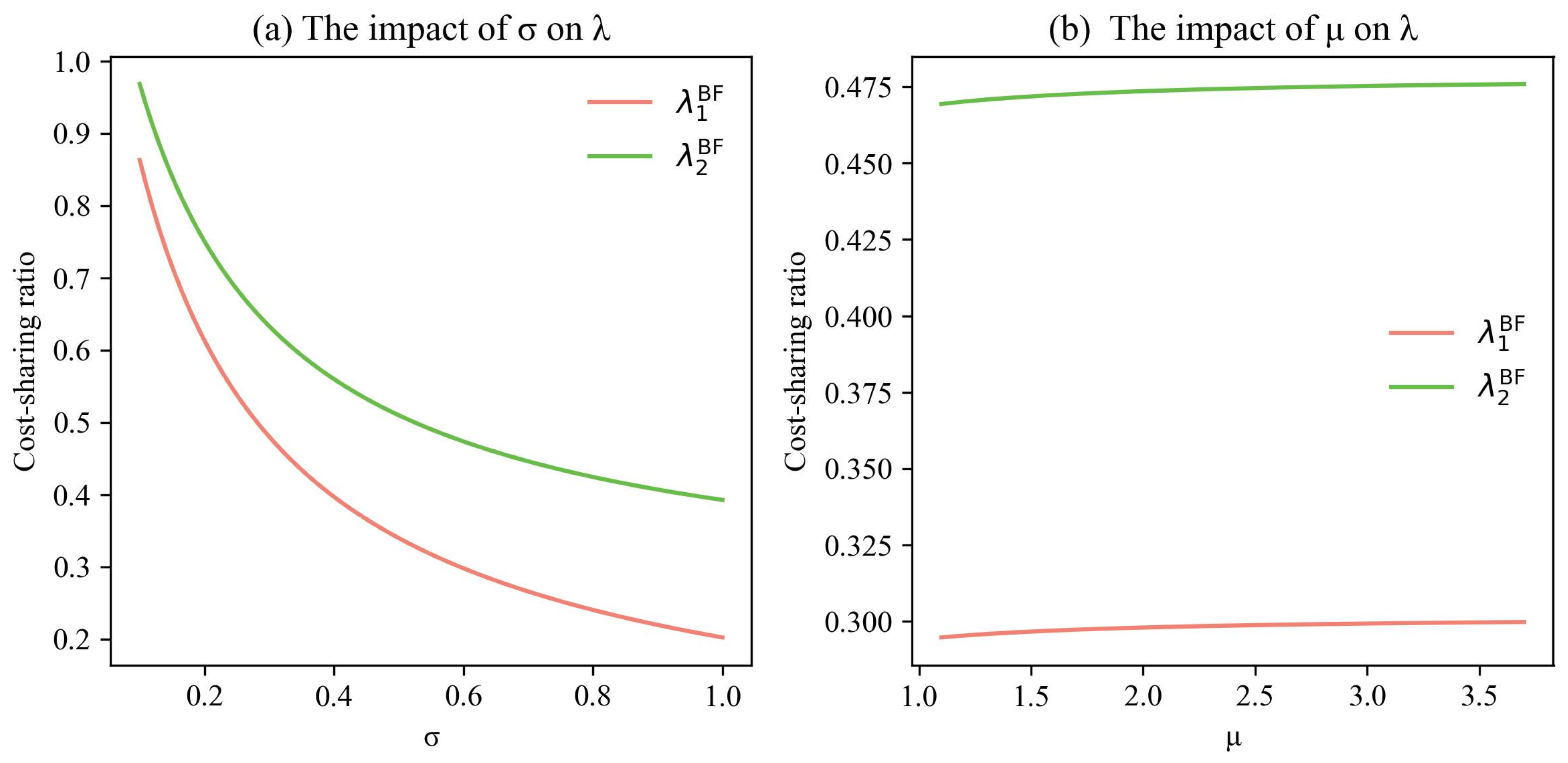
6.2. The Impact of ICH on GPI Decisions
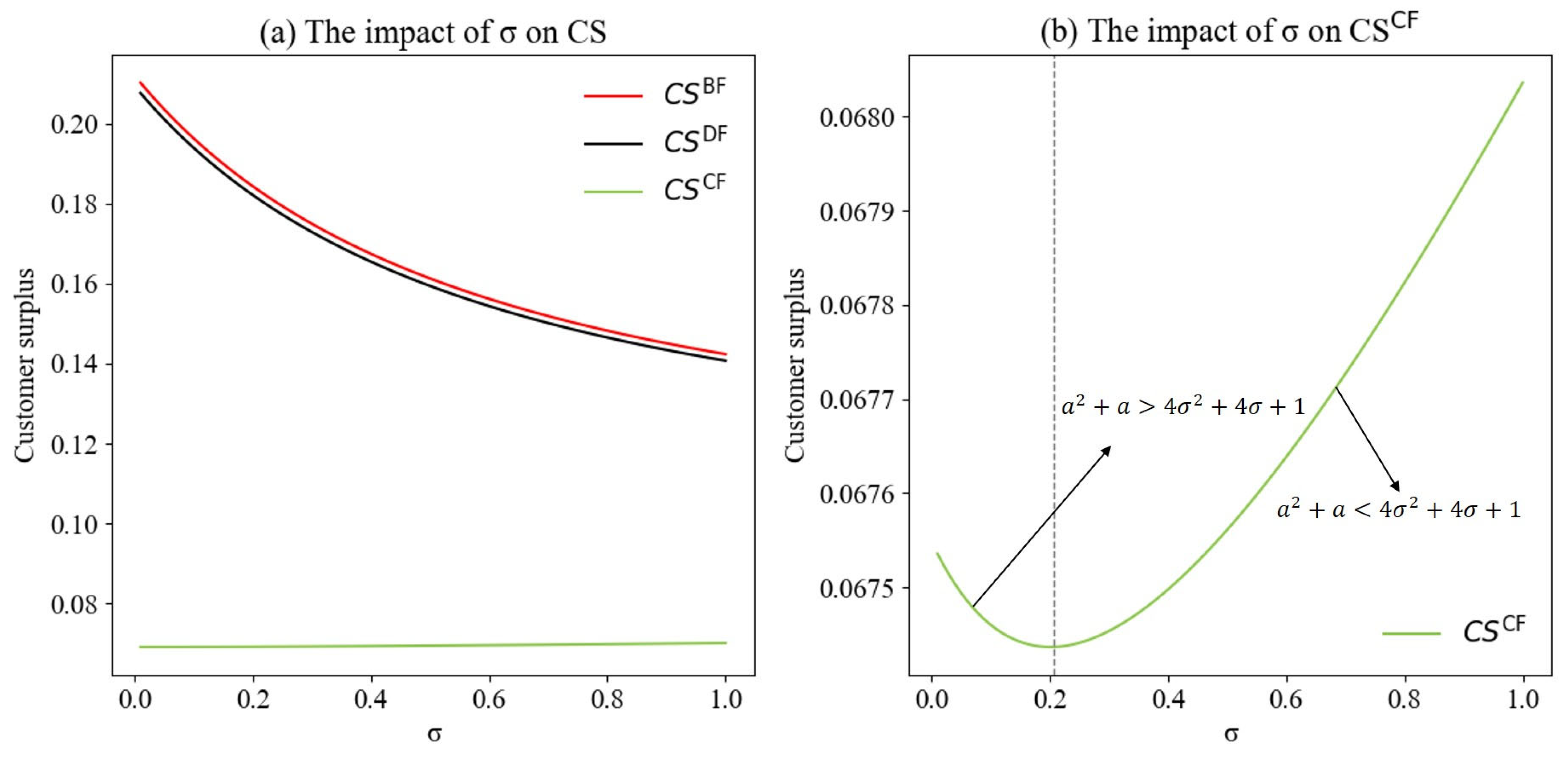
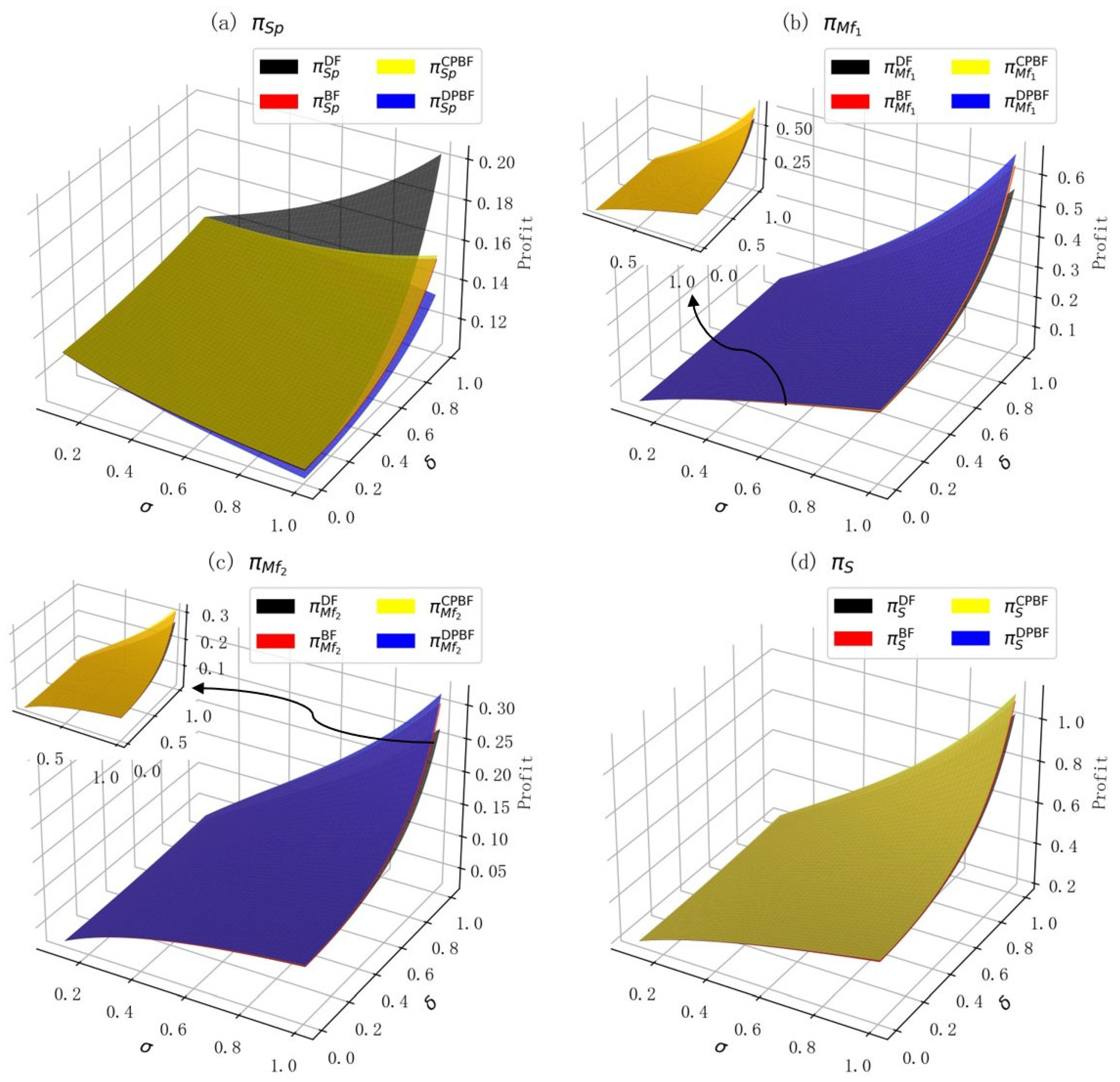
6.3. The Impact of ICH on Profit Allocation and Profits
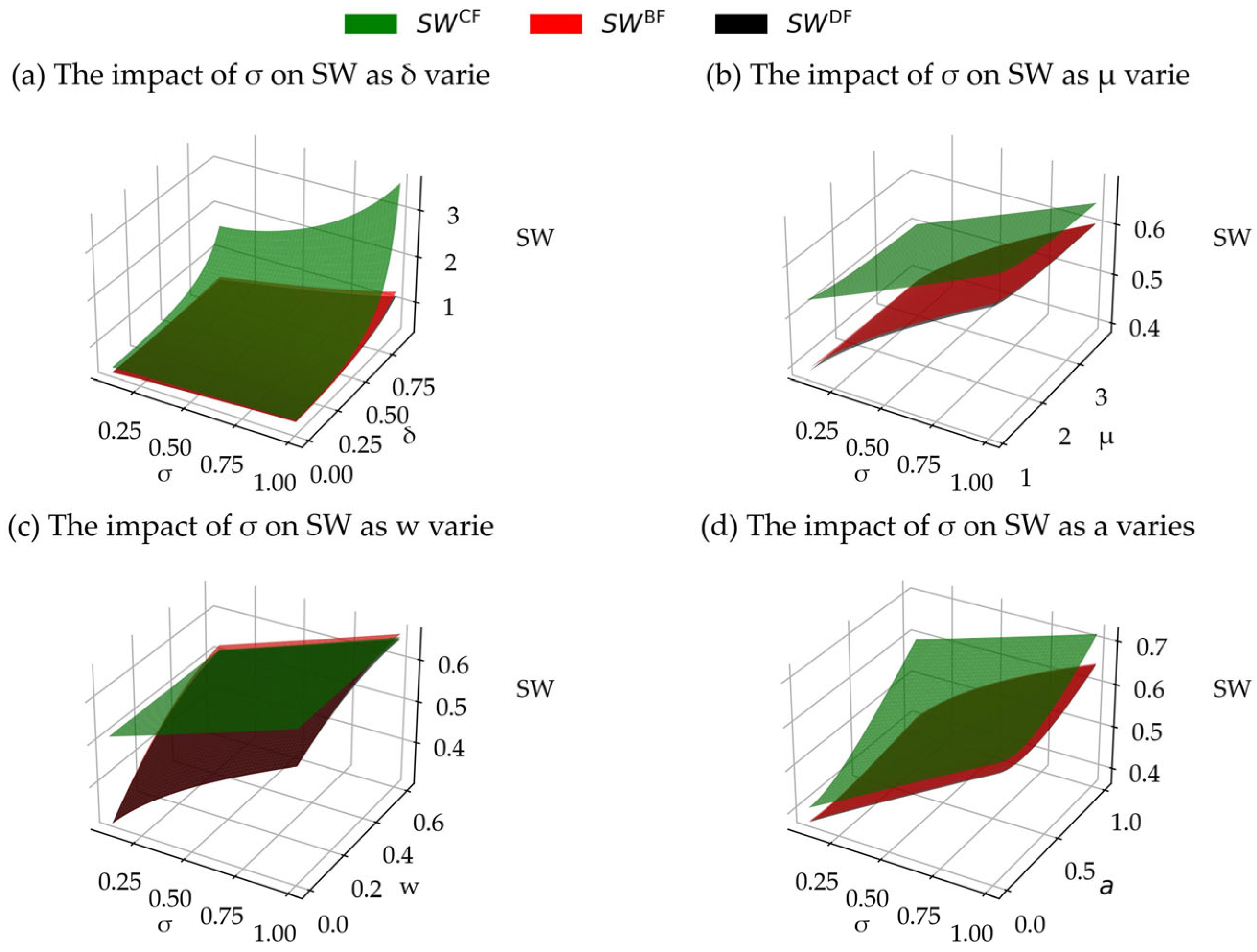
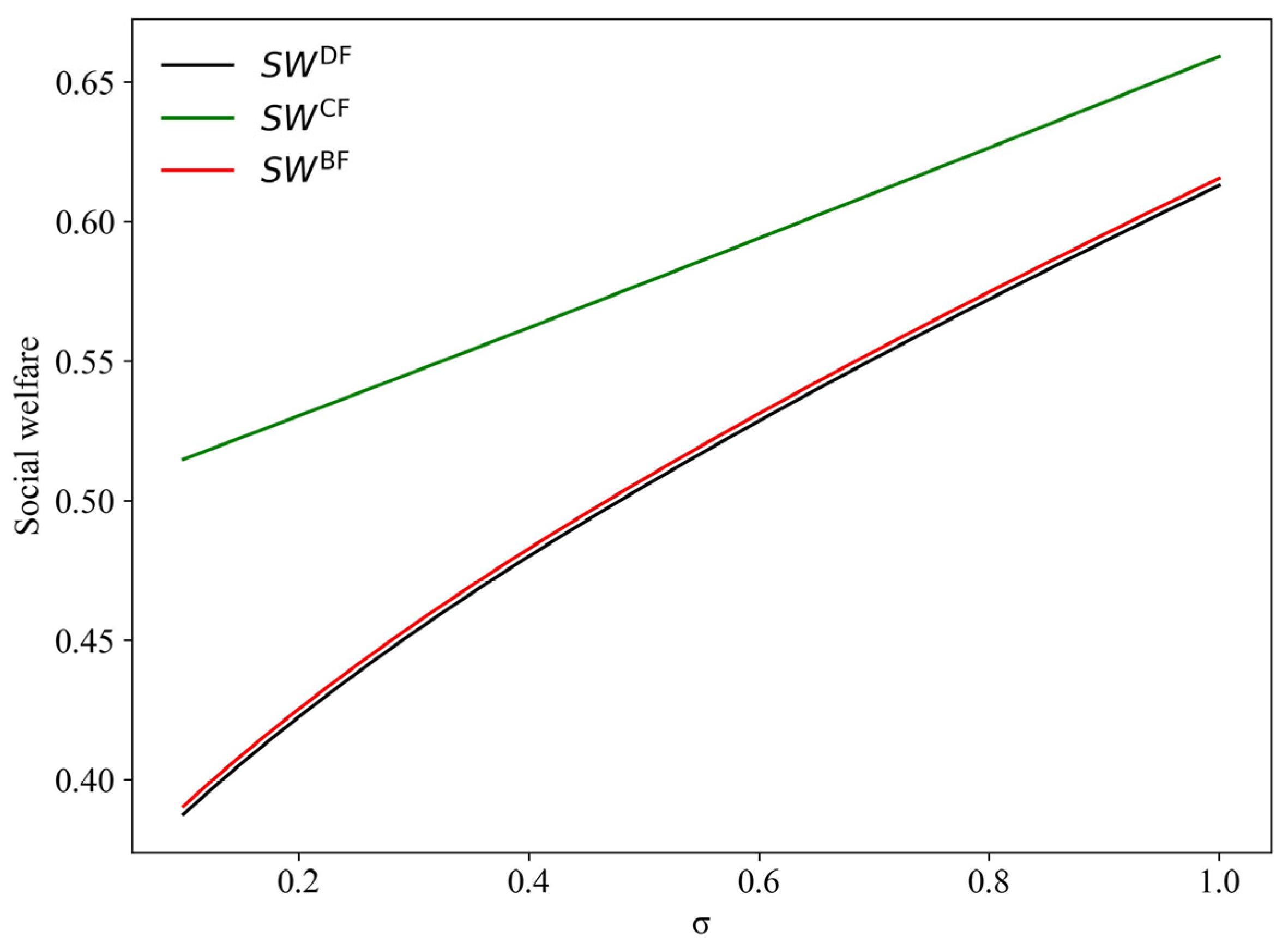
6.4. The Impact of ICH on SW
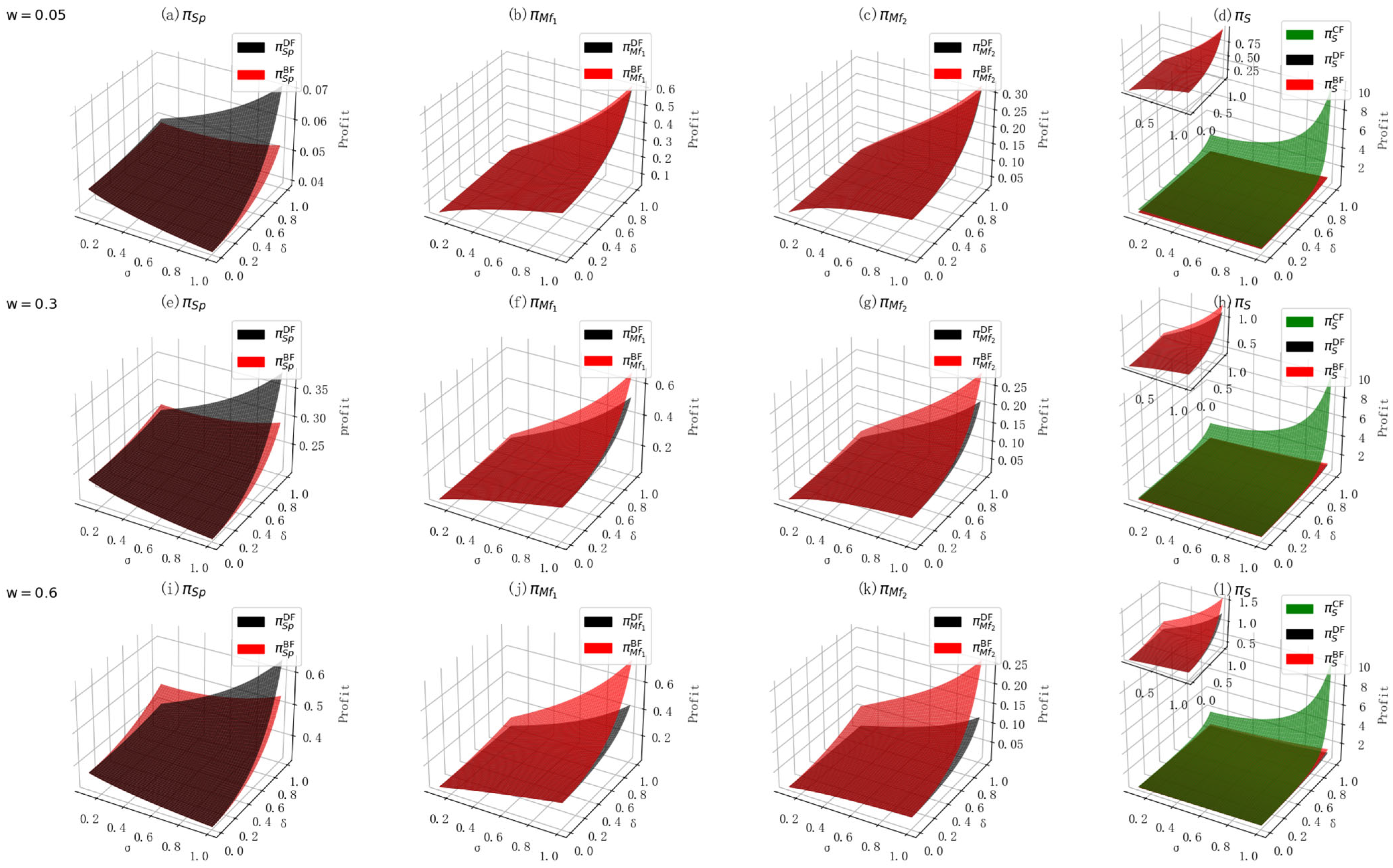
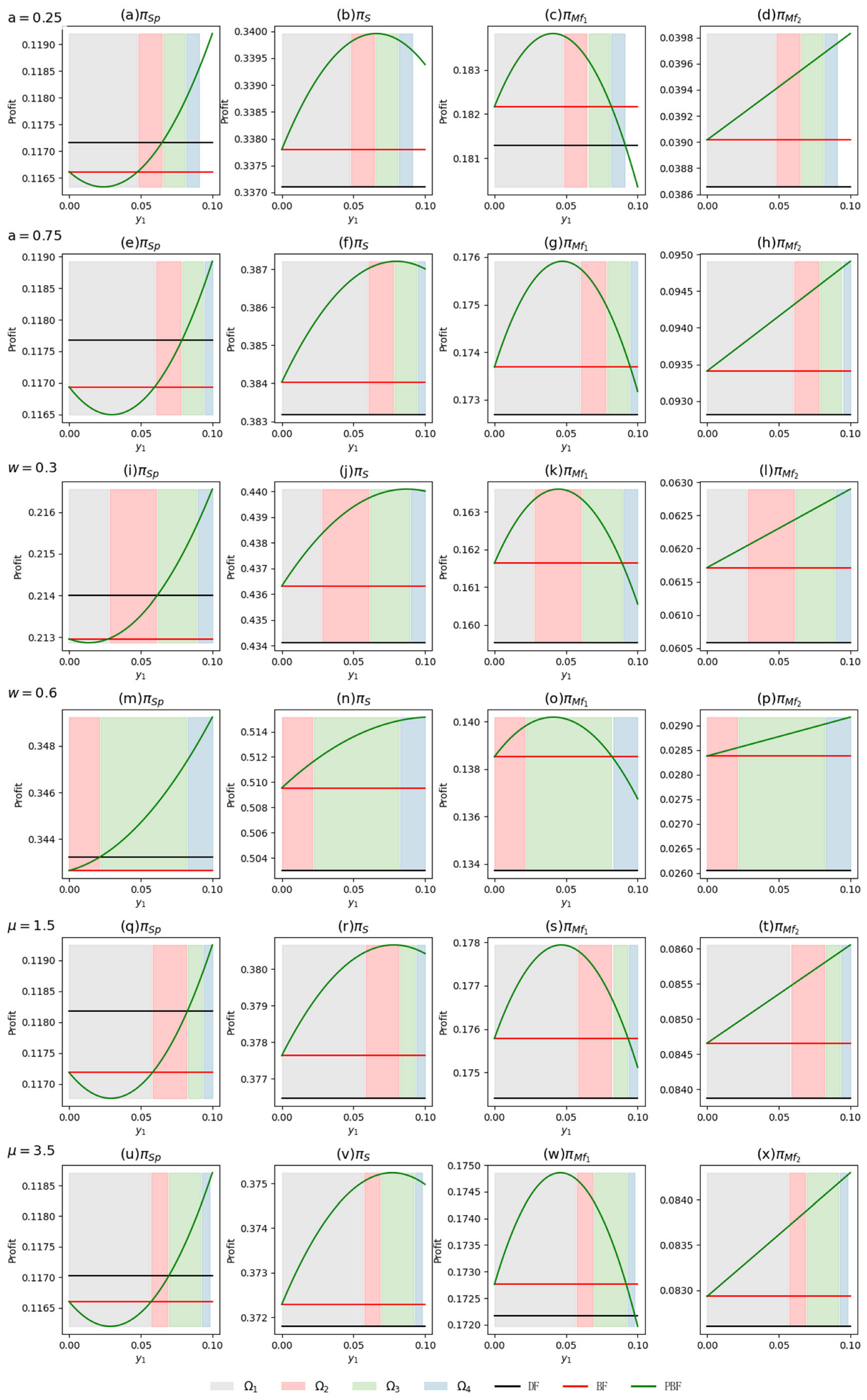
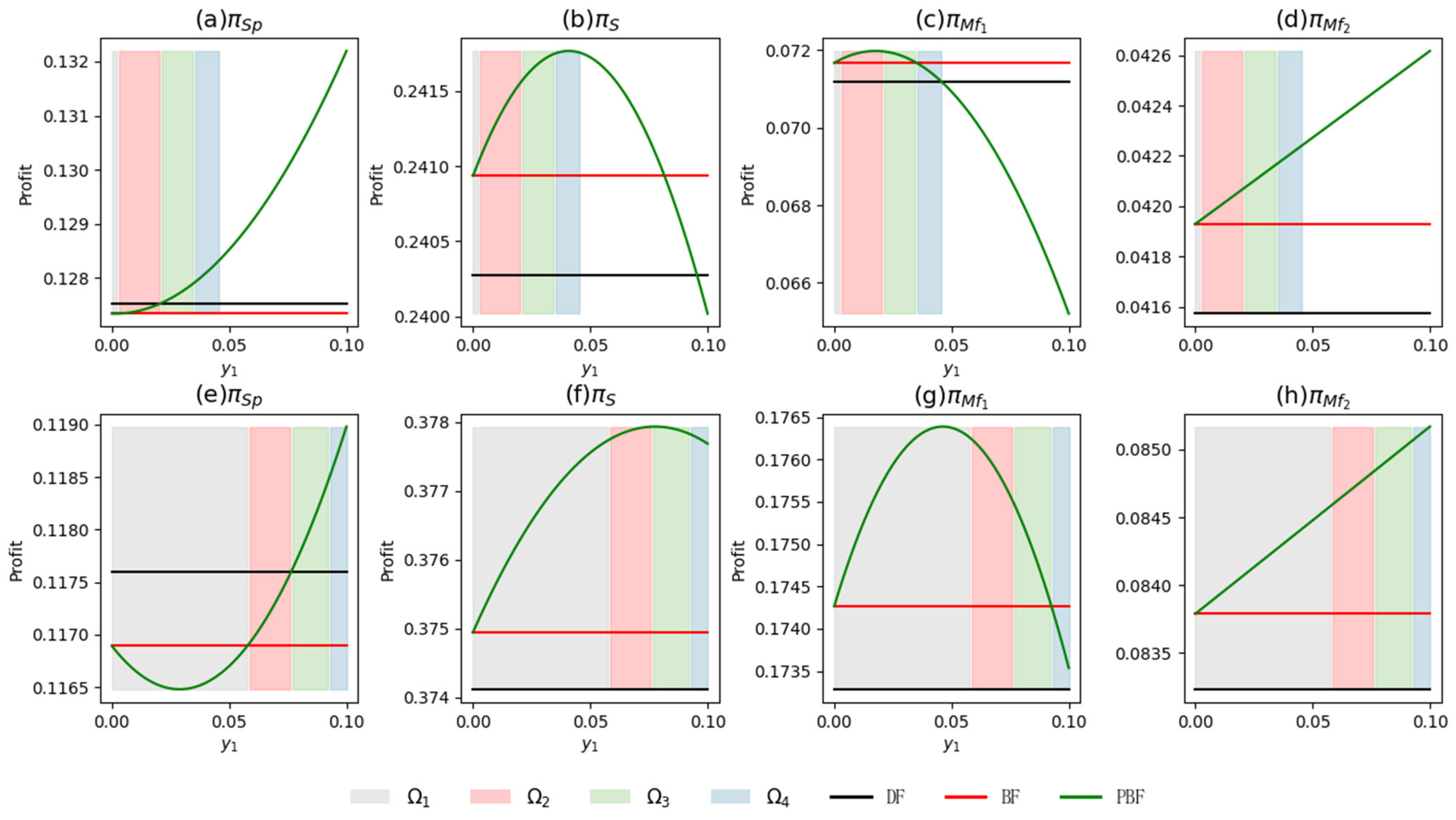
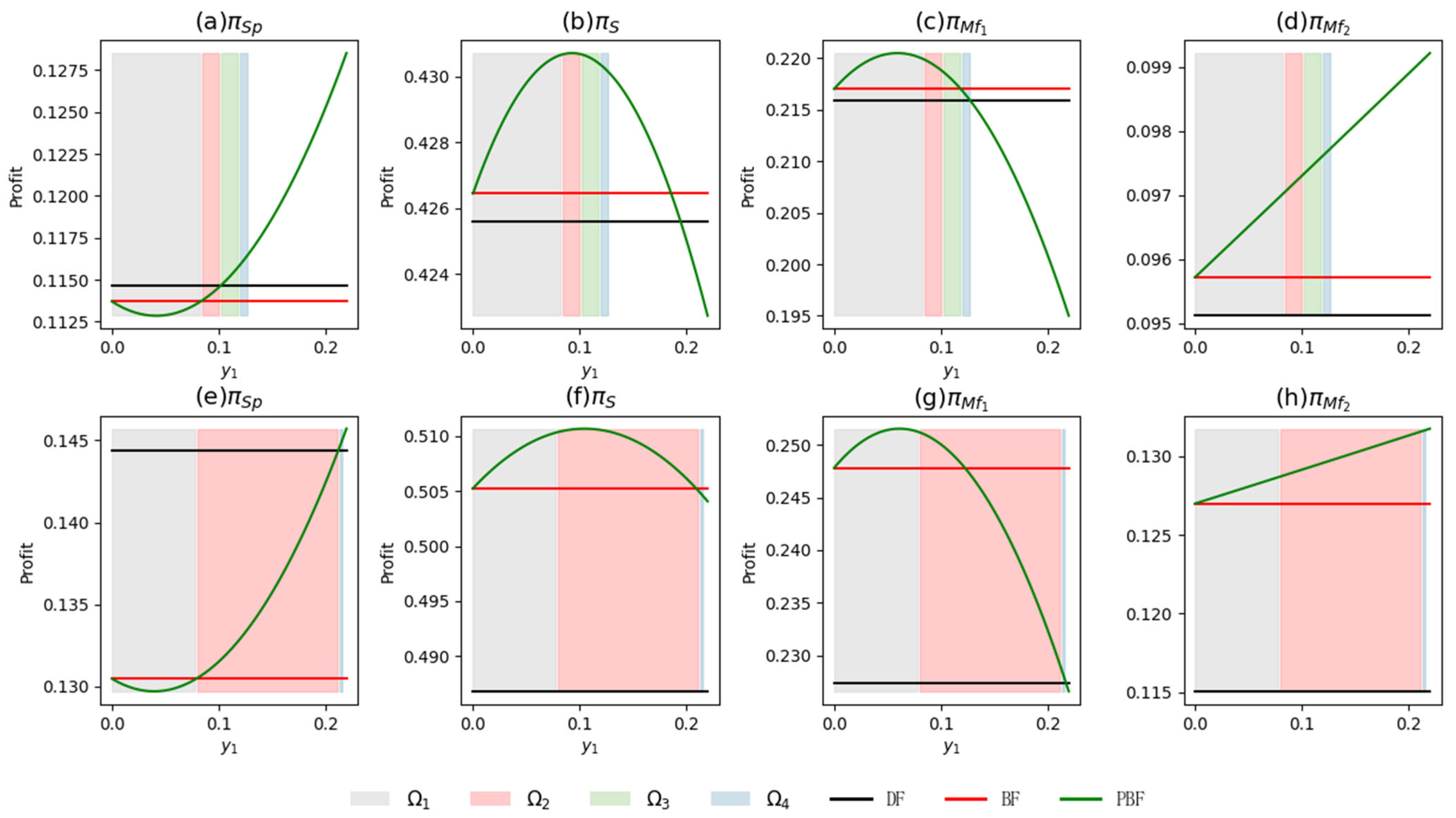
6.5. The Coordination Effect of the Promotion Compensation Contract
6.5.1. Exogenous Promotion Compensation
6.5.2. Endogenous Promotion Compensation
6.5.3. Comparison of the Coordination Results Across Different Decision-Making Mode
7. Conclusions
7.1. Key Findings
7.2. Managerial Implications
7.3. Limitations and Possible Directions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
- (1)
- .
- (2)
- (3)
- (4)
- (5)
- (6)
- (7)
- (8)
Appendix D. Proof for Proposition 1
- (1)
- , ,
- (2)
- , ,
- (3)
- , ,
- (4)
- , ,
- (5)
- , ,
- (6)
- , , , >
Appendix E. Proof for Proposition 3
- (1)
- The proof of , , .
- (2)
- The proof of , , .
- (3)
- The proof of , holds if and holds otherwise, .
- (4)
- The proof of ; .
Appendix F. Proof for Proposition 4
- (1)
- The proof of , , .
- (2)
- The proof of , holds if and otherwise, .
- (3)
- The proof of , , .
- (4)
- The proof of .
Appendix G. Proof for Proposition 5
- (1)
- The proof for , , .
- (2)
- The proof for , holds if , holds if , .
- (3)
- The proof for , , .
- (4)
- The proof for ; .
Appendix H. Proof for Proposition 6
Appendix I. Proof for Proposition 7
Appendix J. Proof for Proposition 8
Appendix K. Proof for Proposition 9
Appendix L. Proof for Proposition 10
Appendix M
References
- Aluminum China. The “Dual Carbon” Goals Bring New Opportunities for the Development of Recycled Aluminum. Available online: https://www.aluminiumchina.com/zh-cn/media-center/hyzxdt/2024/4/2.html (accessed on 4 July 2025).
- Li, Y.; Wang, S.; Wang, N.; Liu, Y.; Xin, H.; Sun, H.; Zhang, R. Exploring the Paths of Energy Conservation and Emission Reduction in Aluminum Industry in Henan Province, China. J. Clean. Prod. 2024, 467, 142997. [Google Scholar] [CrossRef]
- Olanrewaju, O.I.; Enegbuma, W.I.; Donn, M. Challenges in Life Cycle Assessment Implementation for Construction Environmental Product Declaration Development: A Mixed Approach and Global Perspective. Sustain. Prod. Consum. 2024, 49, 502–528. [Google Scholar] [CrossRef]
- Dong, H.; Yu, F.; Bi, Z.; Zhang, C.; Liu, X.; Geng, Y.; Ohnishi, S.; Li, H. Life Cycle Environmental and Economic Assessment of Tetra Pak Recycling Technologies. Resour. Conserv. Recycl. 2024, 202, 107355. [Google Scholar] [CrossRef]
- Godja, N.; Munteanu, F.D. Environmentally Friendly Solutions as Potential Alternatives to Chromium-Based Anodization and Chromate Sealing for Aeronautic Applications. Coatings 2025, 15, 439. [Google Scholar] [CrossRef]
- Li, M.; Gao, F.; Jin, M.; Sun, B.; Liu, Y.; Gong, X.; Nie, Z. Integrating Sustainability into Material Design and Selection through Eco-Design: A Case Study on Aluminum Alloy Plates. J. Clean. Prod. 2024, 482, 144191. [Google Scholar] [CrossRef]
- Cheng, C.H.; Tang, B.J.; Cheng, Y.R. Strategies and Tools for Small- and Medium-Sized Enterprises (SMEs) to Move toward Green Operations: The Case of the Taiwan Metal Industry. Sustainability 2024, 16, 4705. [Google Scholar] [CrossRef]
- Panigrahi, S.S.; Mishra, S.; Sahu, B. What Hinders the Green Supply Chain Management Adoption in the Indian Aluminium Sector? Environ. Dev. Sustain. 2025, 27, 14469–14495. [Google Scholar] [CrossRef]
- Fontoura, P.; Coelho, A. How to Boost Green Innovation and Performance through Collaboration in the Supply Chain: Insights into a More Sustainable Economy. J. Clean. Prod. 2022, 359, 132005. [Google Scholar] [CrossRef]
- Almeida Costa, A.; Zemsky, P. The Choice of Value-Based Strategies under Rivalry: Whether to Enhance Value Creation or Bargaining Capabilities. Strateg. Manag. J. 2021, 42, 2020–2046. [Google Scholar] [CrossRef]
- Zheng, X.; Li, D. A New Biform Game-Based Investment Incentive Mechanism for Eco-Efficient Innovation in Supply Chain. Int. J. Prod. Econ. 2023, 258, 108795. [Google Scholar] [CrossRef]
- Soho. Committed to Green Practices: Yunnan Aluminum Co., Ltd.’s Comprehensive Development of a Green Supply Chain. Available online: https://www.sohu.com/a/www.sohu.com/a/906186300_121613636 (accessed on 31 July 2025).
- Asghari, T.; Taleizadeh, A.A.; Jolai, F.; Moshtagh, M.S. Cooperative Game for Coordination of a Green Closed-Loop Supply Chain. J. Clean. Prod. 2022, 363, 132371. [Google Scholar] [CrossRef]
- Jia, F.; Zhang, S.; Zheng, X.-X.; Choi, T.-M. A Novel Coordination Mechanism to Coordinate the Multi-Agent Reverse Supply Chain with Fairness Concerns. Int. J. Prod. Econ. 2023, 265, 108973. [Google Scholar] [CrossRef]
- Zhao, D.; Zhao, T.; Du, R. TFP Shocks and Endogenous Innovation Ability in Manufacturing Industry: From the Perspective of Structural Stickiness. Technol. Econ. Dev. Econ. 2025, 31, 211–243. [Google Scholar] [CrossRef]
- Barney, J. Firm Resources and Sustained Competitive Advantage. J. Manag. 1991, 17, 99–120. [Google Scholar] [CrossRef]
- Sun, J.; Long, Q.; Teng, C. Indigenous Innovation VS. Technology Outsourcing: R&D Strategy and Contract Design for Green Supply Chain Considering R&D Capability. Chin. J. Manag. Sci. 2024, 32, 1–23. [Google Scholar] [CrossRef]
- Alshammari, K.H.; Alshammari, A.F. Green Innovation and Its Effects on Innovation Climate and Environmental Sustainability: The Moderating Influence of Green Abilities and Strategies. Sustainability 2023, 15, 15898. [Google Scholar] [CrossRef]
- Fadavi, A.; Jolai, F.; Taleizadeh, A.A. Green Product Design in a Supply Chain with Considering Marketing under Competition and Coordination. Environ. Dev. Sustain. 2022, 24, 11721–11759. [Google Scholar] [CrossRef]
- Camel, A.; Belhadi, A.; Kamble, S.; Tiwari, S.; Touriki, F.E. Integrating Smart Green Product Platforming for Carbon Footprint Reduction: The Role of Blockchain Technology and Stakeholders Influence within the Agri-Food Supply Chain. Int. J. Prod. Econ. 2024, 272, 109251. [Google Scholar] [CrossRef]
- Ministry of Industry and Information Technology of the People’s Republic of China. Notice on the Issuance of the “14th Five-Year Plan for Industrial Green Development”; Ministry of Industry and Information Technology of the People’s Republic of China: Beijing, China, 2021.
- Ministry of Industry and Information Technology of the People’s Republic of China (MIIT) and Nine Other Departments. Notice on the Issuance of the Implementation Plan for the High-Quality Development of the Aluminum Industry (2025–2027); Ministry of Industry and Information Technology of the People’s Republic of China (MIIT) and Nine Other Departments: Beijing, China, 2025.
- Guangdong Guangxin Holdings Group Ltd. Guangdong State-Owned Enterprises’ New “Smart” Manufacturing|Advancing Toward Innovation and Intelligent Manufacturing, Xingfa Aluminum Accelerates Digitalization to Promote Global Development. Available online: https://www.gdghg.com/xwzx/ztjj/content/post_92912.html (accessed on 31 July 2025).
- Zhongya Aluminum. Achieving New Success: Zhongya Alumnum Listed Among the “Top 500 Manufacturing Enterprises in Guangdong Province 2024”. Available online: https://www.zhongya-alum.com/news_detail.php?id=674 (accessed on 4 August 2025).
- Wang, M.; Li, Y.; Li, J.; Wang, Z. Green Process Innovation, Green Product Innovation and Its Economic Performance Improvement Paths: A Survey and Structural Model. J. Environ. Manag. 2021, 297, 113282. [Google Scholar] [CrossRef]
- Zhan, H.; Zeng, G.; Wang, Q.; Wang, C.; Wang, P.; Wang, Z.; Xu, Y.; Hess, D.; Crepeau, P.; Wang, J. Unified Casting (UniCast) Aluminum Alloy—A Sustainable and Low-Carbon Materials Solution for Vehicle Lightweighting. J. Mater. Sci. Technol. 2023, 154, 251–268. [Google Scholar] [CrossRef]
- Cheng, W.; Li, Q.; Wu, Q.; Jiang, Y.; Ye, F. Cooperative Promotion and Wholesale Price Discount Incentives in a Closed-Loop Supply Chain with Dynamic Returns. Sage Open 2024, 14, 21582440241264378. [Google Scholar] [CrossRef]
- Xu, C.; Wang, Y.; Yao, D.; Qiu, S.; Li, H. Research on the Coordination of a Marine Green Fuel Supply Chain Considering a Cost-Sharing Contract and a Revenue-Sharing Contract. Front. Mar. Sci. 2025, 12, 1552136. [Google Scholar] [CrossRef]
- Qu, Y.; Guan, Z.; Li, J.; Liu, T. Cooperative or Noncooperative? Green Innovation, Pricing Decisions, and Collaborative Mechanisms in a Supply Chain with Manufacturer’s Disappointment Aversion. IEEE Trans. Eng. Manag. 2024, 71, 9588–9603. [Google Scholar] [CrossRef]
- Cao, K.; Mei, Y. Green Supply Chain Decision and Management under Manufacturer’s Fairness Concern and Risk Aversion. Sustainability 2022, 14, 16006. [Google Scholar] [CrossRef]
- Forward. [Industry Insight] Outlook 2025: Competitive Landscape of China’s Aluminum Profiles Industry. Available online: https://cn.investing.com/news/economy-news/article-2829674 (accessed on 31 July 2025).
- Brandenburger, A.; Stuart, H. Biform Games. Manag. Sci. 2007, 53, 537–549. [Google Scholar] [CrossRef]
- Summerfield, N.S.; Dror, M. Biform Game: Reflection as a Stochastic Programming Problem. Int. J. Prod. Econ. 2013, 142, 124–129. [Google Scholar] [CrossRef]
- Stuart, H.W. Biform Analysis of Inventory Competition. Manuf. Serv. Oper. Manag. 2005, 7, 347–359. [Google Scholar] [CrossRef]
- Feess, E.; Thun, J.-H. Surplus Division and Investment Incentives in Supply Chains: A Biform-Game Analysis. Eur. J. Oper. Res. 2014, 234, 763–773. [Google Scholar] [CrossRef]
- Li, M.; Li, D.; Nan, J. Competition of Green Supply Chains and R&D Cost-sharing within a Chain--Based on Noncooperative-Cooperative Biform Game Approach. Chin. J. Manag. Sci. 2023, 31, 1–13. [Google Scholar] [CrossRef]
- Liang, K.; Li, D. A Noncooperative-Cooperative Biform Game Analysis of Pricing and Investment Decisions in a Low-Carbon Supply Chain. J. Syst. Sci. Math. Sci. 2023, 43, 1389–1412. [Google Scholar]
- Kirchoff, J.F.; Falasca, M. Environmental Differentiation from a Supply Chain Practice View Perspective. Int. J. Prod. Econ. 2022, 244, 108365. [Google Scholar] [CrossRef]
- Tian, C.; Xiao, T.; Shang, J. Channel Differentiation Strategy in a Dual-Channel Supply Chain Considering Free Riding Behavior. Eur. J. Oper. Res. 2022, 301, 473–485. [Google Scholar] [CrossRef]
- Xiao, Y.; Niu, W.; Zhang, L.; Xue, W. Store Brand Introduction in a Dual-Channel Supply Chain: The Roles of Quality Differentiation and Power Structure. Omega 2023, 116, 102802. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, B.; Liu, J. Pricing and Sourcing Strategies for a Combination of Products with Quality Differentiation under the Supply Disruption Risk. Syst. Eng. Theory Pract. 2024, 44, 1068–1084. [Google Scholar]
- Zhang, J.; Mu, J.; Kang, L. Research on decision-making of e-commerce logistics model considering brand differences and power structure. Oper. Res. Manag. Sci. 2024, 33, 1–8. [Google Scholar]
- Lin, Y.; Wu, L.-Y. Exploring the Role of Dynamic Capabilities in Firm Performance under the Resource-Based View Framework. J. Bus. Res. 2014, 67, 407–413. [Google Scholar] [CrossRef]
- ChinaIRN. Current Status, Competitive Landscape, and Future Trends and Prospects of the Aluminum Processing Industry in 2024. Available online: https://www.chinairn.com/hyzx/20250121/101309531.shtml (accessed on 31 July 2025).
- Su, J.; Xu, B.; Li, L.; Wang, D.; Zhang, F. A Green Supply Chain Member Selection Method Considering Green Innovation Capability in a Hesitant Fuzzy Environment. Axioms 2023, 12, 188. [Google Scholar] [CrossRef]
- Sun, W.; Jiang, L.; Dong, K. Research on Supply Chain Coordination Decision Model Based on Green Technology. Sage Open 2023, 13, 21582440231190799. [Google Scholar] [CrossRef]
- Nishino, N.; Okazaki, M.; Akai, K. Effects of Ability Difference and Strategy Imitation on Cooperation Network Formation: A Study with Game Theoretic Modeling and Multi-Agent Simulation. Technol. Forecast. Soc. Change 2018, 136, 145–156. [Google Scholar] [CrossRef]
- Zhou, J.; Zhu, J.; Wang, H. Strategic Cooperation with Differential Suppliers’ Ability under Downstream Competition in Complex Products Systems. J. Syst. Sci. Syst. Eng. 2019, 28, 449–477. [Google Scholar] [CrossRef]
- Chen, J.; Huang, H.; Liu, L.; Xu, H. Price Delegation or Not? The Effect of Heterogeneous Sales Agents. Prod. Oper. Manag. 2021, 30, 1350–1364. [Google Scholar] [CrossRef]
- Helfat, C.E.; Kaul, A.; Ketchen, D.J., Jr.; Barney, J.B.; Chatain, O.; Singh, H. Renewing the Resource-Based View: New Contexts, New Concepts, and New Methods. Strateg. Manag. J. 2023, 44, 1357–1390. [Google Scholar] [CrossRef]
- Jing, F.; Lin, J.; Zhang, Q.; Qian, Y. New Technology Introduction and Product Rollover Strategies. Eur. J. Oper. Res. 2022, 302, 324–336. [Google Scholar] [CrossRef]
- Bloom, N.; Jones, C.I.; Van Reenen, J.; Webb, M. Are Ideas Getting Harder to Find? Am. Econ. Rev. 2020, 110, 1104–1144. [Google Scholar] [CrossRef]
- Aluminum China. Chinalco Yunnan Aluminum Co., Ltd.: Strengthening the Green Aluminum Industry Chain. Available online: http://www.sasac.gov.cn/n4470048/n26915116/n29140421/n29140461/c29281680/content.html (accessed on 31 July 2025).
- Qin, L.; Zhu, Y.; Liu, S.; Zhang, X.; Zhao, Y. The Shapley Value in Data Science: Advances in Computation, Extensions, and Applications. Mathematics 2025, 13, 1581. [Google Scholar] [CrossRef]
- Von Neumann, J.; Morgenstern, O. Theory of Games and Economic Behavior, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 1947. [Google Scholar]
- Shapley, L.S. A Value for N-Person Games; RAND Corporation: Santa Monica, CA, USA, 1952. [Google Scholar]
- Knott, A.M. Persistent Heterogeneity and Sustainable Innovation. Strateg. Manag. J. 2003, 24, 687–705. [Google Scholar] [CrossRef]
- Chen, J.; Liang, L.; Yao, D.-Q.; Sun, S. Price and Quality Decisions in Dual-Channel Supply Chains. Eur. J. Oper. Res. 2017, 259, 935–948. [Google Scholar] [CrossRef]
- Sun, R.; He, D.; Yan, J. Dynamic analysis of green technology innovation in products and processes under supply chain competition scenarios—A study based on stochastic differential game model. J. Environ. Manag. 2025, 373, 123545. [Google Scholar] [CrossRef]
- Li, B. China Aluminum Alloy Market 2025: Aluminum Hydrogen Fuel Bipolar Plate Raid, Aluminum Demand for New Energy Vehicles “Intercepted” by Sodium Battery? Available online: https://www.chinairn.com/hyzx/20250307/152901967.shtml (accessed on 6 May 2025).
- Liu, L.; Han, T.; Jin, H. Differential Game Study of Green Supply Chain Based on Green Technology Innovation and Manufacturer Competition. J. Manag. Bus. Res. 2023, 20, 116–126. [Google Scholar]
- Forward. 2025–2030 Global and Chinese Aluminum Processing Industry Market Research and Investment Outlook Analysis Report. Available online: https://bg.qianzhan.com/report/detail/2012021116312203.html?v=title (accessed on 6 May 2025).
- Trading Economics. China—Core Inflation. Available online: https://zh.tradingeconomics.com/china/core-inflation-rate (accessed on 8 May 2025).
- Zhang, Z.; Yu, L. Differential Game Analysis of Recycling Mode and Power Structure in a Low-Carbon Closed-Loop Supply Chain Considering Altruism and Government’s Compound Subsidy. Ann. Oper. Res. 2024, 1–51. [Google Scholar] [CrossRef]
- Al-Adwan, A.S.; Al-Debei, M.M.; Dwivedi, Y.K. E-Commerce in High Uncertainty Avoidance Cultures: The Driving Forces of Repurchase and Word-of-Mouth Intentions. Technol. Soc. 2022, 71, 102083. [Google Scholar] [CrossRef]
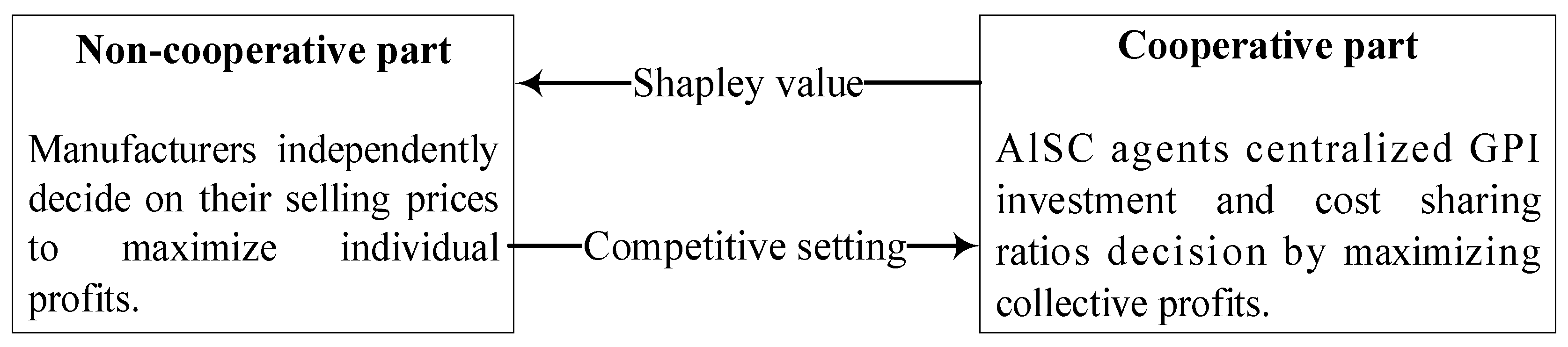





| Ref. | Research Object | Supply Chain Structure | Coordinate Strategy | Methods | Heterogeneity Setting |
|---|---|---|---|---|---|
| [21] | Power battery recycling supply chain | 1 manufacturer, 1 retailer | Promotion/wholesale price contracts | Non-cooperative game | No |
| [22] | General supply chain | 1 manufacturer, 1 retailer | Revenue-sharing/cost-sharing contracts | Non-cooperative game | No |
| [13] | Green closed-loop supply chain | 1 manufacturer, 1 recycler, 1 retailer | Cooperative alliance | Cooperative game | No |
| [29] | General supply chain | 1 supplier, 2 manufacturers | Contracts and cooperative games | Non-cooperative and cooperative games | No |
| [11] | Eco-innovation supply chain | 1 supplier, 2 manufacturers | Cooperative alliance | Biform game | No |
| [32] | General supply chain | 1 supplier, 2 manufacturers | - | Biform game | No |
| [37] | Low-carbon supply chain | 1 manufacturer, 1 retailer | Cooperative alliance | Biform game | No |
| [40] | Retail supply chain | Dual channels: 1 supplier, 1 retailer | - | Non-cooperative game | Brand |
| [41] | Retail supply chain | 2 suppliers, 1 retailer | - | Non-cooperative game | Product quality |
| [42] | E-commerce logistics supply chain | 1 supplier, 2 logistics service providers | - | Non-cooperative game | Brand |
| Item | Subitem | Extant Literature | This Paper |
|---|---|---|---|
| 2.1 Decision making and coordination of supply chain on green innovation | Number of agents | 2 or 3 | 3 |
| Methods | Non-cooperative game and/or cooperative game | Non-cooperative game and biform game | |
| Number of decision-making methods for contract parameters | 1 | 3 (Section 5) | |
| 2.2 The application of biform game in SCM | Non-cooperative game | Profit maximization strategies | Profit maximization strategies |
| Cooperative game | The core or Shapley value | Shapley value | |
| 2.3 The operational research on firm heterogeneity | Heterogeneous agents | Suppliers | Manufacturers |
| Dimensions of heterogeneity | Product, quality or firm ability | Innovation capability |
| Category | Notions | Descriptions |
|---|---|---|
| Parameters | The size of the market for the weak manufacturer, and | |
| The demand-boosting effect of GPI | ||
| ICH | ||
| The cost per unit of GPI for the strong manufacturer | ||
| Wholesale price | ||
| Subscript | , subscripts 1 and 2 distinguish the two manufactures. | |
| Superscripts | Decentralized decision making | |
| Centralized decision making | ||
| Biform game-based decision making | ||
| Biform game-based decision making under exogenous promotion compensation contract | ||
| Biform game-based decision making under cooperative endogenous promotion compensation contract | ||
| Biform game-based decision making under competitive endogenous promotion compensation contract | ||
| Decision variables | Manufacturer’s GPI efforts | |
| Manufacturer’s selling price | ||
| Cost-sharing ratio for GPI investment | ||
| Variables | The manufacturer’s market demand | |
| Total market demand | ||
| Supply chain’s profits | ||
| Supplier’s profits | ||
| Manufacturer’s profits | ||
| Consumer surplus |
| How decisions are made | Coordinate the results |
| Exogenous | Pareto improvement over Models BF or DF (: Manufacturer-biased, : Balanced, : Supplier-biased) |
| Endogenous cooperation | Pareto improvement over Models BF or DF (Supplier-biased) |
| Endogenous competition | No Pareto improvement (Manufacturer-biased) |
| Model | Environment | Economics | Society | |||
|---|---|---|---|---|---|---|
| GPI | Prices | Supplier’s Profit | Manufacturers’ Profit | Supply Chain’s Profit | SW | |
| DF | ↑ | ↑ | ↓↑ | ↑ | ↑ | ↑ |
| CF | ↑, ↓ | ↑, ↓↑ | - | - | ↑ | ↑ |
| BF | ↑, ↓↑ | ↑ | ↓↑ | ↑ | ↑ | ↑ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Kong, R.; Luo, J. Green Product Innovation Coordination in Aluminum Building Material Supply Chains with Innovation Capability Heterogeneity: A Biform Game-Theoretic Approach. Sustainability 2025, 17, 7377. https://doi.org/10.3390/su17167377
Wang M, Kong R, Luo J. Green Product Innovation Coordination in Aluminum Building Material Supply Chains with Innovation Capability Heterogeneity: A Biform Game-Theoretic Approach. Sustainability. 2025; 17(16):7377. https://doi.org/10.3390/su17167377
Chicago/Turabian StyleWang, Mingyue, Rui Kong, and Jianfu Luo. 2025. "Green Product Innovation Coordination in Aluminum Building Material Supply Chains with Innovation Capability Heterogeneity: A Biform Game-Theoretic Approach" Sustainability 17, no. 16: 7377. https://doi.org/10.3390/su17167377
APA StyleWang, M., Kong, R., & Luo, J. (2025). Green Product Innovation Coordination in Aluminum Building Material Supply Chains with Innovation Capability Heterogeneity: A Biform Game-Theoretic Approach. Sustainability, 17(16), 7377. https://doi.org/10.3390/su17167377






