Assessing Sustainable Growth: Evolution and Convergence of Green Total Factor Productivity in Tibetan Plateau Agriculture

Abstract

Accurate assessment of green productivity is essential for advancing sustainable agriculture in ecologically fragile regions. This study examined the evolution of agricultural green total factor productivity (AGTFP) in Tibet over the period 2002–2021 by applying a super-efficiency SBM-GML model that accounts for undesirable outputs. We decompose AGTFP into technical change and efficiency change, conduct redundancy analysis to identify sources of inefficiency and explore its spatiotemporal dynamics through kernel density estimation and convergence analysis. Results show that (1) AGTFP in Tibet grew at an average annual rate of 0.78%, slower than the national average of 1.6%; (2) labor input, livestock scale, and agricultural carbon emissions are major sources of redundancy, especially in pastoral regions; (3) technological progress is the main driver of AGTFP growth, while efficiency gains have a limited impact, reflecting a technology-led growth pattern; (4) AGTFP follows a “convergence-divergence-reconvergence” trend, with signs of conditional β convergence after controlling for regional heterogeneity. These findings highlight the need for region-specific green agricultural policies. Priority should be given to improving green technology diffusion and input allocation in high-altitude pastoral areas, alongside strengthening ecological compensation and interregional coordination to enhance green efficiency and promote high-quality development across Tibet.

1. Introduction

Agriculture, as a fundamental sector underpinning human survival and economic development, increasingly faces challenges arising from the inherent tension between its production systems and the ecosystems on which they depend [1]. Since the mid-20th-century Green Revolution, global agricultural output has consistently increased through the adoption of high-yield crop varieties, intensified use of chemical inputs, mechanization, and expanded irrigation. Despite an increase of only approximately 9% in arable land, food production has nearly doubled, substantially alleviating global hunger [2]. However, this input-intensive growth model has resulted in considerable environmental degradation. Agricultural expansion has become a major driver of land degradation, water depletion, biodiversity loss, and non-point source pollution [3]. Moreover, agriculture is the second-largest contributor to global greenhouse gas (GHG) emissions, accounting for approximately 25% of the total [4]. Key emission sources include fertilizer application in crop production, methane from enteric fermentation, and nitrous oxide from manure management [5]. Methane, with a global warming potential approximately 28 times that of carbon dioxide, has positioned livestock production as a critical focus in climate governance [6]. Simultaneously, climate change is exerting significant feedback effects on agricultural systems. Each 1 °C increase in temperature is projected to reduce yields of major staple crops by 3% to 7% [7], while heat stress lowers the nutritional value of forage and increases disease risks in livestock [8]. Based on multi-regional historical data, Ortiz-Bobea et al. (2021) estimated that global agricultural total factor productivity (TFP) has declined by approximately 21% due to climate change since 1960, equivalent to the loss of seven years’ worth of technological progress [9]. This stark result underscores the importance of distinguishing productivity growth from technical efficiency in assessing agricultural performance. Recent decompositions of TFP change reveal that technical progress and efficiency change play distinct roles in driving sector dynamics [10]. Total factor productivity—the ratio of aggregate outputs to inputs—captures long-term technological shifts and scale economies, whereas technical efficiency measures a producer’s proximity to the ‘best-practice’ frontier under current technology [11,12]. Key drivers of efficiency include farm size, input allocation, and governance structures [13], while TFP growth is fueled by R&D investment, climate variability, and policy support [14,15]. Integrating these perspectives—typically via DEA-based Slack-Based Measures combined with the Global Malmquist–Luenberger index—provides a nuanced framework for evaluating green agricultural transformation.

Amid the significant environmental challenges posed by conventional agricultural growth models and increasing climate change pressures, reconciling food security with ecological protection has become a central concern in global sustainable development. In this context, green total factor productivity (GTFP) has emerged as a critical indicator for assessing agricultural performance from an environmental sustainability perspective. Unlike traditional TFP, which accounts only for desirable outputs relative to inputs, GTFP explicitly incorporates undesirable outputs such as carbon emissions, thereby aligning resource allocation efficiency with ecological carrying capacity and embodying fundamental sustainability principles [16]. Rooted at the intersection of production efficiency theory and environmental economics, GTFP integrates environmental constraints into efficiency assessments to simultaneously capture economic and ecological outcomes. Methodologically, non-parametric data envelopment analysis (DEA) is commonly used to assess green efficiency, as it accommodates multiple inputs and outputs without requiring predefined functional forms [17]. The Slack-Based Measure (SBM), an advanced DEA variant, is particularly effective in detecting inefficiencies related to both input usage and undesirable outputs [18]. Extending this framework, the Global Malmquist–Luenberger (GML) index introduces a temporal dimension that overcomes the base-period dependence of traditional productivity measures, enabling dynamic tracking of technical progress and efficiency changes over time [19].

As methodologies have evolved, GTFP research has expanded across national and subnational levels, forming a relatively comprehensive analytical framework. Existing research has largely concentrated on the evolution and influencing factors of agricultural green transformation over time. For instance, using a non-radial SBM-GML model, researchers have found that GTFP in eastern China improved significantly, driven primarily by technological progress [20]. Others have employed panel fixed-effects models to demonstrate that the digital economy enhances agricultural GTFP, with green innovation acting as a mediating factor [21]. At the micro level, studies have explored green technology adoption and control of undesirable outputs. For example, Alem et al. (2023) incorporated methane emissions into the efficiency evaluation of Norwegian dairy farms and found that both farm size and technological capability had significant effects on green efficiency [22]. More recently, growing attention has been paid to the spatial heterogeneity of GTFP. Researchers have applied spatial analysis tools such as kernel density estimation, spatial autocorrelation, and Markov chains to investigate agricultural GTFP in major river basins, revealing significant club convergence patterns and spatial clustering mechanisms [23]. Others have employed Moran’s I, spatial clustering, and convergence models to trace the spatiotemporal evolution of county-level GTFP, confirming the presence of strong spatial dependence [24]. Liu et al. (2023) further found that urban expansion in eastern China exerted significant positive spatial spillover effects on agricultural GTFP, whereas western regions, constrained by weak infrastructure and ecological fragility, exhibited the opposite trend [25]. These findings underscore the growing spatial imbalance in the evolution of green efficiency.

Despite substantial progress, several key gaps remain. First, most existing studies have focused on agriculturally rich plains with well-developed infrastructure, such as the North China Plain and the Yangtze River Delta, while highland regions, particularly Tibet, have received limited attention. As a region with highly sensitive ecosystems and stringent resource constraints, Tibet offers a representative case for understanding green transitions in ecologically fragile areas and warrants deeper investigation. Second, studies have primarily analyzed GTFP at national or provincial scales, overlooking internal heterogeneity. In Tibet, agriculture can be categorized into farming, pastoral, and agro-pastoral zones, each with distinct natural endowments, production modes, input structures, and ecological pressures. These differences likely lead to divergent trajectories in green productivity, yet few studies have systematically compared these subregions. Third, much of the literature has focused on either farming or livestock production in isolation, ignoring the widespread presence of integrated agricultural systems. In practice, mixed systems such as crop-livestock integration and agro-pastoral rotation constitute the foundation of plateau agriculture and exhibit strong ecological-production coupling. Ignoring these system-level characteristics risks distorting green efficiency assessments and weakening the policy relevance of research findings.

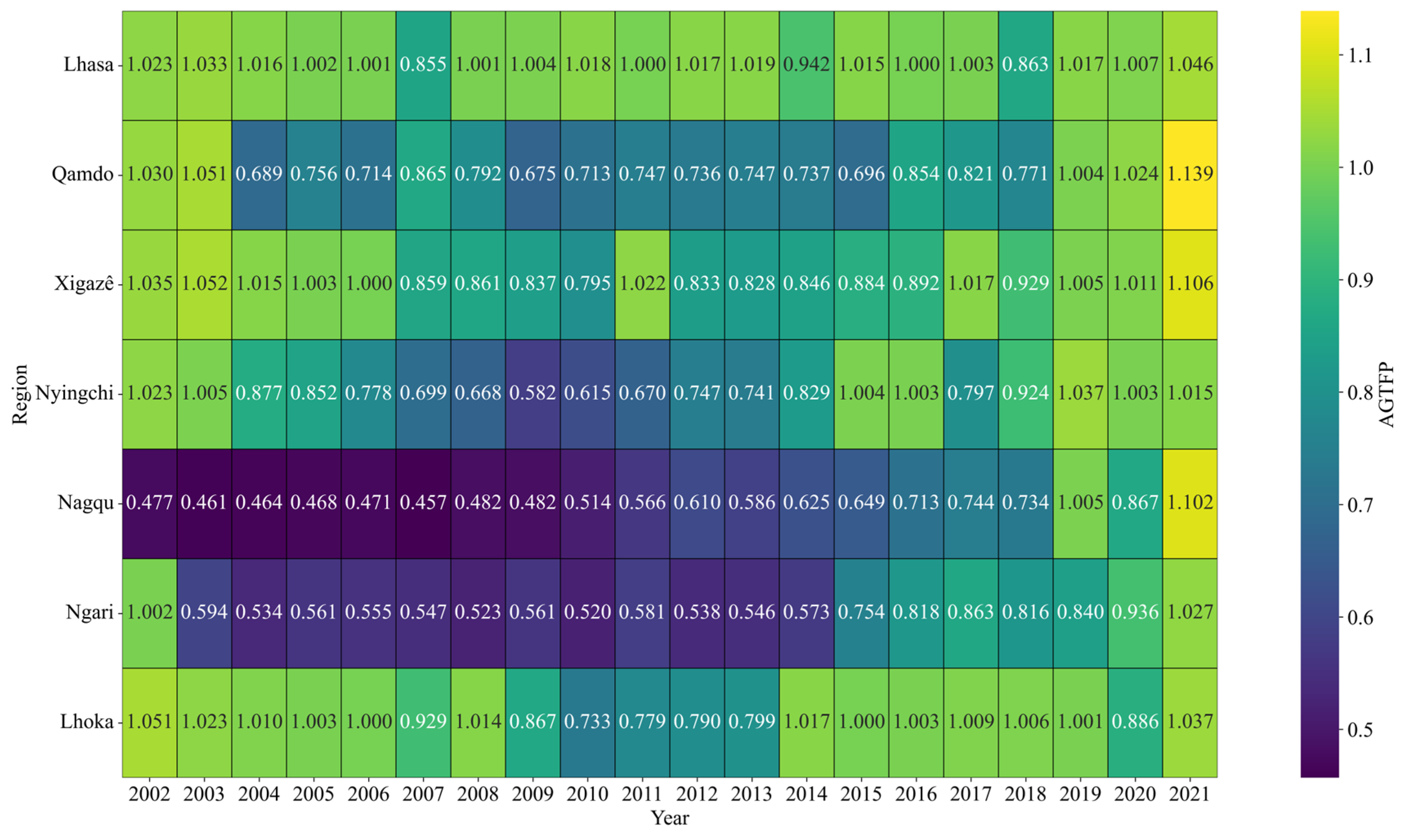
To address these gaps, this study focuses on Tibet’s farming, pastoral, and mixed farming–grazing areas and develops a tailored evaluation framework for integrated agricultural systems. We assess agricultural green total factor productivity (AGTFP) in seven Tibetan prefectures over the period 2002–2021 using an output-oriented super-efficiency Slack-Based Measure model paired with the Global Malmquist–Luenberger index, calculate input and regional redundancy rates to identify structural inefficiencies, decompose productivity change into technical efficiency and technological progress components, apply kernel density estimation to trace the temporal evolution of productivity distributions, and employ σ- and β-convergence tests to assess regional disparities and catch-up dynamics. By integrating systematic measurement, redundancy diagnostics, structural decomposition, distributional analysis, and convergence assessment, this approach delivers a granular evaluation of green agricultural productivity in fragile ecological regions and provides empirical insights to inform differentiated governance strategies for Tibet’s green agricultural transition.

The remainder of this paper is structured as follows. Section 2 describes the data sources, variable selection, and the definitions of productivity and efficiency. Section 3 outlines the methodological framework, including the super efficiency Slack-Based Measure model, the Global Malmquist–Luenberger index, and the convergence analysis methods. Section 4 presents the empirical results, including AGTFP measurement, efficiency decomposition, input and environmental redundancies, and spatiotemporal patterns. Section 5 discusses the key findings and their policy implications for promoting green agricultural development in Tibet. Section 6 concludes with a summary of the main contributions, limitations, and suggestions for future research.

2. Variable Selection and Data Sources

2.1. Construction of the Indicator System

In this study, productivity refers to the rate at which multiple inputs—land, labor, capital, and energy—are transformed into desirable outputs (crop and livestock value), net of undesirable by-products such as CO₂ emissions and nitrogen runoff. We capture productivity change with the Global Malmquist–Luenberger (GML) index, which accommodates both good and bad outputs while avoiding reference-period bias. Technical efficiency, by contrast, denotes each decision-making unit’s performance relative to an empirical best-practice frontier. We estimate technical efficiency using an output-oriented super-efficiency Slack-Based Measure (SBM) model, which both ranks fully efficient units and quantifies slack-based redundancies.

Agricultural production systems must not only pursue output maximization but also operate under resource constraints and environmental externalities. Coordinating energy use, ecological impacts, and social welfare is especially critical in ecologically fragile regions. Based on this principle, we constructed an indicator system that integrates both traditional and environmentally relevant variables for modeling AGTFP. Specifically, alongside traditional inputs like land, labor, capital, and energy, this study incorporated undesirable outputs—including CO₂ emissions and agricultural non-point source pollution—to account for the environmental impacts of agricultural activities. Additionally, carbon sequestration is included as a desirable output, representing the carbon capture ability and ecological services provided by agricultural ecosystems. This multi-dimensional framework enables a more comprehensive assessment of AGTFP by aligning resource use, environmental impacts, and productive outcomes. A detailed description of all variables is provided in

Table 1. Input–output indicator framework for assessing agricultural green total factor productivity (AGTFP) in Tibet.

Indicator’s Type	Indicator’s Name	Meaning	Units	Mean	Standard Deviation	Minimum	Maximum
Input	Labor	The number of agricultural employees	10 thousand people	13.25	8.27	2.86	30.94
	Mechanics	The total power of agricultural machinery	10,000 kW	1,027,546	1,111,395	83,433	6,641,743
	Land	The total planting area of crops	1000 HA	33.09	27.00	1.94	94.04
	Water	Effective irrigation area	1000 HA	19.94	23.26	0.10	90.78
	Fertilizer	The amount of pure fertilizer application	tons	6766	5515	9.00	23,068
	Pesticide	The use amount of pesticide	tons	151	189	0.00	1122
	Plastic sheeting	Consumption of agricultural plastic film	tons	156	246.00	0.00	1147
	livestock	Year-end inventory of livestock	10 thousand heads (only)	127	86	41.4	313.2
Desirable output	GDP	Gross Domestic Product of Agriculture and Animal Husbandry	10,000 yuan	178,000	152,000	23,737	660,179
	Carbon sink	Carbon sequestration in agricultural production	10,000 tons	14.50	13.00	0.41	47.13
Undesirable output	Non-point source pollution	Agricultural non-point source pollution and other standard emissions	10,000 tons	32.00	17.00	10.10	77.30
	Agricultural total carbon emissions	Total carbon emissions from agricultural production and livestock breeding	10,000 tons	0.33	0.24	0.04	0.79

.

2.1.1. Input Variables

Since the emergence of the classical factor production theory, models of agricultural input have evolved from a “three-factor” to a “four-factor” structure and, more recently, toward multi-factor extensions [26]. Building on this progression, we constructed a five-dimensional input framework encompassing labor, land, capital, water, and energy. This structure reflects both the operational fundamentals of agricultural systems and the critical resource constraints inherent to green efficiency assessments. Labor input was quantified as the total workforce engaged in agriculture, forestry, animal husbandry, and fisheries. Given that farming and pastoral activities account for over 98% of the primary sector in Tibet, this variable serves as a reliable proxy for regional labor allocation. Land input was represented by the total sown area of crops over the entire year. Compared with cultivated land area, this measure avoids potential bias arising from fallow or abandoned land [27]. We measured capital input using two main indicators: the quantity of fertilizer applied, standardized to pure nutrient content, and the year-end stock of draft animals. Pesticide and plastic film consumption were also incorporated to reflect resource use and environmental impact. Excessive application of these materials not only represents a substantial input but also generates pollution. Accordingly, both pesticide and plastic-film use serve dual roles in our model, functioning as conventional inputs and as undesirable outputs to reflect their ecological impacts [28]. Water input was measured by the area of effectively irrigated farmland, which reflects the dependency of agricultural production on water resources [29]. Energy input was proxied by the total horsepower of agricultural machinery, which compensates for missing data on actual energy consumption and operation time, and serves to indicate the level of mechanization and energy support capacity [30].

2.1.2. Desirable Outputs

To fully represent the beneficial outputs of the agricultural system, two desirable output indicators were chosen: the total value of crop and livestock production, and the amount of agricultural carbon sequestration. These reflect, respectively, the economic productivity and ecological service capacity of the system.

(1) 

Combined Agricultural Output

Since crop production and livestock raising together constitute more than 95% of Tibet’s primary sector, we adopted the combined gross output value of these two sectors as a desirable output indicator to accurately reflect regional agricultural performance. To control for price-level changes, reported nominal values were adjusted to 1993 constant yuan by applying the National Bureau of Statistics’ agricultural product price index to ensure temporal consistency and cross-period comparability.

(2) 

Carbon Fixation in Crop Production

Agricultural carbon sequestration captures the total quantity of atmospheric CO₂ that is assimilated by crops via photosynthetic activity throughout their growth period. This serves as a crucial indicator for assessing the carbon sequestration capacity of agricultural ecosystems [31]. In this study, we estimated sequestration based on the yield and physiological characteristics of representative staple and cash crops. The carbon sequestration volume was calculated using the following formula:

$$CS={\displaystyle \sum _{i=1}^{m}C{S}_i}={\displaystyle \sum _{i=1}^m{c}_{si}}\times Y_i\times {\displaystyle \frac{1-Q_i}{H{I}_i}}$$

In the equation, $CS$ summarizes the total annual carbon sequestered by all $m$ crops in this study, while $C{S}_i$ gives the annual sequestration for each individual crop $i$; for every crop $i$, $c_{si}$ measures the amount of carbon captured per unit of organic matter produced through photosynthesis; $Y_i$ is its total yearly harvest; $Q_i$ denotes the moisture percentage at maturity; and $H{I}_i$ converts economic yield into the equivalent carbon uptake. Only the principal crops—those with the largest cultivation areas, highest yields, and greatest economic importance—are included in these calculations (see Appendix A,

Table A1. Conversion factors, moisture contents at harvest, and carbon fixation rates for the principal crops in this study.

Crop	Yield-to-Carbon Conversion Factor	Harvest Moisture (%)	Carbon Absorption Rate	Reference
Tibetan hull-less barley	0.51	12	0.485	[57,58,59]
Wheat	0.40	12	0.49	[57,58]
Forage grass	0.34	70	0.15	[58,60]
Rapeseed	0.25	10	0.45	[58,61]
Vegetables	0.6	90	0.45	[58,62]

).

2.1.3. Undesirable Outputs

The selection of undesirable outputs remains a central concern in the evaluation of green agricultural production efficiency. Although no universal standard has been established, the prevailing consensus identifies agricultural non-point source (NPS) pollution and greenhouse gas (GHG) emissions as the two major environmental burdens adversely affecting agricultural ecological performance.

On one hand, agricultural NPS pollution is widely recognized as a critical undesirable output [32,33]. It originates primarily from fertilizer and pesticide residues, livestock waste, and agricultural by-products. Characterized by wide spatial distribution, high concealment, and strong heterogeneity, NPS pollution has been a major driver of eutrophication and ecological degradation in freshwater systems [34]. It is also difficult to monitor, costly to mitigate, and imposes substantial environmental externalities. On the other hand, agricultural activities have been identified by the Intergovernmental Panel on Climate Change (IPCC, 2007) as a significant source of greenhouse gas emissions [35]. Operations such as mechanized tillage, fertilizer application, and pesticide spraying contribute large amounts of carbon dioxide (CO₂), methane (CH₄), and nitrous oxide (N₂O). Agricultural carbon emissions are estimated to constitute about 17% of China’s total emissions [36], making the sector critical to achieving the national carbon peak and neutrality goals.

Accordingly, we treat agricultural non-point source pollution and carbon emissions as by-products in the model, thus accounting for ecological costs and boosting the environmental responsiveness and methodological rigor of the AGTFP evaluation. The specific components are outlined below:

(1) 

Agricultural Non-Point Source Pollution

Following the inventory analysis method developed by Tsinghua University and the Handbook of Emission Coefficients for the Second National Census of Pollution Sources (Agricultural Sources), we systematically estimated the intensity of NPS pollution in Tibet. The analysis focused on two primary sources: fertilizer runoff and livestock waste. Specifically, we selected the annual application of nitrogen and phosphate fertilizers (in pure nutrient form), as well as the year-end inventory of cattle, sheep, and pigs, as the core indicators. The corresponding pollutants include total nitrogen (TN), total phosphorus (TP), and chemical oxygen demand (COD). A detailed inventory of NPS pollution indicators is provided in Appendix A,

Table A2. Emission inventory for agricultural non-point-source pollutants.

Source Category	Survey Unit	Indicator	Unit	Tracked Pollutants
Synthetic fertilizer use	Nitrogen and phosphorus	Pure-equivalent application	10,000 tone	TN, TP
Animal production sector	Cattle, sheep, pigs	Year-end livestock numbers	10,000 heads	COD, TN, TP

.

Nutrient losses from fertilizer were quantified by multiplying annual nitrogen and phosphorus inputs by their respective runoff coefficients to obtain TN and TP emissions. Animal-source pollutants were computed using end-of-year livestock counts together with Tibet-specific generation and excretion factors for COD and other contaminants. Considering Tibet’s highly integrated rural ecosystems, inputs from household waste and straw burning were judged negligible and thus omitted. Pollutant loads were calculated using the following formula:

$$P_j={\displaystyle \sum _i(Q_i}\times E_i),$$

In this formulation, $P_j$ denotes the total emissions of pollutant $j$; $Q_i$ is the scale of the source $i$ (for instance, fertilizer input or livestock stock at year-end), and $E_i$ represents the per-unit emission factor. Subsequently, the yearly emissions for each pollutant category (COD, TN, TP) are computed as follows:

$$P_{\mathrm{COD}}={\displaystyle \sum _i(Q_i}\times E_i^{\mathrm{COD}}),P_{\mathrm{TN}}={\displaystyle \sum _i(Q_i}\times E_i^{\mathrm{TN}}),P_{\mathrm{TP}}={\displaystyle \sum _i(Q_i}\times E_i^{\mathrm{TP}}).$$

To standardize units and enable aggregation, all emissions were converted into equivalent standardized loadings based on Class III thresholds from the Environmental Quality Standards for Surface Water (GB 3838-2002) [37], where COD = 20 mg/L, TN = 1 mg/L, and TP = 0.2 mg/L. The equivalent standardized emission for each pollutant was computed as follows:

$$P_{\mathrm{eq},\mathrm{COD}}={\displaystyle \frac{P_{\mathrm{COD}}}{20\left[\mathrm{mg}/\mathrm{L}\right]}},P_{\mathrm{eq},\mathrm{TN}}={\displaystyle \frac{P_{\mathrm{TN}}}{1\left[\mathrm{mg}/\mathrm{L}\right]}},P_{\mathrm{eq},\mathrm{TP}}={\displaystyle \frac{P_{\mathrm{TP}}}{0.2\left[\mathrm{mg}/\mathrm{L}\right]}}.$$

Finally, the comprehensive indicator for agricultural non-point source pollution was calculated by summing the standardized emissions of all three pollutants:

$$P_{\mathrm{total}}=P_{\mathrm{eq},\mathrm{COD}}+P_{\mathrm{eq},\mathrm{TN}}+P_{\mathrm{eq},\mathrm{TP}}.$$

(2) 

Estimation of Agricultural Carbon Emissions

Drawing on the IPCC’s 2006 guidelines and established studies in the field [38], we grouped farm-based carbon inputs into four categories—synthetic fertilizers, pesticide applications, mulch films, and tillage practices—and calculated their combined emissions using an activity-driven model:

$$C_{\mathrm{total}}={\displaystyle \sum _i{C}_i}={\displaystyle \sum _i{T}_i}\times {\delta }_i$$

In this formulation, $C_{\mathrm{total}}$ signifies the total agricultural carbon emissions (kg CO₂e), $T_i$ indicates the activity level for source $i$, and ${\delta }_i$ denotes its specific emission factor. Reference values from existing studies are listed in Appendix A,

Table A3. Carbon Source Categories, Emission Factors, and Literature Citations.

Carbon Source	Carbon Emission Coefficient	Source
Fertilizer	0.8956 kg CO2e·kg−1	Oak Ridge National Laboratory, ORNL
Pesticides	4.9341 kg CO2e·kg−1	Oak Ridge National Laboratory, ORNL
Agricultural plastic sheeting	5.18 kg CO2e·kg−1	Institute of Resources, Ecosystem and Environment of Agriculture, IREEA, Nanjing Agricultural University
Agricultural ploughing	312.6 kg CO2e·km−1	Institute of Agriculture and Biotechnology of China Agricultural University, IABCAU

.

(3) 

Livestock Carbon Emissions

Greenhouse gas emissions from animal husbandry arise principally from enteric fermentation—yielding methane (CH₄)—and manure management, which emits both CH₄ and nitrous oxide (N₂O). In accordance with the IPCC’s 2019 Refinement to the 2006 Guidelines for National Greenhouse Gas Inventories, we quantified emissions for three representative groups—pigs, cattle (including yaks), and sheep. Annual emissions for each group were then calculated using the following equation:

$$C_{\mathrm{livestock}}={\displaystyle \sum _i{A}_i}(E{F}_{i,{\mathrm{CH}}_4}^{\mathrm{enteric}}\times {\mathrm{GWP}}_{{\mathrm{CH}}_4}+E{F}_{i,{\mathrm{CH}}_4}^{\mathrm{manure}}\times {\mathrm{GWP}}_{{\mathrm{CH}}_4}+E{F}_{i,{\mathrm{N}}_2\mathrm{O}}^{\mathrm{manure}}\times {\mathrm{GWP}}_{{\mathrm{N}}_2\mathrm{O}})$$

In this formula, $C_{\mathrm{livestock}}$ denotes the total annual greenhouse gas emissions from livestock production (kg CO₂e), while $A_i$ represents the year-end population of livestock type $i$; the coefficients $E{F}_{i,{\mathrm{CH}}_4}^{\mathrm{enteric}},E{F}_{i,{\mathrm{CH}}_4}^{\mathrm{manure}},E{F}_{i,{\mathrm{N}}_2\mathrm{O}}^{\mathrm{manure}}$ correspond to emission factors for enteric methane, manure-related CH₄, and manure-derived N₂O, respectively; and the coefficients ${\mathrm{GWP}}_{{\mathrm{CH}}_4}=28$, ${\mathrm{GWP}}_{{\mathrm{N}}_2\mathrm{O}}=265$ were derived from the IPCC Fifth Assessment Report [39]. Appendix A,

Table A4. Emission Coefficients for Representative Livestock Types.

Livestock Species	CH4-Enteric (kg/Head·yr)	CH4-Manure (kg/Head·yr)	N2O-Manure (kg/Head·yr)	GHG Intensity (kg CO2e/Head·yr)
Pig	1	5.08	0.175	68
Cattle (including yak)	78.8	5.82	1.456	774.4
Sheep	9.1	0.27	0.113	107.3

, summarizes the CH₄ and N₂O emission coefficients for major livestock species, along with their associated CO₂-equivalent intensities.

2.2. Data Sources

The analysis was conducted at the prefecture level, encompassing all seven administrative regions within the Tibet Autonomous Region over the 2002–2021 period. The dataset includes key agricultural input variables, desired outputs, and undesirable outputs. Most of the core variables—including agricultural labor, cultivated area, input usage, and output value—were derived from official statistical records covering 2003 to 2022, primarily the Tibet Statistical Yearbook. To construct the environmental constraint indicators, relevant parameters on diffuse pollution and carbon emissions were obtained from two primary sources: the Manual of Discharge Coefficients for Agricultural Pollution (Second National Census of Pollution Sources) and the IPCC’s 2019 Refinement to the 2006 Guidelines for National Greenhouse Gas Inventories. Region-specific coefficients for Tibet were used to ensure scientific rigor and contextual relevance.

For missing values in specific years or variables, we applied linear interpolation in accordance with each series’ temporal profile, covering eight of 147 prefecture-year records (5.4%) for fertilizer use and seven of 147 records (4.8%) for irrigated area. This smoothing method improved dataset continuity and comparability, preserved the robustness and precision of AGTFP estimates, and avoided biases associated with sample deletion, thereby ensuring data integrity for dynamic trend analyses.

3. Modeling Approach

3.1. Efficiency Evaluation Using the Super-SBM Model

In economic production activities, inputs such as labor, capital and energy yield desired outputs but also generate undesirable by-products, notably CO₂ emissions [40]. To account for these undesirable outputs in efficiency analysis, Tone in 2001 developed the Slack-Based Measure (SBM) model, which incorporates such outputs directly into the assessment, thereby providing a more realistic representation of production processes [41]. Since then, the SBM approach has seen widespread application in assessing carbon emission performance [42], ecological efficiency [43], and energy efficiency [44]. Unlike traditional data envelopment analysis models, SBM accounts simultaneously for input and output slacks, producing more precise efficiency scores when undesirable outputs are present [45]. A common challenge in DEA studies is that many decision-making units (DMUs) appear fully efficient and cannot be further discriminated. To overcome this limitation, Tone in 2002 developed the super-efficiency SBM model, which excludes the target DMU from its reference set and allows efficiency scores to exceed one. This modification permits ranking of efficient units and identification of performance drivers. The super-efficiency SBM model’s non-radial, non-oriented structure prevents bias from arbitrary direction choices and enhances the objectivity and robustness of efficiency assessments [46]. For these reasons, it is ideally suited to evaluate AGTFP and its spatial heterogeneity.

In this framework, each decision-making unit (DMU) is modeled as operating a production system characterized by three variable sets: input vector $x\in R^m$, desirable output vector $y\in R^s$, and undesirable output vector $b\in R^t$. Suppose there are $n$ DMUs in total. The corresponding input and output data are organized into the following matrices:

$$X=\left[x_{ij}\right]\in R^{m\times n},Y=\left[Y_{rj}\right]\in R^{s\times n},B=\left[b_{\mathcal{l}j}\right]\in R^{t\times n}$$

Let $x_{ij}$ denote the quantity of the $i$th input associated with the $j$th DMU; $y_{rj}$ indicate the amount of the rth desirable output produced by the $j$th DMU; and $b_{\mathcal{l}j}$ represent the level of the $\mathcal{l}$th undesirable output corresponding to the $j$th DMU.

By incorporating the weight vector $\lambda \in R_{+}^n$, the production possibility set is defined as follows:

$$P=\left\{(x,y,b)\left|x=X\lambda ,y=Y\lambda ,b=B\lambda ,\lambda \ge 0\right.\right\}$$

A DMU is considered inefficient if its observed desirable output falls short of the optimal level on the production frontier or if its undesirable output exceeds the frontier benchmark [47]. To capture such inefficiencies, Tone introduced the Slack-Based Measure (SBM) model, which explicitly accounts for input and output slacks in the efficiency assessment. The model’s original nonlinear formulation, prior to linearization, is given as follows:

$$\min \rho ={\displaystyle \frac{1-\frac{1}{m}{\displaystyle {\sum }_{i=1}^m\frac{s_i^{-}}{x_{io}}}}{1+\frac{1}{s+t}\left({\displaystyle {\sum }_{r=1}^s\frac{s_r^{+}}{y_{ro}}}+{\displaystyle {\sum }_{\mathcal{l}=1}^t\frac{s_{\mathcal{l}}^b}{b_{\mathcal{l}o}}}\right)}}, s.t.\left\{\begin{array}{l}{x}_o=X\lambda +s^{-}, s^{-}\ge 0, \lambda \ge 0\\ y_o=Y\lambda -s^{+}, s^{+}\ge 0, \lambda \ge 0\\ b_o=B\lambda +s^b, s^b\ge 0, \lambda \ge 0\end{array}\right.$$

In this formulation, $s_i^{-}$, $s_r^{+}$, and $s_{\mathcal{l}}^b$ correspond to the excesses or shortfalls in inputs, desirable outputs, and undesirable outputs, respectively. The objective function value $\rho$ reflects the efficiency score of the DMU, taking values within the interval [0, 1]. When $\rho =1$ and all slack variables are zero, the DMU lies on the efficient frontier; when $0\le \rho <1$, the DMU is inefficient, indicating that its inputs and outputs require adjustment.

To facilitate computational tractability, the Charnes–Cooper transformation is applied to reformulate the original nonlinear model into a mathematically equivalent linear programming problem [48]. The resulting linear expression is given as follows:

$$\max \rho \ast ={\displaystyle \frac{1+\frac{1}{s+t}\left({\displaystyle {\sum }_{r=1}^s\frac{s_r^{+}}{y_{ro}}}+{\displaystyle {\sum }_{\mathcal{l}=1}^t\frac{s_{\mathcal{l}}^b}{b_{\mathcal{l}o}}}\right)}{1-\frac{1}{m}{\displaystyle {\sum }_{i=1}^m\frac{s_i^{-}}{x_{io}}}}}, s.t.\left\{\begin{array}{l}{x}_o=X\lambda +s^{-}\\ y_o=Y\lambda -s^{+}\\ b_o=B\lambda +s^b\\ \lambda \ge 0, s^{-}\ge 0, s^{+}\ge 0, s^b\ge 0\end{array}\right.$$

Assuming constant returns to scale (CRS), the Super-SBM model lifts the efficiency cap present in conventional DEA frameworks, enabling efficiency scores of fully efficient DMUs to surpass 1. This feature enables the effective ranking and discrimination of units operating on the efficiency frontier. Moreover, the model is capable of identifying input redundancies and excess undesirable outputs, thereby providing a more precise assessment of the potential for efficiency improvement across regions. Leveraging these advantages, this paper employs the Super-SBM model to assess the temporal evolution of AGTFP across Tibet’s seven prefectures between 2002 and 2021. This methodology furnishes a robust framework for detecting spatial variations in green technology advancement and efficiency in resource utilization.

3.2. Global Malmquist–Luenberger Index

This study adopts the Global Malmquist–Luenberger (GML) index to capture the temporal dynamics of AGTFP in Tibet, explicitly integrating undesirable outputs into the efficiency analysis. Originally proposed by Oh in 2010 and later extended by Tone and Tsutsui, the GML index constructs a unified global reference technology set, thereby eliminating the base-period dependency that often distorts traditional TFP estimates. Due to its strong temporal consistency and dynamic robustness, the GML index has been widely adopted in long-term studies on environmental efficiency and green technological progress [19,45].

Let there be $n$ decision-making units (DMUs). At any given time $t$, each DMU is characterized by an input vector $x\in R_{+}^m$, a desirable output vector $y\in R_{+}^s$, and an undesirable output vector $b\in R_{+}^q$. Let $g=(-x,y,-b)$ denote the directional vector. Based on the global reference technology set $P^G$, the directional distance function is defined as follows:

$$D_0^g(x,y,b)=\max \left\{\beta \left|(x-\beta x^g,y+\beta y^g,b-\beta b^g)\in P^G\right.\right\}$$

Accordingly, the Global Malmquist–Luenberger (GML) index is defined as follows:

$$GM{L}_t^{t+1}={\displaystyle \frac{1+D_0^g(x^{t+1},y^{t+1},b^{t+1}\left|P^G\right.)}{1+D_0^g(x^t,y^t,b^t\left|P^G\right.)}},$$

where $D_0^g(•)$ denote the directional distance functions at time $t$ and $t+1$, respectively, based on the global reference technology set. $GM{L}_t^{t+1}>1$ indicates an improvement in AGTFP, while a value less than 1 suggests a decline.

The change in AGTFP measured using the GML index can be further decomposed into two primary components: efficiency change (EC) and technical change (TC). The EC component captures improvements in resource allocation efficiency and management performance under existing technological conditions, reflecting how effectively a decision-making unit utilizes its available resources in green production. The TC component reflects the movement of the technological frontier, capturing the advancement and diffusion of environmentally friendly innovations—such as the adoption of clean technologies and sustainable crop-livestock systems—across regions.

$$GM{L}_t^{t+1}=E{C}_t^{t+1}\times T{C}_t^{t+1}$$

The efficiency change (EC) component is defined as follows:

$$E{C}_t^{t+1}={\displaystyle \frac{1+D_0^g(x^{t+1},y^{t+1},b^{t+1}\left|P^G\right.)}{1+D_0^g(x^t,y^t,b^t\left|P^G\right.)}}$$

The technical change (TC) component is given by the following:

$$T{C}_t^{t+1}={\displaystyle \frac{1+D_0^g(x^{t+1},y^{t+1},b^{t+1}\left|P^{G+1}\right.)}{1+D_0^g(x^{t+1},y^{t+1},b^{t+1}\left|P^G\right.)}}\times {\displaystyle \frac{1+D_0^g(x^t,y^t,b^t\left|P^G\right.)}{1+D_0^g(x^t,y^t,b^t\left|P^t\right.)}},$$

where $E{C}_t^{t+1}$ reflects changes in relative efficiency with respect to the global production frontier, and $T{C}_t^{t+1}$ captures the shift of the frontier itself between periods $t$ and $t+1$, representing the pace of technological advancement.

Methods like stochastic frontier analysis (SFA) and parametric TFP indices offer valuable perspectives; however, they exhibit constraints when applied to our specific context. SFA separates inefficiency from statistical noise but relies on a specified production function and distributional assumptions. Parametric indices enable productivity decomposition, yet struggle to incorporate undesirable outputs or to rank fully efficient units. By contrast, our nonparametric DEA framework, combined with the Global Malmquist–Luenberger index, imposes no functional form, handles multiple inputs, as well as both desirable and undesirable outputs, and eliminates reference-period bias. Using an output-oriented super-efficiency Slack-Based Measure further improves discrimination among efficient decision-making units by excluding the target unit from the reference set and directly quantifying slacks. This integrated approach offers a robust, flexible, and temporally consistent method for assessing AGTFP and its spatial heterogeneity in Tibet.

3.3. Kernel Density Estimation

To characterize the spatiotemporal evolution of AGTFP in Tibet, this study applied a kernel density estimation approach to the Super-SBM results. By nonparametrically fitting the distribution of AGTFP values across years, this method enables the identification of distributional shifts in efficiency levels, including tendencies toward convergence, dispersion, or polarization [49]. To facilitate periodical comparisons, this study divided the sample period into four distinct stages:

The analysis spans four intervals: 2002–2006 (China’s Tenth Five-Year Plan, T₁ = 5), 2007–2011 (Eleventh Five-Year Plan, T₂ = 5), 2012–2016 (Twelfth Five-Year Plan, T₃ = 5), and 2017–2021 (Thirteenth Five-Year Plan, T₄ = 5).

If period $(p=1,2,3,4)$ spans $T_p$ years, the total number of AGTFP observations across the seven prefectures in that interval is $n_p=7\times T_p$, denoted by $G_i^{(p)},i=1,2,\dots ,n_p$. For any real value $x$, the kernel density estimator for period $p$ is defined as follows:

$${\widehat{f}}_p(x)={\displaystyle \frac{1}{n_p{h}_p}}{\displaystyle \sum _{i=1}^{n_p}K\left(\frac{x-G_i^{(p)}}{h_p}\right)}$$

In this context, ${\widehat{f}}_p(x)$ represents the smoothed density estimate of AGTFP for period $p$; $n_p=7\times T_p$; $G_i^{(p)}$ denotes the AGTFP value of the $i$th prefecture in period $p$; and $h_p>0$ is the bandwidth parameter, employing the Gaussian kernel function $K(u)={\displaystyle \frac{1}{\sqrt{2\pi }}}\exp \left(-{\displaystyle \frac{1}{2}}{u}^2\right)$.

3.4. Convergence Analysis

To systematically examine regional disparities and convergence patterns of AGTFP across different ecological zones in Tibet—including agricultural, pastoral, and agro-pastoral transitional areas—this study employed both σ-convergence and β-convergence models. These approaches allow for empirical assessment of the evolution of efficiency distribution, identifying trends in regional dispersion and the potential for catch-up among low-performing areas.

(1)

σ-convergence

σ-convergence investigates whether the intertemporal variation in AGTFP across observational units tends to decline over time. For any group of units (e.g., the entire region or a specific ecological zone) in year $t$, let $N$ denote the number of units, $G_{i,t}$ the AGTFP of unit $i$, and ${\overline{G}}_t={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N{G}_{i,t}}$ the average AGTFP of the group. The standard deviation of AGTFP in year $t$ is then defined as follows:

$${\sigma }_t=\sqrt{{\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N{(G_{i,t}-{\overline{G}}_t)}^2}}$$

If the standard deviation continues to decline for all observed periods, it suggests that AGTFP disparities within the group are converging over time, indicating a reduction in intra-regional differences.

(2)

β-convergence

The absolute β-convergence test evaluates whether AGTFP across different units tends to converge toward a common steady state in the absence of heterogeneity. Let $t$ and $t+N$ denote the two time periods of interest. The following regression equation is estimated for each unit:

$$\ln G_{i,t+T}-\ln G_{i,t}=\alpha +\beta \ln G_{i,t}+{\epsilon }_i$$

Let $G_{i,t}$ and $G_{i,t+T}$ represent the AGTFP values of unit $i$ at the initial and final periods, respectively; $T$ denotes the number of years between the two periods; $\alpha$ and $\beta$ are the parameters to be estimated; and ${\epsilon }_i$ is the random error term.

If the estimated coefficient $\beta <0$ and is statistically significant, this indicates the existence of absolute convergence in AGTFP across units. The annual rate of convergence is then given by $\lambda =-{\displaystyle \frac{1}{T}}\ln (1+\beta )$.

Conditional β-convergence takes into account unit-specific heterogeneity in economic development, resource endowment, and natural conditions. It assesses whether AGTFP converges toward each unit’s own steady state.

We applied a two-way fixed effects panel model, with the conditional β-convergence specified as follows:

$$\ln G_{i,t+1}-\ln G_{i,t}={\alpha }_i+{\delta }_t+\beta \ln G_{i,t}+{\gamma }^{\prime }{X}_{i,t}+{\epsilon }_{i,t}$$

In this specification, ${\alpha }_i$ denotes the individual (unit-specific) fixed effect, and ${\delta }_t$ captures the time fixed effect. $X_{i,t}$ represents a vector of control variables, $\gamma$ denotes the corresponding vector of coefficients, ${\epsilon }_{i,t}$ is the random disturbance term, and $\beta$ is the convergence coefficient. If the estimated $\beta <0$ and is statistically significant, it indicates the presence of conditional β-convergence. In this case, the annual convergence rate can be computed as $\lambda =-\ln (1+\beta )$.

4. Results and Analysis

4.1. Estimation of AGTFP and Component Decomposition

Applying the AGTFP framework outlined above, AGTFP for Tibet’s seven prefectures over 2002–2021 was computed using MaxDEA 7.0.

4.1.1. AGTFP Estimates for Tibet

The estimation results, shown in Figure 1, reveal substantial spatial heterogeneity in AGTFP across Tibet’s seven prefectures from 2002 to 2021, with an extreme variation of 128.2%. Overall, AGTFP exhibited an upward trend, growing at an average annual rate of 0.78%, although this lagged behind the national average of 1.6% during the same period [50]. Post-2010, the growth rate surged to 4.13%, coinciding with the rollout of major initiatives—most notably the Tibet Ecological Security Barrier Protection and Construction Plan (2008–2030)—thereby illustrating the pivotal role of ecological policies in driving green transformation. Regional disparities followed a three-stage dynamic pattern of convergence, divergence, and reconvergence, reflecting the complex adaptive nature of the plateau agricultural system.

Regarding overall trends, AGTFP across Tibet’s regions generally fluctuated between 2002 and 2021, with most areas showing neither sustained growth nor consistent decline but oscillating within specific ranges. Particularly during 2019–2021, many regions experienced a collective rebound or stabilization at higher levels, indicating significant progress in green agricultural development in the latter period. Regionally, Lhasa, Xigazê, and Lhoka consistently maintained high AGTFP levels—often near or above 1.0—with limited fluctuation, suggesting a strong foundation in green agriculture and relatively efficient resource allocation. Conversely, Qamdo and Nyingchi exhibited a reverse trajectory, characterized by initially low AGTFP values followed by steady recovery, especially after notable declines from 2004 to 2010, driven by the expansion of green technologies and ecological restoration initiatives. In contrast, Nagqu and Ngari displayed persistently low AGTFP values, particularly between 2002 and 2010, with most years below 0.6 and occasional dips below 0.5 (e.g., Nagqu in 2002: 0.477; Ngari in 2004: 0.534). These results reflect weaker green agricultural development and more severe ecological and resource constraints in these regions.

4.1.2. Input and Environmental Redundancy Analysis

Based on the AGTFP measurements and dynamic analysis for Tibet’s seven regions from 2002 to 2021, this section further explores the structural factors underlying low-efficiency performance. Focusing on periods when AGTFP values fell below one, we calculated the redundancy and insufficiency rates of key input–output variables, including labor, land, agricultural inputs, livestock inventory, and carbon emissions. The results indicate that insufficiency rates were close to zero in most cases, suggesting a lack of significant underinvestment in resource inputs. Consequently, our analysis concentrates on redundancy rates, which measure the extent to which actual inputs or emissions exceed the efficiency frontier and thus reveal primary constraints on production efficiency (see

Table 2. Average redundancy rates (%) during inefficient years (super-efficiency score < 1) across seven regions in Tibet, 2002–2021.

Indicator	Ngari	Qamdo	Lhasa	Nyingchi	Nagqu	Xigazê	Lhoka
Primary sector employment	0.75	0.86	0.16	0.28	1.53	0.47	0.21
Sown crop area	0.31	0.16	0.03	0.26	0.00	0.03	0.01
Total agricultural machinery power	0.00	0.00	0.00	0.00	0.00	0.00	0.00
Effectively irrigated farmland	0.60	0.05	0.01	0.23	0.29	0.03	0.05
Fertilizer application	0.00	0.00	0.00	0.00	0.01	0.00	0.00
Pesticide use	0.50	0.06	0.04	0.08	5.17	0.03	0.03
Plastic film use	0.08	0.06	0.03	0.04	13.62	0.01	0.03
Livestock inventory	0.14	0.10	0.00	0.01	0.20	0.02	0.01
Non-point source pollution	0.24	0.09	0.10	0.17	0.24	0.01	0.13
Carbon emissions	6.67	29.33	3.45	0.00	69.44	16.31	29.27

).

Among the production factors, labor redundancy was the most prominent. Regions such as Nagqu (1.53%), Qamdo (0.86%), and Ngari (0.75%) exhibited relatively high redundancy rates in agricultural labor, indicating persistent underutilization of labor resources in pastoral areas characterized by harsh natural conditions and limited industrial diversification. In contrast, more economically developed regions like Lhasa and Lhoka reported substantially lower redundancy rates (approximately 0.2%), reflecting a more optimized labor allocation.

Redundancy in land and irrigation resources was generally lower but displayed notable regional variation. The redundancy rate for sown cropland remained below 0.3% across all regions, implying relatively efficient land use even during low-efficiency periods. However, in ecologically fragile or water-scarce areas such as Ngari (0.60%), Nagqu (0.29%), and Nyingchi (0.23%), irrigated farmland exhibited higher redundancy rates, suggesting diminishing marginal returns on irrigation infrastructure in these specific zones.

Regarding capital inputs, both total agricultural machinery power and fertilizer application exhibited zero redundancy, indicating high resource-use efficiency even during low-efficiency periods. This suggests rational input behavior in the deployment of core agricultural materials across the region. However, pesticide and plastic film inputs revealed localized redundancy issues. In Nagqu, pesticide redundancy reached 5.17% and plastic film redundancy 13.62%, substantially exceeding levels in other regions (generally below 0.1%). These anomalies likely result from inadequate substitution by green technologies, heavy reliance on chemical pest control, and excessive use of plastic mulching, all of which pose significant environmental risks. Livestock inventory redundancy was concentrated in Ngari (0.14%) and Nagqu (0.20%). Within the ecological constraints of grassland systems, sustained overstocking diminishes resource-use efficiency and exacerbates grassland degradation and ecological imbalance. This issue was markedly less pronounced in southeastern farming regions, reflecting regional variations in ecological carrying capacity under the agro-pastoral division.

Redundancy in undesirable environmental outputs presents an even greater concern. While non-point source pollution exhibited limited redundancy (maximum below 0.24%), suggesting relatively controlled pollution in Tibet’s ecologically sensitive zones—likely due to low fertilizer usage and more sustainable farming practices—carbon emission redundancy showed stark spatial variation. Redundancy rates peaked at 69.44% in Nagqu, exceeded 29% in Qamdo and Lhoka, and reached 16.31% in Xigazê, whereas Nyingchi reported no redundancy. These findings highlight that livestock-related methane emissions from enteric fermentation and nitrous oxide from manure management are principal carbon sources in pastoral areas, substantially constraining AGTFP. Notably, Nagqu sustained an average of 2.81 million livestock units during low-efficiency years, far surpassing the 640,000 units in Ngari, explaining its exceptionally high carbon emission redundancy. The spatial clustering of carbon-intensive zones underscores the “high-cost, low-substitution” dilemma facing green transitions in alpine pastoral regions.

In summary, efficiency losses in Tibet’s agricultural system exhibit distinct structural and spatial characteristics. Labor and livestock redundancies are concentrated in high-altitude pastoral regions; pesticide and plastic film redundancies are localized; carbon emission redundancy is spatially polarized, while key capital inputs such as machinery and fertilizer show minimal redundancy. This pattern of “concentrated redundancy” suggests that strategies to enhance green efficiency should eschew uniform approaches and instead target specific inefficiencies with regionally tailored input controls and ecological management interventions.

4.1.3. Decomposition of AGTFP Efficiency in Tibet

To uncover the structural sources of AGTFP change in Tibet, we applied the Global Malmquist–Luenberger index and decomposed it into efficiency change (EC) and technological change (TC). We further disaggregated EC into pure technical efficiency (PEC) and scale efficiency (SEC).

Table 3. Annual average ML index and its decomposition for AGTFP in Tibet’s seven regions (2002–2021).

Region	EC	TC	PEC	SEC	ML
Ngari	1.002	1.010	0.998	1.014	1.011
Qamdo	0.998	1.022	1.005	0.995	1.022
Lhasa	1.002	1.003	1.002	1.000	1.004
Nyingchi	0.997	0.999	1.034	0.983	0.997
Nagqu	0.994	1.085	0.992	1.011	1.074
Xigazê	1.004	0.991	1.001	1.004	0.997
Lhoka	1.006	0.997	1.003	1.002	1.003

reports the annual averages of these indices for Tibet’s seven prefectures over 2002–2021.

Overall, AGTFP rose modestly. In five prefectures, the Malmquist–Luenberger index exceeded one, signalling general gains in green productivity. Nagqu (1.074) and Qamdo (1.022) achieved the largest advances, followed by Ngari (1.011) and Lhasa (1.004). In contrast, Nyingchi (0.997) and Xigazê (0.996) registered slight declines, reflecting periods of stagnation or insufficient innovation.

Technological change drove most of these improvements. Five regions recorded TC values above unity, indicating continual adoption of green practices. Nagqu led with 1.085, likely supported by grassland conservation efforts, mechanized livestock systems, and ecological restoration policies. Qamdo (1.022) and Ngari (1.010) also showed strong technology uptake. By comparison, Nyingchi (0.999) and Xigazê (0.991) fell below one, suggesting lagging progress at the technological frontier.

Efficiency change varied more widely. Lhoka (1.006) and Xigazê (1.004) improved resource allocation and management under existing technology. Lhasa, Qamdo and Ngari remained near unity, indicating stable performance. Nyingchi (0.997) and Nagqu (0.994) declined slightly, revealing that technological advances outstripped gains in organizational and operational efficiency.

A closer look at efficiency components highlights distinct regional profiles. Nyingchi’s PEC of 1.034 suggests strong input management and governance despite modest AGTFP growth. By contrast, Nagqu (PEC = 0.992) and Ngari (PEC = 0.998) depended heavily on innovation with weaker management efficiency. Scale efficiency results further expose imbalances: Ngari (1.014), Xigazê (1.004) and Lhoka (1.002) approach optimal production scale, whereas Nyingchi (0.983) and Qamdo (0.995) exhibit scale mismatches that hinder full exploitation of new technologies.

In summary, AGTFP gains in Tibet stem chiefly from technological progress rather than broad-based efficiency improvements. Nagqu and Qamdo exemplify technology-driven growth, Lhasa and Lhoka maintain steady efficiency-led gains, and Nyingchi and Xigazê face dual challenges of efficiency recovery and technological catch-up. Policy should therefore align with each prefecture’s profile: sustain innovation investment in technology-led areas, support technology adoption where efficiency is strong, and strengthen governance and institutional frameworks in lagging regions to foster integrated productivity growth.

4.2. Temporal Evolution of AGTFP Distribution in Tibet

To examine the temporal evolution and spatial distribution of AGTFP in Tibet from 2002 to 2021, we applied kernel density estimation. As shown in Figure 2, the distribution of AGTFP followed a four-stage pattern: an early peak, a sharp decline, a gradual recovery and a final steady increase. During the 10th Five-Year Plan, the density curve was narrow and peaked between 1.00 and 1.05, indicating high green efficiency and strong regional convergence. In the 11th Five-Year Plan, the peak shifted left to around 0.75 and the curve flattened and widened, reflecting the lowest efficiency levels and the greatest disparities. Under the 12th Five-Year Plan, the distribution began moving right and narrowed, signalling a recovery in green efficiency. By the 13th Five-Year Plan, the peak surpassed 1.00 and the curve became steeper, demonstrating marked efficiency gains, the emergence of high-efficiency clusters and renewed convergence. Overall, these shifts describe an S-shaped diffusion process: a high starting level, a regression phase and a policy-driven rebound leading to consolidation.

At the prefecture level, Lhasa maintained its leading position throughout. Its density peak moved steadily to the right, and a secondary mode appeared in the 13th Five-Year Plan, suggesting the formation of multiple efficiency groups among farming actors. Xigazê showed a gradual rightward shift with consistently tight distributions during the 11th and 12th plans. In the 13th plan, its high-efficiency range returned to the levels seen in the 10th plan, indicating balanced improvement. Qamdo’s density evolved from a single peak in the 12th plan to a bimodal form in the 13th, reflecting both growth and divergence under continuing policy influence. Nyingchi’s distribution was sharply concentrated in the 11th plan; it migrated rightward thereafter but flattened, denoting a movement from a uniform intensive model to more diverse green practices. Lhoka followed a U-shaped trajectory, peaking in the 10th plan, declining over the next two plans and recovering in the 13th, indicating transitional adjustments in its development pathway. Nagqu and Ngari, both pastoral regions, exhibited persistently left-skewed and flat curves with minimal rightward movement, reflecting low green efficiency and substantial heterogeneity and underscoring the need for targeted interventions.

In summary, although AGTFP in Tibet has improved overall, Lhasa and Nyingchi have achieved high-efficiency status, while Nagqu and Ngari lag significantly. This spatial polarization calls for a stratified policy framework that aligns technology dissemination and intervention measures with each region’s distributional characteristics and critical inflection points, thereby accelerating coordinated improvements in green production efficiency.

4.3. Convergence Analysis of AGTFP in Tibet

Employing σ and β-convergence tests, this paper investigated the spatial and temporal dynamics of AGTFP across Tibet and its seven prefectures during 2002–2021. To uncover both inter-regional differences and internal convergence mechanisms, we conducted convergence analyses for each of the three ecological types: farming, pastoral, and agro-pastoral regions.

4.3.1. σ-Convergence

To test for σ-convergence in Tibet’s AGTFP, this study calculated the annual standard deviation of AGTFP from 2002 to 2021 to examine its temporal evolution. According to the σ-convergence criterion, a declining standard deviation over time indicates a reduction in interregional disparities and the presence of σ-convergence; conversely, an increasing standard deviation implies widening disparities and the absence of σ-convergence.

The results show a sustained upward trend in the overall σ coefficient for Tibet, rising from 0.18 in 2002 to 0.35 in 2021. This indicates that regional differences in green efficiency have generally expanded, reflecting a lack of σ-convergence. This pattern reveals that as Tibet advances its agricultural green transformation, differences in development foundations, resource endowments, and policy responsiveness across regions have become increasingly pronounced, leading to evident spatial imbalance in green efficiency evolution.

Examining functional zones separately, the pastoral region consistently exhibits the highest σ coefficient, increasing from 0.26 in 2002 to 0.38 in 2021, indicating the most significant internal disparity in AGTFP. The agro-pastoral region follows, with σ rising from 0.12 to 0.22, while the farming region shows relatively smaller differences, with σ increasing from 0.09 to 0.18. All three zones display an upward trend in standard deviation, suggesting intensified internal divergence in green efficiency. Notably, the pastoral region’s σ growth is the largest, highlighting increasing spatial unevenness within this zone, likely linked to harsher natural conditions, weaker infrastructure, and delayed adoption of green technologies.

4.3.2. β-Convergence

To evaluate AGTFP’s convergence dynamics in Tibet, we performed both absolute and conditional β-convergence analyses. The outcomes are detailed in

Table 4. Results of the β-convergence tests.

	Absolute β-Convergence				Conditional β-Convergence
	Tibet	Pastoral Zone	Agro-Pastoral	Farming Zone	Tibet	Pastoral Zone	Agro-Pastoral	Farming Zone
β coefficient	0.05	0.08	0.03	−0.05	−0.15 ***	−0.18 ***	−0.12 **	−0.09 *
α (intercept)	0.012	0.005	0.012	0.018	0.008	0.007	0.01	0.015
R2	0.06	0.1	0.04	0.12	0.32	0.28	0.35	0.22
p-value	0.682	0.532	0.674	0.41	0.001	0.008	0.023	0.086
Convergence rate (λ)	—	—	—	—	0.8%	0.01%	0.006%	0.004%
Conclusion	No	No	No	No	Convergence	Convergence	Convergence	Weak convergence

Note: * p < 0.10; ** p < 0.05; *** p < 0.01.

.

Absolute β-convergence analysis yields β estimates of 0.05 for the entire region, 0.08 for the pastoral zone, 0.03 for the agro-pastoral zone, and −0.05 for the farming zone. However, none of these coefficients are statistically significant (p > 0.1), and the models show low explanatory power (R² ranging from 0.04 to 0.12). This suggests that, in the absence of controls for regional heterogeneity, there is no clear trend toward absolute convergence in AGTFP across regions. The findings imply that differences in initial green efficiency levels have not naturally diminished over time. Instead, there may be risks of path dependency and persistent efficiency gaps.

In contrast, the conditional β-convergence results offer stronger explanatory insight. After controlling for structural variables—such as differences in resource endowment, policy environments, and development trajectories—the β coefficients become negative and mostly statistically significant. This indicates the presence of conditional convergence in AGTFP across Tibet and within the three functional zones. Specifically, the β coefficient for the entire region is −0.15 and significant at the 1% level (p < 0.01), with a model R² of 0.32, suggesting a robust convergence trend under controlled conditions. The pastoral and agro-pastoral zones also exhibit significant convergence (β = −0.18, p < 0.01; β = −0.12, p < 0.05), while the farming zone shows marginal evidence of “weak conditional convergence” (β = −0.09, p = 0.086), indicating a moderate tendency toward efficiency equalization.

Regarding the speed of convergence (λ), the annual rate for the entire region is estimated at 0.8%, with the pastoral zone at 0.01%, the agro-pastoral zone at 0.006%, and the farming zone at 0.004%. These differences are substantial. Although the pastoral zone has the highest convergence rate, it also exhibits the largest initial disparities, highlighting both the pressure and potential for improvement. In contrast, the farming zone shows weaker convergence dynamics, possibly reflecting a plateau in its green development trajectory.

In summary, while Tibet’s AGTFP does not exhibit absolute β-convergence, there is clear evidence of conditional convergence once regional heterogeneity is accounted for. These results suggest that interregional disparities in green efficiency are partly attributable to differences in baseline conditions and structural characteristics. Targeted promotion of green technologies, optimized resource allocation, and policy interventions can help facilitate convergence in green productivity. Moving forward, greater emphasis should be placed on place-based strategies and tailored support mechanisms to improve the overall coherence and inclusiveness of Tibet’s green transformation process.

5. Discussion

5.1. Green Transformation Pathways: Efficiency and Technological Progress

Based on the decomposition results of the GML index for the entire Tibet Autonomous Region, the growth of AGTFP has been primarily driven by technological progress, suggesting that overall improvements in green efficiency have relied more on advances in technology than on gains in operational efficiency. Nevertheless, notable regional disparities remain. In regions such as Xigazê and Lhoka, TC values fall below 1, indicating that the effectiveness of green technology diffusion remains unstable and that there is a continuing need to strengthen both the introduction of external technologies and the enhancement of local absorptive capacities. Within the highly resource-constrained and ecologically fragile plateau agricultural system, green technological innovation has emerged as the central mechanism for overcoming conventional growth bottlenecks and pushing the production frontier outward [19,51]. This is especially evident in alpine pastoral regions, where the deployment of technologies related to ecological restoration, mechanized livestock farming, and integrated crop–livestock systems has significantly improved resource-use efficiency and environmental adaptability, injecting crucial momentum into the region’s green agricultural transformation.

This technology-led development path deviates from the classical “efficiency–technology sequence” paradigm. According to the theory of induced innovation [26], improvements in total factor productivity in agriculture typically follow a staged pattern: early gains are achieved through more efficient resource allocation and scale management (e.g., enhancements in pure technical efficiency), followed by outward shifts in the technological frontier driven by mechanization and biotechnological inputs. In this framework, efficiency gains are often considered the most accessible entry point for green transition. However, in certain regions of Tibet, a phenomenon of “green technological leapfrogging” has emerged. In these areas, rapid improvements in green productivity have occurred not through prior optimization of production efficiency but rather through direct reliance on policy support and the adoption of external green technologies [52]. This validates the theoretical proposition within the technological catch-up literature that late-developing regions may bypass traditional development stages [53]. This phenomenon highlights a distinctive “nonlinear transformation pathway” for green agriculture in plateau regions, wherein the diffusion of green technologies may precede the enhancement of managerial efficiency, challenging the linear logic assumed in classical development theory. Such findings are instrumental in deepening the understanding of Tibet’s unique pathway toward green agricultural advancement and offer meaningful reference points for exploring green transformation trajectories in other ecologically vulnerable regions.

5.2. Divergence and Convergence in the Spatial Pattern of Green Efficiency

This study finds that AGTFP in Tibet exhibited a dual trajectory of spatial divergence and conditional convergence between 2002 and 2021. This pattern not only reflects the influence of Tibet’s unique geography and stage of development on its green agricultural transition but also echoes and extends the existing literature on the spatiotemporal dynamics of green efficiency.

On one hand, σ-convergence analysis indicates a general upward trend in the standard deviation of AGTFP across the region and its major functional zones, suggesting a widening spatial disparity in green efficiency. Our results resonate with Huang et al. (2023), who showed that green productivity growth in China’s frontier and ecologically vulnerable areas is hindered by environmental constraints, infrastructure shortcomings, and sluggish technology diffusion [54]. This pattern is particularly pronounced in alpine pastoral areas, where the challenges of allocating green inputs and the high costs of resource integration often lead to a persistent cycle of ecological constraints, low efficiency, and resource redundancy, thereby exacerbating intraregional inequality.

On the other hand, the statistical significance of conditional β-convergence provides evidence that, once structural heterogeneity—such as differences in resource endowments and development conditions—is controlled for, lower-efficiency regions exhibit considerable potential for catch-up in green productivity. This result is consistent with Barro’s (1992) theory of conditional convergence [55] and with the findings of Duan and Jin (2022), which suggest that while green technology diffusion may follow different temporal trajectories across regions, a general trend toward convergence can still emerge [56]. In Tibet, low-efficiency regions have increasingly overcome path dependence under the combined effects of policy support, infrastructure investment, and technological spillovers. Notably, during the 13th Five-Year Plan period, AGTFP improved substantially in Chamdo and Nagqu, reflecting the growing effectiveness of institutional guidance and targeted green policy interventions.

According to “green growth-pole theory”, locales such as Lhasa and Xigazê—benefiting from strategic positioning, advanced technological capacity, and superior market linkages—are emerging as the primary drivers of Tibet’s green agricultural transformation. In contrast, remote pastoral zones may risk falling into “low-efficiency traps,” exhibiting a path of polarization in which stronger regions grow stronger while weaker ones continue to lag. This pattern of “efficiency clubs” may also be interpreted within the framework of new structural economics, which posits that varying capacities for technological adaptation and institutional support across regions can lead to multiple equilibrium paths in green productivity convergence.

5.3. Limitations and Directions for Future Research

Although this study rigorously evaluated the spatiotemporal dynamics of agricultural AGTFP in Tibet using the Super-SBM and GML frameworks, several limitations persist and warrant further research. First, our indicator set does not fully reflect the social and ecological dimensions of green agriculture. Critical factors such as farmer income equity and biodiversity conservation were omitted, restricting the framework’s ability to capture the complexity of Tibet’s varied ecosystems and the interactions between cropping and pastoral systems. Second, data availability remains a major obstacle. Despite applying imputation methods to fill gaps, essential micro-level data—such as farm-level input–output records and the adoption rates of green technologies—remain scarce, limiting our understanding of the drivers of efficiency variation and the pathways through which policy measures exert influence. Third, although we addressed policy impacts qualitatively, this study lacks quantitative analysis of policy transmission, market efficiency and heterogeneous farmer responses, leaving the mechanisms of green transformation only partially explained.

Moreover, our analysis is constrained by its regional-level resolution, which overlooks variations in production systems, resource endowments and governance structures among Tibet’s ecological subregions. Future work should enhance analytical granularity by expanding the indicator suite, improving data quality and extending the modeling framework. Integrating fine-scale spatial datasets with spatial econometric methods would reveal localized bottlenecks and critical intervention points for the green transition. These refinements would enable more targeted policy recommendations to promote sustainable, high-quality agricultural development in Tibet. In addition, a comparative assessment of multiple high-altitude plateau regions would provide a valuable perspective on common constraints and inform the design of context-specific technology diffusion strategies.

6. Conclusions and Policy Recommendations

6.1. Main Findings

Based on our dynamic assessment of AGTFP across Tibet’s seven prefectures from 2002 to 2021, the study delivers the following key findings:

(1)

Slow growth with fluctuating trends and three-phase regional divergence: AGTFP in Tibet grew at an average annual rate of 0.78 percent—below the national average—and exhibited a cycle of decline followed by recovery. Spatial disparities evolved through an initial convergence phase, a mid-period divergence, and a later reconvergence, reflecting how high-altitude farming systems adapt to shifting policy incentives and ecological constraints.

(2)

Pronounced structural and spatial inefficiencies: Alpine pastoral areas such as Nagqu and Ngari suffered severe redundancies in labour, draft animals and carbon emissions. In contrast, agricultural centres like Lhasa and Lhoka maintained comparatively low inefficiency levels. Although fertilizer and machinery inputs were managed effectively, pesticide and plastic-film use remained highly redundant, highlighting weak substitution effects and the externalisation of environmental costs during the green transition.

(3)

Dominance of technical progress amid regional heterogeneity: Decomposition of the Malmquist–Luenberger index shows that technical change (TC > 1) was the primary driver of AGTFP gains, especially in Qamdo and Nagqu. Contributions from pure technical efficiency and scale efficiency were limited and varied markedly across regions, indicating that technological advancements outpaced efficiency improvements in many areas.

(4)

Spatial polarisation followed by stratified reconvergence: Kernel density estimates trace AGTFP distributions from concentration to dispersion and then back toward clustering after the Twelfth Five-Year Plan. Prefectures such as Lhasa and Lhoka formed stable, high-efficiency clusters, whereas Nagqu and Ngari displayed flatter, left-skewed distributions that signal persistent low-efficiency zones and the risk of spatial stratification.

(5)

Absence of absolute convergence but presence of conditional convergence: The σ-convergence analysis indicated widening AGTFP disparities across regions, particularly within pastoral areas. Although absolute β-convergence was not detected, conditional β-convergence became significant after controlling for ecological type and resource endowments. This suggests that differentiated policy interventions hold potential to reduce efficiency gaps and promote green productivity convergence across Tibet.

6.2. Policy Implications

Drawing on the above results, the following policy actions are recommended to improve AGTFP and promote more balanced regional development across Tibet:

(1)

Precision input management to address redundancy. Prioritise the reduction of non-green inputs—particularly pesticides and plastic film—by promoting eco-friendly alternatives and precision application technologies in regions where overuse is most pronounced. In pastoral areas, implement controlled livestock stocking plans and support the development of integrated crop-livestock systems that maintain ecological balance. At the same time, optimise labour-transfer schemes to reallocate surplus agricultural workers into emerging rural industries, thereby improving overall resource-allocation efficiency.

(2)

Differentiated strategies to align technological and efficiency gains. Tailor interventions to each prefecture’s performance profile. In technology-driven zones such as Nagqu and Qamdo, strengthen extension services and managerial training to close the gap in technical efficiency. In efficiency-leading centres like Lhasa and Lhoka, incentivise the diversification and upgrading of green industries to capitalise on existing strengths. In structurally lagging areas such as Ngari, prioritise comprehensive technology deployment—such as climate-resilient seed varieties and renewable energy systems—alongside targeted ecological restoration initiatives to build a foundation for sustained green productivity growth.

(3)

Advancing spatially differentiated mechanisms to promote inclusive and coordinated green development. In light of the significant spatial polarization and internal heterogeneity in green agricultural efficiency, a regionally responsive governance framework is needed—one that integrates crop–livestock system dynamics, tiered development pathways, and functional zoning strategies. This framework should include cross-regional resource reallocation, ecological compensation mechanisms for ecologically fragile and low-efficiency zones, and performance-based incentives to encourage the adoption of low-carbon technologies. Targeted policy tools such as region-specific subsidies for eco-friendly inputs (e.g., organic fertilizers and biodegradable mulching film), investments in adaptive green technology extension services, and technical training for farmers—particularly in pastoral and semi-pastoral areas—can help promote convergence in green efficiency and reduce the widening “green divide” between high- and low-performing regions.