Abstract
Innovative demand-responsive transport services are spreading in most urban areas, allowing dynamic matching between demand and supply and enabling travellers to request shared rides in real-time via mobile applications. They are used both as an alternative to public transport and as an access/egress leg to mass transit stations, i.e., acting as a feeder service. In low-demand areas and small-sized cities, it is often difficult to provide effective and cost-efficient public transport, thus resulting in an extensive use of private vehicles. Using an agent-based modelling approach, this study compares the performance of fixed-route transit (FRT) and demand-responsive transit (DRT), where optional stops can be activated on demand. The aim is to identify the conditions allowing DRT to become more advantageous than FRT in small-sized cities, both for travellers and the transport operator. A real-time matching algorithm identifies optimal trip chains (i.e., public transport lines; pick-up, drop-off and transfer stops; and time windows) for travel requests, dynamically updating vehicles’ routes and schedules. The model is applied to the city of Caltanissetta, Italy, where a transit service with six FRT urban lines is currently operating. Travel patterns were reconstructed from thousands of travel requests collected by a Mobility-as-a-Service platform within one-year. The main findings demonstrate the benefits of DRT in providing a higher quality of service, reducing riding times for passengers, and enhancing service efficiency without burdening operating costs. The DRT reduced the vehicle-kilometres travelled by up to 5% compared to FRT while decreasing passenger ride times by approximately 10%. An economic analysis showed reductions in operator unit costs of up to 3.4% for low-demand rates, confirming the advantages of flexible operations in small-sized cities.
1. Introduction
Infomobility is a crucial component as it allows passengers to plan their journeys more effectively, reducing waiting times and increasing user satisfaction with the services provided. It empowers operators to optimise resources and react promptly to disruptions or traffic variations. From a traveller’s perspective, real-time information allows passengers to monitor the expected arrival time at the stop, enabling them to wait comfortably at their place of origin and avoid prolonged waits.
Urban public transport is traditionally considered a frequency-based transport service, where users can reach the stop without consulting the timetable (the headway should be less than 10–15 min). However, thanks to the real-time information provided by current mobility apps, public transport can be treated as a schedule-based service, where users go to the stop based on knowledge of the arrival time, experiencing shorter waiting times at the stop. A broader concept that aims to integrate various transport services into a single digital platform is Mobility as a Service (MaaS), which allows travellers to search, book, and pay for door-to-door trips through a single application [1,2]. MaaS can include transport options from traditional public transport, taxis, and bicycles to modern ride-sharing services and, importantly, demand-responsive transit (DRT).
DRT can be a key component of a MaaS system, providing a flexible and personalised transport option that can be integrated with other transport services. DRT encompasses a range of services, from ride-sharing options to flexible transit systems [3]. The former involves low-capacity vehicles that do not follow any predetermined route, while the latter is often operated by conventional buses or minibuses with routes and schedules that adapt to demand fluctuations. This can be seen as an evolution of traditional public transport, which operates on predetermined routes and timetables, often based on historical demand data. Instead, DRT relies on continuously updated demand data and effective algorithms to handle dynamic scheduling and routing.
In the context of sustainable urban development, small-sized cities (defined as urban areas with populations between 50,000 and 100,000 inhabitants) face unique transportation challenges that directly impact environmental, social, and economic sustainability [4]. These cities represent a significant portion of the European urban landscape and are an often overlooked category in transport research. Traditional fixed-route transit in these settings often operates with low occupancy rates and poor resource utilization, resulting in higher per-passenger emissions and limited accessibility for underserved populations. By optimizing vehicle routing based on actual demand, DRT has the potential to reduce unnecessary vehicle-kilometres travelled, improve transport accessibility, and create more financially sustainable public transport systems. DRT has been investigated and proposed to overcome the inefficiency of conventional transit in contexts like small cities and low-demand areas [5] or even when the transit system is absent.
However, DRT systems have historically faced significant challenges and often struggled to achieve long-term viability due to the strong need for subsidies [6]. This is often due to high operating costs per passenger transported. When a DRT system requires a large fleet, it can be viewed as a heavily subsidised individual taxi service [7]. Additionally, careful planning is essential to avoid DRT competing with fixed-route transit and creating unwanted effects [8]. Without integration, DRT can compete with fixed transit, potentially leading to decreased revenue for fixed-route services and an increase in road congestion. Finally, operating a DRT system, as well as traditional public transport, involves balancing various competing objectives and perspectives. The key challenges revolve around the inherent conflict between what is optimal for the operator (low operating costs) and what is desirable for the user (short travel times). In other words, it is about addressing the trade-off between cost and quality of service (QoS).
The remainder of the paper is structured as follows: Section 2 provides a comprehensive literature review, identifying research gaps and outlining the contributions of this study. Section 3 details the methodology, focusing on the architecture of the simulation model used to analyse demand-responsive transport systems. Section 4 applies the proposed methodology to a real case study, demonstrating its practical implementation and relevance. Section 5 presents and discusses the results, highlighting key findings and their implications for implementing DRT services. Section 6 concludes the paper, summarising the main insights and suggesting directions for future research.
2. Literature Review
In this paper, we define demand-responsive transport (DRT) as a flexible public transport service that adjusts its routes and schedules based on passenger demand [9,10]. It is also known as mobility-on-demand [11,12] or flexible transit [13,14]. DRT encompasses a group of shared mobility solutions that combine a high level of “shareability”, typical of traditional public transport, with adequate flexibility in routes and schedules. Various implementations of DRT systems exist, and the literature has extensively explored their key characteristics, algorithms, and service strategies.
DRT is often utilised in areas with a lower or dispersed population density where fixed-route services are less cost-effective. It is particularly useful in suburban [15] and rural areas [16,17]. Additionally, DRT can serve as a feeder to mass transit, providing first/last mile connections [18]. Combining DRT and FRT systems has the potential to increase service coverage, improve transport accessibility, and reduce reliance on private cars. Therefore, integrating DRT into the existing transport ecosystem is crucial. This integration can be achieved in different ways, depending on the spatial and temporal context [19]. For instance, in cities with extensive transit networks, DRT is likely to complement fixed-route transit (FRT) in specific areas (e.g., suburbs and residential zones). Conversely, in smaller cities, DRT could replace FRT during certain time periods or entirely. In this respect, diverse studies explored the conditions that justify switching between fixed-route and demand-responsive policies [18,20]. Studies also focus on reducing inequality of accessibility by improving connectivity to opportunities [21].
Several strategies can be employed to enhance DRT service efficiency and effectiveness. Zoning involves designating different areas for operation, which helps in managing resources better [22]. Time windows are used to manage passenger requests and scheduling [9,18], ensuring a tailored and timely service. Real-time dispatching [23] allows DRT systems to react promptly to immediate travel requests, while rebalancing [24] involves relocating empty vehicles to areas with higher demand.
DRT services can be either stop-based or door-to-door. Stop-based services require passengers to walk to designated stops for pick-ups and drop-offs, which can save costs by requiring a lower fleet size [3]. Door-to-door services, on the other hand, pick up and drop off passengers at their specific locations within the service area. In this respect, demand consolidation [12] increases efficiency by grouping passenger requests towards the same stops while saving on vehicle detours. Fielbaum et al. [25] analysed the potential of optimising pick-up and drop-off points in ridesharing systems. The study shows that optimising these locations can improve the system’s performance compared to a system without walking.
Recent developments in DRT research have increasingly focused on simulation-based approaches and practical implementation frameworks [7,10], while agent-based modelling has emerged as a preferred methodology for evaluating flexible transit operations [9,26]. This evolution in the literature supports the unified modelling approach proposed in this study, which bridges the gap between theoretical DRT concepts and practical implementation in small-city contexts. Simulation models are extensively used to study DRT and understand the impacts of different operational parameters and strategies [5,11]. Li et al. [27] present an agent-based model for dispatching a real-time demand-responsive feeder bus service. Leffler et al. [28] examine simulation-based evaluations of flexible transit systems and their integration with fixed systems. The study demonstrates how integrating FRT with DRT can improve the QoS for passengers without increasing operational costs, though this depends on the number of passengers requesting the service and the availability of vehicles. From the passenger’s perspective, route detours and flexible schedules can increase uncertainty in waiting and in-vehicle times compared to traditional FRT services. Variations in perceived reliability heavily influence passengers’ mode and route choices when multiple alternatives are available [29].
Finally, recent research explores integrating freight with passenger transport in a Mobility-as-a-Service (MaaS) environment, which could benefit both systems [2]. A noticeable work in this direction was performed by Cavallaro and Nocera [30], who propose an integrated DRT system for rural areas, combining passenger and freight services to improve efficiency and sustainability.
Research Gaps and Contributions
Public transport services can exploit information technologies to offer more flexible and customised services. However, there are inherent challenges in balancing the operator’s needs with the user’s expectations, such as managing costs and ensuring quality of service (QoS). In this regard, the contribution of this research is twofold.
Firstly, it proposes a unified model for fixed-route transit (FRT) and demand-responsive transport (DRT). This model is capable of managing user travel requests and matching them to the optimal trip chains through the proposed matching algorithm. This algorithm is inherently flexible, as it adapts well to both FRT and DRT operations. In the latter case, it shows that there is room for reducing vehicle-kilometres travelled by “skipping” optional stops along the route, and this saving can be used to improve the frequency of service offered to users.
Secondly, this research adopts a different approach from most of the existing literature on DRT. While existing studies often focus on service optimisation, they rarely evaluate the impact on user costs or consider the actual feasibility of implementing such a service from the public transport agency’s perspective. This research, instead, considers DRT as a flexible, demand-adaptive transport service and demonstrates that it is possible, especially in small cities with limited resources, to achieve improvements in transport accessibility and better QoS at virtually unchanged costs and without major changes to the transit structure. The successful application of this model to a real case study verifies that DRT can improve the quality of service for travellers without increasing operating costs for the transit agency, underscoring its practical value and potential for broader implementation in urban transit systems.
3. Model Architecture
The agent-based model presented in this paper simulates the daily operation of an urban public transport network, assuming that potential passengers are informed in real time about the state of the service. This allows them to choose the combination of stops and lines that minimises their travel time from origin to destination. The model was implemented in the NetLogo development environment [31]. The agents in the model are vehicles, stops, and travellers. There are two possible operating policies that can be addressed by the model: fixed-route transit (FRT) and demand-responsive transit (DRT). The former represents the conventional public transport (PT) service operating on fixed routes and schedules, while the latter is based on flexible routes, consisting of mandatory stops (FRT stops) and optional stops (DRT stops) to be activated on demand. A detailed outline of the FRT and DRT model is provided in Section 3.1.
3.1. Setup Phase
Before the simulation start, a setup phase is needed to initialize the input parameters of the model, including the transport demand model and the creation of the vehicles’ daily schedules. A many-to-many demand pattern is considered. The total number of travel requests generated during a simulation run is given by the daily demand rate (requests/day), which is set as an input parameter. To account for demand fluctuations throughout the day, a variable fraction of is allocated to different time periods , ensuring that the sum of all fractions satisfies . The study area is divided into traffic zones, and an origin–destination (OD) matrix is created for each time period. The number and extent of time periods, as well as the size of each traffic zone, should be based on the amount and quality of available demand data.
The PT network consists of a set of operating lines . A generic line is identified by a sequence of stops , with representing the set of PT stops. The first and last elements of are the terminals of the line . Each line has an associated daily schedule, consisting of a series of trips, the associated departure times and the assigned vehicle . Denoting as the position of a generic trip in the daily schedule of line , each trip can be identified by a unique pair . Therefore, we denote as the set of daily trips related to line . The structure behind each trip schedule is assumed to be the same for both FRT and DRT operations in order to guarantee interoperability between the two service strategies. It consists of a sequence of 5-tuples, , … … where
- is the stop at the n-th position of the stop sequence, with ;
- is the estimated vehicle arrival time at ( represents the departure time);
- is the latest vehicle arrival time at (;
- is a Boolean parameter that is equal to 1 if the and equal to 0 if the ;
- is the expected number of passenger (load) when the vehicle departs from .
The last three elements of the tuple are introduced to cope with DRT operations, where PT lines include both FRT and DRT stops. The latter can be “activated” in a given trip by a passenger request, causing a detour from the fixed route. Moreover, the first element of each tuple () remains constant, as well as the position of the tuple itself inside , while the other four elements are dynamically updated during the simulation process due to road traffic conditions (affecting and ) and the insertion of passengers in the trip schedule (affecting , and ). The trip updating process is described in detail in Section 3.3.
Finally, for each vehicle, the trip schedule is created. It consists of a sequence of 3-tuples identifying, respectively, the line ID, the number, and the departure time of the trips scheduled in the simulated day. Vehicles’ locations at the instant corresponds to the terminal of their first scheduled trip.
3.2. Simulation Process
The simulation process takes place between the instants and . At each time step, the timer is incremented by 1 s, and three main sub-processes are carried out, namely,
- Vehicles’ state updating;
- Travellers’ state updating;
- Travel request creation.
The first sub-process governs the vehicles’ behaviours and the transition between three states: “idling”, “travelling”, and “loading/unloading”. Vehicles are in the idling state when waiting at the terminal for the next departure time. The travelling state involves moving between the scheduled stops at a constant speed and updating the expected arrival time at each stop. When the vehicle visits a stop where travellers need to be picked up or dropped off, it switches to the loading/unloading state to allow these operations. In this case, a fixed additional time lost at the stop () and an extra time for each boarded and alighted passenger () are included. These steps are depicted through the vehicle state chart in Figure 1a.
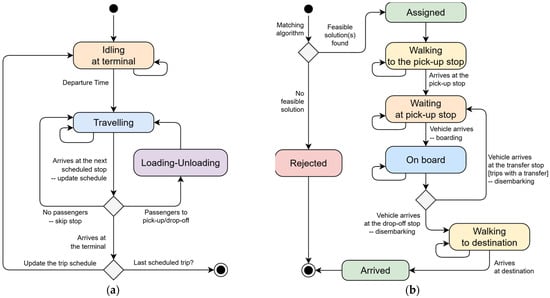
Figure 1.
State charts for vehicles (a) and travellers (b).
The second sub-process governs the travellers’ behaviours during the entire journey, from the travel request at the origin to the arrival at the destination. If a feasible match between the travel request and a (combination of) trip(s) is found (see Section 3.3), the traveller state becomes “assigned”; otherwise, it is “rejected”. Assuming that users are perfectly aware of the PT vehicles’ up-to-date position, they walk (at a speed of ) to the chosen pick-up stop before the expected vehicle arrival time. This assumption is reasonable since modern transit systems use tracking technologies to provide real-time updates on vehicle locations. This information is easily accessible through mobile apps or websites. Travellers switch between the states of “waiting” (at the pick-up stop or at the transfer stop), “on board”, and “walking” (from the drop-off stop to the destination). Finally, when travellers arrive at their destination, they switch to the state “arrived”. Figure 1b illustrates the traveller state chart.
The third sub-process involves the generation of a new travel request that is defined by a tuple of five attributes . Specifically,
- is the non-empty list of travellers. This attribute is needed to cope with the case where travel request involves more travellers sharing the same journey.
- is the origin location of the traveller’s journey.
- is the destination location the traveller’s journey.
- is the time instant of the request.
- is the latest arrival time at the destination (time-window constraint).
At each time instant of the simulation process, the probability that a new travel request arises depends on the demand rate related to the current time period, and is given by , with . Travel requests are processed in real-time through the matching algorithm described in Section 3.3. The objective is to find a set of feasible trip chains able to satisfy the request. Thus, we assume that the minimum-cost trip chain is always chosen, i.e., the one that minimises the cost function (see Section 3.3). In reality, transport users choose among trip chain options based on their own preferences (i.e., their utility function). This choice mechanism is out of the scope of this work.
A candidate trip chain for the i-th travel request is composed of n pairs of 4-tuples including the line ID , the trip position in the daily schedule , the pick-up stop , and the drop-off stop . A trip chain composed of a single 4-tuple implies a direct trip involving a single ride with pick-up at and drop-off at Otherwise, the trip chain involves two lines and and includes an intermediate transfer stop that belongs to both lines. Therefore . We assume that travellers are willing to accept at most one transfer. The set of candidate pick-up stops and the set of candidate drop-off stops are built based on the assumption that travellers are willing to walk within a walking distance threshold , which is a constant input parameter. A schematic illustration of candidate trip chains for the i-th travel request is shown in Figure 2.
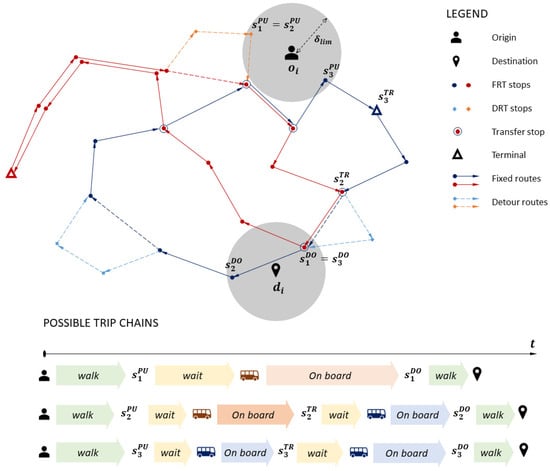
Figure 2.
Example of possible trip chains for travel request .
3.3. Matching Algorithm
The matching algorithm described by Algorithm 1 provides a set of feasible trip chains for the i-th travel request. It explores the possible combinations between candidate pick-up stops and candidate drop-off stops . Then, it evaluates the lines and the trips that can serve the pair () while respecting the traveller’s time window. If the distance from origin to destination is below , travellers are assumed to walk without using public transport. To avoid the proliferation of feasible solutions and limit the computational burden, priority is given to trip chains involving a single line, when possible (see Algorithm 2). This case also includes the possibility of two trips made with the same line, including idling at terminal (which becomes a transfer stop). This implies and . Otherwise, the algorithm tries to build a trip chain involving a transfer between two different lines (see Algorithm 3) through a transfer stop belonging to both lines. This implies and . The matching algorithm considers two time-window constraints and one capacity constraint using the following equation:
Equation (1) ensures that traveller i is able to reach the pick-up stop before the vehicle’s expected arrival time , considering the needed walking time . Equation (2) imposes that the latest vehicle arrival time at the drop-off stop, incremented by the walking time to reach the destination that must not exceed the traveller’s latest arrival time at destination. Equation (3) ensures that the number of passengers of the vehicles associated with the trip chain does not exceed their passenger capacity at any scheduled stop.
| Algorithm 1 Creation of the Feasible Trip Chains’ List |
| 1: Travel request 2: Define sets of candidate pick-up and drop-off stops based on distance threshold 3: For each 4: Compute walking time from origin to 5: For each 6: Compute walking time from to destination 7: For each | 8: If 9: Do Algorithm 2 // OD trip without transfers 10: Else 11: If // solution list is empty 12: Do Algorithm 3 // OD trip with transfer 13: End If 14: End If 15: End For 16: End For 17: End For 18: Return solution-list with feasible trip combination and the related costs |
| Algorithm 2 Identification of Feasible Trip Solutions Without Line Change |
| 1: For each // check possible trips not already concluded 2: If position position // direct trip 3: Check constraints (1–3) for // time windows, vehicle capacity 4: Else // two trips with the same line, including idling at terminal 5: Set transfer stop // the terminal of line l is the transfer stop 6: Check constraints (1–3) for and 7: End If 8: If solution is feasible 9: Compute Cost Function 10: Update solution list 11: End If 12: End For |
| Algorithm 3 Identification of Feasible Trip Chains Involving Two Different Lines |
| 1: For each | 2: For each 3: If pos. pos. And pos. pos. 4: For each 5: For each 6: Check constraints (1–3) for and 7: If solution is feasible 8: Compute Cost Function 9: Update solution list 10: End If 11: End For 12: End For 13: End If 14: End For 15: End For |
Every time that a feasible trip chain is found by the algorithm, the solution list is updated by adding the j-th pair to the list, where is the cost associated with . We assume that is given by the weighted sum of the traveller cost due to the expected travel time and the transport operator cost due to any additional trip time needed to serve . The structure of the cost function is shown in Equation (4):
where is the sum of the first four terms and is the last term. In Equation (4), is the sum of the walking times required to reach the pick-up stop from the origin and the destination from the drop-off stop ; is the sum of the waiting times at the pick-up stop and the transfer stop (if any); is the ride time on board the assigned vehicles; is the ride time needed from to travelling along the shortest path in the road network without intermediate stops; is a time penalty that accounts for the additional disutility caused by transfers [32]; is the additional trip time caused by the insertion of the travel request in the trip schedule; , , are the weight coefficients for traveller walking time, waiting time, and ride time, respectively; while is the weight coefficient for the additional trip time incurred by the transport operator. Note that in the case of direct trips and if and . In other words, if the stops included in the trip chain are FRT stops (or they have been added to the trip schedule due to previous travel requests), no additional trip time is needed. Thus, a high value of can be set to penalize the solutions including DRT stops, and vice versa.
Finally, when the best solution is found, the respective trip chain is assigned to the travellers . The schedules of each trip associated to the best trip chain are updated accordingly. As mentioned in Section 3.1, this procedure involves updating the 5-tuples defining the trip schedule, i.e.,, with , where is the number of stops (both FRT and DRT) of line l. If any stops of the trip chain are DRT stops and ( was not already scheduled), the expected vehicle arrival time is updated ( is known in advance) and is set to 1. The vehicle load is updated between any couple of pick-up and drop-off stops based on the size of . It should be noted that, for DRT stops, the estimated () and latest () vehicle arrival times are not actual unless they are “activated”, i.e., they are included in the trip chain.
3.4. Output Indicators
The results of each simulation run can be assessed through various performance indicators, with the key ones described in Table 1.

Table 1.
Traveller-related and operator-related performance indicators.
The acceptance rate () serves as an important measure of service effectiveness in meeting diverse travel demands, reflecting how reliably the system can accommodate user requests. The time stretch (σ) indicator measures how much longer PT journeys are compared to the shortest possible route, thus providing a measure of service efficiency and reliability from the user’s perspective. Additionally, the Gini coefficient () captures equity in service provision, which directly relates to user satisfaction by measuring inequality in travel time distribution among passengers. These metrics collectively provide insights into the human experience of the transport service beyond purely operational considerations.
The Total Unit Cost () is a performance indicator that encompasses both the traveller’s and operator’s perspectives [33]. To calculate the , the following input parameters are required: the traveller Value of Time () in EUR/h, the distance-related operator cost () in EUR/km, the time-related cost () in EUR/km, and the PT service duration (), which is the number of hours the PT service operates during the day.
4. Case Study
Caltanissetta is a small-sized city located in Southern Italy with nearly 60,000 residents. The urban public transport (PT) network in Caltanissetta is currently structured around six main lines operating six days a week (on weekdays), two additional lines dedicated to school services, and one Sunday line. The network includes a total of 175 stops. The average stop density, considering the urbanized area covered by the PT network, is approximately 15 stops per square kilometre.
4.1. Transport Demand Estimation
To build the transport demand model using public transport data, travel requests from the urban mobility app “Moovle” were analysed. Through collaboration with the Municipality of Caltanissetta, the Moovle app provides real-time arrival times for different stops across all public transport lines. Additionally, adopting the Mobility-as-a-Service (MaaS) paradigm, the app enables users to plan and schedule urban travel using various modes of transport.
In this study, 9767 travel requests made through the Moovle app from 1 January 2024 to 31 December 2024 were analysed. These requests are entirely anonymous and linked to a unique “device ID”. Each row of the request dataset contains data related to a single request submitted via the app. Key information for each travel request includes the device ID code; date and time of the travel request; coordinates (latitude and longitude) of the origin; and coordinates (latitude and longitude) of the destination. Additionally, information about the trip chain suggested by the app is provided, including the start date and time of the journey; end date and time of the journey; total trip duration; walking distance; walking time; waiting time; onboard time; and number of transfers (line changes). A data filtering process was conducted to eliminate duplicate errors (i.e., requests made by the same device within a few minutes with an identical origin, destination, and start time of the journey), requests falling outside the area served by public transport, and travel requests repeated over time with similar patterns. These include travel requests made on different days but sharing the same device ID, and similar start times (considering a 1 h tolerance), origins, and destinations (considering a 400 m tolerance).
Next, origin–destination (OD) matrices were created for one-hour time intervals based on the start time. The daily temporal fluctuation of travel demand from the analysed travel requests, normalised between 0 and 1, is shown in Figure 3. Noticeably, the PT demand profile does not exhibit pronounced peaks, and drops below 70% of the maximum value after the late afternoon.
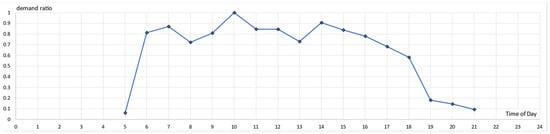
Figure 3.
Temporal profile of transport demand during the day, normalised with respect to the maximum daily value.
Using the coordinates of the origin and destination points for these travel requests, their spatial distribution was reconstructed in a GIS environment and assigned to the corresponding traffic zone (see Section 3.1). Traffic zones were generated through a tessellation process, creating hexagons with a 100 m side (0.3 km2 area). Notably, the central station, which serves as the terminal for all PT lines, emerged as the primary generator and attractor of trips. Nearly 20% of the travel requests either originate or terminate at the station. Regarding the estimation of transport demand in terms of the number of daily travel requests, data from the Italian National Institute of Statistics [34] indicate 0.37 million public transport users per year. Dividing this number by 305 weekdays, we establish a base value for the daily demand rate of 1200 requests per day.
4.2. Simulation Scenarios
In this study, two operating policies, namely fixed-route transit (FRT) and demand-responsive transit (DRT) are simulated and compared from both the perspectives of the passengers (who seek a low travel time) and the operator (who aims at minimising the service cost). Currently, the PT service in the city of Caltanissetta operates on six lines under a FRT policy. The operating PT fleet consists of five vehicles: each line is assigned a vehicle (Line 3 and Line 5 are served by the same vehicle). The number of daily trips ranges from a minimum of 13 for Line 3 to a maximum of 21 trips for Line 4, which connects the city centre with the city hospital. Due to the limited fleet size, the headways (inverse of the service frequency) vary between 40 and 60 min.
We chose FRT as the base scenario, representing the current situation, with a service period of 15 h (from 6:00 a.m. to 9:00 p.m.). In the DRT scenario, the schedule of the PT lines remains unchanged (i.e., same departure times), but some stops are made optional (DRT stops). This way, routes are shorter if no requests for DRT stops are made. Additionally, a third scenario is considered, where the service frequency is increased by adding trips to the lines’ schedule. This adjustment is made due to the expected decrease in the route time of vehicles under the DRT policy. The input parameters chosen for the set of simulations are shown in Table 2.

Table 2.
Demand-related and supply-related input parameters of the simulated scenarios.
For each of the three scenarios, five groups of simulations were performed, with a variable demand rate ranging from 600 to 1800 requests per day. Each group consisted of 10 simulation runs with constant input data and variable seeds. The results of each group of simulations were evaluated by calculating the average of the different output indicators from the ten simulations, ensuring the robustness and generalisability of the results. By analysing demand rates both lower and higher than the base value of 1200, we aim to identify a “threshold” at which DRT becomes preferable to FRT.
5. Results and Discussion
In this section, the results of the simulations performed for the scenarios described in Section 4.2 are presented. First, the performance of the current fixed-route transport (FRT) service is analysed. Next, we evaluate how the performance indicators change if all the public transport (PT) lines were operated in a demand-responsive transport (DRT) fashion. Finally, we compare the “enhanced” DRT scenario, where the service frequency of the PT lines is increased.
5.1. FRT Scenario
A crucial indicator for a PT system is the percentage of travel requests that can be satisfied. The higher the percentage of accepted requests (), the more accessible the service is. Figure 4a shows that this percentage is nearly 80%. The influence of increasing the demand rate () is negligible, as it does not influence the route coverage and only marginally affects travel times (due to a decrease in the average speed from increased boarding and alighting operations). The number of transfers needed would also remain substantially unchanged, constituting between 28% and 30% of total trip chains.
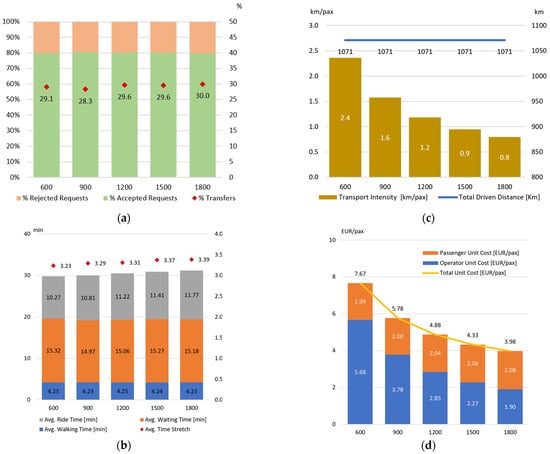
Figure 4.
Key performance indicators (KPIs) for the FRT scenario: (a) percentage of accepted travel requests and percentage of trips with transfer; (b) travel time components for PT passengers and average “time stretch” value; (c) total distance driven by PT vehicles vs. distance driven per transported passenger (transport intensity); (d) Total Unit Cost (TUC) split into passenger-related and operator-related components.
The results of the passenger travel time are shown in Figure 4b. The part that most affects the overall travel time is the waiting time. This is due to the low frequency of the different lines, which values are below the standards of an urban PT service. As expected, higher demand rates cause longer ride times due to a lower average vehicle speed, thus increasing the average time stretch ().
From the operator’s perspective (Figure 4c), the number of kilometres travelled per transported passenger () is inversely correlated with (while remains constant). The same applies for the (Figure 4d). Since , , and remain constant, depends solely on . Moreover, as the remains substantially unchanged, the decrease by nearly 40% when triples from 600 to 1800 requests per day.
To identify which stops can be made optional in the DRT scenario, a preliminary analysis was conducted based on the daily passenger load profile (PLP) of each line. For example, Figure 5 shows the PLP of Line 1 when is set to the base value of 1200 requests per day. Line 1 has the longest and most tortuous route (drawn in red in Figure 6), and includes an extended detour from the city centre to serve a peripheral small village. As confirmed by the simulation results, the stops along this part of the route served a small number of passengers (see the green and orange dots in Figure 5, corresponding to stops 13 to 34) and may be removed from the fixed route, making them available on demand. This approach was applied also to the remaining lines, “cutting” the part of routes circled in red in Figure 6b and transforming the associated stops into DRT stops.
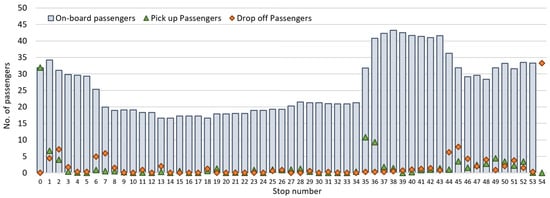
Figure 5.
Passenger load profile for Line 1.
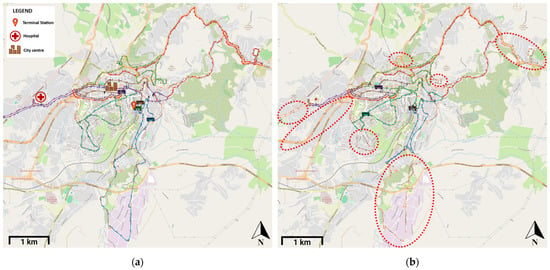
Figure 6.
PT route network in the FRT scenario (a) and in the DRT scenario (b), where DRT stops are highlighted. The maps represent the simulation environment interface where the shapefiles for transit lines are imported and agents (vehicles and users) are visualized during the simulation.
5.2. DRT Scenario
In the DRT scenario, the PT routes are modified by removing the DRT stops, but the line schedule remains unchanged, maintaining the same departure times as in the FRT scenario. The simulation results obtained for increasing demand rates were compared with those of the FRT scenario. The percentage variations are shown in Table 3.

Table 3.
Variations of the KPIs for the DRT scenario compared to the FRT scenario. Improvements are shown in green, deteriorations in red, regardless of sign.
We note a slight decrease in the fraction of accepted requests, which is more pronounced in low-demand scenarios. This can be explained by the fact that if the demand is low, the probability of a route detour to serve DRT stops is low. Consequently, it is less likely that inserting a DRT stop into existing schedules will meet time-window constraints. Specifically, if a travel request arises in an area served only by DRT stops of a given line, it could happen that the corresponding vehicle has already reached the detour point and is not on time to make the detour to serve the DRT stop on that trip.
The DRT also causes a minor increase (0.3–1.4%) in , since the matching algorithm tends to favour the insertion of FRT stops in the trip chains (when possible) even though this could imply greater walking distances. The increase in is more noticeable (up to 5%) due to the higher uncertainties in vehicle arrival times at the stops caused by the dynamic modification of PT routes. This inconvenience is compensated by the shorter time spent onboard (), which drops by more than 5% when the demand is low. As a result, remains substantially unchanged, with only minor oscillations around 1%.
Noticeably, the major benefits of DRT are the significant reductions in and , due to the shorter distance travelled by the PT vehicles. As expected, the lower the , the greater the travel distance saved by PT operator (up to 17%), and therefore the lower the . Consequently, the results show the highest reduction in the for requests per day (−3.4%).
Although the results clearly show that DRT can reduce costs for the PT operator, this comes at the expense of a (albeit small) decrease in service accessibility, due to lower and . Notably, higher values of the Gini coefficient indicate a worsening in the inequality in the distribution of travel times among PT users. Moreover, if the trip schedule remains the same as in the FRT scenario, the shorter distance travelled translates into longer idling times at the terminal, causing unproductive time. Finally, a PT agency should be more interested in increasing the efficiency of the service (i.e., enhancing the QoS provided without increasing operating costs) rather than merely decreasing service costs.
5.3. Enhanced DRT Scenario
The considerations made at the end of the previous section motivated us to analyse a third “enhanced” DRT scenario. In the enhanced DRT scenario, the service frequency is increased due to the expected savings in vehicle driving distances and thus in the (average) route time. Table 4 shows the comparison between the current schedules of PT lines (used in the FRT and DRT scenarios) and the enhanced schedules considered in this scenario. A total of 18 trips are added, broadening the service time windows from the first to the last departure and decreasing the headway by 5 min.

Table 4.
Current schedules of PT lines vs. enhanced schedules for DRT (in bold).
As in the previous case, the simulation results obtained for increasing demand rates are compared with those of the FRT scenario. The percentage variations are shown in Table 5. We notice a higher , which results in a greater number of passengers transported. It means that the PT service becomes more accessible. This helps us explain the increase in , which is higher when is low. In fact, the travellers who could not be served in the FRT scenario, probably due to time-window constraints, are assigned a feasible trip chain in this scenario, increasing . It is reasonable to assume that these travellers are the ones with the higher travel times, thus impacting the average travel time spent by all travellers (i.e., higher ). Real-time information can make waiting times less annoying for those passengers. A positive effect of increasing the service frequency is that it improves the equality in the travel time distribution among travellers, which should be one of the PT agency’s goals towards improving transport accessibility [35].

Table 5.
Variations of the KPIs for the enhanced DRT scenario compared to the FRT scenario. Improvements are shown in green, deteriorations in red, regardless of sign.
Notably, these improvements can be achieved without increasing operating costs. In fact, the and the decrease compared to the FRT scenario, despite the increased number of trips in the daily schedule. This is due the possibility of saving kilometres when DRT stops are not requested, which is more probable in low-demand scenarios.
The enhanced DRT scenario shows environmental implications: the total driven distance decreases by 3% for low-demand rates but increases by 2.2% for high-demand rates. However, the transport intensity (TI) consistently improves across all demand levels, decreasing by up to 5% for low demand rates and nearly 1% for high demand rates, indicating more efficient resource utilization per transported passenger. As a result, based on the cost parameters of this case study, lower demand rates favour the implementation of a DRT policy from a global perspective, including travellers’ needs and the operator’s budget constraints.
5.4. Discussion and Policy Implications
One of the most important elements that emerged from this analysis is the accessibility of the public transport service. This concept includes the time needed to reach the stop, the waiting time, the travel time on board, and therefore the total time to reach the final destination. The results show that the variability of vehicle arrival times at PT stops allowed by the DRT can negatively impact the waiting time. Although this drawback would be compensated by shorter ride times, it primarily depends on the poor service frequency, the values of which are not suitable for an urban PT service. To address this challenge, transit agencies should consider supplementing DRT with robust real-time information systems. Accurate arrival predictions can significantly improve the passenger experience, despite inherent variability in DRT operations. Appropriate scheduling strategies, including modest time buffers at key network points, could help mitigate the waiting time uncertainty revealed in the simulations.
Removing the constraint of the unchanged fleet size among the simulated scenarios (thus allowing for a more pronounced enhancement of the QoS) was out of the scope of this paper. In fact, the primary objective was to show that the efficiency of the system could be improved without major structural modifications. For small cities with constrained resources, this finding is particularly relevant as it demonstrates the potential for service improvement without cost-intensive fleet expansion.
Service flexibility is another crucial aspect. The proposed model can simulate increasing degrees of route flexibility when transport demand drops. This flexibility allows the service to be adapted to the travellers’ needs, reducing the route length when necessary and thus the average travel time spent onboard. However, flexibility must be balanced with demand density. In high-demand contexts, an FRT service might be more efficient. Transit agencies might implement this flexibility through a structured approach that maintains service predictability while introducing demand-responsive elements. This could include identifying core network segments where fixed routing is maintained and designating low-ridership route sections for flexible operation. Nevertheless, while DRT may require additional vehicle-kilometres at high demand rates, it achieves better passenger-to-resource ratios compared to FRT, particularly at low demand rates (i.e., a low transport intensity), potentially mitigating increased fuel consumption through higher service utilization when demand is sparse. Evaluating each context and even the time of day is necessary to determine which transport policy is most efficient, defining policies for when and how routes can be modified. By properly adjusting service frequency and route flexibility, the PT agency can significantly improve service efficiency. Additionally, the same PT operator might decide to switch between FRT and DRT policies on different days of the week or periods of the day as the demand pattern changes over time. In this context, special attention should be given to equity considerations, ensuring that technology-dependent DRT systems remain accessible to all user groups through multiple booking channels and appropriate support mechanisms. The transition between FRT and DRT operations also requires careful communication strategies to help passengers understand and adapt to flexible service concepts.
6. Conclusions
The main objective of this study was to evaluate the efficiency of the current fixed-route transport (FRT) system and compare it with the performance of a flexible public transport strategy capable of integrating demand-responsive transport (DRT) into the existing system. This measure, along with the increasing diffusion of intelligent infomobility systems, aligns with the sustainable urban mobility strategies outlined in the guidelines for Sustainable Urban Mobility Plans.
To evaluate the effectiveness of these changes, an agent-based simulation model was developed and applied to the case study of Caltanissetta, Italy, a small-sized city with a six-line public transport network operating with a limited fleet size. This research makes a contribution by proposing a unified model for FRT and DRT. The model is capable of managing user travel requests and matching them to the optimal trip chains through a flexible matching algorithm. This algorithm adapts well to both FRT and DRT operations, showing that there is potential to reduce vehicle-kilometres travelled and improve the frequency of service offered to users. By analysing the service performance indicators from both the travellers’ and the transport operator’s perspectives, simulations provide valuable insights into the potential benefits of introducing flexible transport services that dynamically adapt to users’ needs in low-demand areas. While this study focuses on a small-sized city, the proposed agent-based model is scalable and can be adapted to broader urban contexts. For medium-sized cities or polycentric regions, particular attention should be paid to defining hierarchical zoning with different service levels, hub-based operations with trunk and feeder services, and differentiated fleet allocation. Recent applications in larger cities like Palermo [15] suggest hybrid approaches combining fixed high-frequency corridors with DRT feeders, whereas our small-city model proposes more comprehensive flexibility.
Future experiments may focus on varying the degree of service flexibility based on the time of the day, proposing a “hybrid” service where DRT operations are provided when transport demand is low (e.g., during the evening). This approach would optimize the service strategy according to the consolidated trend of the transport demand, further improving efficiency and user satisfaction. Additionally, incorporating dynamic external factors such as weather conditions, special events, or infrastructure disruptions would enhance model realism.
In conclusion, improving the current FRT system with DRT strategies, supported by data-driven decision-making, represents a promising approach to creating a more efficient, sustainable, and inclusive urban mobility environment. By integrating FRT and DRT into a single framework, the proposed model enhances service efficiency without major changes to the transit structure. However, there are challenges to consider, such as the potential for inequity due to the digital divide, which penalises individuals who have limited access to modern information and communication technologies. Further research is needed to explore how price, travel time, and convenience impact modal choice. Understanding how travel time variability impacts users’ perceived quality of service (QoS) is essential, as users may choose between feasible solutions instead of the best one. Dynamic pricing strategies can be included within DRT applications to compensate for longer travel times when the demand is higher. Regarding sustainability assessments, future model implementations could incorporate specific environmental metrics such as CO2 emissions and fuel consumption when detailed fleet composition data become available.
Optimizing DRT systems to reduce costs while maintaining high-quality service is a crucial area for future research. This includes exploring various operational strategies and matching algorithms that can help achieve this balance. Additionally, there is potential for integrating freight services, exploiting the extra idling time at terminals due to short turns. This integration could lead to more efficient use of resources and further reduce operational costs, while also providing additional revenue streams for transit agencies.
Funding
This research was funded by the Spoke 9 “Digital Society & Smart Cities” inside the “National Centre for HPC, Big Data and Quantum Computing” (Code CN00000013, unique project code: E63C22001000006)—innovation fund “MIA: Multimodal Interchange Assistant”, funded under PNRR M4C2 Line 1.4, by the Italian Ministry for Research. This research has been partially supported by the project “SMART3R-FLITS: SMART Transport for TRavellers and Freight Logistics Integration Towards Sustainability” (unique project code: E53D23010230006) under the programme “PRIN 2022”).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The code of the simulation model presented in the study is openly available in GitHub at https://github.com/giovanni-cal/Flexible-Transit-microsimulation (accessed on 10 April 2025). The raw data used to generate the transport demand are not publicly available due to privacy restrictions.
Acknowledgments
The author would like to express his sincere gratitude to Riccardo D’Angelo of Moovle (https://www.moovle.me/), for providing access to the data used in this research. The support and collaboration of Moovle have been instrumental in enabling the development and validation of the proposed models.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Butler, L.; Yigitcanlar, T.; Paz, A. Barriers and risks of Mobility-as-a-Service (MaaS) adoption in cities: A systematic review of the literature. Cities 2021, 109, 103036. [Google Scholar] [CrossRef]
- Le Pira, M.; Tavasszy, L.A.; Correia, G.H.A.; Ignaccolo, M.; Inturri, G. Opportunities for integration between Mobility as a Service (MaaS) and freight transport: A conceptual model. Sustain. Cities Soc. 2021, 74, 103212. [Google Scholar] [CrossRef]
- Vansteenwegen, P.; Melis, L.; Aktaş, D.; Montenegro, B.D.G.; Vieira, F.S.; Sörensen, K. A survey on demand-responsive public bus systems. Transp. Res. Part C Emerg. Technol. 2022, 137, 103573. [Google Scholar] [CrossRef]
- Dijkstra, L.; Poelman, H. Cities in Europe: The new OECD-EC definition. Reg. Focus 2012, 1, 1–13. [Google Scholar]
- Calabrò, G.; Le Pira, M.; Giuffrida, N.; Inturri, G.; Ignaccolo, M.; Correia, G.H.D.A. Designing demand responsive transport services in small-sized cities using an agent-based model. Transp. Res. Procedia 2023, 69, 759–766. [Google Scholar] [CrossRef]
- Currie, G.; Fournier, N. Why most DRT/Micro-Transits fail–What the survivors tell us about progress. Res. Transp. Econ. 2020, 83, 100895. [Google Scholar] [CrossRef]
- Melo, S.; Gomes, R.; Abbasi, R.; Arantes, A. Demand-Responsive Transport for Urban Mobility: Integrating Mobile Data Analytics to Enhance Public Transportation Systems. Sustainability 2024, 16, 4367. [Google Scholar] [CrossRef]
- Alonso-González, M.J.; Liu, T.; Cats, O.; Van Oort, N.; Hoogendoorn, S. The potential of demand-responsive transport as a complement to public transport: An assessment framework and an empirical evaluation. Transp. Res. Rec. 2018, 2672, 879–889. [Google Scholar] [CrossRef]
- Leffler, D.; Burghout, W.; Jenelius, E.; Cats, O. Simulation of fixed versus on-demand station-based feeder operations. Transp. Res. Part C Emerg. Technol. 2021, 132, 103401. [Google Scholar] [CrossRef]
- Liu, T.; You, H.; Gkiotsalitis, K.; Cats, O. Human-Machine collaborative decision-making approach to scheduling customized buses with flexible departure times. Transp. Res. Part A Policy Pract. 2024, 187, 104184. [Google Scholar] [CrossRef]
- Basu, R.; Araldo, A.; Akkinepally, A.P.; Nahmias Biran, B.H.; Basak, K.; Seshadri, R.; Ben-Akiva, M. Automated mobility-on-demand vs. mass transit: A multi-modal activity-driven agent-based simulation approach. Transp. Res. Rec. 2018, 2672, 608–618. [Google Scholar] [CrossRef]
- Araldo, A.; Di Maria, A.; Di Stefano, A.; Morana, G. On the Importance of Demand Consolidation in Mobility on Demand. In Proceedings of the 2019 IEEE/ACM 23rd International Symposium on Distributed Simulation and Real Time Applications (DS-RT), Cosenza, Italy, 7–9 October 2019; pp. 1–8. [Google Scholar]
- Errico, F.; Crainic, T.G.; Malucelli, F.; Nonato, M. A survey on planning semi-flexible transit systems: Methodological issues and a unifying framework. Transp. Res. Part C Emerg. Technol. 2013, 36, 324–338. [Google Scholar] [CrossRef]
- Giuffrida, N.; Le Pira, M.; Inturri, G.; Ignaccolo, M.; Calabrò, G.; Cuius, B.; D’Angelo, R.; Pluchino, A. On-demand flexible transit in fast-growing cities: The case of Dubai. Sustainability 2020, 12, 4455. [Google Scholar] [CrossRef]
- Capodici, A.E.; Citrano, M.; D’Orso, G.; Migliore, M.; Ignaccolo, M.; Leonardi, P.; Torrisi, V. Designing microtransit services in suburban areas: A case study in Palermo, Italy. Res. Transp. Bus. Manag. 2024, 56, 101191. [Google Scholar] [CrossRef]
- Schlüter, J.; Bossert, A.; Rössy, P.; Kersting, M. Impact assessment of autonomous demand responsive transport as a link between urban and rural areas. Res. Transp. Bus. Manag. 2021, 39, 100613. [Google Scholar] [CrossRef]
- Lu, C.; Maciejewski, M.; Wu, H.; Nagel, K. Demand-responsive transport for students in rural areas: A case study in Vulkaneifel, Germany. Transp. Res. Part A Policy Pract. 2023, 178, 103837. [Google Scholar] [CrossRef]
- Calabrò, G.; Le Pira, M.; Giuffrida, N.; Inturri, G.; Ignaccolo, M.; Correia, G.H.D.A. Fixed-Route vs. Demand-Responsive Transport Feeder Services: An Exploratory Study Using an Agent-Based Model. J. Adv. Transp. 2022, 2022, 8382754. [Google Scholar] [CrossRef]
- Koffman, D. Operational experiences with flexible transit services. Transp. Res. Board 2004, 53. [Google Scholar] [CrossRef]
- Li, X.; Quadrifoglio, L. Feeder transit services: Choosing between fixed and demand responsive policy. Transp. Res. Part C Emerg. Technol. 2010, 18, 770–780. [Google Scholar] [CrossRef]
- Wang, D.; Araldo, A.; Yacoubi, M.A.E. AccEq-DRT: Planning Demand-Responsive Transit to reduce inequality of accessibility. arXiv 2023, arXiv:2310.04348. [Google Scholar] [CrossRef]
- Shen, S.; Ouyang, Y.; Ren, S.; Chen, M.; Zhao, L. Design and implementation of zone-to-zone demand responsive transportation systems. Transp. Res. Rec. 2021, 2675, 275–287. [Google Scholar] [CrossRef]
- Arslan, O.; Hoffmann, S. Implementation of a spontaneous matching algorithm for on-demand shuttle systems in microsimulation. Transp. Res. Procedia 2024, 78, 418–427. [Google Scholar] [CrossRef]
- Tuncel, K.; Koutsopoulos, H.N.; Ma, Z. An integrated ride-matching and vehicle-rebalancing model for shared mobility on-demand services. Comput. Oper. Res. 2023, 159, 106317. [Google Scholar] [CrossRef]
- Fielbaum, A.; Bai, X.; Alonso-Mora, J. On-demand ridesharing with optimized pick-up and drop-off walking locations. Transp. Res. Part C Emerg. Technol. 2021, 126, 103061. [Google Scholar] [CrossRef]
- Patricio, A.S.; Santos, G.G.D.; Antunes, A.P. Assessing the introduction of regional driverless demand-responsive transit services through agent-based modeling and simulation. Transportation 2023, 52, 1091–1118. [Google Scholar] [CrossRef]
- Li, X.; Wei, M.; Hu, J.; Yuan, Y.; Jiang, H. An Agent-Based Model for Dispatching Real-Time Demand-Responsive Feeder Bus. Math. Probl. Eng. 2018, 2018, 6925764. [Google Scholar] [CrossRef]
- Leffler, D.; Burghout, W.; Cats, O.; Jenelius, E. An adaptive route choice model for integrated fixed and flexible transit systems. Transpmetrica B Transp. Dyn. 2024, 12, 2303047. [Google Scholar] [CrossRef]
- Fielbaum, A.; Tirachini, A.; Alonso-Mora, J. Economies and diseconomies of scale in on-demand ridepooling systems. Econ. Transp. 2023, 34, 100313. [Google Scholar] [CrossRef]
- Cavallaro, F.; Nocera, S. Flexible-route integrated passenger–freight transport in rural areas. Transp. Res. Part A Policy Pract. 2023, 169, 103604. [Google Scholar] [CrossRef]
- Wilensky, U. NetLogo; Center for Connected Learning and Computer Based Modeling: Evanston, IL, USA, 1999. [Google Scholar]
- Garcia-Martinez, A.; Cascajo, R.; Jara-Diaz, S.R.; Chowdhury, S.; Monzon, A. Transfer penalties in multimodal public transport networks. Transp. Res. Part A Policy Pract. 2018, 114, 52–66. [Google Scholar] [CrossRef]
- Inturri, G.; Le Pira, M.; Giuffrida, N.; Ignaccolo, M.; Pluchino, A.; Rapisarda, A.; D’Angelo, R. Multi-agent simulation for planning and designing new shared mobility services. Res. Transp. Econ. 2019, 73, 34–44. [Google Scholar] [CrossRef]
- ISTAT—Italian National Institute of Statistics. Ambiente Urbano. Available online: https://www.istat.it/comunicato-stampa/ambiente-urbano-anno-2019-2 (accessed on 8 April 2025).
- Giuffrida, N.; Ignaccolo, M.; Inturri, G.; Rofè, Y.; Calabrò, G. Investigating the correlation between transportation social need and accessibility: The case of Catania. Transp. Res. Procedia 2017, 27, 816–823. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).