Optothermal Modeling for Sustainable Design of Ultrahigh-Concentration Photovoltaic Systems
Abstract
1. Introduction
2. Optical and Thermal Modeling for UHCPV System
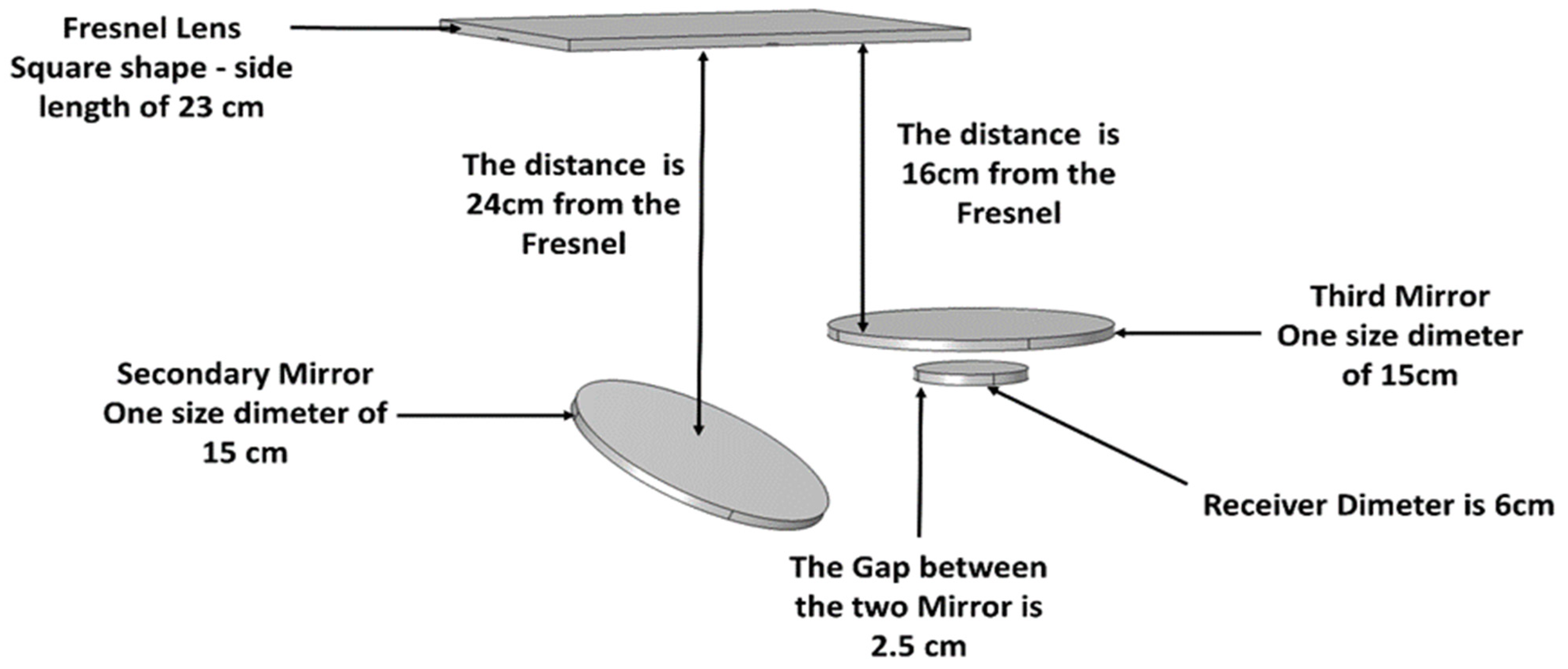
3. Material Geometry and Thermophysical Properties
4. The Governing Equations
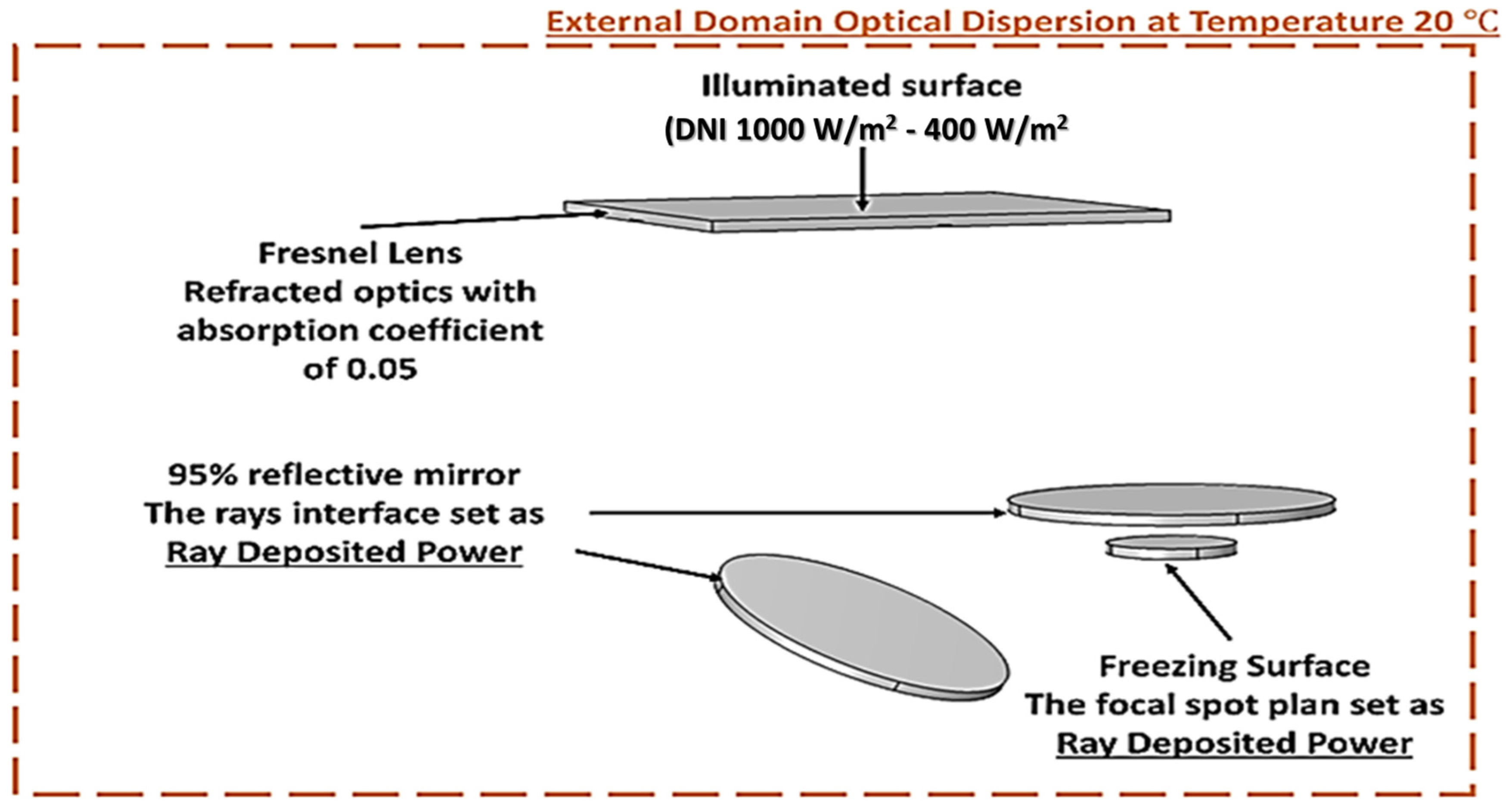
4.1. Optical Model
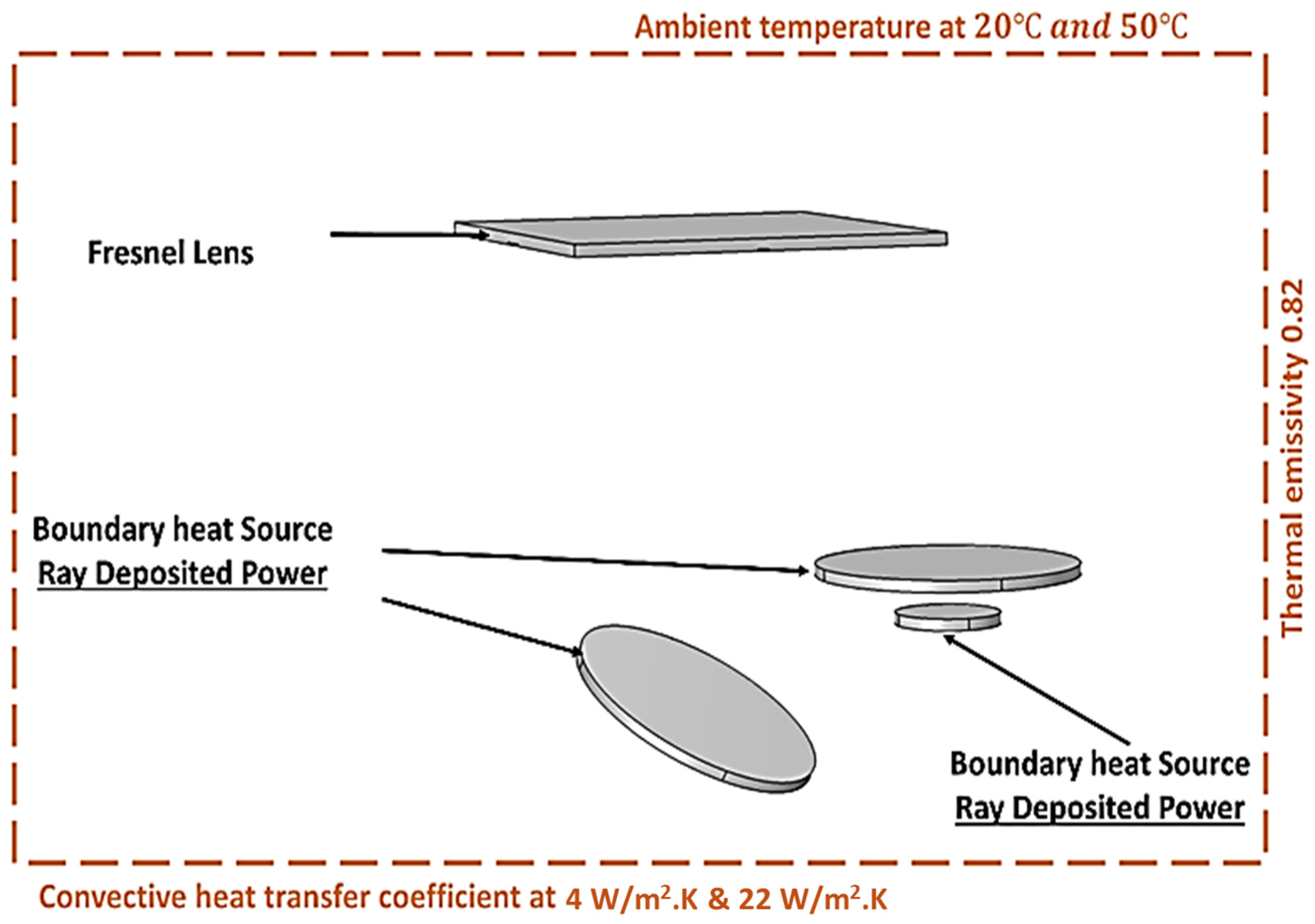
4.2. Thermal Model
5. The Optical and Thermal Model Boundary Conditions
5.1. Optical Model Description
5.2. Thermal Model Description
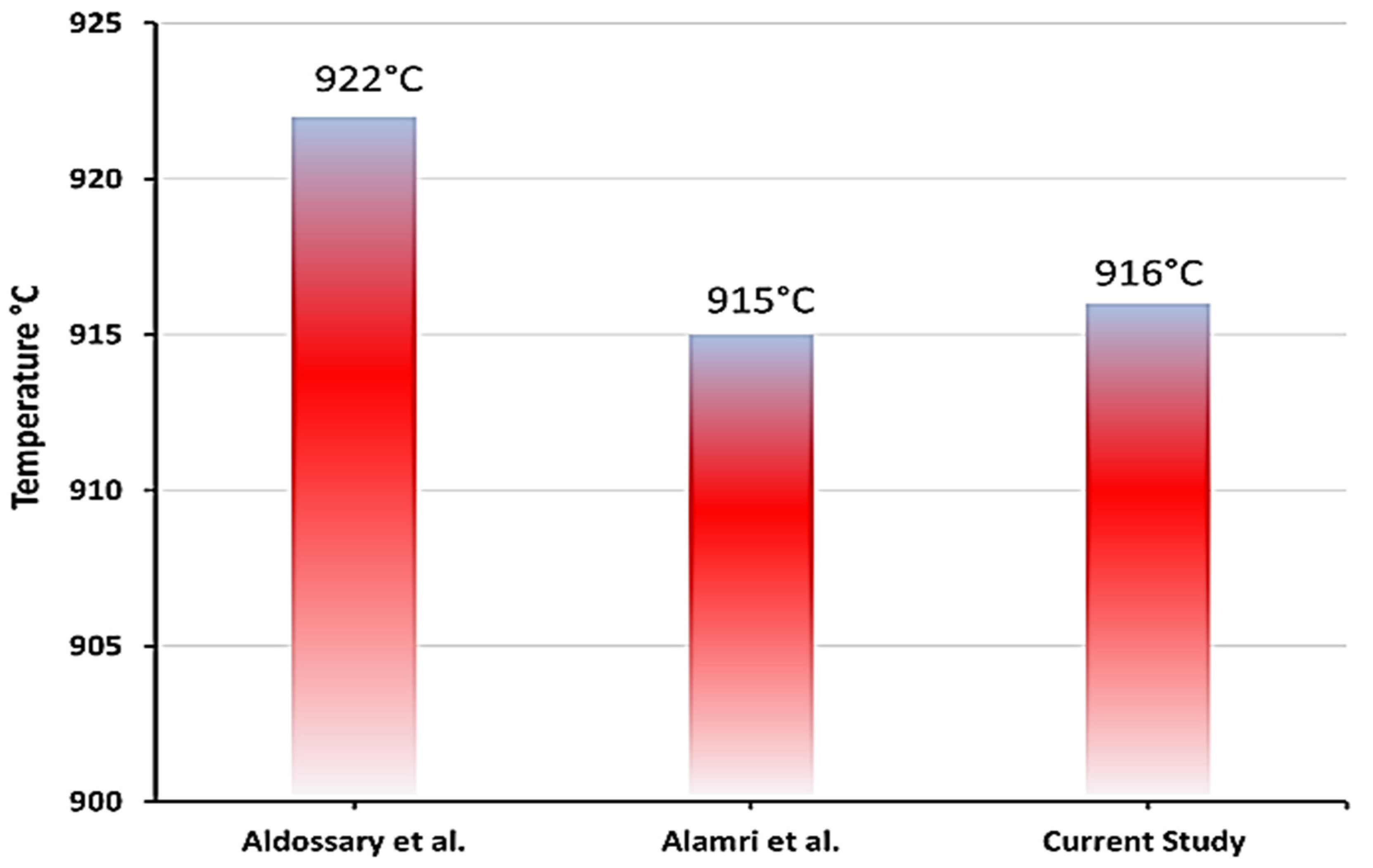
6. Validation
7. Results and Discussion
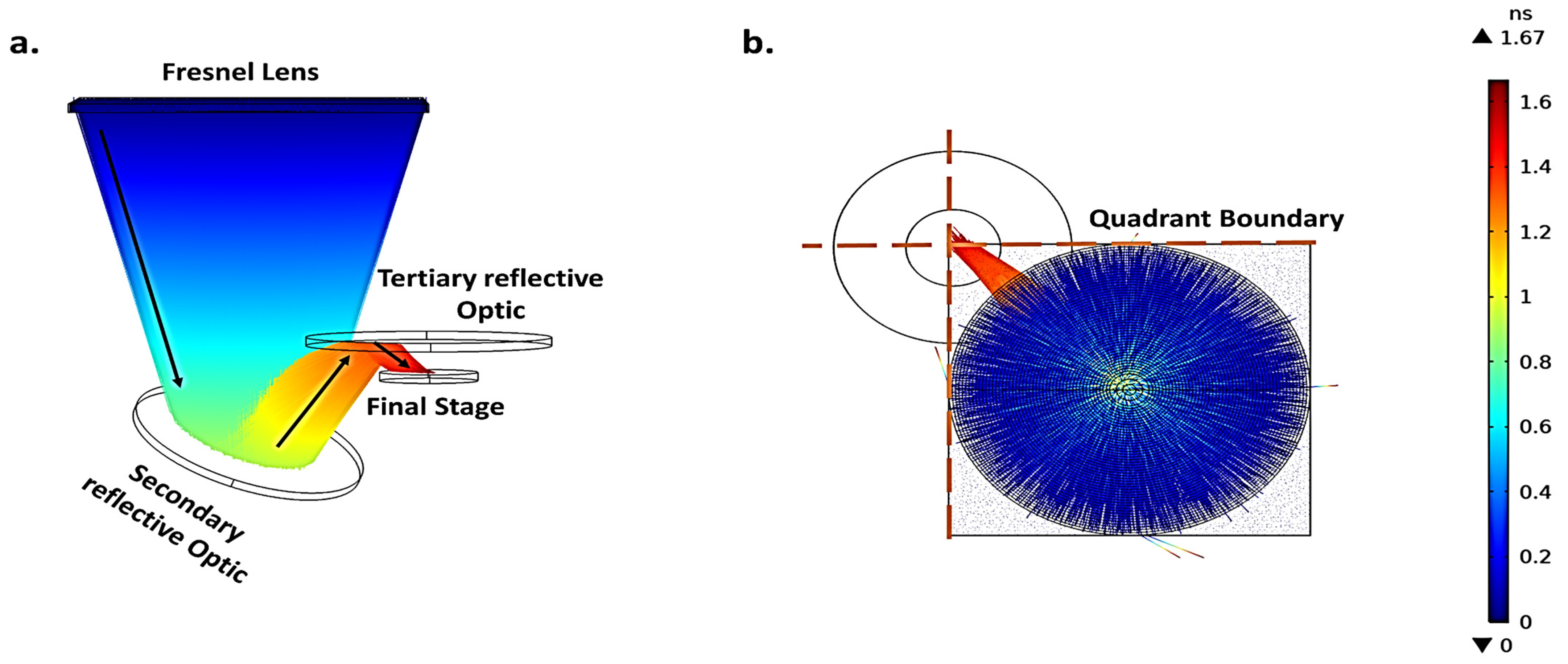
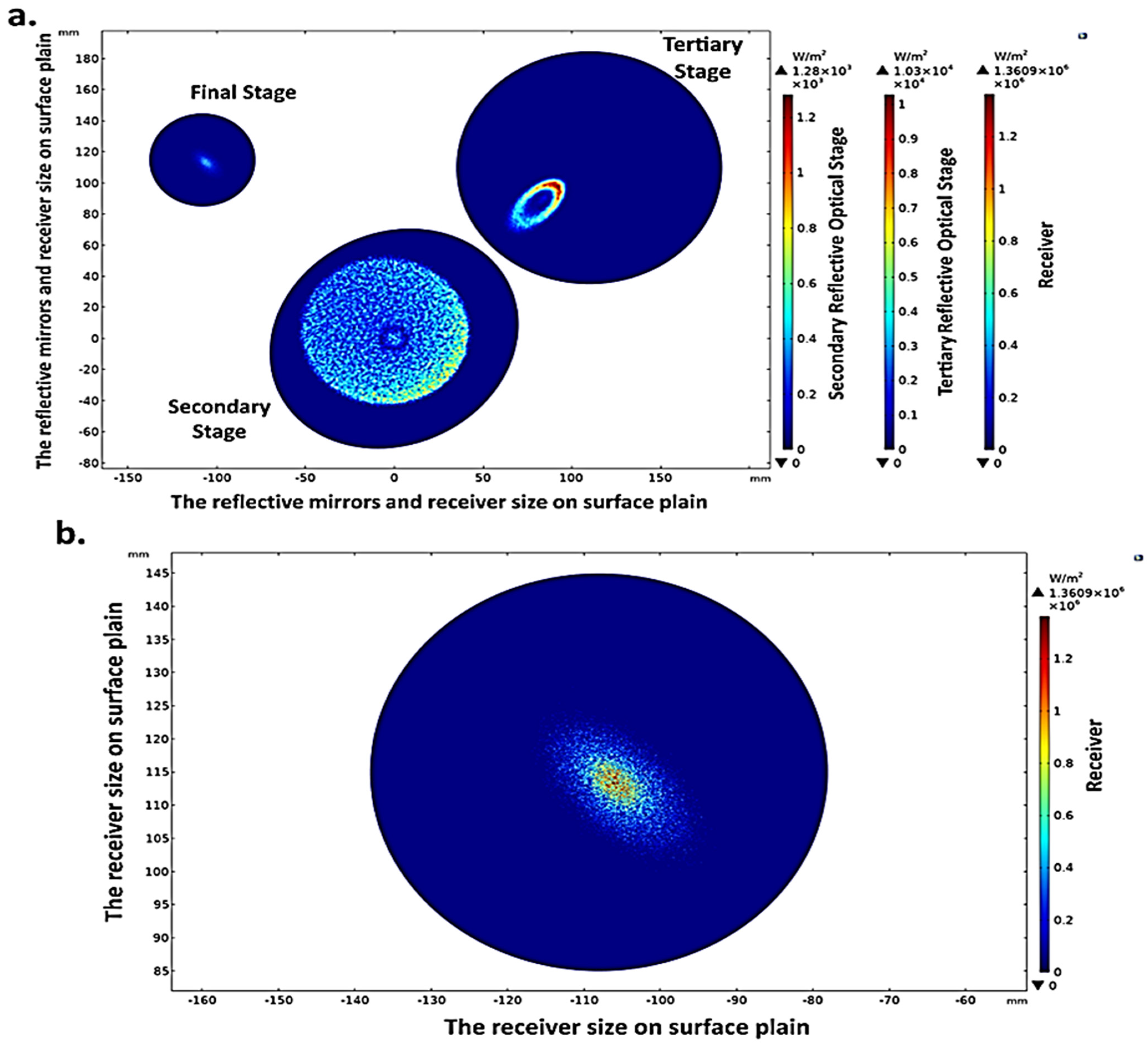
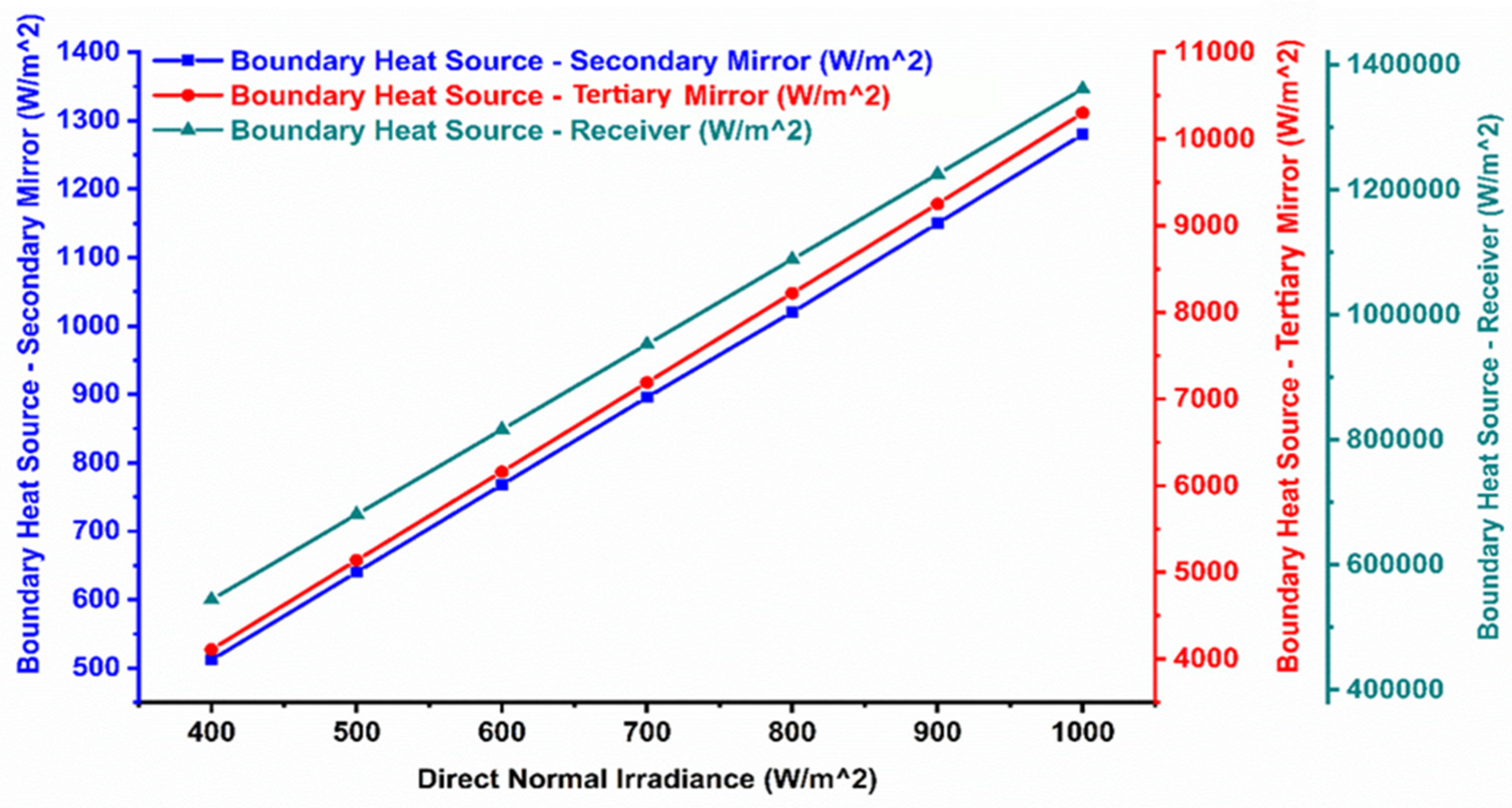
7.1. Quarter of UHCPV Optical System
Solar Divergence Angle
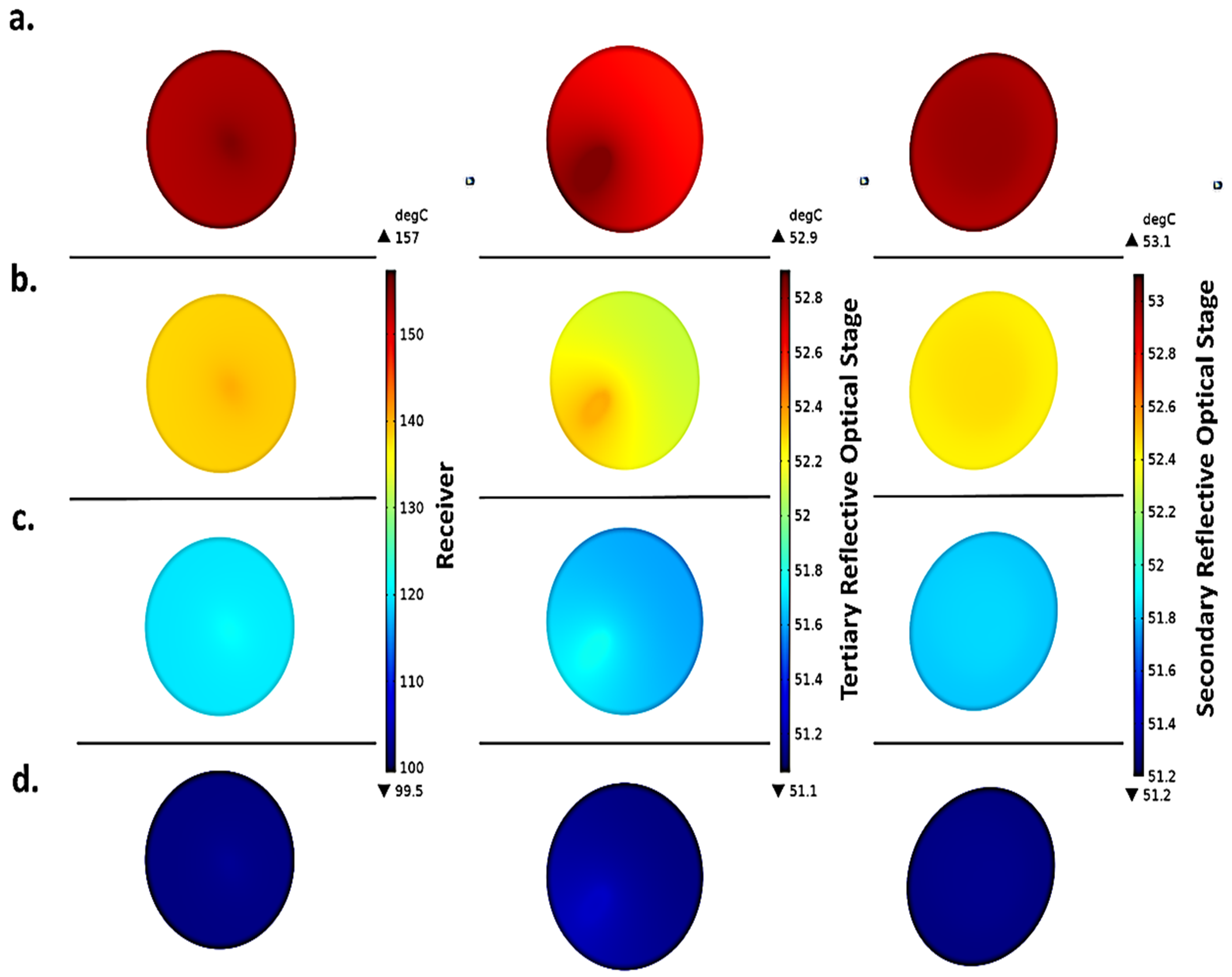
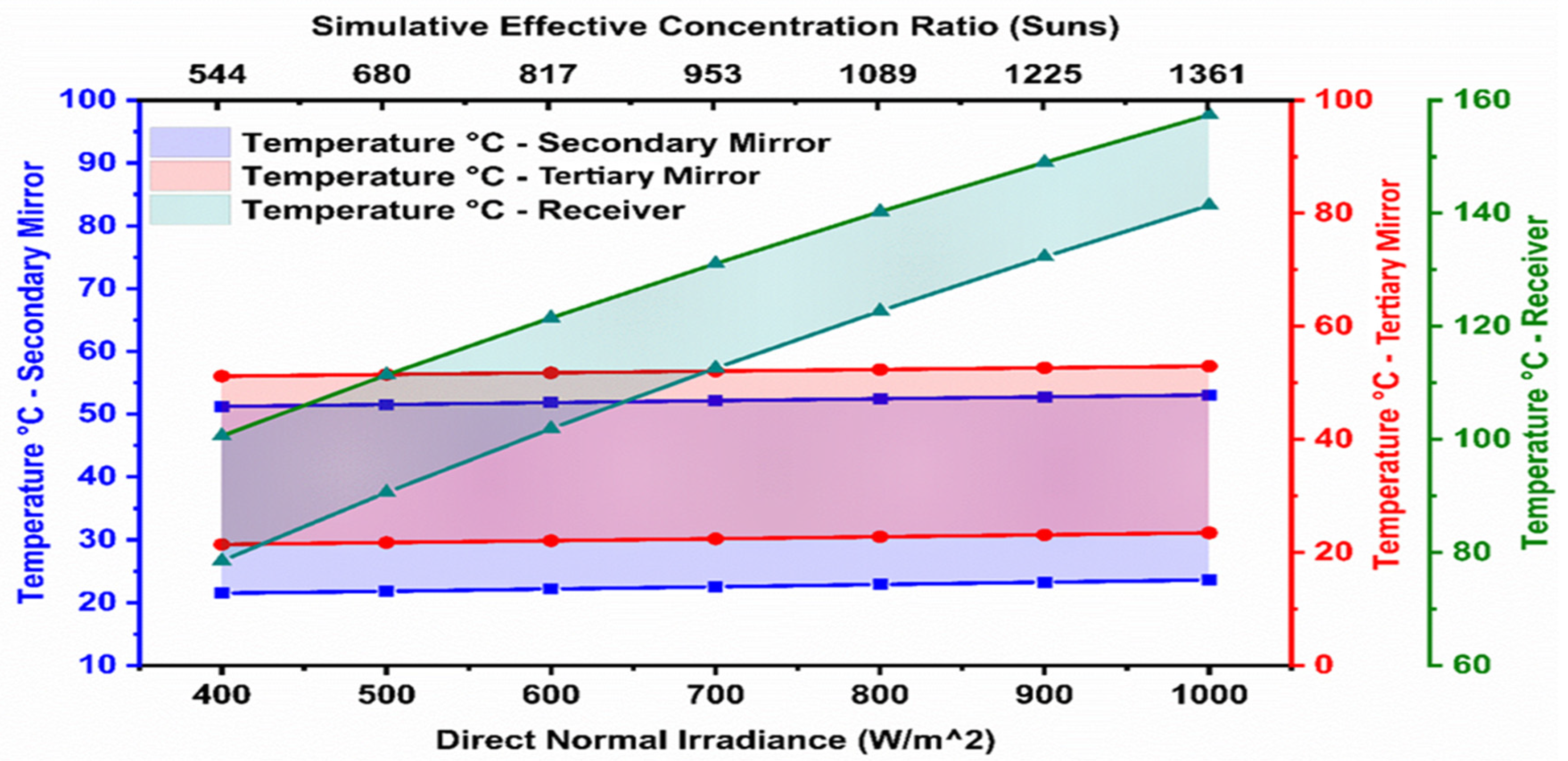
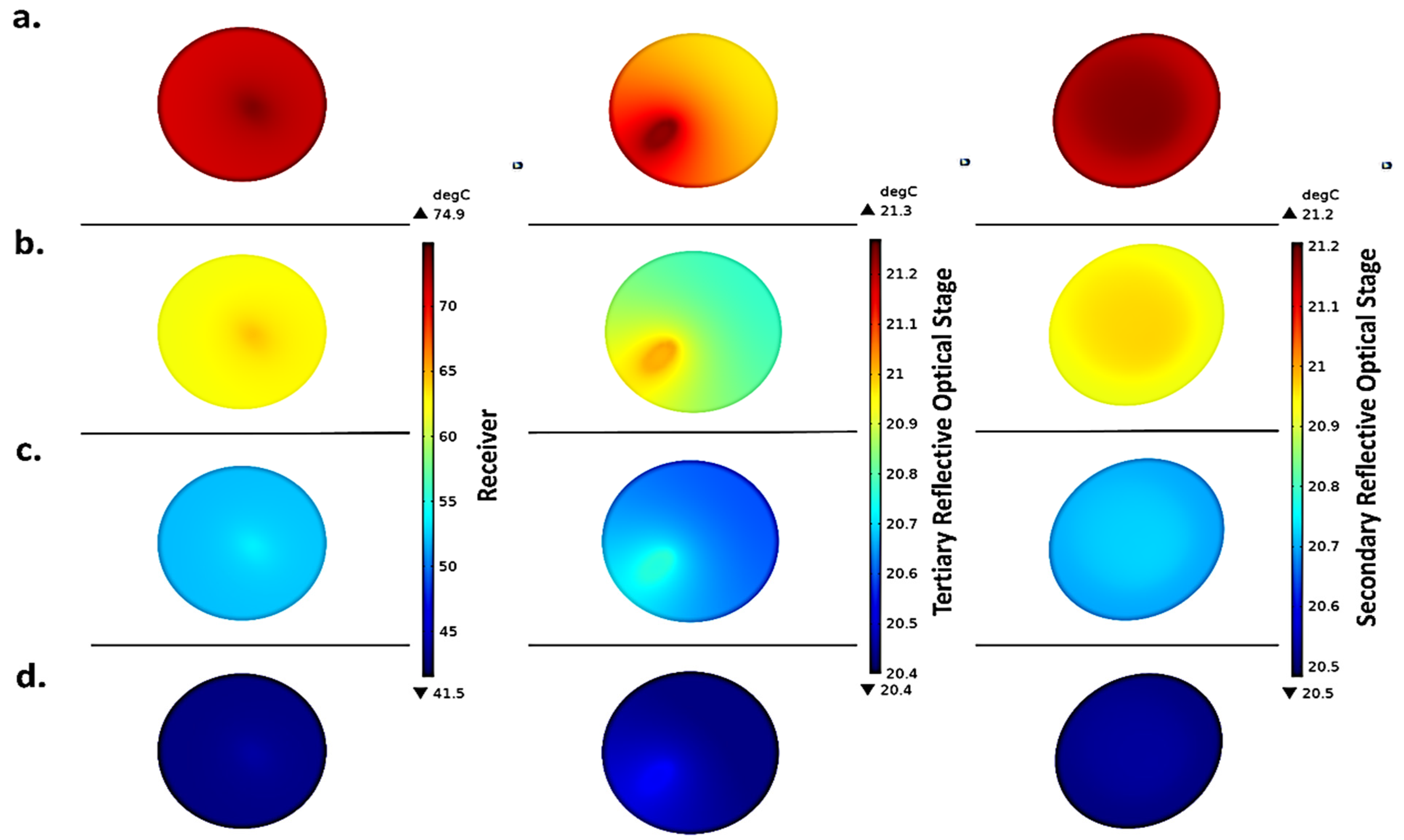
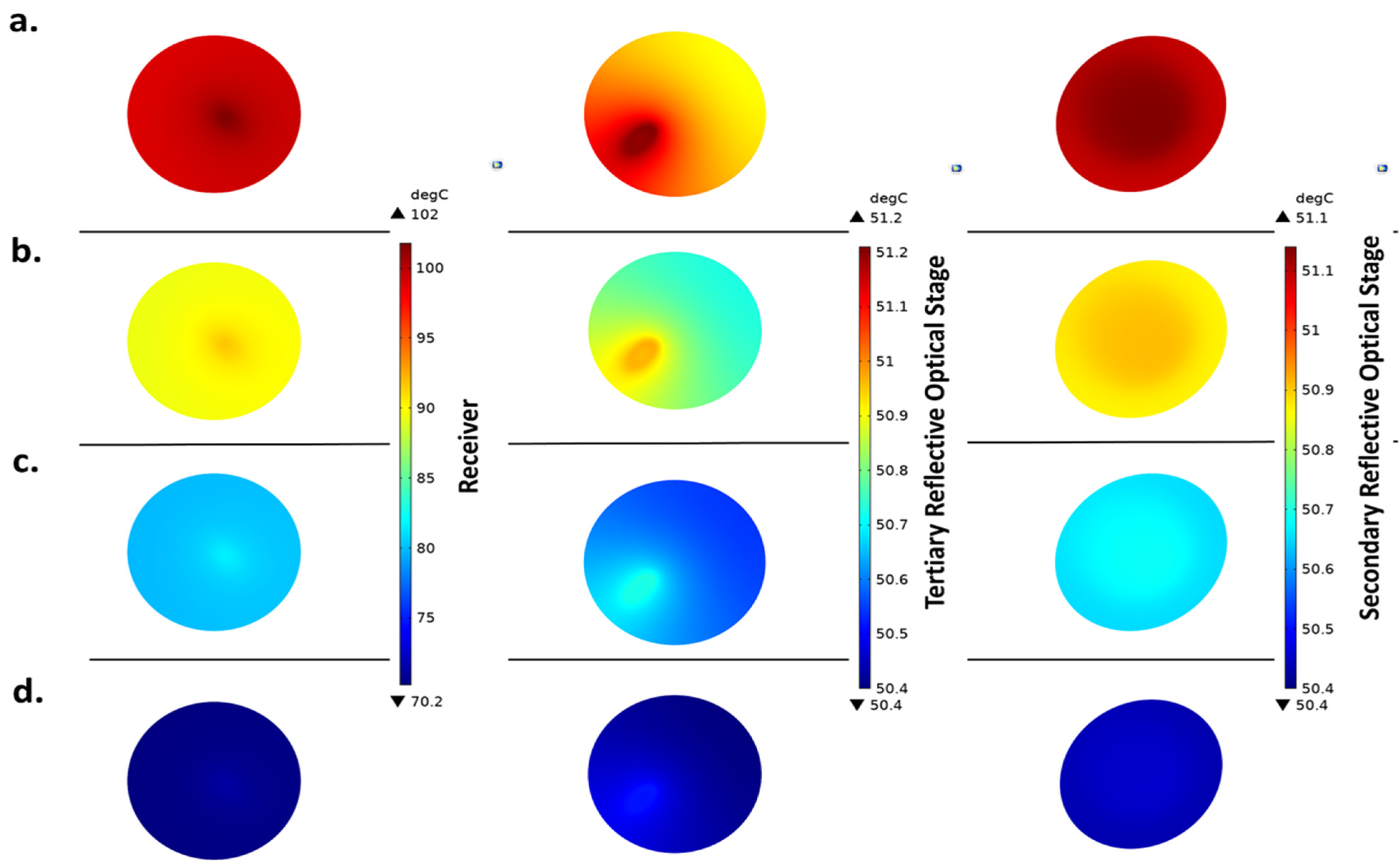
7.2. Thermal Analysis of ¼th of UHCPV System
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Steiner, M.; Siefer, G.; Schmidt, T.; Wiesenfarth, M.; Dimroth, F.; Bett, A.W. 43% Sunlight to Electricity Conversion Efficiency Using CPV. IEEE J. Photovolt. 2016, 6, 1020–1024. [Google Scholar] [CrossRef]
- Shanks, K.; Ferrer-Rodriguez, J.P.; Fernández, E.F.; Almonacid, F. A > 3000 Suns High Concentrator Photovoltaic Design Based on Multiple Fresnel Lens Primaries Focusing to One Central Solar Cell. Sol. Energy 2018, 169, 457–467. [Google Scholar] [CrossRef]
- Wiesenfarth, M.; Steiner, M.; Wolf, J.; Schmidt, T.; Bett, A.W. Investigation of Different Fresnel Lens Designs and Methods to Determine the Optical Efficiency. AIP Conf. Proc. 2014, 1616, 97–101. [Google Scholar] [CrossRef]
- Vallerotto, G.; Victoria, M.; Askins, S.; Herrero, R.; Domínguez, C.; Antón, I.; Sala, G. Design and Modeling of a Cost-Effective Achromatic Fresnel Lens for Concentrating Photovoltaics. Opt. Express 2016, 24, A1245. [Google Scholar] [CrossRef] [PubMed]
- Shanks, K.; Senthilarasu, S.; Mallick, T.K. High-Concentration Optics for Photovoltaic Applications. In High Concentrator Photovoltaics: Fundamentals, Engineering and Power Plants; Springer: Cham, Switzerland, 2015; pp. 85–113. [Google Scholar]
- Vallerotto, G.; Askins, S.; Victoria, M.; Antón, I.; Sala, G. A Novel Achromatic Fresnel Lens for High Concentrating Photovoltaic Systems. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2016; Volume 1766. [Google Scholar] [CrossRef][Green Version]
- Karp, J.H.; Tremblay, E.J.; Hallas, J.M.; Ford, J.E. Orthogonal and Secondary Concentration in Planar Micro-Optic Solar Collectors. Opt. Express 2011, 19, A673. [Google Scholar] [CrossRef]
- Coughenour, B.M.; Stalcup, T.; Wheelwright, B.; Geary, A.; Hammer, K.; Angel, R. Dish-Based High Concentration PV System with Köhler Optics. Opt. Express 2014, 22, A211. [Google Scholar] [CrossRef]
- Dreger, M.; Wiesenfarth, M.; Kisser, A.; Schmid, T.; Bett, A.W. Development and Investigation of a CPV Module with Cassegrain Mirror Optics. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2014; pp. 177–182. [Google Scholar]
- Ferrer-Rodríguez, J.P.; Saura, J.M.; Fernández, E.F.; Almonacid, F.; Talavera, D.L.; Pérez-Higueras, P. Exploring Ultra-High Concentrator Photovoltaic Cassegrain-Koehler-Based Designs up to 6000×. Opt. Express 2020, 28, 6609. [Google Scholar] [CrossRef]
- Variava, J.M.; Ratnadhariya, J.K.; Siddiqui, M.I.H.; Sadasivuni, K.K. 3D Numerical Model of a Concentrated Photovoltaic Thermal (CPV/T) System for Thermal and Electrical Performance Optimization. Case Stud. Therm. Eng. 2024, 61, 104823. [Google Scholar] [CrossRef]
- Nwokolo, S.C.; Eyime, E.E.; Obiwulu, A.U.; Meyer, E.L.; Ahia, C.C.; Ogbulezie, J.C.; Proutsos, N. A Multi-Model Approach Based on CARIMA-SARIMA-GPM for Assessing the Impacts of Climate Change on Concentrated Photovoltaic (CPV) Potential. Phys. Chem. Earth Parts A/B/C 2024, 134, 103560. [Google Scholar] [CrossRef]
- Stsepuro, N.; Kovalev, M.; Podlesnykh, I.; Kudryashov, S. A New Approach to Designing Multi-Element Planar Solar Concentrators: Geometry Optimization for High Angular Selectivity and Efficient Solar Energy Collection. Optics 2025, 6, 6. [Google Scholar] [CrossRef]
- Alzahrani, M.; Shanks, K.; Mallick, T.K. Advances and Limitations of Increasing Solar Irradiance for Concentrating Photovoltaics Thermal System. Renew. Sustain. Energy Rev. 2021, 138, 110517. [Google Scholar] [CrossRef]
- Kiran, M.; Arunachala, U.C.; Varun, K. Effective Thermal Management of Photovoltaic Modules Equipped with Innovative Concentrating Techniques. Int. J. Sustain. Eng. 2025, 18, 2484219. [Google Scholar] [CrossRef]
- Attia, M.E.H.; Zayed, M.E.; Kabeel, A.E.; Khelifa, A.; Arıcı, M.; Abdelgaied, M. Design and Performance Optimization of a Novel Zigzag Channeled Solar Photovoltaic Thermal System: Numerical Investigation and Parametric Analysis. J. Clean. Prod. 2024, 434, 140220. [Google Scholar] [CrossRef]
- Mouaici, K.; Fersadou, B.; Arslan, K.; Kahalerras, H.; Traiche, M. Technological Limit of Solar Concentration Technique Applied to Hybrid Photovoltaic-Thermal Solar Collector Equipped with Thermoelectric Generator Incorporating Ternary Nanofluid. J. Sol. Energy Eng. 2025, 147, 140220. [Google Scholar] [CrossRef]
- Sharaf, O.Z.; Orhan, M.F. Concentrated Photovoltaic Thermal (CPVT) Solar Collector Systems: Part I—Fundamentals, Design Considerations and Current Technologies. Renew. Sustain. Energy Rev. 2015, 50, 1500–1565. [Google Scholar] [CrossRef]
- Obaideen, K.; Olabi, A.G.; Al Swailmeen, Y.; Shehata, N.; Abdelkareem, M.A.; Alami, A.H.; Rodriguez, C.; Sayed, E.T. Solar Energy: Applications, Trends Analysis, Bibliometric Analysis and Research Contribution to Sustainable Development Goals (SDGs). Sustainability 2023, 15, 1418. [Google Scholar] [CrossRef]
- Azur Space Solar Power GMBH. Enhanced Fresnel Assembly—EFA Type: 3C42A—With 10 × 10mm2 CPV TJ Solar Cell Application: Concentrating Photovoltaic (CPV) Modules; Azure Space Solar Power GMBH: Heilbronn, Germany, 2014; pp. 1–4. [Google Scholar]
- Micheli, L.; Sarmah, N.; Fernandez, E.F.; Reddy, K.S.; Mallick, T.K. Technical Issues and Challenges in the Fabrication of a 144-Cell 500× Concentrating Photovoltaic Receiver. In Proceedings of the 2014 IEEE 40th Photovoltaic Specialist Conference (PVSC), Denver, CO, USA, 8–13 June 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 2921–2925. [Google Scholar]
- Abo-Zahhad, E.M.; Ookawara, S.; Radwan, A.; El-Shazly, A.H.; Elkady, M.F. Numerical Analyses of Hybrid Jet Impingement/Microchannel Cooling Device for Thermal Management of High Concentrator Triple-Junction Solar Cell. Appl. Energy 2019, 253, 113538. [Google Scholar] [CrossRef]
- Abo-Zahhad, E.M.; Ookawara, S.; Radwan, A.; El-Shazly, A.H.; El-Kady, M.F.; Esmail, M.F.C. Performance, Limits, and Thermal Stress Analysis of High Concentrator Multijunction Solar Cell under Passive Cooling Conditions. Appl. Therm. Eng. 2020, 164, 114497. [Google Scholar] [CrossRef]
- Alzahrani, M.; Baig, H.; Shanks, K.; Mallick, T. Estimation of the Performance Limits of a Concentrator Solar Cell Coupled with a Micro Heat Sink Based on a Finite Element Simulation. Appl. Therm. Eng. 2020, 176, 115315. [Google Scholar] [CrossRef]
- Shohdy, A.; Emam, M.; Sekiguchi, H.; Hassan, H. Performance of New Hybrid Heat Sink with Trimmed Fins and Microchannels for Thermal Control of a Triple-Junction Concentrator Photovoltaic Cell. Appl. Therm. Eng. 2024, 252, 123695. [Google Scholar] [CrossRef]
- Gupta, A.; Chougule, S.S.; Saha, S.K. Cooling of Highly Concentrated Photovoltaic Cells with Confined Jet Impingement by Introducing Channel Configurations. Renew. Energy 2024, 237, 121600. [Google Scholar] [CrossRef]
- Valera, A.; Fernández, E.F.; Rodrigo, P.M.; Almonacid, F. Feasibility of Flat-Plate Heat-Sinks Using Microscale Solar Cells up to 10,000 Suns Concentrations. Sol. Energy 2019, 181, 361–371. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiao, G.; Luo, Z.; Ni, M.; Yang, T.; Xu, W. Comparison of Different Types of Secondary Mirrors for Solar Application. Optik 2014, 125, 1106–1112. [Google Scholar] [CrossRef]
- Shurtz, R.C. Total Hemispherical Emissivity of Metals Applicable to Radiant Heat Testing; Sandia National Lab.: Albuquerque, NM, USA; Livermore, CA, USA, 2018. [Google Scholar]
- Aldossary, A.; Mahmoud, S.; Al-dadah, R. Technical Feasibility Study of Passive and Active Cooling for Concentrator PV in Harsh Environment. Appl. Therm. Eng. 2016, 100, 490–500. [Google Scholar] [CrossRef]
- Alamri, Y.A.; Albaik, I.; Mahmoud, S.; Al-Dadah, R.; Ismail, M.A. Integration of Concentrated Multi-Junction Solar Cells with Small-Scale Organic Rankine Cycle. Energy Convers. Manag. 2021, 239, 114235. [Google Scholar] [CrossRef]




| Material | Silicon Diameter (Active Area) | Focal Length | Fresnel Lens Prism Spacing | Fresnel Lens Prism per Length | Fresnel Prism Height Increase | Fresnel Constant Angle | Average Prism Angle | Total Number of Grooves | Estimated Optical Edge Loss |
|---|---|---|---|---|---|---|---|---|---|
| Silicon on Glass (SOG) | 21 cm × 21 cm | 420 mm | 0.01 mm | 4 mm | 0.04 mm | 0.55° | 1.2° | 525 | ~4% |
| Optical and Thermal Properties | Silica Glass | Aluminum |
|---|---|---|
| Reflective index, real part [dimensionless] | 1.45 | - |
| Thermal conductivity [] | 1.38 | 238 |
| Density [kg/m3] | 2203 | 2700 |
| Heat capacity [J/(kg.K)] | 703 | 900 |
| Optical Element | Avg. Temp @ 20 °C (°C) | Avg. Temp @ 50 °C (°C) | % Increase |
|---|---|---|---|
| Receiver | 89.2 | 157.4 | 76.5% |
| Secondary Mirror | 37.5 | 58.9 | 56.9% |
| Tertiary Mirror | 36.9 | 57.9 | 56.7% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maatallah, T.; Alzahrani, M.; El Alimi, S.; Ali, S. Optothermal Modeling for Sustainable Design of Ultrahigh-Concentration Photovoltaic Systems. Sustainability 2025, 17, 5262. https://doi.org/10.3390/su17125262
Maatallah T, Alzahrani M, El Alimi S, Ali S. Optothermal Modeling for Sustainable Design of Ultrahigh-Concentration Photovoltaic Systems. Sustainability. 2025; 17(12):5262. https://doi.org/10.3390/su17125262
Chicago/Turabian StyleMaatallah, Taher, Mussad Alzahrani, Souheil El Alimi, and Sajid Ali. 2025. "Optothermal Modeling for Sustainable Design of Ultrahigh-Concentration Photovoltaic Systems" Sustainability 17, no. 12: 5262. https://doi.org/10.3390/su17125262
APA StyleMaatallah, T., Alzahrani, M., El Alimi, S., & Ali, S. (2025). Optothermal Modeling for Sustainable Design of Ultrahigh-Concentration Photovoltaic Systems. Sustainability, 17(12), 5262. https://doi.org/10.3390/su17125262





