1. Introduction
The State Post Bureau of China has announced that by 2024, the volume of express delivery services in China will have reached 174.5 billion items, representing an annual rise of 21.5%. In the same year, the overall amount of same-city express delivery services performed was 15.64 billion items, displaying a 14.6% growth compared to the previous year [
1]. The rising demand for e-commerce and logistics, along with the need for speed in the supply chain [
2], necessitates convenient, efficient, and effective methods for cargo transportation, which are essential for improving logistics services in urban areas and enhancing residents’ quality of life. Currently, traditional logistics transportation relies on fuel-powered vehicles, including three-wheeled motorcycles and small trucks, for ground goods conveyance. However, ongoing population growth in urban areas and the increase in motor vehicle numbers have resulted in issues such as traffic congestion and urban environmental degradation. These issues also limit the effectiveness of urban logistics distribution. At the same time, in response to governmental mandates for energy conservation and emission reduction, green sharing has become the future trend in city logistical development. Some researchers have previously proposed answers to this issue. Using emerging technologies (such as cargo bikes, autonomous vehicles, and drones) and traditional vehicle collaboration, Perboli and Rosano [
3] integrated urban parcel delivery business and operation modes. Schomakers [
4] discussed a novel way of freight transportation, specifically employing Ducktrains for last-mile delivery to address urban freight transportation challenges and its potential benefits. This paper proposes the metro logistics system (M-ULS), namely, the subway as a means of urban cargo transportation.
The metro logistics system (M-ULS) uses the available transportation capacity of the metro system during off-peak passenger periods to deliver freight. This strategy not only ensures the safety and punctuality of logistics operations but also aims to enhance the quality of logistics services and increase customer satisfaction [
5]. The system is composed of a distribution center, metro stations (i.e., distribution sites), the metro network, and end customers, as depicted in
Figure 1. In the first part of the metro logistics system, from the distribution center to the distribution site, distribution can be executed via the metro system or traditional freight trucks. A crisscrossing metro network and most hub stations form the backbone of the system. Workers temporarily store goods at distribution sites near metro stations. In the final phase, specifically from the distribution center to the end consumers, couriers use above-ground transportation tools to collect and send the products to the customers.
The location of distribution centers has always been an important problem in optimizing the logistics system [
6]. The logistics distribution center serves as a bridge connecting the distribution hub and the end-users, and it is also a crucial node in the logistics system, greatly impacting the system’s overall effectiveness and operational quality. Finding suitable distribution hub sites in urban regions is difficult due to considerations such as limited land resources and complex urban planning. Furthermore, an inconvenient site can result in greater transit distances, longer delivery times, higher logistics costs, and inefficient distribution networks, all of which greatly decrease the overall efficiency and effectiveness of the urban logistics system. It is essential to position metro logistics hubs in a way that alleviates urban traffic congestion, reduces transportation expenses, minimizes environmental pollution, and promotes sustainable and intelligent urban logistics development [
7]. However, the majority of metro stations can function as distribution points. Consequently, selecting an optimization model for the placement of logistics distribution hubs to address these practical challenges has become a key focus in logistics studies. This topic continues to be of considerable interest to numerous scholars [
8]. In this paper, we concentrate on two core research questions. Two scientifically sound models are to be developed, one for precise assessment of the feasibility of subway stations as distribution hubs and the other for minimizing urban distribution costs. The second approach involves employing an enhanced heuristic algorithm to address the model and provide an acceptable plan for logistics distribution hubs situated at subway stations.
The next part of this paper is organized as follows:
Section 2 discusses the relevant literature from two perspectives: advancements in underground logistics systems and challenges related to the site selection of distribution hubs. In
Section 3, we introduce two models: the metro-integrated evaluation model and the site selection model for distribution centers. This subsection includes the influencing variables of the models, model assumptions, objective functions, and constraint conditions. A jellyfish search algorithm solves this model in
Section 4.
Section 5 delineates the selection of appropriate logistics hub locations. It takes the Beijing Chaoyang Metro Network as a case study and presents analytical views of the findings.
Section 6 finishes with an analysis of the present circumstances and offers solutions to mitigate this research’s shortcomings.
2. Literature Review
Over the past decade, city logistics has developed efficient and effective ways to transport goods in urban areas. Consequently, the total number of studies on urban logistics issues has increased dramatically. These studies have presented a wide range of innovative solutions for effective cargo distribution in traffic-congested urban areas. The M-ULS model signifies a comparatively innovative methodology. This section gives a literature review from two viewpoints: Initially, we outline the sustainability and advantages of the M-ULS; secondly, we turn to the matter of how to determine the distribution hubs’ location.
In the 19th century, the telegraph system in London, the United Kingdom, laid the foundation for underground cargo transportation. Many nations in Asia, Europe, and other regions have taken steps to create subterranean cargo transit systems for various uses over the years [
9]. For example, in the 20th century, Japan planned a city-wide ULS (underground logistics system) network to alleviate traffic congestion, shifting urban ground transportation to underground transportation [
10]. The Dutch government collaborated to develop dedicated tunnels for underground transportation to carry special goods [
11]. Yiqun Fan et al. [
12] primarily considered the integration of ULS with ports to address traffic congestion caused by container trucks in port cities. In the early 21st century, in the face of the increasingly prominent contradiction between the decline in traditional transportation efficiency and the surge in logistics demand, most research scholars began to explore the feasibility of using subways as a mode of underground logistics transportation [
13,
14,
15]. Researchers believe that the remarkable advantage of utilizing subways for urban freight transit lies in their eco-friendliness and sustainability in the conveyance of commodities. It can reduce resource waste and pollutant emissions generated by the logistics industry, thus promoting urban logistics and green and sustainable development. For example, Zhen Di [
16] and his colleagues optimized the subway freight capacity through a mathematical programming model and simulated traffic flow to calculate the saved TFC. The findings indicate that, without impacting passengers, a portion of freight demand can be shifted from vehicles to subways during non-peak times, thus significantly decreasing traffic-related carbon emissions. By building a model and studying the Madrid scenario, Villa et al. [
17] found that the M4G metro system is a more sustainable and environmentally friendly way to distribute products in cities.
The selection of nodes in the subway logistics distribution network and the pursuit of more effective solutions have emerged as major research topics for scholars recently. The selection of nodes is of vital importance in the subway logistics system, as it plays a crucial role in determining the location of distribution hubs. Researchers use various models and indicators to evaluate subway stations. For instance, scholars such as Laijun Zhao et al. [
18] constructed a metro-integrated logistics system that assessed the significance of each metro station. They employed the TOPSIS model to prioritize all metro stations according to logistical criteria. Shukang Zheng et al. [
19] Considering the differences between various subway stations, several elements, including node degree, inner centrality, and nearby centrality, are suggested as evaluative criteria, and an enhanced fuzzy analytic hierarchy process alongside the entropy weight approach is employed to determine index weights. Zhouyang Du et al. [
20] have put forward an enhanced Topological Potential Model Considering Entropy (ITPE) to consolidate several metrics by incorporating various centrality measures for assessing the significance of nodes in the metro network. Zheng et al. [
21] devised a methodology for site selection of subterranean logistics facilities utilizing the metropolitan metro system. They applied this method to a cost-minimization model for metro transport during off-peak hours. Based on the aforementioned literature and previous studies, this paper considers the dynamic characteristics of logistics demand. By incorporating complex network metrics and subway station passenger flow data, we constructed a metro-integrated evaluation model to determine alternative distribution hub locations. This approach reduces the complexity of the multi-depot location problem and reflects actual logistics service demand across different periods more accurately.
Scholars have employed traditional methods, including the center-of-gravity method [
22,
23] and the analytic hierarchy process [
24,
25], to address the site selection problem for various alternative distribution centers. As the quantity of elements in the site selection model grows and constraints get more complicated, standard methods fail to handle the problem quickly and accurately. Consequently, different scholars have proposed a range of heuristic and optimization algorithms, such as the walrus optimization algorithm, Harris hawks optimization, etc. Mengxiao He et al. [
26] proposed two novel models related to logistics and distribution center layout, and they compared the convergence of an original bat-inspired algorithm with an improved version, demonstrating the reliability of the models. Siying Zhang et al. [
7] used the bilevel programming method to create a location selection model for cold-chain logistics facilities that took consumer preferences and low carbon emissions into account. The model was addressed through the application of the cloud particle swarm optimization algorithm. Wanjie Hu et al. [
27] proposed an enhanced multi-objective cooperative co-evolutionary optimization method for the M-ULS network design issue, accounting for unknown demand and costs.
Although research on M-ULS has gradually matured, most studies focus on a single cost factor when constructing models, rarely accounting for total system costs. In addition, for this NP-hard problem, this paper utilizes the JS algorithm, which has superior optimization performance to solve the model. To prevent the algorithm from falling into local optima during the solving process, which may lead to low solution accuracy, the original JS algorithm is slightly improved. This paper addresses these gaps through optimizations in two key aspects: model formulation and algorithm design. This paper’s primary contributions are as follows:
The model for locating distribution hubs establishes centers around the subway system and aims to minimize overall costs, incorporating comprehensive cost considerations along with various factors and parameters. In practice, it reflects an operational cost structure while also adapting to diverse operating environments and company needs.
The effectiveness of the improved JS algorithm was verified in this paper through a comparison with the original JS algorithm.
4. Artificial Jellyfish Search Algorithm
4.1. Algorithm Principle
Jellyfish are among the most common marine organisms. They live in waters of varied depths and temperatures all over the world and come in a diverse range of colors, sizes, and shapes. These traits illustrate the remarkable adaptability of jellyfish to the marine ecosystem. Additionally, jellyfish are capable of controlling their movements. Their abdomens contract like umbrellas, pushing water out to propel their bodies forward. Despite having this ability, they mostly drift in the water. Jellyfish can only create swarms when living conditions are good.
Various elements, such as ocean currents, oxygen consumption rates, and predation, influence the emergence of a jellyfish swarm. Of these factors, ocean currents are the most critical. The primary drivers of ocean currents are solar heating and wind acting on the ocean surface. This feature, together with the unique movement of each jellyfish within the swarm and its evolution in accordance with ocean currents, allows jellyfish to emerge almost anywhere in the sea. Because the amount of food changes from location to location, comparing it at each site might help establish the ideal position. In 2020, Chou et al. [
29] introduced the Jellyfish Optimization Algorithm based on the aforementioned jellyfish movement and nutrition hunting procedures.
4.2. Algorithm Design
We employ the jellyfish search algorithm, known for its superior optimization features, to deal with the logistics hub site location problem. The precise stages are outlined below, and the algorithmic flow is illustrated in
Figure 3.
Stage 1: initializing the population. The jellyfish search algorithm relies on a more efficient and quickly randomized logistic map to augment population variety, as the limited diversity of the initial population can result in a sluggish convergence rate or predispose the model to local optima. Equation (18) reads as follows:
among them,
is the logistic chaotic value of the position of the
-th jellyfish, and the value range of
is
;
is a control parameter, and the value is 4.
In the code, initialize the jellyfish populations with a population size of and a maximum amount of iterations . The fitness value for each individual is calculated using the fitness function and is stored in . The current set of individual optimal fitness values is . Following this, we need to identify the location of the best jellyfish at the start.
Stage 2: time control mechanism. Over time, the algorithm must implement a temporal control mechanism to regulate the transition between movement modes.
represents the temporal control functions, which are stochastic values that vary between 0 and 1 across time [
30]. Equation (19) reads as follows:
Stage 3: The value of
determines the population’s migration. If
, jellyfish movement aligns with the ocean current, then the position update algorithm is delineated in Equation (20). Vice versa for intra-cluster movement and perform step four calculations.
In the formula, is the literation number, is the optimal position of the current jellyfish population, is the average position of all jellyfish, and is a distribution coefficient ().
Stage 4: simulation of jellyfish swarms. In the initial stage of jellyfish swarm formation, most jellyfish exhibit passive behaviors. However, as time goes by, an increasing number of jellyfish display active behaviors. If
and
, the jellyfish population exhibits passive movement with the following Equation (21) [
29].
where
and
are the upper and lower bounds of the delimited area, respectively, and
is a motion coefficient. Gradually,
rises from 0 to 1, resulting in
prompting jellyfish to transition from a passive to an active mode of locomotion during internal movement 13. This means the revised position of each jellyfish can be seen as follows (Equation (22)):
where
is the original jellyfish, and
is the randomly selected jellyfish.
Stage 5: boundary constraints. Boundary control is executed utilizing Equations (23) and (24) [
12], while the fitness value and the optimal position of each jellyfish are computed.
where
is the position of the
-th jellyfish in the d-dimension,
is the updated position of the
-th jellyfish in the d-dimension, and
and
are the upper and power boundaries of the delimited region, respectively.
Stage 6: Reiterate Steps 2 to 5 until the termination criteria are satisfied, which include reaching the maximum number of iterations and identifying an optimal solution.
The jellyfish search algorithm exhibits rapid convergence and strong optimization ability, yet it is prone to slow convergence in certain instances and may readily become trapped in a local optimum. To enhance the efficacy of the jellyfish search algorithm, we opted to modify the position and velocity of jellyfish via Lévy flight trajectories. The following Formula (25) is used by the improved algorithm to replace the old algorithm’s method for updating speed and location.
where
is the spatial position of the jellyfish in the search
.
is the position of the best jellyfish in this group. Lévy
represents the random searching vector where the step size of the walk is subject to Lévy distribution.
is the scale parameter.
5. Case Study
5.1. Screening of the Alternate Metro Hub Site
The official websites of Beijing Metro and Beijing MTR indicate that Chaoyang District, Beijing, has 13 subterranean lines and 93 metro stops. The degree values of the metro station nodes listed in
Table 3 can be computed using Equation (1) and the topology map of the Chaoyang metro network depicted in
Figure 4.
The topological map of the Chaoyang metro network and Equation (2) reveal 93 metro nodes along with their betweenness values, as presented in
Table 4. It directly shows that some of the 93 metro nodes, like nodes 15, 31, and 57, have relatively high betweenness values. A high betweenness rating, on the one hand, implies that the related node is an important transit point in the metro system. On the other hand, it highlights the key role of these stations in terms of linkage and flow regulation in urban distribution.
Due to the sensitive nature of passenger flow data at each Beijing underground station, we are restricted to accessing flow statistics for each subway line alone. We classify the 93 metro stations into three levels, with each level denoting a specified percentage of the passenger traffic for the respective subway line. This classification enables us to assess the patronage for each station.
Table 5 highlights the stages of metro passenger flow.
Level 1: Numerous metro intersections function as transfer stations, comprising 50% of the overall passenger flow.
Level 2: Within a three-kilometer radius, commercial or enterprise parks constitute 30% of the overall ridership.
Level 3: Alternative stations comprise 20% of the overall passenger traffic.
Official data from Beijing and the Beijing–Hong Kong metros indicate that the average daily passenger flow of the Chaoyang metro lines in 2023 is presented in
Table 6.
The previously mentioned three indications have been rendered dimensionless using Equation (3), and all data can be derived using Equation (4). The integrated evaluation values of ninety-three metro stations are presented in
Table 7.
In conclusion, the node values of 2, 7, 27, 31, 33, 36, 58, and 59 are ranked higher among the 93 metro station nodes, corresponding to the Olympic Park, Wangjing, Sanyuanqiao, Hujialou, Guomao, Panjiayuan, Jintailu and Dawanglu metro stations, respectively. These metro nodes serve as alternative hub sites for researching the greatest rational locations in the Chaoyang District of Beijing.
5.2. Data Acquisition
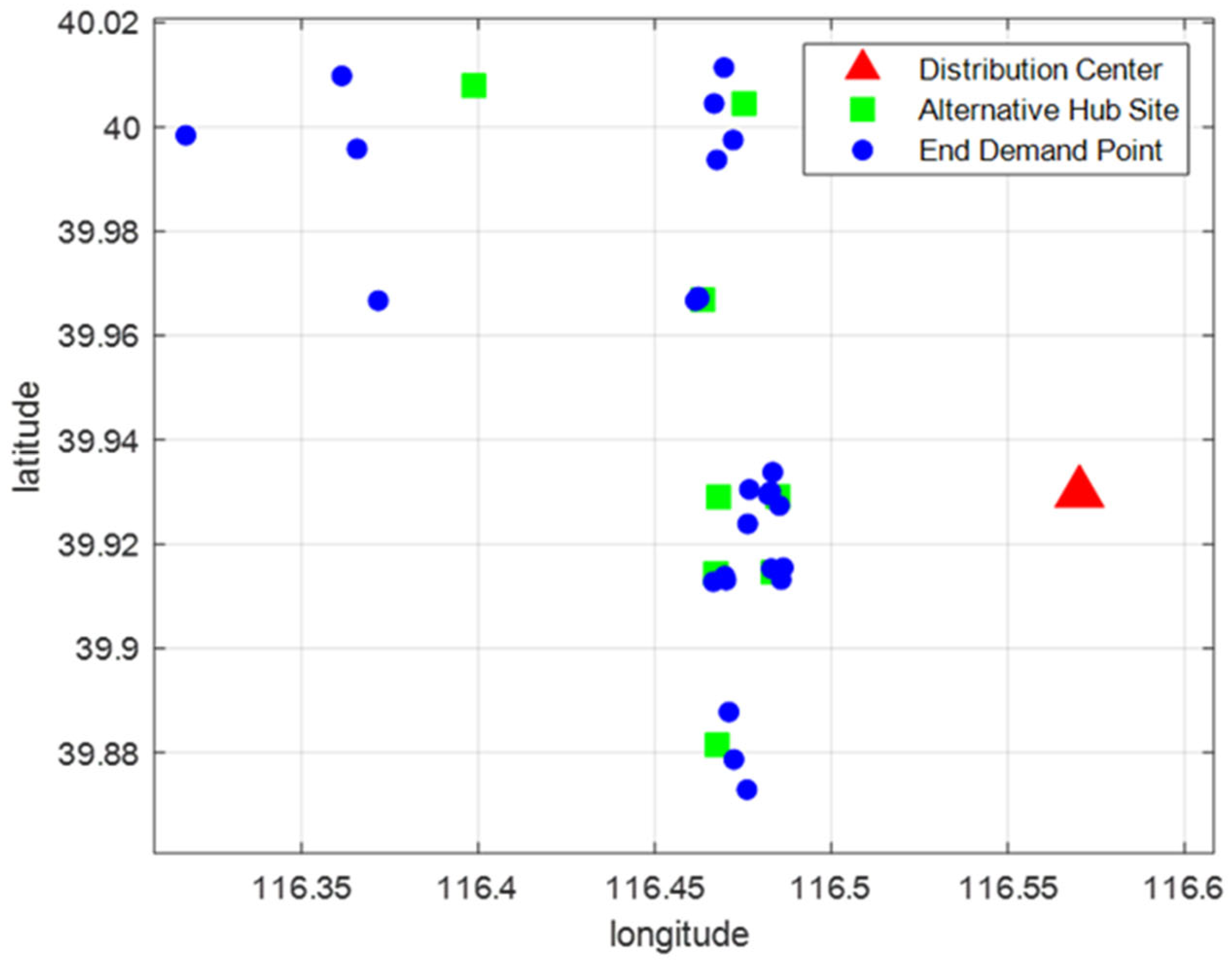
Consultation of the logistics Waybill Information, Beijing Planning, and Gaode map reveals the existence of a large distribution center in Chaoyang District, Beijing, namely the Beijing transit center. The coordinate details of the neighboring subway station, including longitude and latitude, are presented in
Table 8 below.
The integrated importance evaluation analysis of subway stations in
Section 5.1 indicates that in Chaoyang District, Beijing, stations such as Olympic Park, Wangjing, Sanyuanqiao, Hujialou, Guomao, Panjiayuan, Jintailu, and Dawanglu are key to the subway system and play a vital role in improving logistics in Chaoyang District. Consequently, this report designates the aforementioned subway stations as the sites for alternative distribution hubs.
Table 9 presents the fundamental information, including the latitude and longitude coordinates of these metro stations.
The current development models of urban logistics indicate a gradual shift towards collaboration and sharing in last-mile delivery. In the case study, the last-mile demand points, which are the places where customer needs come together, focus on express terminal outlets, express collection sites, and smart lockers. Therefore, based on the population density, the following 26 end demand points are selected as the research targets, and their basic information is presented in
Table 10 as follows.
The distances between the Beijing transit center and alternative hub stations, along with the number of interchanges between subway nodes, were calculated using the latitude, longitude, and the Beijing subway route map, as presented in
Table 11.
For the sake of simplifying mathematical calculations, the Earth is regarded as an ideal sphere. Subsequently, we compute the distance metrics between various hub locations and final demand points utilizing their coordinates, as shown in
Table 12.
5.3. Case Study Solution
This research employs MATLAB R2024a and the jellyfish search algorithm to tackle this location model. We conduct an analogical evaluation based on factors such as subway ticket prices, the pricing of express delivery fees by multiple large-scale express delivery companies, and the consumption of new energy freight vehicles. Then, we define the subsequent expenses: The fee for entering and exiting a metro station is RMB 0.2 per transaction; the charge for transferring between metro lines is RMB 0.1 per transaction; the expense of metro transportation is RMB 0.01 per item for each kilometer; the operational cost of a distribution center is RMB 0.01 per piece; and the expense for end-of-line transport per unit of distance per unit of cargo is RMB 0.01 per piece per kilometer. The relevant parameters of the algorithm are presented in the following
Table 13.
Considering that the locations of the hub sites are all in Chaoyang District, the differences in rental costs and utility costs will not be so huge that the fixed operating costs of the hub sites are all set at 80,000 RMB/year, and the maximum coverage of the hub sites is set at 13 km. According to the related data and demand forecast, we assumed 5.06 billion pieces as the Chaoyang demand of average annual express. But the transportation volumes
between distribution center
and hub sites
and the logistics demands
of end demand point
are obtained difficultly. In this case, based on real conditions, we make a rational assumption for
and
in
Table 14 and
Table 15, the capacities of eight alternative hub sites and the cargo demand volumes of 26 end demand points, respectively.
Utilizing the jellyfish search algorithm and MATLAB R2024a software, we conducted calculations based on the aforementioned data.
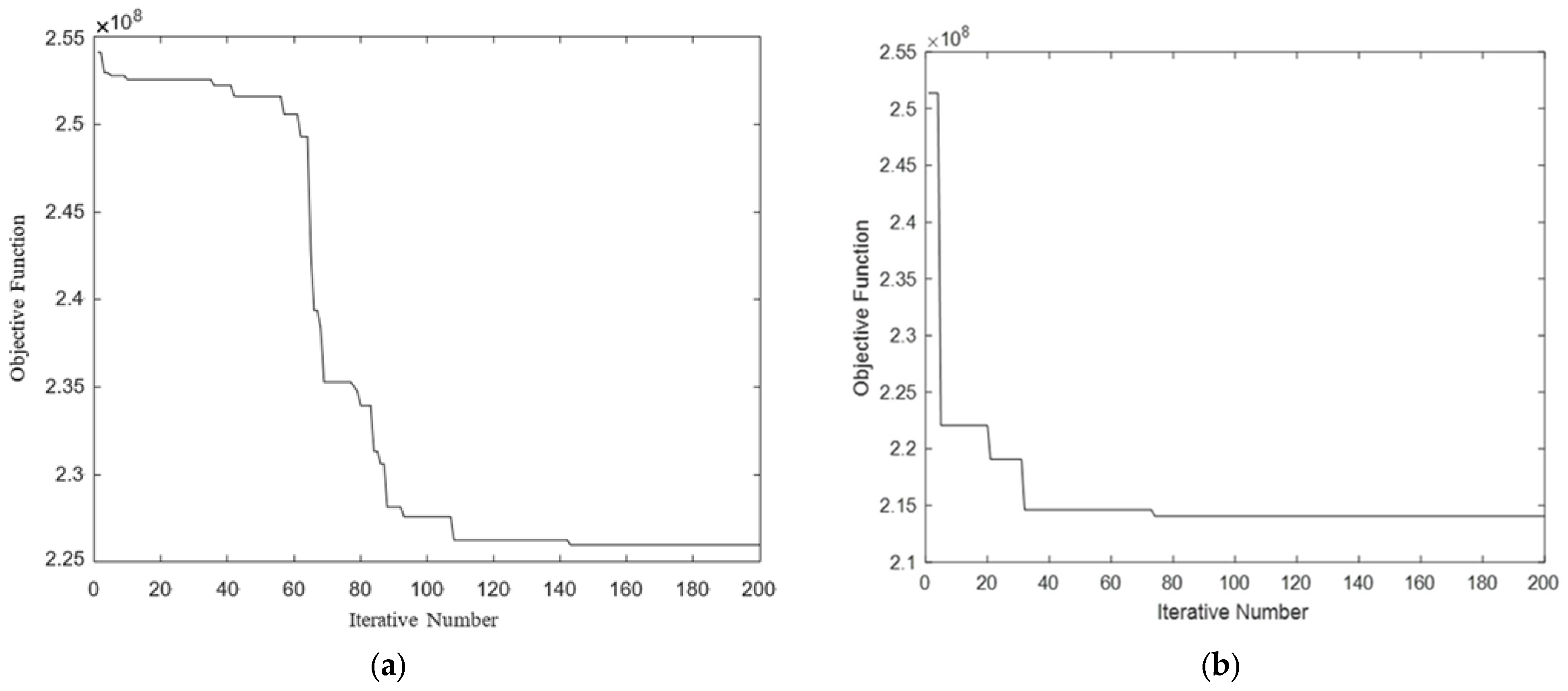
Figure 5 presents a comparative study of the jellyfish search algorithm’s operational procedures before and after enhancements. The two subgraphs clearly demonstrate the variation in objective function values as iteration rates increase, which is essential for assessing the efficacy of algorithms related to the selection of distribution hubs for subway stations.
The convergence diagram above shows that in the early iterations of
Figure 5b particularly from the start to approximately the 40th iteration, the value of the objective function experienced a substantial decline, and by the 80th iteration, the value stabilized, exhibiting only minor fluctuations. The objective function value of
Figure 5a experienced a substantial drop in a ladder-like structure between the 40th and 80th iterations, while the decrease nearly stopped by the 100th iteration as the process continued. The improved jellyfish search algorithm can reach a steady and low objective function value in fewer iterations and also avoids getting stuck in local optima during the process.
To assess the algorithm’s convergence limitations and lessen the risk of premature termination, the first iteration count is established at 1000. The model tends to converge after approximately 80 iterations. Thus, the iteration number is set to = 200 to ensure that we find the approximate optimal solution. Meanwhile, we calculated the total cost to be 214,061,140.00 CNY, the transportation cost between the distribution center and hub sites to be 175,690,100.00 CNY, the running cost of the hub sites to be 5,260,900.00 CNY, and the cost of the end demand points to be 33,110,140.00 CNY.
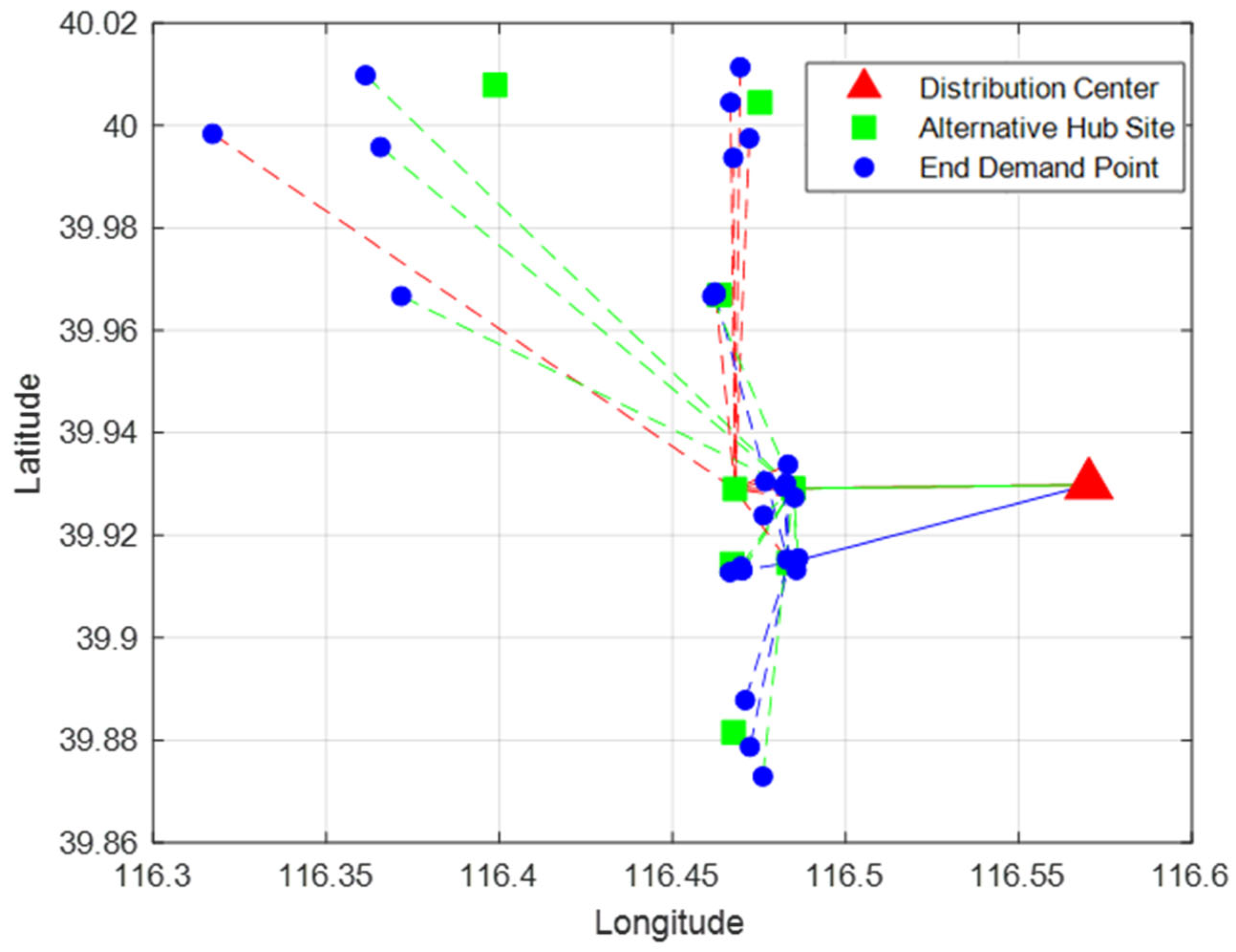
We will choose Hujialou, Jintailu, and Dawanglu as the hub sites for metro logistics in the Chaoyang District, specifically selecting locations 4, 7, and 8. Furthermore, Hujialou encompasses 10 demand points: 3, 5, 6, 7, 8, 9, 12, 14, 23, and 24. The hub site at Jintailu will manage the delivery tasks for 10 end demand points: 1, 2, 4, 11, 13, 15, 16, 19, 25, and 26. Dawanglu will manage the allocation of six demand points: 10, 17, 18, 20, 21, and 22. All delivery relationships are depicted in
Figure 6 and
Figure 7 below.
6. Conclusions
After studying the sustainable urban supply distribution system that uses the subway, we developed a model and an algorithm to help find distribution hubs. This paper first creates a metro-integrated evaluation model using complex network theory. The model takes into account passenger flow, node degree, and node betweenness to provide better options for choosing urban metro distribution hubs. The metro’s internal route selection mode is based on the idea of minimizing transfers. The location model of the distribution hub is established by considering the costs of entering and leaving the subway, transferring lines, subway transportation, the fixed and variable operational costs of the distribution center, and the transportation costs to and from the terminal. The location model constitutes a complex combinatorial optimization challenge. A jellyfish search method is used to give a rough solution to the location model of subway distribution hubs. The model and algorithm’s usefulness and operability to work are finally verified by the real logistics distribution situations and progress in Beijing’s Chaoyang District.
While this study yields valuable findings, several limitations warrant discussion. The proposed integrated evaluation model provides a more comprehensive assessment of subway stations’ potential as distribution hubs than traditional single-index methods. However, additional refinements could further improve its practical applicability. Future studies should incorporate additional metrics such as the H-index and policy environment factors to improve evaluation accuracy. Secondly, the model of locating distribution hubs effectively reduces urban logistics costs, but it ignores essential societal considerations. For example, the model does not assess whether selected areas are consistent with municipal development plans or consider potential community impacts, which could jeopardize implementation viability. Future studies should incorporate these socio-environmental considerations into the optimization approach. While the enhanced jellyfish search algorithm proposed in this study demonstrates improvements over its original version, significant limitations emerge in practical applications. Convergence speed may be significantly reduced when dealing with the large-scale and complex subway distribution hub location problem. When the maximum number of iterations is reached, it still does not converge to a satisfactory result, which affects the timeliness of the location decision. Subsequent research may combine the jellyfish search algorithm with other algorithms with complementary advantages to form a hybrid algorithm. These features will help it jump out of the local optimal solution and improve the probability of finding the global optimal solution.
In addition, the M-ULS proposal highlights the dual potential of subway systems: serving passenger mobility while simultaneously facilitating parcel transportation. To achieve a scientifically sound and balanced integration of these functions, in-depth discussions are required. Specialized parcel storage and sorting facilities will be constructed at the metro station. Designated locations will be furnished with suitable storage racks and sorting equipment. To guarantee the proper functioning of the subway system, we need to set a weight limit for each package. It must be established based on the load capacity of the subway vehicle, the structural integrity of the station, and the safety of the surrounding environment.