Immune-Inspired Multi-Objective PSO Algorithm for Optimizing Underground Logistics Network Layout with Uncertainties: Beijing Case Study
Abstract
:1. Introduction
2. Research Background
2.1. Knowledge of ULS Studies
2.1.1. Planning of ULS Networks
2.1.2. Key Technologies for ULSs
2.2. Topological Paradigm and Layout Decision Boundaries
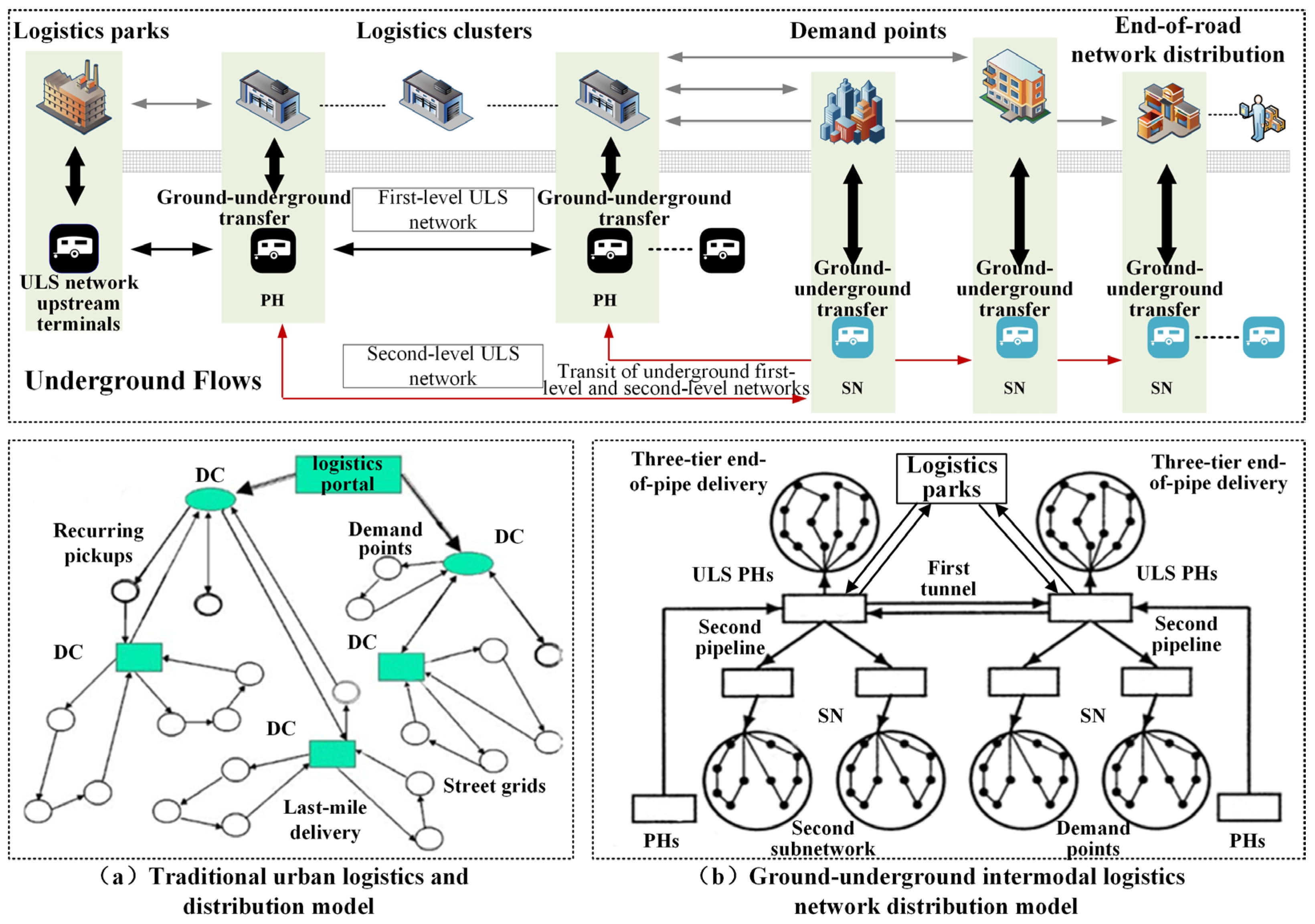
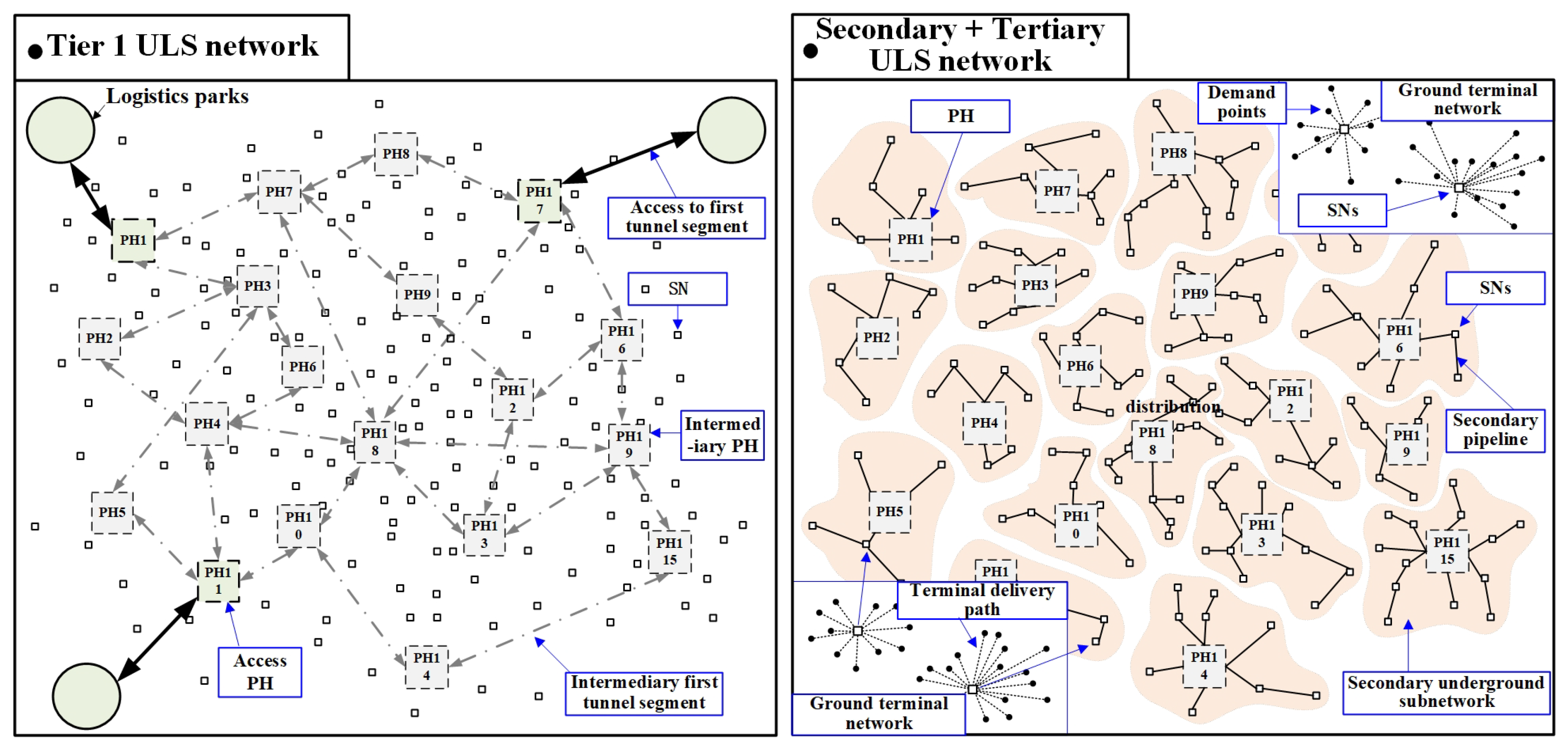
2.2.1. Composition of the Three-Tier Hub-and-Spoke ULS Network
2.2.2. Multi-Objective Capacity Siting, Allocation, and Path Decision-Making
2.2.3. Parameters and Assumption
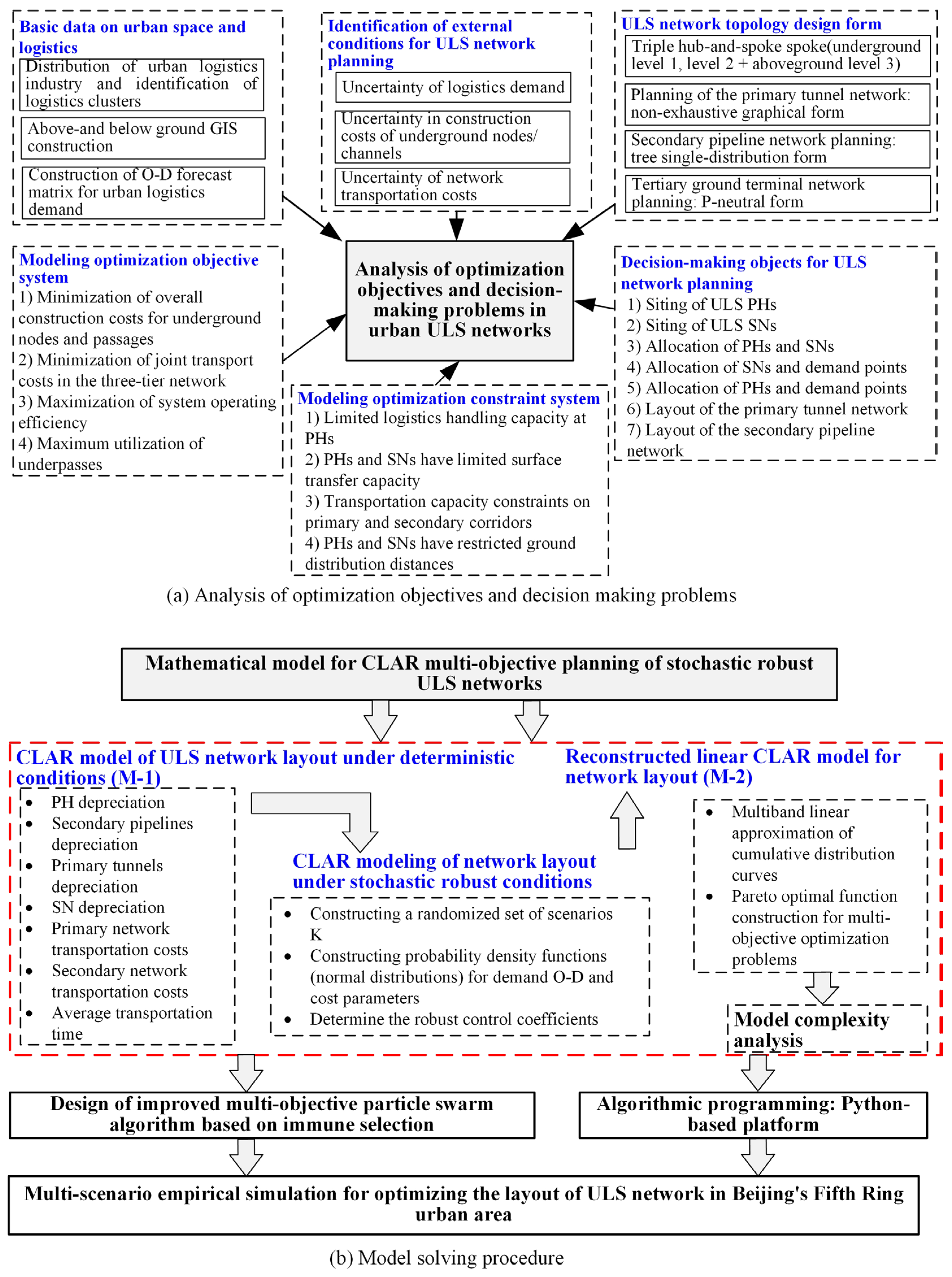
3. Model Development
3.1. Modeling Objectives
3.2. Formulation of Model Constraints
3.3. Optimization Model Reconstruction
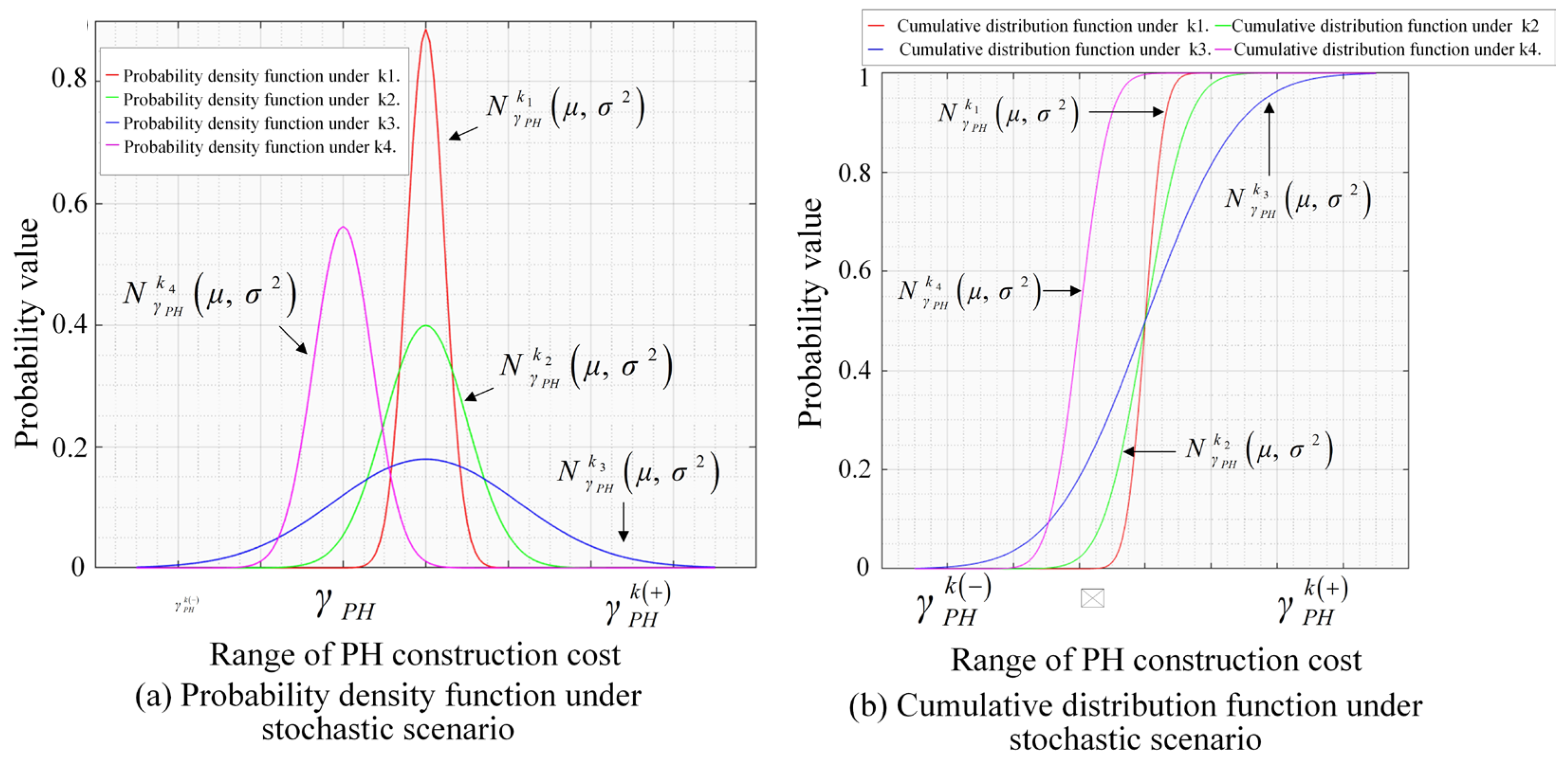
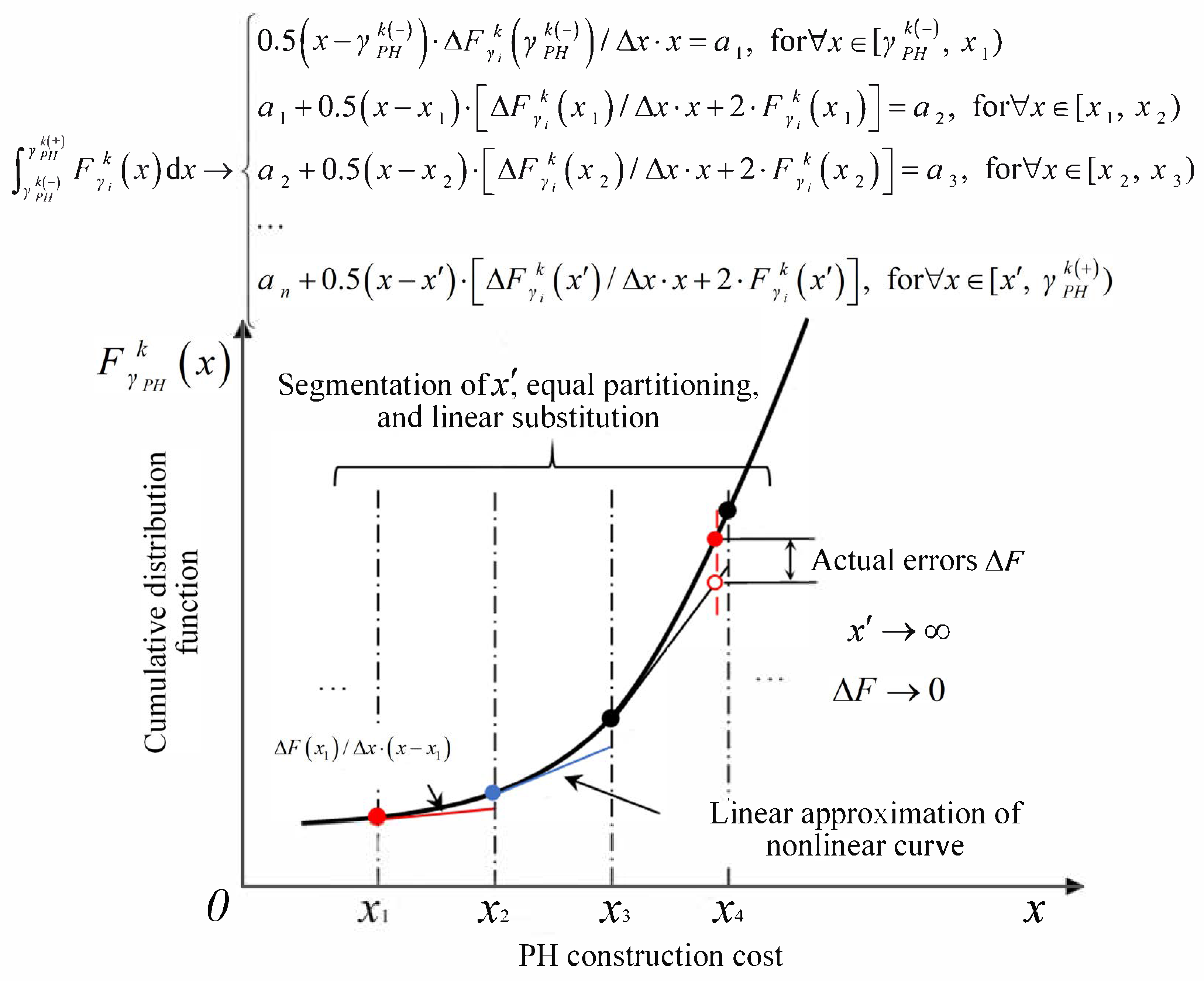
3.3.1. Approximation of Probability Distribution of Stochastic Variables
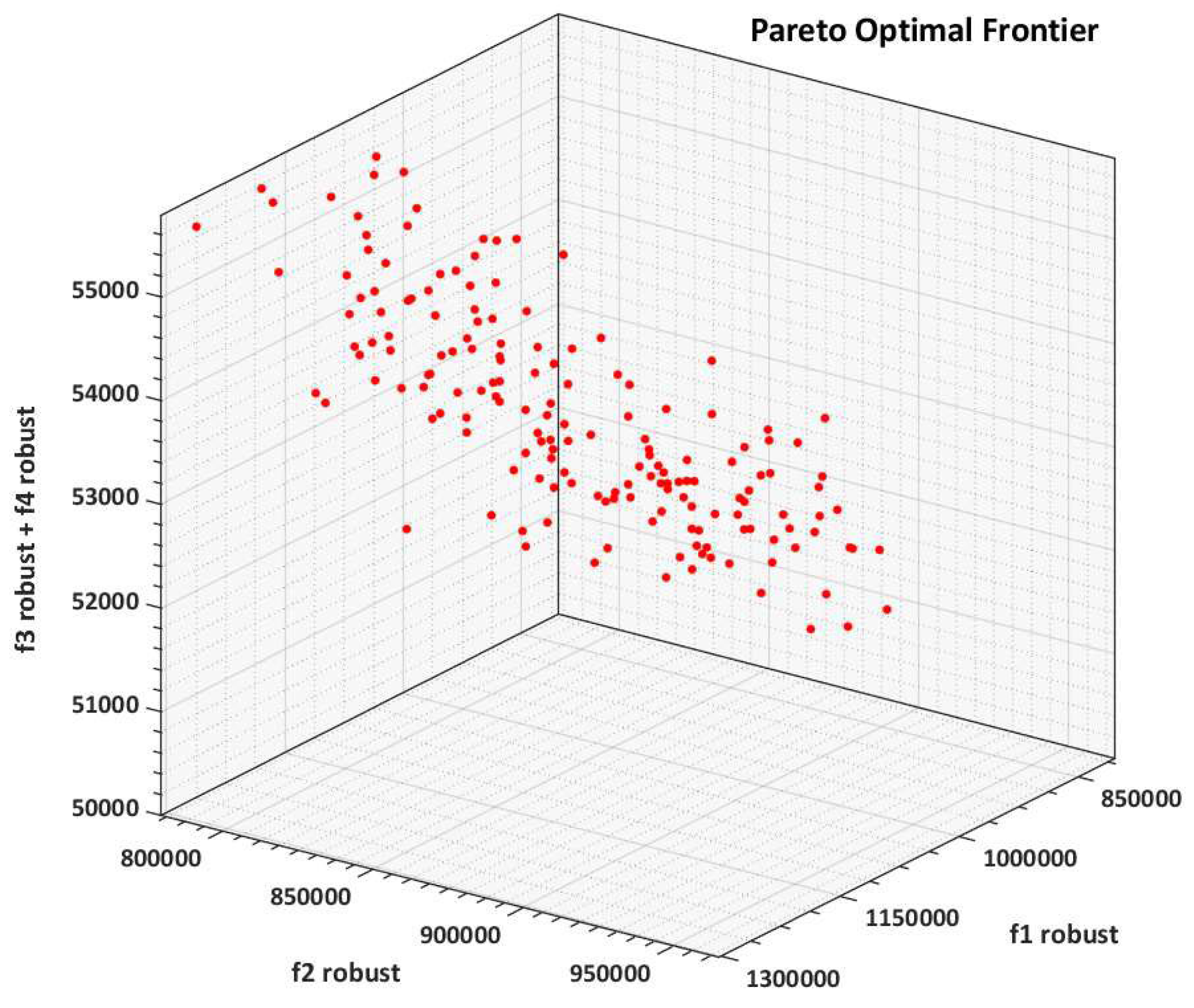
3.3.2. Pareto Fronts Normalized Weighting Method
3.3.3. Model Complexity Analysis
4. Solution Approach
5. Case Study
5.1. Simulation Scenarios
5.2. Comparison of Optimal ULS Layouts
5.3. Sensitivity Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gardrat, M. Urban growth and freight transport: From sprawl to distension. J. Transp. Geogr. 2021, 91, 102979. [Google Scholar] [CrossRef]
- Chen, Z.; Dong, J.; Ren, R. Urban underground logistics system in China: Opportunities or challenges? Undergr. Space 2017, 2, 195–208. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhao, J. Assessment and planning of underground space use in Singapore. Tunn. Undergr. Space Technol. 2016, 55, 249–256. [Google Scholar] [CrossRef]
- Di, Z.; Li, L.; Li, M.; Zhang, S.; Yan, Y.; Wang, M.; Li, B. Research on the contribution of metro-based freight to reducing urban transportation exhaust emissions. Comput. Ind. Eng. 2023, 185, 109622. [Google Scholar] [CrossRef]
- Hou, L.; Xu, Y.; Ren, R.; Yang, J.; Su, L. Optimization of three-dimensional urban underground logistics system alignment: A deep reinforcement learning approach. Comput. Ind. Eng. 2025, 205, 111185. [Google Scholar] [CrossRef]
- Shahooei, S.; Farooghi, F.; Zahedzahedani, S.E.; Shahandashti, M.; Ardekani, S. Application of underground short-haul freight pipelines to large airports. J. Air Transp. Manag. 2018, 71, 64–72. [Google Scholar] [CrossRef]
- Hai, D.; Xu, J.; Duan, Z.; Chen, C. Effects of underground logistics system on urban freight traffic: A case study in Shanghai, China. J. Clean. Prod. 2020, 260, 121019. [Google Scholar] [CrossRef]
- Dong, J.; Hu, W.; Yan, S.; Ren, R.; Zhao, X. Network Planning Method for Capacitated Metro-Based Underground Logistics System. Adv. Civ. Eng. 2018, 2018, 6958086. [Google Scholar] [CrossRef]
- An, N.; Yang, K.; Chen, Y.; Yang, L. Wasserstein distributionally robust optimization for train operation and freight assignment in a metro-based underground logistics system. Comput. Ind. Eng. 2024, 192, 110228. [Google Scholar] [CrossRef]
- He, R.; Bian, R.; Hua, J.; Zhao, L.; Xu, F.; Long, J. Multi-objective optimization of gasoline blending scheduling via NSGA-II algorithm with composite operators considering oil movement path planning. Expert Syst. Appl. 2025, 280, 127426. [Google Scholar] [CrossRef]
- Luo, J.; Gu, Q.; Chen, L.; Li, X.; Li, P. Multi-objective optimization for ore blending schemes in the open-pit phosphate mine using an improved NSGA-II algorithm. Green Smart Min. Eng. 2025, 2, 42–56. [Google Scholar] [CrossRef]
- Zhao, L.; Zhou, J.; Li, H.; Yang, P.; Zhou, L. Optimizing the design of an intra-city metro logistics system based on a hub-and-spoke network model. Tunn. Undergr. Space Technol. 2021, 116, 104086. [Google Scholar] [CrossRef]
- Li, F.; Yuen, K.F. A systematic review on underground logistics system: Designs, impacts, and future directions. Tunn. Undergr. Space Technol. 2025, 159, 106483. [Google Scholar] [CrossRef]
- Li, S.; Zhu, X.; Shang, P.; Wang, L.; Li, T. Scheduling shared passenger and freight transport for an underground logistics system. Transp. Res. Part B Methodol. 2024, 183, 102907. [Google Scholar] [CrossRef]
- Baghalian, A.; Rezapour, S.; Farahani, R.Z. Robust supply chain network design with service level against disruptions and demand uncertainties: A real-life case. Eur. J. Oper. Res. 2013, 227, 199–215. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, J.; Zheng, C.; Wang, B.; Chen, J. Node location of bi-level urban metro-based ground-underground logistics distribution. Multimod. Transp. 2024, 3, 100119. [Google Scholar] [CrossRef]
- Vandersteel, W.; Zhao, Y.; Lundgren, T.S. Automating movement of freight. Transp. Res. Rec. J. Transp. Res. Board 1997, 1602, 71–76. [Google Scholar] [CrossRef]
- Zandi, I.; Allen, W.B.; Morlok, E.K.; Gimm, K.; Plaut, T.; Warner, J. Transport of Solid Commodities via Freight Pipeline: First Year Final Report; University of Pennsylvania: Philadelphia, PA, USA; U.S. Department of Transportation Program of University Research: Washington, DC, USA, 1976. [Google Scholar]
- Braet, J. The environmental impact of container pipeline transport compared to road transport. Case study in the Antwerp Harbor region and some general extrapolations. Int. J. Life Cycle Assess. 2011, 16, 886–896. [Google Scholar] [CrossRef]
- Visser, J. The development of underground freight transport: An overview. Tunn. Undergr. Space Technol. 2018, 80, 123–127. [Google Scholar] [CrossRef]
- Arends, G.; de Boer, E. Tunnelling of infrastructure: From non-considered to ill considered—Lessons from the Netherlands. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2001, 16, 225–234. [Google Scholar] [CrossRef]
- Hu, W.; Dong, J.; Hwang, B.-G.; Ren, R.; Chen, Z. A preliminary prototyping approach for emerging metro-based underground logistics systems: Operation mechanism and facility layout. Int. J. Prod. Res. 2020, 59, 7516–7536. [Google Scholar] [CrossRef]
- Liu, Q.; Chen, Y.; Hu, W.; Dong, J.; Sun, B.; Cheng, H. Underground Logistics Network Design for Large-Scale Municipal Solid Waste Collection: A Case Study of Nanjing, China. Sustainability 2023, 15, 16392. [Google Scholar] [CrossRef]
- Wang, T.; Wang, J.; Wu, P.; Wang, J.; He, Q.; Wang, X. Estimating the environmental costs and benefits of demolition waste using life cycle assessment and willingness-to-pay: A case study in Shenzhen. J. Clean. Prod. 2018, 172, 14–26. [Google Scholar] [CrossRef]
- Hu, W.; Dong, J.; Hwang, B.-G.; Ren, R.; Chen, Z. Network planning of urban underground logistics system with hub-and-spoke layout: Two phase cluster-based approach. Eng. Constr. Arch. Manag. 2020, 27, 2079–2105. [Google Scholar] [CrossRef]
- Hu, W.; Dong, J.; Hwang, B.-G.; Ren, R.; Chen, Z. Hybrid optimization procedures applying for two-echelon urban underground logistics network planning: A case study of Beijing. Comput. Ind. Eng. 2020, 144, 106452. [Google Scholar] [CrossRef]
- Hu, W.; Dong, J.; Xu, N. Multi-period planning of integrated underground logistics system network for automated construction-demolition-municipal waste collection and parcel delivery: A case study. J. Clean. Prod. 2022, 330, 129760. [Google Scholar] [CrossRef]
- Di, Z.; Yang, L.; Shi, J.; Zhou, H.; Yang, K.; Gao, Z. Joint optimization of carriage arrangement and flow control in a metro-based underground logistics system. Transp. Res. Part B Methodol. 2022, 159, 1–23. [Google Scholar] [CrossRef]
- Di, Z.; Luo, J.; Shi, J.; Qi, J.; Zhang, S. Integrated optimization of capacity allocation and timetable rescheduling for metro-based passenger and freight cotransportation. Tunn. Undergr. Space Technol. 2024, 155, 106186. [Google Scholar] [CrossRef]
- Panda, S.; Ganguly, S. Multi-Objective Smart Charging Scheduling Scheme for EV Integration and Energy Loss Minimization in Active Distribution Networks using Mixed Integer Programming. Sustain. Energy Grids Netw. 2025, 43, 101743. [Google Scholar] [CrossRef]
- Wei, H.; Li, A.; Jia, N. Research on optimization and design of sustainable urban underground logistics network framework. Sustainability 2020, 12, 9147. [Google Scholar] [CrossRef]
- Camelo, M.M.; de Andrade, C.F.; de Athayde Prata, B. A mixed-integer linear programming model for optimizing green hydrogen supply chain networks. Int. J. Hydrogen Energy 2025, 118, 134–145. [Google Scholar] [CrossRef]
- Mo, P.; Yao, Y.; D’ariano, A.; Liu, Z. The vehicle routing problem with underground logistics: Formulation and algorithm. Transp. Res. Part E Logist. Transp. Rev. 2023, 179, 103286. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, Q.; Huang, S.; Yu, W.; Yao, S. Resilience quantification and recovery strategy simulation for urban underground logistics systems under node and link attacks: A case study of Nanjing city. Int. J. Crit. Infrastruct. Prot. 2024, 47, 100704. [Google Scholar] [CrossRef]
- He, M.; Sun, L.; Zeng, X.; Liu, W.; Tao, S. Node layout plans for urban underground logistics systems based on heuristic Bat algorithm. Comput. Commun. 2020, 154, 465–480. [Google Scholar] [CrossRef]
- Liang, C.; Hu, X.; Shi, L.; Fu, H.; Xu, D. Joint dispatch of shipment equipment considering underground container logistics. Comput. Ind. Eng. 2022, 165, 107874. [Google Scholar] [CrossRef]
- Shi, Y.; Vanhaverbeke, L.; Xu, J. Electric vehicle routing optimization for sustainable kitchen waste reverse logistics network using robust mixed-integer programming. Omega 2024, 128, 103128. [Google Scholar] [CrossRef]
- Reddy, K.N.; Kumar, A.; Choudhary, A.; Cheng, T.C.E. Multi-period green reverse logistics network design: An improved Benders-decomposition-based heuristic approach. Eur. J. Oper. Res. 2022, 303, 735–752. [Google Scholar] [CrossRef]
- Hu, Y.; Liu, Q.; Li, S.; Wu, W. Robust emergency logistics network design for pandemic emergencies under demand uncertainty. Transp. Res. Part E Logist. Transp. Rev. 2025, 196, 103957. [Google Scholar] [CrossRef]
- De Sá, E.M.; Morabito, R.; de Camargo, R.S. Benders decomposition applied to a robust multiple allocation incom-plete hub location problem. Comput. Oper. Res. 2018, 89, 31–50. [Google Scholar] [CrossRef]
- Ahmadi-Javid, A.; Amiri, E.; Meskar, M. A profit-maximization location-routing-pricing problem: A branch-and-price algorithm. Eur. J. Oper. Res. 2018, 271, 866–881. [Google Scholar] [CrossRef]
- Jenkins, P.R.; Lunday, B.J.; Robbins, M.J. Robust, multi-objective optimization for the military medical evacuation location-allocation problem. Omega 2020, 97, 102088. [Google Scholar] [CrossRef]
- Cardona-Valdés, Y.; Álvarez, A.; Pacheco, J. Metaheuristic procedure for a bi-objective supply chain design problem with uncertainty. Transp. Res. Part B Methodol. 2013, 60, 66–84. [Google Scholar] [CrossRef]
- Beheshti, Z.; Shamsuddin, S.M.; Hasan, S. Memetic binary particle swarm optimization for discrete optimization problems. Inf. Sci. 2015, 299, 58–84. [Google Scholar] [CrossRef]
- Lizondo, D.; Rodriguez, S.; Will, A.; Jimenez, V.; Gotay, J. An artificial immune network for distributed demand-side management in smart grids. Inf. Sci. 2018, 438, 32–45. [Google Scholar] [CrossRef]
- Pan, X.; Dong, J.; Ren, R.; Chen, Y.; Sun, B.; Chen, Z. Monetary evaluation of the external benefits of urban underground logistics System: A case study of Beijing. Tunn. Undergr. Space Technol. 2023, 136, 105094. [Google Scholar] [CrossRef]

| Symbol Definition | Variable Description |
|---|---|
| Constants and continuous variables | |
| Forecasted freight O-D volume between any park and demand point | |
| Forecasted freight O-D volume between any logistics hubs | |
| , | Forecasted fixed construction costs for ULS hub nodes (PHs) and spoke nodes (SNs) |
| Forecasted unit fixed construction costs for first-tier tunnel segments | |
| Forecasted unit fixed construction costs for secondary pipeline segments | |
| Forecasted unit O-D transportation costs for first-tier ULS network | |
| Forecasted unit O-D transportation costs for secondary ULS network | |
| c | Unit transportation costs for road-based freight O-D |
| [cap1], [cap2] | Maximum secondary underground transshipment capacity and tertiary surface transshipment capacity for PHs |
| [cap3] | Maximum tertiary surface transshipment capacity for SNs |
| [cap4], [cap5] | Maximum bidirectional freight transportation capacity for first-tier tunnels and secondary pipelines |
| , | Maximum allowable unsaturation rate for first-tier tunnels and secondary pipelines |
| , | Penalty costs resulting from saturation in first-tier tunnels and secondary pipelines |
| Euclidean distance function reflecting links g, h, p, q | |
| ro | Maximum surface transportation distance for tertiary network |
| , , | Travel speeds for underground and surface transportation systems in first-tier, secondary, and tertiary networks |
| , | Forecasted logistics handling time for O-D at hub and spoke nodes |
| Depreciation coefficient for ULS network infrastructure | |
| Probability of scenario k occurrence | |
| Variables | |
| In random scenario k, if logistics hub i is constructed as PH, then 1; otherwise, 0. | |
| In random scenario k, if demand point j is constructed as SN, then 1; otherwise, 0. | |
| In random scenario k, if link g is constructed as access PT, then 1; otherwise, 0. | |
| In random scenario k, if link h is constructed as intermediary PT, then 1; otherwise, 0. | |
| In random scenario k, if link p is constructed as ST, then 1; otherwise, 0; | |
| In random scenario k, if link q is constructed as ST, then 1; otherwise, 0; | |
| In random scenario k, if undergoes secondary underground transshipment at PH i, then 1; otherwise, 0; | |
| In random scenario k, if undergoes tertiary surface transshipment at SN j, then 1; otherwise, 0; | |
| In random scenario k, if undergoes tertiary surface transshipment at PH i, then 1; otherwise, 0; | |
| In random scenario k, if passes through access PT link g, then 1; otherwise, 0; | |
| In random scenario k, if passes through intermediary PT link h, then 1; otherwise, 0; | |
| In random scenario k, if passes through intermediary PT link h, then 1; otherwise, 0; | |
| In random scenario k, if passes through ST link p, then 1; otherwise, 0; | |
| In random scenario k, if passes through ST link q, then 1; otherwise, 0; | |
| In random scenario k, if passes through LMD link q, then 1; otherwise, 0; | |
| In random scenario k, if passes through LMD link p, then 1; otherwise, 0; |
| Variables | Normally Distributed Mean and Variance | Cumulative Distribution Function | Upper | Lower | Number of Functions |
|---|---|---|---|---|---|
| Variables and Constraints | Maximum Quantity Expression | Beijing Case |
|---|---|---|
| , , Equations (15), (17), (19) and (30) | 4018 | |
| , , Equation (23) | 689,022 | |
| , , Equation (21) | 8930 | |
| Equations (25), (26) and (31) | 32,993 | |
| , , Equation (27) | 864,120 | |
| , , , , Equations (24), (27)–(29) | 7,833,952,740 | |
| , , Equation (28) | 46,086,400 | |
| , , Equations (27) and (28) | 54,473,060 | |
| Total number | 7,936,111,283 |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| CNY 0.5 × 107/km | 0.7 | ||
| CNY 0.14 × 107/km | 0.6 | ||
| CNY 2 per 103 parcel km | CNY 10 per 103 parcel | ||
| CNY 8 per 103 parcel km | CNY 5 per 103 parcel | ||
| c | CNY 10 per 103 parcel km | ro | 3 km |
| CNY 1 × 107 | 60 km/h | ||
| CNY 0.35 × 107 | 30 km/h | ||
| [cap1] | 30 × 104 parcel/d | 10 km/h | |
| [cap2] | 7 × 104 parcel/d | 40 min | |
| [cap3] | 7 × 104 parcel/d | 20 min | |
| [cap4] | 60 × 104 parcel/d | 70 × 365 d | |
| [cap5] | 30 × 104 parcel/d | Objective function weights | [1, 1.2, 0.03, 10] |
| Variable | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| [0,0.85] | [0,1.96] | [0,1.13] | [0,2.48] | [0,1.91] | [0,2.15] | [0,1.49] | [0,1.34] | |
| [0,0.14] | [0,0.16] | [0, 0.2] | [0,0.03] | [0,0.23] | [0,0.38] | [0,0.12] | [0,0.09] | |
| 950 | 1199 | 5389 | 65,524 | 30,999 | 422 | 8391 | 26,804 | |
| 270 | 11,919 | 12,467 | 42,230 | 7926 | 248 | 2748 | 34,715 | |
| 670 | 31,119 | 6638 | 670 | 26,988 | 15,288 | 9644 | 8602 | |
| 8225 | 6578 | 114 | 1288 | 17,660 | 103 | 92 | 24 | |
| 0.10 | 0.84 | 0.67 | 0.80 | 1.49 | 0.98 | 0.97 | 0.33 | |
| 11.80 | 5.25 | 1.28 | 0.11 | 10.32 | 0.10 | 3.80 | 12.80 | |
| 72,253 | 43,718 | 51,495 | 52,706 | 36,000 | 17,424 | 12,617 | 23,963 | |
| 88,744 | 2916 | 55,319 | 16,697 | 4679 | 14,175 | 70,671 | 20,736 | |
| 0.247 | 0.165 | 0.091 | 0.113 | 0.142 | 0.067 | 0.084 | 0.091 | |
| 1.117 1.095 0.898 0.941 | ||||||||
| Algorithms | Traditional PSO | IS-MPSO |
|---|---|---|
| Network cost reduction ratio | 38% | 62% |
| Average number of convergence iterations | 420 | 280 |
| CPU time | 64,356 s | 19,568 s |
| Random Robust Scenario (Model M-1) | Baseline Scenario (Model M-2) | |
|---|---|---|
| Total objective function value | = 3.4 × 106 | = 3.6 × 106 |
| Sub-objective 1 | = 118.9 × 104 CNY | = 116.7 × 104 CNY |
| Sub-objective 2 | = 86.7 × 104 CNY | = 96.9 × 104 CNY |
| Sub-objective 3 | = 2083.2 s | = 2037.2 s |
| Sub-objective 4 | = 5.1 × 104 CNY | = 6.4 × 104 CNY |
| Number of HNs | 30 | 30 |
| Number of SNs | 204 | 220 |
| Total length of first-tier tunnels | 137 km | 144 km |
| Total length of second-tier pipelines | 774 km | 851 km |
| Average end-point ground delivery length of nodes | 1.13 km | 0.94 km |
| Average load rate of first-tier tunnels | 58.83% | 45.14% |
| Average load rate of second-tier pipelines | 40.29% | 36.88% |
| Average ground transport volume at HNs | 6.64 × 104 parcels | 6.54 × 104 parcels |
| Average underground transport volume at HNs | 19.47 × 104 parcels | 19.58 × 104 parcels |
| Average ground transport volume at SNs | 2.88 × 104 parcels | 2.7 × 104 parcels |
| Average travel distance of forward O-D on first-tier and second-tier networks | 28.72 km, 3.98 km | 32.49 km, 4.27 km |
| Average travel distance of same-city O-D on first-tier network | 15.59 km | 17.16 km |
| Ground freight mitigation rate by ULS | RFAR = 98.14% | RFAR = 97.14% |
| Greenhouse gas reducing service | 1.82 × 105 CNY/year | 2.02 × 105 CNY/year |
| Air pollution reducing service | 1.73 × 104 CNY/year | 1.95 × 104 CNY/year |
| [cap4] Perturbation Range | 40% | 60% | 85% | 100% | 120% | 150% | 200% |
|---|---|---|---|---|---|---|---|
| Construction cost (CNY × 104/d) | 127.2 | 121.6 | 116.4 | 116.7 | 114.5 | 112.7 | 110.1 |
| Transport cost (CNY × 104/d) | 100.7 | 99.7 | 97.2 | 96.9 | 95.5 | 92.1 | 89.4 |
| System efficiency (s) | 2088 | 2040 | 2052 | 2034 | 1992 | 1974 | 1926 |
| Penalty cost (CNY × 104/d) | 3.9 | 4.4 | 5.6 | 6.4 | 8 | 8.9 | 10.1 |
| Average load of first-tier tunnels | 86% | 70% | 52% | 45% | 41% | 37% | 30% |
| First-tier network length (km) | 173 | 160 | 148 | 144 | 140 | 135 | 132 |
| Second-tier network length (km) | 863 | 856 | 844 | 851 | 843 | 840 | 832 |
| Number of HNs | 37 | 33 | 30 | 30 | 29 | 28 | 26 |
| Number of SNs | 230 | 222 | 215 | 220 | 216 | 214 | 208 |
| Total objective value of Model M-2 | 3.4 × 106 | 3.4 × 106 | 3.5 × 106 | 3.6 × 106 | 3.7 × 106 | 3.7 × 106 | 3.8 × 106 |
| Perturbation Range | 40% | 60% | 85% | 100% | 120% | 150% | 200% |
|---|---|---|---|---|---|---|---|
| Construction cost (CNY × 104/d) | 118.5 | 118.2 | 116.5 | 116.7 | 117.0 | 117.3 | 116.4 |
| Transport cost (CNY × 104/d) | 50.7 | 68.1 | 86.3 | 96.9 | 112.8 | 139.3 | 183.6 |
| System efficiency (s) | 2070 | 2064 | 2052 | 2034 | 2004 | 1986 | 1968 |
| Penalty cost (CNY × 104/d) | 7 | 6.9 | 6.7 | 6.4 | 6.2 | 5.9 | 5.6 |
| Average load of first-tier tunnels | 40% | 43% | 44% | 45% | 46% | 47% | 45% |
| First-tier network length (km) | 160 | 153 | 147 | 144 | 142 | 140 | 136 |
| Second-tier network length (km) | 842 | 850 | 844 | 851 | 856 | 858 | 861 |
| Number of HNs | 33 | 32 | 30 | 30 | 29 | 29 | 27 |
| Number of SNs | 205 | 213 | 217 | 220 | 226 | 230 | 234 |
| Total objective value of Model M-2 | 3.1 × 106 | 3.3 × 106 | 3.5 × 106 | 3.6 × 106 | 3.7 × 106 | 4 × 106 | 4.5 × 106 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, H.; Shi, A.; Liu, Q.; Liu, J.; Hu, H.; Chen, Z. Immune-Inspired Multi-Objective PSO Algorithm for Optimizing Underground Logistics Network Layout with Uncertainties: Beijing Case Study. Sustainability 2025, 17, 4734. https://doi.org/10.3390/su17104734
Yu H, Shi A, Liu Q, Liu J, Hu H, Chen Z. Immune-Inspired Multi-Objective PSO Algorithm for Optimizing Underground Logistics Network Layout with Uncertainties: Beijing Case Study. Sustainability. 2025; 17(10):4734. https://doi.org/10.3390/su17104734
Chicago/Turabian StyleYu, Hongbin, An Shi, Qing Liu, Jianhua Liu, Huiyang Hu, and Zhilong Chen. 2025. "Immune-Inspired Multi-Objective PSO Algorithm for Optimizing Underground Logistics Network Layout with Uncertainties: Beijing Case Study" Sustainability 17, no. 10: 4734. https://doi.org/10.3390/su17104734
APA StyleYu, H., Shi, A., Liu, Q., Liu, J., Hu, H., & Chen, Z. (2025). Immune-Inspired Multi-Objective PSO Algorithm for Optimizing Underground Logistics Network Layout with Uncertainties: Beijing Case Study. Sustainability, 17(10), 4734. https://doi.org/10.3390/su17104734





