Integrating DEA and AHP for Optimizing Rural Road Network Planning Under the Common Prosperity Framework: A Case Study of Yueqing City

Abstract

Transportation infrastructure serves a pivotal role in driving regional development. This study proposes a decision-making framework for rural road network planning within the context of China’s common prosperity initiative. An integrated model combining Data Envelopment Analysis (DEA) and the Analytic Hierarchy Process (AHP) is developed, where DEA is employed to identify technically efficient planning alternatives and AHP is used to rank these alternatives based on social and environmental benefits. Applying the model to the case of Yueqing City, Zhejiang Province, the findings reveal that common prosperity-oriented schemes, particularly the Scheme, which emphasizes full industrial coverage and balanced equity, achieve a superior balance among construction costs, industrial coverage, regional equity, and carbon emissions. Theoretically, this research advances transportation planning by incorporating equity-focused metrics, such as the Gini coefficient, into efficiency analyses, thus promoting a socially sustainable approach to infrastructure development. Practically, the proposed method offers a systematic and actionable tool for local governments to optimize rural transportation networks in support of common prosperity and balanced regional growth. The resulting framework not only identifies technically efficient and equitable layouts but also offers planners a transparent tool for balancing cost, social equity, and environmental impact in future rural infrastructure projects.

1. Introduction

The concept of “common prosperity” in China emphasizes the gradual realization of wealth, advocating for collective contribution while clarifying that it does not equate to “simultaneous prosperity” or “equal prosperity”, nor is it synonymous with egalitarianism [1]. In contemporary China, this concept serves as a strategic goal of socialism, addressing the challenges of development, distribution, and public goods provision, and embodies the aspirations and pursuit of a better life for all citizens. Over recent years, a series of far-reaching guidelines have been issued to promote the common prosperity strategy, such as the “Opinions on Supporting Zhejiang’s High-Quality Development and Building a Common Prosperity Demonstration Zone”, which have laid out a clear blueprint for achieving this grand objective. With its robust economic strength, well-developed private economy system, high technological innovation level, and relatively balanced urban–rural development, Zhejiang Province is in a unique position to lead the country in building a common prosperity demonstration zone [2]. The rich experiences and solid industrial foundation accumulated in Zhejiang make it a natural and promising candidate to spearhead high-quality development in the common prosperity context, offering valuable lessons and replicable paths for other regions across the nation.

Transportation plays a pivotal role in the national economic development process, acting as a key factor in both infrastructure and service provision. In China, the development of transportation infrastructure largely depends on public finance or state-owned capital, which fundamentally establishes transportation as a significant component of public wealth. A well-developed transportation infrastructure can significantly boost urban economic development. Its hub function strengthens urban innovation capacity, thus driving urban economic growth [3]. Different modes of transportation, however, exhibit distinct trade-offs between speed and cost. For instance, air transport offers the fastest movement of people and goods but incurs the highest operational expenses, while maritime shipping, although the slowest, remains the most cost-effective for bulk cargo. Such variations necessitate careful optimization when selecting transportation modes to balance economic efficiency and service requirements, as highlighted in studies analyzing multimodal transport dynamics [4]. In a sense, actively promoting the development of the transportation sector is essentially contributing to the realization of the ambitious goal of common prosperity [5]. The planning and construction of transportation facilities are inherently interconnected with narrowing the gaps between urban and rural areas, regions, and income levels. For example, extending transportation networks is often closely tied to optimizing industrial layout. A convenient transportation network facilitates the flow and aggregation of industrial resources in economically underdeveloped areas, driving local industrial development, creating more employment opportunities, and generating economic growth, thus contributing to reducing urban–rural and regional development disparities [6]. Moreover, the layout of transportation facilities is closely related to the development and operation of tourist destinations. Improved transportation accessibility can attract more visitors to remote or underdeveloped regions, fostering local tourism and providing additional income sources for residents, thereby narrowing income disparities while promoting economic growth [7].

Under the guidance of the common prosperity goal, the planning of rural road networks is crucial for reducing the development gap between urban and rural areas and promoting rural revitalization. However, research on rural road network layout remains in its early stages, with existing studies primarily focusing on macro-level policy discussions and general strategic analyses. For instance, some research emphasizes the basic principles and policy guidance for rural road layouts within regional development strategies [8], while other studies focus on the role and strategies of rural road infrastructure in promoting rural economic development [9,10]. However, these studies still face significant limitations in constructing scientifically rigorous, systematic road network planning methods, lacking practical, actionable optimization models that can meet the scientific planning needs of rural road networks in the context of common prosperity. Moreover, in many developing countries, rural road construction projects often face challenges in impact assessment, with insufficient data collection and analysis methods, leading to unreliable evaluations of rural roads’ impact on welfare, thus undermining the reliability of decision-making [11].

Achieving common prosperity requires adherence to the principles of “promoting efficiency, ensuring fairness, and achieving sustainable development”, focusing on narrowing the three main disparities: urban–rural, regional, and income. The layout of the road network is a key link in supporting common prosperity and needs to be analyzed in terms of its differences from traditional road network planning models. Understanding how to incorporate the goals of common prosperity into road network layout plans and how to evaluate the effectiveness of these layouts requires the establishment of scientifically sound decision models or methods. At present, the research on rural road layout planning has not comprehensively assessed the costs and benefits of different layout plans. Therefore, conducting a thorough evaluation of planning options is necessary. Due to the unique nature of rural road infrastructure, which involves multiple related factors and varied route choices, this study proposes the integration of Data Envelopment Analysis (DEA) and the Analytic Hierarchy Process (AHP) to construct a decision-making model for optimizing the allocation of funds. These two methods allow for quantitative analysis of rural road network layout plans, providing a more scientific basis for decision-making and laying a solid foundation for finalizing the planning layout [12].

This study proposes a decision model that integrates DEA and AHP for optimizing rural road network planning. The model begins by understanding the characteristics of different planning layouts for rural road networks and investigating the planning needs within the framework of common prosperity. Based on the current rural road network layout, traffic flow, and industrial distribution, it analyzes and extracts the factors influencing rural road network planning and summarizes these factors. The first step involves using DEA to assess the relative efficiency of different planning layout options, selecting those with higher economic and social benefits. Then, using AHP, further analysis is performed to determine the final ranking of the various planning options. The study applies this approach to the rural road network planning of Yueqing City, Zhejiang Province, evaluating different layout options—traditional, intermediate, and common prosperity-oriented—based on economic and social benefits. The primary contribution of this research is the introduction of a common prosperity framework into rural road network optimization, considering economic, social, and environmental objectives to optimize road network planning strategies. By combining DEA for plan selection with AHP for multi-criteria decision analysis, this study enhances the scientific and practical applicability of decision-making. The results provide empirical support for rural road network planning and policy formulation, contributing to the role of transportation infrastructure in achieving common prosperity.

The remainder of this paper is organized as follows. Section 2 reviews relevant literature and identifies the theoretical gap. Section 3 describes the study area, data sources, and the two-stage DEA–AHP methodology. Section 4 presents the DEA and AHP results and interprets key findings. Section 5 offers a dedicated Discussion of practical implications and limitations. Finally, Section 6 draws Conclusions and suggests avenues for future research.

2. Literature Review

Transportation infrastructure is not only a fundamental platform for facilitating the flow of goods but also plays a crucial role in enhancing human capital mobility, fostering social inclusivity, and promoting regional coordination [13]. With the introduction of the concept of “common prosperity”, the optimization of transportation networks has become increasingly important, as it drives urban–rural integration, improves the quality of transportation services in rural areas, alleviates poverty, and narrows regional development gaps [14]. Within the framework of common prosperity, the planning of transportation infrastructure must meet not only the economic efficiency requirements but also consider social equity and regional coordination. In particular, the layout of rural road networks is directly related to regional accessibility, industrial distribution, and the welfare of residents [15]. Scientifically and rationally designed rural road networks can enhance the efficiency of agricultural product circulation, promote rural tourism development, attract industrial capital to rural areas, and facilitate urban–rural integration.

However, existing research primarily focuses on policy guidance and general development strategies, with a lack of specific, actionable decision models. Early transportation network planning methods relied mainly on demand forecasting and economic benefit analysis, employing techniques such as shortest path algorithms, traffic flow distribution models, and linear programming [16,17]. While these methods have achieved good results in urban transportation networks, they often overlook factors such as social benefits and regional equity in rural road network planning. In recent years, multi-objective optimization methods have been increasingly applied to transportation planning, considering multiple competing objectives such as minimizing economic costs, maximizing social benefits, and minimizing environmental impacts. For example, heuristic algorithms such as Genetic Algorithms (GA) and Particle Swarm Optimization (PSO) have been proposed to solve complex transportation network layout problems [18]. Furthermore, ref. [19] introduced the concept of reliability into the layout of road network nodes and established a comprehensive road network planning methodology based on reliability. Ref. [20] constructed urban layout models by extending the Quadratic Assignment Problem (QAP), considering possible traffic distribution between different types of facilities. However, these optimization methods remain relatively limited in their application to road network layout, particularly under the common prosperity framework, where balancing social equity and regional coordination remains an unresolved challenge.

In the decision-making process of transportation planning, effectively assessing the advantages and disadvantages of different planning options—especially under multi-objective and multi-constraint conditions of optimal resource allocation—has always been a core issue in transportation planning [21]. Data Envelopment Analysis (DEA) and the Analytic Hierarchy Process (AHP) are two widely applied decision analysis methods in transportation planning [22]. DEA evaluates the multi-dimensional efficiency of transportation networks by establishing decision-making units (DMUs), making it particularly suitable for assessing the effectiveness and resource allocation issues of transportation networks [23]. For example, Ref. [24] simulated congestion situations and drivers’ perceptions of road network performance, using network DEA techniques to analyze the benefits of collaborative drivers. While DEA can effectively analyze the performance of transportation networks, it overlooks the interrelationships and complexities among decision units, which can limit its application in handling multiple interdependent transportation network elements.

AHP, on the other hand, helps decision-makers consider multiple complex factors comprehensively by determining the relative importance of various indicators, thus facilitating decision-making [25]. AHP provides systematic support for transportation planning by clarifying the weight relationships between indicators when addressing multi-objective decisions. In recent years, hybrid models combining DEA and AHP have gained widespread application in transportation planning, such as in traffic flow forecasting, infrastructure siting and construction, and public transport operation optimization [26]. These composite models leverage the strengths of both methods, offering more comprehensive and precise decision support for transportation network planning. For instance, Ref. [27] conducted a quantitative analysis of road network layouts in 29 Chinese cities based on network centrality, discovering that the higher the centrality of urban road networks, the higher the utilization rate of public transportation by city residents.

Despite the growing use of DEA and AHP in transportation studies, there remains a theoretical gap in combining DEA’s efficiency frontier analysis (including slack variable interpretation) with AHP’s structured weighting of equity and environmental criteria. No prior work systematically integrates these methods within a common prosperity context for rural road networks, where both radial and non-radial inefficiencies must be addressed alongside social and ecological goals.

In summary, existing research on rural road network planning mostly focuses on economic benefit analysis and general strategies, with limited consideration of how to achieve the goals of common prosperity within transportation planning. Although decision methods like DEA and AHP have made some contributions to transportation planning, they still fall short in terms of multi-objective optimization, social benefits, and regional coordination. This study combines DEA and AHP to propose a novel planning decision approach aimed at addressing the shortcomings of existing methods by incorporating social equity and regional coordination, providing a more systematic and comprehensive decision-making framework for rural road network planning

3. Materials and Methods

3.1. Study Area

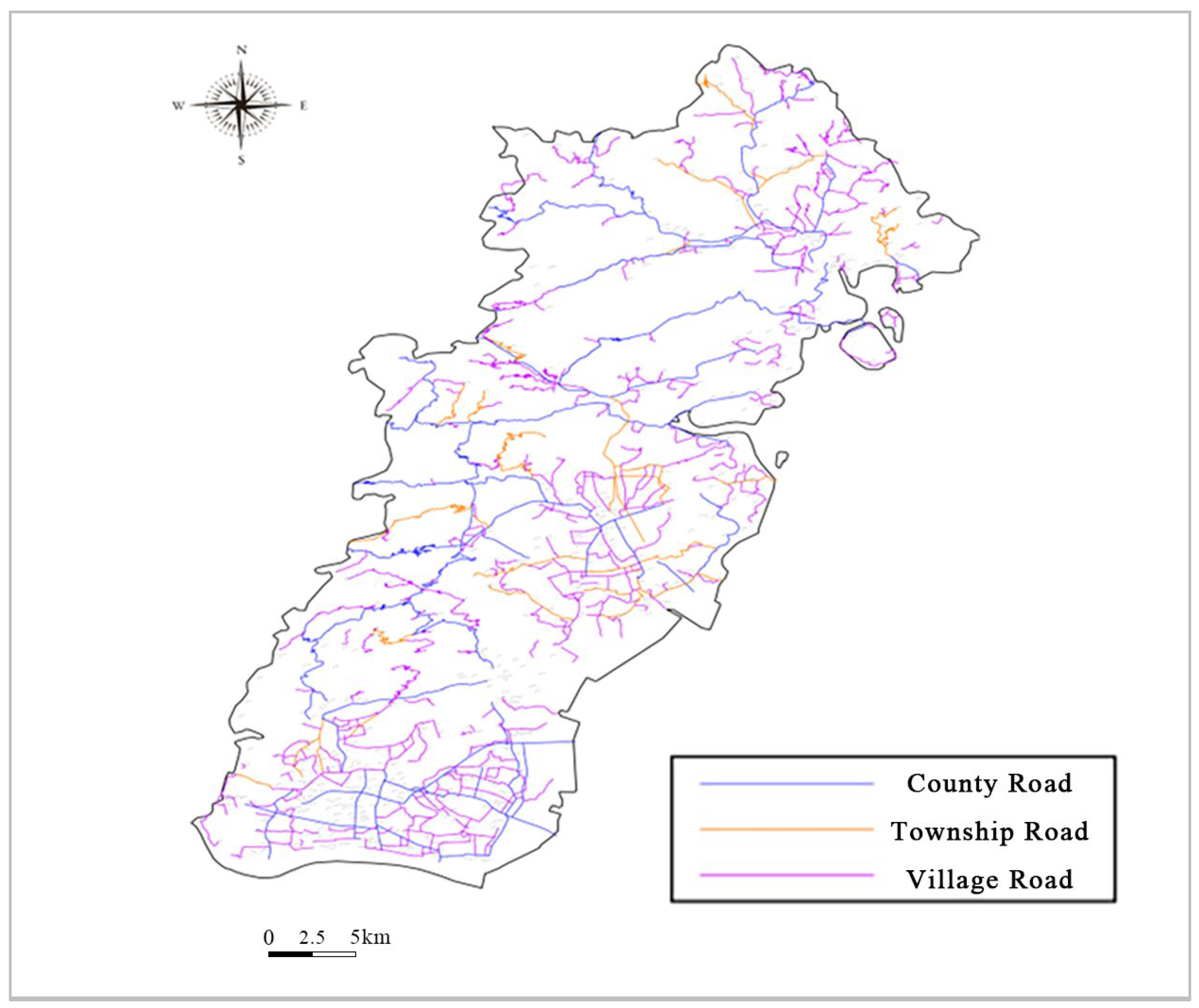
This study uses the rural road network of Yueqing City, Zhejiang Province, as the case for analysis; the current status of its rural road network is depicted in Figure 1. Yueqing City is located within the Yangtze River Delta Economic Zone, where manufacturing and tourism serve as the dominant industries. The city comprises both developed urban areas and underdeveloped rural regions. While the road network covers all townships, regional development remains unbalanced. Some townships suffer from low road classifications and weak traffic capacity, necessitating further optimization of road network planning to enhance the coverage of rural roads.

3.2. Data Description

In evaluating the effectiveness of rural road network planning schemes, the selection of decision-making units (DMUs) must adhere to the “homogeneity” principle. This means that all selected units should share strategic goals aimed at improving regional connectivity and reducing regional development disparities [28]. Additionally, their external environment should exhibit similar geographical and economic characteristics, and their input–output indicator systems must remain strictly consistent. This study designates the rural road network planning schemes of Yueqing City, Zhejiang Province, as the DMUs. All schemes are formulated under a unified policy framework and spatial constraints, with data sourced from the Yueqing City 14th Five-Year Comprehensive Transportation Development Plan, local government fiscal reports, and traffic flow monitoring systems.

Traditional rural road network planning primarily focuses on factors such as funding and road alignment, while often neglecting the role of rural roads in industrial development and in bridging the urban–rural, regional, and income gaps. A road network planning approach aligned with the goal of achieving common prosperity should incorporate not only financial and alignment considerations but also an evaluation framework that integrates multiple dimensions, including economic, social, and environmental benefits. Economic benefits primarily account for construction costs borne by the implementing entity, considering factors such as alignment, mileage, and road classification. Social benefits are assessed across two dimensions: (1) the extent to which the road network layout supports industrial and tourism development, and (2) its impact on reducing regional disparities. Environmental benefits focus on the road network’s effects on the environment and its contribution to overall traffic emissions.

By employing the input–output framework of the Data Envelopment Analysis (DEA) model, this study further refines specific input and output indicators to quantitatively evaluate the rationality and effectiveness of the planning layout.

Input indicators center on resource investment and existing constraints, including:

• Construction cost (CNY 10,000): The total sum of direct and indirect investment, encompassing land acquisition, material procurement, construction expenses, and machinery rental.
• Planned road length (km): The actual mileage of the proposed road network.
• Alignment non-linearity coefficient: Calculated through geometric analysis as the ratio of the actual route length to the straight-line distance, reflecting the degree of road curvature.

Output indicators measure development efficiency and goal attainment, comprising:

• Industrial coverage rate (%): The proportion of industrial nodes, including manufacturing parks, tourist attractions, and agricultural markets, covered within the road network’s influence area.
• Regional Gini coefficient: Adapted from the classical Gini coefficient used to measure inequality, this metric evaluates disparities in transportation infrastructure allocation. Its mathematical form is consistent with the standard definition but adjusted to focus on per capita road mileage across townships, ensuring fair comparisons among regions with different population sizes. In this study, a lower Gini coefficient indicates greater regional equity, directly reflecting residents’ mobility, access to economic opportunities, and public services. The calculation is shown in Equation (1).
• Average daily CO₂ emissions (tons): Estimated using a vehicle energy consumption model, incorporating parameters such as vehicle type distribution, driving conditions, and emission factors to assess the ecological impact of road network operations.

  $$G={\displaystyle \frac{\sum _{i=1}^N\sum _{j=1}^N\left|L_i-L_j\right|}{2N^2\overline{L}}}$$

  (1)

  where $L_i$ represents the per capita road mileage of township $i$ (km per 1000 people); $L_j$ represents the per capita road mileage of township $j$ (km per 1000 people); $\overline{L}$ is the average per capita road mileage across Yueqing City (km per 1000 people); $N$ denotes the number of townships in Yueqing City.

3.3. Method

3.3.1. Determining the Feasible Solution Set Based on the DEA Method

Data Envelopment Analysis (DEA) is used to evaluate the relative efficiency of highway network planning layout schemes by constructing a multi-objective optimization model. This study employs the input-oriented Charles–Cooper–Rhodes (CCR) model, with technical efficiency as the core indicator, to screen the feasible solution set.

Assume there are $M$ decision-making units (DMUs), each corresponding to one candidate planning scheme. For DMU $j$ ($j$ = 1, …, $M$), each containing $I$ input and $O$ output indicators. The input and output of each decision-making unit are represented accordingly, and its efficiency $h_j$ is expressed as follows:

$$h_j={\displaystyle \frac{\sum _{r=1}^O{u}_r{y}_{rj}}{\sum _{i=1}^I{v}_i{x}_{ij}}}, j=\mathrm{1,2},...,\mathrm{M}$$

(2)

where $x_{ij}$ is the i-th input indicator of scheme $j$; $y_{rj}$ is the r-th output indicator of scheme $j$; $v_i$ and $u_r$ are the weight coefficients for output and input indicators, respectively.

By adjusting these coefficients, the efficiency values of all decision-making units are ensured to satisfy $h_j\le 1$, meaning that no unit’s efficiency exceeds the ideal frontier.

To analyze the relative effectiveness of a given decision-making unit, an efficiency evaluation is conducted by constructing a fractional programming model:

$$\begin{gathered} max{h}_{j_0}={\displaystyle \frac{\sum _{r=1}^O{u}_r{y}_{r{j}_0}}{\sum _{i=1}^I{v}_i{x}_{i{j}_0}}} \\ s.t.{\displaystyle \frac{\sum _{r=1}^O{u}_r{y}_{rj}}{\sum _{i=1}^I{v}_i{x}_{ij}}}\le 1 \left(j=\mathrm{1,2},...,M\right), v_i,u_r\ge ϵ \left(ϵ>0\right) \end{gathered}$$

(3)

where ${\mathrm{h}}_{j_0}$ represents efficiency score of the specific DMU indexed by $j_0$; ${ x}_{i{j}_0}$ and $y_{r{j}_0}$ represent the $i$-th input and the $r$-th output of the $j_0$ decision-making unit (DMU), respectively. $v_i$ and $u_r$ are the weight coefficients for output and input indicators, respectively; $\mathsf{ϵ}$ is a small positive constant to prevent zero weights.

Economically, the model aims to find a set of input and output weights $v_i$ and $u_r$ to maximize the relative efficiency $h_{j_0}$ of the DMU under evaluation, while ensuring that the calculated efficiency scores $h_j$ for all DMUs satisfy the constraint $h_j\le 1$. This guarantees a fair comparison under the most favorable weights for the evaluated DMU.

To facilitate computation, the fractional programming problem is converted into an equivalent linear programming model using the Charles–Cooper transformation:

$$t={\displaystyle \frac{1}{\sum _{i=1}^I{v}_i{x}_{i{j}_0}}}, {\mu }_r=t{u}_r, {\omega }_i=t{v}_i$$

(4)

where ${\mu }_r$ and ${\omega }_i$ are the transformed new weight coefficients.

Thus, the fractional programming model transforms into the following linear programming model [29]:

$$\begin{gathered} max\sum _{r=1}^O{\mu }_r{y}_{r{j}_0} \\ s.t.\sum _{i=1}^I{\omega }_i{x}_{ij}-\sum _{r=1}^O{\mu }_r{y}_{rj}\ge 0 \left(j=\mathrm{1,2},...,M\right), \\ s.t.\sum _{i=1}^I{\omega }_i{x}_{i{j}_0}=1, {\mu }_r,{\omega }_i\ge 0 \end{gathered}$$

(5)

Since the dual model of this linear programming problem has significant economic implications, it is necessary to transform it into the dual model. By introducing dual variables ${\lambda }_j$ for the original constraints, as well as slack and surplus variables for inputs and outputs, the dual standard model is obtained:

$$\begin{gathered} min\theta \\ s.t.\sum _{j=1}^n{\lambda }_j{x}_{ij}+s_i^{-}=\theta x_{i{j}_0}+t_i^{-} \left(i=1,...,I\right), \\ s.t.\sum _{j=1}^n{\lambda }_j{y}_{rj}-s_r^{+}=y_{r{j}_0}+t_r^{+} \left(r=1,...,O\right), {\lambda }_j,s_i^{-},s_r^{+}\ge 0 \end{gathered}$$

(6)

where $\theta$ represents the efficiency value; ${\lambda }_j$ represents weight variable for DMU $j$; ${ s}_i^{-}$ and $s_r^{+}$ denote the input redundancy and output shortfall slack variables, respectively.

If $\theta =1$ and all slack variables are zero, the DMU $j_0$ is DEA efficient, indicating it is on the production frontier and does not require input–output structure optimization. Otherwise, efficiency improvements are needed through resource allocation adjustments.

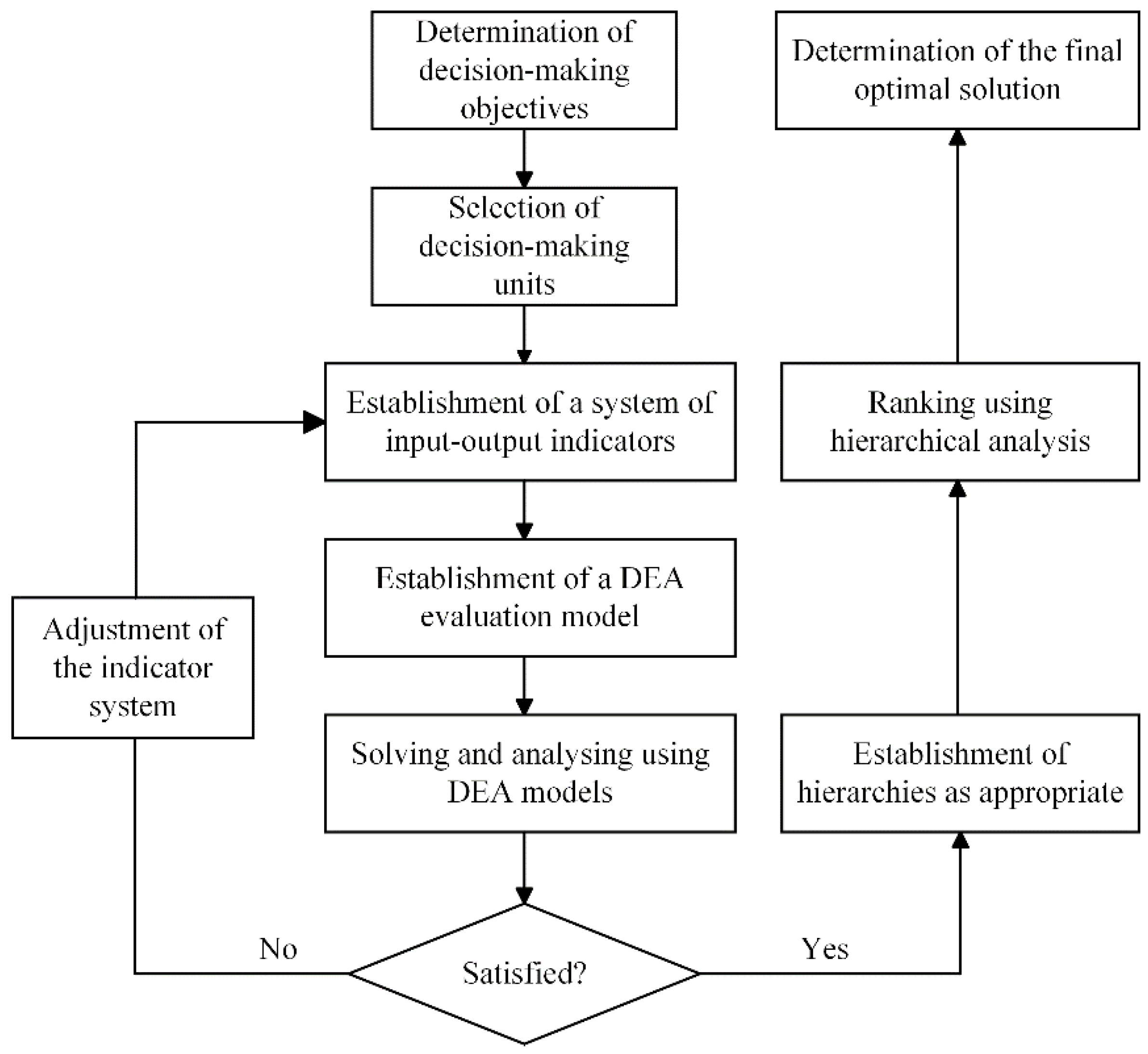
When applying this model, each decision-making unit is analyzed separately, requiring individual computations. If the objective function value meets the specified condition, the decision-making unit is deemed DEA-efficient, forming part of the feasible solution set. The model application process is shown in Figure 2.

3.3.2. AHP Model Construction and Weight Calculation

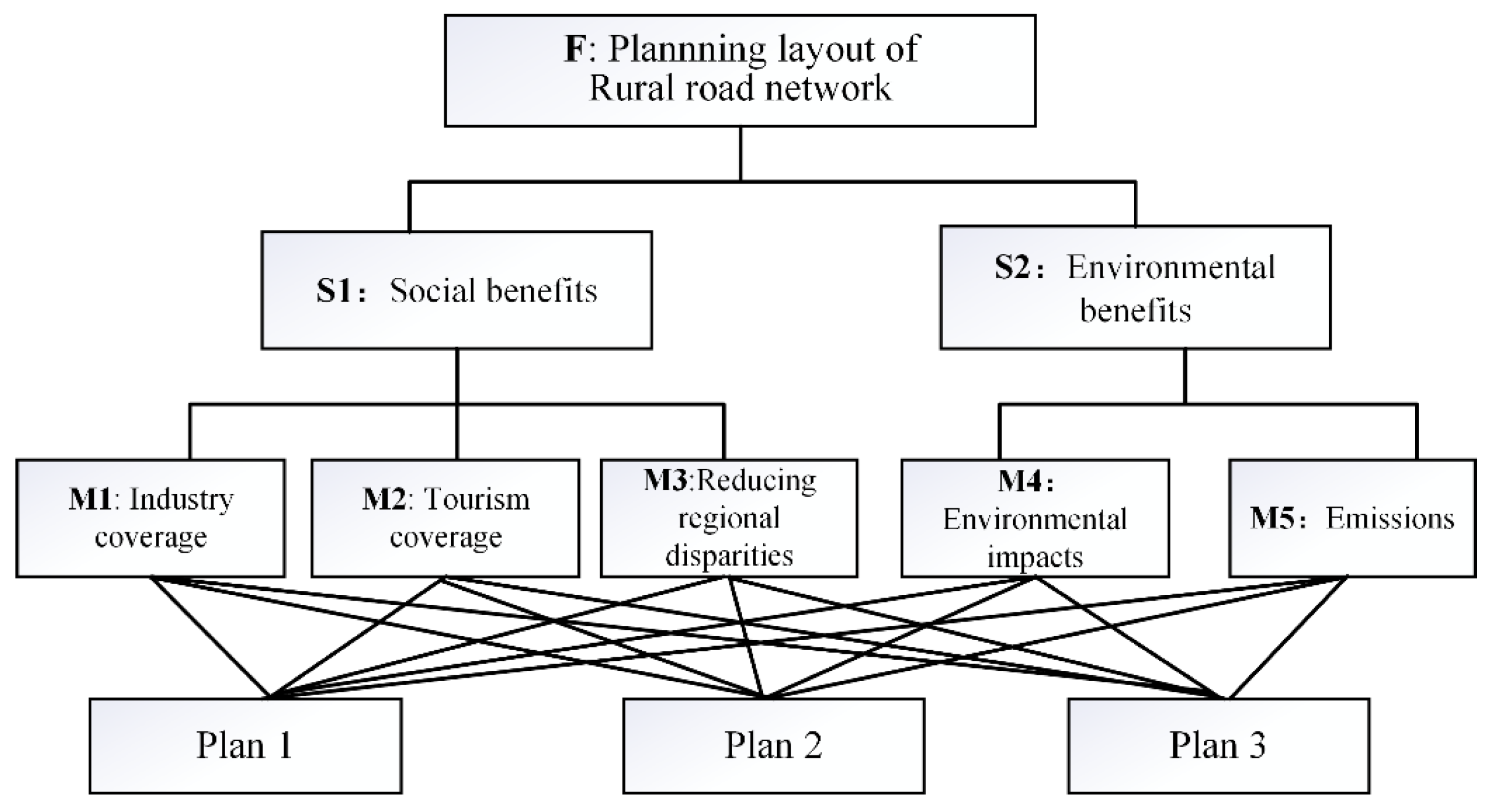
The Analytic Hierarchy Process (AHP) is employed to evaluate highway network planning layout schemes. This method integrates traditional principles with a common prosperity-oriented approach to road maintenance, considering social, economic, environmental, and ecological objectives to assess feasible solutions and determine the optimal highway network planning layout under the common prosperity framework. The basic steps of AHP include: defining the overall goal and establishing the hierarchical structure, calculating weight coefficients for each level, evaluating the alternatives, and conducting consistency tests.

Designing the Hierarchical Structure and Input Parameters

Various factors influence rural highway network planning, which can be summarized into three main aspects: economic benefits, social benefits, and environmental benefits. From the perspective of guiding rural highway networks toward common prosperity, priority is given to social and environmental benefits. Social benefits ensure that the highway network supports common prosperity, while environmental benefits contribute to sustainable development. The planning process should go beyond merely considering topographical constraints and layout patterns, incorporating local industries, tourism, and resources to reduce regional disparities. The hierarchy consists of the following levels, as shown in Figure 3:

• Social benefits (S₁): Industrial coverage (M₁), tourism accessibility (M₂), and regional disparity reduction (M₃).
• Environmental benefits (S₂): Environmental impact (M₄) and emissions reduction (M₅).

Constructing the Judgment Matrix and Weight Calculation

In the decision-making process, each factor influences the next level, requiring comparisons of relative importance. A judgment matrix is constructed using expert scoring or historical data analysis, employing a 1–9 scale for quantification. The weight vector is then determined by computing the maximum eigenvalue of the matrix and normalizing it. For any criterion layer or sub-criterion layer, a judgment matrix in the following form can be constructed:

$$A_p=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \dots & a_{1n_p}\\ a_{21}& a_{22}& \dots & a_{2n_p}\\ ⋮& ⋮& \ddots & ⋮\\ a_{n_{p}1}& a_{n_{p}2}& \dots & a_{n_p{n}_p}\end{array}\right]$$

(7)

where $a_{ij}$ represents the relative importance of factor $i$ compared to factor $j$; $p$ corresponds to different levels in the AHP structure; $n_p$ represents the number of indicators at this level.

The relative importance relationship of the factors satisfies the reciprocal condition satisfying:

$$a_{ij}={\displaystyle \frac{1}{a_{ji}}}, a_{ii}=1, \forall i,j$$

(8)

After constructing the judgment matrix $A_p$, it is necessary to derive the priority weights of each indicator relative to the higher-level goal. The geometric mean method is commonly used to calculate the weights. Specifically, for the $i$-th row of the matrix, the geometric mean $W_i$ is computed to represent the relative importance of element $i$ compared to others. To calculate the weight vector $W$, the eigenvector method is used to solve for the largest eigenvalue ${\lambda }_{max}$ of the judgment matrix and its corresponding normalized eigenvector $W$. The geometric mean is calculated according to Equation (10) to reduce the impact of extreme values and improve the rationality of weight allocation. Normalization processing is performed using Equation (11) to compute the weight vector:

$$A_{p}W={\lambda }_{max}W.$$

(9)

$$W_i={\left(\prod _{j=1}^{n_p}{a}_{ij}\right)}^{{\displaystyle \frac{1}{n_p}}}, i=\mathrm{1,2},...,n_p$$

(10)

$$W_i^{’}={\displaystyle \frac{W_i}{\sum _{i=1}^{n_p}{W}_i}}$$

(11)

where ${\lambda }_{max}$ represents the largest eigenvalue of the matrix, and after normalization, the criterion layer weights are obtained; $W_i$ is the geometric mean of the i-th row in the matrix, representing the preliminary weight of element i; $W_i^{’}$ is the normalized weight of element i.

Similarly, the $A_1$: F-S, $A_2$: S1-M, and $A_3$: S2-M judgment matrices are established. This compares the relative importance of alternatives for each sub-criterion layer.

Consistency Test

After determining the judgment matrix, it is necessary to assess whether the derived weight coefficients are reasonable. To avoid inconsistencies in subjective judgments, a consistency test is conducted for each level of the judgment matrix. The consistency index $CI$ and random consistency ratio $CR$ are calculated as follows:

$$CI={\displaystyle \frac{{\lambda }_{max}-n_p}{n_p-1}}, CR={\displaystyle \frac{CI}{RI}}$$

(12)

where $n_p$ is matrix dimension of $A_p$; $RI$ is the random consistency index corresponding to dimension $n_p$.

If $CR<0.1$, the judgment matrix passes the consistency test; otherwise, the scale values need to be readjusted.

When the judgment matrix is perfectly consistent, the maximum eigenvalue ${\lambda }_{max}$ = n, and all other eigenvalues are zero. When the judgment matrix has satisfactory consistency, its maximum eigenvalue is slightly greater than the matrix order $n$, while the remaining eigenvalues remain zero.

Overall Ranking and Result Output

Finally, the overall ranking of schemes is calculated by integrating the weights at each level. The higher the final score, the more the scheme aligns with the multi-objective optimization requirements under the common prosperity framework.

$$V\left(P_j\right)=\sum _{k=1}^3{W}_k\left(\sum _{l=1}^L{W}_{kl}\cdot W_{klj}\right)$$

(13)

where $W_k$ represents the criterion layer weight, $W_{kl}$ represents the sub-criterion layer weight, and $W_{klj}$ represents the alternative layer weight.

3.3.3. Scheme Design

Based on the concepts and principles of different rural road network layouts, planning schemes can be designed according to three guiding approaches: traditional, intermediate, and common prosperity-oriented. These schemes are then evaluated for their benefits and effectiveness.

The traditional-oriented scheme prioritizes minimizing construction costs, mainly considering direct investment expenditures in the planning process while striving to minimize new road construction mileage. It relies on the existing road network and follows conventional planning methods to reduce financial input. Although this scheme keeps construction costs at the lowest level, it results in poor fairness, a high Gini coefficient, and relatively high carbon emissions, with an average daily emission of 35–50 tons.

The intermediate-oriented scheme improves upon the traditional approach by enhancing industrial coverage and incorporating environmental protection measures. While still based on experience-driven road planning, it strengthens connectivity between major industrial clusters to foster industrial synergy. Additionally, it avoids ecologically fragile areas during construction and incorporates some environmentally friendly materials to reduce environmental impact. The road network alignment ensures partial coverage of industrial parks, though some remote industrial sites remain unconnected. Compared to the common prosperity-oriented scheme, this approach has moderate construction costs but a slightly higher Gini coefficient, with daily carbon emissions controlled between 20–35 tons.

The common prosperity-oriented scheme aims for full industrial coverage, regional equity, and green, low-carbon development. By optimizing road network connectivity with industrial and tourism sites, it enhances resource allocation efficiency while reducing regional disparities. This scheme takes into account the distribution of industries and transportation demands in different regions, ensuring that the road network effectively links industrial parks and tourist destinations. Additionally, it integrates environmental permits and carbon emission controls, keeping daily CO₂ emissions within the range of 10–20 tons. However, due to the comprehensive coverage of industrial and tourism sites, this scheme incurs higher construction costs. Nonetheless, it maintains a low Gini coefficient, ensuring greater fairness and sustainability.

The transition from the traditional to the common prosperity-oriented approach represents an evolution from experience-based planning to data-driven and environmentally prioritized strategies. The planning principles shift from cost minimization to a multi-objective optimization that balances industrial needs, regional equity, and ecological protection.

This paper presents nine distinct planning layout schemes for rural road networks along with their respective benefits. Among them, Schemes 1, 2, and 3 emphasize the common prosperity-oriented approach; Schemes 1–5 incorporate green and environmental principles with extended industrial and tourism coverage while prioritizing sustainability. In contrast, Schemes 6–9 focus more on construction cost control, with Schemes 7, 8, and 9 and following a traditional planning approach.

For each scheme, this paper derived the key evaluation metrics directly from GIS route plans and scheme-specific forecasts. Planned road length and curvature coefficient were measured in ArcGIS by tracing each segment’s centerline and comparing it to its straight-line endpoints; construction cost was estimated by local engineering budget guidelines; industrial coverage rate was calculated by buffering each network by 1 km and computing the percentage of mapped industrial and tourism nodes within the buffer; the regional Gini coefficient follows Equation (1) using township-level per-capita road mileage; average daily CO₂ emissions were estimated with a bottom-up model that multiplies each segment’s forecasted traffic volume. Schemes for planning the layout of the rural road network are summarized in

Table 1. Schemes for planning the layout of the rural road network.

Category	Scheme	Construction Cost (CNY 10,000)	Mileage Scale (km)	Curvature Coefficient (0–1)	Regional Gini Coefficient (0–1)	Major Industry Coverage (%)	CO2 Daily Emissions (tons)
Common prosperity-oriented	1	59,000	3000	1.8	0.1	98	13
	2	50,000	2500	1.7	0.3	99	15
	3	45,000	2200	1.6	0.5	95	20
Medium	4	40,000	2000	1.5	0.6	95	25
	5	38,000	2000	1.5	0.7	95	30
	6	35,000	1500	1.4	0.8	90	32
Traditional	7	30,000	1000	1.3	0.9	90	35
	8	25,000	800	1.2	0.9	90	40
	9	20,000	600	1.1	1.0	88	50

.

4. Results

4.1. DEA Model Results

In this case, the DEA model includes three input variables and three output variables, corresponding to construction cost, road length, alignment non-linearity, industrial coverage, Gini coefficient, and CO₂ emissions. Using Alternative 1 as an example, substituting its input–output data into the input-oriented CCR model yields a solvable linear programming system. For the remaining decision-making units (DMUs), only the right-hand side coefficients need to be adjusted accordingly, resulting in nine separate models to be solved.

In the CCR model, the variables λ₁–λ₉ serve as decision variables that represent the contribution of each peer scheme in constructing the efficiency reference frontier through a convex combination. To capture non-radial inefficiencies, the model also introduces four slack variables, s₁ through s₄, which quantify input excesses or output deficiencies relative to the frontier. Specifically, s₁ represents construction cost redundancy, s₂ represents road length redundancy, s₃ represents industrial coverage shortfall, and s₄ represents CO₂ emissions shortfall. The results are shown in

Table 2. The results of DEA.

Scheme	$\mathit{\lambda }$1	$\mathit{\lambda }$2	$\mathit{\lambda }$3	$\mathit{\lambda }$4	$\mathit{\lambda }$5	$\mathit{\lambda }$6	$\mathit{\lambda }$7	$\mathit{\lambda }$8	$\mathit{\lambda }$9	s1	s2	s3	s4	t1	$\mathit{\theta }$
1	0	0	0	0	0	0.39	0	0	0	0	226.6	68.4	1	0	0.87
2	0	0	0	0	0	0	0.25	0.21	0	0	224.0	71.2	0	0	0.99
3	0	0	0	0	0	0	0.11	0.42	0	0	53.0	50.4	0	0	0.77
4	0	0	0	0	0	0	0	0.66	0	15	66.0	47.9	0	0	0.95
5	0	0	0	0	0	0	0	0.68	0	113	67.9	40.4	0	0	0.98
6	0	0	0	0	0	0	0	0	0	0	0	0	3 × 10−14	0	1
7	0	0	0	0	0	0	1	5 × 10−16	0	0	7 × 10−14	1 × 10−14	0	0	1
8	0	0	0	0	0	0	0	1	0	0	2 × 10−13	0	3 × 10−14	0	1
9	0	0	0	0	0	0	0	0	1	0	0	0	0	0	1

.

The CCR model results indicate that, under both input-oriented and output-oriented conditions, the non-radial variable t₁ for all alternatives is 0, signifying that the industrial coverage rate has reached the assumed maximum value. Four alternatives exhibit an efficiency index (y-value) of 1, with slack variables and surplus variables either at zero or near zero, thus are classified as DEA efficient. These alternatives demonstrate well-organized technical layouts and optimal resource utilization, making them prime investment choices. Alternatives 1, 3, and 4 have relatively low y-values, with large slack variables s₂ and s₃, indicating inefficient resource utilization with either excessive input redundancy or severe output deficiencies. Alternatives 2 and 5 have efficiency indices close to 1, showing potential for further consideration.

Further analysis reveals that the most efficient alternatives identified by the DEA model tend to align with traditional schemes characterized by lower construction costs and low linear non-straightness coefficients. Their slack variables (s₁–s₄) approach zero, suggesting complete resource utilization with no waste or output deficiencies. However, traditional schemes, despite their cost efficiency, have Gini coefficients close to 1, which contradicts the goal of common prosperity.

Thus, the DEA analysis provides an initial selection of alternatives with higher user and social benefits. It is important to note that DEA results are based on the theoretical assumption of maximum industrial point coverage, without considering real-world dynamic changes. Some alternatives may be effective under current static conditions but could become obsolete due to declining actual coverage or stricter carbon emission constraints over time. This highlights the static limitations of DEA analysis. Therefore, DEA results should be supplemented with the Analytic Hierarchy Process (AHP) to optimize weights for cost, equity, and environmental sustainability to address long-term shifts in industrial layouts and regulatory frameworks.

4.2. AHP Model Results

Highway network planning is a strategic activity that requires long-term foresight. Different planning conditions lead to different choices. Relative to the target layer F, environmental benefits (S₂) are prioritized over social benefits (S₁). Thus, judgment matrices F-S, S₁-M, and S₂-M are established, with F-S presented as follows:

Highway network planning is a strategic activity that requires long-term foresight. To systematically reflect the priorities among different planning objectives and evaluation indicators, judgment matrices are established. Specifically, the F-S matrix captures the relative importance between the overall goal (F) and the main criteria (S₁ for social benefits and S₂ for environmental benefits). Considering the overall goal, environmental benefits (S₂) are prioritized over social benefits (S₁).

$$A=\left[\begin{array}{l}1\\ 1\end{array}\right.\begin{array}{cc}& \end{array}\left.\begin{array}{l}3\\ 3\end{array}\right]$$

(14)

Similarly, matrices S₁-M and S₂-M are established to compare the relative importance among detailed evaluation indicators under each main criterion. Here, “M” denotes the set of indicators associated with each criterion. For social benefits (S₁), the indicators include industrial coverage rate, tourism accessibility, and regional disparity reduction. For environmental benefits (S₂), the indicators include environmental impact and CO₂ emissions reduction.

The AHP model employs the same input and output indicators as the DEA model to ensure data consistency between the two methods. Through the analytic hierarchy process, DEA-selected efficient alternatives (Alternatives 6, 7, 8, and 9) and potential alternatives (Alternatives 2 and 5) are ranked comprehensively. The results are presented in

Table 3. Overall ranking results using the Analytic Hierarchy Process.

Scheme	Ranking
Alternative 1	2
Alternative 2	1
Alternative 3	3
Alternative 4	5
Alternative 5	4
Alternative 6	6

.

Alternative 2 ranks first in the overall ranking due to its balanced performance in both social and environmental benefits. Alternatives 1 and 3, guided by the common prosperity principle, rank second and third, respectively. Traditional alternatives 7, 8, and 9 rank lower due to their lower social benefit weights. Alternative 6, with its higher carbon emissions, ranks fourth, highlighting that merely reducing construction costs may compromise long-term sustainability.

The DEA method focuses on technical efficiency, using quantitative analysis to assess resource utilization in various highway network planning alternatives and selecting relatively optimal solutions. However, its evaluation criteria are primarily based on input-output efficiency and fail to fully consider social equity and environmental sustainability within the common prosperity framework. For example, Alternative 7, which follows a traditional approach, is DEA-efficient but contradicts common prosperity goals due to high regional disparities and carbon emissions. The AHP model addresses this limitation by incorporating multi-criteria weighting. Under the AHP model, alternatives must not only exhibit high resource utilization efficiency but also perform well in industrial coverage, regional balance, and environmental friendliness. The analysis confirms that Alternative 2 holds a comprehensive advantage in industrial coverage, regional balance, and low carbon emissions.

Combining DEA and AHP provides a complementary decision-making framework for rural highway network planning. DEA quantitatively filters out technically inefficient alternatives, ensuring compliance with efficiency requirements. AHP then ranks DEA-efficient alternatives based on multidimensional criteria, ensuring that decisions meet both efficiency requirements and align with the strategic goal of common prosperity.

5. Discussion

Alternative 2 offers the most balanced combination of cost, equity and environmental performance, but its practical rollout will demand careful coordination. The slightly higher investment and more winding alignments may stretch limited rural budgets and technical capacity. At the same time, advancing social equity relies on cooperation among multiple agencies, which is an effort that can conflict with near-term traffic efficiency targets. Local officeholders, residents and private stakeholders may also hold divergent priorities, slowing consensus. Addressing these challenges will require clear institutional mandates, transparent decision processes and adaptive implementation strategies.

Compared to previous studies conducted in urban or economically developed areas, which primarily prioritize traffic efficiency and investment returns, this study emphasizes a more balanced evaluation framework tailored to the needs of developing regions. The integration of DEA and AHP provides a complementary decision-making approach for rural highway network planning. DEA quantitatively eliminates technically inefficient alternatives, ensuring alignment with efficiency criteria. Subsequently, AHP ranks the DEA-efficient alternatives based on multidimensional criteria, aligning decisions with both technical feasibility and the strategic goals of common prosperity. This methodology underscores the importance of incorporating multidimensional evaluation metrics that go beyond traditional cost-benefit analysis, integrating efficiency, equity, and sustainability. By introducing indicators such as the Gini coefficient and industrial coverage rate, the study reinforces the paradigm shift toward inclusive infrastructure planning that supports balanced regional development.

However, this study has some limitations. The DEA method relies on static data assumptions for a specific period, whereas industrial point distribution and traffic demand dynamically evolve over time, potentially affecting the long-term validity of selected alternatives. Additionally, this research is based on a single regional case, and the generalizability of conclusions requires further validation.

6. Conclusions

This study focuses on decision-making methods for highway network planning under the common prosperity framework by integrating Data Envelopment Analysis (DEA) and the Analytic Hierarchy Process (AHP). A scientifically sound evaluation model was developed and empirically tested using the rural highway network in Yueqing City, Zhejiang Province. The results indicate that common prosperity-oriented highway network planning alternatives achieve better balance in efficiency, equity, and sustainability, with Alternative 2 ranking highest in AHP priority sorting, owing to its balanced investment, comprehensive industrial and tourism coverage, low regional Gini coefficient, and controlled CO₂ emissions. This method demonstrates advantages in promoting regional coordinated development, optimizing resource allocation, and enhancing social benefits. The key contributions of this study are as follows.

Methodologically, it pioneers the integration of DEA and AHP in highway network planning, providing a novel approach for multidimensional benefit quantification. The DEA method eliminated 55% of alternatives due to input redundancy or output deficiencies, narrowing the feasible solution set to technically efficient candidates. However, DEA alone prioritized cost-efficient schemes with high Gini coefficients, conflicting with equity goals. The AHP model addressed this gap by weighting social and environmental benefits, making the final decisions more scientific and practical.

At the policy level, this study introduces key evaluation indicators such as the Gini coefficient and industrial coverage rate, emphasizing that highway network planning should move beyond mere cost minimization to focus on regional equity and sustainable development. This provides a feasible evaluation framework for local governments in optimizing transportation infrastructure planning under the common prosperity strategy. Local governments should prioritize dynamic evaluation frameworks that update industrial distribution and emission constraints periodically and institutionalize equity metrics in infrastructure planning to avoid over-reliance on cost-driven models.

In engineering practice, a case study of rural highway network planning in Yueqing City validates the advantages of common prosperity-oriented planning. The low Gini coefficient and high industrial coverage of Alternative 2 suggest that moderately increasing construction costs and incorporating non-linear road alignments can effectively enhance social equity and economic connectivity, serving as a reference model for similar county-level planning efforts.

We acknowledge two primary limitations. The DEA component relies on static input–output data and does not capture dynamic changes in traffic demand or industrial distribution, and the case study is confined to a single county-level region; broader validation across multiple geographies and development contexts is needed. Future studies will incorporate dynamic panel data analysis and extend the research scope to regions with varying economic development levels to explore the heterogeneous characteristics of highway network planning in urban–rural integration, industrial synergy, and environmental protection.