Progressing Towards Sustainability: Power-Sharing Control Topologies for Microgrids with Parallel-Connected Inverters for Grid Stability

Abstract

Parallel-connected inverters play a crucial role in the grid interface of distributed generation. The world is now moving towards sustainability, while shifting from traditional power systems to renewable energies. With the emergence of microgrids as an alternative for an uninterruptable power supply, there are significant challenges in terms of control strategies. Ensuring stability and reliability in electrical systems amidst the integration of diverse energy sources with varying power ratings into a distribution network presents the need for advanced control techniques. These techniques must effectively maintain power system quality, stability, and reliability when operating in microgrids with parallel-connected inverters. Achieving accurate power sharing under different operating conditions, compensating for voltage and frequency deviations, and maintaining a well-controlled microgrid system are essential objectives. This paper focuses on the categorization of droop-based control with multi-loop insertion approaches. Additionally, it provides a comprehensive analysis of inverter-based microgrid control techniques, emphasizing power-sharing accuracy in various conditions, and presents a detailed comparison of different control strategies.

1. Introduction

Conventional power systems comprise power generation, transmission, and distribution networks. However, in modern power systems, researchers aim to integrate renewable energy resources into traditional systems to achieve cost-effectiveness, full control, and efficient management [1]. Ensuring power quality and security for various domestic and industrial applications, thus providing uninterrupted services, is crucial for smooth power system operation and control [2]. The development of distributed generation (DG) offers flexibility and reliability, presenting a viable solution for power system operation and control. However, challenges, such as high cost, control issues, and power quality concerns, instability, and protection, still persist [3,4,5,6,7].

A collection of interconnected DG units supplying power to loads is known as a microgrid (MG), which can operate in either an islanded (isolated) or grid-connected mode, depending on its configuration. Islanded MGs manage their power sharing through control actions, while grid-connected MGs are synchronized with the main grid [8,9,10,11]. In conventional grids, a two-way communication system is established to prevent individual units from assuming control. On the other hand, MG systems require two-way communication involving electricity consumers in various aspects, such as electricity usage, storage, and management. Additionally, the parallel operation of inverter-based DG units allows for highly flexible and robust system control [12].

A parallel operation in an MG simplifies maintenance without disrupting the entire system by following a decentralized approach to minimize current ripples [13]. Despite the numerous advantages of MG systems, several issues need to be addressed, including voltage and frequency control, accurate power sharing under various load conditions, stability, power quality, and reliability [3,14]. Ensuring system stability, particularly in a parallel operation, is crucial for the effective functioning of DG units. Analyses of system stability, reliability, and power quality under different load conditions have been conducted in previous studies [15,16].

Control schemes for parallel-connected inverters in MGs can be classified into current accretion, current distribution, and droop control. This paper provides an overview of various control schemes for parallel-connected inverters in MG systems. It focuses on droop-based control techniques, and their advantages and disadvantages concerning power sharing accuracy are discussed. The paper includes the implementation process of different droop-based control schemes, presenting the block diagrams and mathematical equations for each scheme.

This paper addresses the current control system of parallel inverters and the challenges, from centralized control approaches to decentralized control methods. The objectives of a control mechanism in parallel DGs connected with inverters are to attain controlled voltage and power and to resolve power-sharing issues, which are dependent on active load sharing. As for centralized control, a communication link is required for active load sharing when dealing with the control of inverters connected in parallel. For example, the regulated voltage, real and reactive powers, system reliability, system expandability, and stability of a bus system, such as system impedances and local modified references, are controlled in this mode. In parallel-connected inverters, active-load-sharing control is performed by using various techniques, such as current accretion, droop, and current distribution approaches. These control approaches are based on the control loop, as well as the communication and the exchanged control signals between the parallel inverters. It should be noted, furthermore, that droop control is an approach that does not need a communication link, while the others are communication-based.

This paper is organized into six sections. Section 1 serves as the introduction. Section 2, Section 3 and Section 4 delve into the details of droop-based control techniques, linear droop control and non-linear droop control, respectively. In Section 5 and Section 6, the power-sharing control aspects of an MG system and the conclusion of the paper are presented, respectively.

2. Droop Control

Recent advancements in electrical systems have successfully facilitated the integration of an increasing number of renewable energy resources (RERs). To achieve better control and ensure power quality and system stability, the integration of RERs into power electronic devices has become a primary objective in MG systems. However, accomplishing these objectives is not a straightforward task. Various methods exist for MG control, broadly categorized into communication strategies (based on master/slave operations) and communicationless strategies (based on droop-based control) [17,18,19]. This paper focuses specifically on droop-based control techniques. Figure 1 illustrates the further subcategories of droop-based control techniques. An effective MG system needs to meet specific performance criteria, including appropriate system stability, voltage regulation, minimal total harmonic distortion, and harmonic power sharing. Droop control represents an approach or technique that can ensure these performance indices in parallel-connected-inverter systems integrated with RERs.

In addition to achieving these performance goals, droop control enables more accurate sharing of active and reactive powers between inverters. It also facilitates other functionalities, such as hot-swap operation and system impedance [21,22]. The concept of droop control in parallel-connected inverters is derived from the principle of synchronous generators responding to variations in load voltage and frequency [23,24,25]. The basic equations for active and reactive powers, which form the basis of a droop control system, are explained as follows [26]:

$$P={\displaystyle \frac{V_1{V}_2}{X}}sin\delta$$

(1)

$$Q={\displaystyle \frac{V_1^2}{X}}-{\displaystyle \frac{V_1{V}_2}{X}}cos\delta$$

(2)

Considering $sin \delta = \delta \mathrm{and} cos \delta = 1$, Equations (1) and (2) are expressed as

$$\delta ≌{\displaystyle \frac{XP}{V_1{V}_2}}$$

(3)

$$V_1-V_2≌{\displaystyle \frac{XQ}{V_1}}$$

(4)

where V₁, V₂, P, Q, X, and δ are the terminal voltage, load voltage, real power, reactive power, reactance, and power angle, respectively. The above equations are the fundamental equations for P and Q sharing, which originate from the synchronous generator’s principle. Figure 2 depicts the fundamental principle of droop control.

3. Linear Droop Control

Linear droop control enables precise sharing of adjustments in active and reactive powers among parallel-connected inverters. The control method utilizes parameters of frequency, voltage, and power angle. These parameters play a crucial role in creating references for power, frequency, and voltage, thereby facilitating the compensation of these parameters. Linear droop control can be further categorized into modified and conventional droop control methods.

3.1. Conventional Droop Control

The configuration of conventional droop control is depicted in Figure 3, where an increase in voltage at the output of parallel-connected inverters leads to a decrease in frequency. The conventional droop method offers accurate power sharing characteristics, reliability, modularity, and expandability, which have been extensively discussed in the literature. While this method achieves power sharing, it encounters challenges in achieving voltage regulation and exhibits a slow response. In a researchers explored the impact of circulating current on inverters connected in parallel regarding harmonic interaction and resonance. They also examined the system using a low-bandwidth droop control approach, setting predefined values for the frequency, voltage, and harmonic properties [27,28,29].

Table 1. Comparison of conventional droop control techniques combined with different loops.

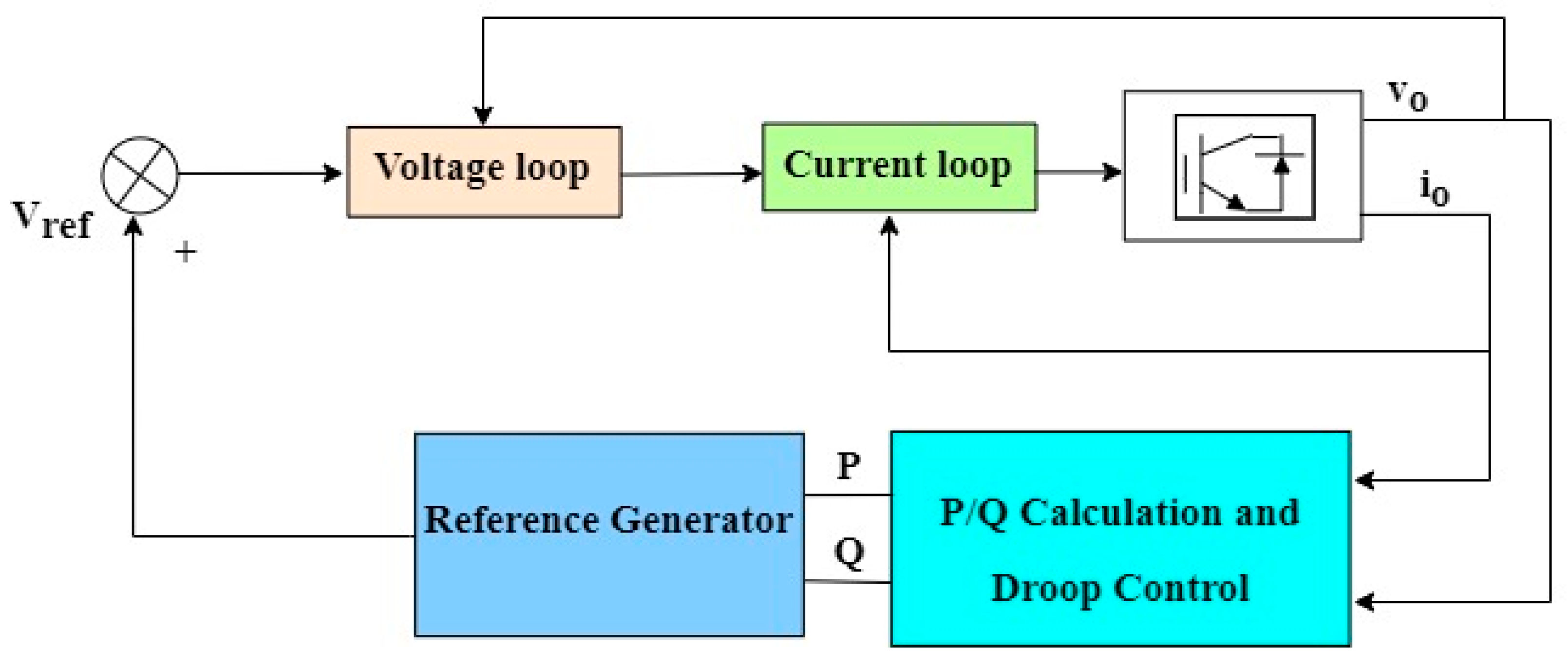
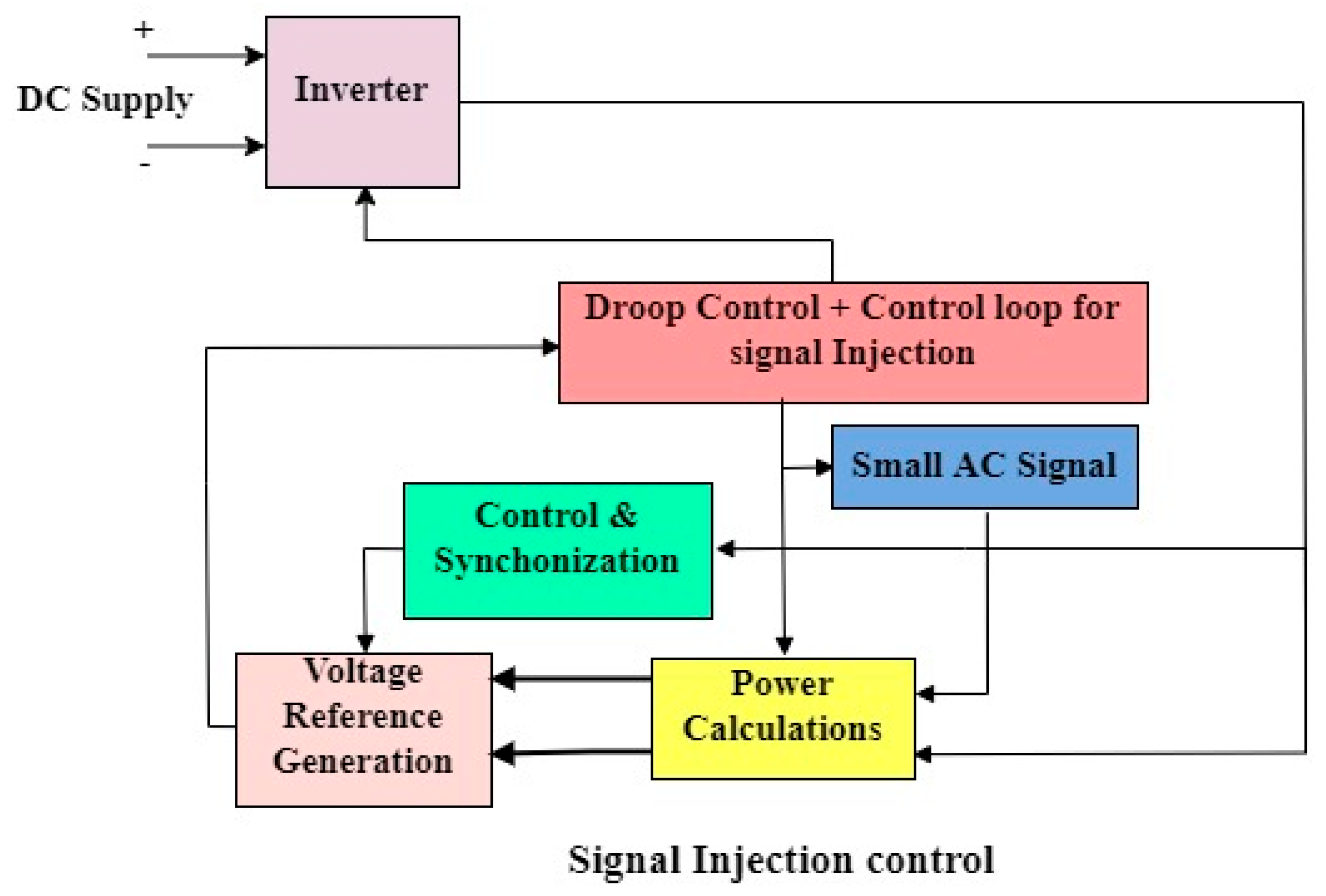
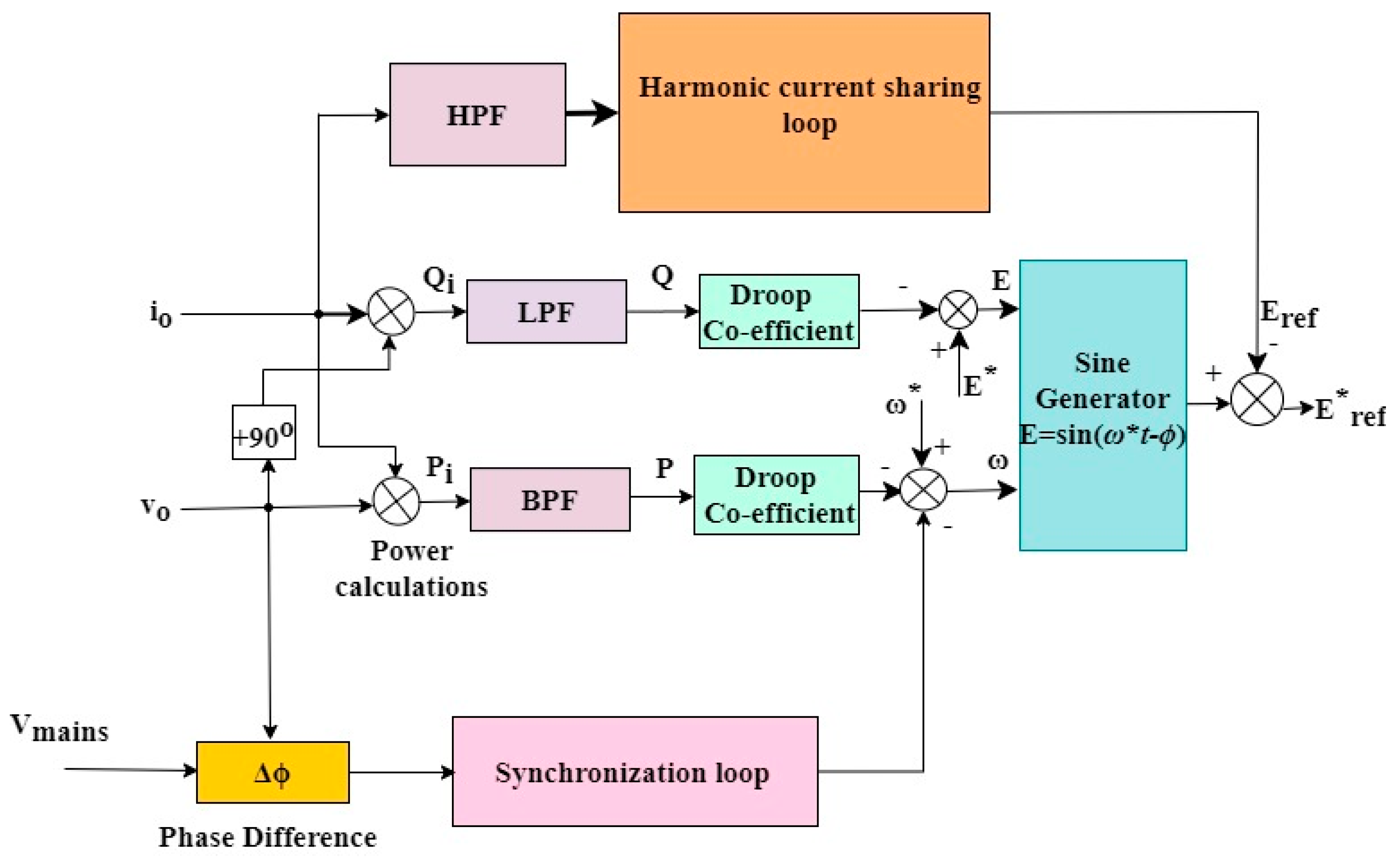
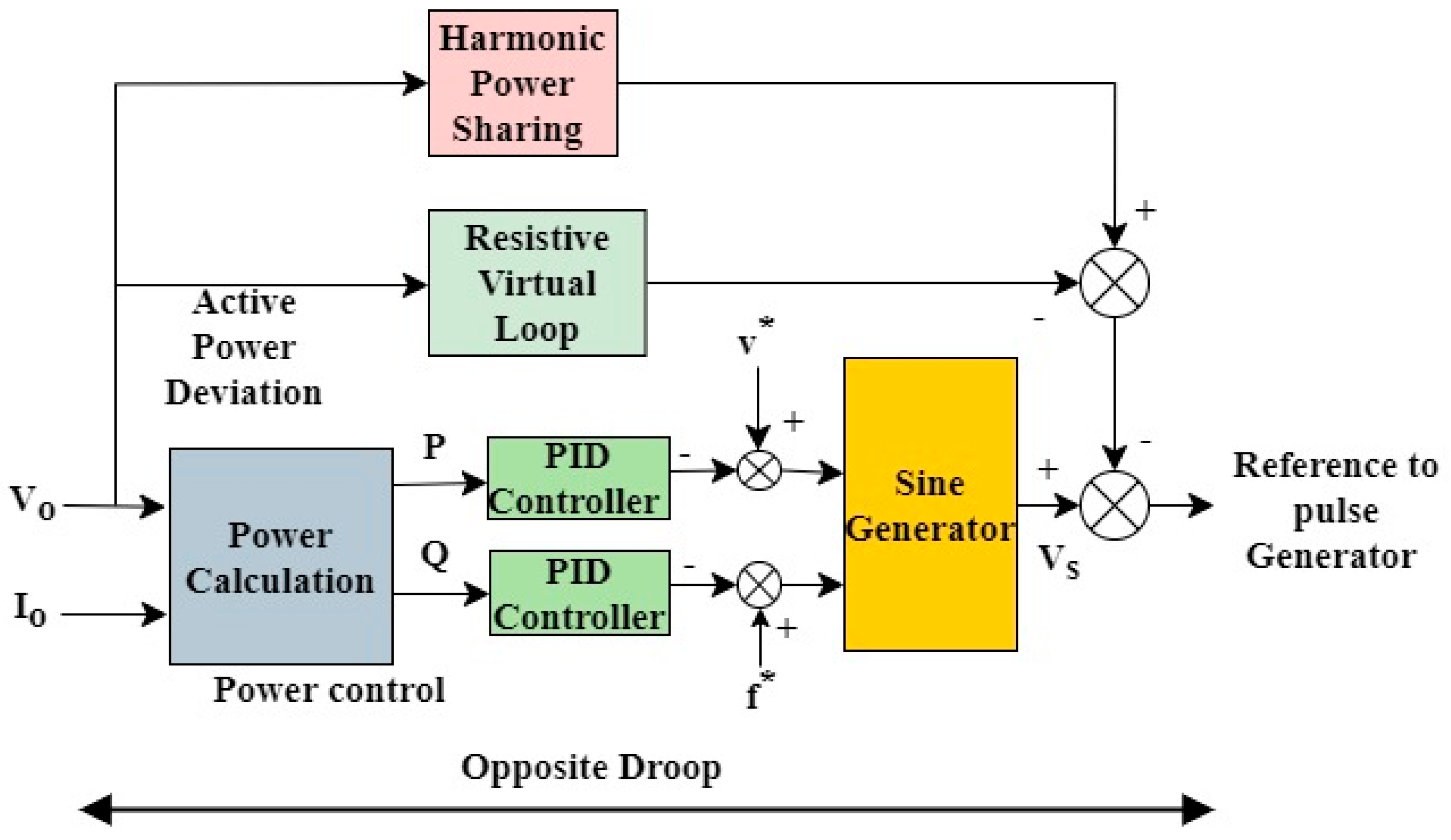
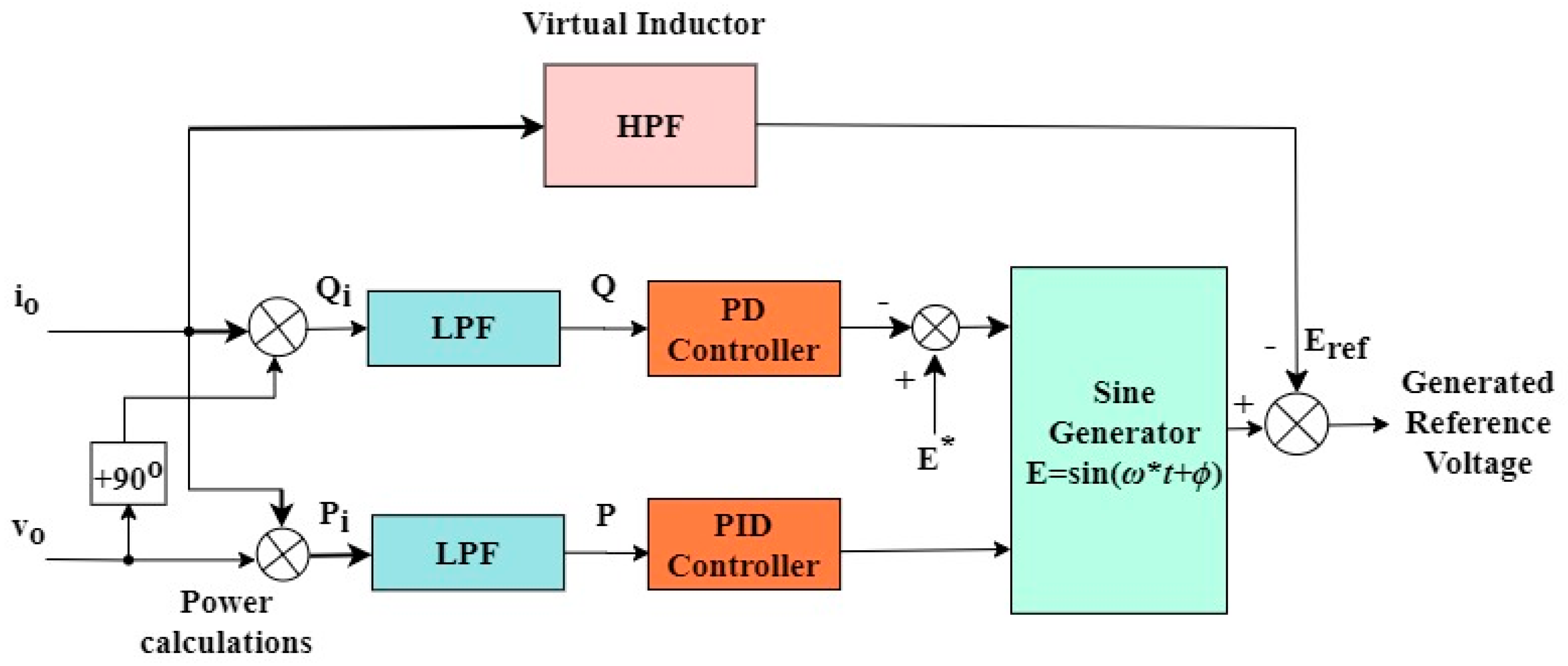
Conventional Droop Control with Additional Loops	Advantages	Limitations	Operational Mode
Conventional droop with addition of virtual impedance loop [30]	Good harmonic current-sharing ability; accuracy in load sharing and voltage regulation	Synchronization error and parameter mismatch; restricted to separate modules only	Grid-connected and islanded
Conventional droop + virtual impedance + separate loops for frequency and amplitude adjustment [31]	Assures system stability and good synchronization characteristics	Power sharing concerns in systems with unevenly distributed line impedances	Grid-connected and islanded
Conventional droop with virtual resistive droop [32]	Ensures active power balancing of system by addition of virtual inductor	Does not address behavior of system under frequency variation condition	Islanded
Conventional droop with effective utilization of harmonic power sharing and virtual impedance [33]	Good power sharing and phase synchronization of system	Trade-off between frequency and amplitude	Islanded

shows conventional droop control techniques combined with different loops, with respect to their advantages, limitations/demerits, and operational modes.

Additionally, Q-V and P-f droop strategies for parallel-connected inverters have been analyzed to attain accurate load sharing in relation to real, active, and reactive powers under linearly varying loads. Subsequently, in [34], the authors demonstrated that the operational control approach proposed in [35] can properly share linear and non-linear loads. However, the control system faces synchronization issues during sudden load changes.

The stability and performance enhancement of parallel-connected inverters in an islanded MG system were explored in [36]. These studies conducted a small-signal analysis, focusing on droop control of voltage and frequency. The authors investigated the determination of optimal gain constants and the selection of filter cut-off frequency to improve system behavior. However, it should be noted that the frequency limitations of the system and the consideration of active and reactive fluxes were not addressed in these studies.

3.2. Modified Droop Control

The modified droop control method introduces changes to droop variables, while retaining the fundamental concept of conventional droop control. When comparing conventional and modified droop methods, notable differences arise in terms of voltage, power, and frequency controls. In [37], a proposal for a static droop boost in low-voltage distributed grids was presented, which follows Equations (5) and (6):

$$E=E^{\mathrm{*}}-nP-n_d{\displaystyle \frac{dP}{dt}}$$

(5)

$$\omega ={\omega }^{\mathrm{*}}-mP-m_d{\displaystyle \frac{dQ}{dt}}$$

(6)

where $m_d,m,n, \mathrm{a}\mathrm{n}\mathrm{d} n_d$ represent the derivative coefficient of real power, proportional coefficient of real power, proportional coefficient of reactive power, and derivative coefficient of reactive power, respectively, while $E^{\mathrm{*}} \mathrm{a}\mathrm{n}\mathrm{d} {\omega }^{\mathrm{*}}$ are the reference voltage and frequency, respectively. In the following subsections, a comprehensive overview of further classes of modified droop control is presented with detailed explanations.

3.2.1. P-V, Q-f, and Q-V Droop Controls

This approach for DG inverters involves the use of finite resistance for controlling parallel-connected inverters. The method, known as reverse droop control, exhibits precise power distribution capabilities, alongside effective voltage regulation characteristics. Typically, all MGs take into account inductive impedance parameters. The origin of the reverse droop control concept can be traced back to the idea of incorporating finite resistance. P-V and Q-f droops were discussed in [38], in which emphasis was placed on controlling the real and reactive powers of parallel-connected inverters. The voltage regulation mechanism, known as P-V control, governs the generation of real power, whereas the frequency droop variation in Q-f control facilitates the production of reactive power [39,40].

In [41], the orthogonal rotational conversion concept utilizing the voltage matrix was introduced, which laid the foundation for a novel control technique known as Q-V droop control. This control technique exhibits novel characteristics related to the reduction in voltage harmonics and suppression of the short-circuit behavior. The exceptional performance of Q-V droop control sets it apart from others regardless of grid impedance. Its operating principle is derived from the tracking of variables through the instantaneous power theory [40]. Additionally, it enables a fast and flexible system operation, striking a balance between voltage regulation and frequency limitations, which is a significant challenge in conventional droop control. The digitalized implementation of this technique enhances its value in improving system performance by reducing the fluctuations of current and voltage in the control section of parallel-connected inverters [42].

A novel and robust control by undertaking deliberate steps will be used to mitigate the inherent slow response issue observed in the conventional method. Therefore, various voltage-power droop controllers utilizing P-V droop control can be integrated into a system with parallel-connected inverters. P-V droop control incorporates pre-established proportional power-sharing techniques. In a novel and robust control by undertaking deliberate steps will use to mitigate the inherent slow response issue observed in the conventional method. Therefore, various voltage-power droop controllers utilizing P-V droop control can be integrated into a system with parallel-connected inverters. P-V droop control incorporates pre-established proportional power-sharing techniques. The combined utilization of both P-V and Q-f techniques enhances power-sharing capabilities, while considering line losses in the system. Furthermore, this combination was tested in a low-voltage MG in the islanded mode of operation and demonstrated good power-sharing behavior and an autonomous controller operation [29,43,44,45,46,47,48,49,50].

3.2.2. Angle Droop Control

The control technique discussed in this section is focused on the stability and power-sharing performances of a system with parallel-connected inverters. The authors concluded that this technique can yield improved results and enhance the transient response of the system. However, the analysis did not consider the system’s performance under variable loads.

In [51], the angle droop control technique was evaluated in a highly resistive network system, considering both web-based communication and communicationless scenarios. The study showcased the technique’s reliability in ensuring effective system operation. To ensure the stability of a system with parallel-connected inverters, high droop gains were introduced, along with additional parameters suggested in [52]. However, this approach resulted in poor damping characteristics due to the high gain quality, adversely affecting system stability.

In [53,54], the authors proposed another control technique, known as gain-scheduling angle droop control, which incorporated the angle droop concept. This technique offered a different approach to system control, allowing for improved performance and stability.

3.2.3. Compensation Droop Control

Compensation droop control addresses the line impedances of a system with parallel-connected inverters by implementing a mechanism for harmonic reduction. This method entails the integration of supplementary control loops, alongside the conventional droop control mechanism, aiming to enhance the overall system performance. The following are several compensation approaches that can be combined with droop control to facilitate compensation droop control.

(a)

Droop control through gain scheduling

By employing gain scheduling, this technique offers superior outcomes compared with those of the master–slave control approach. This modified conventional droop control technique using gain scheduling exhibits significant improvements in voltage regulation. The connections of this technique are illustrated in Figure 4.

Additionally, with the integration of a low-pass filter, this technique efficiently ensures a robust performance in terms of source/load dynamics. However, the effects of gain scheduling during abrupt load changes were not elaborated in [55].

(b)

Droop control through signal injection

The issue raised in [55] pertains to digital implementation that lacks sufficient performance criteria due to the complexity and dynamic consequences caused by line impedance imbalances. Additionally, the behavior of a system with parallel-connected inverters under non-uniform conditions was briefly discussed in [56]. The insertion of control signals aims to share system variables, and a phase-locked loop (PLL) was implemented to ensure efficient measurements and adjustments of droop coefficients. However, the suggested model showed that the use of the PLL resulted in a low transient response. Figure 5 illustrates the compensation droop technique based on signal injection [35].

This technique offers further variations. The following are the different types of droop controls using signal injection.

(c)

Droop control through virtual inductor

During a steady state, stability can be attained using this technique. By incorporating virtual impedance into the traditional approach, the active power balance of a system is ensured through the addition of a virtual inductor, as illustrated in Figure 6. However, it is worth noting that this control technique does not address a system’s behavior under frequency variations [57]. The concerns raised in [57] regarding the performance of a system under variable frequencies, including poor response and transient behavior, were addressed by the authors in [58,59], who introduced an additional loop of virtual impedance in a control system with parallel-connected inverters. This modification of the control circuitry aimed to improve transient response and system behavior when frequency changes occur. However, it is important to note that the authors did not consider the impact of impedance output parameters on current distribution. Furthermore, the proposed method did not yield a satisfactory transient response, and it also did not specifically address the behavior of a system under frequency variations.

(d)

Droop control with synchronization loop

In [60], an alternative technique was proposed, as depicted in Figure 7, which was specifically designed for the non-linear operational mode of a system with parallel-connected inverters. This technique addresses harmonic currents and calculates the virtual impedance at the output to achieve low harmonic distortion. It incorporates a combination of a low-pass filter, band-pass filter, and high-pass filter. Furthermore, this approach guarantees efficient power sharing and phase synchronization in the system, eliminating the need for a DC component. Active power balancing is achieved through the utilization of the transient droop function, while reliable frequency regulation is attained during a steady state in DG inverter-based systems, as stated in [60]. Additionally, Ref. [61] highlighted that the crest factor remained below 3, resulting in a precise transient response of the system.

(e)

Droop control with virtual impedance loop

In [62,63], a novel technique was proposed to address the sensitivity issue in a system with parallel-connected inverters, as illustrated in Figure 8. Sensitivity is a critical concern, and in [64], the authors conducted an analysis of power sharing in a parallel-connected-inverter system, focusing specifically on output impedance. The control system takes into account system sensitivity by utilizing output impedance, as shown in Figure 8. Furthermore, Ref. [65] introduced an extra control loop that followed linear feedback principles, aiming to emulate the characteristics of feedback gain and project virtual output impedance. By mitigating the effects of line impedance, accurate power sharing can be achieved.

The problem discussed in [65] was addressed in [66] by employing a decentralized control approach that incorporated resistive output impedance. This novel technique is specifically implemented in the context of digital controller configurations. In [67,68], the authors investigated the components of a microgrid with a communication-based secondary control mechanism, particularly focusing on systems incorporating renewable energy sources. They explored the adjustment of the voltage-based droop function and achieved power-sharing accuracy through power compensation using virtual impedance and droop. However, it should be noted that this control technique demonstrates droop coefficient errors. In [69], the authors adopted an algorithm-based approach with low-bandwidth communication to examine power sharing, while accounting for constant line resistance. Refs. [70,71] proposed an algorithm-based control technique that incorporated proportional power sharing and showcased the controller’s effectiveness in managing real and reactive powers. However, it is important to note that this control technique does not address dynamic load variations in a system.

In [72], the proposed control technique assumed negligible circulating apparent power. This approach utilized synchronized frequency and parameters of zero steady-state error of inverters to analyze power-sharing performance and stability. Nevertheless, the assumption made by the authors may seem impractical.

Further investigations into this control scheme revealed that precise power sharing can be accomplished by meticulously selecting control parameters. Additionally, this control technique exhibits high efficiency and utilizes output voltage averaging as the reference value. However, it is crucial to acknowledge that this technique does not consider the phase angle, as stated in [73].

(f)

Droop control with harmonic power sharing and resistive virtual loop

The implementation of a decentralized controller, as illustrated in Figure 9, has demonstrated notable effectiveness in managing harmonic power sharing and attaining precise voltage regulation in parallel-connected inverter control. Ref. [74] introduced the integration of virtual resistance into control schemes, alongside the configurations of P-V and Q-f droop controls, to further enhance a system’s capacity for accurate load sharing. In order to improve system characteristics, voltage regulation in the droop frequency of parallel-connected inverters is arranged in an opposing manner. However, it is worth noting that this mechanism exhibits a slow response due to the auxiliary control.

This innovative technique has demonstrated improved results in terms of harmonic current sharing. However, it is important to note that it suffers from synchronization errors and parameter mismatches, which restrict its application to separate modules only. In the control methodology presented in [75], the authors integrated a virtual impedance loop into a control system with parallel-connected inverters. However, subsequent analyses have revealed that the frequency restoration algorithm utilized in this technique is influenced. Parameters crucial for a control system with parallel-connected inverters, such as the damping ratio, real power, and reactive power, can be achieved by compensating within an acceptable bandwidth range, as proposed by the authors. Nevertheless, it is worth noting that the suggested control mechanisms do not extensively address the dynamic load variations encountered in a control system with parallel-connected inverters.

(g)

Droop control with additional adaptive virtual impedance loop

In order to tackle dynamic load variations in a control system with parallel-connected inverters, supplementary loops and adaptive control techniques have been employed. Ref. [76] examined the performance of a system under varying loads by utilizing adaptive mechanisms tailored to droop control, which showcased system synchronization and stability. However, the implementation of this control technique results in system complexity and voltage/frequency errors. In order to mitigate voltage and frequency issues caused by impedance mismatch and synchronization errors, the authors in [77] introduced an additional loop with a gain constant to improve reactive power sharing and enhance system stability. The challenge of achieving reactive power sharing in the localized setpoint of a system with parallel-connected inverters was addressed in [51] by implementing an opposite droop and constant power band. This control scheme, referred to as “twofold” control, was thoroughly analyzed in the context of dispatchable and non-dispatchable loads. The “twofold” control technique demonstrates enhanced stability, transient response, and precise power-sharing characteristics.

Ensuring the reliability of MGs is of utmost importance. Ref. [78] presented a reliable control technique with accurate power sharing by utilizing a communication link for load voltage. The P-Q control technique offers high reliability and synchronization, regardless of system stability. This algorithm-based control technique yields remarkable outcomes in terms of frequency and amplitude restoration, as suggested.

3.2.4. Virtual Flux Droop Control

The control of parallel-connected inverters can be simplified and made more efficient by utilizing a combination of active power control and reactive power control, along with the effective utilization of phase angle proportional to the flux. This control approach proves to be advantageous, particularly during load changes. By exempting the use of additional loops, the system achieves simplicity without compromising its efficiency. Furthermore, this technique enables direct flux control by estimating flux and minimizing frequency deviation, as described in [44]. An extension of this control technique was explored in [79], where the incorporation of secure communication was investigated to enhance the overall performance of a system.

3.2.5. Voltage–Current Droop

The authors in [80] presented a control technique that leveraged the droop signal and feed-forward injection to tackle power- and current-sharing challenges. This technique not only enhances the dynamic response and stability of a system but is also specifically well-suited for small-sized inverters and current applications.

In [45], a stability analysis was conducted using the V-I droop method and a multi-input output model for a system comprising two parallel-connected inverters. This model was based on the dq reference frame and enabled accurate sharing of active and reactive powers between the inverters. The results obtained in [4] were compared with those of the conventional droop control technique, which highlighted the improved performance achieved by the proposed approach. Furthermore, through linear system analysis, the underlying cause of oscillation between the inverters was identified for both grid-connected and autonomous modes.

4. Non-Linear Droop Control

A control technique for parallel-connected inverters demonstrates non-linear droop characteristics when employing metaheuristic optimization algorithms, such as particle swarm optimization, as discussed in [81]. In [82], a system was comprehensively examined under peak-load and low-load conditions to showcase the efficacy of system parameters, including power sharing and flexibility. In the proposed technique, droop resistance is incrementally raised with increasing load. The effectiveness of the control technique proposed in [83] was validated through simulation outcomes and experimental observations.

4.1. Non-Linear Load Sharing with Current Harmonics

Non-linear load sharing is a vital issue in islanded microgrids. In [74], a bank of band-pass filters was introduced to share non-linear loads. The aim was to achieve proper load sharing by adjusting the output voltage’s bandwidth. The bank of band-pass filters extracted the harmonic components from the current’s signal and then the current’s signals were re-injected into the grid. In [83], the concept of resistive output impedance was proposed for both linear and non-linear load sharing for applications of uninterruptible power supply. Harmonic current contents are not easy to share, and hence in [84], the authors introduced a novel concept using closed-loop impedance that certified that the resistive property and current harmonics were shared properly. According to [5], the most suitable nature of an impedance is the inductive output impedance. For non-linear loads, inductive output tends to reduce total harmonic distortion. High-pass filters were utilized in [85], which when linked to the virtual complex output impedance showed inductive behavior of an inductor at the nominal frequency and resistive behavior at harmonic frequencies.

4.2. Non-Linear Load Sharing with Circulating Current

In [86], an inductive power transfer system was discussed to eliminate the fundamental circulating current produced due to parameter mismatch and inner resistances of parallel-connected inverters. A series-parallel resonant tank was used, which very easily eliminated harmonic circulating current, and the current decomposition method was employed to ensure control system accuracy. The fundamental circulating current in parallel-connected inverters was eliminated by decomposing active and reactive currents. The current decomposing approach worked without the phase-locked loop or the phasor control method. High-frequency AC signals were transformed into DC signals for the phasor controller. In this manner, the communicational burden and complexity of the control algorithm were avoided. The current decomposition method was also found to reduce the manufacturing cost. In [87], the control of parallel-connected inverters in terms of unbalanced loads and synchronization was discussed, with a new control technique proposed to address power sharing and circulating current issues, but the control scheme was complex to implement.

5. Active and Reactive Power-Sharing Control with Different Considerations

The power-sharing capability of parallel-connected inverters, each having distinct ratings and R/X ratios, can be enhanced using a control technique founded on the principle of power decoupling. This technique integrates the utilization of P-V and Q-f control techniques with virtual resistance loops, leading to enhanced system stability. However, when unevenly distributed line impedances are present, the technique encounters challenges in achieving accurate power sharing [88]. In [66], the authors proposed a virtual impedance tuning control technique, which enabled precise power sharing. It should be noted that this technique is specifically applicable to distribution systems with the same rating. The accuracy of power sharing under different conditions is discussed in the following subsections.

Table 2. Active and reactive power-sharing control techniques based on fundamental droop characteristics.

Method	P and Q Control Characteristics	Advantages	Disadvantages
Optimization in droop [89,90,91,92,93,94,95,96,97,98]	Improvement in primary level control; addition of inductive feeder impedance	Highly reliable and stable communication-less strategy; suitable to mitigate frequency and voltage deviation	Complexity in design; does not address complex loads; cannot be applied to MG system with multiple DG inverters
Optimization in secondary-level, graph-theory algorithms [99,100,101], multi-agent-based control [102]	Improvement in hierarchal control levels	Simplicity and stability of control technique; low-bandwidth communication	Slow response of controller; deviations with non-linear loads
Decoupling-based control [103,104,105] and modified P-V and Q-f [106,107]	P-V and Q-f droop controls with resistive domination in impedance	Improved stability with good transient response	Cannot be applied to microgrids with complex integrated structure
Network-based control [108,109,110]	Power sharing without pre-knowledge of feeder impedances	Robust performance for P sharing accuracy	Parameter estimation is not easy to obtain; design and implementation complexity
Common linear and non-linear cost-based droop controls [111,112,113,114,115]	Proportional active power sharing	Active power-sharing capability is good; voltage and frequency deviations can be efficiently removed	Communication delay; not suitable for complex feeder impedances

shows the active and reactive power-sharing control techniques based on droop characteristics.

5.1. Active and Reactive Power Control for Mismatched Feeder Impedances

Increasing power losses have a direct impact on system instability when a large external inductor is installed for accurate power sharing, leading to an overall increase in system costs [116]. By assuming negligible transmission line impedance, the authors in [117] employed separate modules for output current feedback and harmonic injection to develop a new control scheme with varying virtual impedances. While this technique improves system stability, it also results in increased circulating current and exhibits unfavorable characteristics under load variations. Building upon the control techniques presented in [118], a further investigation was conducted in [73] to enhance system stability by utilizing adaptive impedance. The study demonstrated the potential for reduced circulating current and improved accuracy in power sharing.

In [33], an online parameter algorithm incorporating periodic modifications was introduced for controlling parallel-connected inverters. In this scheme, droop coefficients are adaptively readjusted to accommodate variations in controller dynamics during a steady-state operation. This control technique incorporates a feed-forward auxiliary control mechanism for controller analysis, and the addition of a decoupling feed-forward gain loop enables autonomous dynamics of a control system with parallel-connected inverters [119]. To enhance damping frequency and transient stability, a novel approach based on the consensus droop control theory was proposed in [33], utilizing non-zero inertia parameters.

By combining droop control with phase shift and virtual impedance loop parameters, a system can achieve both stability and accurate reactive power control. While this control technique provides a broad operating range, it also introduces challenges when employed in multiple inverters, such as increased system complexity, limited flexibility, and delayed response, as highlighted in [75]. Under the condition of small inductive impedance [120], conventional droop control combined with a proportional-resonant controller demonstrates good performance in terms of stability and system dynamics. In [121], an approach similar to equivalent feeder impedances was employed to enhance power sharing. The authors performed individual calculations of the voltage drop across each inverter and employed an averaging technique as part of the control strategy. This approach aimed to achieve precise load sharing, even in scenarios involving load variations.

Table 3. Overview of active and reactive power-sharing techniques in presence of feeder impedance mismatch.

Method	P and Q Sharing Issues	Merits	Demerits
Droop-based adaptive virtual impedance [85,122,123,124,125,126,127,128,129,130]	Modified virtual impedance	Enhanced performance to mitigate Q deviations; addresses complex loading conditions and abrupt load changes	Complexity in design and implementation
Optimization in secondary control [101,131,132,133,134,135]	Mismatch in feeder impedances connected to same system	Frequency and voltage deviations are easily removed; better performance for complex MGs	Accurate power sharing is difficult to achieve under non-linear load condition; slow response of controller
Programmable algorithms [99,136,137,138,139]	Congestion	Easily implemented in MG system with parallel-connected inverters; good performance for Q sharing with stability	Difficult to design control strategy; delayed execution of programmable algorithms
Virtual-impedance-based secondary control [90,140,141]	Linear/non-linear or unbalanced loads	Suitable for unstable loads; ensures stability of system; suitable to mitigate voltage errors	Reactive power-sharing performance is poor; not suitable for complex MG system
Multi-agent system [102,142]	Environmental changes affect performance	Stability and expandability is ensured; information exchange management system is possible	Pre-adjusted values of algorithms cause problems; complicated design

provides an overview of active and reactive power-sharing techniques in the presence of feeder impedance mismatch.

This technique also minimizes circulating current in parallel-connected inverters. It is important to consider the internal and external inductances of the system, as well as the different capacities of DG units and equivalent feeder impedances. This control technique ensures system stability and flexibility. However, voltage deviation can be an issue in the presence of a local load [74,116,143,144,145].

5.2. Active and Reactive Power Control with Unbalanced Loads

For optimizing the virtual impedance loop in a network-based MG with symmetric distributed generation, a metaheuristic algorithm control was suggested in [82] to address dynamic non-linear loads. The mitigation of circulating current in parallel-connected inverters plays a vital role in improving system efficiency and ensuring control system reliability. In [146], the authors employed droop control to suppress circulating current and achieved effective voltage and current regulation. An alternative control technique was introduced in [147], which utilized aggregated parameter values and small-signal analysis specifically for non-linear loads. This innovative technique successfully reduces circulating current and enhances load-sharing accuracy by incorporating the feedback of the circulating current.

The challenges associated with circulating current and power distribution in parallel-connected inverters were thoroughly investigated in [4,10,148,149,150]. These studies proposed modifications to the droop control approach to effectively address output voltage deviations that may occur when connecting local loads. The aim was to optimize the control mechanism and ensure proper management of power distribution in systems with parallel-connected inverters, while minimizing voltage variations. In [151], a communication-based control utilizing a cyber network and the averaging technique was proposed. The behavior of the system under dynamic loads and voltage regulation was examined. However, this technique exhibits a slow dynamic response and encounters challenges in power sharing and graphical connectivity. A dynamic consensus protocol, employed for distributed decision-making in control mechanisms, has been used to estimate average voltage.

Table 4. Comparison of control techniques for active and reactive power sharing with unbalanced loads.

Method	Explanation	Advantages	Limitations
Gain scheduling control [152,153,154,155,156]	Data adjusted by gain scheduler	Good power-sharing accuracy control; provides stability of system	Gain coefficient selection is complex
Predictive control [157,158,159,160]	Predicts unknown parameters	Good power-sharing capability; shows robustness and stability of system	Design complexity is drawback of control scheme
Cooperative distributed control [161,162]	Extra channel is provided for P and Q	Good power-sharing accuracy with stable operation; provides excellent plug-and-play facility	Slow dynamic response; complex structure

provides an overview of control techniques for active and reactive power sharing with respect to non-linear or unbalanced loads.

6. Conclusions

In conclusion, this paper provides a comprehensive review of control techniques applicable in DG-inverter-based MG control systems, as the world is moving towards a future with sustainable energy. The robustness and autonomy of the control techniques primarily rely on the reliability of droop-based control mechanisms. Currently, decentralized or communicationless control techniques utilizing modified droop approaches are commonly employed in modern DG-inverter-based MG systems. The combination of droop control with different loops demonstrates superior performance and addresses power-sharing challenges in systems with parallel-connected inverters. Furthermore, droop-based control techniques ensure system expandability and modularity and minimize current and voltage. The limitations and applications of droop-based control techniques in MG system control were also discussed. A lot of research works for the control of parallel-connected inverters have been carried out in recent years based on communication and communicationless (droop) schemes.

The following are the research directions for future works based on the observations by this paper’s authors:

• A hybrid control mechanism, which enables a control system operating in islanded mode to shift to the grid-connected mode, could be developed. However, it needs to be explored under the non-linear dynamic load condition. The capability of a control system to perform accurate power sharing under such conditions needs to be inspected.
• Optimized tracking of power angle errors in a system with parallel-connected inverters, as well as improvement techniques, should be taken into account in power droop-based control techniques.
• A controller’s performance in terms of stability, harmonic distortion, and current transients under a non-linear load condition through the utilization of a hybrid control scheme of parallel-connected inverters in the grid-connected mode needs more attention from researchers.
• Power-sharing accuracy and the sensitivity of a system integrating parallel inverters under a non-linear load condition, and the response time issue by using algorithm-based techniques, should be explored.
• An efficient and simple control technique for circulating current suspension to improve system stability and flexibility can be explored.
• The performance of control strategies for different RESs and DG failures should be taken into account.
• A flawless, lossless, low-cost, efficient, wireless-network-based, and autonomous control technique for the application of integrated RESs with proper power sharing among inverters should be developed in the future.