Abstract
With the increasing connection between integrated natural gas, thermal energy, and electric power systems, the integrated energy system (IES) needs to coordinate the internal unit scheduling and meet the different load demands of customers. However, when the energy subjects involved in scheduling are engaged in conflicts of interest, aspects such as hierarchical status relationships and cooperative and competitive relationships must be considered. Therefore, this paper studies the problem of achieving optimal energy scheduling for multiple subjects of source, storage, and load under the same distribution network while ensuring that their benefits are not impaired. First, this paper establishes a dual master-slave game model with a shared energy storage system (SESS), IES, and the alliance of prosumers (APs) as the main subjects. Second, based on the Nash negotiation theory and considering the sharing of electric energy among prosumers, the APs model is equated into two sub-problems of coalition cost minimization and cooperative benefit distribution to ensure that the coalition members distribute the cooperative benefits equitably. Further, the Stackelberg-Stackelberg-Nash three-layer game model is established, and the dichotomous distributed optimization algorithm combined with the alternating direction multiplier method (ADMM) is used to solve this three-layer game model. Finally, in the simulation results of the arithmetic example, the natural gas consumption is reduced by 9.32%, the economic efficiency of IES is improved by 3.95%, and the comprehensive energy purchase cost of APs is reduced by 12.16%, the proposed model verifies the sustainability co-optimization and mutual benefits of source, storage and load multi-interested subjects.
1. Introduction
Traditional energy systems are planned and operated independently, with low energy efficiency and serious resource waste [1]. With the increasing depletion of traditional fossil energy sources, the development of multiple energy complementary technologies to improve energy efficiency has become urgent [2]. In the context of carbon neutrality goals, integrated energy systems are one of the typical applications of multi-energy coupling to improve energy efficiency [3]. The grid integration of distributed renewable energy sources, including photovoltaic and wind power, has grown significantly in recent years [4]. However, the inherent variability and uncertainty of renewable energy sources bring new challenges to the safe and stable operation of power systems [5]. Therefore, there is an urgent need to find a feasible method to effectively integrate regional flexible resources, match the renewable energy output, and support the dynamic and balanced operation of the new power system.
Integrated energy systems optimize the scheduling of regional flexible resources by complementing multiple energy sources to effectively respond to the production of renewable energy sources, while their application has become an inevitable trend. With the development of technologies such as Combined Heat and Power (CHP) and Concentrated Solar Thermal Power (CSP), the use of CHP technology to provide energy is a sustainable and economical strategy to reduce fuel consumption [6]. Many studies have decoupled the electro-thermal characteristics of CHP by coupling the system with thermal energy storage (TES), electric boiler (EB), or both to improve the flexibility of CHP [7]. Li [8] proposes a hybrid CSP-CHP energy flow framework to provide additional operational flexibility for renewable energy sources in an integrated energy system (IES). Generating electricity with hybrid CHP-CSP can reduce wind abandonment compared to other renewable energy generation [9]. The configuration plays a crucially important role in the improvement of energy efficiency, flexibility and sustainability of the IES [10]. Therefore, improving the primary energy utilization and renewable energy flexibility in IES and further reducing the primary consumption of energy in the system is the focus of this paper.
Operation optimization is an important technical support for IES practice, and for the IES energy complementary optimal scheduling problem, Liu [11] uses an enhanced Wasserstein deep convolution generative adversarial network with gradient penalty to simulate extreme scenarios and analyze the impact of source-load correlation on the IES economy with respect to source-load uncertainty. Peng [12] proposed an exergoeconomic optimization scheduling method for the IES based on a novel performance indicator, namely, the specific exergy cost, in response to the challenge that traditional scheduling methods can hardly coexist by considering only the operational efficiency or economic performance. When faced with a large number of electric vehicle charge stations (EVCS) joining the construction and use of IESs, there are computationally complex problems of inter-feeding with the grid, system stability, revenue and environmental pollution between EVCS and IESs [13]. To solve this, Fang [14] using improved NSGA-III algorithm combined with fuzzy evaluation, Liao [15] proposes a future value competition strategy for wind and photovoltaic allocation based on goal optimization, Liu [16] proposes a Multi-Objective Sand Cat Swarm Optimization Algorithm based on a mutation-dominated selection strategy, Yin [17] proposes a Many-objective Stochastic Competition Optimization algorithm, Wang [18] introduced an improved moth-flame optimization algorithm.
However, with the continuous and in-depth study of IES, the elements of the system’s internal subject optimization and participation in external energy interactions are becoming more and more complex, which puts forward new requirements for the development of IES in the energy market environment. Game theory is a key technology that can help achieve regional resource integration and dispatch optimization and support the operation of new power systems [19]. Li [20] considers a Stackelberg game energy optimization scheduling framework that balances the interests of operators and users under integrated energy demand response and renewable energy generation uncertainty conditions. Wang [21] developed a Stackelberg game model based on energy pre-transaction behavior between energy service providers and users. Wang [22] established a Stackelberg game model based on the one-master-multiple-slave to maximize the profit of integrated energy operators and minimize the cost of distributed integrated energy. Zhang [23] developed a two-layer Stackelberg game model for integrated energy operators with IESs and integrated energy operators with IESs. Li [24] established an urban community energy optimization model for city managers and community operators based on master-slave game theory. Tan [25] developed a one-master-many-slave Stackelberg game model with a regional energy operator as the leader, building producers and distributors and electric vehicle aggregators as the followers. However, since the energy operator or the master network has a monopoly on IES, most of the previous studies that take advantage of this feature use the leader-follower framework to construct the model, but this also puts the followers in a disadvantageous position, which in turn harms their interests.
To motivate followers to participate in the above mutual feedforward process with increased flexibility, it is necessary to coordinate and avoid conflicts of interest, which can be compensated by game theory. Tan [26] developed a cooperative game model for IES-HGESS and designed a revenue-sharing strategy to stabilize long-term cooperation. Wang [27] established a Nash game-based energy trading model by studying the benefits of cooperation between IES and electric vehicle charge stations. Shi [28] proposed an electricity-hydrogen-heat IES cluster energy scheduling mechanism based on the consideration of peer-to-peer (P2P) electricity and heat transactions between production and sales users. Yang [29] introduced Stackelberg theory and cooperative game theory to establish a two-level game optimal scheduling model for supply and demand equilibrium, respectively. Wang [30] established an IES cooperative game model based on cooperative game theory to minimize carbon emissions and cost. Although the above studies have fully explored the flexible potential of IES in managing regional grids, there are still fewer distributed energy demand response (DR) strategy studies. The installation of renewable energy in the local grid transforms from a traditional electricity consumer to a producer and seller (prosumer, producer and consumer), which makes it challenging to coordinate the producer and seller with the operator while reducing the impact on the local grid [31]. Kotowicz [32] proposes the concept of integrated residential energy systems with rooftop PV as a prosumer, and they can change, to some extent, the consumption patterns of the residential users themselves. Jiang [33] proposes a cooperative model between PV producers and sellers and community energy managers based on Nash bargaining. Kuehnbach [34] establishes a framework for considering households as producers and sellers in local energy markets. In addition to renewable energy sources, producers and sellers, represented by distributed battery storage systems, are a key part of IES flexibility [35]. Zhang [36] investigated a shared energy storage system (SESS) through P2P with a multi-user trading mechanism and modeled a multi-player cooperative game to ensure the distribution of reasonable benefits among the participating parties. Ding [37] established a cooperative game model to collect electricity-heat-hydrogen multi-energy transactions by taking the hydrogen energy generated at the load side as the transaction object. Therefore, it is especially critical to establish an appropriate Stackelberg game model to improve the flexibility of IES and prosumers.
Li [38] proposes a one-master-multiple-slave multi-intelligentsia game operation strategy for energy retailers, suppliers, and users considering demand response and incorporating a non-cooperative game among energy suppliers. Li [39] developed a non-cooperative game model between coupled electricity-heat producers and sellers, taking into account the impact of renewable energy uncertainty on the total cost and verified the effectiveness of the model optimization approach in reducing the consumption cost while increasing the renewable energy penetration. Chen [40] proposes a pre-day cooperative game model for SESS in regional IES and converts it into a two-step optimization problem with a profit-maximizing scheduling strategy for cooperative alliances and an optimal pricing strategy for SESS. Since each member in the alliance of prosumers (APs) belongs to different stakeholders and rationally pursues the minimization of their respective energy purchase costs, there is a need to ensure the fairness of transactions and promote the balance between electricity supply and demand. Therefore, power sharing among APs can be regarded as a cooperative game problem. Chen [41] investigated the cooperative surplus allocation mechanism based on the asymmetric Nash bargaining theory and established a cooperative model for P2P energy trading based on Nash bargaining, which can effectively balance the individual and overall costs of members after cooperation. However, the above studies either only consider the competitive relationship between IESs and APs or only consider the potential for APs to cooperate without seeking cooperation in the context of competition and are unable to further explore the impact of cooperation on their benefits when the producers and sellers are in the situation of being monopolized by IESs. In response to the complex problem of coordination and optimization among subjects of interest., Liu [42] constructed a novel two-layer energy dispatching and collaborative optimization model for a regional integrated energy system considering stakeholders game and flexible load management based on the master-slave game. Li [43] proposes the three-layer Nash-Stackelberg-Nash mixed game model for the IES operator and energy prosumer. Therefore, in addition to constructing SESS-IES and IES-APs as two Stackelberg games, this paper also embeds the Nash game between different producers and sellers, thus forming a Stackelberg-Stackelberg-Nash three-layer game in Table 1, a comparison of key technologies with previous literature is given.

Table 1.
Survey of previous studies.
The main innovations and contributions of this paper are mainly in the following three aspects.
- An integrated SESS-IES-Prosumers energy dispatch model is developed. The model takes into account WT, PV generation uncertainty, and CHP-CSP cooperation and describes the actual operation mechanisms of SESS, IES, and different prosumer energy scheduling. In addition, the potential for utilizing waste heat recovery to improve natural gas utilization is presented.
- In response to the fact that the above SESS-IES-Prosumers model needs to simultaneously consider the self-interests of each independent subject, convey energy price information, and reach a feasible solution for energy trading, a three-layer Stackelberg-Stackelberg-Nash game framework with embedded power sharing among multiple prosumers is proposed for Nash bargaining.
- The three-layer game framework proposed in this paper leads to the following conclusions: the study case can reduce the natural gas loss by 9.32% and the total energy purchase cost of APs by 12.16% under the premise of guaranteeing the interests of each subject and ultimately achieve the source, storage, load multi-interested subjects sustainability co-optimization and mutual benefit and benefit.
The rest of the paper is organized as follows: Section 2 establishes a three-layer master-slave game model of SESS-IES-APs based on the Stackelberg game and establishes a method for distributing the revenues after the cooperation of different prosumers in the lower-layer APs; Section 3 describes the solution method based on this three-layer game model; Section 4 gives the results of the arithmetic example simulation and the analysis; and Section 5 sums up the whole paper and gives an outlook on the next direction of the research.
2. Description of the SESS-IES-APs Three-Layer Game Framework
In analyzing the energy interactions between different energy subjects with different hierarchical statuses, the impact of APs constituted by load-side demand response and energy-sharing cooperation on the energy optimization and dispatch strategies of each subject needs to be further explored. Therefore, the Stackelberg game is introduced to establish a master-slave game model that includes an independent individual SESS, an IES that needs to satisfy different load demands in the region, and prosumers at the lowest level. The transaction framework and hierarchical relationship among SESS, IES, and APs constructed in this paper are shown in Figure 1.
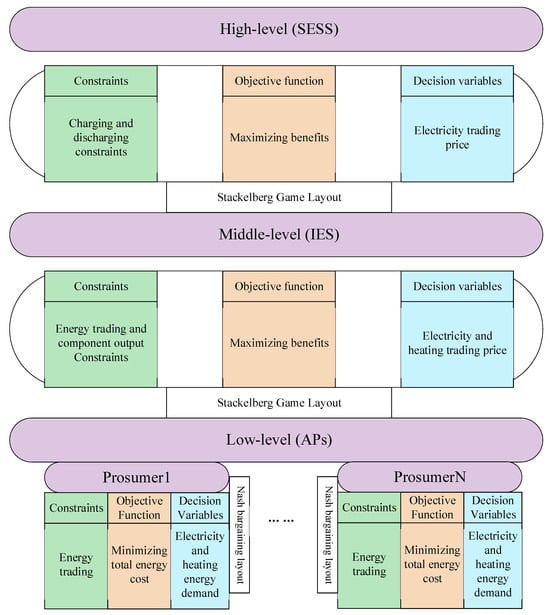
Figure 1.
The transaction framework and hierarchical relationship.
2.1. High-Level Shared Energy Storage System Framework
2.1.1. SESS Optimization Model
From the perspective of the trading market, SESS acts as an intermediary between the grid and IESs and can trade energy with the IES side. Therefore, it is particularly important to formulate the electric energy interaction strategy between SESS and the grid and IES to ensure the development of long-term synergistic scheduling among the grid, SESS, and IES. In summary, in this paper, we set a day divided into periods whose own capacity can be expressed by Equation (1) and constrained by Equation (2).
where: , , denotes the capacity, lower and upper limits of SESS at the time, , , , denotes the charging/discharging power and the upper limits, , denotes the lower and upper limits of the efficiency, , denotes the charging and discharging identification bits.
In addition, the storage state of the SESS is affected by the purchased and sold power of the IES, and its interaction with the distribution grid and the IES can be expressed by Equation (3) and constrained by Equation (4).
where: , indicates the power purchased and sold with the distribution grid, , indicates the power purchased and sold with IES, , indicates the charging and discharging power, , indicates the upper limit of power purchased and sold to the grid, , denote the identification position of power purchased and sold to the grid.
2.1.2. SESS Objective Function
The SESS, as the leader at the top, can issue prices for the purchase and sale of electricity to lower-level IESs. However, from a practical point of view, if the price is too high, the relationship will break down. Therefore, it is especially critical to set appropriate power purchase and sale prices for IESs to achieve long-term synergistic development benefits. SESS operators aim to maximize their benefits, and their objective function can be expressed by Equation (5) and constrained by Equation (9).
where: is the integrated benefit of the SESS during the day, , denotes the gain of trading with the grid, IES at the time of , indicates the cost of charging and discharging operations and maintenance, indicates the cost factor per charge/discharge, , indicates the purchase and sale price of electricity issued by the grid, , indicates the purchase and sale price of electricity set and issued to IES, , , , denotes the lower and upper limits of the power purchase and sale price to IES, in addition, to avoid SESS deliberately increasing the power sale price to IES or suppressing the power purchase price to IES due to profit-seeking, it is necessary to increase the constraints on the average value of the power purchase and sale price of SESS to IES , .
2.2. Middle-Level Integrated Energy System Framework
Since the load-side energy demand is becoming more and more complex and variable, a more integrated and flexible energy-side scheduling strategy is needed to meet the load-side integrated energy demand. In summary, this paper establishes an IES that includes wind turbine (WT), photovoltaic (PV), electrical energy storage (ESS), concentrated solar power (CSP), thermal energy storage (TES), gas turbine (CHP), gas boiler (GB), and Figure 2 shows the relationship of energy flow between the electrical, thermal, and gas networks and the individual devices.
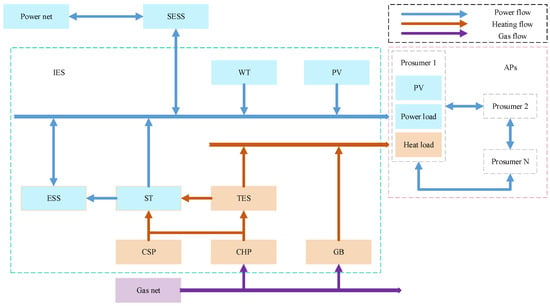
Figure 2.
Energy flow relationships in SESS-IES-APs.
2.2.1. Clean Energy Component Model
In this paper, WT, PV, ESS, and CSP are categorized as the cleaner production parts of the IES energy-providing equipment. Among them, due to the large-scale wind and photovoltaic power generation connected with source-side uncertainty, in IES, stochastic renewable energy sources impact the operation much [44]. Therefore, according to the literature [22], the actual generation power of wind and solar is regarded as the sum of the prediction value and random error in this paper, and since the scope of this paper is considered a day-ahead scheduling problem, the wind and solar output is represented by Equations (10) and (11) and constrained by Equations (12) and (13).
where: , , indicates the predicted wind power, the actual wind power, and the abandoned wind power, , , indicates the predicted PV power, the actual PV power and the abandoned power, , denotes the short-term prediction error of wind power output, , denotes normally distributed variance.
The EES can be used to save a portion of excess power or to compensate for a portion of power deficits, and its capacity can be expressed by Equation (14) and constrained by Equation (15).
where: denotes the capacity of the ESS at the time of , , denote the charging and discharging power, , denote the charge/discharge efficiency, , denote the lower and upper limits of capacity, , indicate the lower and upper limits of charging and discharging power, , indicate the charge/discharge identification bit.
The CSP consists of a mirror field (MF), a steam turbine (ST), and a TES. Its main energy source is aggregated photothermal energy, and the ST is driven by the solar heat absorbed by the MF to generate electricity, and the excess heat is stored in the TES. The power generation output of the CSP can be expressed by Equation (16) and is constrained by Equation (17).
where: denotes the power generated by the CSP at the time of , , denote the thermal power supplied by MF and TES to ST, denotes the coefficient of power generation efficiency, indicates the upper limit of power generation.
The source of TES thermal energy comes from the waste heat of MF and CHP, so the heat stored in the TES can not only drive the ST to generate electricity but also flow directly to the thermal load. Its capacity can be expressed by Equation (18) and constrained by Equation (22).
where: represents the heat storage capacity of TES at the time of , , denote heat exchanger power, , denote charge and discharge thermal efficiency, , denote the absorbed thermal power from CHP and MF, denotes the power to supply heat directly to the heat loads, , denote MF heat gathering power and heat loss power, , indicate the upper limit of charging and discharging thermal power, , denote the charge and discharge heat identification bit.
2.2.2. Gas Boiler and Gas Turbine Model
Since the CSP heat output is always limited by the geographical and climatic environment, it is necessary to consider the inclusion of heat-generating equipment, mainly CHP and GB, which are used to improve the flexibility and reliability of the IES.GB mainly interacts with natural gas and heat loads; its energy source is natural gas, and its heat-generating power is directly supplied to the heat loads. The GB heat-generating power and constraints are as follows:
where: denotes the heat production power of GB at the time of , indicates the gas consumption, denotes the conversion factor of heat production per unit of gas consumption, denotes the upper limit of GB heat production power.
CHP produces electrical power and thermal power by burning natural gas and generating both electrical and thermal energy, which can be expressed by Equations (25) and (26) and constrained by Equation (28).
where: , denote the electrical power and thermal power produced by CHP at the , indicates the gas consumption, , indicate the coefficient of efficiency of electricity and heat production per unit of gas consumption, indicates the thermal power supplied directly to the heat loads, , indicate the upper power limit for electricity and heat production, , indicate the upper limit of power supplied by CHP to TES and thermal loads.
2.2.3. IES Energy Interaction Model
Since there is uncertainty in the wind and light output, the uncertainty is described in this paper in the form of chance constraints according to Equations (10)–(13), which in turn represents the IES electric power balance in Equation (29) and is constrained by Equation (31). Similarly, the IES thermal power balance is shown in Equation (30). In addition, the impact of uncertainty on IES scheduling will be explained in Equations (A1)–(A3) in Appendix A.
where: , represent the power purchased and sold by IES to SESS at the time of , denotes the total electrical load demand of APs, is the inverse function of the standard normal distribution, represents the total heat load demand of APs, , denote the upper limit of power purchased and sold to SESS, , denote that it purchased electricity sales identification bits from SESS.
2.2.4. IES Objective Function
Since the IES is in the middle of the three-tier hierarchy, it is subject to both the SESS tariff-setting constraints and the APs’ energy demand strategies to some extent. Therefore, it is crucial to obtain the optimal scheduling strategy and economics by setting appropriate energy prices for APs under the condition of being constrained by SESS tariffs. In this paper, we set the IES operator to maximize its benefit as the objective, and this objective function can be expressed by Equation (32) and constrained by Equation (38).
where: is the combined IES intraday benefit, , indicate proceeds from power purchases and sales with SESS and energy sales to APs, , , indicate the cost of natural gas, the cost of operation and maintenance of the equipment, and the cost of wind and solar energy, indicates the cost factor for purchasing a unit volume of natural gas, , denote the cost factor of wind and light abandonment, , denote the cost factor of ESS, TES charging and discharging energy, denotes CSP power production cost factor, , is the price of electricity and heat set by IES for different prosumers, , indicate that IES sets the floor and ceiling for electricity sales prices, , indicate that IES sets the lower and upper bounds on the price of heat sales, , denote the IES constraint on the average value of electricity and heat prices.
2.3. Low-Level Alliance of Prosumers Framework
2.3.1. APs Model Considering Demand Response and Peer-to-Peer Electrical Energy Transactions
Prosumer has the ability to produce energy due to the inclusion of rooftop PV. In addition, the multiple energy demand load of the prosumer varies with conditions. Therefore, the total electrical load demand of APs consisting of multiple prosumers can be expressed by Equation (39) and bounded by Equation (41). Similarly, its thermal total load demand can be expressed by Equation (40) and bounded by Equation (42).
where: denotes the predicted power of prosumer at the time of , indicates the predicted power of rooftop PV, , denote curtailable and level-able electrical loads, denotes P2P electrical energy load sharing with other prosumers, denotes the predicted power of the thermal energy load, , denote curtailable and level-able heating loads, , denote the upper limit of curtailable and level-able electrical loads, denotes P2P power-sharing maximum power.
2.3.2. APs Objective Function
Since APs are in the lowest tier, their energy purchase costs are greatly limited by the prices set by the higher tiers. Therefore, it is especially critical to formulate an optimal energy demand strategy to reduce their own energy purchase cost while meeting certain energy demands. In summary, this paper sets the objective function of APs to minimize the comprehensive cost, as shown in Equation (43) and is constrained by Equation (49).
where: is the combined cost of APs, , denote the cost of purchasing electricity from IES and the cost of DR for electricity, , denote the cost of heat purchased from IES and the cost of heat DR, , , , indicate the cost reduction factor and transfer cost factor for electricity and heat loads, is the cost of sharing trade in electrical energy between prosumer, , denotes the trading tariff and trading power of prosumer with , denotes the shared energy tariff between prosumer and , , denotes the upper and lower limits of the shared electricity tariff.
2.4. Nash Bargaining-Based Cooperative APs Model
Although APs are at the lowest level of disadvantage, in addition to the energy DR, their electricity consumption strategy can further reduce the comprehensive cost through inter-prosumer electricity sharing trade. It means that, due to the different time-sharing pricing issued by IES to different prosumers, prosumers can provide part of their electricity to other prosumers in the form of P2P sharing, and in fact, the electricity sharing is delivered through the distribution facilities that prosumers are connected to IES. However, since each prosumer belongs to different independent interests and shares the trading and pricing rights of electricity, they all hope to reach their cost minimization through cooperation. Therefore, it is necessary to ensure that the benefits of each subject will not be damaged after the cooperation. The Nash negotiation in the cooperative game can effectively reach the member contract collaboration through bargaining and negotiation according to the energy sharing among the subjects. The Nash negotiation model of APs constructed in this paper is represented by Equation (50) and constrained by Equation (53).
where: is the combined cost of purchasing energy for intraday coalition members not participating in Nash negotiations, i.e., the point at which bargaining cooperation breaks down, is the combined purchased energy cost of the intraday coalition members participating in the Nash negotiations without regard to the portion of the shared power payment, is the combined cost difference of purchased energy before and after intraday coalition member participation in power sharing.
However, since the Nash negotiation model (50) is a non-convex nonlinear optimization problem, it is difficult to solve it directly, and thus, it is necessary to convert the model into two subproblems of coalition cost minimization and cooperative benefit distribution , which are easier to solve, and solve them sequentially.
Setting for the alliance cooperation does not take into account the sharing of electricity to pay for the purchase of energy costs , then sub-problem alliance cost minimization can be expressed in the following formula:
Setting as the optimal solution obtained in subproblem , the distribution of cooperative benefits in subproblem can be expressed by the following equation:
3. Stackelberg-Stackelberg-Nash Three-Level Game Model Solving
In the three-layer game model, the price and power of the energy interaction between the two subjects must satisfy the constraints of the network and match the optimization solution, and Stackelberg needs to go through an iterative process to acquire an equilibrium solution. To solve this problem effectively, this paper refers to [45] using the lower layer problem as a quadratic problem, the unique optimal solution of the KKT condition is applied, which can transform this middle-lower layer optimization problem into a single-layer optimization problem, and the master-slave part and Nash part are represented in Figure 3 and Figure 4. The lower layer model is restated as follows:
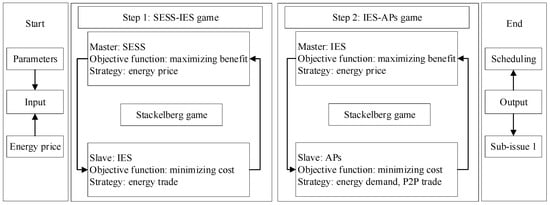
Figure 3.
Flowchart of the Stackelberg game section.
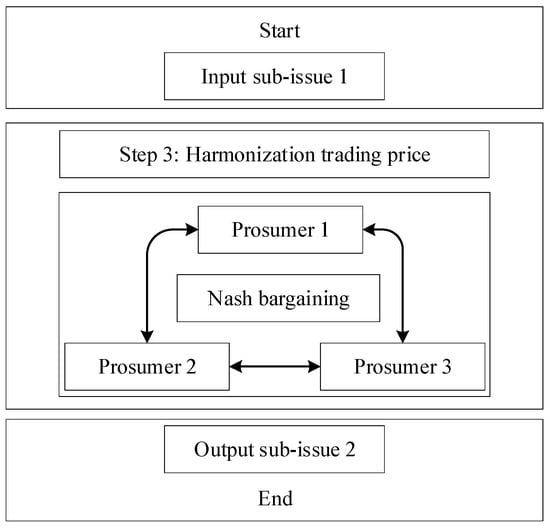
Figure 4.
Flowchart of the Nash Bargaining section.
3.1. Master-Slave Game Solution Section
Since the use of metaheuristic algorithms in solving, it is possible to arrive at a neighboring result with the same boundary twice, which leads to the whole solving process being time-consuming. Based on this, this paper refers to the dichotomous distributed optimization algorithm solution model of the literature [46]. The algorithm will determine whether the results of two adjacent iterations are the same during the iterative solving process, and if so, the boundaries will be processed through the bisection method, and the final iteration results will be locked quickly.
Set to be the energy price at in the iteration, and assume that is upper bounded.
- When , add constraints:
- When , add constraints:
Since Equations (57) and (58) ensure that the boundary of each iteration computation can be rapidly reduced, which in turn improves the computational efficiency of the algorithm, while in each iteration, it is judged whether the convergence condition of Equations (59) and (60) is satisfied, and if it is satisfied with the convergence, then the iteration is ended.
where: , denote the price of purchased and sold electricity set by SESS to IES at in the iteration.
3.2. Cooperative Game Solution Section
Considering that the APs cost minimization problem has separable convex functions and constraints, it can be solved in a distributed manner using ADMM. The augmented Lagrange function is constructed by introducing Lagrange multipliers and penalty factors :
According to the principle of the ADMM algorithm, Equation (61) is decomposed to obtain the distributed optimization operation model for each member of APs, and member 1 is used as an example:
The distributed optimization runtime model for the other members is similar to that of member 1. 3 members are used as an example to finally build the distributed algorithm for the APs subproblem cooperative revenue allocation:
- Setting the maximum number of iterations , convergence precision , penalty factor , the initial number of iterations , initial Lagrange multipliers , and initial sharing of electrical power between initial members .
- Member 2 can accept the shared electricity tariff between member 1 and member 2, member 3 can accept the shared electricity tariff between member 1 and member 3, solve the distributed optimal operation model for member 1, acquire member 1 can accept the shared electricity tariff , with members 2 and 3.
- Member 1 can accept the shared electricity tariff between member 2 and member 1, member 3 can accept the shared electricity tariff between member 2 and member 3, solve the distributed optimal operation model for member 2, acquire member 2 can accept to share the electricity tariff , with members 1 and 3.
- Member 1 can accept the shared electricity tariff between member 3 and member 1, member 2 can accept the shared electricity tariff between member 3 and member 2, solve the distributed optimal operation model for member 3, acquire member 3 can accept to share the electricity tariff , with members 1 and 2.
- Update the Lagrange multipliers:
- Judge the convergence of the algorithm and terminate the iteration if Equation (64) is satisfied.
- If not satisfied, then , repeat (2) to (6).
4. Simulation Experiment and Comparison
In this section, the reasonableness of the proposed model is verified through arithmetic simulations on a computer equipped with a 3.1 GHz Intel Core i5 and 16 GB of RAM. The arithmetic simulation is performed using the MATLAB R2021b platform using Yalmip (https://yalmip.github.io/) to invoke the Gurobi solver 11.0.3 (Gurobi Optimization, 2022) and solve the model using the dichotomous method combined with ADMM. References [13,14,15,16,17,18] set the simulation parameters, and the energy prices for each period are shown in Table 2, and the parameters used in the SESS-IES-APs three-layer hybrid game model are listed in Table 3, Table 4 and Table 5, including each unit of equipment. In addition, each electric and thermal energy input/demand in the simulation experiment is shown in Figure A1a–d in Appendix A.

Table 2.
Hourly energy price.

Table 3.
Parameters related to the SESS of the case study.

Table 4.
IES parameters related to the IES of the case study.

Table 5.
APs parameters related to the case study.
Since whether the lower-level prosumers involve electricity and heat energy DR and whether cooperative alliances are formed among prosumers are important factors affecting the prosumer’s costs, they are also key to directly affecting the outcome of the benefits of the upper-level game players. Therefore, this paper sets up the following four different scenarios and compares and analyzes the optimization results in Section 4.1 and Section 4.2.
Scenario 1: DR of APs is not considered, and cooperative game of APs is not considered.
Scenario 2: DR of APs is not considered, but cooperative game of APs is considered.
Scenario 3: DR of APs is considered, but cooperative game of APs is not considered.
Scenario 4: Consider the DR of APs and consider the cooperative game of APs.
4.1. Analysis of the Results of Energy Optimization Scheduling
In this section, the impacts of different scenarios on the optimal energy scheduling results of the SESS-IES-APs three-tier subject energy optimization are investigated, including the SESS charging and discharging strategy, the IES intra-unit inter-unit scheduling strategy, and the prosumer energy consumption strategy.
Compared with Scenario 1, the cooperative alliance between prosumers in Scenario 2 can theoretically provide more flexible energy scheduling strategies for subjects at all levels. In Figure 5a, due to the dual influence of grid time-of-day tariffs and IES energy purchase and sale strategies, the SESS can purchase electricity as a reserve when the IES residual energy is sufficient and sell it to the grid during peak periods (11:00–14:00; 18:00–20:00). In Figure 5b,c, the total electrical and thermal energy load profiles of the APs are the same before and after optimization because they do not consider the energy demand side response. Since the CSP has a large supply of concentrating heat energy in the 07:00–17:00 time period, a part of it is transferred to the TES to be used as a thermal energy reserve, and the high tariff period set by the SESS is in the 9:00–15:00 time period, at this time, the extra output energy from the CHP and the CSP is converted to electrical energy output to compensate for the electrical energy demand; in the 16:00–20:00 time period which is still a high tariff period, the APs’ larger electric load demand, and at this time GB and CHP output is limited, TES in CSP will produce heat or convert it to electric energy output to compensate for electric energy demand, thus improving the economic efficiency of IES. Compared to Figure 5b,c and Figure 6b,c, the total energy consumption demand remains the same despite the presence of inter-prosumer power sharing. Compared to Scenario 2, the prosumer energy DR is considered in Scenario 3, providing a more flexible energy consumption strategy. Comparing Figure 6a and Figure 7a, SESS no longer provides power to IES during peak power periods (18:00–20:00) and sells surplus energy directly to the grid. Comparing Figure 6b,c and Figure 7b,c, there is a significant change in the energy consumption of the APs, with the largest period of decrease in electrical energy demand being 647.16 kw from 19:00 to 20:00 and the largest period of decrease in thermal energy demand being 294.696 kw from 13:00 to 14:00. In addition, the largest increase in electrical energy demand is 260.14 kw (23:00–24:00), which needs to further explore the effect of adding electrical energy sharing among prosumers on the energy scheduling results.

Figure 5.
Energy-optimized scheduling results for SESS-IES-APs under Scenario 1.
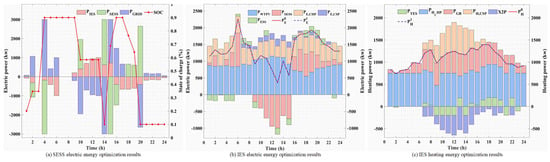
Figure 6.
Energy-optimized scheduling results for SESS-IES-APs under Scenario 2.
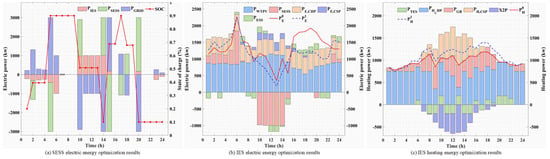
Figure 7.
Energy-optimized scheduling results for SESS-IES-APs under Scenario 3.
Compared to Figure 7a and Figure 8a, the maximum reduction of power purchase from SESS by IES is 149.51 kw (1:00–2:00) due to the further decrease of power needed by IES to satisfy APs. Comparing with Figure 7b,c and Figure 8b,c, the maximum decrease of APs power demand is 166.658 kw (13:00–14:00), and the maximum increase of power demand is 263.17 kw (9:00–10:00), which verifies the validity of the inter-prosumer power-sharing energy on the reduction of its own energy consumption cost. In addition, as AP’s electric demand side response and inter-member electric energy sharing are considered, the amount of electricity that IES needs to satisfy under different periods of the SESS tariff is further adjusted. In the 1:00–4:00 h, the electricity demand is increased by 30.5 kw, 89.18 kw, and 118.92 kw, respectively, and at this time, the portion of electricity that could have been available for ESS to be used as an electric energy reserve is used to compensate for the adjusted increase in the demand for electric energy. During the 9:00–10:00 h, due to the 263.17 kw increase in adjusted load, CHP increased its generation output from 236.829 kw to 500 kw to meet the additional load demand. During the 13:00–14:00 h, due to a decrease in electrical load demand of 167.658 kw, the CHP is reduced from 128.022 kw to 47.582 kw, and the CSP is reduced from 250 kw to 163.782 kw. Similarly, the IES does not need to purchase electrical energy from the SESS during the non-valley hours of 8:00–23:00 to compensate for the load, and in turn, during the 10:00–10:00 h, it does not need to purchase electrical energy from the SESS to pay for the load. Similarly, IES is not required to purchase power from SESS during the off-valley hours of 8:00–23:00 to compensate for the load and, in turn, utilizes the output of ESS, CHP, and CSP during the hours of 10:00–14:00 and sells it to SESS for profit. And the thermal output is reduced from 192.034 kw to 71.3726 kw. It is worth noting that compared with Scenario 1, the IES daily natural gas losses in Scenario 4 are reduced by 9.32%.
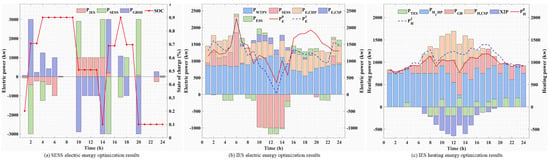
Figure 8.
Energy-optimized scheduling results for SESS-IES-APs under Scenario 4.
4.2. Analysis of Economic Performance Results
In this section, the economics of each subject after optimal scheduling of SESS-IES-APs under different scenarios are investigated. The cost information of the operation results under different scenarios is shown in Table 6, and the cost comparison before and after prosumers’ cooperation is shown in Table 7, where positive values indicate costs and negative values indicate benefits. Finally, in this paper, ADMM combined with a distributed algorithm is used to solve the subproblem , the penalty factor is set to 100, the convergence accuracy is set to 0.001, and the results are shown in Figure 9a,b.

Table 6.
Information on the results of running multiple scenarios.

Table 7.
Cost comparison before and after cooperation.
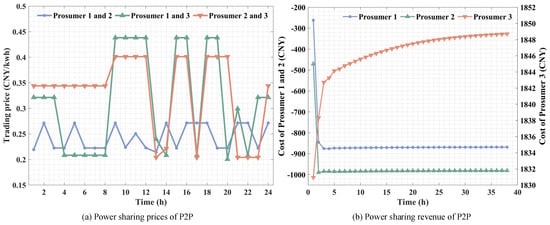
Figure 9.
P2P power-sharing results between prosumers.
Observing Table 6, it can be seen that the SESS gain decreases significantly, which is due to the indirect influence of the lowest level prosumer by changing its energy consumption strategy, but still manages to maintain high economics due to its highest position. However, compared with Scenario 1, IES gains in Scenario 4 are instead boosted by 604.931, which is because the prosumer, by changing its energy consumption strategy, makes the combined cost of the APs lower by 4171.938 at the same time as the IES gradually reduces the amount of power purchased when the SESS sets a high price. Observing Table 7 shows that whether or not the DR of the prosumer is taken into account, its post-cooperation integrated cost is always lower than the original purchased energy cost before the cooperation, but when comparing Scenario 4 with Scenario 1 in combination with Table 6, the integrated purchased energy cost of APs is reduced by 12.16%.
Observing Figure 9a, the electricity sharing tariffs among Prosumer 1–2, Prosumer 1–3, and Prosumer 2–3 fluctuate within the intervals of [0.2195–0.2715], [0.2083–0.4832], [0.2041–0.4011], respectively, which satisfy the constraint intervals set in this paper. Observing Figure 9b, the algorithm converges after 38 iterations of solving, with Prosumer 1 converging to −868.734 from the initial −261.995, Prosumer 2 converging to −980.856 from the initial −470.849, and Prosumer3 converging to 1848.71 from the initial 1830.93. Combining Table 3 and Table 4, the cost of Prosumer 1 and 2 is significantly lower, although it increases the post-cooperation cost of Prosumer 3, which will be compensated by the bargaining portion redistribution, which ensures that Prosumer 3 will not jeopardize its interest by cooperating.
5. Conclusions
For different energy subjects participating in cooperative optimization scheduling involving conflict of interests, how to meet the possible existence of different hierarchical status relationships, cooperation, and competition, etc., so that the interests of multiple subjects participating in the situation will not be damaged, and to achieve the sustainability of participation in the cooperative optimization, high efficiency of energy utilization, and flexibility of the system scheduling. In this study, a Stackelberg-Stackelberg-Nash three-layer game framework is proposed for use in the three-layer optimal scheduling of SESS-IES-APs under the same distribution network. The energy interactions among the regional grid, SESS, IES, and APs are studied, especially the impact of each prosumer energy consumption strategy in APs on other subjects, and the main conclusions are as follows:
- Compared with Scenario 1, the cost of IES energy purchase in Scenarios 3 and 4 is reduced by 4.94% and 3.95%. At this time, IES reduces natural gas consumption by 9.32% after considering certain scenery output uncertainty and adopting CHP-CSP synergistic operation used to realize X2P. TES saves waste heat while gas is powered and uses ST to generate electricity at night when there is excess heat and insufficient electricity, which verifies the validity of the three-layer optimization model proposed in this paper.
- Comparing the simulation results of APs’ energy purchase cost in scenarios 4 and 1, prosumer 1, 2, and 3 reduce their own energy purchase cost by 11.61%, 12.1%, and 12.7%, respectively, and the total energy purchase cost of APs is reduced by 12.16% when considering the cooperation between DR and other prosumers. It is verified that the producers and sellers in the master-slave game framework can further reduce the cost of purchasing energy when they are in the monopolized position by realizing the power-sharing among members to explore cooperation and adjusting the energy consumption strategy by utilizing their energy DR.
This paper provides methodological support for the application of CHP-CSP and producers and sellers to optimize the operation of IES in the future. In addition, the IES model in this paper does not consider the impact of low carbon emissions and P2G on IES energy optimization and economic efficiency. Therefore, in future work, we aim to further explore the enhancement of IES benefits by multi-energy complementarity.
Author Contributions
F.Z.: Conceptualization, Methodology, Design, Experiment, Analysis, Visualization, Writing—original draft. H.H.: Methodology, Analysis, Writing—review and editing. X.L.: Methodology, Analysis, Writing—review and editing, Funding acquisition. K.L.: Analysis, Writing—review and editing. S.O.: Analysis, Writing—review and editing. L.M.: Data collection, Writing—review and editing. W.H.: Data collection, Writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (51809097), the Open Foundation of Hubei Key Laboratory for High-efficiency Utilization of Solar Energy and Operation Control of Energy Storage System (HBSEES202312), and the Open Foundation of Hubei Engineering Research Center for Safety Monitoring of New Energy and Power Grid Equipment (HBSKF202125).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data will be made available on request.
Conflicts of Interest
Authors Hui He and Wei Huang are employed by Changjiang Engineering Group. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Correction Statement
This article has been republished with a minor correction to the existing affiliation information. This change does not affect the scientific content of the article.
Abbreviations
| ADMM | alternating direction multiplier method | MF | mirror field |
| APs | alliance of prosumers | P2P | peer to peer |
| CHP | combined heat and power | PV | photovoltaic |
| CSP | concentrated solar thermal power | SESS | shared energy storage system |
| EB | electric boiler | ST | steam turbine |
| EES | electric energy storage | TES | thermal energy storage |
| EVCS | electric vehicle charge station | WT | wind turbine |
| GB | gas boiler | X2P | gas and heat to power |
Appendix A
Describing electric power balance constraints under wind and light uncertainty in the form of chance constraints:
where denotes the level of confidence probability. Marking the probability cumulative distribution function of the random variable as , then Equation (A1) can be converted into the following equation:
Following the computation of , the above constraints can eventually be converted into the following inequality constraints [27]:
where: is the inverse function of the standard normal distribution.
Each electrical and thermal energy input/demand in the simulation experiment is shown in Figure A1a–d in Appendix A.
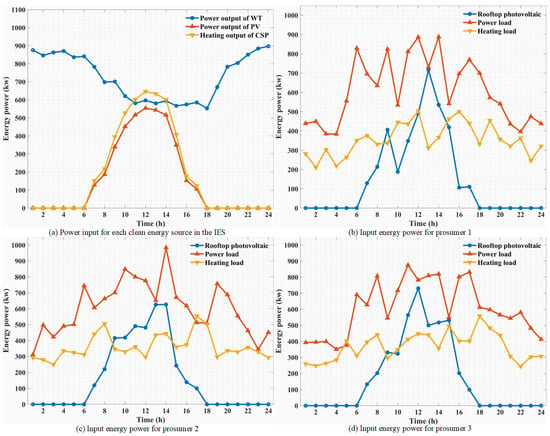
Figure A1.
Electrical and heating energy input/demand.
References
- Li, Y.; Wang, C.; Li, G.; Wang, J.; Zhao, D.; Chen, C. Improving operational flexibility of integrated energy system with uncertain renewable generations considering thermal inertia of buildings. Energy Conv. Manag. 2020, 207, 112526. [Google Scholar] [CrossRef]
- Chen, C.; Wu, X.; Li, Y.; Zhu, X.; Li, Z.; Ma, J.; Qiu, W.; Liu, C.; Lin, Z.; Yang, L.; et al. Distributionally robust day-ahead scheduling of park-level integrated energy system considering generalized energy storages. Appl. Energy 2021, 302, 117493. [Google Scholar] [CrossRef]
- Xiao, X.; Yin, J.; Chen, L.; Wang, M.; Zhao, Y.; Li, Z. Evolutionary Game-theoretic Modeling of Massive Distributed Renewable Energy Deployment Towards Low-carbon Distribution Networks. J. Mod. Power Syst. Clean Energy 2023, 11, 1519–1528. [Google Scholar] [CrossRef]
- Lipu, M.S.H.; Miah, S.; Ansari, S.; Hannan, M.; Hasan, K.; Sarker, M.R.; Mahmud, S.; Hussain, A.; Mansor, M. Data-driven hybrid approaches for renewable power prediction toward grid decarbonization: Applications, issues and suggestions. J. Clean. Prod. 2021, 328, 129476. [Google Scholar] [CrossRef]
- Wang, W.; Yu, T.; Huang, Y.; Han, Y.; Liu, D.; Shen, Y. The situation and suggestions of the new energy power system under the background of carbon reduction in China. Energy Rep. 2021, 7, 1477–1484. [Google Scholar] [CrossRef]
- Milan, C.; Stadler, M.; Cardoso, G.; Mashayekh, S. Modeling of non-linear CHP efficiency curves in distributed energy systems. Appl. Energy 2015, 148, 334–347. [Google Scholar] [CrossRef]
- Haase, P.; Thomas, B. Test and optimization of a control algorithm for demand-oriented operation of CHP units using hardware-in-the-loop. Appl. Energy 2021, 294, 116974. [Google Scholar] [CrossRef]
- Li, X.; Wu, X.; Gui, D.; Hua, Y.; Guo, P. Power system planning based on CSP-CHP system to integrate variable renewable energy. Energy 2021, 232, 121064. [Google Scholar] [CrossRef]
- Li, X.; Li, T.; Liu, L.; Wang, Z.; Li, X.; Huang, J.; Huang, J.; Guo, P.; Xiong, W. Operation optimization for integrated energy system based on hybrid CSP-CHP considering power-to-gas technology and carbon capture system. J. Clean. Prod. 2023, 391, 136119. [Google Scholar] [CrossRef]
- Ao, X.; Zhang, J.; Yan, R.; He, Y.; Long, C.; Geng, X.; Zhang, Y.; Fan, J.; Liu, T. More flexibility and waste heat recovery of a combined heat and power system for renewable consumption and higher efficiency. Energy 2025, 315, 134392. [Google Scholar] [CrossRef]
- Liu, X.; Lu, H.; Zhao, W.; Chen, Y.; Shao, S. Research on optimal scheduling and source-network-load correlation matching of integrated energy system considering uncertainty. Energy 2025, 321, 135421. [Google Scholar] [CrossRef]
- Peng, S.; Liu, S.; Wu, X. Optimal scheduling of integrated energy system considering exergoeconomic performance. Energy 2025, 320, 135171. [Google Scholar] [CrossRef]
- Liao, X.; Qian, B.; Jiang, Z.; Fu, B.; He, H. Integrated Energy Station Optimal Dispatching Using a Novel Many-Objective Optimization Algorithm Based on Multiple Update Strategies. Energies 2023, 16, 5216. [Google Scholar] [CrossRef]
- Fang, N.; Ma, S.; Liao, X.; Ding, H.; Yu, J. Optimized scheduling of integrated community energy stations based on improved NSGA-III algorithm. J. Energy Storage 2024, 99, 113362. [Google Scholar] [CrossRef]
- Liao, X.; Ma, J.; Yin, B.; Qian, B.; Lei, R.; Li, C. Many-objective bi-level energy scheduling method for integrated energy stations based on power allocation strategy. iScience 2024, 27, 109305. [Google Scholar] [CrossRef]
- Liu, K.; He, H.; Liao, X.; Zou, F.; Huang, W.; Li, C. Optimization of Renewable Energy Sharing for Electric Vehicle Integrated Energy Stations and High-Rise Buildings Considering Economic and Environmental Factors. Sustainability 2025, 17, 3142. [Google Scholar] [CrossRef]
- Yin, B.; Liao, X.; Qian, B.; Ma, J.; Lei, R. Optimal Scheduling of Electric Vehicle Integrated Energy Station Using a Novel Many-Objective Stochastic Competitive Optimization Algorithm. IEEE Access 2023, 11, 129043–129059. [Google Scholar] [CrossRef]
- Wang, F.; Liao, X.; Fang, N.; Jiang, Z. Optimal Scheduling of Regional Combined Heat and Power System Based on Improved MFO Algorithm. Energies 2022, 15, 3410. [Google Scholar] [CrossRef]
- Li, Y.; Wang, B.; Yang, Z.; Li, J.; Chen, C. Hierarchical stochastic scheduling of multi-community integrated energy systems in uncertain environments via Stackelberg game. Appl. Energy 2022, 308, 118392. [Google Scholar] [CrossRef]
- Li, Y.; Wang, C.; Li, G.; Chen, C. Optimal scheduling of integrated demand response-enabled integrated energy systems with uncertain renewable generations: A Stackelberg game approach. Energy Conv. Manag. 2021, 235, 113996. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, J. Two-stage energy management method of integrated energy system considering pre-transaction behavior of energy service provider and users. Energy 2023, 271, 127065. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.; Wang, J.; Du, B.; Qin, Y.; Liu, X.; Liu, L. A Stackelberg game-based approach to transaction optimization for distributed integrated energy system. Energy 2023, 283, 128475. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, H.; Li, B.; Wang, X. Research on dynamic pricing and operation optimization strategy of integrated energy system based on Stackelberg game. Int. J. Electr. Power Energy Syst. 2022, 143, 108446. [Google Scholar] [CrossRef]
- Li, P.; Wang, Z.; Yang, W.; Liu, H.; Yin, Y.; Wang, J.; Guo, T. Hierarchically partitioned coordinated operation of distributed integrated energy system based on a master-slave game. Energy 2021, 214, 119006. [Google Scholar] [CrossRef]
- Tan, J.; Li, Y.; Zhang, X.; Pan, W.; Ruan, W. Operation of a commercial district integrated energy system considering dynamic integrated demand response: A Stackelberg game approach. Energy 2023, 274, 126888. [Google Scholar] [CrossRef]
- Tan, C.; Geng, S.; Tan, Z.; Wang, G.; Pu, L.; Guo, X. Integrated energy system-Hydrogen natural gas hybrid energy storage system optimization model based on cooperative game under carbon neutrality. J. Energy Storage 2021, 38, 102539. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Shao, C.; Gong, N. Distributed energy trading for an integrated energy system and electric vehicle charging stations: A Nash bargaining game approach. Renew. Energy 2020, 155, 513–530. [Google Scholar] [CrossRef]
- Shi, M.; Wang, H.; Xie, P.; Lyu, C.; Jian, L.; Jia, Y. Distributed Energy Scheduling for Integrated Energy System Clusters with Peer-to-Peer Energy Transaction. IEEE Trans. Smart Grid 2023, 14, 142–156. [Google Scholar] [CrossRef]
- Yang, S.; Tan, Z.; Zhou, J.; Xue, F.; Gao, H.; Lin, H.; Zhou, F. A two-level game optimal dispatching model for the park integrated energy system considering Stackelberg and cooperative games. Int. J. Electr. Power Energy Syst. 2021, 130, 106959. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.; Cai, C.; Xue, L.; Ma, Y.; Shen, H.; Chen, X.; Liu, L. Research on the optimization method of integrated energy system operation with multi-subject game. Energy 2022, 245, 123305. [Google Scholar] [CrossRef]
- Ullah, M.H.; Park, J. DLMP integrated P2P2G energy trading in distribution-level grid-interactive transactive energy systems. Appl. Energy 2022, 312, 118592. [Google Scholar] [CrossRef]
- Kotowicz, J.; Uchman, W. Analysis of the integrated energy system in residential scale: Photovoltaics, micro-cogeneration and electrical energy storage. Energy 2021, 227, 120469. [Google Scholar] [CrossRef]
- Jiang, A.; Yuan, H.; Li, D. Energy management for a community-level integrated energy system with photovoltaic prosumers based on bargaining theory. Energy 2021, 225, 120272. [Google Scholar] [CrossRef]
- Kuehnbach, M.; Bekk, A.; Weidlich, A. Towards improved prosumer participation: Electricity trading in local markets. Energy 2022, 239, 122445. [Google Scholar] [CrossRef]
- Schick, C.; Klempp, N.; Hufendiek, K. Role and Impact of Prosumers in a Sector-Integrated Energy System With High Renewable Shares. IEEE Trans. Power Syst. 2022, 3286, 3286–3298. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, S.; Gu, W.; Zhu, C. Optimal Operation of Micro-energy Grids Considering Shared Energy Storage Systems and Balanced Profit Allocations. CSEE J. Power Energy Syst. 2023, 9, 254–271. [Google Scholar] [CrossRef]
- Ding, J.; Gao, C.; Song, M.; Yan, X.; Chen, T. Optimal operation of multi-agent electricity-heat-hydrogen sharing in integrated energy system based on Nash bargaining. Int. J. Electr. Power Energy Syst. 2023, 148, 108930. [Google Scholar] [CrossRef]
- Li, K.; Ye, N.; Li, S.; Wang, H.; Zhang, C. Distributed collaborative operation strategies in multi-agent integrated energy system considering integrated demand response based on game theory. Energy 2023, 273, 127137. [Google Scholar] [CrossRef]
- Li, R.; Yan, X.; Liu, N. Hybrid energy sharing considering network cost for prosumers in integrated energy systems. Appl. Energy 2022, 323, 119627. [Google Scholar] [CrossRef]
- Chen, C.; Li, Y.; Qiu, W.; Liu, C.; Zhang, Q.; Li, Z.; Lin, Z.; Yang, L. Cooperative-Game-Based Day-Ahead Scheduling of Local Integrated Energy Systems with Shared Energy Storage. IEEE Trans. Sustain. Energy 2022, 13, 1994–2011. [Google Scholar] [CrossRef]
- Chen, Y.; Pei, W.; Ma, T.; Xiao, H. Asymmetric Nash bargaining model for peer-to-peer energy transactions combined with shared energy storage. Energy 2023, 278, 127980. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, S.; Luo, X.; Huang, Y.-H.; Gu, R.-Z.; Li, J.-X.; Li, L.-L. Two-layer energy dispatching and collaborative optimization of regional integrated energy system considering stakeholders game and flexible load management. Appl. Energy 2025, 379, 124918. [Google Scholar] [CrossRef]
- Li, X.; Wu, N.; Lei, L. Nash-Stackelberg-Nash three-layer mixed game optimal control strategy for multi-integrated energy systems considering multiple uncertainties. Energy 2025, 320, 135418. [Google Scholar] [CrossRef]
- Fan, J.; Yan, R.; He, Y.; Zhang, J.; Zhao, W.; Liu, M.; An, S.; Ma, Q. Stochastic optimization of combined energy and computation task scheduling strategies of hybrid system with multi-energy storage system and data center. Renew. Energy 2025, 242, 122466. [Google Scholar] [CrossRef]
- Nasiri, N.; Zeynali, S.; Ravadanegh, S.N.; Marzband, M. A hybrid robust-stochastic approach for strategic scheduling of a multi-energy system as a price-maker player in day-ahead wholesale market. Energy 2021, 235, 121398. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhang, N.; Zhang, B.; Kang, C.; Xi, W.; Feng, M. Low-Carbon Operation of Multiple Energy Systems Based on Energy-Carbon Integrated Prices. IEEE Trans. Smart Grid 2020, 11, 1307–1318. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).