Economic and Technical Aspects of Power Grids with Electric Vehicle Charge Stations, Sustainable Energies, and Compensators
Abstract
1. Introduction
1.1. The Motivation
1.2. The Development Statuses of EVCSs to Serve EV Growth in Several Countries and Territories
1.3. The Literature Review About the Integration of the ECVS Distribution Power Grid
1.4. The Novelty and Contribution
- -
- Successfully applied novel metaheuristic algorithms, including the black-winged kite algorithm (BKA) and secretary bird optimization algorithm (SBOA), to optimize the placement of an EVCS in the IEEE 69-node DPG. Both the BKA and SBOA have proven their capability in the development phase compared to other previous methods, including the most iconic ones, such as PSO, DE, or GWO. Regarding the SBOA, personally, the method is superior to most of the recent recently developed ones, such as the nutcracker optimization algorithm (NOA) and Rime optimization algorithm (RIME), which were developed in 2023; golden jackal optimization (GJO)—2022; artificial gorilla troops optimizer (GTO)—2021; etc. Regarding the BKA, the algorithm also outperforms a wide range of state-of-the-art metaheuristic algorithms such as the improved moth flame optimization algorithm (IMFA) and sand cat swarm optimization (SCOA), developed in 2023; golden jackal optimization (GJO) and coati optimization algorithm (COA)—2022; hunter–prey optimization (HPO) and quantum-based avian navigation optimizer algorithm (QANAO)—2021; etc.
- -
- Implemented the integration of ECVSs in three different objective functions with five distinctive scenarios for each considered objective function. For each objective function, the placement of EVCSs is executed along with a particular type of auxiliary devices, which could be CAPBs, PVUs, WTs, or combined with all the mentioned devices to offer a detailed look at the real effectiveness of all these implementations. Based on that, the present valuable references are for the planners, dispatchers, and also operators.
- -
- As well as providing a detailed look while solving the considered problem on the aspects of planning and designing through different scenarios, as mentioned above, the study also presented the results of solving the problem based on the viewpoint of operational aspects with real data of load demand variation and supplied power form PVU and WT within 24 h.
- -
- Determine the best-applied algorithm among the three ones using different criteria and specific comparisons.
- -
- The placement of EVCSs is considered to reach the optimal value of different objective functions, including minimizing the overall active power loss, minimizing the power source at the slack bus, and minimizing the total voltage deviation index.
- -
- Clarify the effectiveness of placing EVCSs with other auxiliary devices using particular scenarios for each considered objective function and indicate the best scenario resulting in the best value for each considered objective function.
- -
- Present and analyze in detail the differences in results reached by three objective functions while compared to others, offering a valuable reference for those, especially operators, in terms of optimizing their own DPGs to reach the desired expectations.
- -
- Clarify the contribution of renewable-based distributed generators to the reduction in grid power and present a detailed evaluation using quantitative results while solving the problem considered from an operational viewpoint.
- -
- Using particular case studies to demonstrate the effectiveness of utilizing optimization algorithms to solve the considered problem from both the planning and operational viewpoints.
2. Problem Formulation
2.1. The Main Objective Functions
- Reduction of overall active power loss: Total active power loss (PLossall) is caused due to the flow of electric current in the distribution lines (branches). Hence, the more branches the given grid has, the larger PLossall is; therefore, reducing PLossall is really important. The mathematical expression of PLossall is formulated as follows:
- Reduction in grid power consumption: Grid power is supplied to loads by the transformer at the slack node. So, the second objective is to reduce the total grid power as shown in the following expression.
- Reduction in total voltage deviation (TVD): The deviation between nominal and real voltages reflects the voltage stability of the system. So, minimizing the TVD of the given grid is also crucial, as modeled by the following objective function [41]:
2.2. The Involved Constraints
- Power balance constraints: The most important condition for a stable operation of distribution systems is the balance of power between consumption and supply. The constraints are expressed as follows:
- Operational voltage constraint: Voltage is another critical factor that directly affects the reliability and stability of a particular DPG; therefore, voltage must be maintained in the allowed ranges between the minimum and maximum values as follows:
- Thermal constraint: This constraint is mainly about the current amplitude circulated through a particular branch. The constraint can be expressed as follows:
- PVU operation constraints: These constraints set the legal ranges to the amount of active power supplied to grid by PVUs. The mathematical expression of the constraint is as follows:
- CAPB operation constraints: The amount of reactive power supplied by CAPBs can only vary in the allow ranges as follows:
- WTS operation constraints: WTSs can work safely and efficiently as their designed capability when they are operating within their limits as follows:
- The position constraints of PVUs, CAPBs, and WTSs: This constraint means that the placements of PVUs, CAPBs, and WTSs are considered legally only if they are placed from node 2 onward to the DPG as follows:
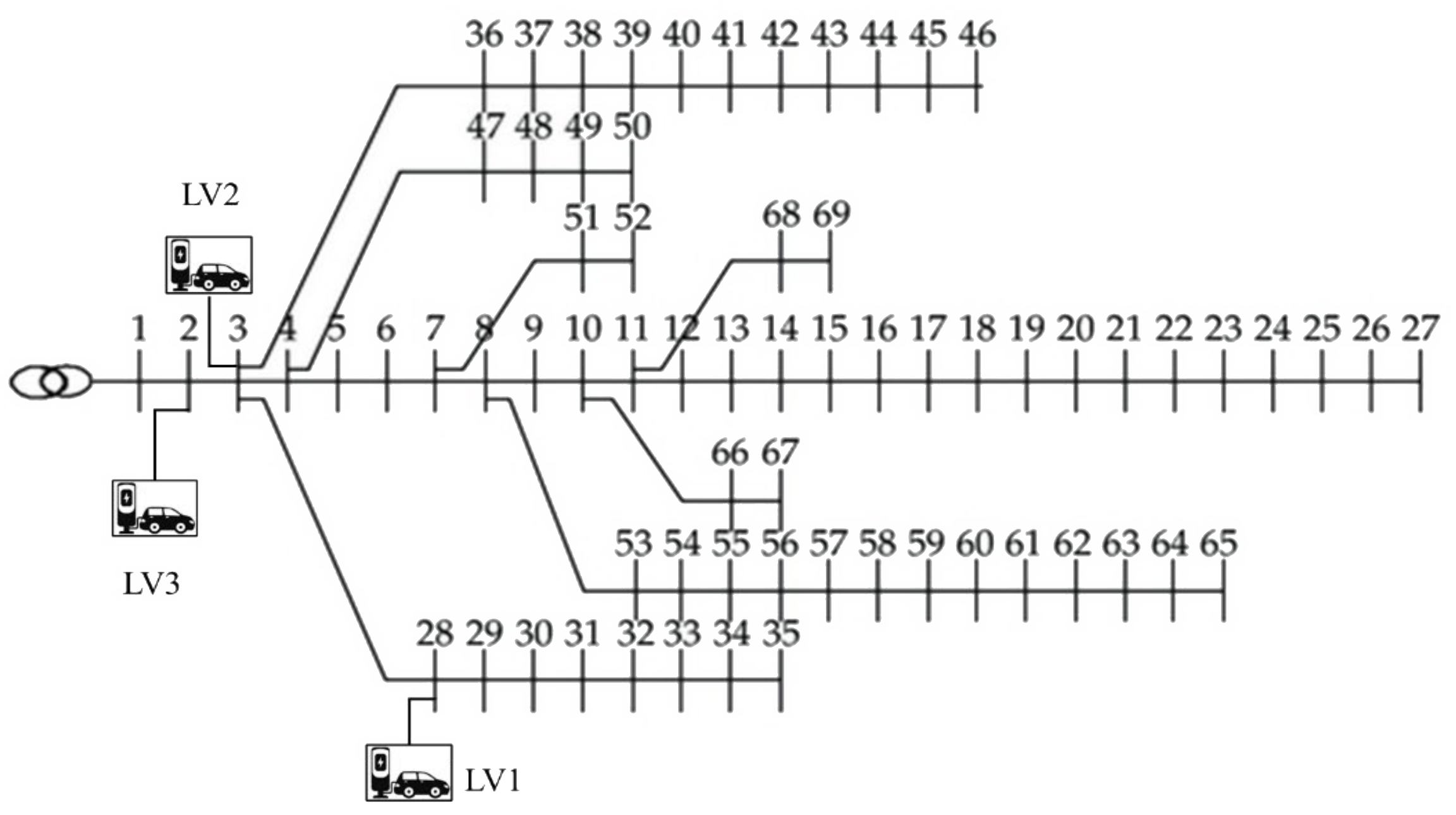
- EVCS site constraints: The placements of EVCSs at all levels are accepted only if they are connected to node 2 onward to the last node on the DPG as follows:
3. Applying EO to Optimize the Allocation of EVCSs and Other Auxiliary Devices
3.1. The Equilibrium Optimizer (EO)
3.2. The Selection of Control and Dependent Variables
- PVUs with a power factor of 1.0.
- WTSs with a power factor between 0.85 and 0.95.
- Placing one Level 1, one Level 2, and one Level 3 EVCS.
3.3. The Fitness Function
3.4. The Implementation of EO for the Problem
4. Results and Discussion
4.1. Simulation Scenarios for the Three Applied Algorithms
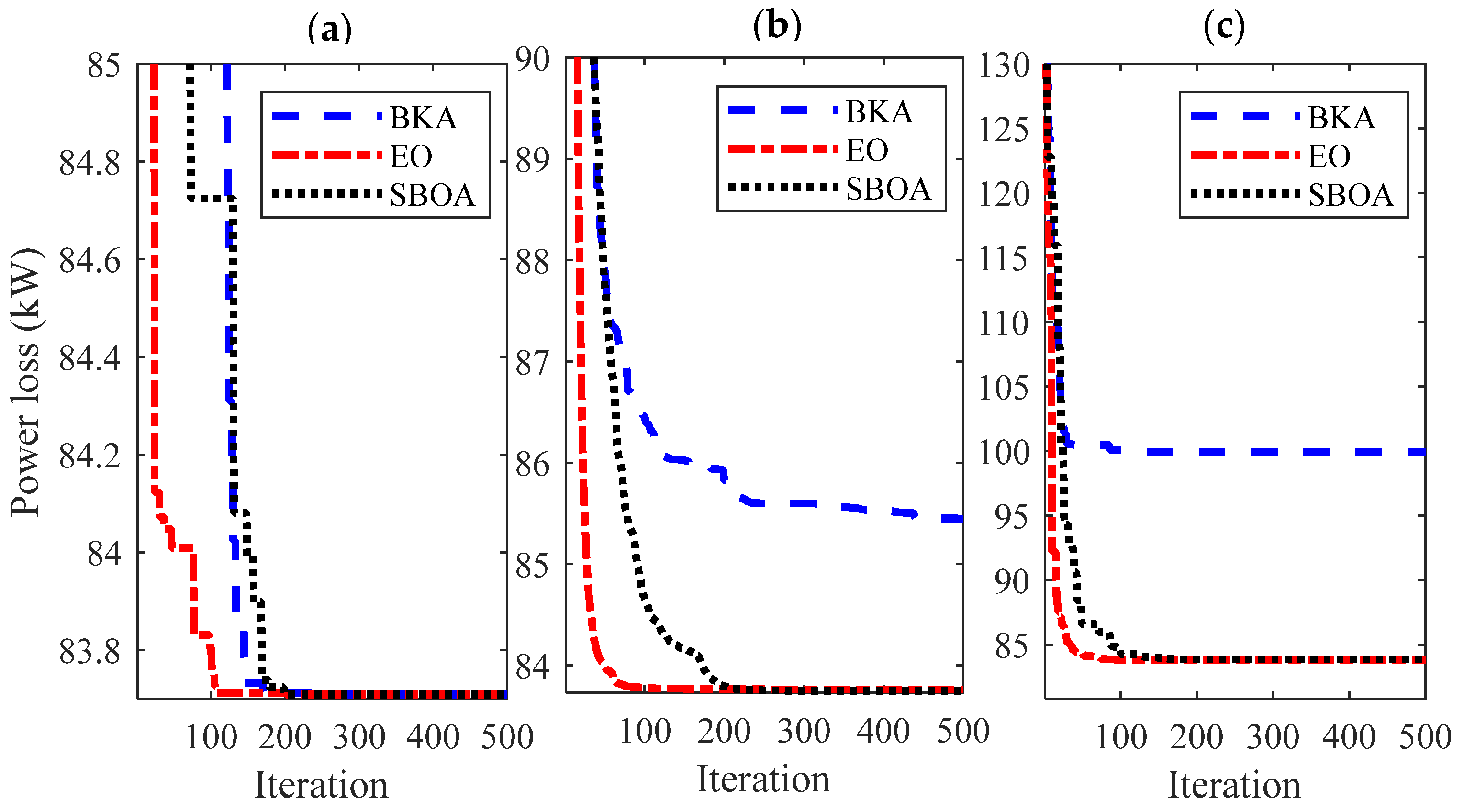
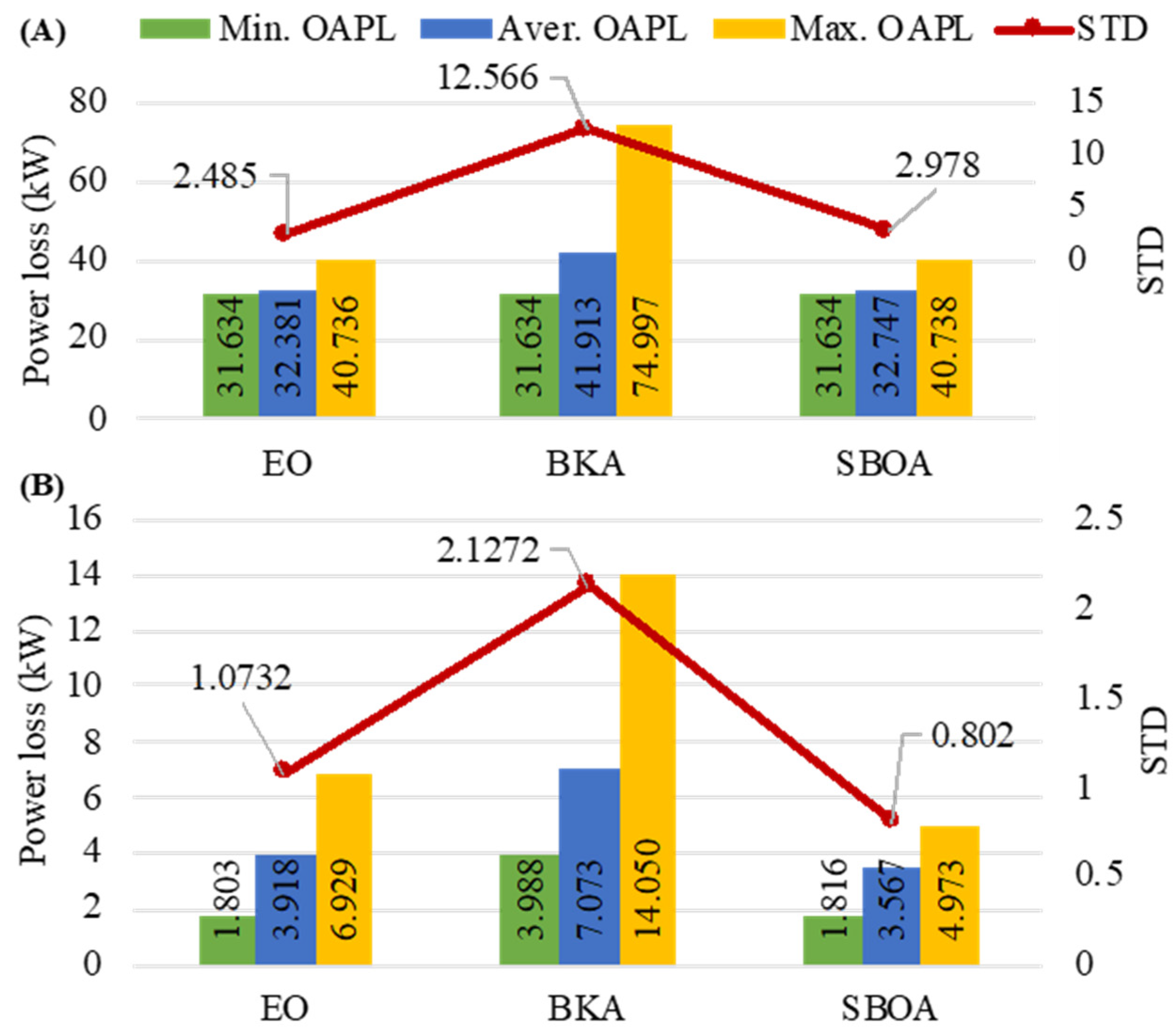
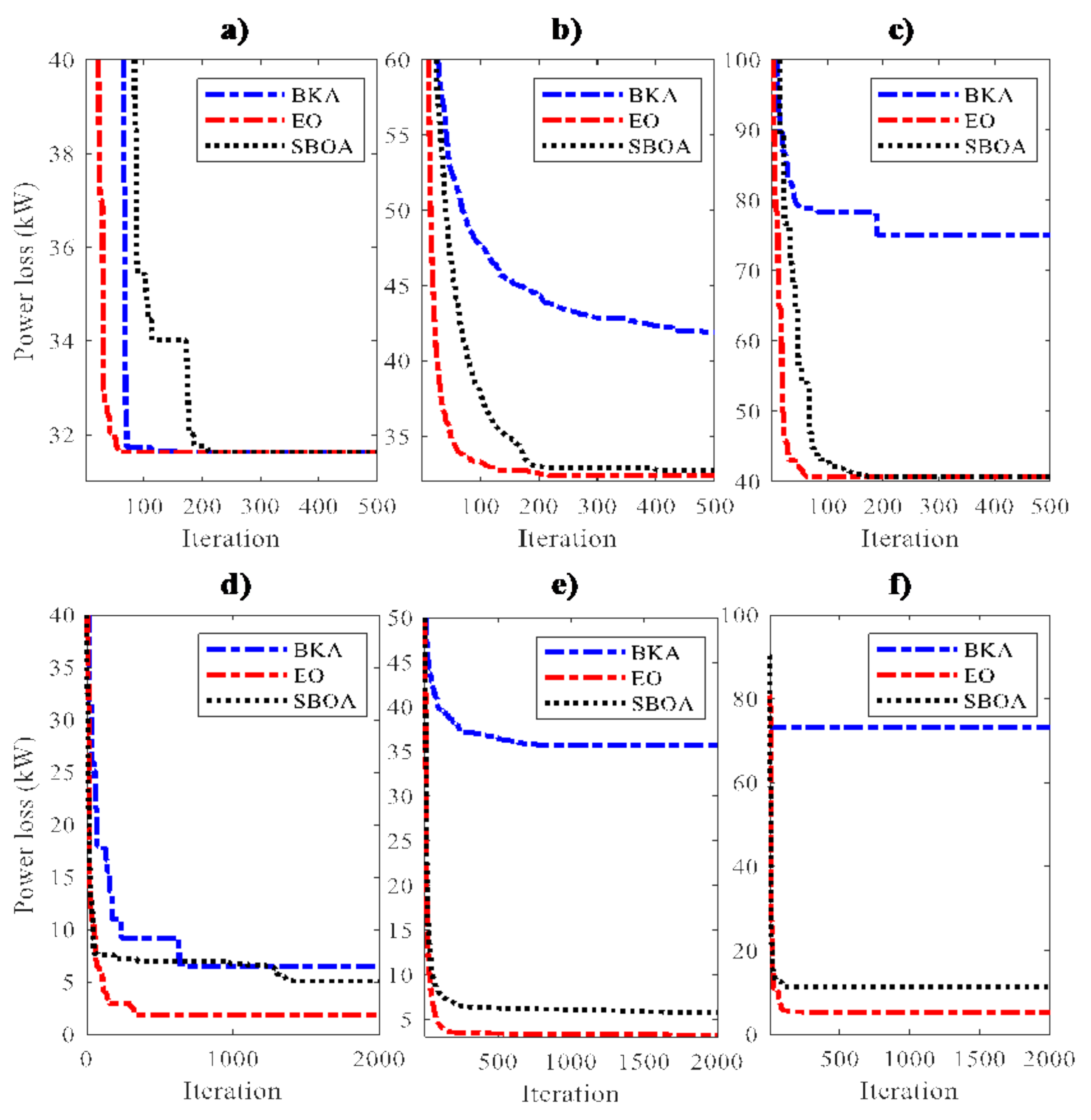
4.2. Simulation Results for Power Loss Reduction
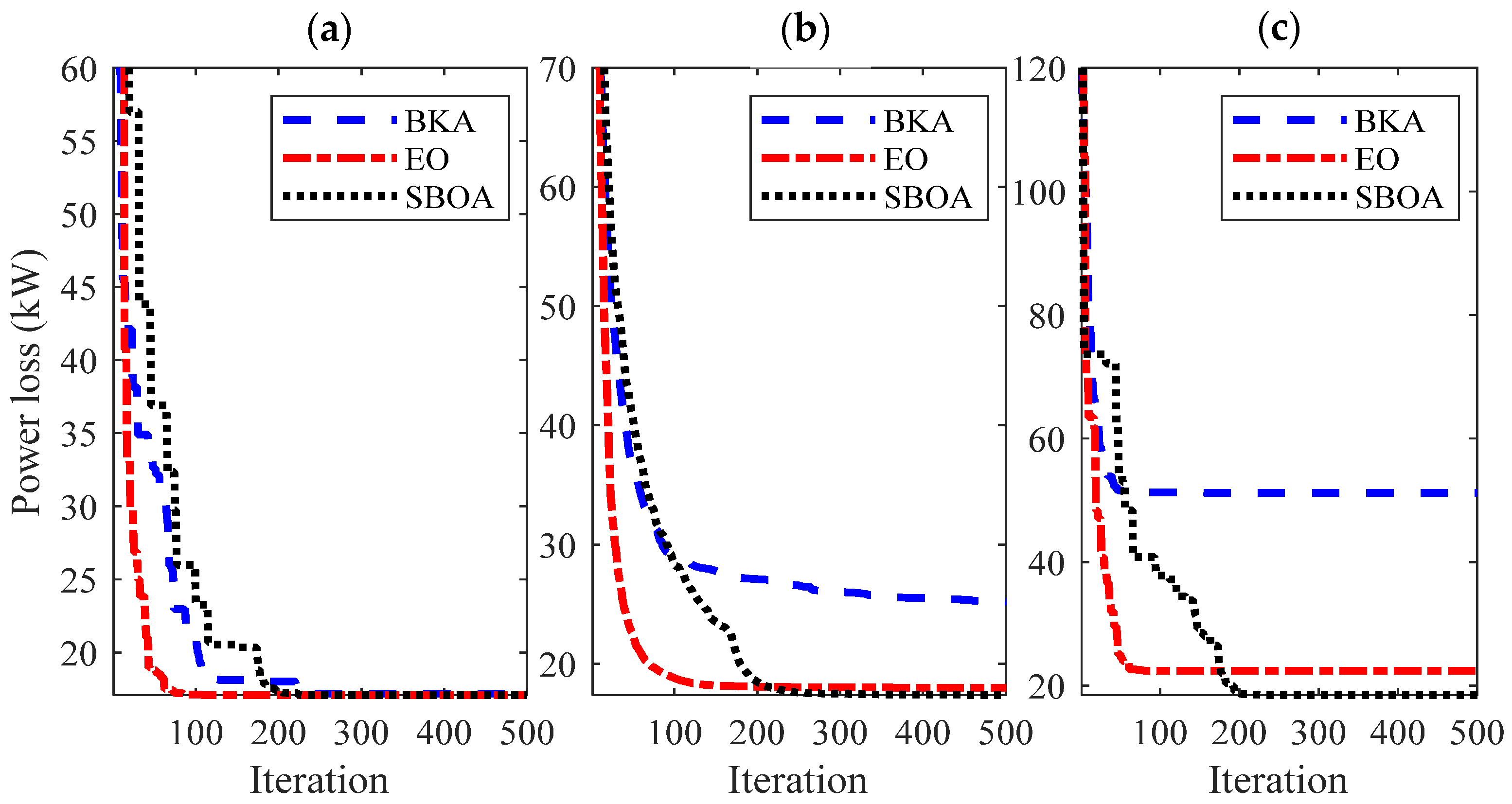
4.3. Simulation Results for Grid Power and TVD Reduction
4.4. Discussion on Simulation Scenarios
4.4.1. The Impact of Added Active and Reactive Power Sources on Objectives
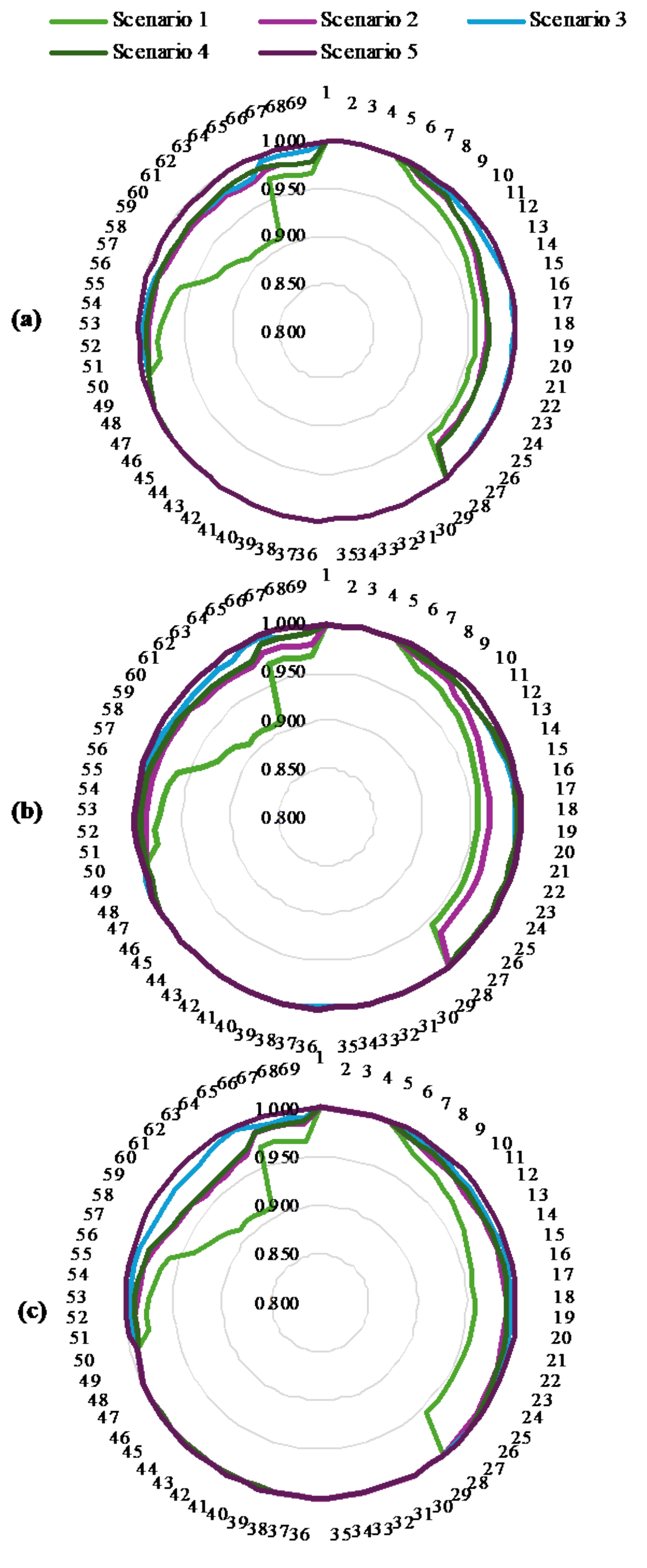
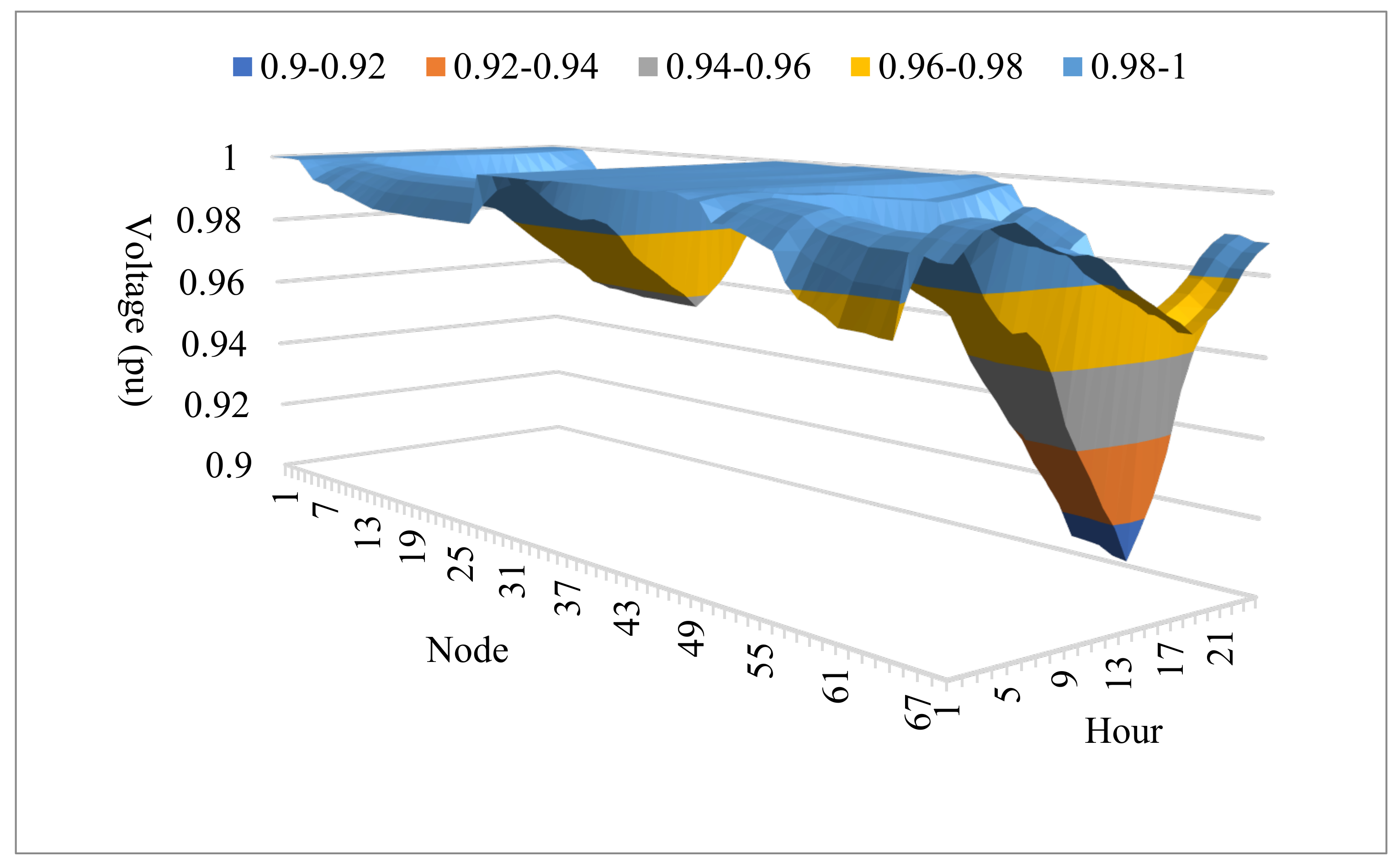
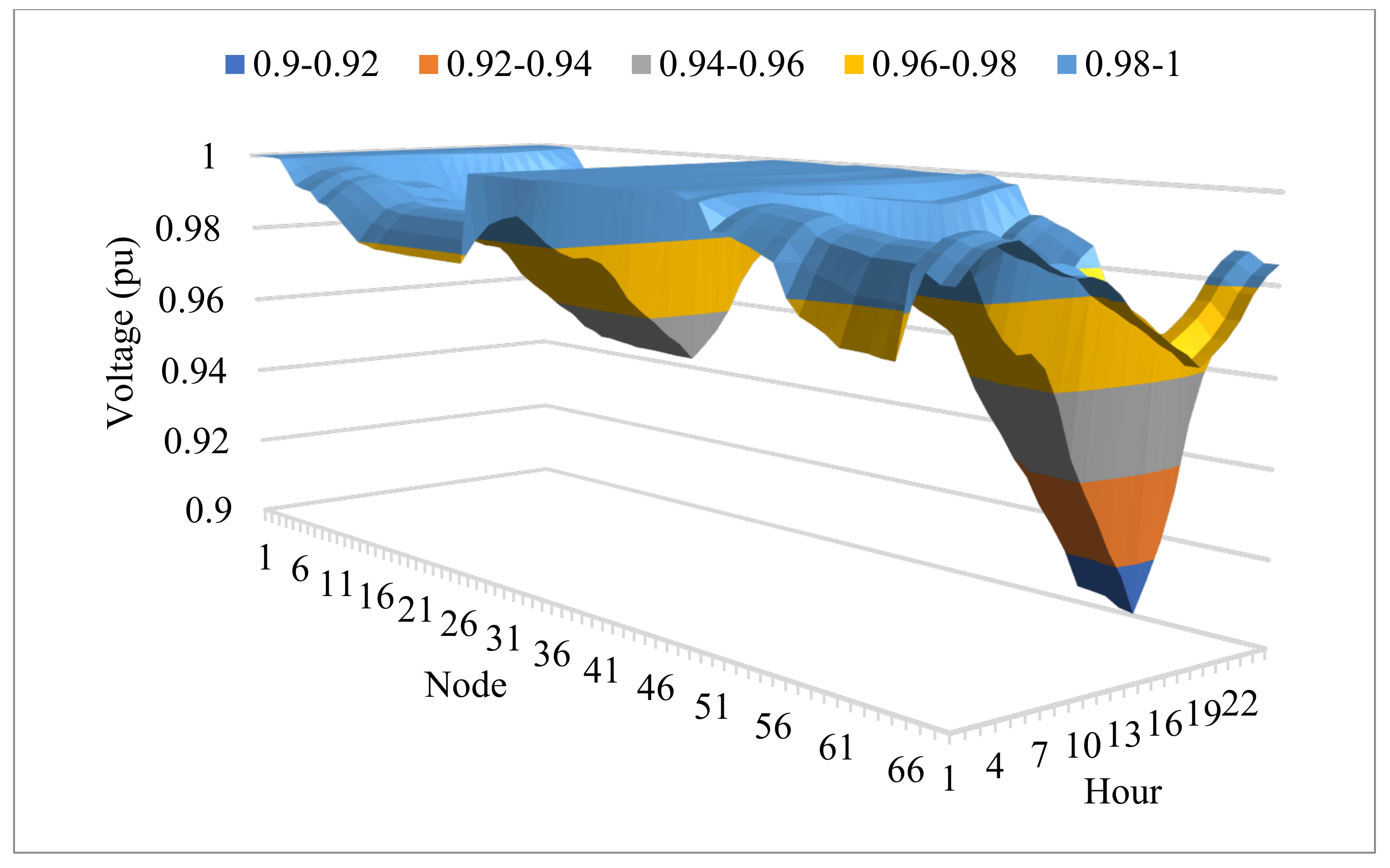
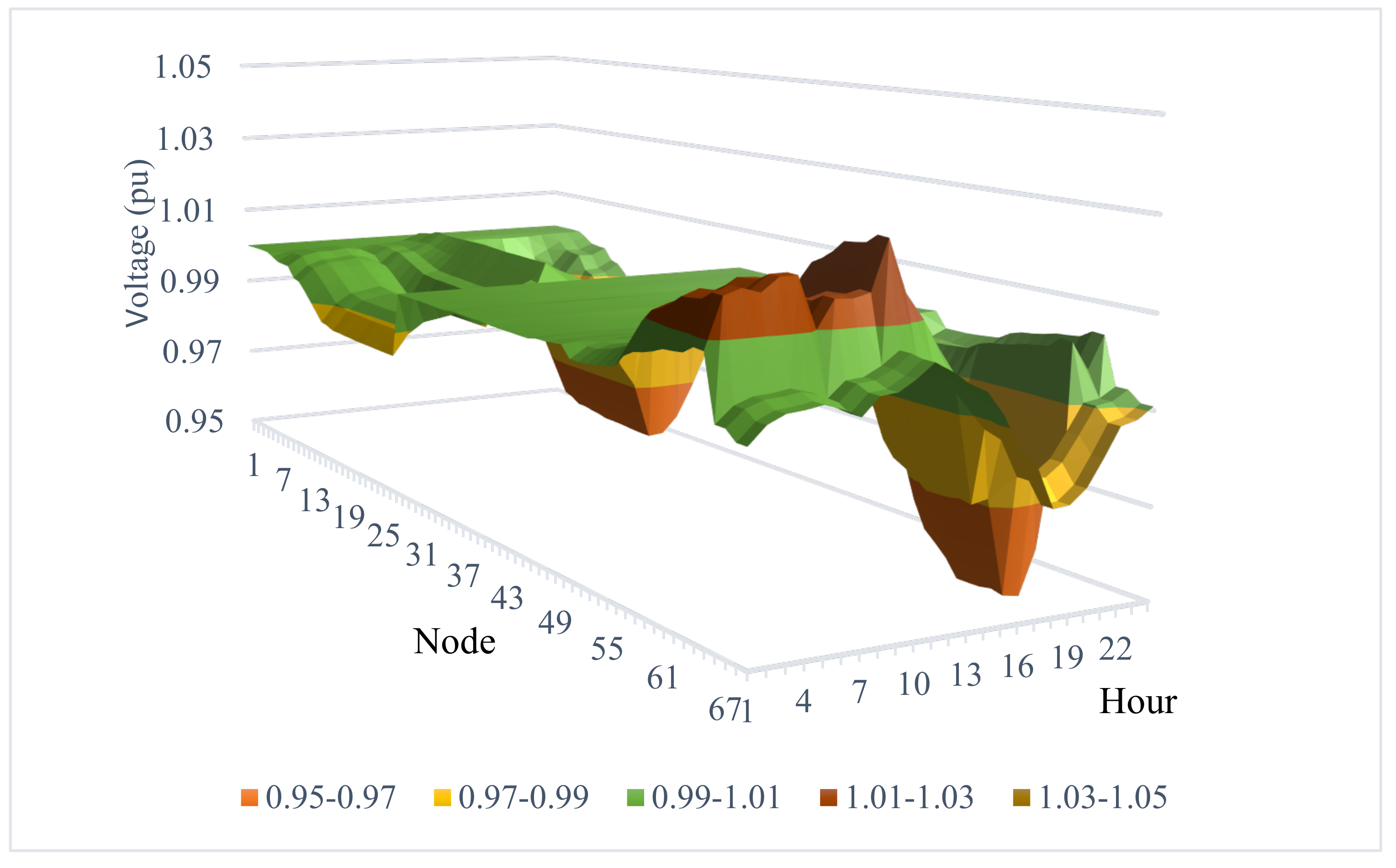
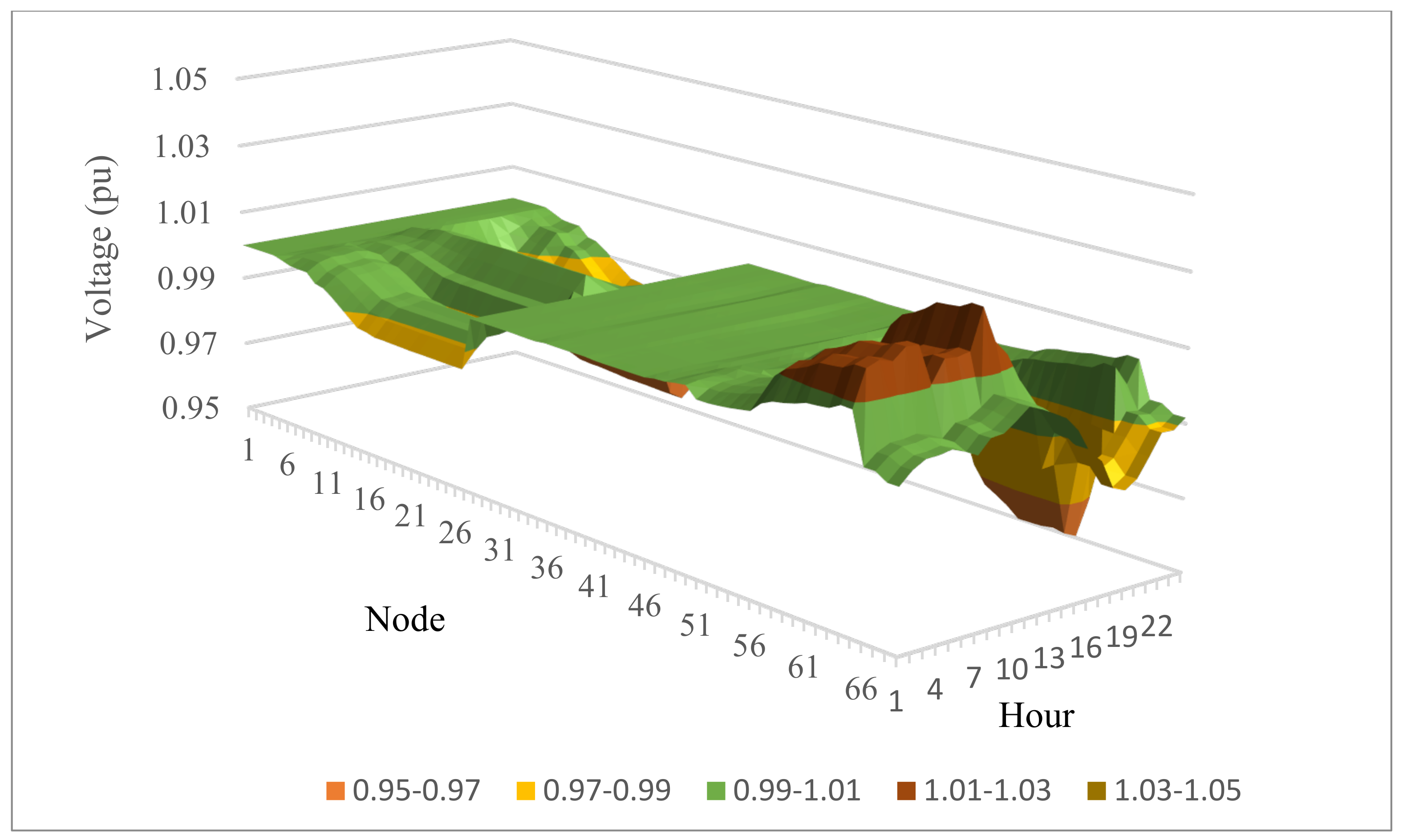
4.4.2. The Improvement of Voltage Fluctuations
4.4.3. The Limitations of the Study
- Costs of electric vehicle charge stations and renewable power sources: This study only focuses on the technical factors, including total voltage deviation, voltage limits, and power loss, but neglects economic aspects, such as the cost of energy loss on all distribution lines [48], the total cost of investment, and operation and maintenance for wind turbines and solar photovoltaic panels [49], the total cost of building charging stations [50], and the costs of investment, operation, and maintenance of the capacitor banks [51]. The study did not present any economic planning strategies regarding the construction of the charge stations and renewable power, so the economic effectiveness could not be reflected by using the obtained solutions proposed by the EO and other metaheuristic algorithms. This study aimed to outline the circumstances for a distribution power grid with the installation of electric vehicle charge stations and additional sources based on wind and solar factors. Derived from the results, it concluded that the installation of charge stations led to a high electricity use demand, high power loss, and high voltage drop. However, the optimal placement of renewable energies-based distributed generators and capacitor banks could overcome faults regarding technical issues such as the overloading status of lines, high fluctuations of node voltage, and high power loss.
- The consideration of a practical distribution power network with a new building plan for an electric vehicle charge station and new installation of renewable power sources: This study employed a standard IEEE distribution power grid with 69 nodes and fixed load demand. In addition, geographical issues were not considered when selecting electric vehicle charge stations and renewable power sources. In practice, areas for constructing the stations are very large and highly expensive.
- Load demand, generation of renewable energies, and configuration of the distribution power grid: Basically, load demand and renewable power cannot be 100% accurate as predicted and obtained from the wind and solar global atlas. The change in load profiles has a high impact on the location and power of renewable power sources and capacitor banks. High load demands require high generations from renewable power sources and capacitor banks to reduce power loss and power grids and increase the voltage profile of loads. If the configuration of grids changes, the power flows will change, leading to changes in location and power supplied by renewable power sources and capacitor banks. So, the optimal placement of added electric components significantly changes under different conditions, and optimal solutions obtained by using optimization algorithms cannot be applied at each hour for a practical distribution power network. Furthermore, the inexact data influence the design problem of placing renewable power sources, i.e., selecting the location to install renewable power sources and selecting the capacity of renewable power sources. All studies cope with the same big problem, and we cannot find an absolute solution for determining the exact power of renewable energy and load demand at each hour.
- The practical implementation of EVCS placement must account for several crucial real-world factors, including traffic conditions, available space, and user convenience. Considering these factors, the research findings can become more realistic and applicable to planning and expansion processes. To further develop this research, future studies should prioritize a comprehensive investigation of the availability of potential EVCS locations. After that, a mathematical model must be formulated to restrict EVCS placement to permissible areas, ensuring optimal and feasible deployment.
4.5. Simulation for One Operating Day with Real Wind and Solar Power
4.5.1. Study Case Simulations
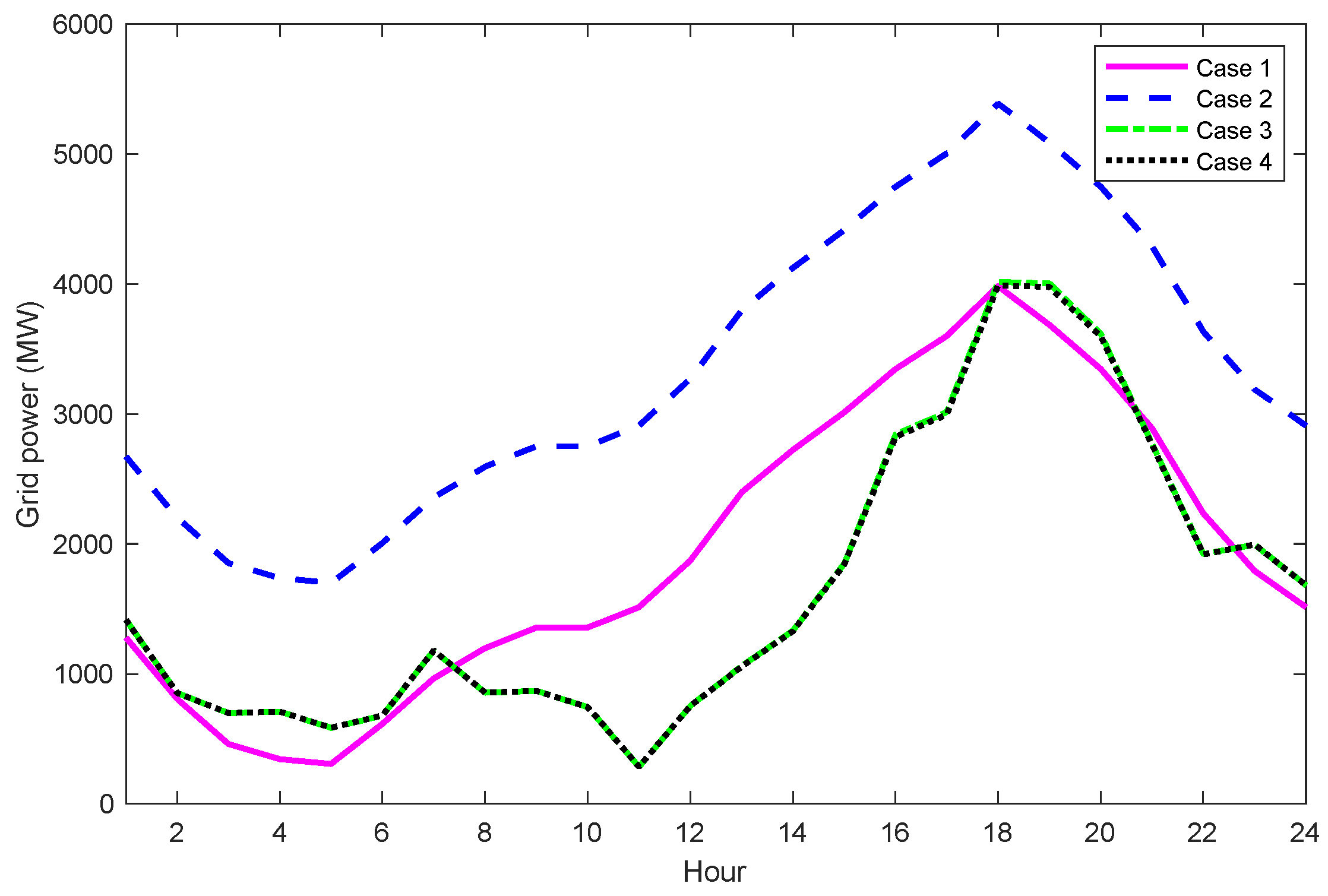
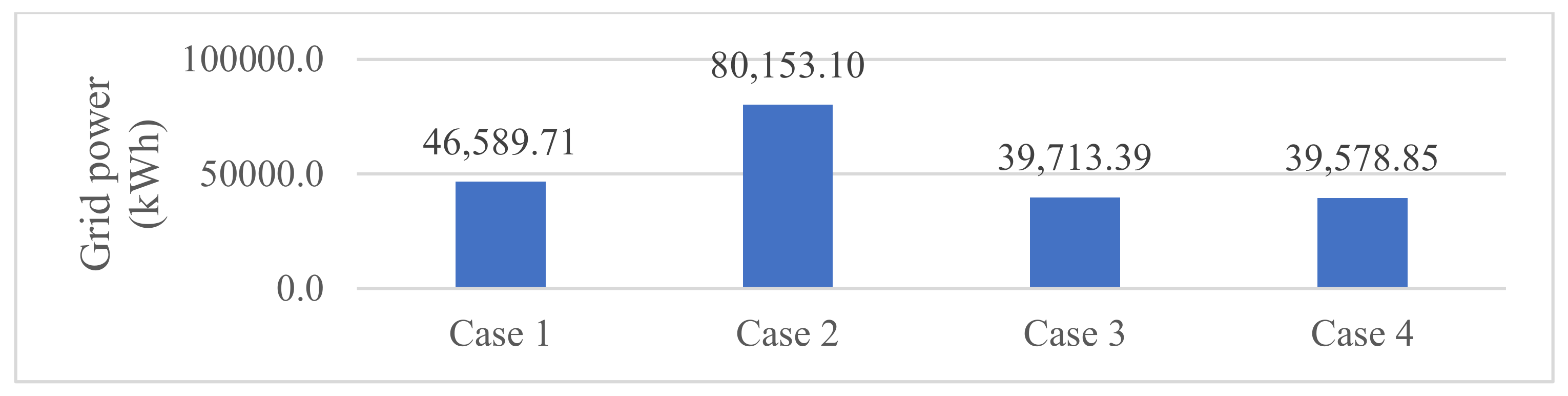
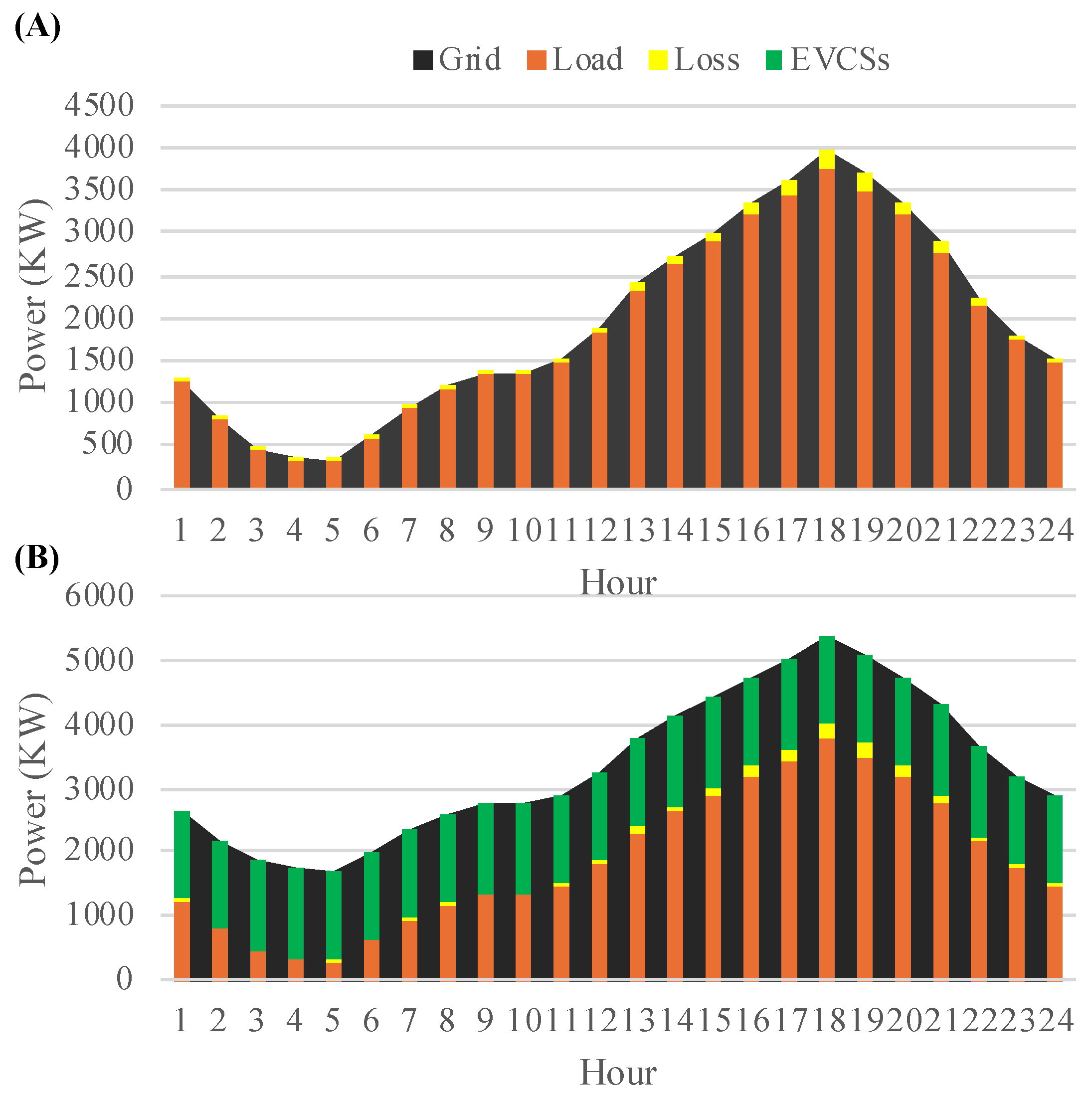
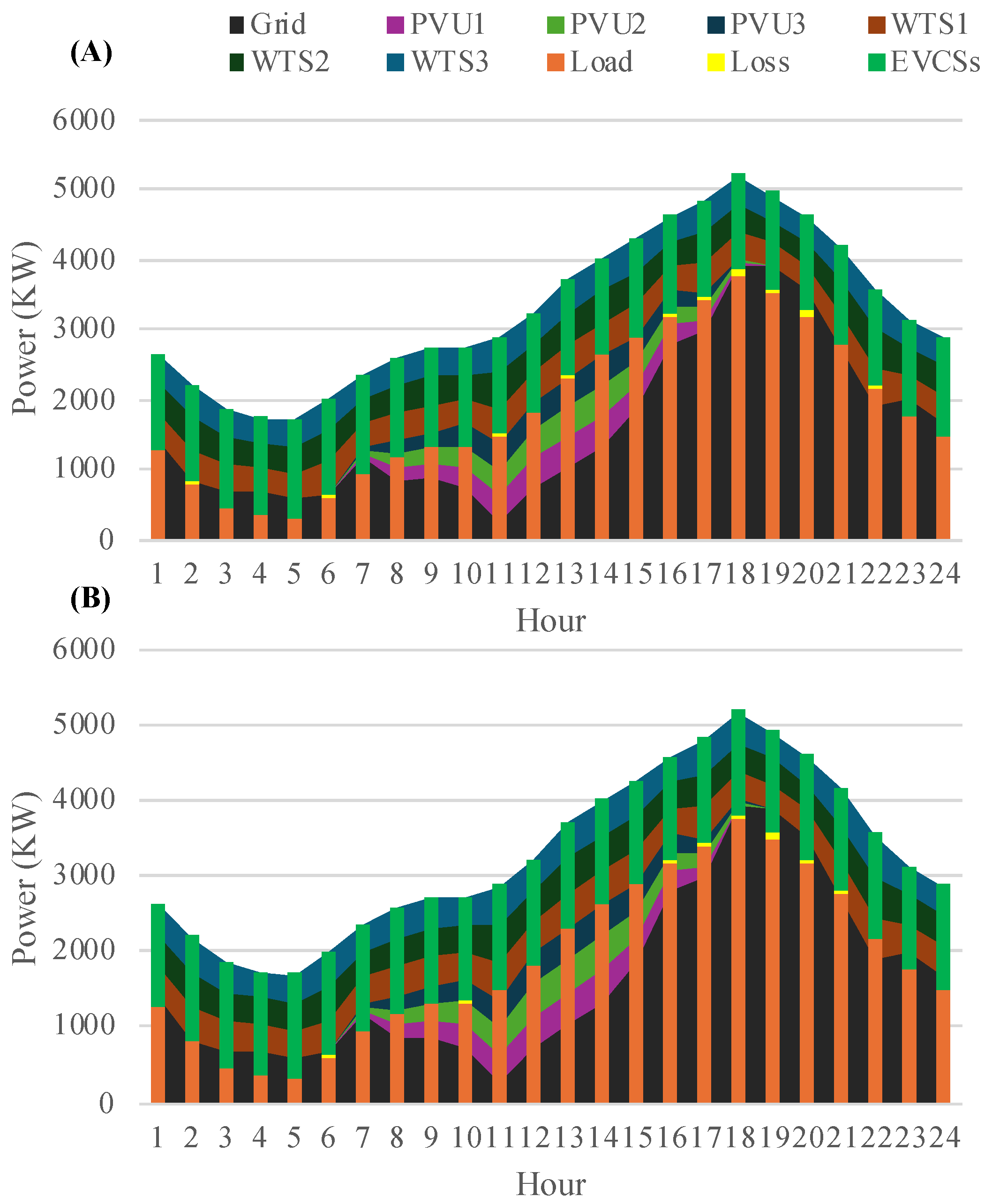
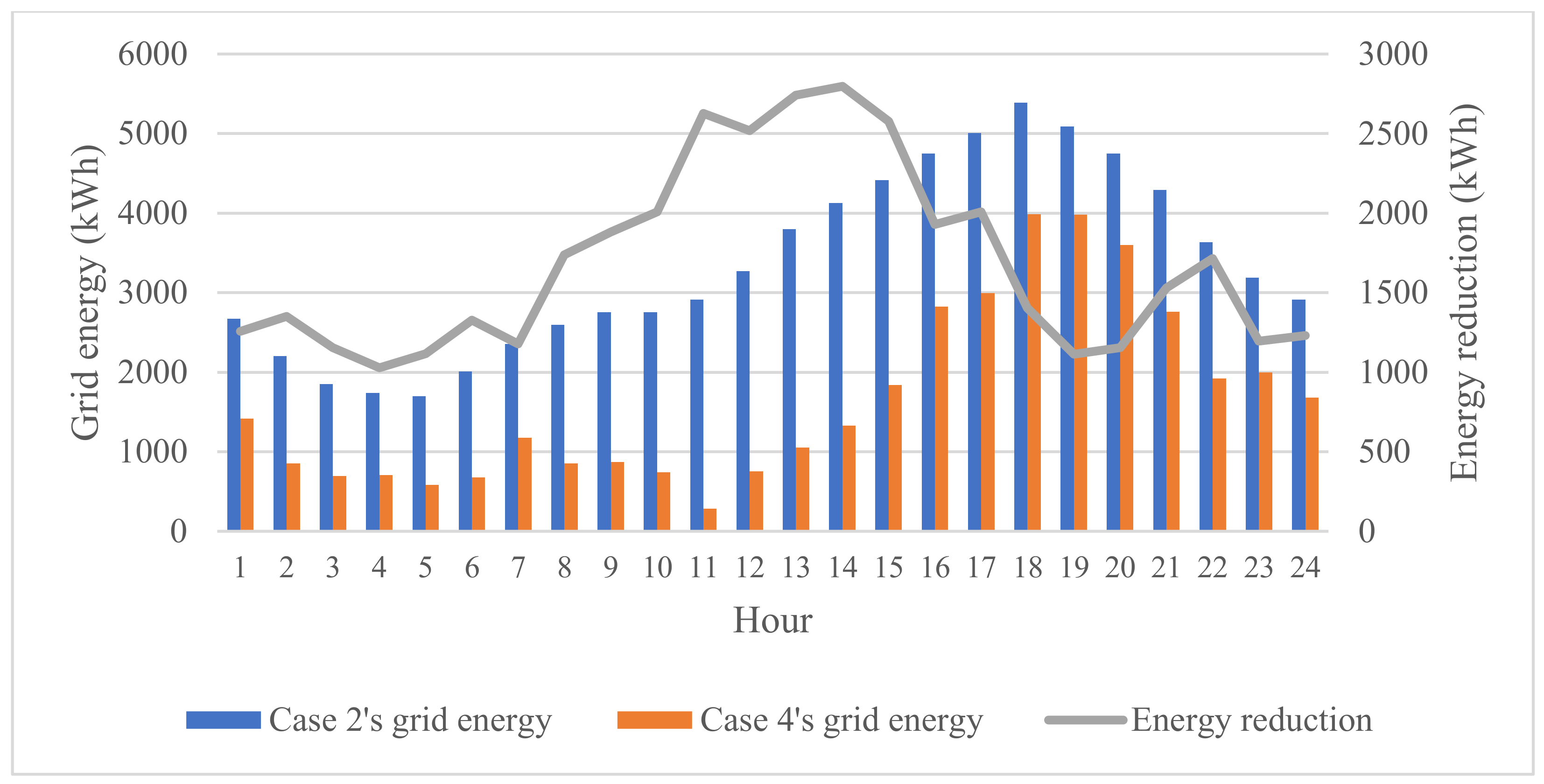
- Case 1: Find grid energy for the base system without EVCS, distributed generators, and capacitors.
- Case 2: Find grid energy for the modified system with EVCS but without distributed generators and capacitors.
- Case 3: Find grid energy for the modified system with EVCS, solar-, and wind-based distributed generators but without capacitors.
- Case 4: Find an energy grid for the modified system with EVCSs, solar- and wind-based distributed generators, and capacitors.
4.5.2. The Benefit of Systems with CAPBs, PVUs, and WTSs
- -
- Capital cost (USD) = Capital price rated power
- -
- Annual cost (USD/20 years) = Annual price rated power 20 years
- -
- O & M cost (USD/20 years) = O & M price
- -
- Total generation 365 days 20 years
- -
- Total cost for PVUs and WTs = Capital cost + O & M cost (USD/20 years)
- -
- Total cost for CAPBs = Capital cost + Annual cost
- -
- Benefit per year = total cost reduction/20 = 1,421,721.82 (USD/year)
- -
- Payback period = total costs/benefit per year = 5.21 (years)
5. Conclusions
- Case 2 provided the highest energy of 80,153.1 kWh, while Case 3 and Case 4 provided the energy of 39,713.4 kWh and 39,578.9 kWh. So, Case 4 can reduce the energy by greater than 50% of Case 2 and 0.34% of Case 3.
- Case 1 and Case 2 suffered the lowest voltage in the range between 0.9 and 0.95 Pu, violating the lower voltage limit of 0.5 Pu. Case 4 reached the best voltage profile among the four cases, with all nodes in the range from 0.95 to 1.0 Pu. The nodes with 0.95 and 0.97 Pu were the fewest in Case 4, and the remaining nodes were in the range of 0.97 and 1.0 Pu.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mariappan, S.; David Raj, A.; Kumar, S.; Chatterjee, U. Global Warming Impacts on the Environment in the Last Century. In Springer Climate; Springer Science and Business Media B.V.: Cham, Switzerland, 2022; pp. 63–93. [Google Scholar]
- Rawat, A.; Kumar, D.; Khati, B.S. A Review on Climate Change Impacts, Models, and Its Consequences on Different Sectors: A Systematic Approach. J. Water Clim. Chang. 2024, 15, 104–126. [Google Scholar] [CrossRef]
- Yoro, K.O.; Daramola, M.O. CO2 Emission Sources, Greenhouse Gases, and the Global Warming Effect. In Advances in Carbon Capture; Elsevier: Amsterdam, The Netherlands, 2020; pp. 3–28. [Google Scholar]
- Paris Agreement Climate Change. Available online: https://unfccc.int/process-and-meetings/the-paris-agreement (accessed on 2 January 2025).
- Riesz, J.; Sotiriadis, C.; Ambach, D.; Donovan, S. Quantifying the Costs of a Rapid Transition to Electric Vehicles. Appl. Energy 2016, 180, 287–300. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, Y.; Lu, Y. Spatial Accessibility of Public Electric Vehicle Charging Services in China. ISPRS Int. J. Geoinf. 2023, 12, 478. [Google Scholar] [CrossRef]
- Kaya, Ö.; Alemdar, K.D.; Campisi, T.; Tortum, A.; Çodur, M.K. The Development of Decarbonisation Strategies: A Three-Step Methodology for the Suitable Analysis of Current Evcs Locations Applied to Istanbul, Turkey. Energies 2021, 14, 2756. [Google Scholar] [CrossRef]
- Haces-Fernandez, F. Risk Assessment Framework for Electric Vehicle Charging Station Development in the United States as an Ancillary Service. Energies 2023, 16, 8035. [Google Scholar] [CrossRef]
- Sheng, K.; Dibaj, M.; Akrami, M. Analysing the Cost-Effectiveness of Charging Stations for Electric Vehicles in the U.K.’s Rural Areas. World Electr. Veh. J. 2021, 12, 232. [Google Scholar] [CrossRef]
- Rathnayake, R.M.D.I.M.; Jayawickrama, T.S.; Melagoda, D.G. The Feasibility of Establishing Electric Vehicle Charging Stations at Public Hotspots in Sri Lanka. In Proceedings of the MERCon 2019—Proceedings, 5th International Multidisciplinary Moratuwa Engineering Research Conference, Moratuwa, Sri Lanka, 3–5 July 2019; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2019; pp. 510–514. [Google Scholar]
- Liu, G.; Kang, L.; Luan, Z.; Qiu, J.; Zheng, F. Charging Station and Power Network Planning for Integrated Electric Vehicles (EVs). Energies 2019, 12, 2595. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Q.; Farnoosh, A.; Chen, S.; Li, Y. GIS-Based Multi-Objective Particle Swarm Optimization of Charging Stations for Electric Vehicles. Energy 2019, 169, 844–853. [Google Scholar] [CrossRef]
- Bilal, M.; Rizwan, M. Integration of Electric Vehicle Charging Stations and Capacitors in Distribution Systems with Vehicle-to-Grid Facility. Energy Sources Part A Recovery Util. Environ. Eff. 2021. [Google Scholar] [CrossRef]
- Liu, Z.; Wen, F.; Ledwich, G. Optimal Planning of Electric-Vehicle Charging Stations in Distribution Systems. IEEE Trans. Power Deliv. 2013, 28, 102–110. [Google Scholar] [CrossRef]
- Zeb, M.Z.; Imran, K.; Khattak, A.; Janjua, A.K.; Pal, A.; Nadeem, M.; Zhang, J.; Khan, S. Optimal Placement of Electric Vehicle Charging Stations in the Active Distribution Network. IEEE Access 2020, 8, 68124–68134. [Google Scholar] [CrossRef]
- Ahmad, F.; Khalid, M.; Panigrahi, B.K. An Enhanced Approach to Optimally Place the Solar Powered Electric Vehicle Charging Station in Distribution Network. J. Energy Storage 2021, 42, 103090. [Google Scholar] [CrossRef]
- Chen, L.; Xu, C.; Song, H.; Jermsittiparsert, K. Optimal Sizing and Sitting of EVCS in the Distribution System Using Metaheuristics: A Case Study. Energy Rep. 2021, 7, 208–217. [Google Scholar] [CrossRef]
- Mehrjerdi, H.; Hemmati, R. Stochastic Model for Electric Vehicle Charging Station Integrated with Wind Energy. Sustain. Energy Technol. Assess. 2020, 37, 100577. [Google Scholar] [CrossRef]
- Hafez, O.; Bhattacharya, K. Optimal Design of Electric Vehicle Charging Stations Considering Various Energy Resources. Renew Energy 2017, 107, 576–589. [Google Scholar] [CrossRef]
- Dai, Q.; Liu, J.; Wei, Q. Optimal Photovoltaic/Battery Energy Storage/Electric Vehicle Charging Station Design Based on Multi-Agent Particle Swarm Optimization Algorithm. Sustainability 2019, 11, 1973. [Google Scholar] [CrossRef]
- Zhang, M.; Yan, Q.; Guan, Y.; Ni, D.; Agundis Tinajero, G.D. Joint Planning of Residential Electric Vehicle Charging Station Integrated with Photovoltaic and Energy Storage Considering Demand Response and Uncertainties. Energy 2024, 298, 131370. [Google Scholar] [CrossRef]
- Chowdhury, R.; Mukherjee, B.K.; Mishra, P.; Mathur, H.D. Performance Assessment of a Distribution System by Simultaneous Optimal Positioning of Electric Vehicle Charging Stations and Distributed Generators. Electr. Power Syst. Res. 2023, 214, 108934. [Google Scholar] [CrossRef]
- Ahmad, F.; Iqbal, A.; Ashraf, I.; Marzband, M.; Khan, I. Optimal Location of Electric Vehicle Charging Station and Its Impact on Distribution Network: A Review. Energy Rep. 2022, 8, 2314–2333. [Google Scholar] [CrossRef]
- Yuvaraj, T.; Devabalaji, K.R.; Thanikanti, S.B.; Aljafari, B.; Nwulu, N. Minimizing the Electric Vehicle Charging Stations Impact in the Distribution Networks by Simultaneous Allocation of DG and DSTATCOM with Considering Uncertainty in Load. Energy Rep. 2023, 10, 1796–1817. [Google Scholar] [CrossRef]
- Kathiravan, K.; Rajnarayanan, P.N. Application of AOA Algorithm for Optimal Placement of Electric Vehicle Charging Station to Minimize Line Losses. Electr. Power Syst. Res. 2023, 214, 108868. [Google Scholar] [CrossRef]
- Krishnamurthy, N.K.; Sabhahit, J.N.; Jadoun, V.K.; Gaonkar, D.N.; Shrivastava, A.; Rao, V.S.; Kudva, G. Optimal Placement and Sizing of Electric Vehicle Charging Infrastructure in a Grid-Tied DC Microgrid Using Modified TLBO Method. Energies 2023, 16, 1781. [Google Scholar] [CrossRef]
- Karmaker, A.K.; Hossain, M.A.; Pota, H.R.; Onen, A.; Jung, J. Energy Management System for Hybrid Renewable Energy-Based Electric Vehicle Charging Station. IEEE Access 2023, 11, 27793–27805. [Google Scholar] [CrossRef]
- Yuvaraj, T.; Devabalaji, K.R.; Thanikanti, S.B.; Pamshetti, V.B.; Nwulu, N.I. Integration of Electric Vehicle Charging Stations and DSTATCOM in Practical Indian Distribution Systems Using Bald Eagle Search Algorithm. IEEE Access 2023, 11, 55149–55168. [Google Scholar] [CrossRef]
- Alshareef, S.; Fathy, A. Efficient Red Kite Optimization Algorithm for Integrating the Renewable Sources and Electric Vehicle Fast Charging Stations in Radial Distribution Networks. Mathematics 2023, 11, 3305. [Google Scholar] [CrossRef]
- Khalid, M.R.; Khan, I.A.; Hameed, S.; Asghar, M.S.J.; Ro, J. A Comprehensive Review on Structural Topologies, Power Levels, Energy Storage Systems, and Standards for Electric Vehicle Charging Stations and Their Impacts on Grid. IEEE Access 2021, 9, 128069–128094. [Google Scholar] [CrossRef]
- Parajuli, A.; Gurung, S.; Chapagain, K. Optimal Placement and Sizing of Battery Energy Storage Systems for Improvement of System Frequency Stability. Electricity 2024, 5, 662–683. [Google Scholar] [CrossRef]
- Saldanha, J.J.; Nied, A.; Trentini, R.; Kutzner, R. AI-based optimal allocation of BESS, EV charging station and DG in distribution network for losses reduction and peak load shaving. Electr. Power Syst. Res. 2024, 234, 110554. [Google Scholar] [CrossRef]
- Alizadeh, M.; Meegahapola, L.; Amani, A.M.; Jalili, M.; Seilsepour, A. Optimal Planning Framework for Battery Energy Storage Systems and Electric Vehicle Charging Stations in Distribution Networks. In Proceedings of the 2024 IEEE International Conference on Industrial Technology (ICIT), Bristol, UK, 25–27 March 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, X.; Huang, Q.; Yan, S.; Xia, J.; Zhao, Y. EVCS Joint BESS Optimal Planning Based on MOTEO Algorithm. In Proceedings of the 2024 IEEE 2nd International Conference on Power Science and Technology (ICPST), Dali, China, 9–11 May 2024; pp. 1949–1954. [Google Scholar] [CrossRef]
- Kazemtarghi, A.; Mallik, A. A two-stage stochastic programming approach for electric energy procurement of EV charging station integrated with BESS and PV. Electr. Power Syst. Res. 2024, 232, 110411. [Google Scholar] [CrossRef]
- Eid, A.; Abdel-Salam, M. Management of electric vehicle charging stations in low-voltage distribution networks integrated with wind turbine–battery energy storage systems using metaheuristic optimization. Eng. Optim. 2024, 56, 1335–1360. [Google Scholar] [CrossRef]
- Kumar, P.M.; Dhilipkumar, R.; Geethamahalakshmi, G.; Sujatha, M. Efficient distribution network based on photovoltaic fed electric vehicle charging station using WSO-RBFNN approach. J. Energy Storage 2025, 106, 114728. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Hu, X.; Qiu, L.; Zang, H. Black-Winged Kite Algorithm: A Nature-Inspired Meta-Heuristic for Solving Benchmark Functions and Engineering Problems. Artif. Intell. Rev. 2024, 57, 98. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium Optimizer: A Novel Optimization Algorithm. Knowl Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Fu, Y.; Liu, D.; Chen, J.; He, L. Secretary Bird Optimization Algorithm: A New Metaheuristic for Solving Global Optimization Problems. Artif. Intell. Rev. 2024, 57, 123. [Google Scholar] [CrossRef]
- Vijay, V.; Venkaiah, C.; Mallesham, V.K.D. Meta Heuristic Algorithm Based Multi Objective Optimal Planning of Rapid Charging Stations and Distribution Generators in a Distribution System Coupled with Transportation Network. Adv. Electr. Electron. Eng. 2023, 20, 493–504. [Google Scholar] [CrossRef]
- Guerraiche, K.; Midouni, F.; Sahraoui, N.E.; Dekhici, L. Application of Equilibrium Optimizer Algorithm for Solving Linear and Non Linear Coordination of Directional Overcurrent Relays. Adv. Electr. Electron. Eng. 2023, 20, 537–548. [Google Scholar] [CrossRef]
- Teng, J.H.; Chang, C.Y. Backward/forward sweep-based harmonic analysis method for distribution systems. IEEE Trans. Power Deliv. 2007, 22, 1665–1672. [Google Scholar] [CrossRef]
- Duong, M.Q.; Pham, T.D.; Nguyen, T.T.; Doan, A.T.; Tran, H.V. Determination of optimal location and sizing of solar photovoltaic distribution generation units in radial distribution systems. Energies 2019, 12, 174. [Google Scholar] [CrossRef]
- Poudyal, R.; Loskot, P.; Parajuli, R. Techno-Economic Feasibility Analysis of a 3-KW PV System Installation in Nepal. Renew. Wind Water Sol. 2021, 8, 5. [Google Scholar] [CrossRef]
- Hadzhiev, I.; Malamov, D.; Balabozov, I.; Yatchev, I. Study of Operational Parameters of a Capacitor Bank with Detuned Reactor for Power Factor Correction in a Low Voltage Network. In Proceedings of the 2020 21st International Symposium on Electrical Apparatus & Technologies (SIELA), Bourgas, Bulgaria, 3–6 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–4. [Google Scholar]
- Hall, J.F.; Chen, D. Performance of a 100 kW wind turbine with a Variable Ratio Gearbox. Renew. Energy 2012, 44, 261–266. [Google Scholar] [CrossRef]
- Pham, T.D.; Nguyen, T.T. Minimize renewable distributed generator costs while achieving high levels of system uniformity and voltage regulation. Ain Shams Eng. J. 2024, 15, 102720. [Google Scholar] [CrossRef]
- Ghiasi, M. Detailed study, multi-objective optimization, and design of an AC-DC smart microgrid with hybrid renewable energy resources. Energy 2019, 169, 496–507. [Google Scholar] [CrossRef]
- Keleshteri, S.F.; Niknam, T.; Ghiasi, M.; Chabok, H. New optimal planning strategy for plug-in electric vehicles charging stations in a coupled power and transportation network. J. Eng. 2023, 2023, e12252. [Google Scholar] [CrossRef]
- Sadeghian, O.; Safari, A. Net saving improvement of capacitor banks in power distribution systems by increasing daily size switching number: A comparative result analysis by artificial intelligence. J. Eng. 2024, 2024, e12357. [Google Scholar] [CrossRef]
- Augusteen, W.A.; Geetha, S.; Rengaraj, R. Economic dispatch incorporation solar energy using particle swarm optimization. In Proceedings of the 2016 3rd International Conference on Electrical Energy Systems (ICEES), Chennai, India, 17–19 March 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 67–73. [Google Scholar]
- Zhang, H.; Yue, D.; Xie, X.; Dou, C.; Sun, F. Gradient decent based multi-objective cultural differential evolution for short-term hydrothermal optimal scheduling of economic emission with integrating wind power and photovoltaic power. Energy 2017, 122, 748–766. [Google Scholar] [CrossRef]
- Oda, E.S.; Abd El Hamed, A.M.; Ali, A.; Elbaset, A.A.; Abd El Sattar, M.; Ebeed, M. Stochastic optimal planning of distribution system considering integrated photovoltaic-based DG and DSTATCOM under uncertainties of loads and solar irradiance. IEEE Access 2021, 9, 26541–26555. [Google Scholar] [CrossRef]
- Zou, K.; Agalgaonkar, A.P.; Muttaqi, K.M.; Perera, S. Distribution system planning with incorporating DG reactive capability and system uncertainties. IEEE Trans. Sustain. Energy 2011, 3, 112–123. [Google Scholar] [CrossRef]
- Petchrompo, S.; Wannakrairot, A.; Parlikad, A.K. Pruning Pareto optimal solutions for multi-objective portfolio asset management. Eur. J. Oper. Res. 2022, 297, 203–220. [Google Scholar] [CrossRef]
- Rao, R.S.; Narasimham, S.V.L.; Ramalingaraju, M. Optimal capacitor placement in a radial distribution system using plant growth simulation algorithm. Int. J. Electr. Power Energy Syst. 2011, 33, 1133–1139. [Google Scholar] [CrossRef]
- Tamilselvan, V.; Jayabarathi, T.; Raghunathan, T.; Yang, X.S. Optimal capacitor placement in radial distribution systems using flower pollination algorithm. Alex. Eng. J. 2018, 57, 2775–2786. [Google Scholar] [CrossRef]
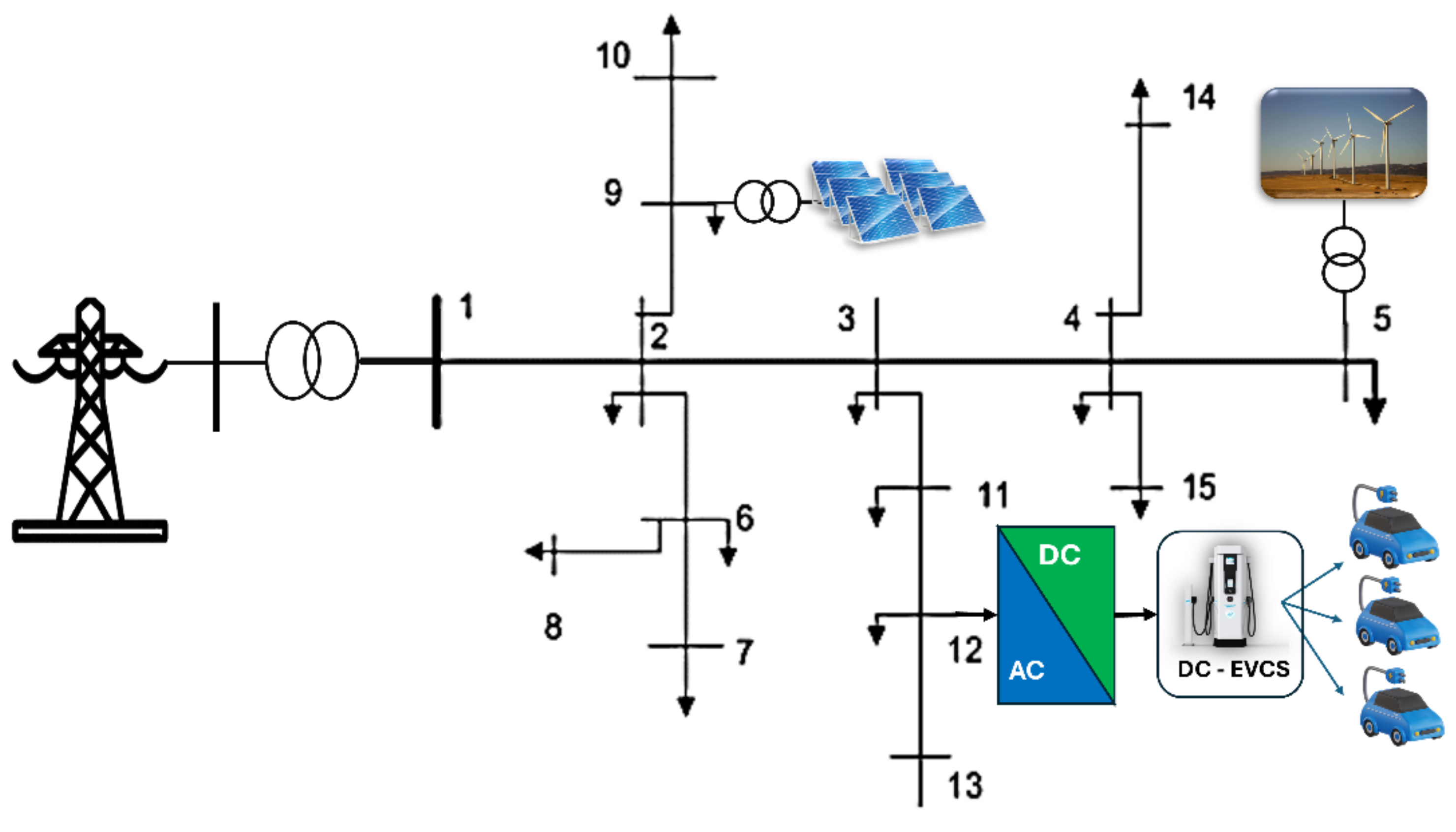
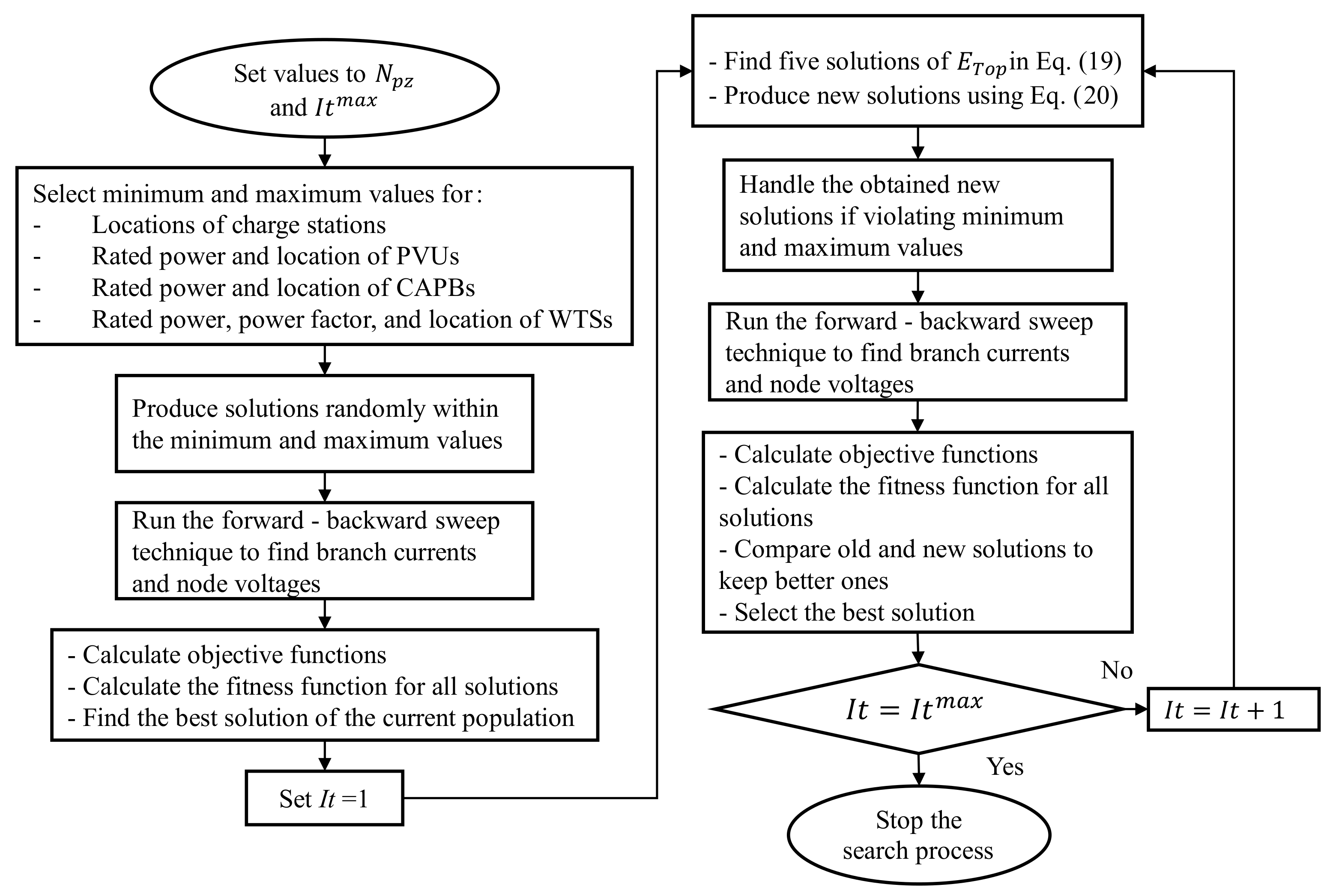
| Scenario | PVUs | CAPBs | WTs | EVCSs |
|---|---|---|---|---|
| 1 | - | - | - | 1 Level 1 station, 1 Level 2 station, and 1 Level 3 station |
| 2 | 3 PVUs with power factor of 1.0 for each PVU | - | - | |
| 3 | 3 PVUs: power factor of 1.0, 3 kW solar panel | 3 CAPBs: 30 kVAr for each step | - | |
| 4 | - | - | 3 WTSs: 100 kW WT and power factor of [0.85, 0.95] | |
| 5 | 3 PVUs: power factor of 1.0, 3 kW solar panel | 3 CAPBs: 30 kVAr for each step | 3 WTSs: 100 kW WT and power factor of [0.85, 0.95] |
| Type | Rated Power of Each Charger (kW) | Number of Chargers/EVs | Rated Power of Each EVCS (kW) |
|---|---|---|---|
| L1 EVCS | 1.9 | 100 | 190 |
| L2 EVCS | 4.0 | 50 | 200 |
| L3 EVCS | 100 | 10 | 1000 |
| Scenario | Description | Population | Maximum Iteration Number | Number of Control Variables |
|---|---|---|---|---|
| Base | Without EVCS and auxiliary devices | - | - | - |
| 1 | 3 EVCSs | 40 | 200 | 3 |
| 2 | 3 EVCSs + 3 PVUs | 40 | 500 | 3 + 6 = 9 |
| 3 | 3 EVCSs + 3 PVUs + 3 CAPBs | 100 | 500 | 3 + 6 + 6 = 15 |
| 4 | 3 EVCSs + 3 WTSs | 100 | 500 | 3 + 9 = 12 |
| 5 | 3 EVCSs + 3 PVUs + 3 CAPBs+ 3 WTSs | 100 | 1000 | 3 + 6 + 6 + 9 = 24 |
| Method | EO | BKA | SBOA |
|---|---|---|---|
| Best loss (kW) | 225.031 | 225.031 | 225.031 |
| Mean loss (kW) | 225.031 | 225.031 | 225.031 |
| Maximum loss (kW) | 225.032 | 225.032 | 225.032 |
| STD | 4.27 × 10−5 | 4.31 × 10−5 | 4.31 × 10−5 |
| Time execution (s) | 102.532439 | 71.980158 | 1026.675761 |
| Scenario | Power Loss (kW) | Percentage of Power Loss Reduction (%) |
|---|---|---|
| Base | 255.0185 (#) | - |
| 1 | 225.031 | - |
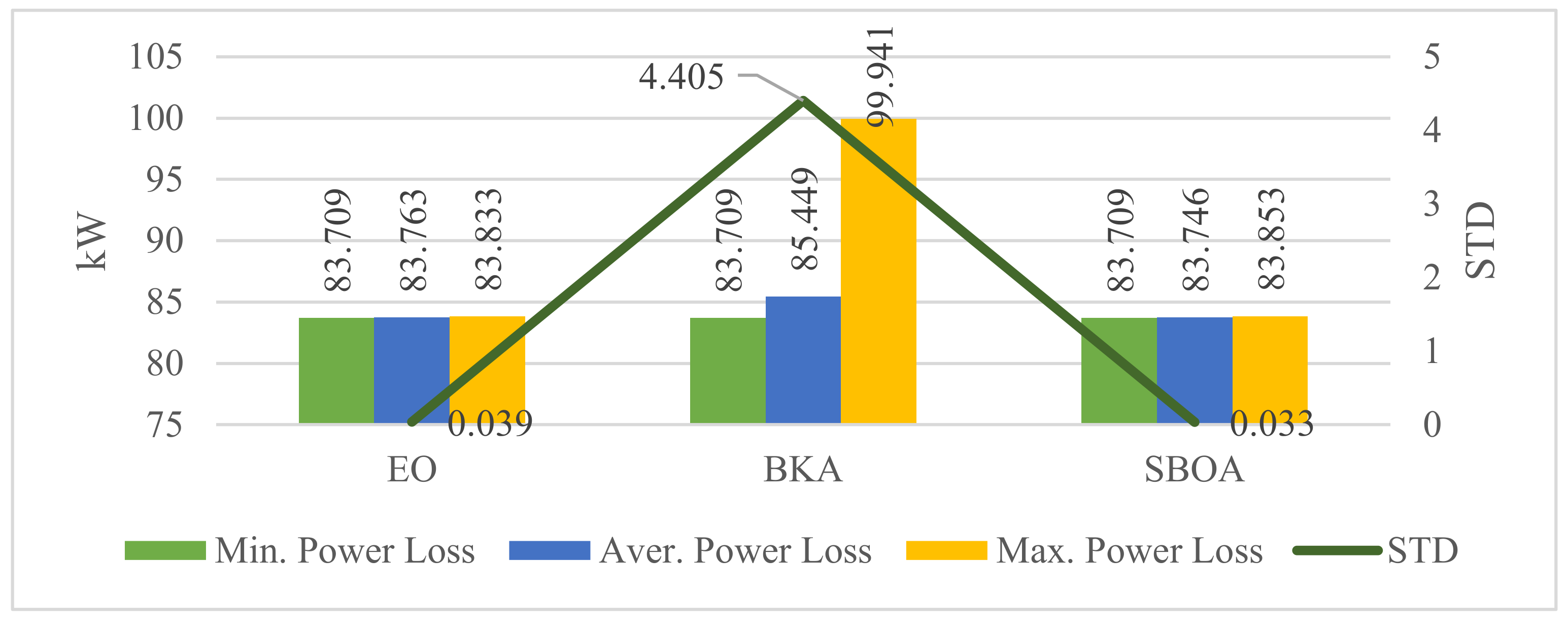
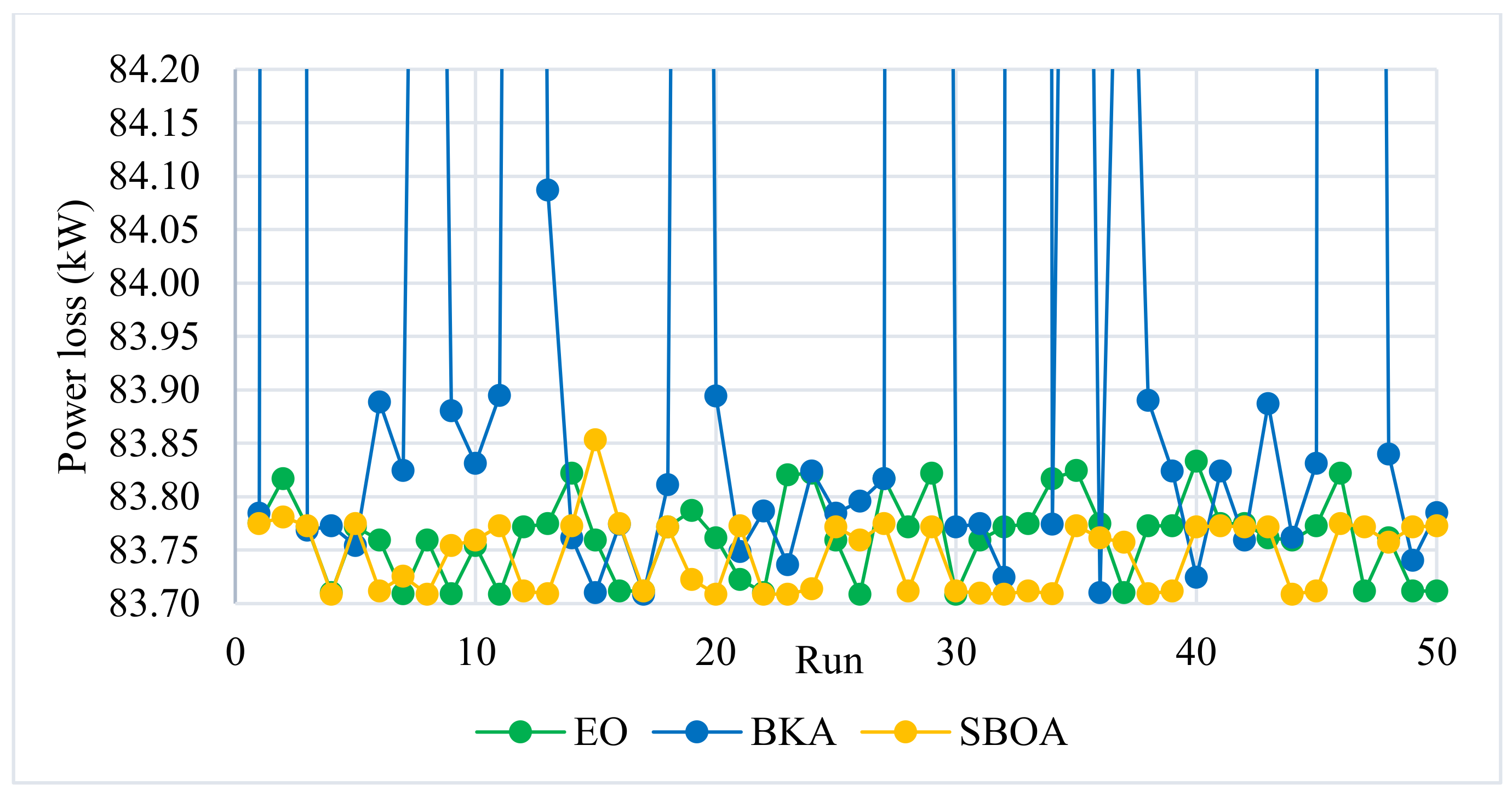
| 2 | 83.709 | 62.80 |
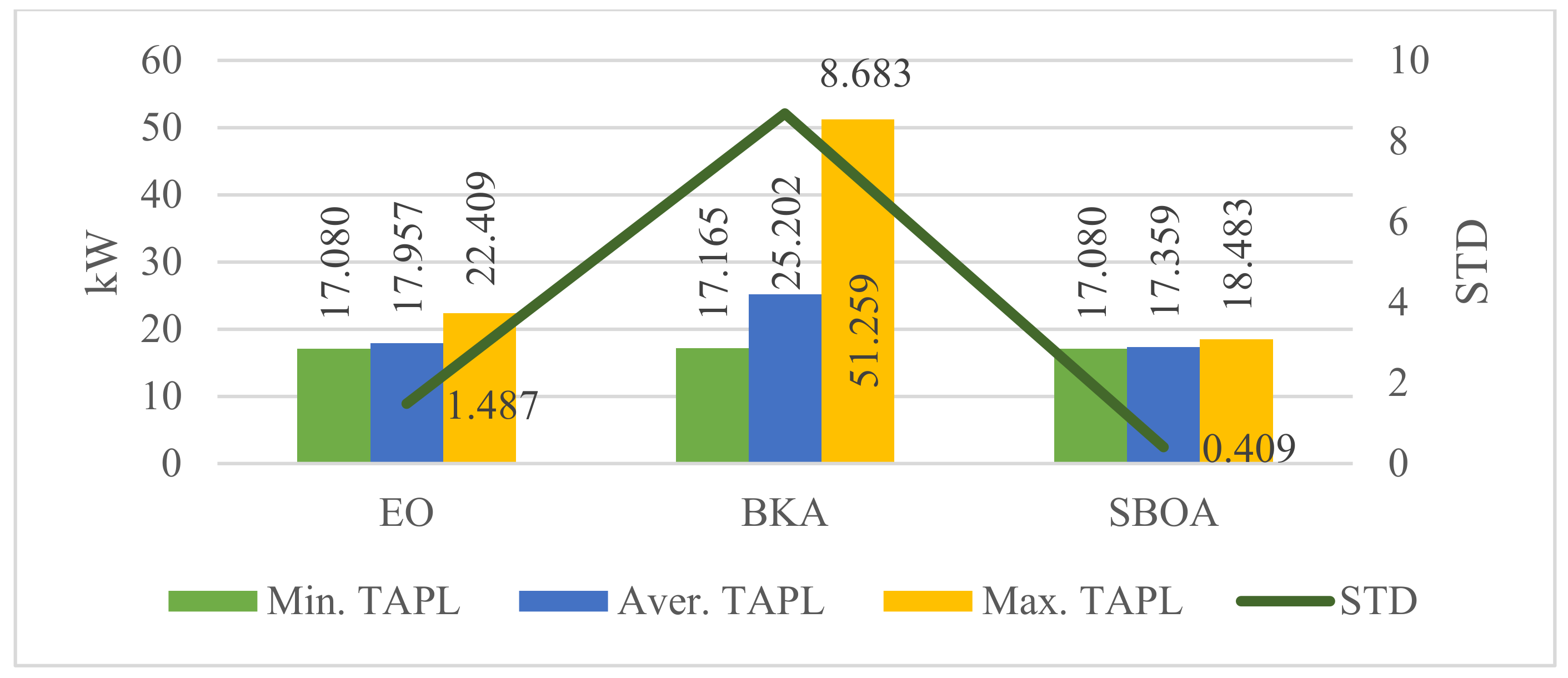
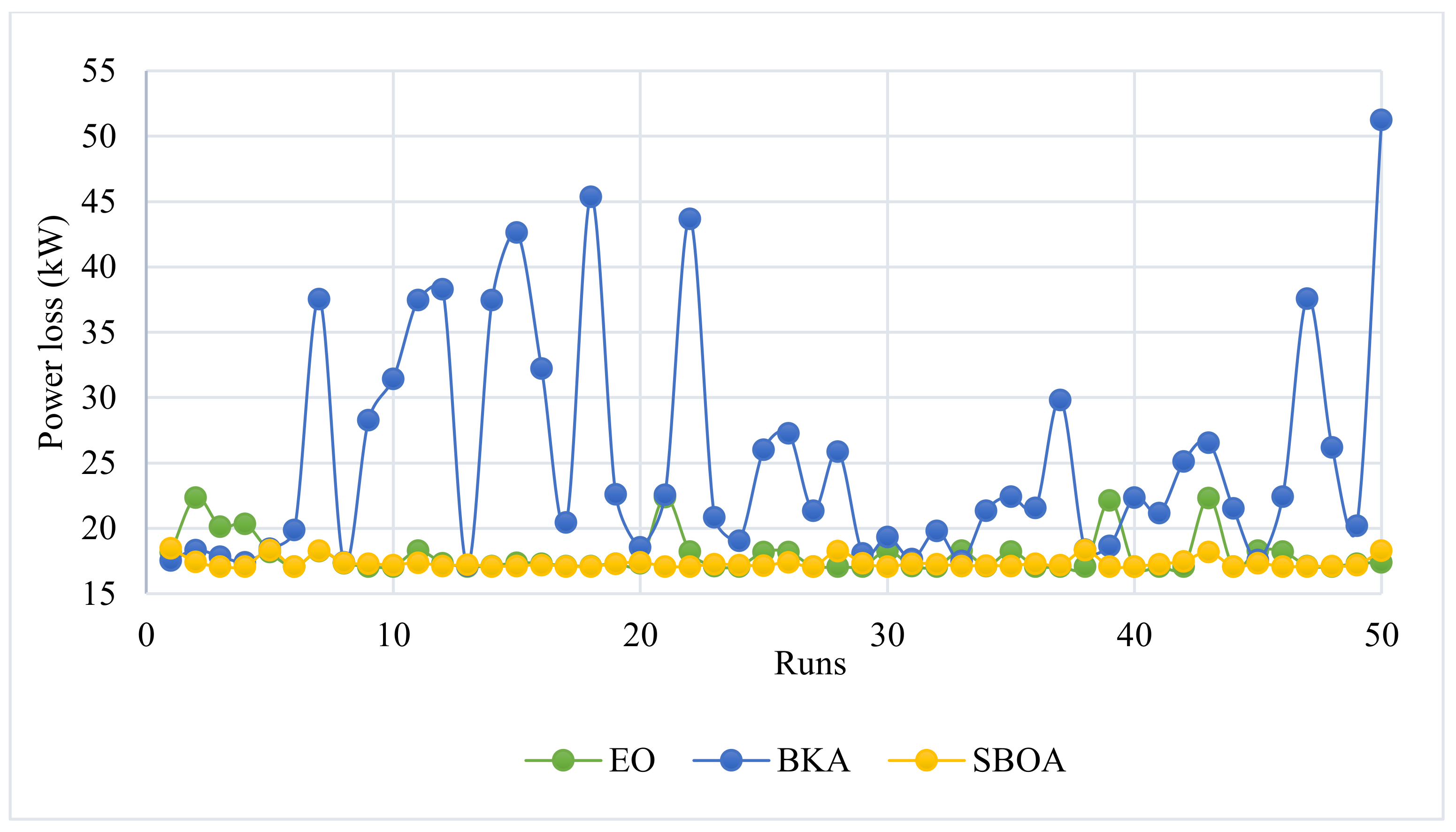
| 3 | 17.080 | 92.41 |
| 4 | 31.634 | 85.94 |
| 5 | 1.803 | 99.20 |
| Scenario | Grid Power (kW) | EO | BKA | SBOA | The Best Algorithm |
|---|---|---|---|---|---|
| 1 | Minimum | 5416.521 * | 5416.521 * | 5416.521 * | EO, BKA, SBOA |
| Mean | 5416.521 | 5416.521 | 5416.521 | ||
| Maximum | 5416.522 | 5416.522 | 5416.522 | ||
| STD | 4.32 × 10−5 * | 4.39 × 10−5 * | 4.31 × 10−5 * | ||
| 2 | Minimum | 3475.199 * | 3475.215 | 3475.199 * | EO, SBOA |
| Mean | 3475.248 | 3484.043 | 3475.252 | ||
| Maximum | 3475.312 | 3522.981 | 3475.334 | ||
| STD | 0.036 ** | 11.476 | 0.040 | ||
| 3 | Minimum | 3408.569 * | 3410.718 | 3408.569 * | EO, SBOA |
| Mean | 3410.571 | 3428.051 | 3409.602 | ||
| Maximum | 3430.959 | 3475.832 | 3420.839 | ||
| STD | 4.432 | 15.205 | 2.369 ** | ||
| 4 | Minimum | 3723.1242 * | 3723.12521 | 3723.1242 * | EO, SBOA |
| Mean | 3725.136 | 3737.0985 | 3724.966 | ||
| Maximum | 3732.2242 | 3763.0824 | 3732.637 | ||
| STD | 3.7844 | 13.8621 | 3.679 * | ||
| 5 | Minimum | 1893.2864 * | 1895.97115 | 1893.471 | EO |
| Mean | 1895.0782 | 1901.5247 | 1895.337 | ||
| Maximum | 1896.7659 | 1936.1058 | 1899.513 | ||
| STD | 1.0645 * | 6.4806 | 1.307 |
| Scenario | TVD (pu) | EO | BKA | SBOA | The Best Algorithm |
|---|---|---|---|---|---|
| 1 | Minimum | 1.838 * | 1.838 * | 1.838 * | EO, BKA, SBOA |
| Mean | 1.838 | 1.838 | 1.838 | ||
| Maximum | 1.838 | 1.838 | 1.838 | ||
| STD | 3.11 × 10−7 * | 8.53 × 10−7 | 4.91 × 10−7 | ||
| 2 | Minimum | 0.6702 * | 0.6702 * | 0.6702 * | EO, SBOA |
| Mean | 0.6819 | 0.6924 | 0.6771 | ||
| Maximum | 0.6926 | 0.7407 | 0.6926 | ||
| STD | 0.011 ** | 0.0176 | 0.011 ** | ||
| 3 | Minimum | 0.2609 * | 0.2694 | 0.2611 | EO |
| Mean | 0.2821 | 0.3892 | 0.2807 | ||
| Maximum | 0.5297 | 0.6603 | 0.4067 | ||
| STD | 0.0457 | 0.0948 | 0.0314 | ||
| 4 | Minimum | 0.5923 * | 0.5923 * | 0.5923 * | EO, BKA, SBOA |
| Mean | 0.6113 | 0.6721 | 0.6067 | ||
| Maximum | 0.6513 | 0.9449 | 0.6602 | ||
| STD | 0.0276 | 0.0921 | 0.0247 ** | ||
| 5 | Minimum | 0.026 * | 0.0356 | 0.0284 | EO |
| Mean | 0.0368 | 0.0798 | 0.043 | ||
| Maximum | 0.0499 | 0.2982 | 0.0971 | ||
| STD | 0.0056 ** | 0.0579 | 0.0103 |
| Scenario | Description | Power Loss (kW) | Grid Power (kW) | TVD (pu) |
|---|---|---|---|---|
| Base | - | 225 | 4026.49 | 1.837 |
| 1 | 3 EVCSs | 225.031 | 5416.521 | 1.838 |
| 2 | 3 EVCSs + 3 PVUs | 83.709 | 3475.199 | 0.6702 |
| 3 | 3 EVCSs + 3 PVUs + 3 CAPBs | 17.08 | 3408.569 | 0.2609 |
| 4 | 3 EVCSs + 3 WTSs | 31.6342 | 3723.124 | 0.5923 |
| 5 | 3 EVCSs + 3 PVUs + 3 CAPBs + 3 WTSs | 1.8242 | 1893.2864 | 0.026 |
| Scenario | Loss Objective | Grid Power Objective | TVD Objective |
|---|---|---|---|
| 1 | 1.838 | 1.838 | 1.838 |
| 2 | 0.916 | 0.916 | 0.67 |
| 3 | 0.346 | 0.346 | 0.261 |
| 4 | 0.816 | 0.816 | 0.592 |
| 5 | 0.0727 | 0.0578 | 0.0265 |
| Hour | Radiation (W/m2) | Hour | Radiation (W/m2) | Hour | Radiation (W/m2) |
|---|---|---|---|---|---|
| 1 | 0 | 9 | 375 | 17 | 291 |
| 2 | 0 | 10 | 503 | 18 | 86 |
| 3 | 0 | 11 | 617 | 19 | 0 |
| 4 | 0 | 12 | 868 | 20 | 0 |
| 5 | 0 | 13 | 703 | 21 | 0 |
| 6 | 0 | 14 | 736 | 22 | 0 |
| 7 | 111 | 15 | 586 | 23 | 0 |
| 8 | 311 | 16 | 425 | 25 | 0 |
| Hour | Wind Speed (m/s) | Hour | Wind Speed (m/s) | Hour | Wind Speed (m/s) |
|---|---|---|---|---|---|
| 1 | 13.25 | 9 | 12.90 | 17 | 13.75 |
| 2 | 14 | 10 | 12.20 | 18 | 12.60 |
| 3 | 12.75 | 11 | 15 | 19 | 11.50 |
| 4 | 11.90 | 12 | 13.25 | 20 | 11.90 |
| 5 | 12.5 | 13 | 14.30 | 21 | 14.50 |
| 6 | 13.90 | 14 | 14.10 | 22 | 16.00 |
| 7 | 11.80 | 15 | 14.25 | 23 | 12.70 |
| 8 | 12.75 | 16 | 11.75 | 25 | 13.00 |
| Power Source | Capital Price | Operating and Maintenance Price | Annual Price |
|---|---|---|---|
| Wind turbines [55] | 1882 (USD/kW) | 0.01 (USD/kWh) | - |
| Solar panel [56] | 770 (USD/kW) | 0.01 (USD/kWh) | - |
| Capacitor (600 kVar) | 1320 (USD) [57] | - | 0.22 (USD/kVar year) [58] |
| Parameters | Total Grid Energy (kWh/day) | Grid Cost (USD/day) | Grid Cost (USD/20 Years) |
|---|---|---|---|
| Case 2 | 80,153.1037 | 7694.69795 | 56,171,295.1 |
| Case 4 | 39,578.8509 | 3799.56969 | 27,736,858.7 |
| Cost Reduction (USD) | 28,434,436.3 | ||
| Device-Rated Power | Total Gen. (kWh/day) | Capital Cost (USD) | Annual Cost (20 Years) | O & M Cost (USD/20 Years) | Total Cost (USD) |
|---|---|---|---|---|---|
| PVU1-500 kW | 3217.98 | 385,000 | - | 234,912.54 | 619,912.5447 |
| PVU2-500 kW | 3216.89 | 385,000 | - | 234,832.71 | 619,832.705 |
| PVU3-500 kW | 3217.38 | 385,000 | - | 234,868.43 | 619,868.4299 |
| WTS1-600 kW | 9825.21 | 1,129,200 | - | 717,240.00 | 1,846,439.998 |
| WTS2-600 kW | 9825.72 | 1,129,200 | - | 717,277.38 | 1,846,477.383 |
| WTS3-600 kW | 9824.12 | 1,129,200 | - | 717,160.94 | 1,846,360.941 |
| CAPB1-600 kVar | - | 1320 | 2640 | - | 3960 |
| CAPB2-600 kVar | - | 1320 | 2640 | - | 3960 |
| CAPB3-600 kVar | - | 1320 | 2640 | - | 3960 |
| Total costs for all devices | 7,410,772 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duong, M.P.; Le, M.-H.; Nguyen, T.T.; Duong, M.Q.; Doan, A.T. Economic and Technical Aspects of Power Grids with Electric Vehicle Charge Stations, Sustainable Energies, and Compensators. Sustainability 2025, 17, 376. https://doi.org/10.3390/su17010376
Duong MP, Le M-H, Nguyen TT, Duong MQ, Doan AT. Economic and Technical Aspects of Power Grids with Electric Vehicle Charge Stations, Sustainable Energies, and Compensators. Sustainability. 2025; 17(1):376. https://doi.org/10.3390/su17010376
Chicago/Turabian StyleDuong, Minh Phuc, My-Ha Le, Thang Trung Nguyen, Minh Quan Duong, and Anh Tuan Doan. 2025. "Economic and Technical Aspects of Power Grids with Electric Vehicle Charge Stations, Sustainable Energies, and Compensators" Sustainability 17, no. 1: 376. https://doi.org/10.3390/su17010376
APA StyleDuong, M. P., Le, M.-H., Nguyen, T. T., Duong, M. Q., & Doan, A. T. (2025). Economic and Technical Aspects of Power Grids with Electric Vehicle Charge Stations, Sustainable Energies, and Compensators. Sustainability, 17(1), 376. https://doi.org/10.3390/su17010376







