Should Charging Stations Provide Service for Plug-In Hybrid Electric Vehicles During Holidays?
Abstract
1. Introduction
2. Literature Review
3. Basic Model
3.1. Resource Allocation Plan
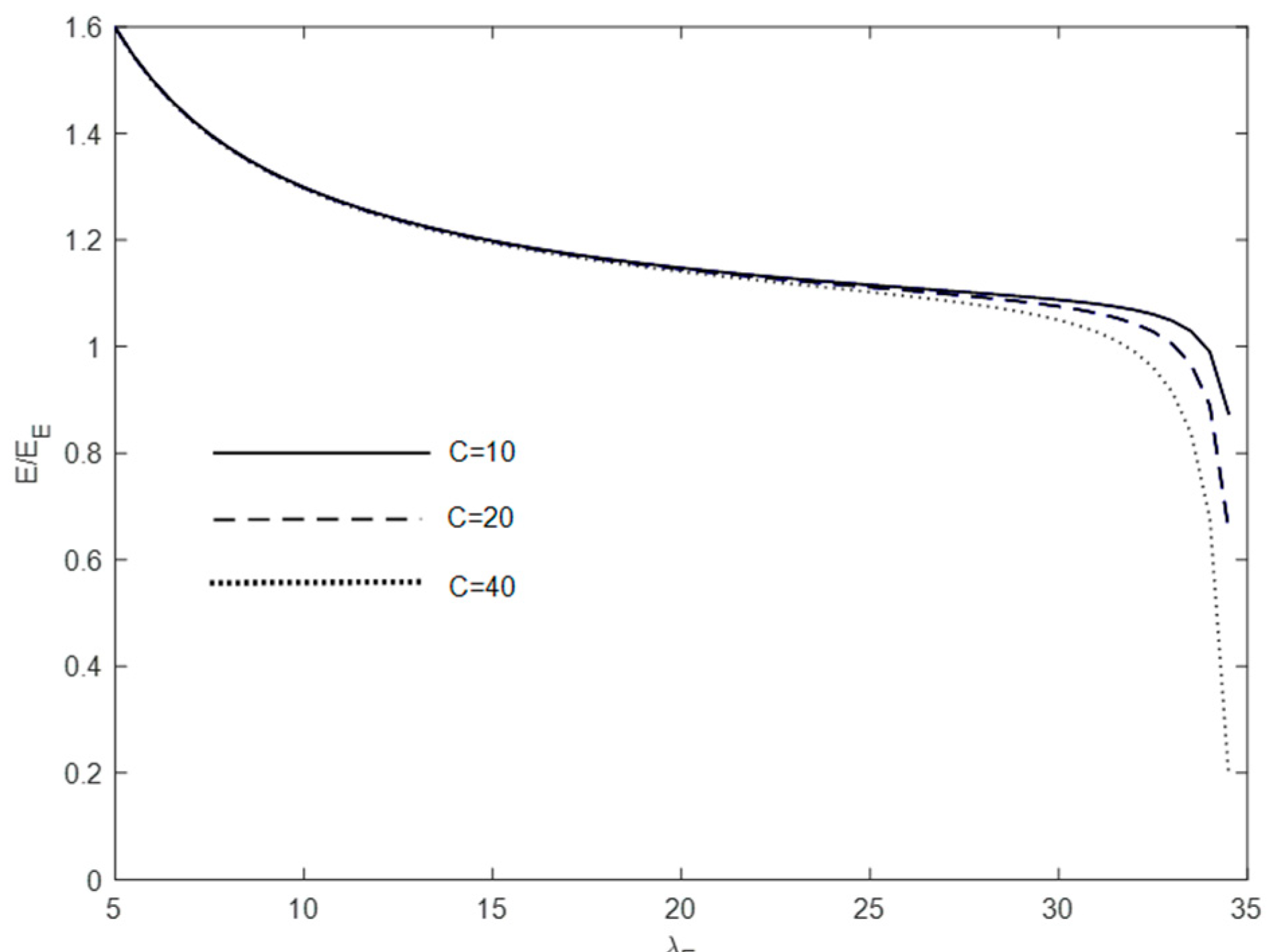
3.2. Economic Situation of Serving PHEVs
4. Extension to Including Impatient NEV Drivers
4.1. Queuing System with Balking
4.1.1. Resource Allocation Plan
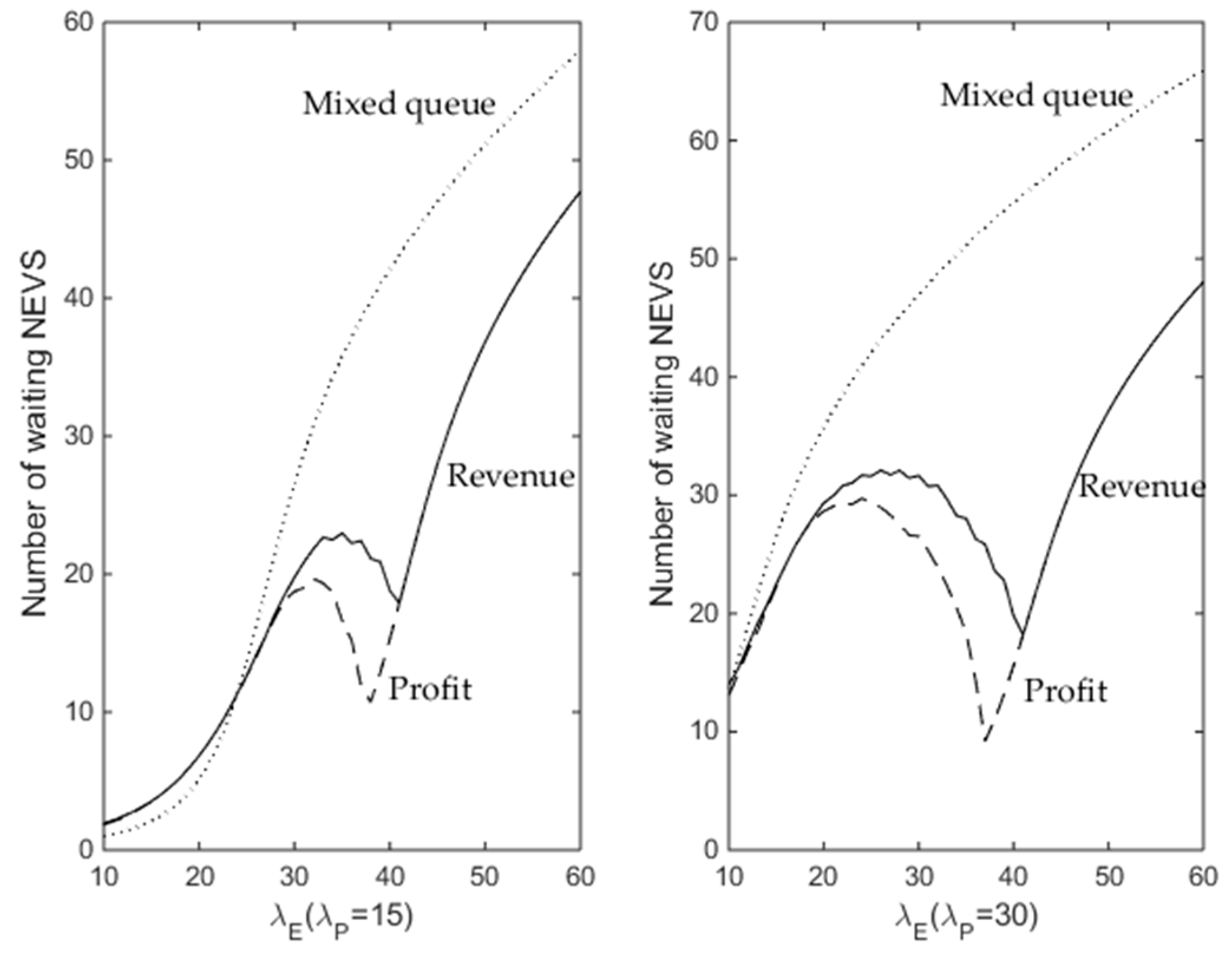
4.1.2. Comparison of Queueing Disciplines
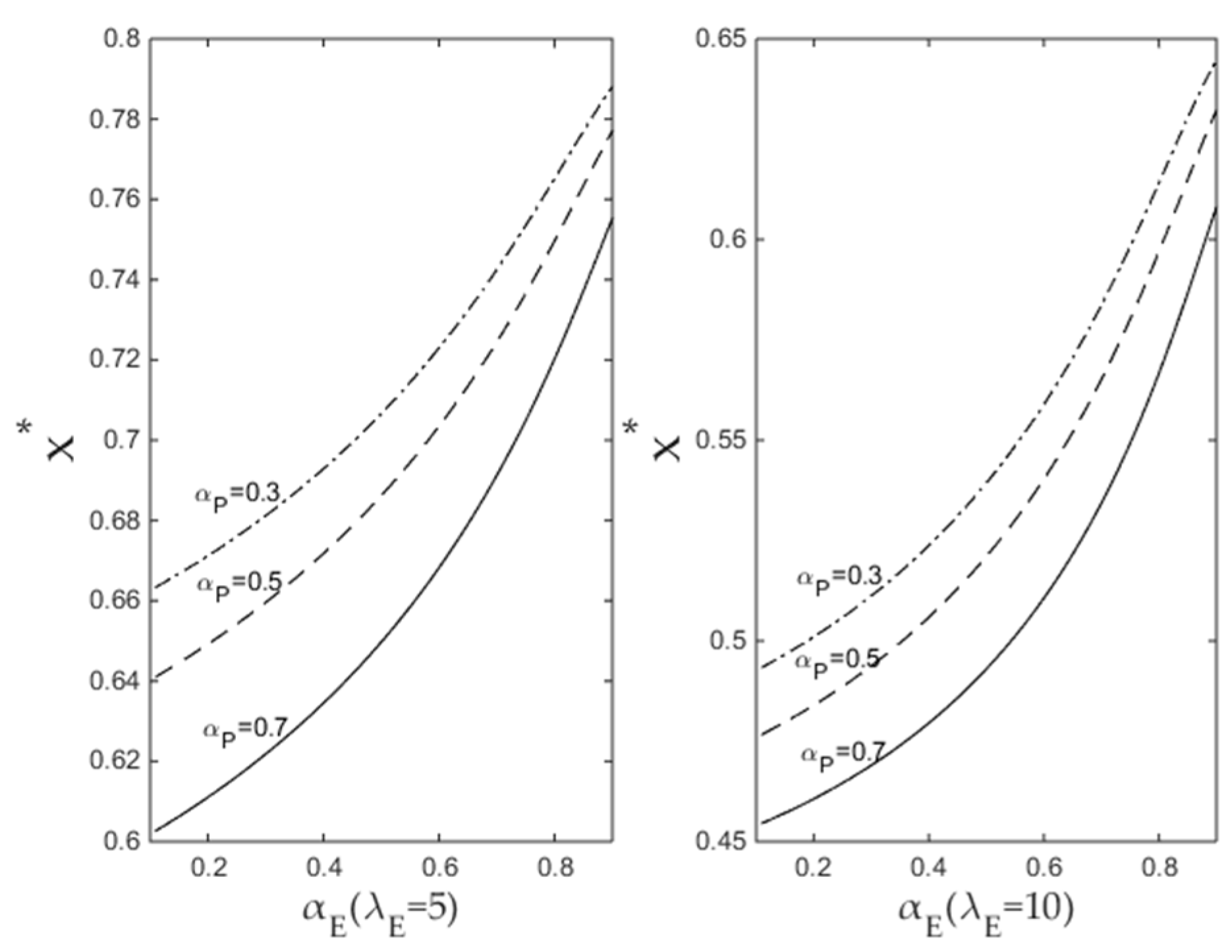
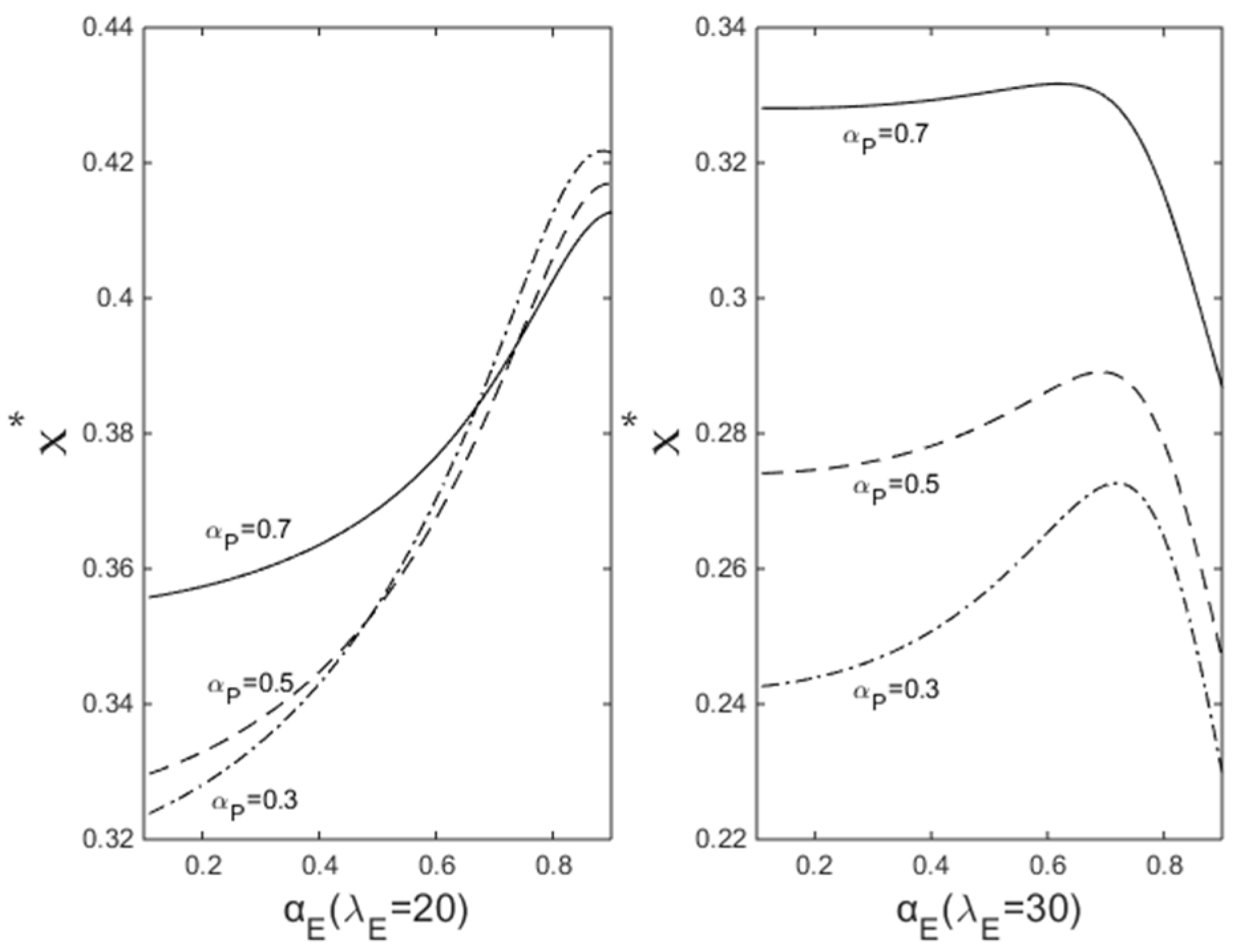
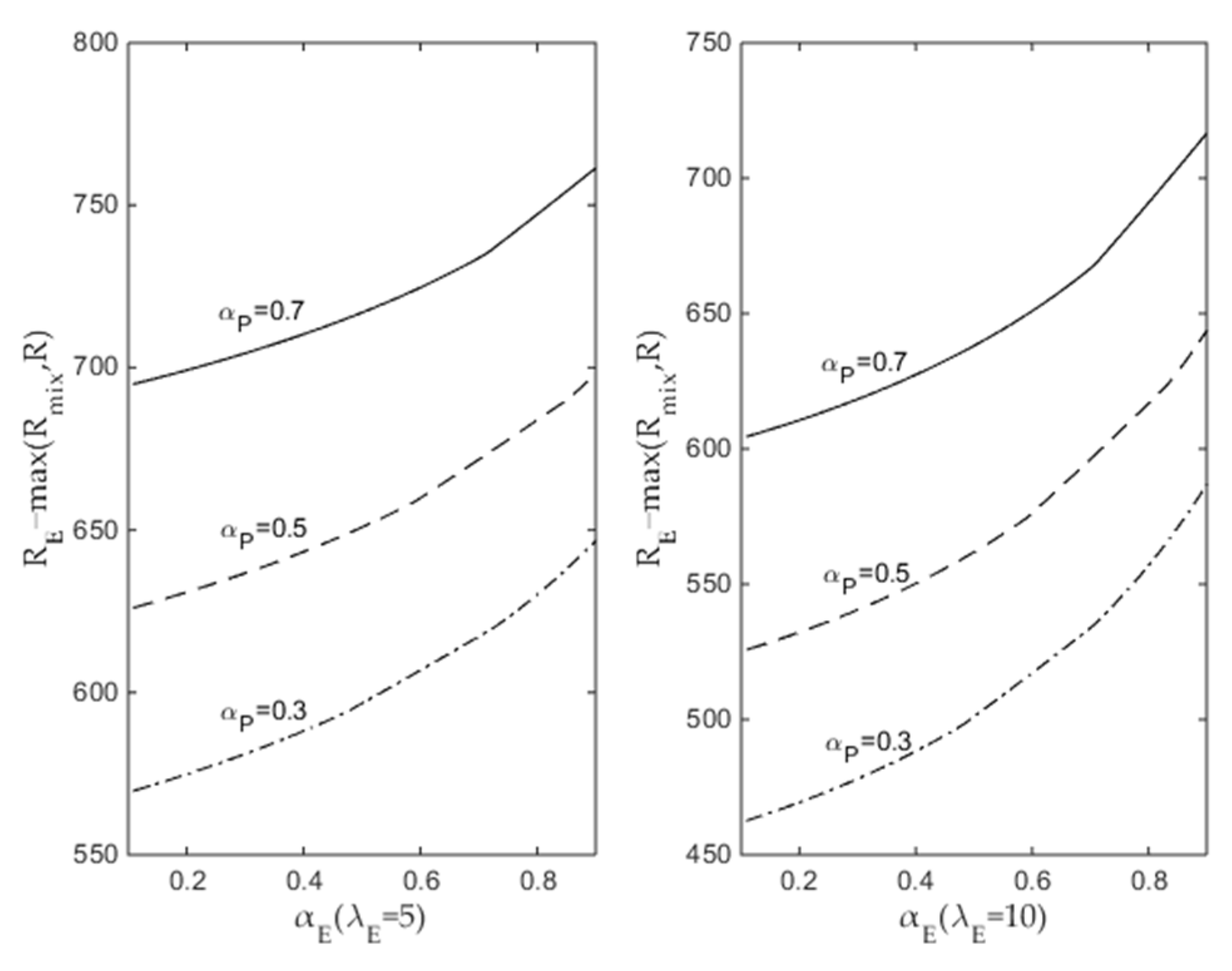
4.1.3. Economic Situation of Serving PHEVs
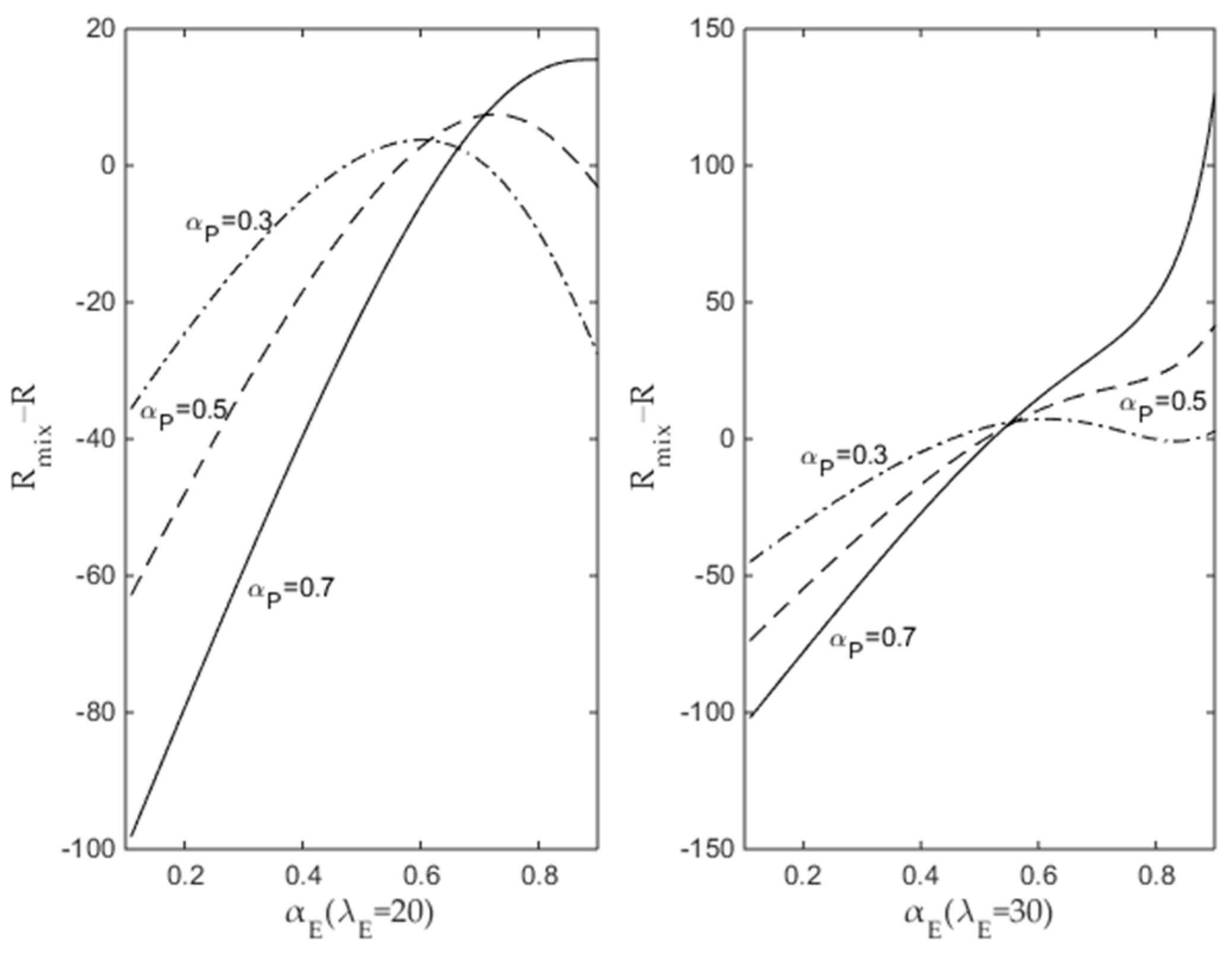
4.2. Queuing System with Balking and Reneging
5. Conclusions
- This research assumes that marginal revenue of charging one NEV is exogenous. In reality, charging stations can adjust the price based on the service ability and the arrival rate of the NEVs. Studying the service resource allocation problem with pricing is an interesting research topic.
- Service resource management is assumed to be static, which means that the manager allocates a fixed amount of charging resources to different kinds of NEVs in advance. In actual operation management, managers may dynamically adjust the service allocation plan based on the length of the EV queue and PHEV queue. Dynamically adjusting resource allocation in order to charge the NEVs is also a promising topic.
- The arrival and service processes are assumed to be Poisson distributed. In practice, the real processes may be more complex. Methods like deep learning can be applied to estimate the arrival and service processes. Expect for queue theory, applying scheduling methods for the operation of charging stations is another research option.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
- From the proof of Proposition 1, we hold that
References
- Zhang, T.; Zhang, J.; Zhao, F.; Ru, Y.; Sutherland, J.W. Allocating resources for a restaurant that serves regular and group-buying customers. Electron. Commer. Res. 2020, 20, 883–913. [Google Scholar] [CrossRef]
- Jarvis, J.; Climent, L.; Arbelaez, A. Smart and sustainable scheduling of charging events for electric buses. Top 2024, 32, 22–56. [Google Scholar] [CrossRef]
- Bac, U.; Erdem, M. Optimization of electric vehicle recharge schedule and routing problem with time windows and partial recharge: A comparative study for an urban logistics fleet. Sustain. Cities Soc. 2021, 70, 102883. [Google Scholar] [CrossRef]
- Syla, A.; Rinaldi, A.; Parra, D.; Patel, M.K. Optimal capacity planning for the electrification of personal transport: The interplay between flexible charging and energy system infrastructure. Sustain. Cities Soc. 2024, 192, 114214. [Google Scholar] [CrossRef]
- Kim, J.; Oh, H.; Lee, J. Data-driven cost-effective capacity provisioning scheme in electric vehicle charging facility. Comput. Ind. Eng. 2022, 173, 108743. [Google Scholar] [CrossRef]
- Wu, Y.; Aziz, S.; Haque, M. Techno-economic modelling for energy cost minimization of a university campus to support electric vehicle charging with photovoltaic capacity optimization. Renew. Energy 2023, 219, 119427. [Google Scholar] [CrossRef]
- Jeon, S.; Park, J.; Kang, B.; Lee, H. Study on Battery Charging Strategy of Electric Vehicles Considering Battery Capacity. IEEE Access 2021, 9, 89757–89767. [Google Scholar] [CrossRef]
- Esmaeilnejad, S.; Kattan, L.; Wirasinghe, S.C. Optimal charging station locations and durations for a transit route with battery-electric buses: A two-stage stochastic programming approach with consideration of weather conditions. Transp. Res. Part C Emerg. Technol. 2023, 156, 104327. [Google Scholar] [CrossRef]
- Wu, X.; Feng, Q.; Bai, C.; Lai, C.; Jia, Y.; Lai, L. A novel fast-charging stations locational planning model for electric bus transit system. Energy 2021, 224, 120106. [Google Scholar] [CrossRef]
- Yin, W.; Ji, J.; Qin, X. Study on optimal configuration of EV charging stations based on second-order cone. Energy 2023, 284, 128494. [Google Scholar] [CrossRef]
- Wang, S.; Bi, S.; Zhang, Y.; Huang, J.; Huang, J. Electrical Vehicle Charging Station Profit Maximization: Admission, Pricing, and Online Scheduling. IEEE Trans. Sustain. Energy 2018, 9, 1722–1731. [Google Scholar] [CrossRef]
- Amin, A.; Tareen, W.U.K.; Usman, M.; Ali, H.; Bari, I.; Horan, B.; Mekhilef, S.; Asif, M.; Ahmed, S.; Mahmood, A. A Review of Optimal Charging Strategy for Electric Vehicles under Dynamic Pricing Schemes in the Distribution Charging Network. Sustainability 2020, 12, 10160. [Google Scholar] [CrossRef]
- Yun, B.; Sun, D.; Zhang, Y.; Deng, S.; Xiong, J. A Charging Location Choice Model for Plug-In Hybrid Electric Vehicle Users. Sustainability 2019, 11, 5761. [Google Scholar] [CrossRef]
- Ma, J.; Zhu, Y.; Chen, D.; Zhang, C.; Song, M.; Zhang, H.; Chen, J.; Zhang, K. Analysis of Urban Electric Vehicle Adoption Based on Operating Costs in Urban Transportation Network. Systems 2023, 11, 149. [Google Scholar] [CrossRef]
- Zhu, T.; Boyles, S.; Unnikrishnan, A. Plug-In Hybrid Electric Vehicle Traveling-Salesman Problem with Drone. Transp. Res. Rec. 2024, 03611981241278351. [Google Scholar] [CrossRef]
- Wu, F.; Adulyasak, Y.; Cordeau, J. Modeling and Solving the Traveling Salesman Problem with Speed Optimization for a Plug-In Hybrid Electric Vehicle. Transp. Sci. 2024, 58, 557–683. [Google Scholar] [CrossRef]
- Kim, T.; Kwak, J.; Chong, S. Dynamic Pricing, Scheduling, and Energy Management for Profit Maximization in PHEV Charging Stations. IEEE Trans. Veh. Technol. 2017, 66, 1011–1026. [Google Scholar] [CrossRef]
- Zhu, Z.; Gao, Z.; Zheng, J.; Du, H. Charging Station Planning for Plug-In Electric Vehicles. J. Syst. Sci. Syst. Eng. 2018, 27, 24–45. [Google Scholar] [CrossRef]
- Yi, T.; Cheng, X.-B.; Zheng, H.; Liu, J.-P. Research on Location and Capacity Optimization Method for Electric Vehicle Charging Stations Considering User’s Comprehensive Satisfaction. Energies 2019, 12, 1915. [Google Scholar] [CrossRef]
- Vijay, V.; Venkaiah, C.; Kumar, D. Multi objective queue theory based optimal planning of rapid charging stations and distributed generators in coupled transportation and distribution network. Energy Storage 2024, 6, e484. [Google Scholar] [CrossRef]
- Xiao, D.; An, S.; Cai, H.A.; Wang, J.; Cai, H. An optimization model for electric vehicle charging infrastructure planning considering queuing behavior with finite queue length. J. Energy Storage 2020, 29, 101317. [Google Scholar] [CrossRef]
- Meng, F.; Pei, W.; Zhang, Q.; Zhang, Y.; Ma, B.; Li, L. Research on the capacity of charging stations based on queuing theory and energy storage scheduling optimization sharing strategy. J. Energy Storage 2024, 96, 112673. [Google Scholar] [CrossRef]
- Oonsivilai, A.; Boribun, B.; Pao-la-or, P. Integration of Distributed Generation and Plug-in Electric Vehicles on Power Distribution System by Using Queuing Theory. Energies 2023, 16, 3146. [Google Scholar] [CrossRef]
- Esmailirad, S.; Ghiasian, A.; Rabiee, A. An Extended M/M/K/K Queueing Model to Analyze the Profit of a Multiservice Electric Vehicle Charging Station. IEEE Trans. Veh. Technol. 2021, 70, 3007–3016. [Google Scholar] [CrossRef]
- Liu, B.; Pantelidis, T.; Tam, S.; Chow, J. An electric vehicle charging station access equilibrium model with M/D/C queueing. Int. J. Sustain. Transp. 2023, 17, 228–244. [Google Scholar] [CrossRef]
- Wu, T.; Fainman, E.; Maïzi, Y.; Shu, J.; Li, Y. Allocate electric vehicles’ public charging stations with charging demand uncertainty. Transp. Res. Part D Transp. Environ. 2024, 130, 104178. [Google Scholar] [CrossRef]
- Huang, S.; Xiong, L.; Zhou, Y.; Gao, F.; Jia, Q.; Li, X.; Li, X.; Wang, Z.; Khan, M.W. Robust distributed fixed-time fault-tolerant control for shipboard microgrids with actuator fault. IEEE Trans. Transp. Electrif. 2024; early access. [Google Scholar] [CrossRef]
- Pourvaziri, H.; Sarhadi, H.; Azad, N.; Afshari, H.; Taghavi, M. Planning of electric vehicle charging stations: An integrated deep learning and queueing theory approach. Transp. Res. Part E 2024, 186, 103568. [Google Scholar] [CrossRef]
- Zhang, X.; Chan, K.; Li, H.; Wang, H.; Qiu, J.; Wang, G. Deep-Learning-Based Probabilistic Forecasting of Electric Vehicle Charging Load With a Novel Queuing Model. IEEE Trans. Cybern. 2021, 51, 3157–3170. [Google Scholar] [CrossRef] [PubMed]
- Gross, D.; Shortle, J.; Thompson, J.; Harris, C. Fundamentals of Queueing Theory; Wileys: Hoboken, NJ, USA, 2008. [Google Scholar] [CrossRef]




| Objective | Queueing Structures | Related Literature |
|---|---|---|
| Minimizing cost, driving distance, or waiting time | M/M/C | [18,19,20] |
| Minimizing cost | M/M/S/N | [21,22,24] |
| Minimizing power loss | M/M/S/N | [23] |
| Calculating waiting time | M/D/C | [25] |
| Minimizing cost | M/G/N/N | [26] |
| Minimizing cost and minimizing waiting time | GI/GI/C | [28] |
| PHEV Queue | EV Queue | |
|---|---|---|
| Length | ||
| Service rate | ||
| Arrival rate | ||
| Traffic intensity | ||
| Actual arrival rate | ||
| Length of the queue | ||
| Average revenue of charging one NEV | ||
| Waiting cost per NEV per unit time | ||
| Profit | ||
| Mixed Queue | |
|---|---|
| Length | |
| Service rate | |
| Arrival rate | |
| Actual arrival rate (PHEV) | |
| Actual arrival rate (EV) | |
| Length of the queue | |
| Average revenue of charging one PHEV | |
| Average revenue of charging one EV | |
| Waiting cost of one NEV per unit time | |
| Profit |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Li, X.; Zhang, Y.; Shu, C. Should Charging Stations Provide Service for Plug-In Hybrid Electric Vehicles During Holidays? Sustainability 2025, 17, 336. https://doi.org/10.3390/su17010336
Zhang T, Li X, Zhang Y, Shu C. Should Charging Stations Provide Service for Plug-In Hybrid Electric Vehicles During Holidays? Sustainability. 2025; 17(1):336. https://doi.org/10.3390/su17010336
Chicago/Turabian StyleZhang, Tianhua, Xin Li, Yiwen Zhang, and Chenhui Shu. 2025. "Should Charging Stations Provide Service for Plug-In Hybrid Electric Vehicles During Holidays?" Sustainability 17, no. 1: 336. https://doi.org/10.3390/su17010336
APA StyleZhang, T., Li, X., Zhang, Y., & Shu, C. (2025). Should Charging Stations Provide Service for Plug-In Hybrid Electric Vehicles During Holidays? Sustainability, 17(1), 336. https://doi.org/10.3390/su17010336







