Optimization Based on Computational Fluid Dynamics and Machine Learning for the Performance of Diffuser-Augmented Wind Turbines with Inlet Shrouds
Abstract
1. Introduction
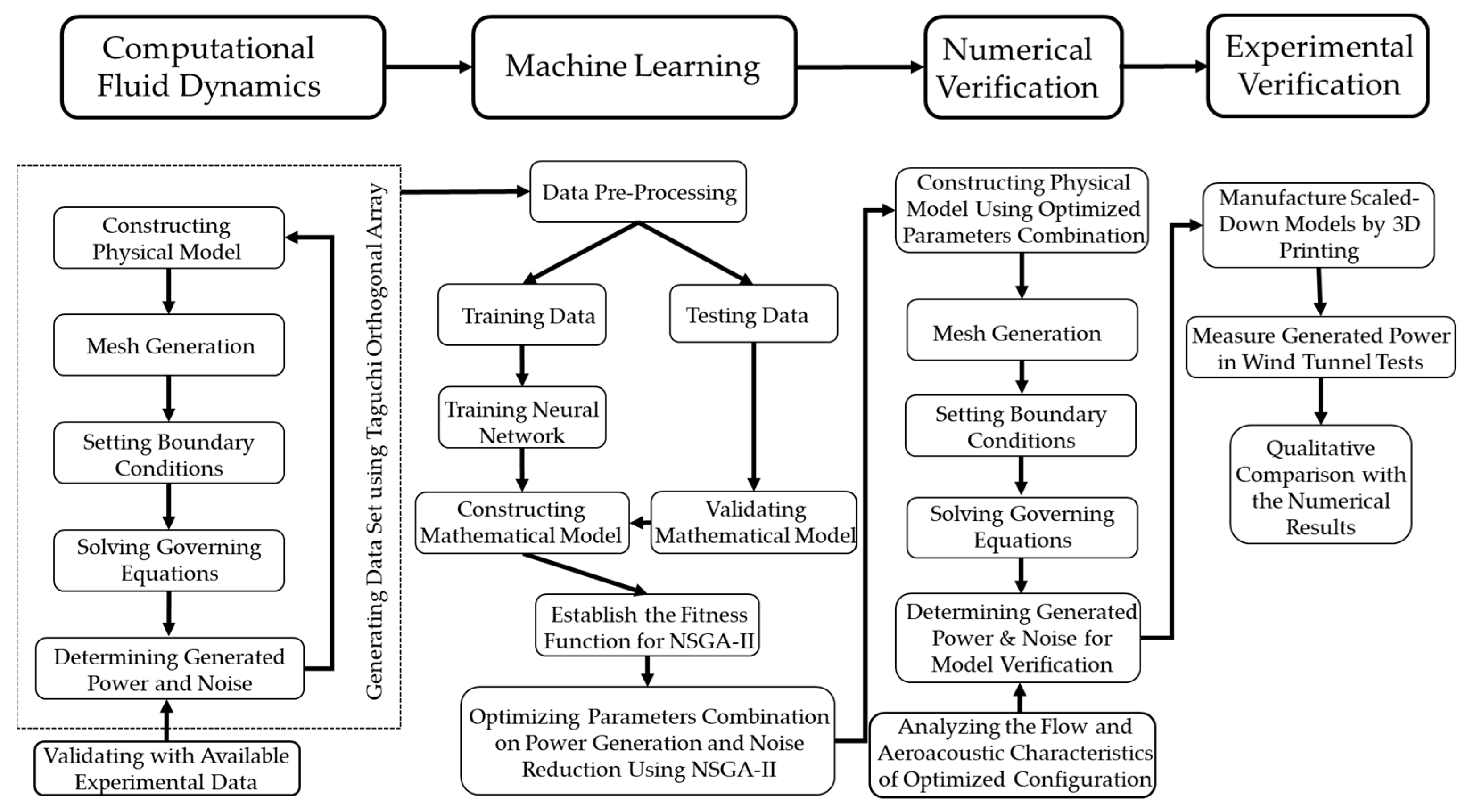
2. Methodology
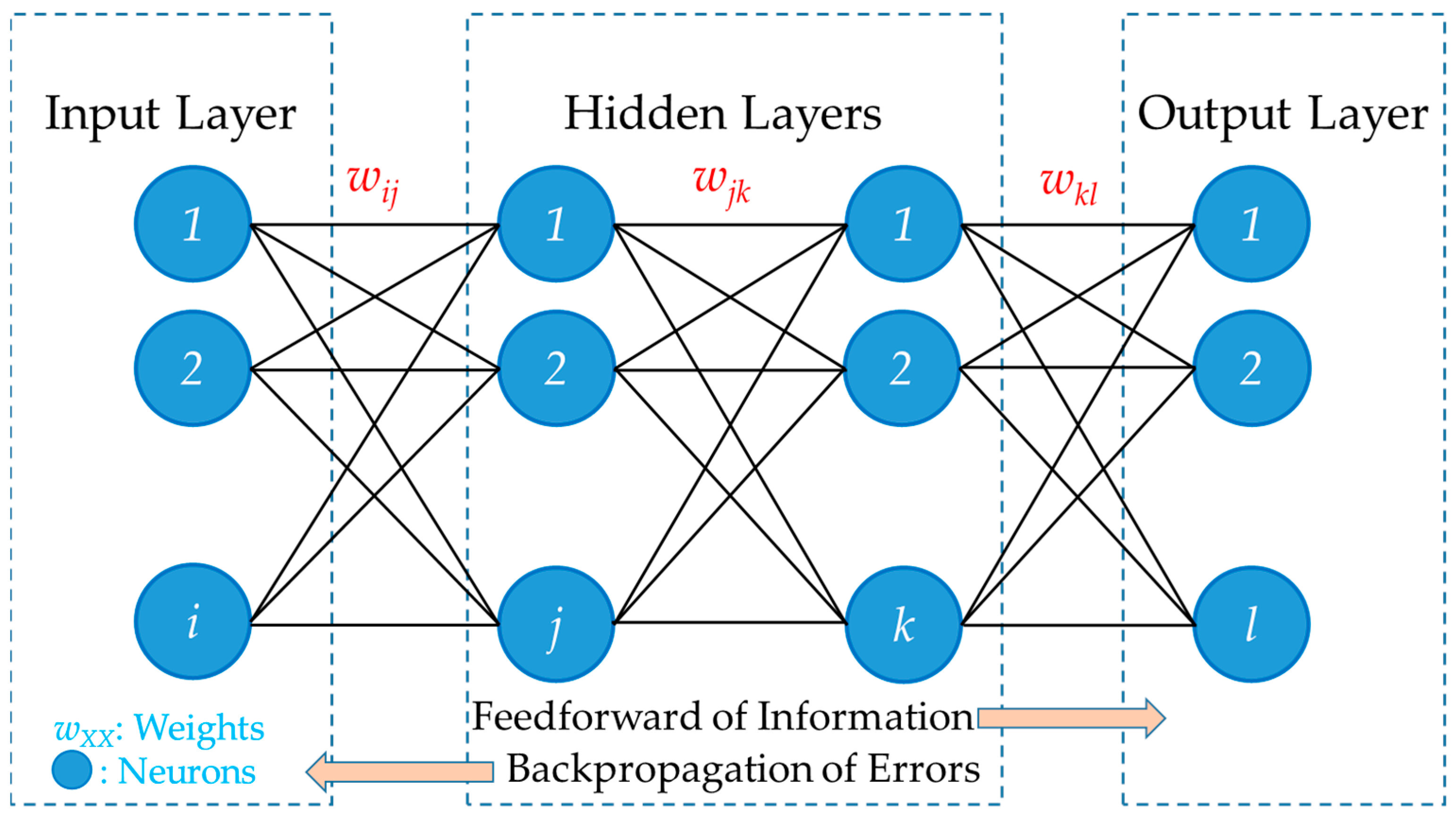
- BPNN algorithm: ML is a branch of artificial intelligence. In the modern era of software, ML depends on the prediction of datasets based on various algorithms for different software modules. A neural network is an ML model that implements a learning/training rule, i.e., when the input nodes are activated, synaptic weights are updated and forwarded to output nodes. Different training algorithms are available, like backpropagation, genetic, and krill herd algorithms [53]. The BPNN is such an ML model, one inspired by the biological neural network, and it is one of the oldest supervised-learning multilayer feed-forward neural network algorithms [54], having been proposed by Rumelhart, Hinton, and Williams in 1986 [55]. As introduced in the 1980s, it quickly became a focal point in neural network research due to its outstanding learning capability and adaptability [56]. Due to its backpropagating ability, it is highly suitable for problems with no relationships between the outputs and inputs [54]. Its flexibility, learning, and powerful fitting capabilities make it a robust tool for addressing complex problems [54,56]. Lillicrap et al. [57] pointed out that neural networks trained with backpropagation of error are at the heart of the recent successes of ML, including state-of-the-art speech and image recognition and language translation. In addition, backpropagation of error even underpins recent progress in unsupervised learning problems such as image and speech generation, language modeling, and other next-step prediction tasks. Over the years, BPNN has been proven to be the best algorithm among the multilayer perceptron algorithms [58]. Thus, the multilayer perceptron neural network trained with BPNN is the most popular and widely used network paradigm employed by engineering applications to solve practical problems, and it has demonstrated exceptional performance [53,54,56,59,60]. Inevitably, the traditional BPNN algorithm has some shortcomings, such as low convergence speed and an easy fall to the local minimum, but some remedies have been proposed to solve these problems [61]. In this study, the BPNN model is selected based on the abovementioned survey and then employed on the MATLAB platform, which will promptly update the latest modifications to the model.
- NSGA-II algorithm: Inspired by Darwin’s theory of species evolution, John Holland proposed the genetic algorithm (GA) in 1975, which is widely used in various fields, including artificial intelligence, logistics distribution, and engineering science applications. It can be employed as an optimization algorithm that simulates the biological evolution process for multi-objective optimization problems (MOPs) [62]. In the real world, it is challenging to determine optimal solutions over MOPs with multiple conflicting objectives in complex systems. In such a situation, it is impossible to compute a single optimal solution. Therefore, the most common solution concept is to compute a set of Pareto optima, solutions that cannot be improved in one objective without accepting a worsening in others, and then let a decision-maker select the final solution based on their preference [63]. As a mainstream method for solving MOPs, the development and application of evolutionary algorithms (EAs) has attracted thousands of researchers since the 1950s [64]. EAs profit from their general ability to work with sets of solutions, are the standard approach to MOPs, and have many successful applications [63]. The NSGA-II algorithm, a model initially proposed by Deb et al. [65] in 2002, is considered the most prominent multi-objective EA [63,66] with the most popular GA framework [64], and has served as a powerful decision-space exploration engine, based on GA, used to solve MOPs [67]. So far, it has been cited more than 50,000 times on Google Scholar [68] and is becoming one of the most widely used algorithms for solving MOPs in various applications in different fields [12,68,69,70]. It has been verified that the Pareto frontier obtained by the NSGA-II algorithm is evenly distributed and has good convergence and robustness. [71]. We take advantage of its high competence, efficiency, and strength in dealing with most MOPs and adopt it in this research.
2.1. Computational Fluid Dynamics (CFD)
2.2. Backpropagation Neural Network (BPNN)
2.3. Multi-Objective Genetic Algorithm-NSGA-II
2.4. Experimental Setup and Measurement
3. Results and Discussion
3.1. Numerical Validation
3.2. Optimized Results Obtained by Taguchi Method
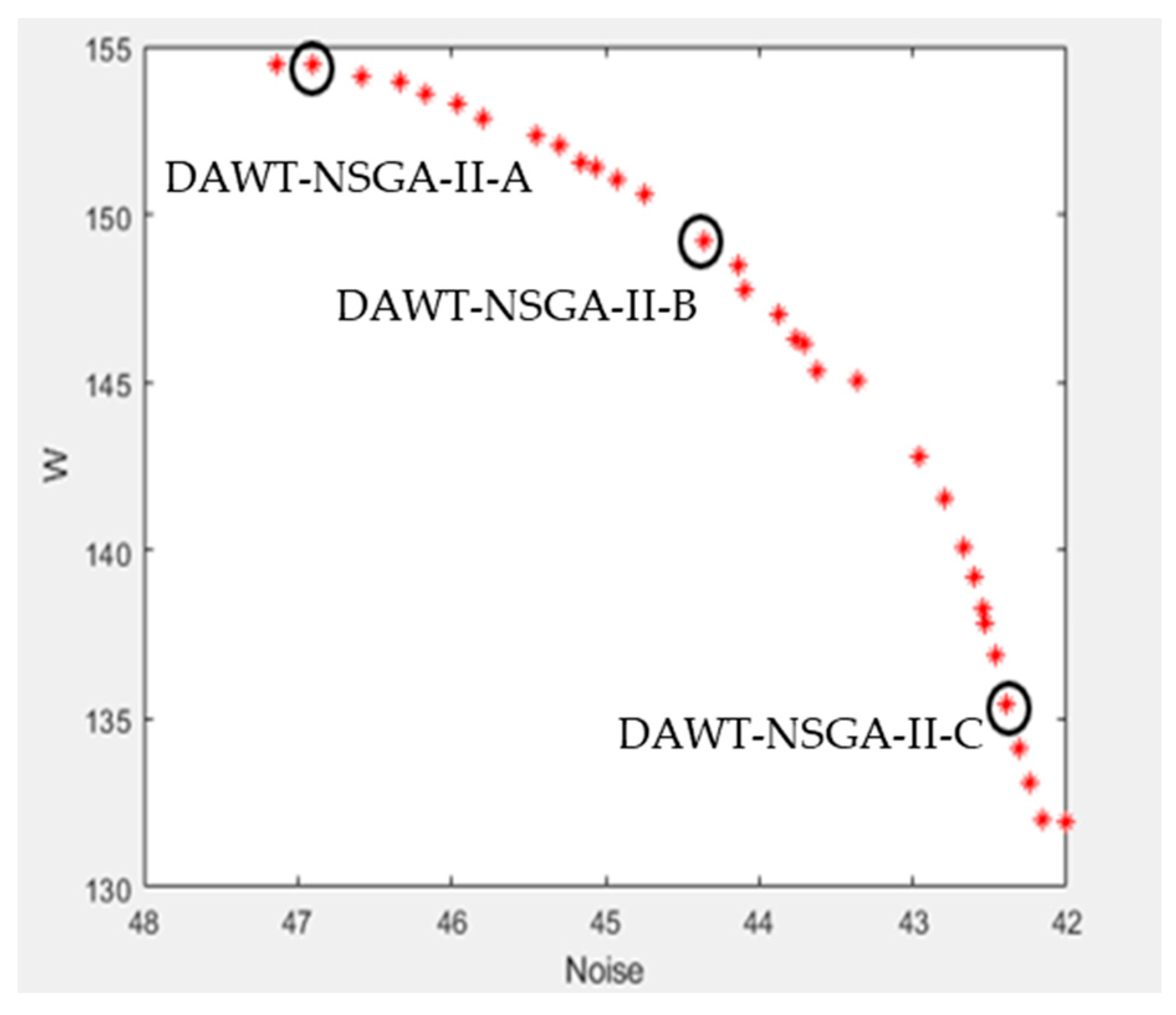
3.3. Optimized Results Obtained by Multi-Objective Optimization
- Training dataset: The training set comprises a subset of the generated datasets obtained from the CFD simulations. This dataset trains the neural network model using the backpropagation algorithm. During training, the neural network learns the underlying patterns and the relationships between the input parameters (flange height/angle, diffuser length, rotor axial position) and the corresponding outputs (power output and generated noise of the DAWT). The Levenberg–Marquardt algorithm was employed in this phase to obtain a lower mean squared error [61].
- Validation dataset: This dataset, separate from the training dataset, tunes hyperparameters and assesses the model’s performance during training. After each epoch of training iterations, the model’s performance is evaluated on the validation dataset to monitor the model’s generalization ability and prevent overfitting.
- Test dataset: This dataset, separate from the training and validation datasets, is used to evaluate the final performance of the trained model and assess how well the trained model generalizes on unseen data.
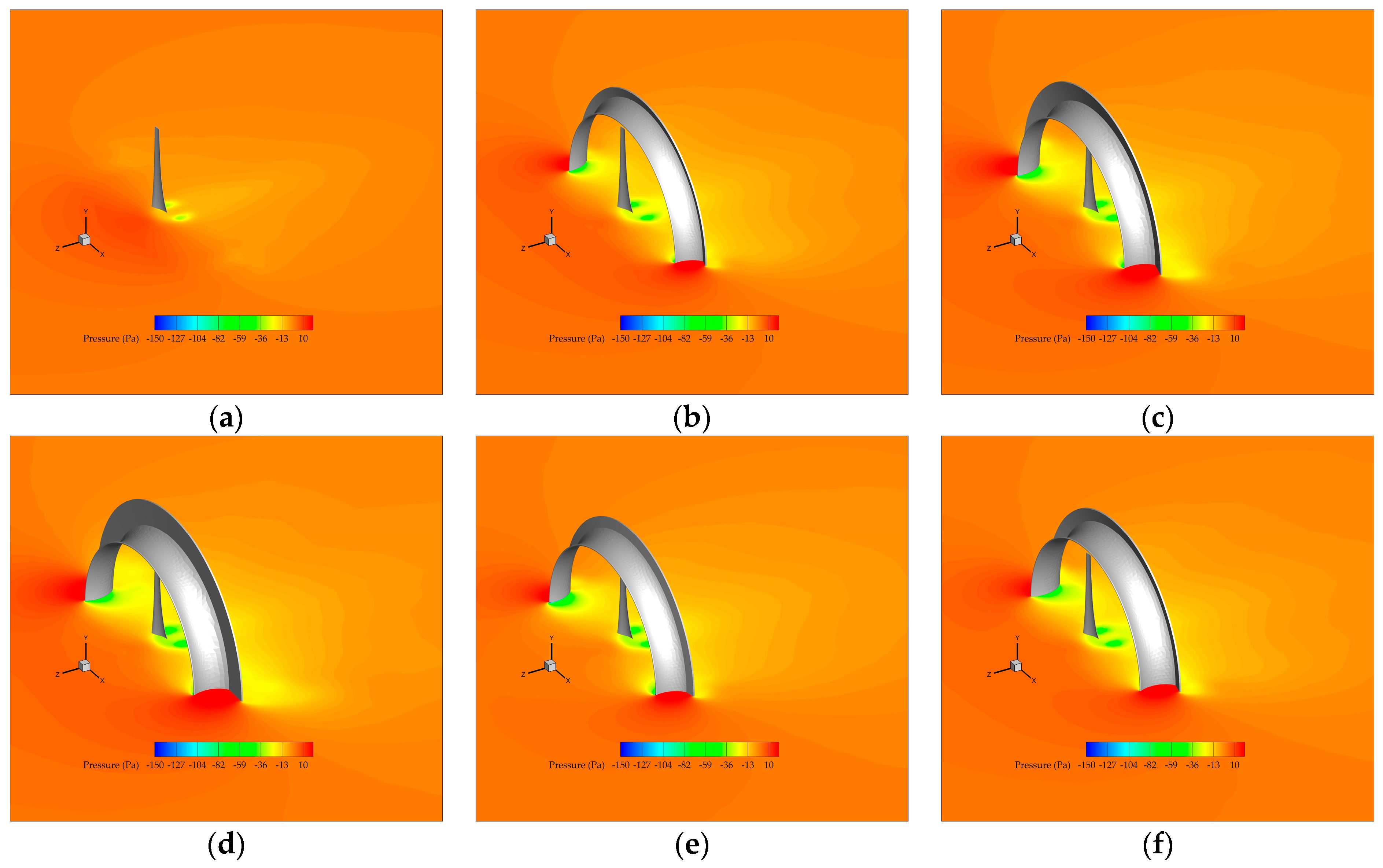
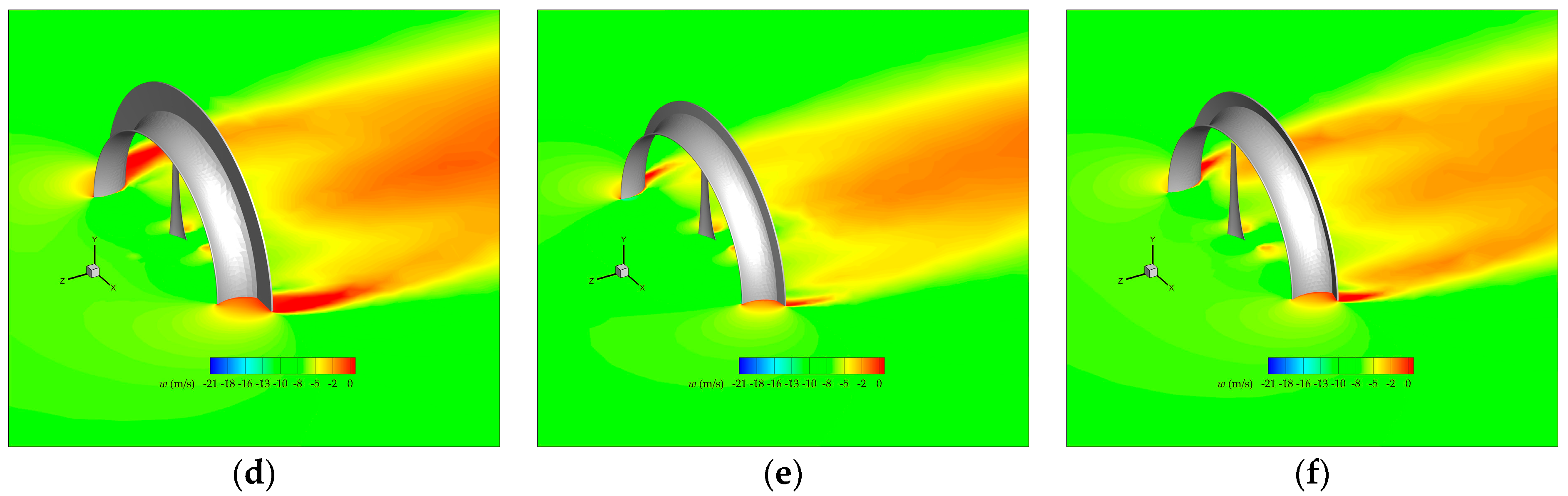
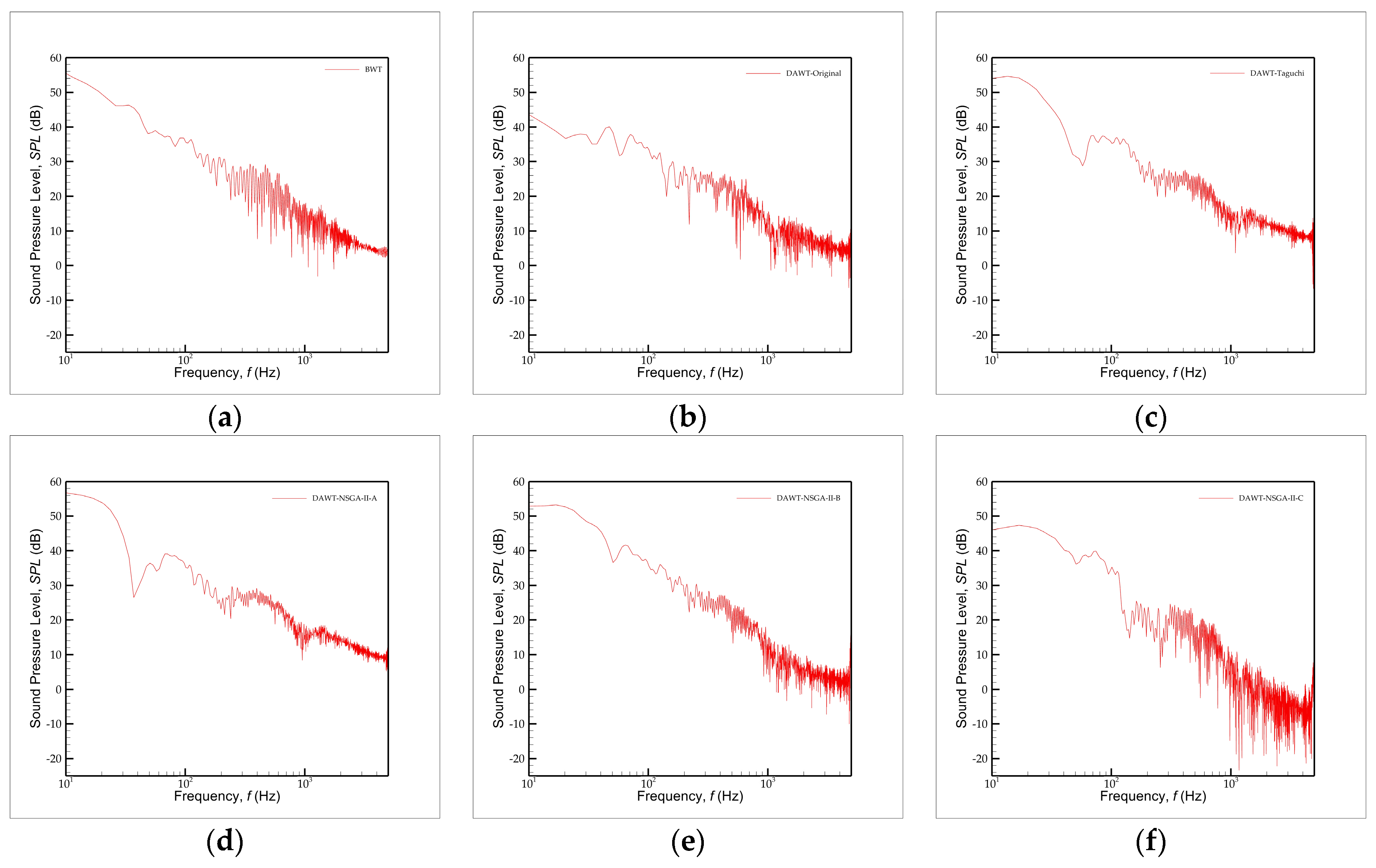
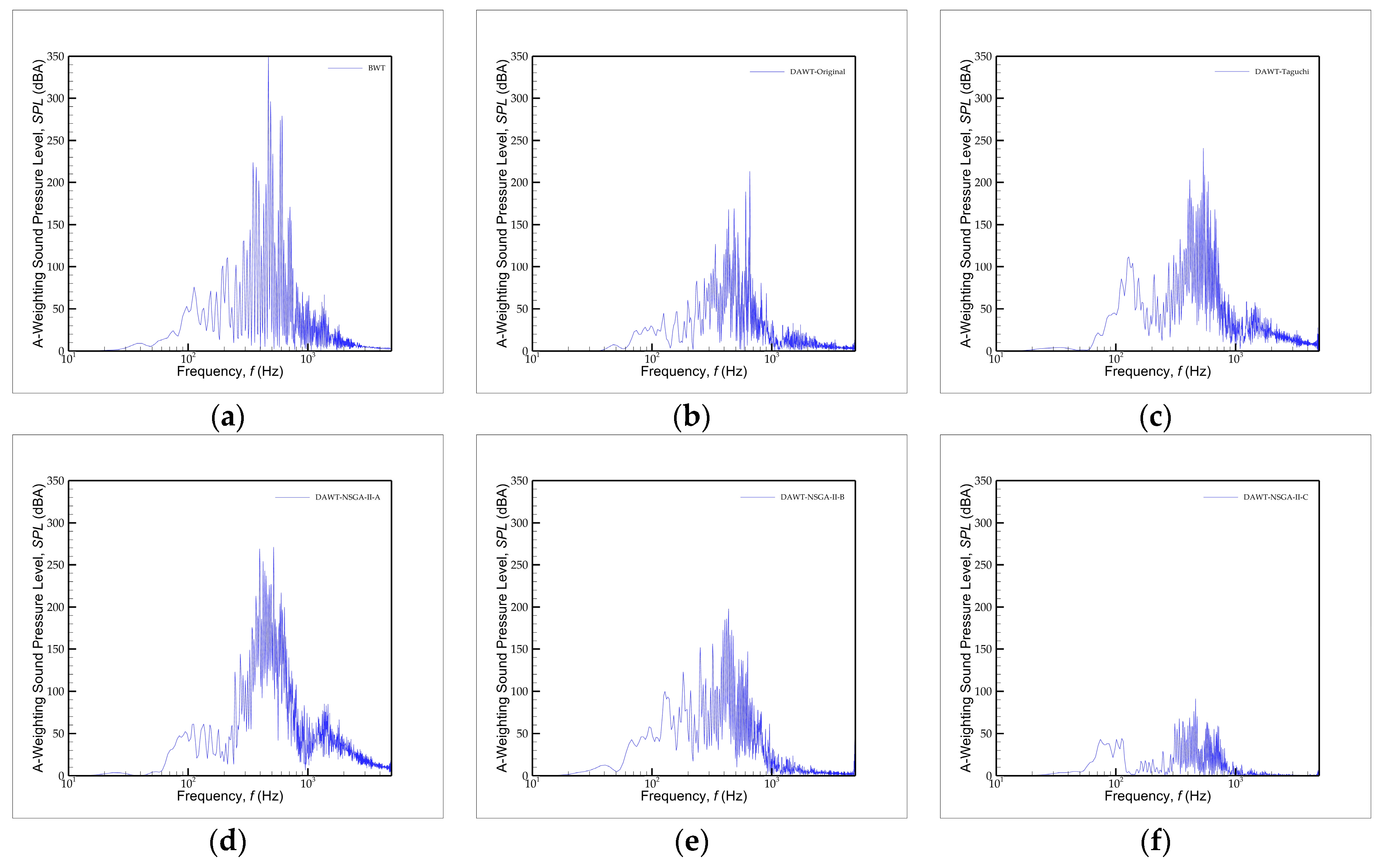
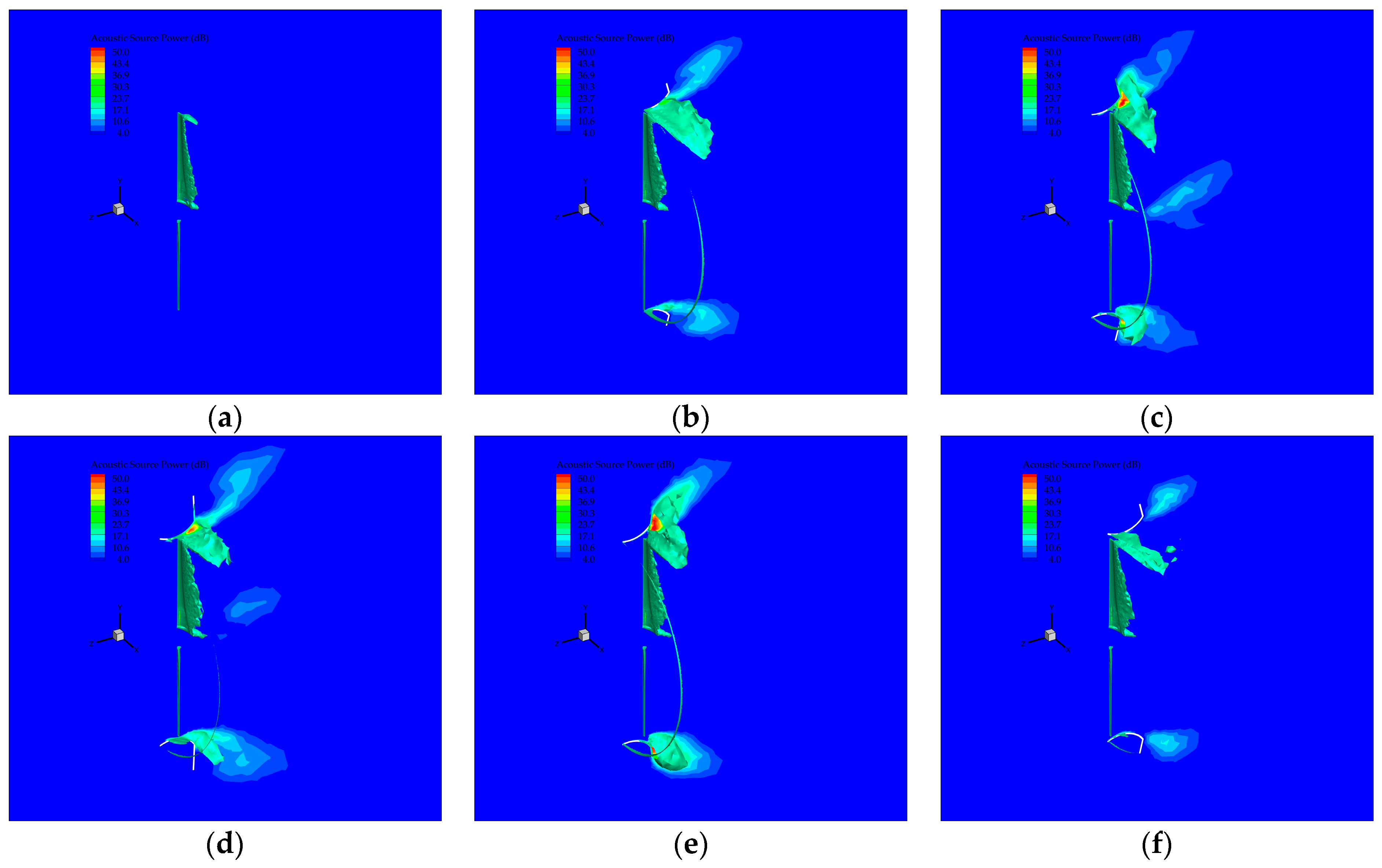
3.4. Flow and Acoustic Fields: Analysis and Comparison
4. Conclusions
- 1.
- This study successfully integrates CFD, BPNN, and NSGA-II to conduct multi-objective optimization of DAWT, using output power and noise as objective functions. Performance evaluation and verification are carried out for the optimized designs. Finally, the diffuser configurations that meet different requirements for power and noise are proposed.
- 2.
- The influence of design parameters can be evaluated through the Taguchi method. It was found that the impact of the rotor’s axial position on the power output of DAWT is the most significant, followed by those of the diffuser length, flange angle, and height.
- 3.
- When employing a cycloid diffuser profile, varying the design parameters, i.e., flange height/angle, diffuser length, and rotor axial position, allows for the indirect incorporation of additional parameters, i.e., tip clearance, diffuser opening angle, and the adding of inlet shroud, allowing these values to be optimized together.
- 4.
- It was evident that a well-designed diffuser requires the acceleration of airflow while maintaining high-pressure recovery.
- 5.
- Under the conditions of this study, introducing a diffuser can reduce the noise in the frequency band of 200 Hz to 800 Hz, but if the induced tip vortex is too strong, it will have the opposite effect on the noise reduction. This finding can be used to interpret the positive and negative impacts on noise of installing a diffuser.
- 6.
- The flange height should not be too high or too low. If it is too low, it will not be able to generate a vortex with sufficient strength behind it to accelerate the airflow inside the diffuser, which will provide limited help to the power output. However, if the flange is too high, it will cause the recirculation zone to be far away from the rotor inside the diffuser, resulting in limited benefit to power output. Moreover, if the flange height is too high, it would lead to structural damage and deformation, resulting in higher maintenance costs and making it unsuitable for practical applications.
- 7.
- An appropriate flange angle can induce vortices to drive and accelerate airflow within the diffuser. Negative flange angles balance power and noise demands, resulting in smoother flow fields with weaker pressure fluctuations and lower noise levels.
- 8.
- If the diffuser length is too long, it is unsuitable for practical applications because it can cause the DAWT to be too heavy for placement in elevated locations. Additionally, excessive length can hinder the vortices generated by the flange from influencing the flow field near the rotor inside the diffuser.
- 9.
- The rotor should ideally be positioned behind the throat (approximately halfway between the throat and the outlet) to receive the accelerated flow field induced by the vortices generated by the flange, thereby enhancing its power output. Placing the rotor near this position between the throat and the outlet yields better results for maximizing power output. However, positioning the rotor in front of the throat is more effective for noise reduction.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gayen, D.; Chatterjee, R.; Roy, S. A review on environmental impacts of renewable energy for sustainable development. Int. J. Environ. Sci. Technol. 2024, 21, 5285–5310. [Google Scholar] [CrossRef]
- Sayed, E.T.; Wilberforce, T.; Elsaid, K.; Rabaia, M.K.H.; Abdelkareem, M.A.; Chae, K.J.; Olabi, A.G. A critical review on environmental impacts of renewable energy systems and mitigation strategies: Wind, hydro, biomass and geothermal. Sci. Total Environ. 2021, 766, 144505. [Google Scholar] [CrossRef] [PubMed]
- Darwish, A.S.; Al-Dabbagh, R. Wind energy state of the art: Present and future technology advancements. Renew. Energy Environ. Sustain. 2020, 5, 7. [Google Scholar] [CrossRef]
- Nazir, M.S.; Ali, N.; Bilal, M.; Iqbal, H.M.N. Potential environmental impacts of wind energy development: A global perspective. Curr. Opin. Environ. Sci. Health 2020, 13, 85–90. [Google Scholar] [CrossRef]
- Joselin Herbert, G.M.; Iniyan, S.; Sreevalsanc, E.; Rajapandian, S. A review on wind energy technologies. Renew. Sustain. Energy Rev. 2007, 11, 1117–1145. [Google Scholar] [CrossRef]
- Hutchinson, M.; Zhao, F. GWEC|Global Wind Report 2023; Global Wind Energy Council: Brussels, Belgium, 2023. [Google Scholar]
- Kassa, B.Y.; Baheta, A.T.; Beyene, A. Current trends and innovations in enhancing the aerodynamic performance of small-scale, horizontal axis wind turbines: A review. ASME Open J. Eng. 2024, 3, 031001. [Google Scholar] [CrossRef]
- Burton, T.; Jenkins, N.; Bossanyi, E.; Sharpe, D.; Graham, M. Wind Energy Handbook, 3rd ed.; John Wiley & Sons, Ltd.: West Sussex, UK, 2021. [Google Scholar]
- Alabdali, Q.A.; Bajawi, A.M.; Fatani, A.M.; Nahhas, A.M. Review of recent advances of wind energy. Sustain. Energy 2020, 8, 12–19. [Google Scholar]
- Jianu, O.; Rosen, M.A.; Naterer, G. Noise pollution prevention in wind turbines: Status and recent advances. Sustainability 2012, 4, 1104–1117. [Google Scholar] [CrossRef]
- Ohya, Y.; Karasudani, T.; Nagai, T.; Watanabe, K. Wind lens technology and its application to wind and water turbine and beyond. Renew. Energy Environ. Sustain. 2017, 2, 2. [Google Scholar] [CrossRef]
- Nunes, M.M.; Brasil Junior, A.C.P.; Oliveira, T.F. Systematic review of diffuser-augmented horizontal-axis turbines. Renew. Sustain. Energy Rev. 2020, 133, 110075. [Google Scholar] [CrossRef]
- Ilhan, A.; Sahin, B.; Bilgili, M. A review: Diffuser augmented wind turbine technologies. Int. J. Green Energy 2022, 19, 1–27. [Google Scholar] [CrossRef]
- Ohya, Y.; Karasudani, T. A shrouded wind turbine generating high output power with wind-lens technology. Energies 2010, 3, 634–649. [Google Scholar] [CrossRef]
- Watson, S.; Moro, A.; Reis, V.; Baniotopoulos, C.; Barth, S.; Bartoli, G.; Bauer, F.; Boelman, E.; Bosse, D.; Cherubini, A.; et al. Future emerging technologies in the wind power sector: A European perspective. Renew. Sustain. Energy Rev. 2019, 113, 109270. [Google Scholar] [CrossRef]
- Calautit, K.; Johnstone, C. State-of-the-art review of micro to small-scale wind energy harvesting technologies for building integration. Energy Convers. Manag. X 2023, 20, 100457. [Google Scholar] [CrossRef]
- Al-Quraishi, B.A.J.; Asmuin, N.Z.B.; Mohd, S.B.; Abd Al-Wahid, W.A.; Mohammed, A.N.; Didane, D.H. Review on diffuser augmented wind turbine (DAWT). Int. J. Integr. Eng. 2019, 11, 178–206. [Google Scholar] [CrossRef]
- Aravindhan, N.; Bibin, C.; Kumar, R.A.; Kalyan, K.S.; Balaji, K.S.; Kugan, R.; Rajesh, K.; Arunkumar, S. Performance analysis of various types of ducted wind turbines—A review. Mater. Today Proc. 2023, 80, 188–194. [Google Scholar] [CrossRef]
- Abe, K.I.; Ohya, Y. An investigation of flow fields around flanged diffusers using CFD. J. Wind. Eng. Ind. Aerodyn. 2004, 92, 315–330. [Google Scholar] [CrossRef]
- Abe, K.; Nishida, M.; Sakurai, A.; Ohya, Y.; Kihara, H.; Wada, E.; Sato, K. Experimental and numerical investigations of flow fields behind a small wind turbine with a flanged diffuser. J. Wind. Eng. Ind. Aerodyn. 2005, 93, 951–970. [Google Scholar] [CrossRef]
- Toshimitsu, K.; Nishikawa, K.; Haruki, W.; Oono, S.; Takao, M.; Ohya, Y. PIV measurements of flows around the wind turbines with a flanged-diffuser shroud. J. Therm. Sci. 2008, 17, 375–380. [Google Scholar] [CrossRef]
- Jafari, S.A.H.; Kosasih, B. Flow analysis of shrouded small wind turbine with a simple frustum diffuser with computational fluid dynamics simulations. J. Wind Eng. 2014, 125, 102–110. [Google Scholar] [CrossRef]
- Roshan, S.Z.; Alimirzazadeh, S.; Rad, M. RANS simulations of the stepped duct effect on the performance of ducted wind turbine. J. Wind. Eng. Ind. Aerodyn. 2015, 145, 270–279. [Google Scholar] [CrossRef]
- El-Zahaby, A.M.; Kabeel, A.E.; Elsayed, S.S.; Obiaa, M.F. CFD analysis of flow fields for shrouded wind turbine’s diffuser model with different flange angles. Alex. Eng. J. 2017, 56, 171–179. [Google Scholar] [CrossRef]
- Amano, R.S. Review of wind turbine research in 21st Century. J. Energy Resour. Technol. 2017, 139, 050801. [Google Scholar] [CrossRef]
- Natesan, M.; Jeyanthi, S.; Sivasathya, U. A review on design of augmented wind turbine blade for low wind speed urban area. Int. J. Mech. Eng. Technol. 2017, 8, 685–691. [Google Scholar]
- Heikal, H.A.; Abu-Elyazeed, O.S.M.; Nawar, M.A.A.; Attai, Y.A. On the actual power coefficient by theoretical developing of the diffuser flange of wind-lens turbine. Renew. Energy 2018, 125, 295–305. [Google Scholar] [CrossRef]
- Klistafani, Y.; Mukhsen, M.I. Development of a shrouded wind turbine with various diffuser type structures. IOP Conf. Ser. Mater. Sci. Eng. 2019, 676, 012040. [Google Scholar] [CrossRef]
- Anbarsooz, M.; Mazloum, M.; Moghadam, D.G. Converging-diverging ducts for efficient utilization of low-grade wind energy: Numerical and experimental studies. J. Renew. Sustain. Energy 2020, 12, 023304. [Google Scholar] [CrossRef]
- Arifin, F.; Kusumanto, R.D.; Bow, Y.; Rusdianasari; Taqwa, A.; Susandi, A.; Herlambang, Y.D.; Wang, M.W.; Sitompul, C.R. Study the effect diffuser length and degree to horizontal wind turbine. In Proceedings of the 4th International Conference on Applied Science and Technology on Engineering Science (iCAST-ES 2021), Samarinda, Indonesia, 23–24 October 2021. [Google Scholar]
- Watanabe, K.; Ohya, Y. A Simple theory and performance prediction for a shrouded wind turbine with a brimmed diffuser. Energies 2021, 14, 3661. [Google Scholar] [CrossRef]
- Ramayee, L.; Supradeepan, K. Influence of axial distance and duct angle in the improvement of power generation in duct augmented wind turbines. J. Energy Resour. Technol. Trans. ASME 2022, 144, 091302. [Google Scholar] [CrossRef]
- Hashem, I.; Hafiz, A.A.; Mohamed, M.H. Characterization of aerodynamic performance of wind-lens turbine using high-fidelity CFD simulations. Front. Energy 2022, 16, 661–682. [Google Scholar] [CrossRef]
- Jauhar, T.A.; Hussain, M.I.; Kiren, T.; Arif, W.; Miran, S.; Lee, G.H. Effect of flanged diffuser divergence angle on wind turbine: A numerical investigation. PLoS ONE 2023, 18, e0287053. [Google Scholar] [CrossRef]
- Mutasher, S.A.; Ahmed, H.M. CFD analysis of brimmed diffuser augmented wind turbine. In Proceedings of the 2023 IEEE 8th International Conference on Engineering Technologies and Applied Sciences (ICETAS), InterContinental Bahrain, Manama, Bahrain, 25–27 October 2023. [Google Scholar]
- Göçmen, T.; Özerdema, B. Airfoil optimization for noise emission problem and aerodynamic performance criterion on small scale wind turbines. Energy 2012, 46, 62–71. [Google Scholar] [CrossRef]
- Reja, R.K.; Amin, R.; Tasneem, Z.; Ali, M.F.; Islam, M.R.; Saha, D.K.; Badal, F.R.; Ahamed, M.H.; Moyeen, S.I.; Das, S.K. A review of the evaluation of urban wind resources: Challenges and perspectives. Energy Build. 2022, 257, 111781. [Google Scholar] [CrossRef]
- Hashem, I.; Mohamed, M.H.; Hafiz, A.A. Aero-acoustics noise assessment for wind-lens turbine. Energy 2017, 118, 345–368. [Google Scholar] [CrossRef]
- Avallone, F.; Ragni, D.; Casalino, D. On the effect of the tip-clearance ratio on the aeroacoustics of a diffuser-augmented wind turbine. Renew. Energy 2020, 152, 1317–1327. [Google Scholar] [CrossRef]
- Sanderse, B.; van der Pijl, S.P.; Koren, B. Review of computational fluid dynamics for wind-turbine wake aerodynamics. Wind Energy 2011, 14, 797–819. [Google Scholar] [CrossRef]
- Rehman, S.; Alam, M.M.; Alhems, L.M.; Rafique, M.M. Horizontal axis wind turbine blade design methodologies for efficiency enhancement—A review. Energies 2018, 11, 506. [Google Scholar] [CrossRef]
- Agha, A.; Chaudhry, H.N.; Wang, F. Diffuser augmented wind turbine (DAWT) technologies: A review. Int. J. Renew. Energy Res. 2018, 8, 1369–1385. [Google Scholar]
- Marugán, A.P.; Márquez, F.P.G.; Perez, J.M.P.; Ruiz-Hernández, D. A survey of artificial neural network in wind energy systems. Appl. Energy 2018, 228, 1822–1836. [Google Scholar] [CrossRef]
- Elyasichamazkoti, F.; Khajehpoor, A. Application of machine learning for wind energy from design to energy-Water nexus: A Survey. Energy Nexus 2021, 2, 100011. [Google Scholar] [CrossRef]
- Bin Abu Sofian, A.D.A.; Lim, H.R.; Siti Halimatul Munawaroh, H.; Ma, Z.; Chew, K.W.; Show, P.L. Machine learning and the renewable energy revolution: Exploring solar and wind energy solutions for a sustainable future including innovations in energy storage. Sustain. Dev. 2024, 1–26. [Google Scholar] [CrossRef]
- Nikolić, V.; Petković, D.; Shamshirband, S.; Ćojbašić, Ž. Adaptive neuro-fuzzy estimation of diffuser effects on wind turbine performance. Energy 2015, 89, 324–333. [Google Scholar] [CrossRef]
- Liu, J.; Song, M.; Chen, K.; Wu, B.; Zhang, X. An optimization methodology for wind lens profile using computational fluid dynamics simulation. Energy 2016, 109, 602–611. [Google Scholar] [CrossRef]
- Oka, N.; Furukawa, M.; Kawamitsu, K.; Yamada, K. Optimum aerodynamic design for wind-lens turbine. J. Fluid Sci. Technol. 2016, 11, JFST0011. [Google Scholar] [CrossRef]
- Khamlaj, T.A.; Rumpfkeil, M.P. Analysis and optimization of ducted wind turbines. Energy 2018, 162, 1234–1252. [Google Scholar] [CrossRef]
- Leloudas, S.N.; Lygidakis, G.N.; Eskantar, A.I.; Nikolos, I.K. A robust methodology for the design optimization of diffuser augmented wind turbine shrouds. Renew. Energy 2020, 150, 722–742. [Google Scholar] [CrossRef]
- Rahmatian, M.A.; Shahrbabaki, A.N.; Moeini, S.P. Single-objective optimization design of convergent-divergent ducts of ducted wind turbine using RSM and GA, to increase power coefficient of a small-scale horizontal axis wind turbine. Energy 2023, 269, 126822. [Google Scholar] [CrossRef]
- Shambira, N.; Makaka, G.; Mukumba, P. Velocity augmentation model for an empty concentrator-diffuser-augmented wind turbine and optimisation of geometrical parameters using surface response methodology. Sustainability 2024, 16, 1707. [Google Scholar] [CrossRef]
- Kuninti, S.; Rooban, S. Backpropagation algorithm and its hardware implementations: A review. J. Phys. Conf. Ser. 2021, 1804, 012169. [Google Scholar] [CrossRef]
- Solanki, S.; Jethva, H.B. A review on back propagation algorithms for feedforward networks. Glob. Res. Anal. 2013, 2, 73–75. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning internal representations by error propagation. In Parallel Distributed Processing: Explorations in the Microstructure of Cognition; Rumelhart, D.E., McClelland, J.L., Eds.; The MIT Press: Cambridge, MA, USA, 1986; Volume 1, pp. 318–362. [Google Scholar]
- Li, M. Comprehensive review of backpropagation neural networks. Acad. J. Sci. Technol. 2024, 9, 150–154. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Santoro, A.; Marris, L.; Akerman, C.J.; Hinton, C. Backpropagation and the brain. Nat. Rev. Neurosci. 2020, 21, 335–346. [Google Scholar] [CrossRef]
- Suliman, A.; Zhang, Y. A review on back-propagation neural networks in the application of remote sensing image classification. J. Earth Sci. Eng. 2015, 5, 52–65. [Google Scholar]
- Primadusi, U.; Cahyadi, A.I.; Prasetyo, D.; Wahyunggoro, O. Backpropagation neural network models for LiFePO4 Battery. AIP Conf. Proc. 2016, 1755, 090009. [Google Scholar]
- Jwo, D.J.; Biswal, A.; Mir, I.A. Artificial neural networks for navigation systems: A review of recent research. Appl. Sci. 2023, 13, 4475. [Google Scholar] [CrossRef]
- Nguyen, T.A.; Ly, H.B.; Pham, B.T. Backpropagation neural network-based machine learning model for prediction of soil friction angle. Math. Probl. Eng. 2020, 2020, 8845768. [Google Scholar] [CrossRef]
- Coley, D.A. An Introduction to Genetic Algorithms for Scientists and Engineers, 1st ed.; World Scientific Publishing Company: Danvers, MA, USA, 1999; pp. 2–3. [Google Scholar]
- Cerf, S.; Doerr, B.; Hebras, B.; Kahane, Y.; Wietheger, S. The first proven performance guarantees for the non-dominated sorting genetic algorithm II (NSGA-II) on a combinatorial optimization problem. In Proceedings of the 32nd International Joint Conference on Artificial Intelligence, Macao SAR, China, 19–25 August 2023. [Google Scholar]
- Qu, Y.; Ma, Z.; Clausen, A.; Jørgensen, B.N. A comprehensive review on evolutionary algorithm solving multi-objective Problems. In Proceedings of the 22nd IEEE International Conference on Industrial Technology (ICIT), Valencia, Spain, 10–12 March 2021. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multi-objective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Damak, N.; Jarboui, B.; Loukil, T. Non-dominated sorting genetic algorithm-II to solve bi-objective multi-mode resource-constrained project scheduling. In Proceedings of the 2013 International Conference on Control, Decision and Information Technologies (CoDIT), Hammamet, Tunisia, 6–8 May 2013. [Google Scholar]
- Verma, S.; Pant, M.; Snasel, V. A comprehensive review on NSGA-II for multi-objective combinatorial optimization problems. IEEE Access 2021, 9, 57757–57791. [Google Scholar] [CrossRef]
- Golchha, A.; Qureshi, S.G. Non-dominated sorting genetic algorithm-II—A succinct survey. Int. J. Comput. Sci. Inf. Technol. 2015, 6, 252–255. [Google Scholar]
- Rahimi, I.; Gandomi, A.H.; Deb, K.; Chen, F.; Nikoo, M.R. Scheduling by NSGA-II: Review and bibliometric analysis. Processes 2022, 10, 98. [Google Scholar] [CrossRef]
- Ma, H.; Zhang, Y.; Sun, S.; Liu, T.; Shan, Y. A comprehensive survey on NSGA-II for multi-objective optimization and applications. Artif. Intell. Rev. 2023, 56, 15217–15270. [Google Scholar] [CrossRef]
- Chang, H.; Zhang, G.; Sun, Y.; Lu, S. Non-dominant genetic algorithm for multi-objective optimization design of unmanned aerial vehicle shell process. Polymers 2022, 14, 2896. [Google Scholar] [CrossRef]
- Singh, R.K.; Ahmed, M.R. Blade design and performance testing of a small wind turbine rotor for low wind speed applications. Renew. Energy 2013, 50, 812–819. [Google Scholar] [CrossRef]
- Taguchi, G. System of Experimental Design: Engineering Methods to Optimize Quality and Minimize Costs, 1st ed.; UNIPUB/Kraus International Publications: Dearborn, MI, USA, 1987; pp. 653–655. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Ffowcs-Williams, J.E.; Hawkings, D.L. Sound generation by turbulence and surfaces in arbitrary motion. Proc. R. Soc. A Math. Phys. Eng. Sci. 1969, 264, 321–342. [Google Scholar]
- Proudman, I. The generation of noise by isotropic turbulence. Proc. R. Soc. A Math. Phys. Eng. Sci. 1952, 214, 119–132. [Google Scholar]
- Curle, N. The influence of solid boundaries upon aerodynamic sound. Proc. R. Soc. A Math. Phys. Eng. Sci. 1955, 231, 505–514. [Google Scholar]
- Singh, R.K.; Ahmed, M.R.; Zullah, M.A.; Lee, Y.H. Design of a low Reynolds number airfoil for small horizontal axis wind turbines. Renew. Energy 2012, 42, 66–76. [Google Scholar] [CrossRef]
- IEC 61400-11; International Standard, Wind Turbines–Part 11: Acoustic Noise Measurement Techniques. International Electrotechnical Commission: Geneva, Switzerland, 2018.
- IEC 61672-1:2013; Electroacoustics–Sound Level Meters–Part 1: Specifications. International Electrotechnical Commission: Geneva, Switzerland, 2013.
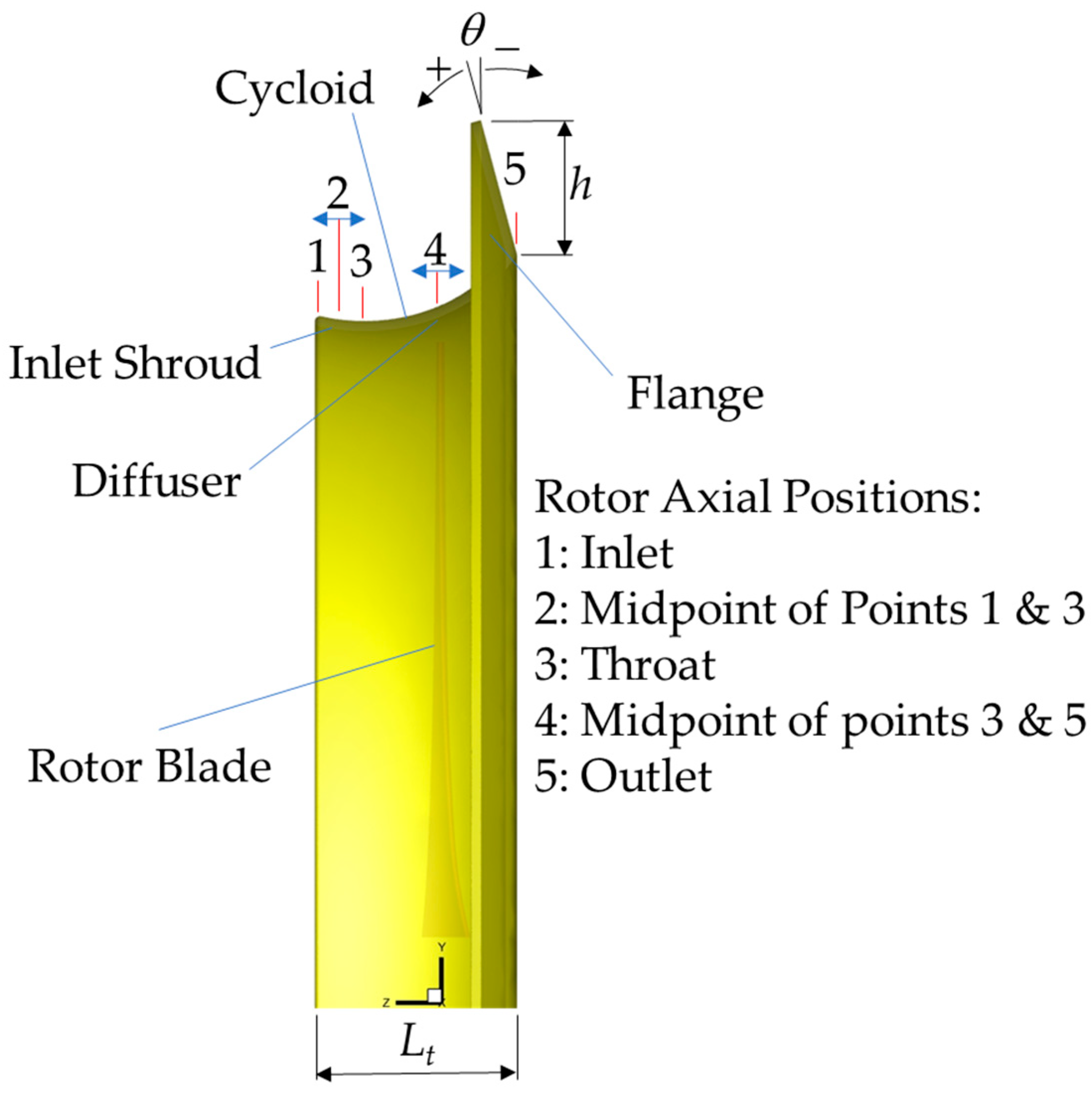


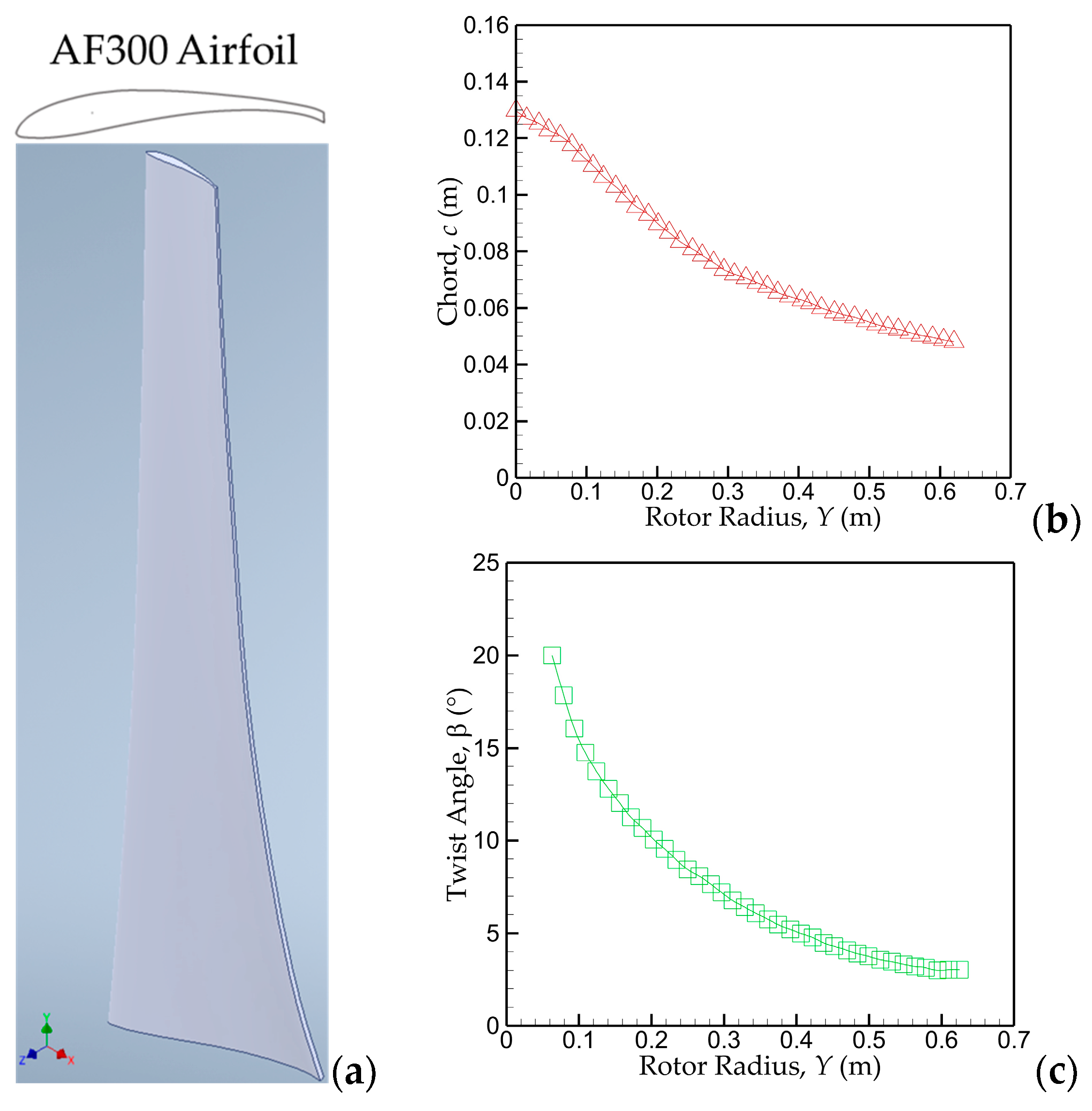

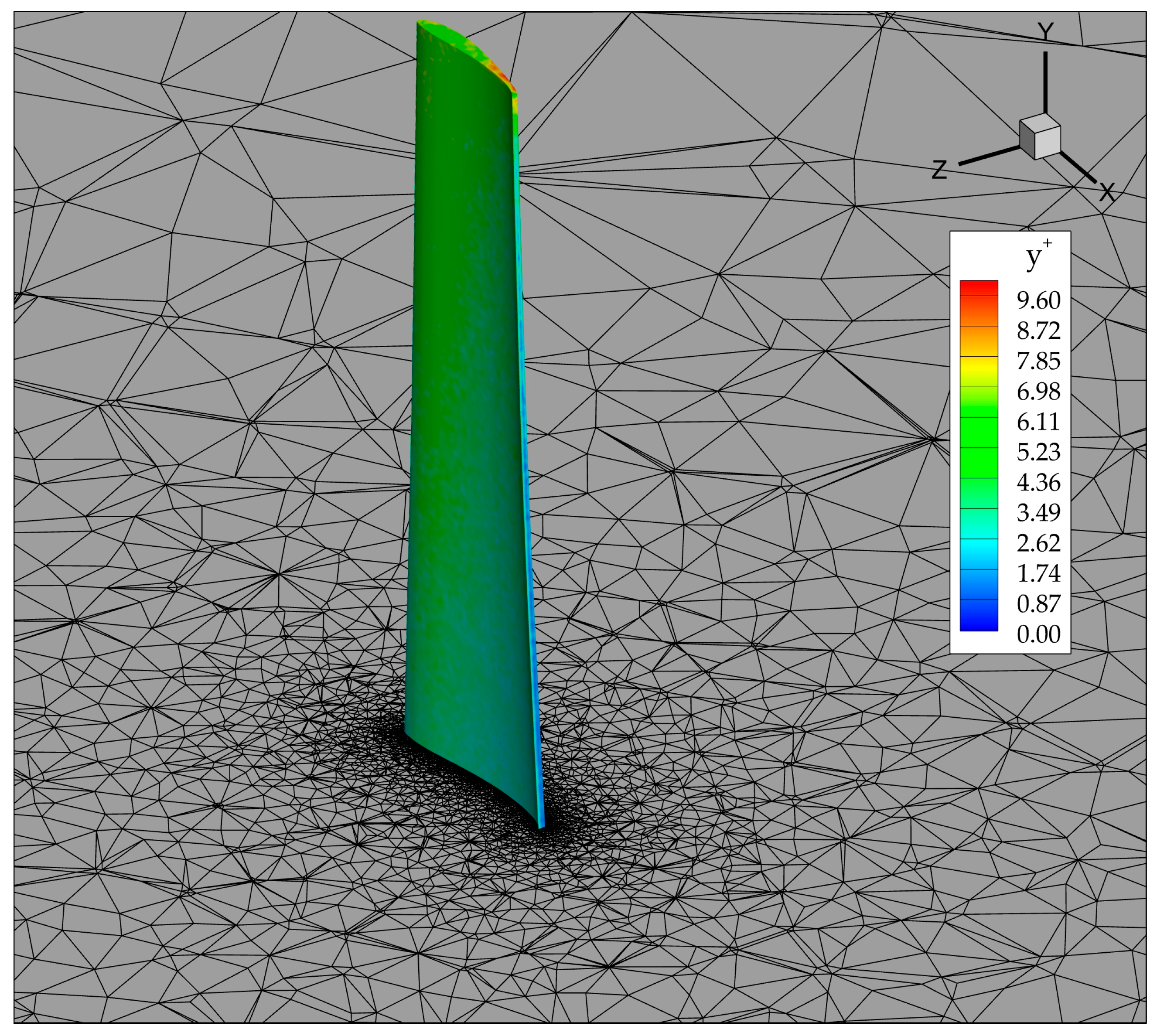


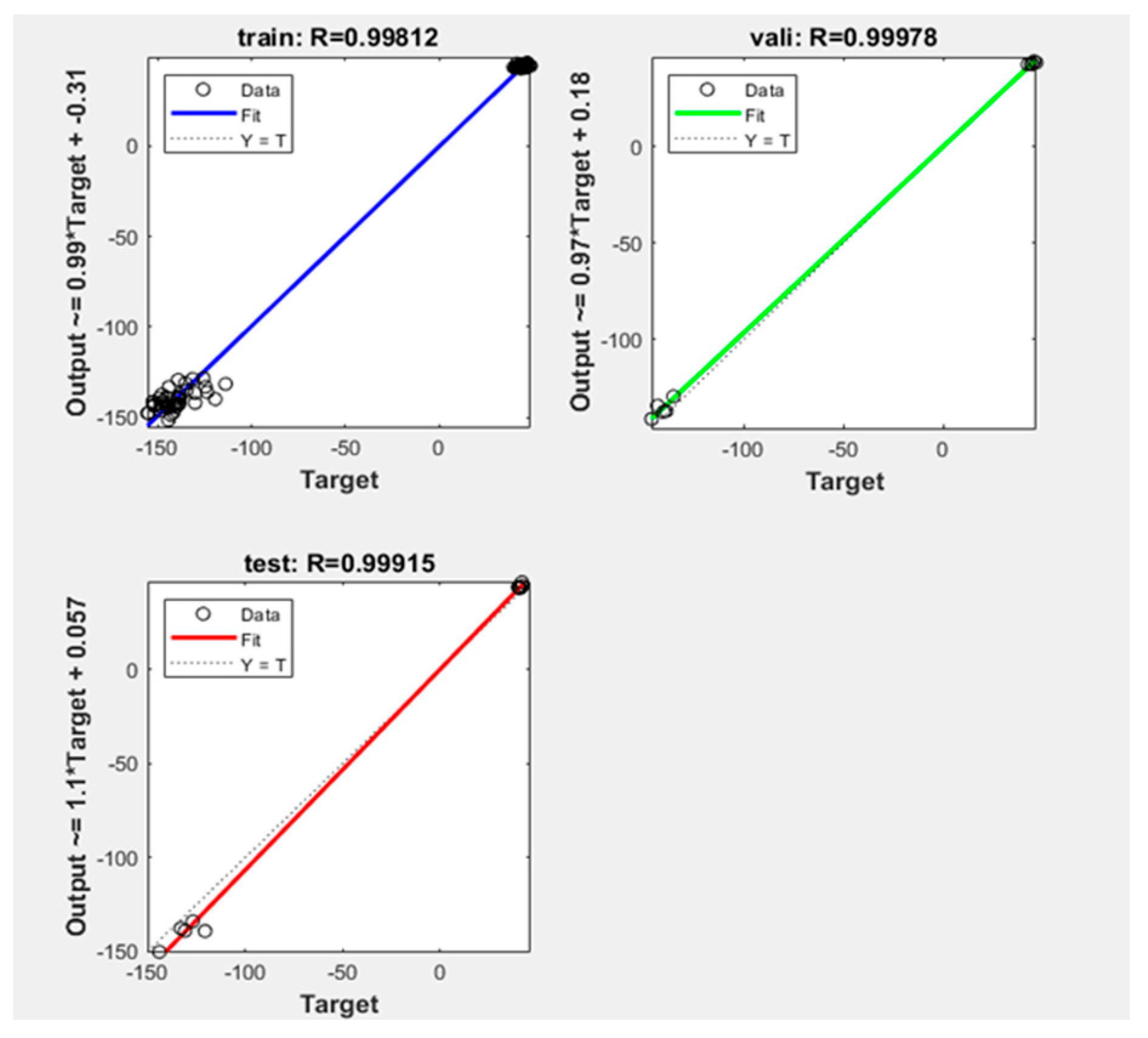


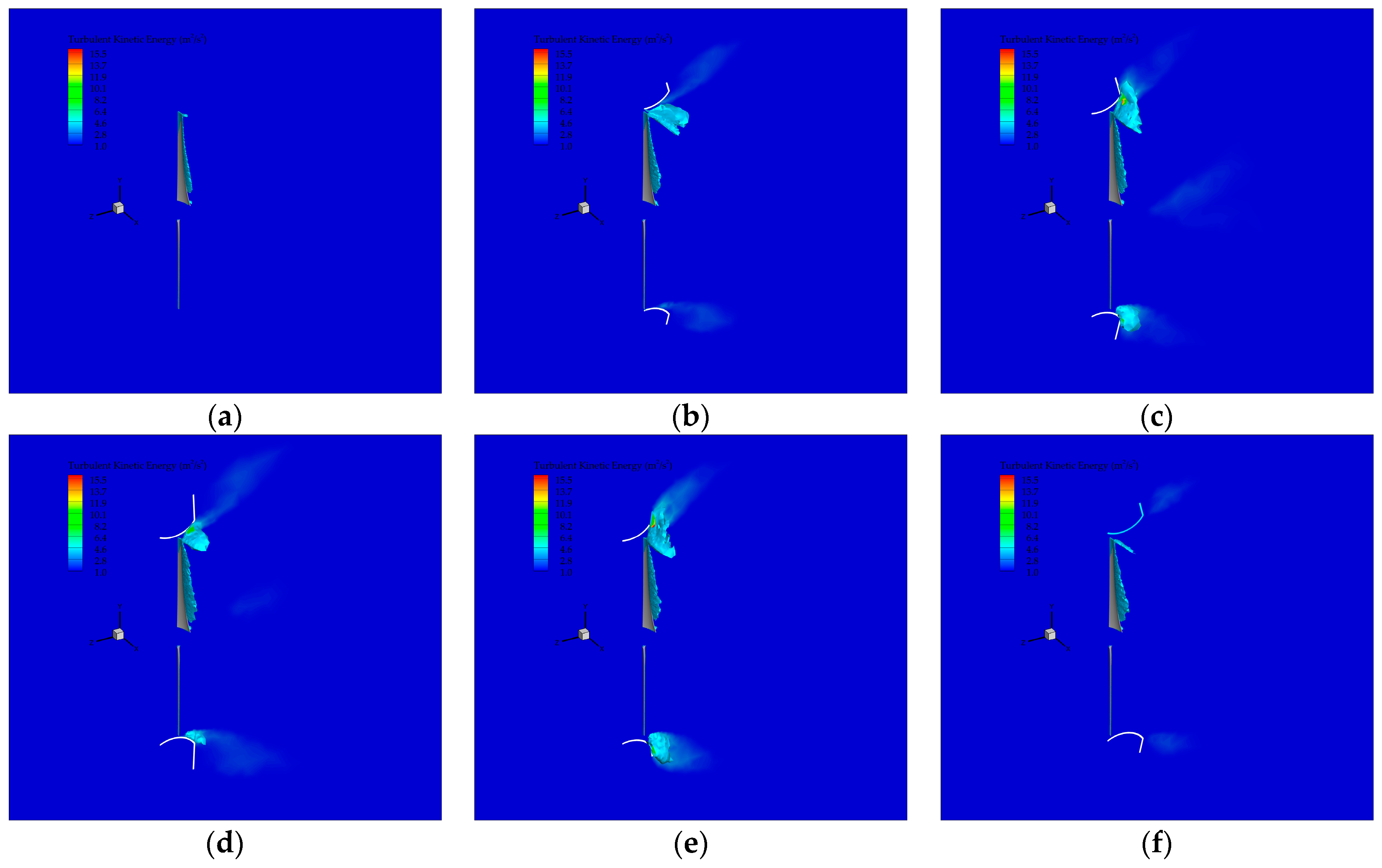
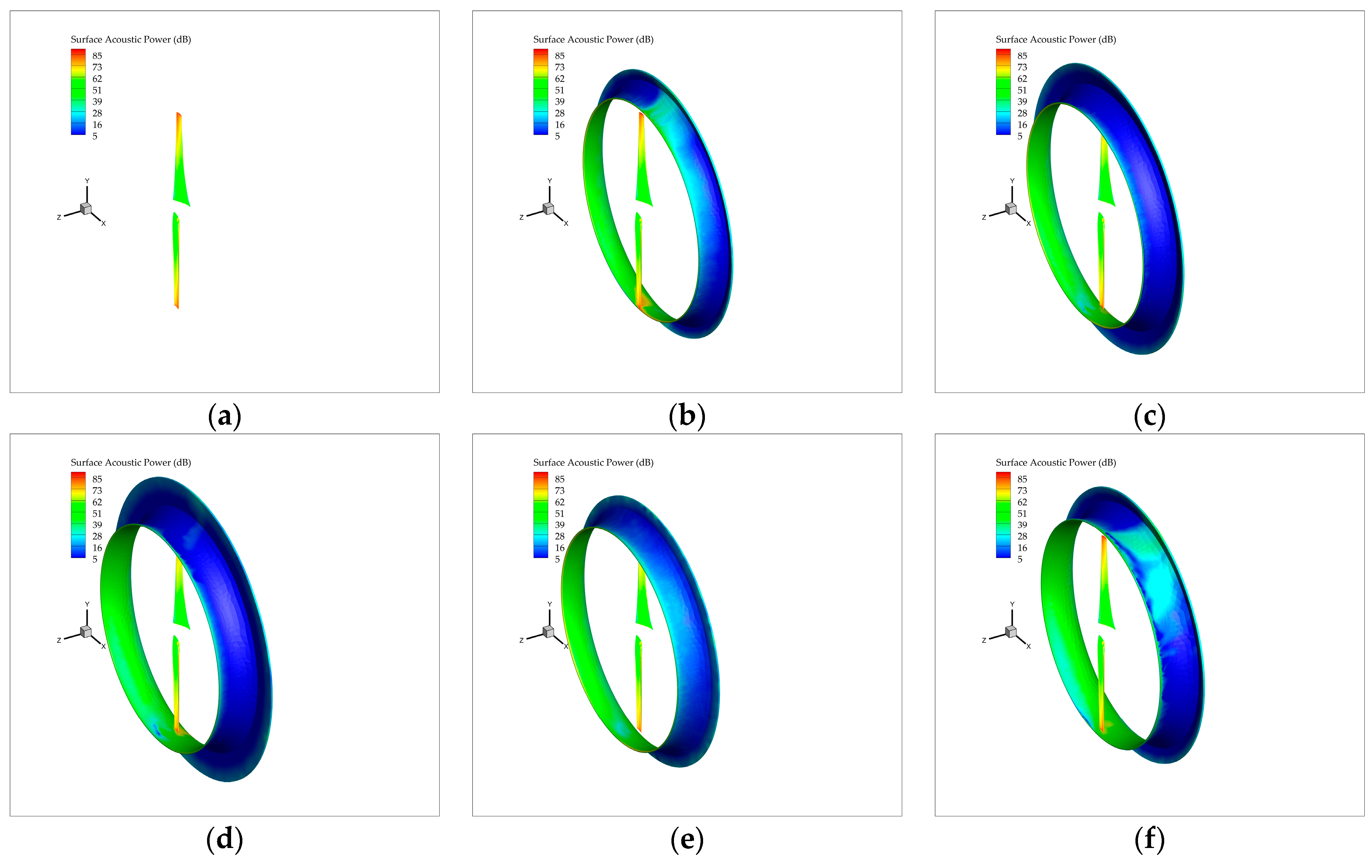
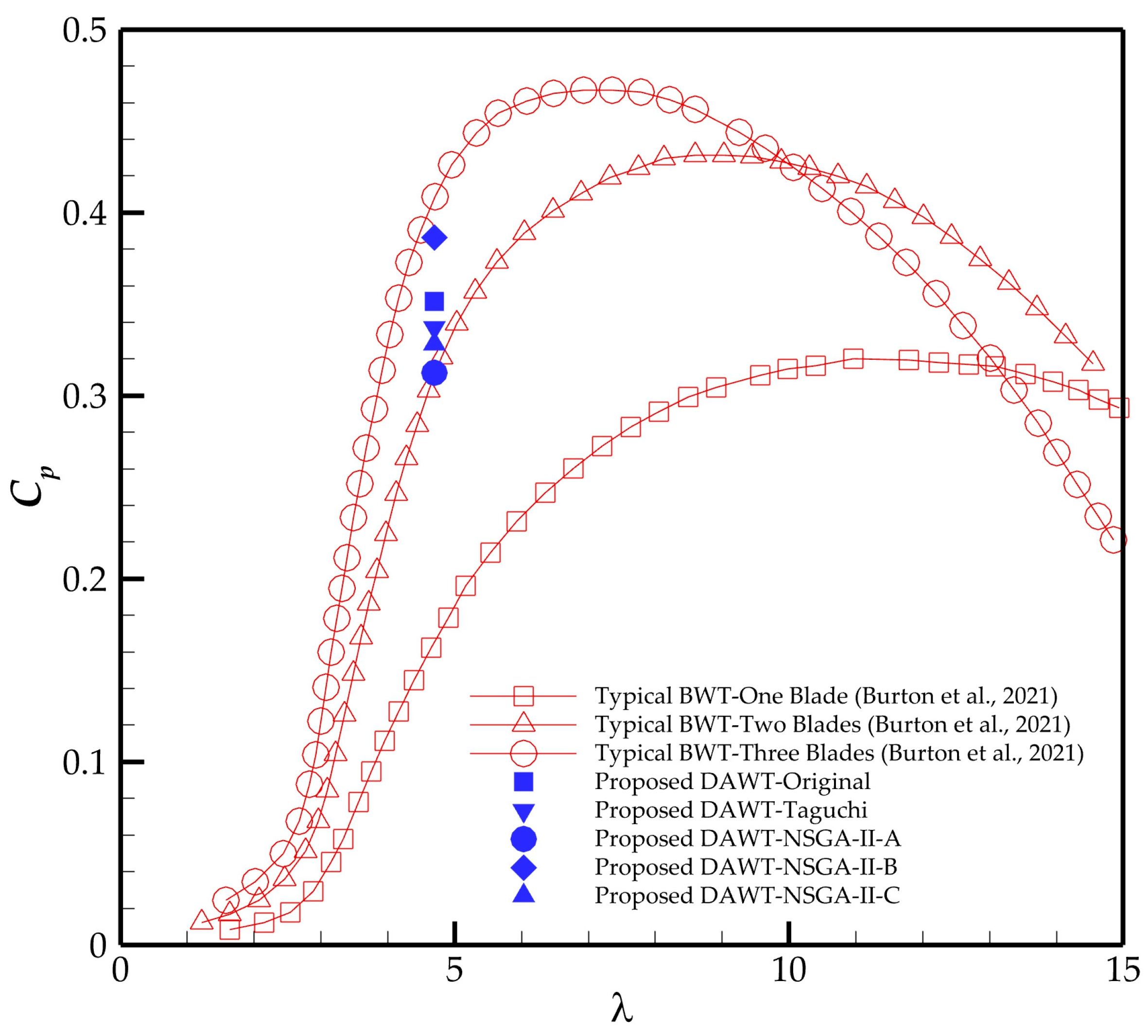
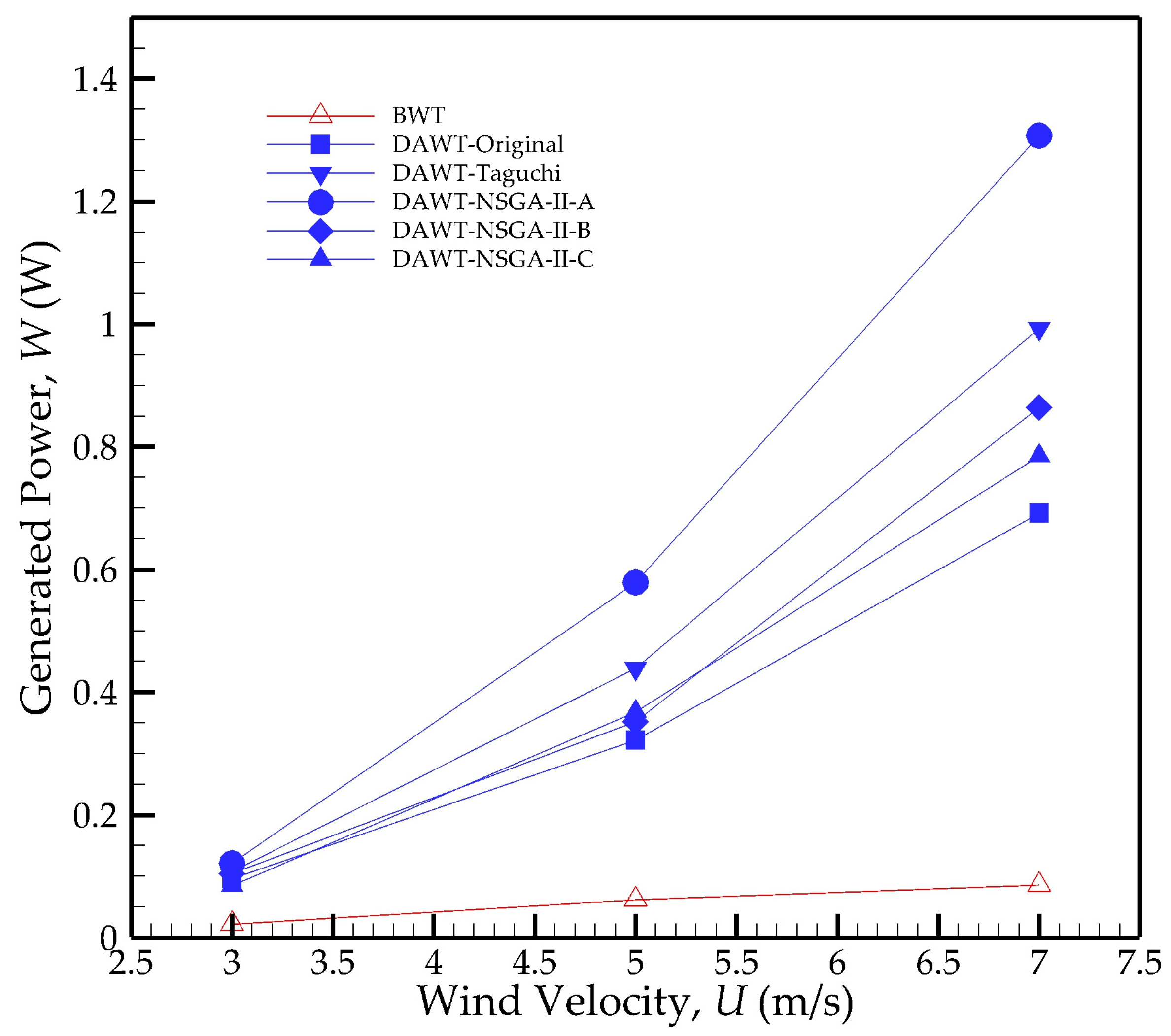
| Diameter | Hub Diameter | Twist Angle | Rotor Solidity | Design Rotational Speed |
|---|---|---|---|---|
| D = 1.26 m | H = 0.13 m | β = 20° − 3° = 17° | σ = 8.27% | ω = 500 rpm |
| Flange Height | Flange Angle | Diffuser Length | Rotor Axial Position |
|---|---|---|---|
| h/D= 0.05–0.25 | θ= −15°–15° | Lt/D = 0.132–0.223 | Five specific positions 1 |
| Flange Height h/D | Flange Angle θ | Diffuser Length Lt/D | Rotor Axial Position z/D |
|---|---|---|---|
| 0.05–0.2 [14] | −25°–25° [24] | 0.1–0.4 [14] | 0.04–0.16 [32] |
| 0–0.05 [19] | −15°–15° [27] | 0.1–0.4 [22] | 0.4–0.8 [34] |
| 0.025–0.35 [22] | −15°–0° [35] | 0.5–1.25 [30] | |
| 0.05–0.2 [33] | 0.013–0.556 [32] | ||
| 0–0.3 [34] | 0.1–0.371 [33] |
| Levels | Flange Height h/D | Flange Angle θ | Diffuser Length Lt/D | Rotor Axial Position Labeled Number |
|---|---|---|---|---|
| 1 | 0.05 | 15° | 0.132 | 1 |
| 2 | 0.1 | 10° | 0.152 | 2 |
| 3 | 0.15 | 0° | 0.183 | 3 |
| 4 | 0.2 | −10° | 0.211 | 4 |
| 5 | 0.25 | −15° | 0.223 | 5 |
| Case | Flange Height, h/D | Flange Angle, θ | Diffuser Length, Lt/D | Rotor Axial Position |
|---|---|---|---|---|
| DAWT-Original | 0.05 | 15 | 0.132 | 1 |
| DAWT-Taguchi | 0.1 | 15 | 0.152 | 4 |
| DAWT-NSGA-II-A | 0.13 | 2.4 | 0.181 | 3.5 |
| DAWT-NSGA-II-B | 0.06 | −8 | 0.149 | 4.3 |
| DAWT-NSGA-II-C | 0.07 | 13.7 | 0.185 | 1.4 |
| Case | Prediction | Power (W) | Noise (dBA) |
|---|---|---|---|
| DAWT-NSGA-II-A | BPNN | 154.51 | 46.91 |
| CFD | 154.44 | 47.2 | |
| Error | 0.04% | 0.6% | |
| DAWT-NSGA-II-B | BPNN | 151.08 | 44.92 |
| CFD | 151.85 | 43.7 | |
| Error | 0.5% | 2.7% | |
| DAWT-NSGA-II-C | BPNN | 135.41 | 42.39 |
| CFD | 134.26 | 38.4 | |
| Error | 0.8% | 9.4% |
| Case | Tip Clearance (mm) | Power (W) | Noise (dBA) | Cpb 2 | Cpd 3 | K 4 |
|---|---|---|---|---|---|---|
| BWT | — | 98.12 | 44.24 | — | — | 0.875 |
| DAWT-Original | 10 (1.6%) 1 | 135.31 | 43.3 | −0.778 | 0.366 | 0.975 |
| DAWT-Taguchi | 25.7 (4.1%) | 152.08 | 45.8 | −0.98 | 0.211 | 1.14 |
| DAWT-NSGA-II-A | 14.1 (2.2%) | 154.44 | 47.2 | −0.924 | 0.304 | 1.142 |
| DAWT-NSGA-II-B | 37.8 (6%) | 151.85 | 43.7 | −0.974 | 0.224 | 1.149 |
| DAWT-NSGA-II-C | 21.7 (3.4%) | 134.26 | 38.4 | −0.834 | 0.311 | 1.006 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hwang, P.-W.; Wu, J.-H.; Chang, Y.-J. Optimization Based on Computational Fluid Dynamics and Machine Learning for the Performance of Diffuser-Augmented Wind Turbines with Inlet Shrouds. Sustainability 2024, 16, 3648. https://doi.org/10.3390/su16093648
Hwang P-W, Wu J-H, Chang Y-J. Optimization Based on Computational Fluid Dynamics and Machine Learning for the Performance of Diffuser-Augmented Wind Turbines with Inlet Shrouds. Sustainability. 2024; 16(9):3648. https://doi.org/10.3390/su16093648
Chicago/Turabian StyleHwang, Po-Wen, Jia-Heng Wu, and Yuan-Jen Chang. 2024. "Optimization Based on Computational Fluid Dynamics and Machine Learning for the Performance of Diffuser-Augmented Wind Turbines with Inlet Shrouds" Sustainability 16, no. 9: 3648. https://doi.org/10.3390/su16093648
APA StyleHwang, P.-W., Wu, J.-H., & Chang, Y.-J. (2024). Optimization Based on Computational Fluid Dynamics and Machine Learning for the Performance of Diffuser-Augmented Wind Turbines with Inlet Shrouds. Sustainability, 16(9), 3648. https://doi.org/10.3390/su16093648







