Study on Spatial and Temporal Changes in Landscape Ecological Risks and Indicator Weights: A Case Study of the Bailong River Basin
Abstract
1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Research Data
3. Research Methodology
3.1. Construction of Landscape Ecological Risk Evaluation System
3.1.1. Establishment of Evaluation Indicators
3.1.2. Methodology for the Assignment of Indicators
3.1.3. Comparison of Different Empowerment Methods
3.1.4. Comparison of the Evaluation Results of Multiple Weights
3.2. Landscape Ecological Risk Calculation
3.3. Spatial Autocorrelation and Hotspot Analysis
4. Results and Analyses
4.1. Analysis of Spatial and Temporal Changes in Land Use Types
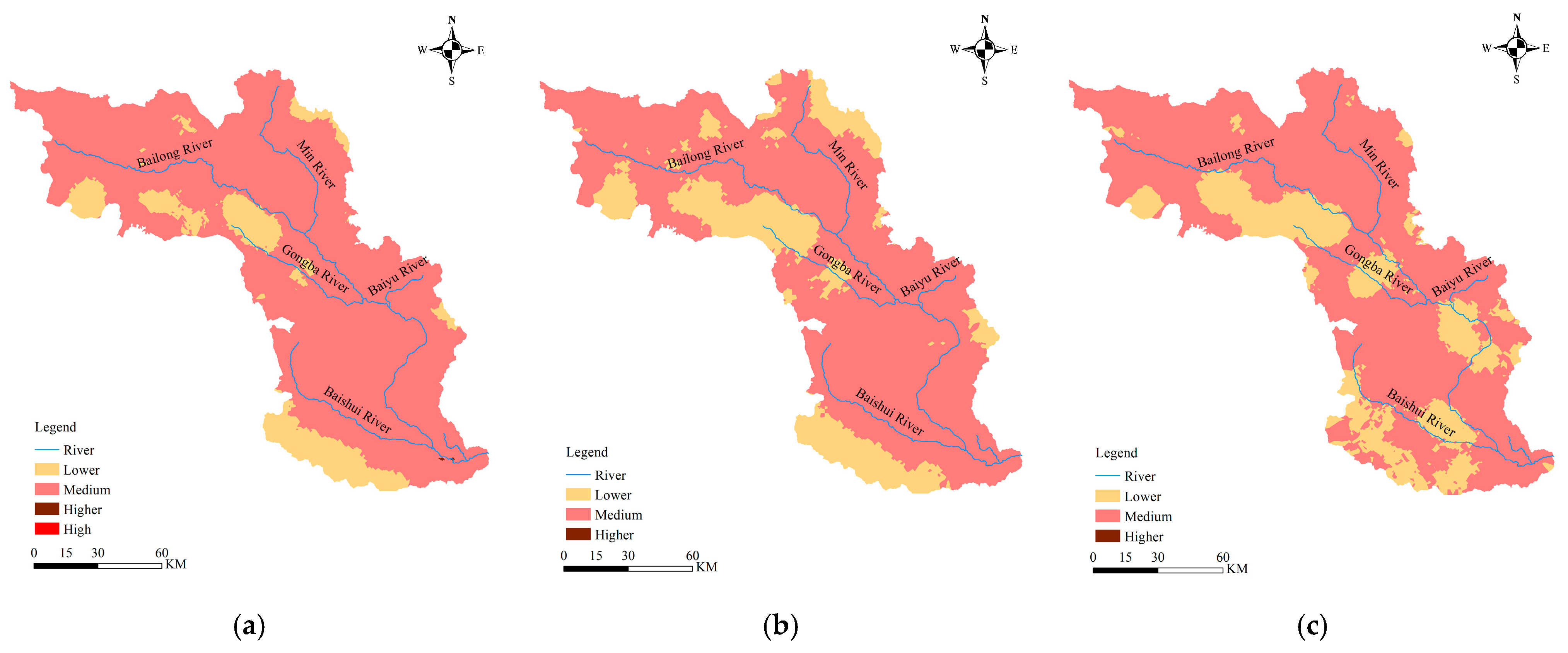
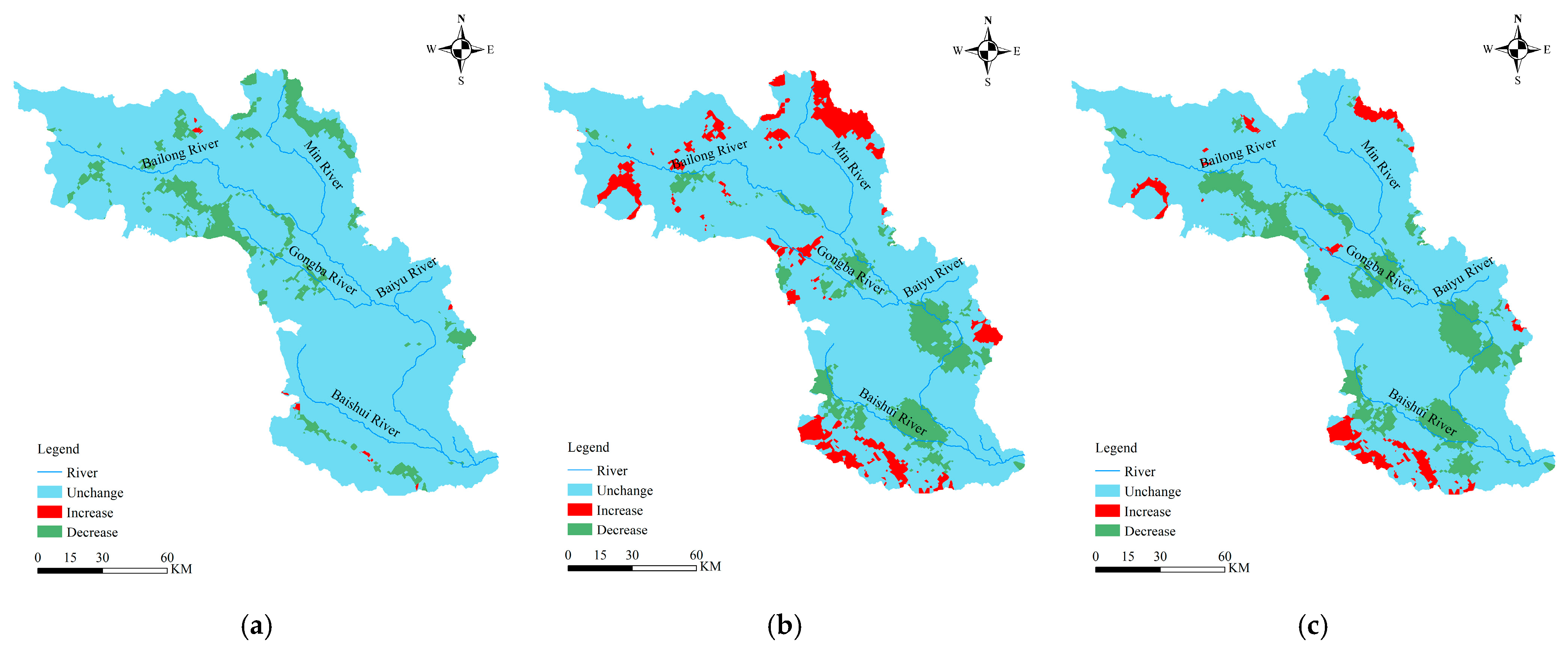
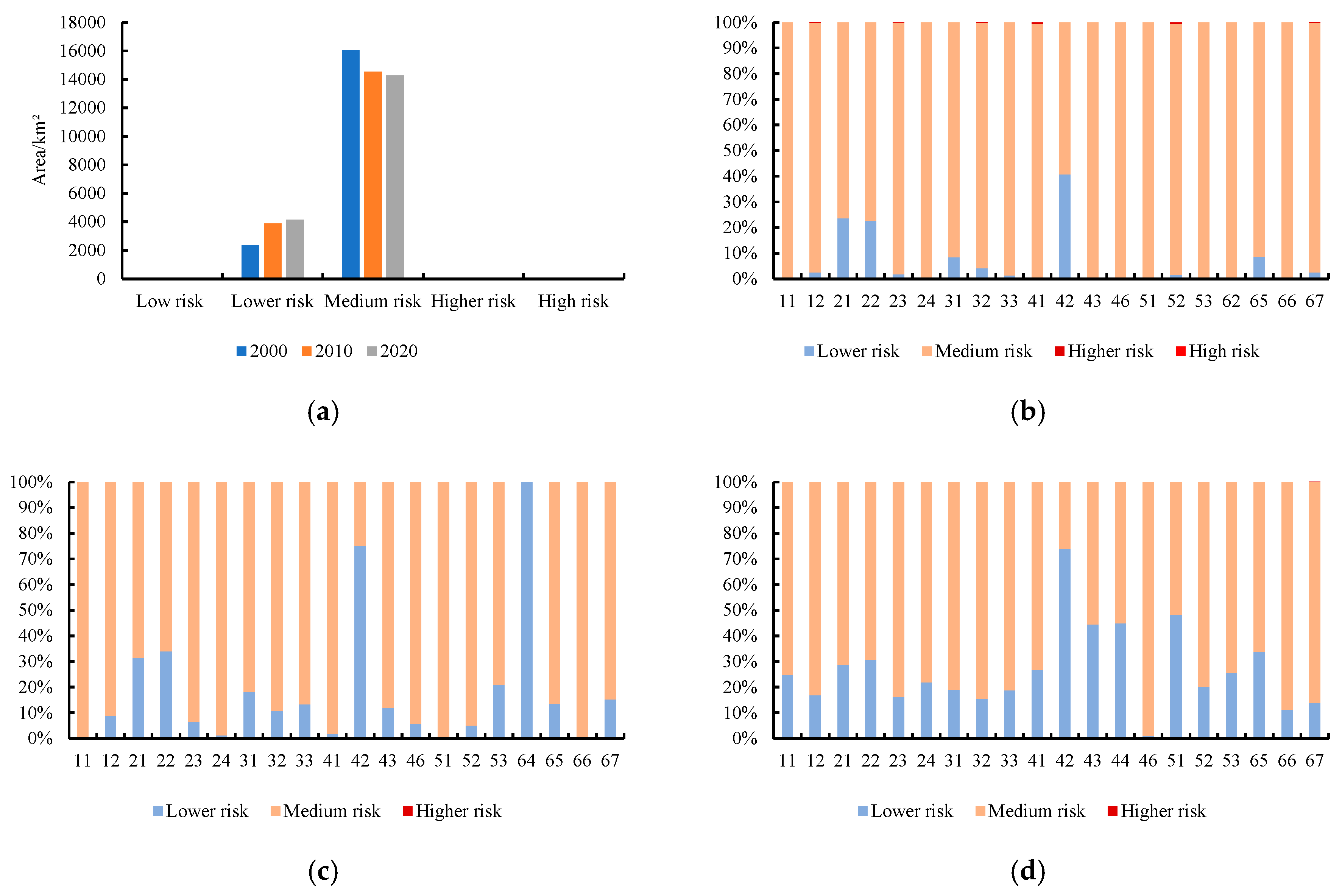
4.2. Analysis of Spatial and Temporal Changes in Landscape Ecological Risk
4.3. Landscape Ecological Risk Analyses for Different Site Types
4.4. Spatial Autocorrelation and Hotspot Analysis
4.4.1. Comparison of Evaluation Results of Multiple Weights
4.4.2. Hot Spot Analysis
5. Discussion
5.1. Scale Dependence of Weight Assignment
5.2. Response Relationship between Land Use and Landscape Ecological Risk
5.3. Spatial Characterization of Landscape Ecological Risk
5.4. Research Shortcomings and Prospects
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gong, J.; Cao, E.; Xie, Y.; Xu, C.; Li, H.; Yan, L. Integrating ecosystem services and landscape ecological risk into adaptive management: Insights from a western mountain-basin area, China. J. Environ. Manag. 2021, 281, 111817. [Google Scholar] [CrossRef] [PubMed]
- Gong, J.; Xie, Y.; Cao, E.; Huang, Q.; Li, H. Integration of InVEST-habitat quality model with landscape pattern indexes to assess mountain plant biodiversity change: A case study of Bailongjiang watershed in Gansu Province. J. Geogr. Sci. 2019, 29, 1193–1210. [Google Scholar] [CrossRef]
- Gong, J.; Liu, D.; Gao, B. Tradeoffs and synergies of ecosystem services in western mountainous China: A case study of the Bailongjiang basin in Gansu, China. J. Appl. Ecol. 2020, 31, 1278–1288. [Google Scholar]
- Wang, H.; Liu, X.; Zhao, C.; Chang, Y.; Liu, Y.; Zang, F. Spatial-temporal Pattern Analysis of Landscape Ecological Risk Assessment Based on Land use/Land Cover Change in Baishuijiang National Nature Reserve in Gansu Province, China. Ecol. Indic. 2021, 124, 107454. [Google Scholar] [CrossRef]
- Tian, P.; Li, J.; Shi, X. Spatial and Temporal Change of Land Use Pattern and Ecological Risk Assessment in Zhejiang Province. Resour. Environ. Yangtze River Basin 2018, 27, 59–68. [Google Scholar]
- Shi, P.; Qin, Y.; Li, P. Development of a landscape index to link landscape patterns to runoff and sediment. J. Mt. Sci. 2022, 19, 2905–2919. [Google Scholar] [CrossRef]
- Peng, J.; Dang, W.; Liu, Y. Progress and Prospects of Landscape Ecological Risk Assessment Research. Acta Geogr. Sin. 2015, 70, 664–677. [Google Scholar]
- Ai, J.; Yu, K.; Zeng, Z.; Yang, L.; Liu, Y.; Liu, J. Assessing the dynamic landscape ecological risk and its driving forces in an island city based on optimal spatial scales: Haitan Island, China. Ecol. Indic. 2022, 137, 108771. [Google Scholar] [CrossRef]
- Cui, L.; Zhao, Y.; Liu, J. Landscape ecological risk assessment in Qinling Mountain. Geol. J. 2018, 53, 342–351. [Google Scholar] [CrossRef]
- Chen, X.; Yang, Z.; Wang, T.; Han, F. Landscape Ecological Risk and Ecological Security Pattern Construction in World Natural Heritage Sites: A Case Study of Bayinbuluke, Xinjiang, China. ISPRS Int. J. Geo-Inf. 2022, 11, 6. [Google Scholar] [CrossRef]
- Lin, X.; Wang, Z. Landscape Ecological Risk Assessment and Its Driving Factors of Multi-mountainous City. Ecol. Indic. 2023, 146, 109823. [Google Scholar] [CrossRef]
- Asada, H.; Minagawa, T. Impact of Vegetation Differences on Shallow Landslides: A Case Study in Aso, Japan. Water 2023, 15, 18. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, J.; Lv, Z.; Yao, L.; Zhang, N.; Zhang, Q. Spatio-Temporal Assessment of Landscape Ecological Risk and Associated Drivers: A Case Study of the Yellow River Basin in Inner Mongolia. Land 2023, 12, 1114. [Google Scholar] [CrossRef]
- Wang, W.; Wang, H.; Zhou, X. Ecological risk assessment of watershed economic zones on the landscape scale: A case study of the Yangtze River Economic Belt in China. Reg. Environ. Chang. 2023, 23, 105. [Google Scholar] [CrossRef]
- Liu, D.; Chen, H.; Zhang, H.; Geng, T.; Shi, Q. Spatiotemporal Evolution of Landscape Ecological Risk Based on Geomorphological Regionalization during 1980–2017: A Case Study of Shaanxi Province, China. Sustainability 2020, 12, 941. [Google Scholar] [CrossRef]
- Wang, S.; Tan, X.; Fan, F. Landscape Ecological Risk Assessment and Impact Factor Analysis of the Qinghai–Tibetan Plateau. Remote Sens. 2022, 14, 4726. [Google Scholar] [CrossRef]
- Lan, Y.; Chen, J.; Yang, Y.; Ling, M.; You, H.; Han, X. Landscape Pattern and Ecological Risk Assessment in Guilin Based on Land Use Change. Int. J. Environ. Res. Public Health 2023, 20, 2045. [Google Scholar] [CrossRef] [PubMed]
- Tan, R.; Zhou, K. Examining the Causal Effects of Road Networks on Landscape Ecological Risk: The Case of Wuhan, China. J. Urban Plan. Dev. 2023, 149, 2. [Google Scholar] [CrossRef]
- Yan, Z.; You, N.; Wang, L.; Lan, C. Assessing the Impact of Road Network on Urban Landscape Ecological Risk Based on Corridor Cutting Degree Model in Fuzhou, China. Sustainability 2023, 15, 1724. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhao, W.; Lv, S.; Huang, D.; Zhao, Z.; Sun, Y. Spatiotemporal Transfer of Source-Sink Landscape Ecological Risk in a Karst Lake Watershed Based on Sub-Watersheds. Land 2023, 12, 1330. [Google Scholar] [CrossRef]
- Zhao, L.; Shi, Z.; He, G.; He, L.; Xi, W.; Jiang, Q. Land Use Change and Landscape Ecological Risk Assessment Based on Terrain Gradients in Yuanmou Basin. Land 2023, 12, 1759. [Google Scholar] [CrossRef]
- Peng, J.; Zong, M.; Hu, Y.; Liu, Y.; Wu, J. Assessing Landscape Ecological Risk in a Mining City: A Case Study in Liaoyuan City, China. Sustainability 2015, 7, 8312–8334. [Google Scholar] [CrossRef]
- Li, C.; Zhang, J.; Philbin, S.; Yang, X.; Dong, Z.; Hong, J.; Ballesteros-Pérez, P. Evaluating the impact of highway construction projects on landscape ecological risks in high altitude plateaus. Sci. Rep. 2020, 12, 5107. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Ma, Y. Ecological Risk Identification and Ecological Security Pattern Construction of Productive Wetland Landscape. Water Resour Manag. 2023, 37, 4709–4731. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, P.; Chang, Y.; Li, G.; Chen, Z.; Zhang, X.; Xing, G.; Lu, R.; Li, M.; Zhou, Z. Landscape pattern evolution and ecological risk assessment of the Yellow River Basin based on optimal scale. Ecol. Indic. 2024, 158, 111381. [Google Scholar] [CrossRef]
- Li, B.; Yang, Y.; Jiao, L.; Yang, M.; Li, T. Selecting ecologically appropriate scales to assess landscape ecological risk in megacity Beijing, China. Ecol. Indic. 2023, 154, 110780. [Google Scholar] [CrossRef]
- Xu, W.; Wang, J.; Zhang, M.; Li, S. Construction of landscape ecological network based on landscape ecological risk assessment in a large-scale opencast coal mine area. J. Clean. Prod. 2021, 286, 125523. [Google Scholar] [CrossRef]
- Aksu, G.; Musaoglu, N.; Uzun, A. Ecological risk analysis based on analytic hierrchy process. Fresenius Environ. Bull. 2017, 26, 84–92. [Google Scholar]
- Zhu, C.; Fang, C.; Zhang, L. Analysis of the coupling coordinated development of the Population-Water-Ecology-Economy system in urban agglomerations and obstacle factors discrimination: A case study of the Tianshan North Slope Urban Agglomeration, China. Sustain. Cities Soc. 2023, 90, 104359. [Google Scholar] [CrossRef]
- Algayer, B.; Wang, B.; Bourennane, H.; Zheng, F.; Duval, O.; Li, G.; Le Bissonnais, Y.; Darboux, F. Aggregate stability of a crusted soil: Differences between crust and sub-crust material, and consequences for interrill erodibility assessment. An example from the Loess Plateau of China. Eur. J. Soil Sci. 2014, 65, 325–335. [Google Scholar] [CrossRef]
- Wang, X.; Che, Q.; Wang, L.; Li, G.; Sun, H.; Qin, W.; Chen, S.; Yao, S.; Meng, L.; Yu, X. Spatial–temporal pattern of urban ecological construction in the Yellow River basin and its optimization and promotion paths. Environ. Inform. Remote Sens. 2023, 11, 1147619. [Google Scholar]
- Long, C.; Pang, Y.; Wang, Z. Study of the Sustainability of a Forest Road Network Using GIS-MCE. Forests 2023, 14, 2410. [Google Scholar] [CrossRef]
- Zhao, L.; Ma, R.; Yang, Z.; Ning, K.; Chen, P.; Wu, J. Ecosystem health risk assessment of lakes in the Inner Mongolian Plateau based on the coupled AHP-SOM-CGT model. Ecol. Indic. 2023, 156, 111168. [Google Scholar] [CrossRef]
- Peng, J.; Zhao, H.; Liu, Y.; Wu, J. Progress and Prospects of Research on the Construction of Regional Ecological Security Patterns. Geogr. Res. 2017, 36, 407–419. [Google Scholar]
- Li, Q.; Ma, B.; Zhao, L.; Mao, Z.; Luo, L.; Liu, X. Landscape Ecological Risk Evaluation Study under Multi-Scale Grids—A Case Study of Bailong River Basin in Gansu Province, China. Water 2023, 15, 3777. [Google Scholar] [CrossRef]
- Chen, M.; Lu, D.; Zhang, H. Comprehensice Evaluation and the Driving Factors of China’s Urbanization. Acta Geogr. Sin. 2009, 64, 387–398+6. [Google Scholar]
- Chen, S.; Zou, Q.; Wang, B.; Zhou, W.; Yang, T.; Jiang, H.; Zhou, B.; Yao, H. Disaster risk management of debris flow based on time-series contribution mechanism (CRMCD): Nonnegligible ecological vulnerable multi-ethnic communities. Ecol. Indic. 2023, 157, 111266. [Google Scholar] [CrossRef]
- Xu, N.; Hu, X.; Wang, X.; Liu, Z.; Tian, J.; Ren, Z. Spatiotemporal variations of eco-environmental vulnerability in Shiyang River Basin, China. Ecol. Indic. 2024, 158, 111327. [Google Scholar] [CrossRef]
- Yang, X.; Shen, J. Landscape Sensitivity Assessment of Historic Districts Using a GIS-Based Method: A Case Study of Beishan Street in Hangzhou, China. ISPRS Int. J. Geo-Inf. 2023, 12, 462. [Google Scholar] [CrossRef]
- Niu, S.; Li, G.; Zhang, S. Driving Risk Assessment Model of Commercial Drivers Based on Satellite positioning Data. China J. Highw. Transp. 2020, 33, 202–211. [Google Scholar]
- Li, W.; Lin, Q.; Hao, J.; Wu, X.; Zhou, Z.; Lou, P.; Liu, Y. Landscape Ecological Risk Assessment and Analysis of Influencing Factors in Selenga River Basin. Remote Sens. 2023, 15, 4262. [Google Scholar] [CrossRef]
- Ma, J.; Khromykh, V.; Wang, J.; Zhang, J.; Li, W.; Zhong, X. A landscape-based ecological hazard evaluation and characterization of influencing factors in Laos. Environ. Inform. Remote Sens. 2023, 11, 1276239. [Google Scholar] [CrossRef]
- Zhang, X.; Dong, X.; Xu, C.; Wang, R.; Lv, T.; Ranagalage, M. Landscape Ecological Risk Assessment in the Dongjiangyuan Region, China, from 1985 to 2020 Using Geospatial Techniques. Geomat. Nat. Hazards Risk 2023, 14, 2173662. [Google Scholar] [CrossRef]
- Gibson, C.C.; Ostrom, E.; Ahn, T.-K. The concept of scale and the human dimensions of global change: A survey. Ecol. Econ. 2000, 32, 217–239. [Google Scholar] [CrossRef]
- Ju, H.; Niu, C.; Zhang, S.; Jiang, W.; Zhang, Z.; Zhang, X.; Yang, Z.; Cui, Y. Spatiotemporal patterns and modifiable areal unit problems of the landscape ecological risk in coastal areas: A case study of the Shandong Peninsula, China. J. Clean. Prod. 2021, 310, 127522. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, J.; Lan, Y.; Zhou, G.; You, H.; Han, X.; Wang, Y.; Shi, X. Landscape Pattern and Ecological Risk Assessment in Guangxi Based on Land Use Change. Int. J. Environ. Res. Public Health 2022, 19, 1595. [Google Scholar] [CrossRef]
- Chen, J.; Yang, Y.; Feng, Z.; Huang, R.; Zhou, G.; You, H.; Han, X. Ecological Risk Assessment and Prediction Based on Scale Optimization—A Case Study of Nanning, a Landscape Garden City in China. Remote Sens. 2023, 15, 1304. [Google Scholar] [CrossRef]
- Zhu, Y.; Hou, Z.; Xu, C.; Gong, J. Ecological Risk Identification and Management Based on Ecosystem Service Supply and Demand Relationship in the Bailongjiang River Watershed of Gansu Province. Sci. Geogr. Sin. 2023, 43, 423–433. [Google Scholar]
- Kumaraswamy, S.; Kunte, K. Integrating biodiversity and conservation with modern agricultural landscapes. Biodivers. Conserv. 2013, 22, 2735–2750. [Google Scholar] [CrossRef]
- Shi, Y.; Feng, C.; Yu, Q.; Han, R.; Guo, L. Contradiction or coordination? The spatiotemporal relationship between landscape ecological risks and urbanization from coupling perspectives in China. J. Clean. Prod. 2022, 363, 132557. [Google Scholar] [CrossRef]
- Qu, Y.; Zong, H.; Su, D.; Ping, Z.; Guan, M. Land Use Change and Its Impact on Landscape Ecological Risk in Typical Areas of the Yellow River Basin in China. Int. J. Environ. Res. Public Health 2021, 18, 11301. [Google Scholar] [CrossRef]
- Sestras, P.; Bondrea, M.V.; Cetean, H.I.; SĂLĂGean, T.; BilaŞCo, Ş.; Sanda, N.A. Ameliorative, ecological and landscape roles of Făget Forest, Cluj-Napoca, Romania, and possibilities of avoiding risks based on GIS landslide susceptibility map. Not. Bot. Horti Agrobot. Cluj-Napoca 2018, 46, 292–300. [Google Scholar] [CrossRef]
- Liu, J.; Wang, M.; Yang, L. Assessing Landscape Ecological Risk Induced by Land-Use/Cover Change in a County in China: A GIS and Landscape-Metric-Based Approach. Sustainability 2020, 12, 9037. [Google Scholar] [CrossRef]
- Hu, J.; Liu, Y.; Dai, Q.; Yang, B.; Zhou, W. Evaluation of ecotourism suitability based on AHP-GIS: Taking Xiaoxiangling area of the Giant Panada National Park and the Surrounding communities as an example. Chin. J. Appl. Ecol. 2024, 1–11. [Google Scholar] [CrossRef]
- Gong, J.; Gao, J.; Zhang, L.; Xie, Y.; Zhao, C.; Qian, D. Distribution Characteristics of Ecological Risks in Land-use Based on Terrain Gradient and Landscape Structure: Taking Bailongjiang Watershed as an Example. J. Lanzhou Univ. (Nat. Sci.) 2014, 50, 692–698. [Google Scholar]
- Zhou, W.; Luo, J. Spatial-temporal Evolution of Ecosystem Service Value and Landscape Ecological Risk in Dry Valleys. Yangtze River 2023, 54, 85–93. [Google Scholar]
- Cao, Y.; Dong, B.; Xu, H.; Xu, Z.; Wei, Z.; Lu, Z.; Liu, X. Landscape Ecological Risk Assessment of Chongming Dongtan Wetland in Shanghai from 1990 to 2020. Environ. Res. Commun. 2023, 5, 105016. [Google Scholar] [CrossRef]
- Wang, D.; Ji, X.; Li, C.; Gong, Y. Spatiotemporal Variations of Landscape Ecological Risks in a Resource-Based City under Transformation. Sustainability 2021, 13, 5297. [Google Scholar] [CrossRef]
- Bai, Y.; Liao, S.; Sun, J. Scale effect and methods for accuracy evaluation of attribute information loss in rasterization. J. Geogr. Sci. 2011, 21, 1089–1100. [Google Scholar] [CrossRef]
- Molinos, J.; Takao, S.; Kumagai, N.; Poloczanska, E.; Burows, M.; Fujii, M.; Yamano, H. Improving the interpretability of climate landscape metrics: An ecological risk analysis of Japan’s Marine Protected Areas. Glob. Chang. Biol. 2017, 23, 4440–4452. [Google Scholar] [CrossRef]
- Fu, B.; Lu, Y. The progress and perspectives of landscape ecology in China. Prog. Phys. Geogr. 2006, 30, 232–244. [Google Scholar] [CrossRef]
- Gao, Y.; Wu, Z.F.; Lou, Q.S.; Huang, H.M.; Cheng, J.; Chen, Z.L. Landscape ecological security assessment based on projection pursuit in Pearl River Delta. Environ. Monit. Assess. 2012, 184, 2307–2319. [Google Scholar] [CrossRef] [PubMed]
- Zhou, K.H.; Liu, Y.L.; Tan, R.H.; Song, Y. Urban dynamics, landscape ecological security, and policy implications: A case study from the Wuhan area of central China. Cities 2014, 41, 141–153. [Google Scholar] [CrossRef]
- Cen, X.T.; Wu, C.F.; Xing, X.S.; Fang, M.; Garang, Z.M.; Wu, Y.Z. Coupling Intensive Land Use and Landscape Ecological Security for Urban Sustainability: An Integrated Socioeconomic Data and Spatial Metrics Analysis in Hangzhou City. Sustainability 2015, 7, 1459–1482. [Google Scholar] [CrossRef]









| Level 1 | Code | Level 2 | Code | Definition |
|---|---|---|---|---|
| Cultivated land | 1 | Wet field | 11 | Refers to arable land with a guaranteed water source and irrigation facilities that can be adequately irrigated, including arable land where rice and dryland crop rotation is practiced. |
| Dry field | 12 | Refers to arable land with no irrigation source or facilities, which relies on natural water to grow crops; dry crop arable land with water source and watering facilities, which can be generally irrigated in average years; arable land mainly for growing vegetables; and recreational land and rotational land with regular crop rotation. | ||
| Forest land | 2 | Natural forest land and artificial forest land | 21 | Refers to natural and plantation forests with a degree of closure more significant than 30 per cent. This includes timber forests, economic forests, protection forests, and other mature woodlands. |
| Shrubland | 22 | Refers to short woodlands and scrub woodlands where the degree of depression is greater than 40 per cent and the height is less than 2 m. | ||
| Sparse forest land | 23 | Refers to woodlands with 10–30 percent stand closure. | ||
| Other land | 24 | Refers to unforested afforestation land, traces of land, nurseries, and various types of gardens. | ||
| Grass land | 3 | High-cover grassland | 31 | Refers to natural grasslands, improved grasslands, and mown grasslands with greater than 50 percent cover. These grasslands generally have good moisture conditions and dense grass growth. |
| Medium-cover grassland | 32 | Refers to natural and improved grasslands with a cover greater than 20 percent, which is generally low in moisture and sparsely grassed. | ||
| Low-cover grassland | 33 | Refers to natural grasslands with less than 20 percent cover. These grasslands lack moisture, have sparse grass cover, and are poorly utilized for pastoral purposes. | ||
| Water body | 4 | Rivers and canals | 41 | The land below the perennial level of a naturally occurring or artificially excavated river and its main stream. Artificial channels include embankments. |
| Lake | 42 | Refers to land below the perennial water level in naturally occurring waterlogged areas. | ||
| Reservoir | 43 | Refer to land below the perennial water level in an artificially constructed water storage area. | ||
| Glacier and Snow | 44 | Refers to land that is covered by glaciers and snow year-round. | ||
| Mudflat | 45 | Refers to the tidal inundation zone between the high and low tide levels of a coastal high tide. | ||
| Beach land | 46 | Refers to the land between the level of the river or lake waters during the levelling period and the level during the flooding period. | ||
| Built-up land | 5 | Urban land | 51 | Refers to land in large, medium, and small cities and built-up areas above the county town level. |
| Rural residential area | 52 | Refers to rural settlements that are independent of towns. | ||
| Other built-up land | 53 | Refers to sites such as factories, mines, large industrial areas, oilfields, saltworks, quarries, etc., as well as transport roads, airports, and unique sites. | ||
| Desert | 61 | Refers to land with a sandy surface and less than 5 percent vegetation cover. | ||
| Unused land | 6 | Gobi | 62 | Refers to land where the surface is dominated by gravel with less than 5 percent vegetative cover. |
| Saline soil | 63 | Refers to land where saline accumulates on the surface and vegetation is so sparse that only strongly saline-tolerant plants can grow. | ||
| Marsh | 64 | Refers to flat, low-lying land, poorly drained, chronically wet, seasonally waterlogged or perennially waterlogged, and where wet vegetation grows on the surface. | ||
| Bare land | 65 | Refers to land with a surface soil cover and less than 5 percent vegetation cover. | ||
| Bare rock | 66 | Refers to land with a rocky or gravelly surface that covers less than 5 percent of the land area. | ||
| Other unused land | 67 | Refers to other unused land, including alpine deserts, tundra, etc. |
| Landscape-Scale | Features | Index Name | Units | Range | Ecological Implications |
|---|---|---|---|---|---|
| Class metrics | Crumbliness | Patch density (PD) | pieces/100 hm2 | >0 | The greater the PD, the greater the landscape fragmentation and the higher the ecological risk posed to the landscape. |
| Dominance | Largest patch index (LPI) | % | [0, 100] | LPI represents the degree of dominance, with a larger LPI indicating that the dominant type in the landscape is more prominent and poses less ecological risk to the landscape. | |
| Stability | Landscape shape index (LSI) | — | ≥1 | LSI stands for stability, and a larger LSI indicates a more complex shape of the landscape component with a more unstable structure and a higher ecological risk posed to the landscape. | |
| Intra-patch connectivity | Average contiguity index (CONTIG_MN) | — | [0, 1] | CONTIG_MN stands for patch internal connectivity. The contiguity index assesses the spatial connectedness, or contiguity, of cells within a grid-cell patch to provide an index of patch boundary configuration and thus patch shape. | |
| Inter-patch connectivity | Connectance index (CONNECT) | % | [0, 100] | CONNECT represents the connectivity between patches. The larger the connectivity index, the better the connectivity between patches and the lower the ecological risk caused to the landscape. | |
| Separability | Split index (SPLIT) | — | ≥1 | SPLIT represents the degree of separation of the same type of patches. The greater the splitting index, the greater the degree of separation between the same kind of patches, resulting in higher ecological risks to the landscape. | |
| Landscape metrics | Diversity | Landscape diversity index (Shannon’s diversity index, SHDI) | — | ≥0 | Reflects the abundance of regional landscape types and changes in landscape diversity characteristics. A higher diversity index indicates more patch types in the landscape. |
| Evenness | Landscape evenness index (Shannon’s evenness index, SHEI) | — | [0, 1] | Smaller SHEI values reflect a landscape dominated by one or more dominant patch types. When the SHEI is close to 1, it indicates that there is no clear dominant type in the landscape and that the patch types are evenly distributed across the landscape. |
| Type | 2000 | 2010 | 2020 | 2000–2010 | 2010–2020 | 2000–2020 |
|---|---|---|---|---|---|---|
| 11 | 75.45 | 68.73 | 58.69 | −6.72 | −10.04 | −16.75 |
| 12 | 2972.35 | 2863.04 | 2804.81 | −109.31 | −58.23 | −167.54 |
| 21 | 5253.34 | 5251.29 | 5252.96 | −2.05 | 1.67 | −0.38 |
| 22 | 2641.63 | 2639.95 | 2644.11 | −1.68 | 4.16 | 2.48 |
| 23 | 162.17 | 162.59 | 162.69 | 0.41 | 0.10 | 0.52 |
| 24 | 22.44 | 40.39 | 40.03 | 17.95 | −0.36 | 17.59 |
| 31 | 3416.04 | 3458.72 | 3463.03 | 42.68 | 4.31 | 46.99 |
| 32 | 3059.66 | 3068.99 | 3071.74 | 9.33 | 2.75 | 12.08 |
| 33 | 263.37 | 299.94 | 293.23 | 36.57 | −6.70 | 29.87 |
| 41 | 60.10 | 59.32 | 57.88 | −0.78 | −1.44 | −2.22 |
| 42 | 0.25 | 0.14 | 0.14 | −0.11 | 0.00 | −0.11 |
| 43 | 1.52 | 4.11 | 10.09 | 2.59 | 5.98 | 8.58 |
| 44 | 0.00 | 0.00 | 1.70 | 0.00 | 1.70 | 1.70 |
| 46 | 22.20 | 22.18 | 22.49 | −0.02 | 0.31 | 0.29 |
| 51 | 5.08 | 6.52 | 15.29 | 1.44 | 8.77 | 10.21 |
| 52 | 63.77 | 84.73 | 104.66 | 20.96 | 19.93 | 40.89 |
| 53 | 0.71 | 1.21 | 5.63 | 0.50 | 4.42 | 4.92 |
| 62 | 0.54 | 0.00 | 0.00 | −0.54 | 0.00 | −0.54 |
| 64 | 0.00 | 1.61 | 0.00 | 1.61 | −1.61 | 0.00 |
| 65 | 7.20 | 12.59 | 21.46 | 5.39 | 8.87 | 14.26 |
| 66 | 9.09 | 50.70 | 49.45 | 41.62 | −1.25 | 40.36 |
| 67 | 372.95 | 313.11 | 329.77 | −59.84 | 16.67 | −43.18 |
| Moran’s I Value | p Value | Z Value | |
|---|---|---|---|
| 2000 | 0.28 | 0.00 | 11.41 |
| 2010 | 0.25 | 0.00 | 10.17 |
| 2020 | 0.12 | 0.00 | 5.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Ma, B.; Zhao, L.; Mao, Z.; Liu, X. Study on Spatial and Temporal Changes in Landscape Ecological Risks and Indicator Weights: A Case Study of the Bailong River Basin. Sustainability 2024, 16, 1915. https://doi.org/10.3390/su16051915
Li Q, Ma B, Zhao L, Mao Z, Liu X. Study on Spatial and Temporal Changes in Landscape Ecological Risks and Indicator Weights: A Case Study of the Bailong River Basin. Sustainability. 2024; 16(5):1915. https://doi.org/10.3390/su16051915
Chicago/Turabian StyleLi, Quanxi, Biao Ma, Liwei Zhao, Zixuan Mao, and Xuelu Liu. 2024. "Study on Spatial and Temporal Changes in Landscape Ecological Risks and Indicator Weights: A Case Study of the Bailong River Basin" Sustainability 16, no. 5: 1915. https://doi.org/10.3390/su16051915
APA StyleLi, Q., Ma, B., Zhao, L., Mao, Z., & Liu, X. (2024). Study on Spatial and Temporal Changes in Landscape Ecological Risks and Indicator Weights: A Case Study of the Bailong River Basin. Sustainability, 16(5), 1915. https://doi.org/10.3390/su16051915





