Enhancement Effect of Phragmites australis Roots on Soil Shear Strength in the Yellow River Delta
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Sample Collection and Determination of Basic Physical Indices
2.3. Direct Shear Test of Root–Soil Composite
2.4. Calculation of Mechanical Indices
2.5. Determination of Root Distribution
2.6. Single-Root Model
3. Results and Analysis
3.1. Relationship Between Shear Stress and Shear Displacement
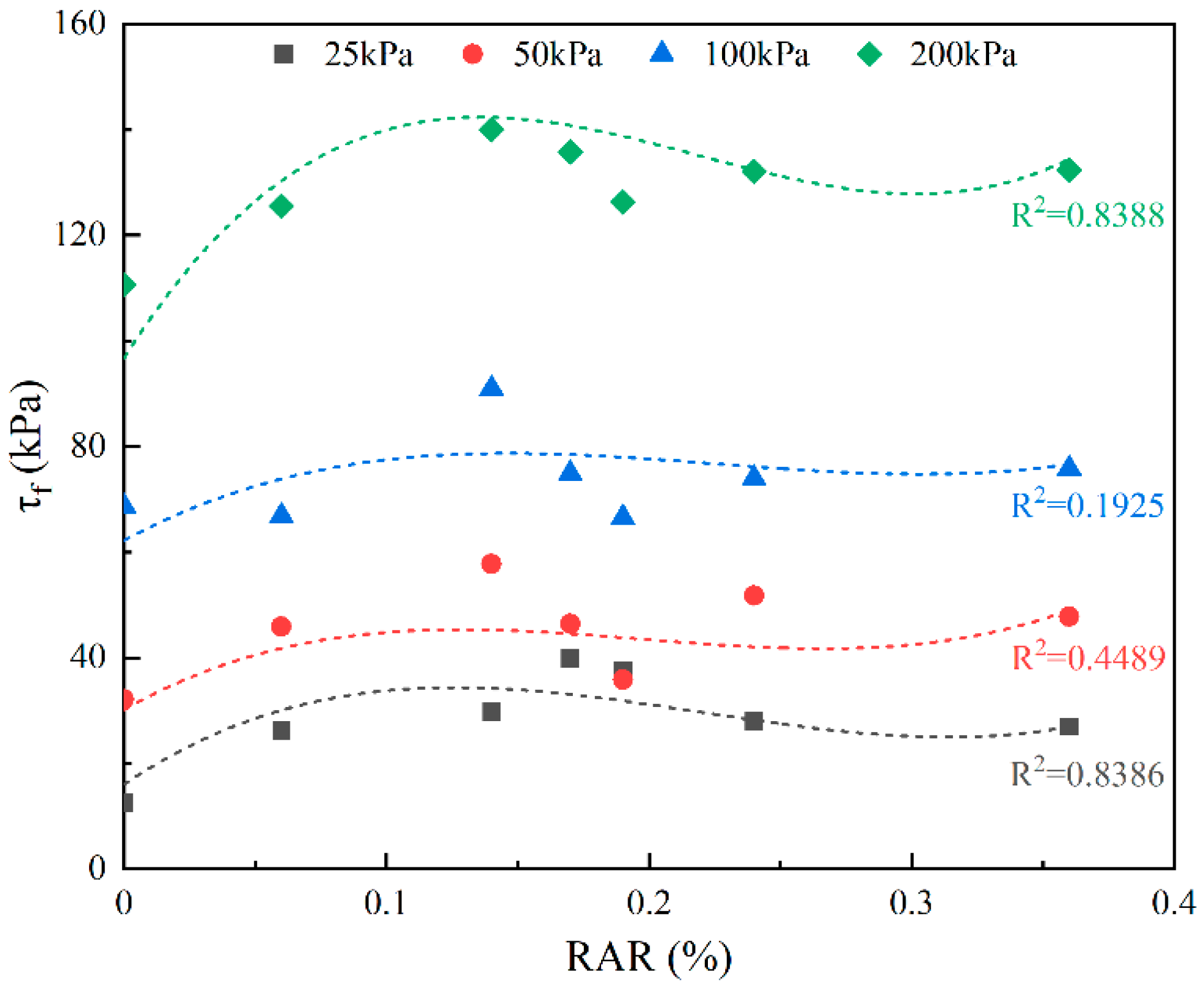
3.2. Shear Strengths of Root–Soil Composites with Different Root Contents
3.3. Shear Indices of Root–Soil Composites with Different Root Contents
4. Discussion
4.1. Enhancement Effect of PA Roots on Soil Shear Resistance
4.2. Differences in Shear Failure of Rootless Soil and Root–Soil Composites
4.3. Influence of Root Distribution on Shear Strength
4.4. Calculation and Verification of Root Deflection Angle During Shearing
5. Conclusions
- (1)
- The shear stress–displacement curves of the rootless soil and PA root–soil composite specimens are of hardened and softened types. Before shear failure, the shear stress increased with the shear displacement, but the growth rate changed from fast to slow. In addition, the shear deformation resistances of rootless soil and root–soil composite specimens are different, with the root–soil composite having a stronger shear deformation resistance than rootless soil.
- (2)
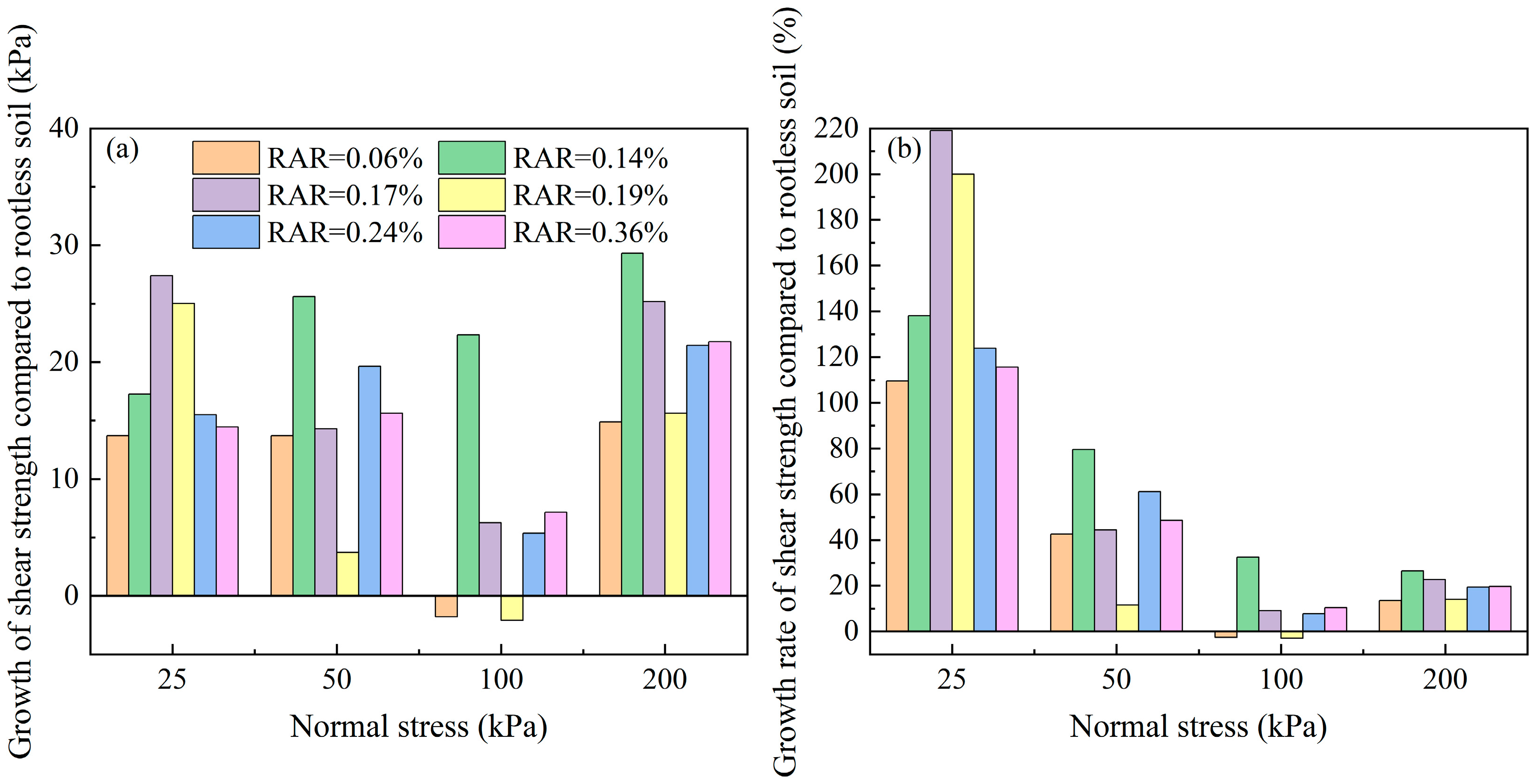
- The shear strength of both rootless soil and the root–soil composite increased with increasing normal stress. The trend of shear strength with RAR under four levels of normal stress was more consistent, and an RAR of 0.14% was optimal in maximizing the shear strength of the root–soil composite within the range of 0~0.36%. Under the same normal stress, the shear strength of most root–soil composite specimens was higher than that of rootless soil, with growth rates ranging at 109.5~219.0% (25 kPa), 11.6~79.6% (50 kPa), 7.8~32.5% (100 kPa), and 13.5~26.5% (200 kPa).
- (3)
- The cohesion of root–soil composites with different root contents was greater than that of rootless soil, with a maximum growth rate of 440.1%. There is an optimum RAR of 0.14%, which maximizes the cohesion of the soil in the range of 0~0.36%. The internal friction angles of root–soil composites with different root contents did not differ significantly from that of the rootless soil. The increase in the shear strength of the root–soil composite was mainly due to the increase in cohesion.
- (4)
- The overall failure mode of the rootless soil is shear failure, in which the shear plane is not completely horizontal. Root–soil composite failure occurs when the root is pulled out of the soil. Under the action of shear stress, the roots are deflected in the direction opposite to the shear stress. With an increase in shear displacement, the angle between the roots and the shear plane gradually increases. The variation in is proportional to that of .
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bardgett, R.D.; Mommer, L.; Vries, F.T.D. Going underground: Root traits as drivers of ecosystem processes. Trends Ecol. Evol. 2014, 29, 692–699. [Google Scholar] [CrossRef] [PubMed]
- Freschet, T.G.; Roumet, C. Sampling roots to capture plant and soil functions. Funct. Ecol. 2017, 31, 1506–1518. [Google Scholar] [CrossRef]
- Bassanelli, C.; Bischetti, G.B.; Chiaradia, E.A.; Rossi, L.; Vergani, C. The contribution of chestnut coppice forests on slope stability in abandoned territory: A case study. J. Agric. Eng. 2013, 44, 68–73. [Google Scholar] [CrossRef][Green Version]
- Bordoni, M.; Meisina, C.; Vercesi, A.; Bischetti, G.B.; Chiaradia, E.A.; Vergani, C.; Chersich, S.; Valentino, R.; Bittelli, M.; Comolli, R.; et al. Quantifying the contribution of grapevine roots to soil mechanical reinforcement in an area susceptible to shallow landslides. Soil Tillage Res. 2016, 163, 195–206. [Google Scholar] [CrossRef]
- Brooks, H.; Möller, I.; Carr, S.; Chirol, C.; Christie, E.; Evans, B.; Spencer, K.L.; Spencer, T.; Royse, K. Resistance of salt marsh substrates to near-instantaneous hydrodynamic forcing. Earth Surf. Process. Landf. 2020, 46, 67–88. [Google Scholar] [CrossRef]
- Gyssels, G.; Poesen, J.; Bochet, E.; Li, Y. Impact of plant roots on the resistance of soils to erosion by water: A review. Prog. Phys. Geogr. 2005, 29, 189–217. [Google Scholar] [CrossRef]
- Mao, Z.J.; Bi, Y.L.; Geng, M.M.; An, N. Pull-out characteristics of herbaceous roots of alfalfa on the loess in different growth stages and their impacts on slope stability. Soil Tillage Res. 2023, 225, 105542. [Google Scholar] [CrossRef]
- Rossi, R.; Picuno, P.; Fagnano, M.; Amato, M. Soil reinforcement potential of cultivated cardoon (Cynara cardunculus L.): First data of root tensile strength and density. Catena 2022, 211, 106016. [Google Scholar] [CrossRef]
- Alam, S.; Manzur, T.; Borquist, E.; Williams, J.; Matthews, J.C. In-situ assessment of soil-root bonding strength to aid in preventing soil erosion. Soil Tillage Res. 2021, 213, 105140. [Google Scholar] [CrossRef]
- Docker, B.B.; Hubble, T.C.T. Quantifying root-reinforcement of river bank soils by four Australian tree species. Geomorphology 2008, 100, 401–418. [Google Scholar] [CrossRef]
- Ghestem, M.; Veylon, G.; Bernard, A.; Vanel, Q.; Stokes, A. Influence of plant root system morphology and architectural traits on soil shear resistance. Plant Soil 2014, 377, 43–61. [Google Scholar] [CrossRef]
- Wang, T.Y.; Guo, Q.L.; Pei, Q.Q.; Chen, W.W.; Wang, Y.W.; Zhang, B.; Yu, J. Destruction or protection? Experimental studies on the mechanism of biological soil crusts on the surfaces of earthen sites. Catena 2023, 227, 107096. [Google Scholar] [CrossRef]
- Xiong, D.W.; Chen, F.Q.; Lv, K.; Tan, X.Q.; Huang, Y.W. The performance and temporal dynamics of vegetation concretes comprising three herbaceous species in soil stabilization and slope protection. Ecol. Eng. 2023, 188, 106873. [Google Scholar] [CrossRef]
- Huang, M.; Sun, S.; Feng, K.; Lin, M.; Shuai, F.; Zhang, Y.; Lin, J.; Ge, H.; Jiang, F.; Huang, Y. Effects of Neyraudia reynaudiana roots on the soil shear strength of collapsing wall in benggang, southeast China. Catena 2022, 210, 105883. [Google Scholar] [CrossRef]
- Li, C.; Jia, Z.H.; Peng, X.N.; Zhai, L.; Zhang, B.; Liu, X.; Zhang, J.C. Functions of mineral-solubilizing microbes and a water retaining agent for the remediation of abandoned mine sites. Sci. Total Environ. 2021, 761, 143215. [Google Scholar] [CrossRef]
- Song, X.H.; Tan, Y. Experimental study on the stability of vegetated earthen slopes under intense rainfall. Soil Tillage Res. 2024, 238, 106028. [Google Scholar] [CrossRef]
- Baets, S.D.; Poesen, J.; Reubens, B.; Wemans, K.; Baerdemaeker, J.D.; Muys, B. Root tensile strength and root distribution of typical mediterranean plant species and their contribution to soil shear strength. Plant Soil 2008, 305, 207–226. [Google Scholar] [CrossRef]
- Comino, E.; Marengo, P.; Rolli, V. Root reinforcement effect of different grass species: A comparison between experimental and models results. Soil Tillage Res. 2010, 110, 60–68. [Google Scholar] [CrossRef]
- Forster, M.; Ugarte, C.; Lamandé, M.; Faucon, M.P. Root traits of crop species contributing to soil shear strength. Geoderma 2022, 409, 115642. [Google Scholar] [CrossRef]
- Liu, Y.F.; Meng, L.C.; Huang, Z.; Shi, Z.H.; Wu, G.L. Contribution of fine roots mechanical property of Poaceae grasses to soil erosion resistance on the Loess Plateau. Geoderma 2022, 426, 116122. [Google Scholar] [CrossRef]
- Su, X.M.; Zhou, Z.C.; Liu, J.E.; Wang, P.P.; Liu, J.Y.; Li, Q.J.; Zhao, F.W. The role of roots traits of climax community species to shear strength in the Loess Hilly Region, China. Soil Tillage Res. 2022, 221, 105417. [Google Scholar] [CrossRef]
- Wang, Y.; Jin, Y.L.; Liang, X.L.; Liu, X.; Tan, B.; He, S.Q.; Zheng, J.K.; Hou, G.R.; Zhang, Y.Q. Fragmentation of soil-root complexes in sloping landscapes during tillage and soil translocation. Biosyst. Eng. 2022, 223, 116–128. [Google Scholar] [CrossRef]
- Gobinath, R.; Ganapathy, G.P.; Akinwumi, I.I. Stabilisation of natural slopes using natural plant root as reinforcing agent. Mater. Today Proc. 2021, 39, 493–499. [Google Scholar] [CrossRef]
- Zhu, H.B.; Zhao, H.R.; Bai, L.Z.; Ma, S.A.; Zhang, X.; Li, H. Mechanical characteristics of rice root-soil complex in rice-wheat rotation area. Agriculture 2022, 12, 1045. [Google Scholar] [CrossRef]
- Brooks, H.; Moeller, I.; Spencer, T.; Royse, K.; Price, S.; Kirkham, M. How strong are salt marshes? Geotechnical properties of coastal wetland soils. Earth Surf. Process. Landf. 2022, 47, 1390–1408. [Google Scholar] [CrossRef]
- Gonzalez-Ollauri, A.; Mickovski, S.B. Plant-soil reinforcement response under different soil hydrological regimes. Geoderma 2017, 285, 141–150. [Google Scholar] [CrossRef]
- Zhu, J.Q.; Mao, Z.; Wang, Y.Q.; Wang, Y.J.; Li, T.; Wang, K.; Langendoen, E.J.; Zheng, B.F. Soil moisture and hysteresis affect both magnitude and efficiency of root reinforcement. Catena 2022, 219, 106574. [Google Scholar] [CrossRef]
- Burak, E.; Dodd, I.C.; Quinton, J.N. Do root hairs of barley and maize roots reinforce soil under shear stress? Geoderma 2021, 383, 114740. [Google Scholar] [CrossRef]
- Bengough, A.G.; Mckenzie, B.M.; Hallett, P.D.; Valentine, T.A. Root elongation, water stress, and mechanical impedance: A review of limiting stresses and beneficial root tip traits. J. Exp. Bot. 2011, 62, 59–68. [Google Scholar] [CrossRef]
- Xu, Z.H.; Zhang, Y.; Tao, Z.P.; Zha, L.L.; Chen, Y.Y. Mechanical characteristics of undisturbed roots soil composites from the Source Area of Lanniqing Landslide, Zhaotong. J. Soil Water Conserv. 2022, 36, 128–134. (In Chinese) [Google Scholar]
- Chen, Y.; Thompson, C.E.L.; Collins, M.B. Saltmarsh creek bank stability: Biostabilisation and consolidation with depth. Cont. Shelf Res. 2012, 35, 64–74. [Google Scholar] [CrossRef]
- Chirol, C.; Spencer, K.L.; Carr, S.J.; Mller, I.; Evans, B.; Lynch, J.; Brooks, H.; Royse, K.R. Effect of vegetation cover and sediment type on 3d subsurface structure and shear strength in saltmarshes. Earth Surf. Process. Landf. 2021, 46, 2279–2297. [Google Scholar] [CrossRef]
- Gray, D.H.; Leiser, A.T. Biotechnical Slope Protection and Erosion Control; Van Nostrand Reinhold Co.: New York, NY, USA, 1982. [Google Scholar]
- Xu, T.; Liu, C.Y.; Hu, X.S.; Zhou, L.H.; Shen, Z.Y.; Yu, D.M. Study on the Mechanical Properties of Roots and the Shear Strengths of Four Halophytic Plants in Qaidam Basin. Res. Soil Water Conserv. 2021, 28, 101–110. (In Chinese) [Google Scholar]
- Qi, Z.X.; Yu, D.M.; Liu, Y.B.; Fu, J.T.; Hu, X.S.; Li, S.X.; Zhao, D. Experimental research on factors affecting shear strength of halophyte root-soil composite systems in cold and arid environments. J. Eng. Geol. 2017, 25, 1438–1448. (In Chinese) [Google Scholar]
- Yu, G.A.; Li, Z.W.; Yang, H.Y.; Lu, J.Y.; Huang, H.Q.; Yi, Y.J. Effects of riparian plant roots on the unconsolidated bank stability of meandering channels in the Tarim River, China. Geomorphology 2020, 351, 106958. [Google Scholar] [CrossRef]
- Ni, J.J.; Leung, A.K.; Ng, C.W.W. Influences of plant spacing on root tensile strength of Schefflera arboricola and soil shear strength. Landsc. Ecol. Eng. 2019, 15, 223–230. [Google Scholar] [CrossRef]
- GB/T 50123-2019; Standard for Geotechnical Testing Method. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2019; pp. 8–20. (In Chinese)
- Meng, X.; Jia, Y.; Shan, H.; Yang, Z.; Zheng, J. An experimental study on erodibility of intertidal sediments in the yellow river delta. Int. J. Sediment Res. 2012, 27, 240–249. [Google Scholar] [CrossRef]
- Liu, H.L.; Jia, Y.G.; Zhang, S.T.; Shan, H.X.; Xue, L.; Sun, Z.W.; Quan, Y.Z.; Li, Z.H.; Chen, T.; Tian, Z.C.; et al. Field measurement of the erosion threshold of silty seabed in the intertidal flat of the Yellow River Delta with a newly developed annular flume. Front. Mar. Sci. 2023, 10, 1177241. [Google Scholar] [CrossRef]
- Tan, H.M.; Chen, F.M.; Chen, J.; Gao, Y.F. Direct shear tests of shear strength of soils reinforced by geomats and plant roots. Geotext. Geomembr. 2019, 47, 103491. [Google Scholar] [CrossRef]
- Wang, X.H.; Ma, C.; Wang, Y.Q.; Wang, Y.J.; Li, T.; Dai, Z.S.; Li, M.Y. Effect of root architecture on rainfall threshold for slope stability: Variabilities in saturated hydraulic conductivity and strength of root-soil composite. Landslides 2020, 17, 1965–1977. [Google Scholar] [CrossRef]
- Docker, B.B.; Hubble, T.C.T. Modelling the distribution of enhanced soil shear strength beneath riparian trees of Southeastern Australia. Ecol. Eng. 2009, 35, 921–934. [Google Scholar] [CrossRef]
- Mahannopkul, K.; Jotisankasa, A. Influences of root concentration and suction on Chrysopogon zizanioides reinforcement of soil. Soils Found. 2019, 59, 500–516. [Google Scholar] [CrossRef]
- Hamidifar, H.; Keshavarzi, A.; Truong, P. Enhancement of river bank shear strength parameters using Vetiver grass root system. Arabian J. Geosci. 2018, 11, 611. [Google Scholar] [CrossRef]
- Zong, Q.L.; Feng, B.; Cai, H.B.; Chen, Z.K.; Wang, J.X. Mechanism of riverbank protection by desert riparian vegetation roots in Tarim River basin. Chin. J. Rock Mech. Eng. 2018, 37, 1290–1300. (In Chinese) [Google Scholar]
- Hu, M.; Li, W.P.; Shi, H.B.; Liang, J.C. Effects of Root Layout and Diameter on Shear Performance in Root-Soil Composite. Bull. Soil Water Conserv. 2012, 32, 42–44. (In Chinese) [Google Scholar]
- Schwarz, M.; Cohen, D.; Or, D. Root–soil mechanical interactions during pullout and failure of root bundles. J. Geophys. Res. 2010, 115, F04035. [Google Scholar] [CrossRef]
- Fan, C.C. A displacement-based model for estimating the shear resistance of root-permeated soils. Plant Soil 2012, 355, 103–119. [Google Scholar] [CrossRef]
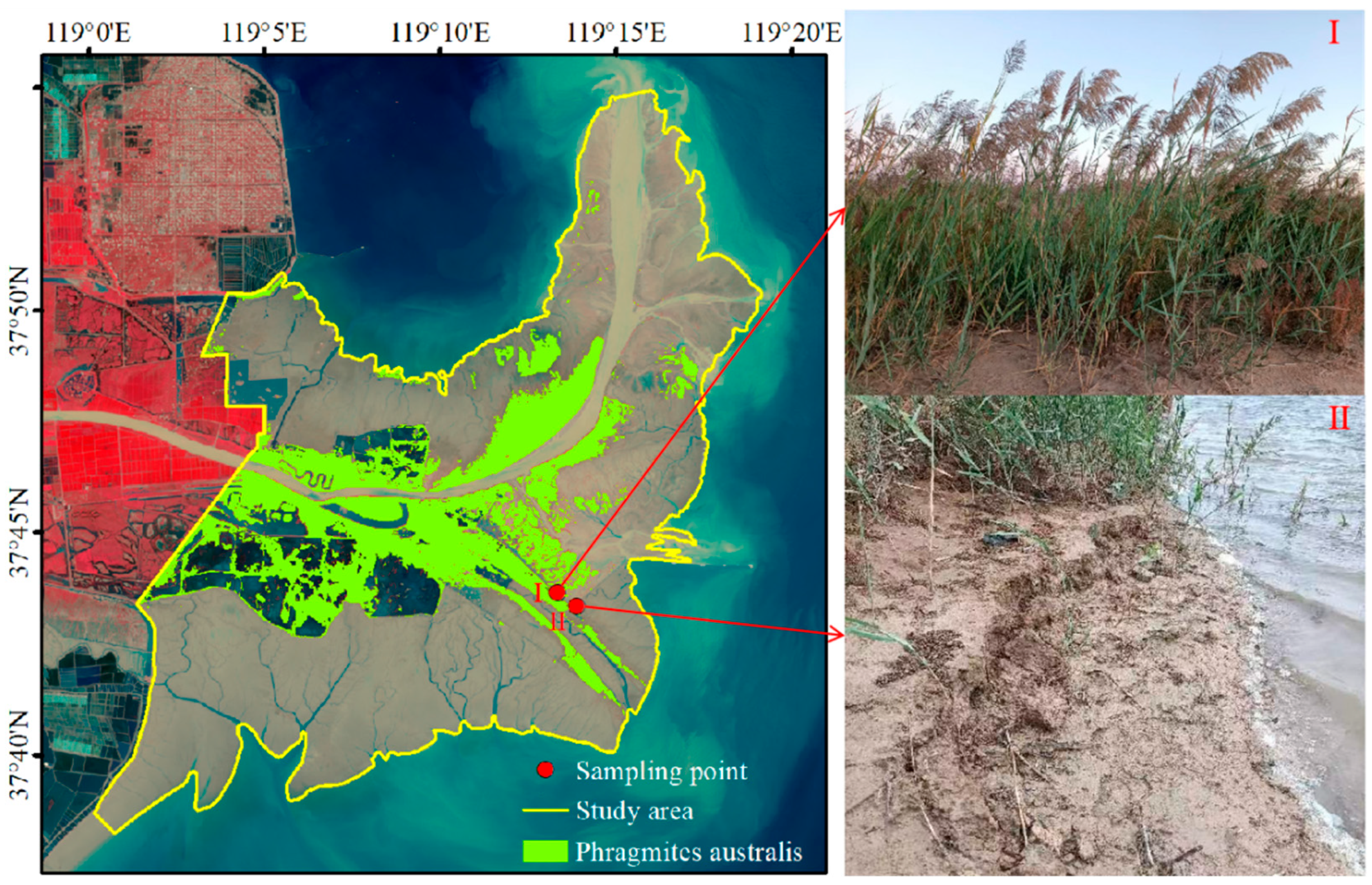
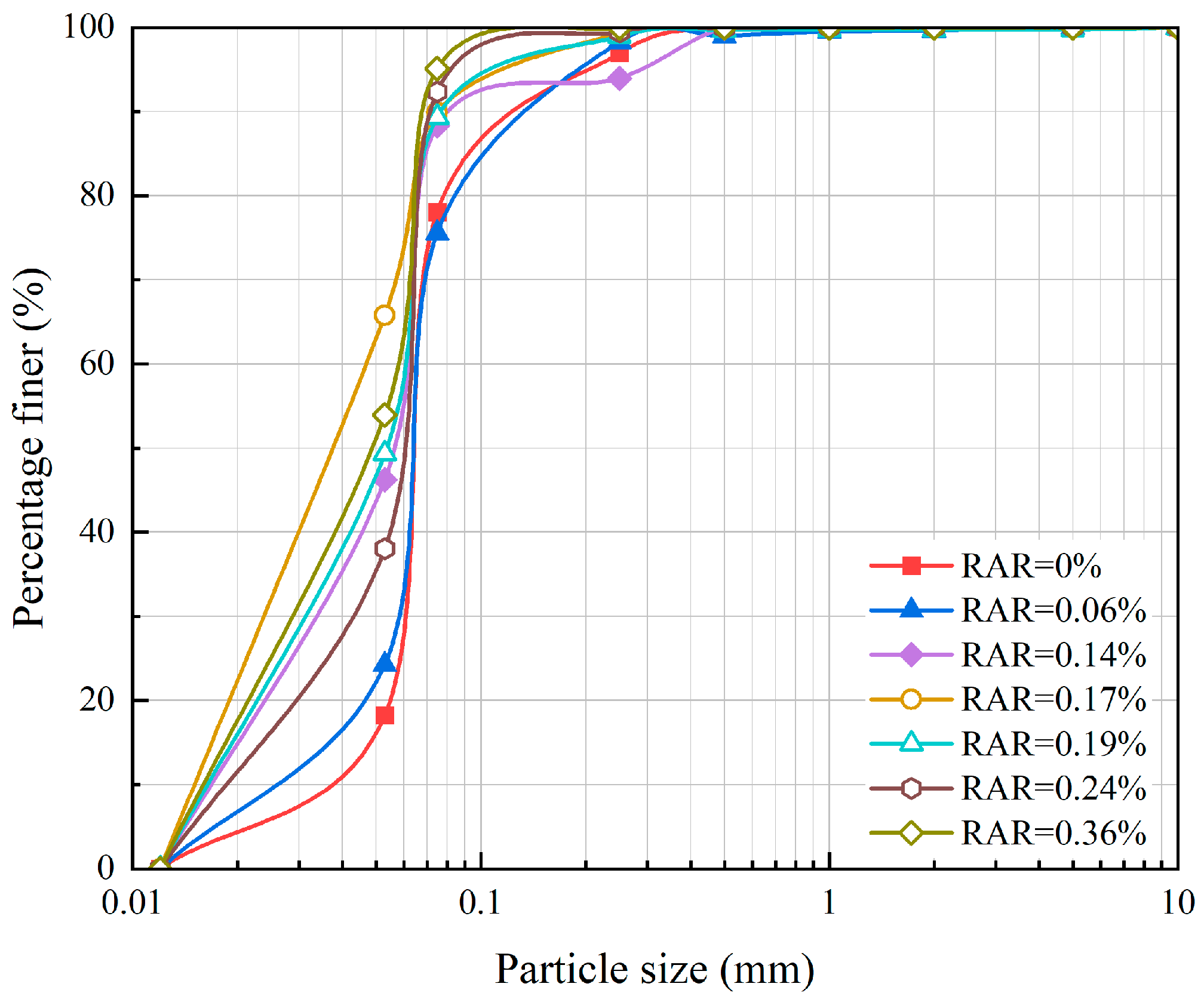
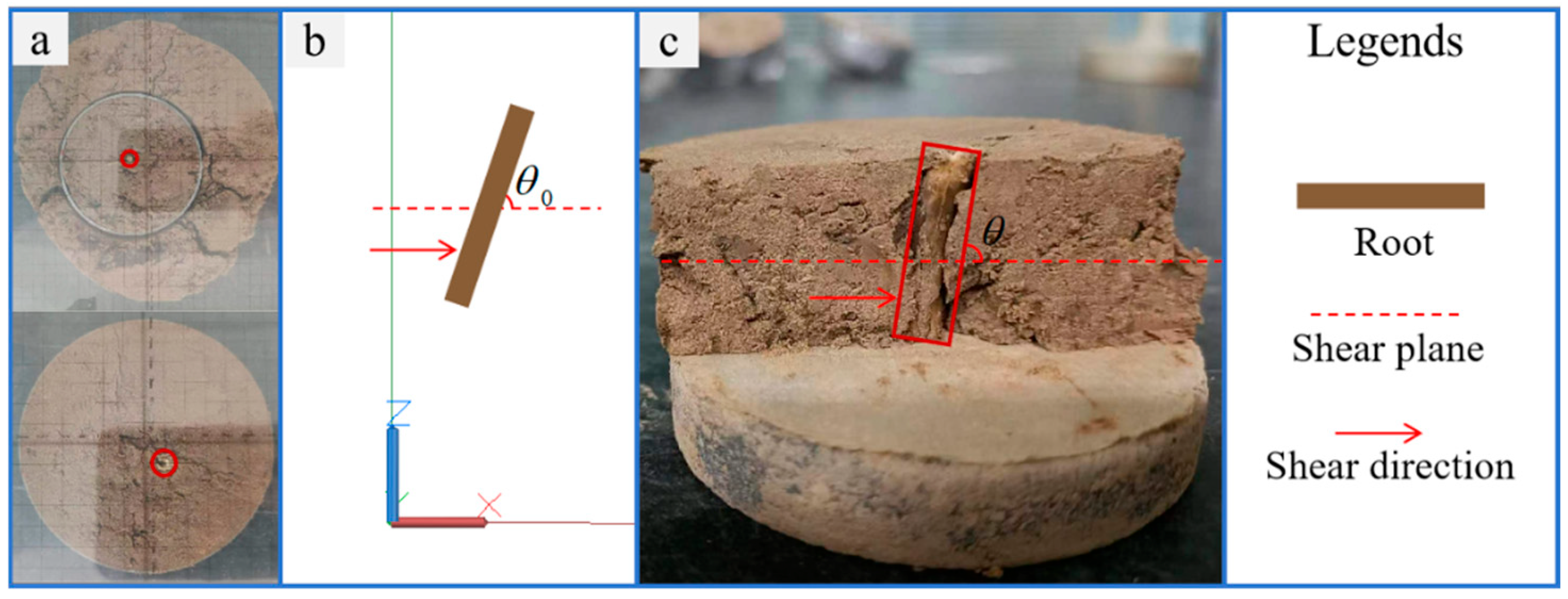

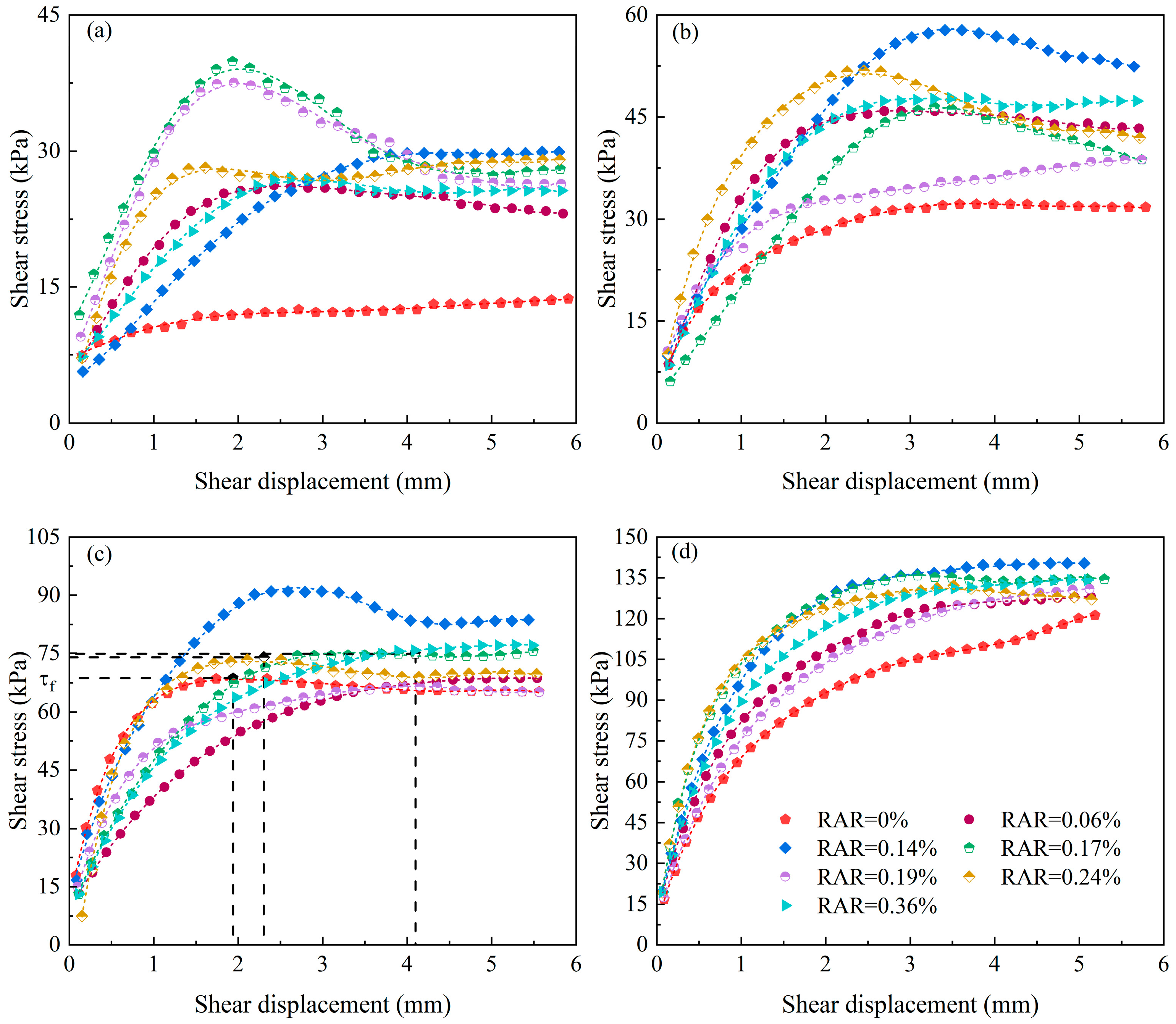




| Serial Number | Coordinates of Sampling Point | Root Number | Average Root Diameter (mm) | RAR (%) | Dry Density (g/cm3) | Water Content (%) |
|---|---|---|---|---|---|---|
| I | 119°12′58″ E, 37°43′23″ N | 0 | 0 | 0 | 1.49 | 21.3 |
| 5 | 3.32 | 0.06 | 1.56 | 22.8 | ||
| II | 119°13′31″ E, 37°43′4″ N | 6 | 4.64 | 0.14 | 1.55 | 22.5 |
| 7 | 4.71 | 0.17 | 1.50 | 26.5 | ||
| 6 | 5.37 | 0.19 | 1.56 | 24.6 | ||
| 8 | 5.15 | 0.24 | 1.56 | 25.3 | ||
| 10 | 5.76 | 0.36 | 1.58 | 24.3 |
| RAR/% | Growth Rate/% | ||
|---|---|---|---|
| 25 → 50 kPa | 50 → 100 kPa | 100 → 200 kPa | |
| 0 | 157.1 | 113.4 | 61.2 |
| 0.06 | 75.0 | 45.8 | 87.8 |
| 0.14 | 94.0 | 57.5 | 53.8 |
| 0.17 | 16.4 | 61.2 | 81.3 |
| 0.19 | −4.4 | 85.5 | 89.7 |
| 0.24 | 85.1 | 42.8 | 78.5 |
| 0.36 | 77.3 | 58.6 | 74.7 |
| RAR/% | Relationship Between Normal Stress and Shear Strength | R2 | c/kPa | c Growth /kPa | c Growth Rate/% | φ/° |
|---|---|---|---|---|---|---|
| 0 | 0.9765 | 4.25 | 0 | 0 | 28.9 | |
| 0.06 | 0.9951 | 14.22 | 9.97 | 234.8 | 29.0 | |
| 0.14 | 0.9759 | 22.94 | 18.69 | 440.1 | 31.2 | |
| 0.17 | 0.9930 | 21.46 | 17.21 | 405.3 | 29.4 | |
| 0.19 | 0.9753 | 16.04 | 11.80 | 277.7 | 28.3 | |
| 0.24 | 0.9921 | 17.71 | 13.47 | 317.1 | 29.8 | |
| 0.36 | 0.9966 | 15.45 | 11.21 | 263.9 | 30.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Jin, K.; Qin, P.; Liu, C.; Zhu, X.; Zhang, Y.; Zong, Q. Enhancement Effect of Phragmites australis Roots on Soil Shear Strength in the Yellow River Delta. Sustainability 2024, 16, 10657. https://doi.org/10.3390/su162310657
Li X, Jin K, Qin P, Liu C, Zhu X, Zhang Y, Zong Q. Enhancement Effect of Phragmites australis Roots on Soil Shear Strength in the Yellow River Delta. Sustainability. 2024; 16(23):10657. https://doi.org/10.3390/su162310657
Chicago/Turabian StyleLi, Xinyue, Kai Jin, Peng Qin, Chunxia Liu, Xiuzhi Zhu, Yuyang Zhang, and Quanli Zong. 2024. "Enhancement Effect of Phragmites australis Roots on Soil Shear Strength in the Yellow River Delta" Sustainability 16, no. 23: 10657. https://doi.org/10.3390/su162310657
APA StyleLi, X., Jin, K., Qin, P., Liu, C., Zhu, X., Zhang, Y., & Zong, Q. (2024). Enhancement Effect of Phragmites australis Roots on Soil Shear Strength in the Yellow River Delta. Sustainability, 16(23), 10657. https://doi.org/10.3390/su162310657






