Soil Strength Parameters for the Sustainable Design of Unsupported Cuts Under Drained Conditions Using Reliability Analysis
Abstract
1. Introduction
2. Description of the Unsupported Cut
3. Methodology
3.1. Overview
3.2. Generation of the Statistical Meshes
3.3. Determination of the Characteristic Values of Strength Parameters
3.4. Design
3.5. RFELA Calculations
3.6. Probability of Failure and Reliability Analysis
4. Cases Analysed
- The value of the effective cohesion, ;
- The dimensionless scale of fluctuation, ;
- The geometry of the cut (h and ) and of the soil friction angle, .
4.1. Influence of the Value of the Effective Cohesion
4.2. Influence of the Dimensionless Scale of Fluctuation
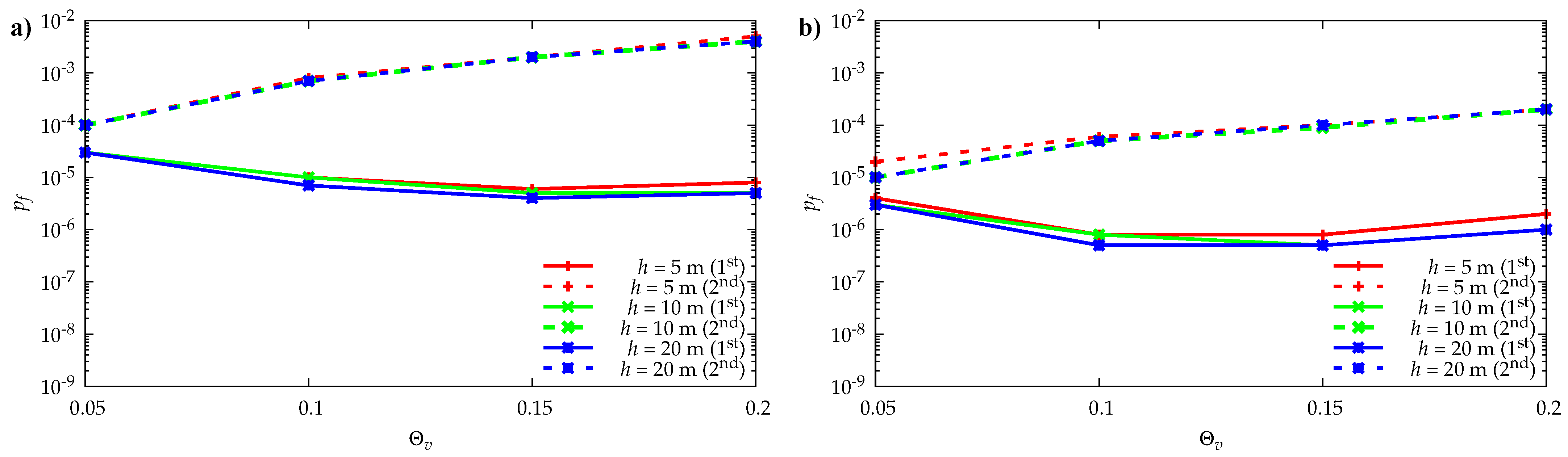
4.3. Influence of the Geometry of the Cut and of the Soil Friction Angle
5. Conclusions
- The value of does not significantly influence the probability of failure for cuts where the design value of the actions equal the design value of the resistances;
- The probability of failure depends on the dimensionless scale of fluctuation, and not on the scale of fluctuation or excavation depth, which is considered isolated;
- Combining careful soil characterisation performed at the exact location of the cut with a partial coefficient of 1.25 applied to the strength parameters ensures a probability of failure less than ;
- For the cases where the soil is not carefully characterised but the soil is very well known, a slightly larger value of the partial coefficient is needed to ensure the same probability of failure if the scale of fluctuation is considered correctly when determining the characteristic values of the strength parameters; if the scale of fluctuation is not considered, a partial factor of 1.4–1.5 is needed.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FELA | Finite Element Limit Analysis |
| RFELA | Random Finite Element Limit Analysis |
References
- Basu, D.; Puppala, A.; Misra, A.; Chittoori, B. Sustainability in Geotechnical Engineering. In Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical, Paris, France, 2–6 September 2013; pp. 3155–3162. Available online: https://www.cfms-sols.org/sites/default/files/Actes/3171-3174.pdf (accessed on 1 September 2024).
- EN1997-1. Eurocode 7: Geotechnical Design—Part 1: General Rules; CEN, European Committee for Standardization: Brussels, Belgium, 2004.
- Lumb, P. Safety factors and the probability distribution of soil strength. Can. Geotech. J. 1970, 7, 225–242. [Google Scholar] [CrossRef]
- Meyerhof, G.G. Safety factors in soil mechanics. Can. Geotech. J. 1970, 7, 349–355. [Google Scholar] [CrossRef]
- Meyerhof, G. Limit states design in geotechnical engineering. Struct. Saf. 1982, 1, 67–71. [Google Scholar] [CrossRef]
- Santamarina, J.C.; Altschaeffl, A.G.; Chameau, J.L. Reliability of Slopes: Incorporating Qualitative Information. National Research Council (U.S.), Transportation Research Board, Report TRR 1343. 1992, pp. 1–5. Available online: http://onlinepubs.trb.org/Onlinepubs/trr/1992/1343/1343-001.pdf (accessed on 1 September 2024).
- Baecher, G.B.; Christian, J.T. Reliability and Statistics in Geotechnical Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Orr, T.L. Selection of characteristic values and partial factors in geotechnical designs to Eurocode 7. Comput. Geotech. 2000, 26, 263–279. [Google Scholar] [CrossRef]
- Ching, J.; Phoon, K.K.; Chen, K.F.; Orr, T.L.; Schneider, H.R. Statistical determination of multivariate characteristic values for Eurocode 7. Struct. Saf. 2020, 82, 101893. [Google Scholar] [CrossRef]
- Länsivaara, T.; Phoon, K.K.; Ching, J. What is a characteristic value for soils? Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2022, 16, 199–224. [Google Scholar] [CrossRef]
- Phoon, K.K.; Kulhawy, F.H. Characterization of geotechnical variability. Can. Geotech. J. 1999, 36, 612–624. [Google Scholar] [CrossRef]
- Cao, Z.; Wang, Y.; Li, D. Probabilistic Approaches for Geotechnical Site Characterization and Slope Stability Analysis; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Kulhawy, F.; Prakoso, W.; Phoon, K. Uncertainty in basic laboratory and field properties of geomaterials. In Geotechnical Engineering Education and Training; CRC Press: London, UK, 2020; pp. 297–302. [Google Scholar] [CrossRef]
- Phoon, K.K.; Shuku, T.; Ching, J. Uncertainty, Modeling, and Decision Making in Geotechnics; CRC Press: Boca Raton, FL, USA, 2023. [Google Scholar] [CrossRef]
- Vanmarcke, E.H. Reliability of Earth Slopes. J. Geotech. Eng. Div. 1977, 103, 1247–1265. [Google Scholar] [CrossRef]
- Mostyn, G.R.; Soo, S. The effect of auto-correlation on the probability of failure of slopes. In Proceedings of the Effect of Auto-Correlation on the Probability of Failure of Slopes, Christchurch, New Zealand, 3–7 February 1992; pp. 542–546. Available online: https://www.issmge.org/uploads/publications/89/99/6ANZ_095.pdf (accessed on 1 September 2024).
- Griffiths, D.V.; Fenton, G.A. Probabilistic Slope Stability Analysis by Finite Elements. J. Geotech. Geoenviron. Eng. 2004, 130, 507–518. [Google Scholar] [CrossRef]
- Cho, S.E. Effects of spatial variability of soil properties on slope stability. Eng. Geol. 2007, 92, 97–109. [Google Scholar] [CrossRef]
- Suchomel, R.; Mašín, D. Comparison of different probabilistic methods for predicting stability of a slope in spatially variable c′ϕ soil. Comput. Geotech. 2010, 37, 132–140. [Google Scholar] [CrossRef]
- Chok, Y.H.; Jaksa, M.B.; Griffiths, D.V.; Fenton, G.A.; Kaggwa, W.S. Probabilistic analysis of a spatially variable c′−ϕ′ slope. Aust. Geomech. J. 2015, 50, 17–27. [Google Scholar]
- Agbaje, S.; Zhang, X.; Ward, D.; Dhimitri, L.; Patelli, E. Spatial variability characteristics of the effective friction angle of Crag deposits and its effects on slope stability. Comput. Geotech. 2022, 141, 104532. [Google Scholar] [CrossRef]
- Chuaiwate, P.; Jaritngam, S.; Panedpojaman, P.; Konkong, N. Probabilistic Analysis of Slope against Uncertain Soil Parameters. Sustainability 2022, 14, 14530. [Google Scholar] [CrossRef]
- Peng, P.; Li, Z.; Zhang, X.; Liu, W.; Sui, S.; Xu, H. Slope Failure Risk Assessment Considering Both the Randomness of Groundwater Level and Soil Shear Strength Parameters. Sustainability 2023, 15, 7464. [Google Scholar] [CrossRef]
- Yang, R.; Huang, J.; Griffiths, D.V.; Meng, J.; Fenton, G.A. Optimal geotechnical site investigations for slope design. Comput. Geotech. 2019, 114, 103111. [Google Scholar] [CrossRef]
- Yang, R.; Huang, J.; Griffiths, D.V.; Li, J.; Sheng, D. Importance of soil property sampling location in slope stability assessment. Can. Geotech. J. 2019, 56, 335–346. [Google Scholar] [CrossRef]
- Jiang, S.H.; Papaioannou, I.; Straub, D. Optimization of Site-Exploration Programs for Slope-Reliability Assessment. Asce-Asme J. Risk Uncertain. Eng. Syst. Part Civ. Eng. 2020, 6, 04020004. [Google Scholar] [CrossRef]
- Yang, R.; Huang, J.; Griffiths, D.V. Optimal geotechnical site investigations for slope reliability assessment considering measurement errors. Eng. Geol. 2022, 297, 106497. [Google Scholar] [CrossRef]
- de Koker, N.; Day, P.; Zwiers, A. Assessment of reliability-based design of stable slopes. Can. Geotech. J. 2019, 56, 495–504. [Google Scholar] [CrossRef]
- Knuuti, M.; Länsivaara, T. Performance of Variable Partial Factor approach in a slope design. In Proceedings of the 13th International Conference on Applications of Statistics and Probability in Civil Engineering(ICASP13), Seoul, Republic of Korea, 26–30 May 2019. [Google Scholar] [CrossRef]
- Länsivaara, T.; Poutanen, T. Slope stability with partial safety factor method. In Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering, Paris, France, 2–6 September 2013; Available online: https://www.cfms-sols.org/sites/default/files/Actes/1823-1826.pdf (accessed on 1 September 2024).
- Kavvadas, M.; Karlaftis, M.; Fortsakis, P.; Stylianidi, E. Probabilistic analysis in slope stability. In Proceedings of the 17th International Conference on Soil Mechanics and Geotechnical Engineering: The Academia and Practice of Geotechnical Engineering, Alexandria, Egypt, 5–9 October 2009; Volume 2, pp. 1650–1653. [Google Scholar] [CrossRef]
- Vicente da Silva, M.; Antão, A.N. Software Mechpy. 2013. Available online: http://geocluster.dec.fct.unl.pt/mechpy/ (accessed on 2 February 2023).
- Simões, J.T.; Neves, L.C.; Antão, A.N.; Guerra, N.M.C. Probabilistic analysis of bearing capacity of shallow foundations using three-dimensional limit analyses. Int. J. Comput. Methods 2014, 11, 1342008. [Google Scholar] [CrossRef]
- Rantanen, T. Influence of the Variability of Soil Properties on the Stability of Shallow Tunnels in Soils Under Undrained Eonditions. Master’s Thesis, Faculdade de Ciências e Tecnologia, Universidade Nova de Lisboa, Lisbon, Portugal, 2016. (In Portuguese). [Google Scholar]
- Andrade Viana, L.; Antão, A.; Vicente da Silva, M.; Guerra, N. The application of limit analysis to the study of basal failure of deep excavations in clay considering the spatial distribution of soil strength. In Proceedings of the XVII European Conference on Soil Mechanics and Geotechnical Engineening, Icelandic Geotechnical Society, Reykjavík, Iceland, 1–6 September 2019. Available online: https://www.ecsmge-2019.com/uploads/2/1/7/9/21790806/0909-ecsmge-2019_viana-v2.pdf (accessed on 1 September 2024).
- Simões, J.; Neves, L.C.; Antão, A.N.; Guerra, N.M. Reliability assessment of shallow foundations on undrained soils considering soil spatial variability. Comput. Geotech. 2020, 119, 103369. [Google Scholar] [CrossRef]
- Vanmarcke, E.H. Probabilistic Modeling of Soil Profiles. J. Geotech. Eng. Div. 1977, 103, 1227–1246. [Google Scholar] [CrossRef]
- Fenton, G.A.; Griffiths, D.V. Risk Assessment in Geotechnical Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2008; p. 461. [Google Scholar]
- Vicente da Silva, M.; Deusdado, N.; Antão, A.N. Lower and upper bound limit analysis via the alternating direction method of multipliers. Comput. Geotech. 2020, 124, 103571. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. Comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 1979, 21, 239–245. [Google Scholar] [CrossRef]
- Olsson, A.; Sandberg, G.; Dahlblom, O. On Latin hypercube sampling for structural reliability analysis. Struct. Saf. 2003, 25, 47–68. [Google Scholar] [CrossRef]
- Huntington, D.E.; Lyrintzis, C.S. Improvements to and limitations of Latin hypercube sampling. Probabilistic Eng. Mech. 1998, 13, 245–253. [Google Scholar] [CrossRef]
- Martin, C.M. The use of adaptive finite-element limit analysis to reveal slip-line fields. GéOtechnique Lett. 2011, 1, 23–29. [Google Scholar] [CrossRef]
- ISSMGE-TC304. State of the art review of inherent variability and uncertainty in geotechnical properties and models. International Society of Soil Mechanics and Geotechnical Engineering (ISSMGE)—Technical Committee TC304 ‘Engineering Practice of Risk Assessment and Management’. Available online: https://issmge.org/files/reports/TC304-State-of-the-art-review-of-inherent-variability-and-uncertainty-in-geotechnical-properties-and-models.pdf (accessed on 2 March 2021).
- Cami, B.; Javankhoshdel, S.; Phoon, K.K.; Ching, J. Scale of Fluctuation for Spatially Varying Soils: Estimation Methods and Values. Asce-Asme J. Risk Uncertain. Eng. Syst. Part Civ. Eng. 2020, 6, 03120002. [Google Scholar] [CrossRef]
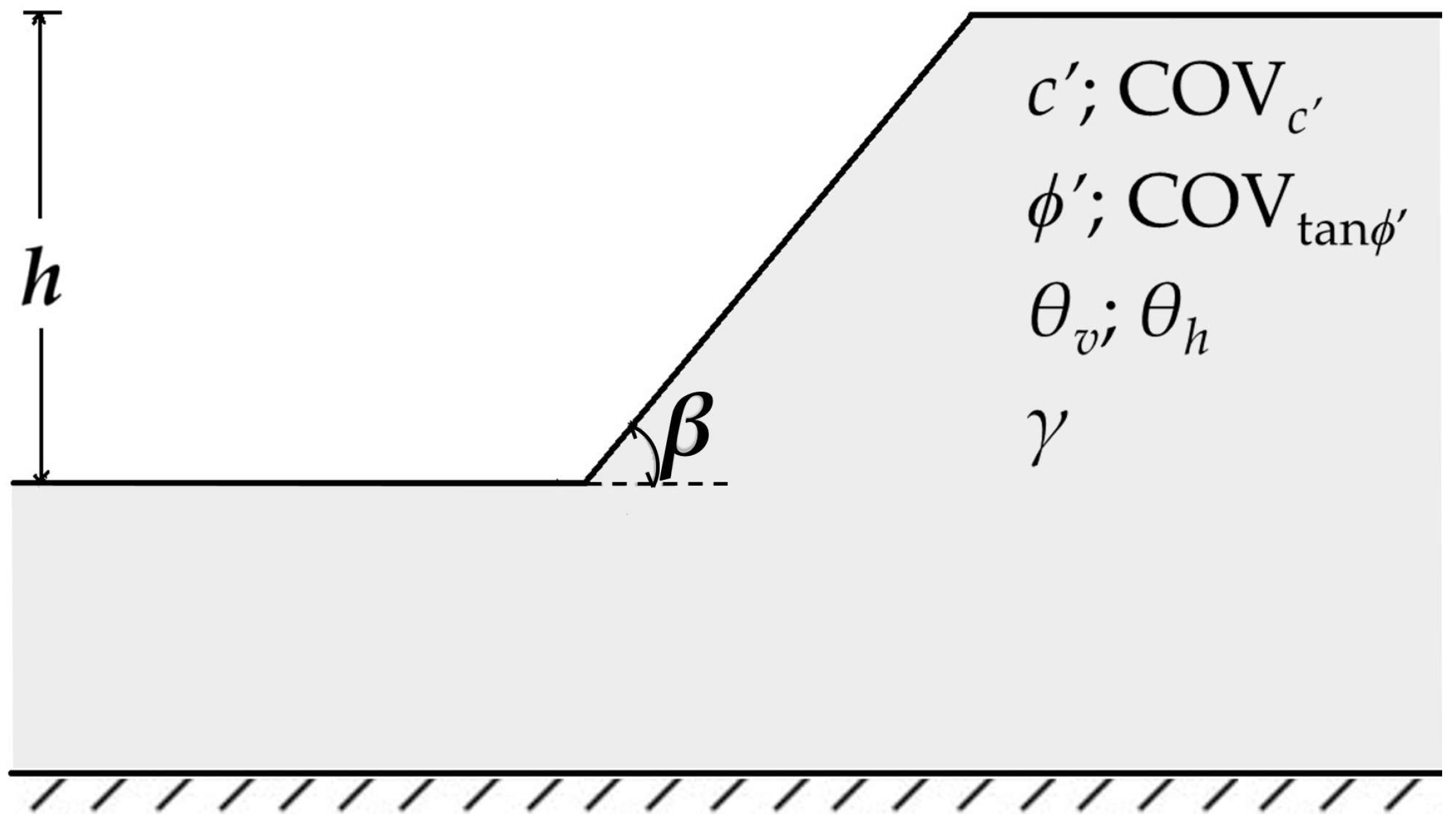

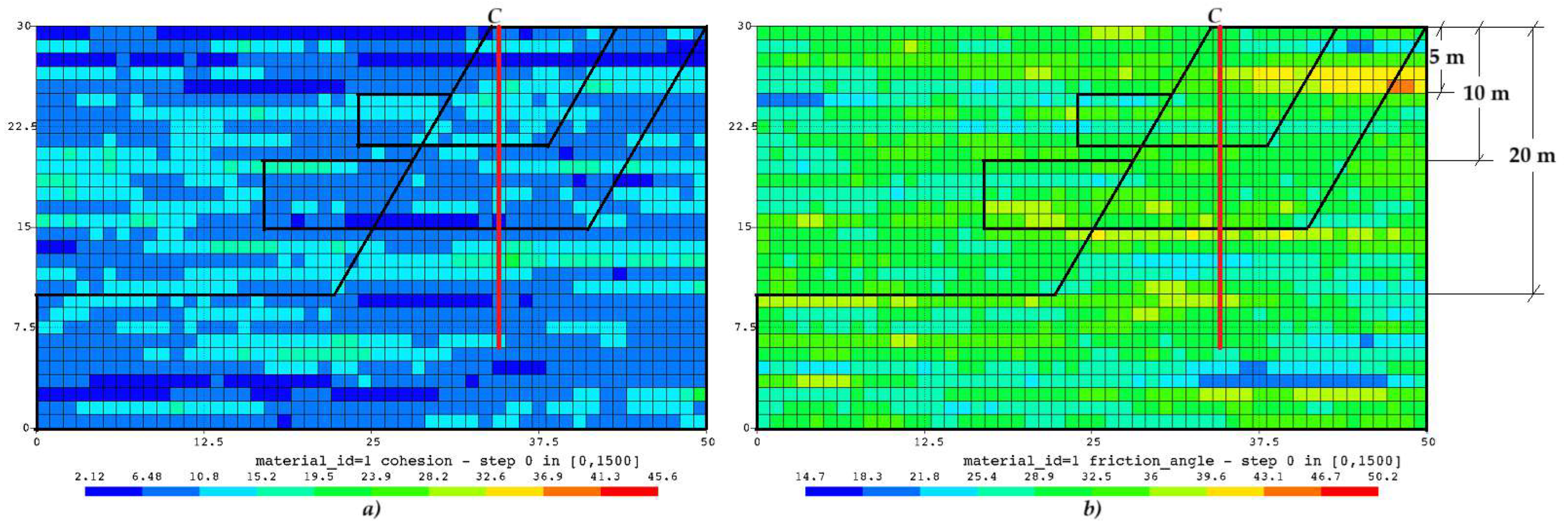
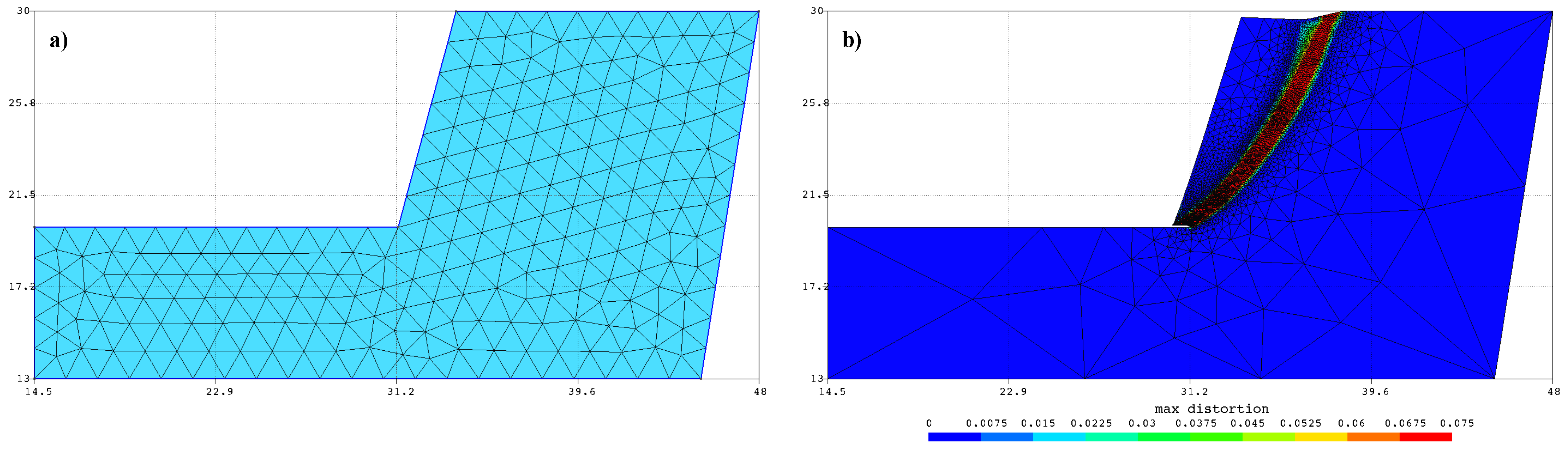


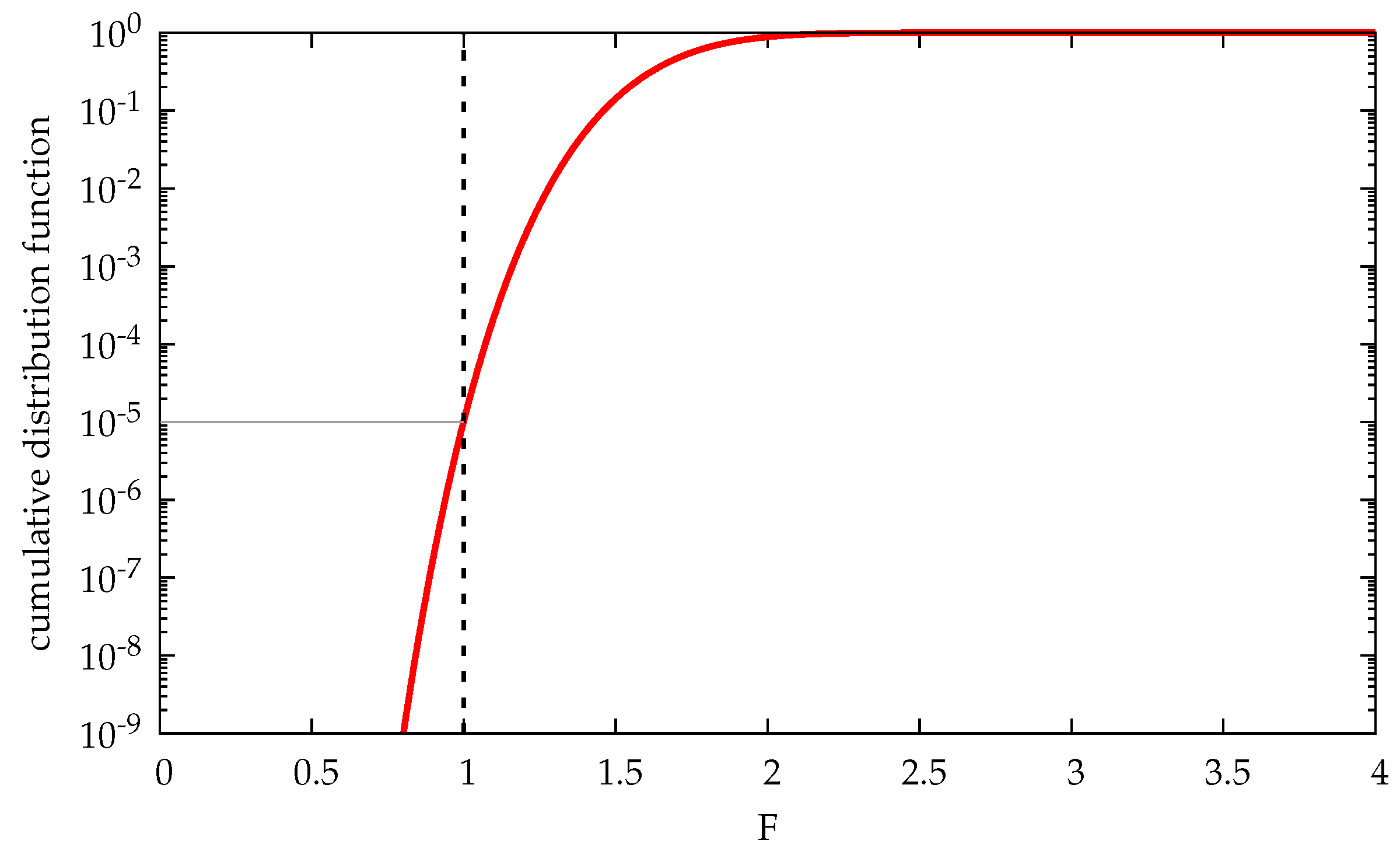


| h | /COV | /COV | 1st Scenario | 2nd Scenario | ||||
|---|---|---|---|---|---|---|---|---|
| (m) | ||||||||
| 5 | 30/0.15 | 1/0.3 | 0.20 | 75 | 4 | 5 | 8 | 4 |
| 2.5/0.3 | 3 | 8 | 1 | 5 | ||||
| 10/0.3 | 1 | 8 | 1 | 5 | ||||
| 100/0.3 | 1 | 5 | 9 | 4 | ||||
| 10 | 30/0.15 | 5/0.3 | 0.1 | 75 | 3 | 8 | 1 | 7 |
| 10/0.3 | 2 | 1 | 9 | 7 | ||||
| h | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1st Scenario | 2nd Scenario | 1st Scenario | 2nd Scenario | |||||||
| (m) | (m) | |||||||||
| 5 | 0.25 | 0.05 | 2 | 3 | 4 | 1 | 6 | 4 | 3 | 2 |
| 0.50 | 0.10 | 1 | 1 | 1 | 8 | 4 | 8 | 1 | 6 | |
| 0.75 | 0.15 | 9 | 6 | 2 | 2 | 7 | 8 | 2 | 1 | |
| 1.00 | 0.20 | 1 | 8 | 1 | 5 | 2 | 2 | 2 | 2 | |
| 10 | 0.50 | 0.05 | 3 | 3 | 3 | 1 | 5 | 3 | 2 | 1 |
| 1.00 | 0.10 | 2 | 1 | 9 | 7 | 9 | 8 | 8 | 5 | |
| 1.50 | 0.15 | 6 | 5 | 2 | 2 | 3 | 5 | 2 | 9 | |
| 2.00 | 0.20 | 2 | 5 | 9 | 4 | 6 | 1 | 9 | 2 | |
| 20 | 1.00 | 0.05 | 6 | 3 | 2 | 1 | 3 | 3 | 1 | 1 |
| 2.00 | 0.10 | 5 | 7 | 1 | 7 | 2 | 5 | 1 | 5 | |
| 3.00 | 0.15 | 2 | 4 | 2 | 2 | 1 | 5 | 2 | 1 | |
| 4.00 | 0.20 | 4 | 5 | 9 | 4 | 1 | 1 | 1 | 2 | |
| 1st Scenario | 2nd Scenario | |||||||
|---|---|---|---|---|---|---|---|---|
| 5 | 30/0.15 | 10/0.30 | 0.2 | 45 | 1 | 3 | 2 | 3 |
| 60 | 2 | 3 | 1 | 3 | ||||
| 75 | 1 | 8 | 1 | 5 | ||||
| 35/0.15 | 45 | — | — | — | — | |||
| 60 | 2 | 1 | 8 | 3 | ||||
| 75 | 6 | 4 | 8 | 4 | ||||
| 40/0.15 | 45 | — | — | — | — | |||
| 60 | 3 | 5 | 9 | 2 | ||||
| 75 | 1 | 1 | 7 | 3 | ||||
| 10 | 30/0.15 | 10/0.30 | 0.1 | 45 | 1 | 7 | 8 | 1 |
| 60 | 3 | 2 | 5 | 3 | ||||
| 75 | 2 | 1 | 9 | 7 | ||||
| 35/0.15 | 45 | — | — | — | — | |||
| 60 | 6 | 8 | 5 | 2 | ||||
| 75 | 4 | 3 | 6 | 5 | ||||
| 40/0.15 | 45 | — | — | — | — | |||
| 60 | 5 | 2 | 6 | 1 | ||||
| 75 | 1 | 1 | 5 | 3 | ||||
| 20 | 30/0.15 | 10/0.30 | 0.05 | 45 | 2 | 5 | 4 | 7 |
| 60 | 3 | 5 | 2 | 3 | ||||
| 75 | 6 | 3 | 2 | 1 | ||||
| 35/0.15 | 45 | 2 | 8 | 3 | 1 | |||
| 60 | 9 | 9 | 6 | 9 | ||||
| 75 | 3 | 8 | 6 | 5 | ||||
| 40/0.15 | 45 | — | — | — | — | |||
| 60 | 3 | 7 | 7 | 3 | ||||
| 75 | 2 | 2 | 5 | 2 | ||||
| 1st Scenario | 2nd Scenario | |||||||
|---|---|---|---|---|---|---|---|---|
| 5 | 30/0.15 | 10/0.30 | 0.2 | 45 | 2 | 3 | 5 | 1 |
| 60 | 1 | 5 | 1 | 1 | ||||
| 75 | 2 | 2 | 2 | 2 | ||||
| 35/0.15 | 45 | — | — | — | — | |||
| 60 | 1 | 2 | 1 | 8 | ||||
| 75 | 1 | 8 | 1 | 1 | ||||
| 40/0.15 | 45 | — | — | — | — | |||
| 60 | 8 | 8 | 2 | 9 | ||||
| 75 | 3 | 3 | 9 | 1 | ||||
| 10 | 30/0.15 | 10/0.30 | 0.1 | 45 | 3 | 3 | 1 | 4 |
| 60 | 4 | 1 | 3 | 1 | ||||
| 75 | 9 | 8 | 8 | 4 | ||||
| 35/0.15 | 45 | — | — | — | — | |||
| 60 | 1 | 4 | 5 | 7 | ||||
| 75 | 2 | 2 | 5 | 3 | ||||
| 40/0.15 | 45 | — | — | — | — | |||
| 60 | 9 | 8 | 9 | 5 | ||||
| 75 | 4 | 6 | 4 | 2 | ||||
| 20 | 30/0.15 | 10/0.30 | 0.05 | 45 | 2 | 3 | 6 | 2 |
| 60 | 1 | 4 | 1 | 3 | ||||
| 75 | 3 | 3 | 1 | 1 | ||||
| 35/0.15 | 45 | 3 | 5 | 9 | 1 | |||
| 60 | 2 | 6 | 5 | 6 | ||||
| 75 | 7 | 9 | 4 | 5 | ||||
| 40/0.15 | 45 | — | — | — | — | |||
| 60 | 6 | 3 | 8 | 2 | ||||
| 75 | 3 | 1 | 3 | 2 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rogério, F.; Guerra, N.; Antão, A.; Vicente da Silva, M. Soil Strength Parameters for the Sustainable Design of Unsupported Cuts Under Drained Conditions Using Reliability Analysis. Sustainability 2024, 16, 10596. https://doi.org/10.3390/su162310596
Rogério F, Guerra N, Antão A, Vicente da Silva M. Soil Strength Parameters for the Sustainable Design of Unsupported Cuts Under Drained Conditions Using Reliability Analysis. Sustainability. 2024; 16(23):10596. https://doi.org/10.3390/su162310596
Chicago/Turabian StyleRogério, Flávio, Nuno Guerra, Armando Antão, and Mário Vicente da Silva. 2024. "Soil Strength Parameters for the Sustainable Design of Unsupported Cuts Under Drained Conditions Using Reliability Analysis" Sustainability 16, no. 23: 10596. https://doi.org/10.3390/su162310596
APA StyleRogério, F., Guerra, N., Antão, A., & Vicente da Silva, M. (2024). Soil Strength Parameters for the Sustainable Design of Unsupported Cuts Under Drained Conditions Using Reliability Analysis. Sustainability, 16(23), 10596. https://doi.org/10.3390/su162310596








