Robotic Edge Intelligence for Energy-Efficient Human–Robot Collaboration
Abstract
1. Introduction
2. Background
3. The Architecture of Robotic Edge Intelligence
3.1. Main Architecture
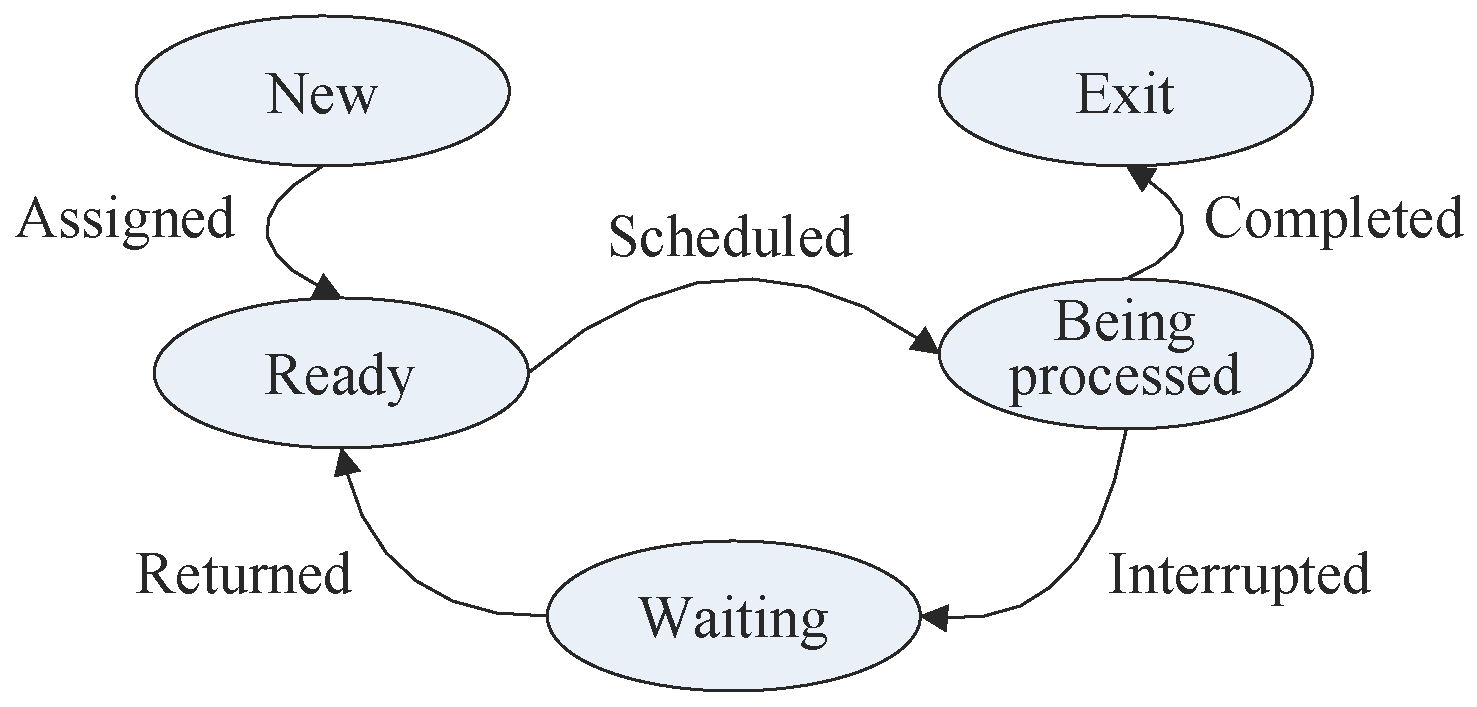
3.2. The Job State Transition
- ●
- New. If a job requests a human/robot, it will be created at first and wait for assignment;
- ●
- Ready. If a new job is assigned to an idle human/robot, it is in a ready state; that is, a human/robot is occupied by the job and cannot be assigned to other jobs;
- ●
- Being processed. If a ready job is scheduled, then it can start immediately. The job is in a being-processed state, and a human/robot is processing it;
- ●
- Waiting. When a job is being processed, any interruption may break it off before its completion, and the interrupted job will be set as in a waiting state. If the interruption is completed in the waiting state, the job will be returned to the ready state;
- ●
- Exit. Whenever a job is completed, it will exit the REI system, and the assigned human/robot will be released.
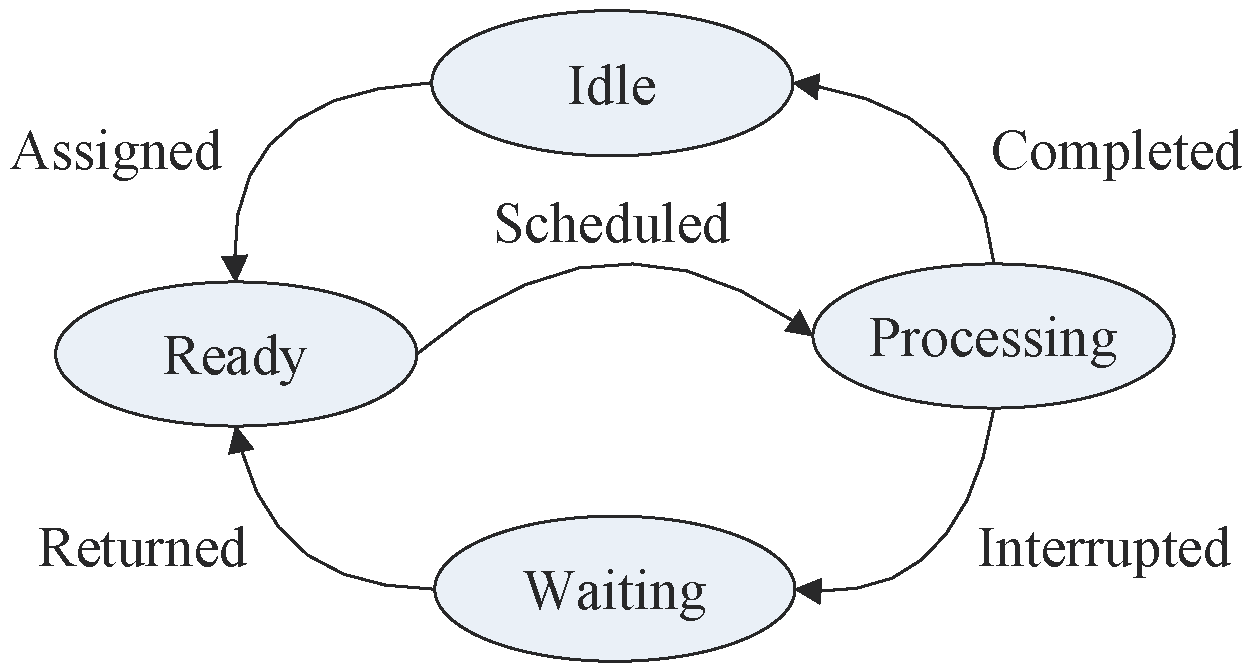
3.3. The Human/Robot State Transition
- ●
- Idle. This is an initial state, when a human/robot is not assigned to any jobs. Only an idle human/robot can be assigned to a job;
- ●
- Ready. If an idle human/robot is assigned to a new job, it is in a ready state; that is, a human/robot is occupied by the job and cannot be assigned to other jobs;
- ●
- Processing. If a ready human/robot is scheduled, then it can process the job immediately, and the job is in a being-processed state. Whenever the processing is completed, the human/robot will be idle again for the next assignments;
- ●
- Waiting. When a human/robot is processing a job, any interruption may break it off before its completion, and the interrupted human/robot will be in a waiting state. If the interruption is completed in the waiting state, the human/robot will be returned to the ready state.
4. A Multi-Objective Model for EHCP
- Assuming that the scheduling in human–machine collaboration is non-preemptive, without considering preemptive scheduling;
- Assuming that different people can complete the same homework operation, regardless of the situation where someone is unable to perform a certain operation, including illness, emotions, and hunger;
- Assuming that different robots can complete the same task operation, regardless of the situation where one robot is unable to perform a certain operation, such as faults, repairs, or power outages;
- Assuming that the energy consumption of humans or robots is only related to their inherent power, without considering the increase or decrease in energy consumption rate under certain operations;
- Assuming no special tasks applicable only to one person or one robot are considered.
4.1. Production Performance of EHCP
4.2. Energy Efficiency of EHCP
5. An Artificial Plant Community Algorithm
5.1. Solution Steps of APC
5.1.1. Step 1: Initialization
5.1.2. Step 2: Seeding of APC
5.1.3. Step 3: Growing of the APC
5.1.4. Step 4: Fruiting of the APC
5.1.5. Step 5: End Judgment
5.2. Pseudo-Codes of APC
| Algorithm 1: Solving EHCP in the job layer | |
| 1: | initialize the parameters of EHCP |
| 2: | initialize the parameters of APC |
| 3: | initialize the parameters of the solving system |
| 4: | if state (job) = new |
| 5: | if state (human) = idle |
| 6: | if state (robot) = idle |
| 7: | encode the APC individual by Equation (29) |
| 8: | select objectives 2 and 3 by Equation (27) |
| 9: | for ite: 1 to |
| 10: | generate the random seeds by |
| 11: | generate seeds from the previous fruits |
| 12: | calculate and compare fitness by Equation (27) |
| 13: | select the best solutions by |
| 14: | select the elite individual with the highest fitness |
| 15: | generate a best fruit through parthenogenesis |
| 16: | generate fruits through social learning by |
| 17: | end judgment by |
| 18: | end for |
| 19: | output the optimal solution |
| 20: | State (job) = ready |
| 21: | State (human) = ready |
| 22: | State (robot) = ready |
6. Benchmark Experiments
6.1. Benchmark Data
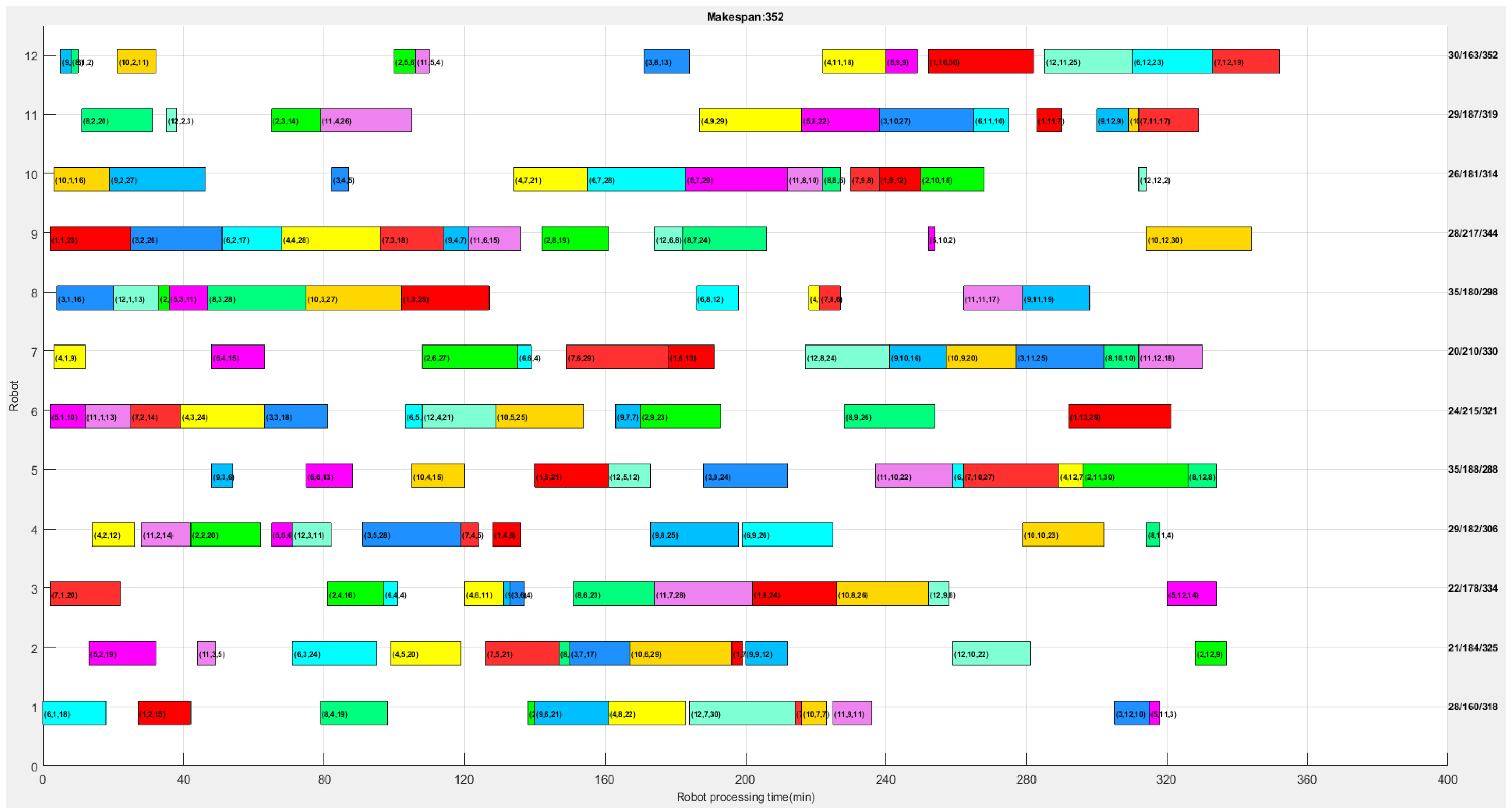
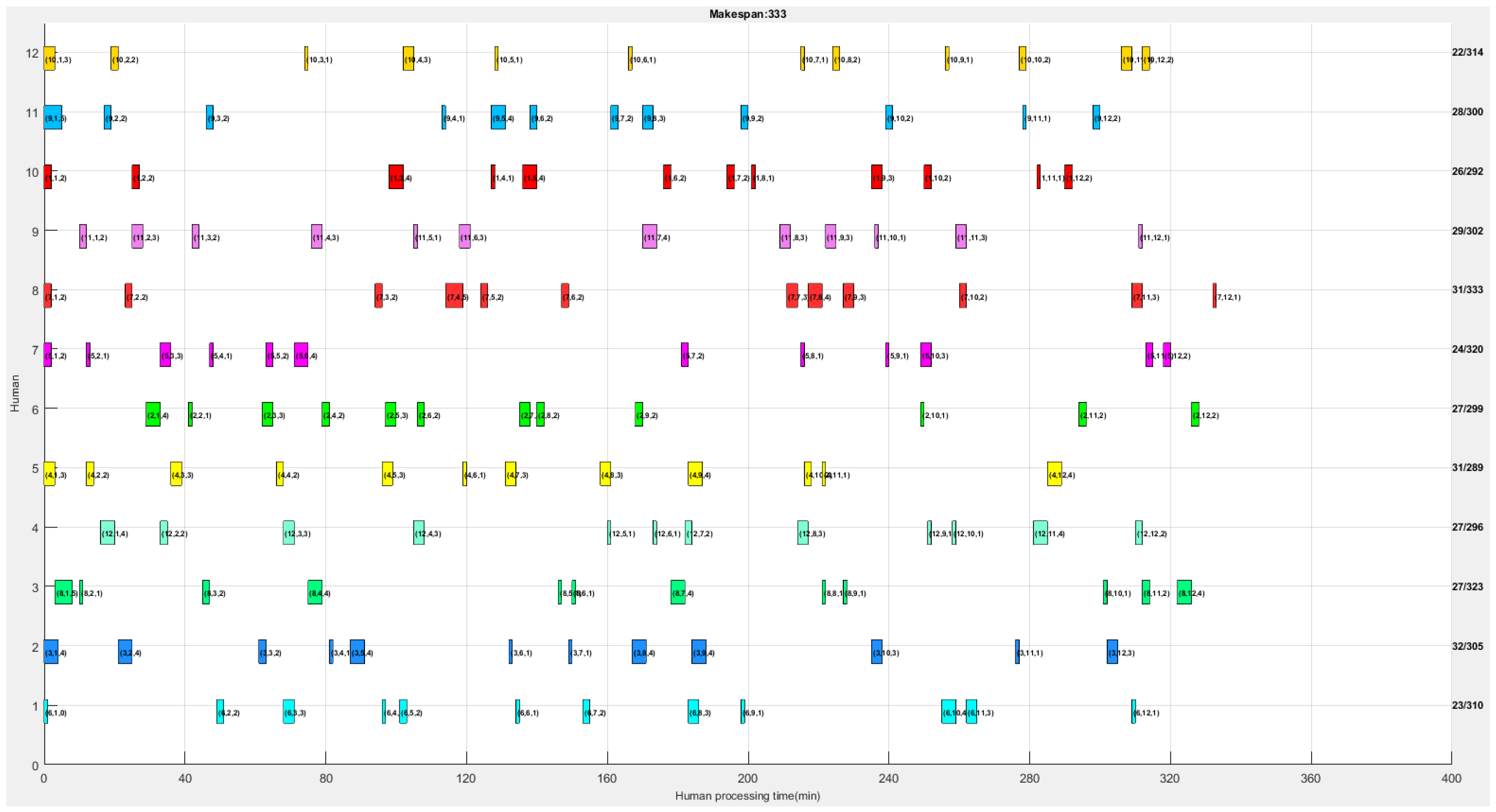
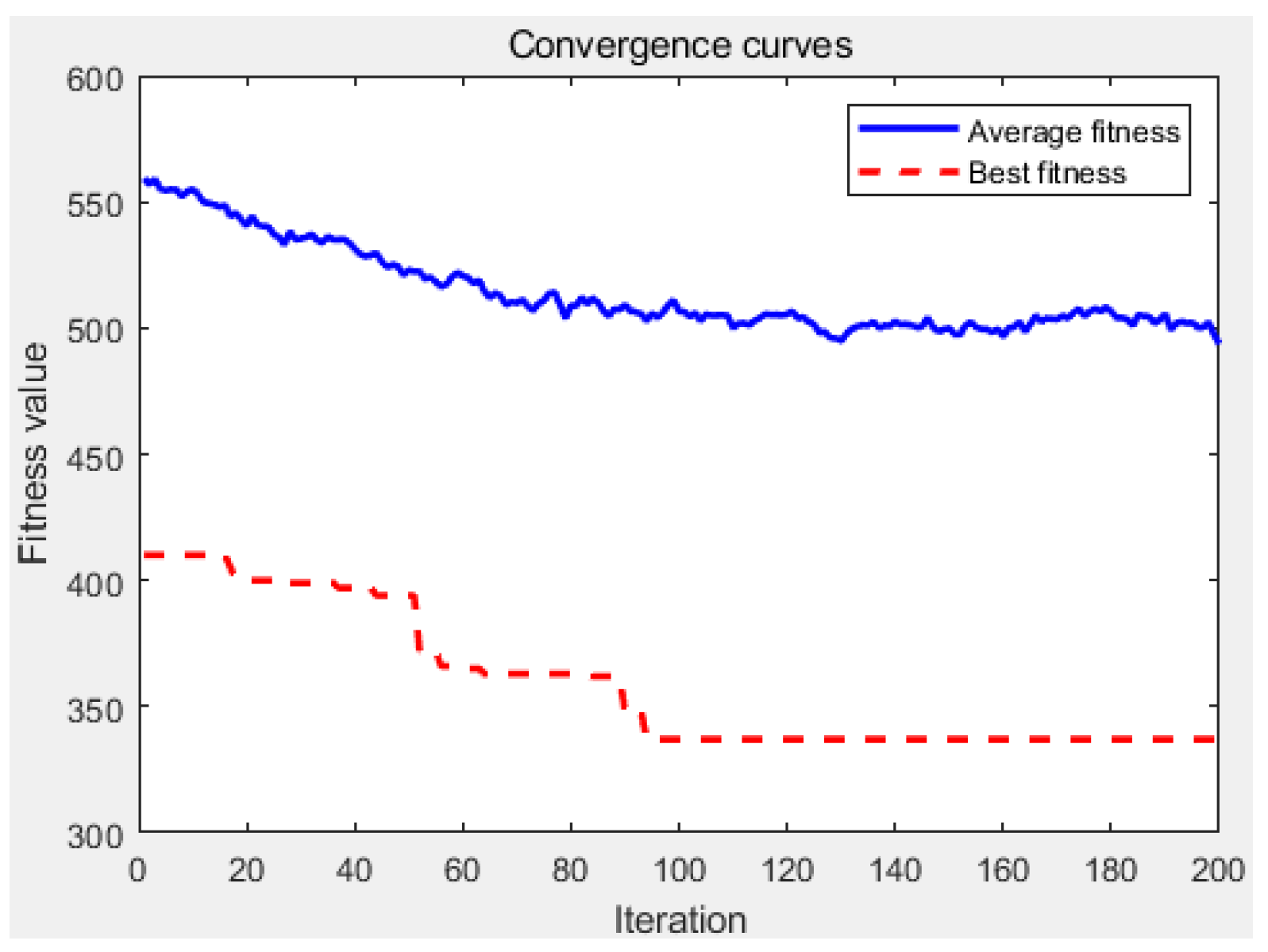
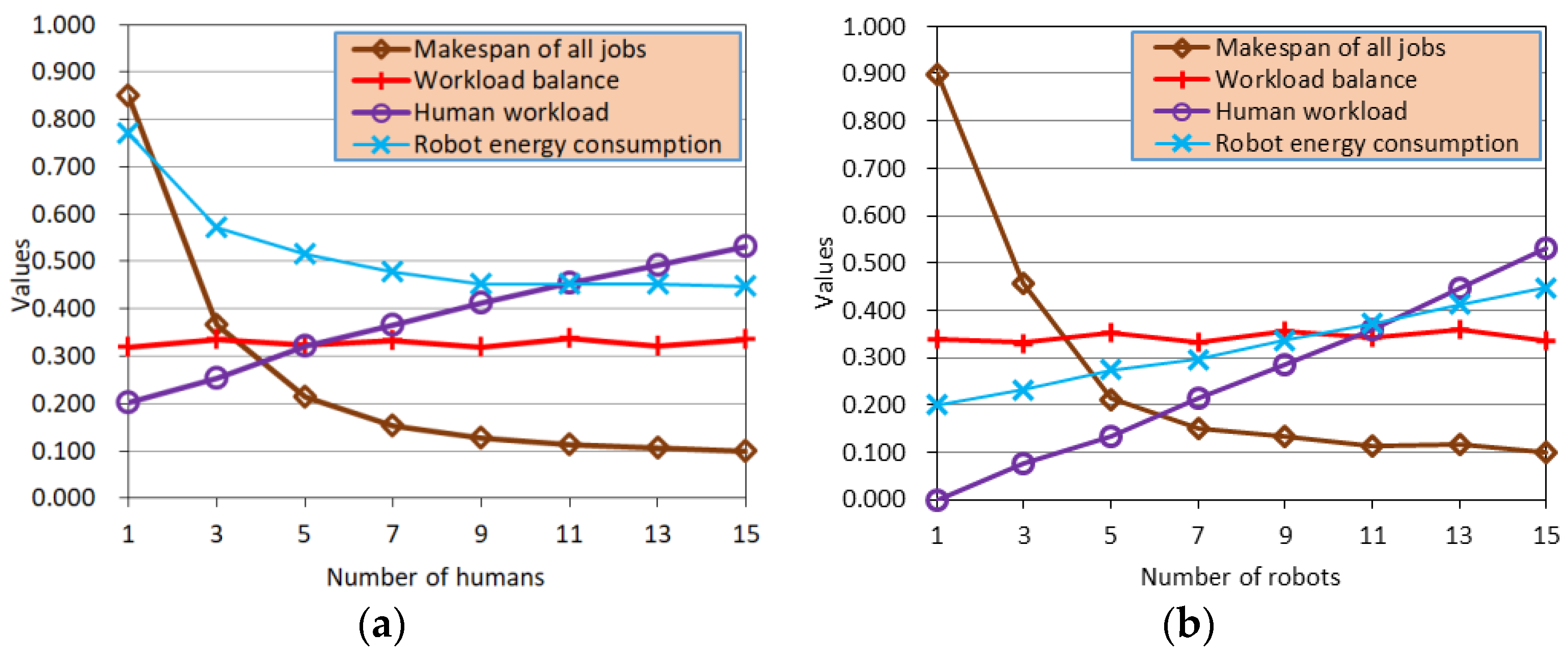
6.2. Experimental Results
6.3. Comparative Analysis
7. Conclusions and Future Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mura, M.D.; Dini, G. Job rotation and human-robot collaboration for enhancing ergonomics in assembly lines by a genetic algorithm. Int. J. Adv. Manuf. Technol. 2022, 118, 2901–2914. [Google Scholar] [CrossRef]
- Lu, C.; Gao, R.; Yin, L.; Zhang, B. Human–robot collaborative scheduling in energy-efficient welding shop. IEEE Trans. Ind. Inform. 2024, 20, 963–971. [Google Scholar] [CrossRef]
- Guo, D. Fast scheduling of human-robot teams collaboration on synchronised production-logistics tasks in aircraft assembly. Robot. Comput. Manuf. 2024, 85, 102620. [Google Scholar] [CrossRef]
- Subramanian, K.; Thomas, L.; Sahin, M.; Sahin, F. Supporting human–robot interaction in manufacturing with augmented Reality and effective human–computer interaction: A review and framework. Machines 2024, 12, 706. [Google Scholar] [CrossRef]
- Zhang, R.; Lv, Q.; Li, J.; Bao, J.; Liu, T.; Liu, S. A reinforcement learning method for human-robot collaboration in assembly tasks. Robot. Robot. Comput. Integr. Manuf. 2022, 73, 102227. [Google Scholar] [CrossRef]
- Mura, M.D.; Dini, G. Designing assembly lines with humans and collaborative robots: A genetic approach. CIRP Nals-Manuf. Technol. 2019, 68, 1–4. [Google Scholar] [CrossRef]
- Qu, C.; Sorbelli, F.B.; Singh, R.; Calyam, P.; Das, S.K. Environmentally-aware and energy-efficient multi-drone coordination and networking for disaster response. IEEE Trans. Netw. Serv. Manag. 2022, 20, 1093–1109. [Google Scholar] [CrossRef]
- Gao, Z.G.; Yang, R.N.; Zhao, K.; Yu, W.H.; Liu, Z.; Liu, L.L. Hybrid convolutional neural network approaches for recognizing col-laborative actions in human-robot assembly tasks. Sustainability 2024, 16, 139. [Google Scholar] [CrossRef]
- Lachner, J.; Allmendinger, F.; Hobert, E.; Hogan, N.; Stramigioli, S. Energy budgets for coordinate invariant robot control in physical human–robot interaction. Int. J. Robot. Res. 2021, 40, 968–985. [Google Scholar] [CrossRef]
- Alevizos, K.I.; Bechlioulis, C.P.; Kyriakopoulos, K.J. Bounded energy collisions in human–robot cooperative transportation. IEEE/ASME Trans. Mechatron. 2022, 27, 4541–4549. [Google Scholar] [CrossRef]
- Elmi, A.; Topaloglu, S. Cyclic job shop robotic cell scheduling problem: Ant colony optimization. Comput. Ind. Eng. 2017, 111, 417–432. [Google Scholar] [CrossRef]
- Wu, T.; Zhang, Z.; Zeng, Y.; Zhang, Y. Mixed-integer programming model and hybrid local search genetic algorithm for human–robot collaborative disassembly line balancing problem. Int. J. Prod. Res. 2023, 62, 1758–1782. [Google Scholar] [CrossRef]
- Huang, Y.; Sheng, B.; Luo, R.; Lu, Y.; Fu, G.; Yin, X. Solving human-robot collaborative mixed-model two-sided assembly line balancing using multi-objective discrete artificial bee colony algorithm. Comput. Ind. Eng. 2024, 187, 109776. [Google Scholar] [CrossRef]
- Omidi, M.; Van de Perre, G.; Hota, R.K.; Cao, H.-L.; Saldien, J.; Vanderborght, B.; El Makrini, I. Improving postural ergonomics during human–robot collaboration using particle swarm optimization: A study in virtual environment. Appl. Sci. 2023, 13, 5385. [Google Scholar] [CrossRef]
- Khosravy, M.; Gupta, N.; Pasquali, A.; Dey, N.; Crespo, R.G.; Witkowski, O. Human-collaborative artificial intelligence along with social values in industry 5.0: A survey of the state-of-the-art. IEEE Trans. Cogn. Dev. Syst. 2024, 16, 165–176. [Google Scholar] [CrossRef]
- Cai, Z.; Wang, X.; Li, R.; Gao, Q. An artificial physarum polycephalum colony for the electric location-routing problem. Sustainability 2023, 15, 16196. [Google Scholar] [CrossRef]
- Cai, Z.; Li, G.; Zhang, J.; Xiong, S. Using an artificial physarum polycephalum colony for threshold image segmentation. Appl. Sci. 2023, 13, 11976. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Y.S. Storage location assignment for improving human-robot collaborative order-picking efficiency in robotic mobile fulfillment systems. Sustainability 2024, 16, 1742. [Google Scholar] [CrossRef]
- Lyu, S.; Cheah, C.C. Human-robot interaction control based on a general energy shaping method. IEEE Trans. Control Syst. Technol. 2020, 28, 2445–2460. [Google Scholar] [CrossRef]
- Aydogan, Ç.; Gürel, S. Energy efficient scheduling of a two machine robotic cell producing multiple part types. Flex. Serv. Manuf. J. 2024, 1–35. [Google Scholar] [CrossRef]
- Ye, X.; Deng, Z.; Shi, Y.; Shen, W. Toward Energy-Efficient Routing of Multiple AGVs with Multi-Agent Reinforcement Learning. Sensors 2023, 23, 5615. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.L.; Du, Y. Hybrid artificial immune algorithm for energy-efficient distributed flexible job shop in semiconductor manufacturing. Clust. Comput. J. Netw. Softw. Tools Appl. 2023, 27, 3075–3098. [Google Scholar] [CrossRef]
- Wei, H.; Li, S.; Quan, H.; Liu, D.; Rao, S.; Li, C.; Hu, J. Unified multi-objective genetic algorithm for energy efficient job shop scheduling. IEEE Access 2021, 9, 54542–54557. [Google Scholar] [CrossRef]
- Luo, S.; Zhang, L.; Fan, Y. Energy-efficient scheduling for multi-objective flexible job shops with variable processing speeds by grey wolf optimization. J. Clean. Prod. 2019, 234, 1365–1384. [Google Scholar] [CrossRef]
- Zhao, F.; Di, S.; Wang, L. A hyperheuristic with Q-learning for the multiobjective energy-efficient distributed blocking flow shop scheduling problem. IEEE Trans. Cybern. 2022, 53, 3337–3350. [Google Scholar] [CrossRef]
- Wang, G.; Li, X.; Gao, L.; Li, P. An effective multi-objective whale swarm algorithm for energy-efficient scheduling of distributed welding flow shop. Ann. Oper. Res. 2022, 310, 223–255. [Google Scholar] [CrossRef]
- Tirkolaee, E.B.; Goli, A.; Weber, G.-W. Fuzzy mathematical programming and self-adaptive artificial fish swarm algorithm for just-in-time energy-aware flow shop scheduling problem with outsourcing option. IEEE Trans. Fuzzy Syst. 2020, 28, 2772–2783. [Google Scholar] [CrossRef]
- Wu, M.; Yeong, C.F.; Su, E.L.M.; Holderbaum, W.; Yang, C. A review on energy efficiency in autonomous mobile robots. Robot. Intell. Autom. 2023, 43, 648–668. [Google Scholar] [CrossRef]
- Czymmek, V.; Köhn, C.; Harders, L.O.; Hussmann, S. Review of energy-efficient embedded system acceleration of convolution neural networks for organic weeding robots. Agriculture 2023, 13, 2103. [Google Scholar] [CrossRef]
- Cai, Z.; Jiang, S.; Dong, J.; Tang, S. An artificial plant community algorithm for the accurate range-free positioning of wireless sensor networks. Sensors 2023, 23, 2804. [Google Scholar] [CrossRef]
- Katare, D.; Perino, D.; Nurmi, J.; Warnier, M.; Janssen, M.; Ding, A.Y. A survey on approximate edge AI for energy efficient au-tonomous driving services. IEEE Commun. Surv. Tutor. 2023, 25, 2714–2754. [Google Scholar] [CrossRef]
- Liu, H.H.; Nasiriany, S.; Zhang, L.C.; Bao, Z.Y.; Zhu, Y.K. Robot learning on the job: Human-in-the-loop autonomy and learning during deployment. arXiv 2024, arXiv:2211.08416. [Google Scholar] [CrossRef]
- Cao, Y.; Zhou, Q.; Yuan, W.; Ye, Q.; Popa, D.; Zhang, Y. Human-robot collaborative assembly and welding: A review and analysis of the state of the art. J. Manuf. Process. 2024, 131, 1388–1403. [Google Scholar] [CrossRef]

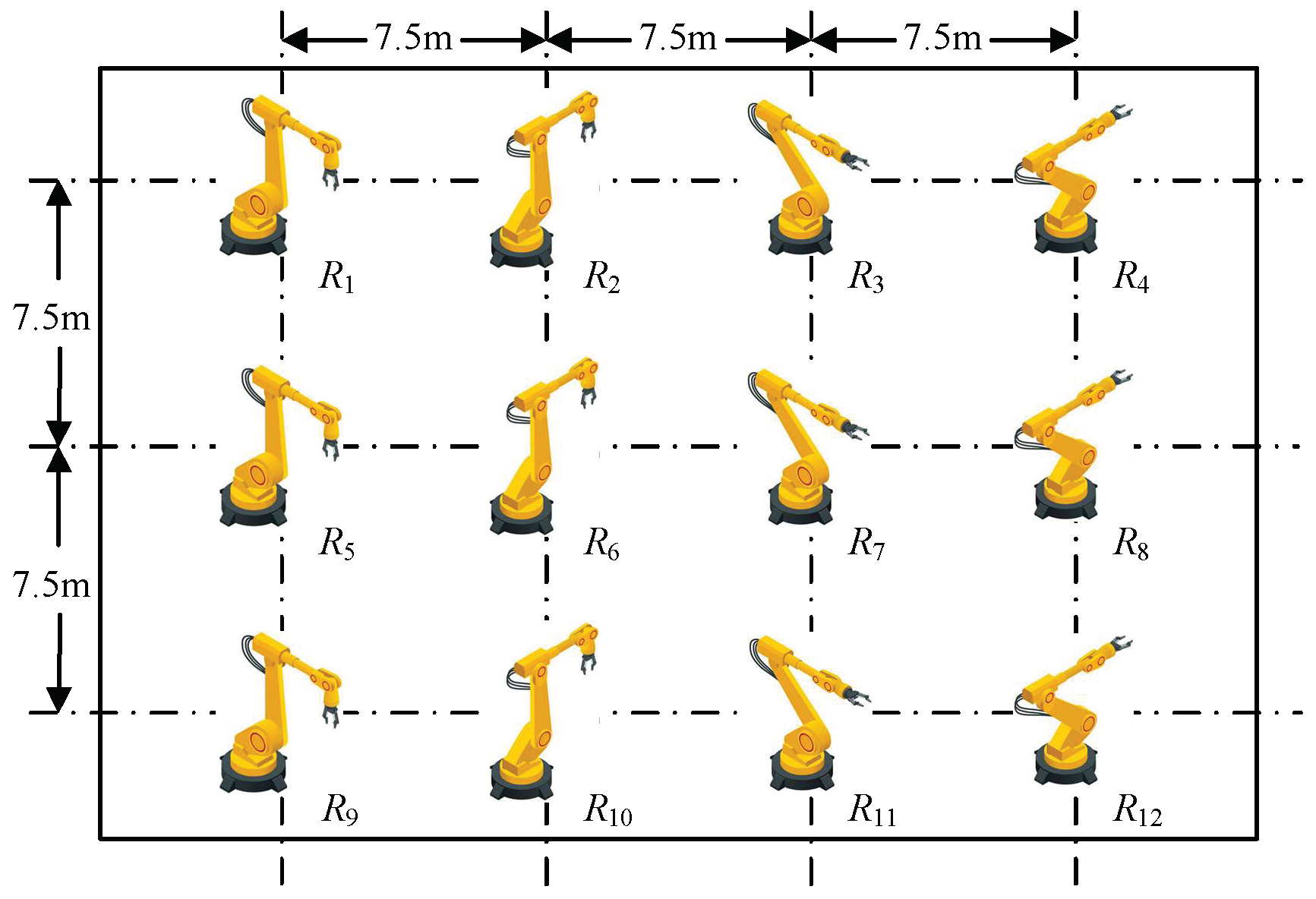
| Robots | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 7.5 | 15 | 22.5 | 7.5 | 15 | 22.5 | 30 | 15 | 22.5 | 30 | 37.5 | |
| 7.5 | 0 | 7.5 | 15 | 15 | 7.5 | 15 | 22.5 | 22.5 | 15 | 22.5 | 30 | |
| 15 | 7.5 | 0 | 7.5 | 22.5 | 15 | 7.5 | 15 | 30 | 22.5 | 15 | 22.5 | |
| 22.5 | 15 | 7.5 | 0 | 30 | 22.5 | 15 | 7.5 | 37.5 | 30 | 22.5 | 15 | |
| 7.5 | 15 | 22.5 | 30 | 0 | 7.5 | 15 | 22.5 | 7.5 | 15 | 22.5 | 30 | |
| 15 | 7.5 | 15 | 22.5 | 7.5 | 0 | 7.5 | 15 | 15 | 7.5 | 15 | 22.5 | |
| 22.5 | 15 | 7.5 | 15 | 15 | 7.5 | 0 | 7.5 | 22.5 | 15 | 7.5 | 15 | |
| 30 | 22.5 | 15 | 7.5 | 22.5 | 15 | 7.5 | 0 | 30 | 22.5 | 15 | 7.5 | |
| 15 | 22.5 | 30 | 37.5 | 7.5 | 15 | 22.5 | 30 | 0 | 7.5 | 15 | 22.5 | |
| 22.5 | 15 | 22.5 | 30 | 15 | 7.5 | 15 | 22.5 | 7.5 | 0 | 7.5 | 15 | |
| 30 | 22.5 | 15 | 22.5 | 22.5 | 15 | 7.5 | 15 | 15 | 7.5 | 0 | 7.5 | |
| 37.5 | 30 | 22.5 | 15 | 30 | 22.5 | 15 | 7.5 | 22.5 | 15 | 7.5 | 0 |
| Operation | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 15 | 3 | 24 | 8 | 21 | 29 | 13 | 25 | 23 | 12 | 7 | 30 | |
| 2 | 9 | 16 | 20 | 30 | 23 | 27 | 3 | 19 | 18 | 14 | 6 | |
| 10 | 17 | 4 | 28 | 24 | 18 | 25 | 16 | 26 | 5 | 27 | 13 | |
| 22 | 20 | 11 | 12 | 7 | 24 | 9 | 3 | 28 | 21 | 29 | 18 | |
| 3 | 19 | 14 | 6 | 13 | 10 | 15 | 11 | 2 | 29 | 22 | 9 | |
| 18 | 24 | 4 | 26 | 3 | 5 | 4 | 12 | 17 | 28 | 10 | 23 | |
| 2 | 21 | 20 | 5 | 27 | 14 | 29 | 6 | 18 | 8 | 17 | 19 | |
| 19 | 3 | 23 | 4 | 8 | 26 | 10 | 28 | 24 | 5 | 20 | 2 | |
| 21 | 12 | 2 | 25 | 6 | 7 | 16 | 19 | 7 | 27 | 9 | 3 | |
| 7 | 29 | 26 | 23 | 15 | 25 | 20 | 27 | 30 | 16 | 3 | 11 | |
| 11 | 5 | 28 | 14 | 22 | 13 | 18 | 17 | 15 | 10 | 26 | 4 | |
| 30 | 22 | 6 | 11 | 12 | 21 | 24 | 13 | 8 | 2 | 3 | 25 |
| 30 | 40 | 50 | 120 | 30 | 40 | 50 | 120 | 30 | 40 | 50 | 120 | |
| 150 | 200 | 300 | 500 | 150 | 200 | 300 | 500 | 150 | 200 | 300 | 500 |
| Metrics | Solutions | ||
|---|---|---|---|
| Minimum | Average | Maximum | |
| The makespan of all jobs (min) | 352 | 371.333 | 406 |
| The workload balance indicator (min) | 30.667 | 36.667 | 41.333 |
| The makespan on the production line (min) | 352 | 371.333 | 406 |
| The maximum workload of all production lines (min) | 245 | 247.667 | 251 |
| The total energy consumption of all robots (kWh) | 12.622 | 12.854 | 13.270 |
| The total workload of humans (min) | 324 | 334.000 | 344 |
| The total workload of robots (min) | 2245 | 2245 | 2245 |
| Total processing energy consumption of all robots (kWh) | 10.596 | 10.596 | 10.596 |
| Total idle energy consumption of all robots (kWh) | 2.026 | 2.258 | 2.674 |
| The maximum processing time of all humans (min) | 32 | 33.333 | 34 |
| The minimum processing time of all humans (min) | 22 | 23.000 | 24 |
| The lowest processing speed of humans (m/min) | 7.50 | 7.50 | 7.50 |
| Objectives | GA [1,6,12,23] | ACO [11] | ABC [13] | PSO [14] | QL [25] | APC | |
|---|---|---|---|---|---|---|---|
| The makespan of all jobs (min) | min | 352 | 352 | 356 | 352 | 352 | 352 |
| avg | 372.133 | 378.033 | 376.367 | 374.767 | 371.667 | 371.333 | |
| The workload balance indicator (min) | min | 32.033 | 31.933 | 31.667 | 32.167 | 30.767 | 30.667 |
| avg | 38.333 | 38.067 | 37.567 | 36.700 | 36.900 | 36.667 | |
| The makespan on the production line (min) | min | 352 | 352 | 356 | 352 | 352 | 352 |
| avg | 373.733 | 371.967 | 372.533 | 376.400 | 371.600 | 371.333 | |
| The maximum workload of all production lines (min) | min | 245 | 245 | 248 | 245 | 245 | 245 |
| avg | 249.100 | 248.867 | 251.033 | 247.800 | 248.733 | 247.667 | |
| The total energy consumption of all robots (kWh) | min | 12.622 | 12.622 | 12.911 | 12.652 | 12.622 | 12.622 |
| avg | 13.138 | 12.973 | 13.064 | 13.143 | 12.955 | 12.854 | |
| The total workload of humans (min) | min | 324 | 326 | 324 | 327.967 | 324 | 324 |
| avg | 335.900 | 336.400 | 338.100 | 336.467 | 334.133 | 334.000 | |
| Solution time (s) | min | 397 | 396 | 401 | 392 | 2157 | 403 |
| avg | 415 | 417 | 422 | 411 | 2576 | 436 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, Z.; Du, X.; Huang, T.; Lv, T.; Cai, Z.; Gong, G. Robotic Edge Intelligence for Energy-Efficient Human–Robot Collaboration. Sustainability 2024, 16, 9788. https://doi.org/10.3390/su16229788
Cai Z, Du X, Huang T, Lv T, Cai Z, Gong G. Robotic Edge Intelligence for Energy-Efficient Human–Robot Collaboration. Sustainability. 2024; 16(22):9788. https://doi.org/10.3390/su16229788
Chicago/Turabian StyleCai, Zhengying, Xiangyu Du, Tianhao Huang, Tianrui Lv, Zhiheng Cai, and Guoqiang Gong. 2024. "Robotic Edge Intelligence for Energy-Efficient Human–Robot Collaboration" Sustainability 16, no. 22: 9788. https://doi.org/10.3390/su16229788
APA StyleCai, Z., Du, X., Huang, T., Lv, T., Cai, Z., & Gong, G. (2024). Robotic Edge Intelligence for Energy-Efficient Human–Robot Collaboration. Sustainability, 16(22), 9788. https://doi.org/10.3390/su16229788





