Optimizing Multi-Channel Green Supply Chain Dynamics with Renewable Energy Integration and Emissions Reduction

Abstract

In response to the global imperative of mitigating greenhouse gas emissions (GHGs) and the shifting landscape of business models toward multi-channel structures, this study delves into the intricacies of a green supply chain. Operating through both online and traditional channels with uncertain demands, the producer’s distribution strategy prompts an exploration of supply chain dynamics. Utilizing an integer programming model, this study calculates optimal prices, optimizes total profit, and minimizes transportation costs to curtail carbon dioxide emissions, depending on the transportation mode. Additionally, this study incorporates renewable energy sources into the production and transportation processes to further minimize carbon dioxide emissions. The integration of renewable energy not only supports environmental goals, but also contributes to the overall profitability of the supply chain by reducing energy costs. Employing a theoretical technique for linearization, the model, resolved through the Jimenez and TH methods, demonstrates efficacy in reconciling economic and environmental goals. The Jimenez method enables the transformation of fuzzy parameters into deterministic equivalents, allowing for a more reliable optimization during uncertainty, while the TH method provides an interactive fuzzy multi-objective approach, aligning the model’s dual objectives for both economic and environmental goals. Notably, when transportation costs to both markets are equal, the model prioritizes devices with a lower environmental impact, showcasing adaptability. Furthermore, the proposed solution empowers decision makers to influence pricing and enhance the entire supply chain’s profitability. In conclusion, this research offers nuanced insights, strategically aligning economic viability with environmental sustainability in the discourse on green supply chains.

1. Introduction

This study introduces a novel approach by designing a two-channel green supply chain network, addressing the uncertainties in key parameters. This research combines green supply chain principles with two-channel networks, focusing on a single product, and a two-level supply chain involving factories and distribution centers. Emphasis is placed on the environmental impact of transportation modes between facilities in each channel, directly influencing greenhouse gas emissions. This study also explores the integration of renewable energy into supply chain operations. Renewable energy sources, such as solar and wind power, are leveraged to reduce the carbon footprint of both production and transportation activities, contributing to the sustainability of the supply chain while maintaining cost-effectiveness. Each mode varies in cost, time, and environmental effects. The study comprehensively considers various aspects of supply chain network design, encompassing production, pricing, lost sales, related costs, capacity limitations, and delivery time. A distinctive feature is the incorporation of two sales channels for product distribution. The first channel involves direct delivery from producer to consumer, while the second utilizes an intermediary for final customer delivery. Pricing differentials between channels influence customer demand, causing shifts. Additionally, diverse transportation methods are evaluated for each market, each with unique characteristics in terms of the cost, delivery time, and carbon dioxide emissions. Variances in fixed and variable transportation costs impact the overall cost of product transportation to each market.

This study tackles the urgent need for sustainable practices in supply chains, particularly as global efforts intensify to reduce greenhouse gas emissions. With industries increasingly adopting multi-channel distribution, there is a critical gap in the research on optimizing dual-channel supply chains to meet both economic and environmental objectives. Current models often lack a comprehensive approach that integrates renewable energy and emissions reduction within the supply chain. To bridge this gap, our study introduces a green supply chain model that incorporates renewable energy and minimizes carbon emissions, thereby aligning financial profitability with environmental responsibility. This approach offers a novel solution to address the dual objectives of economic efficiency and sustainability, catering to the evolving needs of modern supply chains.

This paper presents a mixed-integer programming model with dual objectives, aiming to both maximize the profit of the entire supply chain and minimize greenhouse gas emissions. Given the NP-hard nature of the mathematical model, a two-step approach is employed for resolution. Initially, the model is transformed into an equivalent auxiliary deterministic form, followed by the application of an interactive fuzzy multi-objective programming approach in the second stage to render the model single-objective and derive the Pareto optimal solution set. This process results in an equivalent deterministic single-objective model, effectively solved using IBM CPLEX ILOG software (Version 12.7.1). Motivated by the imperative to address the challenges posed by the NP-hard complexity and the growing need to integrate green supply chain design into contemporary markets, this research seeks to establish a harmonious equilibrium between environmental and economic considerations. The proposed multi-objective model not only focuses on profit maximization, but also incorporates environmental factors, specifically greenhouse gas emissions, as crucial objective functions.

This study’s unique contributions include the development of a dual-channel green supply chain model that integrates renewable energy sources, optimizing both profitability and environmental impact. Unlike previous models, this approach addresses uncertainty through a fuzzy multi-objective framework, which not only accounts for emissions reduction, but also adapts dynamically to shifting market conditions and demand patterns. This integration of sustainability into a multi-channel structure represents a significant advancement in green supply chain research, aligning economic and environmental goals effectively.

2. Literature Review

In contemporary times, the exponential expansion of the economy and human endeavors has resulted in an escalated concentration of greenhouse gases (GHGs) in the Earth’s atmosphere, consequently contributing to global warming. In response to the heightened recognition of the adverse impacts of climate change and the imposition of governmental regulations, there is a pronounced emphasis on mitigating the emissions of greenhouse gases, with particular emphasis on carbon dioxide (CO₂)—the predominant greenhouse gas attributed to human activities. The principal origins of greenhouse gas emissions are human activities across diverse economic sectors, encompassing electricity generation, transportation, industrial processes, commercial and residential domains, and agricultural practices. As delineated in the 2021 report by the United States Environmental Protection Agency (EPA), emissions of greenhouse gases (GHGs) originating from both road and non-road transportation are projected to constitute approximately 29% of the aggregate greenhouse gas emissions in the United States. This percentage is notably higher than the annual growth rate observed in the years spanning from 1990 to 2019 within other sectors [1]. Emissions from transportation predominantly stem from the combustion of fossil fuels in various modes, including automobiles, trucks, maritime vessels, trains, and aircrafts. Recent studies highlight the growing role of renewable energy in supply chains. For instance, renewable energy in production and logistics has been shown to significantly lower greenhouse gas emissions, as well as reduce operational costs. The adoption of solar, wind, and other renewable energy sources offers companies an opportunity to achieving both economic and environmental objectives in their supply chains. Numerous nations have implemented regulatory measures, including carbon tax plans, aimed at mitigating carbon emissions throughout the production-to-transportation continuum. Consequently, there exists a paramount imperative to diminish carbon emissions in logistics operations and concurrently enhance energy consumption efficiency [2].

In light of the accelerated progress in information technology within the industrial landscape, there has been a discernible transformation in consumer procurement patterns. Specifically, consumers are increasingly engaging in both direct procurement from manufacturing facilities and indirect procurement through distribution centers. This shift underscores the evolving dynamics of purchasing behavior within the contemporary industrial context [3]. Conversely, there has been a heightened focus among producers on the establishment and optimization of direct distribution channels. This strategic emphasis is exemplified by the fact that 68% of producers of consumer goods have proactively instituted online sales channels. This strategic realignment underscores a concerted effort within the industrial realm to adapt to contemporary market dynamics and leverage digital platforms for enhanced consumer engagement and commerce [4]. Henceforth, there is a discernible imperative to undertake a comprehensive restructuring of the distribution frameworks within the supply chain. It is pertinent to assert that a pivotal facet in the formulation of dual-channel supply chain networks lies in the judicious determination of competitive pricing dynamics between the two distinct distribution channels. This underscores the criticality of strategic decision making in optimizing supply chain configurations to align with contemporary market demands, thus ensuring competitiveness and operational efficiency [5]. Hence, the imperative in industrial engineering lies in competitively attracting consumers through the strategic calibration of optimal pricing structures, expeditious delivery protocols for goods and services, and establishing direct communication channels. Borovička [6] introduced a fuzzy multi-objective mathematical programming model aimed at the environmental optimization of supply chain design in uncertain conditions. The model addresses the simultaneous minimization of environmental impacts, conventional production costs, and accommodates capacity constraints. Notably, a methodology grounded in product life cycle assessment is employed to identify and quantify environmental impacts within this framework. Porkar et al. [7] proposed a stochastic multi-objective, multi-level, and multi-period model addressing the integrated logistics network within an environment marked by uncertainty. The primary objectives encompass profit maximization, minimization of customer response time, and maximization of product quality. Notably, the model incorporates non-deterministic parameters, such as collection and recycling costs, product price, demand rate, and return rate. Yavari et al. [8] developed a multi-product closed-loop supply chain model that concurrently addresses network design and supplier selection. The model is formulated within a dual-objective framework and incorporates a fuzzy environment to enhance its adaptability to uncertain conditions. Hosseini Dehshiri and Amiri [9] undertook a study focusing on the design of a closed-loop, multi-cycle, multi-product supply chain network. The model incorporates environmental and economic objectives while accounting for parameter uncertainties. Furthermore, the design incorporates the concepts of compensable deficiency and discount to enhance the robustness and practicality of the model. Wang et al. [10] introduced a nonlinear mixed integer programming model addressing the cumulative production planning problem within a multi-product, multi-cycle framework in the context of a green supply chain. The model is developed under the assumption of non-deterministic demand. With a primary focus on minimizing total costs, the model incorporates considerations for the interplay between delivery time, transportation costs, and greenhouse gas emissions levels, emphasizing the integration of environmental and economic factors in decision making. Ahmadi Malakot et al. [11] introduced a stochastic mathematical model and a replenishment policy for perishable products within a centralized two-level supply chain. Their model incorporates costs associated with various transportation modes, inventories, environmental impacts, and uncertain demands. Li et al. [12] addressed a green supply chain network design problem that incorporates a carbon trading program for suppliers. The objective is to maximize the overall profit of the supply chain. The formulated model specifies the optimal placement and capacity of facilities, the ideal product flow between these facilities, and the optimal selling price of goods. Wang and Wan [13] introduced a multi-objective, mixed-integer, mathematical model that concurrently aims at maximizing profit and minimizing carbon emissions. The formulated model accounts for the influence of product price and environmental attributes on customer demand, while also addressing uncertainties in the production process. Pathak et al. [14] developed a mathematical model for a two-channel and two-level supply chain comprising a manufacturer and a distributor. The manufacturer employs both a direct online channel and a traditional retail channel for product distribution. The study employs the Stackelberg game analysis to determine the optimal levels of inventory, sales price, and service level for both sales channels. Soleimani et al. [15] investigated a hierarchical pricing system within a dual distribution channel employing the Stackelberg game analysis. The study aimed to determine the optimal prices for the wholesaler, retailer, and direct channel sales price. Nasrollahi et al. [16] developed a mathematical model to analyze pricing factors in a two-channel system for products with a short life cycle. The study explored a closed-loop supply chain, where the original product is distributed through traditional channels, and the reproduced product is sold via an online channel. The research focused on assessing the influence of two critical factors: the customer’s tendency to buy reproduced goods and their preference for direct sales transactions.

Moreover, recent studies have further advanced the discussion on multi-objective optimization in supply chains, particularly in the context of environmental sustainability and uncertainty. Almotairi et al. [17] introduced a performance analysis of a fully intuitionistic, fuzzy, multi-objective, multi-item, solid fractional transportation model, emphasizing the importance of accounting for uncertainties in transportation parameters. Their model not only addresses the complexities of real-world applications, but also showcases the potential for integrating fuzzy decision-making processes within supply chain optimization, which is another significant contribution. El Sayed and Baky [18] explored a multi-choice, fractional, stochastic, multi-objective transportation problem. Their research highlights the relevance of incorporating uncertainty in the coefficients of fractional objective functions, providing a robust framework that can be applied to various real-world transportation scenarios. Ad, El Sayed et al. [19] developed an interactive approach for solving a bi-level, multi-objective supply chain model, focusing on minimizing transportation costs and delivery time under uncertain demand conditions. This study illustrates the practical applicability of interactive methodologies in supply chain management, further reinforcing the significance of addressing uncertainty in decision-making processes. These contributions underscore the ongoing evolution in supply chain design, particularly concerning the integration of sustainability goals alongside traditional economic objectives. Our research builds on these insights by addressing gaps in the existing literature related to dual-channel distribution strategies, environmental considerations, and the optimization of pricing decisions in a comprehensive framework.

This review of the existing literature highlights a shortage of articles in the field of supply chain design that simultaneously address environmental concerns, the integration of dual online and traditional sales channels, and pricing decisions. Prior research has often been reliant on supply chain models containing restrictive assumptions. This article offers unique contributions, each designed to address the existing research gaps relative to prior studies. We consider each of these contributions as the objectives of this research:

• Development of a Fuzzy Multi-Objective Optimization Model for a Dual-Channel Green Supply Chain

This objective emphasizes the novelty of the proposed model, designed to optimize both economic and environmental outcomes while addressing uncertainties in parameter values.

• Introduction of a Multi-Objective Framework to Integrate Economic and Environmental Dimensions

The model provides a balanced approach that supports decision making across both economic and sustainability goals, ensuring alignment with environmental objectives.

• Linearization of the Nonlinear Model to Enable Computational Efficiency

Using precise linearization techniques, the model’s nonlinear components are transformed into an equivalent linear format, facilitating a more efficient computational solution.

• Evaluation of Capacity Constraints and Optimal Allocation of Transport Resources by Route

This objective addresses the practical limitations in transport capacity and vehicle allocation, tailored for each route to enhance operational feasibility.

• Implementation of a Two-Step Solution Method for the Multi-Objective Fuzzy Model

This objective clarifies the use of a structured two-step approach to resolve the fuzzy multi-objective model, balancing computational efficiency with accuracy in decision making.

3. Model Formulation

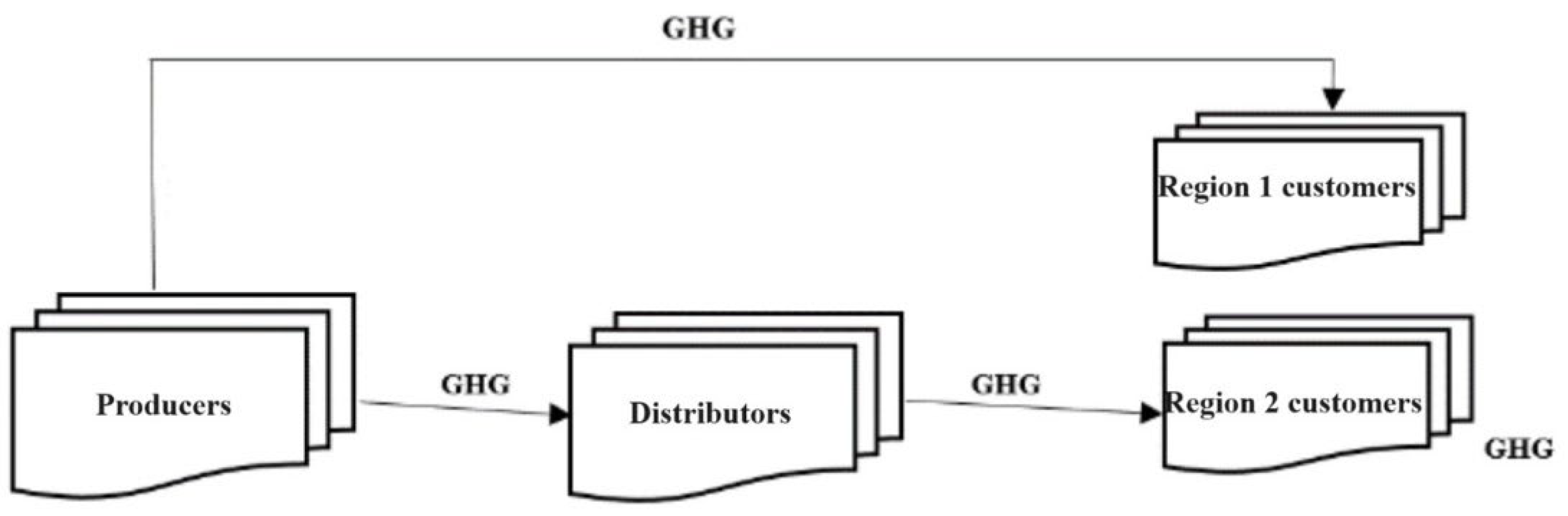
This research introduces a mathematical model for optimizing the design of a two-channel supply chain network, accounting for environmental impacts and parameter uncertainties. The suggested model employs a formulation based on mixed-integer programming, integrating dual objectives to maximize profits and minimize greenhouse gas emissions. The structured supply chain encompasses several manufacturing plants, distributors, a direct channel serving Region 1 customers, and an indirect channel catering to Region 2 customers, as illustrated in Figure 1.

This model is intended to guide strategic decision making in multi-channel green supply chain networks. The dual focus on profitability and environmental sustainability, including emissions reduction and renewable energy integration, underscores its application to long-term planning and optimization. While tactical and operational decisions may be influenced by the outcomes of this model, the primary focus remains on achieving overarching, sustainable goals within a long-term planning horizon.

In Region 1, customers utilize the direct channel (internet) to place orders with factories, employing a singular mode of transportation that results in expedited delivery, but incurs higher pollution levels and increased costs compared to the indirect channel. In a multi-period supply chain scenario, the inventory is consolidated with the primary supplier. Conversely, Region 2 customers engage the traditional channel with a retailer intermediary for order placement in the supply chain. Within this sales channel, goods are dispatched using various transportation modes, each associated with distinct carbon dioxide emissions and fixed and variable transportation costs. The formulated Mixed-Integer Nonlinear Programming (MINLP) model is characterized as single period, single product, and multi-level. The model includes a renewable energy factor (REi) in the production cost and emissions reduction calculations. Renewable energy is assumed to lower production costs and reduce greenhouse gas emissions (GHFis) in comparison to traditional energy sources. The impact of renewable energy on overall supply chain performance is incorporated into both the profit maximization and emissions reduction objectives. The single-round nature of the supply chain leads to the omission of inventory and associated maintenance costs at production and distribution centers. Furthermore, all fixed costs are computed over a single period. This model accounts for uncertainties in the environment, influencing primary customer demand, delivery time to the final customer, and carbon dioxide emissions resulting from product production and transportation.

3.1. Assumptions

The model is predicated on several key assumptions:

• This model uniquely assumes that renewable energy sources (e.g., solar and wind) in production and transportation activities not only reduce carbon emissions, but also contribute to cost-efficiency. Unlike previous models, this approach treats renewable energy integration as a variable factor, allowing the model to dynamically adjust to environmental and operational changes, thus enhancing both economic and environmental objectives within the dual-channel structure.
• The positions of primary customers, factories, and distribution centers are known and remain constant.
• Each producer has the capability to dispatch products to both direct and indirect customers.
• A delivery time constraint is imposed on sending goods to markets for both direct and indirect channels.
• Factories and distribution centers possess a limited capacity for sending goods.
• Deficiency is permissible, and any surplus beyond ordered quantities is considered lost.
• The assumption is made that the entire production during the period is allocated by the factory to the direct market and distribution centers.
• Variations in production costs and greenhouse gas emissions from factories arise due to diverse production technologies.
• Each mode of transport incurs fixed costs for sending and variable costs for each unit of goods dispatched.

3.2. Model Indexes

$i: \mathrm{I}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{x} \mathrm{o}\mathrm{f} \mathrm{c}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{i}\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{e} \mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{s} \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{f}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{o}\mathrm{r}\mathrm{i}\mathrm{e}\mathrm{s}, i=\left\{1, 2, and 3,\dots ., I\right\}$

$j: \mathrm{I}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{x} \mathrm{o}\mathrm{f} \mathrm{c}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{i}\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{e} \mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{s} \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{b}\mathrm{u}\mathrm{t}\mathrm{o}\mathrm{r}\mathrm{s}, j=\left\{1, 2, and 3,\dots ., J\right\}$

$m_1: \mathrm{I}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{x} \mathrm{o}\mathrm{f} \mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{f}\mathrm{i}\mathrm{c} \mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{s} \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{o}\mathrm{n}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e} \mathrm{c}\mathrm{u}\mathrm{s}\mathrm{t}\mathrm{o}\mathrm{m}\mathrm{e}\mathrm{r}\mathrm{s},m_1=\left\{1, 2, and 3,\dots .,M_1\right\}$

$m_2: \mathrm{I}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{x} \mathrm{o}\mathrm{f} \mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{f}\mathrm{i}\mathrm{c} \mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{s} \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{t}\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{a}\mathrm{l} \mathrm{c}\mathrm{u}\mathrm{s}\mathrm{t}\mathrm{o}\mathrm{m}\mathrm{e}\mathrm{r}\mathrm{s},m_2=\left\{1, 2, and 3,\dots .,M_2\right\}$

$n: \mathrm{I}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{x} \mathrm{t}\mathrm{o} \mathrm{i}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{f}\mathrm{y} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{t}\mathrm{y}\mathrm{p}\mathrm{e} \mathrm{o}\mathrm{f} \mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n},n=\left\{1, 2, and 3,\dots ., N\right\}$

3.3. Parameters

$\widetilde{{UD}_1}:Uncertain basic product demand in the market m_1$

$\widetilde{{UD}_2}:Uncertain basic product demand in the market m_2$

${FCF}_i:The fixed cost of setting up the factory i$

${FCD}_j:The fixed cost of setting up the distributor j$

${FCT}_n:The fixed cost of transporting goods by means of transport n$

${VCT}_n:The variable cost of sending goods by means of transport n per unit of distance$

${LV}_n:Product carrying capacity for the n^{th} vehicle$

${CG}_i:The cost of creating a unit of goods in the factory i$

${MF}_i:The maximum capacity of the factory i$

${MD}_j:The maximum capacity of distributor j$

${PL}_{m1}:Penalty for each lost sales unit in the online channel$

${PL}_{m2}:Penalty for each lost sales unit in the triditional channel$

$\widetilde{{DTD}_{j{m}_{2}n}}:Non-deterministic delivery time, from distributor jto indirect$ market m2 through means of transport n

$\widetilde{{DTF}_{i{m}_{1}n}}:Non-deterministic delivery time from factory i to direct market m1 by$ means of transport n

${MDT}_{m1}:Maximum possible delivery time for market m1$

${MDT}_{m2}:Maximum possible delivery time for market m2$

${NFM}_{i{m}_{1}n}^{max}:$ The maximum available number of means of transportation n from factory i to $market m1$

${NFD}_{ijn}^{max}:$ The maximum available number of means of transportation n from factory i to $distribution center j$

${NDM}_{j{m}_{2}n}^{max}:The maximum available number of means of transportationn from the$distributor j to the market m2

$\widetilde{{GHF}_i}:$ Uncertain amount of carbon dioxide emissions for producing each unit of product in $the factory i$

$\widetilde{{GHV}_n}:$ Uncertain amount of carbon dioxide emissions for the n^th means of transport per$unit distance$

${DFD}_{ij}:Distance between factory i and distribution center j$

${DDM}_{j{m}_2}:Distance between distribution center j and market m2$

${DFM}_{i{m}_1}:Distance between factory i and market m1$

$PS:price elasticity of demand$

$\alpha :Substitution degree between two distribution channels (0\le \alpha \le 1)$

$N:A big number$

3.4. Variables

${FL}_i=\left\{\begin{array}{c}1\\ 0\end{array}\right.\begin{array}{c}if an open factory is located in candidate location i\\ Otherwise\end{array}$

$D{L}_j=\left\{\begin{array}{c}1\\ 0\end{array}\right.\begin{array}{c}if a distribution center is placed in candidate location j\\ Otherwise\end{array}$

${TFM}_{i{m}_{1}n}=\left\{\begin{array}{c}1\\ 0\end{array}\right.\begin{array}{c}if there is transportation from factory i to market m1\\ Otherwise\end{array}$

${TDM}_{j{m}_{2}n}=\left\{\begin{array}{c}1\\ 0\end{array}\right.\begin{array}{c}if goods are transported from distributor j to market m2\\ Otherwise\end{array}$

${TFD}_{ijn}=\left\{\begin{array}{c}1\\ 0\end{array}\right.\begin{array}{c}if the shipment is made from factory i to distributor j\\ Otherwise\end{array}$

$D_{m_1}: The amount of customer demand m1 in the direct channel \left(online\right)$

$D_{m_2}: The amount of customer demand m2 in the indirect \left(traditional\right) channel$

${QFD}_{ijn}=$ The amount of goods transported from factory i to distributor j through$the{n}^{th} means of transportation$

${QFM}_{i{m}_{1}n}=$ The amount of goods transported from factory i to market m1 through$the{n}^{th} means of transportation$

${QDM}_{j{m}_{2}n}=$ The amount of goods transported from distributor j to market m2$through the{n}^{th} means of transportation$

$SP{m}_1=Selling price per product unit in the m1 market$

$SP{m}_2=Selling price per product unit in the m2 market$

${NVFD}_{ijn}=The number of means of transportation n from factory i to distributor j$

${NVFM}_{i{m}_{1}n}=Number of means of transportation n from factory i to market m1$

${NVDM}_{j{m}_{2}n}=Number of means of transportation n from distributor j to market m2$

3.5. Objective Functions of the Model

In this section, a conceptual two-objective mathematical programming model is introduced, where two distinct objective functions are delineated, namely economic and environmental considerations. The primary objective function seeks to maximize the aggregate profit within the framework of the supply chain design, encompassing various constituent elements, such as:

Income generated from the sale of products:

$$\sum _{i, m_1, n}SP{m}_1.{QFM}_{i{m}_{1}n}+\sum _{j, m_2, n}SP{m}_2.{QDM}_{j{m}_{2}n}$$

(1)

Fixed cost of setting up factories and distribution centers:

$$\sum _i{FCF}_i.{FL}_i+\sum _j{FCD}_j.{DL}_j$$

(2)

Production cost:

$$\sum _{i, j, n}{CG}_i.{QFD}_{ijn}+\sum _{j, m_1, n}{CG}_i.{QFM}_{i{m}_{1}n}$$

(3)

Fixed cost of transportation:

$$\sum _{i, j, n}{NVFD}_{ijn}.{FCT}_n+\sum _{i, m_1, n}{NVFM}_{i{m}_{1}n}.{FCT}_n+\sum _{j, m_2, n}{NVDM}_{j{m}_{2}n}.{FCT}_n$$

(4)

Variable cost of transportation:

$$\sum _{i, j, n}{NVFD}_{ijn}.{DFD}_{ij}.{VCT}_n+\sum _{i, m_1, n}{NVFM}_{i{m}_{1}n}.{DFM}_{i{m}_1}.{VCT}_n+\sum _{j, m_2, n}{NVDM}_{j{m}_{2}n}.{DDM}_{j{m}_2}.{VCT}_n$$

(5)

Shortage cost (lost sales):

$$\sum _{m_1}{PL}_{m1}\left(D_{m_1}-\sum _{i, n}{QFM}_{i{m}_{1}n}\right)+\sum _{m_2}{PL}_{m2}\left(D_{m_2}-\sum _{j, n}{QDM}_{j{m}_{2}n}\right)$$

(6)

The initial component of the objective function within the context of the problem seeks to optimize the aggregate profit by maximizing the yield derived from the disparity between mathematical expressions 2 through 6 and Equation (1).

Equation (7) constitutes the subsequent component of the model’s objective function, designed to minimize carbon dioxide emissions in the context of production and transportation activities within the supply chain network.

$$\begin{gathered} Min Z_2: \left(\sum _{i, j, m_1, n}\widetilde{{GHF}_i}\left({QFM}_{i{m}_{1}n}+{QFD}_{ijn}\right)+\sum _{i, m_1, n}\widetilde{{GHV}_n}.{DFM}_{i{m}_1}.{NVFM}_{i{m}_{1}n} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\sum _{i, j, n}\widetilde{{GHV}_n}.{DFD}_{ij}.{NVFD}_{ijn}+\sum _{i, m_2, n}\widetilde{{GHV}_n}.{DDM}_{j{m}_2}.{NVDM}_{j{m}_{2}n}\right) \end{gathered}$$

(7)

3.6. Constraints

$$\sum _{i,n}{QFM}_{i{m}_{1}n}\le D_{m_1} \forall m_1$$

(8)

$$\sum _{j, n}{QDM}_{j{m}_{2}n}\le D_{m_2} \forall m_2$$

(9)

$$\sum _{m_2, n}{QDM}_{j{m}_{2}n}\le \sum _{i,n}{QFD}_{ijn} \forall j$$

(10)

$$\sum _{m_1, n}{QFM}_{i{m}_{1}n}+\sum _{i,n}{QFD}_{ijn} \le {MF}_i.{FL}_i \forall i$$

(11)

$$\sum _{i,n}{QFD}_{ijn} \le {MD}_j.D{L}_j \forall j$$

(12)

$$\sum _{i,n}{QFD}_{ijn} \le N.D{L}_j \forall j$$

(13)

$${TFM}_{i{m}_{1}n}.\widetilde{{DTF}_{i{m}_{1}n}} \le {MDT}_{m1} \forall i, m_1, n$$

(14)

$${TDM}_{j{m}_{2}n}.\widetilde{{DTD}_{j{m}_{2}n}} \le {MDT}_{m2} \forall j, m_2, n$$

(15)

$${NVFM}_{i{m}_{1}n} \le {TFM}_{i{m}_{1}n}.{NFM}_{i{m}_{1}n}^{max} \forall i, m_1, n$$

(16)

$${NVFD}_{ijn} \le {TFD}_{ijn}.{NFD}_{ijn}^{max} \forall i, j, n$$

(17)

$${NVDM}_{j{m}_{2}n} \le {TDM}_{j{m}_{2}n}.{NDM}_{j{m}_{2}n}^{max} \forall j, m_2, n$$

(18)

$${\displaystyle \frac{{TFM}_{i{m}_{1}n}}{{NFM}_{i{m}_{1}n}^{max}}} \le {NVFM}_{i{m}_{1}n}\le {TFM}_{i{m}_{1}n}.{NFM}_{i{m}_{1}n}^{max} \forall i, m_1, n$$

(19)

$${\displaystyle \frac{{TFD}_{ijn}}{{NFD}_{ijn}^{max}}} \le {NVFD}_{ijn}\le {TFD}_{ijn}.{NFD}_{ijn}^{max} \forall i, j, n$$

(20)

$${\displaystyle \frac{{TDM}_{j{m}_{2}n}}{{NDM}_{j{m}_{2}n}^{max}}} \le {NVDM}_{j{m}_{2}n}\le {TDM}_{j{m}_{2}n}.{NDM}_{j{m}_{2}n}^{max} \forall j, m_2, n$$

(21)

$${NVFM}_{i{m}_{1}n}-1+{\displaystyle \frac{1}{N}} \le {\displaystyle \frac{{QFM}_{i{m}_{1}n}}{{LV}_n}}\le {NVFM}_{i{m}_{1}n} \forall i, m_1, n$$

(22)

$${NVFD}_{ijn}-1+{\displaystyle \frac{1}{N}} \le {\displaystyle \frac{{QFD}_{ijn}}{{LV}_n}}\le {NVFD}_{ijn} \forall i, j, n$$

(23)

$${NVDM}_{j{m}_{2}n}-1+{\displaystyle \frac{1}{N}} \le {\displaystyle \frac{{QDM}_{j{m}_{2}n}}{{LV}_n}}\le {NVDM}_{j{m}_{2}n} \forall j, m_2, n$$

(24)

$$D_{m_1}=\widetilde{{UD}_1}-{PS}_1. SP{m}_1+{\propto }_{1}SP{m}_2 \forall m_1, m_2$$

(25)

$$D_{m_2}=\widetilde{{UD}_2}-{PS}_2. SP{m}_2+{\propto }_{2}SP{m}_1 \forall m_1, m_2$$

(26)

$${QFD}_{ijn}, {QDM}_{j{m}_{2}n}, {QFM}_{i{m}_{1}n}, SP{m}_1, SP{m}_2\ge 0 \forall i, j, n, m_1, m_2$$

(27)

$${TFD}_{ijn}, {TFM}_{i{m}_{1}n}, {TDM}_{j{m}_{2}n}, {FL}_i,D{L}_j \in \left\{0, 1\right\} \forall i, j, n, m_1, m_2$$

(28)

Constraints (8) and (9) pertain to the fulfillment of customer demand across both direct and indirect sales channels, acknowledging the potential for lost sales in either avenue. Constraint (10) ensures that the flow of output from distributors to the second market remains below the input flow to the distributor, while Constraint (11) posits that the aggregate output from factories does not surpass the production capacity, contingent upon the factory being operational. Constraint (12) guarantees that the total input flow to distributors does not exceed their capacity, contingent upon the distributor facility being operational. Additionally, Constraint (13) ensures the conveyance of products from the factory to the distributor only when the distribution center is operational.

Restrictions (14) and (15) delineate temporal constraints governing the delivery of products to markets. Constraints (16) to (21) prescribe limitations on the available means of transportation between facilities and their utilization for shipments. Restrictions (22) to (24) elucidate the interplay between the number of utilized transportation means and their carrying capacity, affirming that the chosen transportation quantity aligns with the volume of goods dispatched between facilities.

Constraint (25) embodies the customer demand function in the direct channel, while Constraint (26) characterizes the demand function in the indirect channel. In the context of two-channel distribution networks, the demand for each channel is contingent upon the pricing of both channels. The parameters ${PS}_1$ and ${PS}_2$ denote the price elasticity of demand in the direct and indirect channels, respectively, with the assumption that ${PS}_1$ > ${PS}_2$. Parameters ${\propto }_1$ and ${\propto }_2$ signify the price sensitivity of each distribution channel to the product price in the other channel, reflecting the magnitude of demand shift between channels. The hypothesis PS> $\alpha$ posits that an increase in the unit price results in more customers discontinuing purchases in one distribution channel compared to those migrating to the opposing channel due to the price escalation. The non-deterministic parameters $\widetilde{{UD}_1} and \widetilde{{UD}_2}$ signify the market size for products in both the direct and indirect markets.

Constraints (27) and (28) delineate the permissible range for decision variables in the given context.

3.7. Linearization

Equation (1) denotes the multiplication of an integer variable and a continuous variable, introducing nonlinearity to the model. In order to achieve linearization of the model, the variables ${QFM}_{i{m}_{1}n}$ and ${QDM}_{j{m}_{2}n}$ are reformulated through the representation of a set of zero and one binary variables, facilitated by relationships (29) to (31).

$${QFM}_{i{m}_{1}n}=\sum _{h=0}^{r-1}{2}^h{y}_h+(UL-2^r+1)y_r$$

(29)

$$Q<UL$$

(30)

$$2^r<UL<2^{r+1}$$

(31)

In the formulation, the variables $y_{hi{m}_{1}n}$ (for h = 0, …, r − 1) and $y_r$ (for h = r) represent binary variables, assuming values of zero or one. The variable UL denotes the upper limit pertaining to the quantity of goods transported to each market. In the current model, UL is equivalent to the demand quantity for both the direct and indirect markets. Through the implementation of the aforementioned modifications, the initial term of the nonlinear expression (1) is reconfigured and expressed as Equation (32).

$$\sum _{h=0}^{r-1}{2}^h.SP{m}_1.y_{hi{m}_{1}n}+\left(UL-2^r+1\right).SP{m}_1.y_r$$

(32)

Equation (32) presents the multiplication of a binary variable by a continuous variable, thus retaining its inherent nonlinearity. Consequently, an assumption is posited:

$${USP}_{hi{m}_{1}n}=SP{m}_1.y_{hi{m}_{1}n}$$

(33)

Ultimately, through the implementation of the aforementioned modifications, Equation (1) within the objective function, f1, is reformulated as follows:

$$\begin{gathered} \sum _h^{r-1}\sum _{i,m_1,n}{2}^h.{USP}_{hi{m}_{1}n} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\sum _{i,m_1,n}\left(UL-2^r+1\right).{USP}_{hi{m}_{1}n} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +\sum _h^{r-1}\sum _{j,m_2,n}{2}^h.{USP}_{hj{m}_{2}n}+\sum _{j,m_2,n}\left(UL-2^r+1\right).{USP}_{hj{m}_{2}n} \end{gathered}$$

(34)

Subsequently, the ensuing equations are incorporated into the constraints of the model:

$${QFM}_{i{m}_{1}n}={\sum }_{h=0}^{r-1}{2}^h{y}_{hi{m}_{1}n}+({UL}_{m_1}-2^r+1)y_{ri{m}_{1}n} \forall i, m_1, n$$

(35)

$$SP{m}_1-\left[\left(1-y_{hi{m}_{1}n}\right)N\right]\le {USP}_{hi{m}_{1}n}\le SP{m}_1 \forall h, i, m_1, n$$

(36)

$${USP}_{hi{m}_{1}n}\le y_{hi{m}_{1}n}.N \forall h, i, m_1, n$$

(37)

$${QDM}_{j{m}_{2}n}={\sum }_{h=0}^{r-1}{2}^h{y}_{hj{m}_{2}n}+({UL}_{m_2}-2^r+1)y_{rj{m}_{2}n} \forall j, m_2, n$$

(38)

$$SP{m}_2-\left[\left(1-y_{rj{m}_{2}n}\right)N\right]\le {USP}_{hj{m}_{2}n}\le SP{m}_2 \forall h,j, m_2, n$$

(39)

$${USP}_{hj{m}_{2}n}\le y_{rj{m}_{2}n}.N \forall h,j, m_2, n$$

(40)

4. Methodology

To address the presented fuzzy multi-objective model, characterized by imprecise coefficients within both the objective function and constraints, a two-stage solution methodology is employed. During the initial phase, a transformation of the primary model into an equivalent auxiliary deterministic model is executed. This procedure employs a fusion of methodologies previously utilized by researchers in [20,21]. The methodology leverages robust mathematical constructs, such as “expectation interval” and “expectation value”, thereby ensuring computational efficiency. Notably, this approach preserves linearity and avoids augmenting the count of objective functions and inequality constraints.

In the subsequent stage, the interactive, fuzzy, multi-objective programming approach, denoted as the TH method and introduced by Torabi and Hassini [22], is implemented. The proposed methodology incorporates renewable energy in production and transportation, adjusting the model to reflect the associated reduction in both energy costs and carbon emissions. The model quantifies the cost savings and environmental benefits achieved through the use of renewable energy, adding an additional layer of optimization in the pursuit of a sustainable supply chain. This method facilitates the conversion of the single-objective model and facilitates the derivation of the set of Pareto optimal solutions.

4.1. Equivalent Deterministic Model

The approach presented by Jiménez et al. [20] focuses on elucidating the concepts of the “expected interval” (EI) and the “expected value” (EV) for a fuzzy number. Equation (41) explicitly outlines the membership function of the triangular fuzzy number, $\tilde{\omega }$:

$${\theta }_{\tilde{\omega }\left(x\right)}=\left\{\begin{array}{c}{f}_{\omega }\left(x\right)={\displaystyle \frac{x-{\omega }^w}{{\omega }^o-{\omega }^w}} if {\omega }^w\le x\le {\omega }^o\\ \begin{array}{c}1 if x={\omega }^o\\ \begin{array}{c}{g}_{\omega }\left(x\right)={\displaystyle \frac{{\omega }^t-x}{{\omega }^t-{\omega }^o}} if {\omega }^w\le x\le {\omega }^o\\ 0 if x\le {\omega }^w or x\ge {\omega }^t\end{array}\end{array}\end{array}\right.$$

(41)

As outlined in the work by Jiménez and collaborators [20], the articulation of EI and the anticipated value, EV, for a fuzzy number is presented as follows:

$$EI\left(\tilde{\omega }\right)=\left[E_1^{\omega }, E_2^{\omega }\right]=\left[{\int }_0^1{f}_{\omega }^{-1}\left(x\right)dx,{\int }_0^1{g}_{\omega }^{-1}\left(x\right)dx \right]=\left[{\displaystyle \frac{1}{2}}\left({\omega }^w+{\omega }^o\right),{\displaystyle \frac{1}{2}}\left({\omega }^o+{\omega }^t\right) \right]$$

(42)

$$EV\left(\tilde{\omega }\right)={\displaystyle \frac{E_1^{\omega }+E_2^{\omega }}{2}}={\displaystyle \frac{{\omega }^w+2{\omega }^o+{\omega }^t}{2}}$$

(43)

For two given fuzzy numbers, denoted as $\tilde{a}$ and $\tilde{b}$, the quantification of the degree of membership of $\tilde{a}$ surpassing $\tilde{b}$ is explicated as follows:

$${\theta }_N\left(\tilde{a}, \tilde{b}\right)=\left\{\begin{array}{c}0 if E_2^a-E_1^b<0\\ {\displaystyle \frac{E_2^a-E_1^b}{E_2^a-E_1^b-(E_1^a-E_2^b)}} if 0\ni \left[E_1^a-E_2^b,E_2^a-E_1^b \right]\\ 1 if E_1^a-E_2^b>0\end{array}\right.$$

(44)

When the value of ${\theta }_N\left(\tilde{a}, \tilde{b}\right)\ge \beta$, the assertion is made that $\tilde{a}$ is greater than or equal to $\tilde{b}$ by at least the degree represented by $\beta$, as illustrated by the representation ${\tilde{a}}_{\beta }\ge \tilde{b}$.

For any given pair of fuzzy numbers, denoted as $\tilde{a}$ and $\tilde{b}$, it is posited that $\tilde{a}$ relating to $\tilde{b}$ is equivalent to the probability denoted as $\beta$ if the following relationships concurrently hold:

$${\tilde{a}}_{{\displaystyle \raisebox{1ex}{$\beta $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\ge \tilde{b} and {\tilde{a}}_{{\displaystyle \raisebox{1ex}{$\beta $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\le \tilde{b}$$

(45)

Equation (45) is synonymous with Equation (46).

$${\displaystyle \frac{\beta }{2}}\le {\theta }_N\left(\tilde{a}, \tilde{b}\right)\le 1-{\displaystyle \frac{\beta }{2}}$$

(46)

Utilizing the defined concepts of EI and EV within the context of fuzzy numbers, we systematically formulate the auxiliary deterministic model aligned with the proposed two-channel green supply chain network design model as follows:

$$\begin{gathered} Min Z_2: \left(\sum _{i, j, m_1, n}\left({\displaystyle \frac{{GHF}_i^{\omega }+{2GHF}_i^o+{GHF}_i^t}{4}}\right)\left({QFM}_{i{m}_{1}n}+{QFD}_{ijn}\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\sum _{i, m_1, n}\left({\displaystyle \frac{{GHV}_i^{\omega }+{2GHV}_i^o+{GHV}_i^t}{4}}\right).{DFM}_{i{m}_1}.{NVFM}_{i{m}_{1}n} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\sum _{i, j, n}\left({\displaystyle \frac{{GHV}_i^{\omega }+{2GHV}_i^o+{GHV}_i^t}{4}}\right).{DFD}_{ij}.{NVFD}_{ijn} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\sum _{i, m_2, n}\left({\displaystyle \frac{{GHV}_i^{\omega }+{2GHV}_i^o+{GHV}_i^t}{4}}\right).{DDM}_{j{m}_2}.{NVDM}_{j{m}_{2}n}\right) \end{gathered}$$

(47)

S.t.

$$\left[\left({\displaystyle \frac{\beta }{2}}\right){\displaystyle \frac{{UD}_1^t+{UD}_1^o}{2}}+\left(1-{\displaystyle \frac{\beta }{2}}\right){\displaystyle \frac{{UD}_1^{\omega }+{UD}_1^o}{2}}\right]-\left({PS}_1·SP{m}_1+{\alpha }_1.SP{m}_2\right)\le D_{m_1} \forall m_1, m_2$$

(48)

$$\left[\left(1-{\displaystyle \frac{\beta }{2}}\right){\displaystyle \frac{{UD}_1^t+{UD}_1^o}{2}}+\left({\displaystyle \frac{\beta }{2}}\right){\displaystyle \frac{{UD}_1^{\omega }+{UD}_1^o}{2}}\right]-\left({PS}_1·SP{m}_1+{\alpha }_1.SP{m}_2\right)\ge D_{m_1} \forall m_1, m_2$$

(49)

$$\left[\left({\displaystyle \frac{\beta }{2}}\right){\displaystyle \frac{{UD}_2^t+{UD}_2^o}{2}}+\left(1-{\displaystyle \frac{\beta }{2}}\right){\displaystyle \frac{{UD}_2^{\omega }+{UD}_2^o}{2}}\right]-\left({PS}_2·SP{m}_2+{\alpha }_2.SP{m}_1\right)\le D_{m_2} \forall m_1, m_2$$

(50)

$$\left[\left(1-{\displaystyle \frac{\beta }{2}}\right){\displaystyle \frac{{UD}_2^t+{UD}_2^o}{2}}+\left({\displaystyle \frac{\beta }{2}}\right){\displaystyle \frac{{UD}_2^{\omega }+{UD}_2^o}{2}}\right]-\left({PS}_2·SP{m}_2+{\alpha }_2.SP{m}_1\right)\ge D_{m_2} \forall m_1, m_2$$

(51)

$$\left[\left(\beta \right){\displaystyle \frac{{DFD}_{j{m}_{2}n}^o+{DFD}_{j{m}_{2}n}^t}{2}}+\left(1-\beta \right){\displaystyle \frac{{DFD}_{j{m}_{2}n}^{\omega }+{DFD}_{j{m}_{2}n}^o}{2}}\right]{TDM}_{j{m}_{2}n}\le {MDT}_{m2} \forall j, m_2,n$$

(52)

$$\left[\left(\beta \right){\displaystyle \frac{{DFD}_{j{m}_{1}n}^o+{DFD}_{j{m}_{1}n}^t}{2}}+\left(1-\beta \right){\displaystyle \frac{{DFD}_{j{m}_{1}n}^{\omega }+{DFD}_{j{m}_{1}n}^o}{2}}\right]{TDM}_{j{m}_{2}n}\le {MDT}_{m1} \forall i, m_1,n$$

(53)

The formulated mathematical expressions are correspondingly synonymous with the fuzzy objective function denoted as (7) and the fuzzy constraints specified by (14), (15), (25), and (26).

4.2. Fuzzy Solution Approach

In the prescribed methodology for addressing the non-deterministic and multi-objective mathematical model, a dual-stage solution strategy amalgamating the programming elucidated in the antecedent section and the TH method is employed. A key merit of this approach lies in its heightened adaptability, affording the capacity to quantify and modulate the level of goal satisfaction in accordance with the preferences of the decision maker. In the antecedent section, we derived an equivalent deterministic auxiliary model. In this phase, the multi-objective deterministic model undergoes a transformation into a singular-objective model predicated on the priorities set forth by the decision maker. The procedural sequence of this method is delineated as follows:

First Step: Ascertaining the triangular distributions corresponding to the fuzzy parameters inherent in the problem and articulating the multi-objective complex integer linear programming model.

Second Step: Converting the fuzzy objective functions into deterministic objective functions through the application of the expected value methodology based on imprecise parameters.

Third Step: Establishing the value of α and de-fuzzifying the constraints, thereby formulating the equivalent auxiliary deterministic model.

Step Four: Identifying the β-positive ideal solution (β-PIS) and β-negative ideal solution (β-NIS) for every objective function within a β-feasible level.

Fifth Step: Ascertaining the linear membership function associated with each objective function, as articulated by Equations (54) and (55) delineating the functional expressions for the respective objectives.

$${\theta }_1\left(x\right)=\left\{\begin{array}{c}1 if z_1<z_1^{\beta -PIS}\\ {\displaystyle \frac{z_1^{\beta -NIS}-z_1}{z_1^{\beta -NIS}-z_1^{\beta -PIS}}} if z_1^{\beta -PIS}\le z_1\le z_1^{\beta -NIS}\\ 0 if z_1>z_1^{\beta -NIS}\end{array}\right.$$

(54)

$${\theta }_2\left(x\right)=\left\{\begin{array}{c}1 if z_2<z_2^{\beta -PIS}\\ {\displaystyle \frac{z_2^{\beta -NIS}-z_2}{z_2^{\beta -NIS}-z_2^{\beta -PIS}}} if z_2^{\beta -PIS}\le z_2\le z_2^{\beta -NIS}\\ 0 if z_2>z_2^{\beta -NIS}\end{array}\right.$$

(55)

Sixth Step: Converting the multi-objective deterministic complex integer linear model into a singular-objective model through the application of the Torabi and Hassini cumulative function, as expounded in reference [22].

$$\max \delta \left(x\right)=\gamma {\delta }_0+(1-\gamma ){\sum }_r{\phi }_r{\theta }_r\left(x\right)$$

(56)

S.t.

$${\delta }_0<{\theta }_r\left(x\right), r=\mathrm{1,2}$$

(57)

$$x\in F\left(x\right), {\delta }_0 and \delta \in \left[\mathrm{0,1}\right]$$

(58)

This ensures that F(x) constitutes the feasible region encompassing the variables inherent in the equivalent deterministic model, with ${\theta }_r\left(x\right)$ serving as the parameter denoting the degree of satisfaction for the r^th objective function. ${\phi }_{r }$ and $\gamma$ play pivotal roles in delineating the significance attributed to the r^th objective function and determining the compensation coefficient, respectively.

Seventh Step: Identifying the values of γ and ${\phi }_{r }$, and subsequently solving the associated single-objective complex integer linear programming model. Should the decision maker find the current solution satisfactory, the solution process concludes; otherwise, proceed to Step 3 to obtain an alternative solution.

5. Verification of the Model and Analysis of Scenarios

In this section, the proposed model and solution method are validated through a numerical test using IBM ILOG CPLEX Optimization Studio software (Version 12.7.1). Triangular fuzzy numbers are generated by randomly generating the most probable value of each ${\omega }^o$ parameter using

Table 1. Source of random generation of datasets.

Parameter	Random Distribution of Data	Parameter	Random Distribution of Data
${\mathit{U}\mathit{D}}_1$	$U\left(\mathrm{360,400}\right)$	${DTF}_{i{m}_{1}n}$	$U\left(\mathrm{24,35}\right)$
${\mathit{U}\mathit{D}}_2$	$U\left(\mathrm{360,400}\right)$	${DTD}_{j{m}_{2}n}$	$U\left(\mathrm{36,48}\right)$
${\mathit{F}\mathit{C}\mathit{F}}_{\mathit{i}}$	$U\left(\mathrm{80,000,90,000}\right)$	${MDT}_{m1}$	$U\left(\mathrm{30,33}\right)$
${\mathit{F}\mathit{C}\mathit{D}}_{\mathit{j}}$	$U\left(\mathrm{60,000,70,000}\right)$	${MDT}_{m2}$	$U\left(\mathrm{40,45}\right)$
${\mathit{C}\mathit{G}}_{\mathit{i}}$	$U\left(\mathrm{200,205}\right)$	${GHF}_i$	$U\left(\mathrm{4.5,5}\right)$
${\mathit{F}\mathit{C}\mathit{T}}_{\mathit{n}}$	$U\left(\mathrm{70,90}\right)$	${GHV}_n$	$U\left(\mathrm{0.6,2.3}\right)$
${\mathit{V}\mathit{C}\mathit{T}}_{\mathit{n}}$	$U\left(\mathrm{0.02,0.05}\right)$	${LV}_n$	$U\left(\mathrm{30,50}\right)$
${\mathit{M}\mathit{F}}_{\mathit{i}}$	$U\left(\mathrm{200,250}\right)$	${NFM}_{i{m}_{1}n}^{max}$	$U\left(\mathrm{5,8}\right)$
${\mathit{M}\mathit{D}}_{\mathit{j}}$	$U\left(\mathrm{100,110}\right)$	${NFD}_{ijn}^{max}$	$U\left(\mathrm{5,8}\right)$
${\mathit{P}\mathit{L}}_{\mathit{m}1}$	$U\left(\mathrm{50,90}\right)$	${NDM}_{j{m}_{2}n}^{max}$	$U\left(\mathrm{5,8}\right)$
${\mathit{P}\mathit{L}}_{\mathit{m}2}$	$U\left(\mathrm{50,75}\right)$

. Subsequently, utilizing a uniform distribution of two random numbers $\left(h_1, h_2\right)$ within the range of 0.2 to 0.8, optimal pessimistic (${\omega }^w$) and optimistic (${\omega }^t$) values of the fuzzy number are computed based on the provided relations.

The evaluation of model performance is based on two principal criteria: economic performance, quantified by total profit maximization, and environmental performance, quantified by the reduction in carbon emissions. These criteria support a balanced assessment of the model’s dual objectives. Additionally, a sensitivity analysis was performed to examine how fluctuations in pricing and demand impact these criteria, offering further insights into the model’s stability and effectiveness across various scenarios.

$${\omega }^t=\left(1+h_1\right){\omega }^o$$

(59)

$${\omega }^w=\left(1-h_2\right){\omega }^o$$

(60)

To estimate the parameters of $\widetilde{{GHF}_i}$ and $\widetilde{{GHV}_n}$,

Table 2. Emissions levels of greenhouse gases for different vehicles [1].

	Vehicle Type	Weight of Cargo [tons]	Travel Distance [kilometers]	Transportation Effort [ton-kilometers]	CO2 [kg]	Source
1	Petrol van	5	12,000	60,000	19,320	[1]
2	Diesel van	5	12,000	60,000	62,100	[1]
3	Compact truck	5	12,000	60,000	15,120	[1]
4	Intermediate truck	5	12,000	60,000	10,620	[1]
5	Large truck	5	12,000	60,000	7440	[1]
6	Urban trailer	5	12,000	60,000	7380	[1]
7	Standard trailer	5	12,000	60,000	4440	[1]
8	Semi-trailer	5	12,000	60,000	3780	[1]
9	Mega-trailer	5	12,000	60,000	3480	[1]

Note: The CO₂ emissions values provided in this table are sourced from the “EPA Report, 2021” and represent estimated emissions based on average fuel consumption and emissions rates for each vehicle type. The emissions levels are calculated by considering standard transportation distances and weights. The payload capacities listed are based on standardized truck size classifications, reflecting typical values within the industry for each vehicle type. These standardized capacities ensure consistency in emissions calculations and align with industry practices for vehicle classifications.

is utilized. This table provides information on greenhouse gas emissions levels for various types of road transportation, considering both their carrying capacity and per-unit distance.

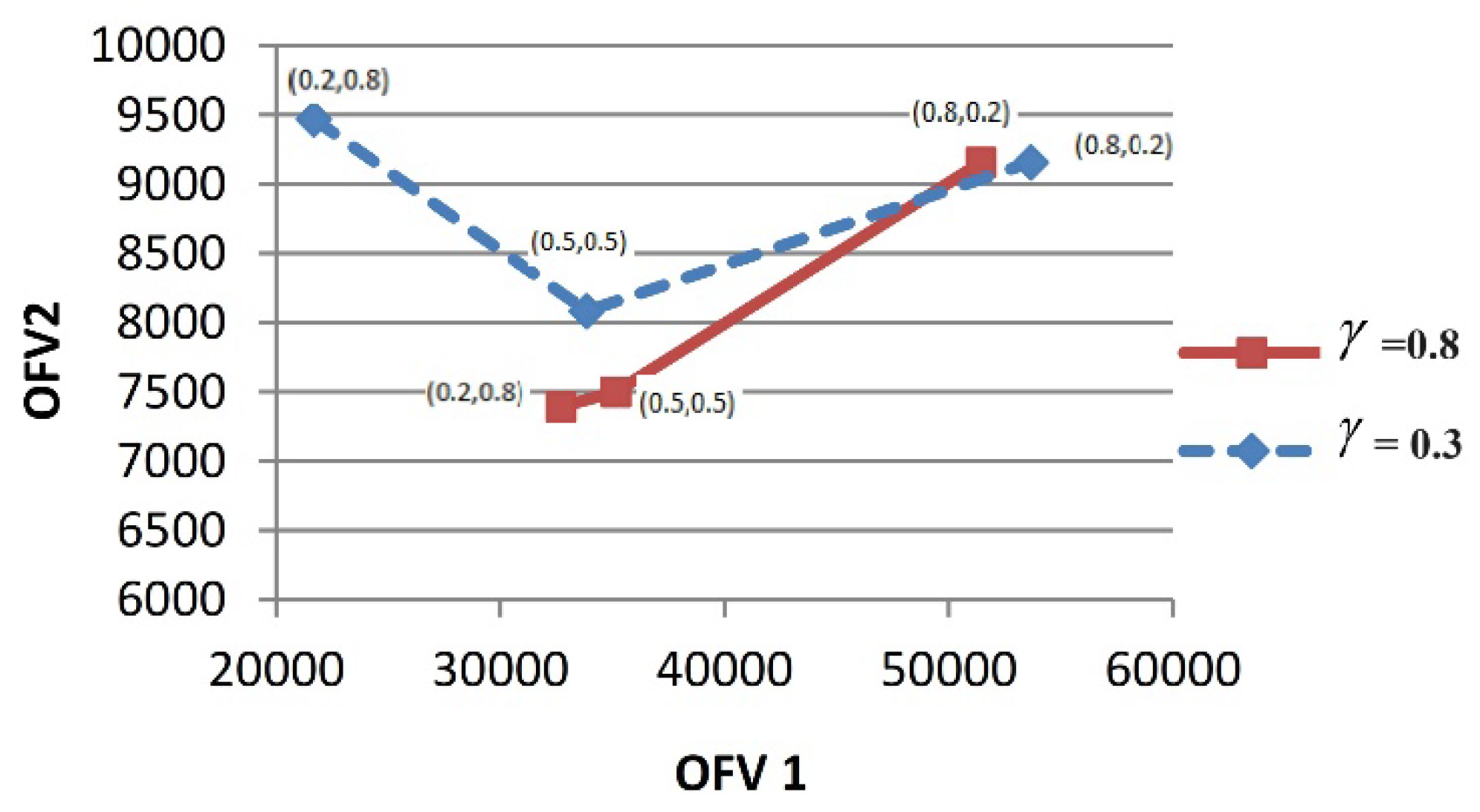
Given the elevated relative importance assigned to the first objective function, we established the values $\left({\phi }_1, {\phi }_2\right)$ as (0.3, 0.7) to address the sample problem. In pursuit of unbalanced solutions with a heightened satisfaction degree level for the first objective function, the parameter γ is set to 0.4.

Table 3. The numerical outcomes of the objective functions within the specified scenario.

$\left({\mathit{\phi }}_1, {\mathit{\phi }}_2\right)=\left(0.7,0.3\right), \mathsf{\gamma }=0.4, \mathsf{\beta }=0.9$
Objective Functions	Components of Objective Functions	Components Value	Objective Function Values	Degree of Satisfaction $\left({\mathit{\theta }}_{\mathit{r}}\left(\mathit{x}\right)\right)$
${\mathit{z}}_1$	Revenue from product sales	409,190	50,717	0.872
	Fixed cost of setting up facilities	307,720
	Production cost	49,400
	Transportation’s constant expense	1290
	Transportation’s fluctuating expenses	59.46
	Cost of deficiency	0
${\mathit{z}}_2$	Co2 emissions	8073.9	8073.9	0.529

presents the values of the objective functions’ components and their respective degrees of satisfaction in the TH method, following the resolution of the sample problem with the parameters outlined in Table 1.

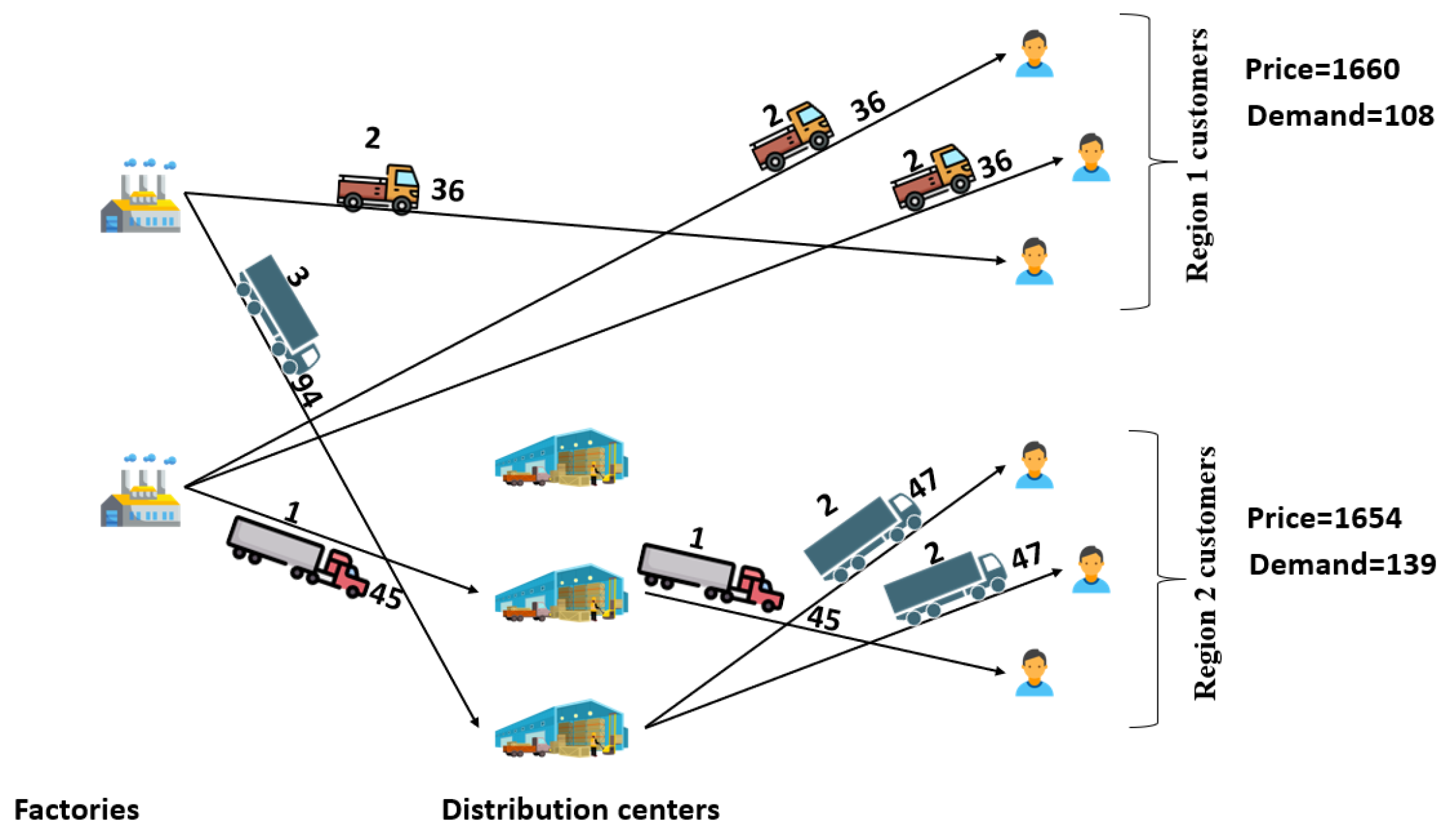
The decision variables for the problem encompass the demand associated with both direct and indirect markets, the pricing of the product in each market, the variable representing the flow of goods among the supply chain facilities, and the quantity and type of transportation means employed for goods transportation, as illustrated in Figure 2.

In assessing the pricing strategy for distribution channels, careful consideration is given to both the price sensitivity of customer demand (PS) and the degree of substitution among distribution channels (α), particularly within the larger direct distribution channel denoted as (α₁, α₂ = (0.3, 0.2) and as (PS₁, PS₂) = (0.5, 0.4).

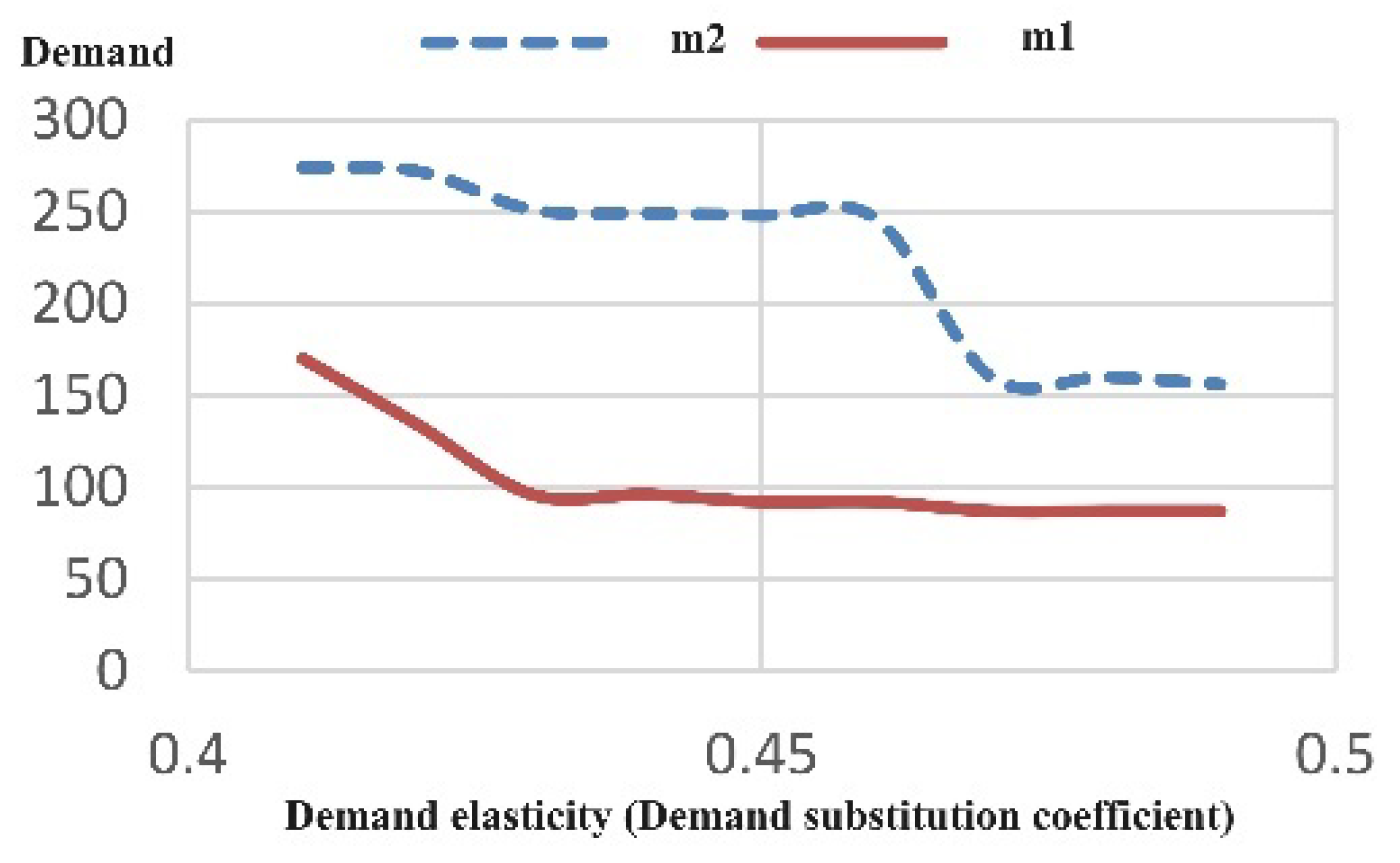
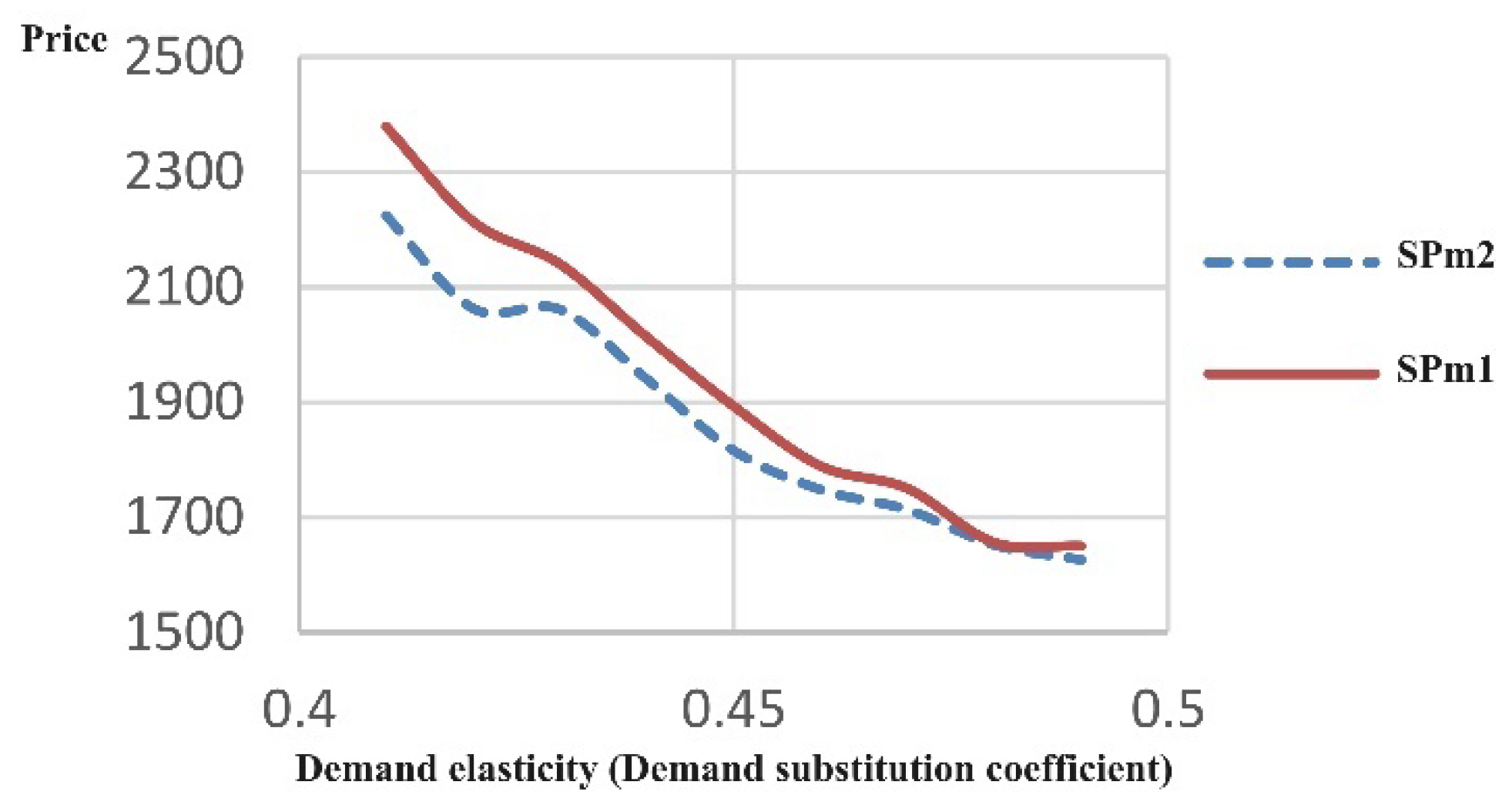
The direct distribution channel exhibits a noticeable disparity in the quantity of demand and dispatched goods when compared to the traditional channel. Additionally, in the resolved sample problem, the model takes into account the higher level of CO₂ emissions associated with transportation vehicles employed in the direct market, owing to the specific vehicle type selected. Consequently, the model exhibits a preference for dispatching fewer goods to the initial market, thereby determining optimal prices within the respective channels. As the demand for each channel is contingent on the pricing of both channels, disparities in prices between the two channels can prompt shifts in customer demands between them. The heightened sensitivity of demand to pricing within the direct channel results in a more pronounced impact on the demand from online customers.

The quantitative and categorical attributes of the transportation fleet employed are systematically documented within

Table 4. The variable values denoting the quantity and classification of vehicles as derived from the model’s output.

		Distribution Centers			Direct Channel Customers (m1)			Indirect Channel Customers (m2)
		1	2	3	1	2	3	1	2	3
Factories	1	0	0	3-2	0	0	2-1	0	0	0
	2	0	1-3	0	2-1	2-1	0	0	0	0
Distribution centers	1	0	0	0	0	0	0	0	0	0
	2	0	0	0	0	0	0	0	0	1-3
	3	0	0	0	0	0	0	2-2	2-2	0

. Each cell in the table is structured to denote the pertinent details, where the initial numerical value signifies the count of transportation vehicles, while the subsequent numerical entry designates the specific type of vehicle. To illustrate, the notation “2-3” conveys that products originating from Manufacturer 1 have been transported to Distribution Center 3, utilizing three distinct transportation vehicles of type 2.

In the envisaged scenario, the selection of transportation modalities has been meticulously orchestrated to facilitate the conveyance of goods to the direct market through vehicles characterized by diminished capacity and reduced transportation costs. Additionally, incorporating renewable energy into production processes, such as solar or wind energy, further reduces operational costs and carbon dioxide emissions. This shift to renewable energy demonstrates a significant impact in lowering the overall environmental footprint of the supply chain, while maintaining cost-effectiveness. Through a comprehensive analysis, encompassing the computation of fixed and variable transportation costs alongside the quantification of goods dispatched to respective markets, the per-unit transportation cost for goods destined for the direct market is determined to be 4.12 units, while that for the indirect market stands at 6.5 units.

Concurrently, the emissions of carbon dioxide (CO₂) attributable to the utilized transportation means within the distribution channel surpass those associated with the conventional channel. Notwithstanding the aforementioned conditions, the volume of goods dispatched to the indirect sales market, as revealed in the output of the sample problem, exceeds that directed to the online market.

To elucidate the influence of individual cost factors and transportation expenses on the demand generated by each market, an additional illustrative problem has been formulated under the premise of equivalent transportation costs for goods in both markets. The ensuing outcomes are systematically presented in

Table 5. The output of scenario 2 in the case of equal transportation costs.

$\left({\mathit{\phi }}_1, {\mathit{\phi }}_2\right)=\left(\mathrm{0.7,0.3}\right), \mathsf{\gamma }=0.4, \mathsf{\beta }=0.9$
Direct distribution channel	Demand	29-30-29
	Price	1653
Indirect distribution channel	Demand	53-55-53
	Price	1642
Objective function values	$z_1$	50,742
	$z_2$	8088.5
The degree of contentment derived from achieving the objective function	${\theta }_1$	0.919
	${\theta }_2$	0.140

for comprehensive analysis and scrutiny.

The outcomes delineated in Table 5 reveal a discernible trend, where the escalation of transportation costs within the direct distribution channel precipitates a concomitant reduction in the demand observed within this particular channel, as juxtaposed against the baseline scenario. The discernible variance in demand between the first and second markets is primarily attributable to the elevated level of equipment wastage linked to transportation in the direct distribution channel. This elucidative scenario underscores that, in instances where transportation costs are equitably distributed for the dispatch of goods to both markets, there is a predilection toward the utilization of transportation means characterized by lower carbon dioxide emissions. Consequently, a discernible reduction in the quantity dispatched to the first market, in comparison to the initial scenario, is evident. The augmentation in demand disparity between the two channels is also reflected in the discernible optimal price differential.

6. Sensitivity Analysis

In this segment, an examination of the sensitivity of the objective functions to variations in the coefficients associated with the price–demand relationship and the cumulative function TH is undertaken. The ensuing results are comprehensively documented, encompassing the values of the objective functions, their respective levels of satisfaction, and the pertinent variables associated with both price and demand.

The assessment seeks to shed light on the impact of alterations in the specified coefficients on the overall optimization objectives. Through a systematic analysis, the sensitivity analysis elucidates the degree to which changes in these coefficients influence the effectiveness and performance of the model, providing valuable insights into the robustness and reliability of the established optimization framework. The reported outcomes provide a nuanced understanding of the interplay between key parameters and the achievement of optimal solutions within the industrial engineering context under consideration.

6.1. Sensitivity Analysis of Price–Demand Parameters in Modeling

Leveraging the dimensions and parameters elucidated in the preceding section, a rigorous sensitivity analysis is performed of the PS and $\alpha$ parameters.

Initially, a systematic exploration involving varied values of parameter $\alpha$ has been conducted, culminating in the determination and documentation of optimal values for $SP{m}_1$, $SP{m}_2$, $D_{m_1}$, and $D_{m_2}$, along with the corresponding outcomes for objective functions and the respective degrees of satisfaction of the defined objectives. These comprehensive findings are systematically presented in

Table 6. Optimal decision variable values and objective function assessment in sensitivity analysis of the PS parameter.

PS	${\mathit{D}}_{{\mathit{m}}_1}$	${\mathit{D}}_{{\mathit{m}}_2}$	$\mathit{S}\mathit{P}{\mathit{m}}_1$	$\mathit{S}\mathit{P}{\mathit{m}}_2$	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{\theta }}_1$	${\mathit{\theta }}_2$
0.21	108	139	1749	1712	72,656	8084.1	0.998	0.534
0.22	134	206	1801	1742	73,843	8149.1	0.706	0.532
0.23	135	212	1901	1807	120,880	8166.6	0.818	0.530
0.24	135	212	2012	1921	160,140	8167.3	0.831	0.530
0.25	136	212	2147	2056	207,050	8168.9	0.852	0.537
0.26	136	212	2297	2207	259,370	8168.9	0.880	0.536
0.27	143	259	2386	2217	318,190	8214.1	0.817	0.533
0.28	144	264	2635	2451	334,970	8296.3	0.715	0.652
0.29	146	298	2875	2691	417,150	8359.1	0.705	0.670
0.41	170	274	2379	2224	320,800	8217.9	0.833	0.534
0.42	134	272	2214	2063	248,250	8215.6	0.823	0.524
0.43	96	251	2140	2061	199,170	8187.7	0.822	0.535
0.44	96	249	2013	1940	150,110	8170.2	0.778	0.531
0.45	92	248	1893	1816	122,730	8145.0	0.831	0.531
0.46	92	246	1789	1748	87,304	8114.4	0.796	0.531
0.47	87	160	1750	1713	69,223	8098.5	0.946	0.137
0.48	87	160	1656	1652	49,140	8084.0	0.897	0.140
0.49	87	156	1650	1626	47,044	8075.1	0.554	0.140

. To execute the numerical assessment, a conjecture is made, where the assumed price sensitivity of demand for both the first and second markets is set at 0.4.

The findings presented in Table 6 elucidate that, under the condition of equality in substitution coefficients across both distribution channels and the symmetrical transfer of demand between online and traditional markets, an increase in said coefficient yields a concurrent augmentation in the demand across both distribution channels (refer to Figure 3). Consequently, the optimally determined prices correspondingly escalate in proportion to the heightened demand levels (refer to Figure 4). It is established that the widening disparity in optimal prices between the two distribution channels corresponds to an increase in the divergence of demand between the direct and indirect markets. As demand and price experience increments, the values of the first and second objective functions follow suit. Specifically, the first objective function attains improved values, while the second objective function exhibits less favorable outcomes. Further analysis, as depicted in Figure 5, reveals that the sensitivity of the first objective function to variations in the demand substitution coefficient, subsequently influenced by changes in price and demand, significantly surpasses the sensitivity observed in the second objective function.

Subsequently, the optimal values of ${ D}_{m_1}$,${ D}_{m_2}$,$SP{m}_1$, and $SP{m}_2$, encompassing the objective functions and the associated degree of satisfaction, are ascertained across varying values of the PS parameter. In conducting this numerical evaluation, a uniform assumption is made for the parameter α within both the direct and indirect distribution channels, with its value set at 0.3.

As evidenced in

Table 7. Model sensitivity analysis based on TH cumulative objective function parameters.

Minimum Degree of Possibility	The Degree of Importance of the Objective Functions	The Degree of Contentment Derived from Achieving the Objective Function		Objective Function Values
$\mathit{\gamma }$	$\left({\phi }_1, {\phi }_2\right)$	${\theta }_1$	${\theta }_2$	$z_1$	$z_2$
0.8	(0.0, 2.8)	0.572	0.572	32,711	7394.9
	(0.5, 0.5)	0.587	0.562	35,164	7504
	(0.8, 0.2)	0.885	0.466	51,450	9158.1
0.3	(0.0, 2.8)	0.372	0.448	21,628	9469.8
	(0.5, 0.5)	0.574	0.529	33,862	8084.1
	(0.8, 0.2)	0.923	0.466	53,680	9160.1

, an observable trend emerges, indicating that an escalation in the PS coefficient is associated with a concurrent reduction in both direct and indirect market demands. This trend is visually depicted in Figure 6 and Figure 7, where a discernible decrease in market demands is illustrated as the PS coefficient experiences an increase. Hence, in a comprehensive context, an anticipatable outcome is that, under the premise of uniformity across all conditions within both distribution channels, the equality of pricing between the two channels would result in an absence of disparity in the magnitude of direct and indirect demand. Consequent to the diminution in both the demand and price, the optimal values pertaining to the first and second objective functions undergo a corresponding reduction. Figure 8 visually delineates this observation, underscoring that the sensitivity of the first objective function to fluctuations in the price sensitivity coefficient of demand substantially surpasses that of the second objective function.

6.2. Sensitivity Analysis of the Model Using Parameters in the Cumulative Objective Function (TH Method)

In this section, a concise compilation of the outcomes derived from the numerical tests conducted with varying values of the parameters ${\phi }_{r }$ and $\gamma$ in the cumulative objective function of the TH method is presented. These parameters, denoting the significance assigned to the objective functions and regulating the minimum degree of satisfaction of said objectives, are systematically documented in Table 7. As illustrated in Table 7, an observation becomes apparent, suggesting that changes in the value of φ for each objective function lead to proportional variations in the satisfaction levels linked to the respective objective function. Conversely, an elevated value assigned to the $\gamma$ parameter signifies a heightened emphasis on the minimum degree of satisfaction of goals (${\delta }_0$), consequently yielding an improved lower limit for goal satisfaction. This emphasis contributes to the generation of more balanced and acceptable solutions within the optimization framework. Hence, through the decrement of the γ parameter value from 0.8 to 0.3, discernible shifts in the optimally derived solutions for the objective functions transpire, resulting in a notable increase in their imbalance. Consequently, it is deduced that a reduction in the $\gamma$ parameter corresponds to a diminished emphasis on achieving an enhanced lower limit for goal satisfaction. The Pareto frontier, delineating the trade-offs between conflicting objectives in the experimental problem, is illustrated in Figure 9 as it evolves in response to variations in the coefficients of the TH function. The numerical annotations associated with distinct points on the optimality diagram serve to denote the relative significance assigned to the first and second objective functions, encapsulated by the respective parameters (${\phi }_1, {\phi }_2$). It is recognized that alterations in the coefficients of the cumulative function TH yield diverse responses and values for the objectives. These variations facilitate the determination of an optimal Pareto state for the problem, contingent upon the decision maker’s preferences.

7. Conclusions

The proposed dual-channel green supply chain model was rigorously examined under two transportation cost scenarios: one with uniform costs across both markets and another with lower costs in the primary market. The results indicate that, when transportation costs are equivalent, a higher volume of goods is routed through environmentally sustainable channels. This finding highlights the model’s efficacy in harmonizing economic and environmental goals, underscoring its value in fostering more sustainable distribution networks. Sensitivity analysis demonstrates that decision makers can strategically adjust price–demand sensitivity coefficients and market-specific substitution rates to optimize pricing strategies, thereby enhancing supply chain profitability. These insights validate the model’s potential to integrate and align economic and environmental objectives, driving distribution networks toward both increased sustainability and profitability.

Furthermore, this study underscores the positive impact of renewable energy on both economic viability and environmental sustainability within the supply chain. Renewable energy not only supports emissions reduction targets, but also reduces operational costs, establishing it as a crucial element of a greener, more efficient supply chain. Future research should explore expanded roles for renewable energy across different supply chain stages to further reinforce sustainability.

Key parameter analysis reveals the model’s adaptability, allowing decision makers to prioritize specific objectives. The flexibility to calibrate the model for either balanced or customized solutions aligned with specific priorities is a significant advantage. This adaptability renders the model suitable for a wide range of decision-making scenarios, strengthening its robustness. Future studies should expand the model’s applicability by exploring omni-channel approaches in green supply chains, integrating permissible deficiency allowances in response to demand, or employing heuristic and metaheuristic methods to enhance scalability and analytical efficiency. These directions highlight a commitment to advancing the model’s capacity to address the evolving complexities of this domain.

Limitations and Future Directions

While this model provides a comprehensive framework for optimizing dual-channel green supply chain operations, it faces several limitations. First, the inherent data uncertainty and model sensitivity, due to the reliance on specific parameter values and stochastic data generation for demand, costs, and emissions factors, present challenges. Although fuzzy multi-objective programming helps mitigate these uncertainties, the model’s accuracy remains highly dependent on high-quality input data. Future studies should enhance model robustness through extensive sensitivity analyses or dynamic data updates.

Additionally, future research could benefit from a more detailed exploration of CO₂ emissions’ differentiation across product segments, particularly in multi-channel retail structures. Retailers in diverse sectors, such as food and non-food, encounter distinct environmental impacts, especially regarding Scope 1, 2, and 3 emissions. These scopes encompass emissions from direct operations, purchased energy, and the broader supply chain. Each segment also faces unique circular economy challenges that merit further investigation. A segment-specific approach could enhance the model by incorporating more precise emissions data, fostering a holistic perspective in green supply chain design.

Finally, the scope of renewable energy sources considered here is limited to solar and wind, which may not represent the full spectrum of global renewable options. Regional variations in integration costs and efficiencies could affect the model’s generalizability. Broadening the range of renewable energy types, along with region-specific considerations, would enhance the model’s practical value. Furthermore, although this study incorporates multiple transportation modes with varied emissions factors, it could benefit from refined metrics, such as vehicle-specific emissions rates or regional regulatory influences on transportation. These refinements would allow for a more nuanced analysis of transportation emissions and costs.