Research on Fault Diagnosis of Agricultural IoT Sensors Based on Improved Dung Beetle Optimization–Support Vector Machine
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Location and Data Sources
2.2. Data Standardization
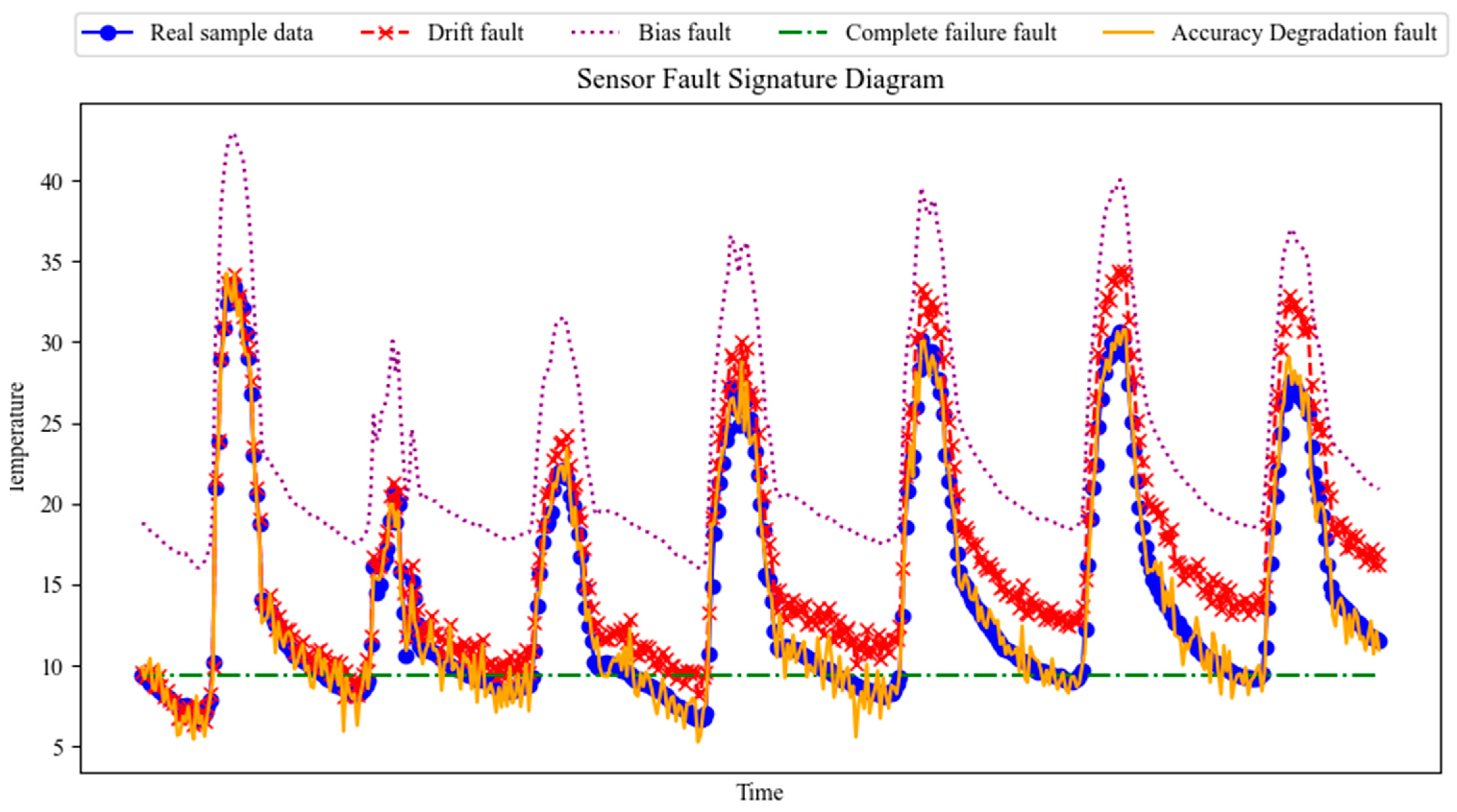
2.3. Theoretical Description of Sensor Faults
2.3.1. Bias Fault
2.3.2. Drift Fault
2.3.3. Accuracy Degradation Fault
2.3.4. Complete Failure Fault
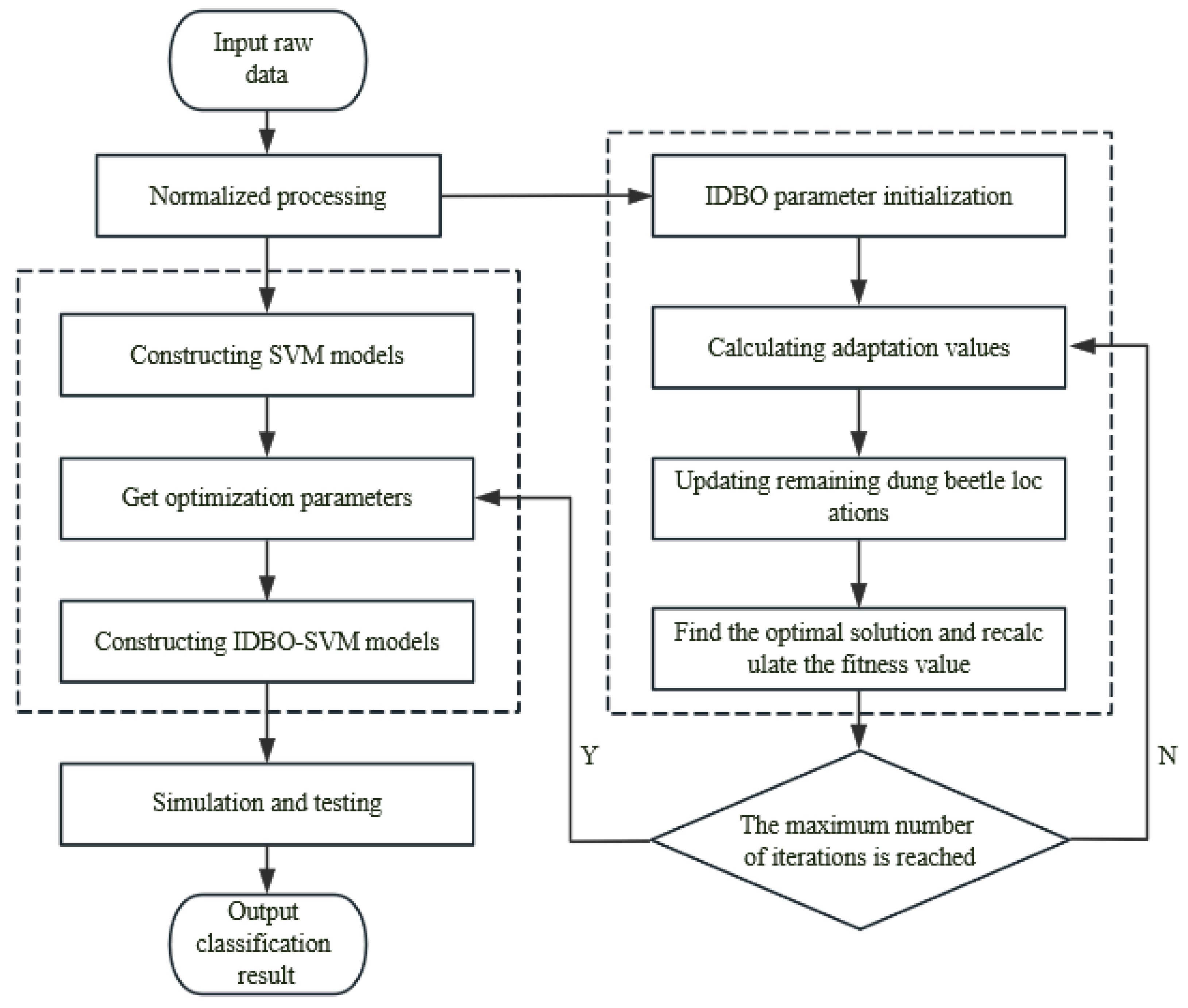
2.4. Construction of Basic Fault Diagnosis Model
2.4.1. SVM (Support Vector Machine) Model
2.4.2. Dung Beetle Optimizer (DBO) Algorithm
2.4.3. Improvements to the Dung Beetle Optimizer (DBO) Algorithm
- (1).
- Incorporation of Bernoulli Chaotic Map
- (2).
- Integration of the Golden Sine Strategy
- (3).
- Dynamic Weight Strategy Update
3. Experiment and Result Analysis
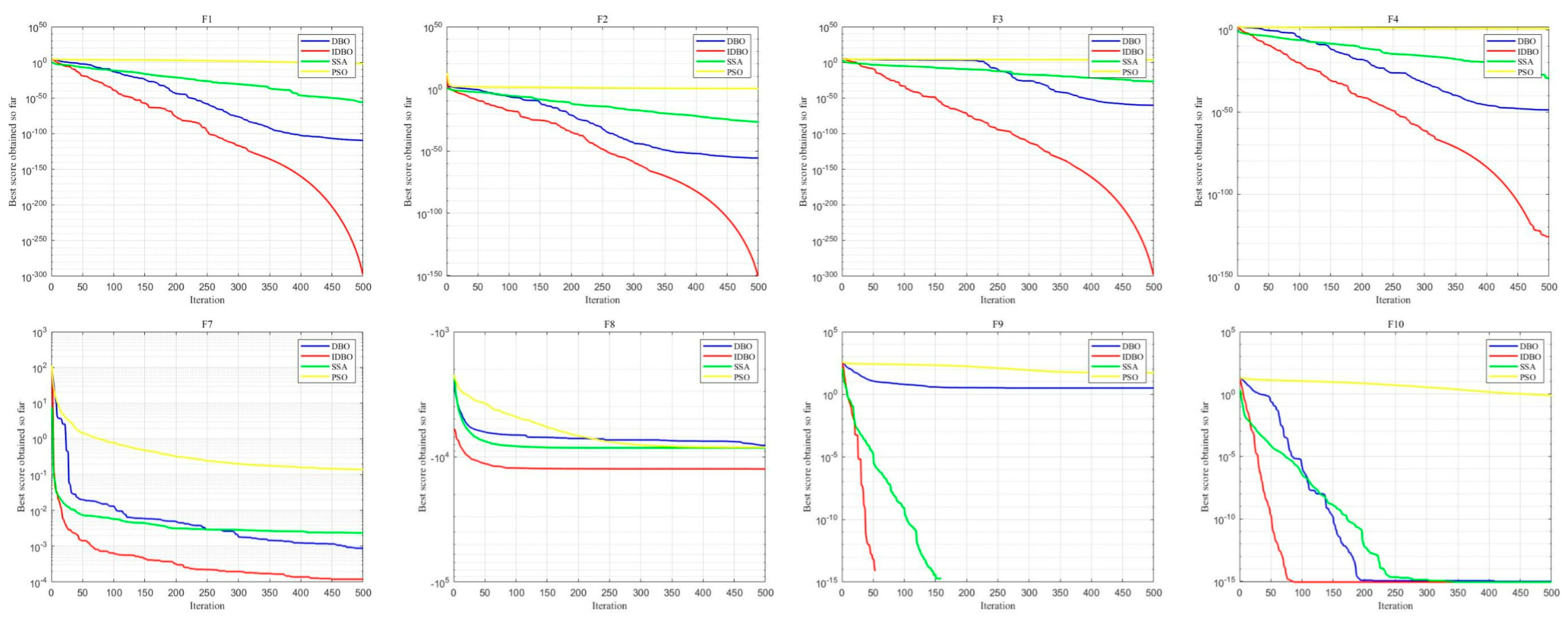
3.1. Performance Testing of the IDBO Algorithm
3.1.1. Performance Comparison Testing of the Improved DBO Algorithm
3.1.2. Comparative Analysis of Algorithm Iterative Convergence Curves
3.2. IDBO-SVM Fault Diagnosis Model
3.3. Model Performance Evaluation
3.4. Model Ablation Study
4. Conclusions
- (1)
- The IDBO algorithm significantly improves the performance of the SVM model by effectively tuning its hyperparameters, especially when handling multimodal data. Compared with other algorithms, IDBO demonstrates faster convergence speed and stronger global search capabilities, enabling it to maintain high classification accuracy even under a high fault ratio. It also shows better computational efficiency, indicating that this model is not only suitable for scenarios requiring high accuracy but also capable of handling real-time application scenarios with high demands on timeliness.
- (2)
- Ablation experiments show that the robustness and generalization performance of the IDBO-SVM model are outstanding under different fault ratios and sample sizes. Compared to other models, IDBO-SVM excels not only on small sample datasets but also in handling high-fault-ratio data. In practical applications, although sensor data were used in the experiments, it can be inferred that the model also has good adaptability and generalization capabilities in other multimodal fault detection tasks.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DBO | Dung Beetle Optimization |
| IDBO | Improved Dung Beetle Optimization |
| SVM | Support Vector Machine |
| BP | Backpropagation |
| ELMAN | Elman neural network |
| KNN | K-Nearest Neighbors |
| SSA | Sparrow Search Algorithm |
| GA | Genetic Algorithm |
| PSO | Particle Swarm Optimization |
References
- Goodrich, P.; Betancourt, O.; Arias, A.C.; Zohdi, T. Placement and drone flight path mapping of agricultural soil sensors using machine learning. Comput. Electron. Agric. 2023, 205, 107591. [Google Scholar] [CrossRef]
- Muangprathub, J.; Boonnam, N.; Kajornkasirat, S.; Lekbangpong, N.; Wanichsombat, A.; Nillaor, P. IoT and agriculture data analysis for smart farm. Comput. Electron. Agric. 2019, 156, 467–474. [Google Scholar] [CrossRef]
- Maheswararajah, S.; Halgamuge, S.K.; Dassanayake, K.B.; Chapman, D. Management of Orphaned-Nodes in Wireless Sensor Networks for Smart Irrigation Systems. IEEE Trans. Signal Process. 2011, 59, 4909–4922. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Thorburn, P.J.; Xiang, W.; Fitch, P. SSIM-A Deep Learning Approach for Recovering Missing Time Series Sensor Data. IEEE Internet Things J. 2019, 6, 6618–6628. [Google Scholar] [CrossRef]
- Bae, J.; Lee, M.; Shin, C. A Data-Based Fault-Detection Model for Wireless Sensor Networks. Sustainability 2019, 11, 6171. [Google Scholar] [CrossRef]
- Bhardwaj, A.; Kumar, M.; Alshehri, M.; Keshta, I.; Abugabah, A.; Sharma, S.K. Smart water management framework for irrigation in agriculture. Environ. Technol. 2024, 45, 2320–2334. [Google Scholar] [CrossRef]
- Kaur, G.; Bhattacharya, M. Intelligent Fault Diagnosis for AIT-Based Smart Farming Applications. IEEE Sens. J. 2023, 23, 28261–28269. [Google Scholar] [CrossRef]
- Rahaman, M.M.; Azharuddin, M. Wireless sensor networks in agriculture through machine learning: A survey. Comput. Electron. Agric. 2022, 197, 106928. [Google Scholar] [CrossRef]
- Erhan, L.; Ndubuaku, M.; Di Mauro, M.; Song, W.; Chen, M.; Fortino, G.; Bagdasar, O.; Liotta, A. Smart anomaly detection in sensor systems: A multi-perspective review. Inf. Fusion 2021, 67, 64–79. [Google Scholar] [CrossRef]
- Purbowaskito, W.; Lan, C.Y.; Fuh, K. The Potentiality of Integrating Model-Based Residuals and Machine-Learning Classifiers: An Induction Motor Fault Diagnosis Case. IEEE Trans. Ind. Inform. 2024, 20, 2822–2832. [Google Scholar] [CrossRef]
- Saeed, U.; Lee, Y.D.; Jan, S.U.; Koo, I. CAFD: Context-Aware Fault Diagnostic Scheme towards Sensor Faults Utilizing Machine Learning. Sensors 2021, 21, 617. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Shen, Q.; Wang, L.X.; Qin, W.W.; Xie, M.M. A New Adaptive Interpretable Fault Diagnosis Model for Complex System Based on Belief Rule Base. IEEE Trans. Instrum. Meas. 2022, 71, 3529111. [Google Scholar] [CrossRef]
- Zou, X.G.; Liu, W.C.; Huo, Z.Q.; Wang, S.Y.; Chen, Z.L.; Xin, C.R.; Bai, Y.A.; Liang, Z.Y.; Gong, Y.; Qian, Y.; et al. Current Status and Prospects of Research on Sensor Fault Diagnosis of Agricultural Internet of Things. Sensors 2023, 23, 2528. [Google Scholar] [CrossRef] [PubMed]
- Hao, H.Y.; Zhang, K.; Ding, S.X.; Chen, Z.W.; Lei, Y.G. A data-driven multiplicative fault diagnosis approach for automation processes. Isa Trans. 2014, 53, 1436–1445. [Google Scholar] [CrossRef]
- Nor, N.M.; Hassan, C.R.C.; Hussain, M.A. A review of data-driven fault detection and diagnosis methods: Applications in chemical process systems. Rev. Chem. Eng. 2020, 36, 513–553. [Google Scholar] [CrossRef]
- Liakos, K.G.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine Learning in Agriculture: A Review. Sensors 2018, 18, 2674. [Google Scholar] [CrossRef]
- Foo, L.K.; Chua, S.L.; Ibrahim, N. Attribute Weighted Naive Bayes Classifier. Cmc-Comput. Mater. Contin. 2022, 71, 1945–1957. [Google Scholar] [CrossRef]
- Kamilaris, A.; Prenafeta-Boldú, F.X. Deep learning in agriculture: A survey. Comput. Electron. Agric. 2018, 147, 70–90. [Google Scholar] [CrossRef]
- Kari, T.; Gao, W.S.; Zhao, D.B.; Abiderexiti, K.; Mo, W.X.; Wang, Y.; Luan, L. Hybrid feature selection approach for power transformer fault diagnosis based on support vector machine and genetic algorithm. Iet Gener. Transm. Distrib. 2018, 12, 5672–5680. [Google Scholar] [CrossRef]
- Maincer, D.; Benmahamed, Y.; Mansour, M.; Alharthi, M.; Ghonein, S.S.M. Fault Diagnosis in Robot Manipulators Using SVM and KNN. Intell. Autom. Soft Comput. 2023, 35, 1957–1969. [Google Scholar] [CrossRef]
- Ye, L.; Chen, Z.; Liu, J.; Lin, C.; Jian, Y. Research on Power Device Fault Prediction of Rod Control Power Cabinet Based on Improved Dung Beetle Optimization-Temporal Convolutional Network Transfer Learning Model. Energies 2024, 17, 447. [Google Scholar] [CrossRef]
- Huang, H.; Yao, Z.; Wei, X.; Zhou, Y. Twin support vector machines based on chaotic mapping dung beetle optimization algorithm. J. Comput. Des. Eng. 2024, 11, 101–110. [Google Scholar] [CrossRef]
- Sharifi, R.; Langari, R. Isolability of faults in sensor fault diagnosis. Mech. Syst. Signal Process. 2011, 25, 2733–2744. [Google Scholar] [CrossRef]
- Xue, J.K.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]



| Sensor Name | Model | Precision | Measurement Range |
|---|---|---|---|
| Air Temperature and Humidity Sensor | DB-171-30 | Temperature: ±0.5 °C Humidity: ±5.0% RH | Temperature: (−40~+120) °C Humidity: 0~100% RH |
| Light Intensity Sensor | TBQ-6 | ±5% | 0.2~200 klux |
| Soil Temperature, Humidity, and Conductivity 3-in-1 Sensor | TEROS12 | Soil Temperature: ±0.1 °C Soil Humidity: ±3% Soil Conductivity: ±5% | Soil Temperature: −40~60 °C Soil Humidity: 1%~100% Soil Conductivity: 0~10 dS/m |
| Soil pH Sensor | RS-PH-*-TR-1 | ±5% | 3~9 PH |
| Wind Direction Sensor | RS-FXA-I20 | ±5% | 0~360° |
| Wind Speed Sensor | RS-FSA-I20 | ±0.2 m/s | 0~60 m/s |
| Rainfall Sensor | RS-YL-I20-4 | ±3% | 0 mm~4 mm/min |
| Air Temperature Normalization | Air Humidity Normalization | Soil Temperature Normalization | Soil Moisture Normalization |
|---|---|---|---|
| 0.35 | 0.62 | 0.16 | 0.92 |
| 0.31 | 0.65 | 0.15 | 0.90 |
| 0.28 | 0.7 | 0.14 | 0.89 |
| 0.27 | 0.68 | 0.13 | 0.87 |
| 0.25 | 0.75 | 0.13 | 0.85 |
| 0.23 | 0.73 | 0.12 | 0.82 |
| 0.21 | 0.78 | 0.10 | 0.79 |
| Series of Functions | IDBO | DBO | SSA | PSO |
|---|---|---|---|---|
| F1 Series | 0.00 (0.00) | 9.78 × 10−164 (1.02 × 10−110) | 9.95 × 10−265 (1.01 × 10−56) | 0.00089212 (0.010301) |
| F2 Series | 0.00 (0.00) | 1.1507 × 10−88 (4.0265 × 10−48) | 2.5063 × 10−109 (1.2556 × 10−31) | 0.0015597 (4.4943) |
| F3 Series | 0.00 (0.00) | 5.3034 × 10−136 (4.0324 × 10−69) | 7.6565 × 10−248 (1.0361 × 10−26) | 533.0801 (2480.233) |
| F4 Series | 0 (1.136 × 10−111) | 3.1903 × 10−78 (1.9221 × 10−50) | 5.1027 × 10−120 (6.4015 × 10−26) | 4.769 (1.4015) |
| F7 Series | 1.2809 × 10−5 (0.00011925) | 0.00015714 (0.00058625) | 6.8396 × 10−5 (0.0020532) | 0.024236 (0.49055) |
| F8 Series | −12569.4865 (1.4191) | −12264.8404 (1948.4593) | −9903.0768 (587.3438) | −9506.6316 (579.1724) |
| F9 Series | 0 (0.00) | 0 (22.8855) | 0 (0.00) | 24.8947 (14.9611) |
| F10 Series | 8.8818 × 10−16 (0) | 8.8818 × 10−16 (0) | 8.8818 × 10−16 (0) | 0.004857 (0.76671) |
| Model Name | SVM | IDBO-SVM | SSA-SVM | ELMAN | BP |
|---|---|---|---|---|---|
| Average accuracy | 89.60% (90.60%) | 94.20% (95.62%) | 91.16% (91.80%) | 86.40% (85.26%) | 87.66% (87.96%) |
| Running time | 22.5S (21.2S) | 18.2S (16.5S) | 16.6S (18.7S) | 26.6S (22.3S) | 31.3S (26.1S) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, S.; Liu, P.; Zhang, Z.; Wu, Y. Research on Fault Diagnosis of Agricultural IoT Sensors Based on Improved Dung Beetle Optimization–Support Vector Machine. Sustainability 2024, 16, 10001. https://doi.org/10.3390/su162210001
Liang S, Liu P, Zhang Z, Wu Y. Research on Fault Diagnosis of Agricultural IoT Sensors Based on Improved Dung Beetle Optimization–Support Vector Machine. Sustainability. 2024; 16(22):10001. https://doi.org/10.3390/su162210001
Chicago/Turabian StyleLiang, Sicheng, Pingzeng Liu, Ziwen Zhang, and Yong Wu. 2024. "Research on Fault Diagnosis of Agricultural IoT Sensors Based on Improved Dung Beetle Optimization–Support Vector Machine" Sustainability 16, no. 22: 10001. https://doi.org/10.3390/su162210001
APA StyleLiang, S., Liu, P., Zhang, Z., & Wu, Y. (2024). Research on Fault Diagnosis of Agricultural IoT Sensors Based on Improved Dung Beetle Optimization–Support Vector Machine. Sustainability, 16(22), 10001. https://doi.org/10.3390/su162210001





