Grid-Based Precipitation Quantile Estimation Considering Homogeneity Using ERA5-Land Data for the Korean Peninsula
Abstract
1. Introduction
2. Methods
2.1. Overview
2.2. Mann–Kendall Test
2.3. Pettitt Test
2.4. Estimation of Probability Precipitation Quantiles
2.5. Goodness-of-Fit Test
2.5.1. Kolmogorov–Smirnov Test
2.5.2. Anderson–Darling Test
3. Data and Study Area
3.1. Precipitation Data
3.2. Study Area
4. Results
4.1. Trend from Mann–Kendall Test
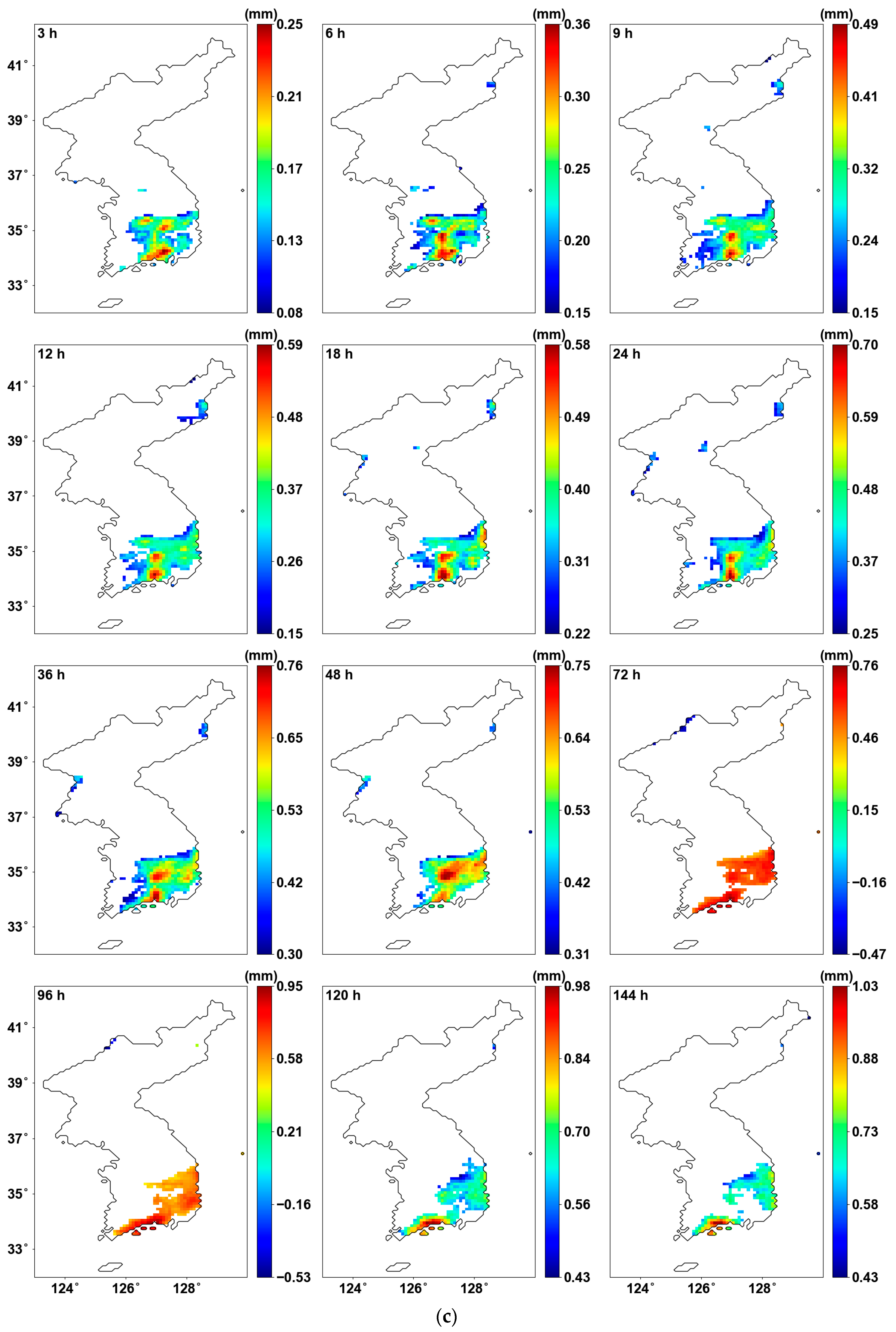
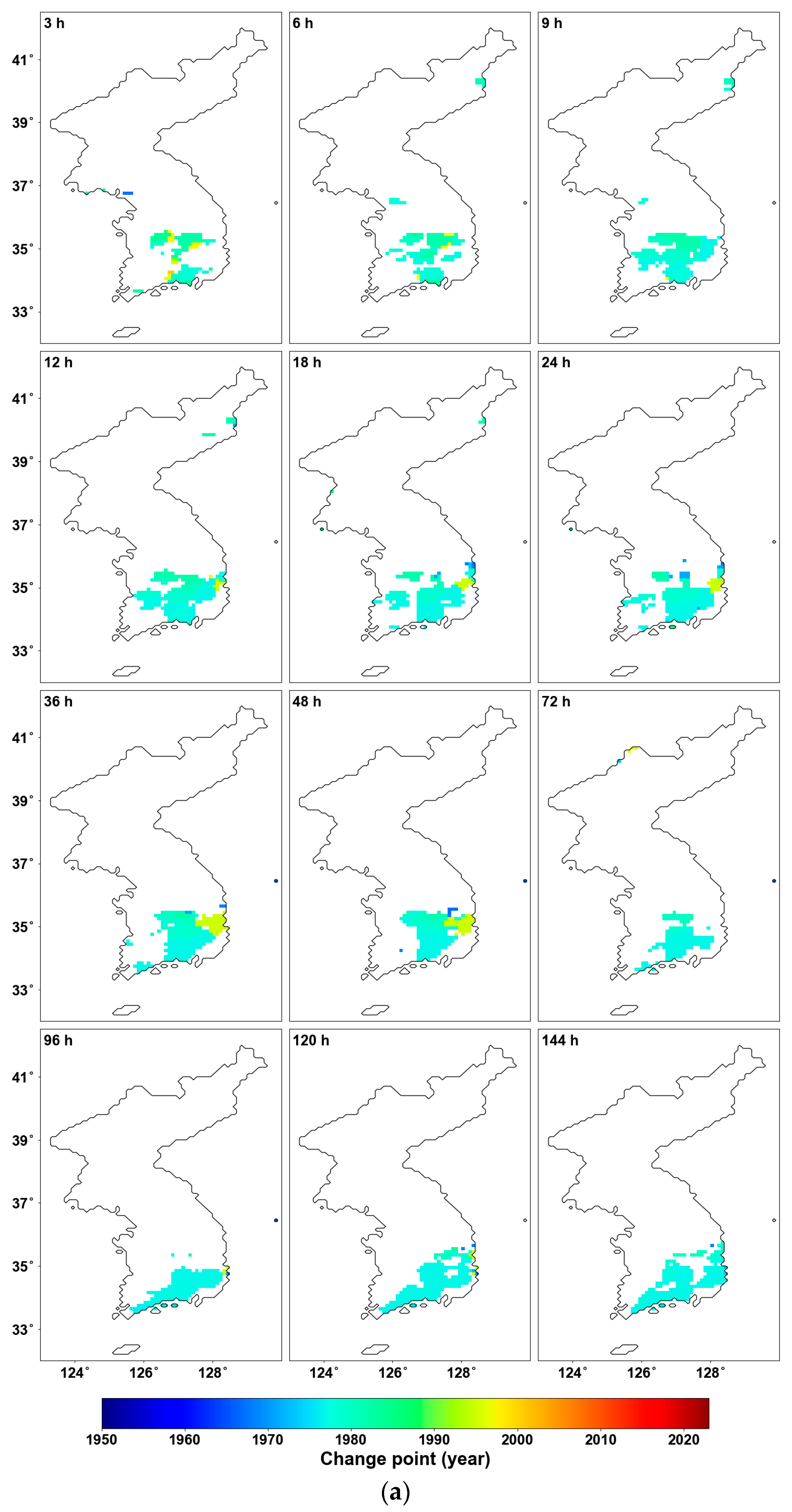
4.2. Homogeneity from Pettitt Test
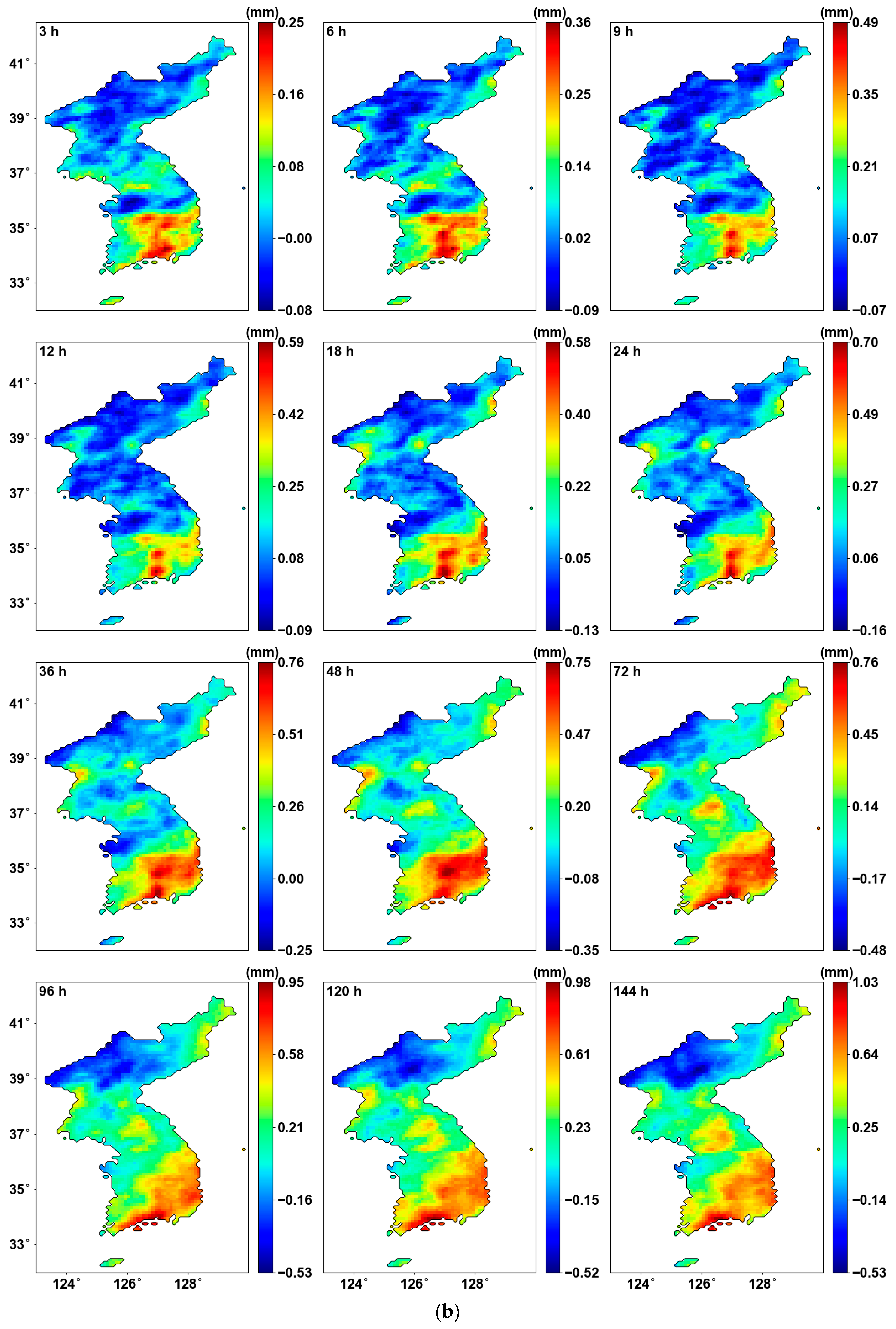
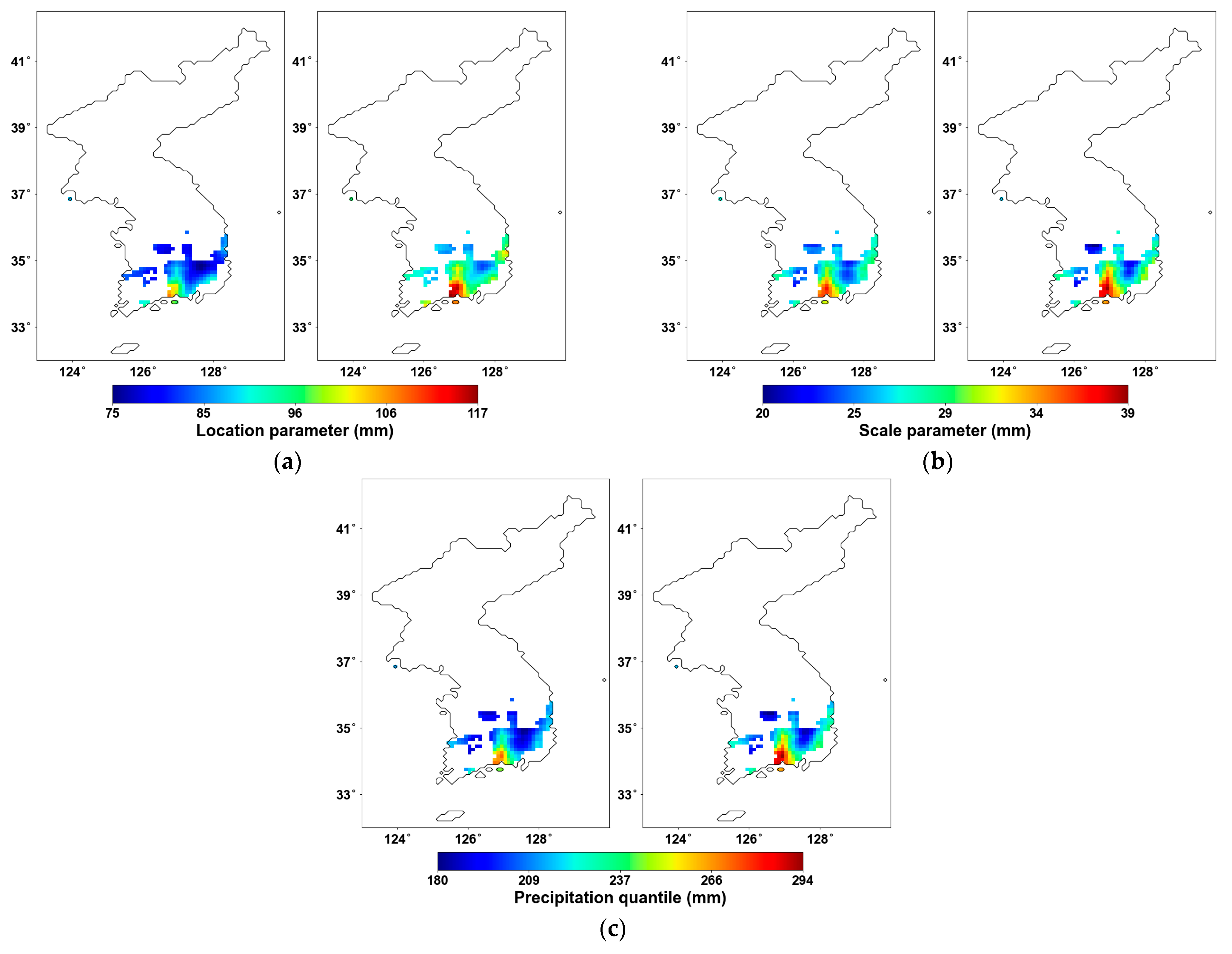
4.3. Estimation of Probability Distribution Parameters Considering Homogeneity from Pettitt Test
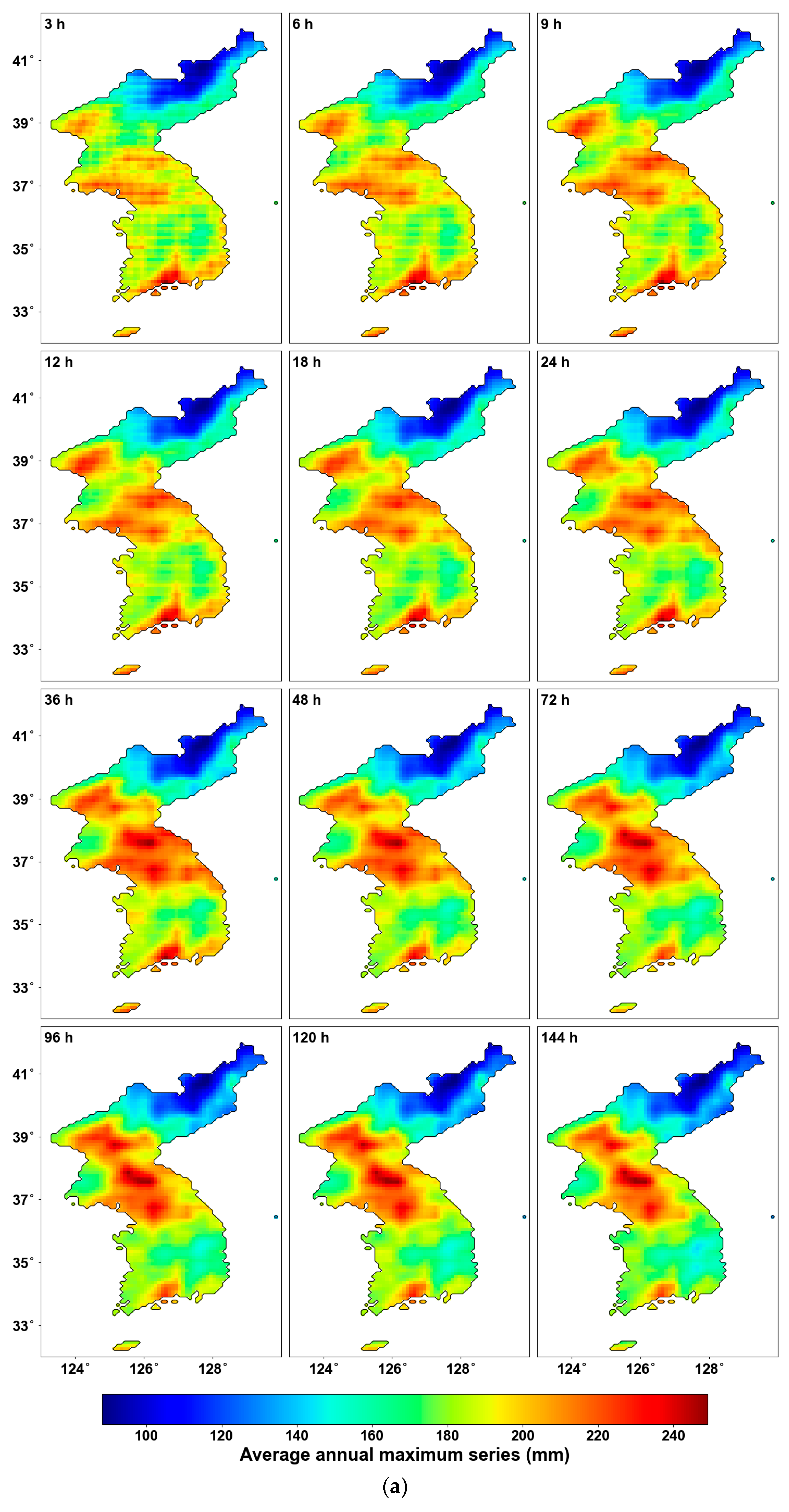
4.4. Precipitation Quantiles
5. Discussions
6. Conclusions
- (1)
- The trend analysis conducted as a preliminary step using the MK test showed a significant increasing trend in the southeastern region of Korea. Homogeneity analysis through the Pettitt test also revealed changes in homogeneity with increasing trends in similar areas. The proportion of affected grid cells was approximately 8.6% of the total.
- (2)
- The parameters of the Gumbel distribution estimated using the original AMS, and the resulting precipitation quantiles generally showed stronger values in the central and southern parts of the Korean Peninsula, while weaker values were observed in the northeastern region.
- (3)
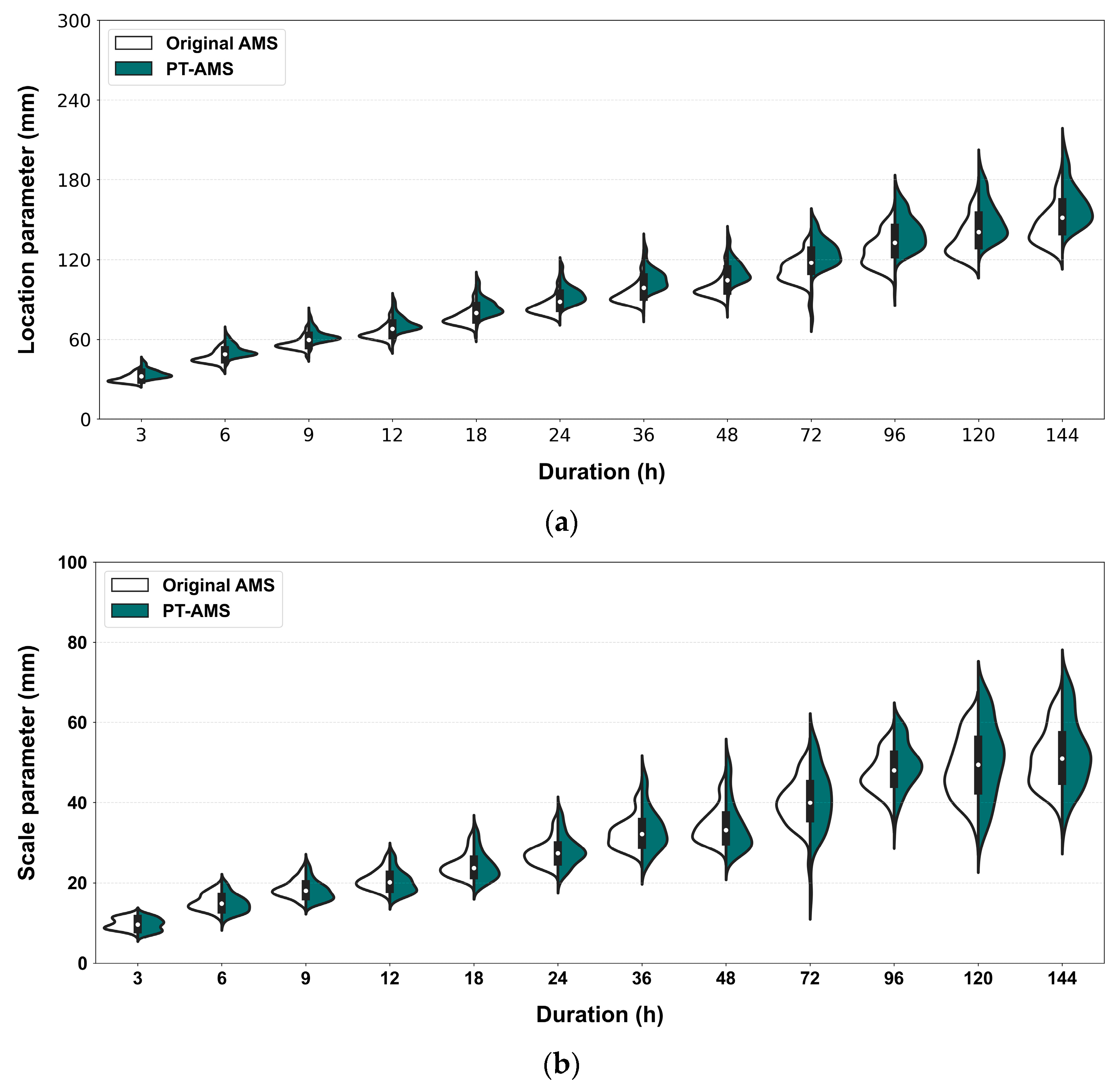
- The frequency analysis performed using PT-AMS showed significant changes in the location parameter, with all values increasing. For the scale parameter, there was a slight decrease for shorter durations, but as the duration increased, a slight upward trend was observed. The resulting precipitation quantiles were largest for a return period of 2 years and a duration of 36 h, with an average increase of approximately +11.5%.
- (4)
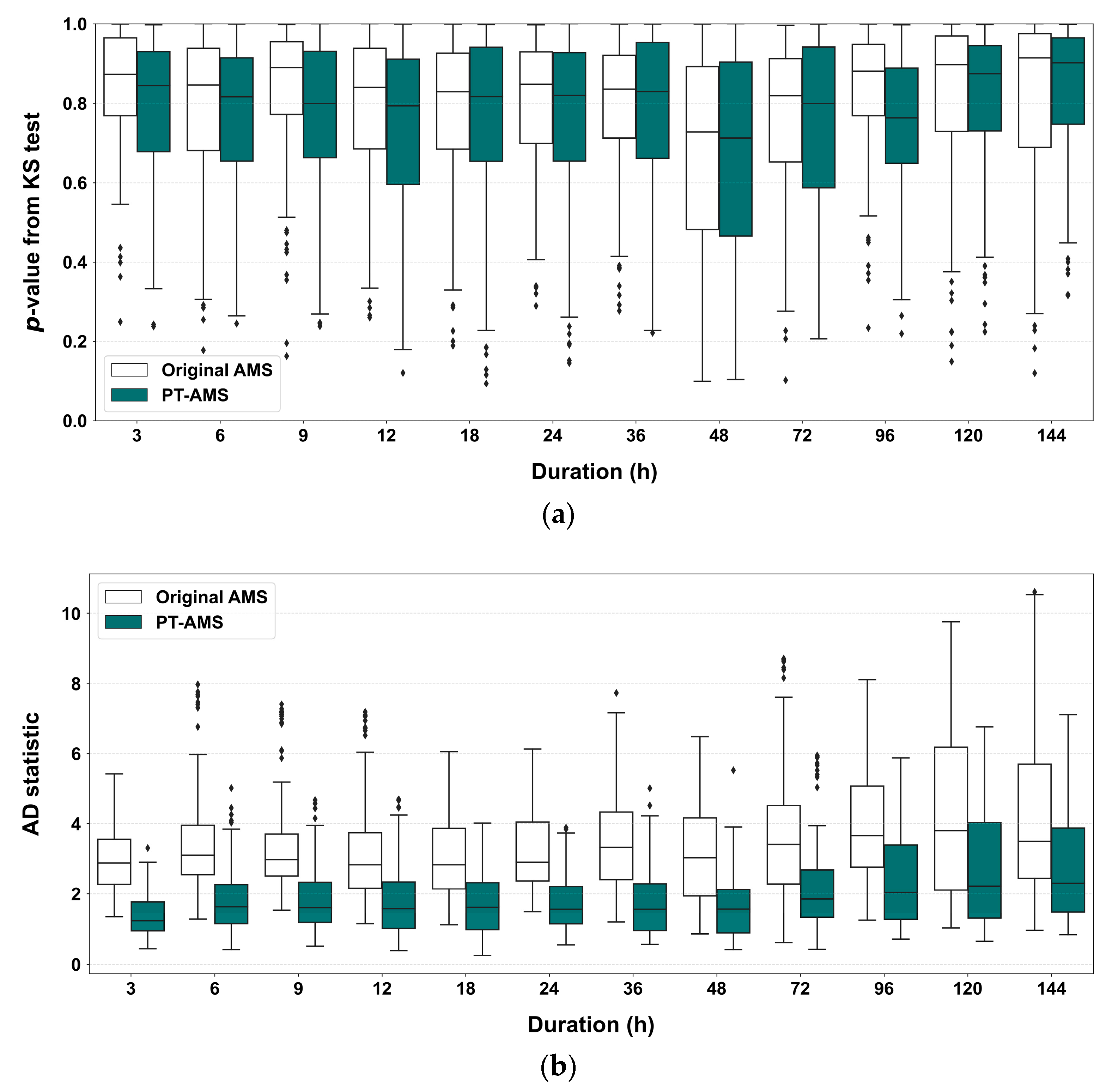
- The goodness-of-fit test results showed no significant differences before and after, with all p-values exceeding 0.05 in the KS test. However, the AD test statistics indicated an improvement in fit.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis: An Approach Based on L-Moments; Cambridge University Press: Cambridge, UK, 1997; ISBN 978-0-521-43045-6. [Google Scholar]
- Wang, Z.; Zeng, Z.; Lai, C.; Lin, W.; Wu, X.; Chen, X. A regional frequency analysis of precipitation extremes in Mainland China with fuzzy C-means and L-moments approaches. Int. J. Climatol. 2017, 37, 429–444. [Google Scholar] [CrossRef]
- Darwish, M.M.; Fowler, H.J.; Blenkinsop, S.; Tye, M.R. A regional frequency analysis of UK sub-daily extreme precipitation and assessment of their seasonality. Int. J. Climatol. 2018, 38, 4758–4776. [Google Scholar] [CrossRef]
- Forestieri, A.; Lo Conti, F.; Blenkinsop, S.; Cannarozzo, M.; Fowler, H.J.; Noto, L.V. Regional frequency analysis of extreme rainfall in Sicily (Italy). Int. J. Climatol. 2018, 38, e698–e716. [Google Scholar] [CrossRef]
- Lee, J.; Jun, C.; Kim, H.-J.; Byun, J.; Baik, J. Estimation of grid-type precipitation quantile using satellite based re-analysis precipitation data in Korean peninsula. J. Korea Water Resour. Assoc. 2022, 55, 447–459. [Google Scholar] [CrossRef]
- Heo, J.-H.; Kim, H. Regional frequency analysis for stationary and nonstationary hydrological data. J. Korea Water Resour. Assoc. 2019, 52, 657–669. [Google Scholar] [CrossRef]
- Nandakumar, N. Estimation of Extreme Rainfalls for Victoria: Application of the Forge Method; Cooperative Research Centre for Catchment Hydrology: Melbourne, VIC, Australia, 1995. [Google Scholar]
- Schaefer, M.G. Regional analyses of precipitation annual maxima in Washington State. Water Resour. Res. 1990, 26, 119–131. [Google Scholar] [CrossRef]
- Courty, L.G.; Wilby, R.L.; Hillier, J.K.; Slater, L.J. Intensity-duration-frequency curves at the global scale. Environ. Res. Lett. 2019, 14, 084045. [Google Scholar] [CrossRef]
- Gado, T.A.; Hsu, K.; Sorooshian, S. Rainfall frequency analysis for ungauged sites using satellite precipitation products. J. Hydrol. 2017, 554, 646–655. [Google Scholar] [CrossRef]
- Yoo, C.; Lee, J.; Ro, Y. Markov Chain Decomposition of Monthly Rainfall into Daily Rainfall: Evaluation of Climate Change Impact. Adv. Meteorol. 2016, 1, 7957490. [Google Scholar] [CrossRef]
- Sung, J.H.; Kim, Y.-O.; Jeon, J.-J. Application of distribution-free nonstationary regional frequency analysis based on L-moments. Theor. Appl. Climatol. 2017, 133, 1219–1233. [Google Scholar] [CrossRef]
- Kim, H.; Shin, J.-Y.; Kim, T.; Kim, S.; Heo, J.-H. Regional frequency analysis of extreme precipitation based on a nonstationary population index flood method. Adv. Water Resour. 2020, 146, 103757. [Google Scholar] [CrossRef]
- Wijngaard, J.B.; Klein Tank, A.M.G.; Können, G.P. Homogeneity of 20th century European daily temperature and precipitation series. Int. J. Climatol. 2003, 23, 679–692. [Google Scholar] [CrossRef]
- Costa, A.C.; Soares, A. Homogenization of Climate Data: Review and New Perspectives Using Geostatistics. Math. Geosci. 2008, 41, 291–305. [Google Scholar] [CrossRef]
- Hurtado, S.I.; Zaninelli, P.G.; Agosta, E.A. A multi-breakpoint methodology to detect changes in climatic time series. An application to wet season precipitation in subtropical Argentina. Atmos. Res. 2020, 241, 104955. [Google Scholar] [CrossRef]
- Hirsch, R.M.; Slack, J.R.; Smith, R.A. Techniques of trend analysis for monthly water quality data. Water Resour. Res. 1982, 18, 107–121. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econom. J. Econom. Soc. 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Charles Griffin: London, UK, 1975. [Google Scholar]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Pettitt, A.N. A Non-Parametric Approach to the Change-Point Problem. J. R. Stat. Soc. C Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Mann, H.B.; Whitney, D.R. On a test of whether one of two random variables is stochastically larger than the other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Fowler, H.J.; Kilsby, C.G. A regional frequency analysis of United Kingdom extreme rainfall from 1961 to 2000. Int. J. Climatol. 2003, 23, 1313–1334. [Google Scholar] [CrossRef]
- Overeem, A.; Buishand, A.; Holleman, I. Rainfall depth-duration-frequency curves and their uncertainties. J. Hydrol. 2008, 348, 124–134. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Koutsoyiannis, D. Battle of extreme value distributions: A global survey on extreme daily rainfall. Water Resour. Res. 2013, 49, 187–201. [Google Scholar] [CrossRef]
- Schiavo, M. The role of different sources of uncertainty on the stochastic quantification of subsurface discharges in heterogeneous aquifers. J. Hydrol. 2023, 617, 128930. [Google Scholar] [CrossRef]
- Park, H.W.; Sohn, H. Parameter estimation of the generalized extreme value distribution for structural health monitoring. Probabilistic Eng. Mech. 2006, 21, 366–376. [Google Scholar] [CrossRef]
- Bali, T.G. A Generalized Extreme Value Approach to Financial Risk Measurement. J. Money Credit Bank. 2007, 39, 1613–1649. [Google Scholar] [CrossRef]
- Martins, E.S.; Stedinger, J.R. Generalized maximum-likelihood generalized extreme-value quantile estimators for hydrologic data. Water Resour. Res. 2000, 36, 737–744. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Statistics of extremes and estimation of extreme rainfall: I. Theoretical investigation/Statistiques de valeurs extrêmes et estimation de précipitations extrêmes: I. Recherche théorique. Hydrol. Sci. J. 2004, 49, 590. [Google Scholar] [CrossRef]
- MLTM (Ministry of Land, Transport and Maritime Affairs). Improvement and Supplement of Probability Rainfall; Ministry of Land, Transport and Maritime Affairs: Seoul, Republic of Korea, 2011.
- ME (Ministry of Environment). Standard Guidelines for Flood Estimation; Ministry of Environment: Sejong, Republic of Korea, 2019.
- Cunnane, C. Statistical Distribution for Flood Frequency Analysis; WMO Operational Hydrology; World Meteorological Organization: Geneva, Switzerland, 1989. [Google Scholar]
- MLTM (Ministry of Land, Transport and Maritime Affairs). Design Flood Estimation Guidelines; Ministry of Land, Transport and Maritime Affairs: Seoul, Republic of Korea, 2012.
- Kim, M.; Lee, E. Validation and Comparison of Climate Reanalysis Data in the East Asian Monsoon Region. Atmosphere 2022, 13, 1589. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data. 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Park, H.; Lee, J.; Yoo, C.; Sim, S.; Im, J. Estimation of Spatially Continuous Near-Surface Relative Humidity Over Japan and South Korea. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8614–8626. [Google Scholar] [CrossRef]
- Wang, Y.-R.; Hessen, D.O.; Samset, B.H.; Stordal, F. Evaluating global and regional land warming trends in the past decades with both MODIS and ERA5-Land land surface temperature data. Remote Sens. Environ. 2022, 280, 113181. [Google Scholar] [CrossRef]
- Zou, J.; Lu, N.; Jiang, H.; Qin, J.; Yao, L.; Xin, Y.; Su, F. Performance of air temperature from ERA5-Land reanalysis in coastal urban agglomeration of Southeast China. Sci. Total Environ. 2022, 828, 154459. [Google Scholar] [CrossRef] [PubMed]
- Ensor, L.A.; Robeson, S.M. Statistical characteristics of daily precipitation: Comparisons of gridded and point datasets. J. Appl. Meteorol. Climatol. 2008, 47, 2468–2476. [Google Scholar] [CrossRef]
- Lee, J.; Park, K.; Yoo, C. Bias from Rainfall Spatial Distribution in the Application of Areal Reduction Factor. KSCE J. Civ. Eng. 2018, 22, 5229–5241. [Google Scholar] [CrossRef]



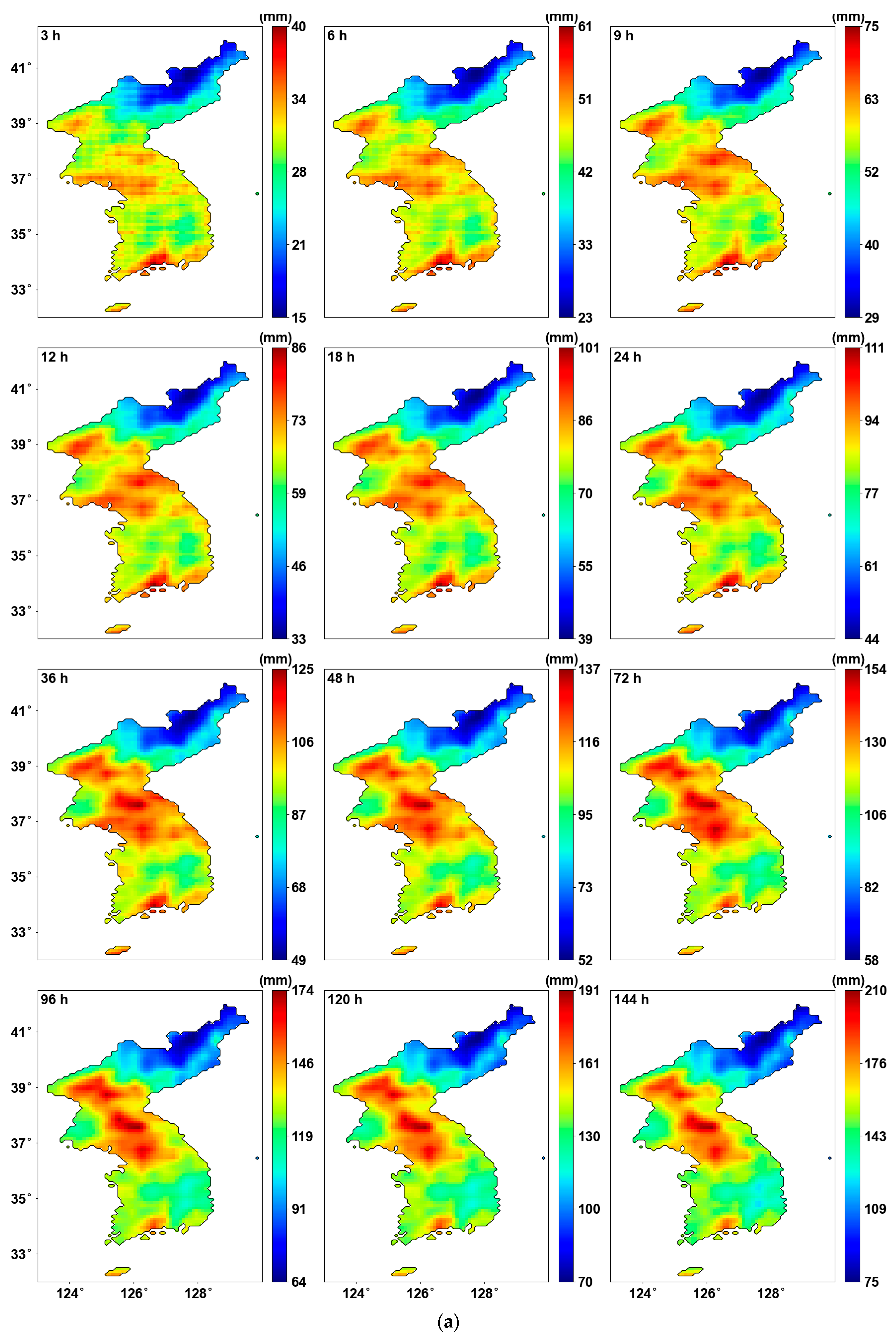
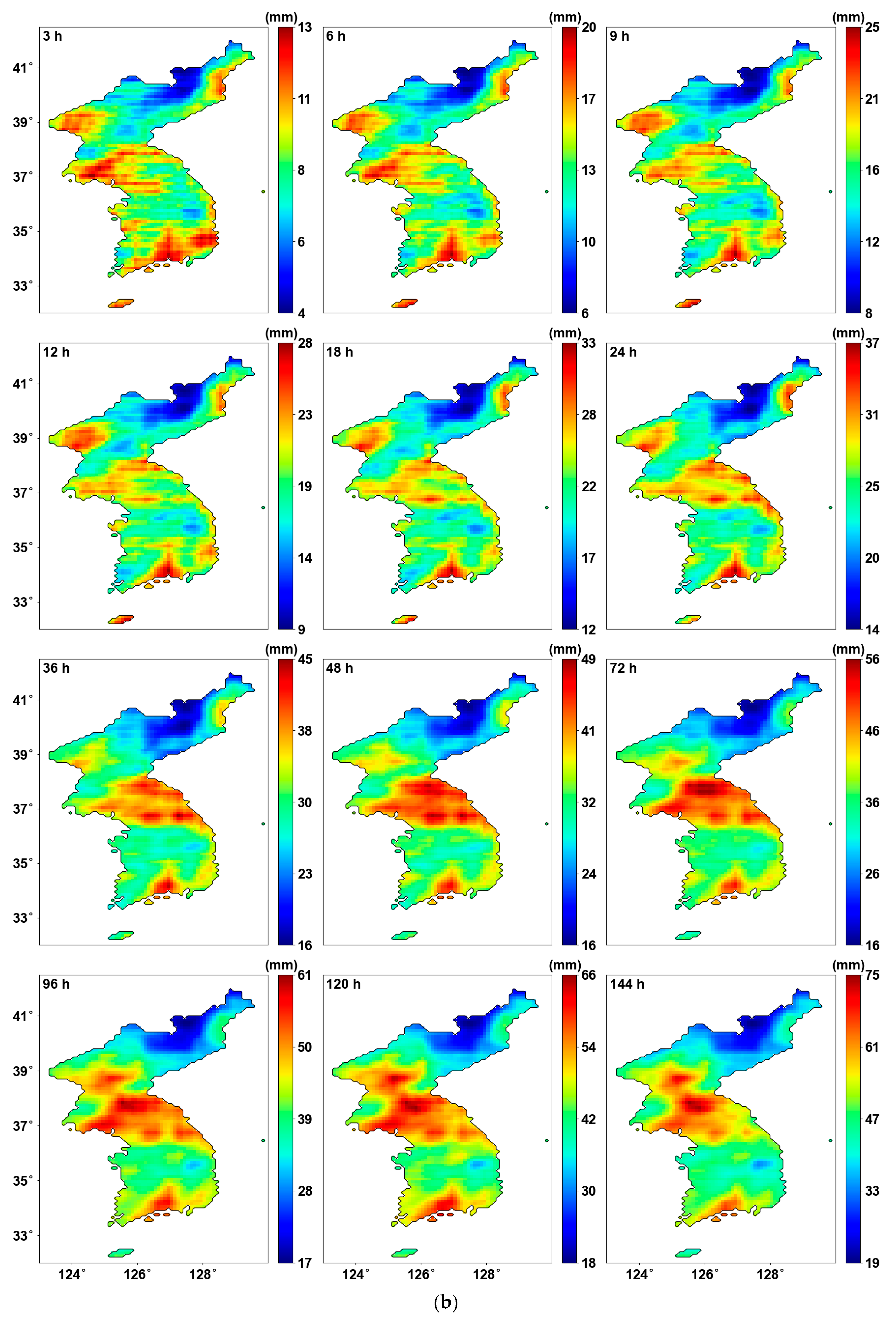
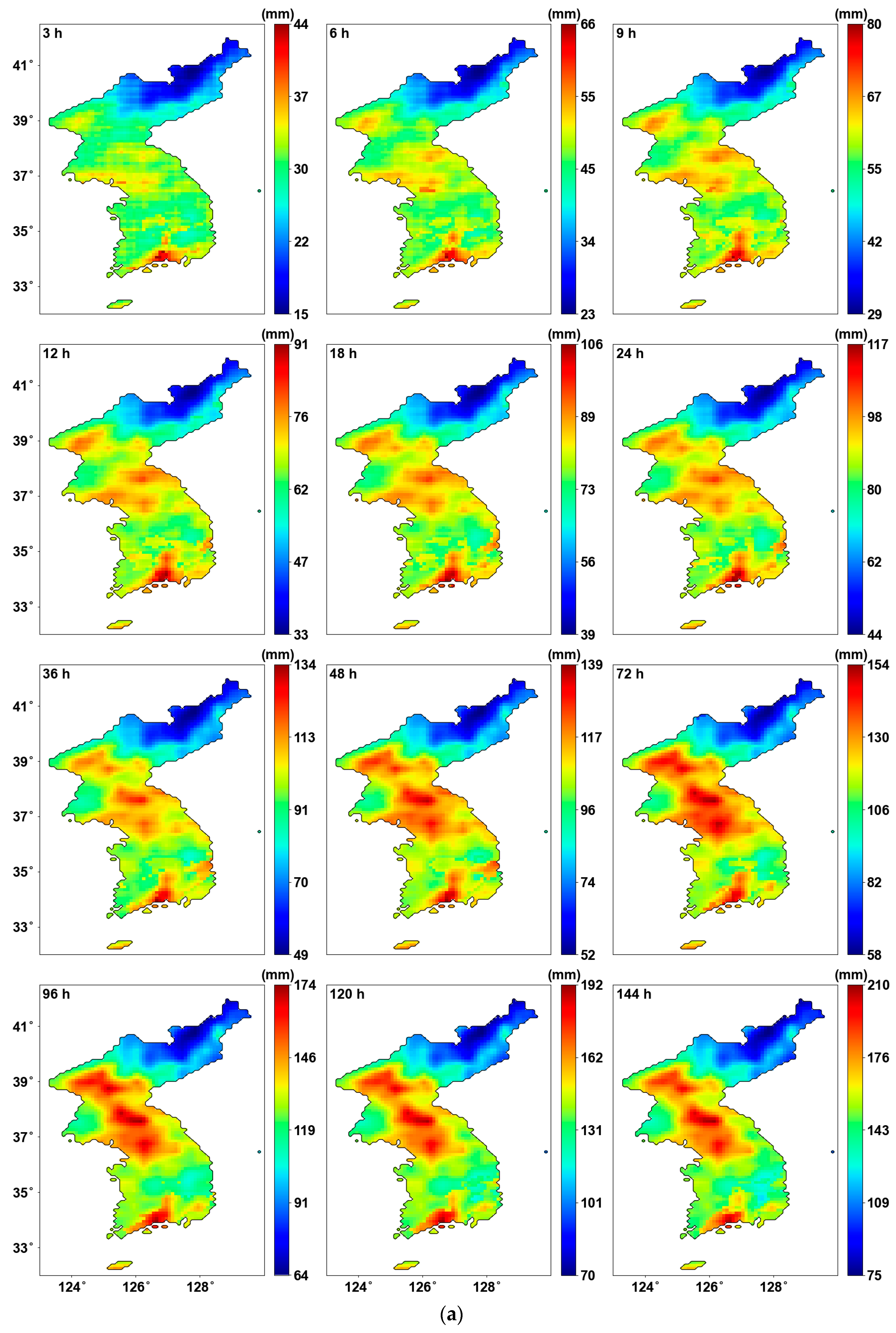

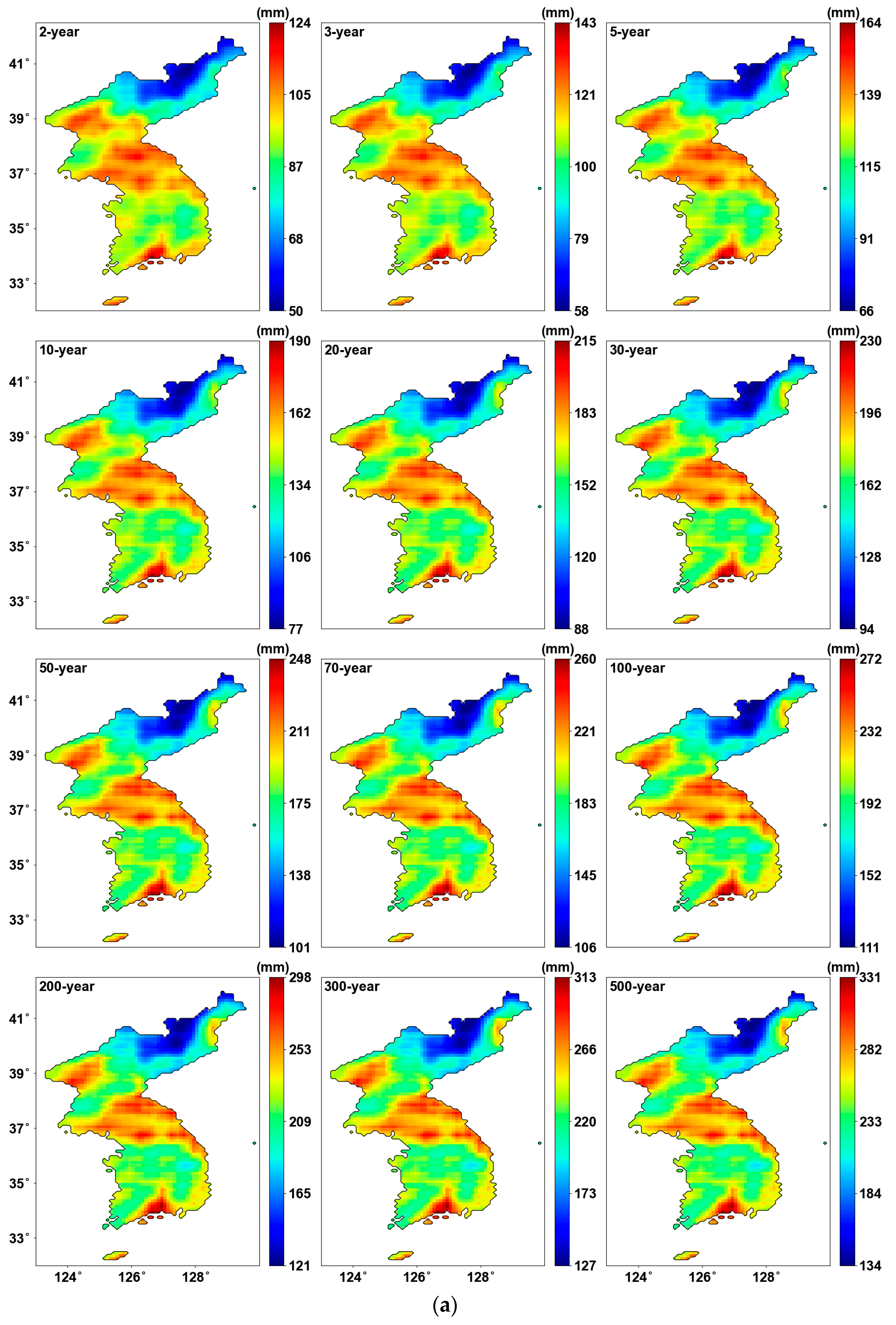



| Duration (h) | Rate (%) |
|---|---|
| 3 | 5.8 |
| 6 | 7.4 |
| 9 | 10.0 |
| 12 | 10.4 |
| 18 | 9.3 |
| 24 | 9.3 |
| 36 | 10.2 |
| 48 | 8.6 |
| 72 | 6.2 |
| 96 | 7.0 |
| 120 | 9.1 |
| 144 | 9.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Oh, S.; Baik, J.; Jun, C.; Seo, J.; Lee, E.H. Grid-Based Precipitation Quantile Estimation Considering Homogeneity Using ERA5-Land Data for the Korean Peninsula. Sustainability 2024, 16, 9295. https://doi.org/10.3390/su16219295
Lee J, Oh S, Baik J, Jun C, Seo J, Lee EH. Grid-Based Precipitation Quantile Estimation Considering Homogeneity Using ERA5-Land Data for the Korean Peninsula. Sustainability. 2024; 16(21):9295. https://doi.org/10.3390/su16219295
Chicago/Turabian StyleLee, Jinwook, Sejeong Oh, Jongjin Baik, Changhyun Jun, Jungho Seo, and Eui Hoon Lee. 2024. "Grid-Based Precipitation Quantile Estimation Considering Homogeneity Using ERA5-Land Data for the Korean Peninsula" Sustainability 16, no. 21: 9295. https://doi.org/10.3390/su16219295
APA StyleLee, J., Oh, S., Baik, J., Jun, C., Seo, J., & Lee, E. H. (2024). Grid-Based Precipitation Quantile Estimation Considering Homogeneity Using ERA5-Land Data for the Korean Peninsula. Sustainability, 16(21), 9295. https://doi.org/10.3390/su16219295








