Abstract
Enhancing flood resilience has become crucial for watershed flood prevention. However, current methods for quantifying resilience often exhibit coarse spatiotemporal granularity, leading to insufficient precision in watershed resilience assessments and hindering the accurate implementation of resilience enhancement measures. This study proposes a watershed flood resilience assessment method based on a system performance curve that considers thresholds of inundation depth and duration. A nested one- and two-dimensional coupled hydrodynamic model, spanning two spatial scales, was utilized to simulate flood processes in plain river network areas with detailed and complex hydraulic connections. The proposed framework was applied to the Hangjiahu area (Taihu Basin, China). The results indicated that the overall trend of resilience curves across different underlying surfaces initially decreased and then increase, with a significant decline observed within 20–50 h. The resilience of paddy fields and forests was the highest, while that of drylands and grasslands was the lowest, but the former had less recovery ability than the latter. The resilience of urban systems sharply declined within the first 40 h and showed no signs of recovery, with the curve remaining at a low level. In some regions, the flood tolerance depth and duration for all land use types exceeded the upper threshold. The resilience of the western part of the Hangjiahu area was higher than that of other regions, whereas the resilience of the southern region was lower compared to the northern region. The terrain and tolerance thresholds of inundation depth were the main factors affecting watershed flood resilience. The findings of this study provide a basis for a deeper understanding of the spatiotemporal evolution patterns of flood resilience and for precisely guiding the implementation and management of flood resilience enhancement projects in the watershed.
1. Introduction
Flood disasters are common and destructive natural events that pose a serious threat to the social economy and human life and property [1]. Despite the construction of high-standard flood prevention projects worldwide, these measures often struggle to withstand extreme floods due to factors such as marginal cost-effectiveness, natural geographical conditions, and limitations on the use of territorial space [2,3,4]. For instance, the 2011 floods in Thailand killed over 800 people, affected millions, and caused direct economic losses of $46 billion, severely impacting global supply chains [5]. Similarly, the 2021 floods in Europe affected Germany, Belgium, and other countries, resulting in over 200 deaths and billions of euros in economic damage [6]. In July 2023, a major flood occurred in the Haihe Basin [7]. In September of the same year, the flood disaster in Libya caused by Storm Daniel resulted in over 11,300 deaths, 10,000 missing, thousands injured, and incalculable economic losses [8]. With the intensification of global climate change and human activities, the frequency and intensity of flood events are expected to increase further, placing higher demands on watershed management and flood disaster prevention. How to make the watershed more resilient under the impact of flood disaster has become a new concept of flood disaster management.
Flood resilience is an important index to measure the ability of river basins to cope with flood disasters, which has received extensive attention in recent years [9]. Resilience has been defined in many different ways and contexts; the term resilience first appeared in the field of physics, and gradually extended to a range of natural and social sciences [10,11,12], such as engineering, psychology, ecology, and disasters science, as shown in Figure 1. In the context of flood management, “flood resilience” represents a shift from traditional flood control methods towards strategies that emphasize adaptability and recovery. It is defined as the ability of a system, community, or society to resist, absorb, accommodate, and recover from the effects of a flood in a timely and efficient manner [13]. However, flood resilience has not been investigated extensively and thoroughly to date, and no clear conceptual frameworks or quantification methods have been defined in regulations or guidelines; these are essential for effective delivery of resilience.

Figure 1.
The development of the resilience concept. (★ represents a milestone event.)
Resilience assessment methods can be divided into qualitative and quantitative assessments. Among these, quantitative assessment has significant advantages in flood resilience assessment due to its objectivity, accuracy, repeatability, and systematic nature, making it widely adopted assessment method. Multi-criteria indices-based metrics and performance-based metrics are two types of quantitative methods for evaluating resilience that have been proposed in some related literature [14,15]. Tayyab et al. [16] constructed a flood resilience evaluation system from four aspects: hazard, exposure, susceptibility, and coping capacity, and used AHP to determine the weights of each index. Fu et al. [17] constructed a comprehensive regional flood resilience index system (RFRI) containing 16 indicators based on the pressure-state-response (PSR) model, and used the analytic hierarchy process (AHP)–efficiency weight method (EWM) to assign weights to the flood resilience evaluation indicators. Zhu et al. [18] proposed a holistic evaluation framework for evaluating urban flood resilience with VIKOR and Grey Relational Analysis (GRA); the proposed framework consisted of indicators of resistance including, coping, recovery, and adaptation capacity for three stages of the flood disaster cycle, namely pre-, during and post-flood. Rezende et al. [13] proposed a multi-criteria index, the Urban Flood Resilience Index (UFRI), composed of 9 sub-indicators and taking into account resilience, adaptation, and resistance. Multi-criteria indices-based metric quantitative evaluation methods are mostly based on statistical data and are characterized by considering the interaction between flood disasters and socio-economic factors. However, the evaluation indicators are relatively subjective, and the temporal and spatial scales of the evaluation are relatively coarse, mostly focusing on assessing the changes in urban flood resilience over different years. Performance-based metrics are also used to calculate flood resilience, with the system performance curve (SPC) being the most commonly used method. Chen et al. [19] proposed a grid-based method for quantifying flood resilience, which considered human risk perception, improving the SPC. Wang et al. [20] proposed a grid-cell-based resilience metric to assess urban flood resilience at the urban drainage catchment scale; the system performance was defined as the ratio of the number of unflooded grid cells to the total grid cell number in an urban drainage catchment. Zhang et al. [21] combined the SPC with a mixed flood model, mainly considering the total simulation time of the system performance curve and the proportion of flooded cities, to simulate and evaluate the UFR in the three stages of resistance, adaptation, and recovery. Compared with the multi-criteria indices-based metrics, the evaluation results of performance-based metrics have mostly been obtained based on the hydrodynamic model, which has outstanding advantages in improving the space-time granularity of the evaluation results and ensuring the objectivity of the evaluation results.
Although performance-based metrics provide a more detailed, dynamic, and objective flood resilience assessment, the following issues remain to be addressed: (1) The traditional system performance curve is primarily used to evaluate the resilience of urban drainage systems but neglects geographic and spatial factors, necessitating a transformation into a grid-based approach; (2) The parameter selection is singular, primarily using inundation depth/flood volume as evaluation parameters. On one hand, this ignores the impact of inundation duration; on the other hand, it does not consider the threshold values of tolerable inundation depth and duration for different land use types. For example, in urban areas, inundation depths exceeding 0.15 m can affect the movement of people and vehicles, whereas in farmland, grassland, and forests, it generally does not cause disruption. Moreover, the duration of inundation is also a critical factor affecting flood resilience. Different entities, such as crops, herbaceous plants, and trees, have varying levels of tolerance to prolonged inundation exposure; (3) The spatial scale and complexity of the evaluation of flood resilience in watersheds and urban areas are very different, making it difficult to use the same index to evaluate them. However, existing research predominantly focuses on urban areas for flood resilience assessment, lacking methods specifically for evaluating flood resilience in watersheds. Therefore, traditional performance-based metrics do not take comprehensive factors into account. By accurately quantifying the differences in the resilience of different land types and providing refined evaluation of resilience, valuable rescue and engineering resources can be allocated to flood-prone areas, which is of great significance for reducing the impact of flood disasters.
The aim of this study is to propose a performance-based analytical framework for assessing flood resilience at the watershed scale. A novel resilience metric is introduced, which accounts for the effects of inundation depth and duration, determining threshold values based on the primary underlying surface type of the watershed. This metric can measure the spatiotemporal variation of watershed resilience in response to extreme rainfall events. Two spatially nested one- and two-dimensional coupled hydrodynamic models were used to simulate flood processes in plain river network areas with detailed, complex hydraulic connections. The proposed framework was applied to the Hangjiahu area (Taihu Basin, China) to identify vulnerable areas and major factors affecting flood resilience, providing guidance for building resilient and sustainable watersheds.
2. Materials and Methods
2.1. Study Area and Data
The Hangjiahu area (7436 km2) in the Taihu Basin, China, was used as the case study. The river channel and drainage systems in this area have limited capacity, with most designed to cope with a 20-year return period rainfall, while some regions can handle only less than a 10-year return period rainfall. The types of flood disaster in this area include plum rain and typhoons, with an annual average precipitation of about 1100 to 1400 mm. As shown in Figure 2, the Hangjiahu area is low-lying, with terrain sloping from the southwest to the northeast. The elevation mostly ranges from 1.2 to 2.2 m, with the highest elevation at 519.9 m and the lowest at 0 m. Eight land use types are included in the study area: paddy field, dryland, forestland, grassland, waters, urban land, rural land, and bare land, with areas of 3336.33, 924.76, 206.71, 11.09, 846.36, 767.02, 1343.00, and 0.72 km2, respectively. The detailed information of all the data used in this study is shown in Table 1.
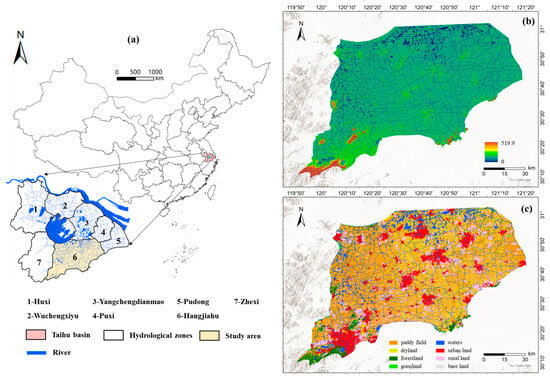
Figure 2.
The geographical location, land use, and topography of the study area: (a) geographical location, (b) the DEM, and (c) land use.

Table 1.
The detailed information of all the data.
2.2. Study Framework
A flowchart of the research is shown in Figure 3. The main steps were as follows: (1) Collect and process the basic data required for the study, including DEM data, land use data, river and hydraulic engineering data, and rainfall data; (2) Conduct flood disaster simulation, which includes three sub-steps: model construction, model calibration and validation, and analysis of simulation results; (3) Analyze the flood resilience of the basin, focusing on the spatial and temporal variation characteristics of basin flood resilience; (4) Discuss the key factors affecting resilience, including the impact of selected calculation indicators for depth and time, and potential influencing factors, and further discuss limitations and directions for improvement.
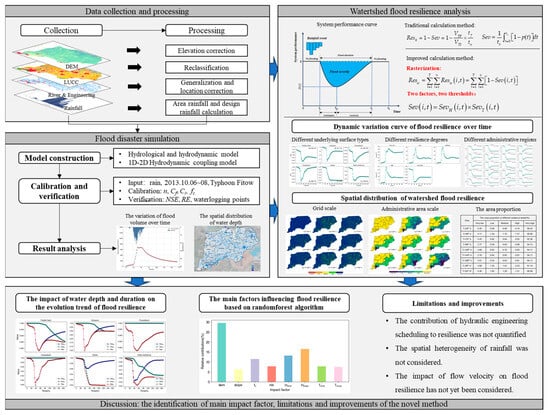
Figure 3.
The flowchart of the watershed flood resilience assessment.
2.3. Flood Disaster Simulation Method
The Taihu Basin, where the study area is located, belongs to a plain river network area and exhibits the following characteristics: (1) complex hydraulic connectivity among rivers, with many experiencing bidirectional flow; (2) numerous hydraulic structures, with flood control and drainage heavily influenced by engineering schedules, requiring coordinated inter-regional scheduling during flood seasons; (3) complex boundary conditions, including inundation levels and tidal boundaries. Therefore, to accurately simulate flood disaster processes, this study developed a watershed–regional nested hydrologic and hydrodynamic coupling model. The characteristics of the model are described in Table 2.

Table 2.
The characteristics of the watershed–regional nested hydrologic and hydrodynamic coupling model.
2.3.1. One-Dimensional Hydrodynamic River Simulation Method
In order to analyze the change processes of water level or discharge in the river channel under the operation of complex sluices, pumps, and other engineering works, the finite difference method was used to solve the Saint-Venant equations that describe the flow movement in the river channel. These equations include the continuity equation and the momentum equation [22]:
where Q is the flow rate, m3/s; q is lateral inflow, m3/s; A is the water flow area, m3; h is the water level, m; R is the hydraulic radius, m; C is the Manning coefficient; α is the momentum correction factor.
2.3.2. Two-Dimensional Surface Hydrodynamic Simulation Method
In order to obtain the dynamics of flood disaster evolution on two-dimensional surface, the semi-implicit finite volume method based on unstructured triangular grid element dispersion was used to solve the two-dimensional shallow water equation. The governing equation is as follows [23]:
The vectors involved in the above formula are:
where h is the inundation depth, m; u and v are vertical mean velocity of water flow in the x direction and y direction, respectively; zb is the bottom elevation; α is the runoff coefficient; P is rainfall intensity; Sfx and Sfy are the frictional resistance of water flow in the x direction and y direction, respectively, which can be calculated via the Manning formula.
2.4. Flood Resilience Assessment Method
2.4.1. System Performance Curve
The system performance curve was used to quantify flood resilience. Drawing on the research of Ganin et al. [24], the change process of flood resilience under an extreme rainfall event is shown in Figure 4. The initial system performance is 1, which decreases from ts following an extreme rainfall event, reaches the minimum value of p(t) at tps, and gradually recovers until full recovery at te.
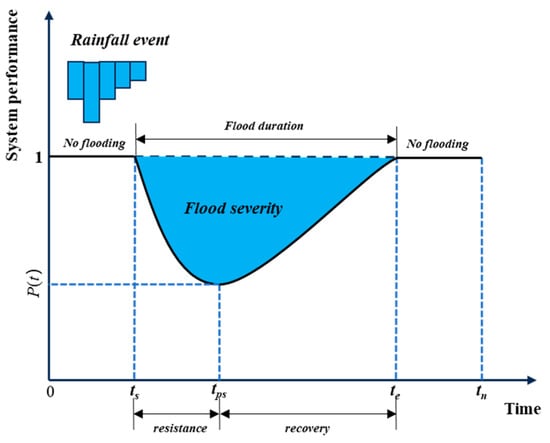
Figure 4.
System performance curve for a watershed under an extreme rainfall event. The black dotted line represents the original performance level of service and the black solid line shows the actual system performance P(t).
The blue area in Figure 4, often referred to as flood severity, represents the total amount of system performance loss during the entire flood event, calculated as follows:
where Sev is the flood severity; tn is the simulation duration.
Equation (4) is the theoretical calculation method of system performance. Mugume et al. [25] proposed a simplified method to calculate the resilience index Res0 for drainage systems. Approximating the flood severity Sev in Equation (4) as a rectangular region, the calculation formula for system resilience is as follows:
where VTF is the total flood volume; VTI is the total inflow into a drainage system, tf is the mean duration of nodal flooding, and tn is the total simulation time.
2.4.2. Flood Resilience Assessment Method Based on Improved System Performance Curve
The method proposed by Mugume et al. [25] provides only a fixed value for the resilience of a system, failing to reflect the spatiotemporal variations of resilience. Therefore, this study improves upon that method to enable a refined assessment of the spatiotemporal processes of resilience. The calculation formula is as follows:
where Resw is the watershed flood resilience; Resw(i,t) is the flood resilience f the ith grid at time t; Sevw(i,t) is the flood severity f the ith grid at time t; T is the total simulation time; n is the number of grids.
When calculating a grid-scale flood resilience index, many studies use the threshold of inundation depth as the criterion [26]. Specifically, the ith grid flood resilience is considered to be 1 if the inundation depth is less than the threshold, and 0 if the inundation depth exceeds the threshold. However, in many cases, the flood resilience begins to be affected by even shallow inundation depths. For instance, an inundation depth of 15 cm on urban land can affect pedestrians, and more than 1 m will endanger personal safety. Additionally, existing studies do not consider the impact of inundation duration. This is especially relevant for different land use types, as their tolerance to inundation duration varies according to their functions. For example, in urban areas, the lower threshold for maximum allowable drainage time is 1 h, while the upper threshold is 24 h. For farmland, the inundation tolerance threshold varies between 2 to 6 days, depending on the crop type. Therefore, traditional resilience calculation methods that consider a single threshold can result in abrupt changes in system performance at the flooding depth threshold. Additionally, neglecting the impact of inundation duration can lead to overestimation of resilience, failing to reflect the true performance of the system. In view of this, this study proposes an improved equation based on Formula (4) to calculate the flood resilience index, taking into account two thresholds of inundation depth and inundation duration, namely the upper threshold and the lower threshold. The calculation is stated as follows:
where SevH(i,t) is the flood severity due to the inundation depth of the ith grid at time t; SevT(i,t) is the flood severity due to the inundation time of the ith grid at time t; H(i,t) is the inundation depth of the ith grid at time t; Hmin(i) is the upper threshold of the inundation depth of the ith grid; Hmax(i) is the lower threshold of the inundation depth of the ith grid; T(i,t) is the inundation time of the ith grid at time t; Tmin(i) is the lower threshold of the inundation time of the ith grid; Tmax(i) is the upper threshold of the inundation time of the ith grid.
The land use types were classified into five categories: urban land, paddy fields, dryland, grassland, and forestland. Referring to technical specifications and the relevant literature [27,28,29,30,31,32,33], the threshold values for the inundation depth and duration for each land use type were determined. The results are shown in Table 3.

Table 3.
The threshold values for the inundation depth and duration for each land use type.
In addition, to compare the resilience of different subjects under the impact of flood disasters, this study proposes a recovery capability (Rc) calculation index, defined as the ratio of resilience recovery value to resilience loss value. The resilience recovery value refers to the difference between the resilience at the end of the simulation (ResE) and the minimum resilience (Resmin), while the resilience loss value refers to the difference between the resilience at the start of the simulation (ResS) and the minimum resilience. The formula is as follows:
3. Results
3.1. Flood Disaster Simulation
3.1.1. Construction of the Hydrological and Hydrodynamic Model
The generalized map of the Taihu Basin model and Hangjiahu regional model is shown in Figure 5. The Taihu Basin model categorizes the hilly area into 125 hydrological zones and the plain area into six hydrological zones for hydrological model calculations. The one-dimensional hydrodynamic river model includes 1793 rivers, 10,112 river sections, 117 lakes outside the embankment, and 210 sluice and pump structures (including ship locks). The boundary conditions encompass tidal boundaries, inflow boundaries from the upstream mountainous areas of the Taihu Basin, and lateral inflow boundaries of the rivers.
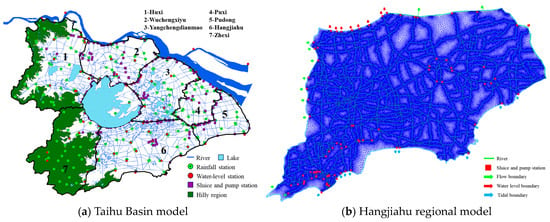
Figure 5.
Generalized map of Taihu Basin model and Hangjiahu regional model.
For the Hangjiahu regional model, the one-dimensional river hydrodynamic model comprises 970 main drainage rivers, 1961 river sections, 86 sluice and pump structures, nine flow boundaries, nine water level boundaries, and 10 tidal boundaries. The two-dimensional hydrodynamic model employs unstructured triangular mesh elements to discretize the modeling area. The mesh resolution is 5 m in the river areas and 500 m in other areas, resulting in a total of 20,498,475 triangular mesh elements and 1,024,928 nodes. The infiltration calculation uses the Horton model, which generalizes the urban drainage capacity of the pipeline network by increasing the infiltration capacity. The one-dimensional and two-dimensional hydrodynamic models were coupled via lateral connection.
3.1.2. Model Calibration and Verification
To assess the validity of the developed hydrological model, calibration and validation were carried out. Data for Typhoon Fitow in October 2013 were used for calibration, while Typhoon Jongdari in August 2018 served as the validation period. The areal rainfall process in the Hangjiahu region is illustrated in Figure 6. During Typhoon Jongdari, the maximum 24 h areal rainfall in the Hangjiahu region reached 166.4 mm, with a 3-day maximum of 173.7 mm, corresponding to a return period of approximately 70 years. For Typhoon Fitow, the maximum 24 h areal rainfall was 204.5 mm, with a return period of about 35 years, and the 3 day maximum was 293.7 mm, with a return period of around 70 years.
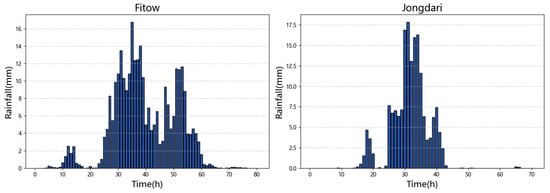
Figure 6.
Areal rainfall process during Typhoon Fitow and Typhoon Jongdari.
The simulation duration for the calibration period was set to 3 days, with output results recorded every hour. After calibration, the Manning coefficient (n) for the main channel was 0.02 and for the floodplain, it was 0.25. The free-flow discharge coefficient (Cf) for the gates was 0.3149, and the submerged flow coefficient was 0.81. Figure 7 presents a comparison of observed and simulated water levels at representative stations. The calibration results indicate that the difference between the observed and simulated maximum water levels ranged from −0.09 m to 0.1 m, with a relative error between −2.58% and 3.64%, demonstrating the accuracy of the model.
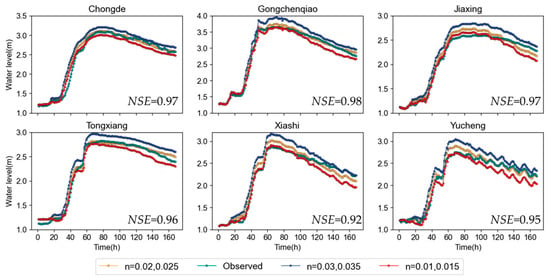
Figure 7.
Sensitivity of simulated rating curves to the variation of a selected range of Manning’s roughness coefficients.
The water level process at various stations during Typhoon Jongdari was simulated based on the calibrated parameters, as shown in Figure 8. The results indicated that the simulated values matched the observed values well. Compared with the observed maximum water levels, the error at Xiashi Station was −0.09 m, and at Jiaxing Station it was 0.05 m. The Nash–Sutcliffe efficiency coefficients were all above 0.95, demonstrating that the model’s generalization and parameter settings were reasonable and suitable for further research.
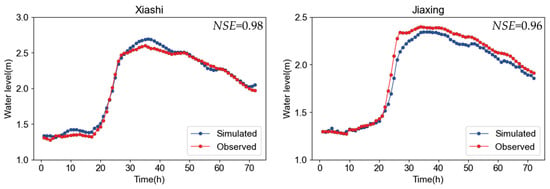
Figure 8.
The verification results of water level processes during Typhoon Jongdari.
For the two-dimensional hydrodynamic model, stable infiltration rates for different underlying surfaces were determined based on the relevant literature [34,35,36], and the corresponding Manning coefficients were calibrated, as shown in Table 4. Additionally, based on news reports and some measured data, the water depths of each water accumulation point were estimated as validation data for the two-dimensional model, as shown in Figure 9. The results showed that the simulation was able to identify all waterlogging point locations. In the study area, the measured inundation depths ranged from 0.2 to 1.7 m, while simulated depths ranged from 0.17 to 1.86 m. The relative errors ranged from −18.76% to 15.62%, with errors less than 20%. The minimum absolute error was 6.14%. Therefore, the two-dimensional hydrodynamic model’s generalization can be considered reasonably accurate.

Table 4.
Steady infiltration rate and manning coefficient after calibration.
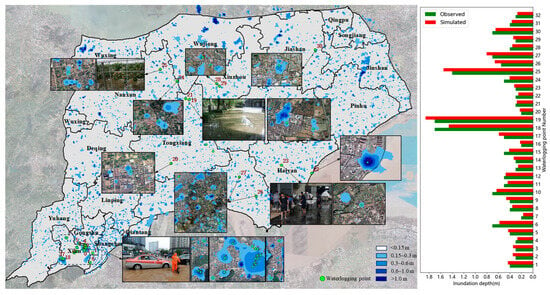
Figure 9.
Comparison of measured and simulated water depth at urban waterlogging points.
3.1.3. Flood Disaster Simulation Based on the Typhoon Fitow Rain Pattern Under a 100-Year Return Period
Based on the Typhoon Fitow rainfall pattern, the same-frequency amplification method was used to obtain the areal rainfall under a 100-year return period for the Hangjiahu region. The maximum one-hour rainfall was 21.7 mm, the maximum one-day rainfall was 262 mm, and the maximum three-day rainfall was 316 mm. The corresponding flood disaster was simulated, with a rainfall duration of 3 days, a simulation duration of 7 days, and result output intervals of 2 h. As seen in Figure 10a, the overall trend in flood volume included four stages: slow increase, rapid increase, fluctuating change, and decrease. The flood volume showed a lag relative to the peak times of rainfall, with the rainfall peak occurring at the 35th hour and the flood volume peak at the 38th hour. This lag was due to the fact that, after the rainfall reached its peak intensity, the subsequent rainfall still exceeded the drainage capacity of the study area, causing further water accumulation. Between the 38th and 52nd hours, the fluctuation in flood volume was mainly due to the reduced rainfall being approximately equal to the drainage capacity of the entire region. The peak flood volume time was considered the most severe moment of the flood disaster, and a spatial distribution map of water depth was drawn, as shown in Figure 10b. According to the spatial distribution of water depth, areas with high water depth were mainly distributed around the Hangjiahu region, including the main urban area of Hangzhou in the southwest, Songjiang District in the northwest, Wujiang District in the north, Pinghu City in the east, and Haining City in the south. Although the central area of Hangjiahu had a wide distribution of flood volume greater than 0.15 m at the most severe moment, the central area’s flood control and drainage projects, such as the Pinghu Pond extension and dredging project, the expansion of the southern drainage project in Hangjiahu, and pump stations in the embankment area, resulted in rapid discharge of floodwater. By the end of the simulation, water depth in most areas had reduced to below 0.15 m.
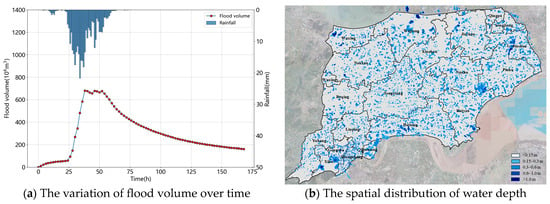
Figure 10.
The variation curve and spatiotemporal distribution of flood volume.
3.2. Flood Resilience Assessment Results
3.2.1. Dynamic Variation Curve of Flood Resilience over Time
The dynamic curves of flood resilience for different land use types at 2 h intervals were plotted, as shown in Figure 11. The results showed that the time at which the resilience of different underlying surfaces reached the minimum value varied slightly, between 38 and 52 h. The overall trend decreased initially and then increased, consistent with the theoretical resilience curve pattern. The resilience of dryland and grassland was most affected by rainfall, with the lowest resilience values being approximately 0.65 for dryland and 0.88 for grassland. Paddy fields and forestland had higher flood tolerance depth and duration, resulting in lower loss of resilience values. The resilience trend in urban areas differed from that of other land use types, lacking the recovery phase after reaching the minimum point. The resilience values for all land use types did not recover to 1, indicating that there were areas of each land use type where the flood tolerance depth and duration exceeded the upper threshold. Regarding recovery ability, in descending order, they were grassland (98.7%), dryland (71.1%), forestland (67.3%), paddy fields (30.1%), and urban areas (0). The average recovery capacity of the whole basin was 29%. Overall, due to the influence of surface characteristics, drainage capacity, and other factors, different land use types exhibited significant differences in their recovery ability following flood events.
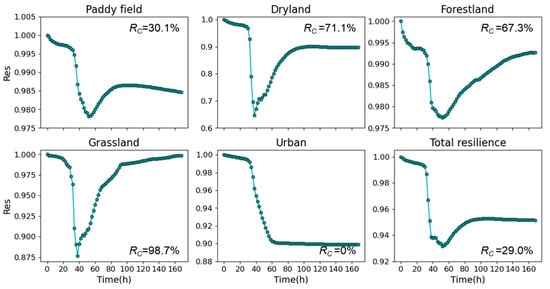
Figure 11.
The dynamic changes in flood resilience across different underlying surface types.
The dynamic curves of flood resilience for different resilience degrees at 2 h intervals were plotted, as shown in Figure 12. The results indicated that from very low to high resilience, the area initially increased, then decreased, followed by a fluctuating trend over time, whereas the area of very high resilience first decreased, then increased, finally remaining stable. For very low and very high resilience, significant changes in area occurred between the 30th and 38th hour. For low, medium, and high resilience, significant area changes occurred between the 30th and 60th hour. From very low to very high resilience, the times when the area increased or decreased to its peak were at the 58th, 52nd, 46th, 40th, and 40th hours, respectively. In terms of the peak area, from largest to smallest, they were very high, very low, high, medium, and low, respectively.
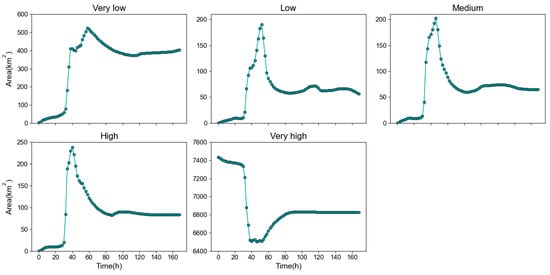
Figure 12.
The dynamic changes in area across different resilience degrees.
The dynamic curves of flood resilience for different administrative regions at 2 h intervals were plotted, as shown in Figure 13. The results showed that the process of resilience change in different regions could be analyzed in two stages. The first stage was from the beginning to the moment of the lowest resilience value, reflecting the basin’s resistance to flood disasters. The second stage was from the moment of the lowest resilience value to the end of the simulation, reflecting the basin’s recovery ability after being impacted by flood disasters. Significant differences were observed among different administrative regions in both the resistance and recovery stages. During the resistance stage, the resilience trends in some regions decreased slowly at first and then rapidly, such as Deqing, Gongshu, and Jiashan, etc. In contrast, some regions experienced a rapid decrease from the start, such as Jinshan and Qingpu, etc. During the recovery stage, resilience in some regions, such as Haiyan, Songjiang, and Qingpu, showed significant recovery. In contrast, resilience in regions like Gongshu, Shangcheng, and Xihu showed minimal recovery, while regions like Qiantang continued to decrease. Moreover, in the stage of rapid resilience decline, most regions, such as Gongshu and Linping, directly decreased to the lowest value, while some regions, such as Haining and Pinghu, showed a fluctuating decline to the lowest value. Regarding the resilience values, Deqing had the highest resilience at approximately 0.98, while Shangcheng had the lowest at approximately 0.84. The resilience in Gongshu, Haiyan, and Shangcheng decreased below 0.9. Regarding the recovery ability of each administrative region, 30% of the areas had a recovery ability of less than 10%, 20% had a recovery ability between 10% and 30%, and 50% had a recovery ability greater than 30%. Among them, Xiuzhou had the highest recovery ability at 56.2%, while Qiantang has the lowest recovery ability at 0.
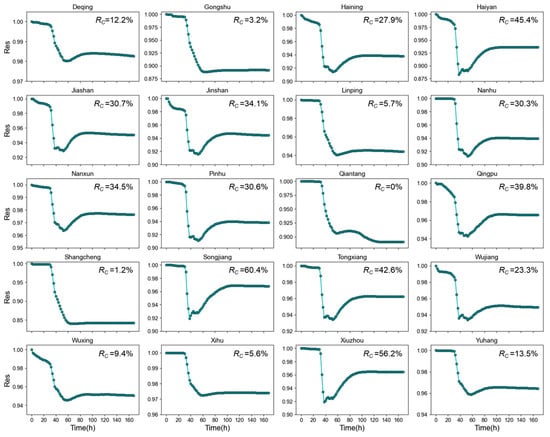
Figure 13.
Dynamic changes in flood resilience across different administrative regions.
3.2.2. Spatial Distribution of Watershed Flood Resilience Considering the Dynamic Process of Floods
Spatial distribution maps of resilience at 24 h intervals were drawn. Meanwhile, based on the total resilience change curve in the Hangjiahu area, spatial distribution maps corresponding to the peak rainfall time and the time of minimum resilience were also created, as shown in Figure 14. From the spatial distribution of flood resilience, the decrease in resilience primarily begins in the northern, southern, and eastern parts of the basin. Subsequently, as the rainfall intensity increases, resilience significantly decreases in all areas of the basin except the western region. As the rainfall intensity decreases, flood resilience in the central and eastern regions begins to gradually recover. Overall, the grid distribution of resilience loss is relatively dispersed, but there are two more concentrated areas in the southwestern and southeastern parts of the basin (marked by red boxes in the figure). The southwestern area, which is located in the main urban area of Hangzhou, exhibits lower resilience due to the high proportion of urban land, smaller tolerance threshold of inundation depth, poor drainage, a long northern drainage path, and southern drainage affected by tidal levels, resulting in inundation exceeding the threshold. The southeastern area has lower resilience due to its low-lying terrain, and the surrounding waterlogging water collects here. In addition, the land type is paddy field, with weak infiltration capacity, and lack of effective drainage facilities is also a factor.
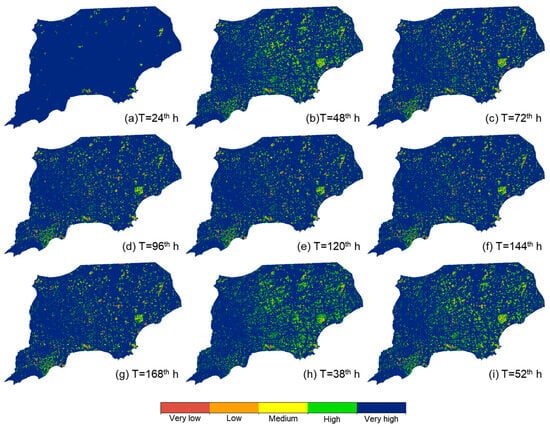
Figure 14.
Spatial distribution of flood resilience on grid scale at different times.
Based on the spatial distribution of resilience at different stages of flood disasters, the area proportions of different resilience levels at corresponding times were calculated, as shown in Table 5. The result showed that the area proportion of very high resilience is generally between 90% and 95%, the area proportion of very low resilience is approximately 0% to 5%, and the area proportions of other resilience levels are about 0% to 2%. When the basin reaches its overall lowest resilience, this is mainly due to significant increases in the areas of extremely low and low resilience, which together account for approximately 6.31% of the total area.

Table 5.
The area proportion of different resilience levels at different stages of flood disasters.
The spatial distribution maps of flood resilience across different administrative regions at various times are shown in Figure 15. The result showed that the spatial pattern of flood resilience in the basin featured three stages. At the beginning of the disaster, the flood resilience of the entire basin was at a very high level. As the flood disaster progressed, the flood resilience in the central and eastern regions began to decrease. The overall trend showed that the resilience in the western region was higher than in other regions, and the resilience in the northern region was higher than in the southern region. Subsequently, the flood resilience gradually recovered, with the overall trend indicating that the southern region had relatively lower resilience. The low-resilience areas were concentrated in Gongshu District, Shangcheng District, and Qiantang District of Hangzhou. The main reason for this phenomenon is that high-resilience areas are primarily composed of paddy fields and forest land, which have higher thresholds for flood tolerance in terms of depth and duration. Therefore, it is difficult for low-resilience areas to form. Shangcheng District has lower resilience because its main land use is urban, which has a lower flood tolerance threshold. Additionally, the runoff from the southern mountainous areas causes the resilience to be low. In parts of Haiyan County, there are low-lying areas where floodwater accumulates and cannot be drained, resulting in lower resilience. The low resilience in Haining, Pinghu, and Jinshan Districts along Hangzhou Bay is due to poor drainage caused by tidal forces hindering southern and eastern drainage. The higher resilience of the western region is mainly influenced by the drainage pattern of the watershed. Overall, the drainage paths flow from south to north and from west to east. There is no external water accumulation in the western region, and the floodwaters in this area flow into the central and eastern regions.
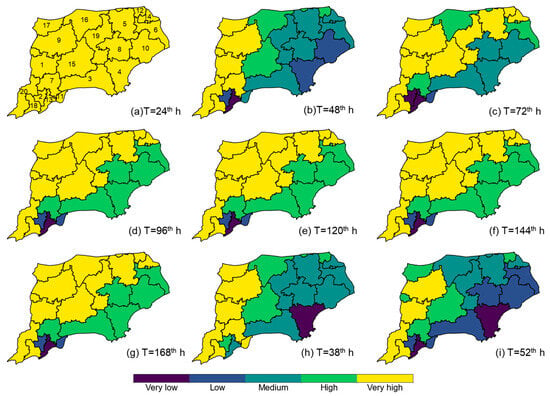
Figure 15.
Spatial distribution of flood resilience at different times for different administrative regions at different times, where the corresponding relationship between the serial number in (a) and the name of the administrative region is shown in Table 6.
The statistical results of the area proportion of flood disasters for different administrative regions at different resilience levels at the lowest resilience moment are shown in Table 6. The results show that the proportion of areas with very low resilience ranged from 0.94% to 7.76%, with Deqing having the smallest proportion and Haiyan the largest. The proportion of areas with low resilience ranged from 0.63% to 6.09%, with Deqing having the smallest proportion and Shangcheng the largest. The proportion of areas with medium resilience ranged from 0.33% to 2.06%, with Xihu having the smallest proportion and Qiantang the largest. The proportion of areas with high resilience ranged from 0.53% to 2.46%, with Xihu having the smallest proportion and Qiantang the largest. The proportion of very-high-resilience areas ranged from 82.35% to 97.04%. Among them, eight administrative regions had an area proportion of less than 90%. Shangcheng had the smallest resilience proportion, while Deqing had the largest resilience proportion. In terms of average resilience values, Shangcheng had the lowest flood resilience, while Deqing had the highest.

Table 6.
The area proportion of flood disasters for different administrative regions at different resilience levels.
4. Discussion
4.1. The Impact of Inundation Depth and Inundation Time on the Evolution Trend of Flood Resilience
Historically, water depth has been the primary indicator for assessing flood resilience [37]. However, Najibi et al. [38] highlighted that flood duration is a crucial factor influencing the impact of flood disasters. The longer the flood duration, the greater is the effect on human populations, with the impact being particularly pronounced in urban areas [39]. To further understand the impact of inundation depth and inundation time on resilience, we defined two new variables, ResH and ResT. ResH represents resilience based on inundation depth and is calculated as 1 − SevH, while ResT represents resilience based on inundation time and is calculated as 1 − SevT. The variation curves of ResH, ResT, and Res were plotted, as shown in Figure 16. The results indicated that the trends of ResH and ResT for paddy fields and drylands were consistent. Specifically, ResH initially decreased and then increased, while ResT remained unchanged at first and then decreased. Therefore, for paddy fields and drylands, inundation depth primarily affects flood resilience during the resistance phase, determining the minimum resilience values, whereas waterlogging duration mainly impacts resilience during the recovery phase, affecting their post-flood recovery capabilities. For forests and grasslands, because they have a higher tolerance for waterlogging duration [40], there were no significant changes throughout the flooding event. The lower thresholds of inundation time for grasslands and forests were 144 h and 240 h, respectively. Therefore, inundation depth is also the main factor affecting the flood resilience of forests and grasslands. For urban areas, the change in flood resilience differed from other studies, mainly due to ResT. Because urban areas are relatively important and have a lower tolerance in terms of inundation time, many areas experience reduced water depth but still exceed the upper threshold for inundation time (24 h). Consequently, even if inundation depth decreases, ResT does not recover in many areas, and thus, according to Formula (7), resilience in urban areas does not increase. However, considering only the trend of ResH, its pattern is consistent with previous studies [19,37]. At the watershed scale, the trend of ResH showed an initial decrease followed by an increase, while ResT gradually decreased but with three plateau periods. This phenomenon occured because water depth is influenced by rainfall and drainage capacity, leading to both increases and decreases, whereas inundation time only increased or remained unchanged.
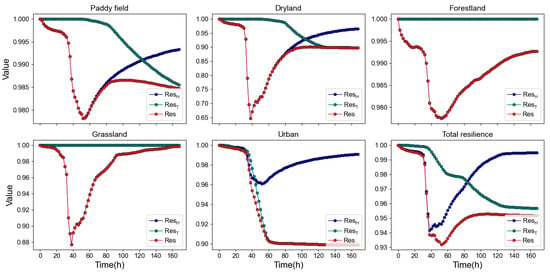
Figure 16.
The dynamic changes in ResH, ResT, and Res across different underlying types, where ResH represents flood resilience based on inundation depth, ResT represents flood resilience based on inundation time, and Res represents resilience based on this study.
In summary, the results of this study highlight that watershed resilience is more sensitive to changes in inundation depth, as these changes are more pronounced compared with flood duration. However, both inundation depth and flood duration are critical factors influencing flood resilience, and these findings are consistent with previous studies [13,41].
4.2. Identification of the Main Factors Influencing Flood Resilience
The contributions of eight indicators to flood resilience: elevation (dem), terrain slope (slope), steady infiltration rate (fc), Manning’s coefficient (mn), lower threshold of water depth (Hmin), upper threshold of water depth (Hmax), upper threshold of waterlogging time (Tmin), and lower threshold of waterlogging time (Tmax) were calculated based on the random forest model, as shown in Figure 17. The results showed that the contributions, in order of significance from highest to lowest, were from dem, Hmax, Hmin, fc, mn, Tmin, Tmax, and slope. These findings are similar to previous studies [42]. Among the aforementioned indicators, DEM and slope represent the impact of terrain on resilience by altering flow paths, with a combined contribution rate of 35.8%. fc and mn represent the impact of the underlying surface properties on resilience. fc indicates the infiltration and drainage capacity in different regions in this study, while mn represents the resistance to water flow in various regions, leading to localized water level increases. Together, they contribute 19.2%. Hmin and Hmax represent the tolerance of different underlying surfaces to the depth of water accumulation, with a combined contribution rate of 29.7%. Tmin and Tmax represent the tolerance of different underlying surfaces to the duration of water accumulation, with a combined contribution rate of 15.3%. Therefore, terrain is the main factor affecting flood resilience [43], and compared with the duration of water accumulation, the depth of water accumulation has a more significant impact on resilience [44].
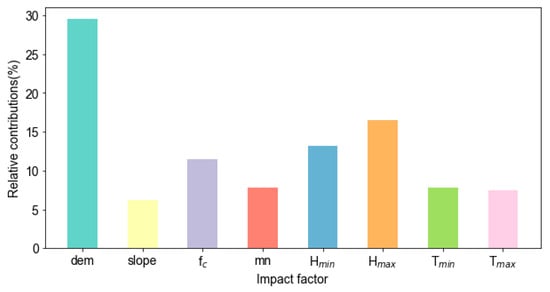
Figure 17.
The relative contributions of eight indicators to flood resilience.
4.3. Analysis of the Reasons for Differences in Inundation Depth and Duration Thresholds Among Four Land Use Types
There were differences in inundation depth and duration thresholds between the four land use types—paddy fields, drylands, forestland, grassland, and urban areas. The specific reasons for these differences are as follows:
(1) Paddy Fields: Higher thresholds for both depth and duration. Paddy fields are usually designed for irrigation and are inherently more tolerant of prolonged water accumulation. The crops and soil in paddy fields can withstand longer periods of inundation and deeper water levels without significant damage. However, once these thresholds are exceeded, crop growth may be adversely affected, and the field may suffer from soil saturation issues [45].
(2) Dryland: Lower thresholds for both depth and duration. Drylands are typically used for crops that are not water-tolerant, and the soil in these areas is not suited for prolonged waterlogging. Excessive water accumulation, even for short periods, can lead to root suffocation, crop failure, and soil compaction, which decreases the land’s agricultural productivity [46].
(3) Forestland: Moderate depth threshold, high duration threshold. Forestland has a good natural drainage system, and the deep root systems of trees help maintain soil aeration and drainage. Forests can tolerate prolonged inundation, but only up to a certain depth. If water levels exceed the root zone, tree health may be compromised [47].
(4) Grassland: Moderate thresholds for depth and duration. Grassland has intermediate resilience, with the ability to tolerate moderate water accumulation due to its soil and vegetation characteristics. Grass roots can absorb water and help with drainage, but excessive inundation can lead to root rot and vegetation loss [48].
(5) Urban Areas: due to the combination of high vulnerability, impermeable surfaces, dense population, and critical infrastructure needs, urban areas have much lower thresholds for inundation depth and duration compared with other land use types [49]. Firstly, urban areas consist largely of impermeable surfaces such as roads and buildings, which prevent natural water infiltration. This leads to rapid water accumulation during heavy rainfall, unlike rural or natural areas where permeable soils can help absorb and drain excess water. Secondly, key infrastructure components in urban areas, such as power grids, communication networks, transportation systems, and water supply, are highly sensitive to flooding [50]. Even shallow water can cause significant disruptions, including power outages, traffic paralysis, and communication failures. Prolonged inundation can also severely damage underground drainage systems and building foundations. Thirdly, urban areas typically have dense populations, and the movement of people and vehicles is critical. Shallow water can quickly obstruct pedestrian and vehicular movement, causing widespread disruption to daily life and emergency responses. Finally, although cities have dedicated drainage systems, these systems often have limited capacity to handle extreme rainfall or flood events. Prolonged water accumulation can overwhelm drainage systems, leading to persistent flooding and exacerbating urban flood risks.
4.4. The Potential Impact on Practical Flood Resilience Enhancement Measures
This study provides a fine-scale, grid-based analysis of flood resilience, allowing precise identification of vulnerable areas within a watershed. The improved resilience assessment model, which accounts for the thresholds of inundation depth and duration for different land use types, offers insights into how different areas respond to floods. This understanding can be utilized by planners and engineers to prioritize areas for flood-proof infrastructure [51]. For instance, the spatiotemporal resilience curves can guide more precise allocation of resources during flood events by identifying regions with slower recovery times or higher vulnerability due to extended inundation periods. In areas with low resilience, such as urban centers with poor drainage, these findings could support the prioritization of flood-proof infrastructure, such as the installation of high-capacity drainage systems or flood barriers. The resilience analysis for agricultural areas with significant crop losses due to prolonged flooding can inform the development of flood-tolerant farming practices or the construction of retention basins to mitigate the impact of future flood events [52]. Additionally, by identifying the main factors influencing flood resilience, such as terrain and tolerance thresholds, the findings provide actionable information for policymakers and watershed managers. They can develop more effective flood prevention strategies tailored to the specific characteristics of different regions within the watershed [53].
4.5. Limitations and Improvements
(1) The contribution of hydraulic engineering scheduling to resilience was not quantified. Flood control in a watershed is a crucial task in flood management, with the main objective being to maintain the water levels of basin-wide rivers within a reasonable range to ensure the drainage safety of towns along the river. Therefore, hydraulic engineering, as the main flood control measure in the watershed, plays a crucial role in enhancing watershed resilience [54]. Although this study considered the impact of hydraulic engineering scheduling on watershed resilience through a one-dimensional hydrodynamic model during the modeling process, it does not provide an appropriate quantitative method to characterize the scheduling capacity of hydraulic engineering when analyzing key factors affecting basin resilience. Hence, future research should adopt a reasonable method to quantify the scheduling capacity of hydraulic engineering, to calculate its contribution to basin resilience;
(2) The spatial heterogeneity of rainfall was not considered. Compared with the evaluation of urban flood resilience, the spatial scale of basin flood resilience evaluation is larger. Therefore, rainfall within a basin exhibits spatial variability. Unfortunately, this study considered only the impact of areal rainfall on resilience and did not reflect the spatial variability of rainfall on the resilience assessment, which may have led to less accurate evaluation results to some extent [55]. Future research should establish rainfall scenarios with spatial heterogeneity based on the rainfall characteristics of the basin to make the resilience evaluation results more consistent with actual conditions;
(3) The impact of flow velocity on flood resilience has not yet been considered. Many studies have shown that water flow velocity significantly affects crops, trees, people, vehicles, and more [26]. This study did not consider water flow velocity when calculating flood resilience because the study area is a plain region with minimal elevation changes. Compared to inundation depth and duration, the impact of water flow velocity on flood resilience is relatively small. However, within a comprehensive, holistic, and universally applicable method, water flow velocity should be included in the resilience evaluation system. This is also an important research area that needs further study;
(4) The contribution of this study lies in integrating both inundation depth and duration thresholds into a watershed flood resilience assessment framework. This dual-threshold approach addresses a major limitation in previous methods, which typically considered only a single threshold or focused solely on depth. By combining depth and duration, our approach provides a more comprehensive and dynamic assessment, capturing the long-term impacts of flooding on resilience. This is particularly important for certain disaster-affected areas, where prolonged water retention can have irreversible effects, such as crop loss or damage to buildings. Additionally, this study expands on how this approach enhances existing frameworks by offering more refined spatiotemporal granularity, allowing more targeted flood management interventions. This improvement is particularly critical for regions that experience slow recovery due to extended inundation periods, an aspect often underestimated in current resilience models.
5. Conclusions
This study proposes a method to quantify flood resilience at the watershed scale by considering the tolerance of key underlying surfaces to inundation depth and duration. Applied to the 7462 km2 Hangjiahu area, the method analyzed spatiotemporal flood resilience distributions under extreme rainfall scenarios and identified the key factors influencing resilience. The main conclusions are as follows:
(1) Compared with the peak rainfall time, there was a noticeable lag between the time of minimum resilience and the rainfall peak. For different land use types, the lag time ranged from 3 to 17 h. Drylands and grasslands exhibited lower flood resilience, while paddy fields and forests demonstrated higher flood resilience. Urban areas showed a unique resilience trend, lacking a recovery phase. In terms of recovery capacity, grasslands had the highest recovery rate (98.7%), while urban areas had the lowest (0%). Xiuzhou District exhibited the highest recovery rate (56.2%), and Qiantang District the lowest (0%);
(2) Regarding the spatial distribution of flood resilience, as rainfall intensity increases, resilience significantly decreases across the basin, except in the western region. The overall trend shows that the western region has higher resilience compared with other areas, and the northern region has higher resilience than the southern region. Low-resilience grids exhibit a fragmented distribution overall, but two concentrated areas were identified in the southwestern and southeastern parts of the basin. The resilience assessment of different administrative regions revealed that Shangcheng District has the lowest flood resilience, while Deqing County has the highest;
(3) The inundation depth and inundation time are both critical factors affecting watershed resilience. The watershed’s resilience is more sensitive to changes in inundation depth because these changes are more drastic compared to inundation time. The terrain and tolerance thresholds of inundation depth are the main factors affecting watershed flood resilience, with a combined contribution rate of 65.5%.
Although the method proposed in this study has significant advantages in quantify-ing flood resilience in watersheds, future research needs to continue in-depth studies on quantifying the contribution of hydraulic engineering to resilience improvement, considering the spatial heterogeneity of rainfall, and incorporating flow velocity into the resilience evaluation system.
Author Contributions
Conceptualization, X.S. and L.W.; methodology, X.S. and L.W.; software, X.S. and L.L.; validation, X.S., L.W. and L.L.; formal analysis, X.S. and X.L.; investigation, X.S., X.L. and Y.L.; resources, Y.W.; data curation, Y.L. and Q.H.; writing—original draft preparation, X.S.; writing—review and editing, X.S.; visualization, X.S.; supervision, Q.H.; funding acquisition, Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Chinese National Key Research and Development Program, grant numbers 2021YFC3000101, 2021YFC3000105; the Chinese National Natural Science Foundation, grant numbers 52309026, 52239008; China Postdoctoral Science Foundation, grant number 2023M741769; Central Public Interest Scientific Institution Basal Research Fund of China, grant numbers Y523005, Y523007, Y523010; Huadong Engineering Corporation commissioned project, grant number Hj522087.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data will be made available on request.
Acknowledgments
Thanks are given to the anonymous reviewers and editors for their constructive comments.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Rentschler, J.; Avner, P.; Marconcini, M.; Su, R.; Strano, E.; Vousdoukas, M.; Hallegatte, S. Global evidence of rapid urban growth in flood zones since 1985. Nature 2023, 622, 87–92. [Google Scholar] [CrossRef]
- Alipour, A.; Ahmadalipour, A.; Moradkhani, H. Assessing flash flood hazard and damages in the southeast United States. J. Flood Risk Manag. 2020, 13, e12605. [Google Scholar] [CrossRef]
- Ionita, M.; Nagavciuc, V. Extreme floods in the eastern part of Europe: Large-scale drivers and associated impacts. Water 2021, 13, 1122. [Google Scholar] [CrossRef]
- Zhu, S.; Li, D.; Feng, H.; Zhang, N. The influencing factors and mechanisms for urban flood resilience in China: From the perspective of social-economic-natural complex ecosystem. Ecol. Indic. 2023, 147, 109959. [Google Scholar] [CrossRef]
- Nakmuenwai, P.; Yamazaki, F.; Liu, W. Automated extraction of inundated areas from multi-temporal dual-polarization RADARSAT-2 images of the 2011 central Thailand flood. Remote Sens. 2017, 9, 78. [Google Scholar] [CrossRef]
- Chan FK, S.; Yang, L.E.; Mitchell, G.; Guan, M.; Lu, X.; Wang, Z.; Montz, O.; Adekola, O. Comparison of sustainable flood risk management by four countries–the United Kingdom, the Netherlands, the United States, and Japan–and the implications for Asian coastal megacities. Nat. Hazards Earth Syst. Sci. 2022, 22, 2567–2588. [Google Scholar] [CrossRef]
- Jiao, Z.; Zhang, Z.; Wu, L. SAR-based dynamic information retrieving of the Beijing-Tianjin-Hebei flood-inundation happened in July 2023, North China. Geomat. Nat. Hazards Risk 2024, 15, 2366361. [Google Scholar] [CrossRef]
- Oduoye, M.O.; Karim, K.A.; Kareem, M.O.; Shehu, A.; Oyeleke, U.A.; Zafar, H.; Muhsin Umar, M.; Raja, H.A.; Adegoke, A.A. Flooding in Libya amid an economic crisis: What went wrong? IJS Glob. Health 2024, 7, e0401. [Google Scholar] [CrossRef]
- Sun, R.; Shi, S.; Reheman, Y.; Li, S. Measurement of urban flood resilience using a quantitative model based on the correlation of vulnerability and resilience. Int. J. Disaster Risk Reduct. 2022, 82, 103344. [Google Scholar] [CrossRef]
- Alexander, D.E. Resilience and disaster risk reduction: An etymological journey. Nat. Hazards Earth Syst. Sci. 2013, 13, 2707–2716. [Google Scholar] [CrossRef]
- McClymont, K.; Morrison, D.; Beevers, L.; Carmen, E. Flood resilience: A systematic review. J. Environ. Plan. Manag. 2020, 63, 1151–1176. [Google Scholar] [CrossRef]
- Koliou, M.; van de Lindt, J.W.; McAllister, T.P.; Ellingwood, B.R.; Dillard, M.; Cutler, H. State of the research in community resilience: Progress and challenges. Sustain. Resilient Infrastruct. 2020, 5, 131–151. [Google Scholar] [CrossRef]
- Rezende, O.M.; de Oliveira AK, B.; Jacob AC, P.; Miguez, M.G. A framework to introduce urban flood resilience into the design of flood control alternatives. J. Hydrol. 2019, 576, 478–493. [Google Scholar] [CrossRef]
- Argyroudis, S.A.; Mitoulis, S.A.; Hofer, L.; Zanini, M.A.; Tubaldi, E.; Frangopol, D.M. Resilience assessment framework for critical infrastructure in a multi-hazard environment: Case study on transport assets. Sci. Total Environ. 2020, 714, 136854. [Google Scholar] [CrossRef] [PubMed]
- Zheng, J.; Li, J.; Zeng, J.; Huang, G.; Chen, W. Application of a time-dependent performance-based resilience metric to establish the potential of coupled grey-green infrastructure in urban flood management. Sustain. Cities Soc. 2024, 112, 105608. [Google Scholar] [CrossRef]
- Tayyab, M.; Zhang, J.; Hussain, M.; Ullah, S.; Liu, X.; Khan, S.N.; Baig, M.A.; Hassan, W.; Al-Shaibah, B. Gis-based urban flood resilience assessment using urban flood resilience model: A case study of peshawar city, khyber pakhtunkhwa, pakistan. Remote Sens. 2021, 13, 1864. [Google Scholar] [CrossRef]
- Fu, X.; Liu, Y.; Xie, Z.; Jiang, F.; Xu, J.; Yang, Z.; Deng, Z.; Wang, Q.; Liao, M.; Wu, X.; et al. A coupled PSR-based framework for holistic modeling and flood resilience assessment: A case study of the 2022 flood events in five southern provinces of China. J. Hydrol. 2024, 636, 131255. [Google Scholar] [CrossRef]
- Zhu, S.; Li, D.; Huang, G.; Chhipi-Shrestha, G.; Nahiduzzaman, K.M.; Hewage, K.; Sadiq, R. Enhancing urban flood resilience: A holistic framework incorporating historic worst flood to Yangtze River Delta, China. Int. J. Disaster Risk Reduct. 2021, 61, 102355. [Google Scholar] [CrossRef]
- Chen, J.; Chen, W.; Huang, G. Assessing urban pluvial flood resilience based on a novel grid-based quantification method that considers human risk perceptions. J. Hydrol. 2021, 601, 126601. [Google Scholar] [CrossRef]
- Wang, Y.; Meng, F.; Liu, H.; Zhang, C.; Fu, G. Assessing catchment scale flood resilience of urban areas using a grid cell based metric. Water Res. 2019, 163, 114852. [Google Scholar] [CrossRef]
- Zhang, Y.; Yue, W.; Su, M.; Teng, Y.; Huang, Q.; Lu, W.; Rong, Q.; Xu, C. Assessment of urban flood resilience based on a systematic framework. Ecol. Indic. 2023, 150, 110230. [Google Scholar] [CrossRef]
- Ferreira, D.M.; Fernandes CV, S.; Kaviski, E.; Bleninger, T. Calibration of river hydrodynamic models: Analysis from the dynamic component in roughness coefficients. J. Hydrol. 2021, 598, 126136. [Google Scholar] [CrossRef]
- Yang, Q.; Huang, H.; Wang, C.; Lei, X.; Feng, T.; Zuo, X. Improving the Accuracy of Urban Waterlogging Simulation: A Novel Computer Vision-Based Digital Elevation Model Refinement Approach for Roads and Densely Built-Up Areas. Remote Sens. 2023, 15, 4915. [Google Scholar] [CrossRef]
- Ganin, A.A.; Massaro, E.; Gutfraind, A.; Steen, N.; Keisler, J.M.; Kott, A.; Mangoubi, R. Igor Linkov Operational resilience: Concepts, design and analysis. Sci. Rep. 2016, 6, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Mugume, S.N.; Gomez, D.E.; Fu, G.; Farmani, R.; Butler, D. A global analysis approach for investigating structural resilience in urban drainage systems. Water Res. 2015, 81, 15–26. [Google Scholar] [CrossRef] [PubMed]
- Zheng, J.; Huang, G. A novel grid cell–based urban flood resilience metric considering water velocity and duration of system performance being impacted. J. Hydrol. 2023, 617, 128911. [Google Scholar] [CrossRef]
- Zhao, G.; Xu, Z.; Pang, B.; Tu, T.; Xu, L.; Du, L. An enhanced inundation method for urban flood hazard mapping at the large catchment scale. J. Hydrol. 2019, 571, 873–882. [Google Scholar] [CrossRef]
- Li, C.; Cheng, X.; Li, N.; Du, X.; Yu, Q.; Kan, G. A framework for flood risk analysis and benefit assessment of flood control measures in urban areas. Int. J. Environ. Res. Public Health 2016, 13, 787. [Google Scholar] [CrossRef]
- GB 50014—2021; Standard for Design of Outdoor Wastewater Engineering. China Planning Press: Beijing, China, 2021. (In Chinese)
- SL723—2016; Standard for Waterlogging Control. China Water Resources and Hydropower Press: Beijing, China, 2016. (In Chinese)
- SL/T 4—2020; Technical Code for Farmland Drainage Projects. China Water Resources and Hydropower Press: Beijing, China, 2020. (In Chinese)
- Begum, M.; Juraimi, A.S.; Amartalingam, R.; Bin Man, A.; Bin Syed Rastans, S.O. The effects of sowing depth and flooding on the emergence, survival, and growth of Fimbristylis miliacea (L.) Vahl. Weed Biol. Manag. 2006, 6, 157–164. [Google Scholar] [CrossRef]
- Nie, G.P.; Chen, M.M.; Yang, L.Y.; Cai, Y.; Xu, F.; Zhang, Y. Plant response to waterlogging stress: Research progress. Chin. Agric. Sci. Bull. 2021, 37, 57–64. (In Chinese) [Google Scholar]
- Chen, S.K.; Liu, C.W. Analysis of water movement in paddy rice fields (I) experimental studies. J. Hydrol. 2002, 260, 206–215. [Google Scholar] [CrossRef]
- Mo, B.; Chen, X.Y.; Yang, Y.C.; Luo, B.L.; Tang, J.; Gong, C.M.; Lin, Z.X.; Zhou, S.J.; Shen, Y.K. Research on soil infiltration capacity and its influencing factors in different land uses. Res. Soil Water Conserv. 2016, 23, 13–17. (In Chinese) [Google Scholar]
- Berhanu, B.; Melesse, A.M.; Seleshi, Y. GIS-based hydrological zones and soil geo-database of Ethiopia. Catena 2013, 104, 21–31. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, C.; Chen, A.S.; Wang, G.; Fu, G. Exploring the relationship between urban flood risk and resilience at a high-resolution grid cell scale. Sci. Total Environ. 2023, 893, 164852. [Google Scholar] [CrossRef] [PubMed]
- Najibi, N.; Devineni, N. Recent trends in the frequency and duration of global floods. Earth Syst. Dyn. 2018, 9, 757–783. [Google Scholar] [CrossRef]
- Hammond, M.J.; Chen, A.S.; Djordjević, S.; Butler, D.; Mark, O. Urban flood impact assessment: A state-of-the-art review. Urban Water J. 2015, 12, 14–29. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z.; Ge, W.; Wang, J.; Guo, X.; Wang, T.; Li, W. Assessment of the impact of floods on terrestrial plant biodiversity. J. Clean. Prod. 2022, 339, 130722. [Google Scholar] [CrossRef]
- Prashar, N.; Lakra, H.S.; Shaw, R.; Kaur, H. Urban Flood Resilience: A comprehensive review of assessment methods, tools, and techniques to manage disaster. Prog. Disaster Sci. 2023, 20, 100299. [Google Scholar] [CrossRef]
- Chen, J.; Huang, G.; Chen, W. Towards better flood risk management: Assessing flood risk and investigating the potential mechanism based on machine learning models. J. Environ. Manag. 2021, 293, 112810. [Google Scholar] [CrossRef]
- Bertilsson, L.; Wiklund, K.; de Moura Tebaldi, I.; Rezende, O.M.; Veról, A.P.; Miguez, M.G. Urban flood resilience–A multi-criteria index to integrate flood resilience into urban planning. J. Hydrol. 2019, 573, 970–982. [Google Scholar] [CrossRef]
- Sidek, L.M.; Jaafar, A.S.; Majid, W.H.A.W.A.; Basri, H.; Marufuzzaman, M.; Fared, M.M.; Moon, W.C. High-resolution hydrological-hydraulic modeling of urban floods using InfoWorks ICM. Sustainability 2021, 13, 10259. [Google Scholar] [CrossRef]
- Rahman, M.C.; Islam, M.A.; Rahaman, M.S.; Sarkar, M.A.R.; Ahmed, R.; Kabir, M.S. Identifying the threshold level of flooding for rice production in Bangladesh: An Empirical Analysis. J. Bangladesh Agric. Univ. 2021, 19, 243–250. [Google Scholar] [CrossRef]
- Cocks, P.S. Ecology of herbaceous perennial legumes: A review of characteristics that may provide management options for the control of salinity and waterlogging in dryland cropping systems. Aust. J. Agric. Res. 2001, 52, 137–151. [Google Scholar] [CrossRef]
- Vreugdenhil, S.J.; Kramer, K.; Pelsma, T. Effects of flooding duration,-frequency and-depth on the presence of saplings of six woody species in north-west Europe. For. Ecol. Manag. 2006, 236, 47–55. [Google Scholar] [CrossRef]
- Grimoldi, A.A.; Insausti, P.; Vasellati, V.; Striker, G.G. Constitutive and plastic root traits and their role in differential tolerance to soil flooding among coexisting species of a lowland grassland. Int. J. Plant Sci. 2005, 166, 805–813. [Google Scholar] [CrossRef]
- Wu, L.; Tong, J.; Wang, Z.; Li, J.; Li, M.; Li, H.; Feng, Y. Post-flood disaster damaged houses classification based on dual-view image fusion and Concentration-Based Attention Module. Sustain. Cities Soc. 2024, 103, 105234. [Google Scholar] [CrossRef]
- Wu, L.; Liu, Y.; Zhang, J.; Zhang, B.; Wang, Z.; Tong, J.; Li, M.; Zhang, A. Identification of flood depth levels in urban waterlogging disaster caused by rainstorm using a CBAM-improved ResNet50. Expert Syst. Appl. 2024, 6, 124382. [Google Scholar] [CrossRef]
- Murdock, H.J.; De Bruijn, K.M.; Gersonius, B. Assessment of critical infrastructure resilience to flooding using a response curve approach. Sustainability 2018, 10, 3470. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, H.; Hu, L.; Meng, J.; Sun, F. Analysis of Short-Term Heavy Rainfall-Based Urban Flood Disaster Risk Assessment Using Integrated Learning Approach. Sustainability 2024, 16, 8249. [Google Scholar] [CrossRef]
- Yang, F.; Xiong, S.; Ou, J.; Zhao, Z.; Lei, T. Human settlement resilience zoning and optimizing strategies for river-network cities under flood risk management objectives: Taking Yueyang City as an example. Sustainability 2022, 14, 9595. [Google Scholar] [CrossRef]
- Xia, J.; Chen, J. A new era of flood control strategies from the perspective of managing the 2020 Yangtze River flood. Sci. China Earth Sci. 2021, 64, 1–9. [Google Scholar] [CrossRef]
- Deng, P.; Zhang, M.; Hu, Q.; Wang, L.; Bing, J. Pattern of spatio-temporal variability of extreme precipitation and flood-waterlogging process in Hanjiang River basin. Atmos. Res. 2022, 276, 106258. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).