Demand Forecast Information Sharing in Low-Carbon Supply Chains

Abstract

In view of the crucial role of consumer data concerning low-carbon preferences, a low-carbon supply chain was established, encompassing one manufacturer and one retailer. Both entities employed technological tools to predict consumer demand. This study assessed the profitability of supply chain participants under two strategies, “make-to-order” and “make-to-stock”, considering scenarios with and without demand forecast sharing information. Furthermore, we investigated how factors such as demand variability, forecast biases from the manufacturer and the retailer, and the forecast correlation coefficient affect the performance of the supply chain and the benefits of sharing information. Our findings indicate that the strategies of supply chain members remain unaffected by the chosen production models and that information sharing proves advantageous for the manufacturer and the retailer. Especially for manufacturers, profits in a “make-to-order” scenario surpass those in a “make-to-stock” scenario. Our numerical analysis showed that profits for the manufacturer and the retailer were consistently higher in scenarios where information was shared than in cases where it was not for “make-to-order” and “make-to-stock” strategies.

1. Introduction

Climate change has introduced significant economic risks to corporate operations. A 2020 report highlighted that over a thousand enterprises across 60 countries have initiated emission reduction initiatives, adopting various strategies to mitigate the severe effects of climate change [1]. Furthermore, the report revealed an increasing trend of corporate participation in emission reductions over the past five years, with many enterprises, including AbInBev, Tesco, and Honda, implementing carbon reduction measures in their supply chains. The adverse effect of global warming on human habitats influences consumer choices, a fact supported by empirical studies. A pivotal survey by McKinsey in 2020 focusing on US consumer sentiments found that over 60% of respondents were willing to pay a premium for sustainably packaged products [2]. Moreover, an investigation by NielsenIQ emphasized the importance of sustainable living for American consumers, with 78% emphasizing the need for sustainable practices in their daily lives [2]. A Carbon Trust study indicated that 78% of respondents want their favorite brands to reduce their carbon footprint [3], and another study showed growing demand for low-carbon products despite economic recessions [4]. Consumer choices affect business activities. Reducing carbon emissions is also beneficial for corporate image and brand reputation for consumers. Research focusing on Marcao residents by Zhang et al. [3] revealed that 90% of respondents were willing to purchase EVs, with 57% ready to pay for them. Xu et al. [4] discovered that 77.60% of respondents were prepared to pay extra for agricultural products with carbon labels, indicating that awareness of low-carbon practices significantly influences the acceptance of carbon-labeled products.

Given these circumstances, organizations must align their offerings with evolving consumer preferences for low-carbon products while embracing corporate social responsibility. Concurrently, the supply chain, which constitutes cooperative companies and integrated resources, must transform from a traditional to a low-carbon model. However, compared to the conventional supply chain, the low-carbon supply chain faces several unique challenges, including the need to reduce carbon emissions and growing consumer preference for low-carbon products. Addressing these novel challenges requires examining how manufacturers and retailers can be effectively coordinated. Notably, existing literature on supply chain coordination does not fully encompass these considerations.

This study analyzed the effect of the sharing of demand forecasting information on the performance of the manufacturer, the retailer, or both in a low-carbon context. Information sharing provides two fundamental benefits for the supply chain. First, it can prevent information distortion and improve the efficiency of customer feedback, helping companies align supply with demand and improve their fast response capabilities, thereby reducing the financial costs of maintaining inventory and addressing shortages. Second, information sharing improves the accuracy of forecasting unusual demand peaks and fluctuations, allowing suppliers and retailers to be fully prepared and proactive.

This paper makes a significant contribution to the field of supply chain management as evidenced by the following: (1) The existing literature on low-carbon supply chains primarily focuses on minimizing carbon emissions or examining the influence of carbon emission reduction on a company’s performance. However, it does not consider the influence of consumer preferences on the supply chain or the effect of demand forecasting information sharing on the performance of retailers and manufacturers. This study considers the influence of information sharing on demand forecasting and decision-making processes related to carbon reduction. (2) The extant literature on information sharing mainly discusses savings in inventory and replenishment due to information sharing but does not address issues resulting from global warming. Our model recognizes the importance of consumer environmental consciousness and corporate social responsibility in addressing global warming. Accordingly, our model helps analyze the influence of information sharing on reducing emissions.

The following sections are organized as follows. Section 2 provides a literature review. Section 3 presents the model framework considering low-carbon consumer preferences. Section 4 and Section 5 analyze the value of information sharing in two distinct scenarios: “make-to-order” and “make-to-stock.” In Section 6, we demonstrate the influence of forecast precision on the manufacturer and the retailer, and we offer conclusions in Section 7.

2. Literature Review

This paper is influenced by several distinct research traditions. The literature can be classified into two main categories: studies focused on supply chains in low-carbon con-texts and those concentrated on information sharing within supply chains. One stream of literature related to low-carbon supply chains analyzes the influence of carbon reduction. Benjaafar et al. [5] were pioneers in incorporating emission reduction into a supply chain framework, demonstrating that such reductions affect supply chain operations. Similarly, Sundarakani et al. [6] investigated carbon emissions in supply chains, analyzing heat transfer mechanisms and developing a model to measure emissions from static and nonstatic processes. Some scholars have employed game theory or optimization to assess the effects of carbon emissions on supply chains. Cachon [7] explored how supply chain retailers’ network layouts affect consumer behavior, discussing how to minimize operation costs under carbon emission constraints. Dong et al. [8] examined sustainable product investment in centralized and decentralized supply chains under the cap-and-trade mechanism, finding that only a revenue-sharing contract could effectively coordinate the supply chain. Liu et al. [9] focused on repurchase issues, developing a supply chain model within a carbon tax and repurchase contract framework. They critically evaluated the optimal decision strategies for producers and retailers, contrasting centralized versus decentralized approaches, under the constraint of carbon taxation. Cai and Jiang [10] devised single-supplier, single-manufacturer low-carbon supply chain models, examining optimal pricing strategies and carbon emission reduction choices while considering consumer preferences for ecofriendly products, cap-and-trade regulations, and the underlying power dynamics within the supply chain. Mao et al. [11] studied manufacturing and remanufacturing supply chains under carbon emission quota polices. Li et al. [12] integrated fairness considerations into low-carbon supply chain coordination mechanisms. Their analysis of four distinct scenarios revealed that fairness concerns negatively affect retailers but benefit manufacturers and the system. However, this literature overlooks the significance of consumer preferences and issues related to demand information.

The second body of literature concerns supply chain information sharing. Chen et al. [13] and Aviv [14] provided extensive literature reviews. Most of the existing research has analyzed savings from sharing information about inventory and replenishment [15,16] or pricing [17,18,19]. Lee, So, and Tang [20] highlighted the high value of demand information sharing, especially when demands are significantly correlated over time. In a two-stage supply chain, Chen et al. [13] demonstrated that centralizing demand information reduces the bullwhip effect, thereby significantly decreasing variability. A substantial body of literature exists on demand forecasting. Aviv [14] examined the value of collaborative forecasting and integrating retailers into manufacturers’ replenishment processes. Zhao et al. [21] studied the effect of forecasting models on the value of information sharing in a supply chain with one supplier and multiple retailers. Their findings demonstrated that substantial cost savings can be achieved through effective information sharing strategies. Li and Zhang [22] examined the effects of three distinct information-sharing scenarios on the profits of manufacturers and retailers. Ren et al. [23] employed game theory to examine forecast sharing and supply chain coordination. Huo, Haq, and Gu [24] empirically examined the effect of information sharing on various aspects of supply chain learning, i.e., internally and with regards to the supplier and customer—and its influence on enhancing flexibility. Huang, Ho, and Kao [25] evaluated the quality of information sharing based on reliability and availability. Li, Tian, and Zheng [26] conducted a study on information sharing within an ecommerce ecosystem comprising an online marketplace, an upstream producer, and a distributor. Their analysis delved into four distinct information-sharing configurations: no sharing, comprehensive sharing, selective sharing with the producer, and exclusive sharing with the distributor. Ma, Li, and Kong [27] examined retailer strategies in consumer information sharing. Chen, Li, and Wang [28] examined the question of which manufacturer should share information within a supply chain with two manufacturers and one platform. However, the aforementioned literature only analyzed information sharing issues and did not discuss problems arising from climate change currently and consumer responses to it. This paper analyzes demand information sharing among supply chain members, considering consumer preference for low-carbon options.

3. Model Framework

This study examines a two-level supply chain comprising a single manufacturer $M$ and a single retailer $R$. The manufacturer produces a low-carbon product, which is then sold by the retailer to the end consumer. The financial outlay per unit of production for the manufacturer is $c$. Wholesale price $w$ per unit is the cost to the retailer. The other cost to the retailer is normalized to zero. The manufacturer initially sets wholesale price $w$ and carbon reduction level $\epsilon$, and the retailer then sets retail price $p$ after observing the manufacturer’s decision. The firms are assumed to be rational and risk-neutral.

The consumer demand D is assumed to be as follows:

$$D=\alpha -\beta p+\gamma \epsilon ,$$

(1)

where $\alpha$ shows the market potential of the product, $\beta$ is the slope of the demand function, and $\gamma$ is the impact coefficient of the carbon emission reduction level on consumer demand. All the parameters are positive.

The cost of emission reduction is considered to be a variable input that increases convexly with carbon reduction level $e$. This suggests that greater capital, technology, and resource investments are required to achieve higher emission reductions, implying a rise in carbon reduction levels. The mathematical properties of the aforementioned carbon reduction cost can be given by $C(e)>0$, $C^{\prime }(e)>0$, and $C^{″}(e)>0$. Thus, we use a quadratic function of the carbon reduction level to represent the cost of carbon reduction, i.e., $C(e)=k{e}^2/2$, where $k$ represents the emission reduction cost coefficient. The quadratic functional form is commonly used to denote the costs associated with environmental improvements, as reflected in the literature by Nordhaus [29] and Bai, Xu, and Chauhan [30].

The broad adoption of data mining and machine learning techniques based on big data provides a robust technological foundation for demand forecasting. Therefore, we can assume that each firm employs available market information-gathering techniques to forecast demand for low-carbon products ($\alpha$). We assume the manufacturer’s forecast of the base level of demand, designated as $\alpha$, is $f_1$, whereas the retailer’s forecast is $f_2$.

We assume that $f_i=\alpha +{\xi }_i,(i=1,2)$, where ${\xi }_i$ is distributed normally and is independent of the base level of demand $\alpha$. Furthermore, ${\xi }_i$ is assumed to have a mean of zero and a variance of ${\sigma }_i$. We denote that the manufacturer’s and the forecast errors made by the retailer (i.e., $(f_m-\alpha )$ and $(f_r-\alpha )$) are normally spread with zero as the mean and variances of ${\sigma }_1^2$ and ${\sigma }_2^2$, respectively. A lower variance for the forecast error indicates that the firm has a higher forecast capability. The errors in the manufacturer’s and the retailer’s forecasts can be correlated, although this is independent of $\alpha$. Correlation $\rho$ is dependent upon the data and methodology utilized by the retailer and manufacturer in their forecasting process.

We also assume that the covariance is not greater than the individual variance, that is, $\rho {\sigma }_r{\sigma }_m\le {\sigma }_m^2$ and $\rho {\sigma }_r{\sigma }_m\le {\sigma }_r^2$. The observed discrepancies between the two forecasts suggest that the data may have originated from independent sources ($\rho$ close to 0). In the event of significant similarities between the variances in question, a high degree of correlation is to be expected ($\rho$ close to 1), i.e., assuming that both members of the supply chain have access to the same probability distribution parameters and the prior probability distribution of $\alpha$ is reasonable. Concurrently, each agent is privy solely to its own forecast, unless forecasts are disseminated. Conditional expectations and variances are shown in Appendix A.

Moreover, we assume that the retailer places an order with the manufacturer, who then assumes responsibility for pricing and carbon emission reduction decisions once market demand has been established. This is known as a make-to-order case, where neither the manufacturer nor the retailer maintains any inventory. We also consider an alternative scenario where the manufacturer determines its pricing and carbon reduction strategy before market demand has been established. This is referred to as the make-to-stock case. Here, the manufacturer makes decisions regarding production, pricing, and carbon emission reduction before knowing the market demand and assumes responsibility for inventory and shortage costs. In this scenario, after demand has been established, the retailer then makes its pricing decision.

4. Analysis of the Make-to-Order Scenario

The action sequence in this bespoke scenario is outlined as follows. First, the players forecast consumer demand. Second, the manufacturer sets wholesale price $w$ and carbon reduction level $e$. Third, the retailer establishes the retail price based on the manufacturer’s decisions. Finally, the players become aware of the actual demand. Following the temporal framework, we now employ backward induction to determine the optimal strategy.

4.1. No Information Sharing in the Make-to-Order Scenario

In this section, we assume that the manufacturer and the retailer refuse to share demand forecast information for low-carbon products. This could be to avoid compromising their own interests during price negotiations or due to a lack of sufficient trust. In this instance, the supply chain participants do not share their respective forecasts with each other. The manufacturer’s demand information remains limited to forecast $f_1$, whereas the retailer’s information includes $f_2$, $w$, and $\epsilon$. In accordance with the game’s timeline, backward induction is employed to achieve optimal results.

The profit function of the retailer is as follows

$$E[{\pi }_R(p)|f_2]=(p-w)(\overline{\alpha }+E[\epsilon |f,w]-\beta p+\gamma \epsilon ),$$

(2)

The initial order condition of Equation (3) with respect to $p$ is given by

$${\displaystyle \frac{\partial {\pi }_R}{\partial p}}=\overline{\alpha }+E[\xi |f_2,w,\epsilon ]-2\beta p+\gamma \epsilon +\beta w=0,$$

(3)

In the absence of information sharing, the optimal price for the retailer, given the parameters $f_2$, $w$, $\epsilon$, is given by

$$p={\displaystyle \frac{\overline{\alpha }+\gamma e+\beta w+f}{2\beta }},$$

(4)

It is anticipated that the supplier will realize a profit of

$$E[{\pi }_M(\epsilon ,w)|f_1]=(w-c)(\alpha -\beta E[p]+\gamma \epsilon )-{\displaystyle \frac{1}{2}}k{\epsilon }^2,$$

(5)

By substituting Equation (5) into Equation (6), we can obtain the first-order conditions of Equation (6) with respect to $\epsilon$ and $w$.

As demonstrated by the findings of Mishra, Raghunathan, and Yue [19] and Yue and Liu [17], the retailer can access the manufacturer’s forecasting data contingent on the manufacturer’s decision. We can therefore obtain the following:

$$w^{*}={\displaystyle \frac{2\overline{\alpha }k+2\beta ck-c{\gamma }^2}{4\beta k-{\gamma }^2}},$$

(6)

$${\epsilon }^{*}={\displaystyle \frac{\overline{\alpha }\gamma -c\gamma \beta }{4\beta k-{\gamma }^2}},$$

(7)

Plugging Equations (6) and (7) into Equation (4), we have

$$p^{*}={\displaystyle \frac{f}{2\beta }}+{\displaystyle \frac{3k\alpha +ck\beta -c{\gamma }^2}{4k\beta -{\gamma }^2}},$$

(8)

The financial gains of the retailer and the manufacturer are outlined below:

$$E[{\mathsf{\Pi }}_R]={\displaystyle \frac{{\left(2\beta k(2{\alpha }_{12}-{\alpha }_1)-{\gamma }^2({\alpha }_{12}-{\alpha }_1)-2ck{\beta }^2\right)}^2}{4\beta {(4\beta k-{\gamma }^2)}^2}}{\displaystyle \frac{{[2k\beta (\alpha -c\beta )+f(4k\beta -{\gamma }^2)]}^2}{4\beta {(4k\beta -{\gamma }^2)}^2}},$$

(9)

$$E[{\mathsf{\Pi }}_M]={\displaystyle \frac{k({\alpha }_1-\beta c)}{2{(4\beta k-{\gamma }^2)}^2}}(8{\alpha }_{12}\beta k+\beta c{\gamma }^2+{\alpha }_1{\gamma }^2-2{\alpha }_{12}{\gamma }^2-4{\alpha }_1\beta k-4kc{\beta }^2){\displaystyle \frac{k{\left(\alpha -c\beta \right)}^2}{2\left(4k\beta -{\gamma }^2\right)}},$$

(10)

Equation (6) indicates that the manufacturer will avoid using $w$ or $e$ to present a false forecast. Providing inaccurate forecasts would lead the retailer to set prices at either extreme of the expected range, resulting in excessively high or low demand. This variability would significantly challenge the manufacturer in terms of production efficiency and supply chain stability, ultimately hindering profit growth.

Equation (10) demonstrates that the manufacturer’s carbon emission reduction level is directly correlated with its demand forecast. As forecasted demand increases, the manufacturer is more likely to invest additional resources in reducing carbon emissions, driven by the positive effect of $e$ on consumer demand.

4.2. Information Sharing in the Make-to-Order Scenario

In this section, we assume that the manufacturer and the retailer are willing to share forecasted demand information for various reasons, such as improving supply chain efficiency, reducing costs, enhancing collaboration, boosting customer satisfaction, mitigating risks, promoting technological innovation and upgrades, and establishing long-term cooperative relationships. In this scenario, both parties involved in the supply chain, namely, the manufacturer and the retailer, have agreed to share information related to market demand forecasting (e.g., $E\{\alpha |f_1,f_2\}$). Therefore, no information asymmetry occurs between them, allowing the manufacturer to accurately anticipate the retailer’s reaction function when deciding on its pricing and carbon reduction strategies.

The retailer is confronted with the following optimization problem, which can be expressed as follows:

$$E[{\mathsf{\Pi }}_R(p)|f_1,f_2]=E\{(p-w)(\alpha -\beta p+\gamma \epsilon )|f_1,f_2\},$$

(11)

The initial order of Equation (14) with respect to $p$ is

$$p={\displaystyle \frac{{\alpha }_{12}+\gamma \epsilon +\beta w}{2\beta }},$$

(12)

The manufacturer is confronted with the following optimization problem:

$$E[{\mathsf{\Pi }}_M(w,e)|f_1,f_2]=(w-c)({\alpha }_{12}-\beta p+\gamma \epsilon )-{\displaystyle \frac{1}{2}}k{\epsilon }^2,$$

(13)

Plugging Equation (12) into Equation (13), we can obtain the optimal results from the FOC of the expected profit for the manufacturer for $w$ and $\epsilon$.

Accordingly, we can get

$$w={\displaystyle \frac{2k({\alpha }_{12}+c\beta )-c{\gamma }^2}{4k\beta -{\gamma }^2}},$$

(14)

$$\epsilon ={\displaystyle \frac{\gamma \left({\alpha }_{12}-c\beta \right)}{4k\beta -{\gamma }^2}},$$

(15)

And then

$$p^{*}={\displaystyle \frac{3{\alpha }_{12}k+ck\beta -c{\gamma }^2}{4\beta k-{\gamma }^2}},$$

(16)

The financial gains of the retailer and the manufacturer can be quantified as follows:

$$E[{\mathsf{\Pi }}_R]={\displaystyle \frac{\beta k^2{({\alpha }_{12}-\beta c)}^2}{{(4k\beta -{\gamma }^2)}^2}},$$

(17)

$$E[{\mathsf{\Pi }}_M]={\displaystyle \frac{k({\alpha }_{12}-\beta c)(4{\alpha }_{12}\beta k+\beta c{\gamma }^2-4ck{\beta }^2-{\alpha }_{12}{\gamma }^2)}{2{(4\beta k-{\gamma }^2)}^2}}.$$

(18)

5. Analysis of a Make-to-Stock Scenario

In this scenario, the manufacturer and the retailer follow these steps sequentially. First, both parties initially forecast consumer demand. Second, the production quantity ($Q$), the wholesale price ($w$), and the carbon reduction level ($\epsilon$) at which carbon emissions are reduced are all set by the manufacturer. Third, the retailer determines its selling price after receiving the manufacturer’s approach ($p$). Finally, the retailer places the order, the demand materializes, and inventory or shortage costs arise.

In the second stage, we assume that the manufacturer begins scheduling its production before receiving the retailer’s order, and in the fourth stage, the demand is realized. The manufacturer bears the burden of handling inventory and shortages. If the demand is lower than the production quantity ($Q$), then the manufacturer incurs holding costs $h$ per inventory unit. Conversely, if demand exceeds $Q$, then we presume that the manufacturer will have to find alternative sources of supply and will pay shortage costs $s$ per inventory item.

5.1. No Information Sharing in the Make-to Stock Scenario

The retailer and the manufacturer’s anticipated profit functions are as follows

$$E[{\mathsf{\Pi }}_R|f_2,p]=E\{(p-w)(\alpha -\beta p+\gamma \epsilon )|f_1,w,\epsilon \},$$

(19)

$$E[{\mathsf{\Pi }}_M|f_1,Q,w,e]=E\{w\min (Q,D)-h\max (Q-D,0)-s\max (D-Q,0)-{\displaystyle \frac{1}{2}}k{\epsilon }^2\},$$

(20)

We have the retailer’s best response function as follows.

$$p={\displaystyle \frac{E\{\alpha |f_1,f_2\}+\gamma \epsilon +\beta w}{2\beta }},$$

(21)

With $Q$ as the manufacturer’s production quantity, we now solve the first-order condition for profit with respect to the wholesale price, the level of carbon reduction, and the production quantity, allowing us to obtain the following results.

$${\epsilon }^{*}={\displaystyle \frac{{\alpha }_1\gamma -c\beta \gamma }{4k\beta -{\gamma }^2}},$$

(22)

$$w^{*}={\displaystyle \frac{2k{\alpha }_1+2kc\beta -c{\gamma }^2}{4k\beta -{\gamma }^2}},$$

(23)

$$Q^{*}={\sigma }_N{F}^{-1}({\displaystyle \frac{s}{s+h}})+{\displaystyle \frac{{\alpha }_{1}k\beta -ck{\beta }^2}{4k\beta -{\gamma }^2}},$$

(24)

Substituting Equations (22) and (23) into Equation (21), we obtain

$$p^{*}={\displaystyle \frac{1}{2\beta }}\left({\alpha }_{12}+{\displaystyle \frac{{\alpha }_1{\gamma }^2+2k{\alpha }_1\beta +2ck{\beta }^2-2\beta c{\gamma }^2}{4k\beta -{\gamma }^2}}\right),$$

(25)

Then, the profits of the retailer and the manufacturer are

$$E[{\mathsf{\Pi }}_R]={\displaystyle \frac{{(4{\alpha }_{12}\beta k+{\alpha }_1{\gamma }^2-2{\alpha }_1\beta k-2ck{\beta }^2-{\alpha }_{12}{\gamma }^2)}^2}{4\beta {(4\beta k-{\gamma }^2)}^2}},$$

(26)

$$\begin{array}{l}E[{\mathsf{\Pi }}_M]={\displaystyle \frac{k({\alpha }_1-\beta c)}{2{(4k\beta -{\gamma }^2)}^2}}(8{\alpha }_{12}\beta k+{\alpha }_1{\gamma }^2+\beta c{\gamma }^2-2{\alpha }_{12}{\gamma }^2-4k{\alpha }_1\beta -4ck{\beta }^2)\\ -{\sigma }_N[(s+h)\mathsf{\Phi }(\tau )+h\tau ]\end{array},$$

(27)

where ${\sigma }_{NI}^2={\displaystyle \frac{{\sigma }_1^2{\sigma }_0^2}{{\sigma }_1^2+{\sigma }_0^2}}$, $\tau =F^{-1}\left({\displaystyle \frac{s}{s+h}}\right)$, $\mathsf{\Phi }(x)={\displaystyle {\int }_x^{\infty }(y-x)}d\mathsf{\Phi }(y)$.

We notice that the results in the make-to-stock scenario are identical to those in the make-to-order scenario.

5.2. Information Sharing of Make-to-Stock Scenario

In the information sharing case, the manufacturer has $f_1$ and $f_2$; thus, the manufacturer uses a different probability distribution of $\alpha$ from that under the no information sharing case.

The optimal results under information sharing in the make-to-stock scenario are as follows:

$${\epsilon }^{*}={\displaystyle \frac{{\alpha }_{12}\gamma -c\beta \gamma }{4k\beta -{\gamma }^2}},$$

(28)

$$w^{*}={\displaystyle \frac{2k{\alpha }_{12}+2kc\beta -c{\gamma }^2}{4k\beta -{\gamma }^2}},$$

(29)

$$Q^{*}={\sigma }_S{F}^{-1}({\displaystyle \frac{s}{s+h}})+{\displaystyle \frac{k{\alpha }_{12}\beta -ck{\beta }^2}{4k\beta -{\gamma }^2}},$$

(30)

$$p^{*}={\displaystyle \frac{3k{\alpha }_{12}+kc\beta -c{\gamma }^2}{4k\beta -{\gamma }^2}}.$$

(31)

Then, the profits of the retailer and the manufacturer are

$$E[{\mathsf{\Pi }}_R]={\displaystyle \frac{\beta k^2{({\alpha }_{12}-\beta c)}^2}{{(4k\beta -{\gamma }^2)}^2}},$$

(32)

$$E[{\mathsf{\Pi }}_M]={\displaystyle \frac{k({\alpha }_{12}-\beta c)(4k{\alpha }_{12}\beta +\beta c{\gamma }^2-{\alpha }_{12}{\gamma }^2-4ck{\beta }^2)}{2{(4k\beta -{\gamma }^2)}^2}}-{\sigma }_I[(s+h)\mathsf{\Phi }(\tau )+h\tau ],$$

(33)

where ${\sigma }_I^2={\displaystyle \frac{(1-{\rho }^2{\sigma }_1^2{\sigma }_2^2{\sigma }_0^2)}{(1-{\rho }^2){\sigma }_1^2{\sigma }_2^2+{\sigma }_0^2({\sigma }_1^2+{\sigma }_2^2-2\rho {\sigma }_1^2{\sigma }_2^2)}}$.

6. Numerical Analysis

To examine the effects of relevant parameters on supply chain performance under various scenarios (i.e., ${\sigma }_0$, ${\sigma }_1$, ${\sigma }_2$, and $\rho$), we have included a numerical simulation in this section. In reference to Zhao, Wang, and Wu [31] and Quadir [32], we utilize the following parameter values for our simulation example under the condition that the decision variables are nonnegative and there is an optimal solution for the above four scenarios: $\overline{\alpha }=250$, $\beta =2$, $\gamma =3$, $c=10$, $k=20$, ${\sigma }_0\in \{2,3,4,5,6,7,8,9,10,11\}$, ${\sigma }_1\in \{2,3,4,5,6,7,8,9,10,11\}$, ${\sigma }_2\in \{2,3,4,5,6,7,8,9,10,11\}$, and $\rho \in \{0.1,0.15,0.2,0.25,0.3,0.35,0.4,0.45,0.5,0.55\}$.

In this section, we analyze the effects of ${\sigma }_0$, ${\sigma }_1$, ${\sigma }_2$, $h$, $s$, and $\rho$ on the profits of the manufacturer for the make-to-order and make-to-stock scenarios, in which we determine their profits for the information sharing and no information sharing cases, respectively. When we study the effect of ${\sigma }_0$, we set ${\sigma }_r={\sigma }_m=5$ and $\rho =0.3$. When studying the effect of ${\sigma }_1$, we set ${\sigma }_0={\sigma }_2=5$ and $\rho$= 0.3. When analyzing the effect of ${\sigma }_2$, we set ${\sigma }_0={\sigma }_1=5$ and $\rho =0.3$. When we study the effect of $\rho$, we set ${\sigma }_0={\sigma }_1={\sigma }_2=5$.

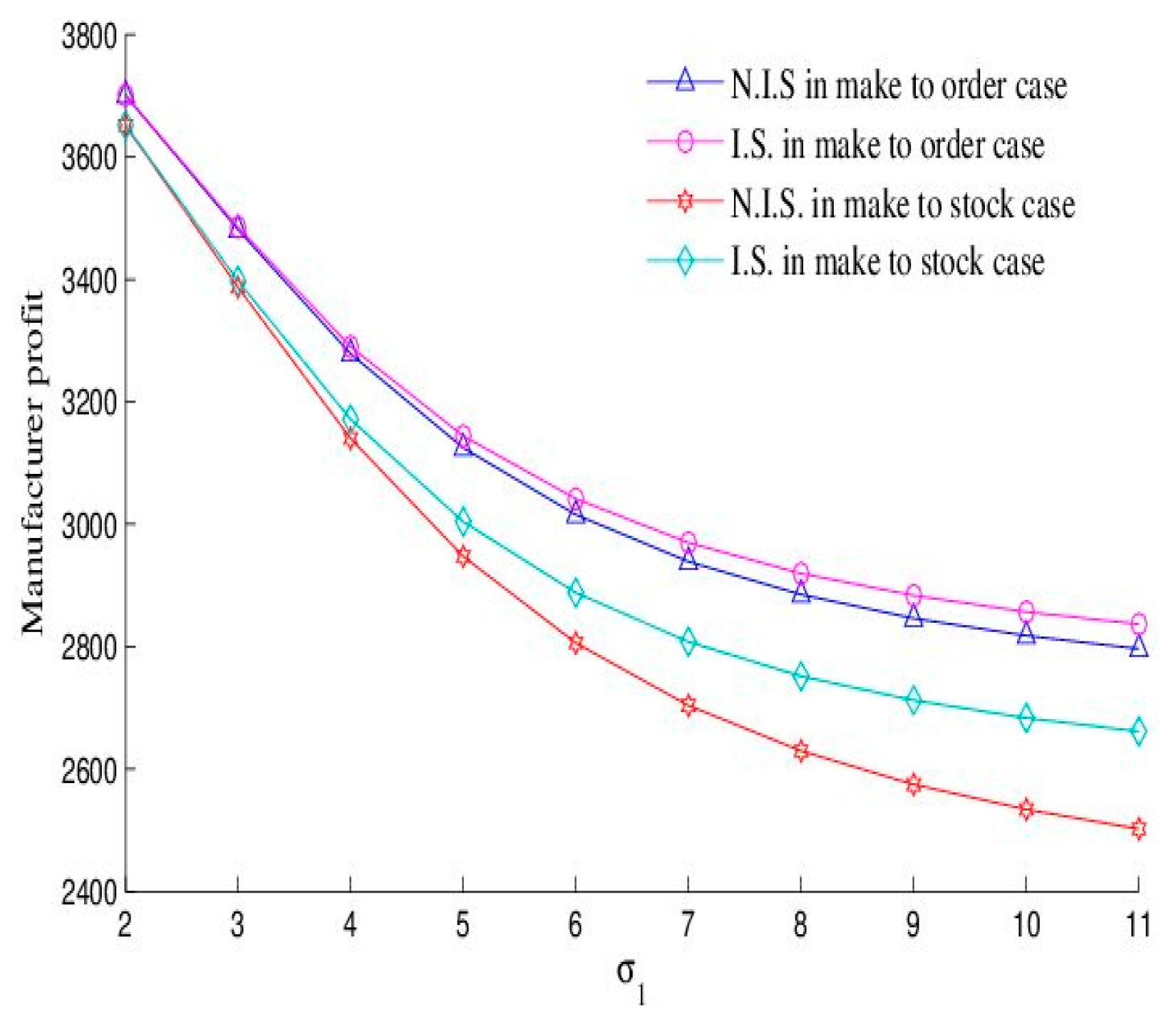
6.1. Effect of ${\sigma }_0$

Figure 1 and Figure 2 illustrate the effect of standard deviation ${\sigma }_0$ on the profits of manufacturers and retailers in make-to-order and make-to-stock scenarios, with and without information sharing, respectively. Evidently, the manufacturer’s profit surpasses that of the retailer. This is determined by the leadership positions among members of the supply chain, thereby resulting in the manufacturer’s profit surpassing that of the retailer. In addition, the manufacturer’s and the retailer’s profits decrease in ${\sigma }_0$ due to the increasing fluctuation of the market demand, which makes demand forecasting considerably more difficult for the manufacturer and the retailer. The figures also reveal that the value of information sharing for the manufacturer and the retailer increases with ${\sigma }_0$ due to the fact that greater demand fluctuations amplify the need for information sharing. By sharing information, manufacturers and retailers can better manage these fluctuations, thereby enhancing the benefits of information sharing. This suggests that as ${\sigma }_0$ and the corresponding value of information sharing increase, the motivation for supply chain members to share information will also strengthen, ultimately leading to a shift from neglecting to strongly emphasizing the importance of information sharing. Therefore, when ${\sigma }_0$ is small, supply chain members may hesitate to share information due to various concerns. However, when ${\sigma }_0$ is large, to avoid a significant decrease in profits, supply chain members are more likely to share information to optimize their profits.

6.2. Effect of ${\sigma }_1$

Figure 3 and Figure 4 demonstrate that ${\sigma }_1$ affects the manufacturer’s and retailer’s profits similarly to ${\sigma }_0$, so we will skip the detailed description and focus on the reasons behind the manufacturer’s and the retailer’s profit direction. Even without information sharing, a manufacturer’s declining accuracy in demand forecasting affects the retailer’s profit through decisions related to wholesale prices, emission reductions, and other factors. As forecast accuracy drops, the retailer’s profit also diminishes. In addition, the retailer’s profit is higher when information is shared compared to when it is not. In the scenario without information sharing, the manufacturer’s profit decreases due to worsening demand forecast accuracy. By contrast, in the scenario with information sharing, the integrated demand forecast also deteriorates due to continuously poor data, which lowers the manufacturer’s and retailer’s profits. The increase in the value of information sharing can be explained as follows. When manufacturers have less accurate demand forecasts, retailer information becomes more crucial for their decision making. This increases the value of information sharing for manufacturers. For retailers, the value of sharing information rises in scenarios without information sharing, as manufacturers lower wholesale prices to encourage more orders from retailers.

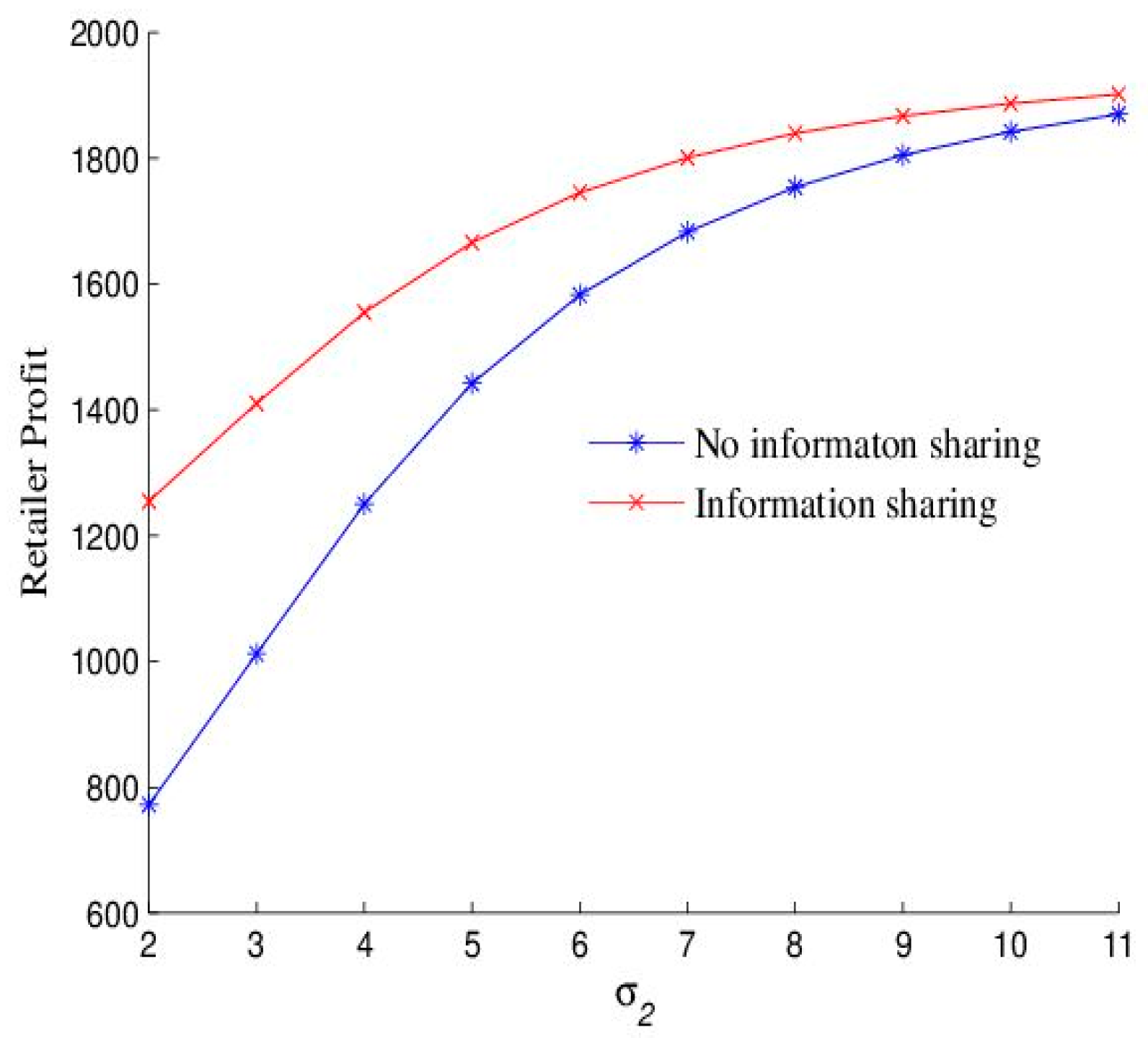
6.3. Effect of ${\sigma }_2$

Figure 5 and Figure 6 illustrate the effect of the retailer’s forecast accuracy on the profits of the manufacturer and the retailer. The manufacturer’s profit consistently exceeds that of the retailer across all values of ${\sigma }_2$, the retailer’s forecast standard error, due to the manufacturer acting as a Stackelberg leader in the supply chain. Different from the effects of ${\sigma }_0$ and ${\sigma }_1$ on the manufacturer’s and the retailer’s profits, the manufacturer and the retailer experience an increase in profits as ${\sigma }_2$ rises. However, the value of information sharing between the manufacturer and the retailer decreases as ${\sigma }_2$ increases. As shown in Figure 5 and Figure 6, the value of information sharing is consistently higher for the retailer than for the manufacturer across all values of ${\sigma }_2$. Different from situations where an increase in the manufacturer’s forecast bias leads to higher wholesale prices, increasing retail prices, and diminishing market demand, a decrease in the retailer’s demand forecast accuracy results in an increase in order quantity. This leads to an illusion of increased demand, creating a superficial appearance of prosperity and contributing to an increase in profits for supply chain members. However, as demand forecast accuracy further declines, its ability to drive profit growth diminishes until it becomes ineffective. Furthermore, for the manufacturer and the retailer, the value of information sharing diminishes as the retailer’s forecast information bias increases, eventually rendering it valueless. This occurs because significant deviations in the retailer’s forecast demand information make the effect of information sharing on decision making negligible, thereby eliminating its value.

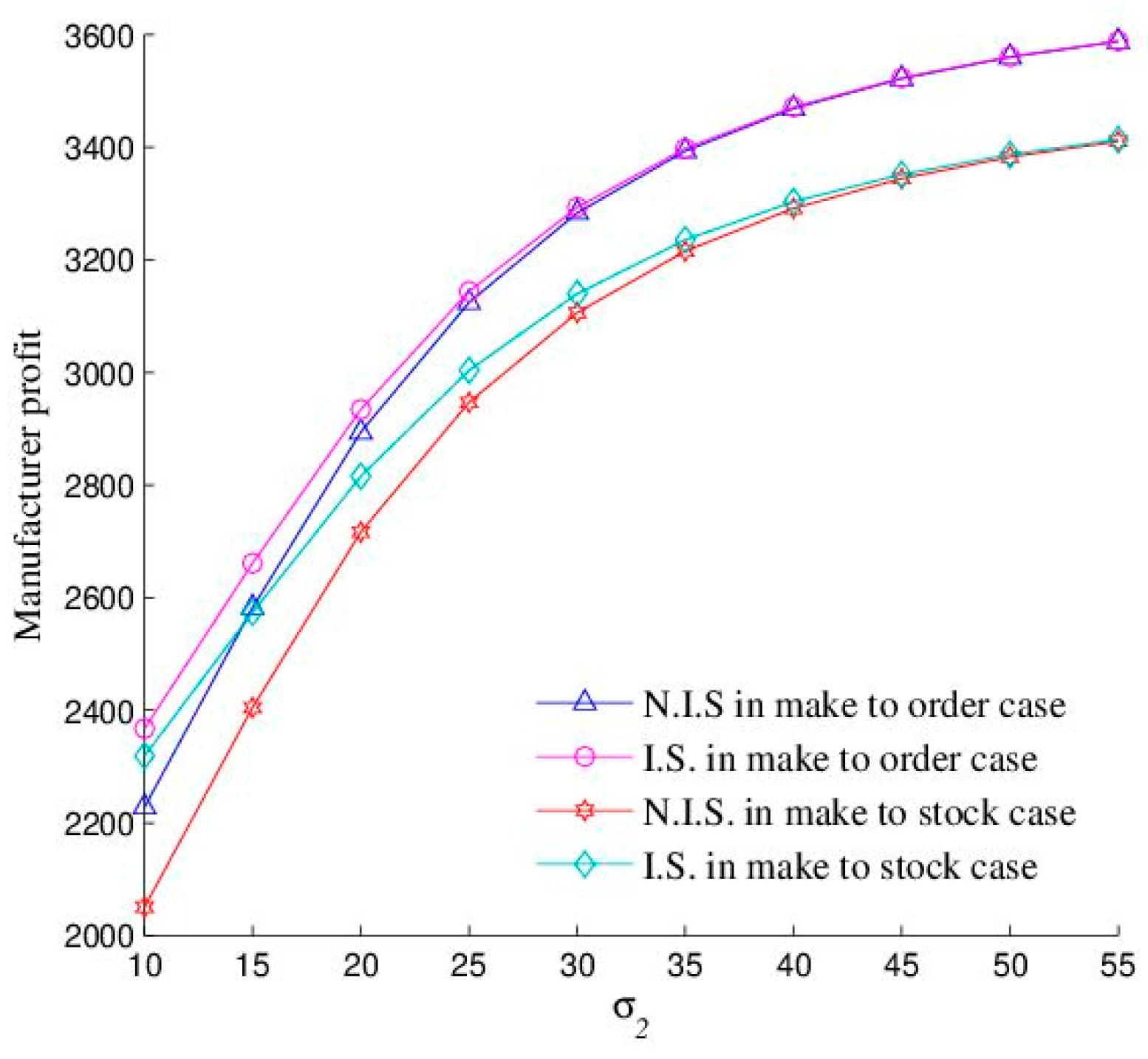
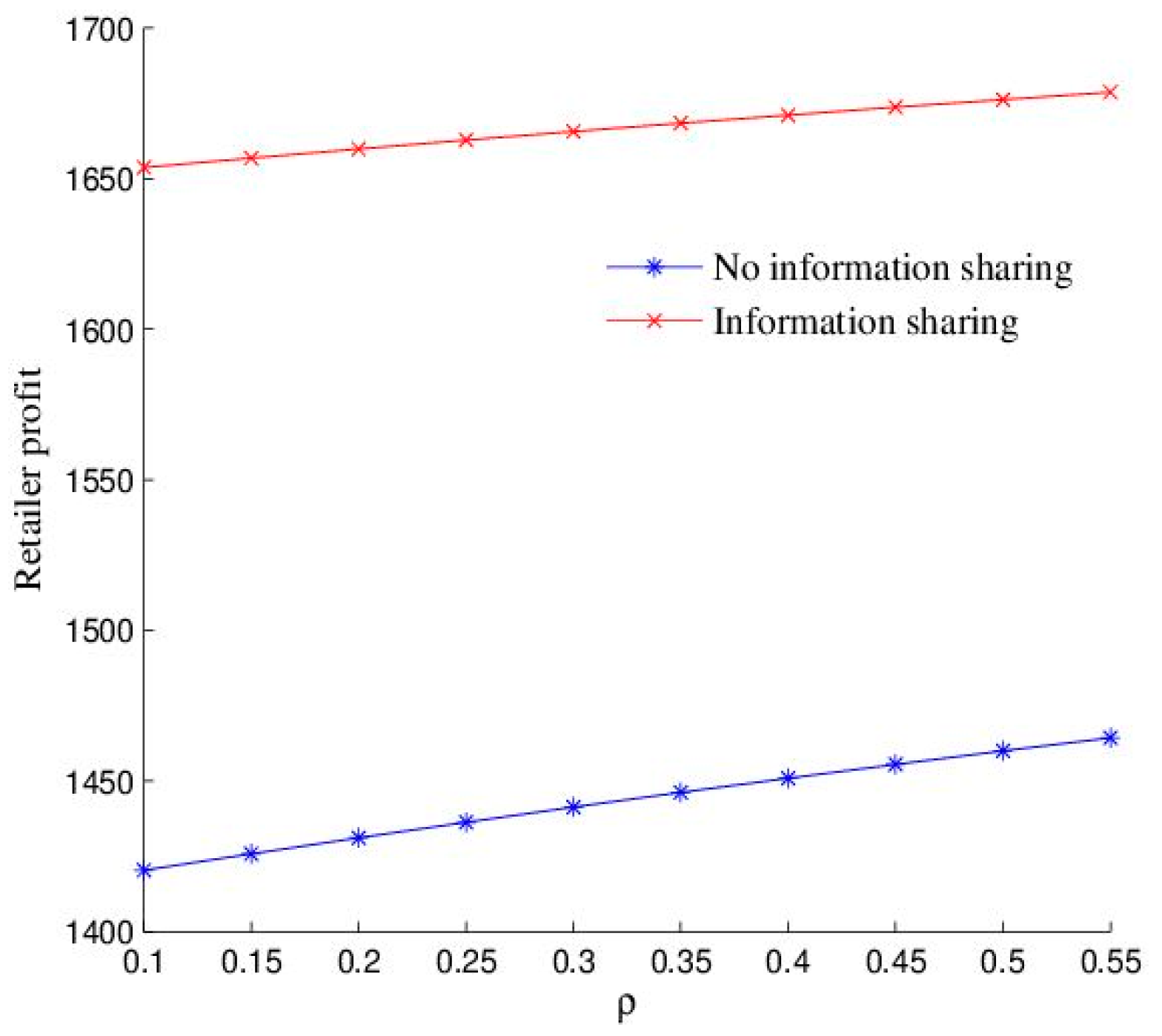
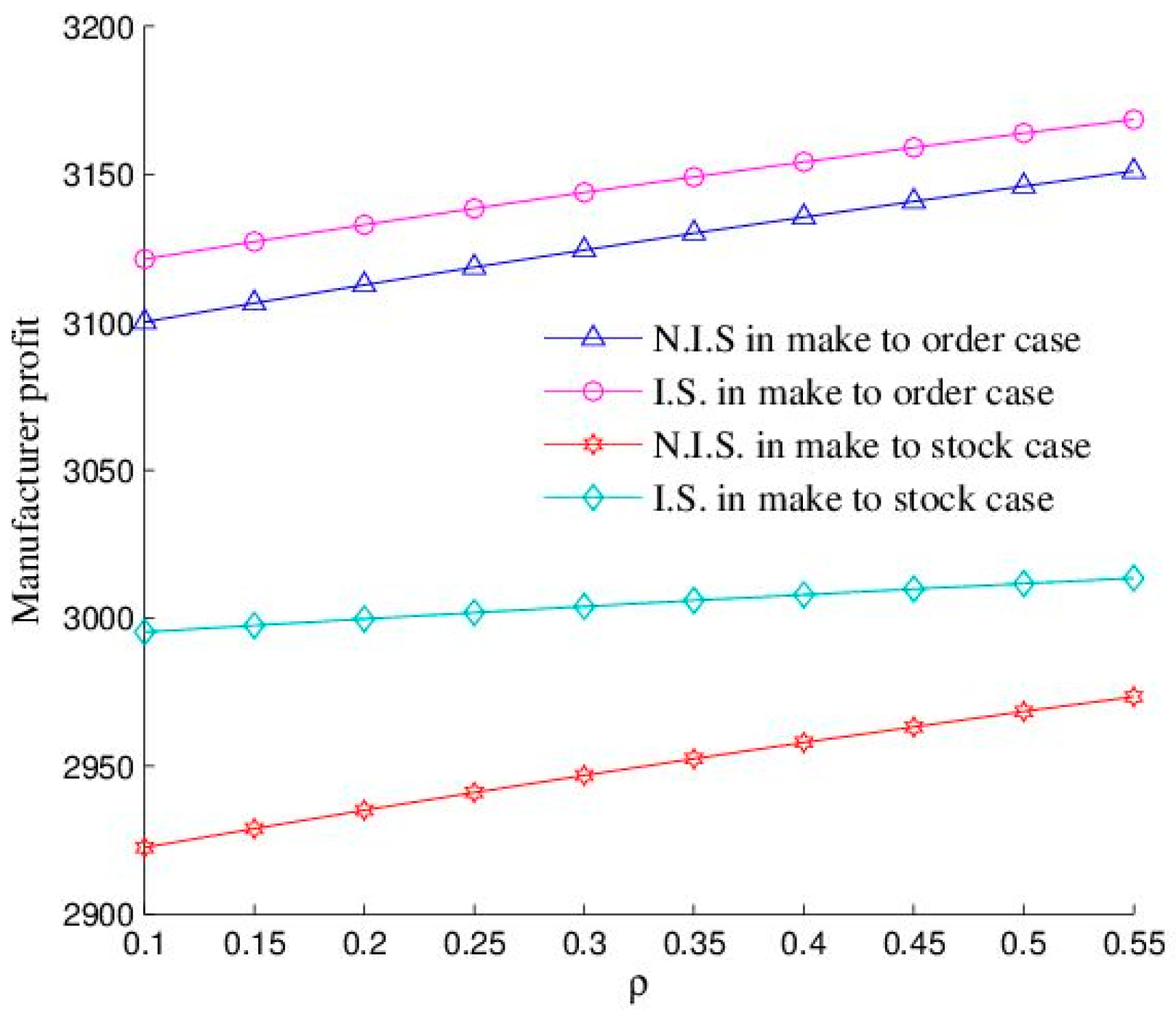
6.4. Effect of $\rho$

Figure 7 and Figure 8 illustrate the effects of $\rho$, the correlation between the manufacturer’s and the retailer’s forecasting information, on the performance of supply chain members. In the make-to-order and make-to-stock scenarios, the expected profits for the manufacturer and the retailer increase with $\rho$, whereas the value of information sharing decreases. The reason for this trend is that a higher correlation between the manufacturer’s and retailer’s demand forecasts leads to greater forecast homogeneity and makes their forecasts more substitutable, indicating that their information sources are becoming increasingly similar. As a result, the proportion of the manufacturer’s and the retailer’s forecasts in the expected demand decreases, whereas the proportion of $\overline{\alpha }$ in the expected demand increases. Given the value assignments of $\overline{\alpha }$, $f_1$, and $f_2$, the expected demand increases with $\rho$, thereby boosting the profits of the manufacturer and the retailer. However, as the rate of increase in expected demand slows down, the value of information sharing for the manufacturer and the retailer declines.

7. Conclusions

Amid continuous global warming, primarily driven by greenhouse gases emitted through human activities since the industrial revolution, the role of consumer preference for low-carbon products in influencing companies to adjust their business practices is being increasingly recognized. Given the importance of consumer information concerning low-carbon demands, a low-carbon supply chain consisting of one manufacturer and one retailer was established. In this setup, the manufacturer is responsible for reducing emissions to attract consumers who prefer low-carbon products. Meanwhile, both supply chain members utilize technological means to forecast consumer demand information. We analyzed the profits of supply chain members under two scenarios, i.e., make-to-order and make-to-stock, considering non-sharing and sharing of forecasted demand information. We also examined how the performance of supply chain members and the value of information sharing are influenced by factors such as the standard deviation of demand, the manufacturer’s forecast bias, the retailer’s forecast bias, and the forecast correlation coefficient.

Our findings indicated that the strategies of supply chain members are unaffected by the different production models adopted and that information sharing is beneficial to the manufacturer and the retailer. For manufacturers, their profits in a make-to-order scenario were shown to be higher than those in a make-to-stock scenario. In our numerical analysis, we observed that the profits of the manufacturer and the retailer in the information sharing scenario were consistently greater than those in the no information sharing scenario for the make-to-order and make-to-stock cases. In both scenarios, the retailer benefited more from information sharing than the manufacturer. The importance of information exchange to the retailer remained constant despite changes in production strategies. However, in a make-to-stock situation, information sharing was found to be more valuable to the manufacturer than in a make-to-order one.

In this paper, we assumed that the company was willing to voluntarily reduce its carbon emissions. Therefore, extending the model to scenarios where firms are required to reduce their emissions is a natural step to analyze the effect of government regulations on the performance of those firms.