Enhancing Sustainability: Quantifying and Mapping Vulnerability to Extreme Heat Using Socioeconomic Factors at the National, Regional and Local Levels
Abstract
1. Introduction
2. Materials and Methods
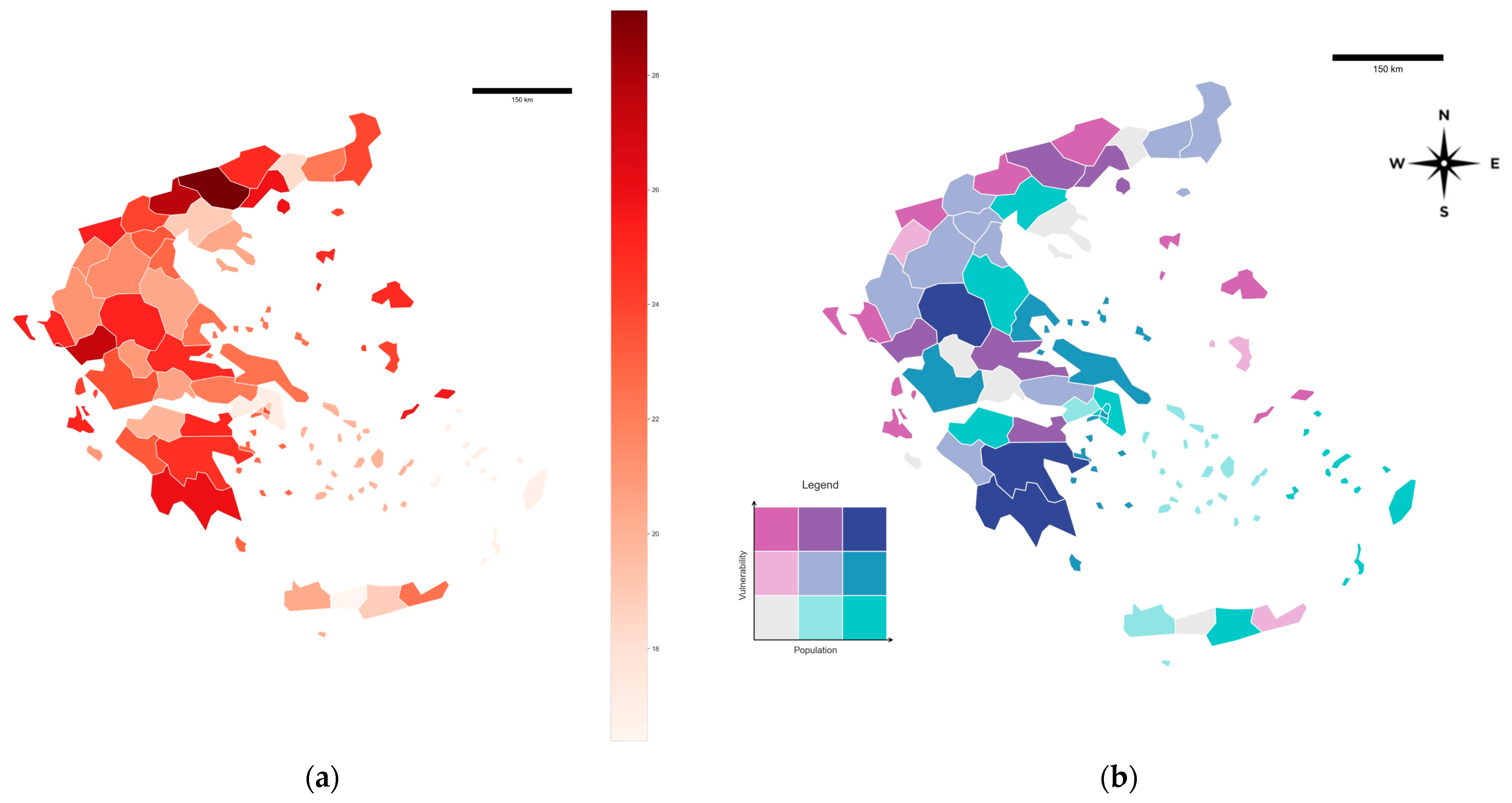
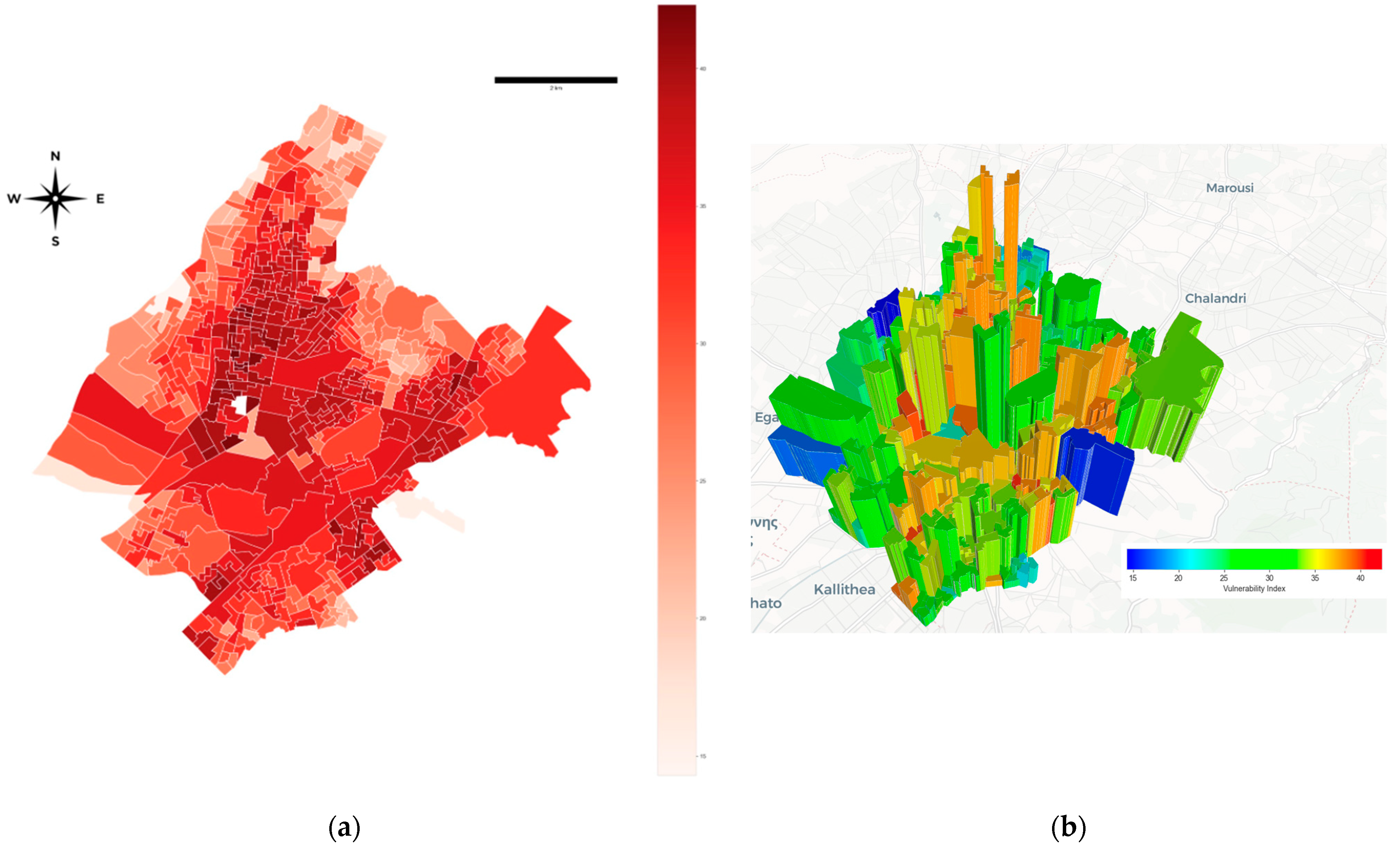
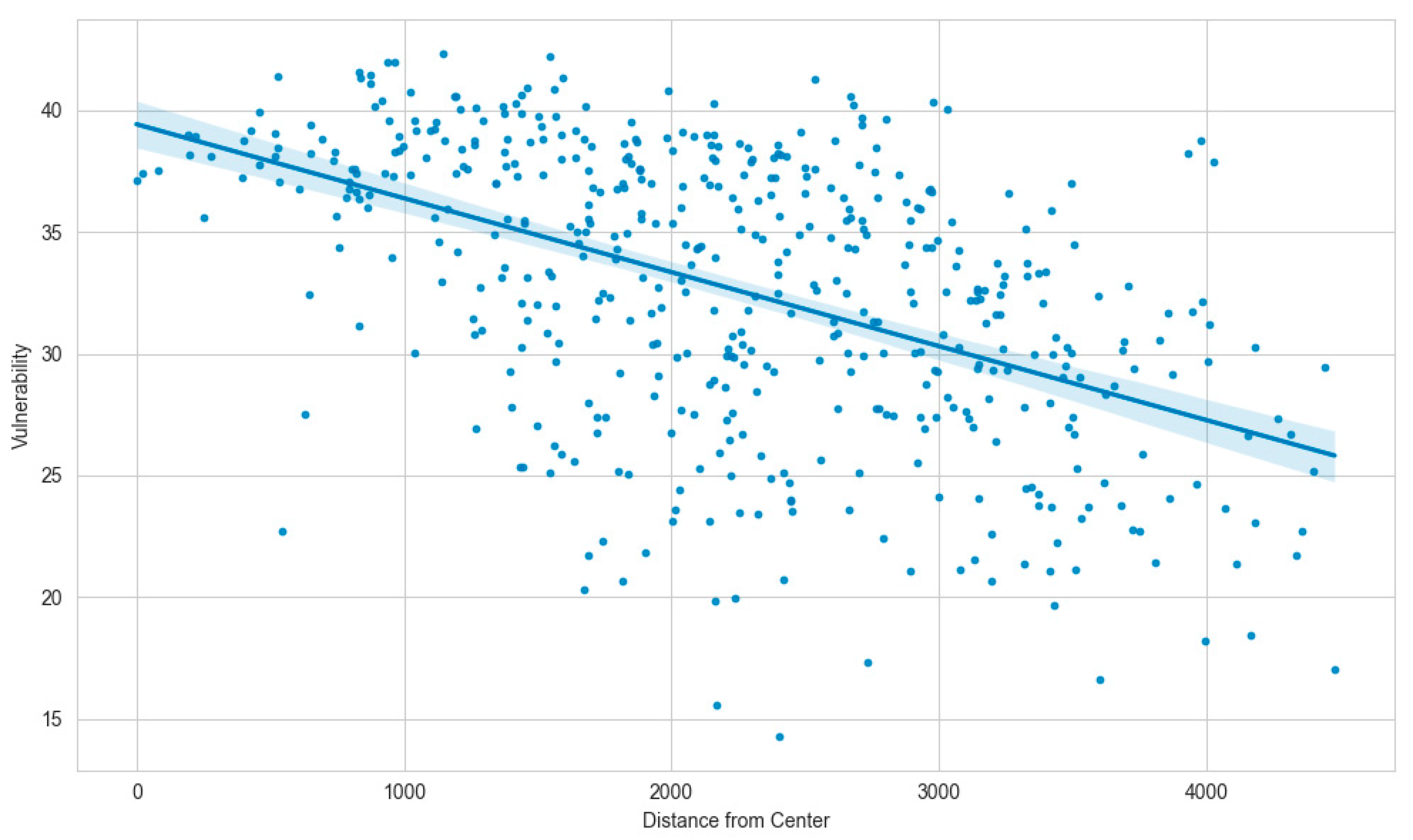
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Meehl, G.A.; Tebaldi, C. More intense, more frequent, and longer lasting heat waves in the 21st century. Science 2004, 305, 994–997. [Google Scholar] [CrossRef] [PubMed]
- Ballester, J.; Quijal-Zamorano, M.; Méndez Turrubiates, R.F.; Pegenaute, F.; Herrmann, F.R.; Robine, J.M.; Basagana, X.; Tonne, C.; Anto, J.M.; Achebak, H. Heat-related mortality in Europe during the summer of 2022. Nat. Med. 2023, 29, 1857–1866. [Google Scholar] [CrossRef] [PubMed]
- Ellena, M.; Breil, M.; Soriani, S. The heat-health nexus in the urban context: A systematic literature review exploring the socio-economic vulnerabilities and built environment characteristics. Urban Clim. 2020, 34, 100676. [Google Scholar] [CrossRef]
- Guo, Y.; Gasparrini, A.; Li, S.; Sera, F.; Vicedo-Cabrera, A.; Coêlho, M.; Saldiva, P.; Lavigne, É.; Tawatsupa, B.; Punnasiri, K.; et al. Quantifying excess deaths related to heatwaves under climate change scenarios: A multicountry time series modelling study. PLoS Med. 2018, 15, e1002629. [Google Scholar] [CrossRef]
- Kearl, Z.; Vogel, J. Urban extreme heat, climate change, and saving lives: Lessons from Washington state. Urban Clim. 2023, 47, 101392. [Google Scholar] [CrossRef]
- Hammer, J.; Ruggieri, D.G.; Thomas, C.; Caum, J. Local Extreme Heat Planning: An Interactive Tool to Examine a Heat Vulnerability Index for Philadelphia, Pennsylvania. J. Urban Health 2020, 97, 519–528. [Google Scholar] [CrossRef]
- Zaidi, R.; Pelling, M. Institutionally configured risk: Assessing urban resilience and disaster risk reduction to heat wave risk in London. Urban Stud. 2015, 52, 1218–1233. [Google Scholar] [CrossRef]
- Paravantis, J.; Santamouris, M.; Cartalis, C.; Efthymiou, C.; Kontoulis, N. Mortality Associated with High Ambient Temperatures, Heatwaves, and the Urban Heat Island in Athens, Greece. Sustainability 2017, 9, 606. [Google Scholar] [CrossRef]
- Romero-Lankao, P.; Qin, H.; Dickinson, K. Urban vulnerability to temperature-related hazards: A meta-analysis and meta-knowledge approach. Glob. Environ. Chang. 2012, 22, 670–683. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Pachauri, R.K., Meyer, L.A., Eds.; IPCC: Geneva, Switzerland, 2014; p. 151. [Google Scholar]
- Nayak, S.G.; Shrestha, S.; Kinney, P.L.; Ross, Z.; Sheridan, S.C.; Pantea, C.I.; Hsu, W.; Muscatiello, N.; Hwang, S.A. Development of a heat vulnerability index for New York State. Public Health 2018, 161, 127–137. [Google Scholar] [CrossRef]
- Kaiser, R.; Le Tertre, A.; Schwartz, J.; Gotway, C.A.; Daley, W.R.; Rubin, C.H. The effect of the 1995 heat wave in Chicago on all-cause and cause-specific mortality. Am. J. Public Health 2007, 97 (Suppl. S1), S158–S162. [Google Scholar] [CrossRef]
- Semenza, J.C.; Rubin, C.H.; Falter, K.H.; Selanikio, J.D.; Flanders, W.D.; Howe, H.L.; Wilhelm, J.L. Heat-related deaths during the July 1995 heat wave in Chicago. N. Engl. J. Med. 1996, 335, 84–90. [Google Scholar] [CrossRef] [PubMed]
- Hayhoe, K.; Sheridan, S.; Kalkstein, L.; Greene, S. Climate change, heat waves, and mortality projections for Chicago. J. Great Lakes Res. 2010, 36 (Suppl. S2), 65–73. [Google Scholar] [CrossRef]
- Founda, D.; Santamouris, M. Synergies between Urban Heat Island and Heat Waves in Athens (Greece), during an extremely hot summer (2012). Sci. Rep. 2017, 7, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Bunker, A.; Wildenhain, J.; Vandenbergh, A.; Henschke, N.; Rocklöv, J.; Hajat, S.; Sauerborn, R. Effects of Air Temperature on Climate-Sensitive Mortality and Morbidity Outcomes in the Elderly; a Systematic Review and Meta-analysis of Epidemiological Evidence. EBioMedicine 2016, 6, 258–268. [Google Scholar] [CrossRef]
- Cutler, M.; Marlon, J.; Howe, P.; Leiserowitz, A. The Influence of Political Ideology and Socioeconomic Vulnerability on Perceived Health Risks of Heat Waves in the Context of Climate Change. Weather Clim. Soc. 2018, 10, 731–746. [Google Scholar] [CrossRef]
- Rohat, G.; Wilhelmi, O.; Flacke, J.; Monaghan, A.; Gao, J.; Dao, H.; Maarseveen, M. Characterizing the role of socioeconomic pathways in shaping future urban heat-related challenges. Sci. Total. Environ. 2019, 695, 133941. [Google Scholar] [CrossRef]
- Romero-Lankao, P.; Gnatz, D.M.; Wilhelmi, O.; Hayden, M. Urban Sustainability and Resilience: From Theory to Practice. Sustainability 2016, 8, 1224. [Google Scholar] [CrossRef]
- Russo, S.; Sillmann, J.; Fischer, E.M. Top ten European heatwaves since 1950 and their occurrence in the coming decades. Environ. Res. Lett. 2015, 10, 124003. [Google Scholar] [CrossRef]
- Hu, L.; Li, L. Using Tree-Based Machine Learning for Health Studies: Literature Review and Case Series. Int. J. Environ. Res. Public Health 2022, 19, 16080. [Google Scholar] [CrossRef]
- Meerow, S.; Newell, J.P.; Stults, M. Defining urban resilience: A review. Landsc. Urban Plan. 2016, 147, 38–49. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Hancock, J.T.; Khoshgoftaar, T.M. CatBoost for big data: An interdisciplinary review. J. Big Data 2020, 7, 1–45. [Google Scholar] [CrossRef] [PubMed]
- Ho, T.K. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; Volume 1, pp. 278–282. [Google Scholar]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. Adv. Neural Inf. Process. Syst. 2018, 31, 1–11. Available online: https://dl.acm.org/doi/pdf/10.5555/3327757.3327770 (accessed on 14 March 2022).
- Bergstra, J.; Yamins, D.; Cox, D. Making a science of model search: Hyperparameter optimization in hundreds of dimensions for vision architectures. In International Conference on Machine Learning; PMLR: Birmingham, UK, 2013; pp. 115–123. Available online: https://proceedings.mlr.press/v28/bergstra13.pdf (accessed on 8 March 2022).
- Toms, J.D.; Lesperance, M.L. Piecewise regression: A tool for identifying ecological thresholds. Ecology 2003, 84, 2034–2041. [Google Scholar] [CrossRef]
- Xiang, L.; Cai, M.; Ren, C.; Ng, E. Modeling pedestrian emotion in high-density cities using visual exposure and machine learning: Tracking real-time physiology and psychology in Hong Kong. Build. Environ. 2021, 205, 108273. [Google Scholar] [CrossRef]
- Ziliaskopoulos, K. Athens Socioeconomic Heat Vulnerability Index—Features and Index Per Region; Zenodo: Geneva, Switzerland, 2023. [Google Scholar] [CrossRef]
- Charakopoulos, A.; Karakasidis, T.; Ziliaskopoulos, K.; Laspidou, C. Complex network analysis of climate and landscape satellite data to explore spatio-temporal patterns in urban environment: The case of Athens. Appl. Netw. Sci. 2024, 9, 42. [Google Scholar] [CrossRef]
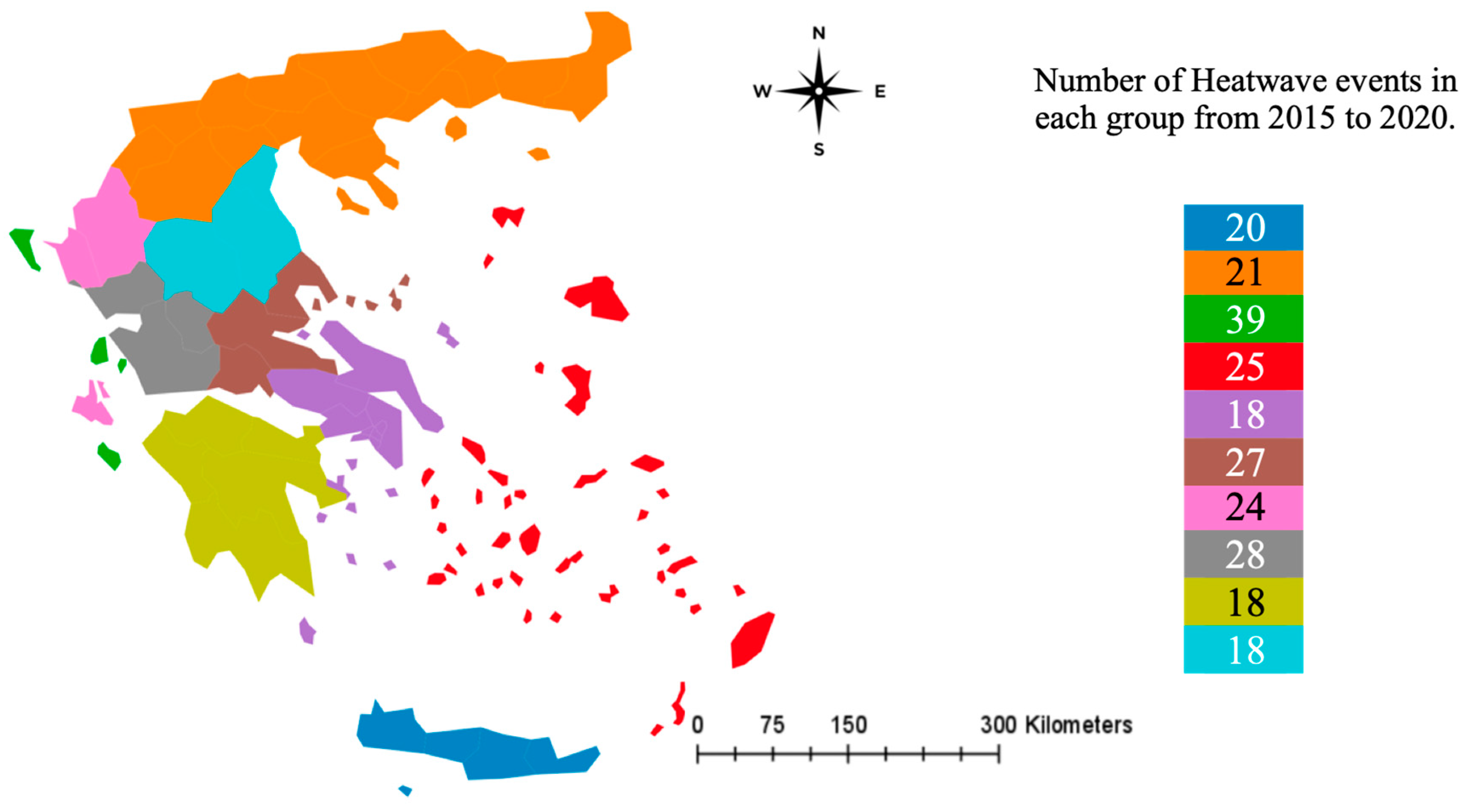
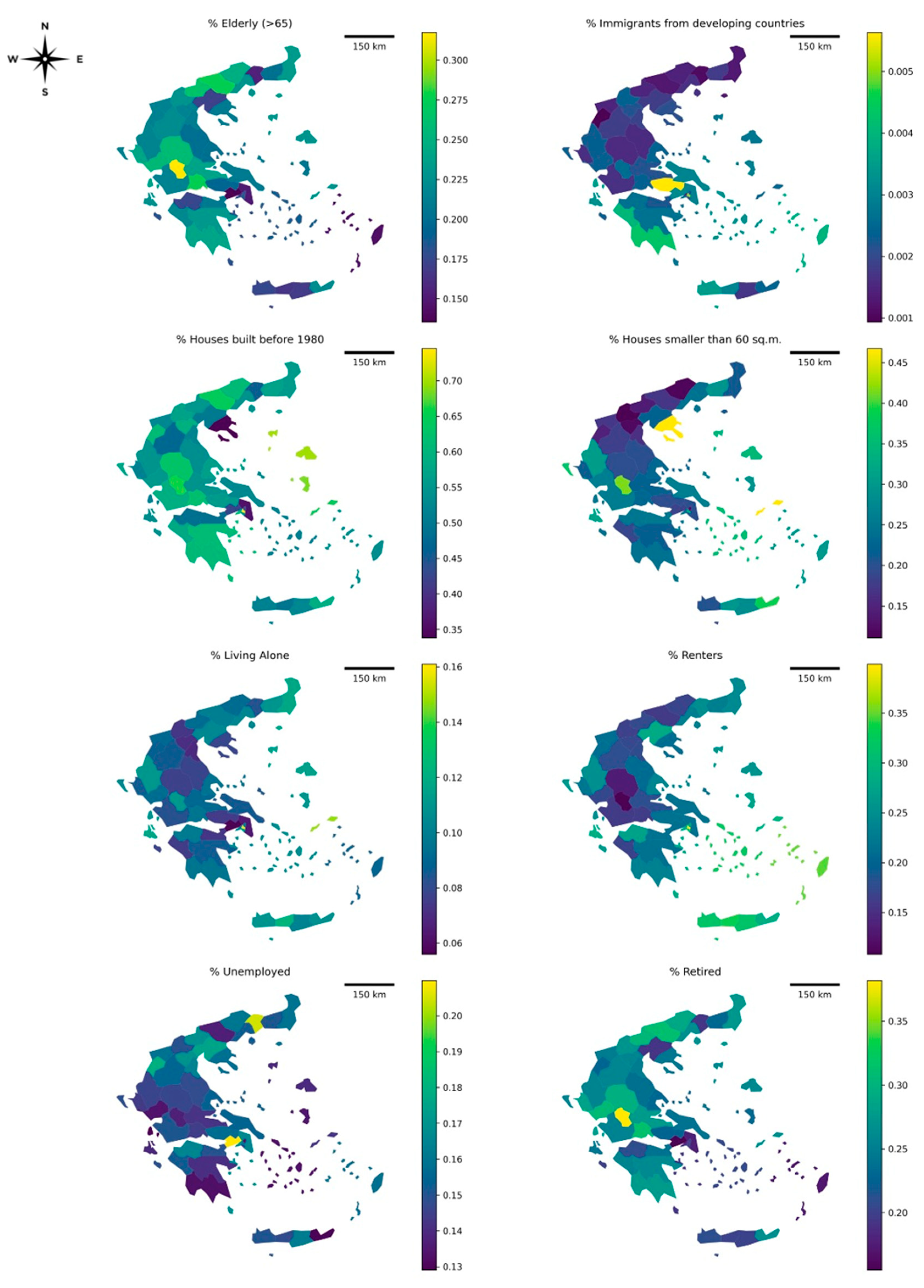
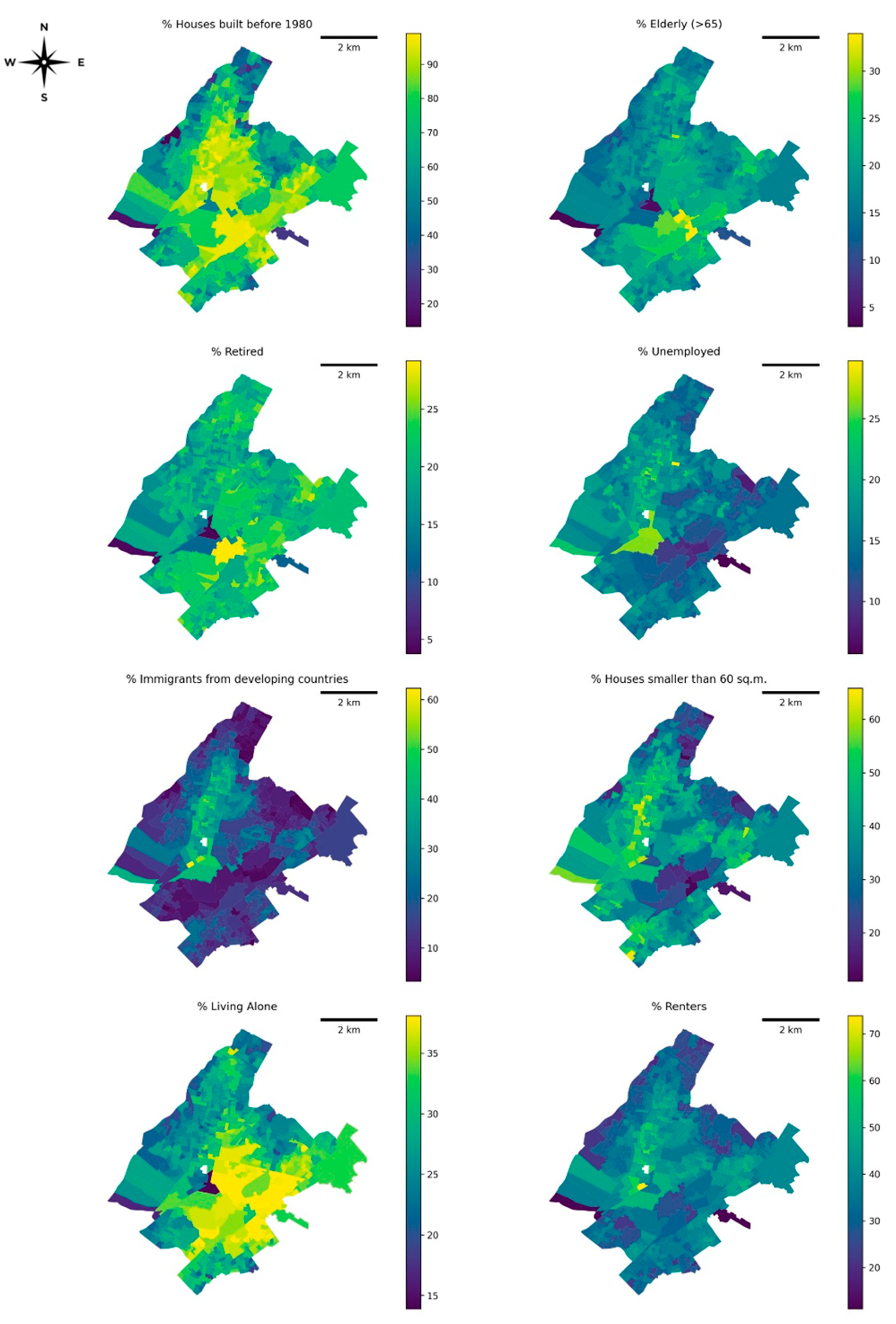
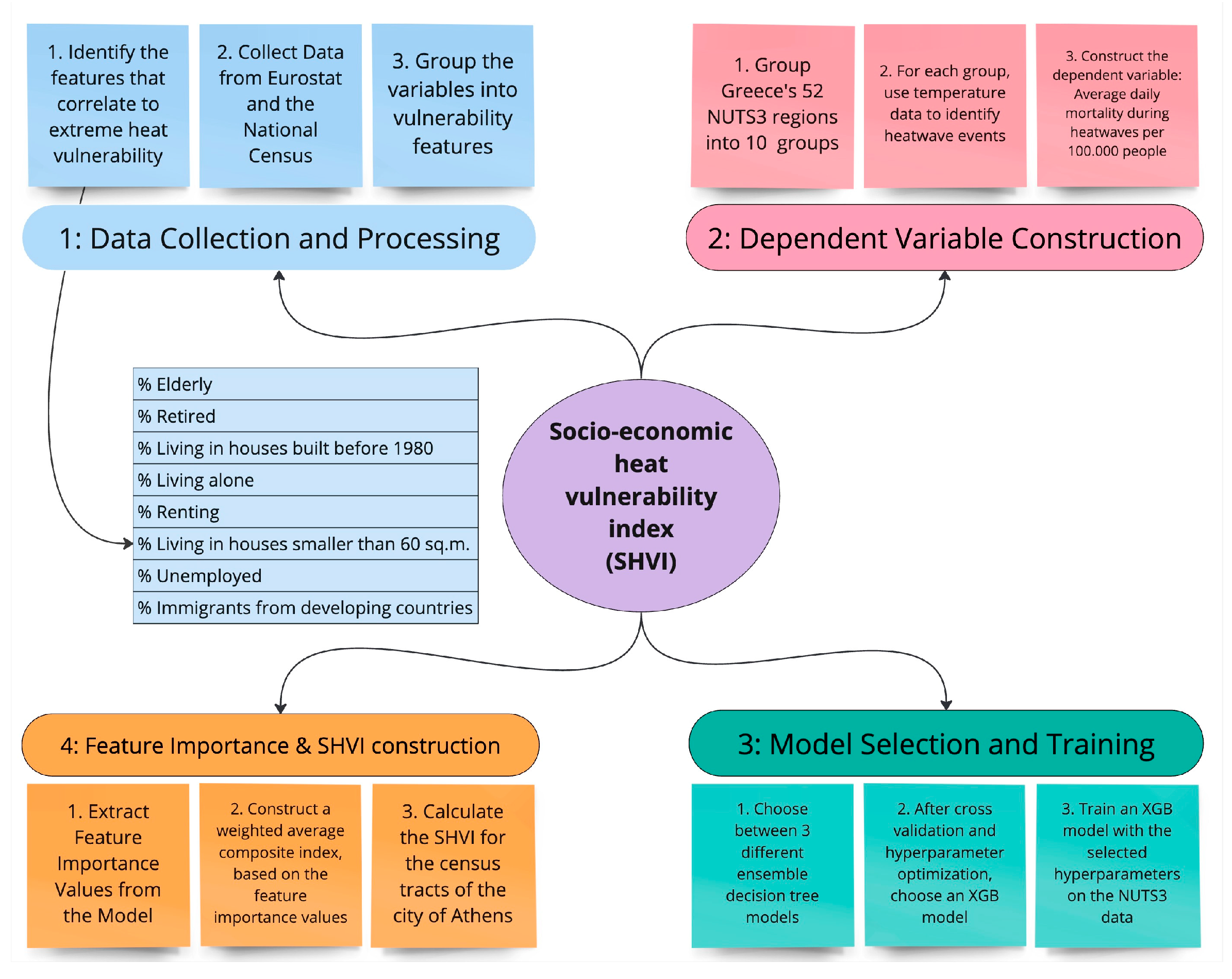


| Data Description | Scale and Units | Data Source |
|---|---|---|
| Maximum temperature for 10 Greek cities, 2015–2020 | Hourly, Celsius | Open Weather Map https://openweathermap.org/ (accessed on 10 December 2022) |
| Number of people by age group, from the 2011 national census | Per NUTS3 region and per census tract in Athens | Hellenic Statistical Authority |
| Number of people by country of origin, from the 2011 national census | Per NUTS3 region and per census tract in Athens | Hellenic Statistical Authority |
| Number of people by different household sizes (e.g., 2-people households, 4-people households, etc.) from the 2011 census | Per NUTS3 region and per census tract in Athens | Hellenic Statistical Authority |
| Number of people by employment status, (employed, looking for work, first-time looking, student, retired, independent, housework, other) from the 2011 census | Per NUTS3 region and per census tract in Athens | Hellenic Statistical Authority |
| Number of dwellings by living status (owner, renting, cooperative ownership, communal housing, other) from the 2011 census | Per NUTS3 region and per census tract in Athens | Hellenic Statistical Authority |
| Number of dwellings by square footage, from the 2011 census | Per NUTS3 region and per census tract in Athens | Hellenic Statistical Authority |
| Number of dwellings by age of building, from the 2011 census | Per NUTS3 region and per census tract in Athens | Hellenic Statistical Authority |
| Number of deaths by age group, 2015–2020 | Per NUTS3 region, weekly | Eurostat |
| Method | MSE | MAE | R2 |
|---|---|---|---|
| XGB | 2.1437 | 0.9 | 0.737 |
| CatBoost | 3.724 | 1.688 | 0.726 |
| Random Forest | 4.882 | 1.9 | 0.642 |
| Hyperparameter Name | Hyperparameter Value |
|---|---|
| Column sample by tree | 0.862 |
| Gamma | 1.309 |
| Learning rate | 952 × 10−5 |
| Max depth | 17 |
| Minimum child weight | 2 |
| Number of estimators | 1372 |
| Alpha regularization | 0.2086 |
| Lambda regularization | 1.007 |
| Subsample | 0.96 |
| No. Observations | 2983 | |||||
| No. Model Parameters | 4 | |||||
| Degrees of Freedom | 2979 | |||||
| Res. Sum of Squares | 1.29253 × 105 | |||||
| Total Sum of Squares | 1.55617 × 105 | |||||
| R Squared | 0.169419 | |||||
| Adjusted R Squared | 0.168303 | |||||
| Converged | True | |||||
| Estimate | Std Err | t-value | p > |t| | 95% CI (LL) | 95% CI (UL) | |
| Constant | 31.2981 | 0.395 | 79.296 | 0 | 30.524 | 32.072 |
| Alpha1 | 0.23707 | 0.0159 | 14.957 | 7.94 × 10−49 | 0.206 | 0.26815 |
| Beta | 3.99292 | 0.387 | 10.326 | - | 3.2347 | 4.7511 |
| Breakpoint | 37.3017 | 0.253 | - | - | 36.806 | 37.797 |
| These alphas (gradients of segments) are estimated from betas (change in gradient) | ||||||
| Alpha2 | 4.23 | 0.386 | 10.948 | 2.23 × 10−27 | 3.4724 | 4.9875 |
| No. Observations | 2983 | |||||
| No. Model Parameters | 6 | |||||
| Degrees of Freedom | 2977 | |||||
| Res. Sum of Squares | 1.85371 × 106 | |||||
| Total Sum of Squares | 2.65208 × 106 | |||||
| R Squared | 0.301034 | |||||
| Adjusted R Squared | 0.299624 | |||||
| Converged | True | |||||
| Estimate | Std Err | t-value | p > |t| | 95% CI (LL) | 95% CI (UL) | |
| Constant | 274.319 | 2.33 | 117.8 | 0 | 269.75 | 278.89 |
| Alpha1 | −3.34262 | 0.121 | −27.629 | 8.9 × 10−150 | −3.5798 | −3.1054 |
| Beta1 | 5.68021 | 0.573 | 9.9095 | - | 4.5563 | 6.8041 |
| Beta2 | 3.92391 | 0.759 | 5.1673 | - | 2.4349 | 5.4129 |
| Breakpoint1 | 26.8632 | 0.418 | - | - | 26.043 | 27.683 |
| Breakpoint2 | 32.9795 | 0.649 | - | - | 31.707 | 34.252 |
| These alphas (gradients of segments) are estimated from betas (change in gradient) | ||||||
| Alpha2 | 2.33759 | 0.56 | 4.1721 | 3.1 × 10−5 | 1.239 | 3.4362 |
| Alpha3 | 6.2615 | 0.513 | 12.216 | 1.6 × 10−33 | 5.2565 | 7.2665 |
| Feature Name | Feature Importance Value |
|---|---|
| % Elderly | 0.455 |
| % Retired | 0.245 |
| % Living in houses built before 1980 | 0.130 |
| % Living alone | 0.063 |
| % Renting | 0.058 |
| % Living in houses smaller than 60 m2 | 0.023 |
| % Unemployed | 0.014 |
| % Immigrants from developing countries | 0.010 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ziliaskopoulos, K.; Petropoulos, C.; Laspidou, C. Enhancing Sustainability: Quantifying and Mapping Vulnerability to Extreme Heat Using Socioeconomic Factors at the National, Regional and Local Levels. Sustainability 2024, 16, 7603. https://doi.org/10.3390/su16177603
Ziliaskopoulos K, Petropoulos C, Laspidou C. Enhancing Sustainability: Quantifying and Mapping Vulnerability to Extreme Heat Using Socioeconomic Factors at the National, Regional and Local Levels. Sustainability. 2024; 16(17):7603. https://doi.org/10.3390/su16177603
Chicago/Turabian StyleZiliaskopoulos, Konstantinos, Christos Petropoulos, and Chrysi Laspidou. 2024. "Enhancing Sustainability: Quantifying and Mapping Vulnerability to Extreme Heat Using Socioeconomic Factors at the National, Regional and Local Levels" Sustainability 16, no. 17: 7603. https://doi.org/10.3390/su16177603
APA StyleZiliaskopoulos, K., Petropoulos, C., & Laspidou, C. (2024). Enhancing Sustainability: Quantifying and Mapping Vulnerability to Extreme Heat Using Socioeconomic Factors at the National, Regional and Local Levels. Sustainability, 16(17), 7603. https://doi.org/10.3390/su16177603







