Analyzing Cooling Island Effect of Urban Parks in Zhengzhou City: A Study on Spatial Maximum and Spatial Accumulation Perspectives

Abstract

As a result of urbanization, cities worldwide are experiencing urban heat island (UHI) challenges. Urban parks, which are essential components of urban blue and green landscapes, typically have lower temperatures in providing outdoor comfort than their surroundings with impervious surfaces. This phenomenon, known as the park cooling island effect (PCIE), has been recognized as an effective approach to mitigate the negative effects of the UHI in the context of sustainable development of urban environment. To cope with the serious UHI challenge and to guide urban park planning and design for Zhengzhou City, which is one of the China’s new first-tier cities, 35 urban parks in the city were analyzed in this study. Remotely sensed land surface temperature ($LST$) and reflectance images by Landsat 9 and Sentinel-2 were selected as data sources. A cubic polynomial model that depicts the relationship between the $LST$ and the distance from the park edge was first built for each park. Based on this model, the spatial maximum perspective metrics (including the park cooling area ($PCA$) and park cooling efficiency ($PCE$)) and the spatial accumulation perspective metrics (including park cooling intensity ($PCI$) and park cooling gradient ($PCG$)) were calculated to quantify the PCIE of each park. The 35 parks were divided into three groups using the hierarchical clustering method for further analysis. For each group, the metrics of the PCIE were statistically analyzed, and the main factors influencing the PCIE were identified by the Spearman correlation coefficient. The results indicate the following: (1) The 35 urban parks exhibit an obvious PCIE. The maximum cooling distance is 133.95 ± 41.93 m. The mean $LST$ of the park is 3.01 ± 1.23 °C lower than that within the maximum cooling distance range. (2) The PCIE varies among different types of parks. Parks with large areas and covered by certain water bodies generally exhibit higher $PCA$, $PCI$, and $PCG$ values. However, parks with small areas and mainly covered by vegetation show higher $PCE$ values, which makes them more economical in exerting the PCIE. (3) Park area and landscape shape index ($LSI$) were positively correlated with $PCA$, $PCI$, and $PCG$. However, there is a threshold in the relationship between the park area and the $PCI$. A park area of approximately 19 ha can produce a higher $PCI$ than a smaller one. In central urban areas with limited space, parks with small areas, complex shapes, and predominant vegetation coverage can be designed to achieve higher cooling efficiency.

1. Introduction

Rapid urbanization dramatically changes land use and land cover, thereby directly affecting the capacity of a land surface to absorb solar radiation, which poses strong impacts on the local climatic conditions. One notable consequence is the urban heat island (UHI), which refers to the phenomenon that urban areas exhibit higher atmospheric or surface temperatures than their non-urbanized counterparts. The UHI effect is a major concern due to its adverse effects [1,2], such as increased energy consumption [3], worsened air quality [4], and higher risks of morbidity and mortality from heat-related diseases [5]. Studies have shown a clear link between land cover types and the UHI effect [6,7]. Urban parks, as an essential component of urban blue and green infrastructure, are the most nature-like areas, with a combination of water bodies and green space patches. Therefore, urban parks are cooler than the surrounding built-up areas and have a cooling effect on the adjoining areas like a cool island. For instance, previous studies have found that the temperature of surrounding areas within hundreds of meters around the urban parks can be decreased by 2∼3 °C [8,9,10]. The phenomenon is denoted as the park cooling island effect (PCIE). Because of the significant PCIE, urban parks have been recognized as a promising solution to mitigate the UHI effect [11,12,13].

By adjusting and controlling the key factors that significantly influence the PCIE, urban parks can be reasonably designed to maximize their cooling effect. Considerable studies on the cooling effects of green space and water bodies have revealed the crucial factors that influence PCIE. Both the landscape composition and landscape configuration of the parks were found to be correlated to the PCIE [12,14,15,16,17]. The common parameters used to describe the landscape characteristics of the parks include park size, geometric characteristics, and the composition of the land cover. Their relationships to the PCIE have been discussed to identify the key factors affecting the PCIE [18,19,20]. However, it is still uncertain regarding the key factors impacting the PCIE. Studies in different regions even reach contradicting conclusions. While the park size, which has been found to explain more than 50% of the variation in the PCIE in eastern China [21,22], is usually identified as the dominant factor, there exists a threshold size beyond which its impact on the PCIE diminishes [12]. There are contradictory findings regarding the shape complexity of parks. Some researches suggest that more intricate shapes enhance the PCIE [23,24], whereas other studies indicate that circular park shapes strengthen PCIE [18,25]. Moreover, the PCIE is affected not only by parks’ interior landscapes but also by their exterior conditions. The landscape composition of the surroundings [26,27], the 3D building morphology [28], the local climate zone (LCZ) [29], and the geographic background climate [21,30], have also been reported to significantly influence the PCIE. Therefore, regional studies that consider the specific features of each city are necessary to better understand the driving factors of the PCIE and thus to effectively guide the construction of urban parks.

The quantitative evaluation of the PCIE is essential for understanding its influencing factors. Due to the extensive spatial coverage, land surface temperature ($LST$) images derived from thermal infrared remote sensors have been widely used in the quantitative evaluation of the PCIE. The $LST$ difference between the interior of the park and its surrounding area is a commonly used metric for the PCIE assessment [31,32,33]. To define the surrounding area, a buffer zone outside the park needs to be built. Two approaches that are commonly used in the community to determine the buffer radius are the fixed distance method and the “$LST$–Distance” curve turning point method [33]. While the fixed distance method uses a uniform buffer radius for all parks [31], the “$LST$–Distance” curve turning point method determines a unique buffer radius for each park by identifying the first turning point of a “$LST$–Distance” curve [24,26]. A series of buffer zones with equal distance intervals are created from the boundary of the park to construct the “$LST$–Distance” curve. The average value of the $LST$ in each buffer zone is calculated to analyze how the $LST$ changes with the distance from the park (i.e., the “$LST$–Distance” curve). Affected by the PCIE, the $LST$ initially rises as the distance from the park increases and then tends to stabilize because the effect of the PCIE gradually diminishes. This also assumes that the first turning point of “$LST$–Distance” curve is the point at which the $LST$ stabilizes. This turning point can be identified through various methods, including visual inspection [24,32], setting a threshold for $LST$ differences between the buffers [34,35], or evaluating the derivative of the cubic polynomial function fitted to the curve [26,36]. The spatial distance corresponding to the first turning point is taken as the buffer radius.

The advantages of the fixed distance method are straightforward and easy to implement [33,37]. However, the method may introduce uncertainties in the evaluation of the PCIE [38]. The distribution of the $LST$ around the park exhibits continuous spatial patterns that generally vary across different parks. The “$LST$–Distance” curve provides valuable insights into the patterns. With the first turning point of the “$LST$–Distance” curve, additional metrics can be calculated to further evaluate the PCIE. For example, Yu et al. proposed metrics to evaluate the extent and intensity of the PCIE based on the first turning point [39]. The extent of the PCIE is the buffer zone from the edge of the park to the distance corresponding to the first turning point. The intensity of the PCIE is the difference between the $LST$ at the first turning point and the average $LST$ of the park. Since the first turning point represents the maximum extent influenced by the PCIE, these metrics evaluate the PCIE from the perspective of the spatial maximum. Due to the spatial continuity and non-linearity of the “$LST$–Distance” curve, the first turning points may be same for parks with different “$LST$–Distance” curves. This suggests that the above metrics may fail to capture the continuous spatial patterns and spatial heterogeneity inherent in the PCIE. To address this limitation, Peng et al. [40] recently proposed metrics for evaluating the PCIE from both spatial maximum and spatial accumulation perspectives. The metrics from the spatial maximum perspective, which evaluate the maximum influence extent of the PCIE, include the park cooling area ($PCA$) and the park cooling efficiency ($PCE$). Additionally, the metrics from the spatial accumulation perspective, which evaluate the accumulated continuous influence within the maximum influence extent, include the park cooling intensity ($PCI$) and the park cooling gradient ($PCG$). These metrics have been widely applied to enhance the evaluation of the PCIE [41,42,43,44,45,46]. For example, Shi et al. investigated the PCIE of green spaces in major cities of the Yangtze River Economic Belt in China [45]. Zhang et al. comprehensively evaluated the PCIE of urban parks in the temperate monsoon climate zone of China [46].

Zhengzhou, honored as a “Green City” in the 1980s, was awarded the title of National Ecological Garden City in January 2020. However, due to rapid urbanization, the city faces challenges related to UHI effects, as highlighted in recent studies [47,48]. The latest research in 2023 ranked Zhengzhou at the top among the 10 “furnace” cities in provincial capitals [49], thus emphasizing the pressing need for sustainable urban planning strategies. In line with its commitment to enhancing the urban ecological environment and meeting the diverse needs of its residents, Zhengzhou aims to achieve a total park green space area of 10007 ha in the main urban area by 2030 according to the Zhengzhou Urban Green Space System Plan (2013–2030). How to plan and build urban parks to achieve these goals has become an urgent practical issue. However, there is limited research on the PCIE of parks in Zhengzhou.

Aiming to provide objective, practical, and economic insights into the design and construction of parks that maximize the PCIE to mitigate the UHI effect, this study (1) comprehensively evaluates the PCIE of 35 urban parks in Zhengzhou from the perspectives of spatial maximum and spatial accumulation during the summer hot extremes; (2) investigates the differences in the PCIEs of typical park types; and (3) identifies the primary factors that influence the PCIE through an analysis of park characteristics. Our study aims to improve an understanding of the PCIE of urban parks and to support the optimization or planning of urban parks to mitigate thermal environment problems in urban areas.

2. Materials and Methods

2.1. Study Site

Zhengzhou city, the capital of Henan province, is located at 112°42′ to 114°14′ E, 34°16′ to 34°58′ N. The built-up area was 774.32 km² in 2022. It has a temperate continental monsoon climate with four distinct seasons. The winter is long, dry, and cold, while the summer is relatively hot. The average annual temperature is 16 °C. The hottest month in Zhengzhou is July, with an average maximum temperature of 33.8 °C. It faces serious UHI problems during the summer.

The park boundary data were extracted from Gaode Map (https://map.amap.com, accessed on 10 March 2024). Two key principles for selecting parks were the following: (1) Each park should have an area greater than 1 ha, and (2) the parks should be situated in the urban core region. Therefore, 35 parks with an average area of 36.10 ha (1.71 ha to 232.36 ha) were selected (Figure 1). The largest one is Xiliuhu Park (232.36 ha), and the smallest is Qicai Park (1.71 ha). Among the 35 parks, 16 parks are located within the third ring road of Zhengzhou City, and 15 parks are located between the third ring road and the fourth ring road. Moreover, the 35 urban parks were categorized into three types according to their area, land cover, and shape.

2.2. Data Collection

The Landsat 9 satellite with the latest Thermal Infrared Sensor 2 (TIRS-2) has a fine spatial resolution in $LST$ retrieval [50]. The released Collection 2 Level 2 $LST$ product has shown good performance according to the evaluation [51]. To analyze the PCIE of the parks during hot extremes, an image of Zhengzhou City with an acquisition date of 7 July 2022 was downloaded from the LandsatLook website (https://landsatlook.usgs.gov/explore, accessed on 20 March 2024). The cloud contamination was measured at 0.27%. The spatial resolution of the $LST$ band in the product was resampled to 30 m, and the $DN$ value was converted to $LST$ in the unit °C through the following equation:

$$LST=DN\times 0.00341802+149-273.15,$$

(1)

A Sentinel-2B satellite image of Zhengzhou City was employed to classify the land cover and land use. The Sentinel-2 L2A surface reflectance product was downloaded from the ESA website (https://scihub.copernicus.eu/, accessed on 20 March 2024). The acquisition date was 16 June 2022, which is close to the Landsat 9 image. The Sentinel-2B satellite’s MultiSpectral Instrument (MSI) comprises four bands with a spatial resolution of 10 meters, thus offering better spatial detail than the Operational Land Imager 2 (OLI-2) onboard the Landsat 9 satellite, which has a spatial resolution of 30 m. Initially, the normalized vegetation index (NDVI) and normalized water body index (NDWI) were derived from the 10 m resolution bands. By integrating NDVI, NDWI, and the 10 m resolution reflectance bands, land cover and land use were classified into four categories(build-up, vegetation, water bodies, and unused land) using the maximum likelihood classification method. However, there were significant classification errors between the “build-up” and “unused land” categories, as well as between “water bodies” and “building shadows”, which were further corrected through visual interpretation. To assess the classification precision, 200 samples were randomly selected for each category. The overall accuracy achieved was 86.5%, with a kappa coefficient of 0.82.

2.3. Quantification of PCIE from Both Spatial Maximum and Spatial Accumulative Perspectives

Previous studies have indicated that PCIE gradually decreases with distance from the boundary of parks and disappears beyond a certain distance. The relationship between $LST$ and distance is non-linear, and the “$LST$–Distance” curve can be fitted using a cubic polynomial function [26,36,39,40,52,53]. Function $T\left(D\right)$ is as follows:

$$T\left(D\right)=a\times D^3+b\times D^2+c\times D+d(a\ne 0),$$

(2)

where D denotes the spatial distance (in meters) from the park boundary, and a, b, c, and d are the coefficients of the function. To investigate the “$LST$–Distance” relationship, the average $LST$ within the park is taken as $T\left(0\right)$, with the park boundary designated as $D=$ 0 m. By creating a series of buffer rings starting from the park boundary at intervals of 30 m (a total of 20 rings), each corresponding to distances of $D=$ 30 m, 60 m, …, 600 m. The average $LST$ inside each buffer was regarded as $T\left(D\right)$. This approach allows for a detailed examination of the $LST$ profile along the distance from the park boundary (see Figure 2 for visualization).

The study employed the non-linear least squares method to determine the coefficients of the fitted function. Considering the different characteristics of the parks, four models were fitted at various distances using 270 m, 360 m, 450 m, and 600 m buffer widths. The model with the highest $R^2$ was considered to best fit the “$LST$–Distance” relationship. The red curve in Figure 2b illustrates the model fitted using data from 0∼450 m.

As depicted by the red curve in Figure 2b, the buffer zone’s $LST$ increases as the D increases. But the increase rate continually decreases until it reaches zero, at which point the first derivative of the $T\left(D\right)$ is zero. This point is referred to the first turning point. The first turning point of $T\left(D\right)$ indicates the maximum cooling distance of PCIE, and the corresponding distance D is symbolized as L. The value of L can be calculated as

$$L=\frac{-2b-\sqrt{\mathsf{\Delta }}}{6a},$$

(3)

where $\mathsf{\Delta }=4b^2-12ac$. If $\mathsf{\Delta }\le 0$, then $L=-b/3a$.

Taking L and $T\left(D\right)$ as the foundation, Peng et al. [40] introduced $PCA$, $PCE$, $PCI$, and $PCG$ to quantify the PCIE. The $PCA$ represents the area of the buffer zone that extends outward from the park, with L serving as the buffer distance, thereby representing the maximum extent that the park can cool significantly. The $PCE$ is defined as the ratio of $PCA$ to the park’s area, thus indicating the cooling area generated per unit of the park’s area and providing insights into the efficiency and effectiveness of the PCIE. The maximum cooling distance L represents the maximum extent influenced by PCIE. Therefore, $PCA$ and $PCE$ provide an evaluation of PCIE from a spatial maximum perspective.

Since the process of PCIE is spatially non-linear, the L may be same even though the “$LST$–Distance” curves vary, e.g., the blue curve in Figure 2b. Therefore, assessing PCIE solely from a spatial maximum perspective is insufficient to fully capture the diverse characteristics present in different parks. It is essential to incorporate the spatial accumulative metrics to understand the spatial continuity influence of PCIE. To achieve this, $PCI$ and $PCG$ are established using the following:

$$PCI=\frac{L\times T\left(L\right)-{\int }_0^{L}T\left(D\right)\mathrm{d}D}{L\times T\left(L\right)},PCG=\frac{L\times T\left(L\right)-{\int }_0^{L}T\left(D\right)\mathrm{d}D}{L}.$$

(4)

Since the cooling process around a park is considered to be spatially continuous, the accumulated $LST$ within the buffer zone ranges from the park edge to L can be integrated. Hence, the integration of ${\int }_0^{L}T\left(D\right)\mathrm{d}D$ in Equation (4) corresponds to the shaded area in Figure 2b, thus representing the spatial accumulative $LST$ within the buffer zone when influenced by PCIE. The $T\left(L\right)$ denotes the modeled $LST$ at the maximum cooling distance L. $T\left(L\right)$ represents the $LST$ of the surroundings that are unaffected by the PCIE, because the maximum influence range of PCIE is within L. Therefore, the $L\times T\left(L\right)$ in Equation (4), corresponds to the area enclosed by the black dotted lines and coordinate axes in Figure 2b, thus representing the spatial accumulative $LST$ if the buffer zone is uninfluenced by PCIE. The difference between the accumulated $LST$ when the park is absent and in place, which is denoted as $L\times T\left(L\right)-{\int }_0^{L}T\left(D\right)\mathrm{d}D$ in Equation (4), representing the accumulative cooling effect of a park on its surroundings. According to Equation (4), the $PCI$, the ratio of the accumulative cooling effect to the initial temperature, implies the intensity of PCIE. And, the $PCG$ implies the accumulated cooling effect per cooling distance of the park. Overall, $PCI$ and $PCG$ provide an evaluation of PCIE from a spatial accumulation perspective.

2.4. Selection of the Influencing Factors of PCIE

Previous studies have revealed that PCIE is influenced not only by the park’s intrinsic attributes but also by the surrounding urban characteristics. In this study, the influencing factors were selected based on specific criteria: (1) a comprehensive depiction of the internal and external environmental characteristics of the parks in this region; (2) factors that can be adjusted and managed through park planning and design; and (3) factors that are easily quantifiable and understandable [35].

Six influencing factors chosen for analysis are detailed in

Table 1. Definition of influencing factors on PCIE.

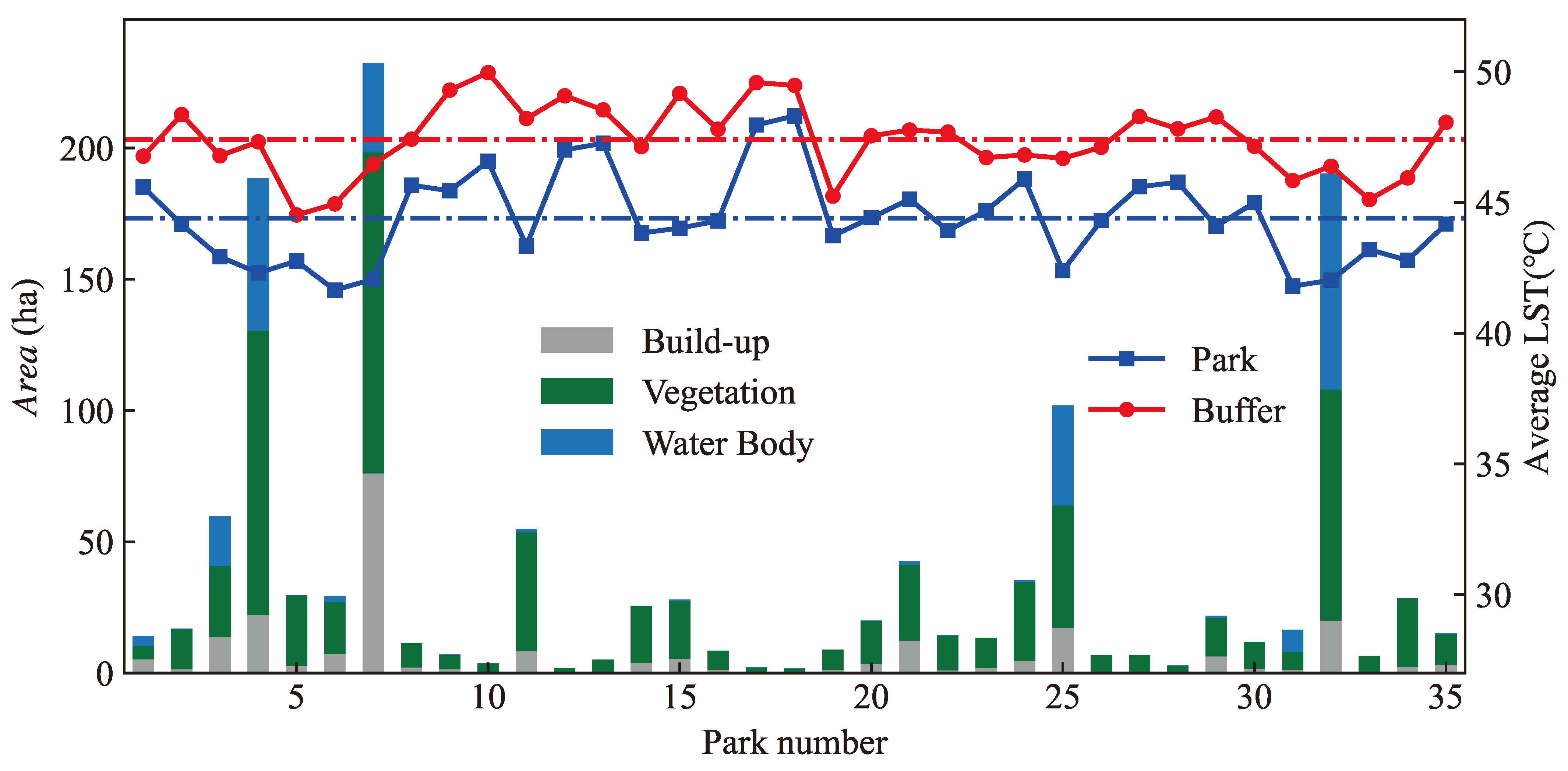
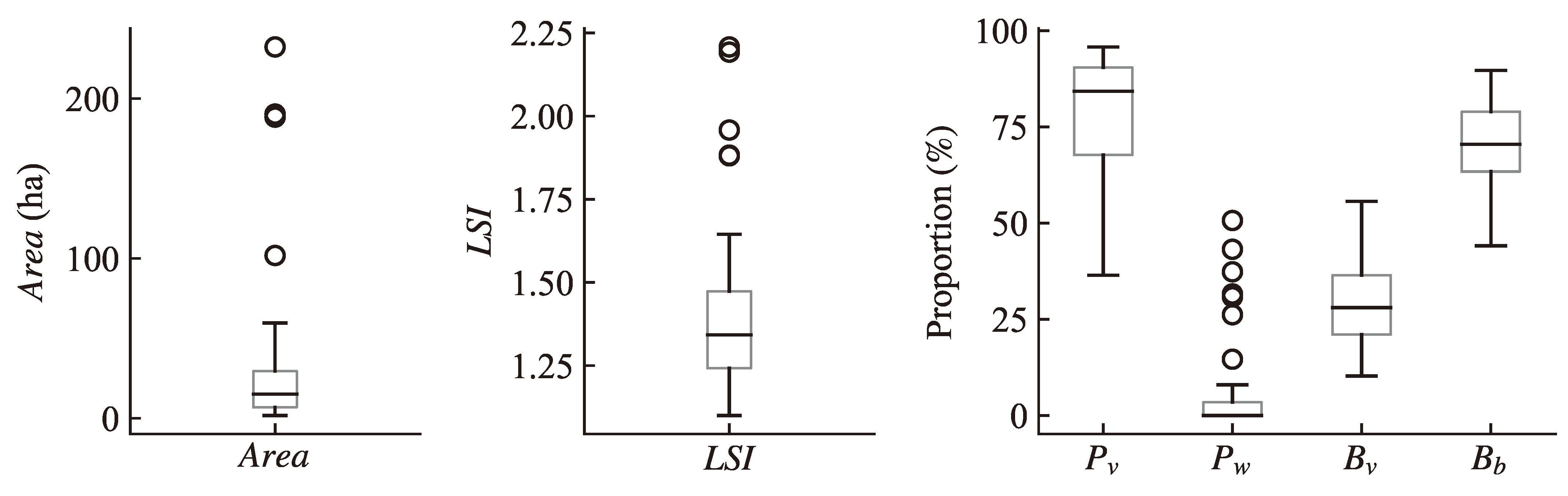
Categories	Influencing Factors	Formula and Range
A. Park patch characteristics	1. Park area ($Area$)	≥ 1 ha
	2. Landscape shape index ($LSI$)	$LSI=\frac{C}{2\sqrt{\pi \times Area}}$, where C is the perimeter of the park,  $LSI>1$
B. Park composition	3. Vegetation area proportion in park $P_v$	$P_v=\frac{A_v^P}{Area}$, where $A_v^P$ is the area of vegetation in the park.   $1\ge P_v\ge 0$
	4. Water area proportion in park $P_w$	$P_w=\frac{A_w^P}{Area}$, where $A_w^P$ is the area of water body in the park.   $1\ge P_w\ge 0$
C. Surrounding composition	5. Vegetation area proportion in buffer $B_v$	$B_v=\frac{A_v^B}{PCA}$, where $A_v^B$ is the area of vegetation in the buffer.  $1\ge B_v\ge 0$
	6. Build-up area proportion in buffer $B_b$	$B_b=\frac{A_b^B}{PCA}$, where $A_b^B$ is the area of build-up in the buffer.  $1\ge B_b\ge 0$

. The size of the parks ($Area$) and their geometry, as measured by the Landscape Shape Index ($LSI$), were employed to assess the patch characteristics. The $LSI$ was set to 1 for a circle and 1.13 for a square, with the $LSI$ value increaseing as the shape becomes more irregular. Additionally, factors related to park composition, such as the proportion of vegetation area ($P_v$) and water area ($P_w$), were considered, as they significantly influence the temperature within the park. Moreover, we examined the land cover composition of the areas surrounding the parks, specifically within a buffer zone at a distance L from the park boundary. This included the proportion of built-up area ($B_b$) and vegetation area ($B_v$), as they are predominant land covers in the surrounding environment.

2.5. Categorization of the Parks

The PCIE exhibits variations across different types of parks. This study utilized park patch and park composition factors, specifically $Area$, $LSI$, $P_v$, and $P_w$, to categorize the parks into different types, as these factors represent the general characteristics of the parks under consideration. To ensure comparability, the values corresponding to these factors were first normalized to the range of [0, 1] through the min–max normalization method. Hierarchical clustering, a clustering algorithm that builds nested clusters by successively merging or splitting them, was employed to cluster the 35 parks. The hierarchical clustering method was implemented with scikit-learn [54] using the “average” linkage criterion and “euclidean” metric. The 35 parks were ultimately categorized into three distinct types. The clustering results are shown in Figure 3, and the spatial distribution of different types of parks is shown in Figure 1.

The radar diagrams (Figure 3b) reveal the distinguishing characteristics of different park types. Type 1 includes three parks: Xushuihe Riverfront Park (No. 4), Xiliuhu Park (No. 7), and Longzihu Park (No. 32). Type 1 parks are characterized by large $Area$ and $LSI$ values, with a notable presence of water bodies. Type 2 consists of 28 parks that are small in size and are mainly covered by vegetation. The $P_v$ values of this type range from 67.13% to 95.77%. Although eight parks contain water bodies, the average $P_w$ is only 3%. Type 3 consists of four parks: Yuehu Park (No. 1), Tianjianhu Park (No. 3), Diehu Park (No. 25), and Jinshui Riverfront Park (No. 31). The main feature of Type 3 is the relatively large proportion of water area, with the $P_w$ ranging from 26.19% to 50.67%. Three parks were specifically chosen to exemplify these characteristics (Figure 3c).

2.6. Statistical Analysis between the PCIE Metrics and Influencing Factors

This study employed the correlation coefficient and regression analysis to investigate the relationship between influencing factors and evaluation metrics of the PCIE. The Kolmogorov–Smirnov test revealed that certain variables, such as $PCA$ in the evaluation metrics of the PCIE, as well as $Area$ and $P_w$ among the influencing factors, exhibited non-normal distributions. As a result, we used the Spearman correlation coefficient, which is more appropriate for analyzing non-normally distributed data [55], to assess the relationship between the evaluation metrics and the influencing factors. Subsequently, a regression analysis model was constructed based on the correlation analysis to predict the evaluation metrics from the main influencing factors. Insights drawn from the quantitative analysis were then used to develop recommendations for park planning and design.

3. Results

3.1. Evaluation of PCIE

As shown in Figure 4, the average $LST$ of the 35 urban parks in Zhengzhou City ranged from 41.65 °C to 48.31 °C, with an average of 44.40 ± 1.75 °C. Notably, Diaosu Park (No. 6) had the lowest $LST$, while Qicai Park (No. 18) recorded the highest $LST$ among all the parks. Furthermore, the $LST$ of the buffer zones within the maximum cooling distance L surpassed the parks’ average $LST$, thus showing an average difference of 3.01 ± 1.23 °C. Specifically, Renmin Park (No. 15), located in the city center, exhibited the largest difference of 5.15 °C, while Jingkaibinhe Park (No. 24) showed the smallest difference of only 0.92 °C.

The spatial distribution of the $LST$ in Zhengzhou City, as depicted in Figure 5a, clearly indicates a significant disparity in the temperatures between the city center and the suburban districts, thus suggesting the presence of a UHI effect. The central areas of the city exhibited notably higher $LST$ values compared to the outlying regions. Areas with high $LST$ were predominantly situated in the western Zhongyuan District and the eastern Guancheng Hui District, where industrial facilities are more concentrated. Regions with water bodies demonstrated lower $LST$, including the Yellow River in the north, the Beilong Lake in the east, and the Jiangang Reservoir in the southwest. Additionally, cooler temperatures can also be observed in vegetated areas in the suburban districts of Zhengzhou city.

The spatial aggregation and differentiation characteristics of $LST$ in Zhengzhou City were further analyzed by the Getis-Ord Gi* hot spot analysis tool. The result is shown in Figure 5b. The hot and cold spots in the figure represent the spatial aggregation areas of high and low $LST$ values, respectively. It is noteworthy that cold spot areas with confidence levels exceeding 90% were identified in 19 parks, thus encompassing roughly 45.17% of the total park area. In contrast, hot spot areas within parks, with confidence levels exceeding 90%, only occupied about 0.51% of the total park area, thus indicating a significant PCIE.

The model $T\left(D\right)$ is the basis for calculating the PCIE evaluation metrics $PCA$, $PCE$, $PCI$, and $PCG$. The model fitting accuracy was measured by the $R^2$ and root mean square errors ($RMSE$). The statistical results of $R^2$, $RMSE$, and the four PCIE evaluation metrics are shown in

Table 2. Statistical results of model fitting indicators and park cooling island effect indexes.

	Model ${\mathit{R}}^2$	Model $\mathit{RMSE}$ (°C)	L (m)	$\mathit{PCA}$ (hm2)	$\mathit{PCE}$	$\mathit{PCI}$	$\mathit{PCG}$ (°C)
min	0.8558	0.0373	76.95	7.51	0.4620	0.0072	0.3373
max	0.9993	0.4733	243.96	142.30	7.0427	0.0351	1.7670
avg	0.9618	0.1762	133.95	40.09	2.5820	0.0205	0.9846
std	0.0383	0.1213	41.93	32.66	2.0036	0.0080	0.3924

. The fitting accuracy was generally high, with an average $R^2$ of 0.9618 ± 0.0383 and an average RMSE of 0.1762 ± 0.1213 °C. The average maximum cooling distance of the 35 parks was 133.95 ± 41.93 m.

The distributions of the PCIE evaluation metrics $PCA$, $PCE$, $PCI$, and $PCG$ in each park are shown in Figure 6a. The fluctuations in high and low values of the $PCA$ and $PCE$ were not consistent among different parks. Parks with larger $PCA$ generally had smaller $PCE$ values, such as the Type 1 parks. The calculation formulas for the $PCI$ and $PCG$ are similar, thus leading to consistent trends in their variations across the parks. To analyze and compare the four metrics, they were normalized to a range of 0∼1. The variances of the normalized metrics were calculated as 0.24 ($PCA$), 0.30 ($PCE$), 0.29 ($PCI$), and 0.27 ($PCG$), thus suggesting that the fluctuation amplitudes from the mean values have no significant discernible difference across the four metrics.

For different types of parks, the statistical results of PCIE evaluation metrics are shown in Figure 6b. The average values of $PCA$, $PCI$, and $PCG$ were the highest in Type 1 parks, and the average values of $PCA$, $PCI$, and $PCG$ were slightly higher in Type 3 than in Type 2 parks, but the $PCE$ was the highest in Type 2 parks.

3.2. Analysis of Factors Influencing the PCIE

The distribution of the values of influencing factors across 35 parks is shown in Figure 7. The $Area$ ranged from 1.71 ha to 232.36 ha. The average value of the $LSI$ was 1.42 ± 0.28. Most of the parks had a predominantly internal land cover type of vegetation, with an average $P_v$ of 77.43 ± 17.54%. Only 14 parks had a $P_w$ greater than 1%, thus resulting in a lower average value of $P_w$. The external land cover type of the parks was dominated by built-up areas and vegetation, with a combined average area proportion exceeding 99%.

The Spearman’s correlation coefficients presented in

Table 3. The Spearman correlation analysis of impact factors and park cooling island effect indexes.

	$\mathit{PCE}$	$\mathit{PCI}$	$\mathit{PCG}$	$\mathit{Area}$	$\mathit{LSI}$	${\mathit{P}}_{\mathit{v}}$	${\mathit{P}}_{\mathit{w}}$	${\mathit{B}}_{\mathit{v}}$	${\mathit{B}}_{\mathit{b}}$
$PCA$	−0.3703 *	0.7098 ***	0.6812 ***	0.7465 ***	0.4280 *	−0.4915 **	−0.2143	0.0597	−0.0490
$PCE$		−0.2720	−0.2557	−0.8731 ***	0.0070	0.2999	0.1786	−0.2697	0.2667
$PCI$			0.9938 ***	0.516 **	0.4560 **	−0.3766 *	−0.0714	−0.1725	0.1751
$PCG$				0.4958 **	0.4440 **	−0.3716	−0.0714	−0.2193	0.2221
$Area$					0.1496	−0.5249 **	−0.2143	0.2174	−0.2118
$LSI$						0.0066	−0.0714	−0.1986	0.2126
$P_v$							−0.2500	0.1711	−0.1647
$P_w$								−0.0750	0.0666
$B_v$									−0.9969 ***

Note: *** indicates that the correlation is significant at 0.001; ** indicates that the correlation is significant at 0.01; * indicates that the correlation is significant at 0.05.

illustrate the relationships between the PCIE evaluation metrics and the influencing factors. Notably, the correlation coefficients in column $P_v$ in Table 3 were calculated using data from 28 Type 2 parks, where vegetation land cover is dominant. The correlation coefficients in column $P_w$ were derived from seven Type 1 and Type 3 parks, which are characterized by a significant presence of water bodies. The remaining columns in Table 3 were based on data from all 35 parks.

The results reveal that the PCIE evaluation metrics were all significantly correlated with $Area$. Specifically, $PCA$, $PCI$, and $PCG$ were positively correlated with $Area$, thus indicating that parks with larger areas tend to have larger cooling range and intensity. Since $PCA$ is the area of a buffer zone with a buffer distance of L from the park boundary, its value increased as the value of $Area$ or L increased. Consequently, the value of $PCE$, which is the ratio of $PCA$ to $Area$, decreased as the $Area$ increased. Therefore, there is a negative correlation between the $PCE$ and $Area$.

Furthermore, the $PCA$, $PCI$, and $PCG$ had significant positive correlations with $LSI$, thus indicating that parks with complex shapes tend to have more pronounced PCIE values. Although vegetation is the main land cover in Type 2 parks, the $P_v$ was significantly negatively correlated with the $Area$. The parks with smaller $Area$ values had relatively higher vegetation cover proportion, which led to a more significant negative correlation between the $PCA$ and $P_v$. The $PCI$ and $PCG$ were not significantly correlated with the $P_v$. Despite the prevalence of water bodies in the Type 1 and Type 3 parks, none of the PCIE evaluation metrics showed significant correlations with the $P_w$. This may be attributed to the limited count of parks with water bodies. Additionally, the analysis indicates that the distribution of vegetation and buildings outside the park does not significantly influence the PCIE evaluation metrics.

In conclusion, the correlation analysis sheds light on the relationships between the park characteristics and PCIE evaluation metrics, thus emphasizing the impact of the park area, vegetation cover, and park shape on the PCIE. Therefore, the regression models were developed for the variables $PCA$, $PCE$, $PCI$, and $Area$ with the results presented in Figure 8. The relationship between the $PCA$ and the $Area$ appeared to be approximately linear, with the $PCA$ increasing as the $Area$ increased. On the other hand, the $PCE$ exhibited a trend of rapid decrease and then stabilization as the $Area$ increased. In the case of the $PCI$, there was an initial increase as the $Area$ increased, but the increase rate became smaller after exceeding a specific threshold value. A logarithmic regression was used to approximate the correlation between the $PCI$ and the $Area$. The second derivative of the fitted logarithmic model represents the change in the increase rate. By identifying the $Area$ at which the second derivative value first fell below $-{10}^5$, i.e., the increase rate approximates stability, the optimal park size was estimated to be 19 ha.

4. Discussion

4.1. Influence of Park Patch Characteristics on PCIE

The $PCA$, $PCI$, and $PCG$ were positively correlated with the $Area$, whereas the $PCE$ was negatively correlated with the $Area$, which is consistent with the findings of Peng et al. [40] and Du et al. [41]. Notably, the $PCA$ reflects the spatial maximum cooling extent of the park, and Peng et al. [40] reported a non-linear relationship between the $PCA$ and the $Area$, where the increase in the $PCA$ was negligible beyond a certain threshold. However, our study found a more linear relationship between the $PCA$ and the $Area$. The two conclusions are inconsistent but not necessarily contradictory. It is important to consider that the parks selected in the study by Peng et al. [40] were larger compared to those in our study. The range of park areas in Peng et al.’s study was between 10.86 ha to 519.81 ha, with an average value of 96.08 ha, while in our study, the park areas ranged from 1.71 ha to 232.36 ha, with an average value of 36.10 ha. The $Area$ threshold identified by Peng et al. [40] was approximately 429 ha, which is significantly larger than the largest park area in our study. Consequently, within the range of areas below this threshold, it can be assumed that the $PCA$ increases linearly with the $Area$.

Additionally, the $PCI$ and $PCG$ exhibited a significant positive correlation with the $Area$. As the $Area$ increased, so did the $PCI$, although the increase rate decelerated once the $Area$ exceeded a threshold of 19 ha. This pattern is consistent with previous research, which determined the intensity of the PCIE by measuring the difference between the average $LST$ within a specific buffer zone outside the park and the average $LST$ inside the park. For instance, Zhao et al. [56] found a similar threshold of 20 ha in their study of the PCIE in 44 parks in Zhengzhou City.

This study found that the $PCA$, $PCI$, and $PCG$ were positively correlated with the $LSI$, whereas the $PCE$ showed no significant correlation with the $LSI$. This result is consistent with the findings of Yao et al. [42] for parks in Fuzhou City. Previous studies have suggested that parks with complex shapes tend to have enhanced heat exchange with their surroundings and demonstrate stronger PCIE values, as highlighted by studies such as [57,58]. However, the relationship between the PCIE and the $LSI$ was found to vary across different studies. By identifying the “source-sink” landscape of UHI, Wu et al. [59] found that simplifying the shape of the “sink” landscape can help mitigate the UHI in the neighboring area. Ma et al. [60] observed that when the $LSI$ was smaller than 1.2, the cooling efficiency of the “sink” landscape increased with increases in the $LSI$, while when the $LSI$ exceeded 1.2, the cooling efficiency of the “sink” landscape decreased. Moreover, in a study encompassing Xiamen, Zhangzhou, and Quanzhou, Shen et al. [61] discovered regional differences in the relationship between the surface temperature and the $LSI$ of green landscapes. Since the PCIE is also affected by park area, internal structure, and surface cover type, it is crucial to consider these factors, along with the park’s functional needs when designing parks.

4.2. Influence of Park Composition on the PCIE

Vegetation is the main land cover type in Type 2 parks. Based on these parks, the correlation coefficients between the PCIE evaluation metrics and the $P_v$ were calculated. This study found that the $PCA$ was negatively correlated with the $P_v$. The $PCA$ evaluates the PCIE from the perspective of the spatial maximum cooling extent, which was significantly and positively correlated with the $Area$. However, as the $Area$ increases, the area proportion of built-up may also increase, resulting in the decrease of $P_v$, i.e., there was a negative correlation between the $P_v$ and the $Area$ in this study. This also led to a negative correlation between the $PCA$ and the $P_v$. The study of Du et al. [41] also showed that there is a non-significant negative correlation between the $PCA$ and the NDVI. The $PCI$ and $PCG$ evaluate the PCIE from the perspective of spatial accumulation. This study found no significant correlations between the $PCI$ and $P_v$ or between the $PCG$ and the $P_v$. Similarly, Wang et al. [62] found no significant correlation between green space coverage and cold island intensity in parks. However, Peng et al. [40] reported that the $PCI$ and the $PCG$ were significantly positively correlated with the product of the NDVI and vegetation coverage. Additionally, Du et al. [41] discovered that the correlation between the $PCI$, $PCG$, and NDVI varied seasonally, with a positive correlation only occurring in summer when extremely high temperatures were present. Xie et al. [63] showed that the cooling amplitude of green space was closely related to the ambient temperature and was more pronounced when the temperature was higher.

The differences between previous studies may be attributed to inconsistent definitions of the $P_v$ and the NDVI, as well as variations in the cooling effect due to the type of vegetation and its spatial arrangement [64]. For example, woodland has been found to have a more pronounced cooling effect than grassland [34]. Therefore, when examining the influence of vegetation on the PCIE, it is crucial to analyze the mechanism from various perspectives.

The $LST$ of water bodies is usually lower, and their cooling effect is more significant [16,65,66]. This study shows that parks with a larger $P_w$ have higher $PCI$ and $PCG$ values. Zhengzhou is mainly located in the Jialu River basin, with water bodies in the main urban area consisting mainly of artificially modified river channels and artificial lakes [67]. In a situation where water resources are relatively scarce, it is necessary to further explore the scientific issues of rationally planning and designing river corridors, artificial lakes, and other water body landscapes to improve the ecological benefits of the urban thermal environment while ensuring the healthy operation of urban water bodies.

4.3. Implications for Sustainable Park Planning

The $PCA$, $PCI$, and $PCG$ increase as the park area increases. Nevertheless, indiscriminate park enlargement is not feasible because of the economic expenses associated with construction and the spatial limitations in urban centers. To attain the most cost-effective PCIE, developers and urban planners must carefully manage land resources. Drawing from our research outcomes, we suggest specific planning strategies to address varying cooling requirements.

In regions with high-temperature aggregations, such as the Guancheng Hui District, which has constructed large industrial parks with massive heat emissions, it is recommended to plan and construct a Type 1 park covering hundreds of hectares with a considerable proportion of water bodies. This park facilitates a more effective reduction in the temperature and provides a cooler island for the surroundings by generating large $PCA$, $PCI$, and $PCG$ values.

In highly developed urban areas where space for construction is limited, the park size is often restricted. To optimize the cooling effect of parks on the surroundings, it is recommended to plan and construct Type 2 parks with areas under 19 ha. Increasing the proportion of green spaces by rationally unitizing various plant types, such as trees, shrubs, and grass, while decreasing the proportion of impermeable surfaces as appropriate is significant to achieve cost-effective PCIE. Moreover, if hydrological conditions allow, incorporating water bodies into the park’s landscape is recommended. Additionally, the constructions of green corridors that link fragmented and intricately shaped green spaces can increase cooling benefits per park unit (i.e., high $PCE$ value) and extend radiative services to encompass more distant residential areas.

4.4. Limitations of the Study

However, this study has a few limitations that need to be acknowledged. Firstly, there is an inadequate representation of diverse park features due to the small sample size of urban parks, which was restricted to only 35. For instance, there were only three Type 1 parks and four Type 3 parks. This limited number of parks may also affect the reliability of identifying key factors that influence the PCIE. Secondly, this study exclusively focused on the summer season characteristics of the PCIE. Although summers typically experience high temperatures and heat waves, previous studies have reported that PCIE and its key influencing factors vary across seasons [41,68]. Therefore, investigating the seasonal variations, even diurnal variations [69], of the PCIE is essential to gain a more comprehensive understanding when designing urban parks. Thirdly, previous studies revealed that the PCIE may differ according to the LCZ [29] and 3D building morphology [28]. It is necessary to delve deeper into understanding how various different LCZ types (e.g., open high-rises and compact low-rises) and 3D landscape features (such as building height and sky view factor) contribute to the PCIE.

5. Conclusions

This study evaluated the PCIE of 35 urban parks in Zhengzhou City from both spatial maximum and spatial accumulative perspectives by using Landsat 9 and Sentinel-2 satellite images. The influencing factors of the PCIE were also analyzed. The selected parks in this study demonstrated a significant PCIE, and the main influencing factors were the park area, landscape shape index, and proportion of vegetation area within the parks. In terms of the spatial maximum PCIE, the maximum cooling distance of the parks ranged from 76.95 to 243.96 m. Parks with larger areas and more complex shapes had higher $PCA$, but the $PCE$ values of parks with larger areas were generally smaller. For the spatial accumulation PCIE, the trends of the $PCI$ and $PCG$ were consistent, with the PCI of larger parks being higher. However, there was a threshold in the relationship between the $PCI$ and the area of parks. The $PCA$, $PCE$, $PCI$, and $PCG$ of different types of parks varied significantly. Parks with a larger proportion of water body area had relatively high $PCA$, $PCI$, and $PCG$ values. Conversely, parks with smaller areas but higher vegetation coverage exhibited the highest $PCE$, which makes them highly economical in exerting the PCIE. In the central urban area with limited spaces, by considering the service groups and functional needs of parks, the planning and design of parks with smaller areas, complex shapes, and a higher proportion of vegetation coverage can obtain higher cold island efficiency.