Multi-Objective Evcuation Planning Model Considering Post-Earthquake Fire Spread: A Tokyo Case Study
Abstract
1. Introduction
2. Literature Review
2.1. Objective of Shelter Location-Allocation Model
2.2. Risk Assessment during Evacuation
3. Methodology
3.1. Estimation of Fire Risk
3.2. Multi-Objective Location-Allocation Model for Hierarchical Shelters
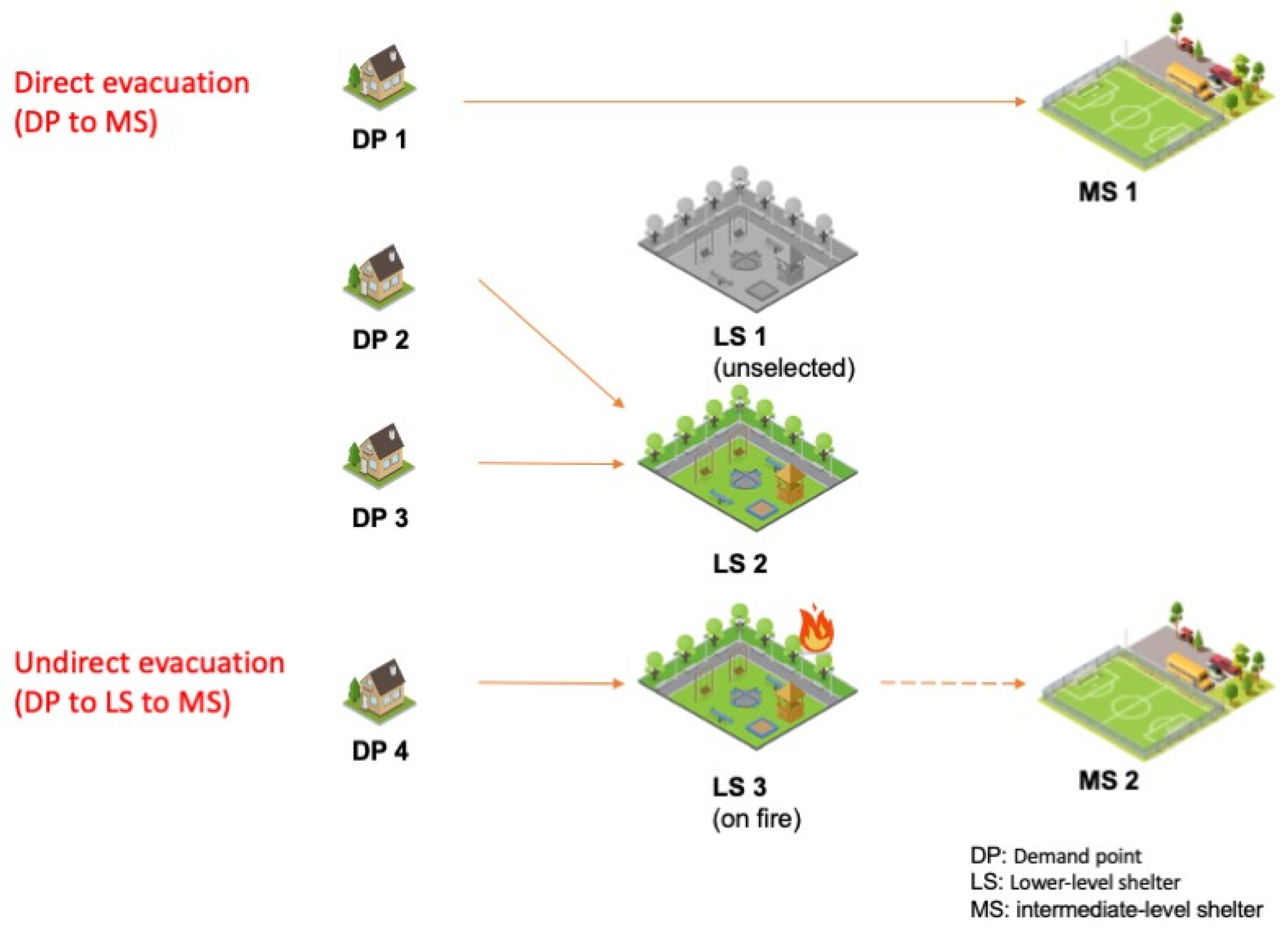
- A major earthquake is assumed, requiring all residents to initially relocate to LSs or MSs.
- For the sake of convenience in management, residents within one DP will be assigned to the same LS or MS. Additionally, evacuees in one LS can only be assigned to the same MS.
- People will choose evacuation routes that do not exceed 20% of the shortest path length with equal probability. This ratio of 20% is also referred to as the tolerance factor or level of tolerance by Jahn et al. [46] and Bayram et al. [29]. This level typically falls within the range of 0 to 100%. To avoid excessive computational workload, we assume it as 20%. In the remaining part of the paper, we refer to these paths as “tolerant paths”.
- Objective 0: minimize the total evacuation distance.
- Objective 1: minimize the risk in LSs.
- Objective 2: minimize the risk along paths.
- Objective 3: maximize the pass ratio.
- Constraints.
3.3. Solution Procedure
- Step1: construct payoff table
- Step2: solve epsilon-constraint problem to obtain Pareto solutions.
- Step3: Pareto pruning.
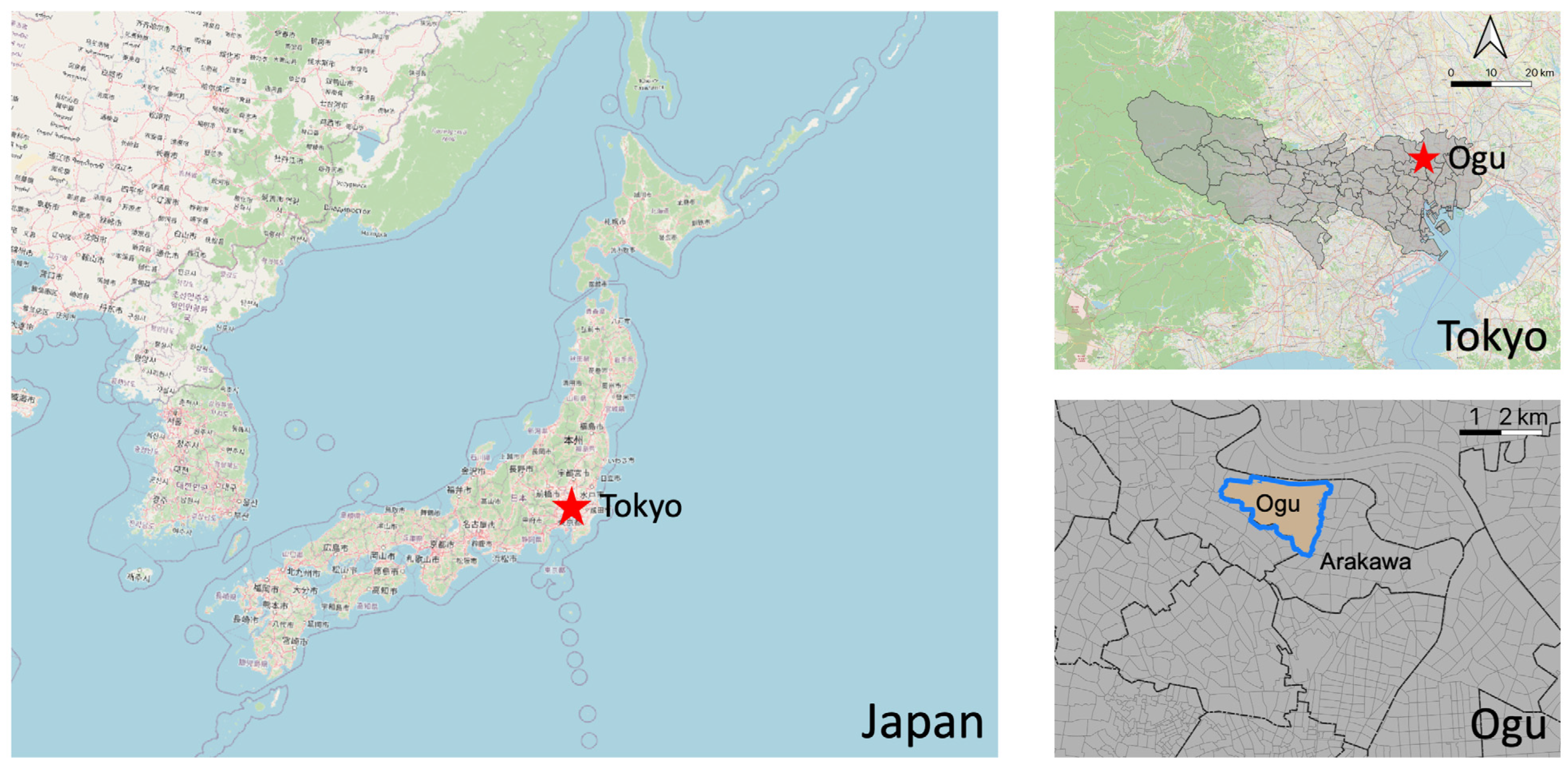
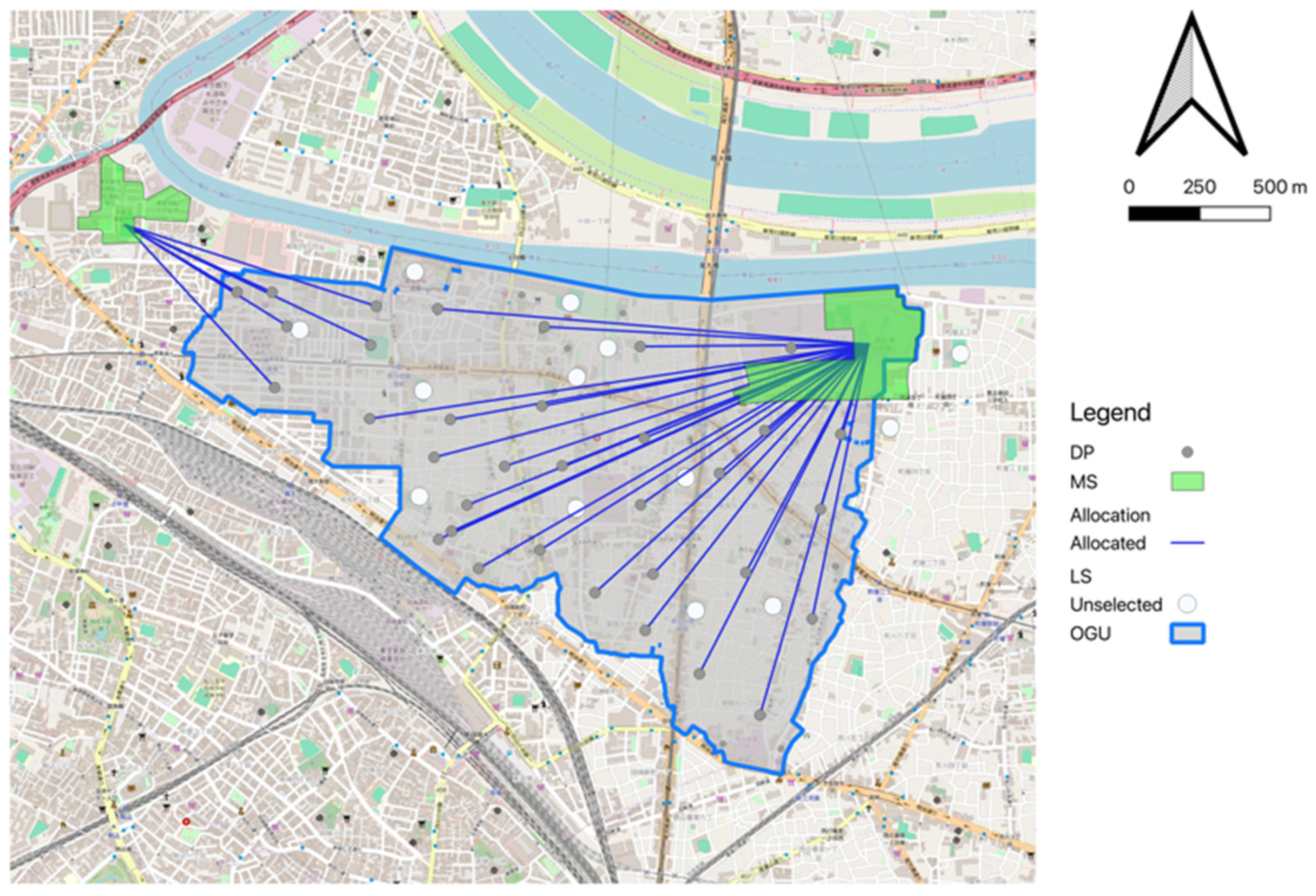
4. Case Study
4.1. Data Generation
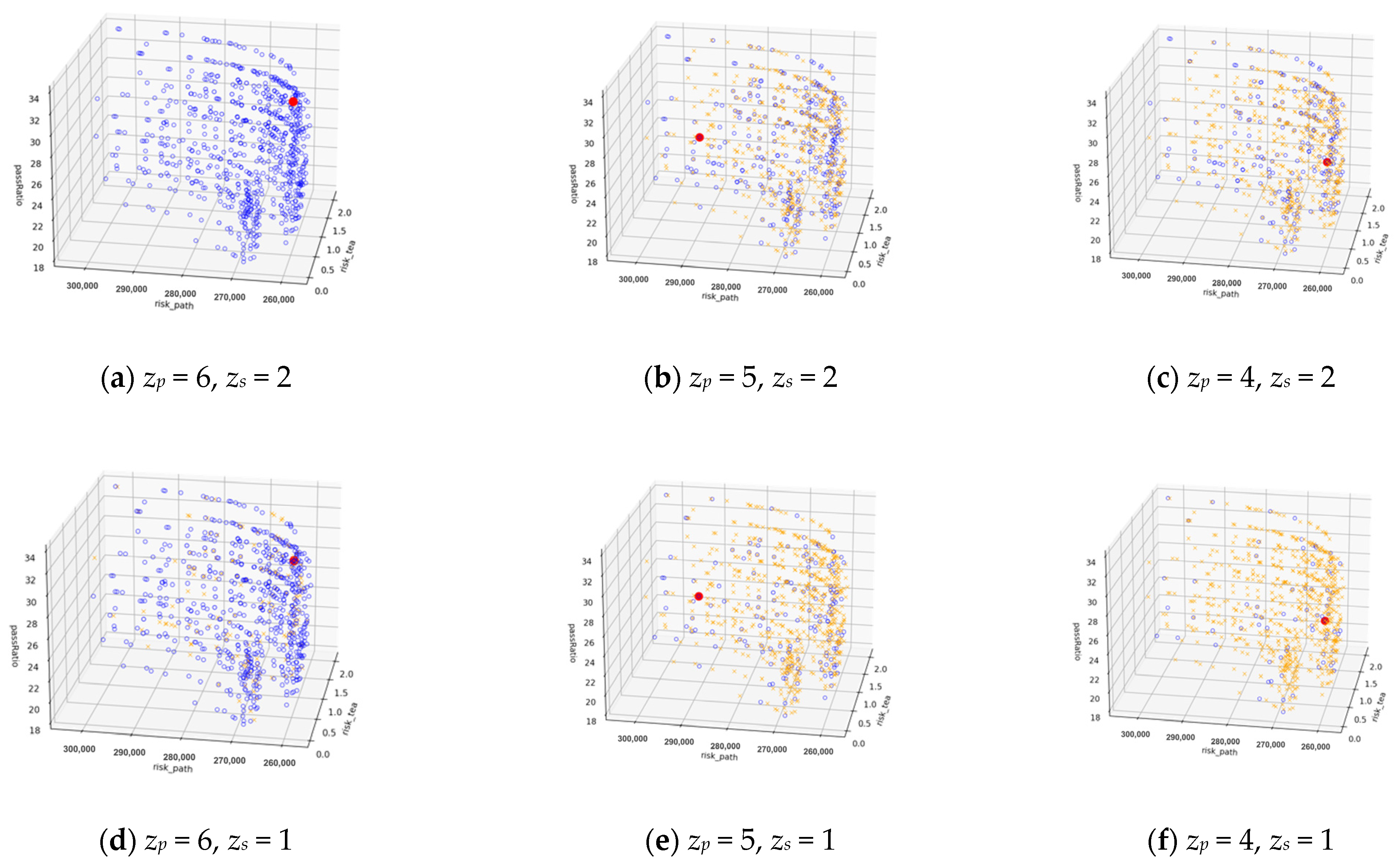
4.2. Result Discussion
4.2.1. Result of Distance Minimization Model (DMM)
4.2.2. Result of Risk Reduction Model (RRM)
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- UNDRR. Annual Report 2022; United Nations Office for Disaster Risk Reduction (UNDRR): Geneva, Switzerland, 2023. [Google Scholar]
- Yazdani, M.; Kabirifar, K.; Haghani, M. Optimising post-disaster waste collection by a deep learning-enhanced differential evolution approach. Eng. Appl. Artif. Intell. 2024, 132, 107932. [Google Scholar] [CrossRef]
- JST. The Great East Japan Earthquake Information from Official Websites; Department of International Affairs of Japan Science and Technology Agency (JST): Tokyo, Japan, 2011. [Google Scholar]
- Wang, J.; Gu, X.; Huang, T. Using Bayesian networks in analyzing powerful earthquake disaster chains. Nat. Hazards 2013, 68, 509–527. [Google Scholar] [CrossRef]
- Marano, K.D.; Wald, D.J.; Allen, T.I. Global earthquake casualties due to secondary effects: A quantitative analysis for improving rapid loss analyses. Nat. Hazards 2009, 52, 319–328. [Google Scholar] [CrossRef]
- Cabinet Office Government of Japan. The Great Hanshin-Awaji Earthquake Lesson Information Compilation [04]: Occurrence and Spread of Fires. Available online: https://www.bousai.go.jp/kyoiku/kyokun/hanshin_awaji/data/detail/1-1-4.html (accessed on 5 January 2024).
- Hyogo Prefecture Medical Association. Data: Human Casualties of the Great Hanshin-Awaji Earthquake. Available online: http://www.hyogo.med.or.jp/jmat-hyogo/day-after/siryo/ (accessed on 5 January 2024).
- Wang, L.; Zhou, Y.; Nagarajaiah, S.; Shi, W. Bi-directional semi-active tuned mass damper for torsional asymmetric structural seismic response control. Eng. Struct. 2023, 294, 116744. [Google Scholar] [CrossRef]
- Homsy, G.C.; Liao, L.; Warner, M.E. Sustainability and Disaster Planning: What Are the Connections? Rural Sociol. 2019, 84, 516–540. [Google Scholar] [CrossRef]
- Arain, F. Knowledge-based Approach for Sustainable Disaster Management: Empowering Emergency Response Management Team. Procedia Eng. 2015, 118, 232–239. [Google Scholar] [CrossRef]
- Li, H.; Zhao, L.; Huang, R.; Hu, Q. Hierarchical earthquake shelter planning in urban areas: A case for Shanghai in China. Int. J. Disaster Risk Reduct. 2017, 22, 431–446. [Google Scholar] [CrossRef]
- Yamada, T. A network flow approach to a city emergency evacuation planning. Int. J. Syst. Sci. 1996, 27, 931–936. [Google Scholar] [CrossRef]
- Tokyo Metropolitan Government. Evacuation Centers & Evacuation Areas. Available online: https://www.bousai.metro.tokyo.lg.jp/bousai/1000026/1000316.html (accessed on 5 January 2024).
- Osaragi, T.; Kishimoto, M. Construction of Simulation Model of Evacuation Behavior and Analysis of Evacuation Measures during Post-earthquake Fire Considering Diverse Information Acquisition and Evacuee Behavioral Characteristics. J. Archit. Plan. (Trans. AIJ) 2023, 88, 1313–1322. [Google Scholar] [CrossRef]
- Aghaie, S.; Karimi, B. Location-allocation-routing for emergency shelters based on geographical information system (ArcGIS) by NSGA-II (case study: Earthquake occurrence in Tehran (District-1)). Socio-Econ. Plan. Sci. 2022, 84, 101420. [Google Scholar] [CrossRef]
- Li, A.C.Y.; Nozick, L.; Xu, N.; Davidson, R. Shelter location and transportation planning under hurricane conditions. Transp. Res. Part E Logist. Transp. Rev. 2012, 48, 715–729. [Google Scholar] [CrossRef]
- Gama, M.; Santos, B.; Scaparra, M. A multi-period shelter location-allocation model with evacuation orders for flood disasters. EURO J. Comput. Optim. 2016, 4, 299–323. [Google Scholar] [CrossRef]
- Yazdani, M.; Loosemore, M.; Mojtahedi, M.; Sanderson, D.; Haghani, M. An integration of operations research and design science research methodology: With an application in hospital disaster management. Prog. Disaster Sci. 2023, 20, 100300. [Google Scholar] [CrossRef]
- Hu, F.; Yang, S.; Xu, W. A non-dominated sorting genetic algorithm for the location and districting planning of earthquake shelters. Int. J. Geogr. Inf. Sci. 2014, 28, 1482–1501. [Google Scholar] [CrossRef]
- Kılcı, F.; Kara, B.Y.; Bozkaya, B. Locating temporary shelter areas after an earthquake: A case for Turkey. Eur. J. Oper. Res. 2015, 243, 323–332. [Google Scholar] [CrossRef]
- Ozbay, E.; Çavuş, Ö.; Kara, B.Y. Shelter site location under multi-hazard scenarios. Comput. Oper. Res. 2019, 106, 102–118. [Google Scholar] [CrossRef]
- Zhong, G.; Zhai, G.; Shang, K.; Chen, W. A two-stage hierarchical model for spatial location and evacuation allocation problem of urban earthquake shelters: A case study in Central urban area of Yangbi county, Yunnan province, China. Geomat. Nat. Hazards Risk 2022, 13, 1721–1761. [Google Scholar] [CrossRef]
- Hammad, A.W.A. A Bilevel Multiobjective Optimisation Approach for Solving the Evacuation Location Assignment Problem. Adv. Civ. Eng. 2019, 2019, 1–11. [Google Scholar] [CrossRef]
- Hallak, J.; Koyuncu, M.; Miç, P. Determining shelter locations in conflict areas by multiobjective modeling: A case study in northern Syria. Int. J. Disaster Risk Reduct. 2019, 38, 101202. [Google Scholar] [CrossRef]
- Mollah, A.K.; Sadhukhan, S.; Das, P.; Anis, M.Z. A cost optimization model and solutions for shelter allocation and relief distribution in flood scenario. Int. J. Disaster Risk Reduct. 2018, 31, 1187–1198. [Google Scholar] [CrossRef]
- Li, L.; Jin, M.; Zhang, L. Sheltering network planning and management with a case in the Gulf Coast region. Int. J. Prod. Econ. 2011, 131, 431–440. [Google Scholar] [CrossRef]
- Kulshrestha, A.; Wu, D.; Lou, Y.; Yin, Y. Robust Shelter Locations for Evacuation Planning with Demand Uncertainty. J. Transp. Saf. Secur. 2011, 3, 272–288. [Google Scholar] [CrossRef]
- Bayram, V.; Yaman, H. Shelter Location and Evacuation Route Assignment Under Uncertainty: A Benders Decomposition Approach. Transp. Sci. 2018, 52, 416–436. [Google Scholar] [CrossRef]
- Bayram, V.; Tansel, B.Ç.; Yaman, H. Compromising system and user interests in shelter location and evacuation planning. Transp. Res. Part B: Methodol. 2015, 72, 146–163. [Google Scholar] [CrossRef]
- Li, W.J.; Zhai, G.F.; Chen, W. Location-allocation of fixed shelters for the elderly from the perspective of needs for refuge: A case of Hefei, China. Int. J. Disaster Risk Reduct. 2023, 92, 103717. [Google Scholar] [CrossRef]
- Xu, W.; Ma, Y.; Zhao, X.; Li, Y.; Qin, L.; Du, J. A comparison of scenario-based hybrid bilevel and multi-objective location-allocation models for earthquake emergency shelters: A case study in the central area of Beijing, China. Int. J. Geogr. Inf. Sci. 2017, 32, 236–256. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, X.; Li, Q.; Chen, J. The temporal hierarchy of shelters: A hierarchical location model for earthquake-shelter planning. Int. J. Geogr. Inf. Sci. 2013, 27, 1612–1630. [Google Scholar] [CrossRef]
- Coutinho-Rodrigues, J.; Tralhão, L.; Alçada-Almeida, L. Solving a location-routing problem with a multiobjective approach: The design of urban evacuation plans. J. Transp. Geogr. 2012, 22, 206–218. [Google Scholar] [CrossRef]
- Alçada-Almeida, L.; Tralhão, L.; Santos, L.; Coutinho-Rodrigues, J. A Multiobjective Approach to Locate Emergency Shelters and Identify Evacuation Routes in Urban Areas. Geogr. Anal. 2009, 41, 9–29. [Google Scholar] [CrossRef]
- Moshashaei, P.; Alizadeh, S.S. Fire Risk Assessment: A Systematic Review of the Methodology and Functional Areas. Iran. J. Health Saf. Environ. 2016, 4, 654–669. [Google Scholar]
- Nishino, T.; Tanaka, T.; Hokugo, A. An evaluation method for the urban post-earthquake fire risk considering multiple scenarios of fire spread and evacuation. Fire Saf. J. 2012, 54, 167–180. [Google Scholar] [CrossRef]
- Zhang, Y. Analysis on Comprehensive Risk Assessment for Urban Fire: The Case of Haikou City. Procedia Eng. 2013, 52, 618–623. [Google Scholar] [CrossRef][Green Version]
- Esposito Amideo, A.; Scaparra, M.P.; Kotiadis, K. Optimising shelter location and evacuation routing operations: The critical issues. Eur. J. Oper. Res. 2019, 279, 279–295. [Google Scholar] [CrossRef]
- Chowdhury, J.U.; Watkins, D.W.; Rahman, M.R.; Karim, M.F. Models for Cyclone Shelter Planning in Bangladesh. Water Int. 1998, 23, 155–163. [Google Scholar] [CrossRef]
- Erik, M.S.; Tomas, R. Risk Assessment of Timberframe Multistorey Apartment Buildings; Department of Fire Safety Engineering, Lund University: Lund, Sweden, 1998. [Google Scholar]
- Lämmel, G.; Klüpfel, H.; Nagel, K. Risk Minimizing Evacuation Strategies under Uncertainty. In Pedestrian and Evacuation Dynamics; Springer: Berlin/Heidelberg, Germany, 2011; pp. 287–296. [Google Scholar] [CrossRef]
- Opasanon, S.; Miller-Hooks, E. The Safest Escape problem. J. Oper. Res. Soc. 2017, 60, 1749–1758. [Google Scholar] [CrossRef]
- Xiongfei, Z.; Qixin, S.; Rachel, H.; Bin, R. Network Emergency Evacuation Modeling: A Literature Review. In Proceedings of the 2010 International Conference on Optoelectronics and Image Processing, Haikou, China, 11–12 November 2010; pp. 30–34. [Google Scholar]
- Göttlich, S.; Kühn, S.; Peter Ohst, J.; Ruzika, S.; Thiemann, M. Evacuation dynamics influenced by spreading hazardous material. Netw. Heterog. Media 2011, 6, 443–464. [Google Scholar] [CrossRef]
- Farahani, R.Z.; Hekmatfar, M.; Fahimnia, B.; Kazemzadeh, N. Hierarchical facility location problem: Models, classifications, techniques, and applications. Comput. Ind. Eng. 2014, 68, 104–117. [Google Scholar] [CrossRef]
- Jahn, O.; Möhring, R.H.; Schulz, A.S.; Stier-Moses, N.E. System-Optimal Routing of Traffic Flows with User Constraints in Networks with Congestion. Oper. Res. 2005, 53, 600–616. [Google Scholar] [CrossRef]
- Mavrotas, G. Effective implementation of the ε-constraint method in Multi-Objective Mathematical Programming problems. Appl. Math. Comput. 2009, 213, 455–465. [Google Scholar] [CrossRef]
- Khalili-Fard, A.; Parsaee, S.; Bakhshi, A.; Yazdani, M.; Aghsami, A.; Rabbani, M. Multi-objective optimization of closed-loop supply chains to achieve sustainable development goals in uncertain environments. Eng. Appl. Artif. Intell. 2024, 133, 108052. [Google Scholar] [CrossRef]
- Gharib, Z.; Yazdani, M.; Bozorgi-Amiri, A.; Tavakkoli-Moghaddam, R.; Taghipourian, M.J. Developing an integrated model for planning the delivery of construction materials to post-disaster reconstruction projects. J. Comput. Des. Eng. 2022, 9, 1135–1156. [Google Scholar] [CrossRef]
- Petchrompo, S.; Coit, D.W.; Brintrup, A.; Wannakrairot, A.; Parlikad, A.K. A review of Pareto pruning methods for multi-objective optimization. Comput. Ind. Eng. 2022, 167, 108022. [Google Scholar] [CrossRef]
- Government, T.M. The Ninth Community Earthquake Risk Assessment Study; Bureau of Urban Development, Tokyo Metropolitan Government: Tokyo, Japan, 2022. [Google Scholar]
- Hirokawa, N.; Osaragi, T. Earthquake Disaster Simulation System: Integration of Models for Building Collapse, Road Blockage, and Fire Spread. J. Disaster Res. 2016, 11, 175–187. [Google Scholar] [CrossRef]
- Torisawa, K.; Matsuoka, M.; Horie, K.; Inoguchi, M.; Yamazaki, F. Building Fragility Curves Based on Disaster-Victim Certificate Data of Multiple Local Governments Covering a Wide Range of Seismic Motion in the 2016 Kumamoto Earthquake. J. Jpn. Assoc. Earthq. Eng. 2021, 21, 5_98–95_118. [Google Scholar] [CrossRef]
- Yen, J.Y. An algorithm for finding shortest routes from all source nodes to a given destination in general networks. Q. Appl. Math. 1970, 27, 526–530. [Google Scholar] [CrossRef]
- Yazdani, M.; Haghani, M. Hospital evacuation in large-scale disasters using limited aerial transport resources. Saf. Sci. 2023, 164, 106171. [Google Scholar] [CrossRef]
- Yazdani, M.; Haghani, M. Logistics of patient evacuation in response to disease Outbreaks: Critical considerations for transportation planning. Transp. Res. Interdiscip. Perspect. 2023, 22, 100975. [Google Scholar] [CrossRef]

| Author | Preparedness Stage Objective | Response Stage Objective | Method |
|---|---|---|---|
| Li et al. [30] | - | Total evacuation distance, Covered demand | Genetic algorithm, Simulated annealing algorithm |
| Aghaie and Karimi [15] | Shelter cost construction | Relief transportation time | NSGA-II |
| Hammad [23] | Shelter cost construction | Total evacuation time, Individual evacuation time | Lexicographic optimization |
| Hallak et al. [24] | Shelter construction cost, Cash-for-work amount, Number of facilities that have portable WASH facilities, Number of facilities with future scale-up flexibility | Covered demand, Covered demand with vulnerability | Weighted-goal programming (WGP) |
| Xu et al. [31] | Total shelter area | Total evacuation distance | Particle swarm optimization (PSO) |
| Hu et al. [19] | Shelter construction cost | Total evacuation distance | NSGA-II |
| Li et al. [16] | - | Unmet demand, Total evacuation time | Weighted-goal programming (WGP) |
| Coutinho-Rodrigues et al. [33] | Risk of shelters, Num of shelters | Total evacuation distance, Total evacuation time, Risk of paths | Hierarchical method |
| Type | Symbol | Description |
|---|---|---|
| Suffix | d | DP (demand point) |
| t | LS (lower-level shelter) | |
| e | MS (intermediate-level shelter) | |
| b | Building | |
| l | Link | |
| p | Path | |
| dt | From DP to LS | |
| de | From DP to MS | |
| te | From LS to MS |
| Type | Symbol | Description |
|---|---|---|
| Decision variable | 1 if LS t is available, 0 otherwise | |
| 1 if people in DP d is allocated to LS t, 0 otherwise | ||
| 1 if people in DP d is allocated to MS e, 0 otherwise | ||
| 1 if people in LS t is allocated to MS e, 0 otherwise. People will evacuee to MS e if LS t is on fire | ||
| Parameter | Pass ratio for link l | |
| Demand in DP d | ||
| Risk of link l | ||
| Risk of path p | ||
| Average risk of tolerant paths from DP d to LS t | ||
| Average risk of tolerant paths from LS t to MS e | ||
| Average risk of tolerant paths from DP d to MS e | ||
| Average length of tolerant paths from DP d to LS t | ||
| Average length of tolerant paths from LS t to MS e | ||
| Average length of tolerant paths from DP d to MS e | ||
| Risk of LS t | ||
| Fire probability of building b | ||
| Collapse probability of building b | ||
| Blockage probability of link l | ||
| Capacity of LS t | ||
| u | The maximum distance between a node and the node to which it is allocated | |
| A big number | ||
| Number of tolerant paths between DP d and LS t | ||
| Set of all tolerant paths between DP d and LS t | ||
| Set | D | Set of DPs |
| T | Set of LSs | |
| E | Set of MSs | |
| Set of links in path p | ||
| Set of links in shortest path from DP d to LS t | ||
| Set of links in shortest path from DP d to MS e | ||
| Set of links in shortest path from LS t to MS e | ||
| Set of street-facing buildings along link l | ||
| Set of buildings within 50 m range of LS t |
| R11: Independently optimization result for f1 | R21: Optimization result for f2 by setting f1 = R11 | R31: Optimization result for f3 by setting f1 = R11 and f2 = R21 |
| R12: Optimization result for f1 by setting f2 = R22 | R22: Independently optimization result for f2 | R32: Optimization result for f3 by setting f2 = R22 and f1 = R12 |
| R13: Optimization result for f1 by setting f3 = R33 | R23: Optimization result for f2 by setting f3 = R33 and f1 = R13 | R33: Independently optimization result for f3 |
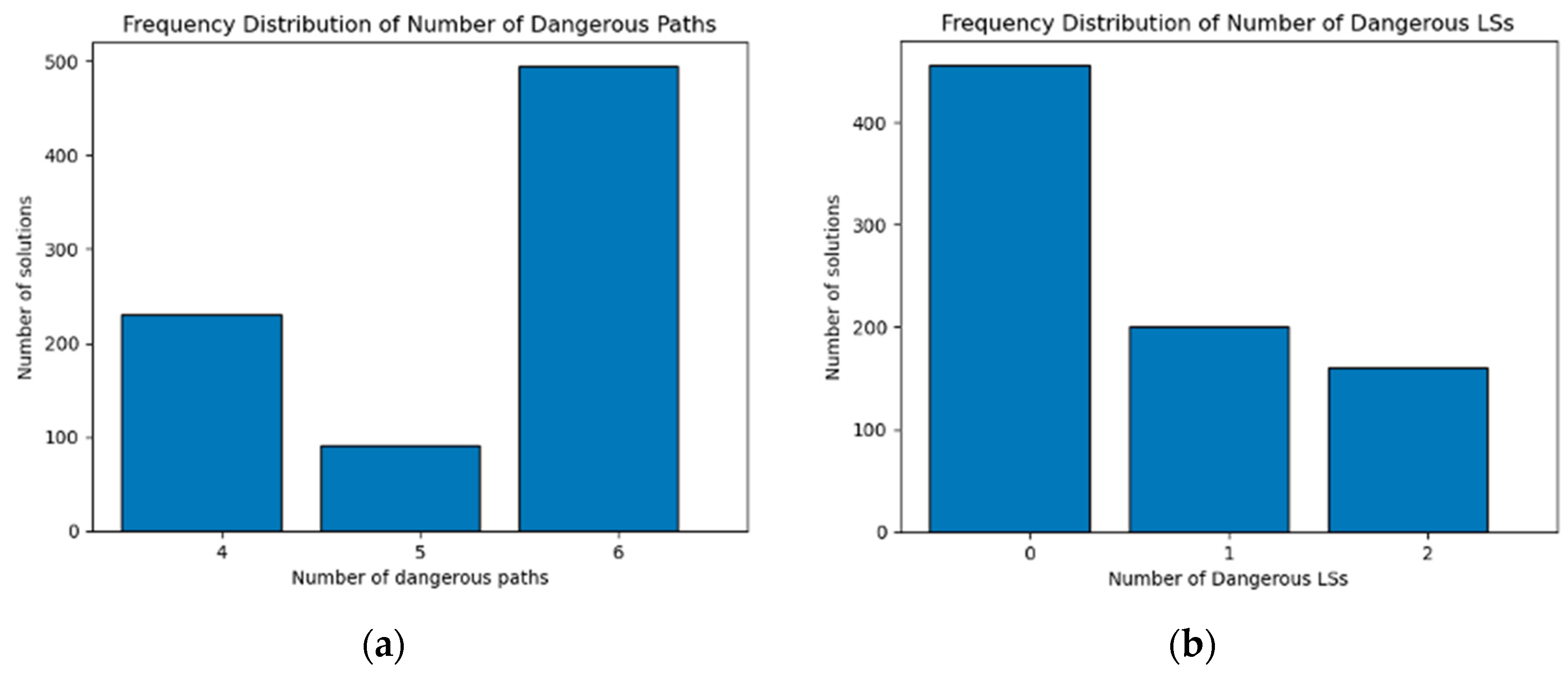
| Pruning Step | Indicator | Description |
|---|---|---|
| 1 | Number of generated dangerous paths for solution k | |
| 1 | Number of selected dangerous LSs for solution k | |
| 2 | Ratio of total travel distance obtained by RRM to the one obtained by DMM |
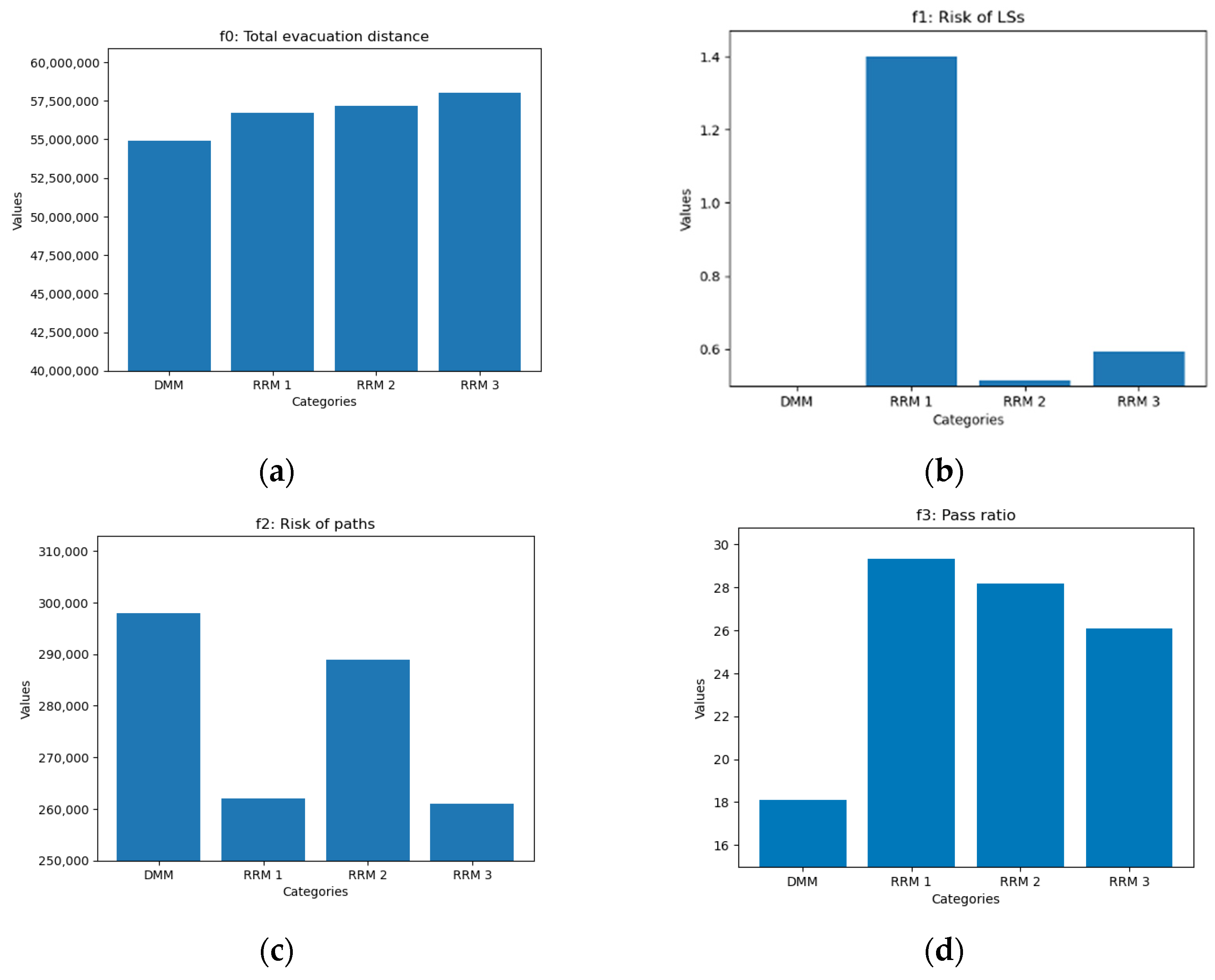
| DMM Solution Value | ||
|---|---|---|
| Objective values | f0 value | 5.49 × 107 |
| f1 value | 0 | |
| f2 value | 2.98 × 105 | |
| f3 value | 18.107 | |
| Location results | Available LS | 0/13 |
| Direct allocation (from DP to MS) | 34 | |
| Allocation results | Indirect allocation (from DP to LS) | 0 |
| RRM Solution 1 Value zp = 6, zs = 1 or 2 | RRM Solution 2 Value zp = 5, zs = 1 or 2 | RRM Solution 3 Value zp = 4, zs = 1 or 2 | ||
|---|---|---|---|---|
| Objective values | f0 value | 5.67 × 107 | 5.72 × 107 | 5.80 × 107 |
| f1 value | 1.401 | 0.516 | 0.594 | |
| f2 value | 2.62 × 105 | 2.89 × 105 | 2.61 × 105 | |
| f3 value | 29.309 | 28.165 | 26.099 | |
| Location results | Available LS | 5/13 | 6/13 | 9/13 |
| Direct allocation (from DP to MS) | 29 | 27 | 22 | |
| Allocation results | Indirect allocation (from DP to LS) | 5 | 7 | 12 |
| Indicator | rtDis | 1.032 | 1.042 | 1.056 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, K.; Osaragi, T. Multi-Objective Evcuation Planning Model Considering Post-Earthquake Fire Spread: A Tokyo Case Study. Sustainability 2024, 16, 3989. https://doi.org/10.3390/su16103989
Tang K, Osaragi T. Multi-Objective Evcuation Planning Model Considering Post-Earthquake Fire Spread: A Tokyo Case Study. Sustainability. 2024; 16(10):3989. https://doi.org/10.3390/su16103989
Chicago/Turabian StyleTang, Kai, and Toshihiro Osaragi. 2024. "Multi-Objective Evcuation Planning Model Considering Post-Earthquake Fire Spread: A Tokyo Case Study" Sustainability 16, no. 10: 3989. https://doi.org/10.3390/su16103989
APA StyleTang, K., & Osaragi, T. (2024). Multi-Objective Evcuation Planning Model Considering Post-Earthquake Fire Spread: A Tokyo Case Study. Sustainability, 16(10), 3989. https://doi.org/10.3390/su16103989






