The Water–Energy–Carbon Coupling Coordination Level in China
Abstract
:1. Introduction
- (I)
- Water system:
- (II)
- Energy system:
- (III)
- Carbon system:
2. Materials and Methods
2.1. Index System Construction
2.2. Entropy Weight Method
2.3. WEC Coupling Coordination Model
2.4. Classification of the Coupling Coordination Evaluation Levels
2.5. Multiple Linear Regression
2.6. Spatial Durbin Model
3. Results
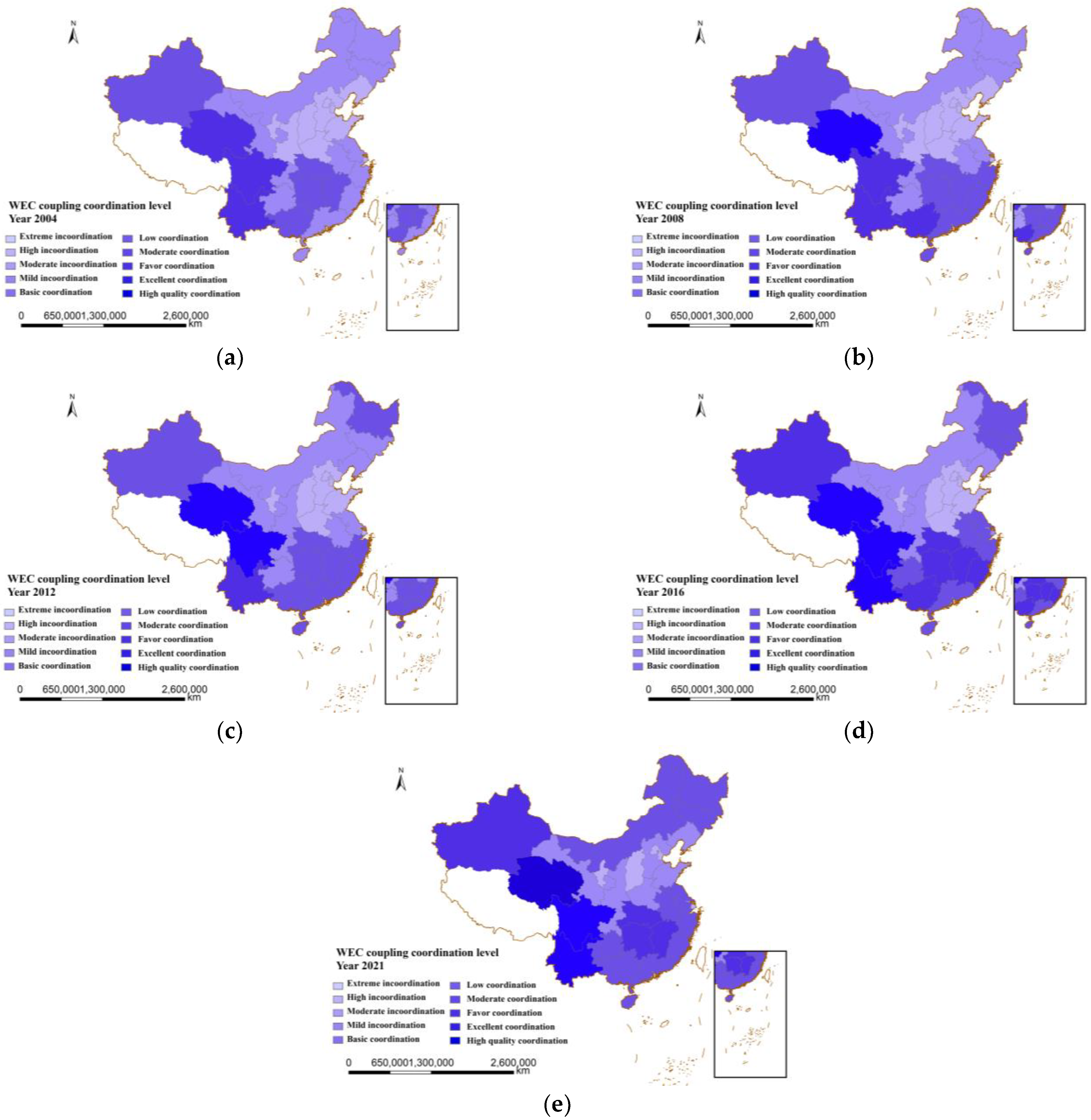
3.1. Temporal Variation in the WEC Coupling Coordination Level
3.2. Spatial Distribution Characteristics of the WEC Coupling Coordination Level
3.3. Spatial Correlation Analysis
3.4. Analysis of Influential Factors
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Duan, C.C.; Chen, B. Energy-water nexus of international energy trade of China. Appl. Energy 2017, 194, 725–734. [Google Scholar] [CrossRef]
- Meng, F.X.; Liu, G.Y.; Liang, S.; Su, M.R.; Yang, Z.F. Critical review of the energy-water-carbon nexus in cities. Energy 2019, 171, 1017–1032. [Google Scholar] [CrossRef]
- Cao, Y.Q.; Li, J.; Xie, L.F.; Yao, J.Q.; Li, K.X.; Zhang, N.Y.; Ji, X.H.; Wang, M.R.; Mo, F.; Zhai, H.R. Coupling coordination of the water-energy-carbon system in three provinces of Northeastern China. Front. Environ. Sci. 2023, 11, 1261339. [Google Scholar] [CrossRef]
- Ding, X.; Wang, S.G.; Chen, B. Impacts of different low-carbon development pathways on water consumption in China based on input-output analysis. In Proceedings of the 9th International Conference on Applied Energy (ICAE), Cardiff, UK, 21–24 August 2017; pp. 3122–3128. [Google Scholar]
- Zheng, H.R.; Zhang, Z.Y.; Zhang, Z.K.; Li, X.; Shan, Y.L.; Song, M.L.; Mi, Z.F.; Meng, J.; Ou, J.M.; Guan, D.B. Mapping Carbon and Water Networks in the North China Urban Agglomeration. One Earth 2019, 1, 126–137. [Google Scholar] [CrossRef]
- Zhou, Y.; Zou, S.; Duan, W.; Chen, Y.; Takara, K.; Di, Y. Analysis of energy carbon emissions from agroecosystems in Tarim River Basin, China: A pathway to achieve carbon neutrality. Appl. Energy 2022, 325, 119842. [Google Scholar] [CrossRef]
- Chhipi-Shrestha, G.; Hewage, K.; Sadiq, R. Water-Energy-Carbon Nexus Modeling for Urban Water Systems: System Dynamics Approach. J. Water Resour. Plan. Manag. 2017, 143, 04017016. [Google Scholar] [CrossRef]
- Wang, X.C.; Jiang, P.; Yang, L.; Fan, Y.V.; Klemes, J.J.; Wang, Y.T. Extended water-energy nexus contribution to environmentally-related sustainable development goals. Renew. Sustain. Energy Rev. 2021, 150, 111485. [Google Scholar] [CrossRef]
- Du, Z.; Su, T.; Ge, J.; Wang, X. Towards the carbon neutrality: The role of carbon sink and its spatial spillover effects. Econ. Res. J. 2021, 56, 187–202. [Google Scholar]
- Gao, J.J.; Li, C.L.; Zhao, P.; Zhang, H.W.; Mao, G.Z.; Wang, Y. Insights into water-energy cobenefits and trade-offs in water resource management. J. Clean. Prod. 2019, 213, 1188–1203. [Google Scholar] [CrossRef]
- Rothausen, S.G.S.A.; Conway, D. Greenhouse-gas emissions from energy use in the water sector. Nat. Clim. Change 2011, 1, 210–219. [Google Scholar] [CrossRef]
- Alresheedi, M.T.; Haider, H.; Shafiquzzaman, M.; AlSaleem, S.S.; Alinizzi, M. Water-Energy-Carbon Nexus Analysis for Water Supply Systems with Brackish Groundwater Sources in Arid Regions. Sustainability 2022, 14, 5106. [Google Scholar] [CrossRef]
- Stokes, J.R.; Horvath, A. Energy and Air Emission Effects of Water Supply. Environ. Sci. Technol. 2009, 43, 2680–2687. [Google Scholar] [CrossRef]
- Griffiths-Sattenspiel, B.; Wilson, W. The Carbon Footprint of Water; River Network: Portland, OR, USA, 2009. [Google Scholar]
- Shrestha, S.; Parajuli, K.; Babel, M.S.; Dhakal, S.; Shinde, V. Water-energy-carbon nexus: A case study of Bangkok. Water Sci. Technol. Water Supply 2015, 15, 889–897. [Google Scholar] [CrossRef]
- Sowby, R.B.; Capener, A. Reducing carbon emissions through water conservation: An analysis of 10 major U.S. cities. Energy Nexus 2022, 7, 100094. [Google Scholar] [CrossRef]
- Achakulwisut, P.; Erickson, P.; Guivarch, C.; Schaeffer, R.; Brutschin, E.; Pye, S. Global fossil fuel reduction pathways under different climate mitigation strategies and ambitions. Nat. Commun. 2023, 14, 5425. [Google Scholar] [CrossRef]
- Liu, Z.; He, X. Balancing-oriented hydropower operation makes the clean energy transition more affordable and simultaneously boosts water security. Nat. Water 2023, 1, 778–789. [Google Scholar] [CrossRef]
- Naveed, U.; Rozali NE, M.; Mahadzir, S. Energy-Water-Carbon Nexus Study for the Optimal Design of Integrated Energy-Water Systems Considering Process Losses. Energies 2022, 15, 8605. [Google Scholar] [CrossRef]
- Ma, J.; Yin, Z.; Cai, J. Efficiency of urban water supply under carbon emission constraints in China. Sustain. Cities Soc. 2022, 85, 104040. [Google Scholar] [CrossRef]
- Regnier, P.; Resplandy, L.; Najjar, R.G.; Ciais, P. The land-to-ocean loops of the global carbon cycle. Nature 2022, 603, 401–410. [Google Scholar] [CrossRef]
- Lin, B.; Ge, J. Valued forest carbon sinks: How much emissions abatement costs could be reduced in China. J. Clean. Prod. 2019, 224, 455–464. [Google Scholar] [CrossRef]
- Sun, Y.; Zhi, Y.; Zhao, Y. Indirect effects of carbon taxes on water conservation: A water footprint analysis for China. J. Environ. Manag. 2021, 279, 111747. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wang, J.; Zhang, L.; Liu, J.; Zheng, H.; Fang, J.; Hou, S.; Chen, S. Optimization of China’s electric power sector targeting water stress and carbon emissions. Appl. Energy 2020, 271, 115221. [Google Scholar] [CrossRef]
- Miller, L.; Carriveau, R. Balancing the carbon and water footprints of the Ontario energy mix. Energy 2017, 125, 562–568. [Google Scholar] [CrossRef]
- Karimov, A.K.; Amirova, I.; Karimov, A.A.; Tohirov, A.; Abdurakhmanov, B. Water, Energy and Carbon Tradeoffs of Groundwater Irrigation-Based Food Production: Case Studies from Fergana Valley, Central Asia. Sustainability 2022, 14, 1451. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Q.; Xu, L.; Tong, Y.; Jia, X.; Tian, H. Water-energy-carbon nexus assessment of China’s iron and steel industry: Case study from plant level. J. Clean. Prod. 2020, 253, 119910. [Google Scholar] [CrossRef]
- Hou, J.J.; Wang, Z.; Zhang, J.T.; Yu, S.W.; Liu, L.C. Revealing energy and water hidden in Chinese regional critical carbon supply chains. Energy Policy 2022, 165, 112979. [Google Scholar] [CrossRef]
- Yu, L.; Liu, S.L.; Wang, F.F.; Liu, Y.X.; Liu, H.; Wang, Q.B.; Tran, L.S.P.; Dong, Y.H.; Li, W.Q. Strategies for agricultural production management based on land, water and carbon footprints on the Qinghai-Tibet Plateau. J. Clean. Prod. 2022, 362, 132563. [Google Scholar] [CrossRef]
- McCarthy, B.; Anex, R.; Wang, Y.; Kendall, A.D.; Anctil, A.; Haacker EM, K.; Hyndman, D.W. Trends in Water Use, Energy Consumption, and Carbon Emissions from Irrigation: Role of Shifting Technologies and Energy Sources. Environ. Sci. Technol. 2020, 54, 15329–15337. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, X.; Liu, J.; Zhang, Y.; Chau, S.; Bhattarai, N.; Wang, Y.; Li, Y.; Connor, T.; Li, Y. Impacts of irrigated agriculture on food–energy–water–CO2 nexus across metacoupled systems. Nat. Commun. 2020, 11, 5837. [Google Scholar] [CrossRef]
- Chen, S.Q.; Tan, Y.Q.; Liu, Z. Direct and embodied energy-water-carbon nexus at an inter-regional scale. Appl. Energy 2019, 251, 113401. [Google Scholar] [CrossRef]
- Shaikh, M.A.; Kucukvar, M.; Onat, N.C.; Kirkil, G. A framework for water and carbon footprint analysis of national electricity production scenarios. Energy 2017, 139, 406–421. [Google Scholar] [CrossRef]
- Liang, M.; Huang, G.; Chen, J.; Li, Y. Energy-water-carbon nexus system planning: A case study of Yangtze River Delta urban agglomeration, China. Appl. Energy 2022, 308, 118144. [Google Scholar] [CrossRef]
- Tian, P.P.; Lu, H.W.; Reinout, H.; Li, D.; Zhang, K.L.; Yang, Y.Y. Water-energy-carbon nexus in China’s intra and inter-regional trade. Sci. Total Environ. 2022, 806, 150666. [Google Scholar] [CrossRef] [PubMed]
- Zhao, R.; Li, Z.; Han, Y.; Milind, K.; Zhang, Z.; Ding, M. The coupling interaction mechanism of regional water-land-energy-carbon system. Acta Geogr. Sin. 2016, 71, 1613–1628. [Google Scholar]
- Xiang, W.Q.; Yang, X.H.; Bian, D.H.; Pan, Z.S.; Chen, H.; Chen, Y.J.; Li, M.S. Evaluation and prediction of water-energy-carbon nexus efficiency in China based on a new multiregional input-output perspective. J. Environ. Manag. 2023, 339. [Google Scholar] [CrossRef]
- Dong, F.; Li, X.H.; Long, R.Y.; Liu, X.Y. Regional carbon emission performance in China according to a stochastic frontier model. Renew. Sustain. Energy Rev. 2013, 28, 525–530. [Google Scholar] [CrossRef]
- Van der Heijden, G.M.; Schnitzer, S.A.; Powers, J.S.; Phillips, O.L. Liana Impacts on Carbon Cycling, Storage and Sequestration in Tropical Forests. Biotropica 2013, 45, 682–692. [Google Scholar] [CrossRef]
- Xue, L.; Luo, X.; Li, Z.; Wu, X. Spatial spillover effects and influencing factors of forest carbon sink in China—Spatial econometric analysis based on forest resources inventory in 31 provinces of the mainland of China. J. Nat. Resour. 2017, 32, 1744–1754. [Google Scholar]
- Xue, L.; Luo, X.; Wu, X. Carbon sequestration efficiency of four forest regions in China: Measurement, driving factors and convergence. J. Nat. Resour. 2016, 31, 1351–1363. [Google Scholar]
- Zhang, K.; Shen, J. Optimal allocation of water resources based on firefly algorithm and entropy method. Water Resour. Prot. 2016, 32, 50. [Google Scholar]
- Geng, Y.Q.; Wei, Z.J.; Zhang, H.; Maimaituerxun, M. Analysis and Prediction of the Coupling Coordination Relationship between Tourism and Air Environment: Yangtze River Economic Zone in China as Example. Discret. Dyn. Nat. Soc. 2020, 2020, 1406978. [Google Scholar] [CrossRef]
- Li, W.W.; Yi, P.T. Assessment of city sustainability-Coupling coordinated development among economy, society and environment. J. Clean. Prod. 2020, 256, 120453. [Google Scholar] [CrossRef]
- Yang, C.; Zeng, W.; Yang, X. Coupling coordination evaluation and sustainable development pattern of geo-ecological environment and urbanization in Chongqing municipality, China. Sustain. Cities Soc. 2020, 61, 102271. [Google Scholar] [CrossRef]
- Li, W.; Wang, Y.; Xie, S.; Cheng, X. Coupling coordination analysis and spatiotemporal heterogeneity between urbanization and ecosystem health in Chongqing municipality, China. Sci. Total Environ. 2021, 791, 148311. [Google Scholar] [CrossRef]
- Yuan, T.; Lu, P.; Liu, Y.J.; Ren, F.; Zhang, H.R. Distribution Characteristics and Influence Factors of Carbon in Coal Mining Subsidence Wetland. Sustainability 2023, 15, 7042. [Google Scholar] [CrossRef]
- Zhu, Y.; Tian, Z.; Wang, L.; Ji, D.; Yang, Z.; Meng, J.; Tian, P.; Liu, J. Characteristics and influencing factors of the rising period of carbon sink flux in East Dongting Lake waters. China Environ. Sci. 2023, 43, 843–853. [Google Scholar]
- Zhao, R.; Liu, Y.; Tian, M.; Ding, M.; Cao, L.; Zhang, Z.; Chuai, X.; Xiao, L.; Yao, L. Impacts of water and land resources exploitation on agricultural carbon emissions: The water-land-energy-carbon nexus. Land Use Policy 2018, 72, 480–492. [Google Scholar] [CrossRef]
- Jiang, W.; Zhang, Z.; Wen, J.; Yin, L.; Song, B. Spatio-temporal variation and influencing factors of industrial carbon emission effect in China based on water-land-energy-carbon nexus. Ecol. Indic. 2023, 152, 110307. [Google Scholar] [CrossRef]
- Liu, J.H.; Pu, L.Y.; Huang, L.C.; Shi, T.L. Research on the Coupling Evaluation and Driving Factors of Water-Energy-Carbon in the Yellow River Basin. Water 2023, 15, 2377. [Google Scholar] [CrossRef]
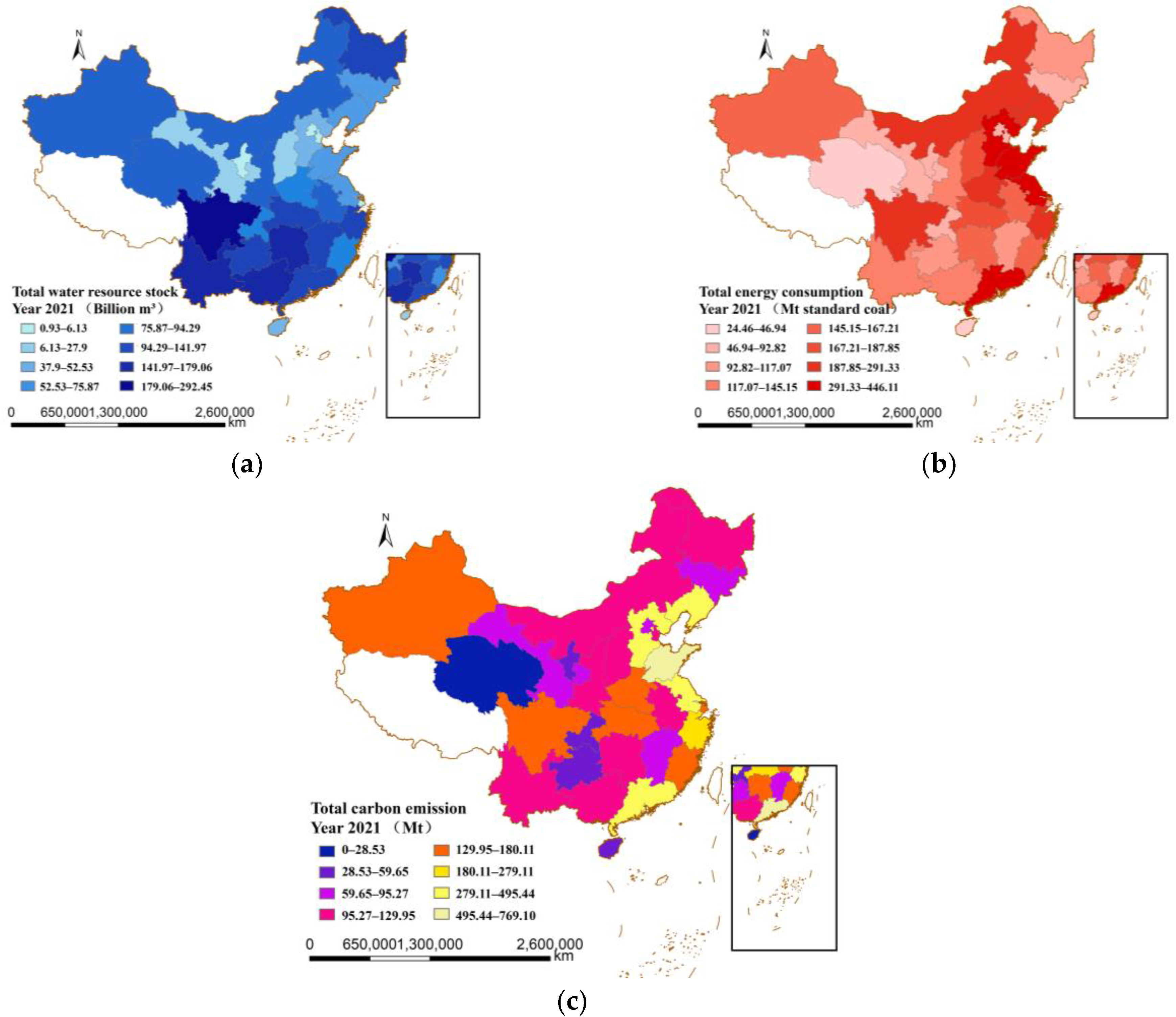



| Subsystem | Category | Evaluation Index | Property |
|---|---|---|---|
| Water resources | Water resource utilization | Water consumption per GDP (CNY 10,000) | Negative |
| Total wastewater discharge | Negative | ||
| Total water consumption in each region | Negative | ||
| Water resource endowment | Water production modulus | Positive | |
| Total water resources | Positive | ||
| Water resources per capita | Positive | ||
| Energy system | Energy consumption | Energy consumption per GDP (CNY 10,000) | Negative |
| Energy consumption structure | Negative | ||
| Total energy consumption | Negative | ||
| Energy production | Total coal and crude oil production | Negative | |
| Hydropower generation | Positive | ||
| The share of non-fossil fuels in energy production | Positive | ||
| Carbon cycle system | Carbon emissions | Total carbon emissions | Negative |
| CO2 emissions per capita | Negative | ||
| CO2 emission intensity | Negative | ||
| Carbon sinks | Carbon sequestration by vegetation | Positive | |
| Carbon sequestration by water bodies | Positive |
| Level | Degree |
|---|---|
| 0–0.1 | Extreme incoordination |
| 0.1–0.2 | High incoordination |
| 0.2–0.3 | Moderate incoordination |
| 0.3–0.4 | Mild incoordination |
| 0.4–0.5 | Basic coordination |
| 0.5–0.6 | Low coordination |
| 0.6–0.7 | Moderate coordination |
| 0.7–0.8 | Favorable coordination |
| 0.8–0.9 | Excellent coordination |
| 0.9–1 | High-quality coordination |
| Explained Variable | Explanatory Variable | Coefficient | p |
|---|---|---|---|
| WEC coupling coordination level | Water production investment | −0.0105 | 0.000 |
| Hydraulic engineering investment | 0.0079 | 0.001 | |
| Water consumption per capita | 0.0126 | 0.178 | |
| Urbanization level | 0.0360 | 0.169 | |
| Industrial structure | −0.0113 | 0.017 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Z. The Water–Energy–Carbon Coupling Coordination Level in China. Sustainability 2024, 16, 383. https://doi.org/10.3390/su16010383
He Z. The Water–Energy–Carbon Coupling Coordination Level in China. Sustainability. 2024; 16(1):383. https://doi.org/10.3390/su16010383
Chicago/Turabian StyleHe, Zigao. 2024. "The Water–Energy–Carbon Coupling Coordination Level in China" Sustainability 16, no. 1: 383. https://doi.org/10.3390/su16010383
APA StyleHe, Z. (2024). The Water–Energy–Carbon Coupling Coordination Level in China. Sustainability, 16(1), 383. https://doi.org/10.3390/su16010383






